Antenna Design by Means of the Fruit Fly Optimization Algorithm
Abstract
:1. Introduction
2. Description of the Algorithm
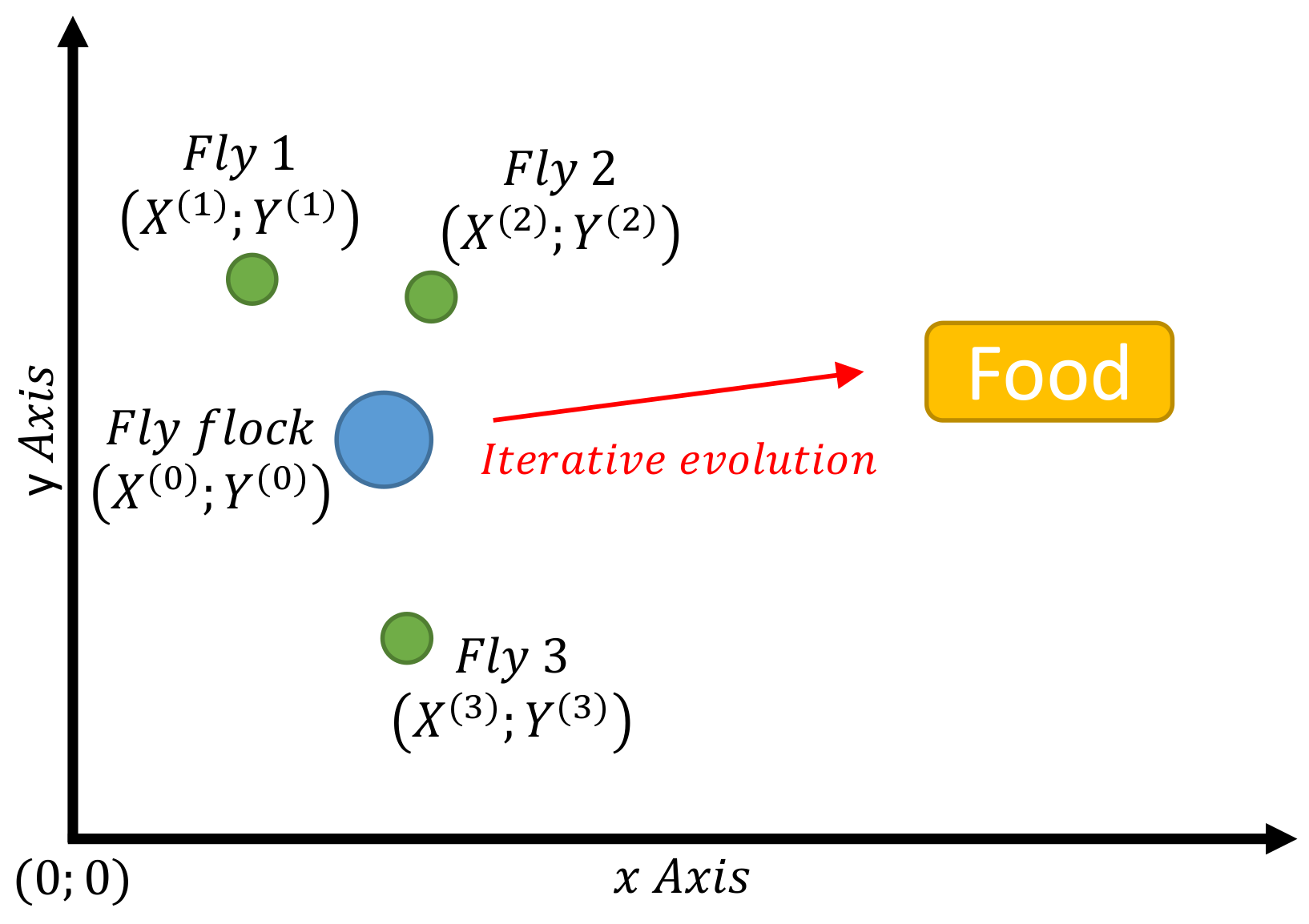
- The swarm is positioned at the location , with a given smell concentration . For each fly i in the swarm:
- The fly moves around a random distance, searching for food by using the osphresis:where and are random values.
- The smell concentration judgement value is defined as the reciprocal of the distance to the origin of coordinates:
- Compute the smell concentration of the fly’s current location by using the smell concentration function (equivalent to a fitness function):
- Look for the specific fly I with the best smell concentration. If this value is better than the value in the initial location of the swarm then move the swarm towards the position of the fly I by using the vision sense:
3. Numerical Examples
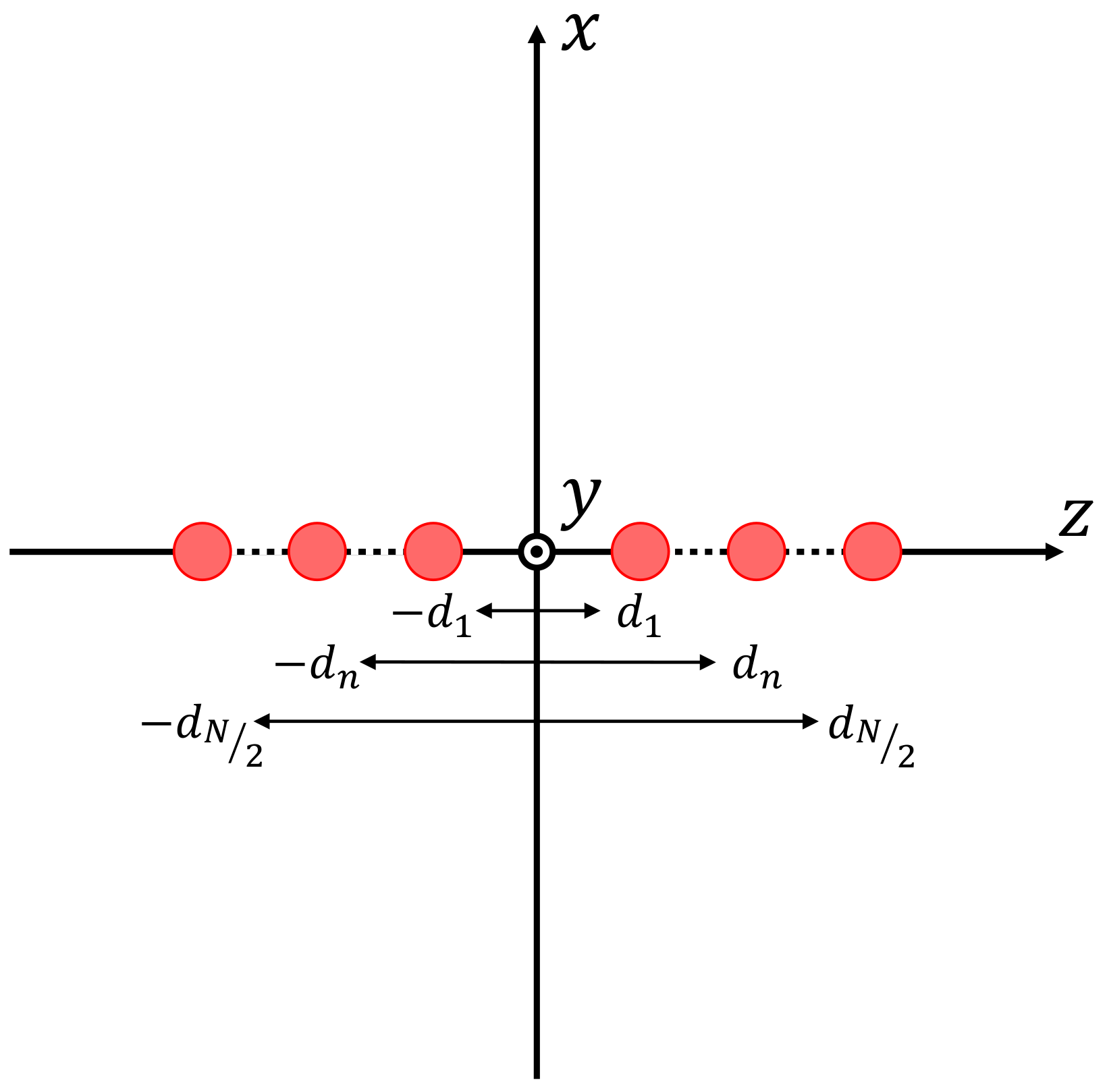
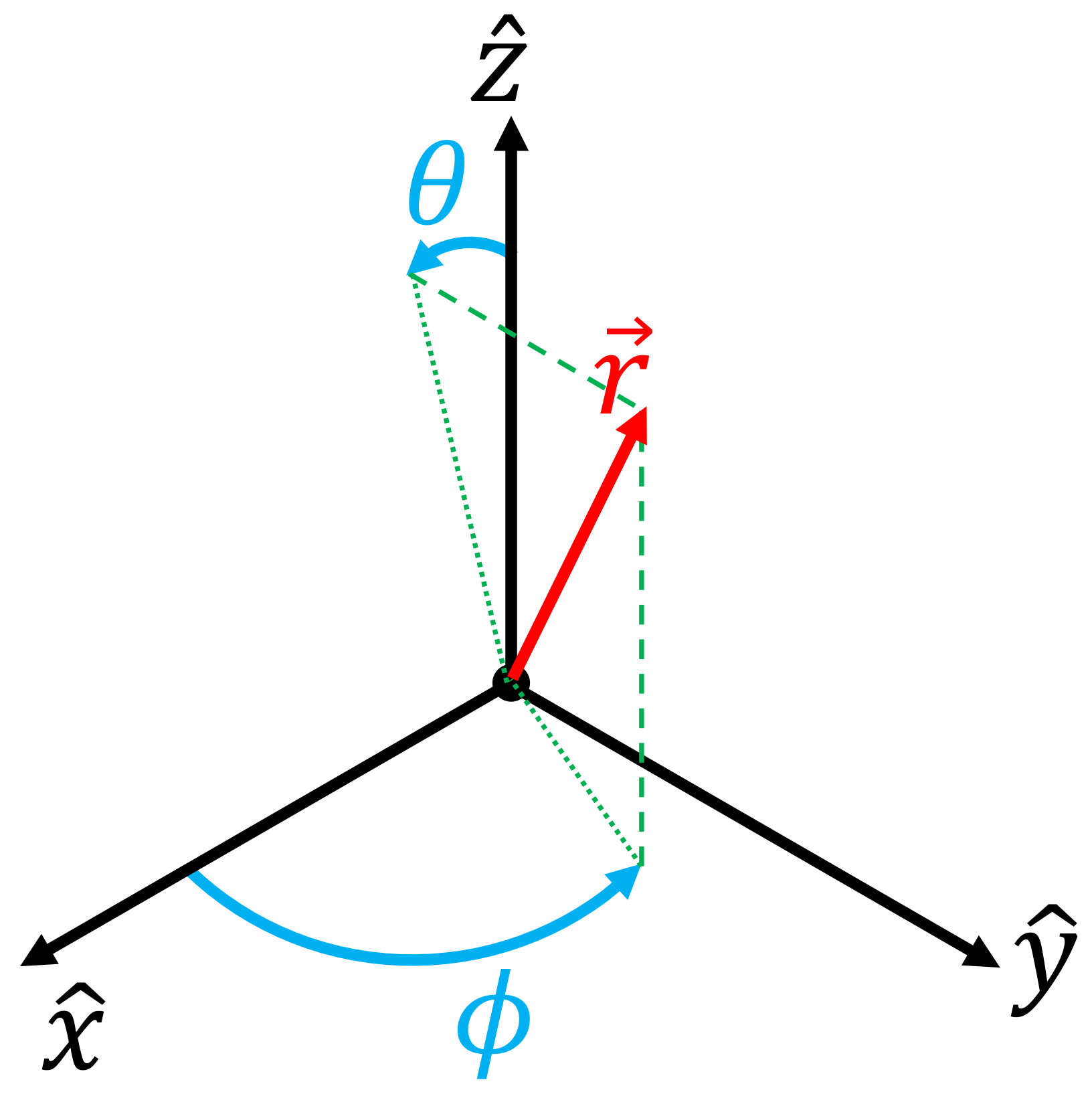
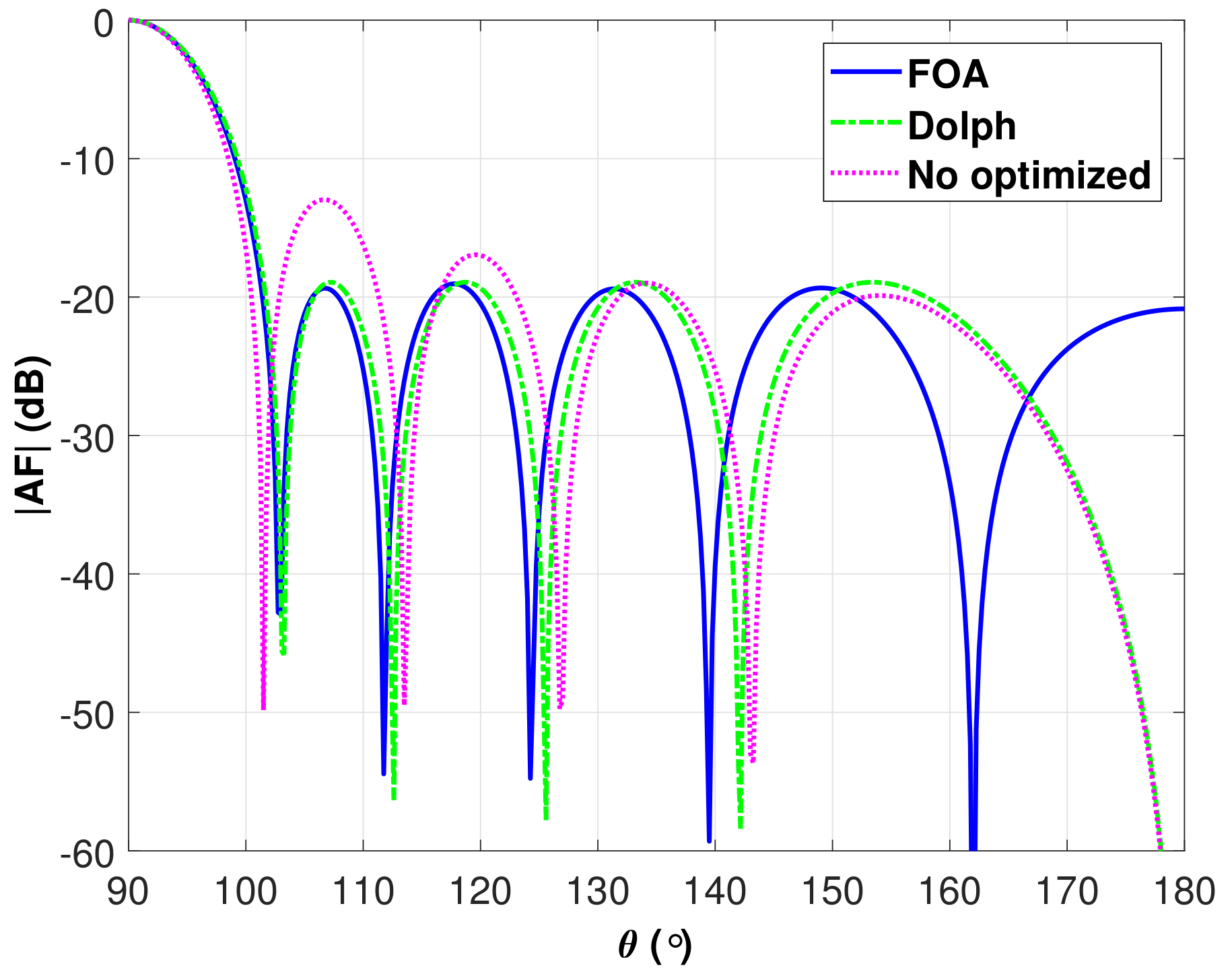
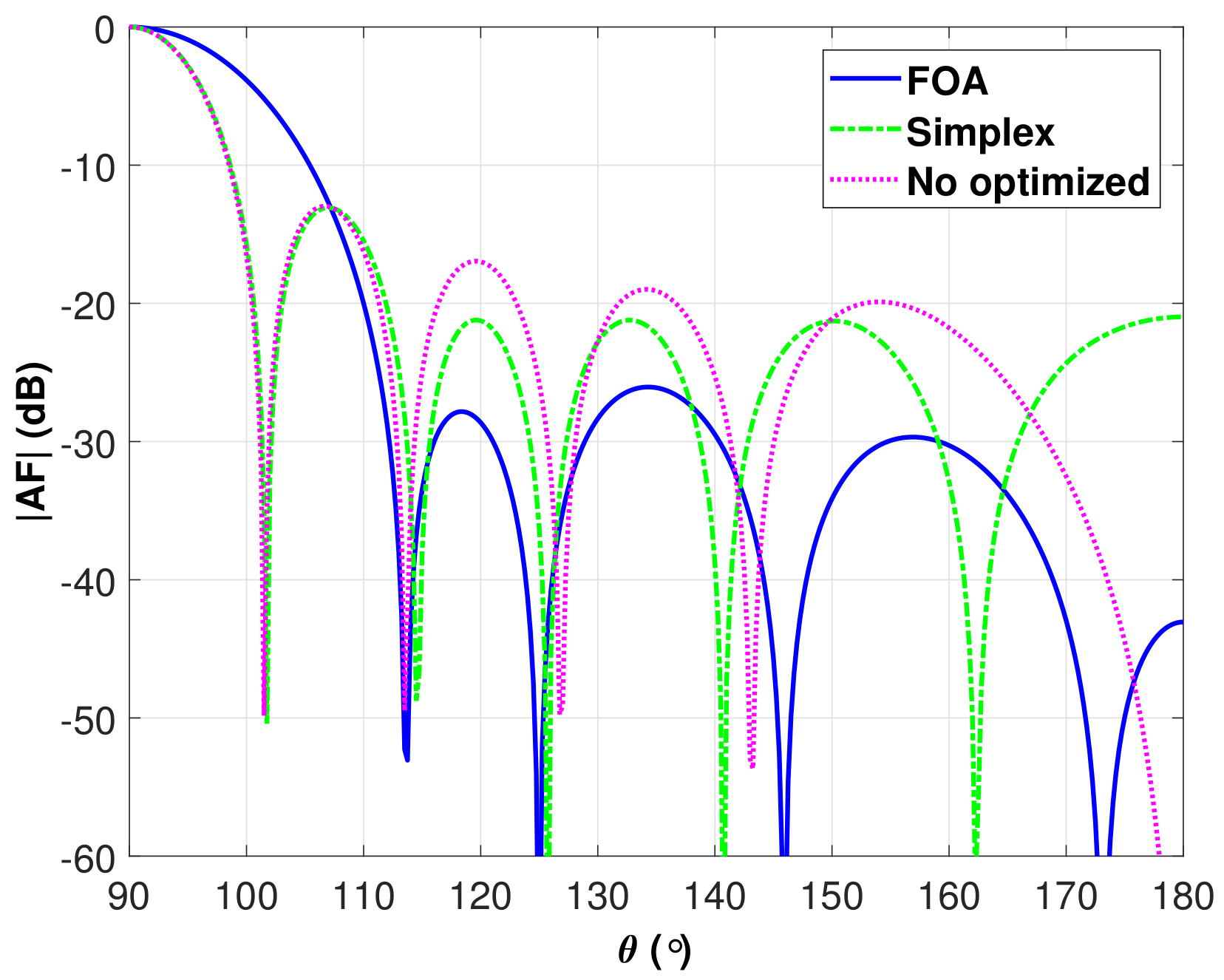
3.1. Application to Array Factor Synthesis
- Flies per swarm: 20.
- Total smell function evaluations: 5000.
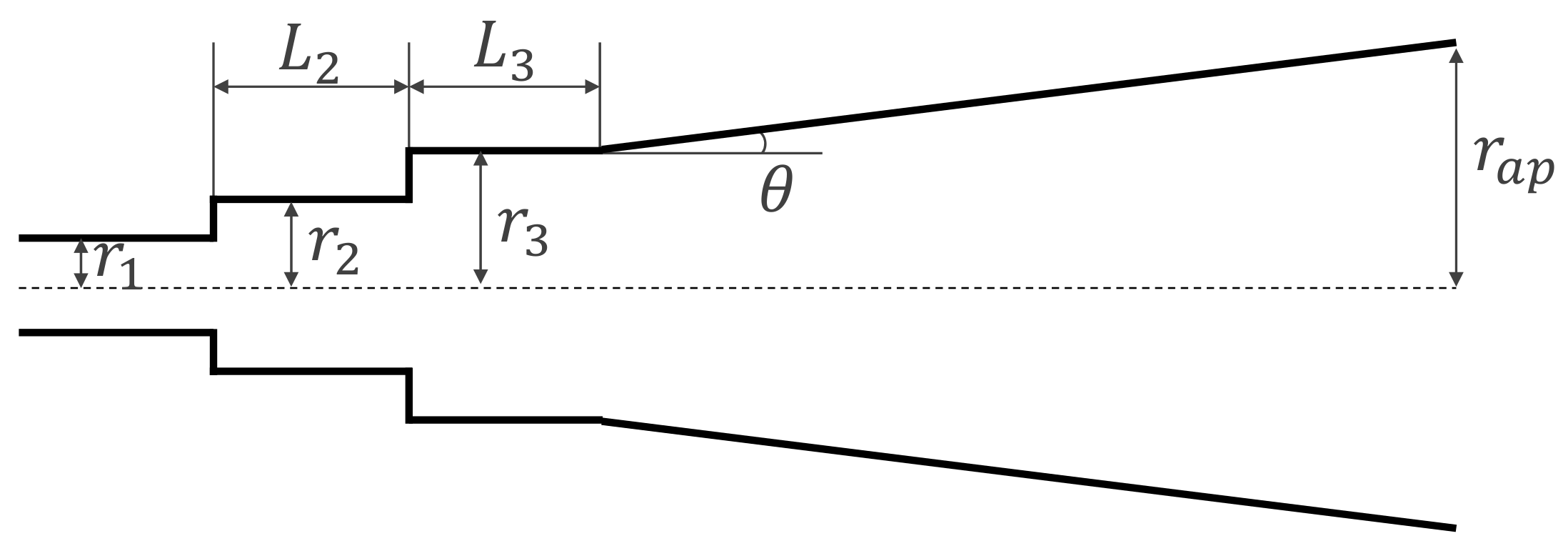
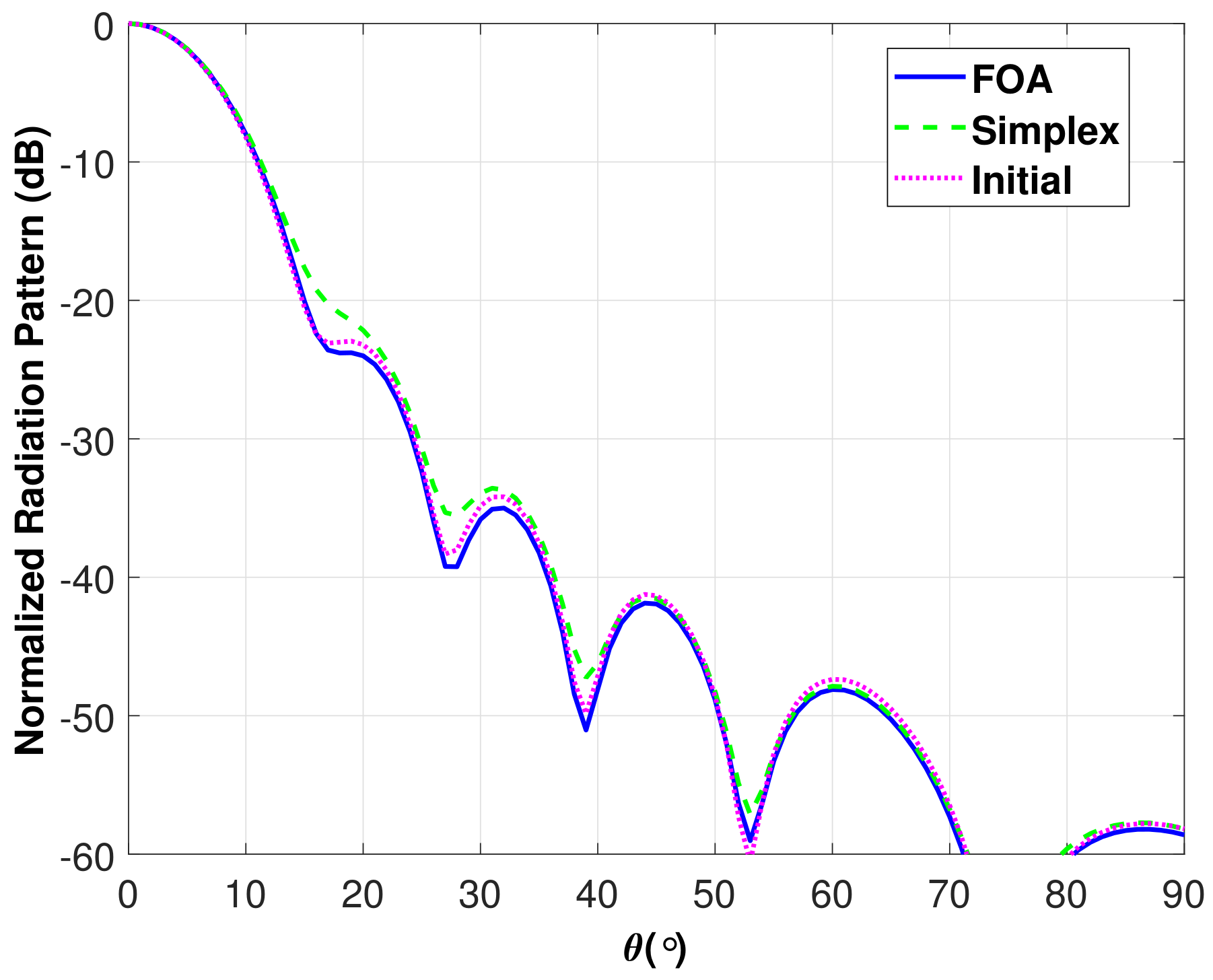
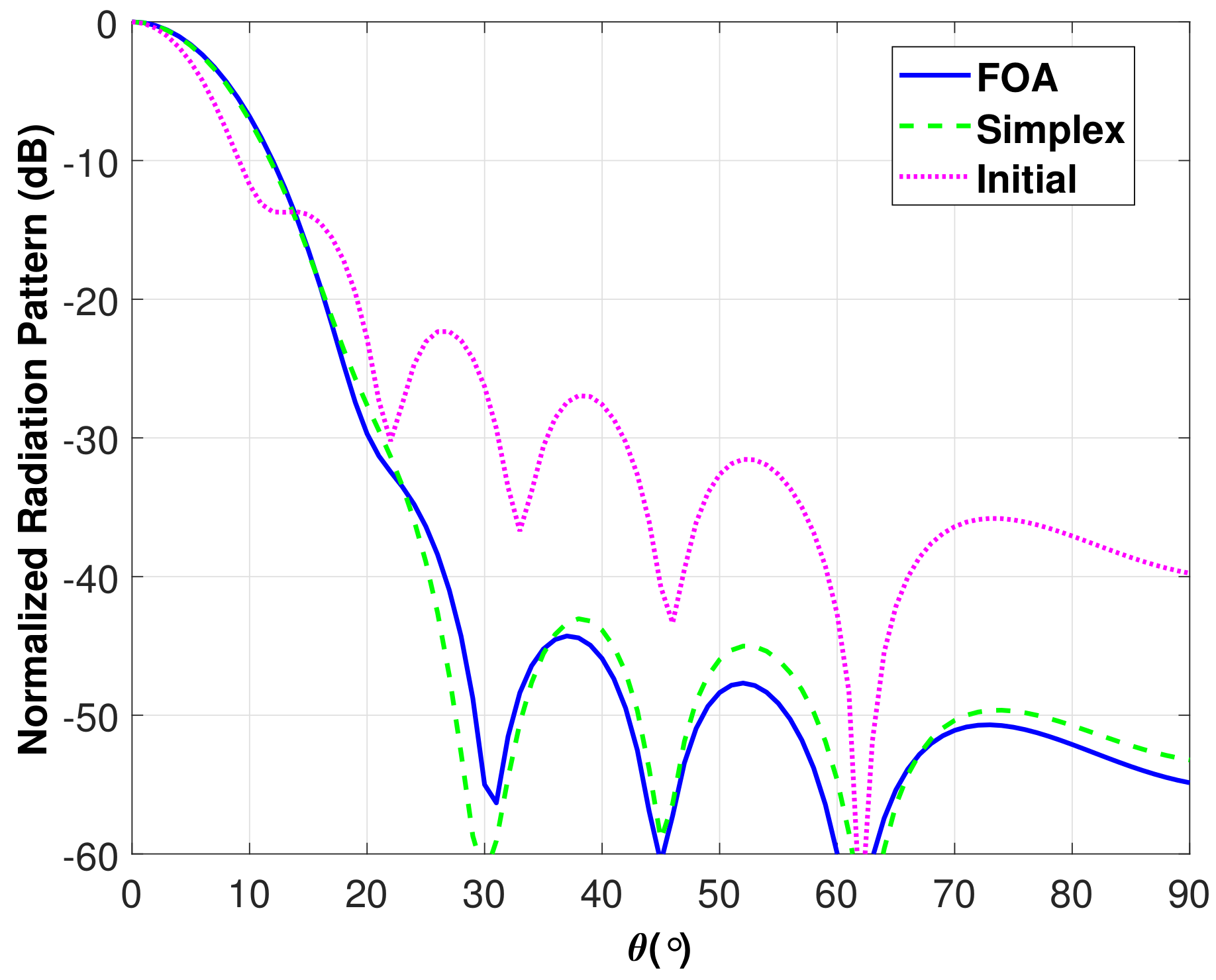
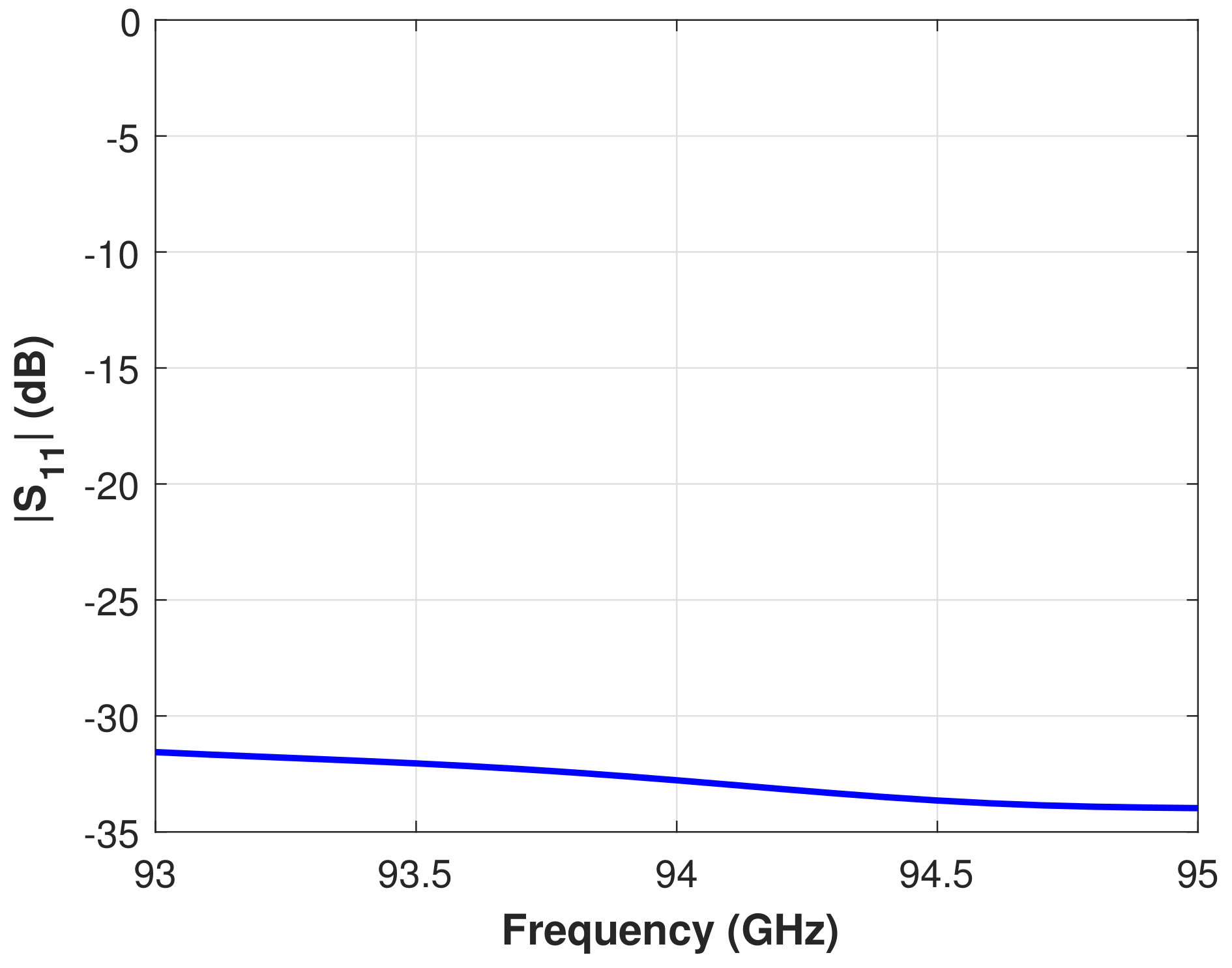
3.2. Application to Horn Antennas
- Radii: 0.15 mm
- Lengths:
- Angle:
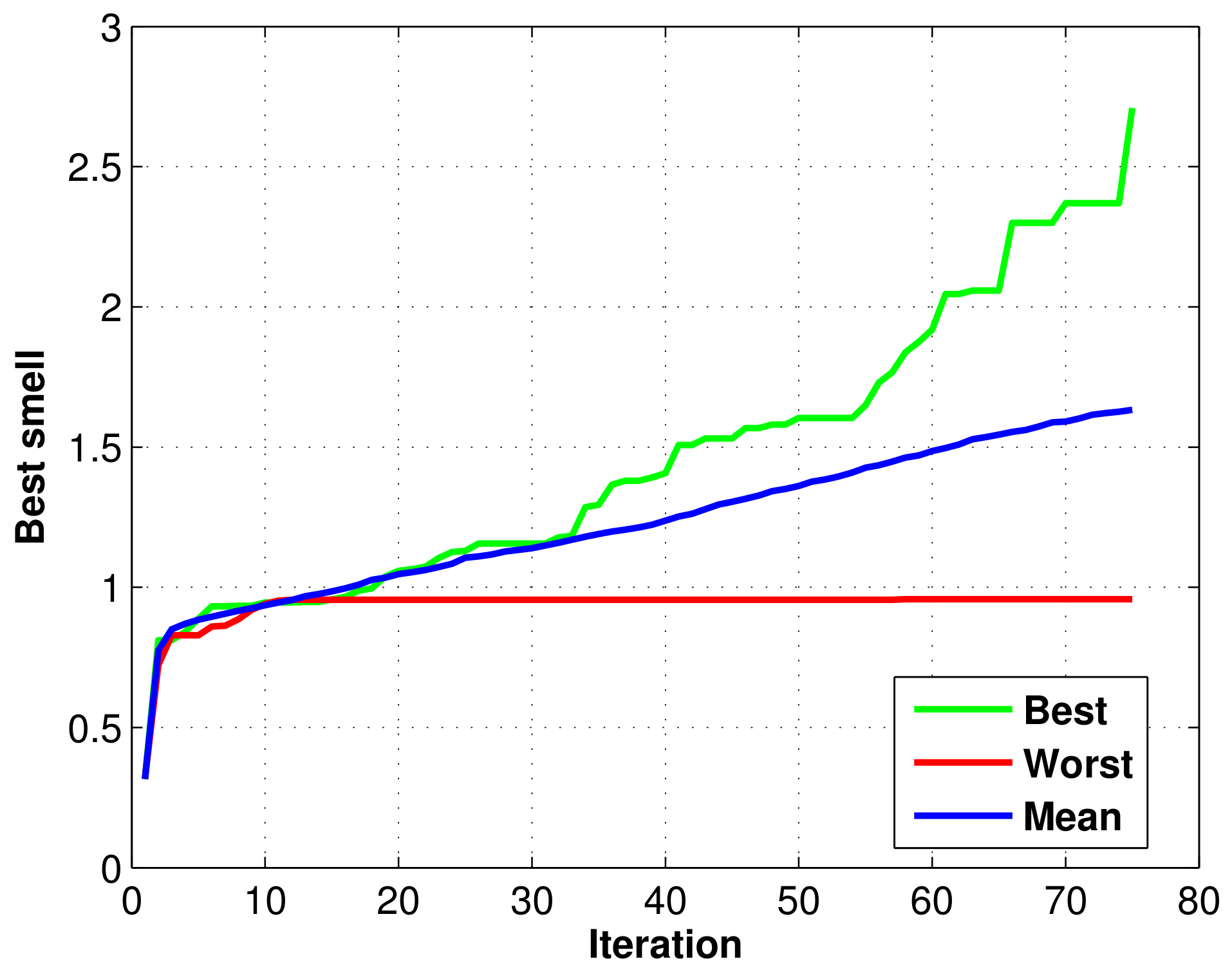
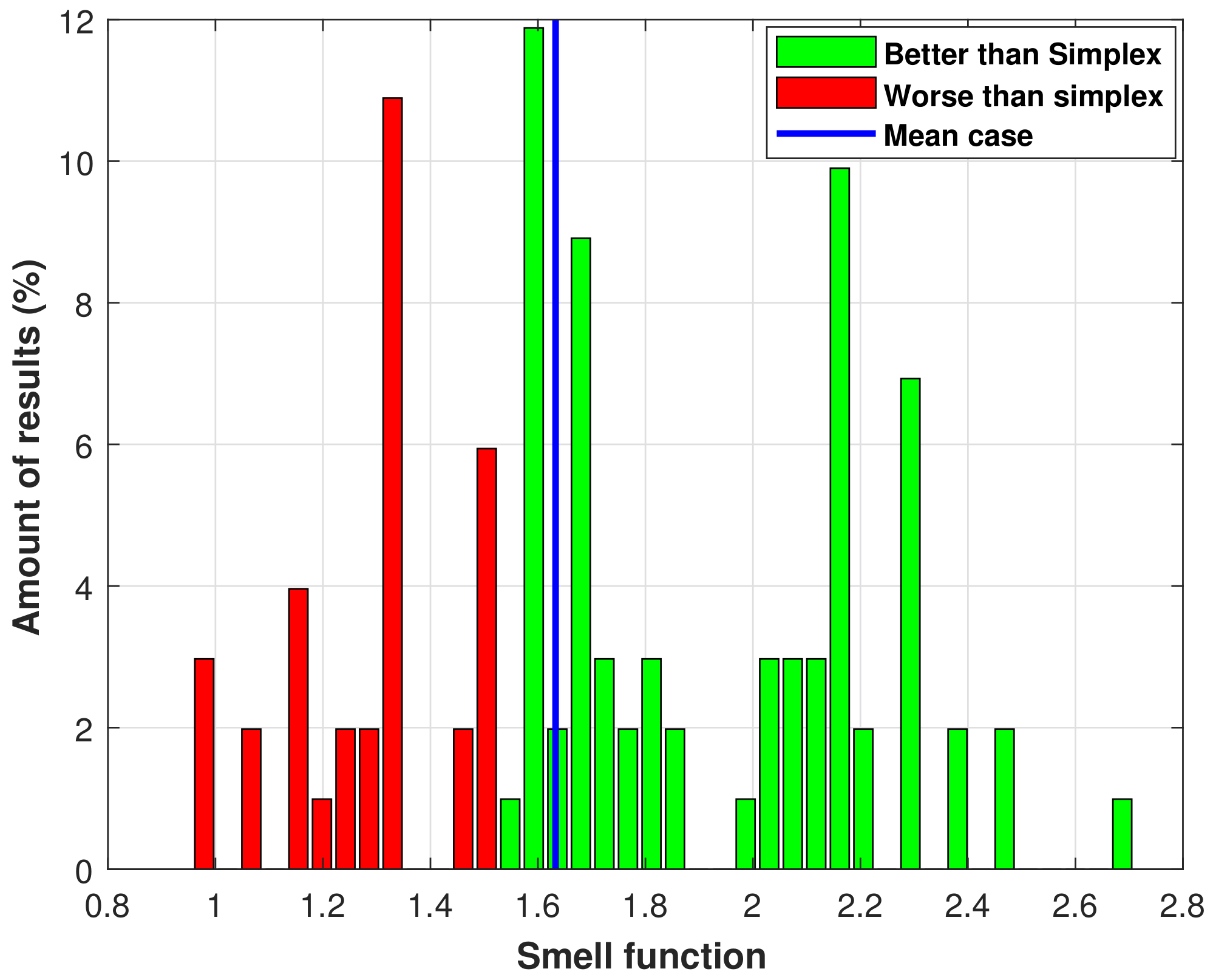
3.3. Statistical Analysis of the Results
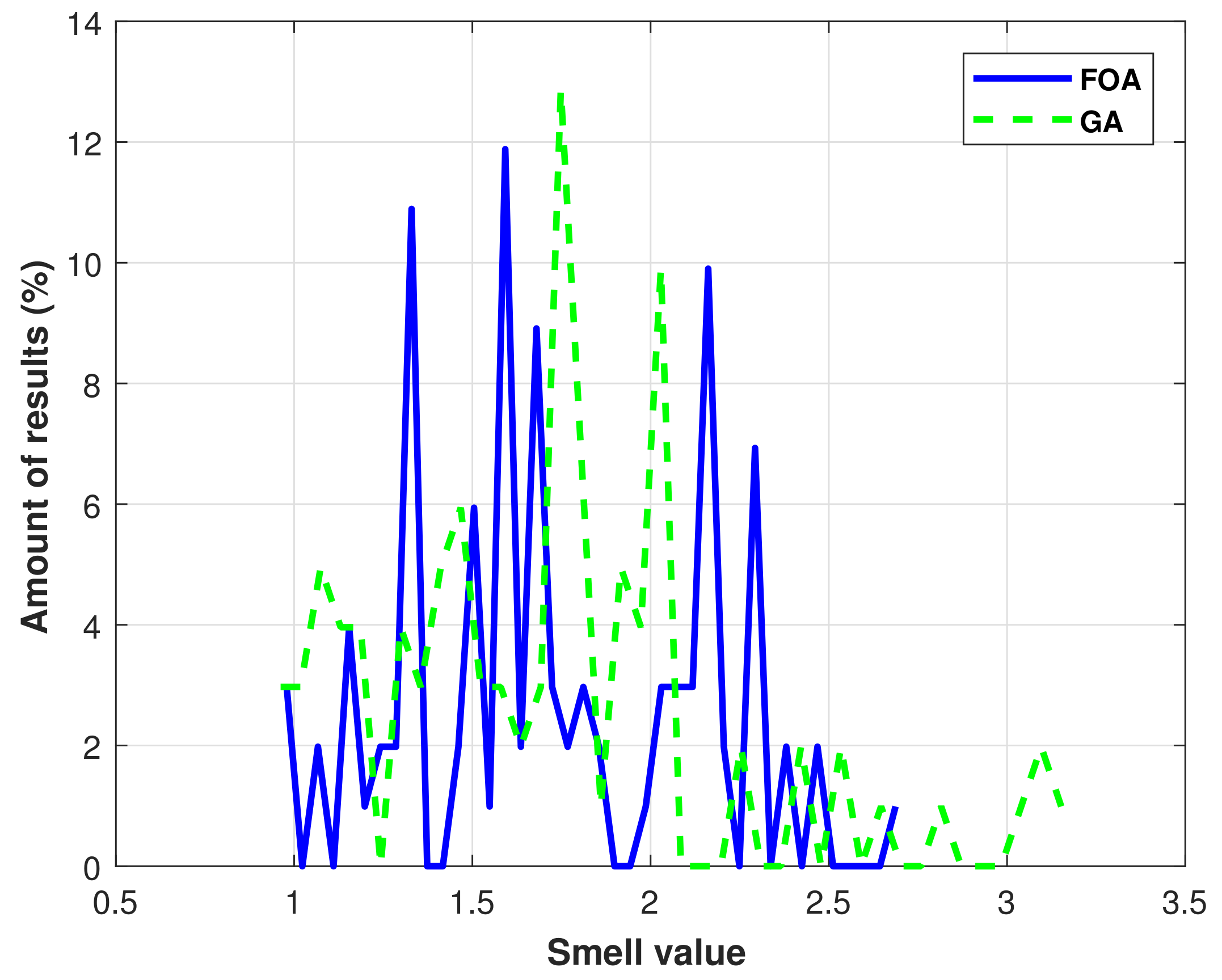
3.4. Comparison with a Genetic Algorithm
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| FOA | Fruit fly Optimization Algorithm |
| SLL | Side Lobe Level |
| TE | Transverse Electric |
| TM | Transverse Magnetic |
| GA | Genetic Algorithm |
References
- Haupt, R.L.; Menozzi, J.J.; McCormack, C.J. Thinned arrays using genetic algorithms. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Ann Arbor, MI, USA, 28 June–2 July 1993; Volume 2, pp. 712–715. [Google Scholar]
- Johnson, J.M.; Rahmat-Samii, V. Genetic algorithms in engineering electromagnetics. IEEE Antennas Propag. Mag. 1997, 39, 7–21. [Google Scholar]
- Ares-Pena, F.J.; Rodriguez-Gonzalez, J.A.; Villanueva-Lopez, E.; Rengarajan, S.R. Genetic algorithms in the design and optimization of antenna array patterns. IEEE Trans. Antennas Propag. 1999, 47, 506–510. [Google Scholar] [CrossRef]
- Dey, R.; Chakrabarty, S.; Jyoti, R.; Kurian, T. Synthesis and analysis of multi-mode profile horn using mode matching technique and evolutionary algorithm. IET Microw. Antennas Propag. 2016, 10, 276–282. [Google Scholar] [CrossRef]
- Rolland, A.; Ettorre, M.; Drissi, M.; Coq, L.L.; Sauleau, R. Optimization of Reduced-Size Smooth-Walled Conical Horns Using BoR-FDTD and Genetic Algorithm. IEEE Trans. Antennas Propag. 2010, 58, 3094–3100. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Rajo-Iglesias, E. Ant Colony Optimization in Thinned Array Synthesis With Minimum Sidelobe Level. IEEE Antennas Wirel. Propag. Lett. 2006, 5, 349–352. [Google Scholar] [CrossRef]
- Mosca, S.; Ciattaglia, M. Ant Colony Optimization to Design Thinned Arrays. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 4675–4678. [Google Scholar]
- Rajo-Iglesias, E.; Quevedo-Teruel, O. Linear array synthesis using an ant-colony-optimization-based algorithm. IEEE Antennas Propag. Mag. 2007, 49, 70–79. [Google Scholar] [CrossRef]
- Khodier, M.M.; Christodoulou, C.G. Linear array geometry synthesis with minimum sidelobe level and null control using particle swarm optimization. IEEE Trans. Antennas Propag. 2005, 53, 2674–2679. [Google Scholar] [CrossRef]
- Donelli, M.; Martini, A.; Massa, A. A Hybrid Approach Based on PSO and Hadamard Difference Sets for the Synthesis of Square Thinned Arrays. IEEE Trans. Antennas Propag. 2009, 57, 2491–2495. [Google Scholar] [CrossRef]
- Robinson, J.; Sinton, S.; Rahmat-Samii, Y. Particle swarm, genetic algorithm, and their hybrids: Optimization of a profiled corrugated horn antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium (IEEE Cat. No.02CH37313), San Antonio, TX, USA, 16–21 June 2002; Volume 1, pp. 314–317. [Google Scholar]
- Moradi, A.; Mohajeri, F. Reduction of SLL in a square horn antenna in presence of metamaterial surfaces by using of particle swarm optimization. In Proceedings of the 2016 24th Iranian Conference on Electrical Engineering (ICEE), Shiraz, Iran, 10–12 May 2016; pp. 598–603. [Google Scholar]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar]
- Pelusi, D.; Mascella, R.; Tallini, L. Revised Gravitational Search Algorithms Based on Evolutionary-Fuzzy Systems. Algorithms 2017, 10. [Google Scholar] [CrossRef]
- Pan, W.T. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl.-Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Li, Y. A Modified Fruit-Fly Optimization Algorithm aided PID controller designing. In Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China, 6–8 July 2012; pp. 233–238. [Google Scholar]
- Li, H.Z.; Guo, S.; Li, C.J.; Sun, J.Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm. Knowl.-Based Syst. 2013, 37, 378–387. [Google Scholar] [CrossRef]
- Mhudtongon, N.; Phongcharoenpanich, C.; Kawdungta, S. Modified Fruit Fly Optimization Algorithm for Analysis of Large Antenna Array. Int. J. Antennas Propag. 2015, 2015, 124675. [Google Scholar] [CrossRef]
- Mhudtongon, N.; Phongcharoenpanich, C.; Watanabe, K. Linear antenna synthesis with maximum directivity using improved fruit fly optimization algorithm. In Proceedings of the 2016 URSI International Symposium on Electromagnetic Theory (EMTS), Espoo, Finland, 14–18 August 2016; pp. 698–701. [Google Scholar]
- Pan, W.T. Fruit Fly Optimization Algorithm (Using MATLAB). 2014. Available online: https://www.mathworks.com/matlabcentral/answers/uploaded_files/20100/Fruit%20Fly%20Optimization%20Algorithm_Second%20Edition.pdf (accessed on 1 February 2014).
- Stutzman, W.L.; Thiele, G. Antenna Theory and Design; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Conciauro, G.; Guglielmi, M.; Sorrentino, R. Advanced Modal Analysis: CAD Techniques for Waveguide Components and Filters; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Olver, A.; Clarricoats, P.; Kishk, A.; Shafai, L. Microwave Horns and Feeds; Electromagnetic Waves Series; IEE: London, UK; IEEE: New York, NY, USA, 1994. [Google Scholar]
- Granet, C.; James, G.L.; Bolton, R.; Moorey, G. A smooth-walled spline-profile horn as an alternative to the corrugated horn for wide band millimeter-wave applications. IEEE Trans. Antennas Propag. 2004, 52, 848–854. [Google Scholar] [CrossRef]
- MATLAB R2016b; The MathWorks, Inc.: Natick, MA, USA, 2017.
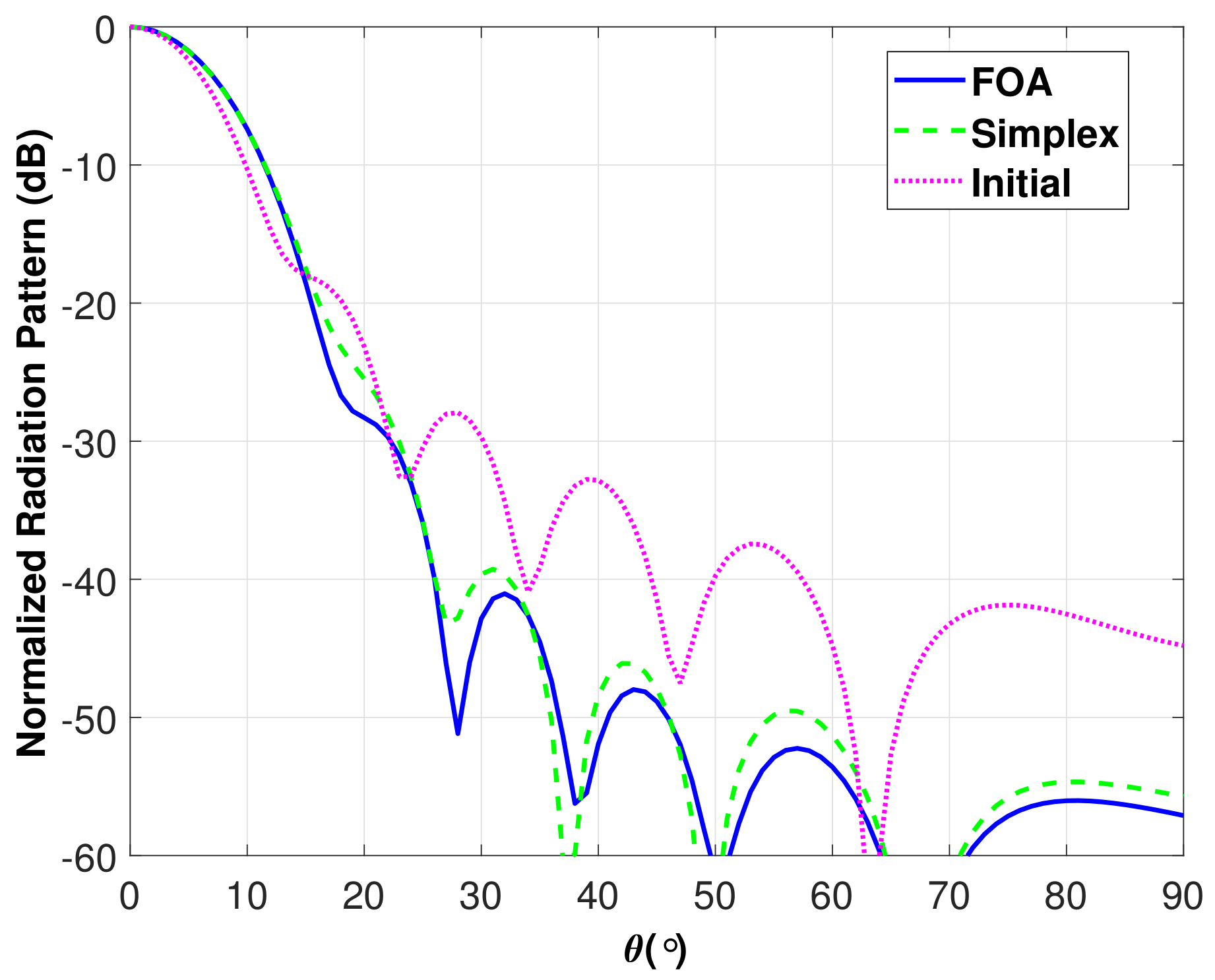
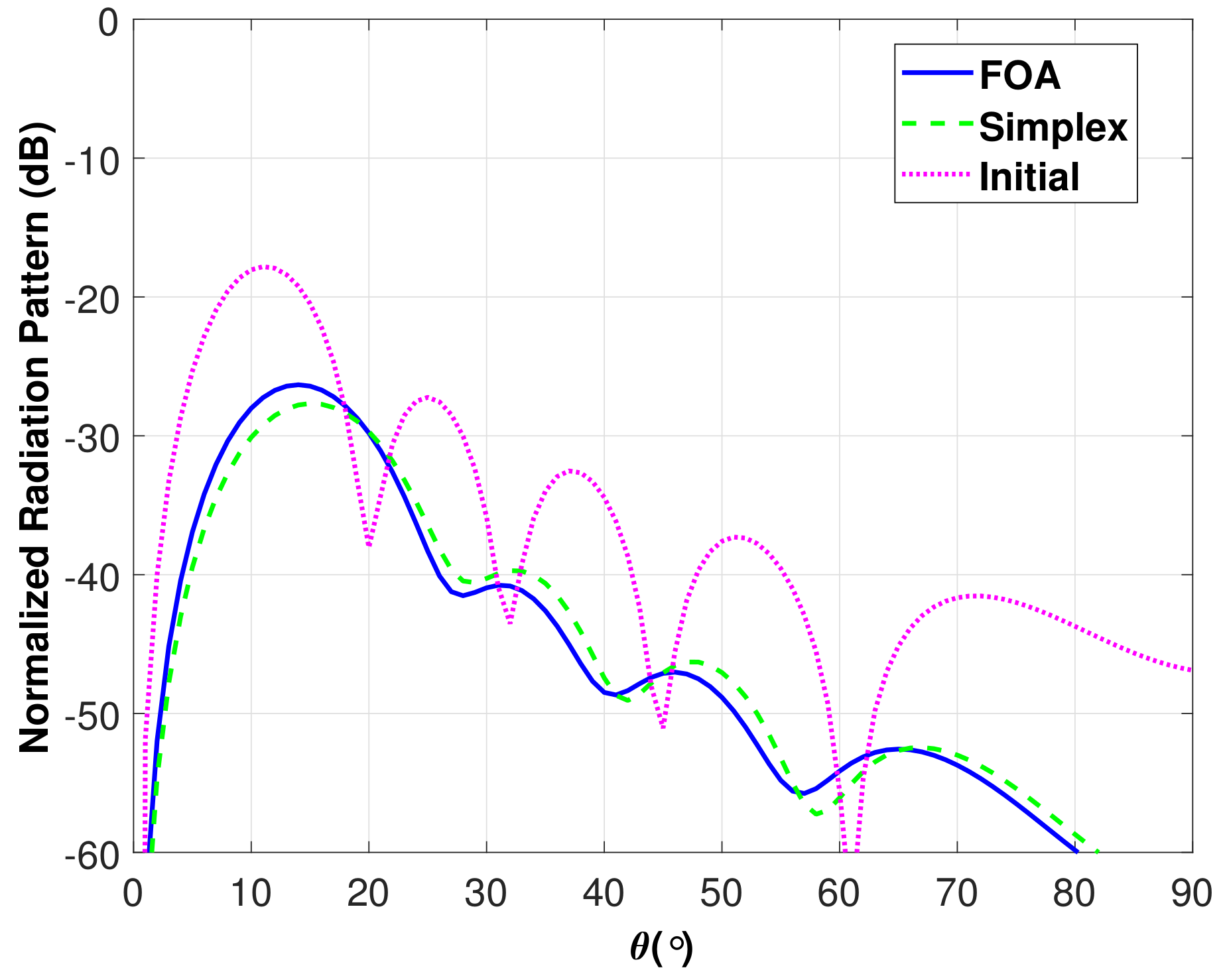
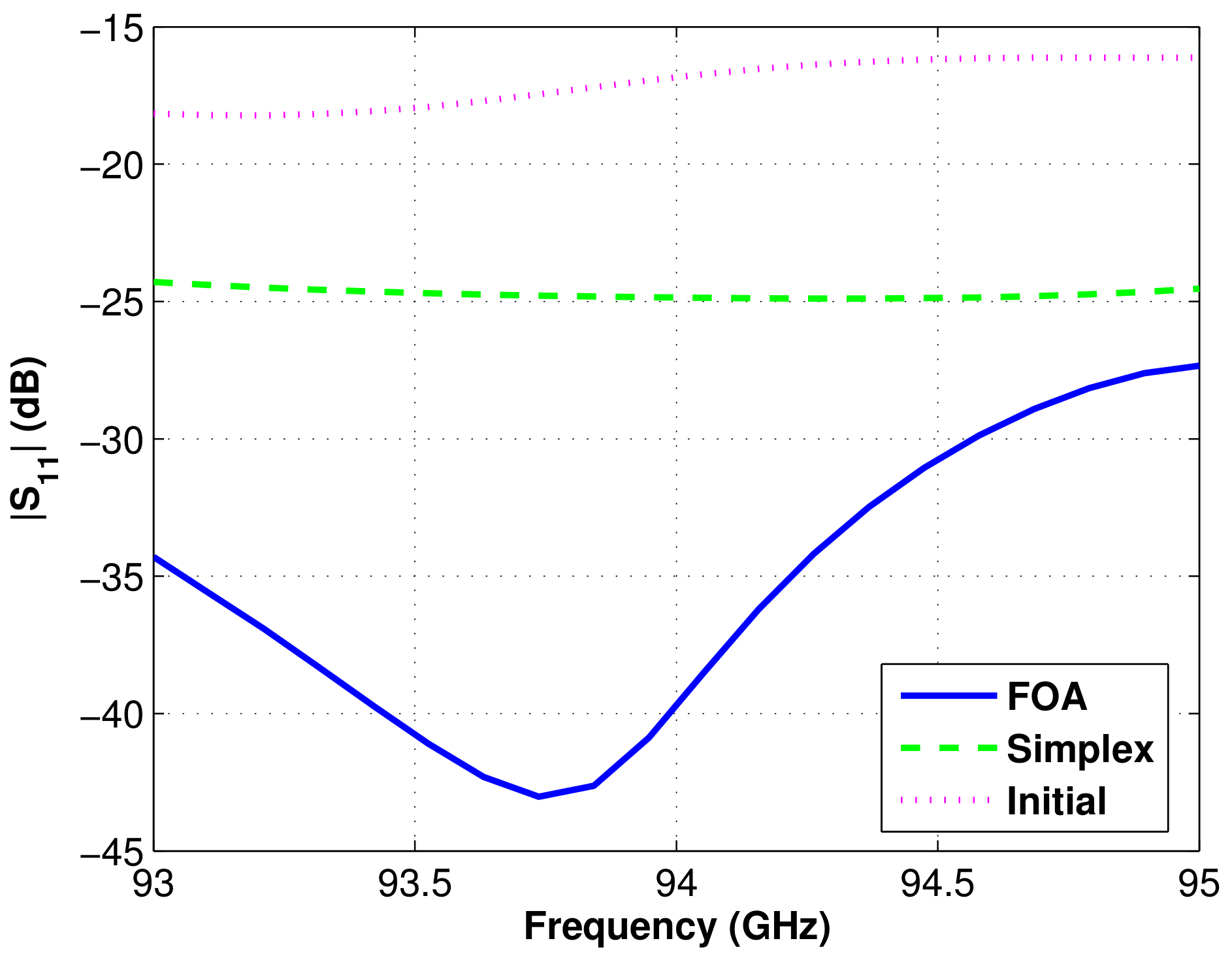

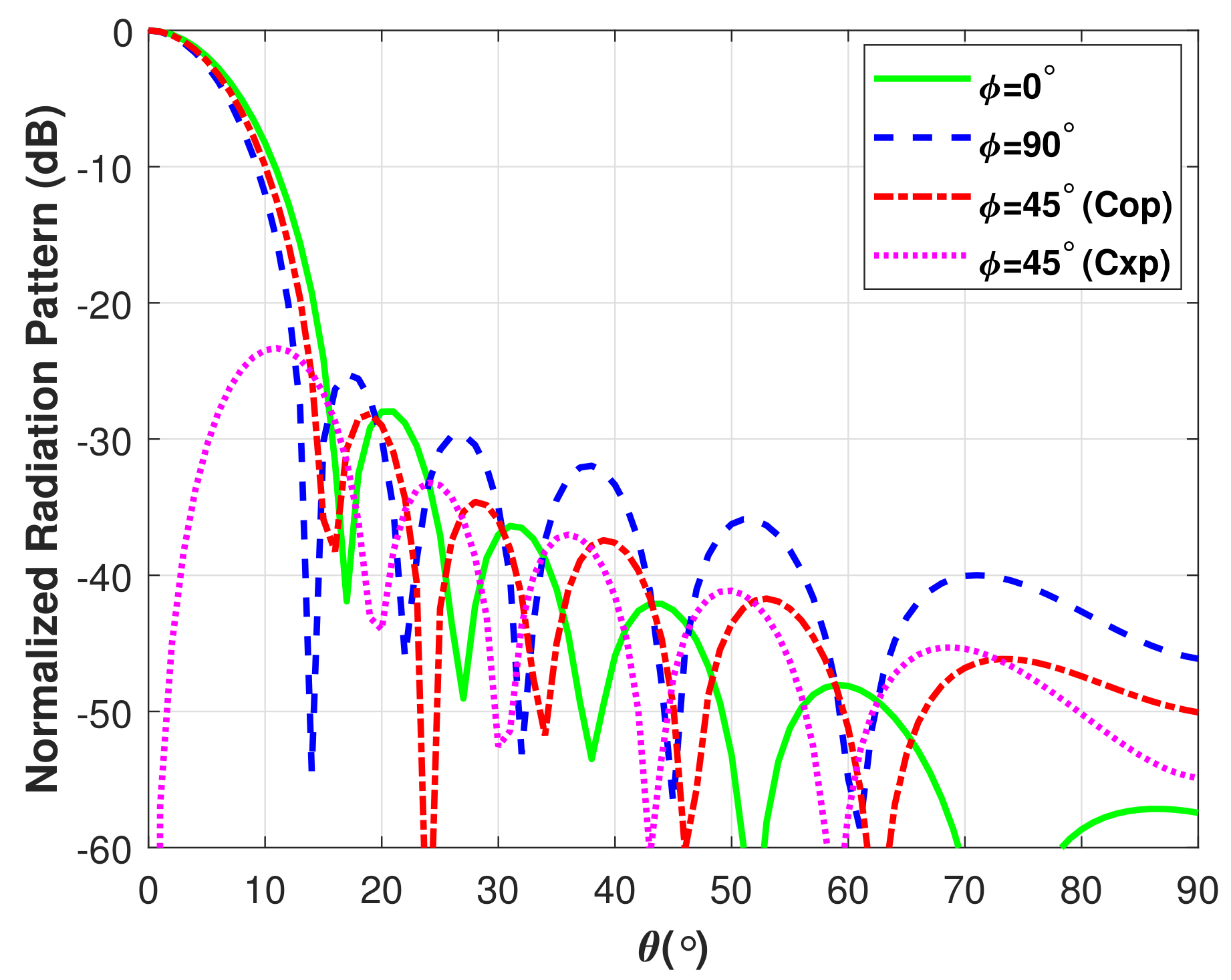
| Parameter | Initial / Dolph | FOA |
|---|---|---|
| Parameter | Initial | FOA | Simplex |
|---|---|---|---|
| Parameter | Initial | FOA | Simplex |
|---|---|---|---|
| 1.50 mm | 1.70 mm | 1.64 mm | |
| 1.60 mm | 6.11 mm | 2.78 mm | |
| 1.95 mm | 2.44 mm | 2.13 mm | |
| 3.99 mm | 2.64 mm | 2.76 mm | |
| Parameter | Lower Boundary | Upper Boundary |
|---|---|---|
| 1.13 mm | 9.57 mm | |
| 1.00 mm | 10.00 mm | |
| 1.13 mm | 9.57 mm | |
| 1.00 mm | 10.00 mm | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polo-López, L.; Córcoles, J.; Ruiz-Cruz, J.A. Antenna Design by Means of the Fruit Fly Optimization Algorithm. Electronics 2018, 7, 3. https://doi.org/10.3390/electronics7010003
Polo-López L, Córcoles J, Ruiz-Cruz JA. Antenna Design by Means of the Fruit Fly Optimization Algorithm. Electronics. 2018; 7(1):3. https://doi.org/10.3390/electronics7010003
Chicago/Turabian StylePolo-López, Lucas, Juan Córcoles, and Jorge A. Ruiz-Cruz. 2018. "Antenna Design by Means of the Fruit Fly Optimization Algorithm" Electronics 7, no. 1: 3. https://doi.org/10.3390/electronics7010003
APA StylePolo-López, L., Córcoles, J., & Ruiz-Cruz, J. A. (2018). Antenna Design by Means of the Fruit Fly Optimization Algorithm. Electronics, 7(1), 3. https://doi.org/10.3390/electronics7010003






