High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach
Abstract
:1. Introduction
Power Amplifier Design Challenges
The Back-Off Efficiency Issue
2. Back-Off Efficiency Enhancement Techniques
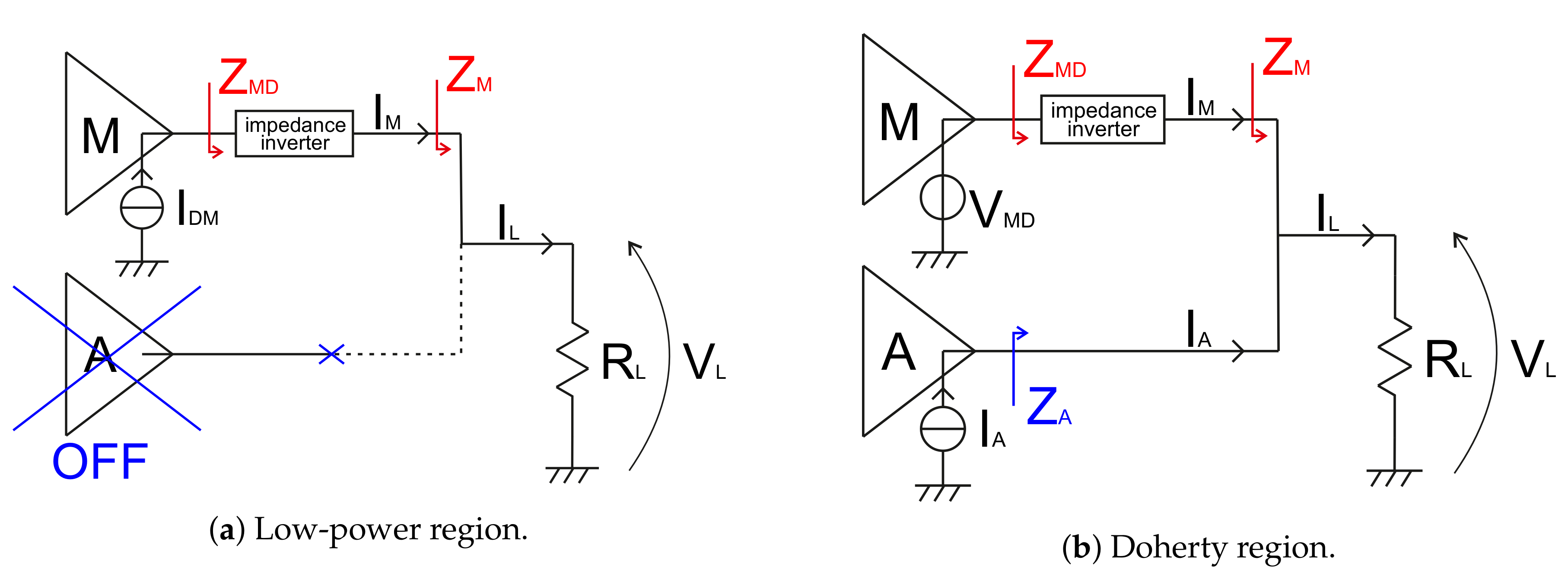
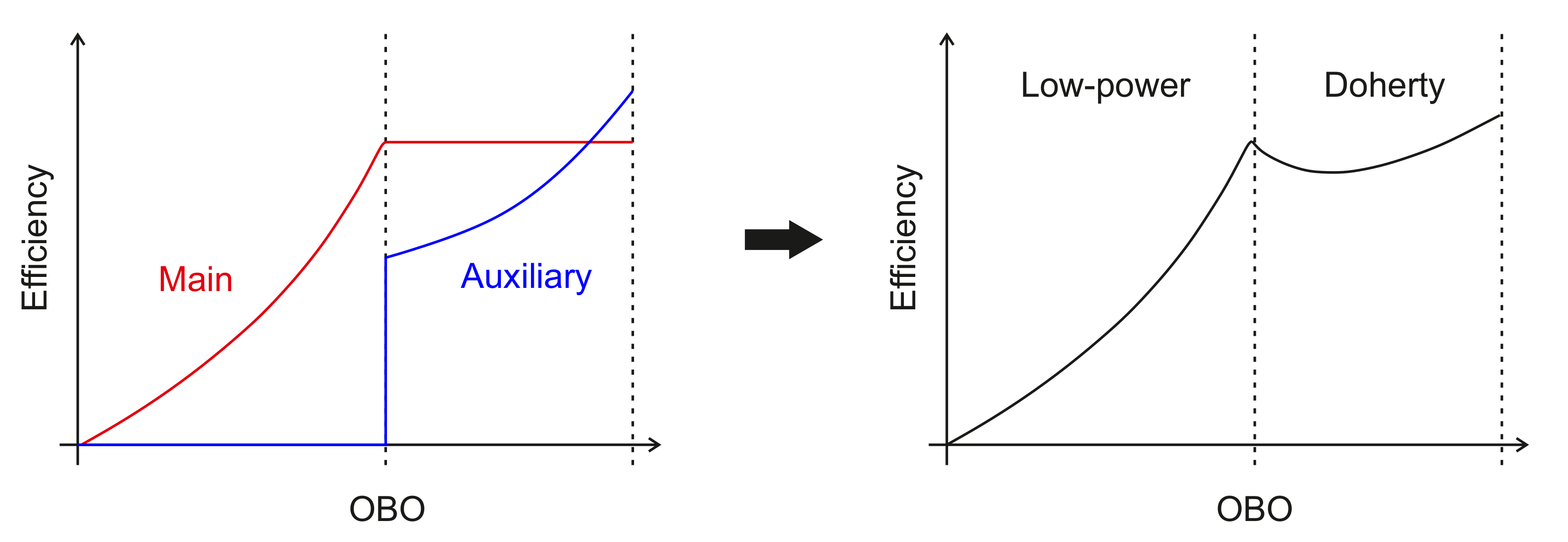
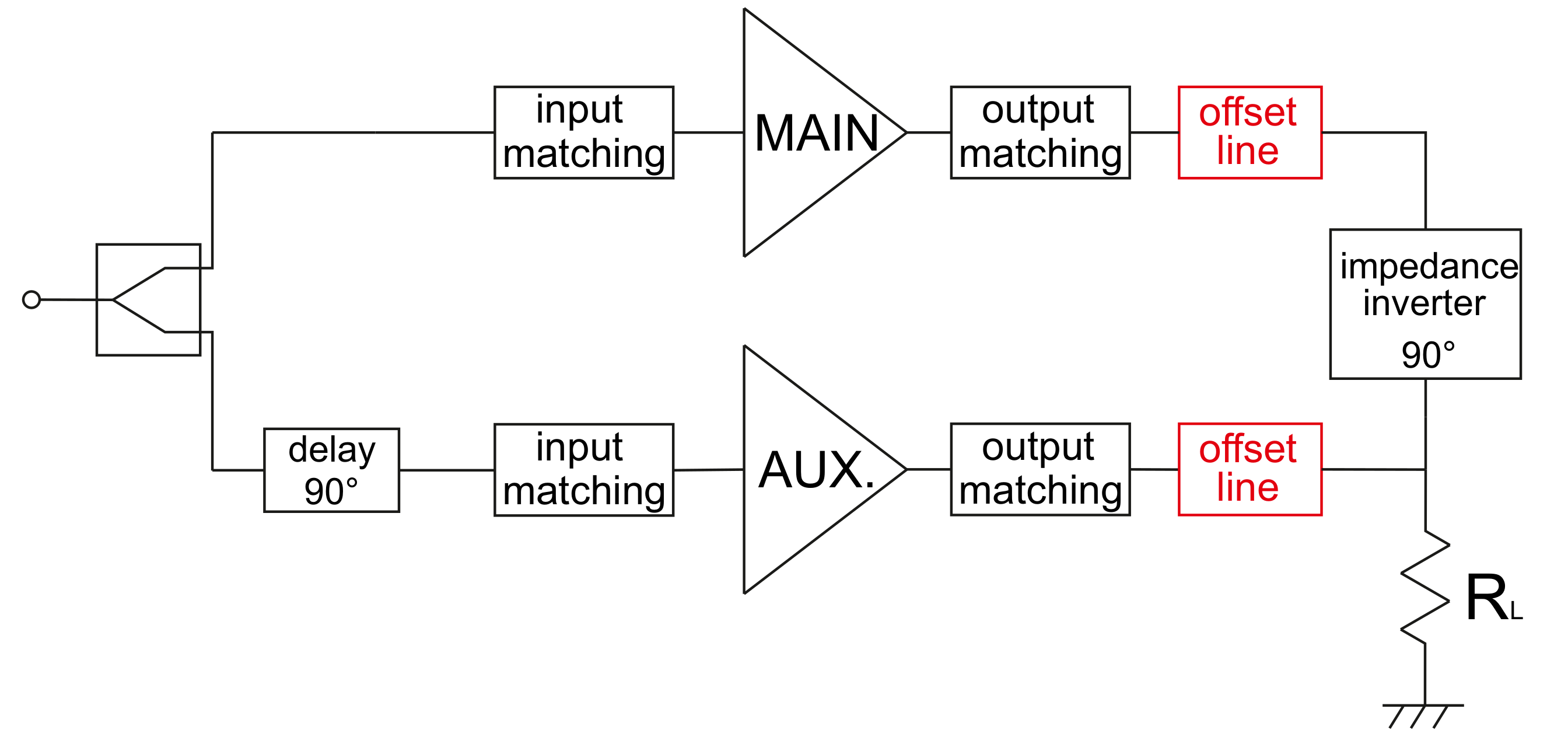
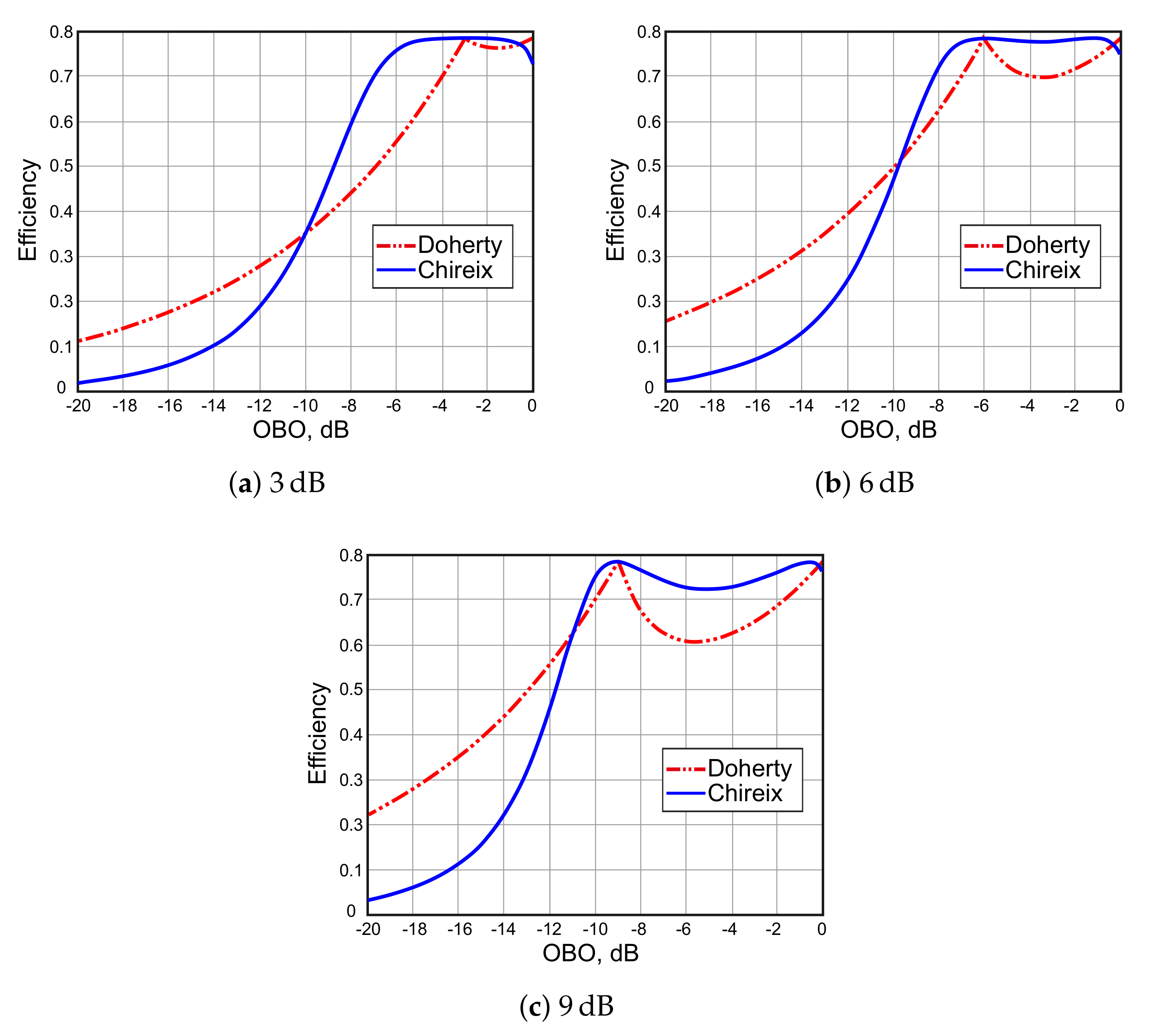
3. Doherty Power Amplifier
3.1. Doherty PA Limitations
3.1.1. High-Efficiency Power Range
3.1.2. Linearity and Efficiency Drop
3.1.3. Bandwidth
3.1.4. Frequency
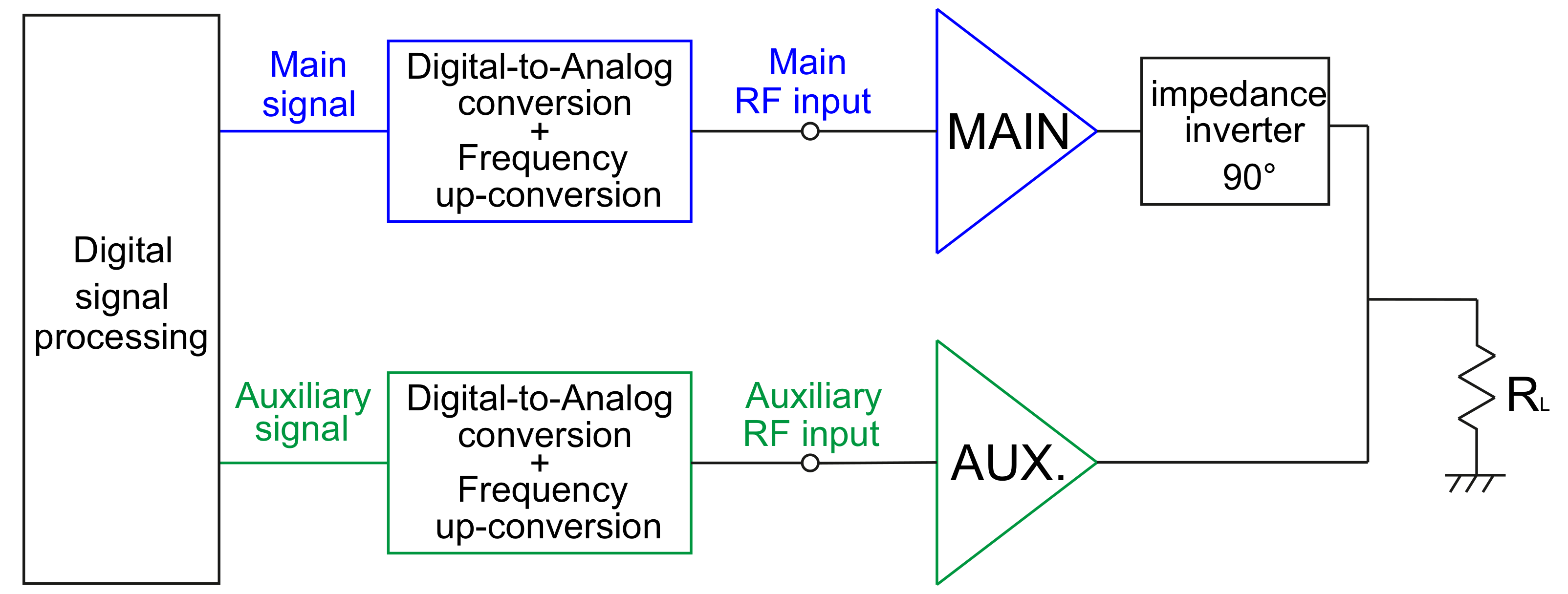
3.2. Digital/Dual-Input DPA
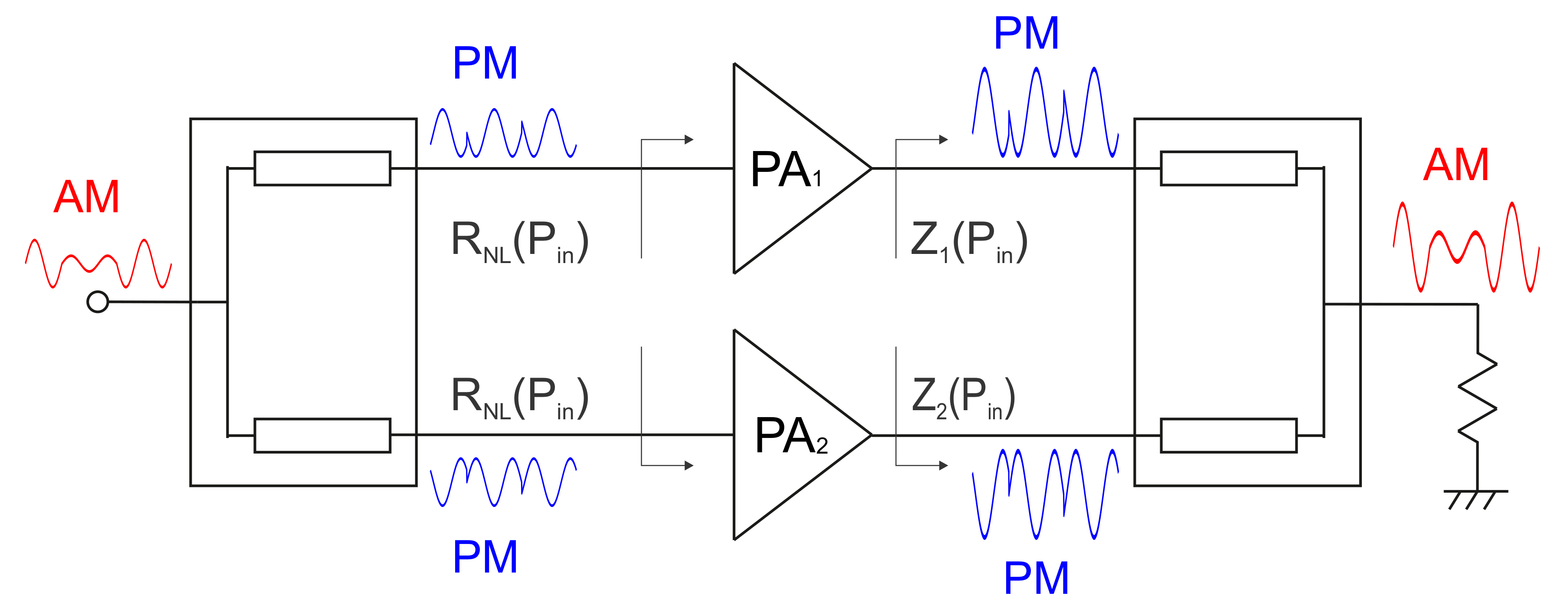
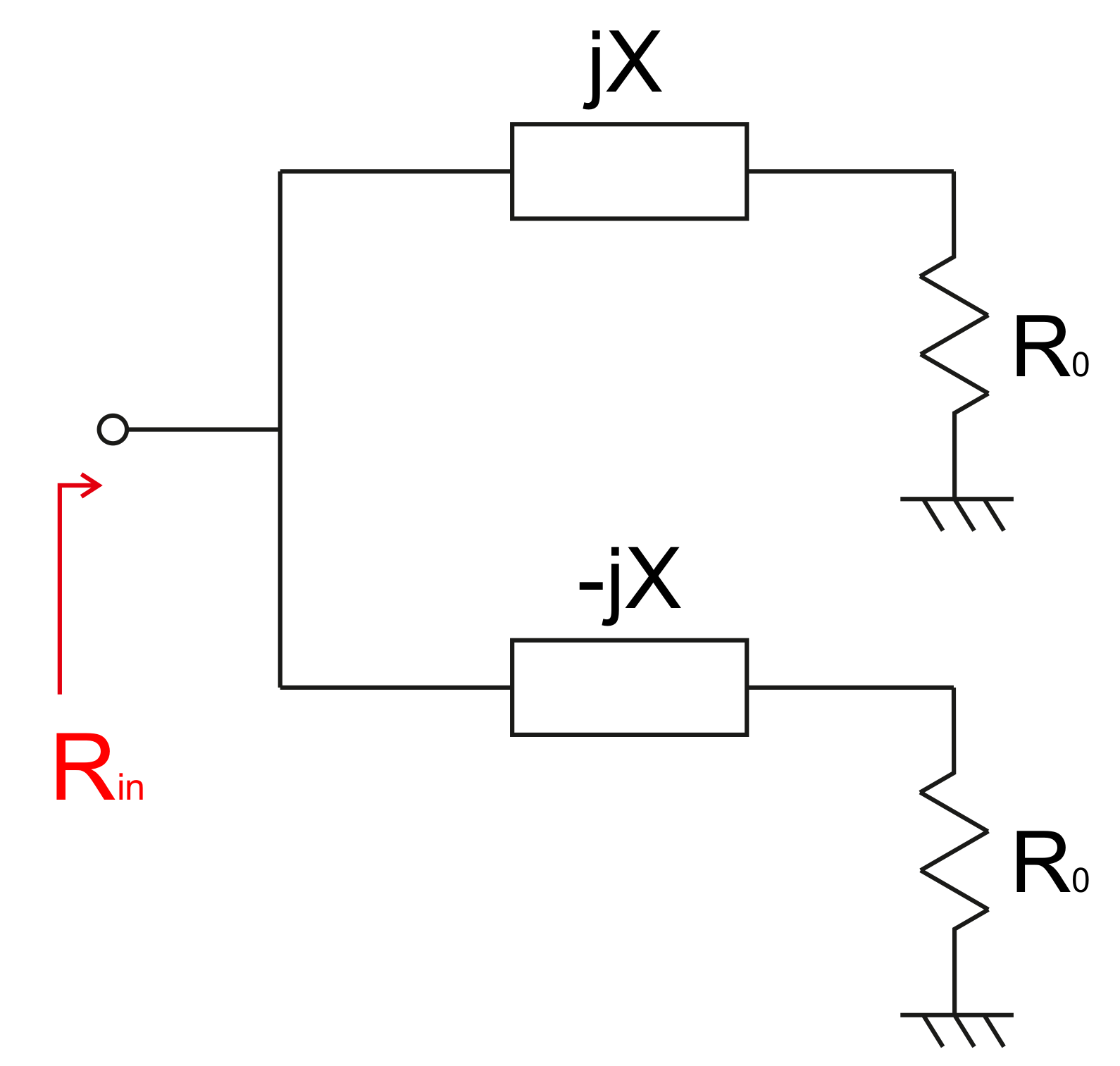
4. Chireix Outphasing Power Amplifier
4.1. Chireix Outphasing PA Limitations
4.1.1. High Efficiency Power Range and Stability
4.1.2. The Voltage Source Issue
4.1.3. Bandwidth
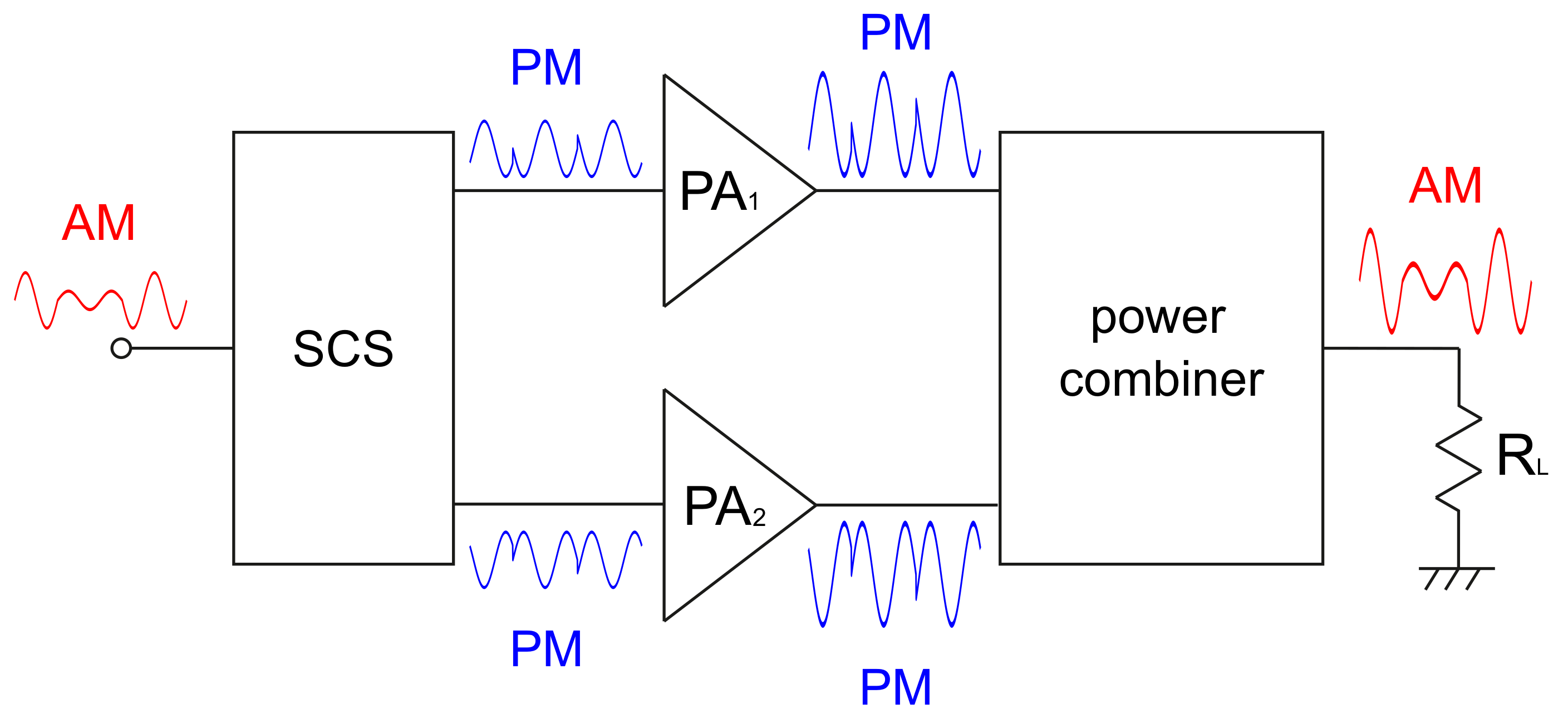
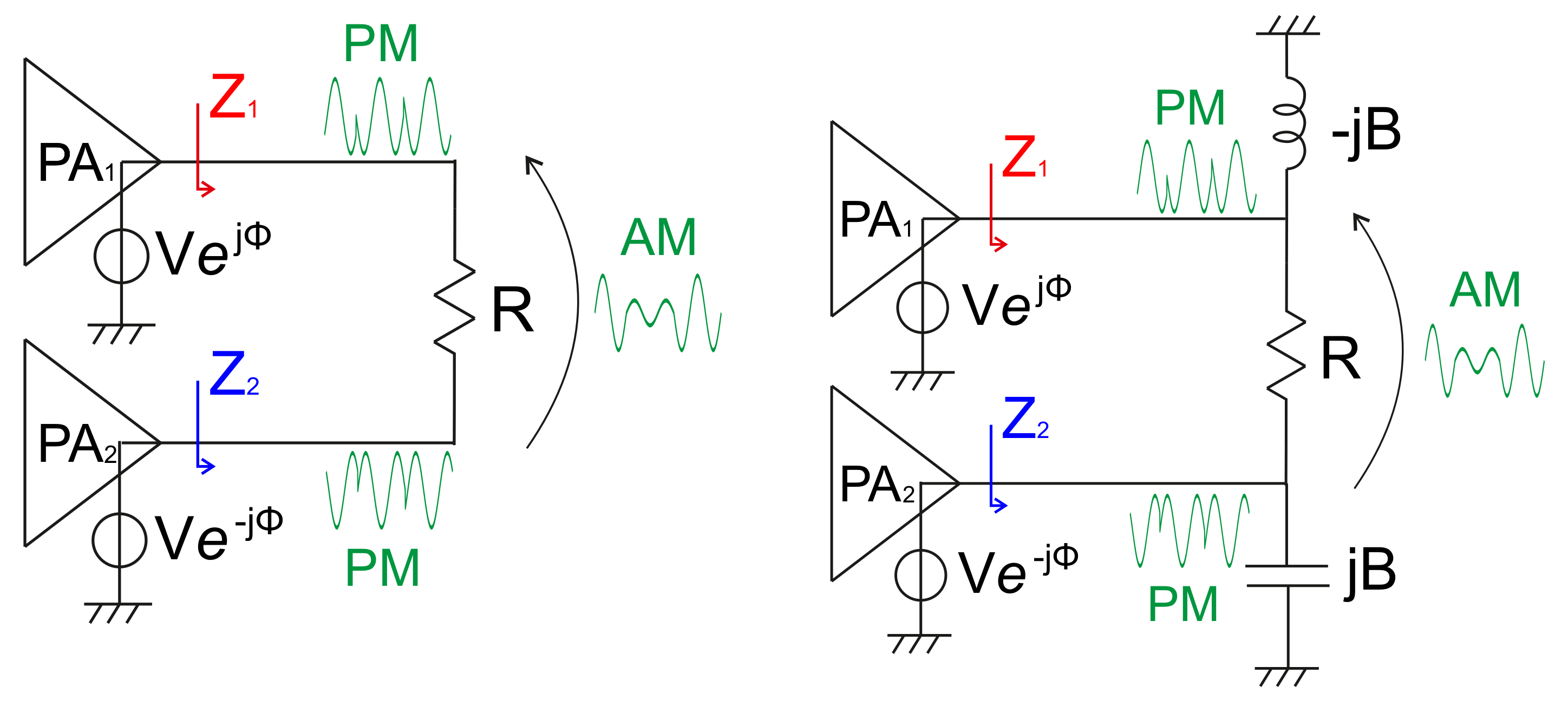
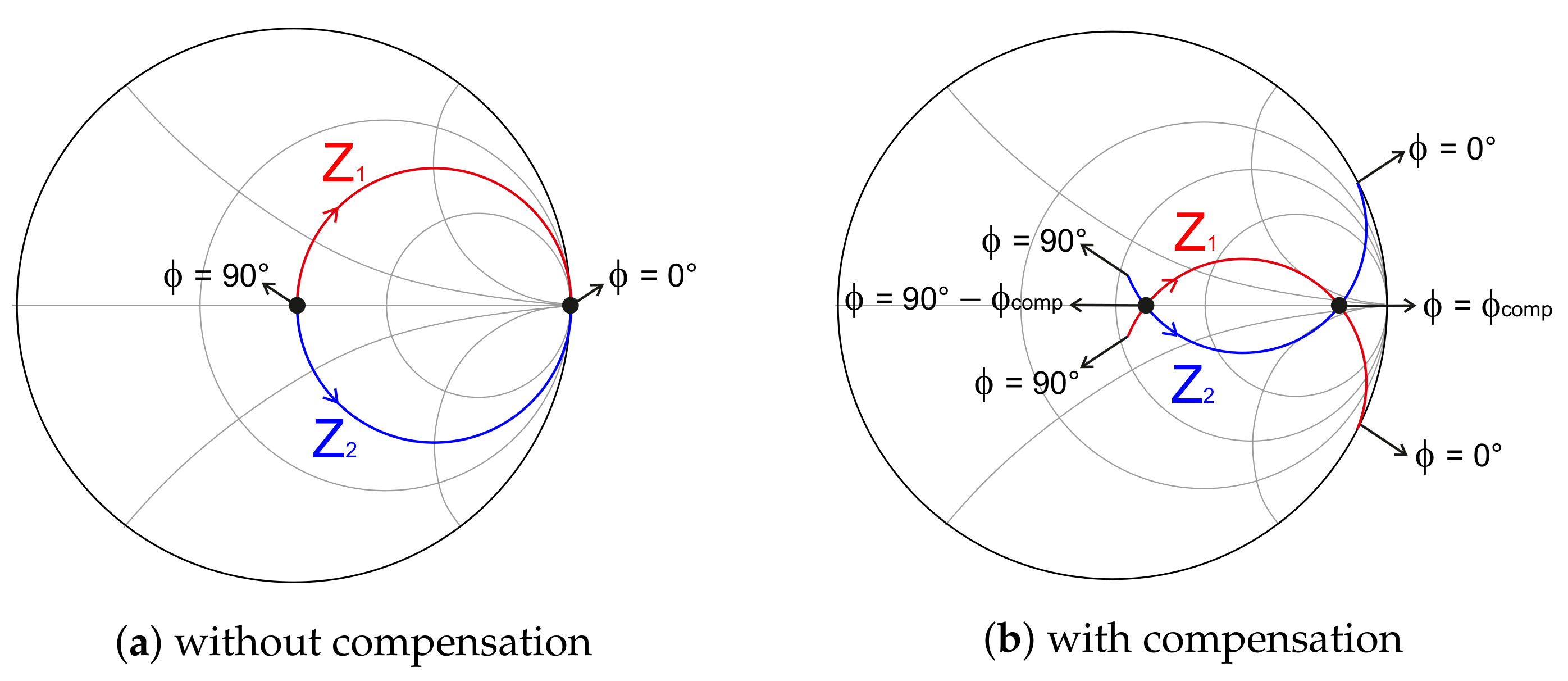
4.1.4. Single-Input Architectures
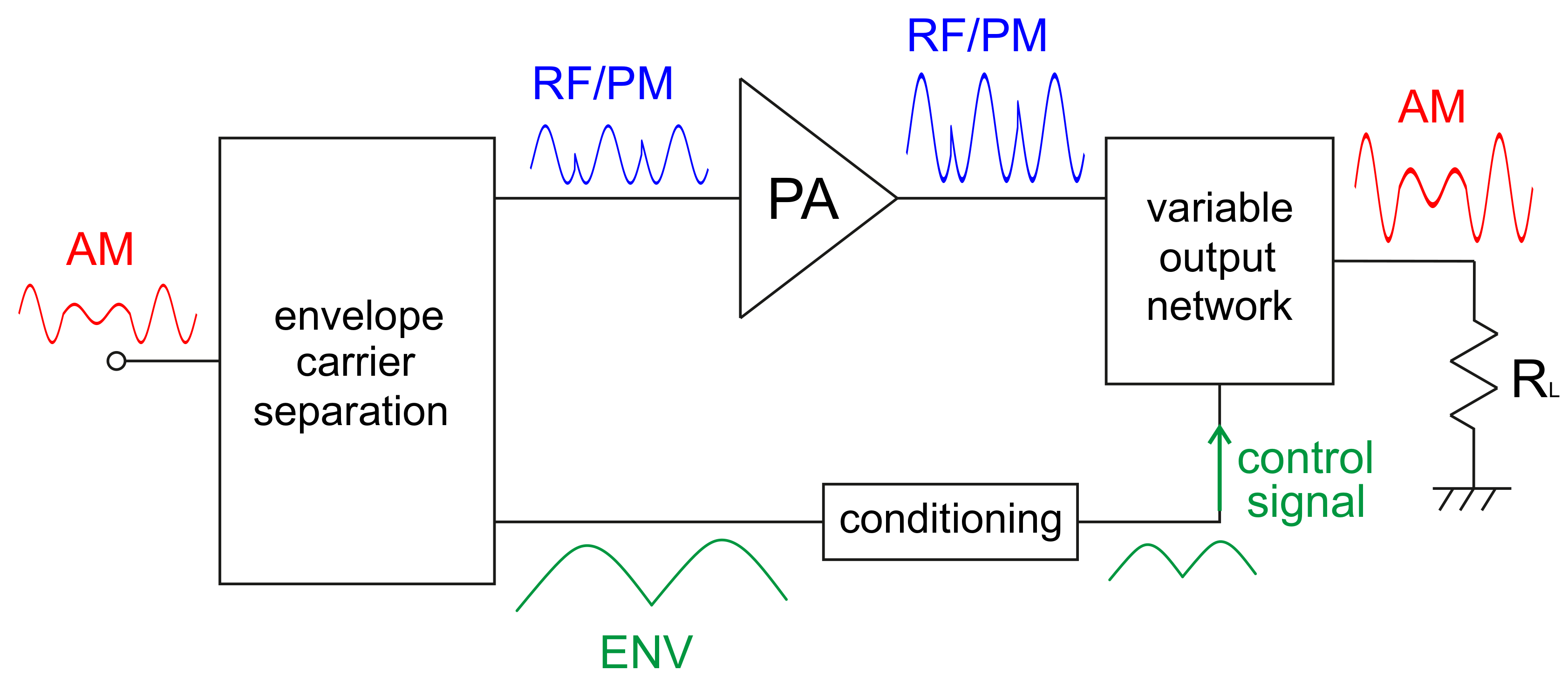
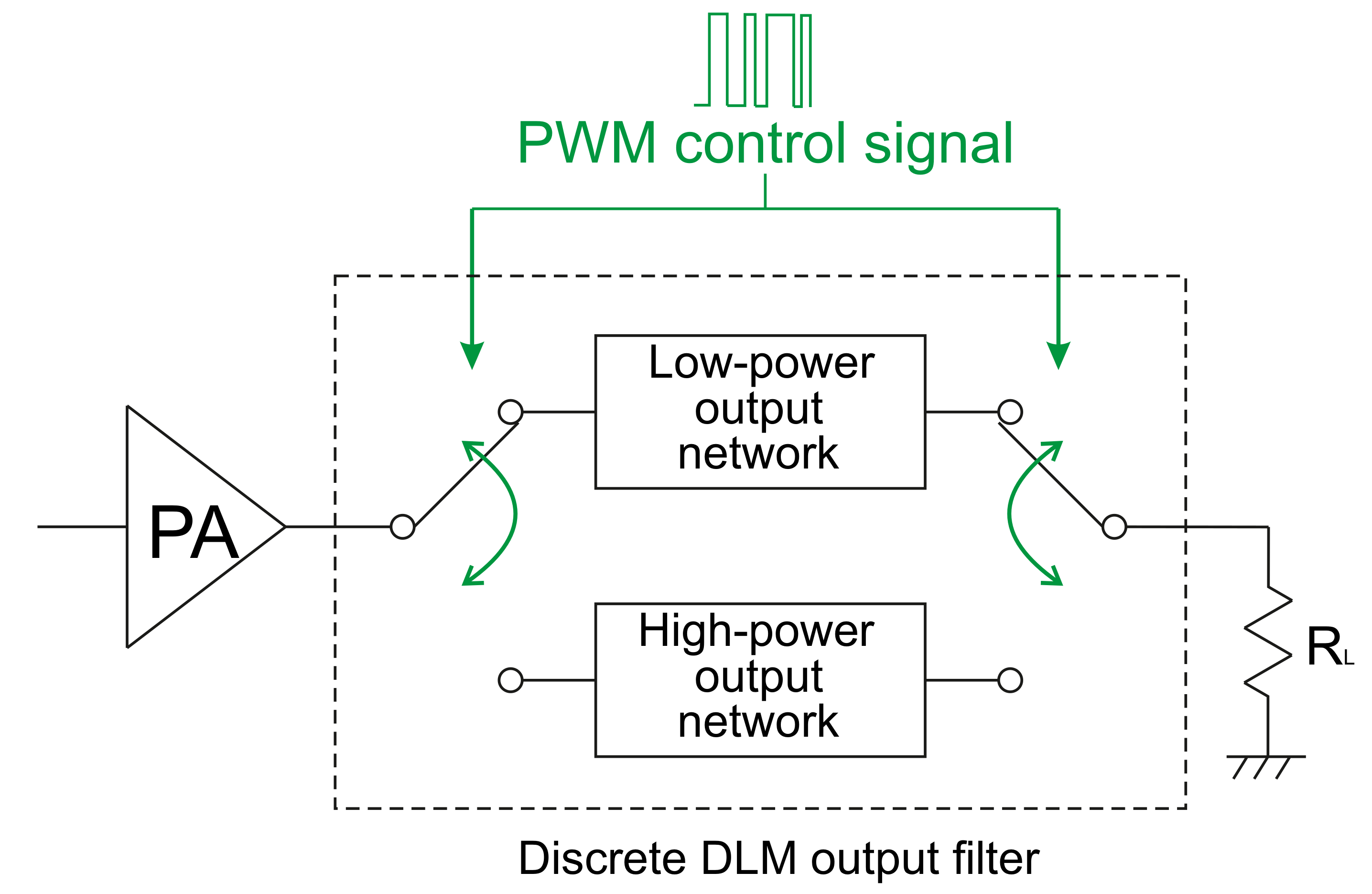
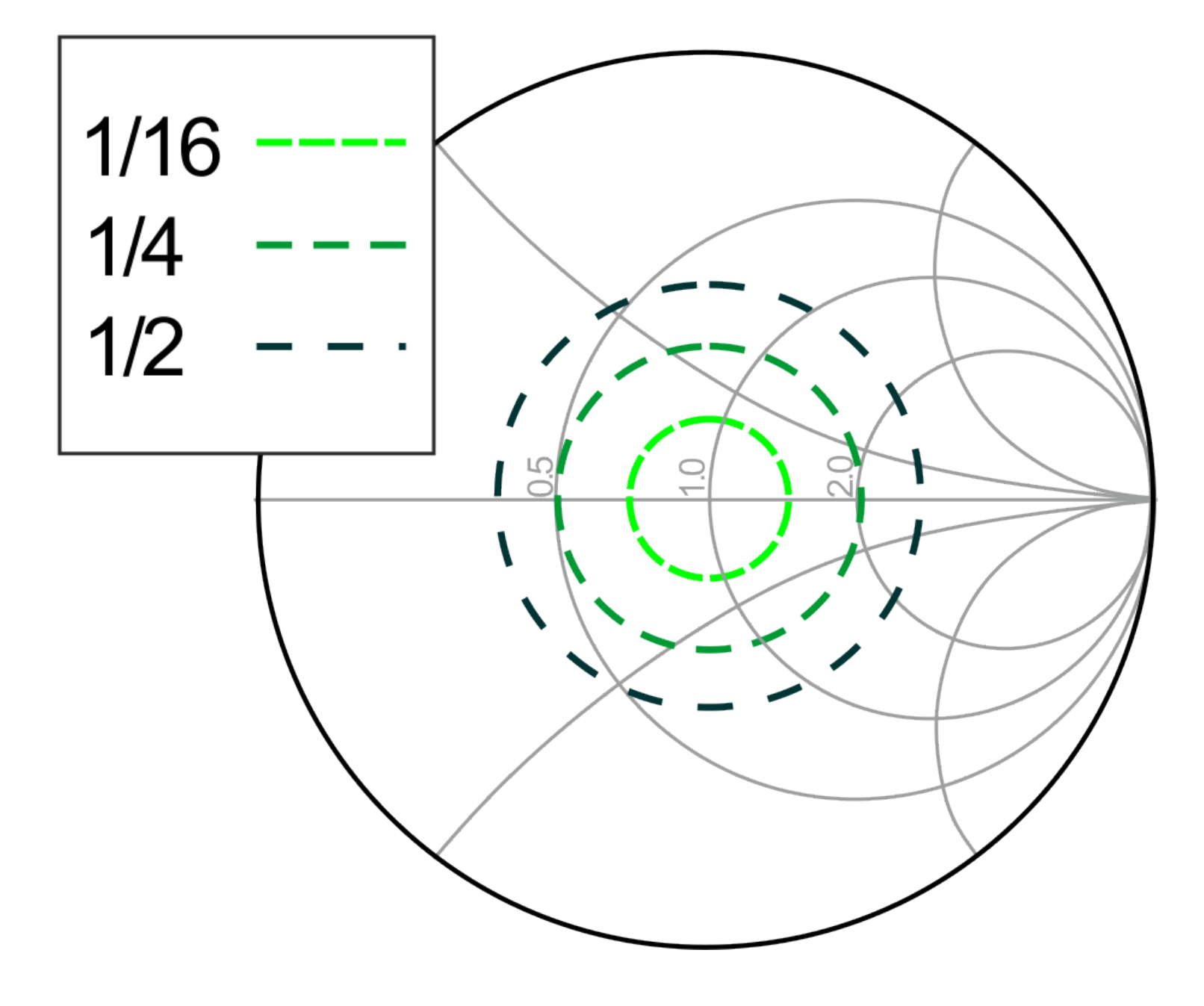
5. Dynamic Load Modulation
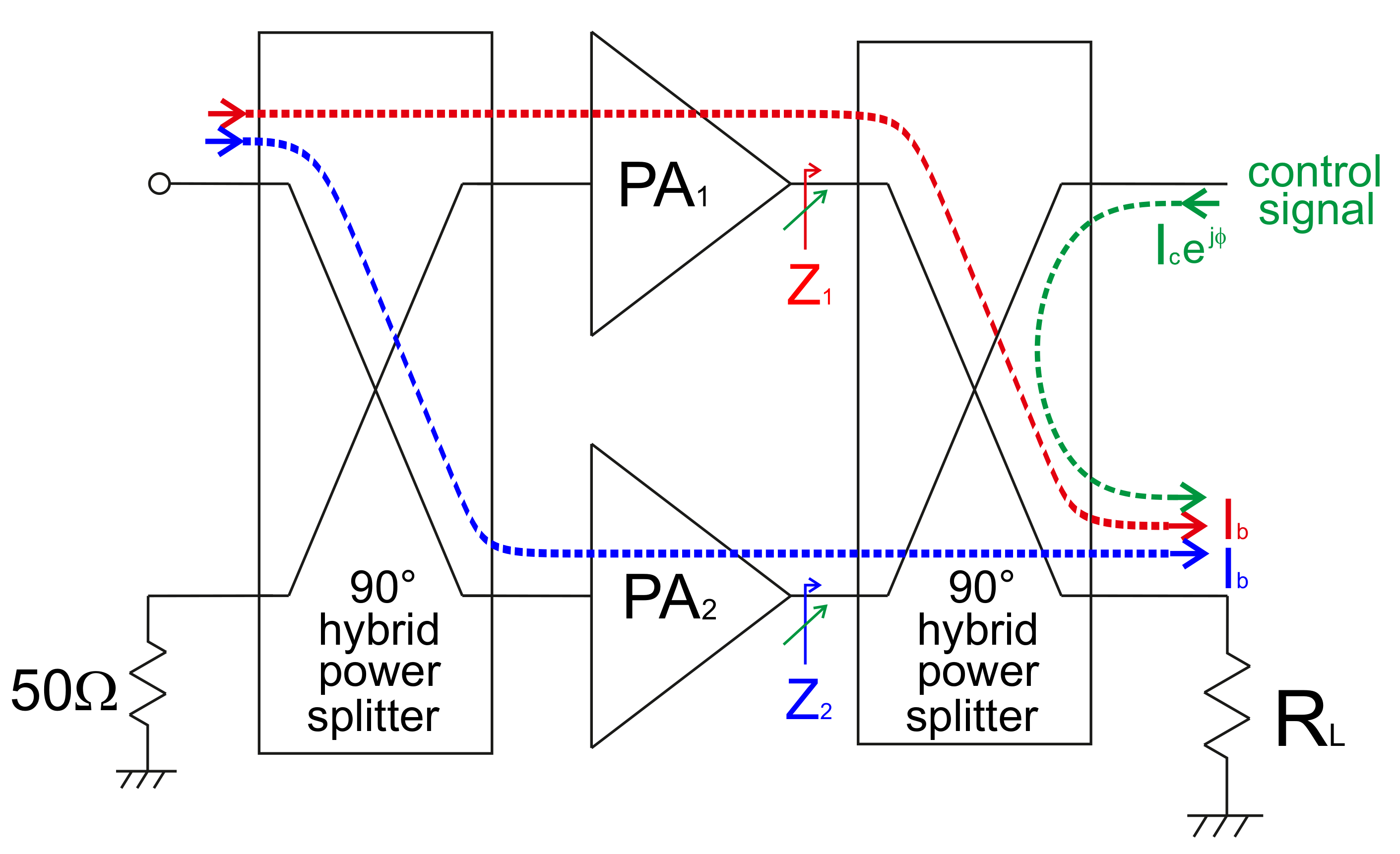
6. Load Modulated Balanced Amplifier
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Requirements Related to Technical Performance for IMT-Advanced Radio Interface(s). 2008. Available online: http://www.itu.int/pub/R-REP-M.2134-2008 (accessed on 15 September 2017).
- Huawei. 5G: A Technology Vision. 2014. Available online: www.huawei.com/ilink/en/download/HW_314849 (accessed on 15 September 2017).
- NGMN. 5G White Paper. 2015. Available online: https://www.ngmn.org/5g-white-paper.html (accessed on 15 September 2017).
- Camarchia, V.; Quaglia, R.; Pirola, M. Electronics for Microwave Backhaul; Artech House: Norwood, MA, USA, 2016. [Google Scholar]
- Ghavidel, A.; Tamjid, F.; Fathy, A. GaN Widening Possibilties for PAs: Wide-band GaN Power Amplifiers Utilize the Technology’s Special Properties. IEEE Microw. Mag. 2017, 18, 46–55. [Google Scholar] [CrossRef]
- Reveyrand, T.; Ciccognani, W.; Ghione, G.; Jardel, O. GaN transistor characterization and modeling activities performed within the frame of the KorriGaN project. Int. J. Microw. Wirel. Technol. 2010, 2, 51–61. [Google Scholar] [CrossRef]
- Ciccognani, W.; Giannini, F.; Limiti, E. GaN Device Technology: Manufacturing, Characterization, Modelling and Verification. In Proceedings of the 14th Conference on Microwave Techniques, Prague, Czech Republic, 23–24 April 2008; pp. 1–6. [Google Scholar]
- Cripps, S.C. RF Power Amplifiers for Wireless Communications; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Colantonio, P.; Giannini, F.; Limiti, E. High Efficiency RF and Microwave Solid State Power Amplifiers; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Quaglia, R.; Camarchia, V.; Pirola, M. Linear GaN MMIC Combined Power Amplifiers for 7-GHz Microwave Backhaul. IEEE Trans. Microw. Theory Tech. 2014, 62, 2700–2710. [Google Scholar] [CrossRef]
- Braithwaite, R.N. A Combined Approach to Digital Predistortion and Crest Factor Reduction for the Linearization of an RF Power Amplifier. IEEE Trans. Microw. Theory Tech. 2013, 61, 291–302. [Google Scholar] [CrossRef]
- Hammi, O.; Carichner, S.; Vassilakis, B. Synergetic Crest Factor Reduction and Baseband Digital Predistortion for Adaptive 3G Doherty Power Amplifier Linearizer Design. IEEE TranS. Microw. Theory Tech. 2008, 56, 2602–2608. [Google Scholar] [CrossRef]
- Chen, X.; Chen, W.; Huang, F. Systematic Crest Factor Reduction and Efficiency Enhancement of Dual-Band Power Amplifier Based Transmitters. IEEE Trans. Broadcast. 2017, 63, 111–122. [Google Scholar] [CrossRef]
- Doherty, W.H. A new high-efficiency power amplifier for modulated waves. Bell Syst. Tech. J. 1936, 15, 469–475. [Google Scholar] [CrossRef]
- Chireix, H. High Power Outphasing Modulation. Proc. IRE 1935, 23, 1370–1392. [Google Scholar] [CrossRef]
- Kahn, L.R. Single-Sideband Transmission by Envelope Elimination and Restoration. Proc. IRE 1952, 40, 803–806. [Google Scholar] [CrossRef]
- Wang, Z. Demystifying Envelope Tracking: Use for High-Efficiency Power Amplifiers for 4G and Beyond. IEEE Microw. Mag. 2015, 16, 106–129. [Google Scholar] [CrossRef]
- Pengelly, R.; Baker, R. GaN Devices and AMO Technology Enable High Efficiency and Wide Bandwidth. Microw. J. 2014, 57, 66. [Google Scholar]
- Merrick, B.; King, J.; Brazil, T. A wideband Sequential Power Amplifier. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS), Tampa, FL, USA, 1–6 June 2014; pp. 1–3. [Google Scholar]
- Shao, J.; Ma, R.; Teo, K.H.; Shinjo, S.; Yamanaka, K. A fully analog two-way sequential GaN power amplifier with 40% fractional bandwidth. In Proceedings of the 2015 IEEE International Wireless Symposium (IWS), Shenzhen, China, 30 March–1 April 2015; pp. 1–3. [Google Scholar]
- Lv, G.; Chen, W.; Feng, Z. A millimeter-wave sequential power amplifier. In Proceedings of the 10th Global Symposium on Millimeter-Waves, Hong Kong, China, 24–26 May 2017; pp. 123–125. [Google Scholar]
- Ren, H.; Shao, J.; Zhou, M. Design of a dual-band sequential power amplifier. In Proceedings of the 2016 IEEE Topical Conference on Power Amplifiers for Wireless and Radio Applications (PAWR), Austin, TX, USA, 24–27 January 2016; pp. 33–35. [Google Scholar]
- Shao, J.; Ma, R.; Shinjo, S. Design of broadband three-way sequential power amplifiers. In Proceedings of the 2016 IEEE International Symposium on Radio-Frequency Integration Technology (RFIT), Taipei, Taiwan, 24–26 August 2016; pp. 1–3. [Google Scholar]
- Giofrè, R.; Colantonio, P.; Giannini, F.; Ramella, C. A comprehensive comparison between GaN MMIC Doherty and combined class-AB power amplifiers for microwave radio links. Int. J. Microw. Wirel. Technol. 2016, 8, 673–681. [Google Scholar] [CrossRef]
- Giofrè, R.; Piazzon, L.; Colantonio, P.; Giannini, F.; Camarchia, V.; Mustazar, I.; Pirola, M.; Quaglia, R.; Ramella, C. GaN MMICs for microwave backhaul: Doherty vs. combined class-AB power amplifier. In Proceedings of the 2015 10th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 7–8 September 2015; pp. 33–36. [Google Scholar]
- Oh, H.; Kang, H.; Lee, H. Doherty Power Amplifier Based on the Fundamental Current Ratio for Asymmetric cells. IEEE Trans. Microw. Theory Tech. 2017, 65, 4190–4197. [Google Scholar] [CrossRef]
- Camarchia, V.; Fang, J.; Ghione, G.; Khoshkholgh, A.J.; Rubio, J.M.; Pirola, M.; Quaglia, R.; Ramella, C. Bandwidth extension of GaN Doherty power amplifier: Effect on power, efficiency and linearity. In Proceedings of the 2013 IEEE International Wireless Symposium (IWS), Beijing, China, 14–18 April 2013; pp. 1–4. [Google Scholar]
- Colantonio, P.; Giannini, F.; Giofre, R.; Piazzon, L. Theory and Experimental Results of a Class F AB-C Doherty Power Amplifier. IEEE Trans. Microw. Theory Tech. 2009, 57, 1936–1947. [Google Scholar] [CrossRef]
- Barakat, A.; Thian, M.; Fusco, V. A High-Efficiency GaN Doherty Power Amplifier With Blended Class-EF Mode and Load-Pull Technique. IEEE Trans. Circuits Syst. II 2017. accepted for publication. [Google Scholar] [CrossRef]
- Kim, S.; Lee, J.; Moon, K.; Park, Y.; Minn, D.; Kim, B. Optimized peaking amplifier of Doherty amplifier using an inductive input second harmonic load. In Proceedings of the 2016 11th European Microwave Integrated Circuits Conference (EuMIC), London, UK, 3–4 October 2016; pp. 129–132. [Google Scholar]
- Cho, Y.; Moon, K.; Park, B.; Kim, J.; Jin, H.; Kim, B. Compact design of linear Doherty power amplifier with harmonic control for handset applications. In Proceedings of the 2015 10th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 7–8 September 2015; pp. 37–40. [Google Scholar]
- Colantonio, P.; Giannini, F.; Giofre, R.; Piazzon, L. GaN Doherty Amplifier With Compact Harmonic Traps. In Proceedings of the 2008 IEEE Microwave Integrated Circuit Conference, Amsterdam, The Netherlands, 27–28 October 2008; pp. 526–529. [Google Scholar]
- Eccleston, K.W.; Smith, K.J.I.; Gough, P.T. Harmonic load modulation in Doherty amplifiers. Electron. Lett. 2008, 44, 128–129. [Google Scholar] [CrossRef]
- Cripps, S. Advanced Techniques in RF Power Amplifier Design; Artech House: Norwood, MA, USA, 2002. [Google Scholar]
- Iwamoto, M.; Williams, A.; Chen, P.-F.; Metzger, A.; Wang, C.; Larson, L.E.; Asbeck, P.M. An extended Doherty amplifier with high efficiency over a wide power range. In Proceedings of the 2001 IEEE MTT-S International Microwave Symposium Digest, Phoenix, AZ, USA, 20–24 May 2001; pp. 931–934. [Google Scholar]
- Kim, J.; Fehri, B.; Boumaiza, S.; Wood, J. Power Efficiency and Linearity Enhancement Using Optimized Asymmetrical Doherty Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2011, 59, 425–434. [Google Scholar] [CrossRef]
- Kitahara, T.; Yamamoto, T.; Hiura, S. Asymmetrical Doherty amplifier using GaN HEMTs for high-power applications. In Proceedings of the 2012 IEEE Topical Conference on Power Amplifiers for Wireless and Radio Applications (PAWR), Santa Clara, CA, USA, 15–18 January 2012; pp. 57–60. [Google Scholar]
- Camarchia, V.; Fang, J.; Rubio, J.M.; Pirola, M.; Quaglia, R. 7 GHz MMIC GaN Doherty Power Amplifier With 47% Efficiency at 7 dB Output Back-Off. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 34–36. [Google Scholar] [CrossRef]
- Nghiem, X.A.; Guan, J.; Negra, R. Broadband Sequential Power Amplifier With Doherty-Type Active Load Modulation. IEEE Trans. Microw. Theory Tech. 2015, 63, 2821–2832. [Google Scholar] [CrossRef]
- Kim, B.; Kim, I.; Moon, J. Advanced Doherty Architecture. IEEE Microw. Mag. 2010, 11, 72–86. [Google Scholar] [CrossRef]
- Blednov, I. Wideband 3 way Doherty RFIC with 12 dB back-off power range. In Proceedings of the 2016 11th European Microwave Integrated Circuits Conference (EuMIC), London, UK, 3–4 October 2016; pp. 17–20. [Google Scholar]
- Golestaneh, H.; Malekzadeh, F.A.; Boumaiza, S. An Extended-Bandwidth Three-Way Doherty Power Amplifier. IEEE Trans. Microw. Theory Tech. 2013, 61, 3318–3328. [Google Scholar] [CrossRef]
- Moronval, X.; Gajadharsing, J. A 100 W multi-band four-way integrated Doherty amplifier. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–3. [Google Scholar]
- Kitahara, T.; Yamamoto, T.; Hiura, S. Doherty power amplifier with asymmetrical drain voltages for enhanced efficiency at 8 dB backed-off output power. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium Digest (MTT), Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Jang, H.; Roblin, P.; Quindroit, C.; Lin, Y.; Pond, R.D. Asymmetric Doherty Power Amplifier Designed Using Model-Based Nonlinear Embedding. IEEE Trans. Microw. Theory Tech. 2014, 62, 3436–3451. [Google Scholar] [CrossRef]
- Gustafsson, D.; Cahuana, J.C.; Kuylenstierna, D.; Angelov, I.; Fager, C. A GaN MMIC Modified Doherty PA With Large Bandwidth and Reconfigurable Efficiency. IEEE Trans. Microw. Theory Tech. 2014, 62, 3006–3016. [Google Scholar] [CrossRef]
- Pang, J.; He, S.; Dai, Z.; Huang, C.; Peng, J.; You, F. Design of a Post-Matching Asymmetric Doherty Power Amplifier for Broadband Applications. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 52–54. [Google Scholar] [CrossRef]
- Özen, M.; Andersson, K.; Fager, C. Symmetrical Doherty Power Amplifier With Extended Efficiency Range. IEEE Trans. Microw. Theory Tech. 2016, 64, 1273–1284. [Google Scholar] [CrossRef]
- Fang, X.H.; Cheng, K.K.M. Extension of High-Efficiency Range of Doherty Amplifier by Using Complex Combining Load. IEEE Trans. Microw. Theory Tech. 2014, 62, 2038–2047. [Google Scholar] [CrossRef]
- Mohamed, A.M.M.; Boumaiza, S.; Mansour, R.R. Doherty Power Amplifier With Enhanced Efficiency at Extended Operating Average Power Levels. IEEE Trans. Microw. Theory Tech. 2013, 61, 4179–4187. [Google Scholar] [CrossRef]
- Shi, W.; He, S.; Gideon, N. Extending high-efficiency power range of symmetrical Doherty power amplifiers by taking advantage of peaking stage. IET Microw. Antennas Propag. 2017, 11, 1296–1302. [Google Scholar] [CrossRef]
- Colantonio, P.; Giannini, F.; Giofre, R.; Piazzon, L. Increasing Doherty Amplifier Average Efficiency Exploiting Device Knee Voltage Behavior. IEEE Trans. Microw. Theory Tech. 2011, 59, 2295–2305. [Google Scholar] [CrossRef]
- Quaglia, R.; Pirola, M.; Ramella, C. Offset Lines in Doherty Power Amplifiers: Analytical Demonstration and Design. IEEE Microw. Wirel. Compon. Lett. 2013, 23, 93–95. [Google Scholar] [CrossRef]
- Yang, Y.; Yi, J.; Woo, Y.Y.; Kim, B. Optimum design for linearity and efficiency of a Microwave Doherty amplifier using a new load matching technique. Microw. J. 2001, 44, 20–36. [Google Scholar]
- Kim, S.; Moon, J.; Lee, J.; Park, Y.; Minn, D.; Kim, B. Accurate Offset Line Design of Doherty Amplifier With Compensation of Peaking Amplifier Phase Variation. IEEE Trans. Microw. Theory Tech. 2016, 64, 3224–3231. [Google Scholar] [CrossRef]
- Rubio, J.M.; Fang, J.; Camarchia, V.; Quaglia, R.; Pirola, M.; Ghione, G. 3–3.6-GHz Wideband GaN Doherty Power Amplifier Exploiting Output Compensation Stages. IEEE Trans. Microw. Theory Tech. 2012, 60, 2543–2548. [Google Scholar] [CrossRef]
- Giofrè, R.; Piazzon, L.; Colantonio, P.; Giannini, F.; Camarchia, V.; Quaglia, R.; Pirola, M.; Ramella, C. GaN-MMIC Doherty power amplifier with integrated reconfigurable input network for microwave backhaul applications. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium (IMS), Phoenix, AZ, USA, 17–22 May 2015; pp. 1–3. [Google Scholar]
- Quaglia, R.; Camarchia, V.; Rubio, J.J.M.; Pirola, M.; Ghione, G. A 4-W Doherty Power Amplifier in GaN MMIC Technology for 15-GHz Applications. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 365–367. [Google Scholar] [CrossRef]
- Rawat, K.; Ghannouchi, F.M. Design Methodology for Dual-Band Doherty Power Amplifier With Performance Enhancement Using Dual-Band Offset Lines. IEEE Trans. Ind. Electron. 2012, 59, 4831–4842. [Google Scholar] [CrossRef]
- Hallberg, W.; Özen, M.; Gustafsson, D.; Buisman, K.; Fager, C. A Doherty Power Amplifier Design Method for Improved Efficiency and Linearity. IEEE Trans. Microw. Theory Tech. 2016, 64, 4491–4504. [Google Scholar] [CrossRef]
- Özen, M.; van der Heijden, M.; Acar, M.; Jos, R.; Fager, C. A Generalized Combiner Synthesis Technique for Class-E Outphasing Transmitters. IEEE Trans. Circuits. Syst. I 2017, 64, 1126–1139. [Google Scholar] [CrossRef]
- Raffo, A.; Scappaviva, F.; Vannini, G. A New Approach to Microwave Power Amplifier Design Based on the Experimental Characterization of the Intrinsic Electron-Device Load Line. IEEE Trans. Microw. Theory Tech. 2009, 57, 1743–1752. [Google Scholar] [CrossRef]
- Vadalà, V.; Schreurs, D.M.M.-P.; Raffo, A.; Crupi, G.; Vannini, G.; Nauwelaers, B. Nonlinear embedding and de-embedding techniques for large-signal FET measurements. Microw. Opt. Technol. Lett. 2012, 54, 2835–2838. [Google Scholar] [CrossRef]
- Jung, S.-C.; Hammi, O.; Ghannouchi, F.M. Design Optimization and DPD Linearization of GaN-Based Unsymmetrical Doherty Power Amplifiers for 3G Multicarrier Applications. IEEE Trans. Microw. Theory Tech. 2009, 57, 2105–2113. [Google Scholar] [CrossRef]
- Nick, M.; Mortazawi, A. Adaptive Input-Power Distribution in Doherty Power Amplifiers for Linearity and Efficiency Enhancement. IEEE Trans. Microw. Theory Tech. 2010, 58, 2764–2771. [Google Scholar] [CrossRef]
- Camarchia, V.; Colantonio, P.; Giannini, F.; Giofrè, R.; Jiang, T.; Pirola, M. A design strategy for AM/PM compensation in GaN Doherty Power Amplifiers. IEEE Access 2017, 5, 22244–22251. [Google Scholar] [CrossRef]
- Nunes, L.C.; Cabral, P.M.; Pedro, J.C. AM/PM distortion in GaN Doherty power amplifiers. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Piazzon, L.; Giofrè, R.; Quaglia, R.; Camarchia, V.; Pirola, M.; Colantonio, P.; Giannini, F.; Ghione, G. Effect of Load Modulation on Phase Distortion in Doherty Power Amplifiers. IEEE Microw. Wirel. Compon. Lett. 2014, 24, 505–507. [Google Scholar] [CrossRef]
- Katz, A.; Wood, J.; Chokola, D. The Evolution of PA Linearization: From Classic Feedforward and Feedback Through Analog and Digital Predistortion. IEEE Microw. Mag. 2016, 17, 32–40. [Google Scholar] [CrossRef]
- Boumaiza, S.; Golestaneh, H. Joint circuit-level and digital predistortion strategies for enhancing the linearity-efficiency tradeoff of Doherty power amplifiers. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–3. [Google Scholar]
- Jiang, T.; Quaglia, R.; Camarchia, V.; Pirola, M. FPGA-based digital predistortion of A 3.5 GHz GaN Doherty power amplifier. In Proceedings of the 10th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM 2014), Beijing, China, 26–28 September 2014; pp. 20–24. [Google Scholar]
- Nair, M.V.D.; Piazzon, L.; Colantonio, P. A comparative study on digital predistortion techniques for Doherty amplifier for LTE applications. In Proceedings of the 2014 International Workshop on Integrated Nonlinear Microwave and Millimetre-wave Circuits (INMMiC), Leuven, Belgium, 2–4 April 2014; pp. 1–3. [Google Scholar]
- Cao, H.; Qureshi, J.; Eriksson, T.; Fager, C.; de Vreede, L. Digital predistortion for dual-input Doherty amplifiers. In Proceedings of the 2012 IEEE Topical Conference on Power Amplifiers for Wireless and Radio Applications (PAWR), Santa Clara, CA, USA, 15–18 January 2012; pp. 45–48. [Google Scholar]
- Bathich, K.; Markos, A.Z.; Boeck, G. Frequency Response Analysis and Bandwidth Extension of the Doherty Amplifier. IEEE Trans. Microw. Theory Tech. 2011, 59, 934–944. [Google Scholar] [CrossRef]
- Sun, G.; Jansen, R.H. Broadband Doherty Power Amplifier via Real Frequency Technique. IEEE Trans. Microw. Theory Tech. 2012, 60, 99–111. [Google Scholar] [CrossRef]
- Qureshi, J.H.; Li, N.; Neo, W.C.E.; van Rijs, F.; Blednov, I.; de Vreede, L.C.N. A wide-band 20W LMOS Doherty power amplifier. In Proceedings of the 2010 IEEE MTT-S International Microwave Symposium Digest (MTT), Anaheim, CA, USA, 23–28 May 2010; pp. 1504–1507. [Google Scholar]
- Abadi, M.N.A.; Golestaneh, H.; Sarbishaei, H.; Boumaiza, S. An extended bandwidth Doherty power amplifier using a novel output combiner. In Proceedings of the 2014 IEEE MTT-S International Microwave Symposium (IMS), Tampa, FL, USA, 1–6 June 2014; pp. 1–4. [Google Scholar]
- Akbarpour, M.; Helaoui, M.; Ghannouchi, F.M. A Transformer-Less Load-Modulated (TLLM) Architecture for Efficient Wideband Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2012, 60, 2863–2874. [Google Scholar] [CrossRef]
- Giofrè, R.; Piazzon, L.; Colantonio, P.; Giannini, F. A Doherty Architecture With High Feasibility and Defined Bandwidth Behavior. IEEE Trans. Microw. Theory Tech. 2013, 61, 3308–3317. [Google Scholar] [CrossRef]
- Carlin, H.; Komiak, J.J. A New Method of Broad-Band Equalization Applied to Microwave Amplifiers. IEEE Trans. Microw. Theory Tech. 1979, 27, 93–99. [Google Scholar] [CrossRef]
- Wu, D.Y.T.; Boumaiza, S. A Modified Doherty Configuration for Broadband Amplification Using Symmetrical Devices. IEEE Trans. Microw. Theory Tech. 2012, 60, 3201–3213. [Google Scholar] [CrossRef]
- Park, Y.; Lee, J.; Jee, S.; Kim, S.; Kim, B. Optimized Doherty power amplifier with a new offset line. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium (IMS), Phoenix, AZ, USA, 17–22 May 2015; pp. 1–4. [Google Scholar]
- Pengelly, R.; Fager, C.; Ozen, M. Doherty’s Legacy: A History of the Doherty Power Amplifier from 1936 to the Present Day. IEEE Microw. Mag. 2016, 17, 41–58. [Google Scholar] [CrossRef]
- Campbell, C.F. A fully integrated Ku-band Doherty amplifier MMIC. IEEE Microw. Guided Wave Lett. 1999, 9, 114–116. [Google Scholar] [CrossRef]
- Camarchia, V.; Quaglia, R.; Ramella, C.; Pirola, M. Power amplifier MMICs for 15 GHz microwave links in 0.25 um GaN technology. In Proceedings of the Integrated Nonlinear Microwave and Millimetre-wave Circuits Workshop (INMMiC) 2017, Graz, Austria, 20–21 April 2017; pp. 1–3. [Google Scholar]
- Quaglia, R.; Camarchia, V.; Jiang, T.; Pirola, M.; Guerrieri, S.D.; Loran, B. K-Band GaAs MMIC Doherty Power Amplifier for Microwave Radio With Optimized Driver. IEEE Trans. Microw. Theory Tech. 2014, 62, 2518–2525. [Google Scholar] [CrossRef]
- Campbell, C.F.; Tran, K.; Kao, M.-Y.; Nayak, S. A K-Band 5W Doherty Amplifier MMIC Utilizing 0.15 um GaN on SiC HEMT MTechnology. In Proceedings of the 2012 IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), La Jolla, CA, USA, 14–17 October 2012; pp. 1–4. [Google Scholar]
- Nguyen, D.P.; Pham, B.L.; Pham, A.V. A compact 29% PAE at 6 dB power back-off E-mode GaAs pHEMT MMIC Doherty power amplifier at Ka-band. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 1683–1686. [Google Scholar]
- Nguyen, D.P.; Pham, T.; Pham, A.V. A Ka-band asymmetrical stacked-FET MMIC Doherty power amplifier. In Proceedings of the 2017 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Honolulu, HI, USA, 4–6 June 2017; pp. 398–401. [Google Scholar]
- Darraji, R.; Mousavi, P.; Ghannouchi, F.M. Doherty Goes Digital: Digitally Enhanced Doherty Power Amplifiers. IEEE Microw. Mag. 2016, 17, 41–51. [Google Scholar] [CrossRef]
- Darraji, R.; Ghannouchi, F.M.; Hammi, O. A Dual-Input Digitally Driven Doherty Amplifier Architecture for Performance Enhancement of Doherty Transmitters. IEEE Trans. Microw. Theory Tech. 2011, 59, 1284–1293. [Google Scholar] [CrossRef]
- Darraji, R.; Ghannouchi, F.M. Digital Doherty Amplifier With Enhanced Efficiency and Extended Range. IEEE Trans. Microw. Theory Tech. 2011, 59, 2898–2909. [Google Scholar] [CrossRef]
- Neo, W.C.E.; Qureshi, J.; Pelk, M.J.; Gajadharsing, J.R.; de Vreede, L.C.N. A Mixed-Signal Approach Towards Linear and Efficient N-Way Doherty Amplifiers. IEEE Trans. Microw. Theory Tech. 2007, 55, 866–879. [Google Scholar] [CrossRef]
- Darraji, R.; Ghannouchi, F.M. RF/DSP Codesign Methodology of Enhanced Doherty Amplifiers. IEEE Trans. Circuits Syst. II 2012, 59, 219–223. [Google Scholar] [CrossRef]
- Darraji, R.; Ghannouchi, F.M.; Helaoui, M. Mitigation of Bandwidth Limitation in Wireless Doherty Amplifiers With Substantial Bandwidth Enhancement Using Digital Techniques. IEEE TranS. Microw. Theory Tech. 2012, 60, 2875–2885. [Google Scholar] [CrossRef]
- Darraji, R.; Kwan, A.K.; Ghannouchi, F.M.; Helaoui, M. Digitally Equalized Doherty RF Front-End Architecture for Broadband and Multistandard Wireless Transmitters. IEEE Trans. Microw. Theory Tech. 2015, 63, 1978–1988. [Google Scholar] [CrossRef]
- Andersson, C.M.; Gustafsson, D.; Cahuana, J.C.; Hellberg, R.; Fager, C. A 1-3-GHz Digitally Controlled Dual-RF Input Power-Amplifier Design Based on a Doherty-Outphasing Continuum Analysis. IEEE Trans. Microw. Theory Tech. 2013, 61, 3743–3752. [Google Scholar] [CrossRef]
- Quaglia, R.; Greene, M.D.; Poulton, M.J.; Cripps, S.T. Design and characterization of a 1.7–2.7 GHz quasi-MMIC Doherty power amplifier. In Proceedings of the 2017 IEEE MTT-S International Microwave Symposium (IMS), Honololu, HI, USA, 4–9 June 2017; pp. 771–773. [Google Scholar]
- Cox, D. Linear Amplification with Nonlinear Components. IEEE Trans. Commun. 1974, 22, 1942–1945. [Google Scholar] [CrossRef]
- Raab, F. Efficiency of Outphasing RF Power-Amplifier Systems. IEEE Trans. Commun. 1985, 33, 1094–1099. [Google Scholar] [CrossRef]
- Hakala, I.; Choi, D.K.; Gharavi, L.; Kajakine, N.; Koskela, J.; Kaunisto, R. A 2.14-GHz Chireix outphasing transmitter. IEEE Trans. Microw. Theory Tech. 2005, 53, 2129–2138. [Google Scholar] [CrossRef]
- Godoy, P.A.; Perreault, D.J.; Dawson, J.L. Outphasing Energy Recovery Amplifier With Resistance Compression for Improved Efficiency. IEEE Trans. Microw. Theory Tech. 2009, 57, 2895–2906. [Google Scholar] [CrossRef]
- Barton, T.W.; Jurkov, A.S.; Pednekar, P.H.; Perreault, D.J. Multi-Way Lossless Outphasing System Based on an All-Transmission-Line Combiner. IEEE Trans. Microw. Theory Tech. 2016, 64, 1313–1326. [Google Scholar] [CrossRef]
- Litchfield, M.; Cappello, T.; Florian, C.; Popovic, Z. X-Band GaN Multi-Level Chireix Outphasing PA with a Discrete Supply Modulator MMIC. In Proceedings of the 2016 IEEE Compound Semiconductor Integrated Circuit Symposium (CSICS), Austin, TX, USA, 23–26 October 2016; pp. 1–4. [Google Scholar]
- Jang, H.; Wilson, R.; Canning, T.; Seebacher, D.; Schuberth, C.; Arigong, B.; Trang, F.; Ward, S. RF-Input Self-Outphasing Doherty-Chireix Combined Amplifier. IEEE Trans. Microw. Theory Tech. 2016, 64, 4518–4534. [Google Scholar] [CrossRef]
- Qureshi, A.; Acar, M.; Qureshi, J.; Wesson, R.; de Vreede, L.C.N. A 112W GaN dual input Doherty-Outphasing Power Amplifier. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Wentzel, A.; Chevtchenko, S.; Kurpas, P.; Heinrich, W. A dual-band voltage-mode class-D PA for 0.8/1.8 GHz applications. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (IMS), Seattle, WA, USA, 2–7 June 2013; pp. 1–4. [Google Scholar]
- Wentzel, A.; Martinez-Mendoza, M.; Heinrich, W. A compact tri-band GaN voltage-mode class-D/S PA for future 0.8/1.8/2.6 GHz LTE picocell applications. In Proceedings of the 2015 10th European Microwave Integrated Circuits Conference (EuMIC), Paris, France, 7–8 September 2015; pp. 309–312. [Google Scholar]
- Qureshi, J.H.; Pelk, M.J.; Marchetti, M.; Edmund Neo, W.C.; Gajadharsing, J.R.; van der Heijden, M.P. A 90-W Peak Power GaN Outphasing Amplifier With Optimum Input Signal Conditioning. IEEE Trans. Microw. Theory Tech. 2009, 57, 1925–1935. [Google Scholar] [CrossRef]
- Qureshi, J.; Lium, R.; de Graauw, A.J.M.; van der Heijden, M.P.; Gajadharsing, J.; de Vreede, L.C.N. A highly efficient chireix amplifier using adaptive power combining. In Proceedings of the 2008 IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008; pp. 759–762. [Google Scholar]
- Barton, T.W.; Perreault, D.J. An RF-input outphasing power amplifier with RF signal decomposition network. In Proceedings of the 2015 IEEE MTT-S International Microwave Symposium (IMS), Phoenix, AZ, USA, 17–22 May 2015; pp. 1–4. [Google Scholar]
- Barton, T.W.; Perreault, D.J. Theory and Implementation of RF-Input Outphasing Power Amplification. IEEE Trans. Microw. Theory Tech. 2015, 63, 4273–4283. [Google Scholar] [CrossRef]
- Roblin, P.; Chang, H.-C.; Martinez-Rodriguez, F.J.; Martinez-Lopez, J.I. On the design of GaN Chireix power amplifiers using an embedding device model. Int. J. Numer. Model. Electron. Net. Dev. Fields 2017, 30, e2148. [Google Scholar] [CrossRef]
- van der Heijden, M.P.; Acar, M.; Vromans, J.S.; Calvillo-Cortes, D.A. A 19W high-efficiency wide-band CMOS-GaN class-E Chireix RF outphasing power amplifier. In Proceedings of the 2011 IEEE MTT-S International Microwave Symposium Digest (MTT), Baltimore, MD, USA, 5–10 June 2011; pp. 1–4. [Google Scholar]
- Perreault, D.J. A New Power Combining and Outphasing Modulation System for High-Efficiency Power Amplification. IEEE Trans. Circuits Syst. I 2011, 58, 1713–1726. [Google Scholar] [CrossRef]
- Hamill, D.C. Time reversal duality between linear networks. IEEE Trans. Circuits Syst. I 1996, 43, 63–65. [Google Scholar] [CrossRef]
- Han, Y.; Leitermann, O.; Jackson, D.A.; Rivas, J.M.; Perreault, D.J. Resistance Compression Networks for Radio-Frequency Power Conversion. IEEE Trans. Power Electron. 2007, 22, 41–53. [Google Scholar] [CrossRef]
- Jang, H.; Wilson, R.; Canning, T.; Seebacher, D.; Schuberth, C.; Arigong, B. Self-outphasing Chireix power amplifier using device input impedance variation. In Proceedings of the 2016 IEEE MTT-S International Microwave Symposium (IMS), San Francisco, CA, USA, 22–27 May 2016; pp. 1–4. [Google Scholar]
- Raab, F.H. High-efficiency linear amplification by dynamic load modulation. In Proceedings of the 2003 IEEE MTT-S International Microwave Symposium Digest, Philadelphia, PA, USA, 8–13 June 2003; Volume 3, pp. 1717–1720. [Google Scholar]
- Ozen, M.; Jos, R.; Andersson, C.M.; Acar, M.; Fager, C. High-Efficiency RF Pulsewidth Modulation of Class-E Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2011, 59, 2931–2942. [Google Scholar] [CrossRef]
- Andersson, C.M.; Gustafsson, D.; Yamanaka, K.; Kuwata, E.; Otsuka, H.; Nakayama, M.; Hirano, Y.; Angelov, I.; Fager, C.; Rorsman, N. Theory and Design of Class-J Power Amplifiers With Dynamic Load Modulation. IEEE Trans. Microw. Theory Tech. 2012, 60, 3778–3786. [Google Scholar] [CrossRef]
- Amirpour, R.; Darraji, R.; Ghannouchi, F.; Quay, R. Enhancement of the Broadband Efficiency of a Class-J Power Amplifier With Varactor-based Dynamic Load Modulation. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 180–182. [Google Scholar] [CrossRef]
- Sánchez-Pérez, C.; Özen, M.; Andersson, C.M.; Kuylenstierna, D.; Rorsman, N.; Fager, C. Optimized Design of a Dual-Band Power Amplifier With SiC Varactor-Based Dynamic Load Modulation. IEEE Trans. Microw. Theory Tech. 2015, 63, 2579–2588. [Google Scholar] [CrossRef]
- Nemati, H.M.; Fager, C.; Gustavsson, U.; Jos, R.; Zirath, H. Design of Varactor-Based Tunable Matching Networks for Dynamic Load Modulation of High Power Amplifiers. IEEE Trans. Microw. Theory Tech. 2009, 57, 1110–1118. [Google Scholar] [CrossRef]
- Cao, H.; Nemati, H.M.; Tehrani, A.S.; Eriksson, T.; Grahn, J.; Fager, C. Linearization of Efficiency-Optimized Dynamic Load Modulation Transmitter Architectures. IEEE Trans. Microw. Theory Tech. 2010, 58, 873–881. [Google Scholar]
- Nemati, H.M.; Cao, H.; Almgren, B.; Eriksson, T.; Fager, C. Design of Highly Efficient Load Modulation Transmitter for Wideband Cellular Applications. IEEE Trans. Microw. Theory Tech. 2010, 58, 2820–2828. [Google Scholar] [CrossRef]
- Chen, K.; Peroulis, D. Design of Adaptive Highly Efficient GaN Power Amplifier for Octave-Bandwidth Application and Dynamic Load Modulation. IEEE Trans. Microw. Theory Tech. 2012, 60, 1829–1839. [Google Scholar] [CrossRef]
- Fu, J.S.; Mortazawi, A. Improving Power Amplifier Efficiency and Linearity Using a Dynamically Controlled Tunable Matching Network. IEEE Trans. Microw. Theory Tech. 2008, 56, 3239–3244. [Google Scholar]
- Sudow, M.; Nemati, H.M.; Thorsell, M.; Gustavsson, U.; Andersson, K.; Fager, C.; Nilsson, P.-A.; ul Hassan, J.; Henry, A.; Janzen, E.; et al. SiC Varactors for Dynamic Load Modulation of High Power Amplifiers. IEEE Electron Device Lett. 2008, 29, 728–730. [Google Scholar] [CrossRef]
- Jeon, M.S.; Woo, J.-L.; Park, S.; Kwon, Y. A Pulsed Dynamic Load Modulation Technique for High-Efficiency Linear Transmitters. IEEE Trans. Microw. Theory Tech. 2015, 63, 2854–2866. [Google Scholar] [CrossRef]
- Liao, S.H.; Wang, Y.E. High Efficiency WCDMA Power Amplifier With Pulsed Load Modulation (PLM). IEEE J. Solid-State Circuits 2010, 45, 2030–2037. [Google Scholar] [CrossRef]
- Shepphard, D.J.; Powell, J.; Cripps, S.C. An Efficient Broadband Reconfigurable Power Amplifier Using Active Load Modulation. IEEE Microw. Wirel. Compon. Lett. 2016, 26, 443–445. [Google Scholar] [CrossRef]

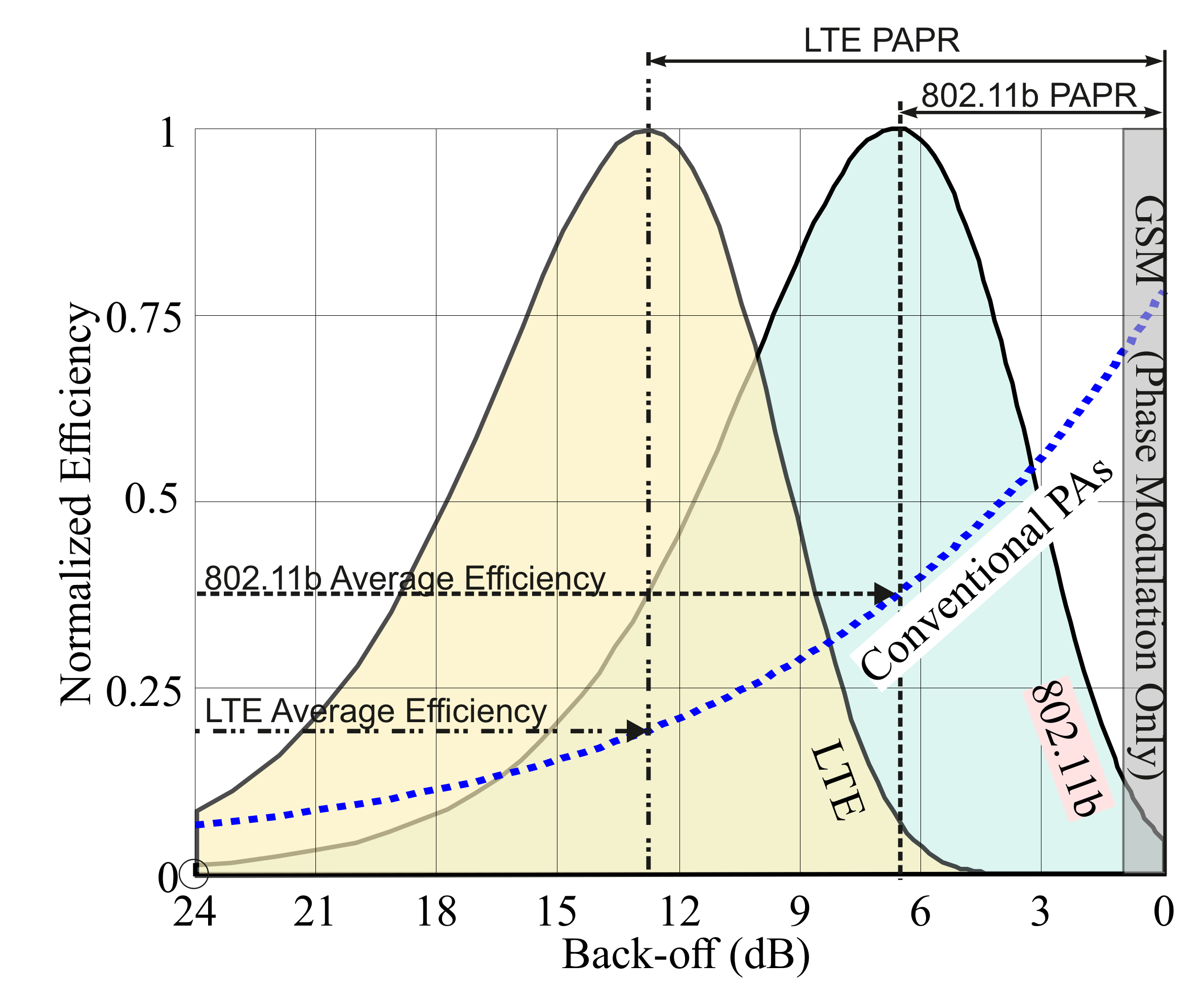




| Gen. | Standard | Interface and Modulation | Max. Frequency (GHz) | Bandwidth (MH) | Max. Bit-Rate (Mbit/s) | Max. PAPR (dB) |
|---|---|---|---|---|---|---|
| 2G | GSM/EDGE | TDMA/FDMA, GMSK, 8PSK | 1.9 | 0.2 | <1 | 3.3 |
| 3G | UMTS | W-CDMA, QPSK/64QAM | 3 | 5 | 100 | 10.6 |
| 4G | LTE | OFDMA, MIMO 4x4, 64QAM | 5.9 | 20 | 300 | 12 |
| 4G | LTE-Advanced | OFDMA/SC-FDMA, MIMO 8x8, CA, 64QAM | 5.9 | 20 (100 with CA) | >300 | 12 |
| 4G | WiMAX | OFDMA, MIMO 2x2, QPSK/64QAM | 5.8 | 20 | 100 | 12 |
| 5G | 5G | OFDMA, HetNet, massive MIMO, advanced CA, CoMP, … | 40 | >100 (800–2000) | >1000 | >12? |
| 3G/4G backhaul | point-to-point | 4096QAM | 86 GHz | 56 | >800 | 12 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramella, C.; Piacibello, A.; Quaglia, R.; Camarchia, V.; Pirola, M. High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach. Electronics 2017, 6, 96. https://doi.org/10.3390/electronics6040096
Ramella C, Piacibello A, Quaglia R, Camarchia V, Pirola M. High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach. Electronics. 2017; 6(4):96. https://doi.org/10.3390/electronics6040096
Chicago/Turabian StyleRamella, Chiara, Anna Piacibello, Roberto Quaglia, Vittorio Camarchia, and Marco Pirola. 2017. "High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach" Electronics 6, no. 4: 96. https://doi.org/10.3390/electronics6040096
APA StyleRamella, C., Piacibello, A., Quaglia, R., Camarchia, V., & Pirola, M. (2017). High Efficiency Power Amplifiers for Modern Mobile Communications: The Load-Modulation Approach. Electronics, 6(4), 96. https://doi.org/10.3390/electronics6040096







