A Microcontroller-Based Adaptive Model Predictive Control Platform for Process Control Applications
Abstract
1. Introduction
2. Previous Work
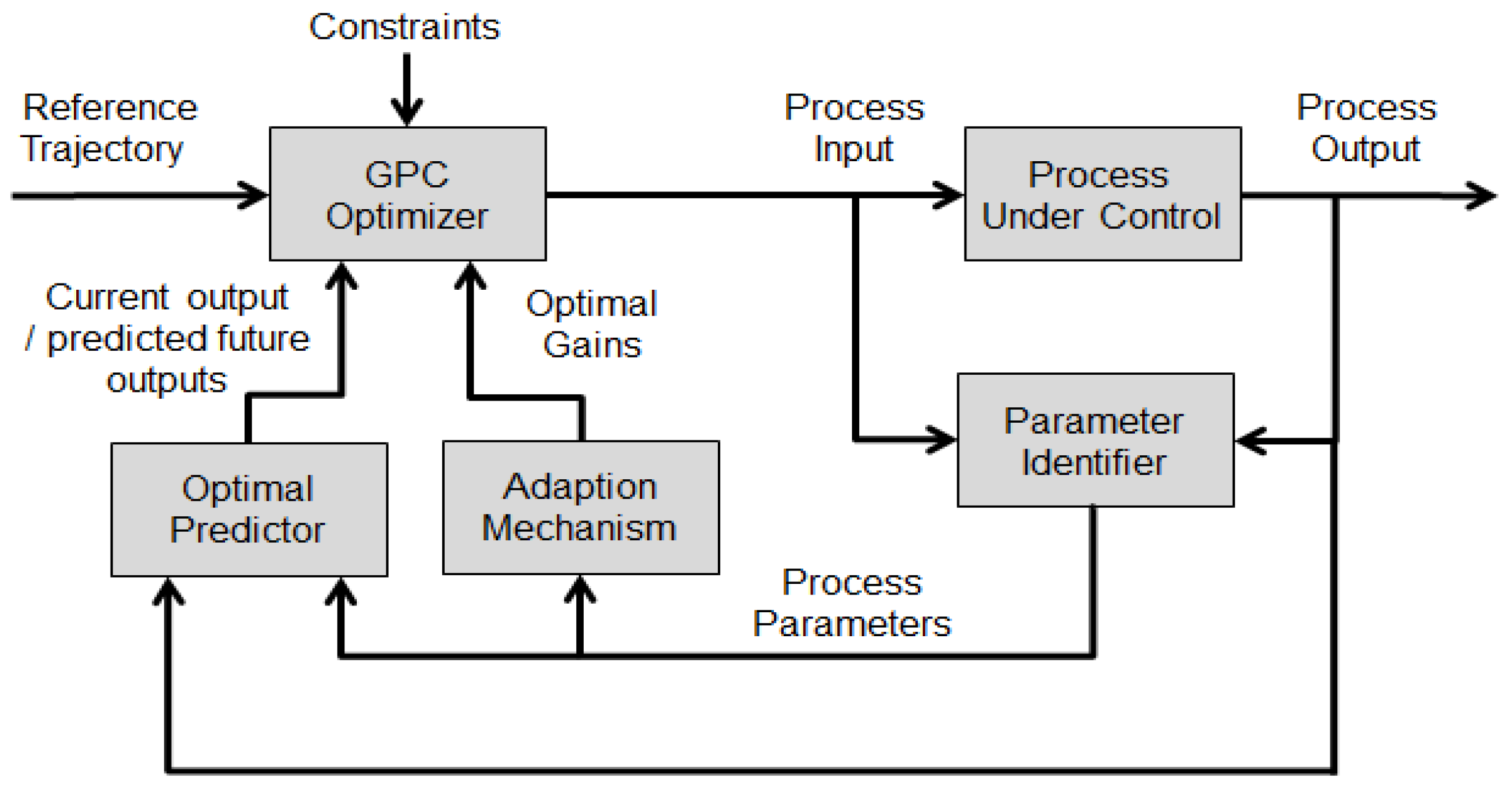
3. An Efficient Adaptive MPC Design for Microcontroller Platforms
3.1. Process Models and Identification
3.2. Constrained Model Predictive Controller
3.2.1. Short-Horizon MPC with Rate-Only Constraints
3.2.2. Short-Horizon MPC with Amplitude-Only Constraints
3.2.3. Short-Horizon GPC with Both Rate and Amplitude Constraints
3.3. Optimal Predictions
3.4. Move Suppression
3.5. Reference Trajectory Generation
4. Experimental Evaluation
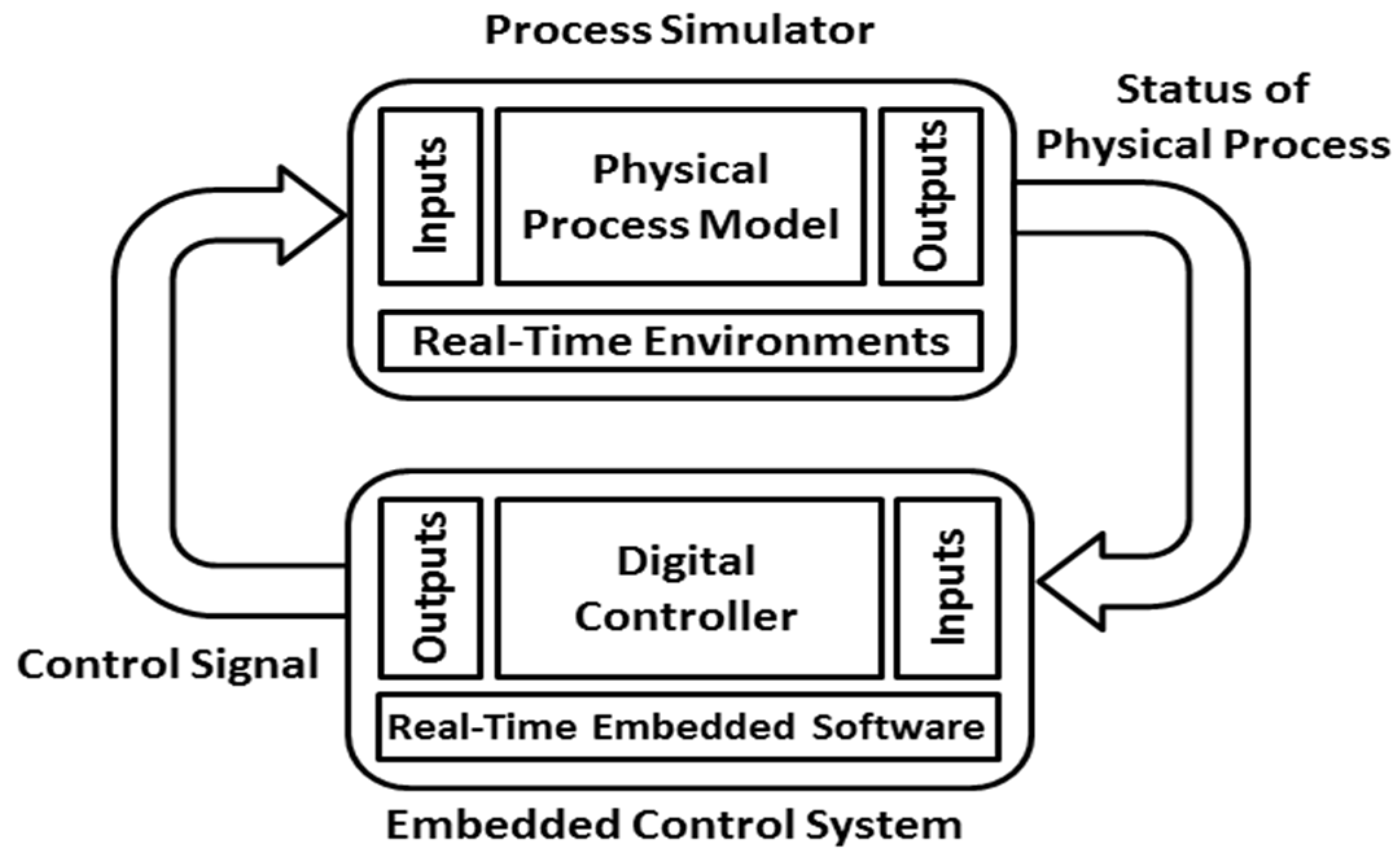
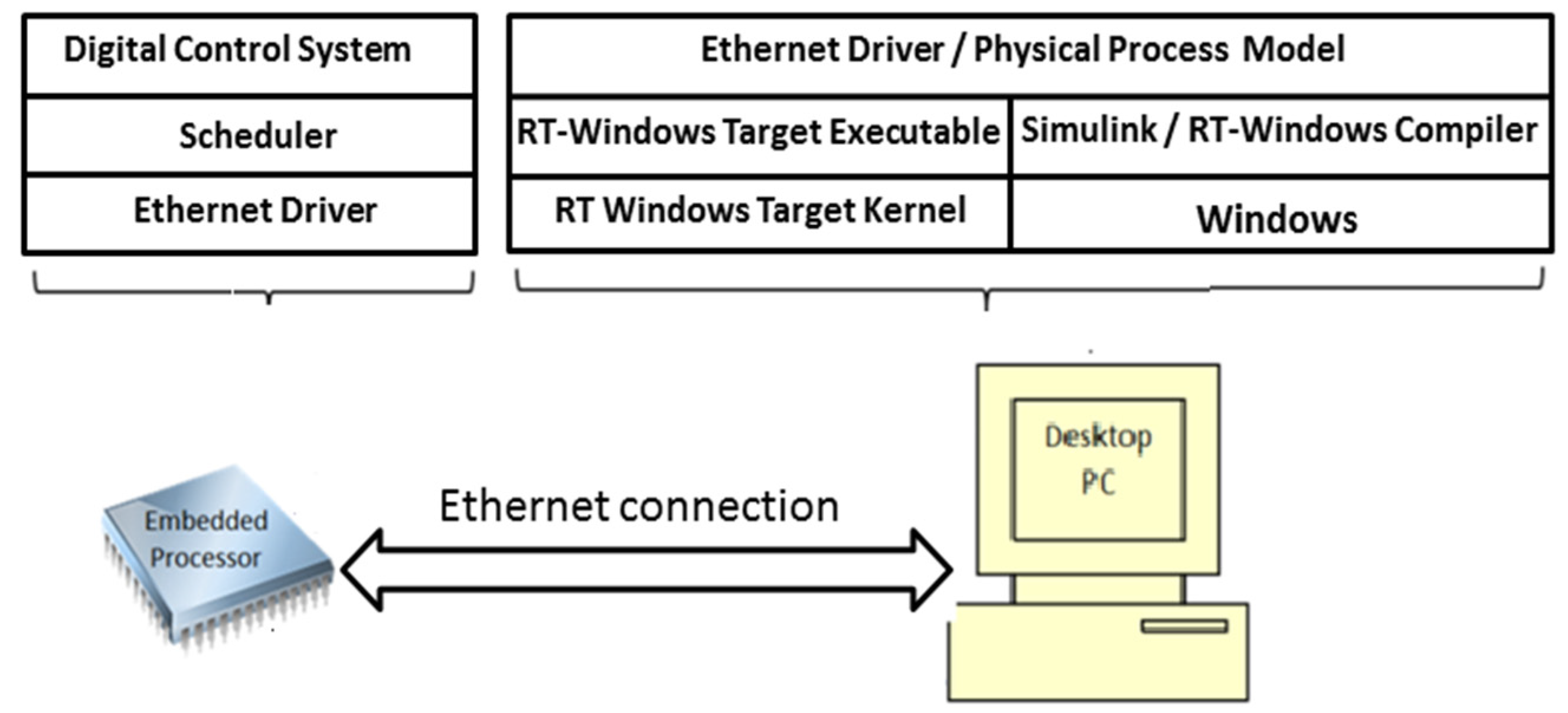
4.1. HIL Testing Facility
4.2. Experiment Design
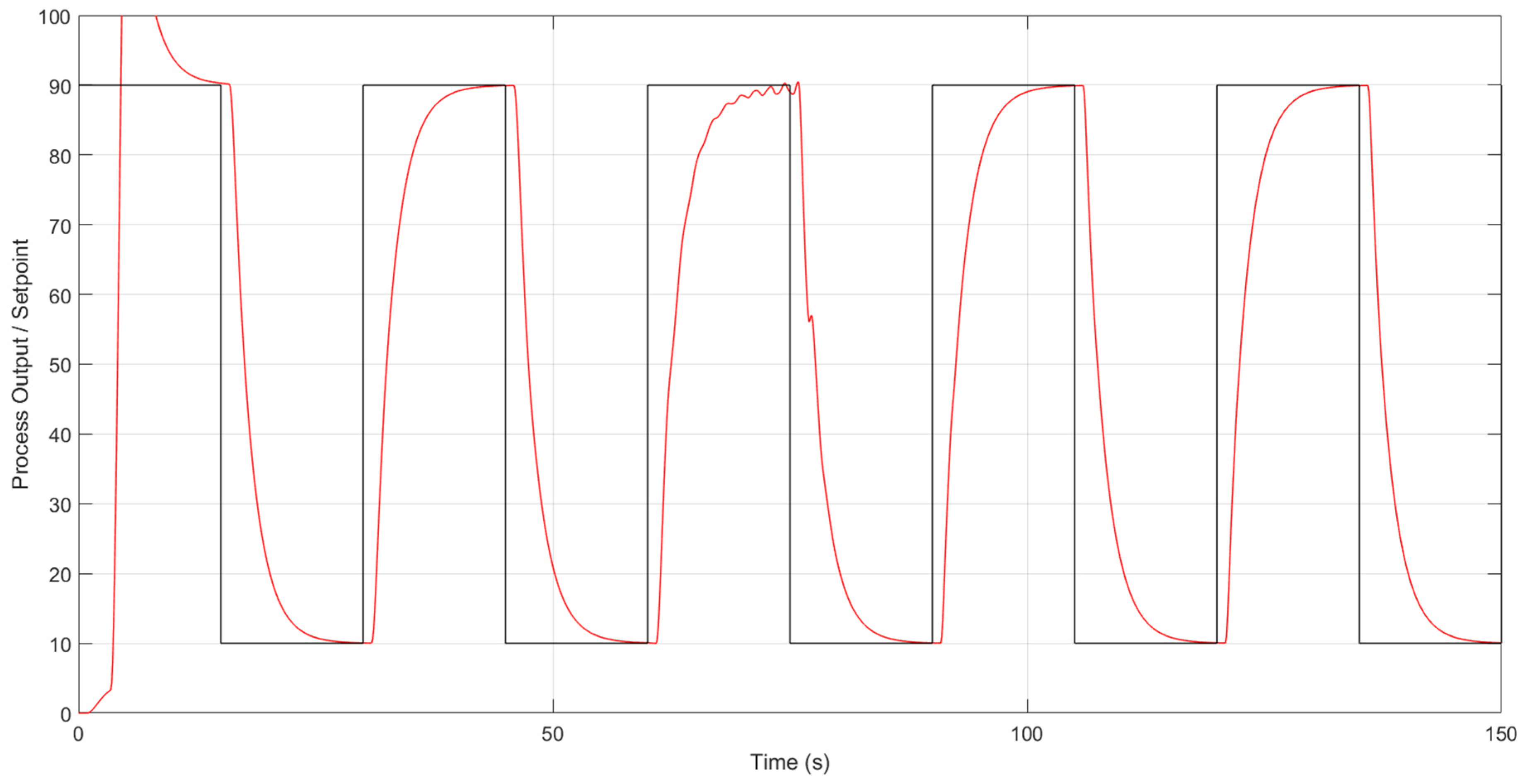
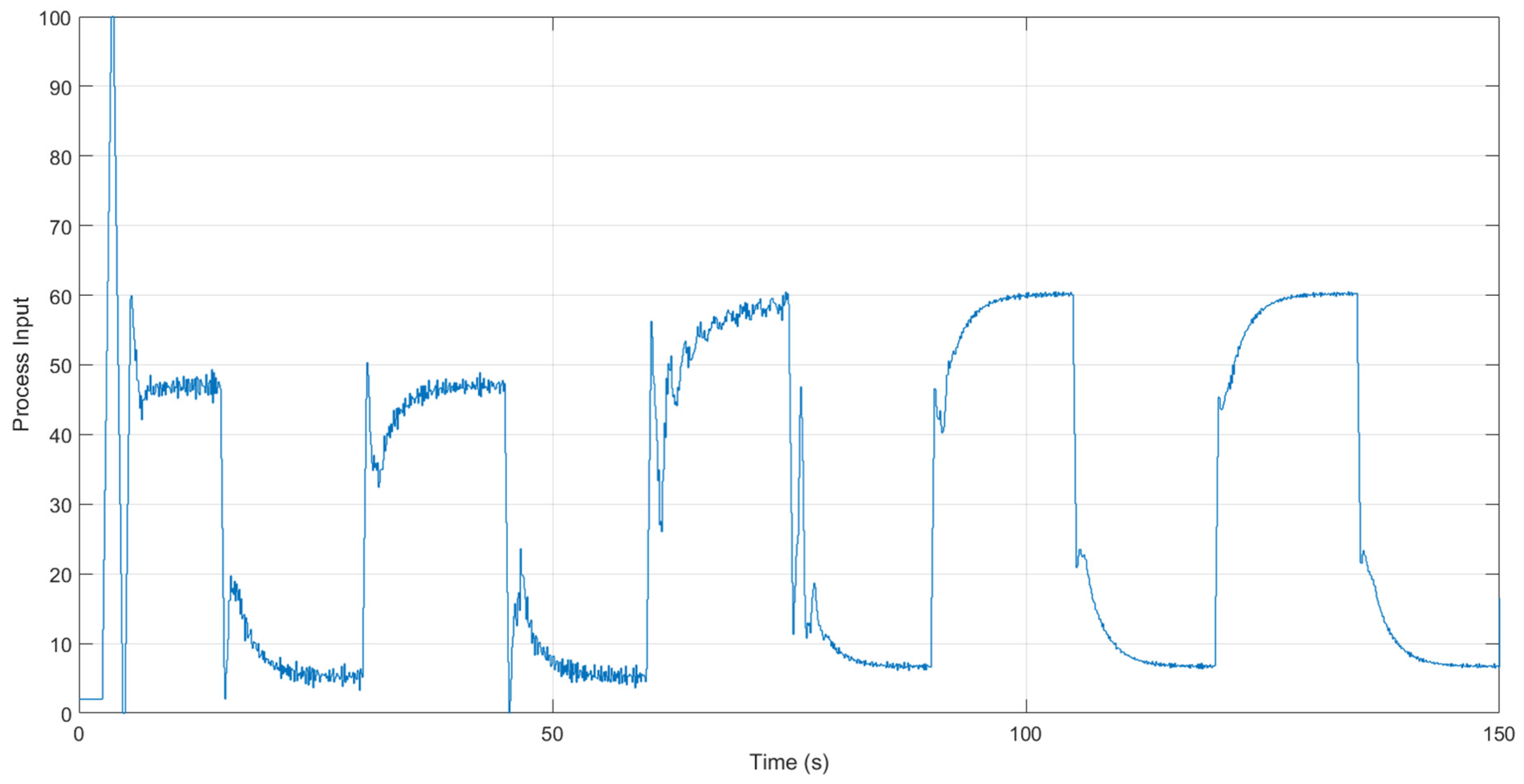
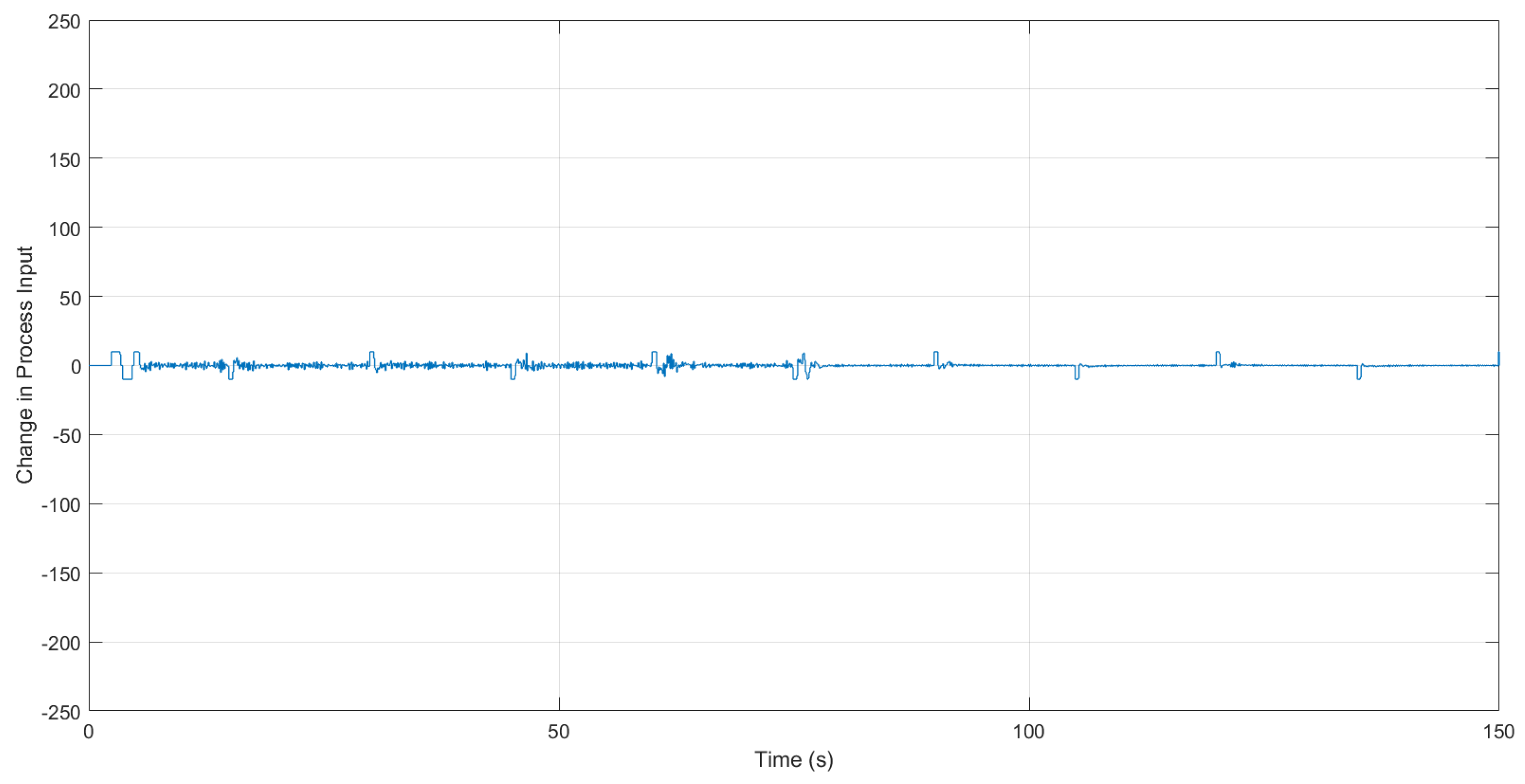
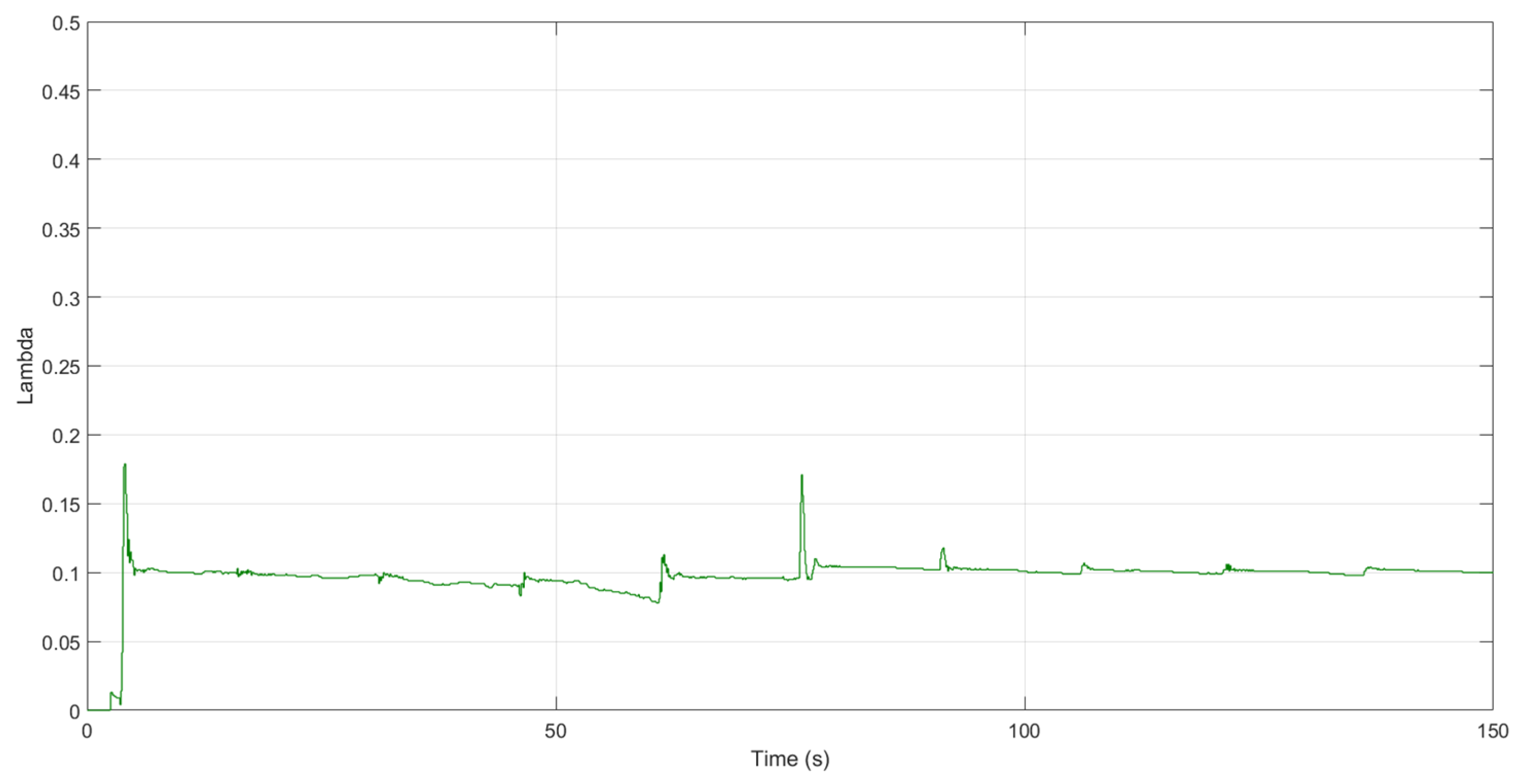
4.3. Experimental Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer-Verlag: Berlin, Germany, 2003. [Google Scholar]
- Morari, M.; Lee, J.H. Model predictive control: past, present and future. Comput. Chem. Eng. 1999, 23, 667–682. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized Predictive Control—Parts I & II. Automatica 1997, 23, 137–160. [Google Scholar]
- Astrom, K.J.; Wittenmark, B. Adaptive Control, 2nd ed.; Addison-Wesley Publishing: Boston, MA, USA, 1995. [Google Scholar]
- Saffer, D.R., II; Doyle, F.J., III. Analysis of linear programming in model predictive control. Comput. Chem. Eng. 2004, 28, 2749–2763. [Google Scholar] [CrossRef]
- Short, M. A simplified approach to Multivariable Model Predictive Control. Int. J. Eng. Technol. Innov. 2015, 5, 19–32. [Google Scholar]
- Short, M. Move Suppression Calculations for Well-Conditioned MPC. ISA Trans. 2017, 67, 371–381. [Google Scholar] [CrossRef] [PubMed]
- Garriga, J.L.; Soroush, M. Model Predictive Control Tuning Methods: A Review. Ind. Eng. Chemisty Res. 2010, 49, 3505–3515. [Google Scholar] [CrossRef]
- Marjanovik, O.; Lennox, B.; Goulding, P.; Sandoz, D. Minimising conservatism in infinite-horizon LQR control. Syst. Control Lett. 2002, 46, 271–279. [Google Scholar] [CrossRef]
- Mare, J.B.; De Dona, J.A. Solution of the input-constrained LQR problem using dynamic programming. Syst. Control Lett. 2006, 56, 342–348. [Google Scholar] [CrossRef]
- Pannocchi, G.; Laachi, N.; Rawlings, J.B. A Fast, Easily Tuned SISO Model Predictive Controller. In Proceedings of the 7th IFAC Symposium on Dynamics and Control of Process Systems 2004 (DYCOPS -7), Cambridge, MA, USA, 5–7 July 2014; pp. 907–912. [Google Scholar]
- Mare, J.B.; De Dona, J.A. Elucidation of the state-space regions wherein model predictive control and anti-windup strategies achieve identical control policies. In Proceedings of the American Control Conference, Chicago, IL, USA, 28–30 June 2000; pp. 1924–1928. [Google Scholar]
- Short, M. Real-Time Infinite Horizon Adaptive/Predictive Control for Smart Home HVAC Applications. In Proceedings of the 17th IEEE International Conference on Emerging Technology Factory Automation, Krakow, Poland, 17–21 September 2012. [Google Scholar]
- Camacho, E.F. Constrained Generalized Predictive Control. IEEE Trans. Autom. Control 1993, 38, 327–332. [Google Scholar] [CrossRef]
- Tsang, T.T.C.; Clarke, D.W. Generalized predictive control with input constraints. IEE Proc. Part D Control Theory Appl. 1988, 135, 451–460. [Google Scholar] [CrossRef]
- Kheriji Abbes, A.; Bouani, F.; Ksouri, M. A Microcontroller Implementation of Constrained Model Predictive Control. World Acad. Sci. Eng. Technol. 2011, 5, 655–662. [Google Scholar]
- Huyck, B.; Brabanter, J.D.; Moor, B.D.; Van Impe, J.F.; Logist, F. Online model predictive control of industrial processes using low-level control hardware: A pilot-scale distillation column case study. Control Eng. Pract. 2014, 28, 34–48. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Tuffs, P.S.; Clarke, D.W. Self-tuning control of offset: a unified approach. IEE Proc. 1985, 132, 100–110. [Google Scholar] [CrossRef]
- Abugchem, F.; Short, M.; Xu, D. A Test Facility for Experimental HIL Analysis of Industrial Embedded Control Systems. In Proceedings of the 17th IEEE International Conference on Emerging Technologies Factory Automation (ETFA), Krakow, Poland, 17–21 September 2012. [Google Scholar]
- Sun, Y.P. The Development of a Hardware-in-the-Loop Simulation System for Unmanned Aerial Vehicle Autopilot Design Using LabVIEW. In Practical Applications and Solutions Using LabVIEW™ Software; Dr., Silviu, F., Ed.; InTech: Vienna, Austria, 2011. [Google Scholar]
- Bacic, M. On hardware-in-the-loop simulation. In Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference, Seville, Spain, 12–15 December 2005; pp. 3194–3198. [Google Scholar]
- Short, M.; Pont, M.; Fang, J. Assessment of performance and dependability in embedded control systems: methodology and case study. Control Eng. Pract. 2008, 16, 1293–1307. [Google Scholar] [CrossRef]
- Lu, B.; Wu, X.; Figueroa, H.; Monti, A. A Low-Cost Real-Time Hardware-in-the-Loop Testing Approach of Power Electronics Controls. IEEE Trans. Ind. Electron. 2007, 54, 919–931. [Google Scholar] [CrossRef]
- Skjetne, R.; Egeland, O. Hardware-in-the-loop testing of marine control system. Model. Ident. Control 2006, 27, 239–258. [Google Scholar] [CrossRef]

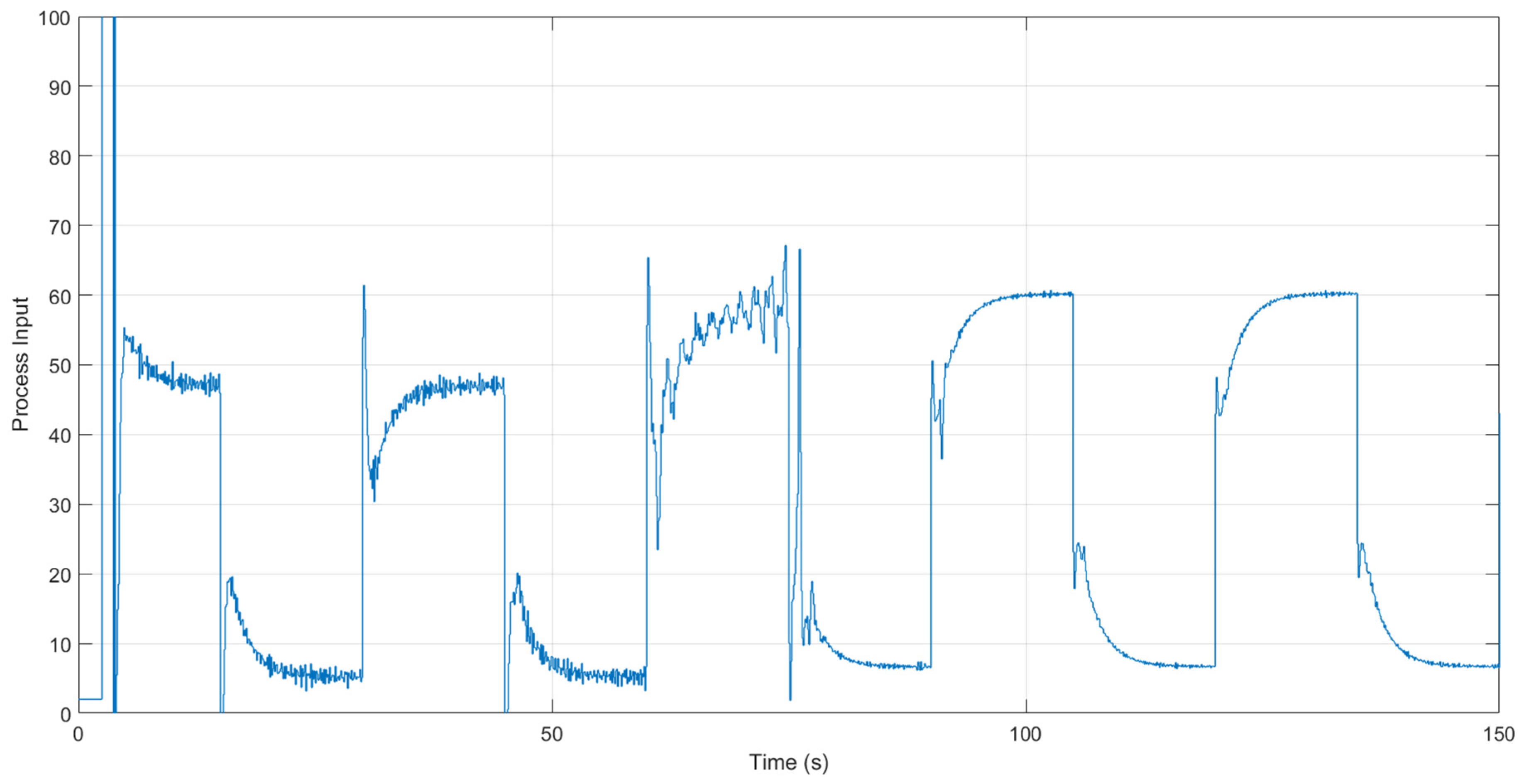
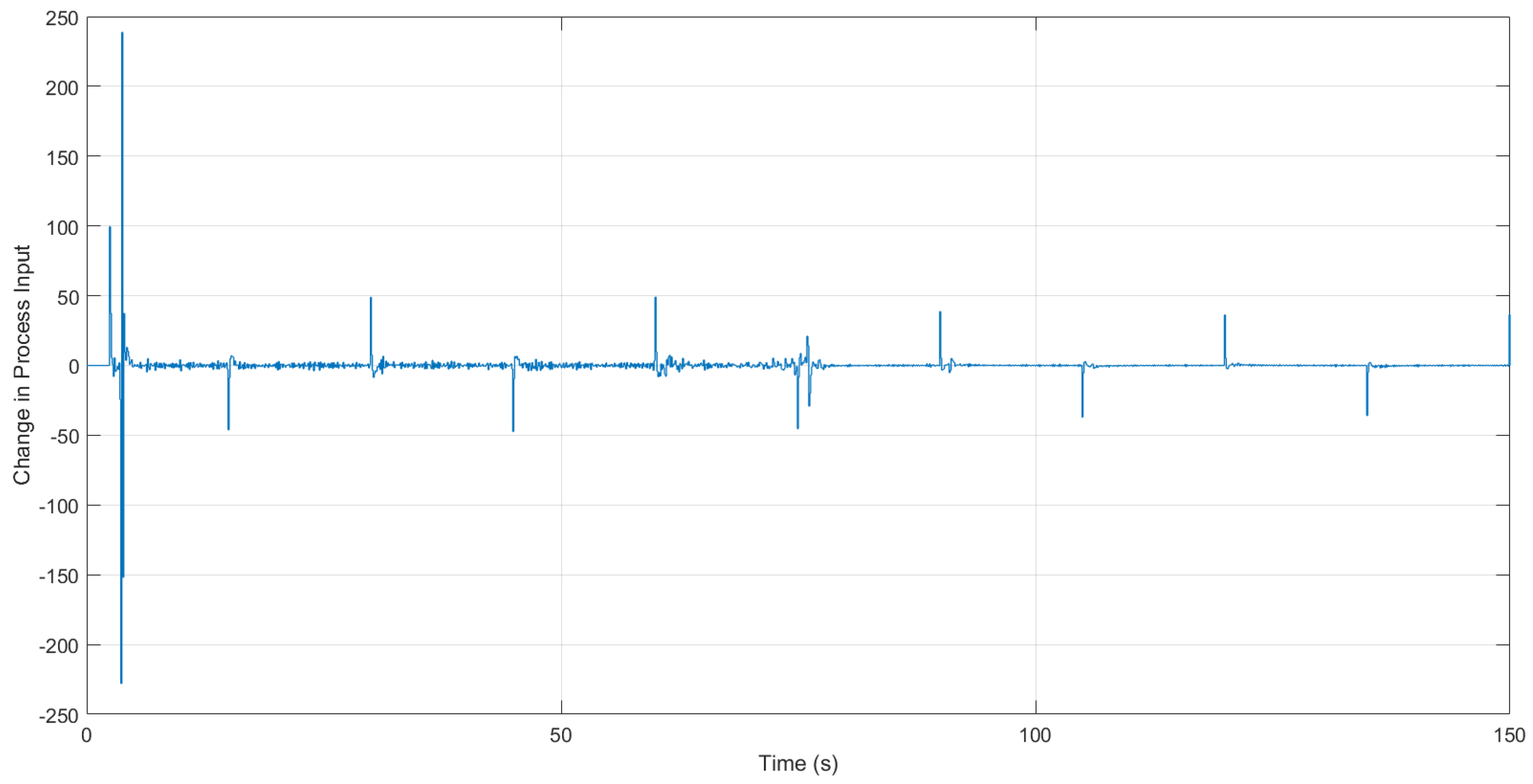
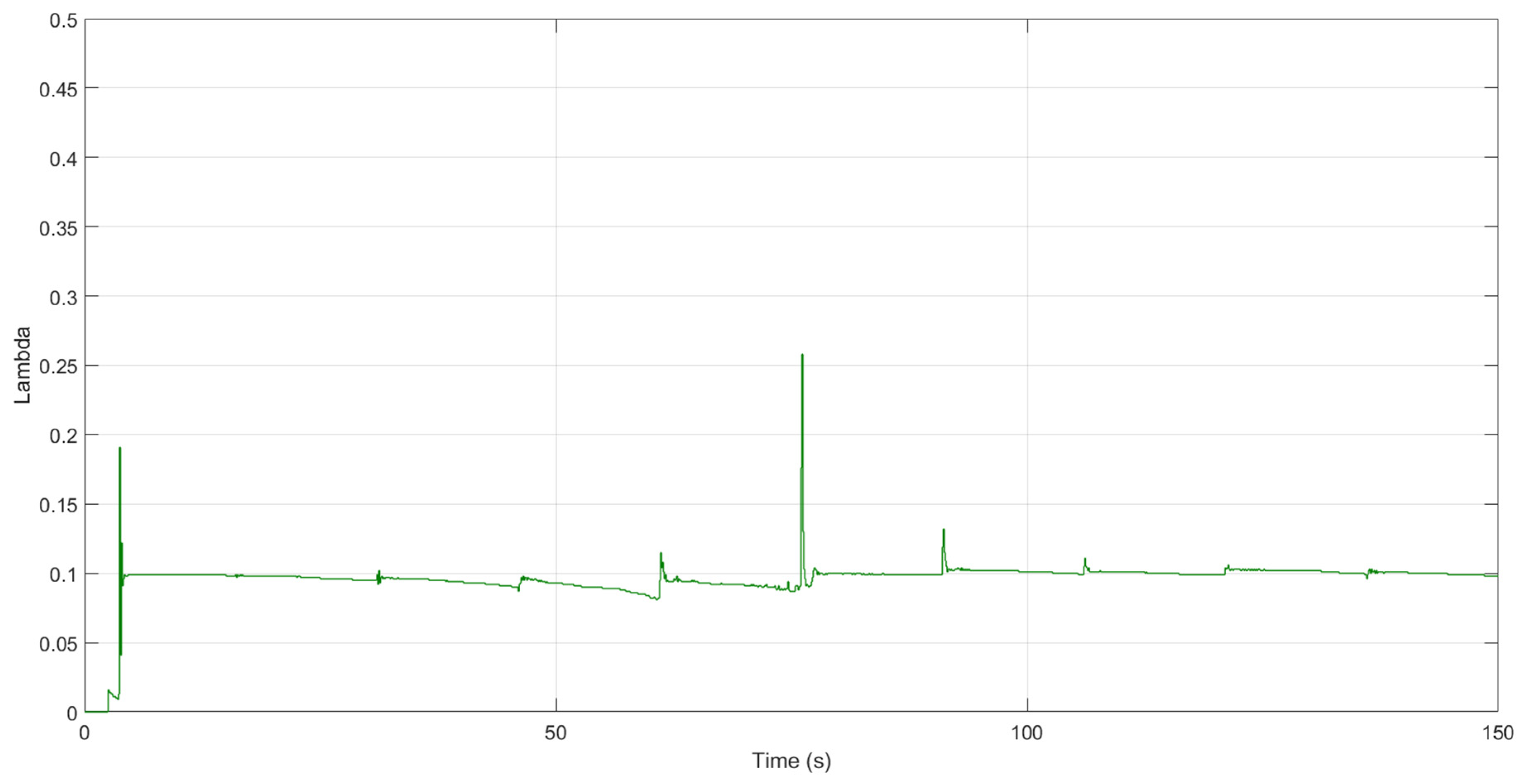
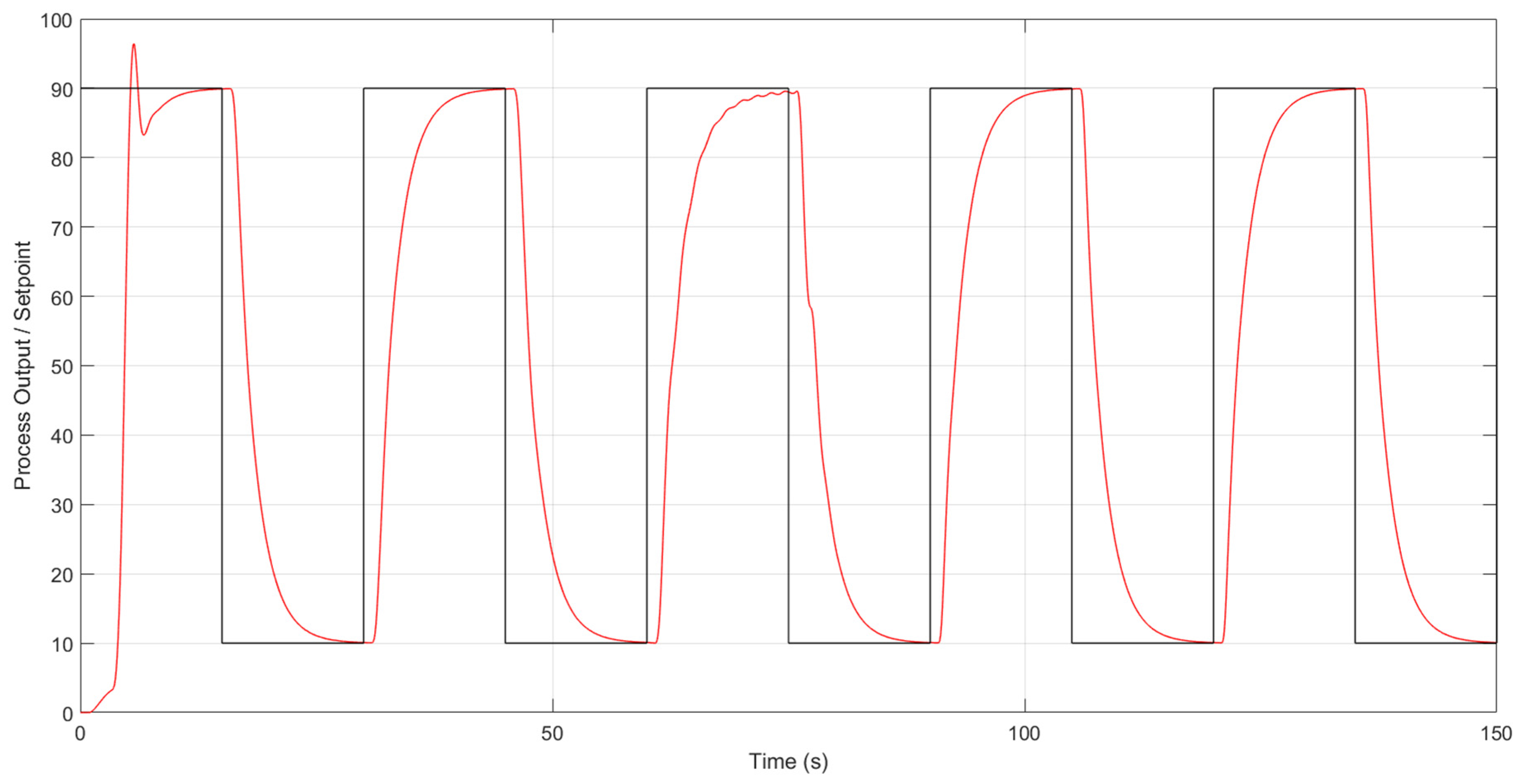
| Parameter | Initial Value | Final Value |
|---|---|---|
| K | 2 | 1.5 |
| ωn | 2 | 1.75 |
| ζ | 0.75 | 1.25 |
| θ | 1 | 0.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Short, M.; Abugchem, F. A Microcontroller-Based Adaptive Model Predictive Control Platform for Process Control Applications. Electronics 2017, 6, 88. https://doi.org/10.3390/electronics6040088
Short M, Abugchem F. A Microcontroller-Based Adaptive Model Predictive Control Platform for Process Control Applications. Electronics. 2017; 6(4):88. https://doi.org/10.3390/electronics6040088
Chicago/Turabian StyleShort, Michael, and Fathi Abugchem. 2017. "A Microcontroller-Based Adaptive Model Predictive Control Platform for Process Control Applications" Electronics 6, no. 4: 88. https://doi.org/10.3390/electronics6040088
APA StyleShort, M., & Abugchem, F. (2017). A Microcontroller-Based Adaptive Model Predictive Control Platform for Process Control Applications. Electronics, 6(4), 88. https://doi.org/10.3390/electronics6040088






