ROBI’: A Prototype Mobile Manipulator for Agricultural Applications
Abstract
:1. Introduction
2. Design and Realization
- low cost, in order to have a research prototype that can be easily realized in multiple examples to study fleet management algorithms;
- low weight, in order to increase, as much as possible, the batteries’ discharge time and, thus, the mission length;
- simple mechanical design, so that the robot can be easily built, without requiring complex machining, from a mounting kit (and thus, easily distributed as an open source project).
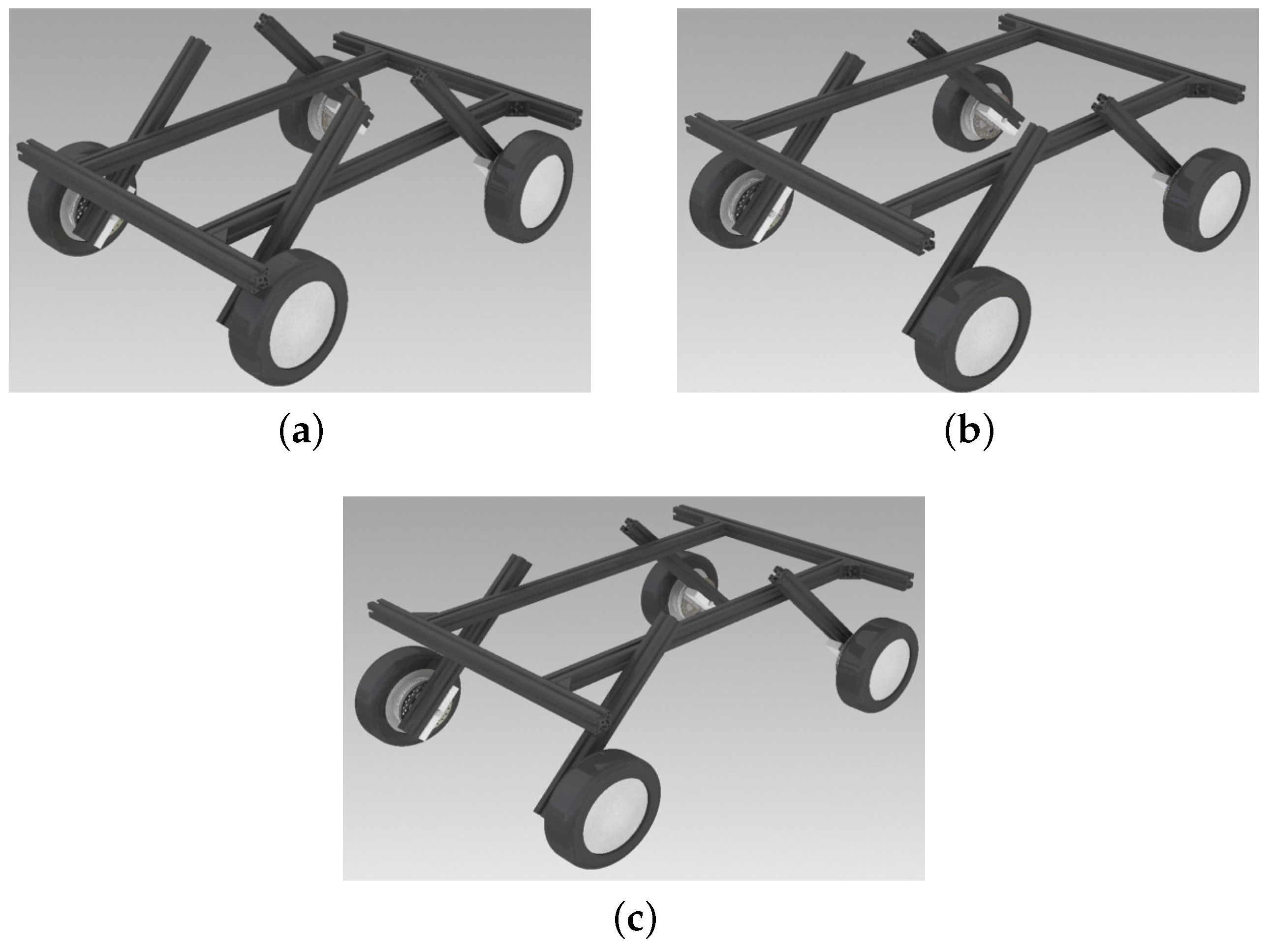
2.1. Chassis
- lightness, to reduce the amount of energy needed to drive the robot;
- flexibility, to easily adapt the robot geometrical configuration keeping the same components.
2.2. In-Wheel Motors
2.3. Power System
2.4. Robotic Arms
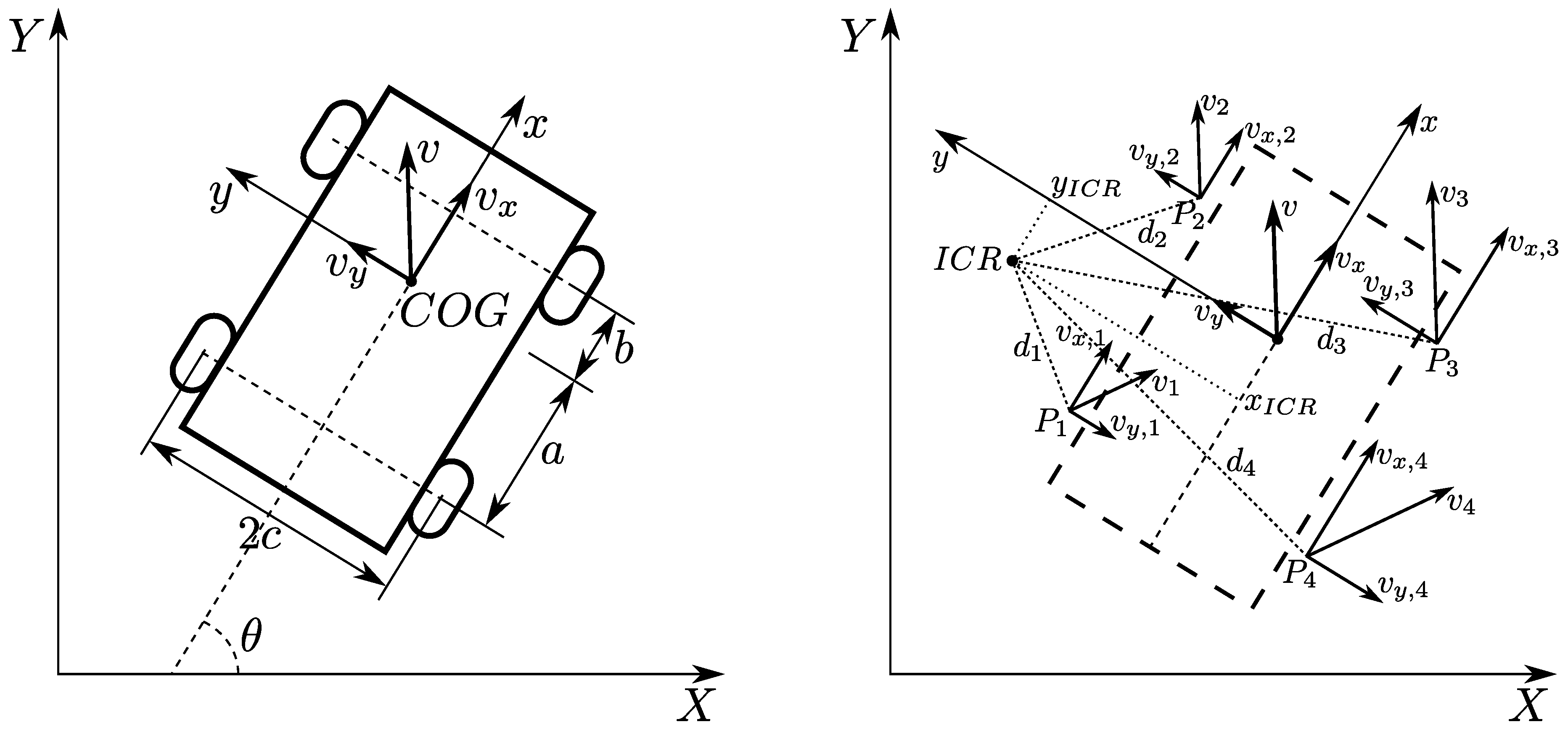
3. Modeling a Skid Steering Robot
3.1. Kinematic Model
3.2. Dynamic Model
4. Simulation Results
- standard motion control systems, based on cascaded velocity/current loops, have been designed (see Table 5 for the main characteristics);
- numerical values of the mechanical parameters required to simulate the model have been derived from the nominal values reported in Section 2 and from the CAD model;
- numerical values of the electrical parameters of the in-wheel motors have been experimentally identified, as will be described in the following part of this section;
- numerical values describing wheel-ground interaction forces have been derived from standard models [32] of motor-scooter tires (as the in-wheel motors used are usually manufactured for electric motor-scooter);
- as the design of a trajectory tracker controller is out of the scope of this work, robot trajectories used in this section have been planned using the kinematic model.
4.1. In-Wheel Motor Parameter Identification
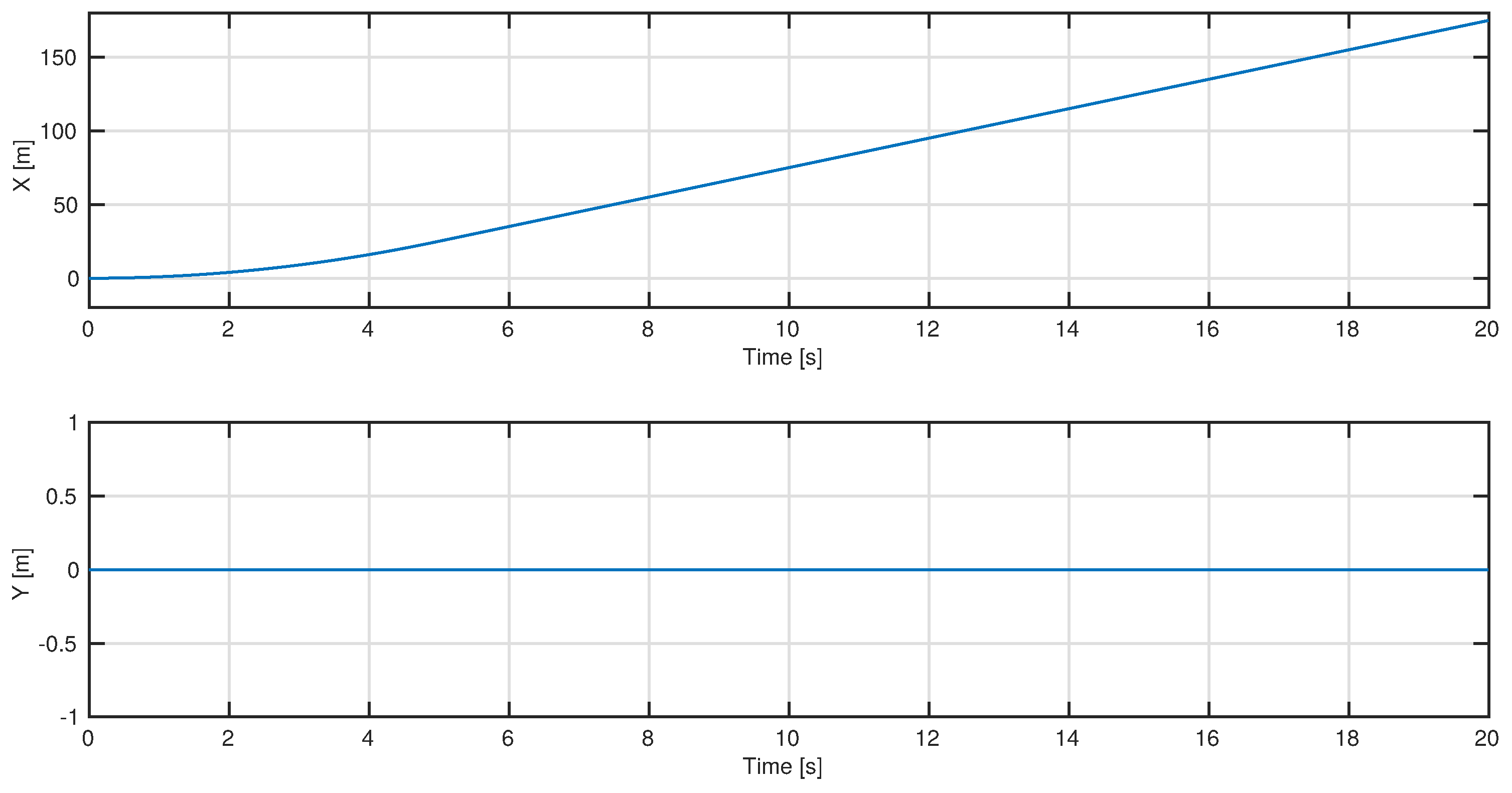
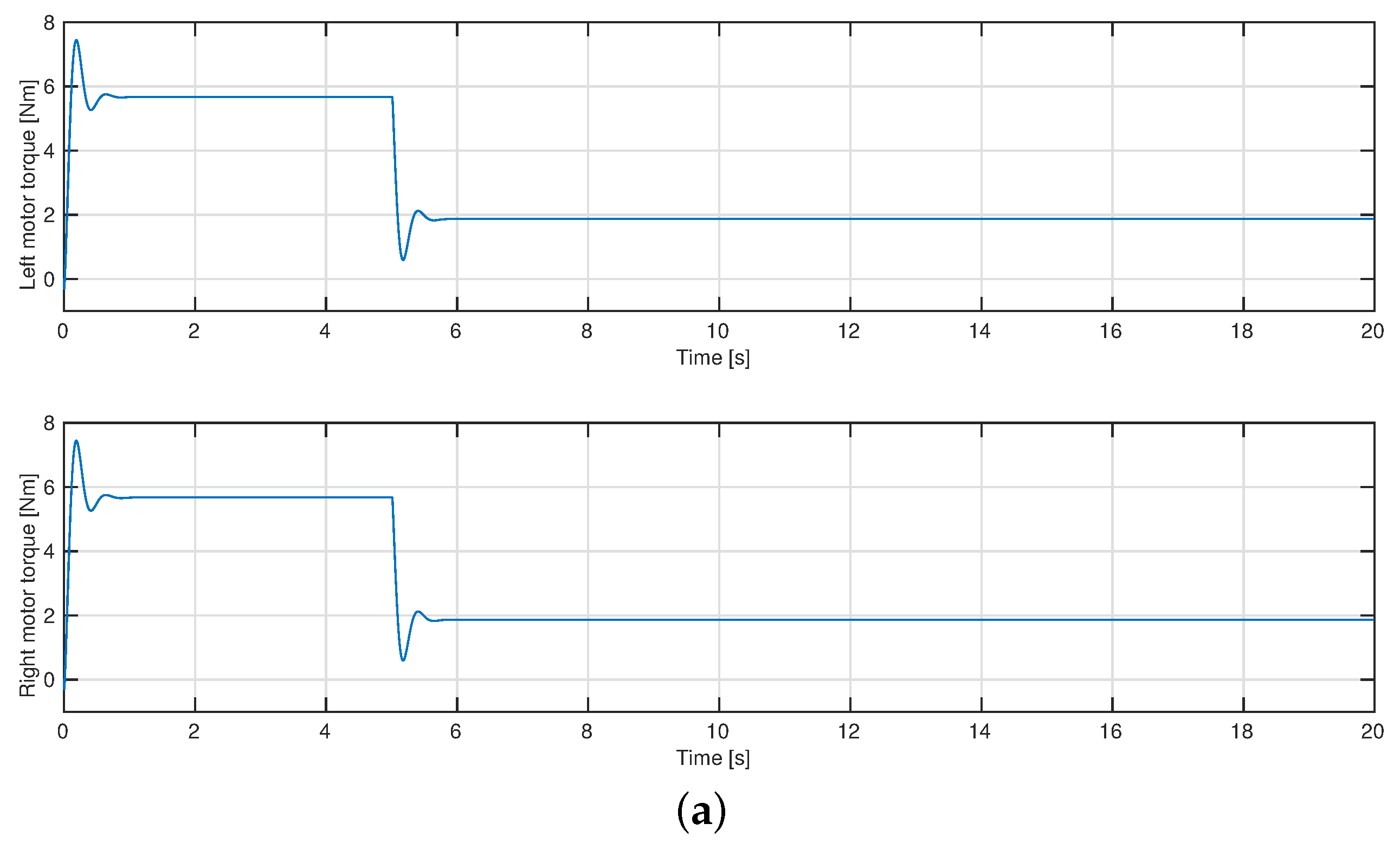
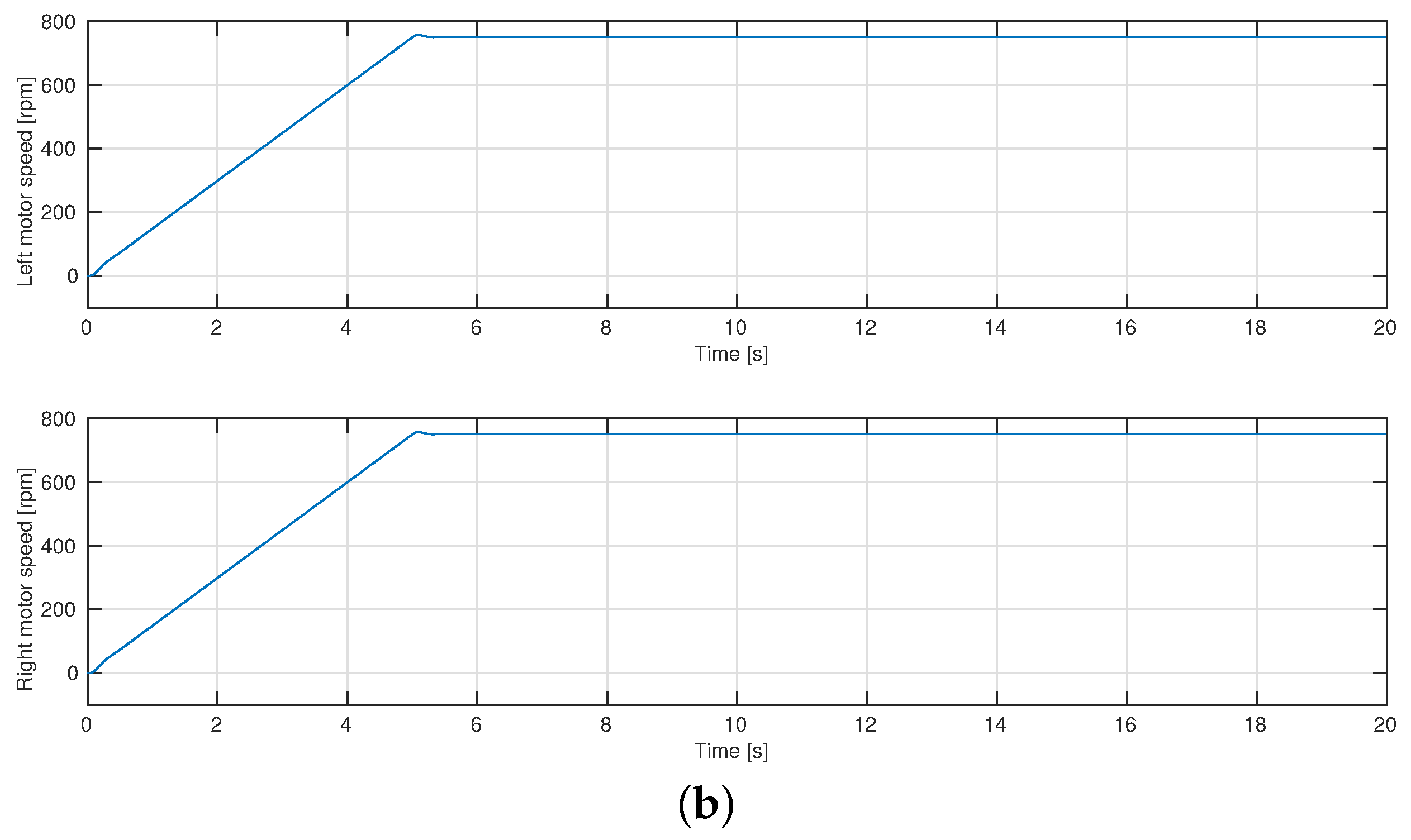
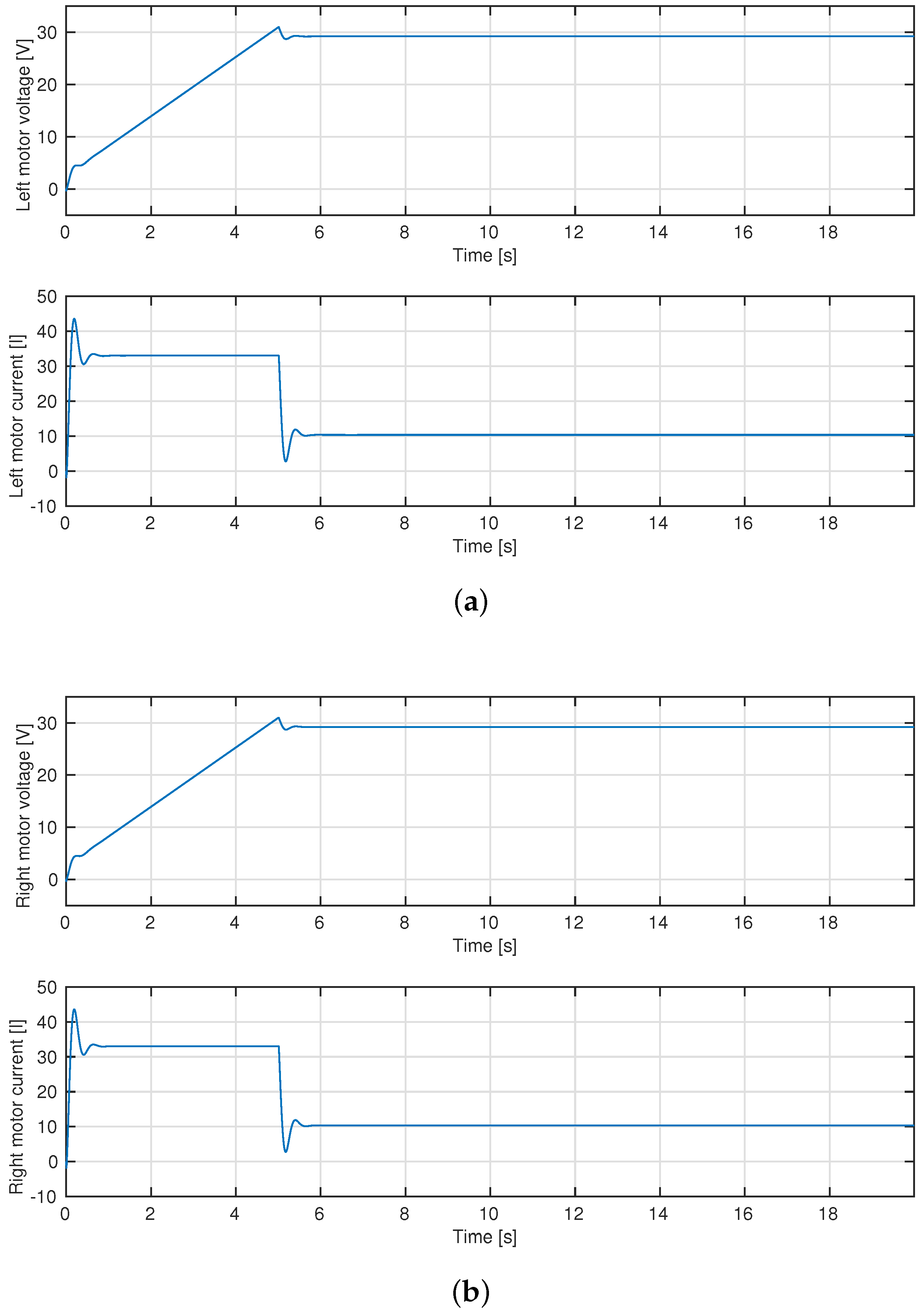
4.2. A Rectilinear Trajectory
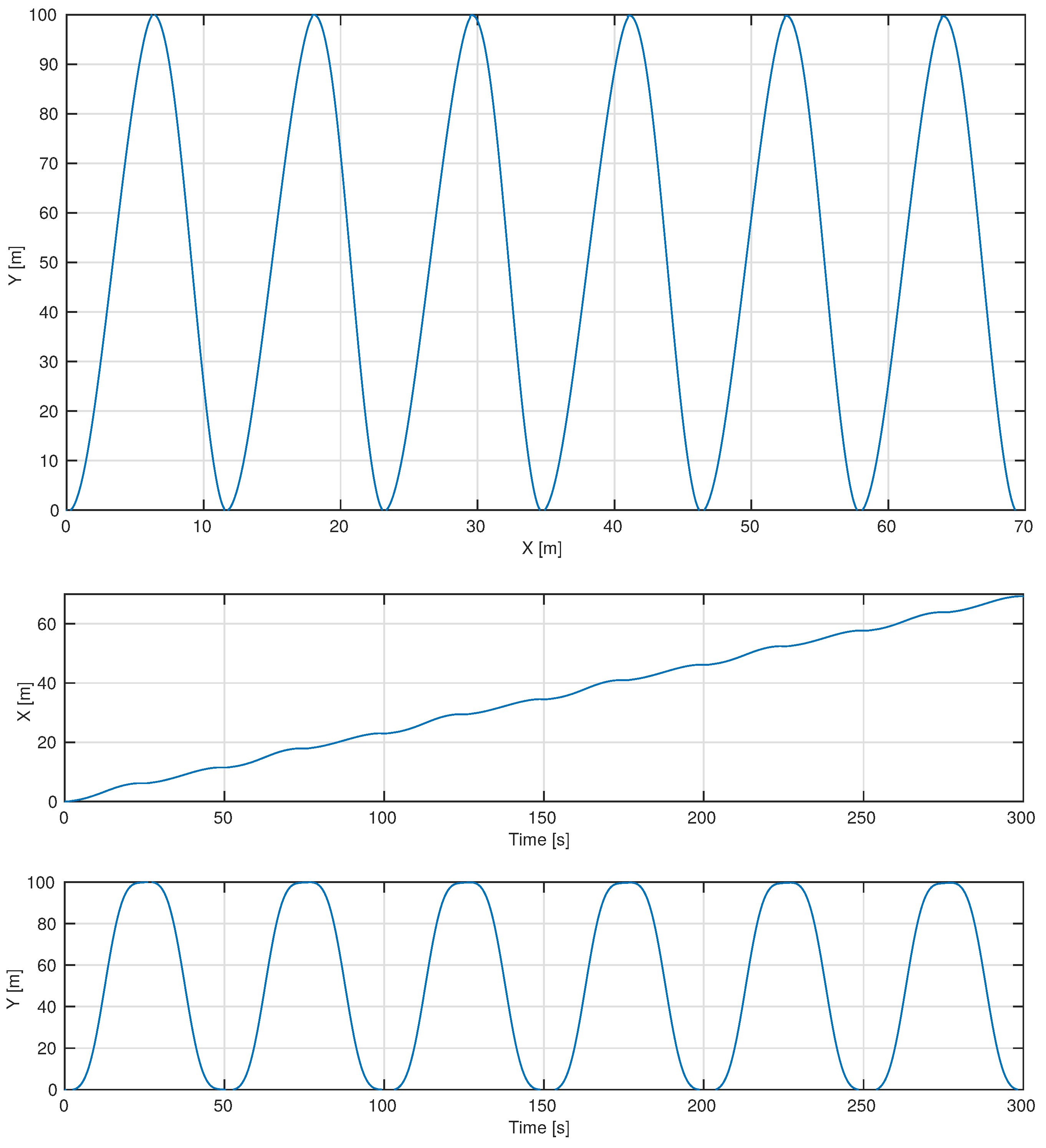
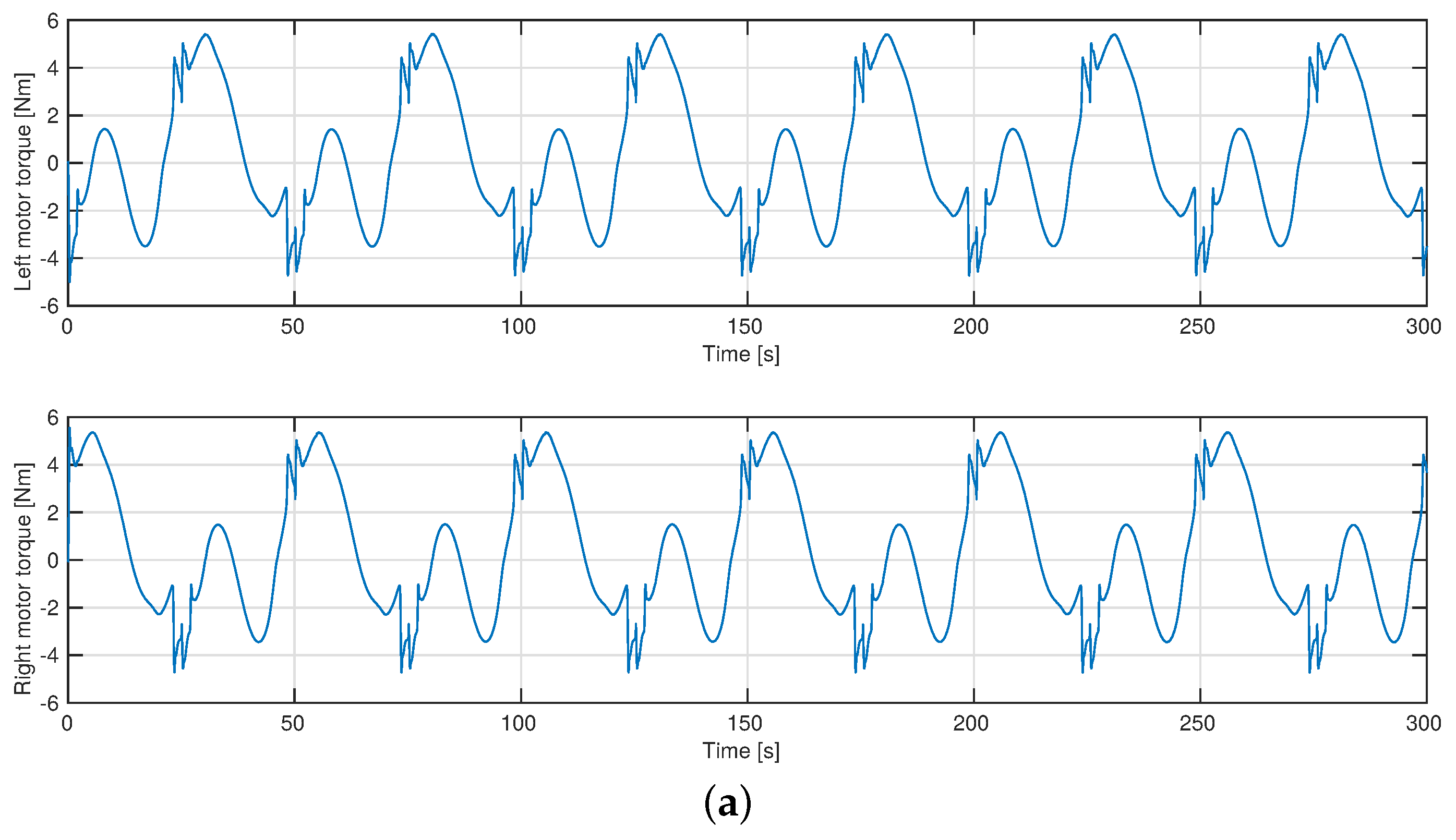
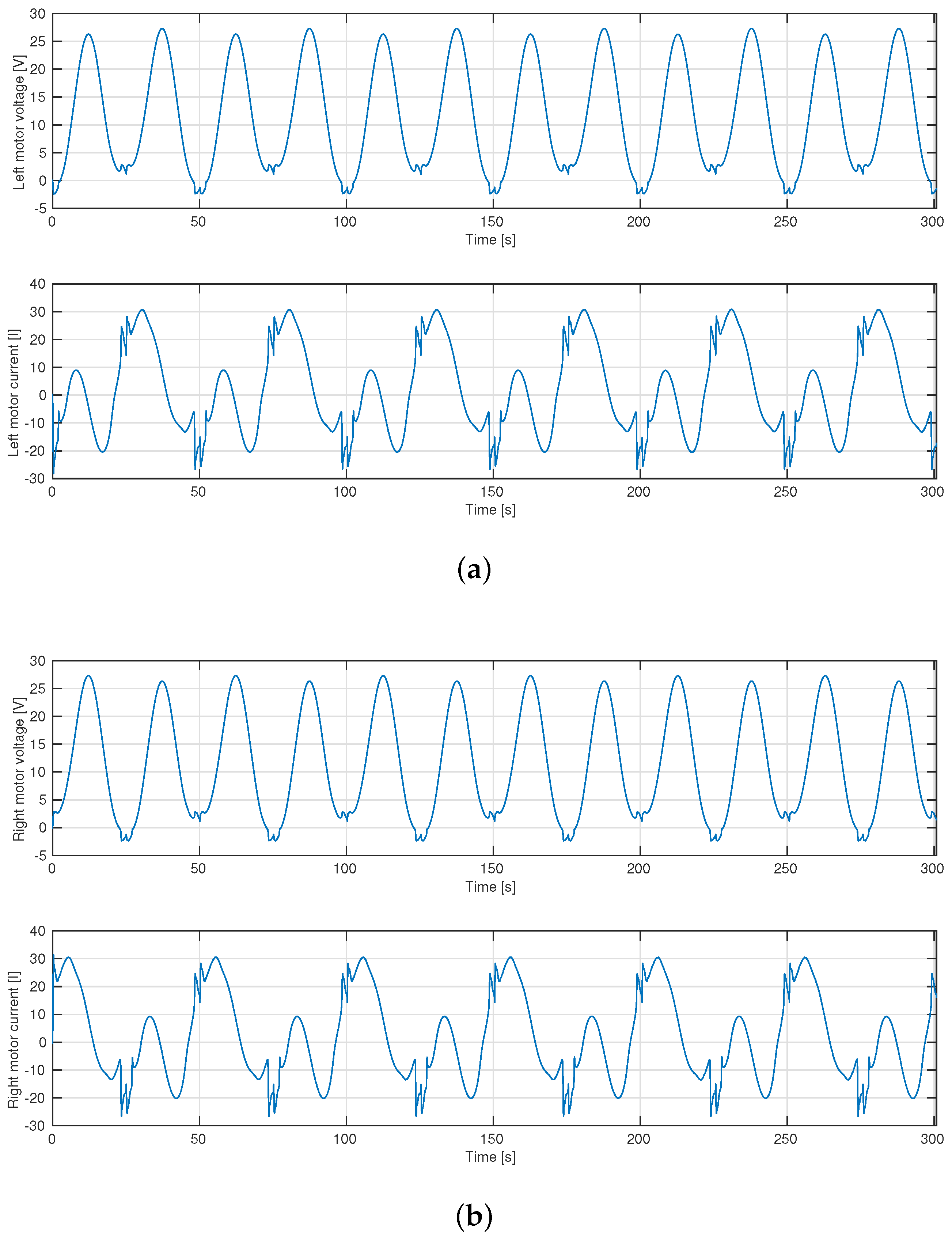
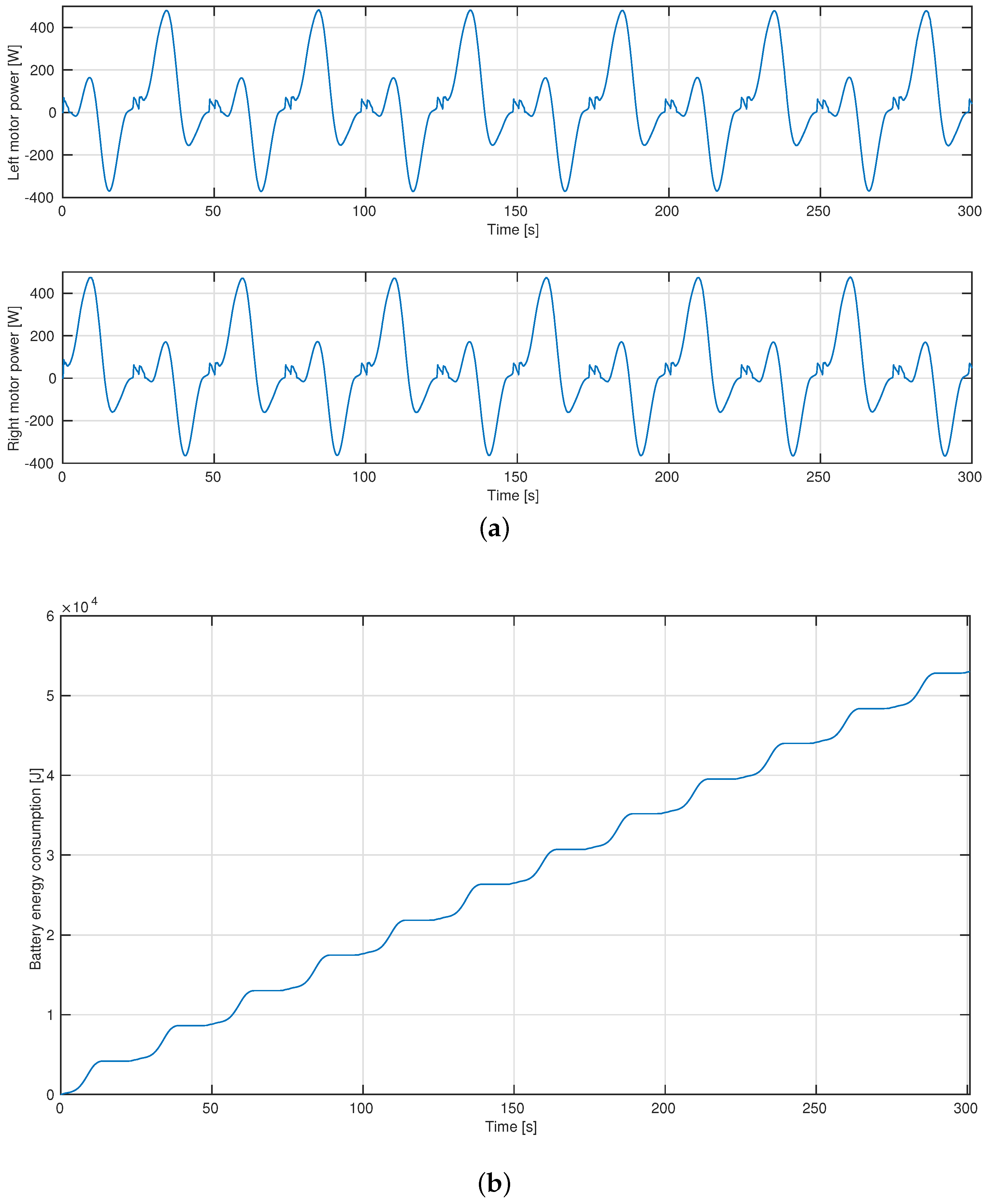
4.3. Exploring an Agricultural Field
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Herring, D. Precision Farming: Feature Articles. In NASA Earth Obs.; 29 January 2001. Available online: https://earthobservatory.nasa.gov/Features/PrecisionFarming/ (accessed on 14 March 2017).
- Cucci, D.; Matteucci, M. On the development of a generic multi-sensor fusion framework for robust odometry estimation. J. Softw. Eng. Robot. 2014, 5, 48–62. [Google Scholar]
- Cucci, D.; Matteucci, M.; Bascetta, L. Pose tracking and sensor self-calibration for an all-terrain autonomous vehicle. In IFAC-PapersOnLine, Prodceedings of 9th IFAC Symposium on Intelligent Autonomous Vehicles IAV 2016, Leipzig, Germany, 29 June—1 July 2016; Springer: Berlin/Hedelberg, Germany, 2016; Volume 49, pp. 25–31. [Google Scholar]
- Tahirović, A.; Magnani, G. General framework for mobile robot navigation using passivity-based MPC. IEEE Trans. Autom. Control 2011, 56, 184–190. [Google Scholar] [CrossRef]
- Tahirović, A.; Brkić, M.; Magnani, G.; Bascetta, L. A planner for All-Terrain Vehicles on unknown rough terrains based on the MPC paradigm and D*-like algorithm. In Proceedings of the IEEE International Conference on Robotics and Automation, Workshop on Modelling, Estimation, Perception and Control of All Terrain Mobile Robots, Hong Kong, China, 1 June 2014. [Google Scholar]
- Bascetta, L.; Cucci, D.; Matteucci, M. Kinematic trajectory tracking controller for an all-terrain Ackermannn steering vehicle. In IFAC-PapersOnLine, Prodceedings of 9th IFAC Symposium on Intelligent Autonomous Vehicles IAV 2016, Leipzig, Germany, 29 June—1 July 2016; Springer: Berlin/Hedelberg, Germany, 2016; Volume 49, pp. 13–18. [Google Scholar]
- D’Amelio, E.; Bascetta, L.; Cucci, D.; Matteucci, M.; Bardaro, G. A Modelica simulator to support the development of the control system of an autonomous All-Terrain mobile robot. In IFAC-PapersOnLine, Proceedings of the Vienna Conference on Mathematical Modelling, Vienna, Austria, 18–20 February 2015; Springer: Berlin/Hedelberg, Germany, 2015; Volume 48, pp. 274–279. [Google Scholar]
- Bardaro, G.; Cucci, D.; Bascetta, L.; Matteucci, M. A simulation based architecture for the development of an autonomous all terrain vehicle. In Proceedings of the Simulation, Modeling, and Programming for Autonomous Robots—Lecture Notes in Computer Science, Bergamo, Italy, 20–23 October 2014; pp. 74–85. [Google Scholar]
- Edan, Y.; Miles, G. Systems engineering of agricultural robot design. IEEE Trans. Syst. Man Cybern. 1994, 24, 1259–1265. [Google Scholar] [CrossRef]
- Chatzimichali, A.; Georgilas, I.; Tourassis, V. Design of an advanced prototype robot for white asparagus harvesting. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Singapore, 14–17 July 2009; pp. 887–892. [Google Scholar]
- Feng, Q.; Wang, X.; Wang, G.; Li, Z. Design and Test of Tomatoes Harvesting Robot. In Proceedings of the IEEE International Conference on Information and Automation, Lijiang, Yunnan, China, 8–10 August 2015; pp. 949–952. [Google Scholar]
- Yaguchi, H.; Nagahama, K.; Hasegawa, T.; Inaba, M. Development of an Autonomous Tomato Harvesting Robot with Rotational Plucking Gripper. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Daejeon, Korea, 9–14 Octorber 2016; pp. 652–657. [Google Scholar]
- Gonzalez-de-Santos, P.; Ribeiro, A.; Fernandez-Quintanilla, C.; Lopez-Granados, F.; Brandstoetter, M.; Tomic, S.; Pedrazzi, S.; Peruzzi, A.; Pajares, G.; Kaplanis, G.; et al. Fleets of robots for environmentally-safe pest control in agriculture. Precis. Agric. 2016, 1–41. [Google Scholar] [CrossRef]
- Grimstad, L.; Pham, C.; Phan, H.; From, P. On the design of a low-cost, light-weight, and highly versatile agricultural robot. In Proceedings of the IEEE International Workshop on Advanced Robotics and Its Social Impacts, Lyon, France, 30 June–2 July 2015. [Google Scholar]
- Roshanianfard, A.; Noguchi, N. Development of a 5DOF robotic arm (RAVebots-1) applied to heavy products harvesting. In IFAC-PapersOnLine, Proceedings of 5th IFAC Conference on Sensing, Control and Automation Technologies for Agriculture AGRICONTROL 2016, Seattle, WA, USA, 14—17 August 2016; Springer: Berlin/Hedelberg, Germany, 2016; Volume 49, pp. 155–160. [Google Scholar]
- Wang, G.; Yu, Y.; Feng, Q. Design of End-effector for Tomato Robotic Harvesting. In IFAC-PapersOnLine, Proceedings of 5th IFAC Conference on Sensing, Control and Automation Technologies for Agriculture AGRICONTROL 2016, Seattle, WA, USA, 14–17 August 2016; Springer: Berlin/Hedelberg, Germany, 2016; Volume 49, pp. 190–193. [Google Scholar]
- Levin, M.; Degani, A. Design of a Task-Based Modular Re-Configurable Agricultural Robot. In IFAC-PapersOnLine, Proceedings of 5th IFAC Conference on Sensing, Control and Automation Technologies for Agriculture AGRICONTROL 2016, Seattle, WA, USA, 14–17 August 2016; Springer: Berlin/Hedelberg, Germany, 2016; Volume 49, pp. 184–189. [Google Scholar]
- Hanhui, L.; Ken, C.; Huazhou, C.; Zhaofeng, Z. Optimization design of fruit picking end-effector based on its grasping model. INMATEH-Agric. Eng. 2014, 47, 81–90. [Google Scholar]
- Ryoo, Y.J.; Lee, K.N.; Choi, P.G. Intelligent Platform Design of Agricultural Robot Inspired by Farmer Assistance (AGRIFA). In Proceedings of the Joint International Conference on Soft Computing and Intelligent Systems, and International Symposium on Advanced Intelligent Systems, Kobe, Japan, 20–24 November 2012; pp. 2037–2039. [Google Scholar]
- Corpe, S.; Tang, L.; Abplanalp, P. GPS-Guided Modular Design Mobile Robot Platform for Agricultural Applications. In Proceedings of the 7th International Conference on Sensing Technology, Wellington, New Zealand, 3–5 December 2013; pp. 806–810. [Google Scholar]
- Durmuş, H.; Güneş, E.; Kirci, M.; Üstündağ, B. The design of general purpose autonomous agricultural mobile-robot: “AGROBOT”. In Proceedings of the International Conference on Agro-Geoinformatics (Agro-geoinformatics), Istanbul, Turkey, 20–24 July 2015. [Google Scholar]
- Ko, M.; Ryuh, B.S.; Kim, K.; Suprem, A.; Mahalik, N. Autonomous Greenhouse Mobile Robot Driving Strategies From System Integration Perspective: Review and Application. IEEE/ASME Trans. Mechatron. 2015, 20, 1705–1716. [Google Scholar] [CrossRef]
- Hassan, M.; Ullah, M.; Iqbal, J. Towards autonomy in agriculture: Design and prototyping of a robotic vehicle with seed selector. In Proceedings of the International Conference on Robotics and Artificial Intelligence, Rawalpindi, Pakistan, 1–2 November 2016; pp. 37–44. [Google Scholar]
- Bechar, A.; Vigneault, C. Agricultural robots for field operations: Concepts and components. Biosyst. Eng. 2016, 149, 94–111. [Google Scholar] [CrossRef]
- Bechar, A.; Vigneault, C. Agricultural robots for field operations. Part 2: Operations and systems. Biosyst. Eng. 2017, 153, 110–128. [Google Scholar] [CrossRef]
- Bloch, V.; Bechar, A.; Degani, A. Development of an environment characterization methodology for optimal design of an agricultural robot. Ind. Robot Int. J. 2017, 44, 94–103. [Google Scholar] [CrossRef]
- Bogue, R. Robots poised to revolutionise agriculture. Ind. Robot Int. J. 2016, 43, 450–456. [Google Scholar] [CrossRef]
- ISO 17396:2014: Synchronous Belt Drives—Metric Pitch, Trapezoidal Profile Systems T and AT, Belts and Pulleys; Technical Report; International Organization for Standardization: Geneva, Switzerland, January 2014.
- VESC—Open Source ESC. Available online: http://vedder.se/2015/01/vesc-open-source-esc (accessed on 14 January 2017).
- Cook, G. Mobile Robots: Navigation, Control and Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pacejka, H. The magic formula tire model. Veh. Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]






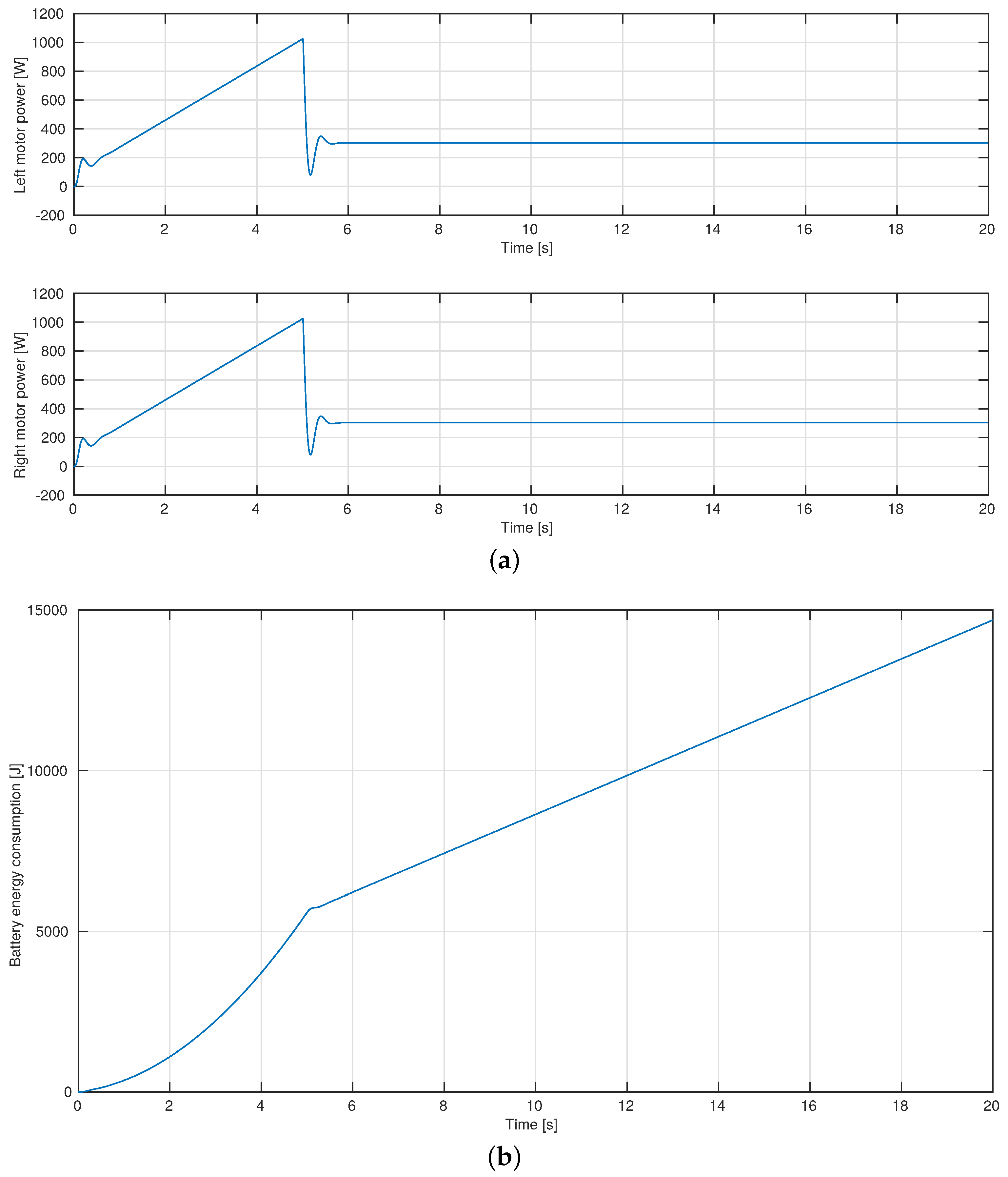


| Ground clearance | |
| Track | |
| Wheelbase |
| Motor mass | kg |
| Motor and tire mass | kg |
| Power | 500 |
| Voltage | 36 |
| Maximum speed | 1350 |
| Maximum operating voltage | 36 |
| Tire diameter | 10 |
| Manufacturer | FIAM |
| Model | |
| Type | sealed lead acid |
| Voltage | |
| Capacity |
| Joint | Servomotor Model | Nominal Torque () |
|---|---|---|
| 0 | MX/RX-64 | 7.3 |
| 1 | MX/RX-28 | 3.1 |
| 2 | MX/RX-64 | 7.3 |
| 3 | MX/RX-64 dual axis | 14.6 |
| 4 | AX12A | 1.5 |
| 5 | AX18A | 1.8 |
| Rise Time ms | Settling Time ms | Overshoot % | |
|---|---|---|---|
| Current loop | 1.0 | 6.0 | 11.10 |
| Speed loop | 9.4 | 93.4 | 6.97 |
| Frequency Hz | Voltage V | Vs/rad | Speed rpm | V/rpm | Magnetic Flux Wb |
|---|---|---|---|---|---|
| 10.076 | 2.284 | 0.3608 | 60.456 | 0.0378 | 0.0208 |
| 20.515 | 4.655 | 0.3611 | 123.09 | 0.0378 | 0.0209 |
| 30.717 | 6.965 | 0.3609 | 184.302 | 0.0378 | 0.0208 |
| 40.839 | 9.256 | 0.3607 | 245.034 | 0.0378 | 0.0208 |
| 51.598 | 11.689 | 0.3605 | 309.588 | 0.0378 | 0.0208 |
| 61.991 | 14.036 | 0.3604 | 371.946 | 0.0377 | 0.0208 |
| 72.559 | 16.426 | 0.3603 | 435.354 | 0.0377 | 0.0208 |
| 83.063 | 18.774 | 0.3597 | 498.378 | 0.0377 | 0.0208 |
| 93.679 | 21.164 | 0.3596 | 562.074 | 0.0377 | 0.0208 |
| Frequency Hz | Current Arms | Voltage Vrms | Back-EMF V | Ω | mH | Ω | mH |
|---|---|---|---|---|---|---|---|
| 14.424 | 3.27 | 1.62 | 1.88 | 0.495 | 0.137 | 0.080 | 0.313 |
| 25.719 | 5.85 | 2.87 | 3.35 | 0.491 | 0.046 | 0.080 | 0.351 |
| 33.088 | 7.53 | 3.67 | 4.32 | 0.487 | 0.033 | 0.080 | 0.396 |
| 45.662 | 10.33 | 5.03 | 5.96 | 0.486 | 0.025 | 0.080 | 0.370 |
| 60.336 | 13.54 | 6.55 | 7.87 | 0.484 | 0.021 | 0.080 | 0.365 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bascetta, L.; Baur, M.; Gruosso, G. ROBI’: A Prototype Mobile Manipulator for Agricultural Applications. Electronics 2017, 6, 39. https://doi.org/10.3390/electronics6020039
Bascetta L, Baur M, Gruosso G. ROBI’: A Prototype Mobile Manipulator for Agricultural Applications. Electronics. 2017; 6(2):39. https://doi.org/10.3390/electronics6020039
Chicago/Turabian StyleBascetta, Luca, Marco Baur, and Giambattista Gruosso. 2017. "ROBI’: A Prototype Mobile Manipulator for Agricultural Applications" Electronics 6, no. 2: 39. https://doi.org/10.3390/electronics6020039
APA StyleBascetta, L., Baur, M., & Gruosso, G. (2017). ROBI’: A Prototype Mobile Manipulator for Agricultural Applications. Electronics, 6(2), 39. https://doi.org/10.3390/electronics6020039







