A Soft-Switching SEPIC with Multi-Output Sources
Abstract
:1. Introduction
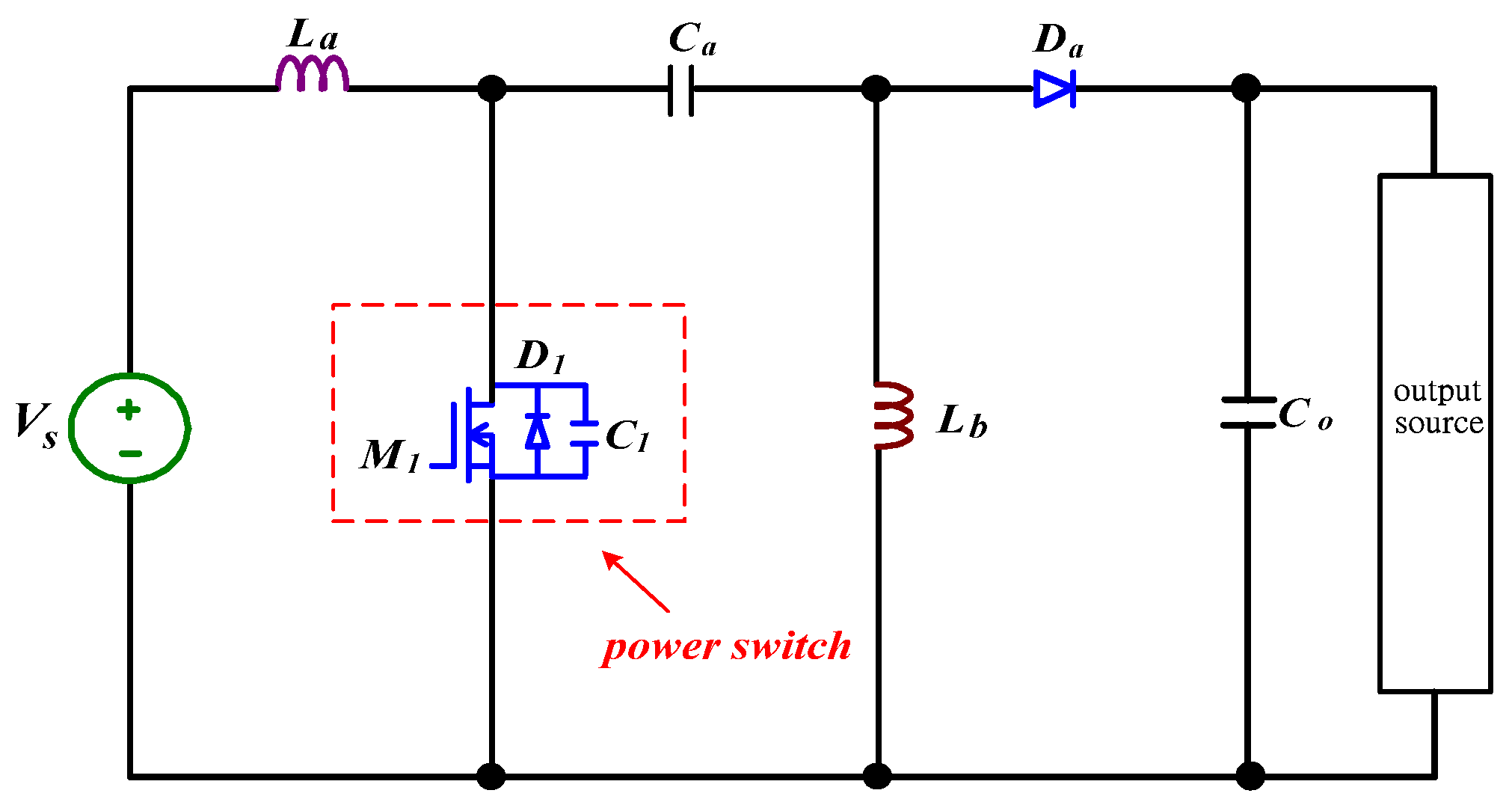
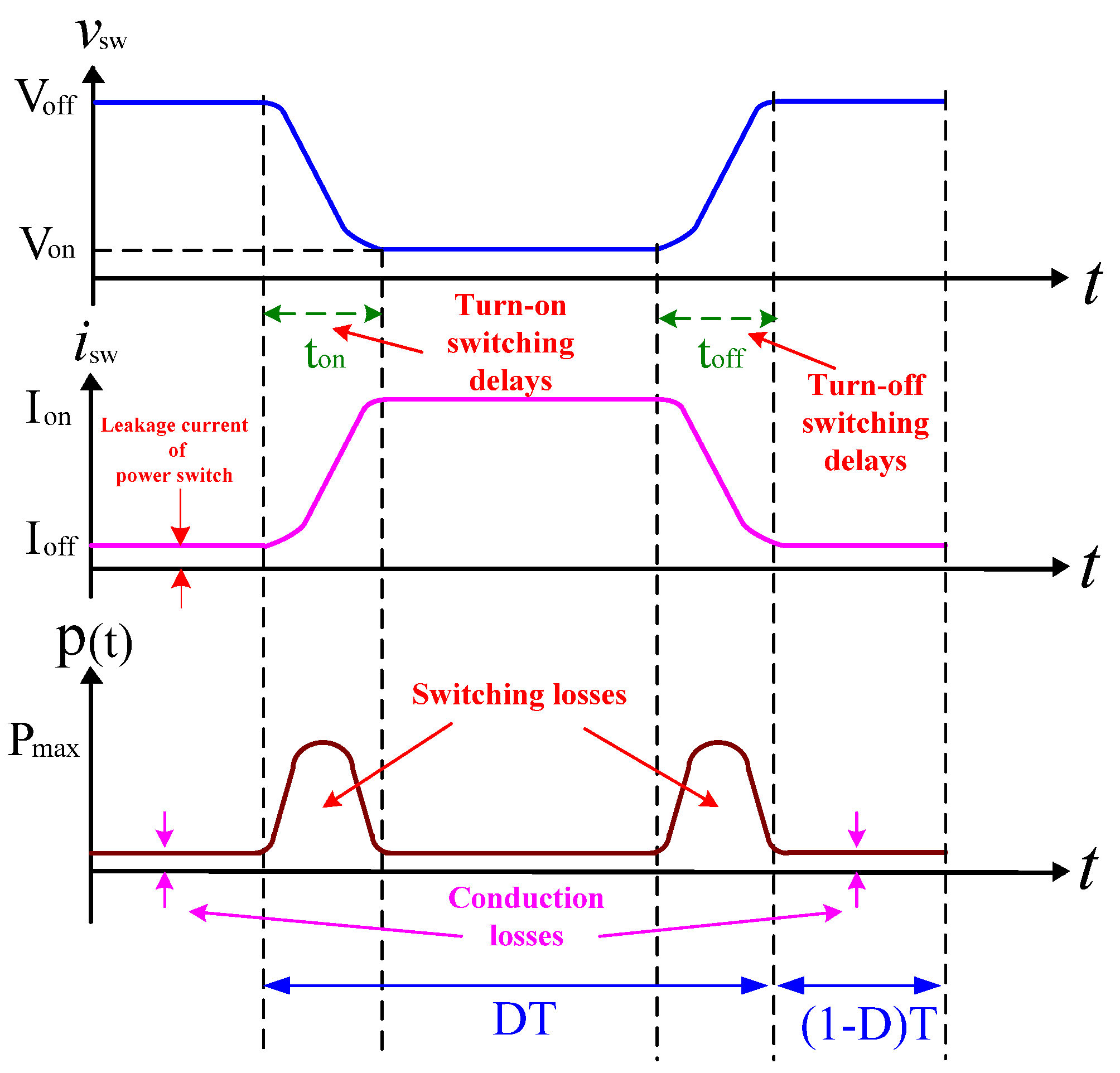
2. Power Estimation of Hard-Switching SEPIC
- (1)
- Low switching losses and high conversion efficiency,
- (2)
- Low di/dt and dv/dt, and thus low voltage spikes and EMI emissions, and
- (3)
- High reliability and low cost.
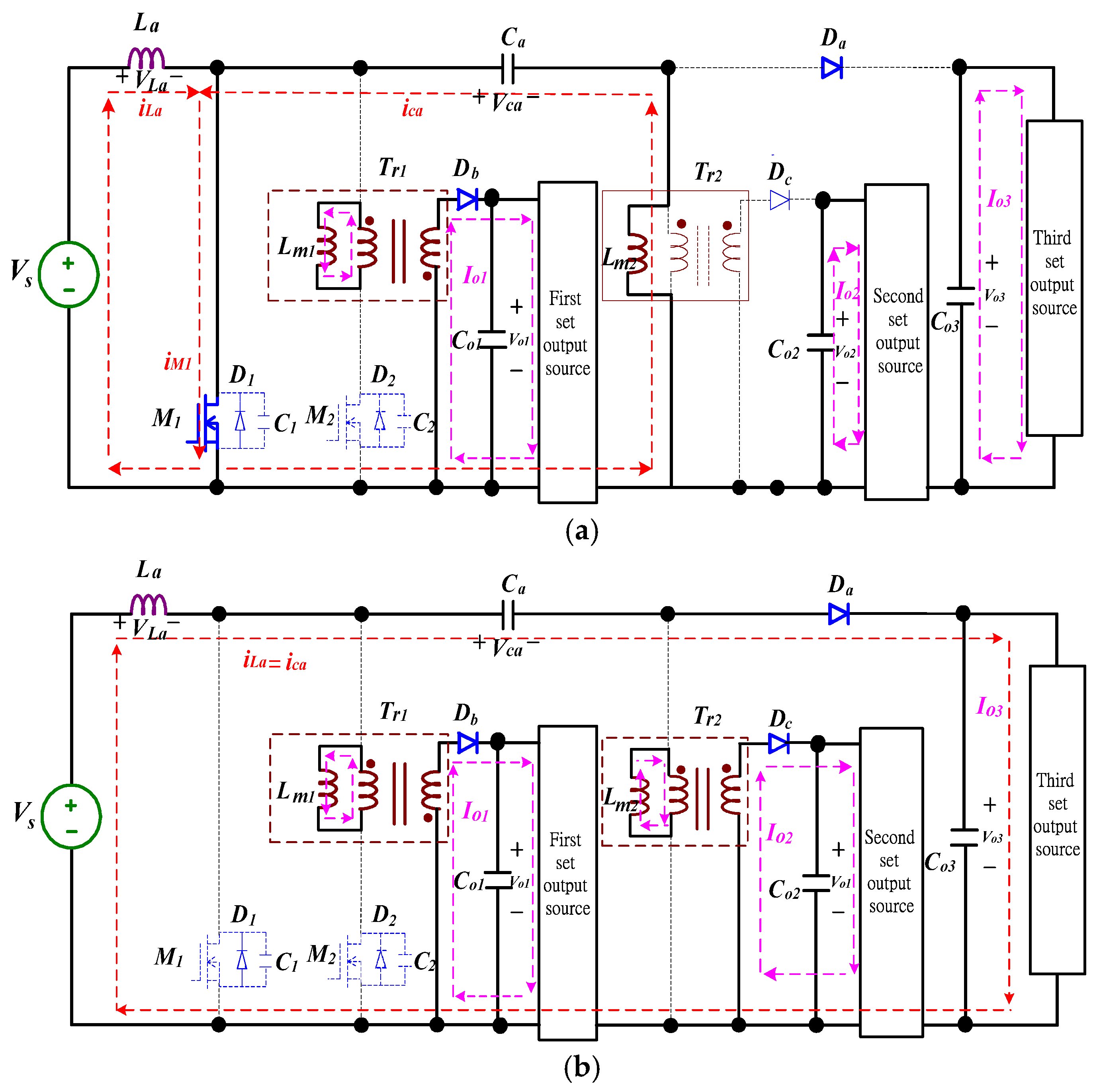
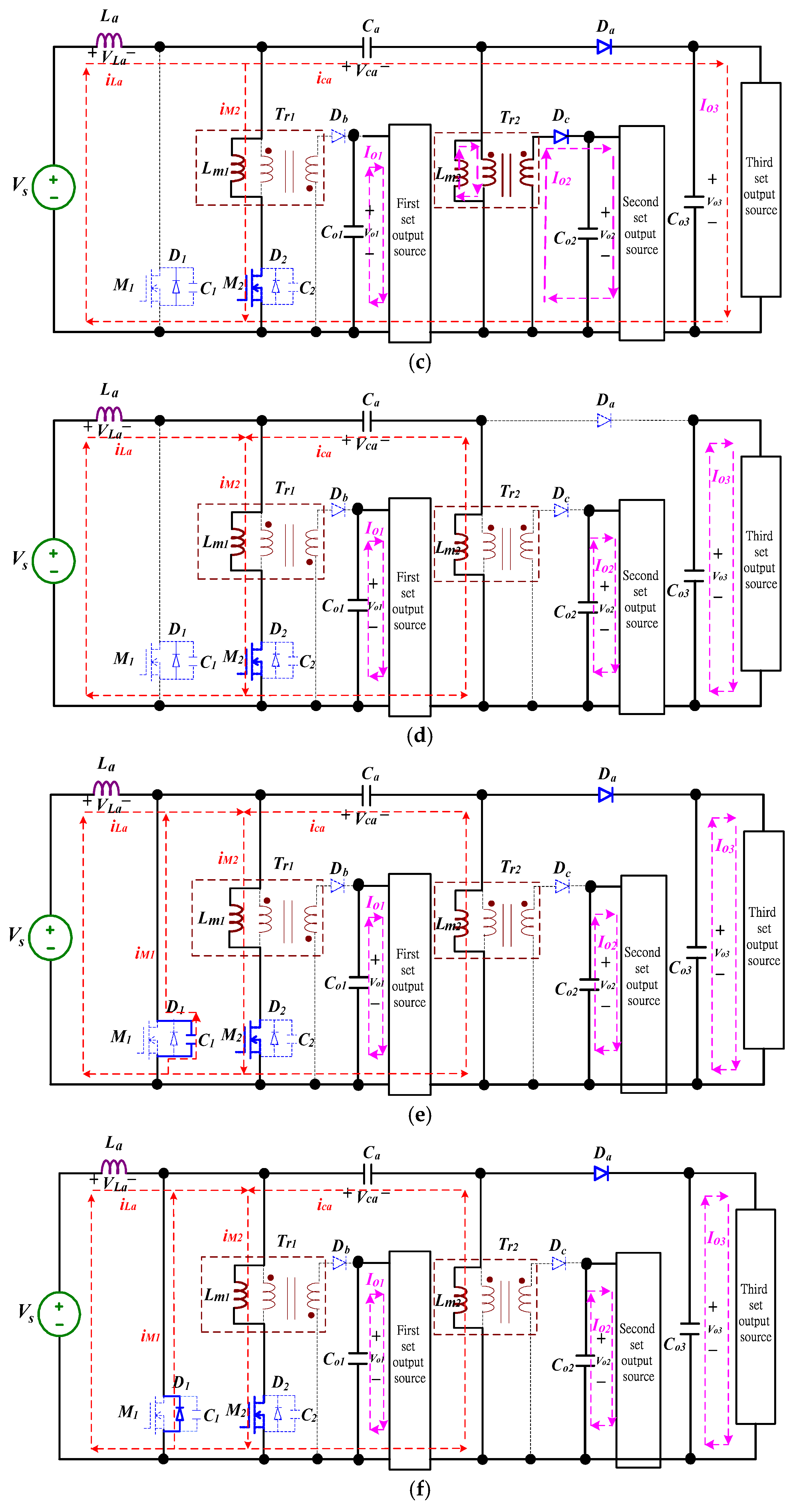
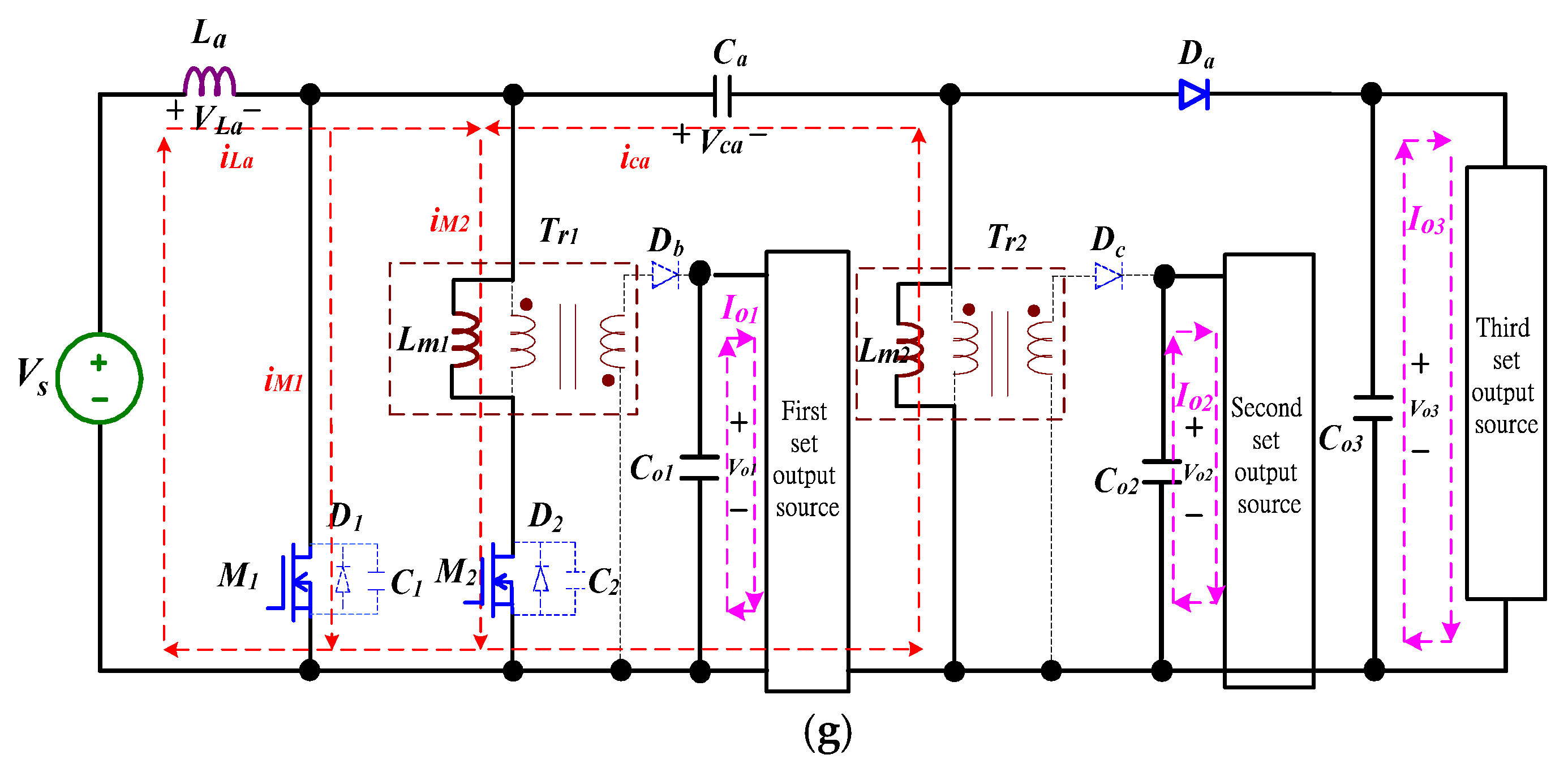
3. Operational Principles
- (1)
- Capacitances of Ca, Co1, Co2, and Co3 are large enough that the voltages across them are constant over a switching cycle.
- (2)
- All of the switching devices, MOSFETs, and diodes are ideal.
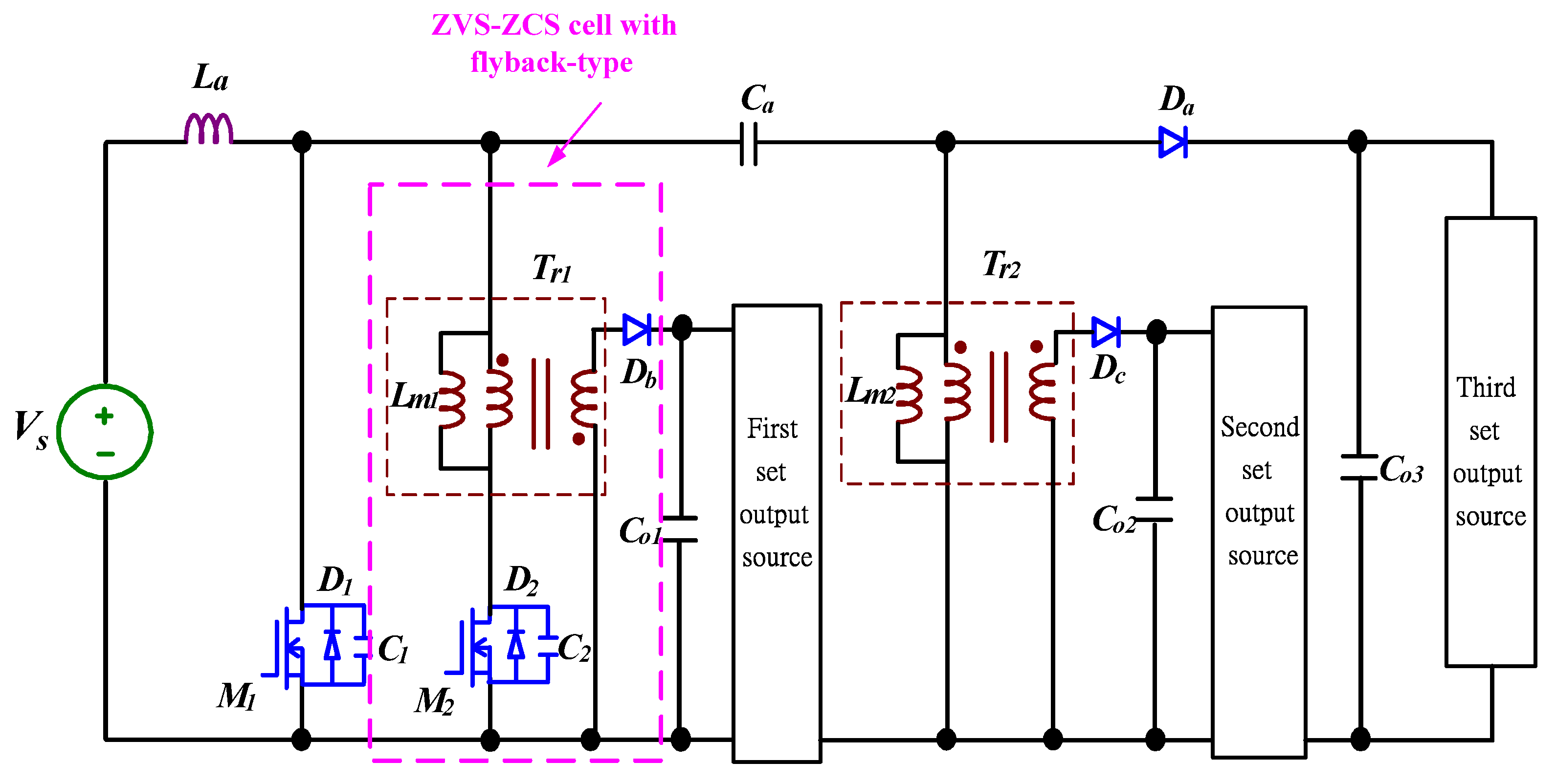
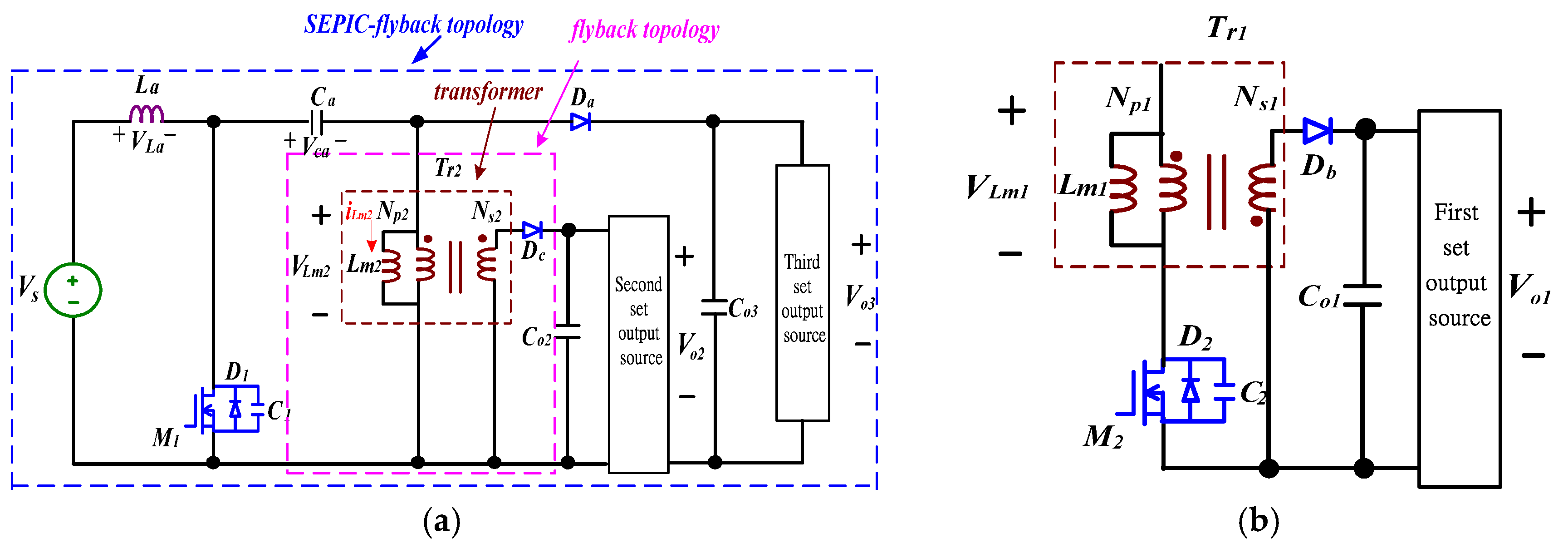
4. Analysis of the Proposed Converter
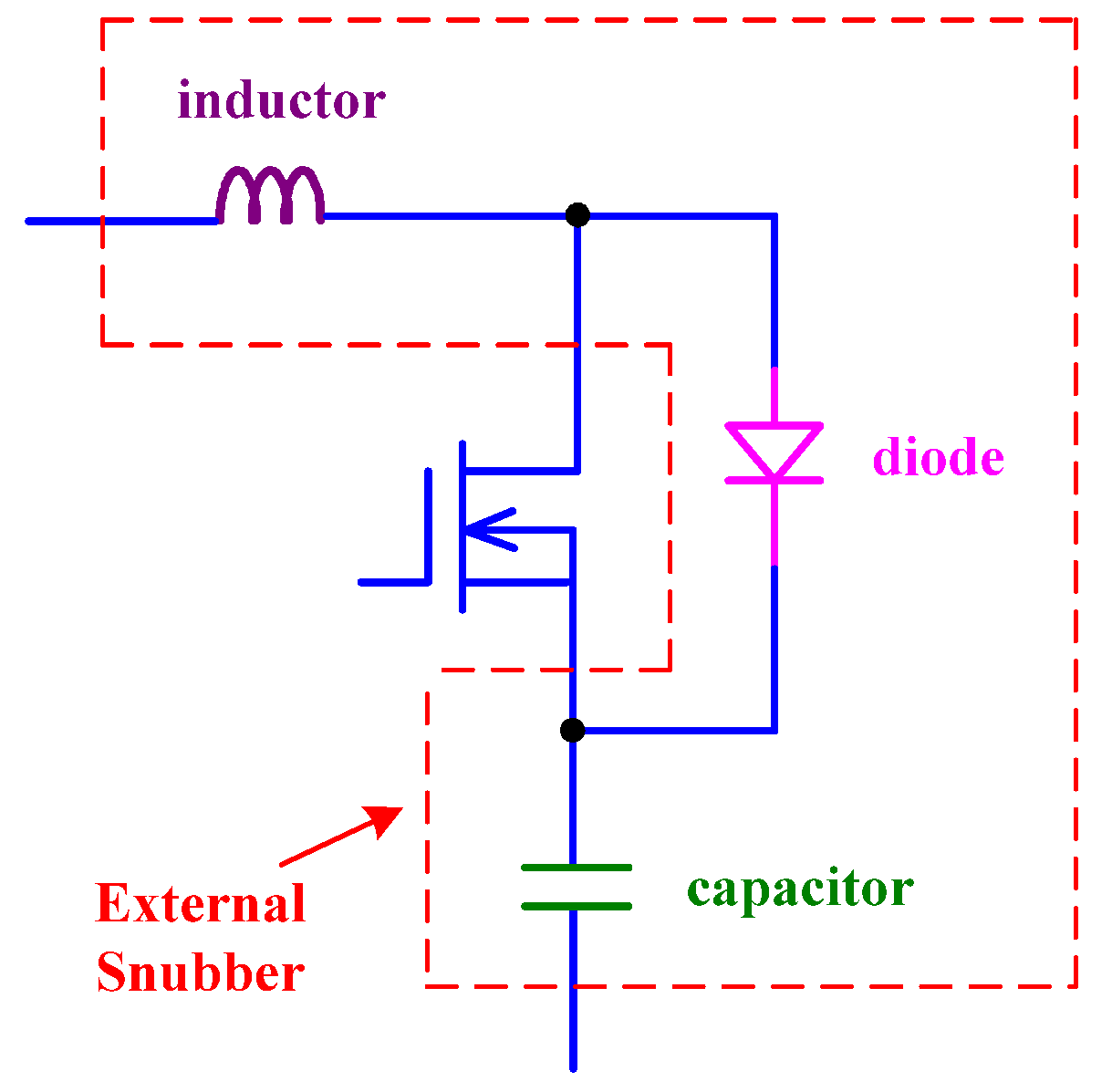
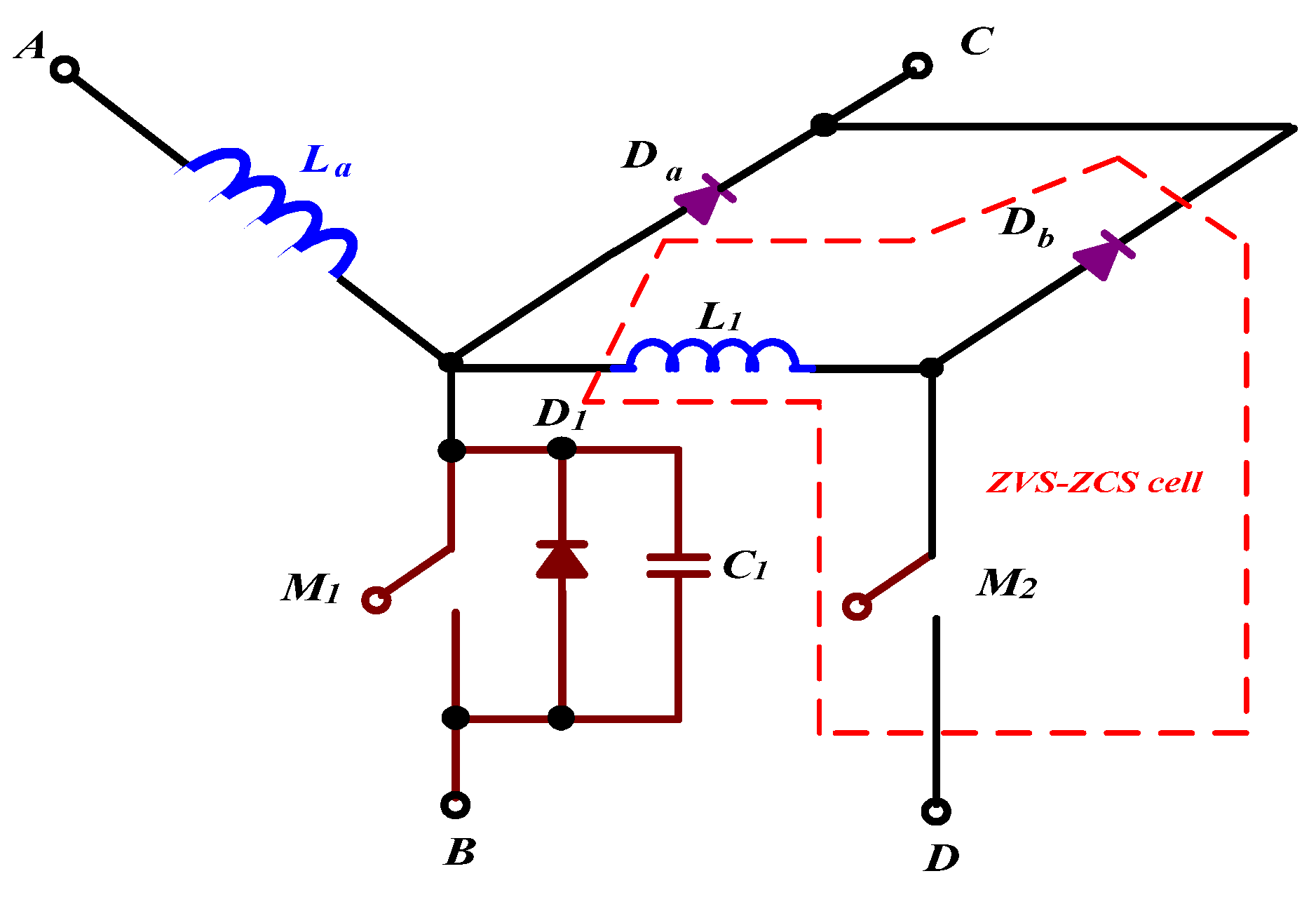
4.1. Derivations of a ZVS-ZCS Cell with Flyback-Type
4.2. Analysis of the Voltage Gain
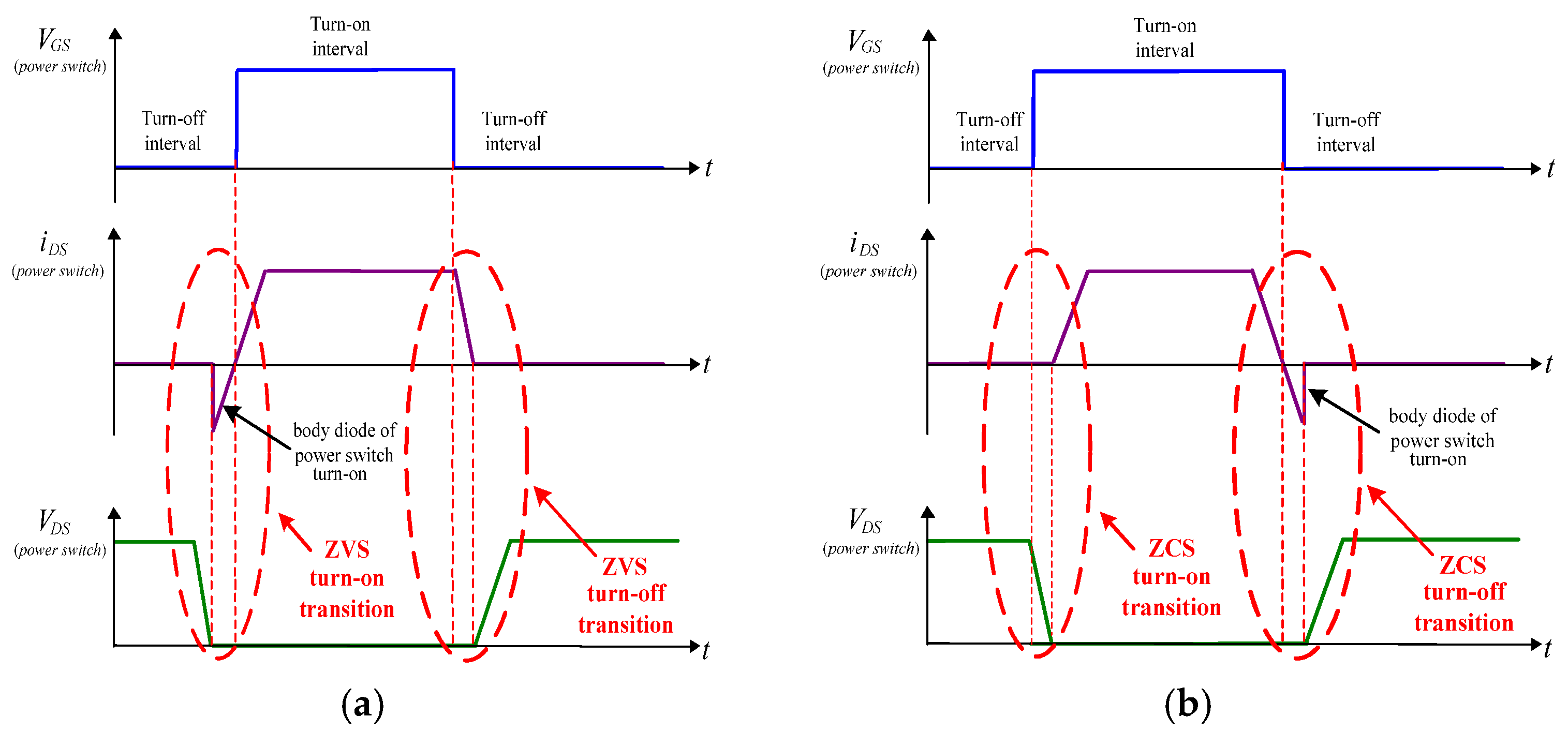
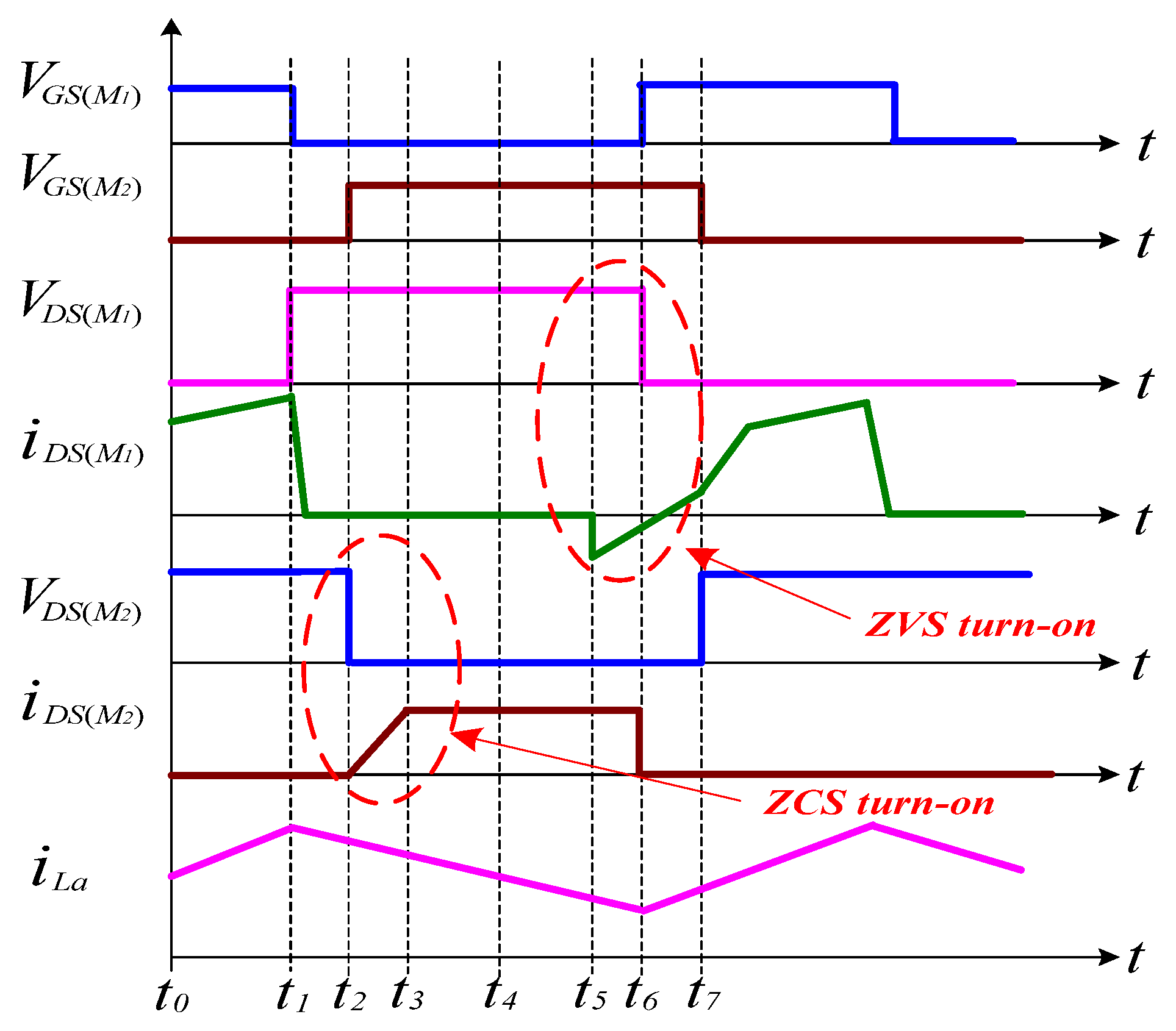
4.3. Region of ZVS and ZCS
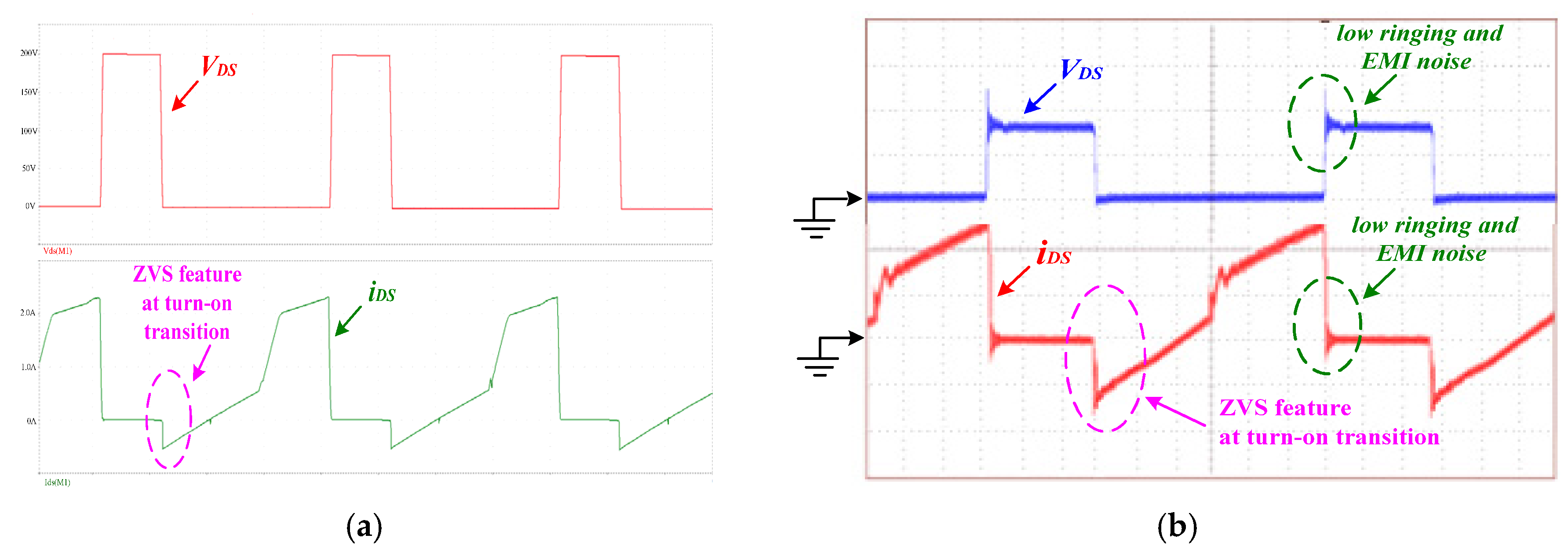
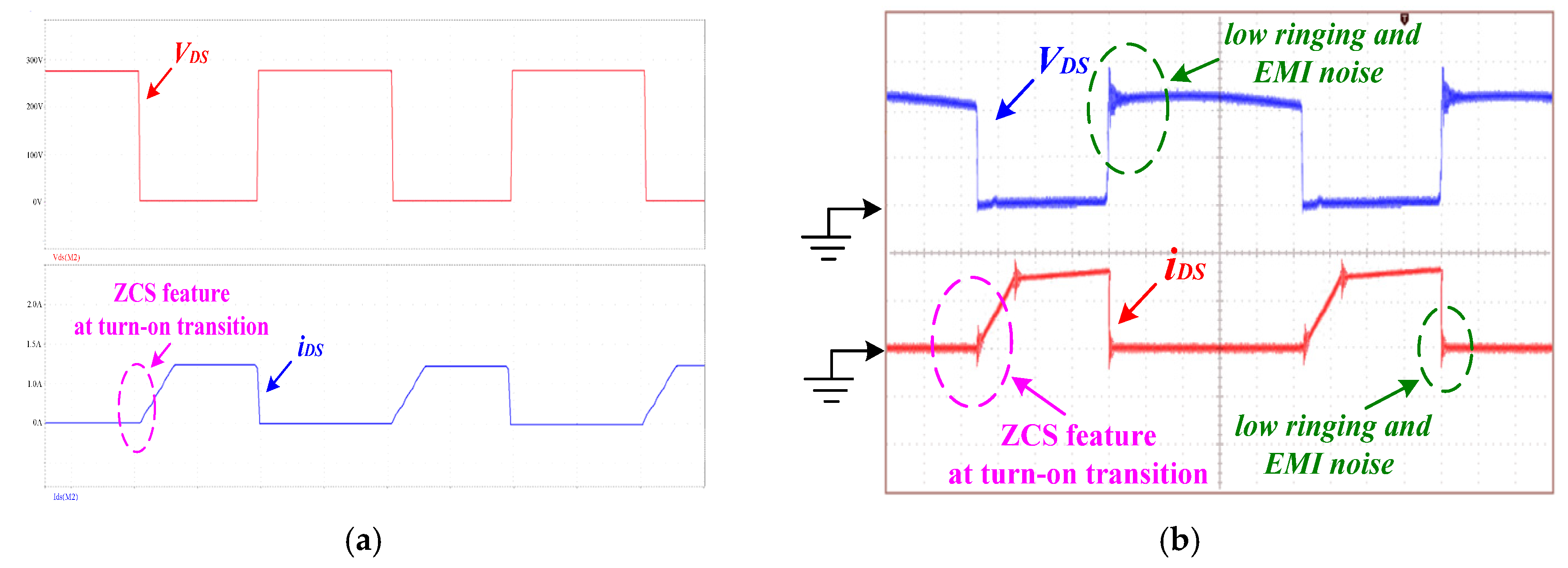
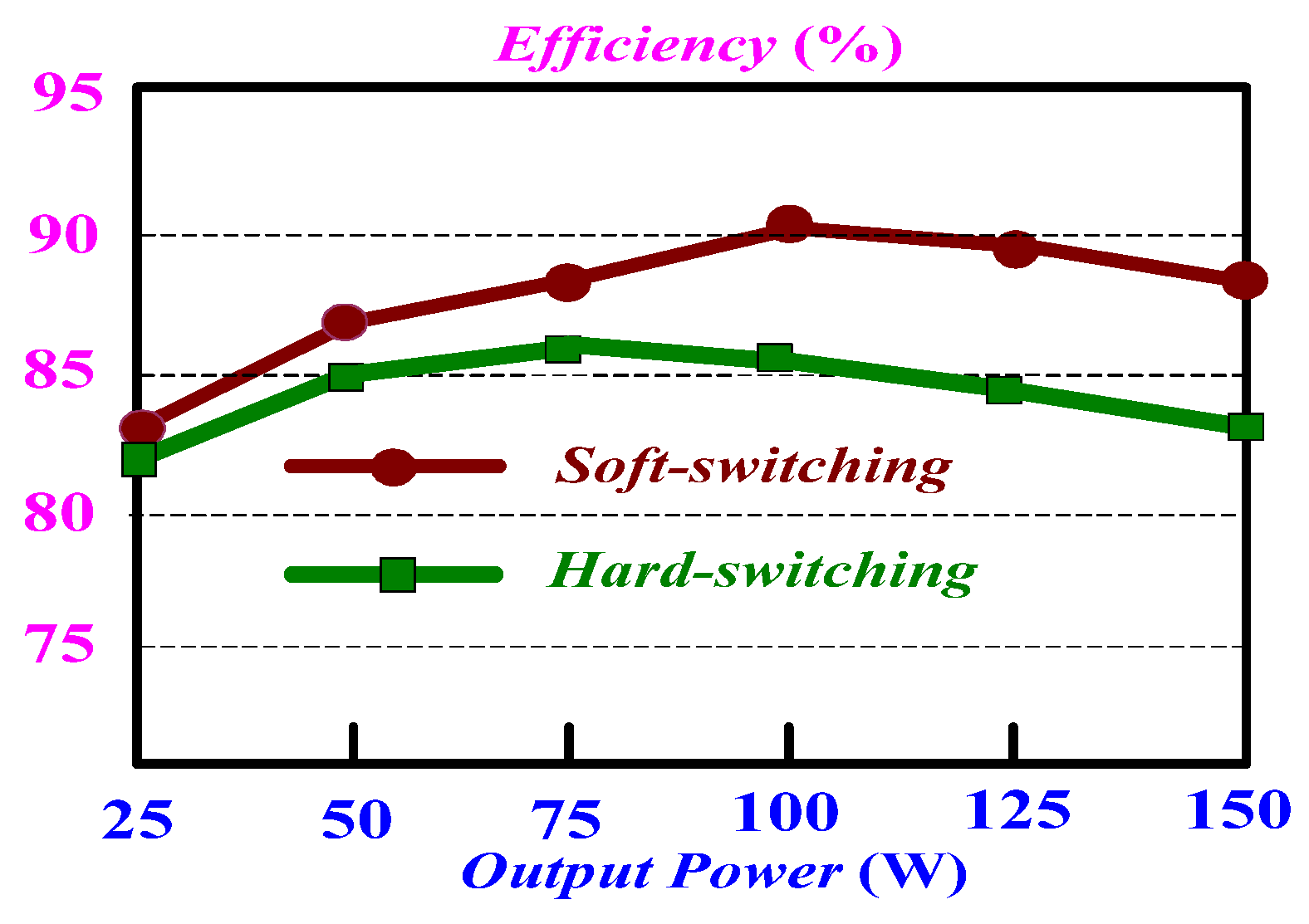
5. Simulated and Experimental Results
- input voltage: Vs = 60 Vdc,
- first-set output voltage: Vo1 = 12 Vdc,
- second-set output voltage: Vo2 = 24 Vdc,
- third-set output voltage: Vo3 = 100 Vdc,
- total output power: 150 W, and
- switching frequency: f = 55 kHz.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shen, C.L.; Tsai, C.T. Double-linear approximation algorithm to achieve maximum-power-point tracking for photovoltaic arrays. Energies 2012, 5, 1982–1997. [Google Scholar] [CrossRef]
- Vasilj, J.; Sarajcev, P.; Jakus, D. Estimating Future Balancing Power Requirements in Wind-PV Power System. Renew. Energy 2016, 99, 369–378. [Google Scholar] [CrossRef]
- Adhikari, J.; Prasanna, I.V.; Panda, S.K. Power Conversion System for High Altitude Wind Power Generation with Medium Voltage AC Transmission. Renew. Energy 2016, 92, 562–578. [Google Scholar] [CrossRef]
- Tsai, C.T.; Chen, W.M. Buck Converter with Soft-Switching Cells for PV Panel Applications. Energies 2016, 9, 148. [Google Scholar] [CrossRef]
- Ridley, R. Analyzing the SEPIC Converter; Power Systems Design Europe: Roswell, NM, USA, 2006; pp. 14–18. [Google Scholar]
- Axelrod, B.; Berkovich, Y. New Coupled-Inductor SEPIC Converter with Very High Conversion Ratio and Reduced Voltage Stress on the Switches. In Proceedings of the 2011 IEEE 33rd International Telecommunications Energy Conference (INTELEC), Amsterdam, The Netherlands, 9–13 October 2011; pp. 1–7. [Google Scholar]
- Gu, W.; Zhang, D. Designing a SEPIC Converter; Excellent Design Guidelines, National Semiconductor in Application Note: Los Angeles, CA, USA, 2008; pp. 1–6. [Google Scholar]
- Ali, M.; Orabi, M.; Ahmed, M.E.; El-Aroudi, A. Design Consideration of Modified SEPIC Converter for LED Lamp Driver. In Proceedings of the 2010 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Heifei, China, 16–18 June 2010; pp. 394–399. [Google Scholar]
- Do, H.L. Soft-Switching SEPIC Converter with Ripple-Free Input Current. IEEE Trans. Power Electron. 2012, 27, 2879–2887. [Google Scholar] [CrossRef]
- Chen, S.M.; Liang, T.J.; Yang, L.S.; Chen, J.F. A Cascaded High Step-up DC–DC Converter with Single Switch for Micro source Applications. IEEE Trans. Power Electron. 2011, 26, 1146–1153. [Google Scholar] [CrossRef]
- Hu, J.; Sagneri, A.D.; Rivas, J.M.; Davis, S.M.; Perreault, D.J. High Frequency Resonant Sepic Converter with Wide Input and Output Voltage Ranges. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 1397–1406. [Google Scholar]
- Wang, C.M. New Family of Zero-Current-Switching PWM Converters Using a New Zero-Current-Switching PWM Auxiliary Circuit. IEEE Trans. Ind. Electron. 2006, 33, 768–777. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, J.; Ye, X.; Qian, Z. Analysis and Derivations for a Family ZVS Converter Based on a New Active Clamp ZVS Cell. IEEE Trans. Ind. Electron. 2008, 55, 773–781. [Google Scholar] [CrossRef]
- Kavitha Unnikrishnan, C.; Reshma Raj, C. High Frequency Quasi Resonant SEPIC Converter for Wide Range of Operation. In Proceedings of the 2014 International Conference on Circuit, Power and Computing Technologies (ICCPCT), Tamil Nadu, India, 20–21 March 2014; pp. 984–989. [Google Scholar]
- Ongaro, F.; Saggini, S. ZVS Isolated Active Clamp Sepic Converter for High Power LED Applications. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 957–962. [Google Scholar]
- Lin, B.R.; Shih, K.L.; Chen, J.J.; Chiang, H.K. Implementation of a Zero Voltage Switching Sepic-Cuk Converter. In Proceedings of the 2008 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 3–5 June 2008; pp. 394–399. [Google Scholar]
- Silva Costa, P.J.; Illa Font, C.H.; Lazzarin, T.B. Improvement of Stability in Current-Programmed SEPIC DC/DC Converters. In Proceedings of the 2015 IEEE 13th Brazilian Power Electronics Conference and 1st Southern Power Electronics Conference (COBEP/SPEC), Fortaleza, CE, Brazil, 29 November–2 December 2015; pp. 1–6. [Google Scholar]
- Maged, N.F. Design of a Digital PWM Controller for a Soft Switching SEPIC Converter. J. Power Electron. 2004, 4, 152–160. [Google Scholar]
- Corradini, L. Zero voltage switching technique for bidirectional DC/DC converters. IEEE Trans. Power Electron. 2014, 29, 1585–1594. [Google Scholar] [CrossRef]
- Elasser, A.; Torry, D.A. Soft Switching Active Snubbers for DC/DC Converters. IEEE Trans. Power Electron. 1996, 11, 710–722. [Google Scholar] [CrossRef]
- Smith, K.M., Jr.; Smedley, K.M. Properties and Synthesis of Lossless, Passive Soft Switching Converters. In Proceedings of the 1st International Congress in Israel on Energy, Power & Motion Contrtol, Tel-Aviv, Israel, 5–6 May 1997; pp. 112–119. [Google Scholar]
- Xu, D.H.; Chen, M.; Lou, J.; Luo, M. Transformer secondary leakage inductance based ZVS dual bridge DC/DC converter. IEEE Trans. Power Electron. 2004, 19, 1408–1416. [Google Scholar] [CrossRef]
- Tseng, C.-J.; Chen, C.-L. Passive Lossless Snubbers for DC/DC Converters. In Proceedings of the 1998 Thirteenth Annual Conference on Applied Power Electronics Conference and Exposition, Anaheim, CA, USA, 15–19 February 1998; pp. 1049–1054. [Google Scholar]
- Watson, R.; Hua, G.; Lee, F.C. Characterization of an Active Clamp Flyback Topology for Power Factor Correction Applications. IEEE Trans. Power Electron. 1996, 11, 191–198. [Google Scholar] [CrossRef]
- Duarte, C.M.C.; Barbi, I. A Family of ZVS-PWM Active-Clamping Dc-to-Dc Converters: Synthesis, Analysis, Design, and Experimentation. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1997, 44, 698–704. [Google Scholar] [CrossRef]
- Jitaru, I.D. Constant Frequency, Forward Converter with Resonant Transition. In Proceedings of the High Frequency Power Conversion Conference, Toronto, ON, Canada, 9–14 June 1991; pp. 282–292. [Google Scholar]
- Liu, K.H.; Lee, F.C. Zero-Voltage Switching Technique in DC/DC Converter. IEEE Trans. Power Electron. 1990, 5, 293–304. [Google Scholar] [CrossRef]
- Wang, H.; Chung, H.S.; Ioinovici, A. A New Concept of High-Voltage DC–DC Conversion Using Asymmetric Voltage Distribution on the Switch Pairs and Hybrid ZVS–ZCS Scheme. IEEE Trans. Power Electron. 2012, 27, 2242–2259. [Google Scholar] [CrossRef]
- Wang, C.M. A Novel ZCS-PWM Flyback Converter with a Simple ZCS-PWM Commutation Cell. IEEE Trans. Ind. Electron. 2008, 55, 749–757. [Google Scholar] [CrossRef]
- Chiang, C.; Chen, C. Zero-Voltage-Switching Control for a PWM Buck Converter under DCM/CCM Boundary. IEEE Trans. Power Electron. 2009, 24, 2120–2126. [Google Scholar] [CrossRef]
- Lee, Y.S.; Chen, G.T. ZCS bi-directional DC-to-DC converter application in battery equalization for electric vehicles. In Proceedings of the IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–26 June 2004; Volume 4, pp. 2766–2772. [Google Scholar]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-T.; Su, J.-C. A Soft-Switching SEPIC with Multi-Output Sources. Electronics 2017, 6, 35. https://doi.org/10.3390/electronics6020035
Tsai C-T, Su J-C. A Soft-Switching SEPIC with Multi-Output Sources. Electronics. 2017; 6(2):35. https://doi.org/10.3390/electronics6020035
Chicago/Turabian StyleTsai, Cheng-Tao, and Jye-Chau Su. 2017. "A Soft-Switching SEPIC with Multi-Output Sources" Electronics 6, no. 2: 35. https://doi.org/10.3390/electronics6020035
APA StyleTsai, C.-T., & Su, J.-C. (2017). A Soft-Switching SEPIC with Multi-Output Sources. Electronics, 6(2), 35. https://doi.org/10.3390/electronics6020035





