1. Introduction
MIMO communication is a key technology for the forthcoming generation of personal wireless communications. Starting from the point-to-point communication networks, the MIMO concept was extended to multi-users introducing new strategies for inter-user interference reduction such as Multi-User MIMO and Massive MIMO. The potential benefits associated to the efficient use of the spatial resources allowed by MIMO communication strategy include higher bit rate, higher reliability of the connection, lower interference level, and a larger number of subscribers in the cell [
1].
All this is made possible by the knowledge of the response of the MIMO channel, i.e., the knowledge of the channel state information (CSI). The accuracy of the CSI is of paramount importance for a MIMO system, and incorrect CSI information can strongly degrade the performance of the communication system.
On the other hand, CSI estimation is an expensive process in terms of throughput of the communication system, since generally pilot signals must be sent during CSI identification, reducing the bit rate at which the payload can be transmitted.
Furthermore, CSI must be refreshed at a rate depending on the correlation time of the channel. While in relatively stationary channels associated to low-mobile devices in almost stationary environments (as for example lap-top connection in a library) the overload due to CSI is small, in fast-changing environments (such as a mobile phone connection in a moving car) the CSI update process can cause a significant loss of performance of the system.
Degradation of MIMO throughput is particularly relevant in presence of deep fading, since the CSI process must be repeated many times before obtaining full CSI identification.
The increase of the number of antennas in MIMO systems makes these problems more and more relevant since the number of measurements as well as the probability of data missing due to deep fading linearly increase with the number of antennas at the receiver/transmitters.
The aim of this paper is to investigate a method able to estimate the CSI from incomplete data. The idea at the basis of this method was briefly sketched for the first time in [
2] and takes advantage of some recent results regarding the connections between electromagnetic theory and information theory. These results allow relating some properties of the channel matrix to the ones of the electromagnetic radiation operator [
3]. As a consequence, in the presence of partially known channel matrix the remaining elements can be estimated considering the minimum rank solution among all the channel matrices compatible with the available data using the matrix completion theory developed in the framework of information theory and signal processing [
4,
5].
2. Number of Subchannels of MIMO Communication Systems and Rank of the Radiation Operator
Let us consider a MIMO communication channel with
N transmitter antennas, and
M receiving antennas. Without loss of generality, we suppose that the channel has unit bandwith (i.e., 1 Hz) and is of flat frequency over this bandwidth. Let
be the total average energy available at the transmitter over a symbol period, that in our specific case is also equal to the total average transmitted power. Given the channel transfer matrix
the input–output relation for the MIMO communication system is [
1]:
where
is the received signal vector,
is the transmitted signal vector, and
is the noise vector. The supposed zero mean circular symmetric complex Gaussian (ZMCSCG) with covariance matrix
,
being the unit
matrix. We suppose that the transmitted signal vector has zero mean, and the trace of its covariance matrix
is equal to
N in order to verify the constraint on the total energy.
As is well known, the channel capacity of the MIMO channel is [
1]:
An insight of the role of the channel matrix
in the channel capacity can be obtained by expanding the matrix using singular value decomposition (SVD),
wherein
and
are unitary matrices whose column vectors
and
are the left and right singular vectors of the matrix, and
is a matrix whose elements are all nulls except the first
r elements
, called singular values, placed along the main diagonal of the
upper-left submatrix. Accordingly, we have:
wherein
stands for the inner product.
The channel capacity can be represented as the sum of the channel capacity of
r parallel SISO channels:
wherein
is the optimal energy allocation along each SISO subchannel, obtained by the waterpouring algorithm.
As indicated above, this analysis in terms of subchannels highlights the importance of the channel matrix structure. The large increase of the channel capacity of MIMO systems arises from the presence of several communication subchannels, each of them able to transmit statistically independent information. The number of such subchannels is bounded by the rank
r of the channel matrix. The number of effectively used subchannels depends on the available average energy (or equivalently on the average transmitted power) [
1]. The number of subchannels conveying reliable information is called the effective degrees of freedom of the MIMO system.
In order to maximize the throughput of a MIMO system it is of paramount importance to estimate the channel matrix . As described in the Introduction, this step, known as channel state information, generally requires the transmission of known signals and causes a decrease of the throughput of the system. Consequently, it is of great interest to estimate the channel state from incomplete data avoiding the repetition of the CSI in case of intermittent received data.
A commonly adopted model for the channel capacity is the Gaussian random matrix. Since Gaussian matrices are low structured, this seems to prevent an effective estimation of missed elements. However, in real cases the channel matrix is much more structured as a consequence of the underlying physical processes involved in MIMO propagation.
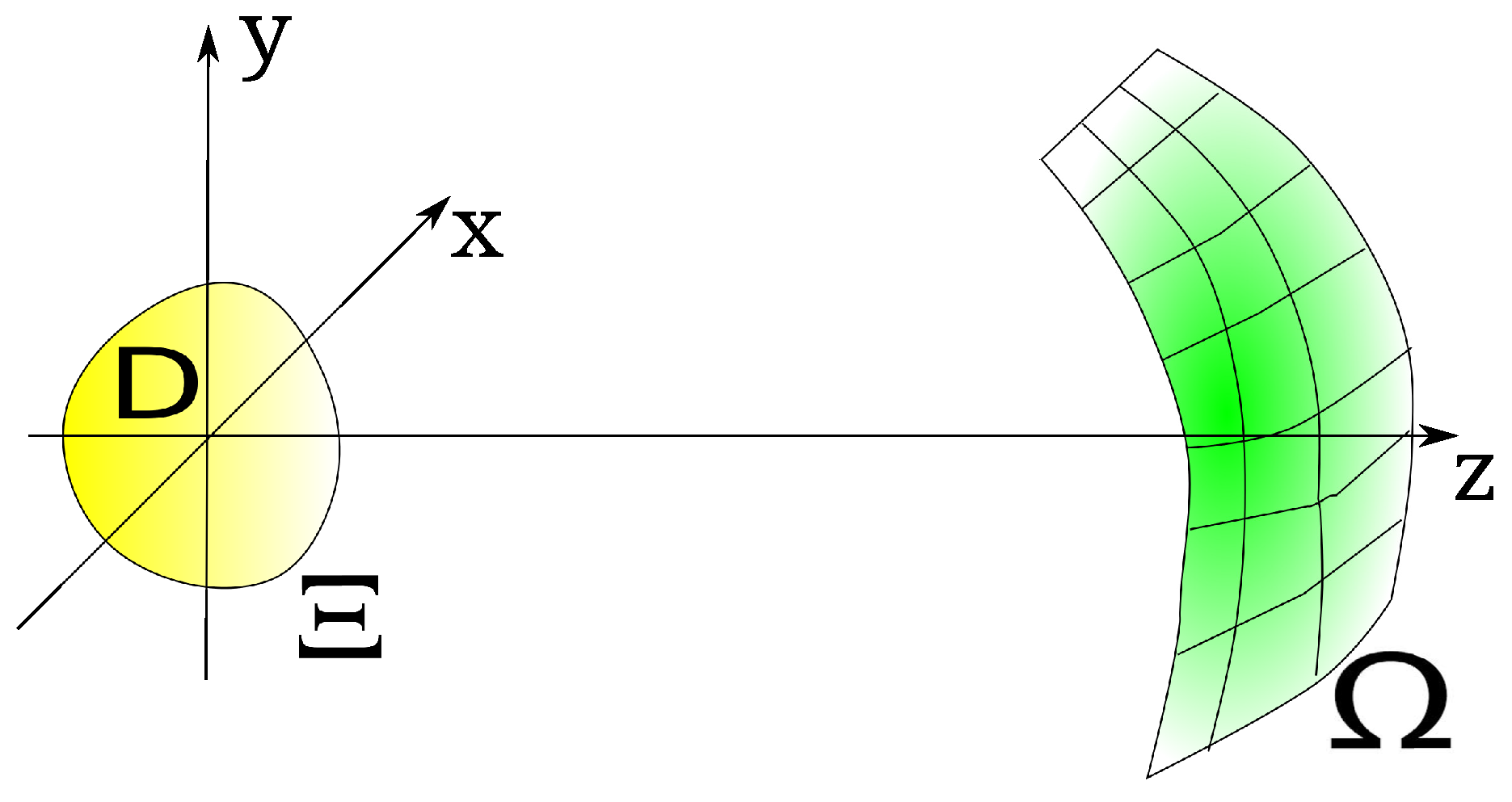
In order to clarify this point let us consider a harmonic electromagnetic source placed in a domain
D bounded by a surface
(see
Figure 1). The field, observed on the domain
(supposed as not intersecting
) is [
6,
7]:
wherein
,
is the source current density,
is the dyadic Green’s function and · denotes the matrix-vector product.
It is possible to recast the problem in functional spaces using standard functional analysis tools. We consider
as an element
x of the set
X,
an element
y of the set
Y and
the radiation operator mapping
X onto
Y, whose elements are the values of the electric field
on the observation surface
[
3]. In the following discussion we suppose that the currents and the fields belong to separable Hilbert spaces equipped with
norm. Furthermore, the set of the currents is supposed to be bounded with the unit
radius.
Since the operator
is completely continuous (also called compact) [
8] and
X is bounded,
can be represented by the Hilbert–Schmidt decomposition [
3,
8]:
wherein
n takes into account additive noise or uncertainty on the observed quantity,
is the singular system of
, and
are the singular values of the operator.
By comparing Equation (
7) to Equation (
4) we can note a strong similarity. Indeed, the electromagnetic model is a continuous version of a MIMO system, and in fact in the case of discrete sources (i.e., radiating arrays) and discrete observation points the continuous model can be straightforwardly modified considering finite-dimensional Euclidean spaces; in this case
turns out to be the channel matrix
, while the Hilbert–Schmidt expansion becomes the well known singular value decomposition of a matrix.
The range of the radiation operator
, i.e., the set of the radiated fields, can be approximated with a finite dimensional space at any degree of accuracy. The number of dimensions of the range of the operator is equal to the effective number of singular values of the operator. This number is the effective rank of the operator, also known as the number of degrees of freedom of the electromagnetic field (NDF) [
9].
Analysis of the NDF in scattering environments has been carried out in [
10], showing that in the case of dense scattering environment and receivers surrounding the source the maximum NDF is limited by the value of the NDF of the field in free space and depends on the electrical dimension of the source. However, this condition is rarely obtained and in practical cases the observation surface, i.e., the surface where the receivers are placed, is a limited portion of the surface surrounding the source, causing a decrease of the NDF.
Comparing Equation (
7) to Equation (
4) we can note that the MIMO channel matrix is a discretized version of the radiation operator, and its rank is limited by the NDF of the field. Consequently, in case of a large number of radiating elements the MIMO channel matrix has generally low rank, with a number of communication subchannels that is lower than the number of RX/TX antennas. This suggests estimating the channel matrix in case of lost matrix elements using this low-rank property. The basic idea is that in presence of lost data it is reasonable to find the channel matrix having lower rank. This is equivalent to identifying the ’simplest’ multipath scenario, i.e., the scenario giving the smallest number of subchannels.
3. MIMO Channel Matrix Estimation from Incomplete and Noisy Data
As discussed in the previous section, the basic idea in order to estimate an incomplete MIMO channel matrix is to identify the matrix having the smallest effective rank. Let us consider an MIMO system and let us suppose that deep fading conditions occurred during the channel state identification procedure causing the loss of a number of entries of the channel matrix. As a consequence of the fading, only a part of (the noise-affected) entries of the channel matrix is available in the CSI process.
Let
be the channel matrix. The available
data are collected in the vector
. As above recalled, in order to estimate the channel matrix from the
p entries we can use a rank minimization strategy:
where
is the linear map:
that selects the
p available entries of the channel matrix among the
entries of the matrix , while
depends on the noise level affecting the measured data
. The problem (
8), known as matrix completion [
4], is a very hard non-convex problem, and requires an exhaustive search or global minimization algorithms. However, recent literature has shown that the trace norm (also called Schatten 1-norm or nuclear norm), defined as:
(wherein
is
k-th singular values of
) can be effectively used as a surrogate of the rank in minimization algorithms [
4,
5].
The nuclear norm can be seen as a relaxed version of the rank norm: while the rank function counts the number of non-zero singular values, the nuclear norm sums their amplitude. Consequently, in some way the nuclear norm is to the rank functional what the convex
-norm is to the
-norm in the sparse recovery area. In order to clarify this point, let us recall that in sparse recovery the goal is to identify the sparsest vector (i.e., the vector having the largest number of null components) compatible with the available data [
11]. This requires minimization of the so called
norm, wherein
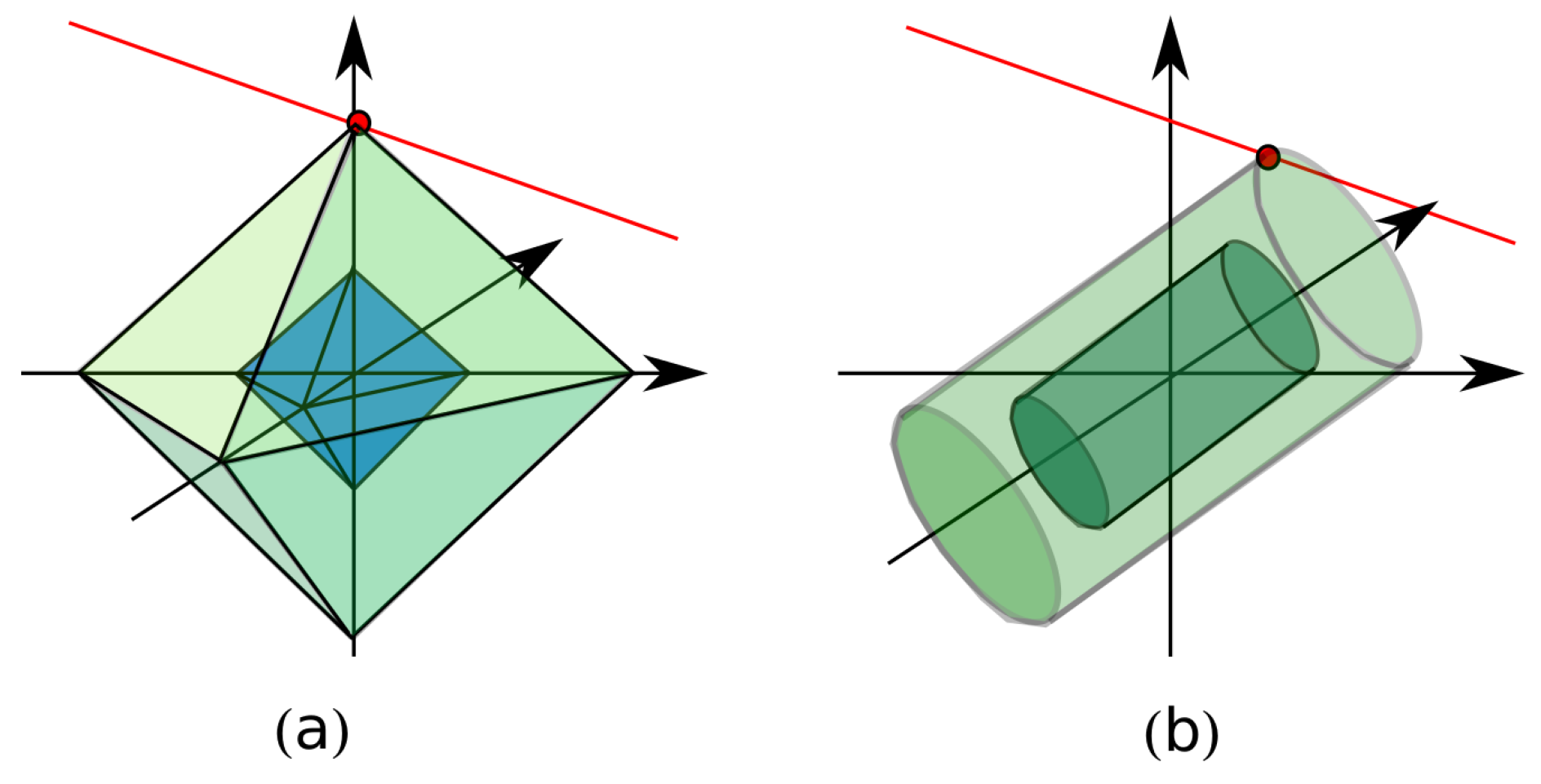
is the number of non null elements of the unknown vector. Such a minimization is a challenging non-convex problem. For the sake of simplicity, let us consider a three-entry vector,
. The vector is supposed to be 1-sparse, i.e., only one of the three entries of the vector is different from zero. Let us consider the convex hull of the 1-sparse vectors. Such a convex hull turns out to be the unit ball of the
norm, wherein the
norm is
. A graphical picture of the unit
ball is drawn in
Figure 2a. The solution of the
minimization (red point in
Figure 2a is the tangent point between the affine space associated to the available data (drawn as a red line in
Figure 2a) and the scaled convex hull.
Now, let us consider the problem of matrix completion. Paralleling the approach followed for sparse recovery, we build the convex hull of the (unit-norm) rank-one matrices, obtaining the nuclear norm ball, shown in
Figure 2b as a cylinder. The solution of the completion problem (red point in
Figure 2b) is given by the tangent point between the affine space associated to the available data (drawn as a red line in
Figure 2b) and the scaled convex hull. Consequently, both methods are based on the construction of a proper convex hull, that turns out to be the unit ball in a suitable norm.
As discussed above, the rank minimization problem is non-polynomial (NP). Instead, the trace norm minimization is a
convex problem and consequently can be solved using efficient convex programming algorithms [
12].
In fact, the trace minimization problem is equivalent to the following problem [
13]:
The solution can be numerically found using a semidefinite programming solver. The examples shown in this paper were obtained using the CVX software [
14] that calls an interior point optimizer. It allows specification of constraints and objectives in standard MatLab expression syntax. For example, the minimization (
8) turns out in the following simple CVX instructions, originally reported in [
13]:
wherein ind is a vector containing the indexes of the entries associated to available data.
CVX is based on MatLab, and hence it is not optimized for speed. The results showed in this paper required the following times of elaboration on an i5 Mac Airbook (evaluated by the CVS time estimation algorithm):
channel matrix: 130 ms;
channel matrix: 150 ms;
channel matrix: 170 ms;
channel matrix: 240 ms;
channel matrix: 410 ms.
However, implementation on FPGA is possible taking into account that the dimension of the matrix is fixed. This should give a large improvement in the elaboration time.
4. Numerical Examples
In order to study the effectiveness of the MIMO channel estimation technique, let us consider a simple MIMO communication system consisting in two linear arrays of half-wavelength equispaced wire antenna elements. The number of elements of the transmitting antenna, N, is supposed equal to the number of elements of the receiving antenna (M) for the sake of simplicity. In all the following examples the measured data are affected by 20-dB noise level, i.e., Gaussian random noise with power 20 dB below the signal power. It is understood that such a noise level limits the dynamic of estimated singular values to around 20 dB also in case of no loss of channel matrix elements.
For example let us consider a MIMO system in an environment with randomly placed perfectly conducting point-like scatterering objects, with a distance between the transmitter and the receiver. In the numerical analysis we considered non light of sight (NLOS) propagation, i.e., the line of sight (LOS) component was neglected.
The mean error of the reconstruction is evaluated as:
wherein
and
are respectively the exact channel matrix and estimated channel matrix of the
trial and
is the Frobenius norm of the matrix.
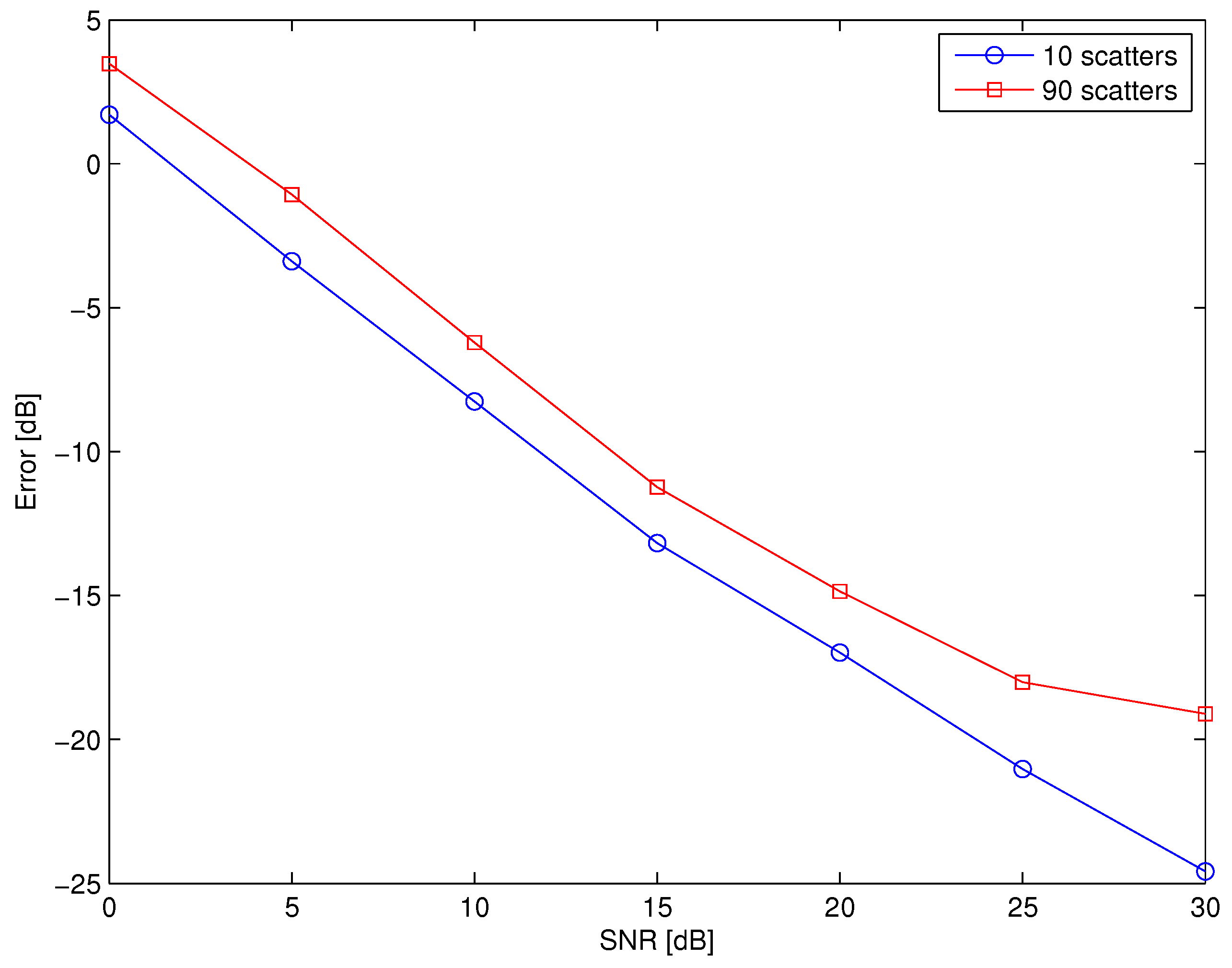
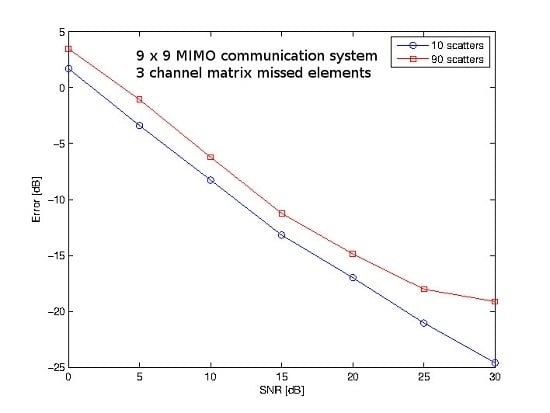
We consider the mean reconstruction error varying the signal-to-noise ratio (SNR) from 0 to 30 dB with 3 matrix elements missed; a number of 10 and 90 scatterers and 50 trials (i.e., 50 random environments) for each value of SNR were considered. The reconstruction error [dB] is plotted in
Figure 3 showing a good estimation of the channel matrix both in case of poor and rich scattering environment.
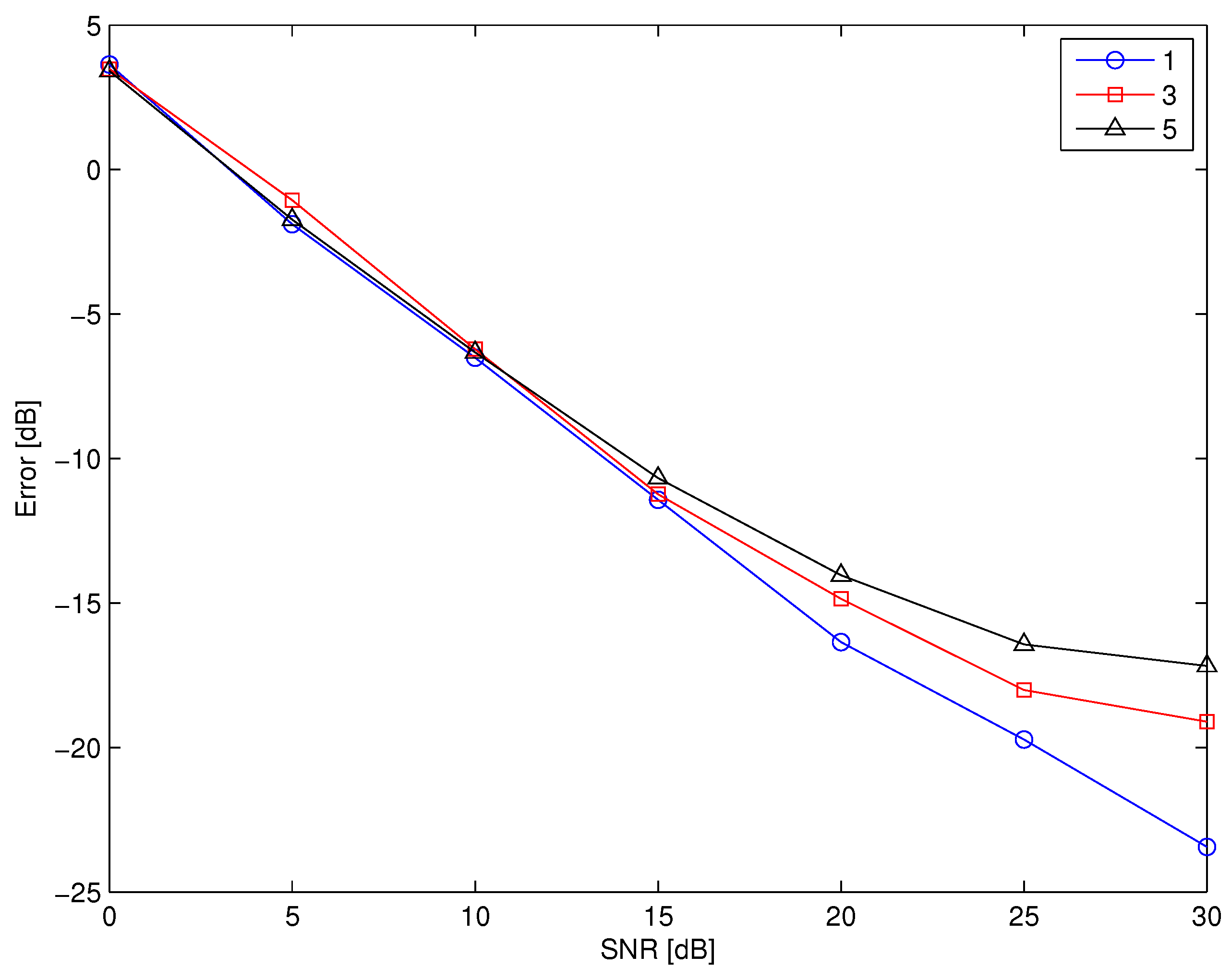
The mean reconstruction error in case of 90 scatterers and 1, 3, and 5 lost elements as a function of the SNR is shown in
Figure 4, showing again a good reconstruction of the matrix
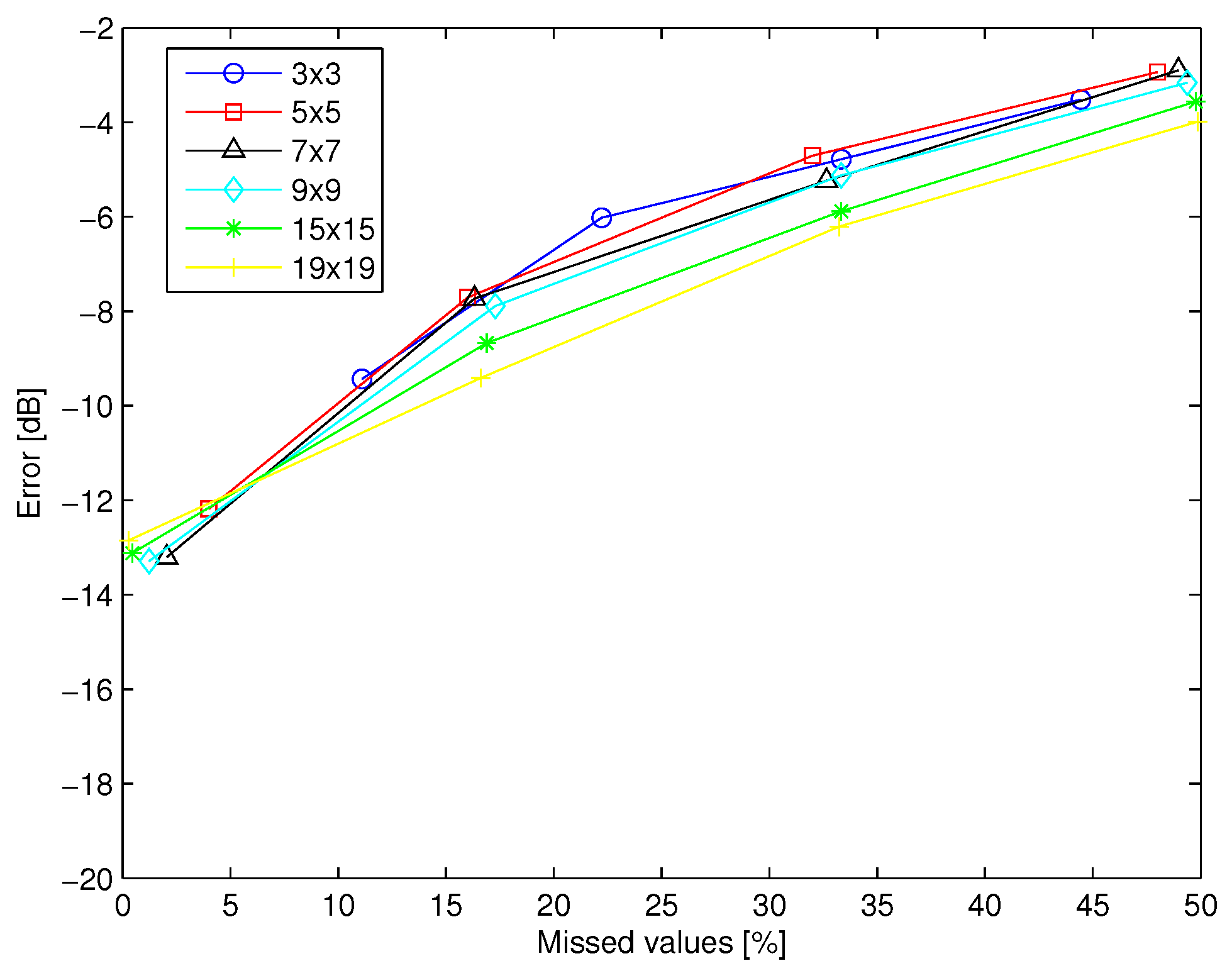
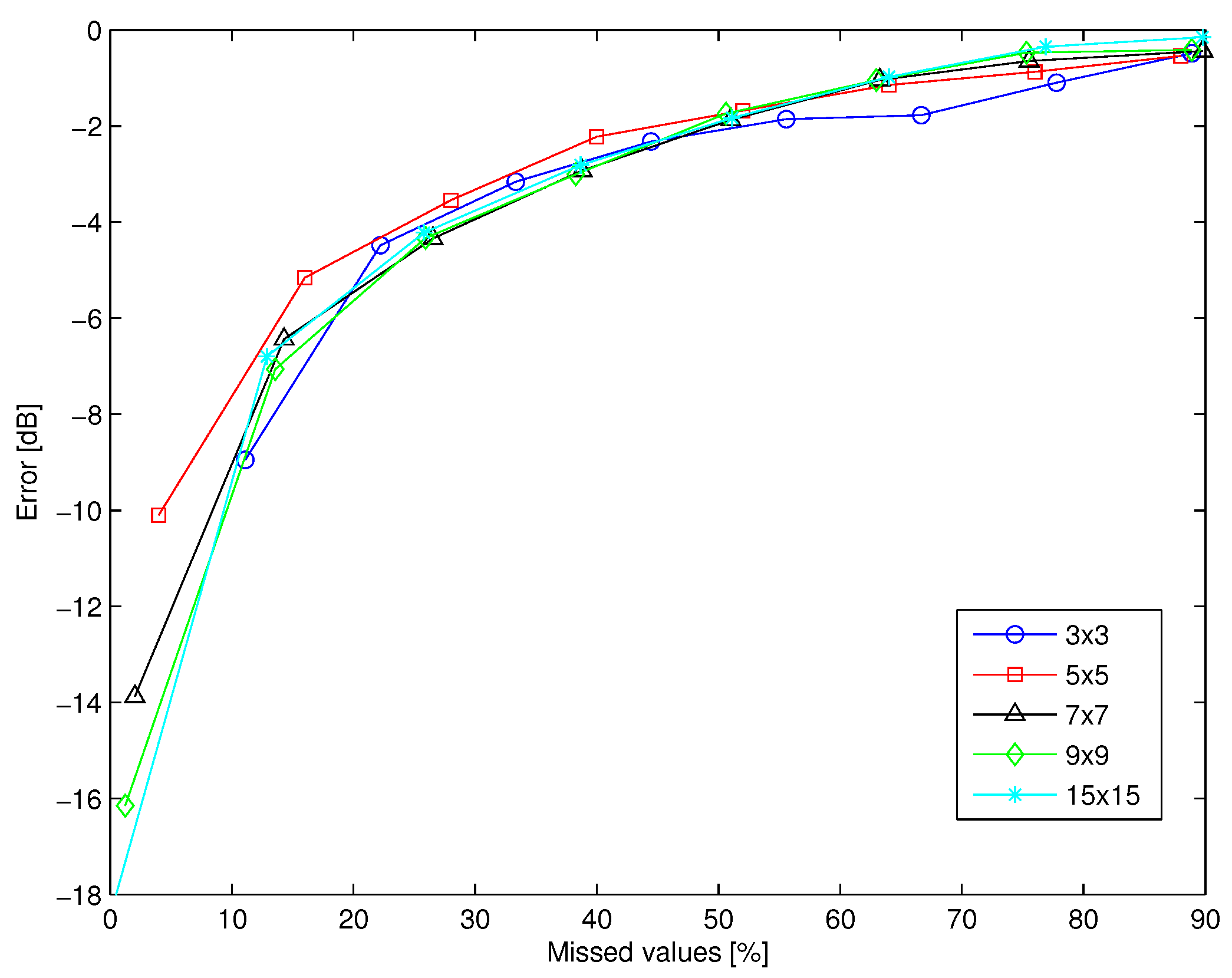
The proposed method is particularly useful in case of large MIMO systems, in which the probability of losing an element is significant. However, it can be used also in smaller MIMO systems, as in IEEE 802.11n radios, that can use up to four radiating elements. In order to investigate the use of the technique in small MIMO systems, the average error (dB) is plotted as a function of the percentage of the missed elements of the channel matrix in case of small (
,
,
,
) and large (
,
) MIMO systems supposing 10 scatterers and a noise level equal to −15 dB and −20 dB in
Figure 5 and
Figure 6 respectively. The plots show that also in case of small MIMO systems we have an interesting performance of the technique.
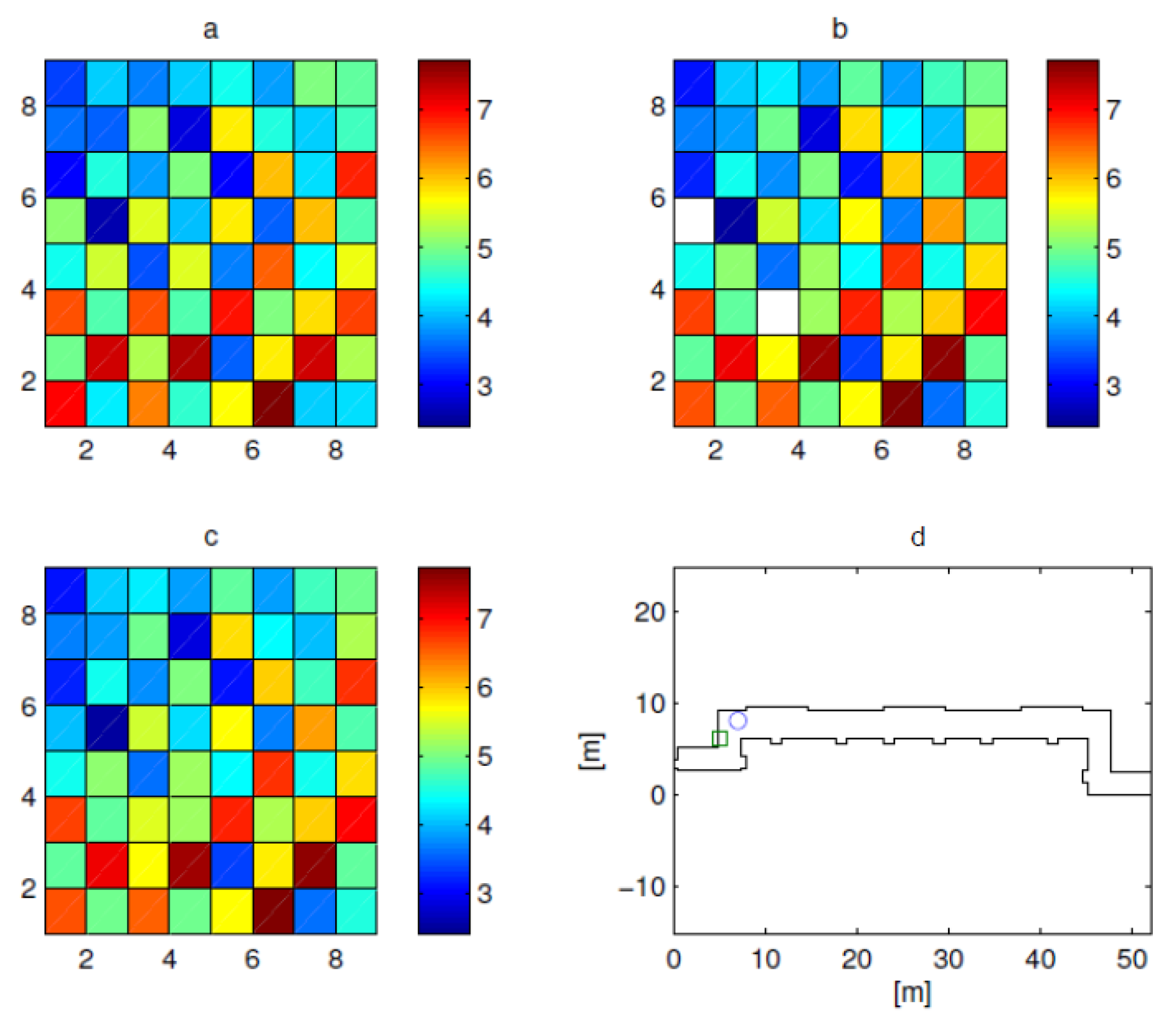
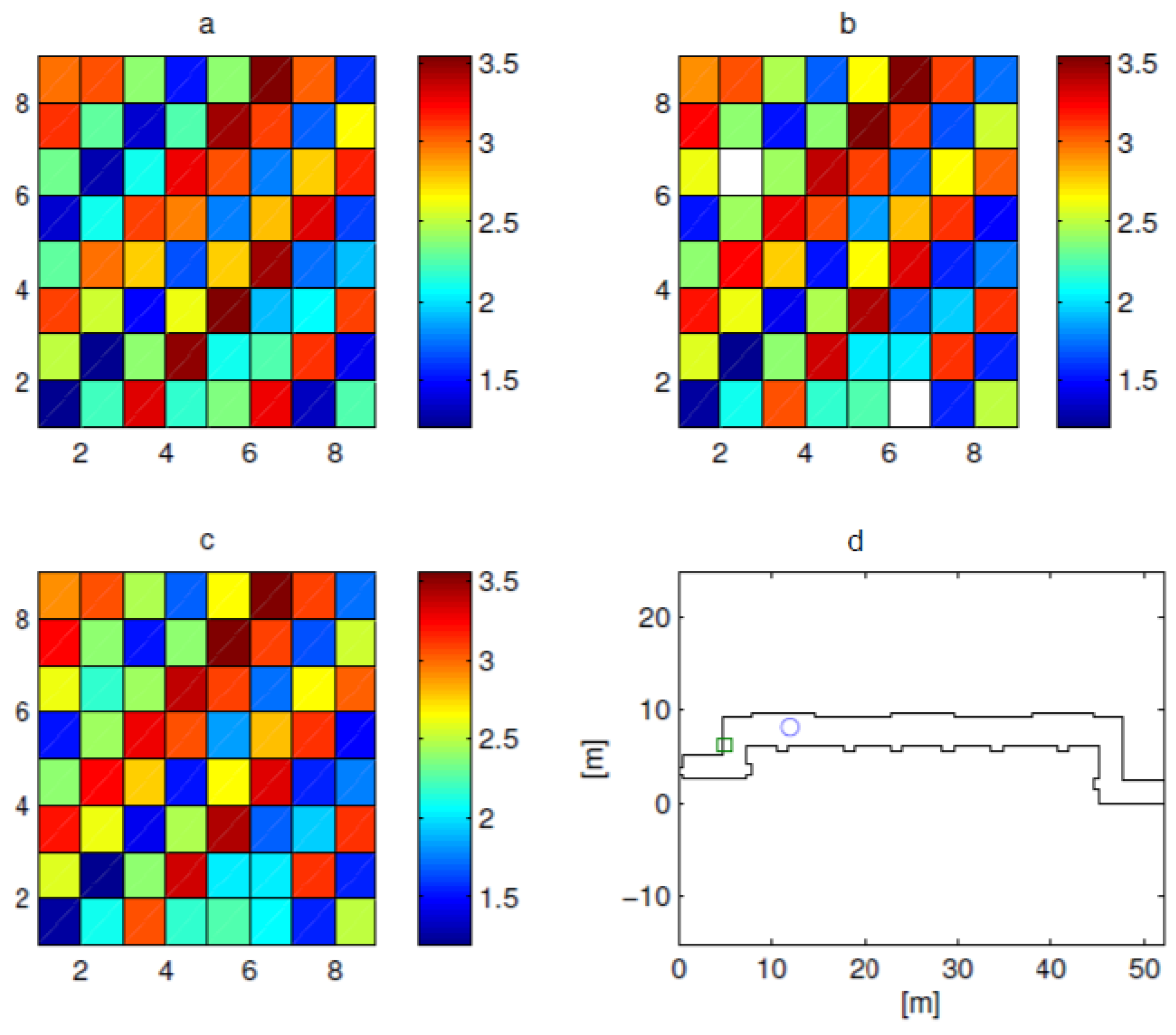
Now, let us show a more realistic scenario, consisting of the corridor shown in
Figure 7d, with a
MIMO communication system. The model is 3D, and the height of the corridor is 3.0 m. The position of the transmitting antenna and receiving antenna is indicated as a green square and a blue circle respectively. Each antenna consists of an array of nine half-wavelength wire antenna radiating elements parallel to the
z axis of the figure working at 2.4 GHz.
The channel matrix was obtained using a 3D ray-tracing algorithm. The algorithm is based on image theory method and considers the dielectric properties of the walls, the roof and the floor, that were supposed to be made by dry bricks with permittivity
[
15]. The simulations were carried out considering a single reflection.
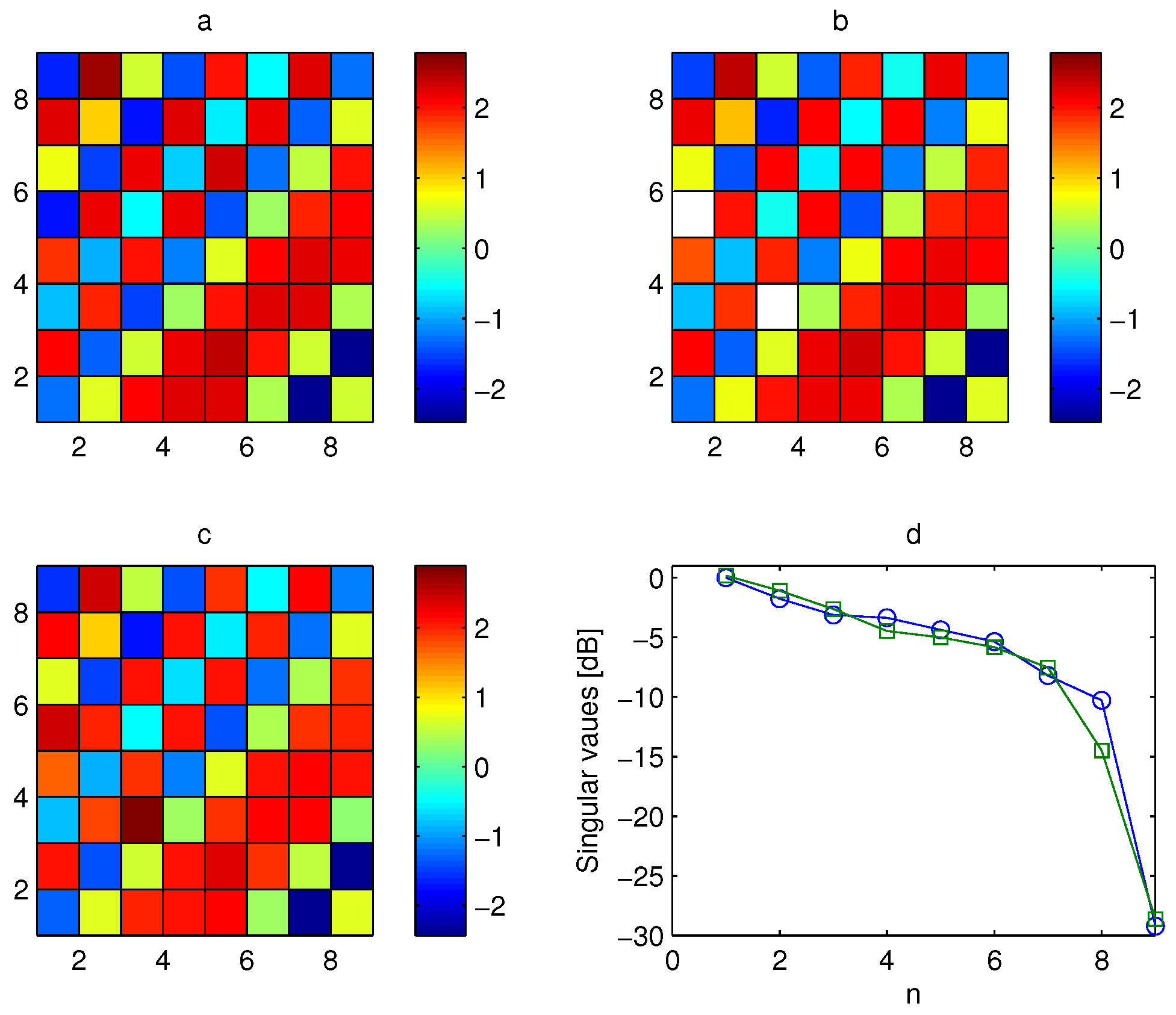
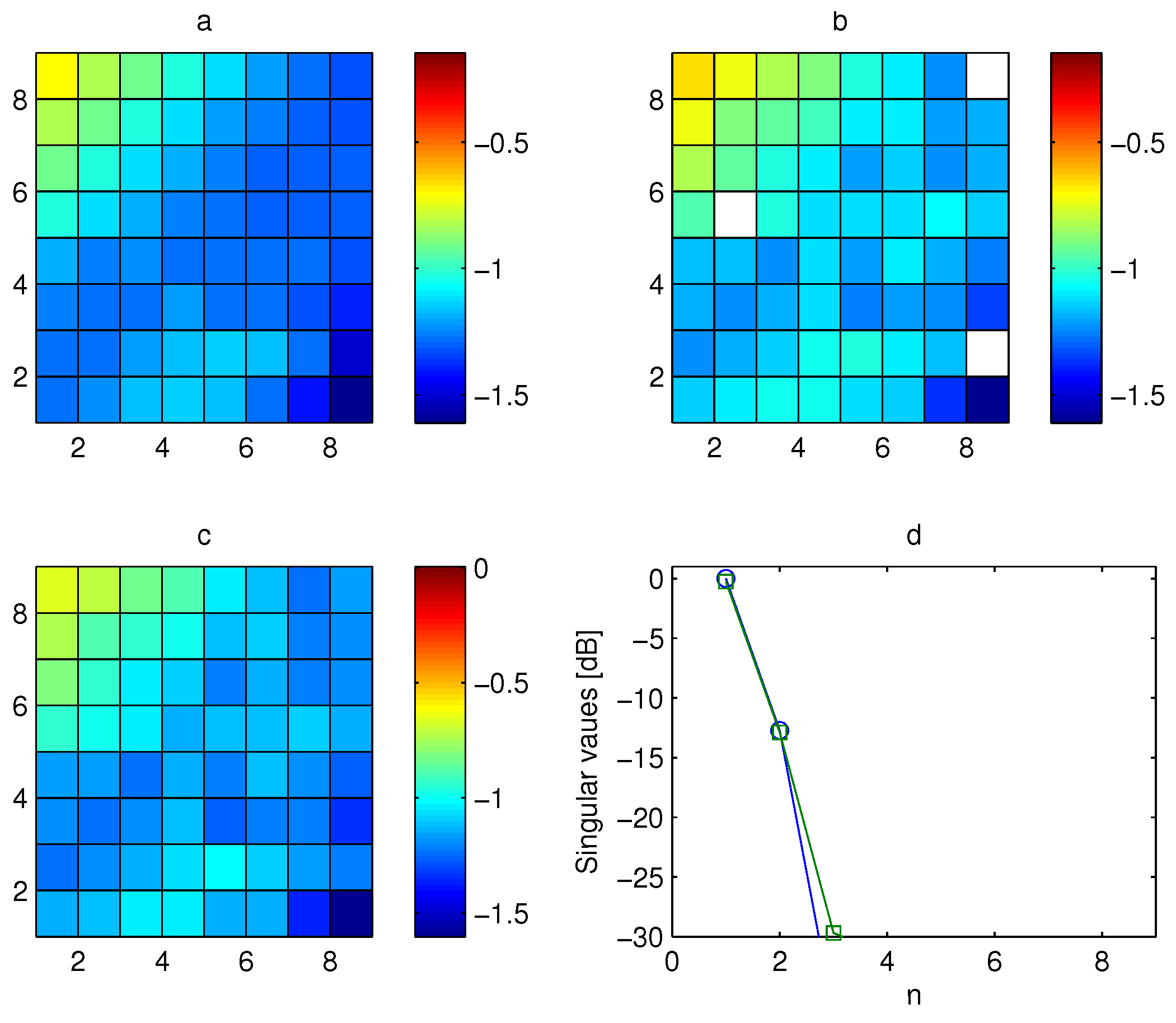
The amplitude and the phase of the channel matrix of the MIMO system are shown in
Figure 7a and
Figure 8a. Two missed elements and 20 dB noise level are assumed during the CSI measurement process. The measured data are affected by 20-dB noise level. The amplitude and the phase of the available data are shown in
Figure 7b and
Figure 8b. The data were elaborated using the proposed algorithm, and amplitude and phase of the estimated channel matrix are shown in
Figure 7c and
Figure 8c. The singular values of the exact channel matrix and of the estimated channel matrix are shown in
Figure 8d respectively as blue circles and green squares. The figures show a good estimation of the channel matrix.
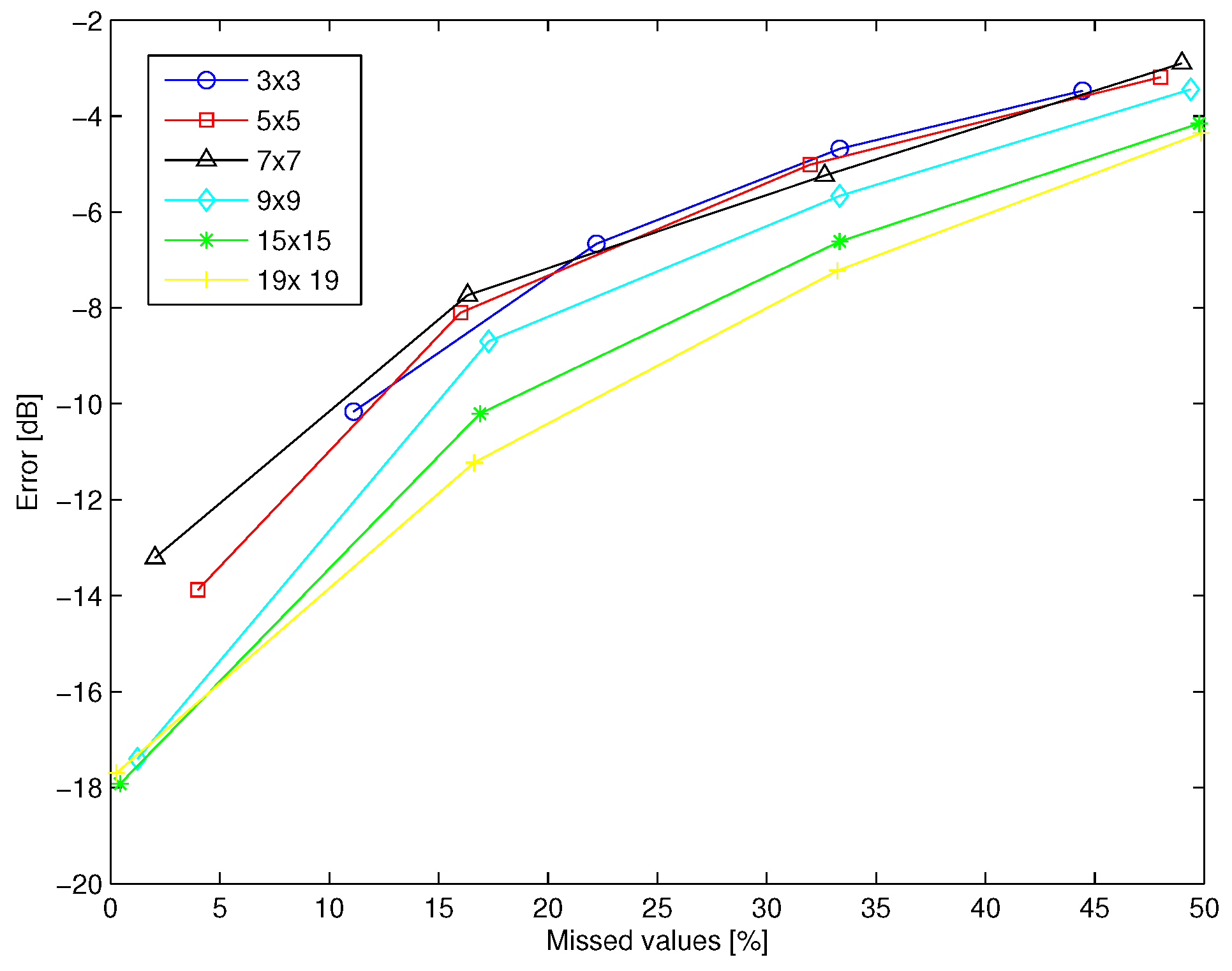
In order to give a more complete view of the performance of the method, in
Figure 9 the error affecting the estimated channel matrix is plotted versus the percentage of the missed elements in case of MIMO systems ranging from
to
elements. The figure shows that the method gives acceptable results also in case of small MIMO systems. However, it is useful to stress that the same value of percentage of missed elements are associated to different absolute number in case of different MIMO systems.
In this example the short distance between transmitter and receiver gives a quite rich channel matrix in terms of number of subchannels, as shown by the relatively slow decrease of the singular values.
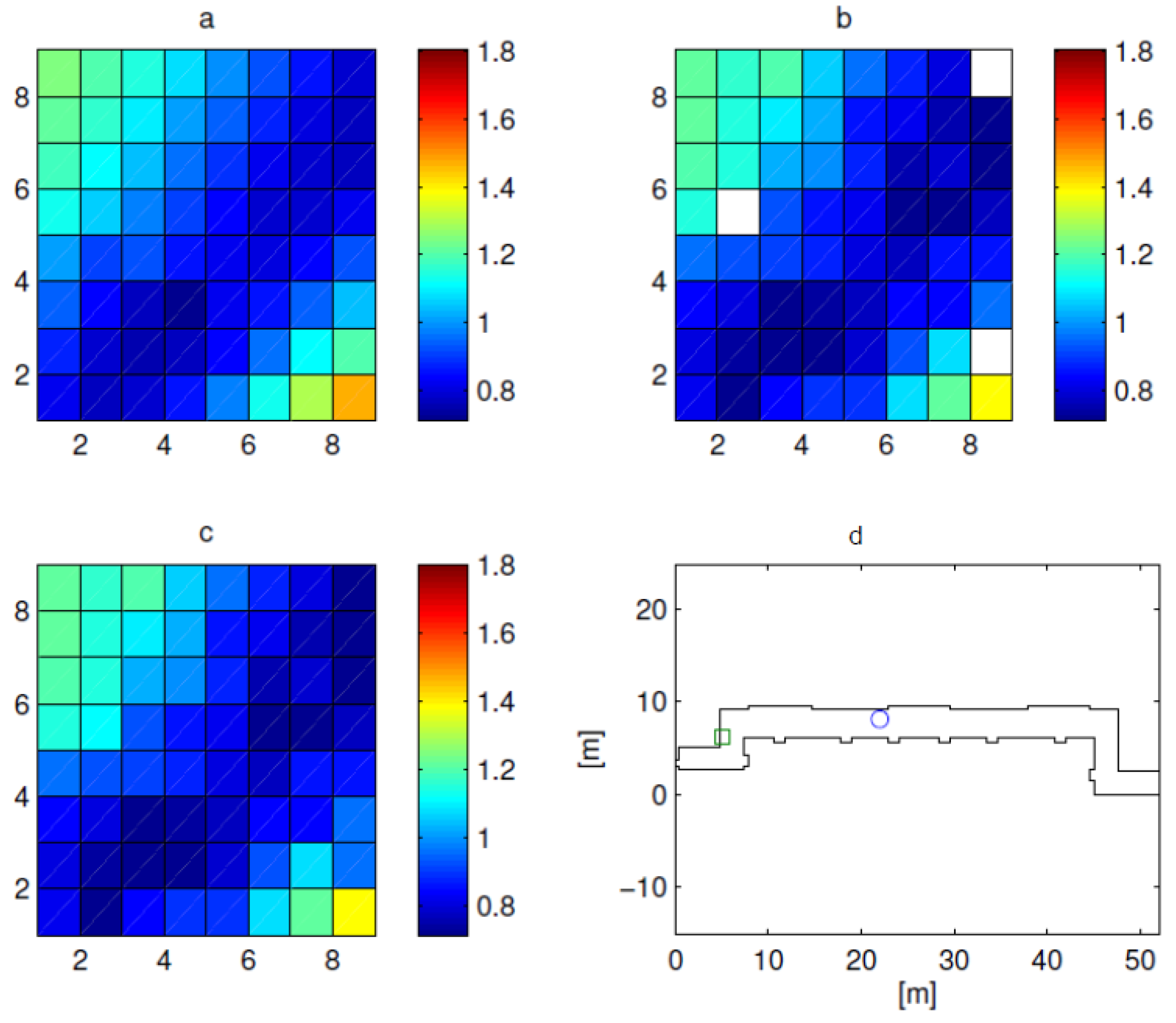
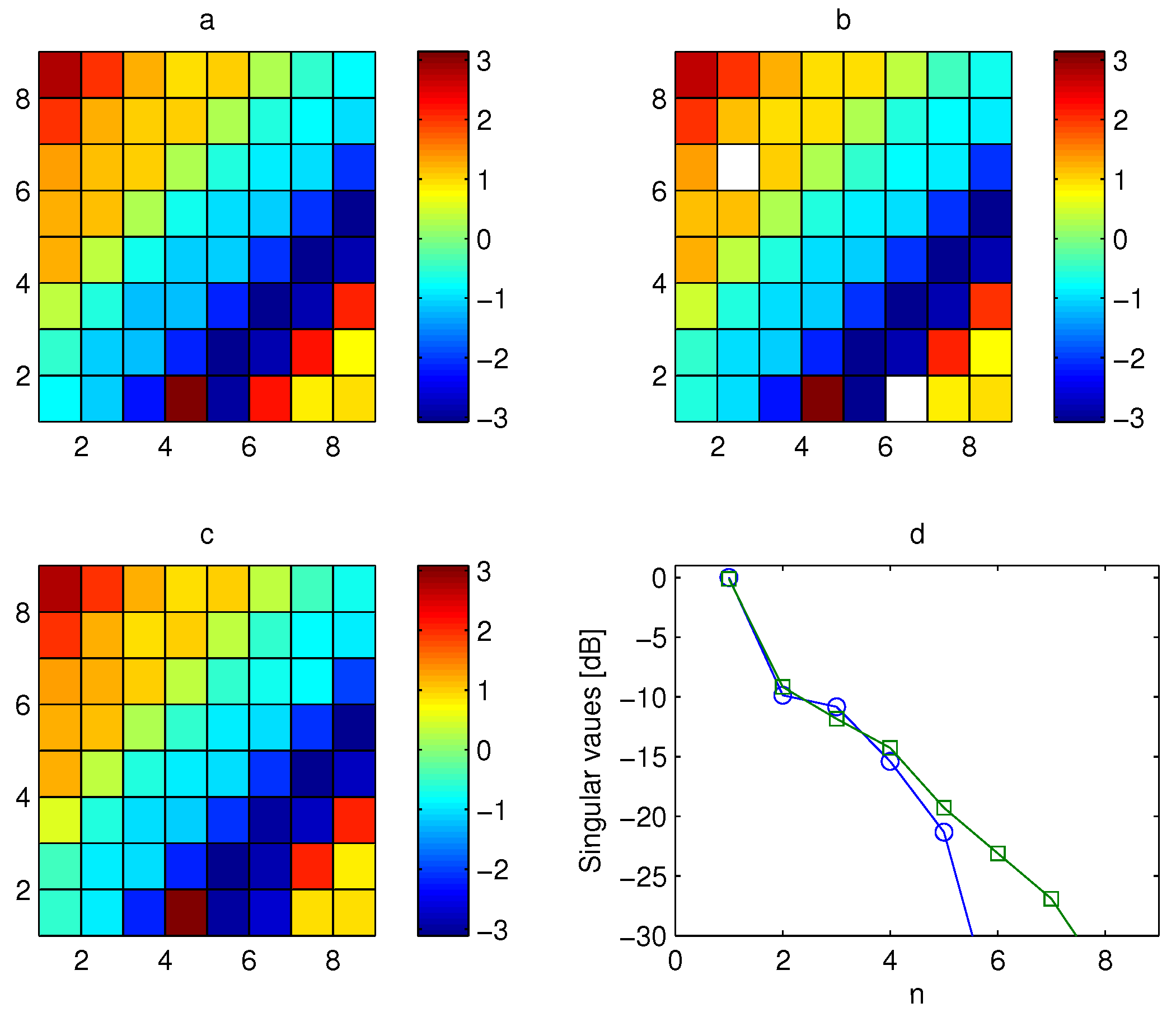
The position of the receiver was moved along the corridor to study the performance of the estimation algorithm in different situations. As an example, the results obtained in two other receiving positions are shown. The positions are reported in
Figure 10d and
Figure 11d. The amplitudes of the channel matrices of the MIMO system are shown in
Figure 10a and
Figure 11a while the phases are shown in
Figure 12a and
Figure 13a. The amplitude of the measured channel matrices, with 25% of the entries lost and the remaining entries affected by 20 dB noise level is shown in
Figure 10b and
Figure 11b while the phase is shown in
Figure 12b and
Figure 13b. Finally the amplitude of the estimated channel matrices is shown in
Figure 10c and
Figure 11c while the phase is shown in
Figure 12c and
Figure 13c. The singular values of the exact channel matrices and of the estimated channel matrices are shown in
Figure 12d and
Figure 13d respectively as blue circles and green squares, confirming the effectiveness of the technique.
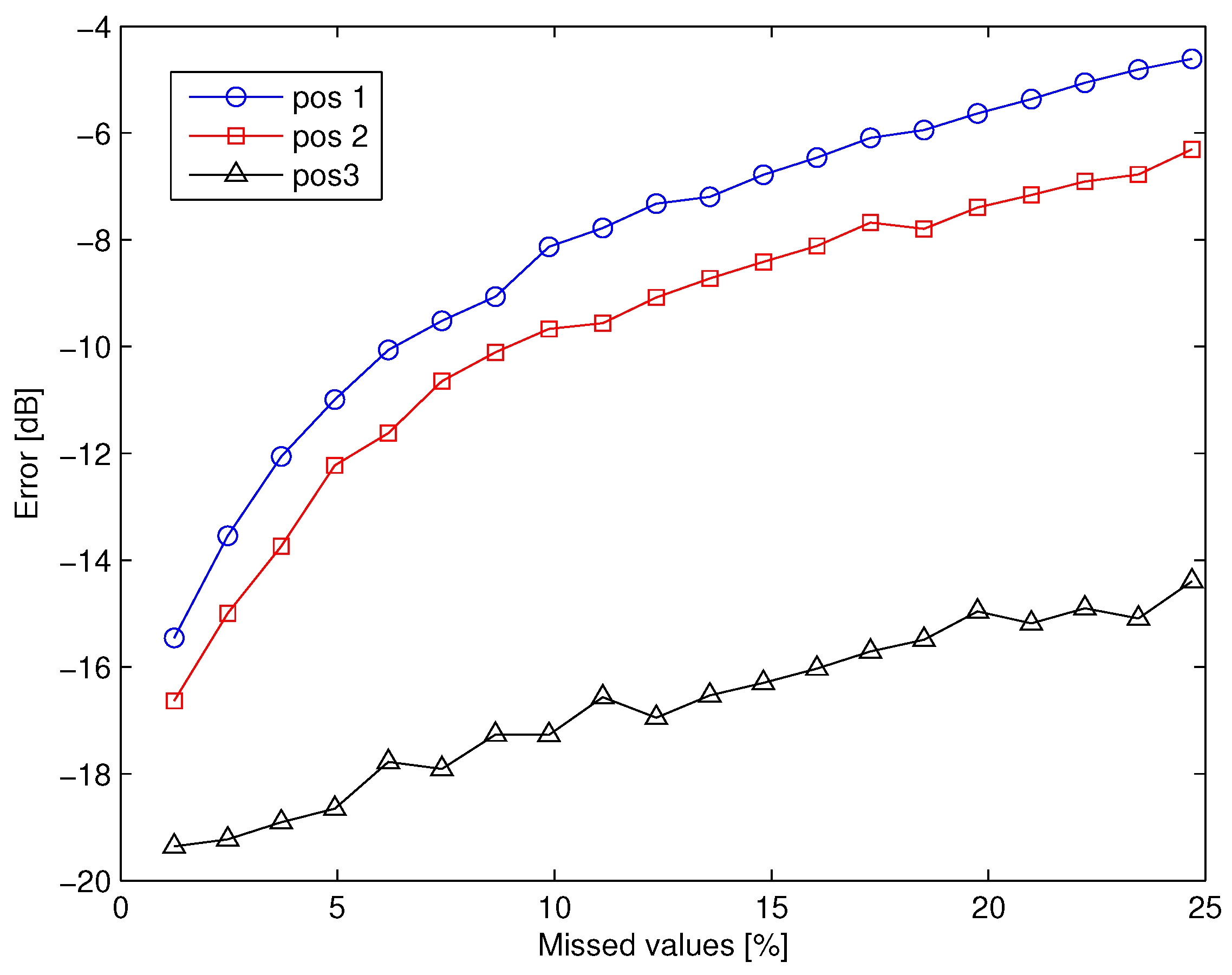
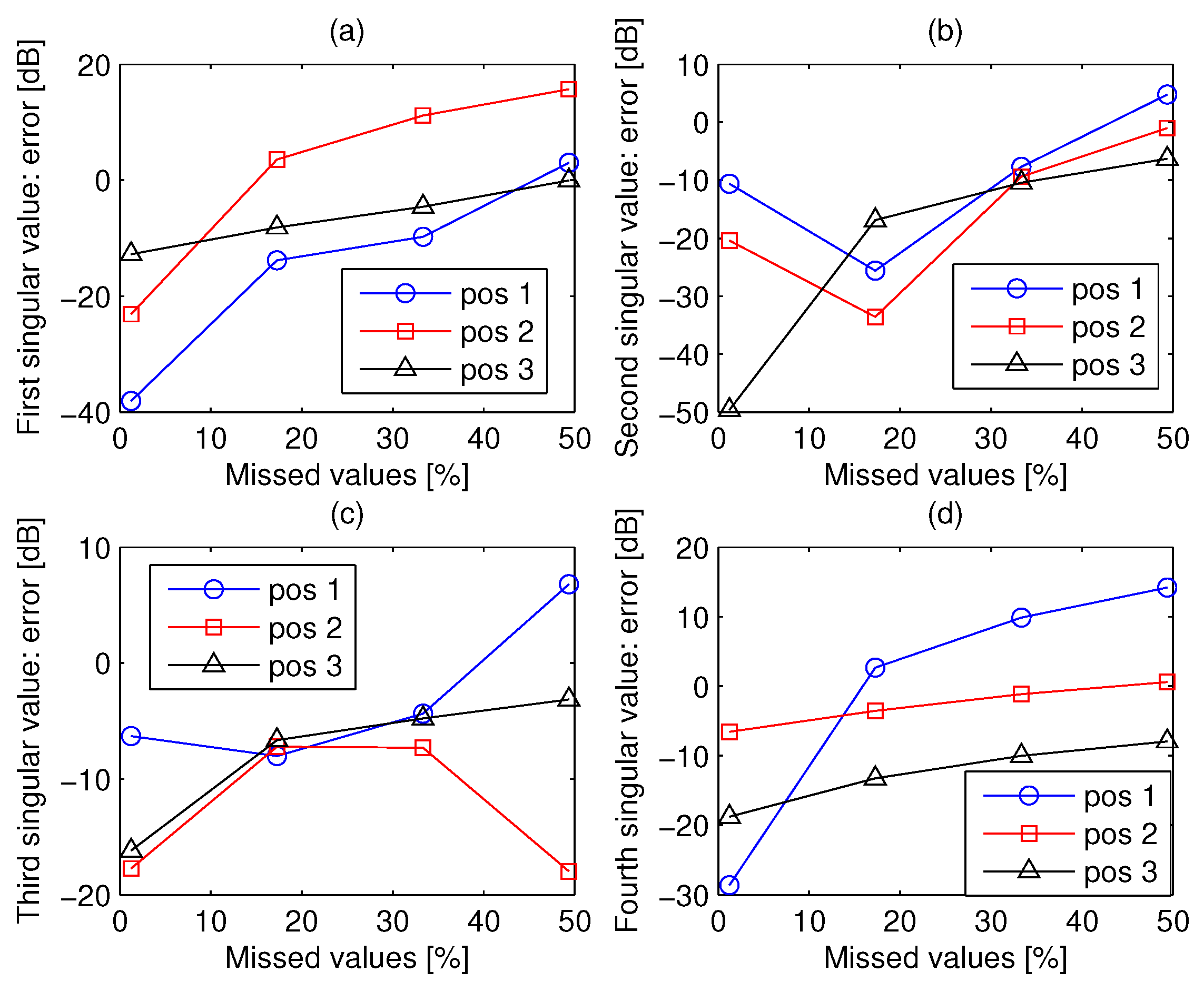
In order to further investigate the technique, in
Figure 14 the estimation error (dB) of the channel matrix in the three positions of the receiving antenna is plotted versus the percentage of the missed elements up to 25%. The figure shows that the best performance is obtained in position 3. This result well matches the electromagnetic model describing the spatial channel. In fact, the number of effective singular values of the radiation operator, and hence the number of MIMO spatial subchannels, becomes smaller when the distance between sources (including scatterers) and receiver increases. Consequently, the channel matrix in case of receiver position 3 is highly rank deficient, making the estimation algorithm more effective. This behavior is confirmed by the error affecting the singular values of the channel matrix, shown in
Figure 15 (first four singular values normalized to the first singular value).