1. Introduction
Like many other cyber-physical systems, the development of drones—which we take here for convenience as also including UAV (Unmanned Aerial Vehicle) systems—is growing at a remarkable rate [
1,
2,
3,
4,
5,
6,
7] in terms of on-board sensing, computing, communication, hovering and locomotion capabilities. There is also increasing diversity in their design, particularly among smaller autonomous drones which can hover and maneuver freely and are sweeping the commercial market [
7]. Indeed, hobby drones that are ready-to-fly off-the-shelf are now in the hands of people of all ages and backgrounds, including children. A casual look at a well-known online shopping site shows that over the past few years there has been a near ten-fold increase in the range of designs and companies building them. Civilian drones now vastly outnumber military drones, and there is an upward trend with the Federal Aviation Administration (FAA) estimating that consumer sales could grow from 1.9 million in 2016 to as many as 4.3 million by 2020 [
7].
This rapidly expanding market among the general population and companies (e.g., Amazon) for such small but agile autonomous devices, will likely drive a rapid increase in the heterogeneity of drones that are airborne at any moment, as well as their number. Just as happens with regular road traffic, they will likely often be trying to access the same part of airspace, or send messages using the same bandwidth range, meaning that they can produce congestion and potential traffic pile-ups as in regular road traffic but with the added risk that they then may fall out of the sky and/or fly into buildings or other human obstacles. Hence, there is an urgent need to understand the tendency of an airborne population of autonomous drones to produce congestion. Since congestion means crowding, this, in turn, means there is a scientific need to understand the dynamics of real-time crowding behavior in a population of heterogeneous, adaptive drones, and how this might affect public safety [
2,
7].
The question that we attempt to address here, albeit in a simple way, is: Is there a set of minimal yet generic design features that can be employed across a heterogeneous population of drones, such that those that happen to be airborne at any one time access a popular region of airspace, or popular communications bandwidth,
without generating large fluctuations due to crowding and hence lessen the chances for accidents? One way to approach this issue might be through regulation. However, just as with everyday car traffic, regulation alone does not prevent accidents [
7]. Another approach is to install additional software that pins down more precisely exact flight paths. However, given the rapidly changing environment seen by a flying drone in terms of obstacles and other drones, this would require a significant increase in on-board processing, together with additional power use, hence adding to the drone’s weight and reducing the total time that it can remain airborne. The use of a virtual tether has also been considered, but this could be challenged as favoring certain businesses of neighborhoods while punishing others. Various crash-avoidance technologies comprising low-powered anti-collisions systems with sensors and machine-learning algorithms, are also possible, but smaller drones would suffer from the same issue of increasing the need for sophisticated on-board computing while draining the power more quickly and adding to the weight [
2,
7]. Indeed, as emphasized in Reference [
2], ‘Flight is energetically expensive, particularly when the size of the device is reduced’. Even the proposal to micromanage every trajectory of every drone in real-time, and send out system alerts, is unrealistic given the wide variety of adaptive behaviors that may characterize a heterogeneous drone population—just like everyday traffic on the street cannot be micromanaged. A solution for a small number of drones
if one has complete control of the environment, is to calculate numerically some optimal solution based on the details of the machines themselves and the environment, and then implement this or embed it in each component’s software and firmware design. However, in the real world, this would need to be done in real-time and would involve accounting for possible other drones in the vicinity. In addition, many commercial drones may have proprietary information in their design and data storage, thereby making conventional optimization and control approaches impractical and unscalable to large numbers of drones
N. Added to this, there is always the unknown natural factor of gusts of wind, etc., which add additional variability to the environment, in particular for smaller drones.
We propose here a different approach that is built around collective competition and only requires feedback of global information about overall system behavior, as opposed to the requirements for real-time cooperation between individual drones. Specifically, it eliminates the need for costly drone-to-drone communications, which, for a population of
N drones, would require keeping open approximately
possible communication links. It also requires minimal on-board computational capabilities within each drone. Indeed, we show that the required memory storage grows sub-linearly with the number of drones
N, as opposed to possibly growing as ∼
for schemes involving drone-to-drone communication. We stress that our scheme will tend to reduce collisions by diluting pockets of crowding in the
N drone population, but does not eliminate them—however, simple proximity sensors can then be added to each drone to detect and hence avoid others that are within a certain radius, without the need to know their identity or specific missions. For concreteness, we will describe our approach in terms of a population of
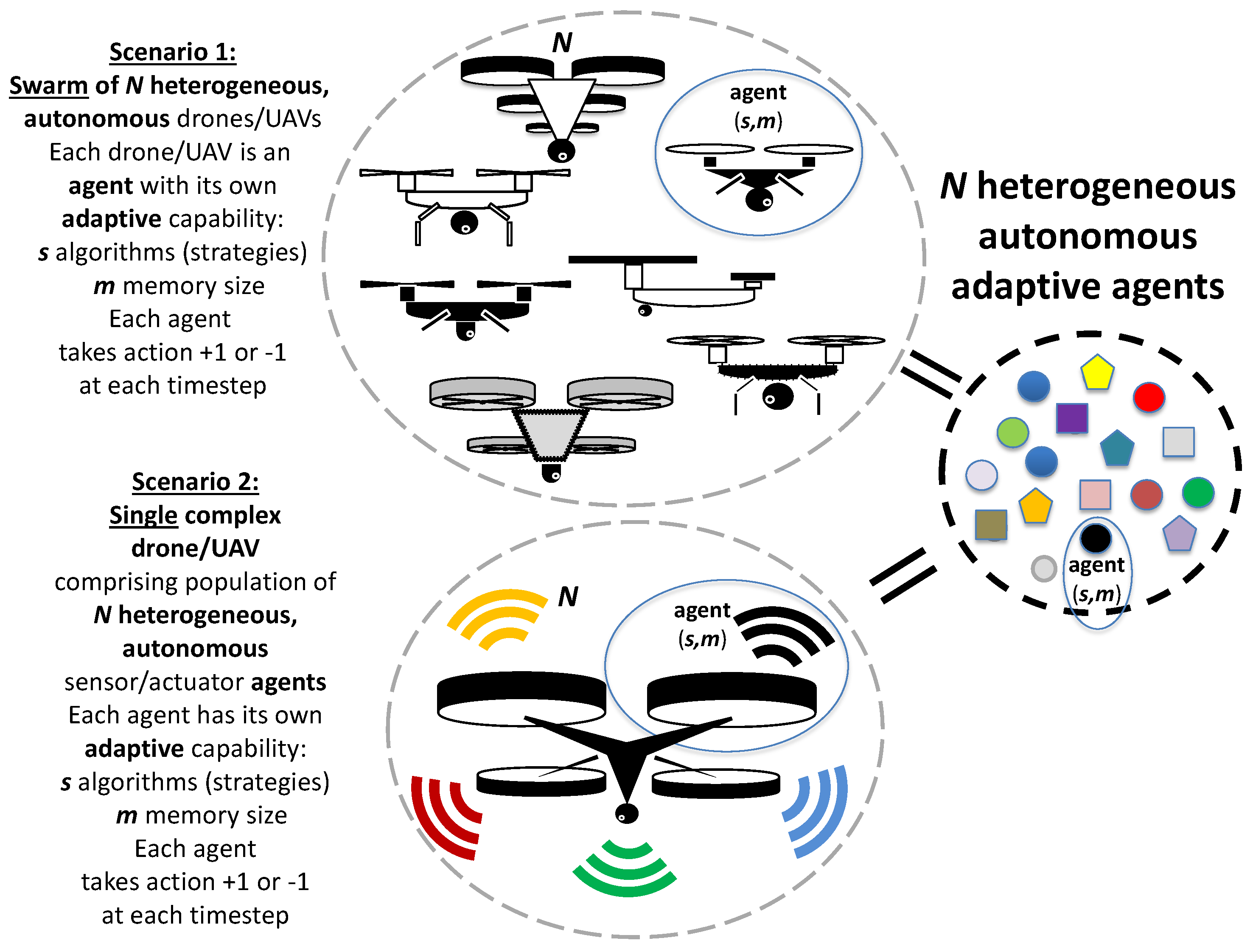
N heterogeneous, autonomous drones as in Scenario 1 (
Figure 1). Using analysis inspired by the physics of many-body systems [
8,
9,
10], we provide closed-form formulae for the optimal range of on-board computational capabilities as a function of the number of drones
N that are airborne in a given region of airspace. Our results are obtained for a system in which the capabilities of each drone (which are measured by
s and
m) are independent of the number of drones
N. This is in stark contrast to schemes which depend on two-way interactions between drones for coordination, and hence whose required on-board resources will need to scale up as
. In addition to populations of drones, the same competition-based design and mathematical results that we provide can be applied to the case of a single complex drone shown schematically in Scenario 2 (
Figure 1), i.e., it can be used to reduce crowding in terms of battery use by the population of on-board sensor/actuators in a single drone, and also reduce message congestion within the drone’s central processor.
Though Scenario 2 is not realistic given current technology, it instead is aimed at exploring a futuristic possibility inspired by living systems. Specifically, it is known [
11] that Drosophila larvae show remarkable abilities in terms of being able to regulate and balance the tasks for movement, momentary stationarity and turning, without the potentially costly overhead of a large, centralized control. In particular, large turns are achieved by the collective output of individual segments of the larva’s body which are effectively like the individual agents in Scenario 2. Each acts as a sensor and actuator, and is semi-autonomous as in Scenario 2. More generally, we note that the idea that advances in system design can usefully learn from Nature’s own evolutionary solutions, has attracted significant attention in recent years and looks set to make an impact on future generation designs—see, for example, References [
12,
13]. Our intention in this paper is to look toward a future set of design ideas which could act as guiding principles as systems become more complex and hence centralized control and management becomes impractical for certain real-world situations where security is a prime concern. It is not our intention to provide a detailed review of the state of the art of current UAS (Unmanned Aircraft Systems) traffic management, either in terms of current technology (e.g., ADS-B which stands for Automatic Dependent Surveillance-Broadcast) or current regulations. The current ADS-B technology, which is reviewed in Reference [
14], is a surveillance technology in which a drone establishes its position by means of satellite navigation and then regularly broadcasts it, meaning that it can then be tracked by a centralized controller. Scenario 1 imagines a future situation in which the density for satisfying ADS-B, and any future variations, has been saturated to the extent that centralized control becomes impractical or unsafe—or, equally, where the threat of intentional system attacks is so significant that a centralized controller is deemed too vulnerable as a design option. Whatever the specific numbers for which these settings might arise, there will be a feasible future scenario in which decentralized control becomes favorable in terms of security.
We also wish to stress that large swarms of very simplified drones are currently considered desirable for certain future operations such as infrastructure testing in scenarios where robustness against the loss of a number of drones is a primary requirement, and where each drone has minimal on-board processing requirements (see Reference [
15]). Our Scenarios address precisely this setting. We therefore continue this paper with a forward-looking discussion of future generation scenarios in which decentralization is the preferred choice.
2. Model Motivation and Setup
Our approach is inspired by, and draws together in a unified way, machinery from the field of complex systems and many-body statistical physics [
8,
9,
10]; recent works on a market-based approach to the distribution problem [
16]; and works on scaling laws for such systems [
17]. We refer to References [
8,
9] for more detail, as well as Reference [
10] for a more general formulation in the language of many-body physics. We start by recognizing the fact that despite their diversity in design details, size and weight, all drones tend to comprise some level of computing capability such as a single-board computer; sensors which give information about internal and external state of the craft; actuators which link through to engines or motors and propellers; some software which manages the system in real time and responds quickly to the changes observed in the sensor data; and of course a power supply, which is typically a lithium-polymer battery for small drones [
2]. The key features of a drone that we incorporate explicitly into our modeling here are: the ability for data storage; the ability to sense information from the outside; the ability to take an action, for example to turn left or right in an attempt to access the less congested of two options, or to decide to transmit or not transmit through a potentially congested bandwidth; and the ability to adapt their decision making over time by having several algorithms stored whose relative ranking in terms of past performance is known (i.e., the drone processor knows at each timestep which is the better of the two operating algorithms (strategies)).
The specific scenario that we imagine in this paper, though generalizable, is that of competition among the
N drones in Scenario 1 (
Figure 1) for the less crowded of two options. This could be spatial, i.e., as in regular road traffic, with the more crowded of two otherwise identical roads being the worse choice. Since all
N cars (drones) are making this binary choice at the same time, and the winning choice will depend on the aggregate of these
N actions after the fact, there will be no way for any individual car (drone) to work out this correct option deductively without having to contact each other car (drone) in turn and then trust that each has reported reliably what they will do. Instead, each drone has
s algorithms and at any given timestep will use the one which happens to be the better of the two in terms of past performance, in order to decide its next action. Alternatively, the same two-option scenario arises in the decision of whether or not to make a communications transmission at a particular instant in time or not, with the consequence that if it does transmit and the channel is overcrowded, then the energy spent transmitting will be wasted. Hence, the action to transmit would have been the wrong one. Indeed, it is known that a growing challenge for designers and engineers in the area of communication and control of drones is the narrow transmission bandwidth available since it is finite and constantly shrinking [
18,
19]: the fast advancement of wireless technological tools demands open networks to operate properly and hence contributes to the bandwidth shrinking process. Any purely cooperative approach is heavy on resource consumption since a system of
N units has
interaction pairs that each need to be made available to create a consensus. In addition and in contrast to the scheme presented here, if one link is lost in such cooperative approaches, then the unity of the system may collapse and unwanted outcomes generated. As mentioned above, many other two-option scenarios are possible such as a choice between two patches over which to hover, with the less crowded choice being the better since it will reduce the chance of random collisions. For the scenario of the individual drone designed with a collection of semi-autonomous sensors and actuators as in Scenario 2 (
Figure 1), this two-option competition could be used to represent the decision to draw power or not, and hence the systemic risk lies in potentially overloading the system and bringing the drone down from the sky. Hence, these binary scenarios, while lacking in specific detail, capture a wide range of relevant safety situations for drone and UAV systems. Indeed, any complex real-world situation will have a tree of decisions that can each likely be broken down into a succession of such binary decisions, hence the broader relevance of our discussion and mathematical analysis for general cyber-physical systems (CPS).
All these limited resource scenarios have the common setup of having two options which are
a priori equally good, but for which the less crowded one is subsequently deemed as the winning option. This enables the problem to be mapped onto the so-called minority game as studied in the many-body physics of complex systems [
8,
9,
10]. The minority game has also been considered in the area of energy resource management [
20] and wireless networks [
21], though not with the same analytic results and insight that we present here. Indeed, our analytic results provide closed-form mathematical expressions which are valid for any
N and for any such binary choice scenario involving drone navigation or communications—or for an individual drone. Our results therefore provide insight for both individual machines and swarms of such machines, and avoid demanding pair-wise communication between the components pieces (
Figure 1). By contrast, conventional distributed approaches, including those of traditional game theory, become increasingly complex for such a system as
N becomes larger, since they depend on the number of possible links between agents (i.e.,
) and hence generally increase as some power of
N or even exponentially.
The main method used in this paper is the basic minority game simulation whose code is available freely online from a number of different sources: see, for example, the NetLogo version of the code which is explained in detail in Reference [
22]. This version is preferable since it is platform independent and requires no particular knowledge of programming in order to run it. A full description of the minority game model is given in References [
8,
9,
10], where the derivations are given in more detail. Together, these provide sufficient details to fully replicate our results.
3. Collective Coordination through Competition
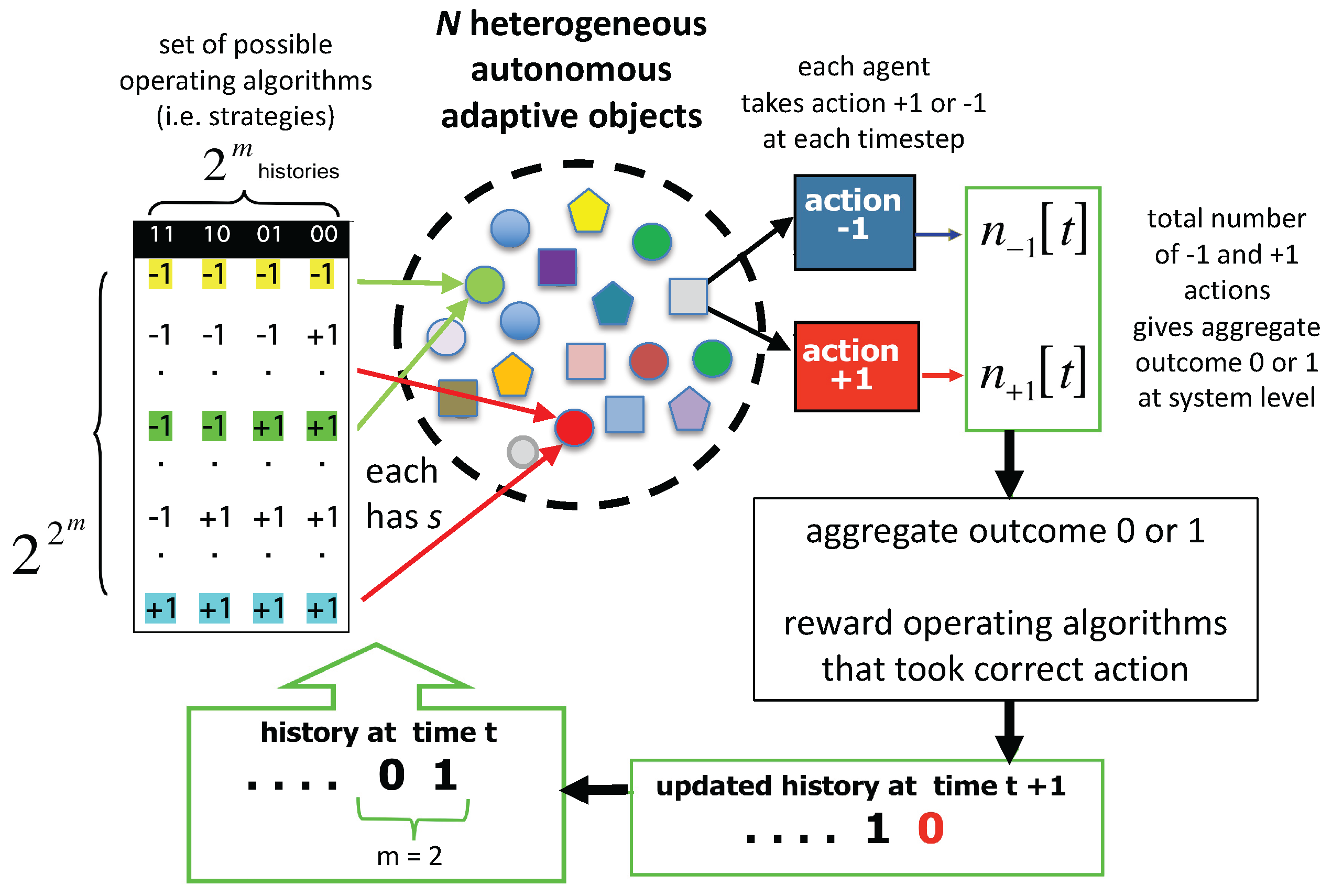
Figure 2 summarizes the dynamics of the population of
N heterogeneous, autonomous drones (i.e., agents) that we consider. The key features of our setup are that each drone has some memory of the past (
m) system outcomes (i.e., history) and also has a modest number (
s) of on-board algorithms (i.e., strategies) among which it can choose its highest performing one at any given timestep, when deciding what action to take. The reason why the
possible combinations of action outputs (i.e., strategies) listed in
Figure 2 corresponds to a complete set, i.e., full strategy space, is worth stressing. Irrespective of its nature, any algorithm that the drone could conceivably have, will necessarily be deterministic. Hence when fed with any of the
possible inputs corresponding to the global outcomes over the prior
m timesteps (00, 01, etc.. for
), it must either produce as its output the action
or the action
. Thus, for every possible algorithm, the output for each of the
possible inputs is either
or
. Each of these permutations of
and
(i.e., each row of the table in
Figure 2) can be regarded equivalently as a strategy. There are
possible permutations of
and
for a given
m, i.e., there are
possible strategies. This means that the full strategy space contains precisely
distinct strategies. Strategies are assigned randomly among the different drones at the outset of the simulation. Due to the random strategy assignment from this strategy space at the start of the simulation, the subset of
s strategies held by each drone is generally not the same for different drones. This mimics the fact that the drones are heterogeneous in their design, being made by a different company and/or for a different purpose.
There is no central controller, other than the equivalent of a central scoreboard which collects the aggregate actions and updates the string of m most recent global outcomes with the winning (i.e., minority) choice, i.e., 0 or 1. These m most recent outcomes are then fed back to each drone which stores them in its memory (or, equivalently, it updates its memory with the most recent outcome) along with the relative success of its s on-board algorithms in predicting the correct action since the beginning of the simulation. At each timestep, every strategy is rewarded or penalized according to its ability to predict the winning group (i.e., less crowded option). Drones adapt their decision-making process by selecting the strategy that happens to rank the highest based on prior outcomes. All units receive the same feedback but since they hold different strategy sets, the highest scored strategy can differ from one drone to another. No communication is necessary among them (i.e., no cooperation) to execute the next decision. The agents themselves (i.e., each drone) are adaptive in that they can switch between the strategies that they possess, according to past performance of these strategies. In future settings, if one wished to model a drone that could adapt by real-time rewriting parts of its operating algorithms and hence strategies, it would be possible to incorporate this in the model by having the agent sporadically pick up new strategies from the pool when the ones that the drone has are not performing well.
While this setup is clearly a significant oversimplification, it does contain the basic principles and competition that a realistic system would have, without getting lost in the detail of individual designs and implementations. The combination of the heterogeneity in operating algorithms combined with feedback of the same global information, leads the N drones to unwittingly divide themselves into two groups at each timestep without any external controller deciding the split. Moreover, the precise split in terms of numbers and membership changes over time, since each drone continually adapts by choosing to use the best of its s operating algorithms in taking its next action. The smaller group is considered to be the winner since it is less crowded and will therefore likely have less accidents due to collisions.
We now proceed to calculate the fluctuations in this system, and, in particular, their dependence on the three variables
N,
m and
s, i.e., the number of drones
N, the size of the on-board memory
m and the number of operating algorithms
s per drone. A convenient system output quantity whose fluctuations we will calculate is the ’excess demand’ given by:
In an ideal world,
for all time
t meaning that the occupation of 0 and 1 would always be essentially equal. For example, for a number of drones
, the occupancies would be 50 and 51 always no matter whether 0 or 1 was the minority choice, and hence
always. If instead the
N drones each flipped a coin to decide their action, then
is the same as a coin-toss for
N coins. We are interested here in the standard deviation of
since this gives a measure of the fluctuations in the system, and hence the size of typical fluctuations in the system—and ultimately the risk in the system. For a full derivation of the closed-form mathematical expressions associated with
Figure 3 and
Figure 4, we refer to References [
8,
9,
10]. Here, we content ourselves with a calculation of the small
m case with
, but for any
N, since this will enable us to identify the minimal value of the drone memory
m that is required in order for the system’s fluctuations to be smaller than the coin-toss (i.e., random) value, hence demonstrating the emergence of collective coordination in the
N drone system as a result of global competition.
The key first step is to understand the correlations in the
N drones’ actions, which, in turn, depend on their respective strategies. Such correlated actions can arise spontaneously even though this is a competitive system because subsets of drones may happen to use the same strategy at the same time, giving rise to sudden crowding and hence congestion, and therefore large fluctuations in
. These correlations have their root in the details of the strategy space, shown in
Figure 2 for
. There are subsets of strategies in this full strategy space such that any pair within this subset has one of the following characteristics:
anti-correlated, e.g.,
and
, or
and
. Any two drones using the (
) strategies
and
, respectively, would take the opposite action irrespective of the sequence of previous outcomes and hence the history. Hence, one drone will always do the opposite of the other drone. This is the key observation that leads to our crowd–anticrowd description and hence the mathematical results presented in
Figure 3,
Figure 4 and
Figure 5. When one of these drones chooses
at a given timestep, the other drone will choose
. The net effect of this on the excess demand
then cancels out at each timestep, irrespective of the history, and so does not contribute to fluctuations in
.
uncorrelated, e.g., and . Any two drones using the strategies and , respectively, would take the opposite action for two of the four histories, while they would take the same action for the remaining two histories. If the histories occur equally often, the actions of the two drones will be uncorrelated on average.
Based on this observation, we can now construct a reduced strategy space which provides a minimal set that spans the full strategy space and yet is easier to deal with mathematically. The results for the fluctuations in
simulated numerically using this reduced strategy space and the full strategy spaces are almost identical since the reduced strategy space respects the correlations in the fuller structure. Consider the following two groups of strategies:
and
Any two within are uncorrelated, likewise any two within are uncorrelated. Moreover, each strategy in has an anti-correlated strategy in : for example, is anti-correlated to , is anti-correlated to etc. This subset of strategies comprising and forms a reduced strategy space that has a smaller number of strategies .
We stress that our approach does not use vehicle-to-vehicle communications but instead employs simple vehicle-to-infrastructure interaction as in present designs. However, the amount of data required is small compared to location and trajectories data of the many drones that might be present within a swarm. Although global monitoring is still needed, it is only required in its simplest form, i.e., a simple +1 or −1 from each vehicle. No knowledge of which drone is sending the information is required, meaning that if this information were illegally intercepted, the information would not be significantly beneficial to the eavesdropping entity. Thus, our approach could be implemented when the number of UASs is large to the point of slowing down the data processing and bandwidth access due to the large volume of transfer.
4. Results
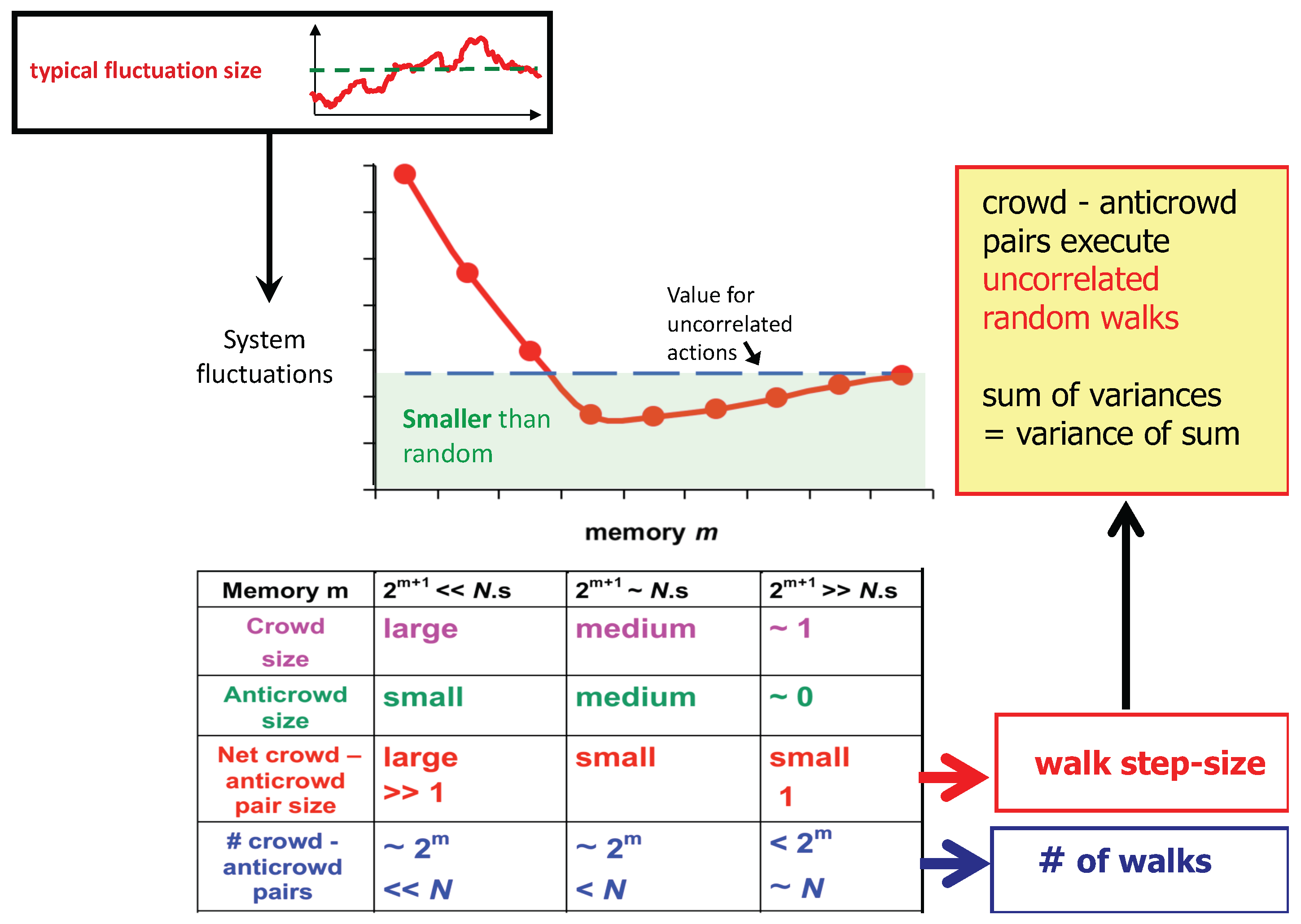
Figure 3 demonstrates schematically the variation that this crowding into strategies and their anti-correlated partners will have on the fluctuations in the
N-drone system. The correlations that drive the
N-drone dynamics effectively separate into crowd–anticrowd pairs containing a crowd of drones using a particular strategy (e.g.,
in
Figure 2) and an anticrowd which uses the anticorrelated strategy (
in
Figure 2). The anticrowd will therefore always take the opposite actions to the crowd, and so the net impact of a given crowd–anticrowd pair on the dynamics is given by the difference between the crowd and anticrowd sizes. The crowd–anticrowd pairs themselves are uncorrelated, hence their aggregate impact of all crowd–anticrowd pairs on the fluctuations can be approximated by using the fact that the sum of the variances is given by the variance of the sum. Assuming that each crowd–anticrowd pair executes a stochastic walk that resembles a random walk, one can then obtain an expression for the overall
N-drone fluctuations (see later). Remarkably, above a certain critical value of
, the fluctuations are predicted to be
smaller than they would be if the drones behaved randomly with respect to each other. This is because of the near cancellations when a given crowd and anticrowd have similar sizes, meaning that the net variance of this crowd–anticrowd pair is far smaller than if its drones were uncorrelated. We stress that this collective action is entirely involuntary among the population of drones—it arises spontaneously and is hence an emergent phenomenon. This particular curve shape in
Figure 3 is confirmed by the numerical calculations in
Figure 4. Even though the
N drones are continually competing for space, coordination can be seen to emerge for ’free’.
We now calculate a closed-form expression for
in the case of
operating algorithms per drone, which is applicable to
any number of drones, i.e., it is perfectly scalable to any
N value and actually gets more accurate as
N increases. As mentioned above, the way that we have grouped together the correlations between drones means that we can use the known mathematical identity that the variance of the sum will be equal to the sum of the variances in order to write the square of the standard deviation (i.e., variance) of
as:
where
is the crowd size (i.e., average number of drones) that uses the strategy ranked
K in terms of performance (i.e., points) while
is the anticrowd size (i.e., average number of drones) that uses the strategy ranked
(i.e., the anticorrelated strategy). Equation (
4) for the total system variance
is simply the sum of the variances for each crowd–anticrowd pair. The detailed explanation is as follows: irrespective of the history bit-string, the
drones using strategy
K are doing the
opposite of the
drones using strategy
. This means that the effective group-size for each crowd–anticrowd pair is
. This in turn represents the net step-size
d of the crowd–anticrowd pair in a random-walk contribution to
. Therefore, the net contribution by this crowd–anticrowd pair to
is given by
where
for a random walk. All the strong correlations have been removed and so the separate crowd–anticrowd pairs execute random walks which are uncorrelated with respect to each other. This means that the total
is given by the sum of the crowd–anticrowd variances, as stated in Equation (
4). It is easy to show [
8,
9] for
and
that the number of agents playing the
K’th ranked (i.e.,
K’th highest-scoring) strategy is given approximately by:
while for
:
assuming that strategies are scattered uniformly across the drone population (i.e., the drone population is indeed heterogeneous). Hence,
and so we obtain the expression for the upper-bound curve shown in
Figure 4 for
at small
m:
In the case that the disorder in the initial strategy assignments to drones is not uniform, it can be shown [
8,
9] that the result differs simply by a factor of
:
We have attached the subscripts ’upper bound’ and ’lower bound’ since they consider the impact of two limits of the drone population’s heterogeneity on the fluctuations in and hence the value of .
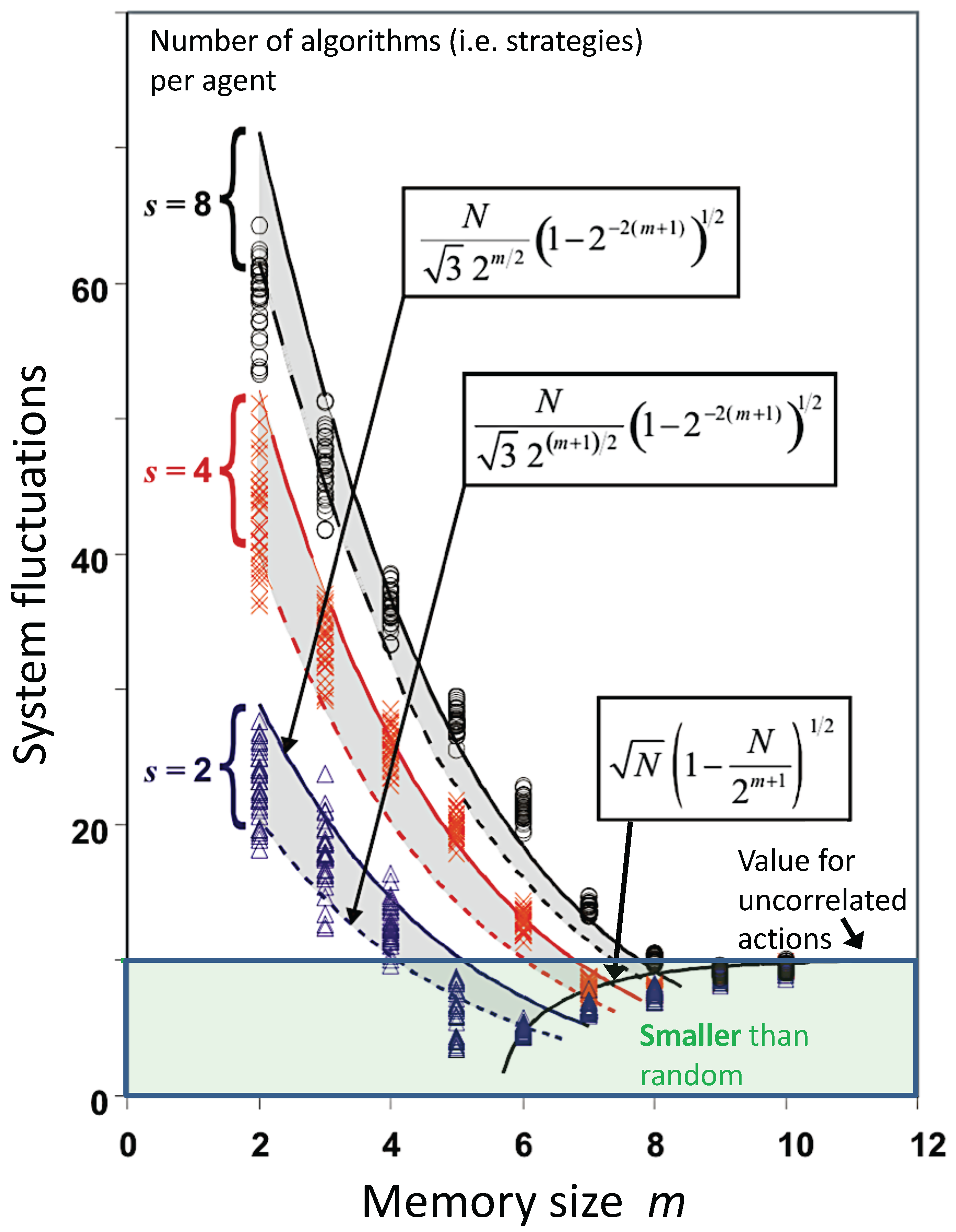
Figure 4 shows these closed-form results, and others from References [
8,
9], for
which measures the system fluctuations due to crowding and hence congestion, as a function of drone memory size
m. For each
m, the spread in numerical values from individual simulation runs is also shown. The analytic expressions indeed capture the essential physics (i.e., the strong correlations) driving the fluctuations in the
N-drone system.
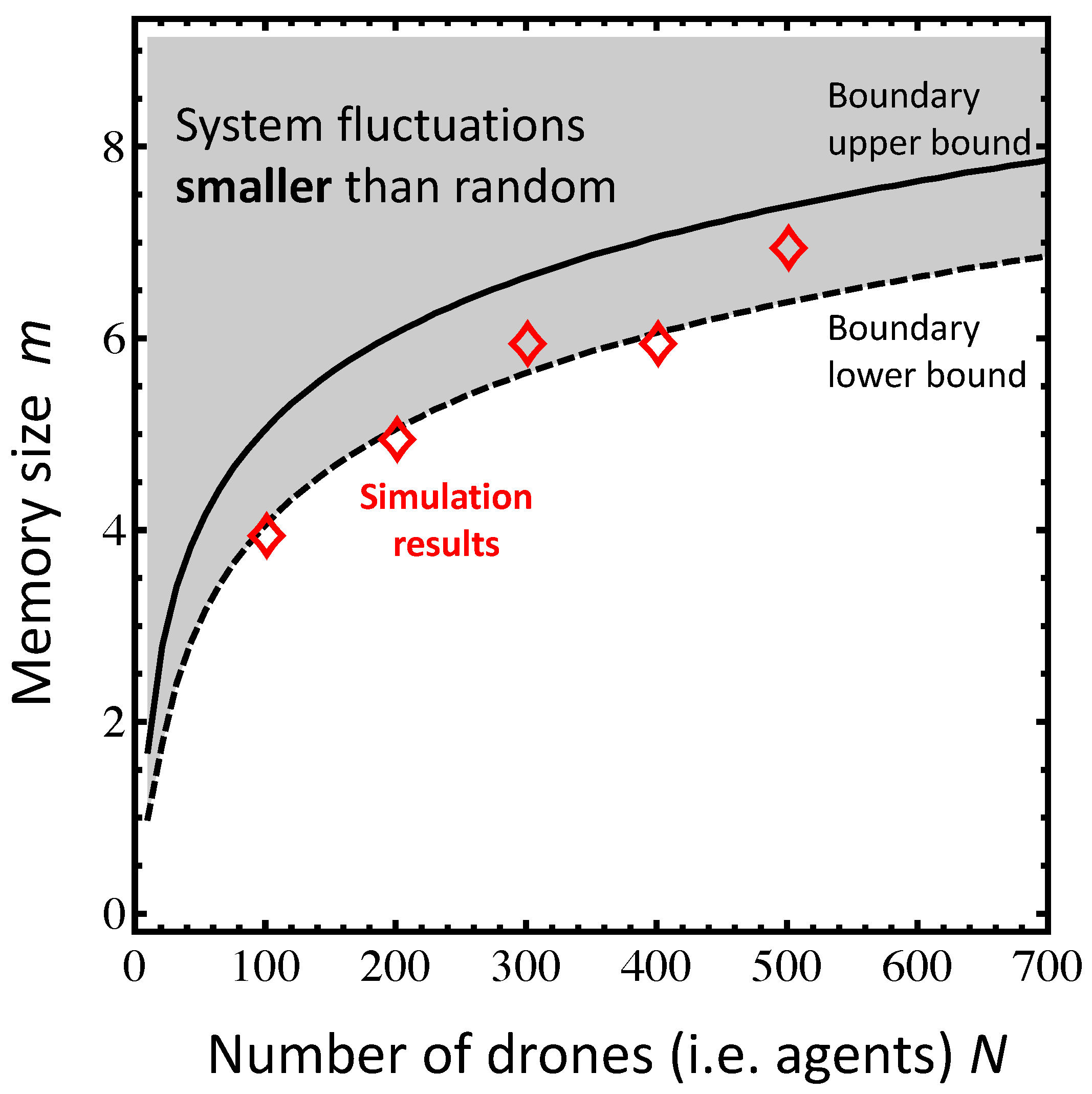
We can now use these results to calculate the minimal value of
m for
and any
N, above which these system fluctuations are
smaller than those obtained in a system of
N independent drones, and hence the regime in which coordination emerges from the system despite the system design being entirely competitive. Specifically, for
N independent drones whose actions are uncorrelated, we can calculate
from the known variance of random walks, and it is given by
. This better-than-random coordinated regime for a collection of
N drones that compete to be in a minority space, and receive only global information about the past, is given by
where
satisfies
This uses the lower-bound estimate for
. The upper-bound estimate of
is obtained from the corresponding expression with an extra factor of
as discussed above. These results are summarized in
Figure 5. The close agreement between the average of the numerical values (red diamonds) and the curves obtained from our closed-form formulae, show that our theoretical analysis is indeed accurate.
5. Conclusions
We have shown that a simple management system built around inter-drone competition, as opposed to cooperation, can reduce the fluctuations that underlie crowding in systems of multiple drones operating simultaneously in the same space, while also keeping the on-board processing requirements minimal. We have provided closed-form formulae that describe the on-board processing required to obtain this coordination regime as a function of the number of drones that are airborne. In addition to populations of drones (Scenario 1 in
Figure 1), the same results can be applied directly to the problem of a single drone (Scenario 2 in
Figure 1) in which each agent is an on-board sensor/actuator that is competing with the others to draw power from the limited central battery, or to provide a communication message in moments where there is no congestion. As such, these measures can reduce the fluctuations in energy use in a single drone and congestion in communication channels.
Moreover, these results are applicable for a system in which the resources and programs in each drone (i.e., each agent) do not have to be adjusted to account for the total number of drones in the population (i.e., s and m are independent of N). This is in stark contrast to schemes which depend on two-way interactions with other members for coordination, and hence will scale up in required resources by . Future work will consider particular sets of designs and operating characteristics for real-world implementations.
We also note that it is of course very difficult to model accurately the flight of even a single drone. There are complicated effects such as interactions with the fluid through which the drone is passing, including wind gusts which themselves are hard to predict yet correlated in time in complex ways, as well as interactions between the blades and motors and general nonlinearities. However, as with road traffic, one need not understand fully a single car in order to start modeling traffic behavior as a collective property. Indeed, one could rightly argue that no amount of understanding of the dynamics of an individual car will ever explain the occurrence of a particular traffic jam due to congestion. In this sense, our modeling moves beyond focusing on specific details and optimizations for particular drone designs, and instead aims to provide a more generic yet arguably deeper understanding of the important collective properties of such systems.
We have not specifically calculated the probability of collision. This is because this probability would depend on many different variables, most of which do not fit into the scope of our paper. However, the key ingredient we have shown is that using our proposal will effectively reduce the crowding of drones when compared to a random approach and the collision probability will definitely increase with increased crowding. This crowding effect is quantified analytically and numerically by the system’s fluctuation. We have shown explicitly that our approach yields system fluctuations that are smaller than that for a random approach, and without implementing cooperative drone-to-drone communication, which can be costly.
Other limitations of the scheme that we explore in this paper include the need for global monitoring, which assumes the existence of a non-cooperative or cooperative central surveillance system. It could also arise in practical, time-evolving scenarios that the success of previous strategies could become small for future decisions. We also acknowledge that the proposed scheme is a departure from the conventional scope of present and future traffic management concepts. In particular, we believe that the most likely application of our control approach is probably in swarming scenarios, more than in the UTM (Unmanned Aerial System Traffic Management) context. Even in such a futuristic perspective, applicability of this proposed architecture to traffic management scenarios requires further studies.
An immediate concern for our study is that it appears highly non-trivial to integrate it into existing aviation practices. Currently proposed UTM frameworks are similar to ADS-B in their design; however, this needn’t be the case if the present approach can be proven to be safe in practice. There is a benefit to having a low bandwidth version of UTM for interaction between swarms. This is analogous to manned military aircraft that fly in formation, where one pilot will communicate directly to Air Traffic Control whilst all pilots will also directly communicate with one another as necessary to maintain safety. We believe that our proposed approach serves this second function within drone swarms, but it may be less likely that this will be via a dedicated system. If future drones will be required to comply with UTM, our proposed approach will need to be designed to fit in with this, rather than simply replace it. Fortunately, since UTM is still very much a work in progress, it is legitimate to propose UTM as a communications infrastructure to support our approach.
Finally, we again stress that our approach aims for a transparent, generic and hence necessarily oversimplified view of future drone system designs. However, by so doing, our analysis highlights the highly non-trivial collective behavior that can emerge from the
N-drone system, a behavior which would otherwise be lost if all manufacturing details were included. Indeed, we do not know of these results being reported before in the drone literature. We also stress that even when additional details are added in, the principle and results that we present should still hold since the result is robust and mathematically grounded. It is also scalable to any value of
N, and so provides a guiding principle irrespective of how many drones are being considered. As noted earlier, such large swarms of very simplified drones are currently considered desirable for certain future operations such as infrastructure testing in scenarios where robustness against the loss of a number of drones is a primary requirement, and where each drone has minimal on-board processing requirements (see Reference [
15]). Our Scenarios address precisely this setting.