Static and Moving Target Imaging Using Harmonic Radar
Abstract
:1. Introduction
2. Harmonic Radar
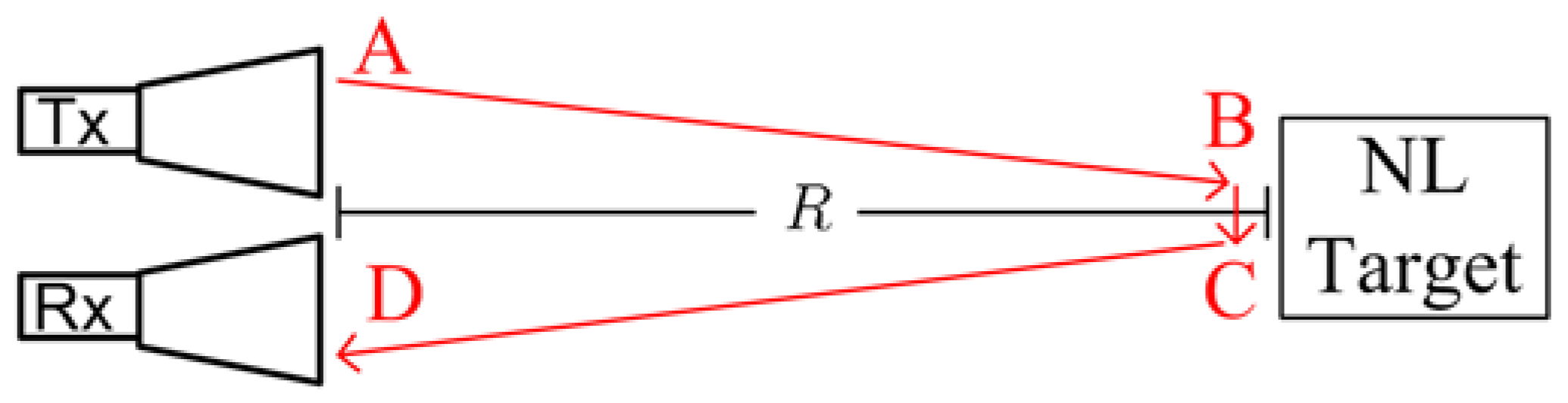
2.1. Harmonic Radar Range Equation
2.2. Unambiguous Range and Range Resolution
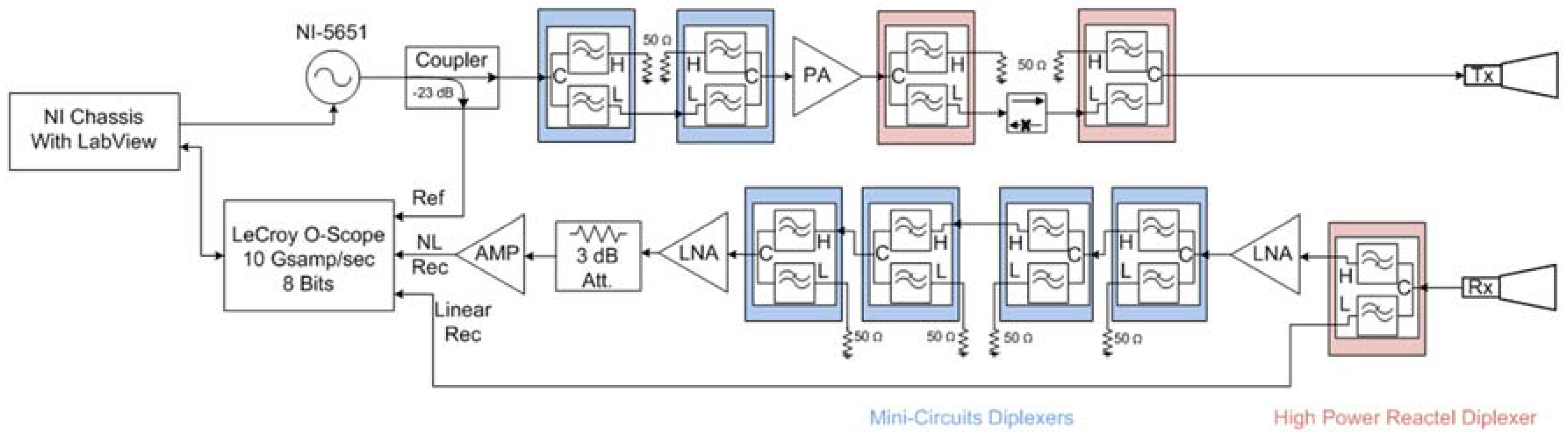
2.3. Description of Harmonic Radar
3. Imaging of Moving Targets
3.1. Moving Target Imaging Approach
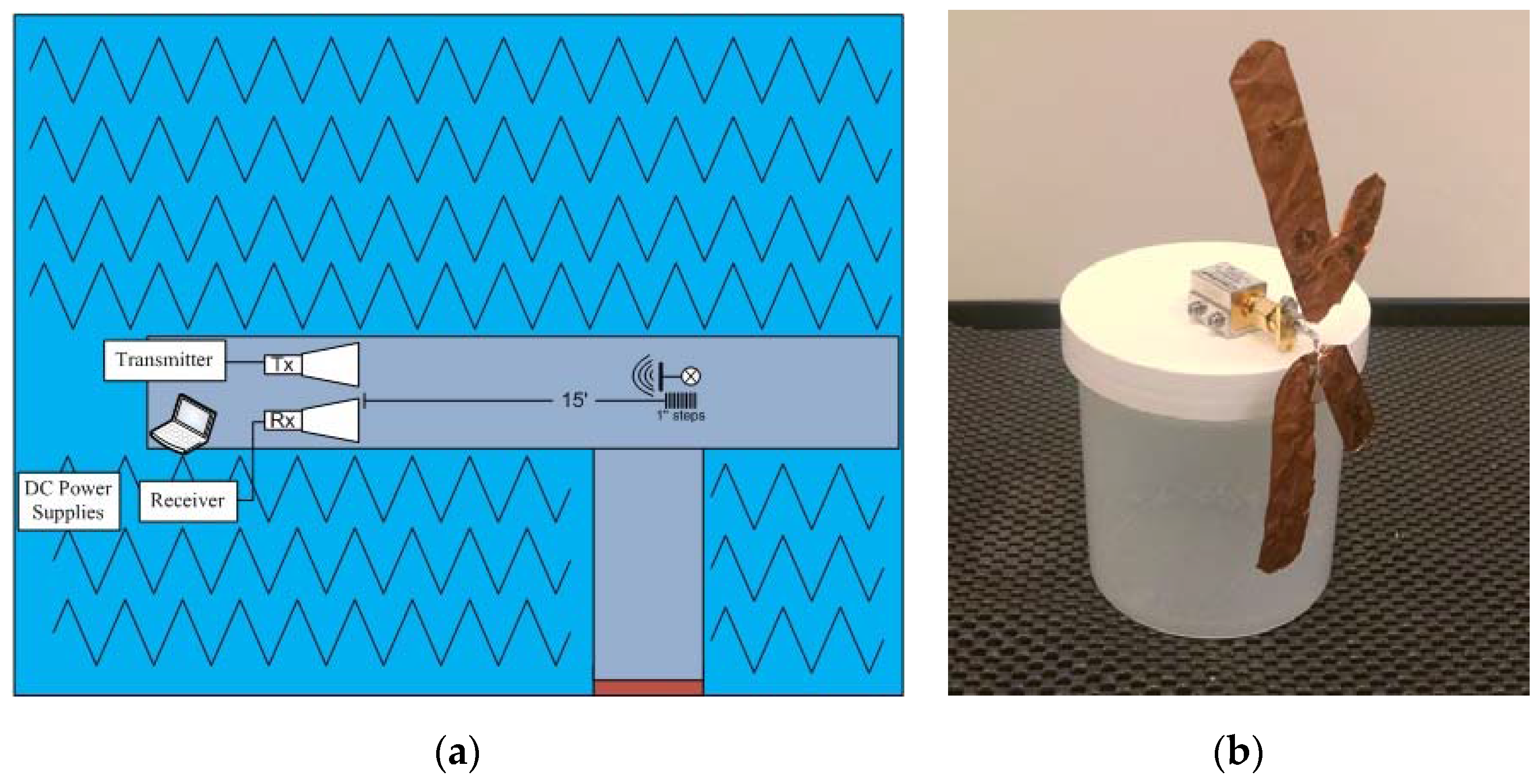
3.2. Moving Target Imaging Setup
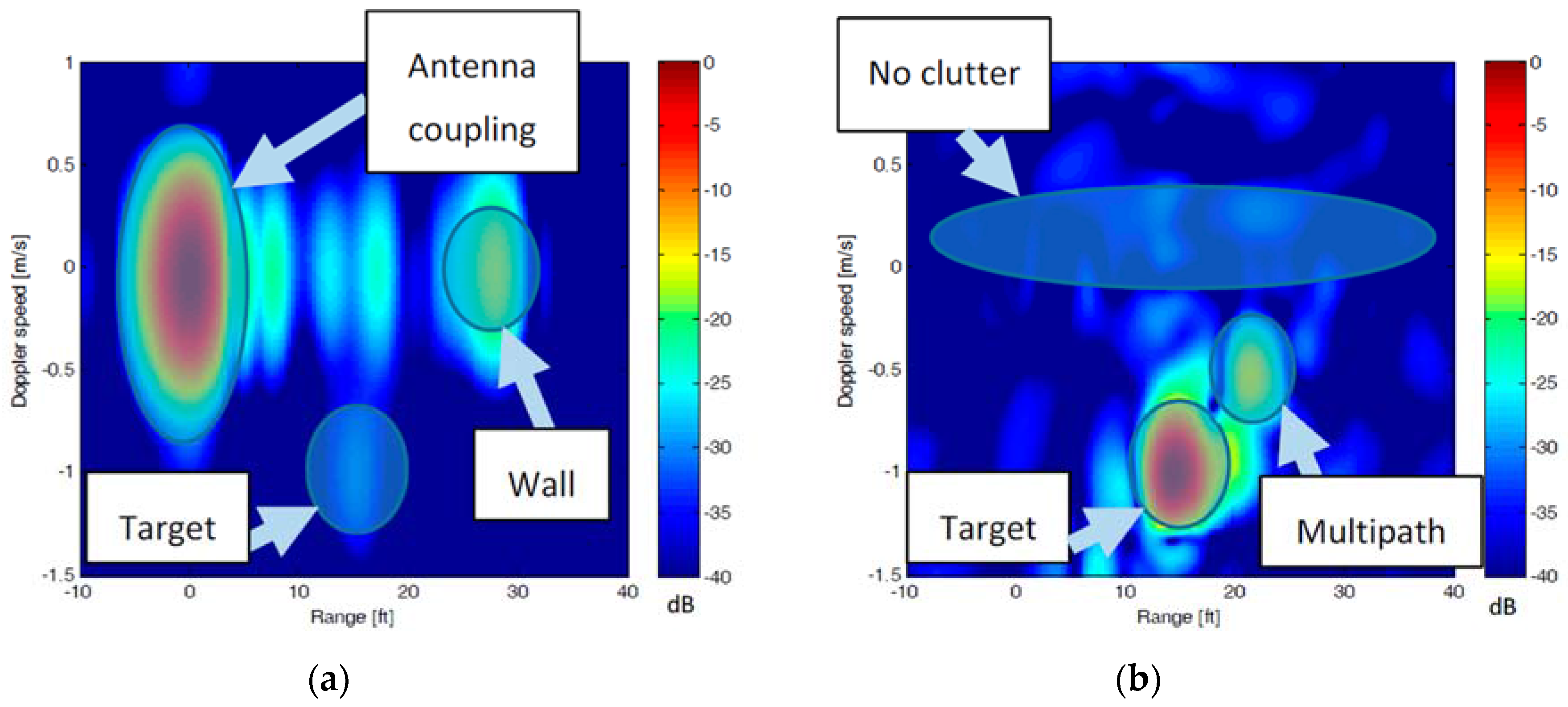
3.3. Data Acquisition and Analysis
4. Synthetic Aperture Radar (SAR) Imaging
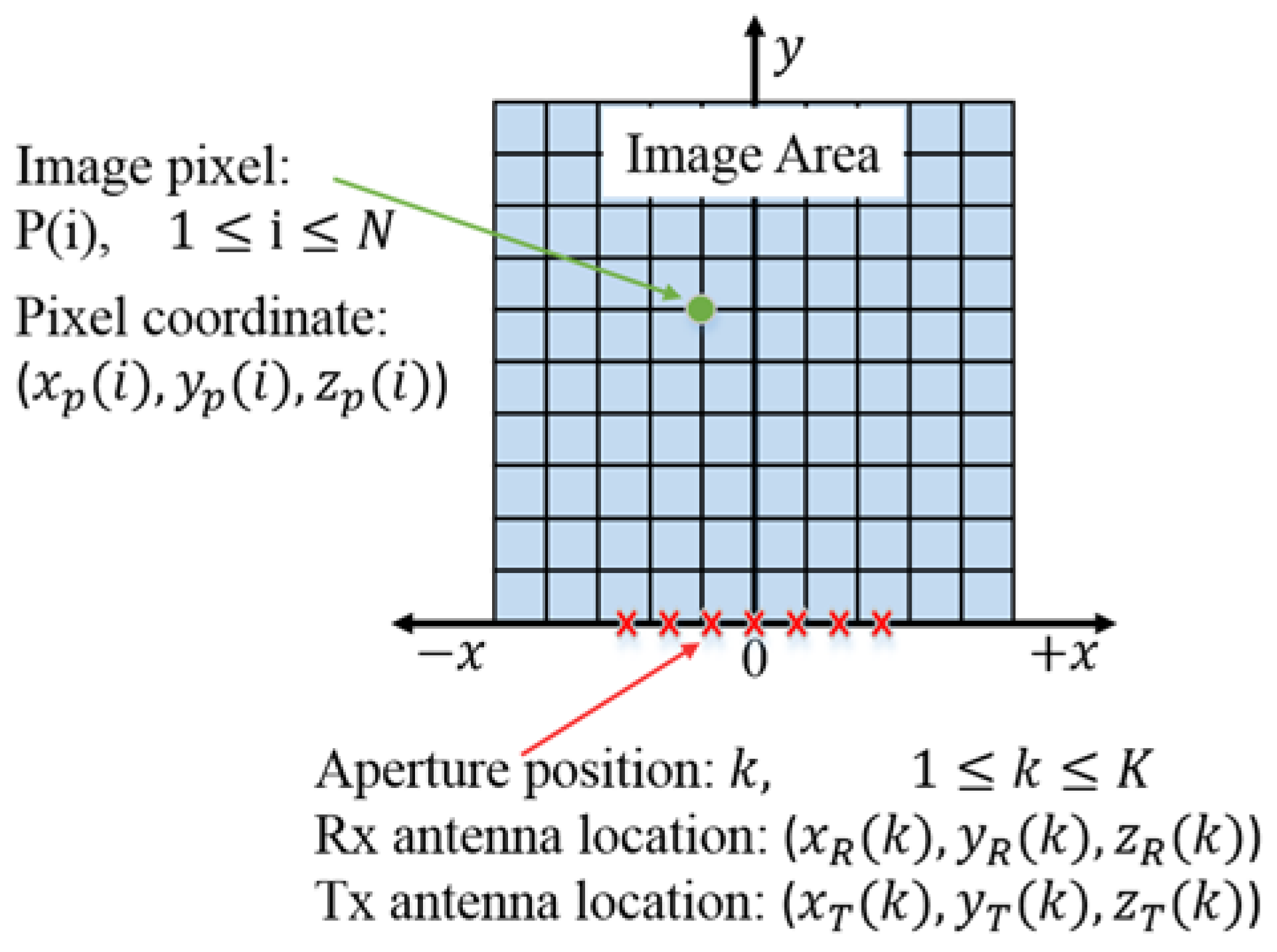
4.1. SAR Image Processing Approach
4.2. Moving Aperture SAR Imaging
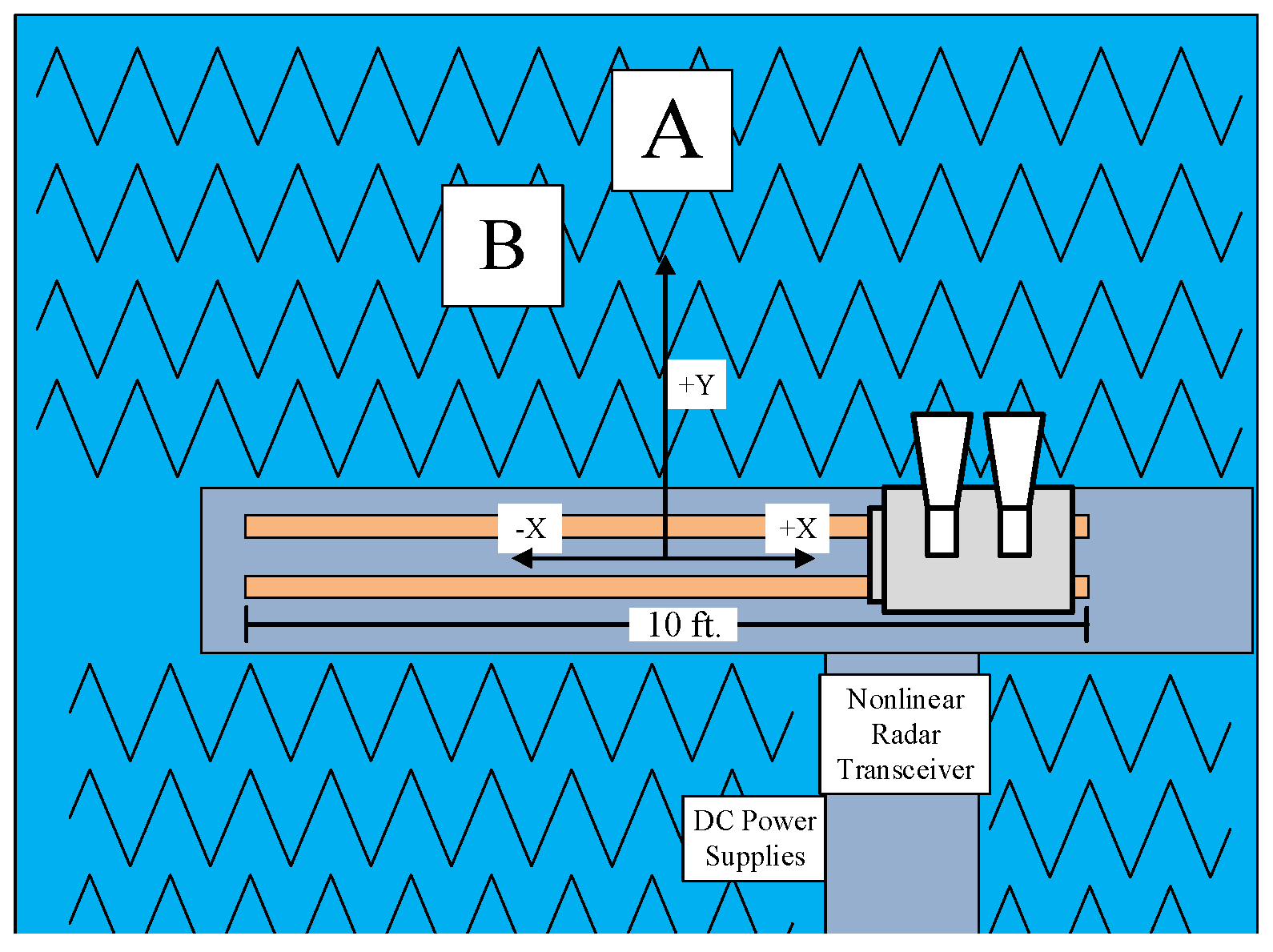
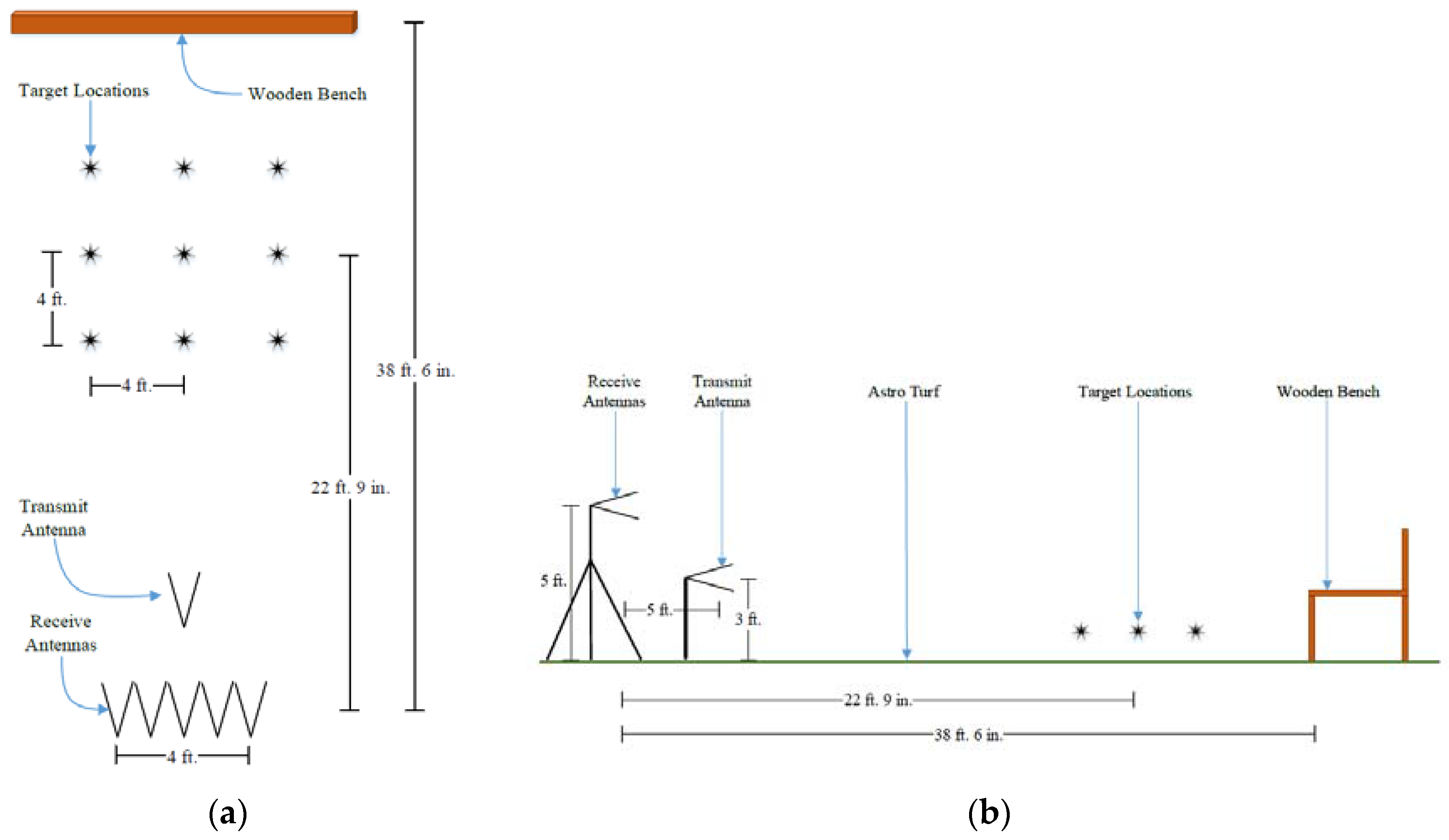
4.2.1. Experimental Setup
4.2.2. Description of Targets
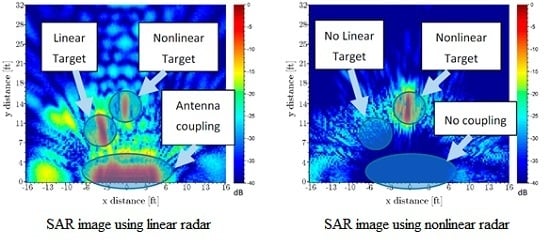
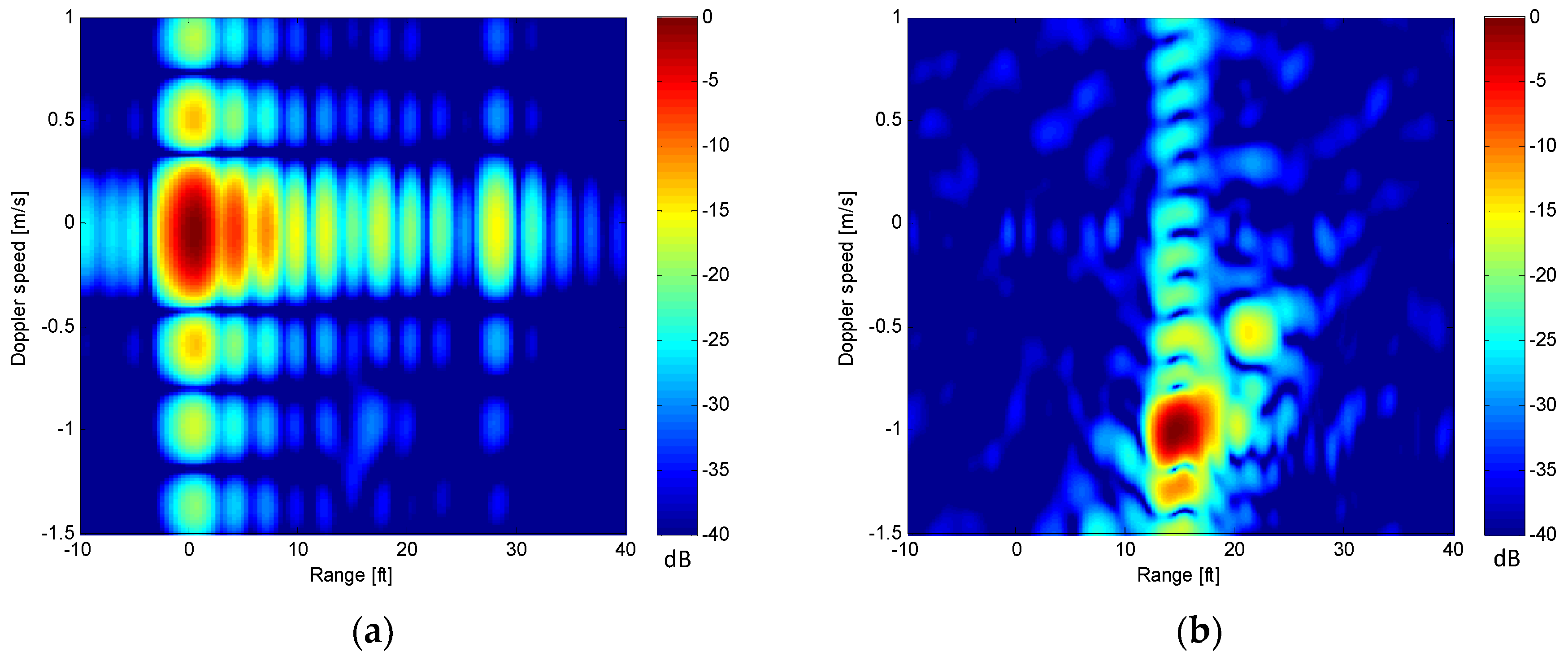
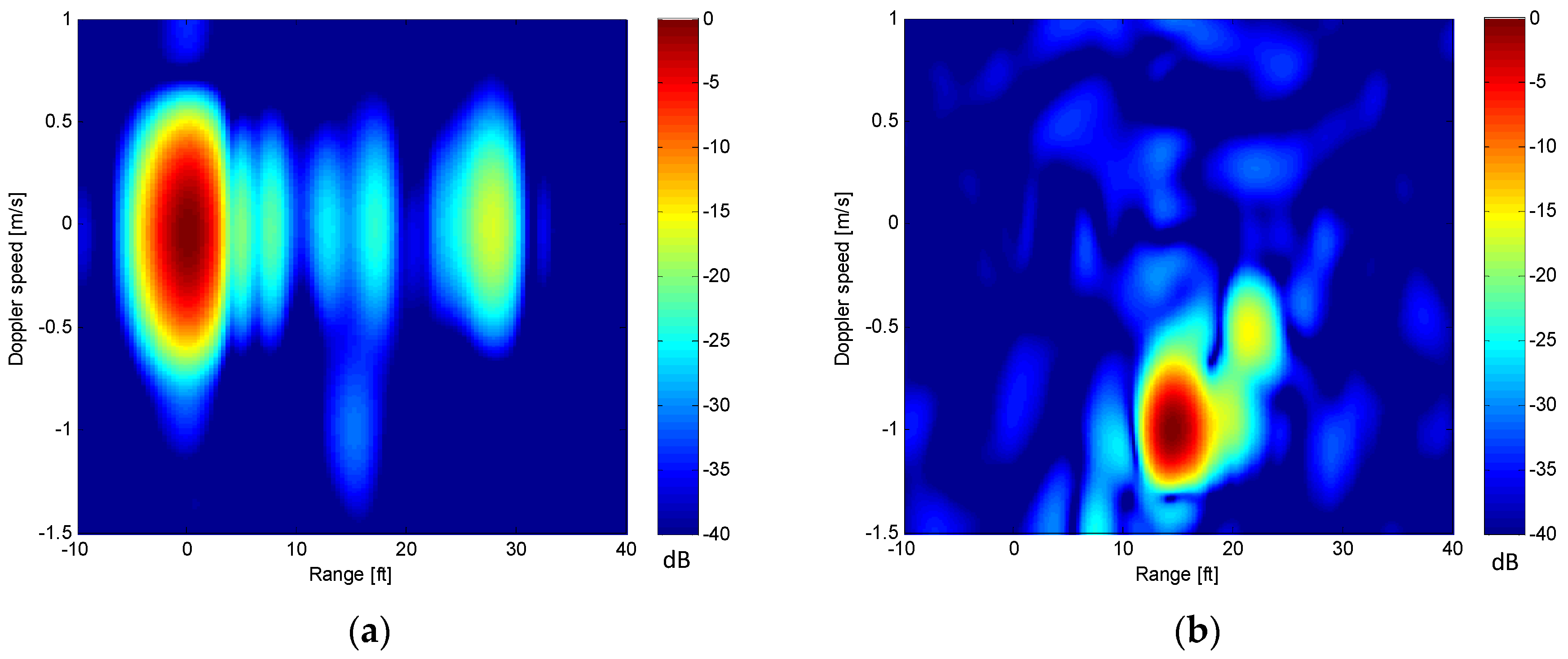
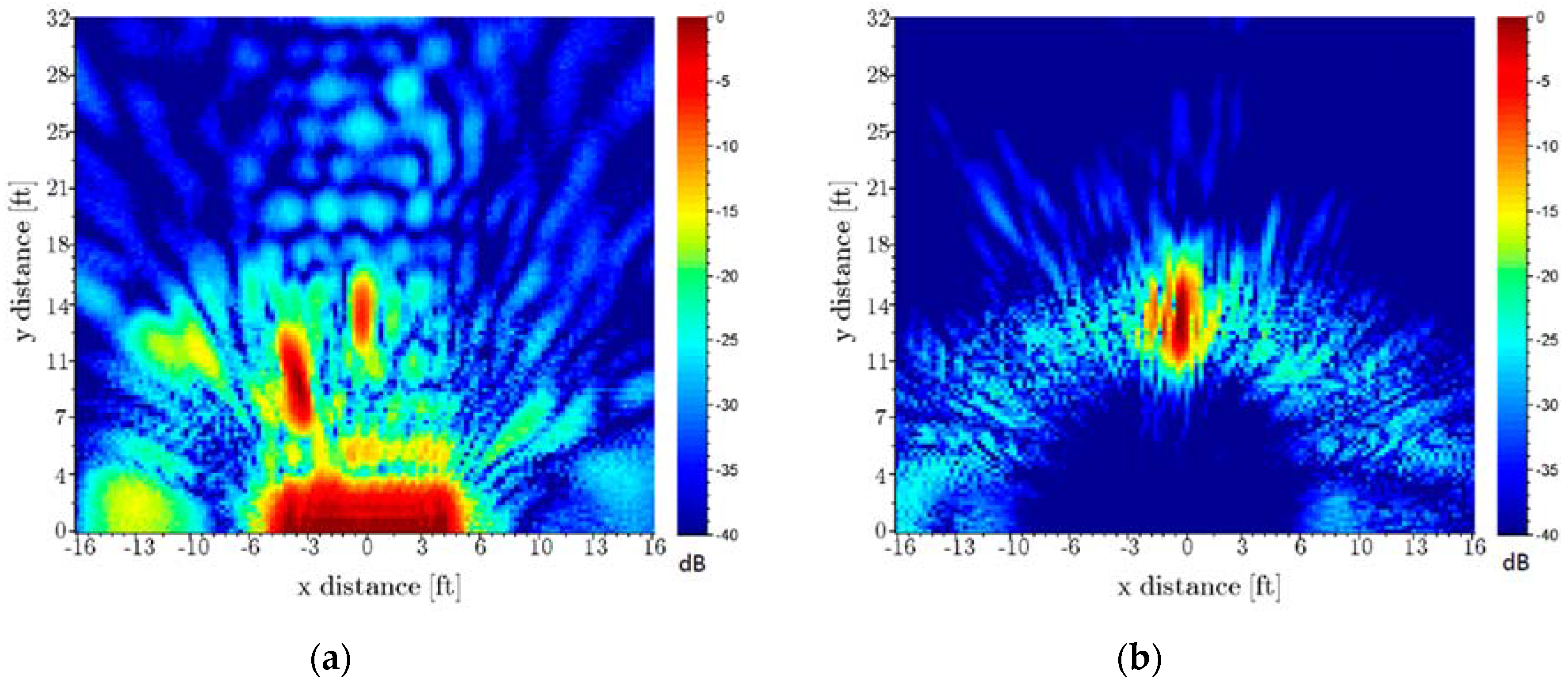
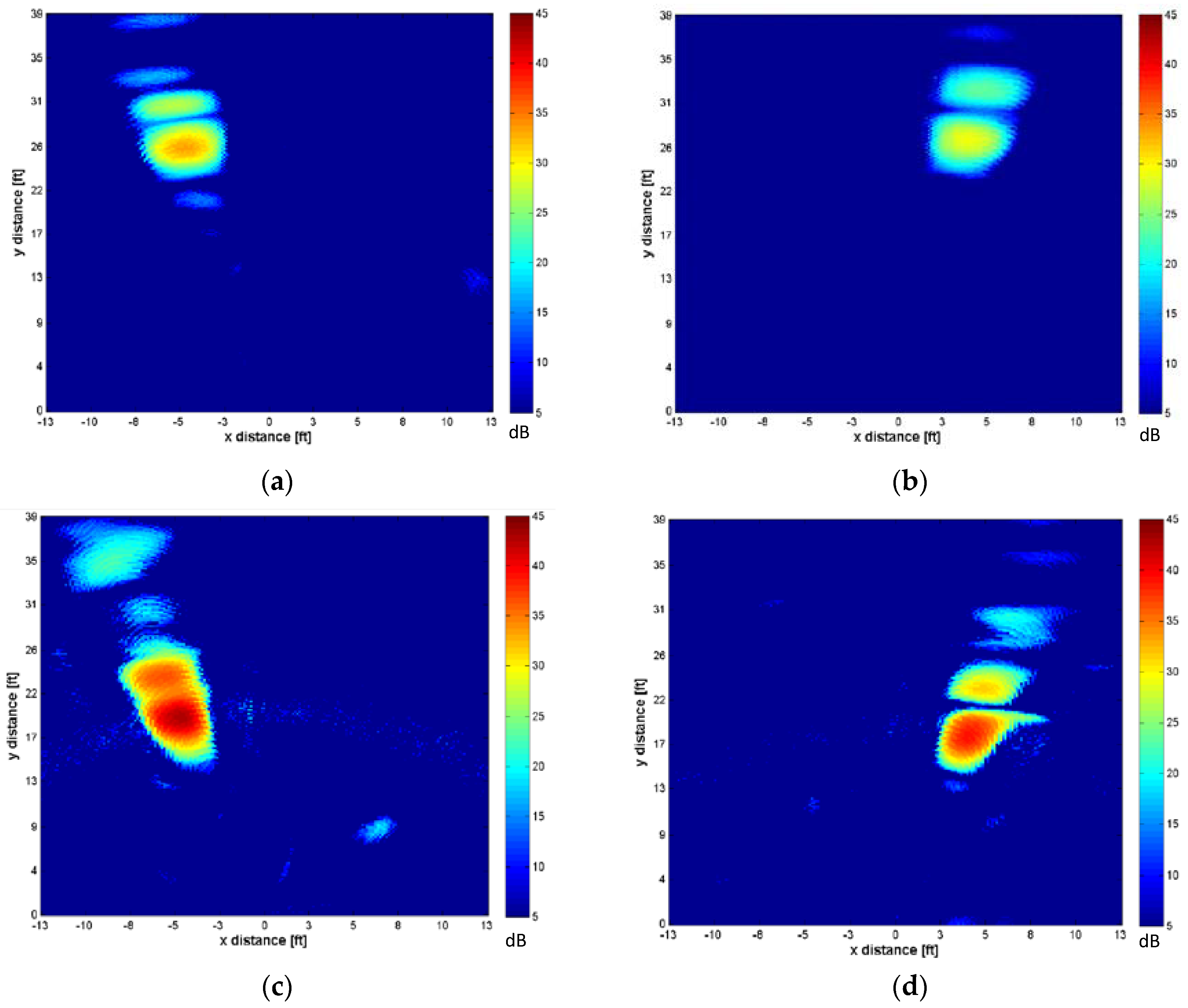
4.2.3. SAR Imaging Results
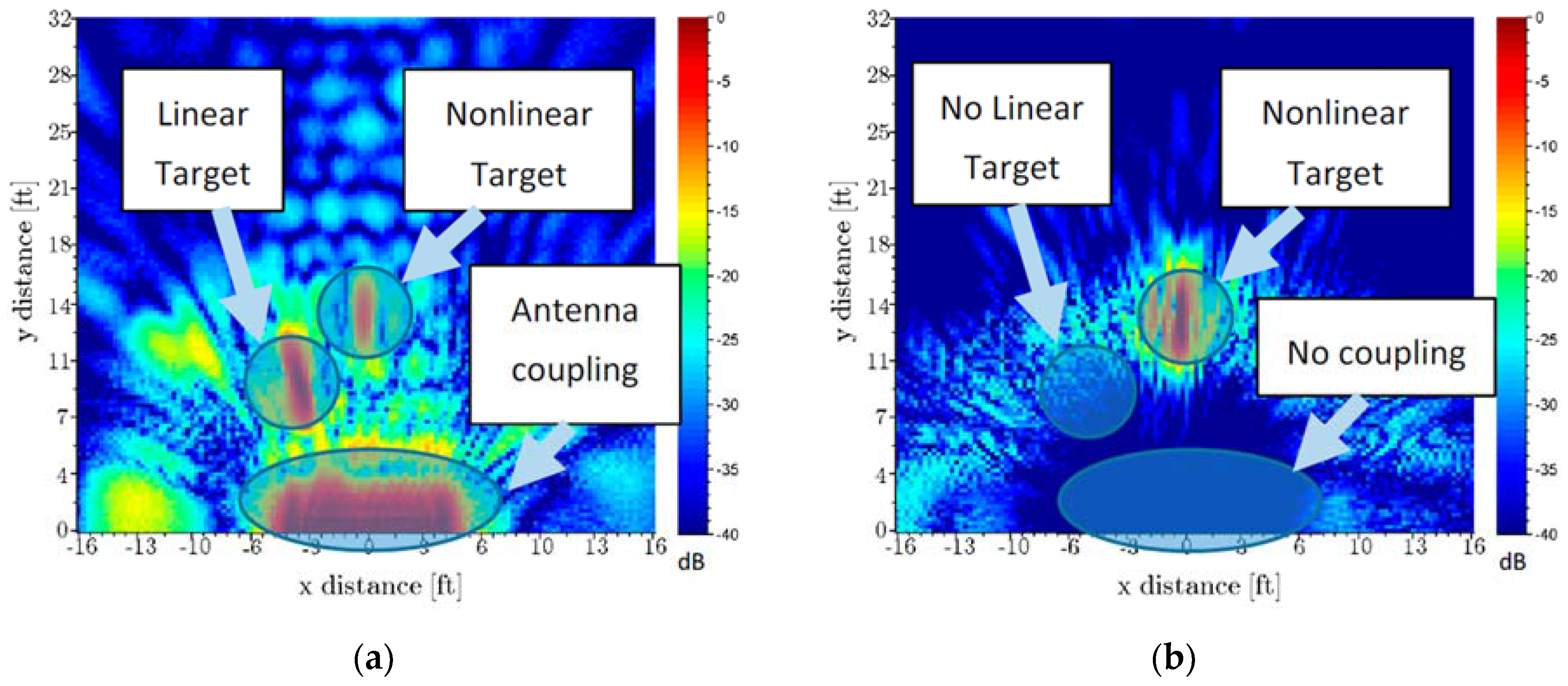
4.3. SAR Imaging with Fixed 16-Channel Receiver
4.3.1. Experimental Setup
4.3.2. Description of Targets
4.3.3. SAR Imaging Results
5. Conclusions
Acknowledgments
Author Contributions
Dedication
Conflicts of Interest
References
- Faraday, M. Experimental Researches in Electricity; Dover Publications: New York, NY, USA, 1965; (Reprint). [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. BSTJ 1948, 27, 379–423. [Google Scholar]
- Steer, M.B.; Khan, P.J. Large signal analysis of nonlinear microwave systems. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, San Francisco, CA, USA, 30 May–1 June 1984; pp. 402–403. [Google Scholar]
- Jakabosky, J.; Ryan, L.; Blunt, S. Transmitter-in-the-loop optimization of distorted OFDM radar emissions. In Proceedings of the IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013. [Google Scholar] [CrossRef]
- Tjora, S.; Lundheim, L. Distortion modeling and compensation in step frequency radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 360–374. [Google Scholar] [CrossRef]
- Wetherington, J.M.; Steer, M.B. Robust analog canceller for high-dynamic range radio frequency measurement. IEEE Trans. Microwave Theory Tech. 2012, 60, 1709–1719. [Google Scholar] [CrossRef]
- Bodson, M.; Sacks, A.; Khosla, P. Harmonic generation in adaptive feedforward cancellation schemes. IEEE Trans. Autom. Control 1994, 39, 1939–1944. [Google Scholar] [CrossRef]
- Pedro, J.C.; De Carvalho, N.B. Evaluating co-channel distortion ratio in microwave power amplifiers. IEEE Trans. Microwave Theory Tech. 2001, 49, 1777–1784. [Google Scholar] [CrossRef]
- Gallagher, K.A.; Mazzaro, G.J.; Narayanan, R.M.; Sherbondy, K.D.; Martone, A.F. Automated cancellation of harmonics using feed-forward filter reflection for radar transmitter linearization. In Proceedings of the SPIE Conference on Radar Sensor Technology XVIII, vol. 9077, Baltimore, MD, USA, 5–7 May 2014. [Google Scholar] [CrossRef]
- Gallagher, K.A.; Narayanan, R.M.; Mazzaro, G.J.; Sherbondy, K.D. Linearization of a harmonic radar transmitter by feed-forward filter reflection. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 1363–1368. [Google Scholar]
- Tellegen, B.D.H. Interaction between radio-waves? Nature 1933, 131, 840. [Google Scholar] [CrossRef]
- Bailey, V.A.; Martyn, D.F. Interaction of radio waves. Nature 1934, 133, 218. [Google Scholar] [CrossRef]
- Helme, B.G.M. Passive intermodulation of ICT components. In Proceedings of the IEE Colloquium on Screening Effectiveness Measurements (Ref. No. 1998/452), London, UK, 6 May 1998; pp. 1/1–1/8. [Google Scholar]
- Shitvov, A.; Schuchinsky, A.G.; Steer, M.B.; Wetherington, J.M. Characterisation of nonlinear distortion and intermodulation in passive devices and antennas. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, Netherlands, 6–11 April 2014; pp. 1454–1458. [Google Scholar]
- Golikov, V.; Hienonen, S.; Vainikainen, P. Passive intermodulation distortion measurements in mobile communication antennas. In Proceedings of the 54th IEEE Vehicular Technology Conference (VTC Fall 2001), Atlantic City, NJ, USA, 7–11 October 2001; pp. 2623–2625. [Google Scholar]
- Ranta, T.; Ella, J.; Pohjonen, H. Antenna switch linearity requirements for GSM/WCDMA mobile phone front-ends. In Proceedings of the European Conference on Wireless Technology, Paris, France, 3–4 Oct 2005; pp. 23–26. [Google Scholar]
- Moriya, A.; Inoue, M.; Kawachi, O. Development of high linearity duplexers with low passive intermodulation component. In Proceedings of the IEEE International Ultrasonics Symposium (IUS), Prague, Czech Republic, 21–25 July 2013; pp. 737–740. [Google Scholar]
- Wilkerson, J.R.; Gard, K.G.; Schuchinsky, A.G.; Steer, M.B. Electrothermal theory of intermodulation distortion in lossy microwave components. IEEE Trans. Microwave Theory Tech. 2008, 56, 2717–2725. [Google Scholar] [CrossRef]
- Opitz, C.L. Metal-detecting radar rejects clutter naturally. Microwaves 1976, 15, 12–14. [Google Scholar]
- Steele, D.W.; Rotondo, F.S.; Houck, J.L. Radar system for manmade device detection and discrimination from clutter. US Patent 7,830,299, 9 November 2010. [Google Scholar]
- Low, G.; Morissette, S.; Frazier, M. Junction range finder. U.S. Patent 3,732,567, 8 May 1973. [Google Scholar]
- Johnson, R.H. Metal target detection system. U.S. Patent 3,972,042, 27 July 1976. [Google Scholar]
- Opitz, C.L. Radar object detector using non-linearities. U.S. Patent 4,053,891, 11 October 1977. [Google Scholar]
- Danze, P.M.; Brienza, M.J. Radar target signature detector. U.S. Patent 5,191,343, 2 March 1993. [Google Scholar]
- Belyaev, V.V.; Mayunov, A.T.; Razin’kov, S.N. Effects of a metal-insulator-metal contact on the antenna in a radar monitoring system. Meas. Tech. 2001, 44, 871–875. [Google Scholar] [CrossRef]
- Belyaev, V.V.; Mayunov, A.T.; Razin’kov, S.N. Potential accuracy and resolving power of a nonlinear radar station with linear frequency modulation. Meas. Tech. 2003, 46, 698–701. [Google Scholar] [CrossRef]
- Belyaev, V.V.; Mayunov, A.T.; Razin’kov, S.N. Object detection range enhancement by means of nonlinear radar employing two signals with linear frequency modulation. Meas. Tech. 2003, 46, 802–805. [Google Scholar] [CrossRef]
- Khakimov, N.T. Recognition method of radio eavesdropping devices by radar sensing. Telecommun. Radio Eng. 2005, 63, 499–502. [Google Scholar] [CrossRef]
- Semyonov, E.V.; Semyonov, A.V. Applying the difference between the convolutions to investigate the nonlinearity of the transformation of test signals and object responses of ultrawideband signals. J. Commun. Technol. Electron. 2007, 52, 451–465. [Google Scholar] [CrossRef]
- Yakubov, V.P.; Shipilov, S.E.; Satarov, R.N.; Yurchenko, A.V. Remote ultra-wideband tomography of nonlinear electronic components. Tech. Phys. 2015, 60, 279–282. [Google Scholar] [CrossRef]
- Shefer, J.; Staras, H. Harmonic radar detecting and ranging system for automotive vehicles. U.S. Patent 3,781,879, 25 December 1973. [Google Scholar]
- Shefer, J.; Klensch, R.J.; Kaplan, G.; Johnson, H.C. Clutter-free radar for cars. Wireless World 1974, 80, 117–122. [Google Scholar]
- Shefer, J.; Klensch, R.J.; Kaplan, G.; Johnson, H.C. Clutter-free radar for cars – conclusion: frequency measurement and application. Wireless World 1974, 80, 199–202. [Google Scholar]
- Brazee, R.D.; Miller, E.S.; Reding, M.E.; Klein, M.G.; Nudd, B.; Zhu, H. A transponder for harmonic radar tracking of the black vine weevil in behavioral research. Trans. ASAE 2005, 48, 831–838. [Google Scholar] [CrossRef]
- O’Neal, M.E.; Landis, D.A.; Rothwell, E.; Kempel, L.; Reinhard, D. Tracking insects with harmonic radar: A case study. Am. Entomol. 2004, 50, 212–218. [Google Scholar] [CrossRef]
- Psychoudakis, D.; Moulder, W.; Chen, C.-C.; Zhu, H.; Volakis, J.L. A portable low-power harmonic radar system and conformal tag for insect tracking. IEEE Antennas Wireless Propag. Lett. 2008, 7, 444–447. [Google Scholar] [CrossRef]
- Aumann, H.; Kus, E.; Cline, B.; Emanetoglu, N. A low-cost harmonic radar for tracking very small tagged amphibians. In Proceedings of the International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 234–237. [Google Scholar]
- Aumann, H.M.; Emanetoglu, N.W. A wideband harmonic radar for tracking small wood frogs. In Proceedings of the IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 108–111. [Google Scholar]
- Gallagher, K.A. Harmonic Radar: Theory and Applications to Nonlinear Target Detection, Tracking, Imaging and Classification. Ph.D. Dissertation, The Pennsylvania State University, University Park, PA, USA, December 2015. [Google Scholar]
- Harger, R.O. Harmonic radar systems for near-ground in- foliage nonlinear scatterers. IEEE Trans. Aerosp. Electron. Syst. 1976, 12, 230–245. [Google Scholar]
- Powers, E.J.; Hong, J.Y.; Kim, Y.C. Cross sections and radar equation for nonlinear scatterers. IEEE Trans. Aerosp. Electron. Syst. 1981, 17, 602–605. [Google Scholar] [CrossRef]
- Bucci, O.M.; De Bonitatibus, A.; Pinto, I. Harmonic radar cross-section of bistatic nonlinear responder. Alta Freq. 1984, 53, 172–176. [Google Scholar]
- Shteĭnshleĭger, V.B. Nonlinear scattering of radio waves by metallic objects. Sov. Phys. Usp. 1984, 27, 60–68. [Google Scholar] [CrossRef]
- Powers, E.J.; Im, S. The utilization of higher-order spectra to determine nonlinear radar cross sections. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP-94), Adelaide, SA, Australia, 19–22 April 1994; pp. IV/437–IV/440. [Google Scholar]
- Shteinshleiger, V.B.; Misezhnikov, G.S.; Melnikov, L.Y. Study of the effect of nonlinear scattering of radio waves by real metallic objects. Record of the IEEE International Radar Conference, Alexandria, VA, USA, 8–11 May 1995; pp. 435–437. [Google Scholar]
- Vernigorov, N.S. Nonlinear transformation and scattering of an electromagnetic field by electrically nonlinear objects. J. Commun. Technol. Electron. 1997, 42, 1097–1101. [Google Scholar]
- Fazi, C.; Crowne, F.; Ressler, M. Design Considerations for Nonlinear Scattering; US Army Research Laboratory Technical Report ARL-TR-5684: Adelphi, MD, USA, September 2011. [Google Scholar]
- Fazi, C.; Crowne, F.; Ressler, M. Link budget calculations for nonlinear scattering. In Proceedings of the 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 1146–1150. [Google Scholar]
- Dardari, D. Detection and accurate localization of harmonic chipless tags. EURASIP J. Adv. Signal Process. 2015, 2015, 77. [Google Scholar] [CrossRef]
- Flemming, M.A.; Mullins, F.H.; Watson, A.W.D. Harmonic Radar Detection Systems. In Proceedings of the IEE International Conference on Radar (Radar-77), London, UK, 25–28 October 1977; pp. 552–554. [Google Scholar]
- Gallagher, K.A.; Mazzaro, G.J.; Martone, A.F.; Sherbondy, K.D.; Narayanan, R.M. Derivation and validation of the nonlinear radar range equation. In Proceedings of the SPIE Conference on Radar Sensor Technology XX, vol. 9829, Baltimore, MD, USA, 18–21 April 2016. [Google Scholar] [CrossRef]
- Gallagher, K.A.; Mazzaro, G.J.; Ranney, K.I.; Nguyen, L.H.; Sherbondy, K.D.; Narayanan, R.M. Nonlinear synthetic aperture radar imaging using a harmonic radar. In Proceedings of the SPIE Conference on Radar Sensor Technology XIX and Active and Passive Signatures VI, vol. 9461, Baltimore, MD, USA, 20–24 April 2015. [Google Scholar] [CrossRef]
- Stimson, G.W. Introduction to Airborne Radar, 2nd ed.; SciTech Publishing: Raleigh, NC, USA, 1998. [Google Scholar]
- Bruder, J.A. Measurement of the performance of moving target indication radars. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 7–10 May 1990; pp. 170–175. [Google Scholar]
- Klemm, R. Introduction to space-time adaptive processing. Electron. Commun. Eng. J. 1999, 11, 5–12. [Google Scholar] [CrossRef]
- Mazzaro, G.J.; Martone, A.F.; McNamara, D.M. Detection of RF electronics by multitone harmonic radar. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 477–490. [Google Scholar] [CrossRef]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. Principles of Modern Radar – Basic Principles; SciTech Publishing: Raleigh, NC, USA, 2010. [Google Scholar]
- Pilkay, G.L.; Reay-Jones, F.P.F.; Greene, J.K. Harmonic radar tagging for tracking movement of Nezara viridula (Hemiptera: Pentatomidae). Environ. Entomol. 2013, 42, 1020–1026. [Google Scholar] [CrossRef] [PubMed]
- Milanesio, D.; Saccani, M.; Maggiora, R.; Laurino, D.; Porporato, M. Design of an harmonic radar for the tracking of the Asian yellow-legged hornet. Ecol. Evol. 2016, 6, 2170–2178. [Google Scholar] [CrossRef] [PubMed]
- Chioukh, L.; Boutayeb, H.; Wu, K.; Deslandes, D. Monitoring vital signs using remote harmonic radar concept. In Proceedings of the 41st European Microwave Conference, Manchester, UK, 10–13 October 2011; pp. 1269–1272. [Google Scholar]
- Gallagher, K.A.; Narayanan, R.M.; Mazzaro, G.J.; Ranney, K.I.; Martone, A.F.; Sherbondy, K.D. Moving target indication with non-linear radar. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 1428–1433. [Google Scholar]
- Beane, E.F. Prediction of mixer intermodulation levels as function of local oscillator power. IEEE Trans. Electromagn. Compat. 1971, 13, 56–63. [Google Scholar] [CrossRef]
- Linnehan, R.; Schindler, J. Multistatic scattering from moving targets in multipath environments. In Proceedings of the IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009. [Google Scholar] [CrossRef]
- Fitch, J.P. Synthetic Aperture Radar; Springer: New York, NY, USA, 1988. [Google Scholar]
- Davis, M.E.; Kapfer, R. Bistatic SAR using illumination from a tethered ground moving target indication radar. In Proceedings of the IEEE Radar Conference, Pasadena, CA, USA, 4–8 May 2009. [Google Scholar] [CrossRef]
- McCorkle, J.; Nguyen, L. Focusing of Dispersive Targets using Synthetic Aperture Radar; US Army Research Laboratory Technical Report ARL-TR-305: Adelphi, MD, USA, August 1994. [Google Scholar]
- Lim, D.; Xu, L.; Gianelli, C.; Li, J.; Nguyen, L.; Anderson, J. Time- and frequency-domain MIMO FLGPR imaging. In Proceedings of the IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015; pp. 1305–1310. [Google Scholar]
- Nguyen, L.; Koenig, F. Augmented reality for forward-looking synthetic aperture radar. In Proceedings of the IEEE Virtual Reality Short Papers and Posters, Costa Mesa, CA, USA, 4–8 March 2012; pp. 145–146. [Google Scholar]
- Ahmad, F.; Amin, M.G.; Kassam, S.A. Synthetic aperture beamformer for imaging through a dielectric wall. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 271–283. [Google Scholar] [CrossRef]
- Dogaru, T.; Le, C.; Nguyen, L. Synthetic Aperture Radar Images of a Simple Room Based on Computer Models; US Army Research Laboratory Technical Report ARL-TR-5193: Adelphi, MD, USA, May 2010. [Google Scholar]
- Berger, T.; Hamran, S.-E. Harmonic synthetic aperture radar processing. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2066–2069. [Google Scholar] [CrossRef]
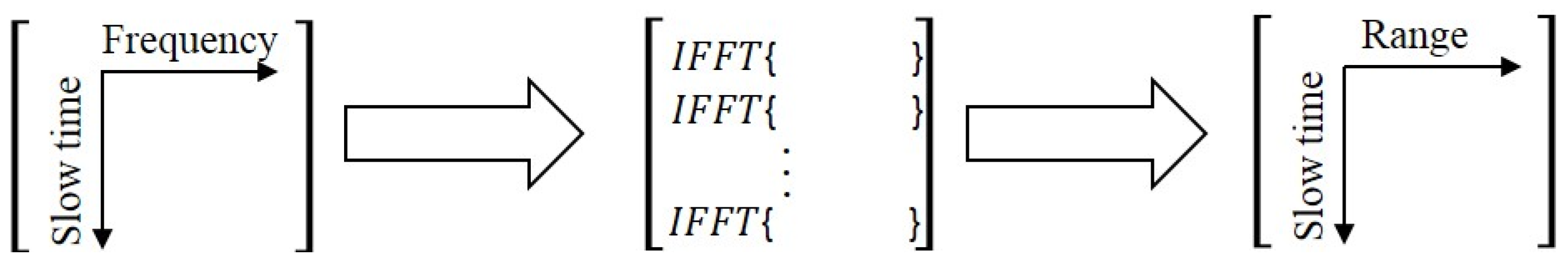
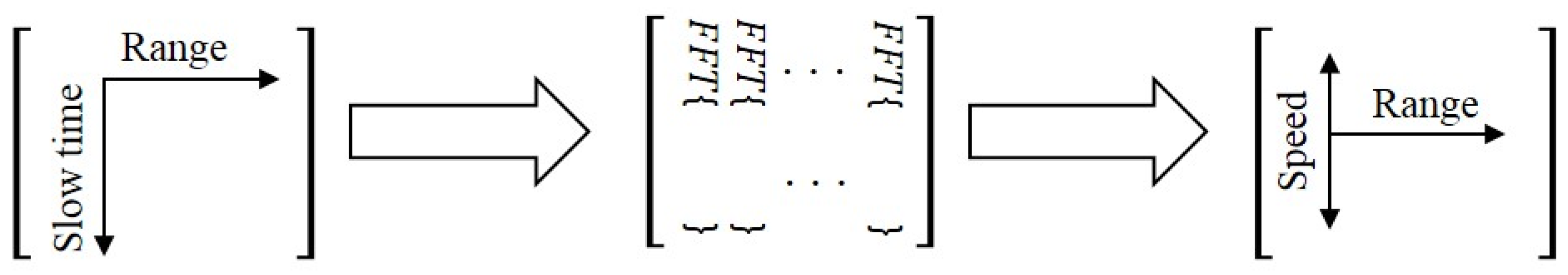





| Parameter | Value |
|---|---|
| Linear frequency range | 800–1000 MHz |
| Harmonic frequency range | 1.6–2 GHz |
| Transmit power | +40 dBm |
| Transmit antenna gain at fundamental | 10 dBi |
| Receive antenna gain at fundamental | 10 dBi |
| Receive antenna gain at second harmonic | 8 dBi |
| Range resolution at fundamental | 75 cm (2.46 feet) |
| Range resolution at second harmonic | 37.5 cm (1.23 feet) |
| System noise floor | −125 dBm |
| Position | x-Coordinate (m/ft) | y-Coordinate (m/ft) |
|---|---|---|
| A | 0/0 | 4.57/15 |
| B | −0.91/−3 | 3.66/12 |
| Target | Description |
|---|---|
| 1 | Hand Held Radio 1 |
| 2 | Hand Held Radio 2 |
| 3 | Hand Held Radio 3 |
| 4 | Commercial RF amplifier, powered on using batteries |
| 5 | Commercial RF amplifier, no power |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallagher, K.A.; Narayanan, R.M.; Mazzaro, G.J.; Martone, A.F.; Sherbondy, K.D. Static and Moving Target Imaging Using Harmonic Radar. Electronics 2017, 6, 30. https://doi.org/10.3390/electronics6020030
Gallagher KA, Narayanan RM, Mazzaro GJ, Martone AF, Sherbondy KD. Static and Moving Target Imaging Using Harmonic Radar. Electronics. 2017; 6(2):30. https://doi.org/10.3390/electronics6020030
Chicago/Turabian StyleGallagher, Kyle A., Ram M. Narayanan, Gregory J. Mazzaro, Anthony F. Martone, and Kelly D. Sherbondy. 2017. "Static and Moving Target Imaging Using Harmonic Radar" Electronics 6, no. 2: 30. https://doi.org/10.3390/electronics6020030
APA StyleGallagher, K. A., Narayanan, R. M., Mazzaro, G. J., Martone, A. F., & Sherbondy, K. D. (2017). Static and Moving Target Imaging Using Harmonic Radar. Electronics, 6(2), 30. https://doi.org/10.3390/electronics6020030