2. Prior Work
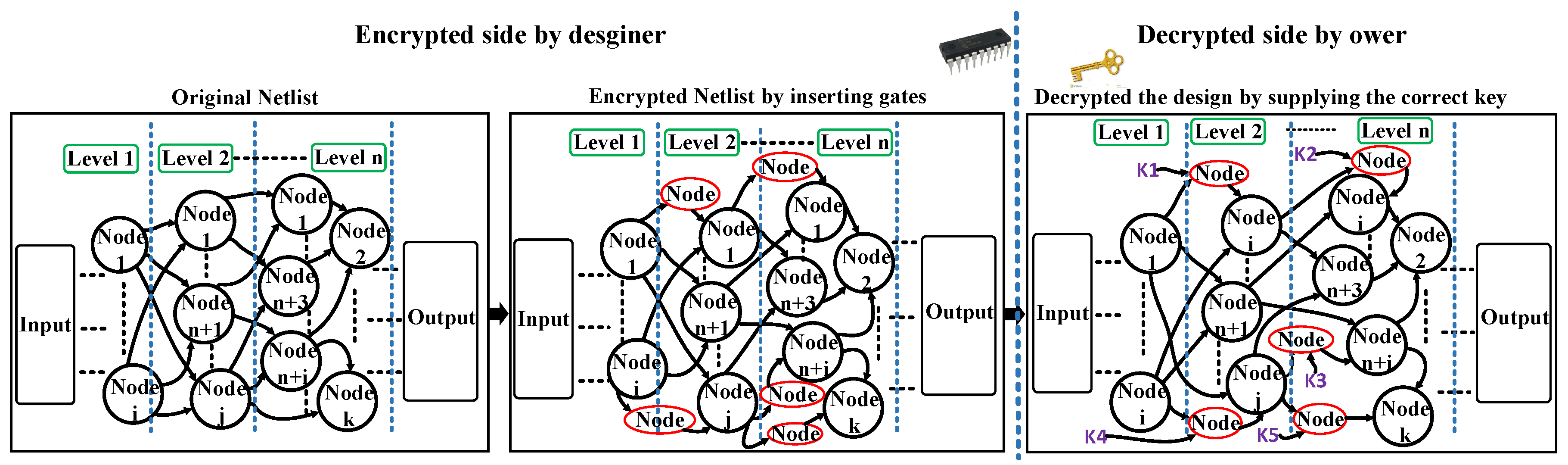
Rogue copy, mask theft, overproduction and overbuilding are the main reasons to secure the IC from various assailants leveraging the logic encryption approaches. The cipher design can be done via inserting a few gates into the original design to conceal the functionality, while the deciphering can be rendered once the owner provides the circuit by the correct external key bit inputs.
Logic encryption can mainly be classified into two types: sequential and combinational. For sequential, new states with transitions have to be added to the original finite state machine (FSM) to produce a boosted and security-enhanced FSM that provides a strong secured circuit [
16]. In [
17] and [
18], the authors proposed two modes: obfuscated and normal. By inserting some state elements into the original FSM, the obfuscated mode is produced to create a counterfeit state. The functionality is always wrong unless the correct sequence of the key bits is applied. An untrusted foundry is not able to figure out the correct sequence of the new FSM without knowing the whole state transition graph, which means going through all of the possible cases. Furthermore, the design goes into an unknown state when the sequence of the key is pulled out. The security strength of these techniques was not evaluated in terms of comparing the corrupt and correct outputs.
For combinational encryption, many methods have been introduced, such as random insertion, fault impact analysis and robust logic obfuscation. In [
19,
20,
21], the authors presented a technique to insert XOR/XNOR gates randomly into an original circuit to conceal its functionality. Upon inserting the valid key, the end-user can get the correct output. The drawback of this approach is that it is not always the case that the wrong key produces the wrong output. In some cases, the true output can be revealed even though an invalid key is supplied. In [
6], Rajendran presented a fault impact analysis (FA) method to increase the security level of the random logic encryption. In the FA approach, the new gates are inserted based on the stuck-at fault model. First, the fault impact for each gate is calculated by computing the stuck at zero and at one. Afterwards, for each iteration, a new gate can be inserted at the highest fault impact on the output until the HD becomes 50% (or close to 50%) or all of the supplied 128 key bits are finished. For robust logic obfuscation, the key-related gate-bits are injected in a certain way into the design that causes the key information extraction process to be hard to achieve [
22]. Yasin et al. improved on the work through inserting more pairwise keys [
5]. In [
23], IC protection is done by insertion of process variation (PV) sensors inside the design at specific selected nodes along with generation of a unique key for each IC. The maximum achieved HD from this technique was around 18%. The authors in [
24] proposed a lightweight technique for defending against Boolean satisfiability (SAT)-based attacks and other threats related to IP piracy. Their technique, namely SAT-Attack Resistant Logic Locking (SARLock), works based on maximizing the required number of distinct input data vectors for preventing data leakage and consequently key revealing. In this way, an attacker’s effort for finding the secret key increases exponentially.
Besides the logic encryption techniques, passive metering [
16] and watermarking [
25] methods can only be used to distinguish IC piracy; however, they cannot preserve the IC from piracy that may occur [
6]. From the above, the logic locking is considered to be one of the most important methodologies in terms of IC piracy prevention and IC protection.
4. Our Techniques
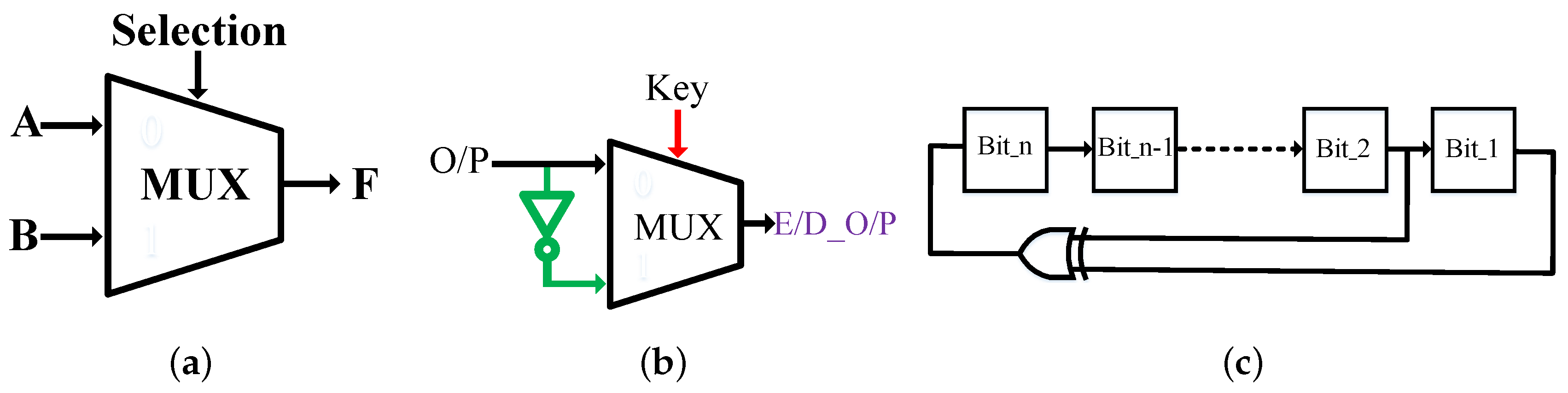
In this section, we demonstrate our methodology to secure a circuit design by leveraging multiplexers as key gates in a way that the output is corrupted by around 50% unless the correct key is supplied. The operation of the multiplexer is to propagate one of the input signals to the output based on the input selection. For instance, if the input selection is zero, then the output F is equal to input A, otherwise F is equal to input B.
Figure 2a demonstrates a two-to-one basic multiplexer diagram. Equation (
1) explains the Boolean operation. A and B are two inputs, while selection is the chosen input and F the output.
Figure 2b illustrates an example of how the output can be determined by the key bit. If the key input is one, the Encryption/Decryption output (E/D_O/P) is equal to the complementary of the original output to encrypt the design; however, to decrypt the design, the E/D_O/P is equal to the original output (O/P) when the key input is zero. The functionality of the circuit can be changed based on the key value.
Since the true random number generator (TRNG) is costly and not fast for several applications, such as creating keys and padding for encryption techniques, the linear feedback shift register (LFSR) is broadly employed to generate a pseudo random number generator (PRNG) instead, as in [
33]. Generally, the LFSR is fast and inexpensive because it demands only a shift register operation and an XOR or an XNOR operation, as shown in
Figure 2c. We employ the LFSR to generate pseudo random keys with half of the key bits ones and the other half zeros to increase the security level of the design. Basically, there are two types of LFSR: standard LFSR (also called internal feedback LFSR) and modular LFSR (referred to as external feedback LFSR) [
34]. We choose the external feedback with 128 bits as a maximum length of the LFSR (number of flip-flops), and we consider the initial value of the LFSR as a constant value. The LFSR counts to
as a maximum number (periodicity) where n is the number of D Flip Flops (DFFs). An attacker needs more than five years to get all of the LFSR possible values once the length is larger than 63 bits [
35]. We use Table 3 in [
35] to get the polynomial equation with the maximum length LFSR counter, where the taps are an XNOR gate among bits 99, 101, 126 and 128.
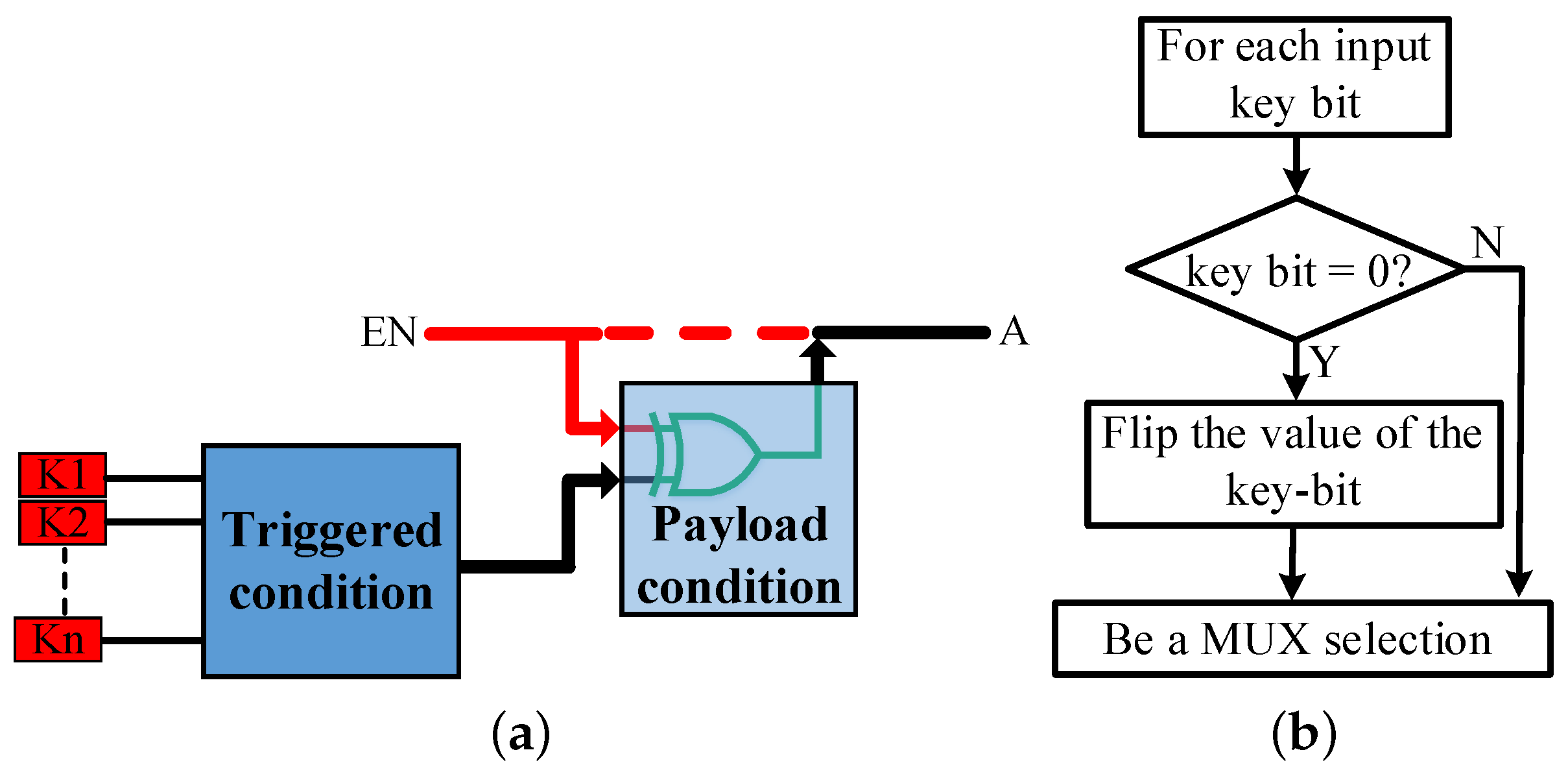
The hardware Trojan mainly consists of two parts; trigger and payload. Trigger is the bare condition to activate the Trojan, while the payload is the act of the Trojan (the payload contains XOR/XNOR gates). We use this idea to conceal/expose the functionality of the design, and we refer to it as the “hardware logic unit (HLU)”. The user key is considered as an input to a trigger; meanwhile, the payload is regarded as the activation of the design.
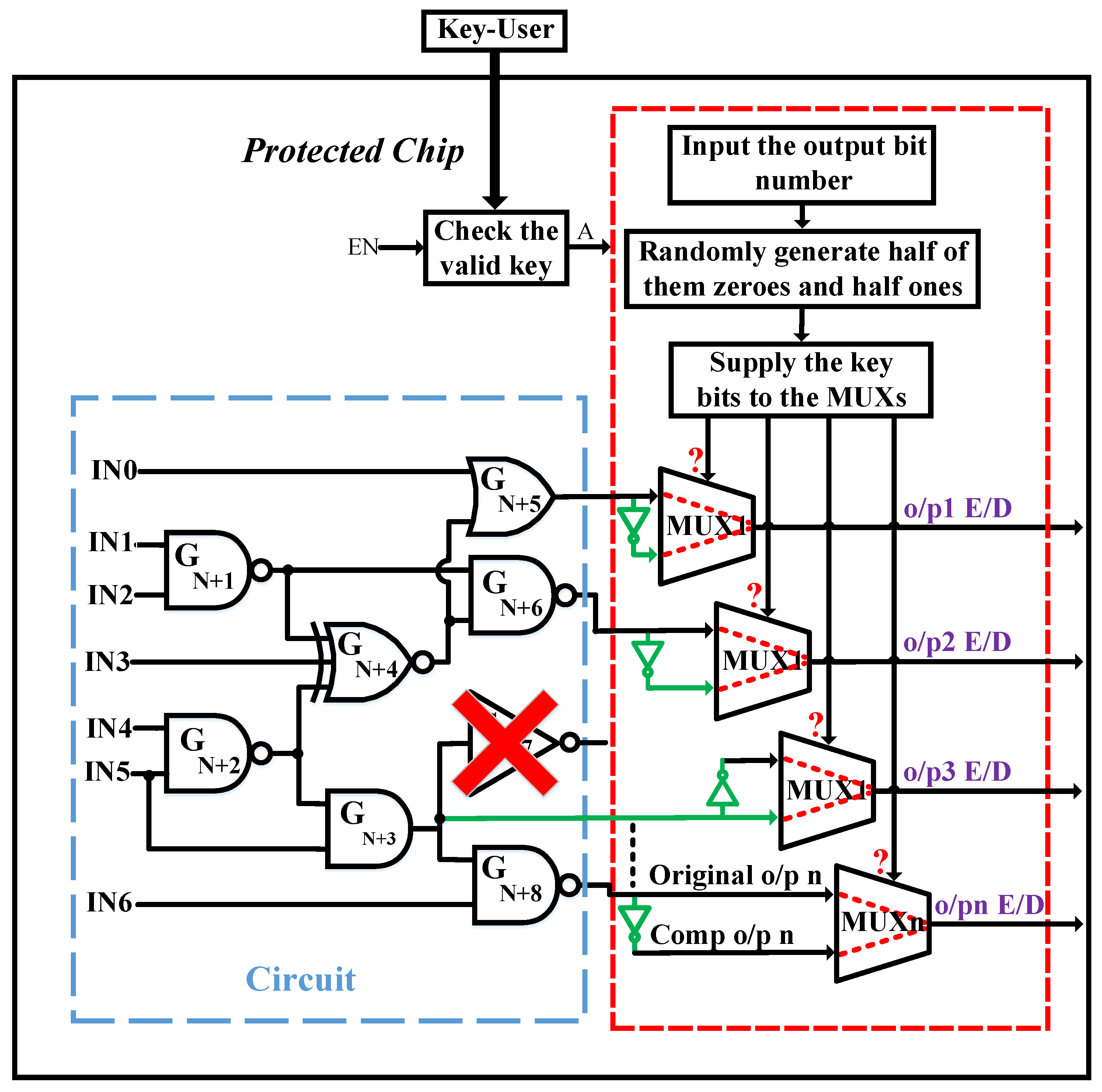
Figure 3a illustrates the key idea of leveraging the HLU to protect the design, where K1, K2, ..., Kn are the user key bits, A is the target to give the initial values of each MUX and EN is to enable the LFSR generator. The functionality of the circuit will be correct if the output of the trigger is activated by supplying the valid user key. Meanwhile, the activation (A) will give the default of the MUX selections. Otherwise, the output will always be wrong. The fault analysis mode was used to affect as many outputs as possible, but it does not affect half of the output for every circuit. We insert the MUXs, at the output, in two ways based on the number of output bits in order to hit around 50% HD. The logic encryption based on MUX insertion is classified as follows:
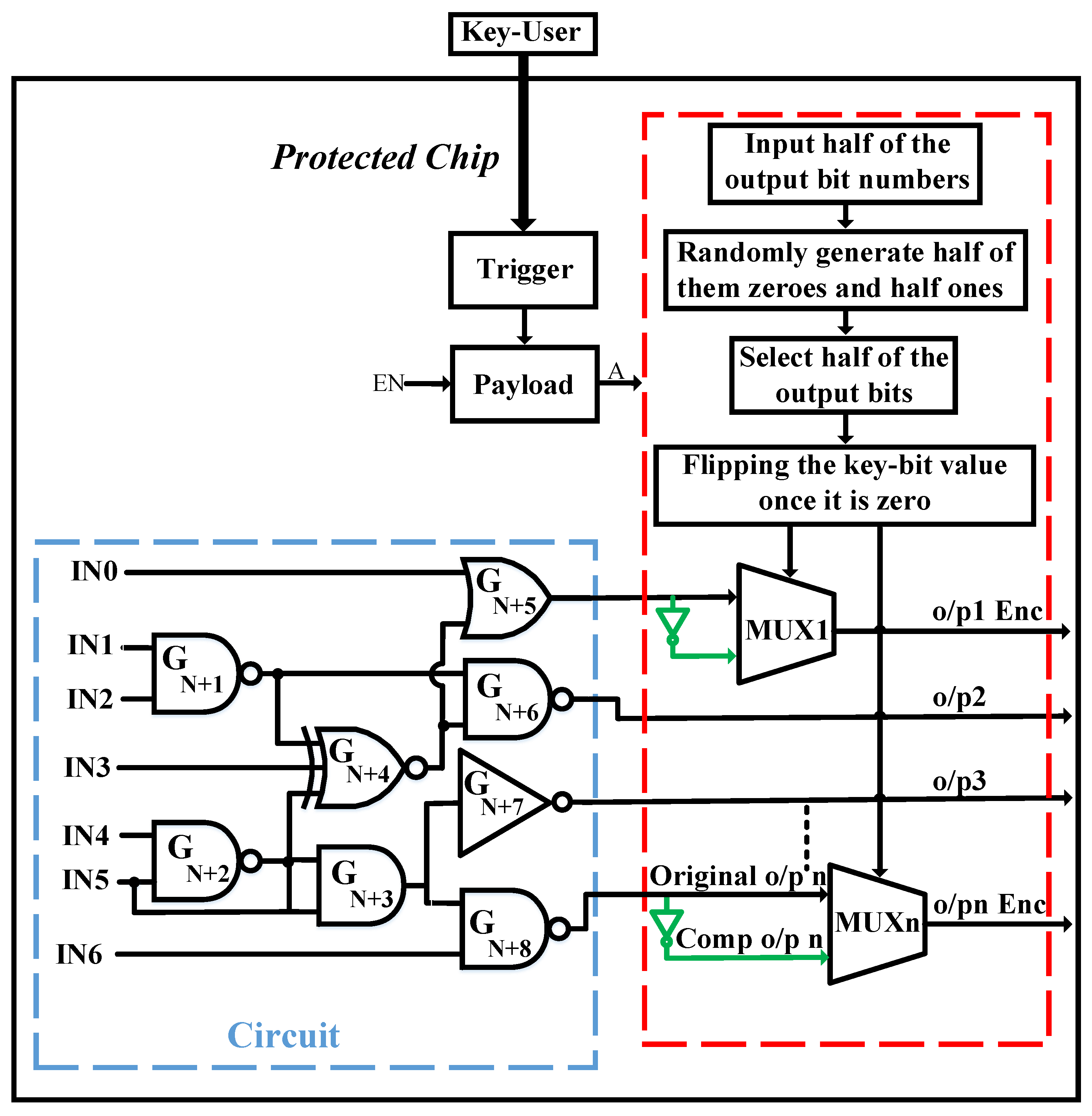
4.1. MUX Insertion Based on Half Output Bits
To insert the multiplexers, we need to count the number of output bits in the design. Then, we randomly select and complement half of the output bits, as well as inserting an MUX with these two (output bit and its complementary) as inputs and a key bit as a selection. Due to the insertion, the Hamming distance between the correct and corrupt outputs is always 50% when the number of output bits is even or close to 50% when the number is odd. Even though the HD is around 50%, the design is not secure enough since the input key selections for all inserted MUXs are weak (all of the input key values have to be ones), which means that the key is very easily exposed to the attackers. In order to make the key more secure and increase the ambiguity of the attackers, we randomly create half of the input key bits as zeros and the other half as ones, then flip the value of the key bit once it is zero to make sure that all of the outputs of MUXs are equal to the complementary of the original output bits. Instead of changing the key bit value, one can invert the output of the MUX (but it also needs one more inverter) or exchange the inputs of the MUX when the key bit value is zero.
To make the design much more secure, RSA cryptography and PUF were proposed in [
12] to provide a fully-encrypted design. This was done without actual evaluation for the power, area and delay overheads, where the overhead of RSA cryptography is too large and the reliability issue of PUF is a concern. Instead of using RSA and PUF, we implement the HLU idea and the LFSR pseudo-random generation with some constraints to ensure that each generated random key consists of half zeros and half ones. The detailed constraints for the LFSR are: (1) making less than half of the initial values of the LFSR as ones to accelerate the generation of half zeros and half ones of the key value; (2) checking whether the new pattern has half zeros and half ones; if not, it neglects the pattern and picks up the next pattern, and so on, until reaching the correct pattern; (3) providing the MUX selection with the correct pattern. If the value of the key bit is zero, it must be inverted before providing it to the MUX selector, which is an additional simple condition after the key generation.
Figure 3b displays the completed flipping key bit technique.
The maximum protection level can be achieved by combining the inserted MUXs, the HLU idea, flipping the key bits and distributing its values. The output will keep malfunctioning with random keys unless the valid user key is provided. With the right key, the output of the trigger will be activated, and the payload will set the activation (A). Once A is set, the value of the secret key will be provided to the MUX selections, and the functionality of the circuit will be correct. Otherwise, the LFSR enable (EN) will be activated to generate random key patterns with half zeros and half ones.
Figure 4 shows the whole protected design based on half MUX insertions, where o/p, Comp, n and Enc are the output, the complementary, the number of the output bits and encryption, respectively. Assuming that n is an odd number, half of the output number is considered as (n−1)/2. Although this technique is efficient against various threats, such as IP piracy and counterfeiting, it might be vulnerable to an attacker who may figure out the functionality of an IC based on some exposed output bits. To prevent experienced attackers, we then propose the full MUX insertion technique.
4.2. MUX Insertion Based on All Output Bits
To maximize the protection of an IC from various attackers, we propose to insert an MUX at each output bit, as shown in
Figure 5. The inputs of the MUX will be the original output bit and its complementary, along with a key bit for the selection of each MUX. The values of the key bit selection must be random with half zeros and half ones to produce 50% HD. Since each output bit and its complementary are connected to a MUX with a random key bit selection, each output bit of the IC is changeable once the key is changed. In this case, not only the HD between the corrected and corrupted outputs is around 50%, but also the value of each output bit is variable.
An assailant cannot figure out the functionality of the design because each output bit will be varied by changing the supplied key via the LFSR generator, which is used to generate random keys (each key is generated to have randomly half zeros and half ones, as mentioned). Since the key value is unpredictable due to the random generation, each output bit will be consequently arbitrary. Once the correct user key is inserted, the output of the payload will be set, and then, the enable (EN) of the LFSR generator will be disabled, while the activation signal (A) will be activated to initialize the values of the MUX’s selections. Then, the functionality of the circuit will be correct. If the value of one bit in the user key is incorrect, the corrupted output ratio will still be around 50%.
Although inserting MUX at each output bit will obviously maximize the protection of the design, as well as the ambiguity of an attacker, the power and area overheads will largely increase. Therefore, this technique is more suitable either for large circuits that include a large amount of output bits or for an expensive IC chip. In both half and full MUX insertions, if there is an inverter at an output, we replace it by an MUX with switching its inputs. Furthermore, all components of the encrypted circuit (in half and full MUX insertion techniques) are made at a pre-layout stage.
5. Results
5.1. Experimental Results
Both the IEEE International Symposium on Circuits and Systems (ISCAS)-85 (combinational) and ISCAS-89 (sequential) benchmarks are employed to analyze our methodology. The C language is used to randomly select and add key gates (or replace an inverter with a key gate if the gate at the output is an inverter) for both half and full MUX insertions. The performance is evaluated by Synopsys Design Compiler.
The Verilog language is also leveraged to design two LFSR random generations; one of them is used to generate 1000 random patterns for the inputs of each netlist, and the second is utilized to generate random keys with equal probability, so the value of the output bits will be controlled by these key bits (each selected output bit is inverted when each key bit is set). We adopted the 1000 random input patterns that the first LFSR generated for the original netlist, and the output results were saved in an array. Afterwards, we supplied the same 1000 random input patterns to the same netlist with a random key that the second LFSR generated, and the results were also saved in an array. We make the initial value of the second LFSR as a constant value. In order to evaluate the Hamming distance between the corrected output when the key selection is at the default value (the valid key is given) and the corrupted output when the second LFSR key generator provides a random wrong key with equal probability to the MUX selections, we designed a shift register to provide each random key bit for each of the 1000 random input patterns starting from the first key bit till the last one in the register.
5.2. Hamming Distance Evaluation
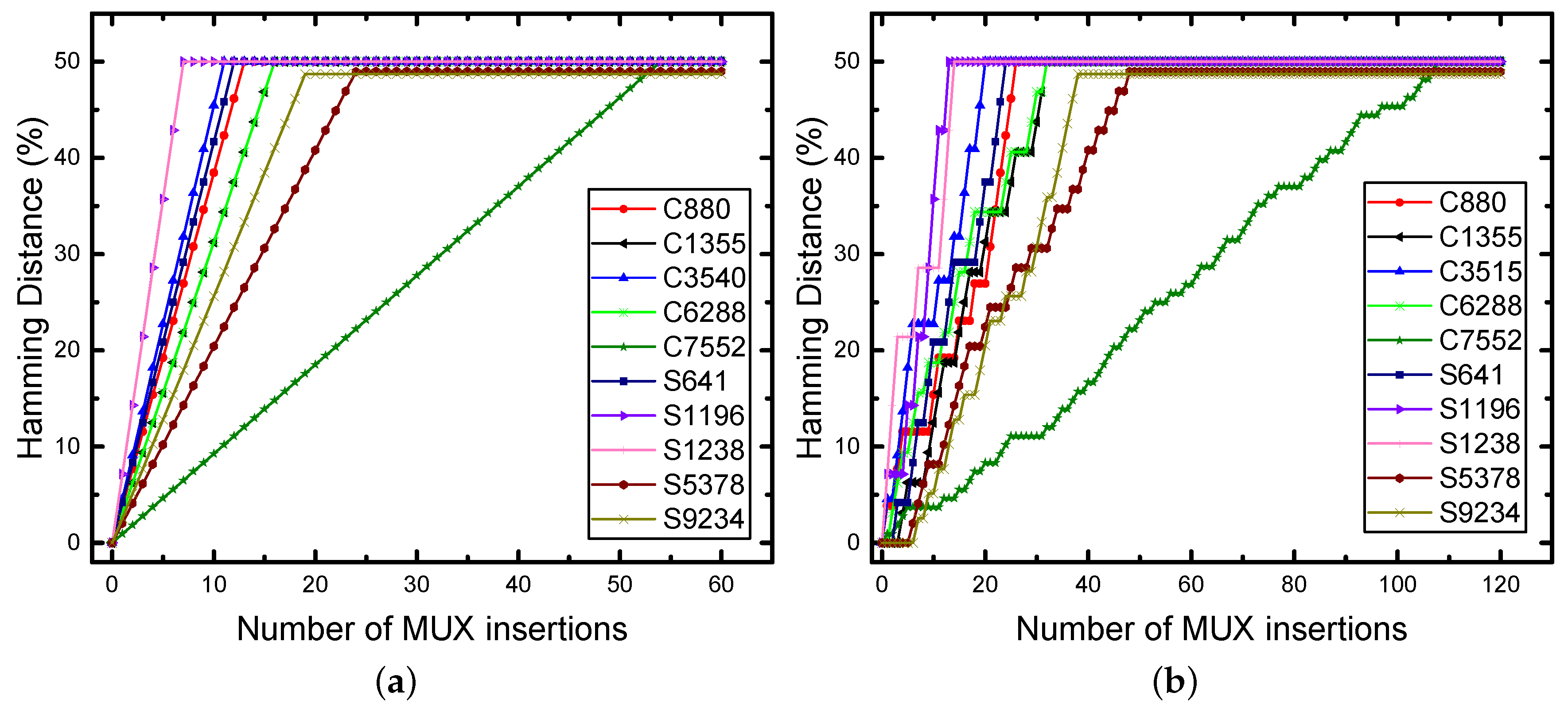
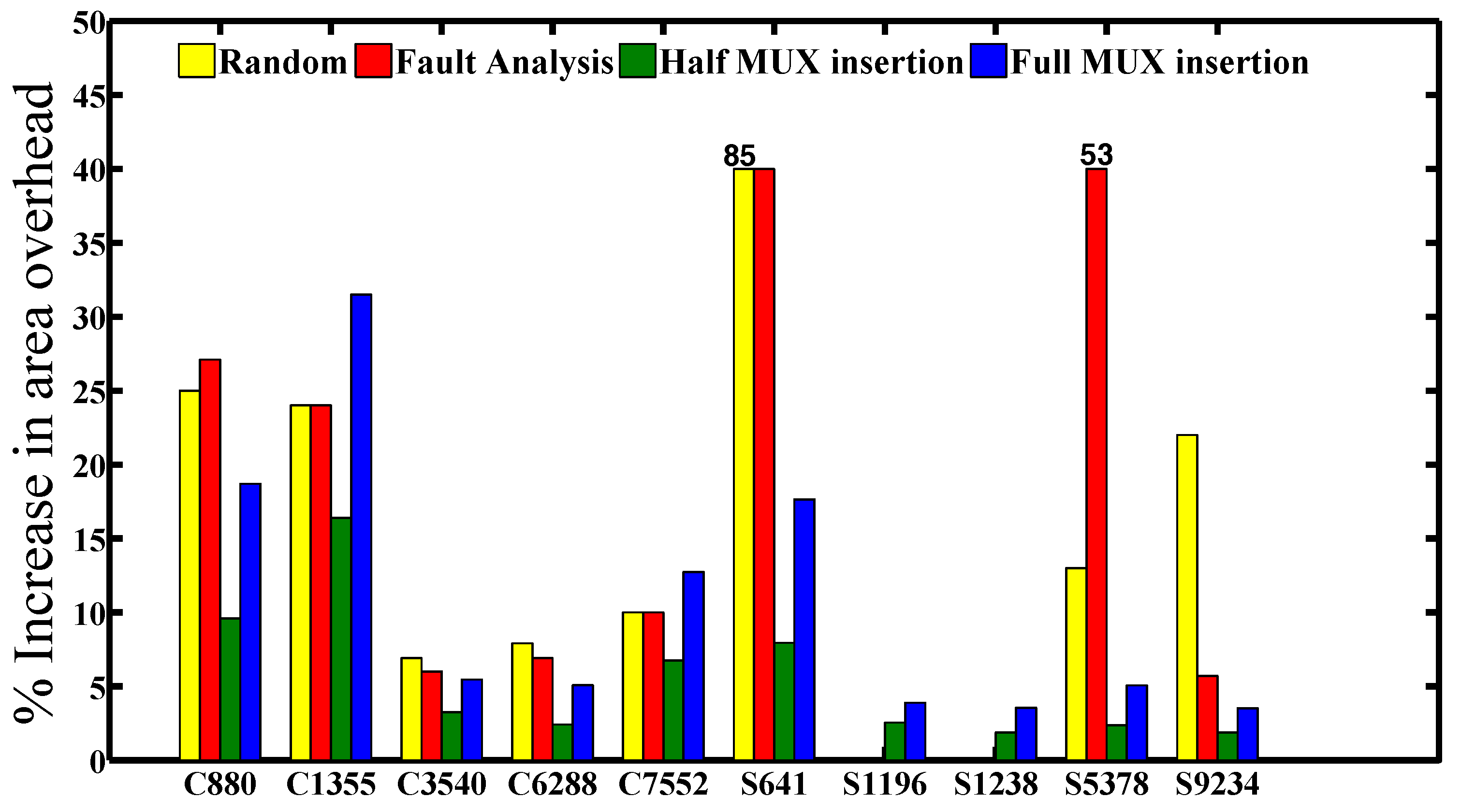
The inserted MUX method based on half and full output bit numbers is compared with both the random and fault impact analysis-based on XOR/XNOR insertion approaches, and the illustrated outcomes for the minimum required number of inserted MUX key gates to achieve the hamming distance (for each benchmark circuit) are depicted in
Table 1, where sequential circuits S1196 and S1238 were not tested by the random and fault impact methods.
The use of the random insertion method did not achieve 50% HD, while the fault impact analysis achieved 50% HD, but not for any circuit and not for any input patterns, especially when the number of output bits is very high (more than 100 output bits), such as the combinational benchmark circuit C7552 , besides the complexity of the fault impact algorithm to find the highest impact gates on the output, which will take a very long time to test the whole design for a large circuit, such as C7552. In contrast, our methodology ensures that the HD will be 50% or close to it (such as S9234) once the design has an even or odd output bit number, relatively.
In addition, we evaluated the HD for all of the benchmarks that are mentioned in
Table 1. For each benchmark, we only picked up one random key that was generated by the LFSR random key generation and fed it to each netlist to evaluate the HD between the correct and corrupt outputs based on half and full MUX insertions.
Figure 6a,b demonstrates the analyzed HD for the ISCAS-85 and ISCAS-89 benchmarks based on the full and half MUX insertions for logic encryption, where the minimum required length of LFSR to achieve the HD in the figure is equal to the number of output bits. The HD for these benchmarks is 50%, except for S9234, which is 48.72% due to having an odd output number.
In our work, not only the functionality of the circuit is incorrect when the wrong user key is entered, but also the Hamming distance is always 50% or close to it, for whatever the input test patterns, the wrong input key and the size of the circuit are, unless the correct user key is inserted. To analyze the effectiveness of the random keys that the LFSR generated, we tested the C880 benchmark with five random keys using the full MUX insertion technique. First, we supplied 1000 random input patterns to the original C880 and monitored the correct output, then we supplied each key bit in each of these random keys with the same 1000 random inputs starting from the first bit until the last one by leveraging a shift register, to evaluate the HD for these five random keys. The HD was always 50% with different output patterns, as shown in
Figure 7. This means that all of the output bits are always changeable and cannot be predicted, even if there is only one bit in the user key that is incorrect.
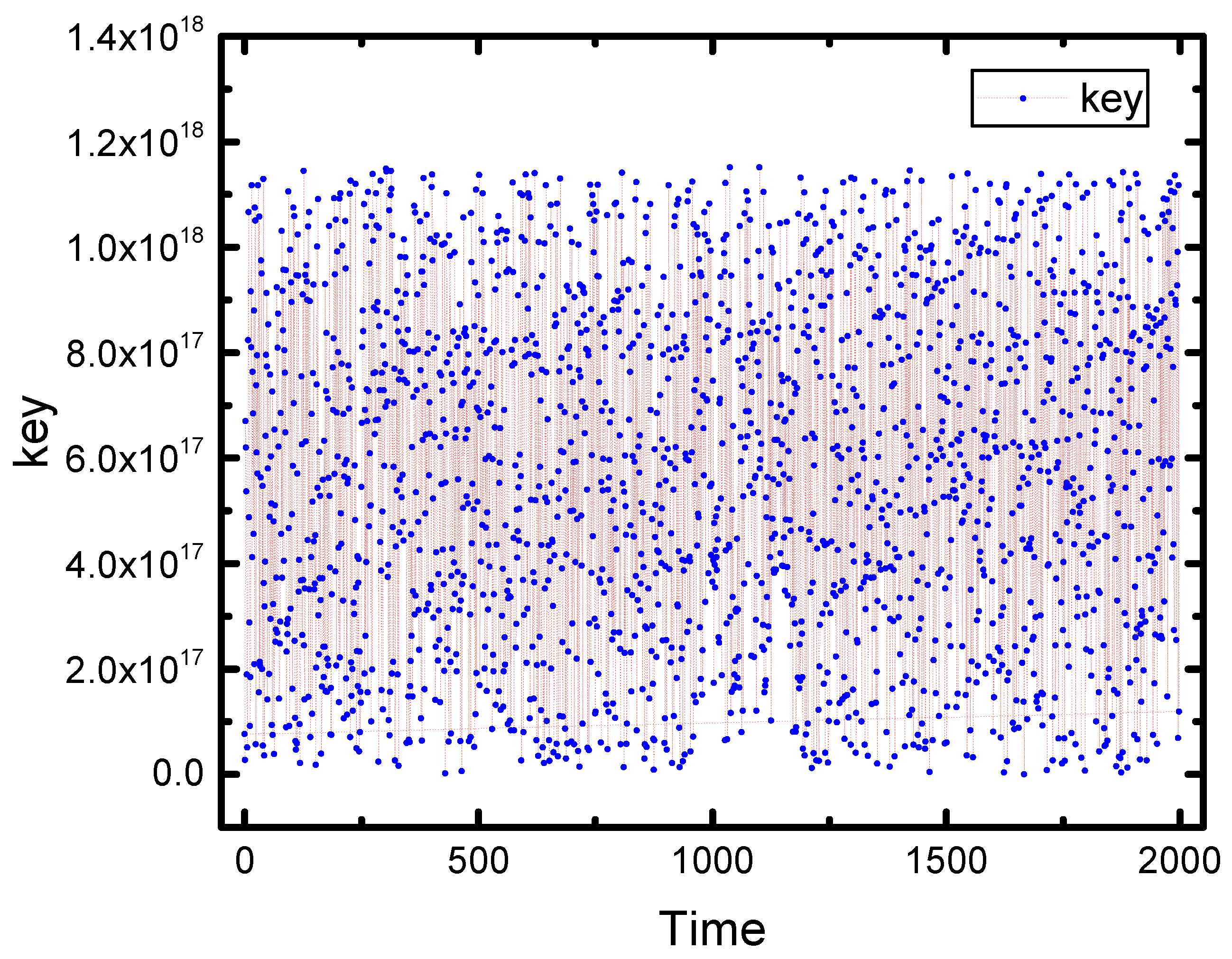
5.3. Random Key Generation
The selections of all MUXs must be provided with the right key bit values at any time for whatever the input patterns are to maximize the protection of the circuit. LFSR always provides the MUX selections with these values to corrupt half of the output bits when the enable signal (EN) is set. Once the valid key (user key) is inserted, the payload will provide the selections of the MUXs with their default values, and the functionality of the circuit will be correct. To make sure that the generated keys by the LFSR are random with equal probability, we observed and saved the outputs of the LFSR in a file only for the first 2000 numbers by making its initial length 60 bits (each output key has 30 zeros and 30 ones), and the outputs are as shown in
Figure 8.
5.4. Delay, Power and Area Performances
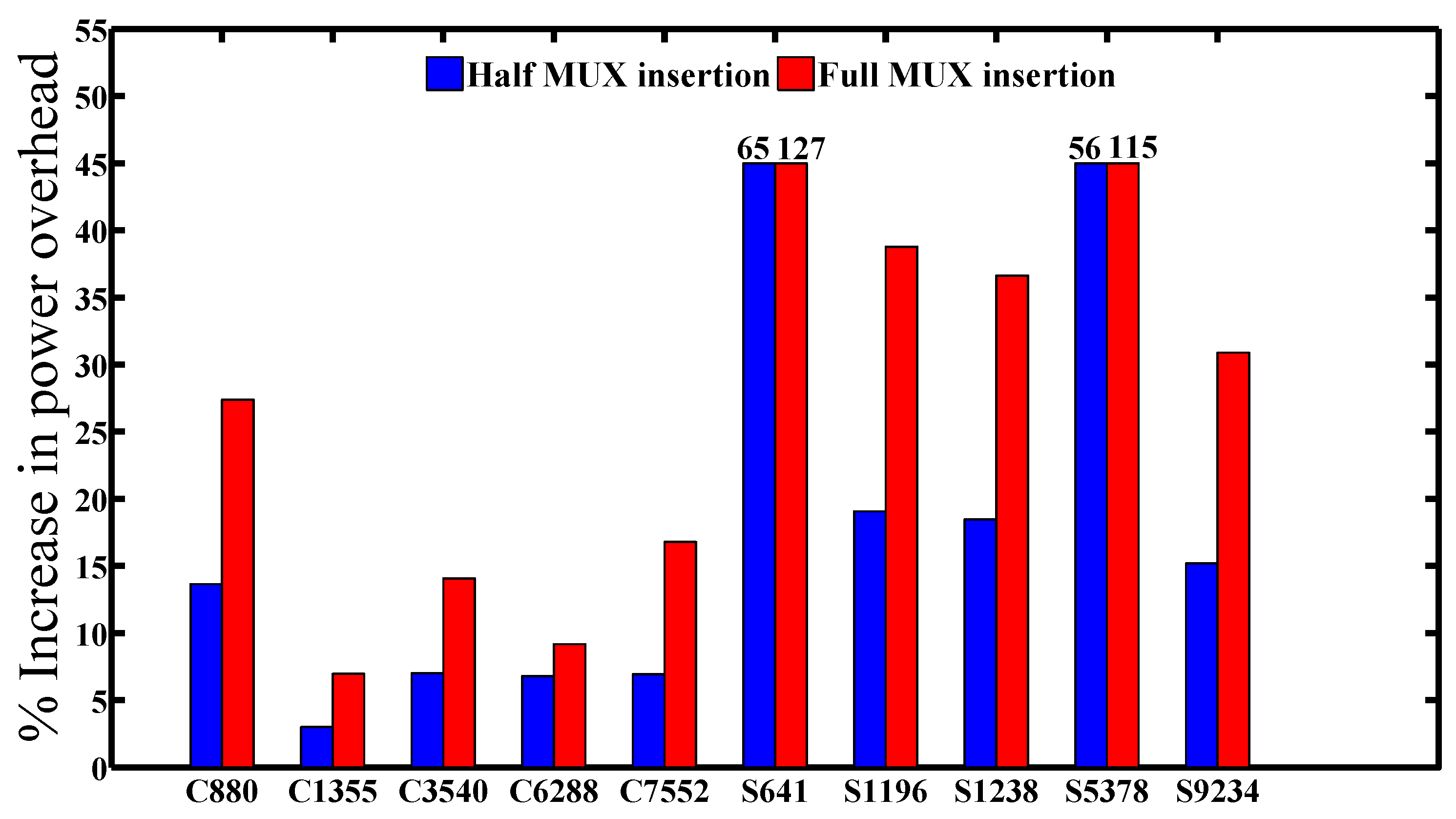
We measured the delay, power and area overheads for each benchmark circuit using the Synopsys design compiler as a tool with the 45-nm CMOS library. Since the MUXs were inserted only at the output of the netlist, the delay overhead (timing path) is almost zero for all of the benchmark circuits. Meanwhile, the power and area overheads for each benchmark depend on the number of output bits. Increasing the number of output bits will significantly increase the overheads for the area and power.
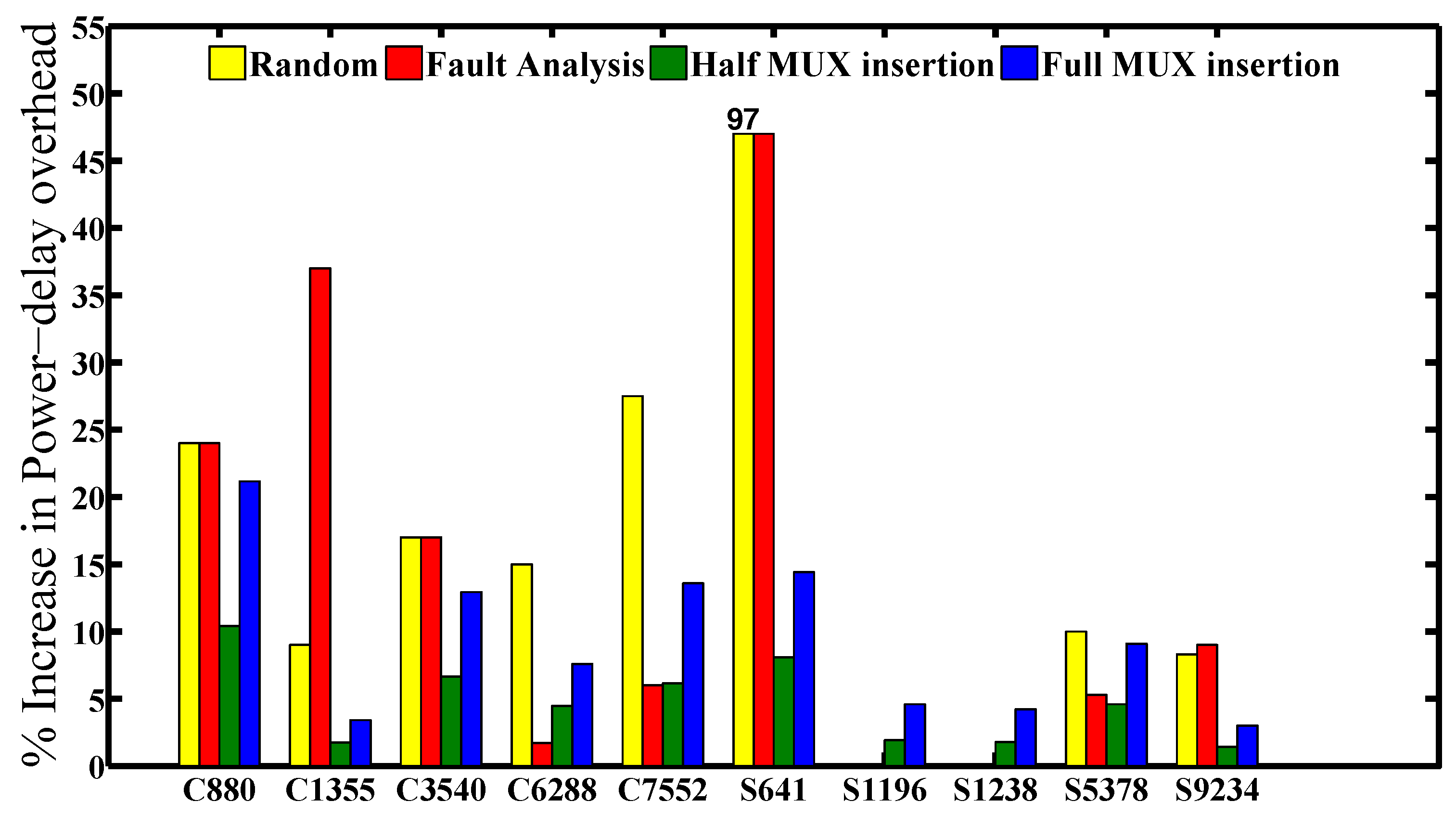
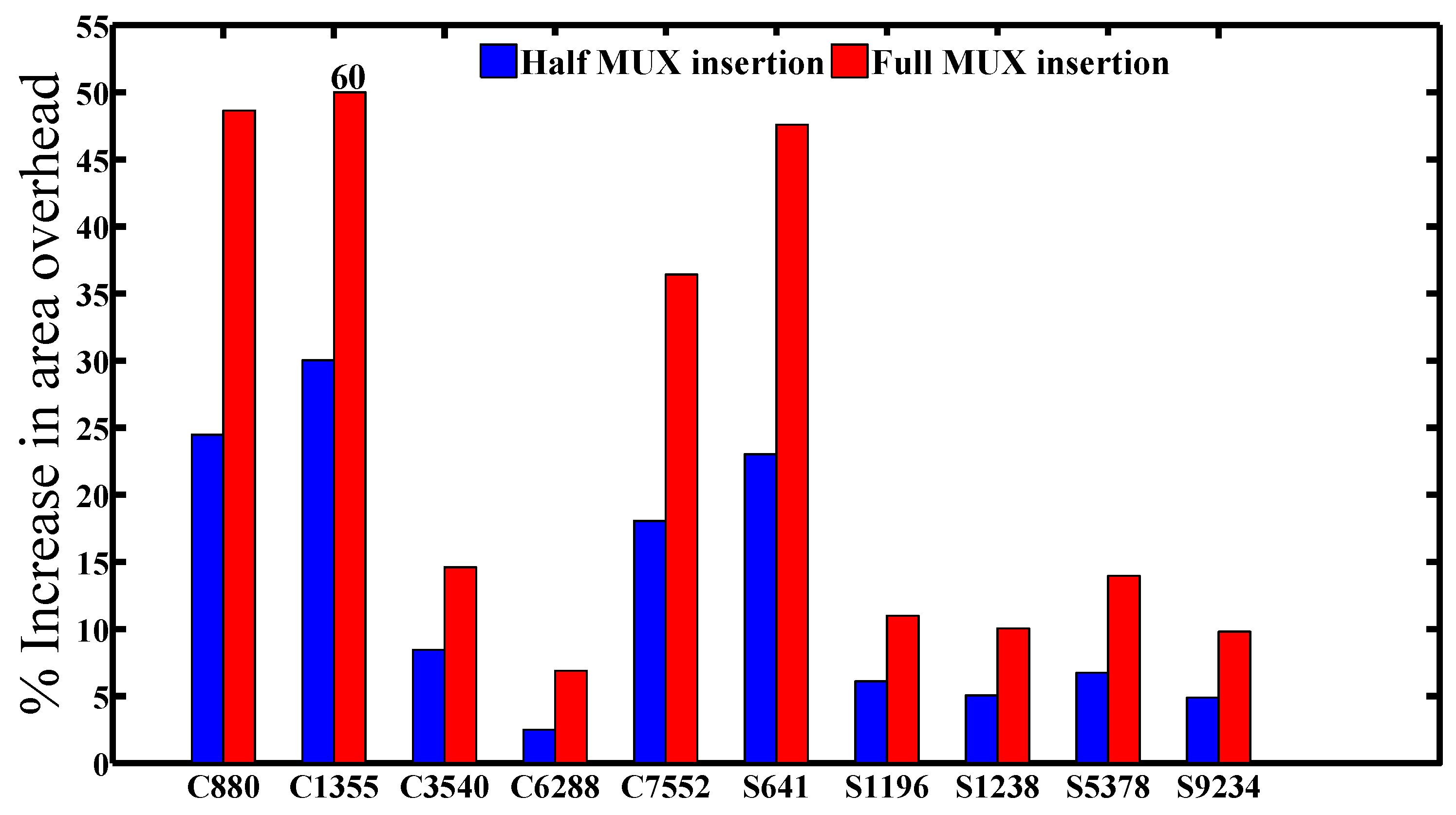
Figure 9 and
Figure 10 show the power-delay product and area overheads for all of the benchmark circuits that are listed in
Table 1 with the corresponding number of MUX insertions that are mentioned in Column 3. From the figures, we can see the full MUX insertions consuming power and area approximately twice a half of the MUX insertions. The reason is obviously because the number of MUX insertions in full insertion is twice a half MUX insertions. It is worth noting that the half and full MUX insertions save area more than 2× and 3.6× and the power-delay product with more than 2× and 3.4× on average, respectively, compared to fault impact analysis.
Furthermore, in order to enhance the security level for the design by generating a unique key for each IC, Rajendran et al. in [
12] employed the PUF circuit and RSA encryption asymmetric cryptography. The RSA overhead will be very high (it overrides the area of VIRTEX5, as mentioned in
Section 1.2), where the authors only proposed using PUF with RSA cryptography without a true evaluation for the delay, power and area overheads.
Instead of using RSA and PUF, we adopt both HLU and LFSR as a different technique to protect the secret key and generate random keys with 0.5 probability for each one, respectively, as mentioned in
Section 4.1. Both the HLU and the LFSR random key generation are designed and synthesized with the full and half MUX insertions using Xilinx ISE. We also evaluate the delay, power and area overheads for the whole design, including all components.
Figure 11 and
Figure 12 demonstrate the total power and area overheads for the whole design, which are appropriate for several benchmark circuits, but are not suitable for other benchmarks, such as C880 and S641, due to the small area compared with S9234 and C6288. Moreover, the delay (timing path) overhead is very small for most of the benchmarks, except for C6288, which was 8.49%.
6. Discussion
6.1. Durability of the Logic Encryption
The most substantial part in the encrypted circuit is the valid key. Once it is known by an attacker, the functionality will be revealed despite how strong the encryption technique is. The attackers can utilize many different ways to expose the functionality of the circuit, but the most dangerous attacks are in the following:
6.1.1. Using the Brute Force Algorithm
An attacker can use the traditional brute force algorithm to get the right key and expose the functionality of the circuit. The number of different combinations that an attacker needs to decipher the design can be computed by Equation (
2), where K is the key size, and the input test patterns are different from one circuit to another. If the length of the user key is large enough, such an attack becomes infeasible [
27]. However, increasing the key size means inserting more gates (each new key needs an inserted XOR/XNOR gate), which leads to a great increase of the power, area and delay overheads, where the designer has the limitation of increasing the key size. In our work, increasing the user key size will not increase the performance overhead that much, since the user key size will only increase in the trigger part (see
Figure 3a). Adding a new key bit to the user key requires only to add either an inverter or a wire if the designer needs the value of the new key bit to be zero or one, correspondingly.
6.1.2. Removing Both LFSR and MUX Key Gate Insertions
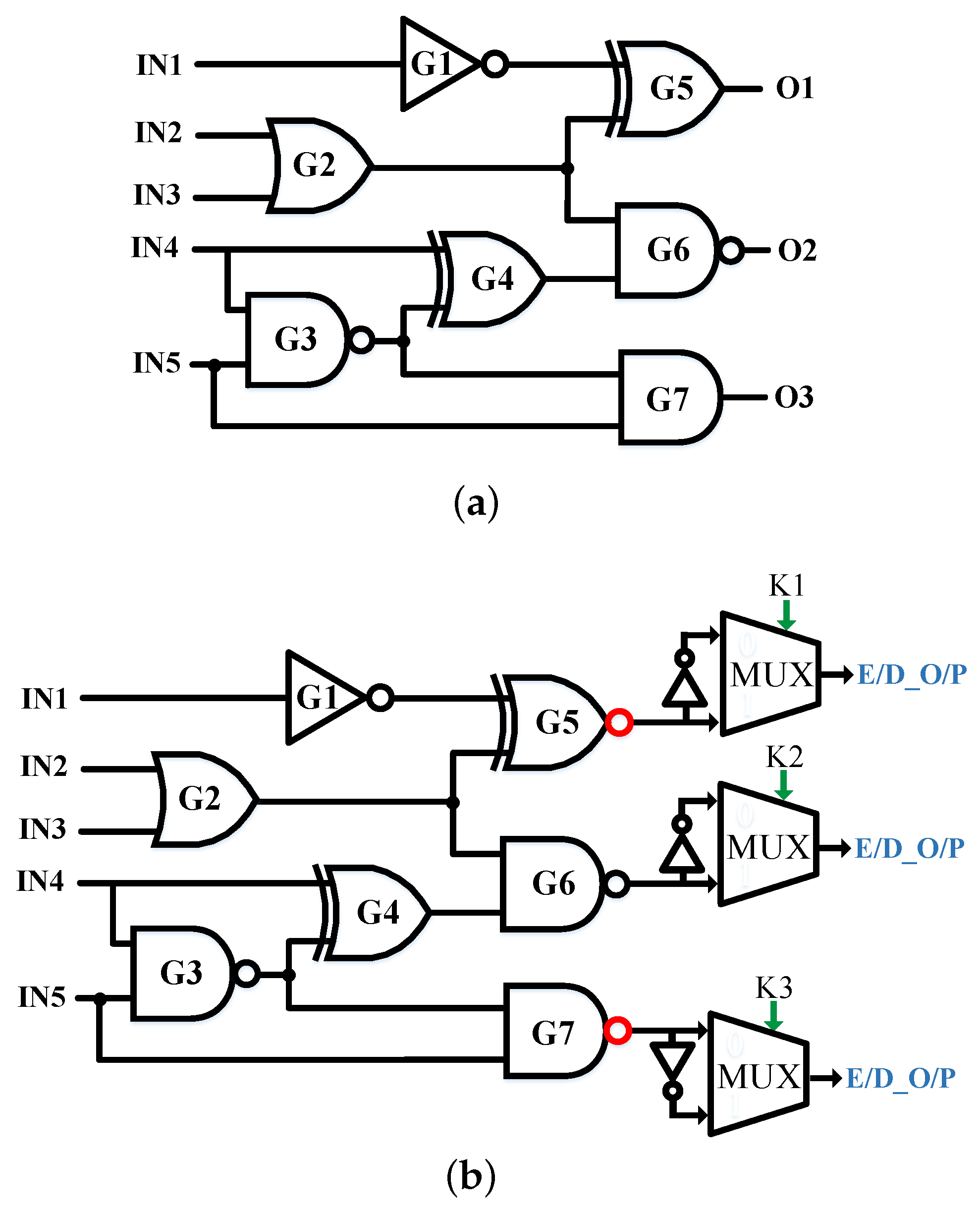
An attacker can remove the LFSR random generator and the inserted MUX key gates to get the original design. Then, he or she can copy the IC illegally. However, the attacker can not get the correct functionality by removing the LFSR and the MUX key gate insertions for two reasons: (1) The MUXs are not only inserted at the outputs, but also some of them are exchanged with inverters in the original design. In this case, the attacker will not know whether the inserted MUX at each output is added or replaced by an inverter. If the original circuit has no inverters at all of the outputs or each primary-output has an inverter, then the attacker can easily get the original IC. In this case, a designer can use another way to prevent such an attack by adding inverters before some of the inserted MUXs and combining them with their previous gates [
6]. For example,
Figure 13a shows an original circuit, and
Figure 13b shows the encrypted circuit with three different key values as “K1K2K3=011”. An attacker cannot know whether an inverter is added and combined with the last gate before the inserted key gate or not. Furthermore, we consider adding or replacing the key gates at the outputs as a minimum requirement to achieve 50% HD. One can increase the ambiguity of the attacker by randomly adding more key gates and replacing others with inverters through the circuit with keeping the correct value of the key bit (without changing the correct value of the internal net signal after the insertion). (2) The synthesis tools can also help prevent an attacker from realizing whether there is an inverter added since the synthesis tools use inverters through the regular synthesis of a design (not for logic locking purposes) [
6].
6.1.3. Isolating the Secret Key and SAT Attacks
An attacker can access the primary input and output signals for a circuit and expose its structure if he or she buys an unlocked IC from the open market [
27]. Rajendran et al. emphasized that the secured key bits can be propagated to the outputs in the traditional XOR/XNOR insertion technique via employing automatic test pattern generation (ATPG) algorithms to create special test input patterns [
22,
32]. If an attacker uses the same input patterns (special test input patterns), there is no need for leveraging logic encryption techniques, since the functionality will be realized, and he or she can illegally copy and sale the ICs. The reason behind this is that the attacker can mute some key bits to expose the values of others to primary outputs, which is known as “isolated key gate” [
22]. To prevent such attack, the author in [
22] suggested that the relationship between the key bits has to be non-mutable using the interference graph, such as two key bits are connected to the same gate, where muting a key bit, it is impossible to propagate the value of the second key bit to an output, which is called “non-mutable convergent key gate”. In this case, the number of attempts that an attacker needs to reveal the correct key will be
, where N is only the number of the affected bits in the key (non-mutable key bits). The security level of the design can be very robust once the effective key size is large where the computational time will be very long. For example, if the effective key size is larger than 100, an assailant needs many years to obtain the correct key [
22]. However, this technique cannot be successfully applied to any circuit because the inserted key gates based on the interference graph rely on the topology of the circuit, and also, the performance overhead will be large compared with other techniques [
5]. Another good way to prevent such an attack [
6] is to consider each flip flop as a pseudo-input and pseudo-output because, to propagate the key, an attacker needs: pseudo-input-output pairs, pseudo-input-primary output pairs and primary input-pseudo-output pairs to successfully get the secret key. The scan test port of the design is disabled after the fabricating test to prohibit accessing of the flip-flops [
6,
36].
Another very serious type of attack is SAT-based attacks. By acquiring the structure of the IC and accessing its primary input and output signals, the attacker can extract the valid key using the satisfiability checking (SAT) algorithm in a short time [
27]. More specifically, he or she applies distinguishing input patterns with different key bits to get all of the various output patterns. Each special I/O pair can recognize a part of the incorrect key combinations, and all of these pairs together will guarantee the correct key in the SAT formula. These two attacks, isolated secret key and SAT attacks, are very powerful to reveal the right key from a locked IC. A designer can prevent an attacker from accessing the correct I/O pair patterns in a locked circuit by adding the ANTi-SAT attack, which is an additional small circuit, namely the anti-SAT block [
28]. This renders an attacker unsuccessful in correctly obtaining the I/O pairs from the encrypted design, which leads the correct key being exposed. On applying random input patterns, using the ANTi-SAT block with a valid key, the output of ANTi-SAT will always be zero, and thus, the functionality of the original circuit will not change. With the invalid key, however, the output of the ANTi-SAT will always be one, which produces the wrong functionality. A designer can get full IC protection by combining ANTi-SAT with our technique (MUX insertion). Note that SAT-based attacks break all existing logic locking techniques, and so far, only this way (adding extra hardware (e.g., ANTi-SAT attack)) can prevent the attacker from exposing the valid key via getting the correct I/O pairs.
Designers can prohibit an attacker in an untrusted company from getting unlocked ICs using the secure split-test (SST) method before sending the ICs to the trusted facility to activate their functionality [
37]. The SST protocol is based on communicating and exchanging generated keys between the foundry and the designer, where only the IP owner can know whether the IC is passing the test successfully or not. A refinement on this protocol, called Connecticut SST (CSST), reduces the complexity communication between the IP owner and the foundry, as well as providing more protection than the SST. In this way, the designer can fully control the chip, and only he or she can understand the analyzed result of the locked chip [
38].
6.2. Limitations and Future Works
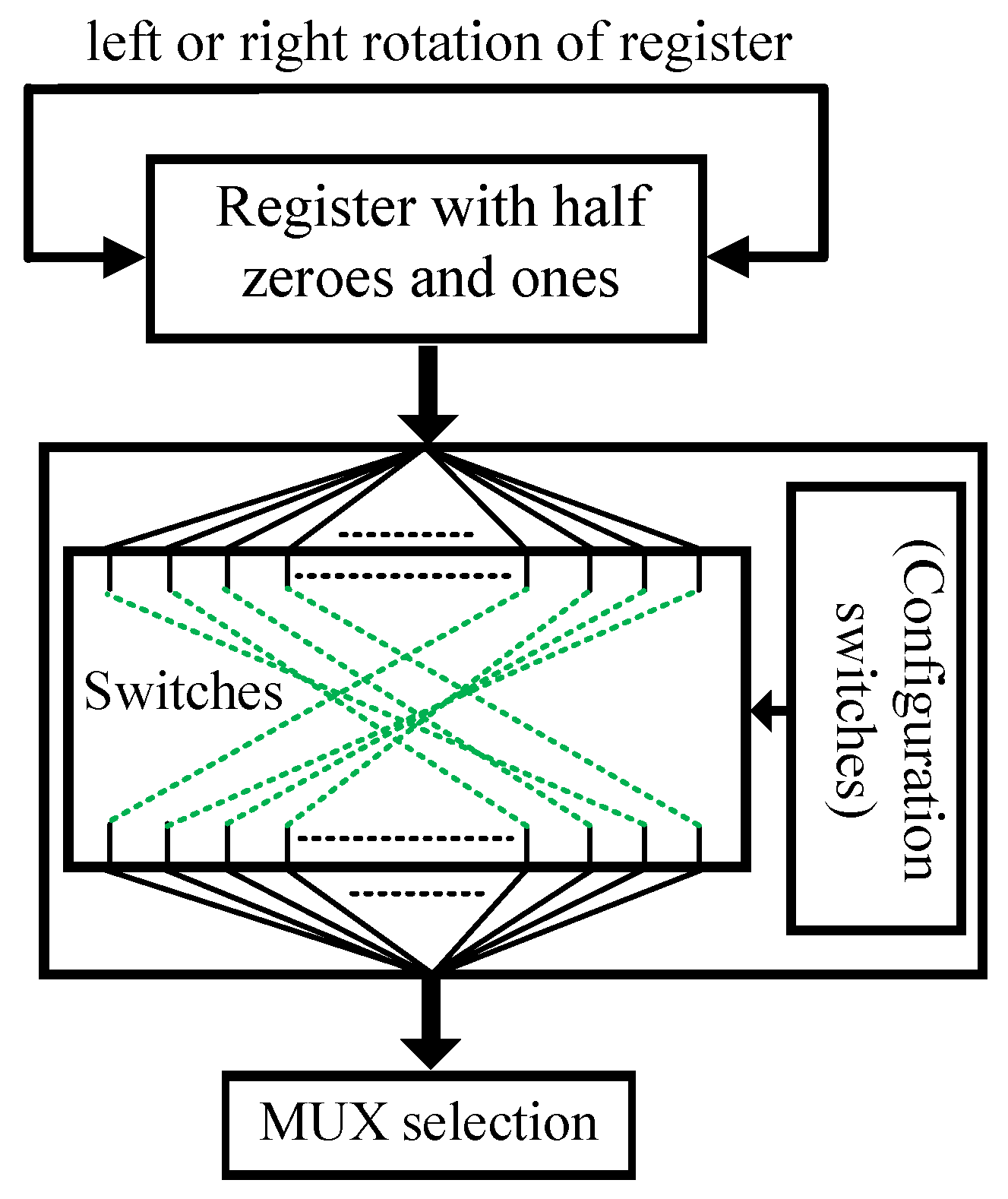
Although using the LFSR random generation produces random keys with 0.5 probability, it will not guarantee generating each key during each clock cycle, especially when the number of output bits in the design is too large (larger than 100). In this case, the old generated key will still be used by the selections of the MUXs until the new generated key by the LFSR is created, even when a new input pattern is supplied. Besides, the power, area and delay overheads increase for a circuit having a large number of output bits. In [
39], Dubeuf et al. utilized dynamic scrambling to change the order of instructions before storing them in the main memory and after reading from it to protect the system from several types of Trojans. A designer can use one register with 0.5 probability of a random key as an initial value, where the length of the register is the same as the number of output bits, then scrambles the key value before providing it to the MUX selections and makes a rotate right or left operation after each clock cycle to change the initial value in the register and to ensure generating a new random key for each input pattern.
Even though the half and full MUX insertion techniques achieve 50% HD for most of the benchmark circuits with a reasonable cost, both might not be strong enough against an experienced assailant. More specifically, the MUX insertion method based on the half output number gives lower power, area and delay overheads, but it might be vulnerable to the uniformity distribution attack. A proficient attacker could get the correct functionality of the design based on some true output bits, since half of the output bit number is always exposed. For instance, an attacker can input a constant vector with the wrong user key and makes the clock run for a long number of cycles, where the LFSR will switch the outputs. Afterwards, he or she will realize that some of the outputs are constant and tries to infer the internal functionality. Furthermore, the MUX insertion at each output bit is very strong against many types of attacks, including this one, because each output bit in the design will become changeable once a random key is supplied to the selections of the MUXs. Nevertheless, both half and full MUX insertion approaches are vulnerable against the LFSR tracking attacks. Since the initial value of the LFSR is constant and the LFSR sequence can be tracked, an attacker can use the temporal repeatable response to figure out the functionality of the design. For instance, an attacker can first supply a constant input vector (e.g., Input vector A (I_A)) with the wrong user key and then record the secured output in an array Secured Output A (SOA(t)). After that, he or she can reset the circuit, use another input vector (e.g., Input vector B (I_B)) and record the output in another array Secured Output B (SOB(t)). Next, the attacker compares the two secured output vectors and produces a post-process data as follows: SOA(t) XOR SOB(t) = OA(t) XOR OB(t), where OA(t) and BO(t) are the correct outputs for the input vectors IA and IB, respectively because the key is the same in both cases (due to the temporal repeatable response of the LFSR). Finally, he or she can take SOA(t) as a reset response and generate new outputs for other inputs (Input vector C (I_C), Input vector D (I_D), Input vector E (I_E), etc.), and from the post-processing results, he or she might infer the correct functionality of the circuit. Preventing an attacker from tracking the LFSR may be achieved by using a dynamic scrambling to scramble the seed value of the LFSR, where its configuration bits should be coming from a true random number generation. In this way, an attacker cannot use the temporal repeatable response to track the LFSR because its initial value will be changed by the dynamic scrambling.
In addition, the designer can leverage our dynamic scrambling proposal instead of employing LFSR random generation for two purposes: (1) reduce the performance overhead; (2) expedite creating a new random key with 0.5 probability and then providing the selections of the MUXs with the new one. The direction of the rotating operation and the configuration of the dynamic scrambling should be changed for each IC to evade the rogue duplicating by the untrusted companies and/or adversaries.
Figure 14 manifests the way of using the rotating operation with the dynamic scrambling.
7. Conclusions
In this paper, multiplexer insertion-based logic encryption has been presented. Compared to previous literature, the fault impact analysis approach will not guarantee achieving a 50% Hamming distance for any circuit, and the execution time of its algorithm is very long and unacceptable in practice for a large chip. On the other hand, our methodology can accomplish 50% (or close to it) Hamming distance between the corrupted and corrected outputs, even if one bit in the user key is incorrect, unless all of the right valid key bits are supplied, and it is very fast. Moreover, instead of using both RSA cryptography and PUF, we employed the HLU and the LFSR random generator to protect the secret key and generate random keys with 0.5 probability, respectively. The power, area and delay overheads are gradually decreased for a large circuit that has appropriate output bits, such as C6288 and S9234. In conclusion, our proposed technique can outperform the previous state-of-the-art work in terms of less performance overhead while achieving a higher security level.