Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS
Abstract
:1. Introduction
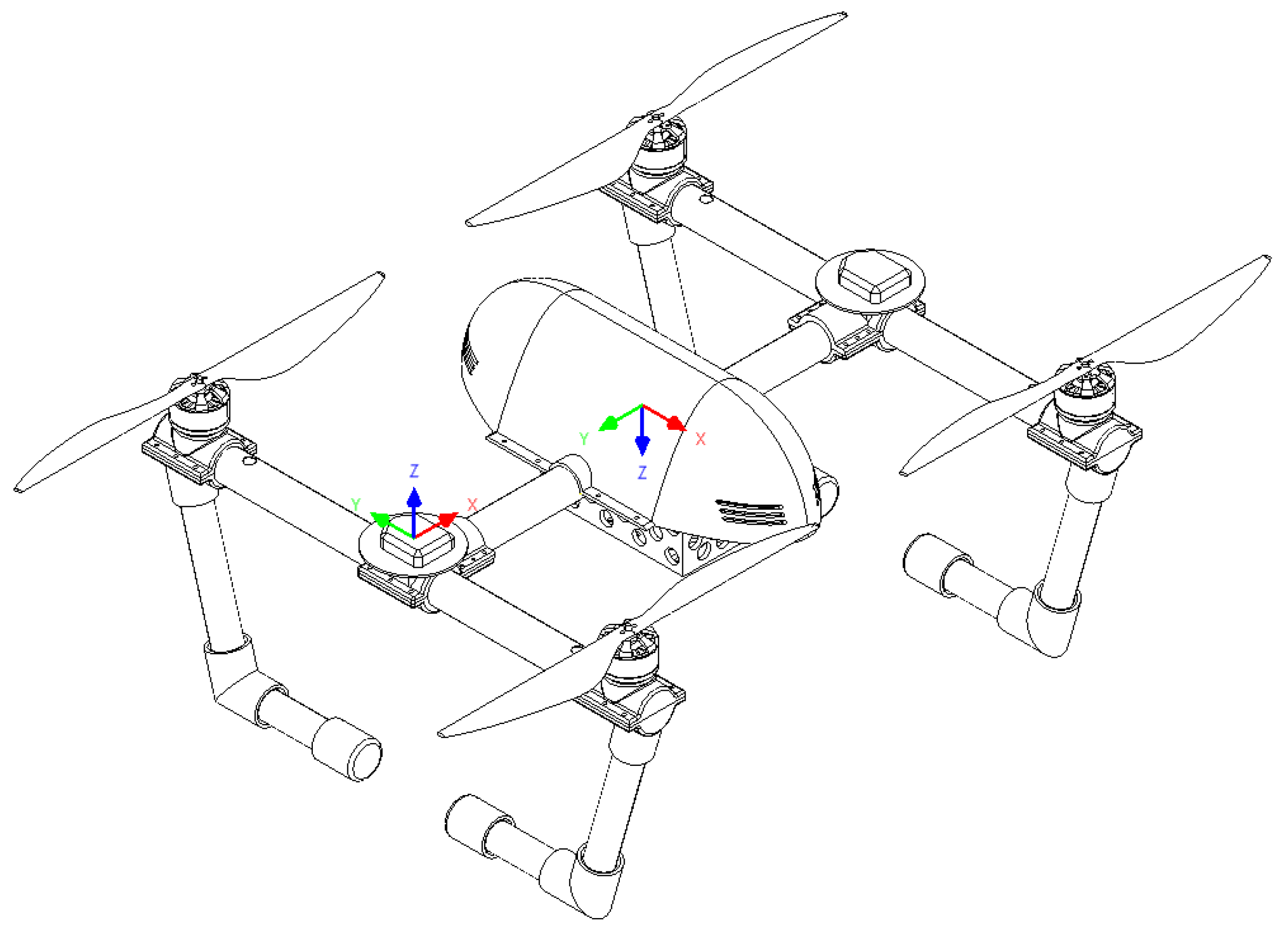
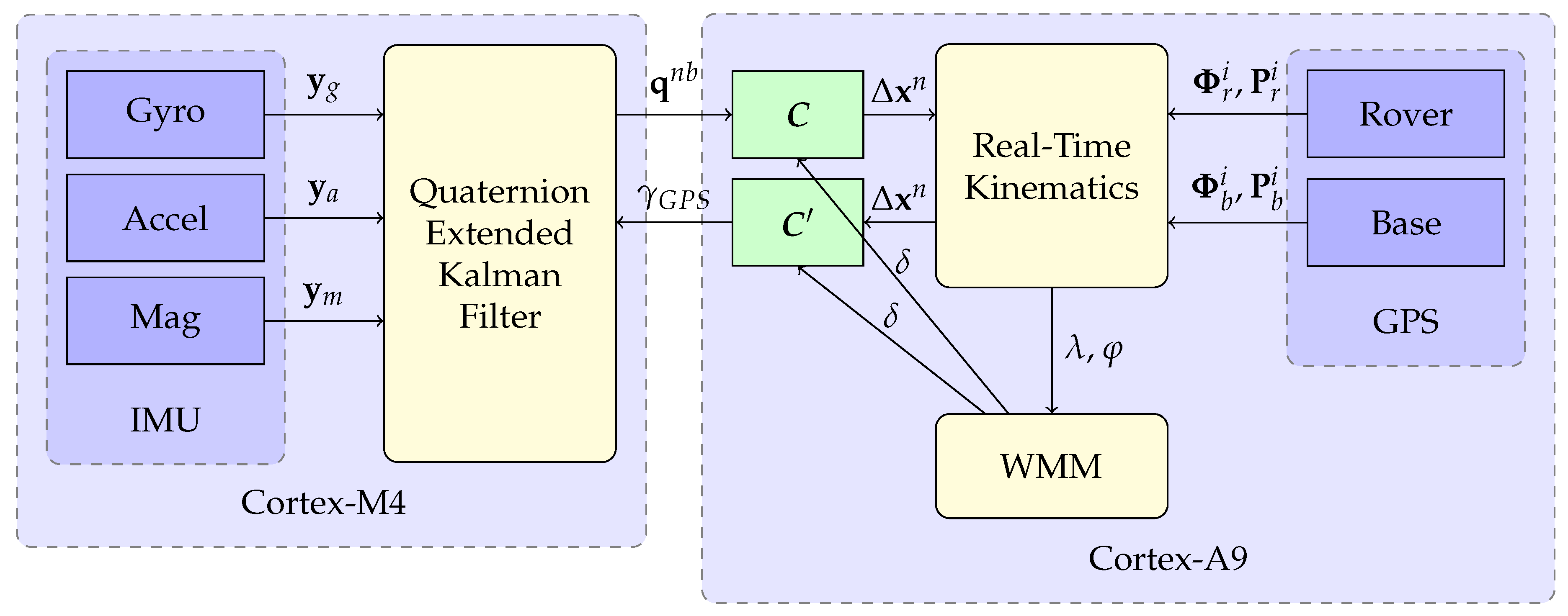
2. System Architecture
2.1. Quaternion Math
2.2. Quaternion Extended Kalman Filter
2.2.1. Measurement Models
2.2.2. System Propagation
2.2.3. System Updates
2.2.4. Roll and Pitch Update
2.2.5. Yaw Update
2.3. Real-Time Kinematics
3. Evaluation
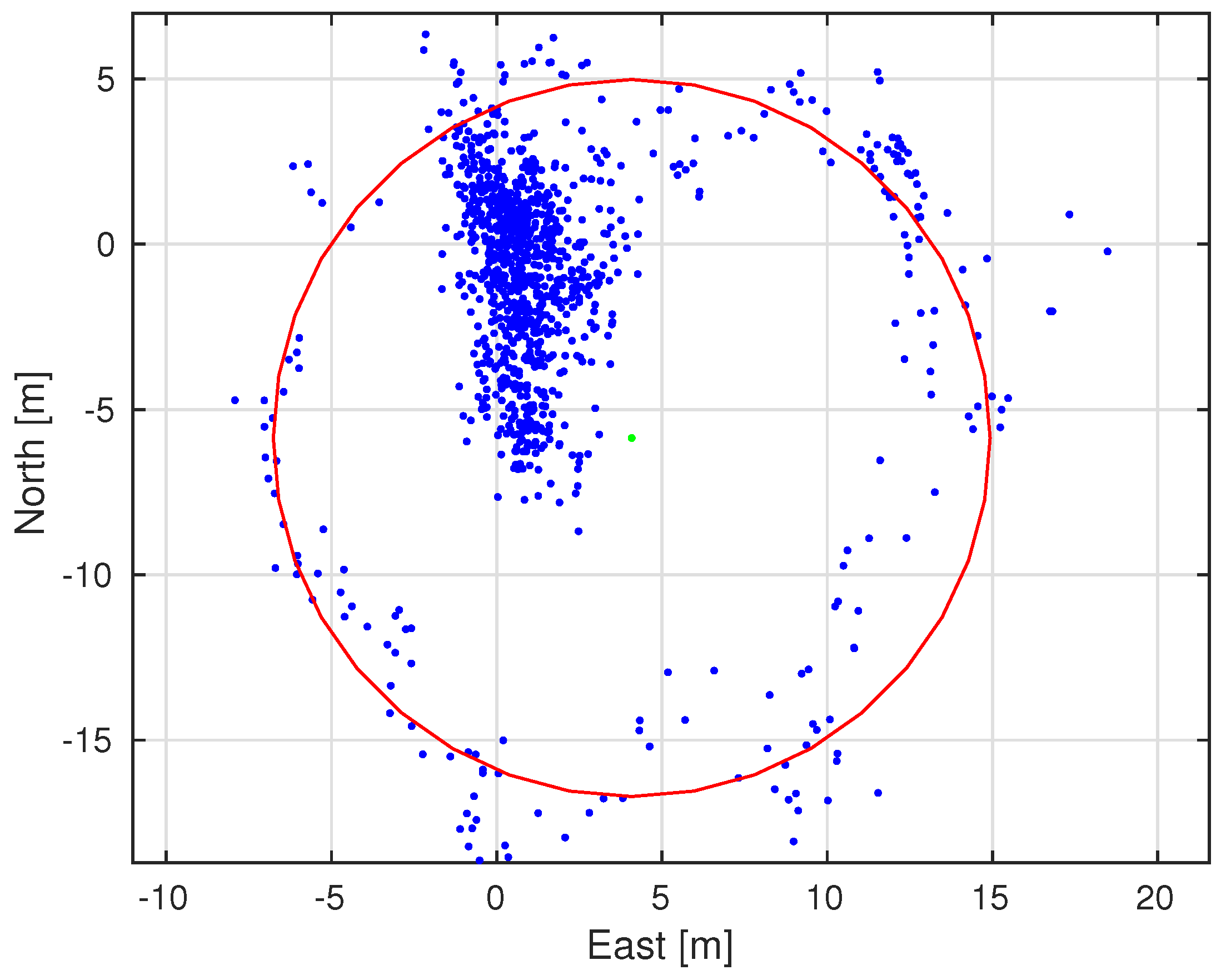
3.1. Static Evaluation
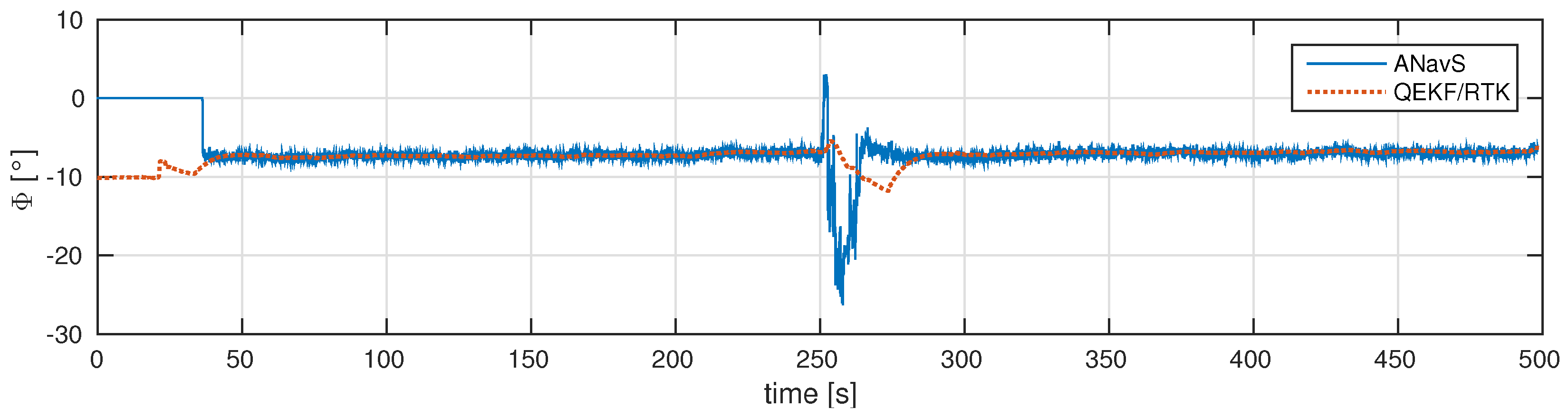
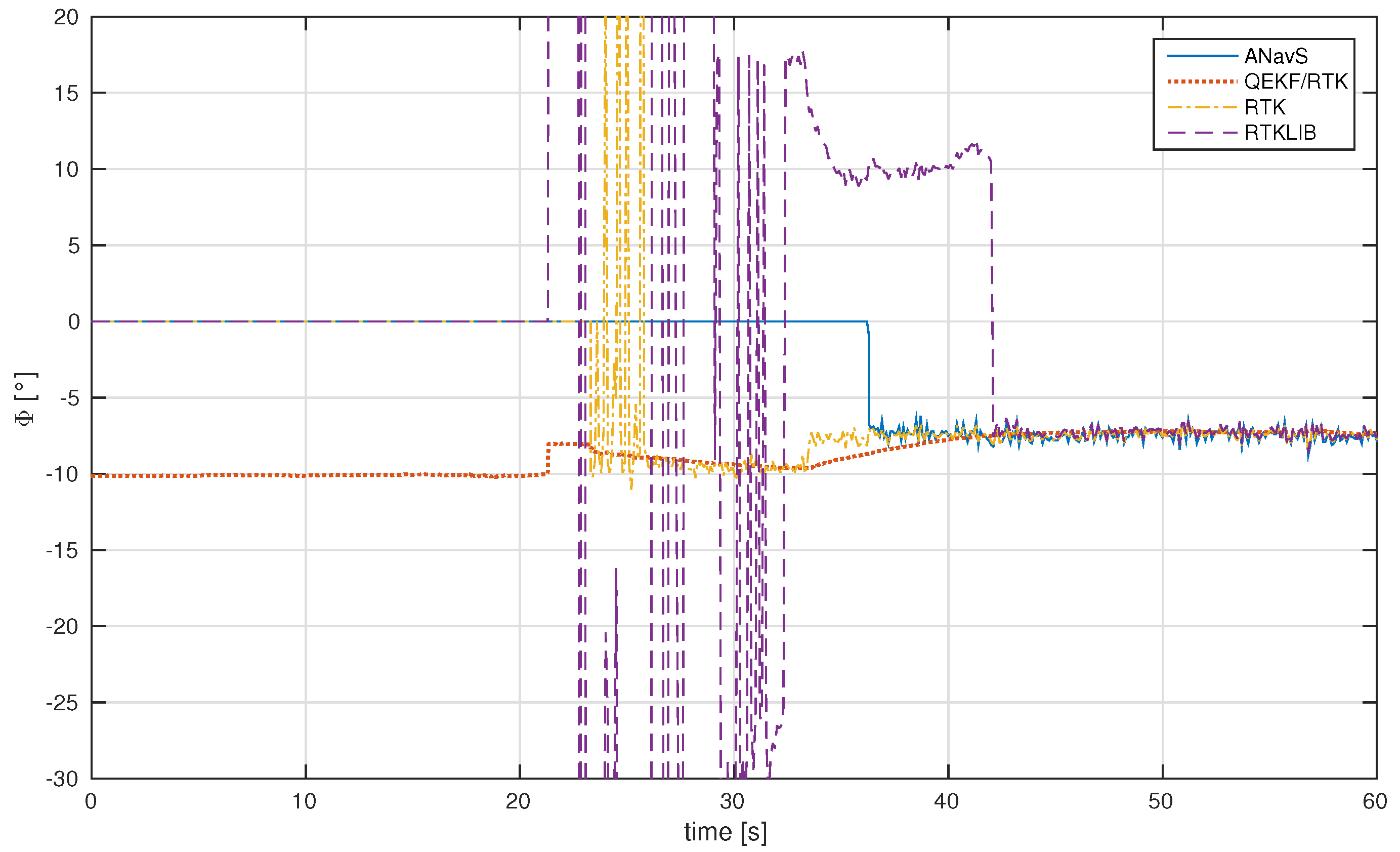
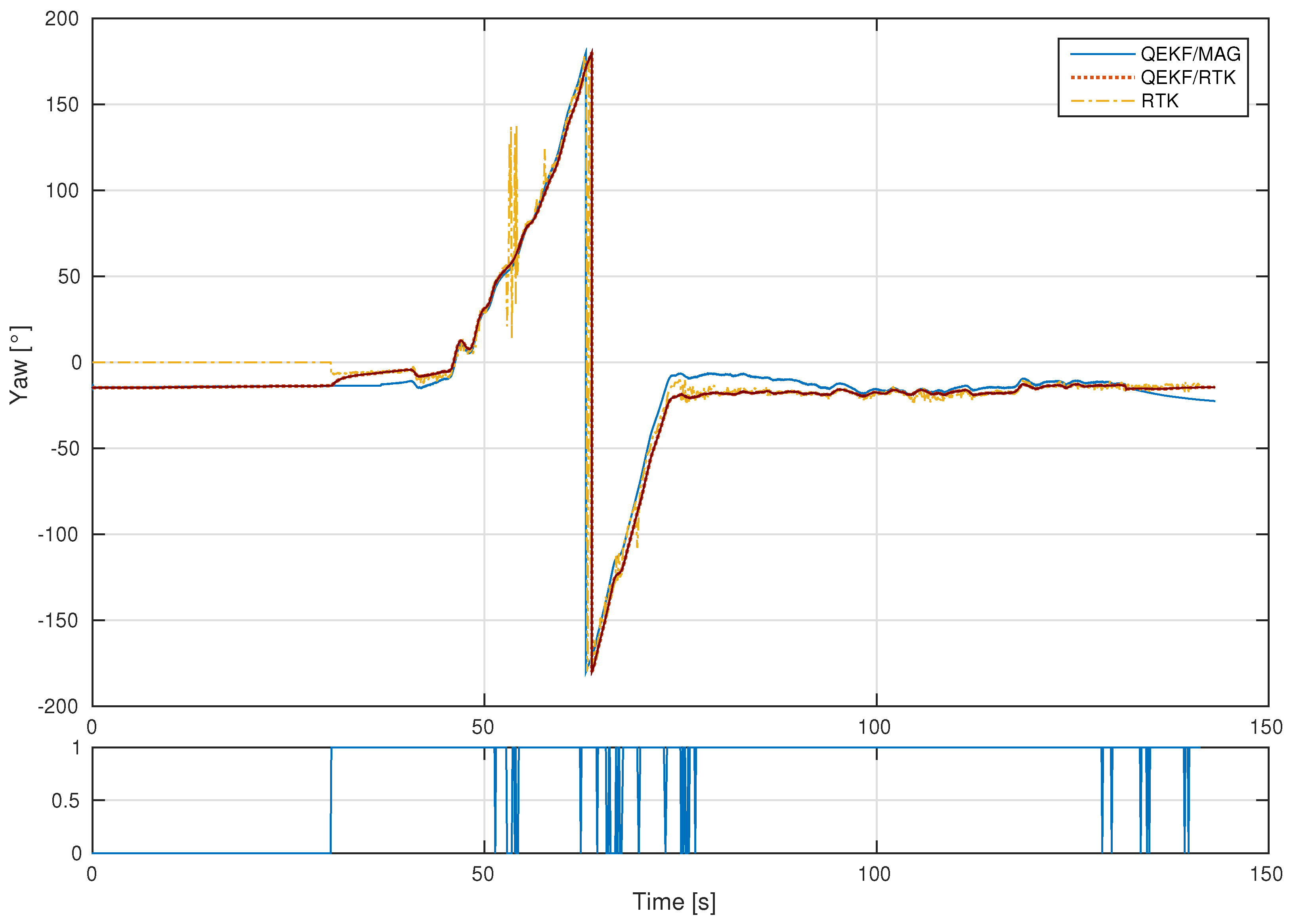
3.2. Dynamic Evaluation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ANavS | Advanced Navigation Solution |
| AUV | Autonomous Underwater Vehicle |
| AWI | Alfred Wegener Institute for Polar and Marine Research |
| COTS | Components-Off-The-Shelf |
| DD | Double-Difference |
| ECEF | Earth-Centered Earth-Fixed |
| EKF | Extended Kalman Filter |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| IMU | Inertial Measurement Unit |
| NED | North-East-Down |
| MEMS | Micro-Electro-Mechanical System |
| ROBEX | Helmholtz Alliance for Robotic Exploration of Extreme Environments |
| ROS | Robot Operating System |
| RODOS | Real-time Onboard Dependable Operating System |
| RTKLIB | Real-Time Kinematics Library |
| RTK | Real-Time Kinematics |
| SD | Single-Difference |
| SNR | Signal-to-Noise Ratio |
| UAV | Unmanned Aerial Vehicle |
| WMM | World Magnetic Model |
References
- Lehmenhecker, S.; Wulff, T. Flying Drone for AUV Under-Ice Missions. Sea Technol. Compass Publ. 2012, 55, 61–64. [Google Scholar]
- King, B.; Cooper, E. Comparison of ship’s heading determined from an array of GPS antennas with heading from conventional gyrocompass measurements. Deep Sea Res. Part I Oceanogr. Res. Pap. 1993, 40, 2207–2216. [Google Scholar] [CrossRef]
- Lachapelle, G.; Cannon, M.E.; Lu, G.; Loncarevic, B. Shipborne GPS attitude determination during MMST-93. IEEE J. Ocean. Eng. 1996, 21, 100–104. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Giorgi, G.; Buist, P.J. Testing of a new single-frequency GNSS carrier phase attitude determination method: Land, ship and aircraft experiments. GPS Solut. 2011, 15, 15–28. [Google Scholar] [CrossRef]
- Henkel, P.; Günther, C. Attitude determination with low-cost GPS/INS. In Proceedings of the 26-th ION GNSS+, Nashville, TN, USA, 16–20 September 2013; pp. 2015–2023.
- Hayward, R.C.; Gebre-Egziabher, D.; Schwall, M.; Powell, J.D.; Wilson, J. Inertially aided GPS based attitude heading reference system (AHRS) for general aviation aircraft. In Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997), Kansas City, MO, USA, 16–19 September 1997; pp. 1415–1424.
- Graas, F.; Braasch, M. GPS interferometric attitude and heading determination: Initial flight test results. Navigation 1991, 38, 297–316. [Google Scholar] [CrossRef]
- Cohen, C.E.; Parkinson, B.W.; McNally, B.D. Flight tests of attitude determination using GPS compared against an inertial navigation unit. Navigation 1994, 41, 83–97. [Google Scholar] [CrossRef]
- Consoli, A.; Ayadi, J.; Bianchi, G.; Pluchino, S.; Piazza, F.; Baddour, R.; Parés, M.E.; Navarro, J.; Colomina, I.; Gameiro, A.; et al. A Multi-Antenna Approach for UAV’s Attitude Determination. In Proceedings of the 2015 IEEE Metrology for Aerospace (MetroAeroSpace), Benevento, Italy, 4–5 June 2015; pp. 401–405.
- Falco, G.; Gutiérrez, M.; Serna, EP.; Zachello, F.; Bories, S. Low-cost Real-time Tightly-Coupled GNSS/INS Navigation System Based on Carrier-phase Double-differences for UAV Applications. In Proceedings of the 27th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2014), Tampa, FL, USA; 2014; pp. 841857–841873. [Google Scholar]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-time Single-frequency GPS/MEMS-IMU Attitude Determination of Lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [PubMed]
- About ROS. Available online: http://www.ros.org/about-ros/ (accessed on 15 November 2016).
- RODOS–Real-Time Onboard Dependable Operating System. Available online: https://software.dlr.de/p/rodos/home/ (accessed on 15 November 2016).
- Chulliat, A.; Macmillan, S.; Alken, P.; Beggan, C.; Nair, M.; Hamilton, B.; Woods, A.; Ridley, V.; Maus, S.; Thomson, A. The US/UK World Magnetic Model for 2015–2020; NOAA: Silver Spring, MD, USA, 2015. [Google Scholar]
- Pedley, M. High Precision Calibration of a Three-Axis Accelerometer; Freescale Semiconductor Application Note; Freescale Semiconductor, Inc.: Austin, TX, USA, 2013. [Google Scholar]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Munguía, R.; Grau, A. A Practical Method for Implementing an Attitude and Heading Reference System. Int. J. Adv. Robot. Syst. 2014, 11. [Google Scholar] [CrossRef]
- Ozyagcilar, T. Calibrating an Ecompass in the Presence of Hard and Soft-Iron Interference; Freescale Semiconductor Ltd.: Hong Kong, China, 2012. [Google Scholar]
- Skog, I.; Handel, P.; Nilsson, J.O.; Rantakokko, J. Zero-velocity detection–An algorithm evaluation. IEEE Trans. Biomed. Eng. 2010, 57, 2657–2666. [Google Scholar] [CrossRef] [PubMed]
- Takasu, T. RTKLIB ver. 2.4.2 Manual. Available online: http://www.rtklib.com/prog/manual2.4.2.pdf (accessed on 16 November 2016).
- Chang, X.W.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Buist, P. The baseline constrained LAMBDA method for single epoch, single frequency attitude determination applications. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 2962–2973.
- Achieving Centimeter Level Performance with Low Cost Antennas; u-Blox: Thalwil, Switzerland, 2016.

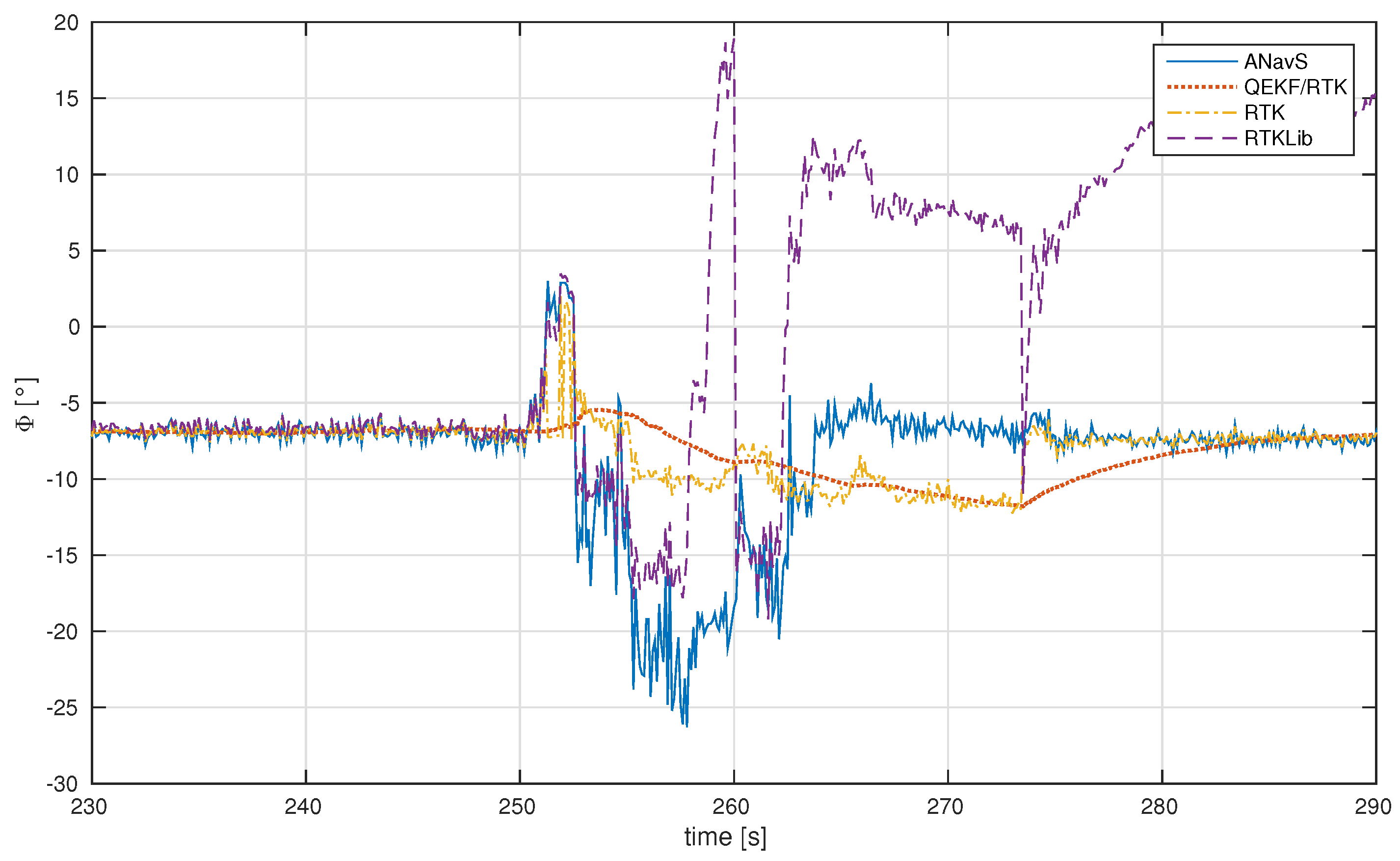
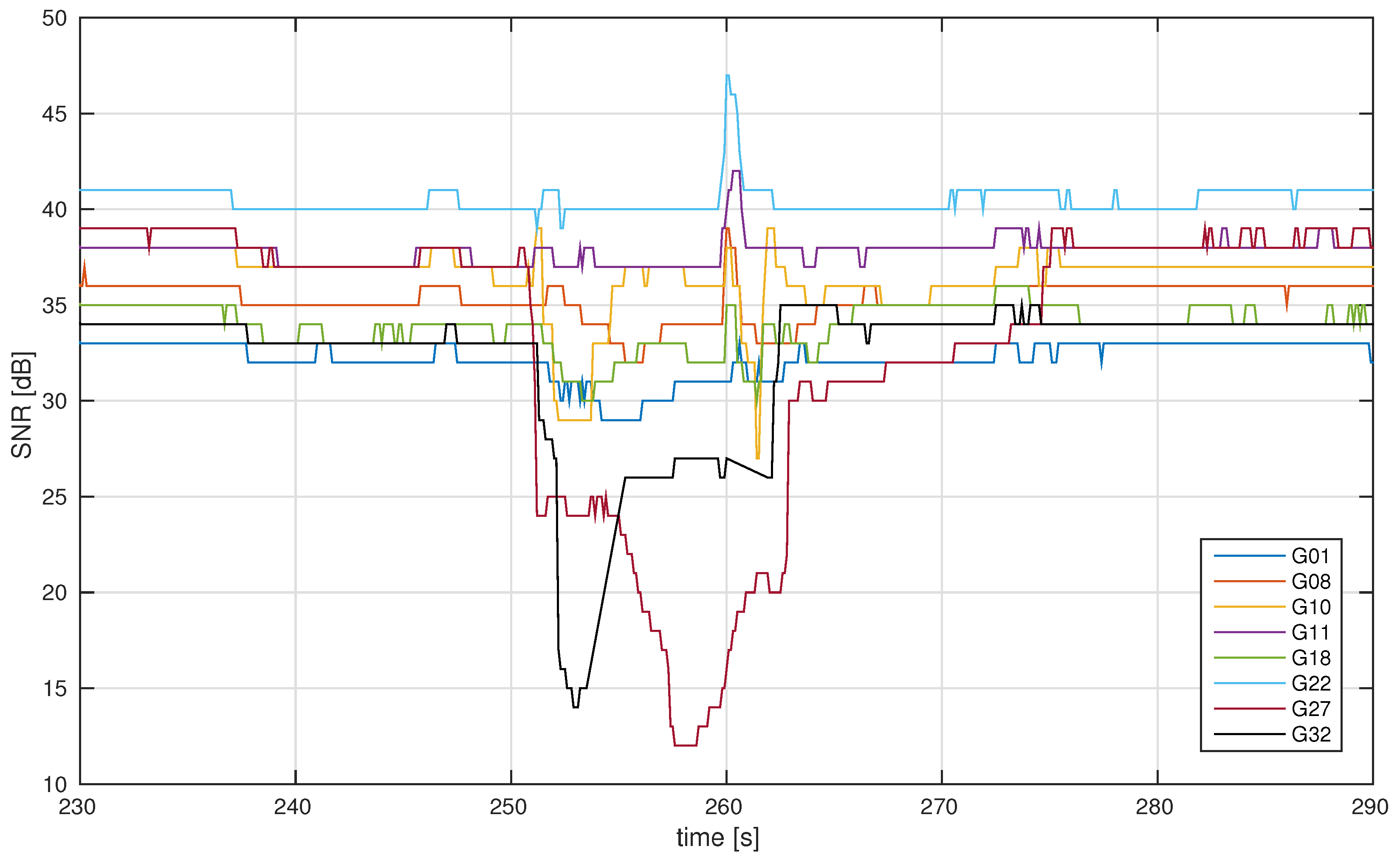
| System | ANavS | QEKF/RTK | RTK | RTKLIB |
|---|---|---|---|---|
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strohmeier, M.; Montenegro, S. Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS. Electronics 2017, 6, 15. https://doi.org/10.3390/electronics6010015
Strohmeier M, Montenegro S. Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS. Electronics. 2017; 6(1):15. https://doi.org/10.3390/electronics6010015
Chicago/Turabian StyleStrohmeier, Michael, and Sergio Montenegro. 2017. "Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS" Electronics 6, no. 1: 15. https://doi.org/10.3390/electronics6010015
APA StyleStrohmeier, M., & Montenegro, S. (2017). Coupled GPS/MEMS IMU Attitude Determination of Small UAVs with COTS. Electronics, 6(1), 15. https://doi.org/10.3390/electronics6010015





