Sudoku Inspired Designs for Radar Waveforms and Antenna Arrays
Abstract
:1. Introduction
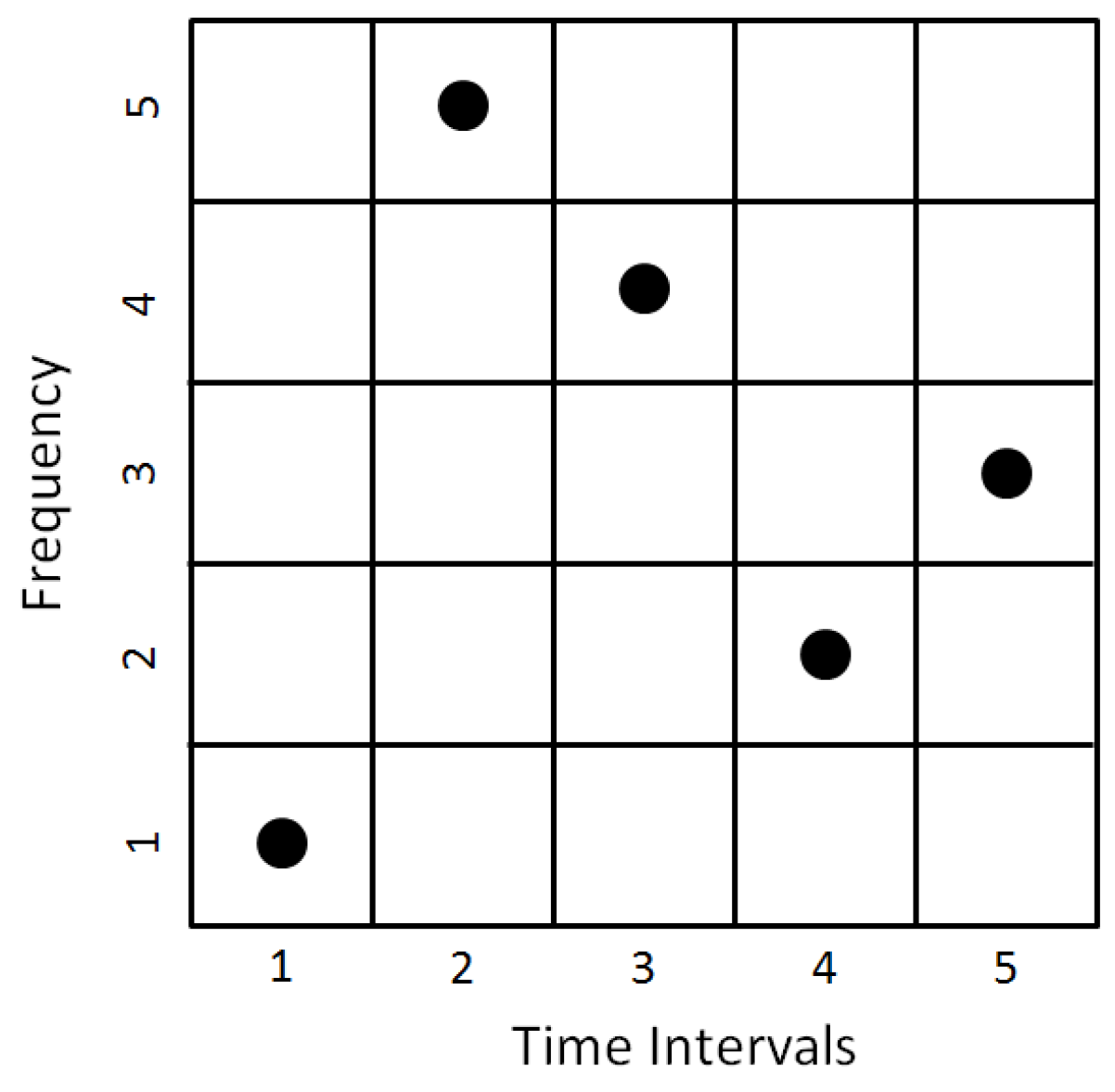
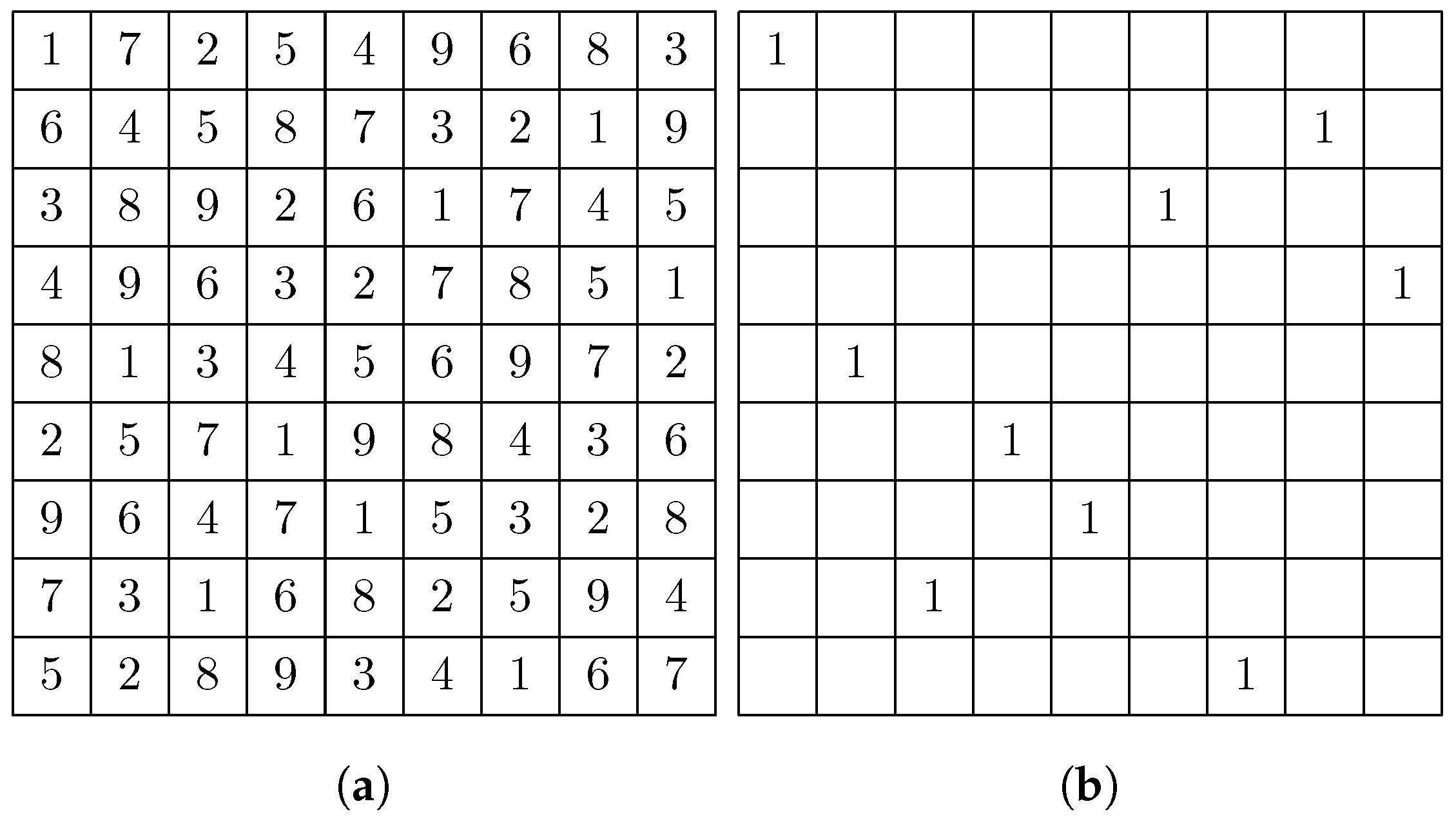
2. Sudoku-Coded Waveforms
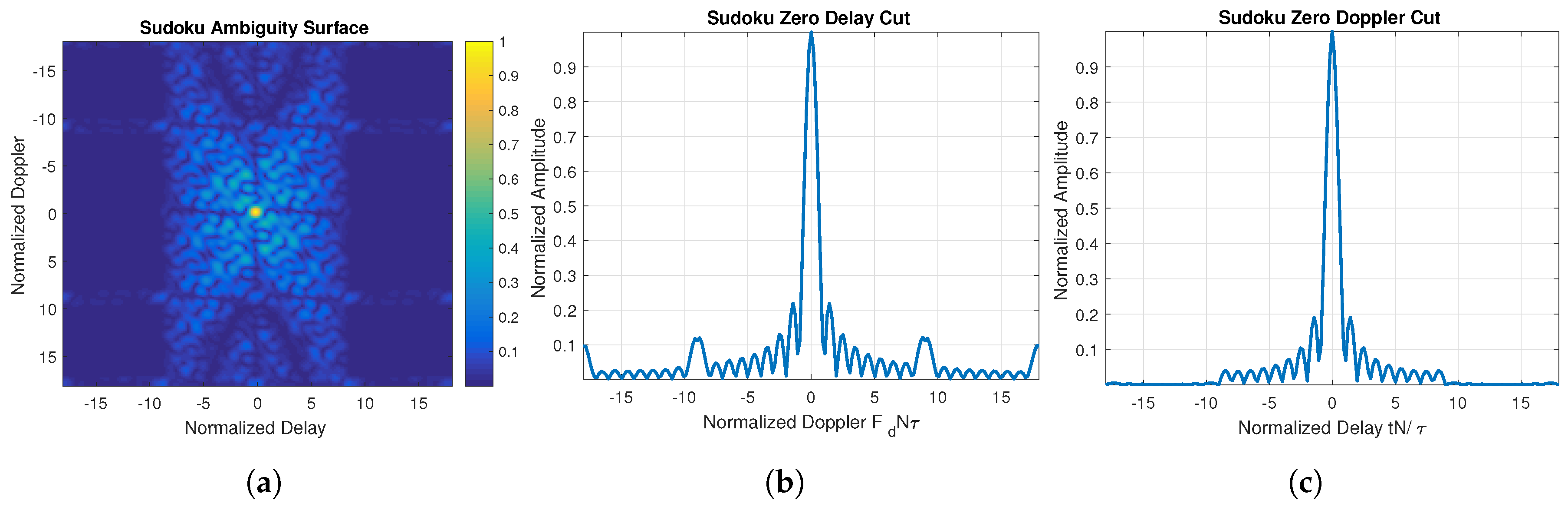
3. Sudoku Ambiguity Function Analysis
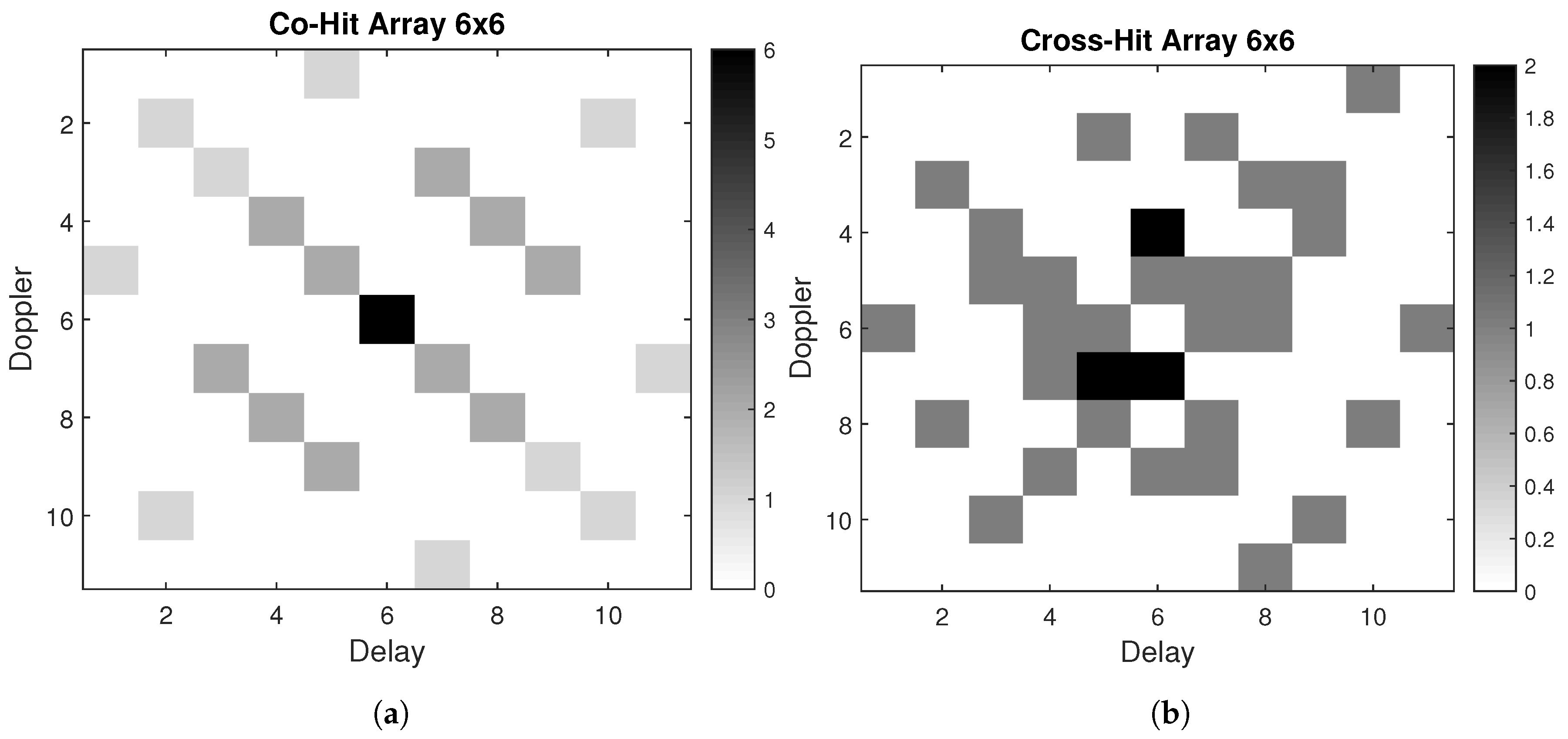
3.1. Sudoku Puzzle Coincidence Analysis
3.1.1. Co-Hit Array Analysis
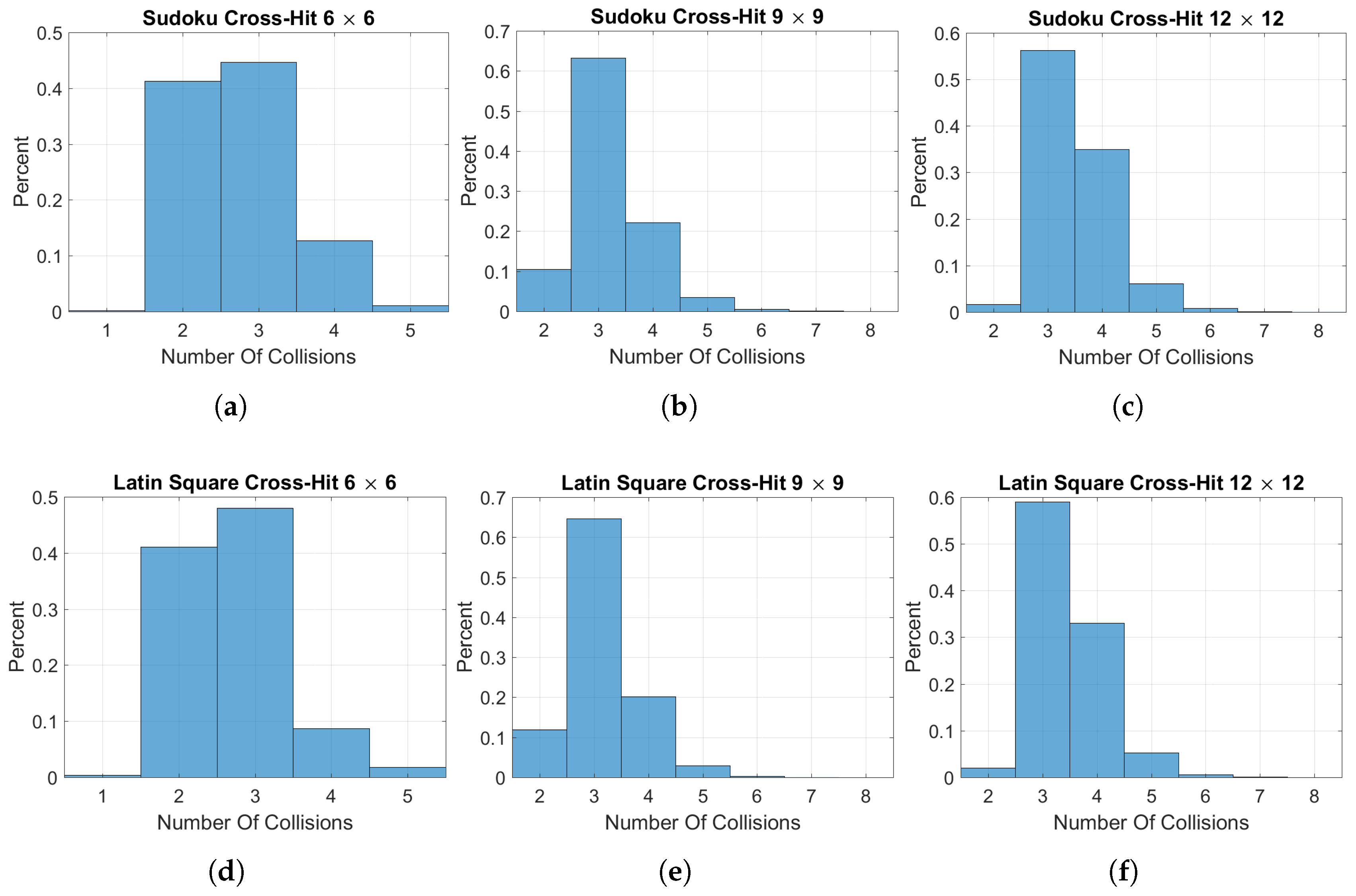
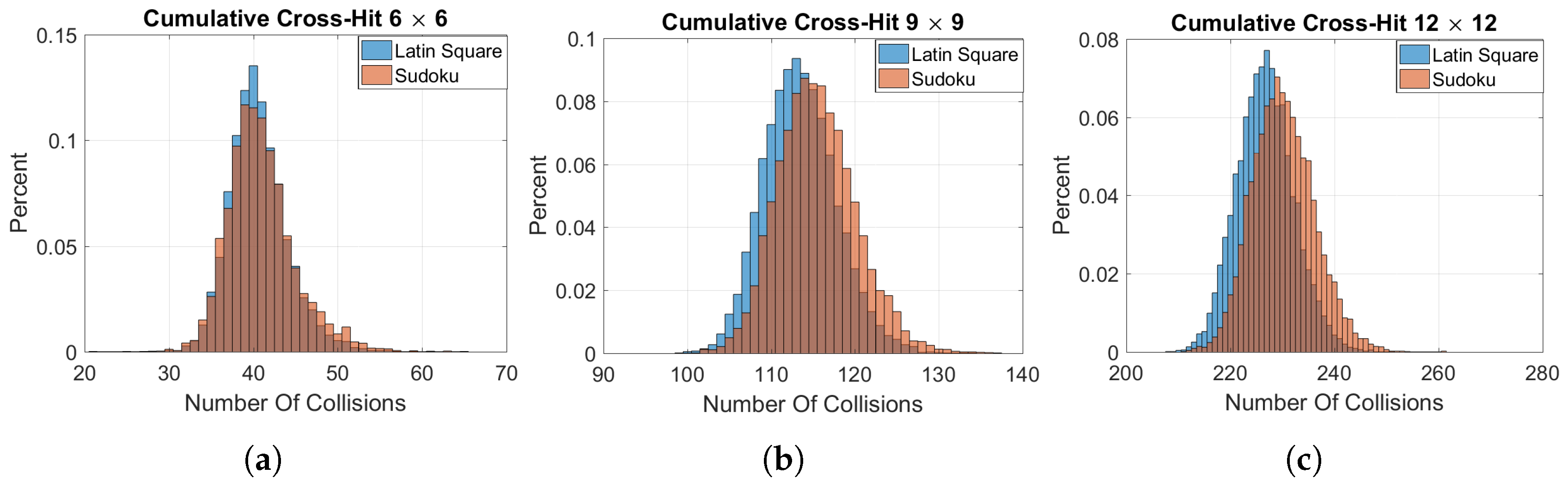
3.1.2. Cross-Hit Array Analysis
3.2. Costas Sudoku Solutions
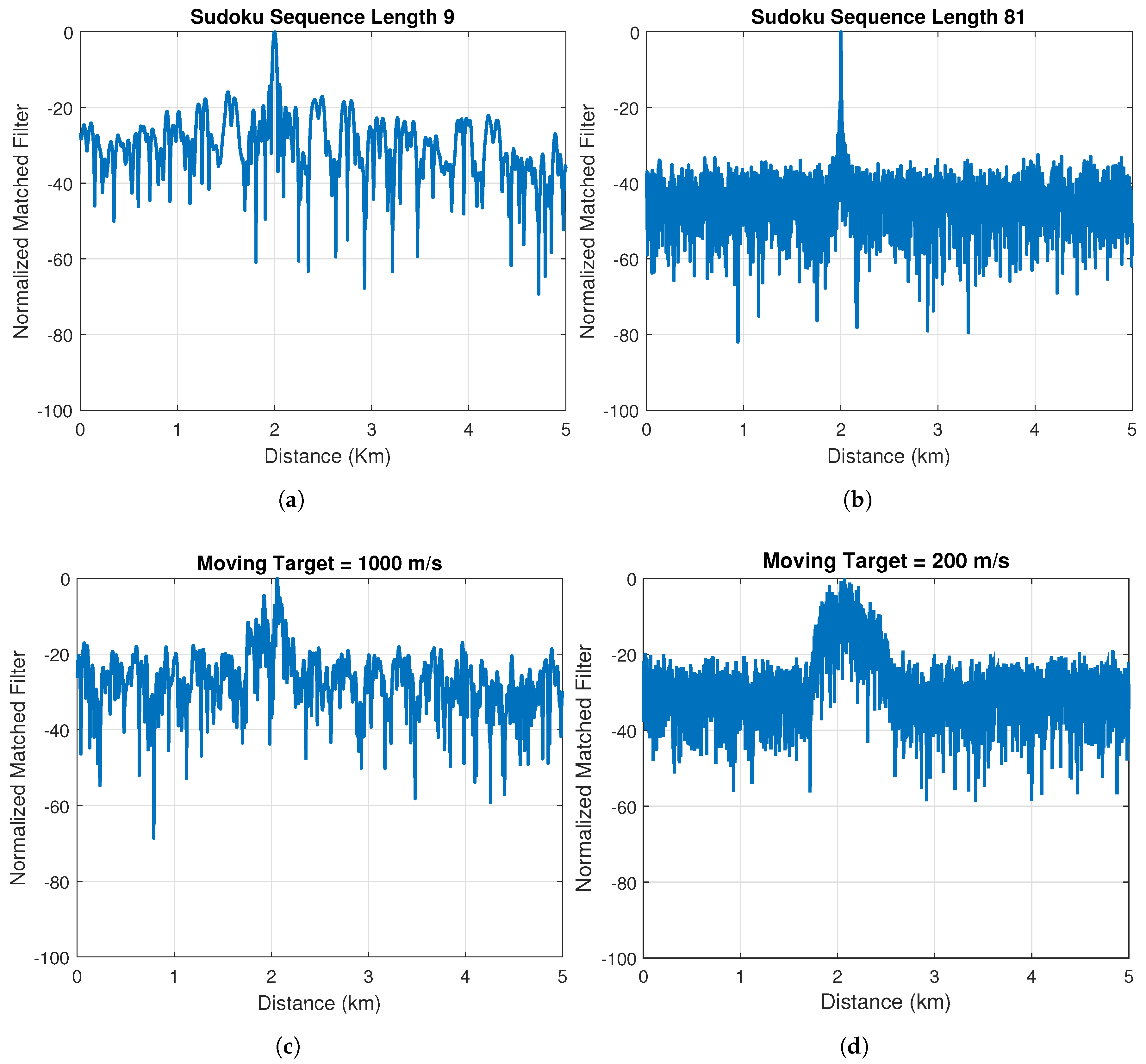
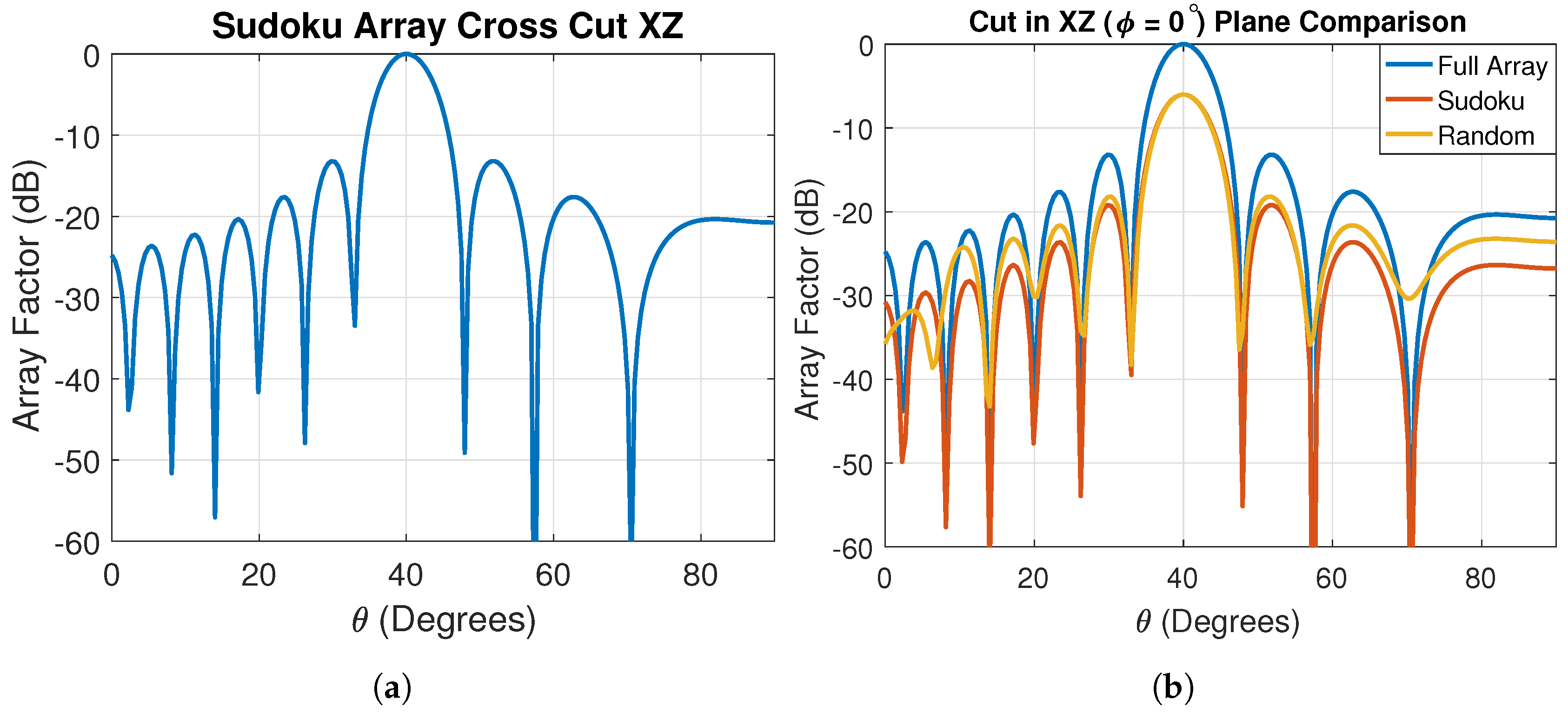
3.3. Sudoku Radar Simulations
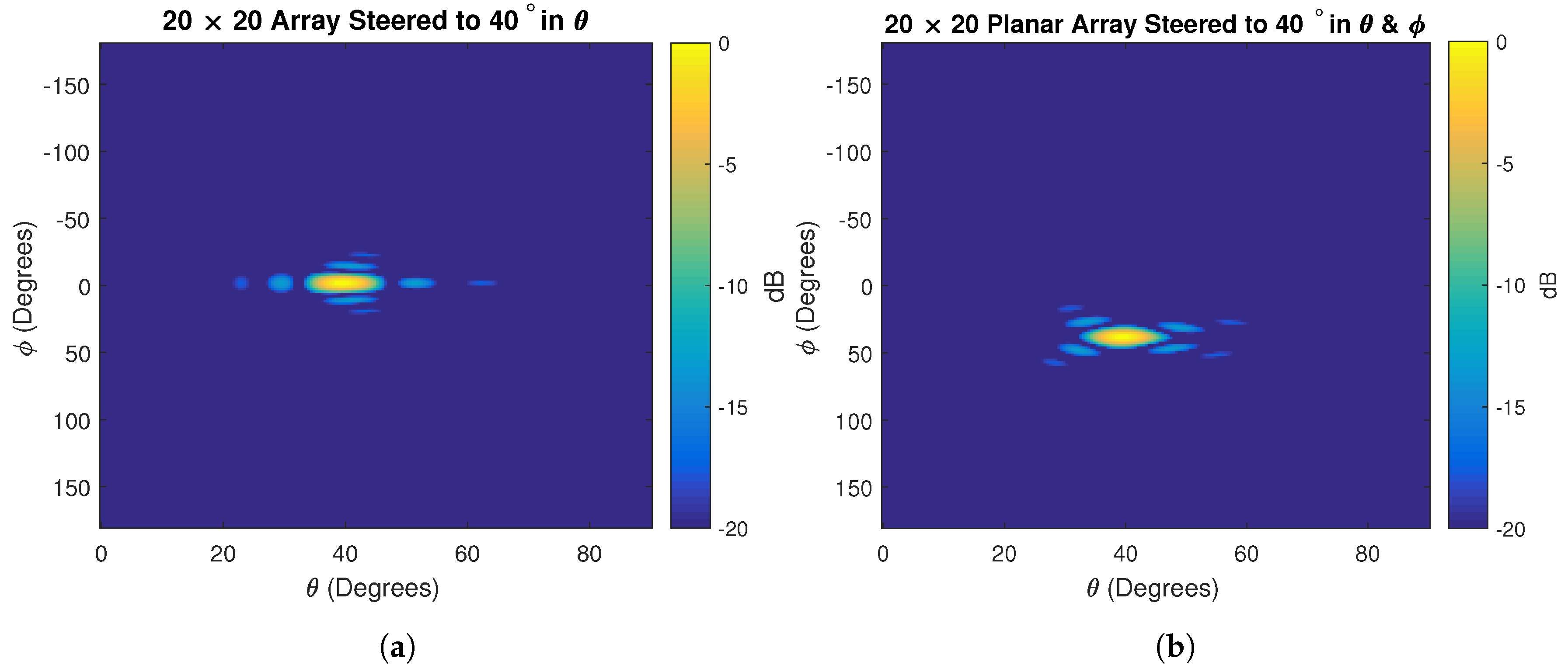
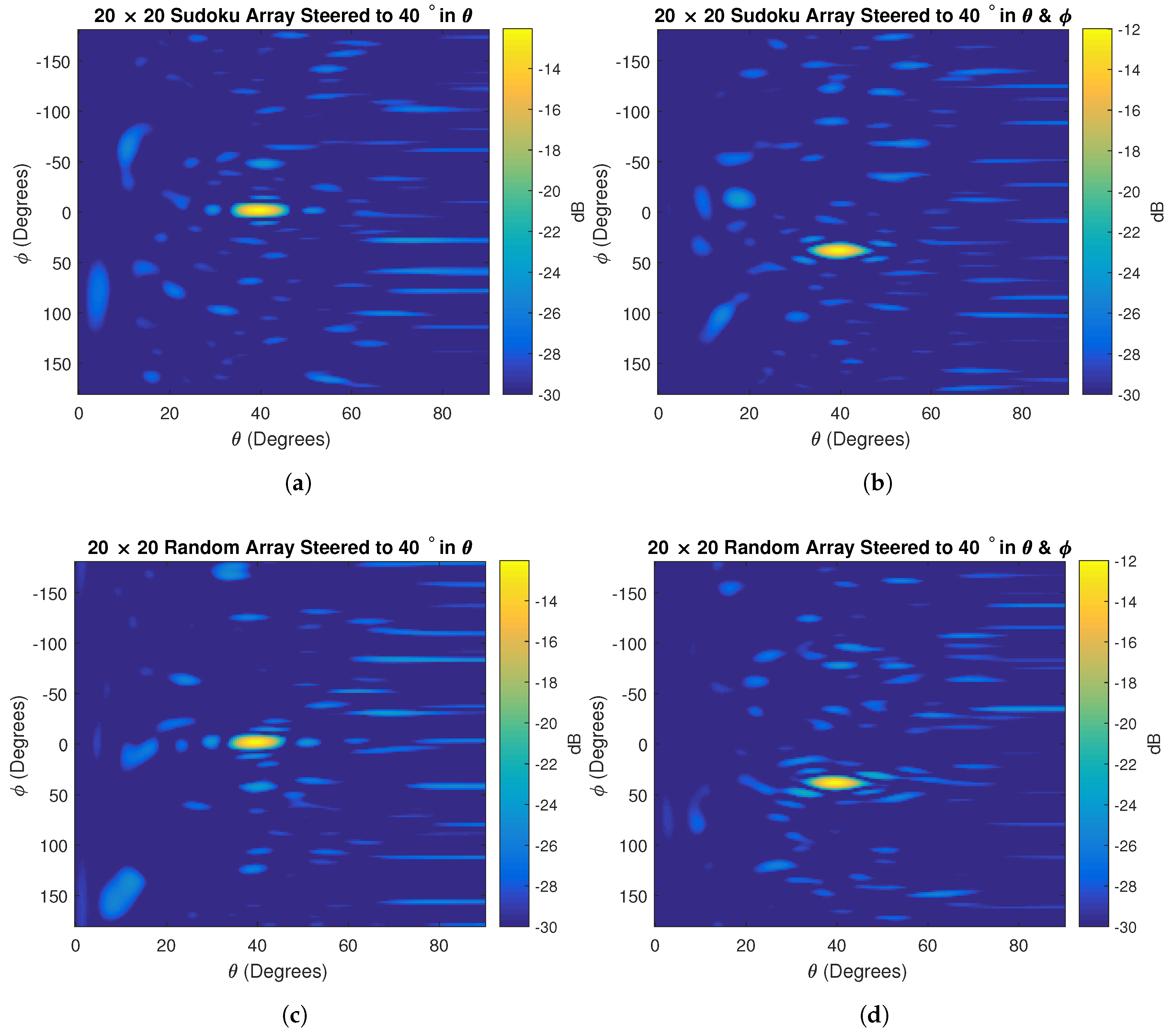
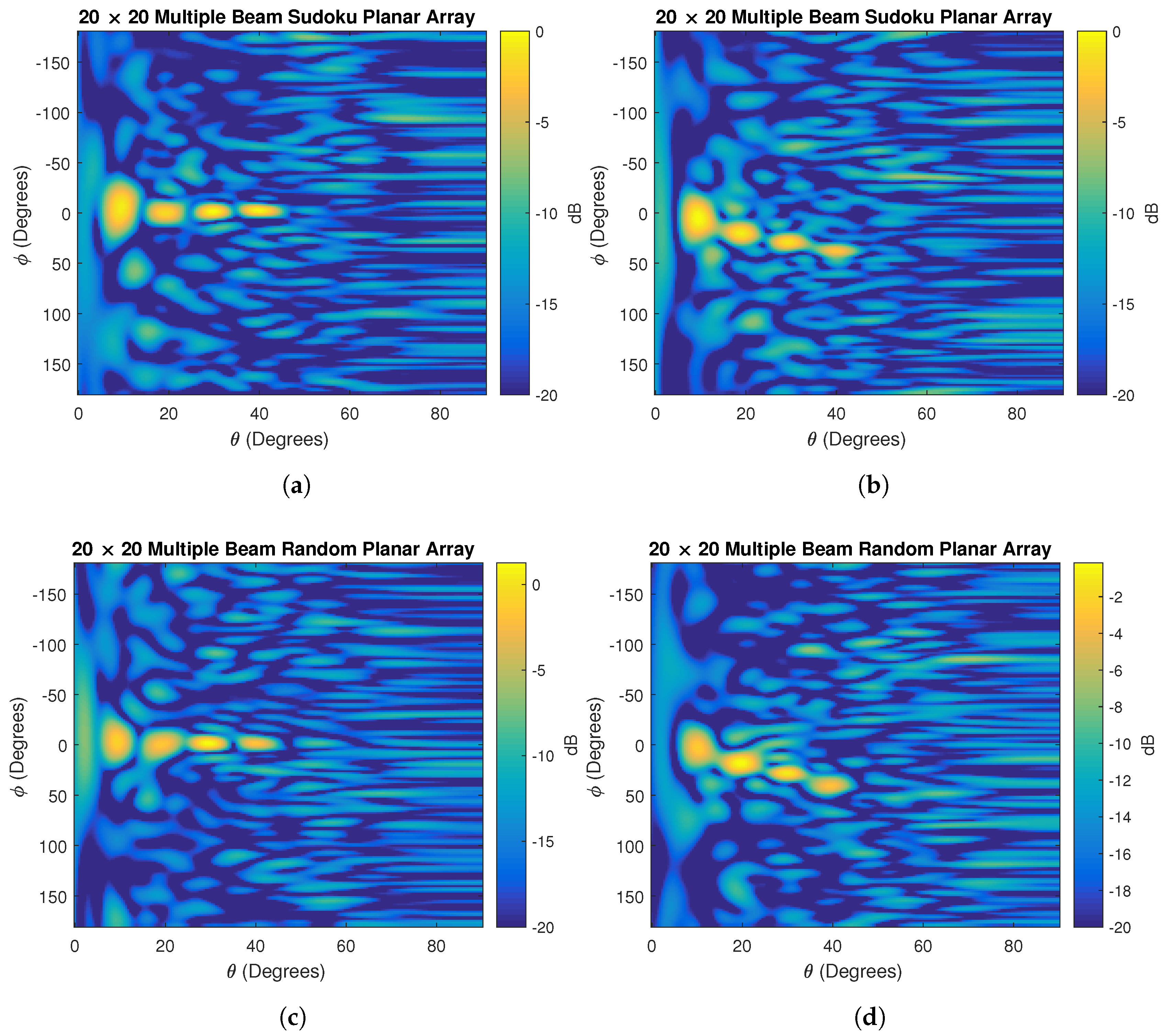
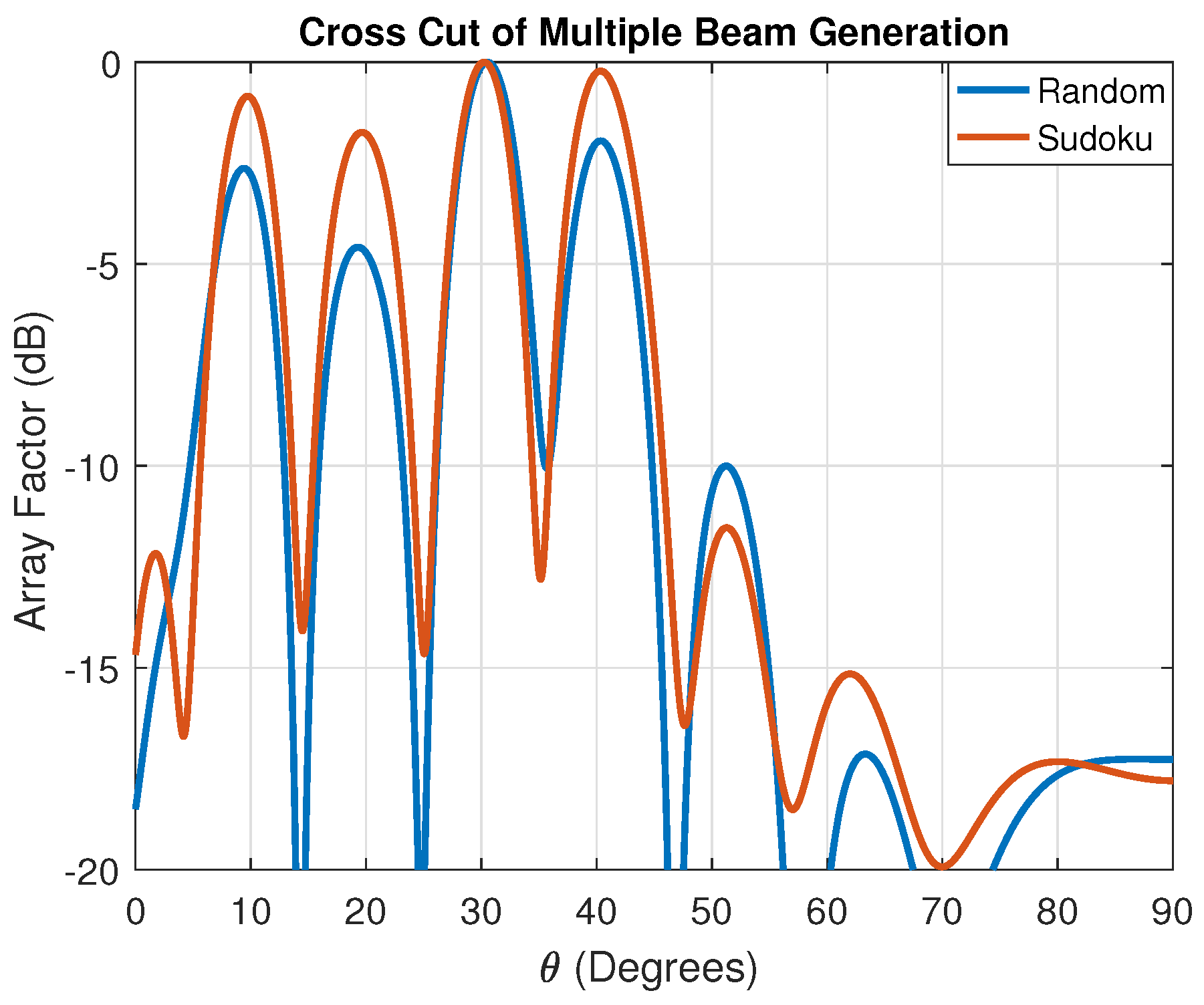
4. Sudoku Antenna Arrays
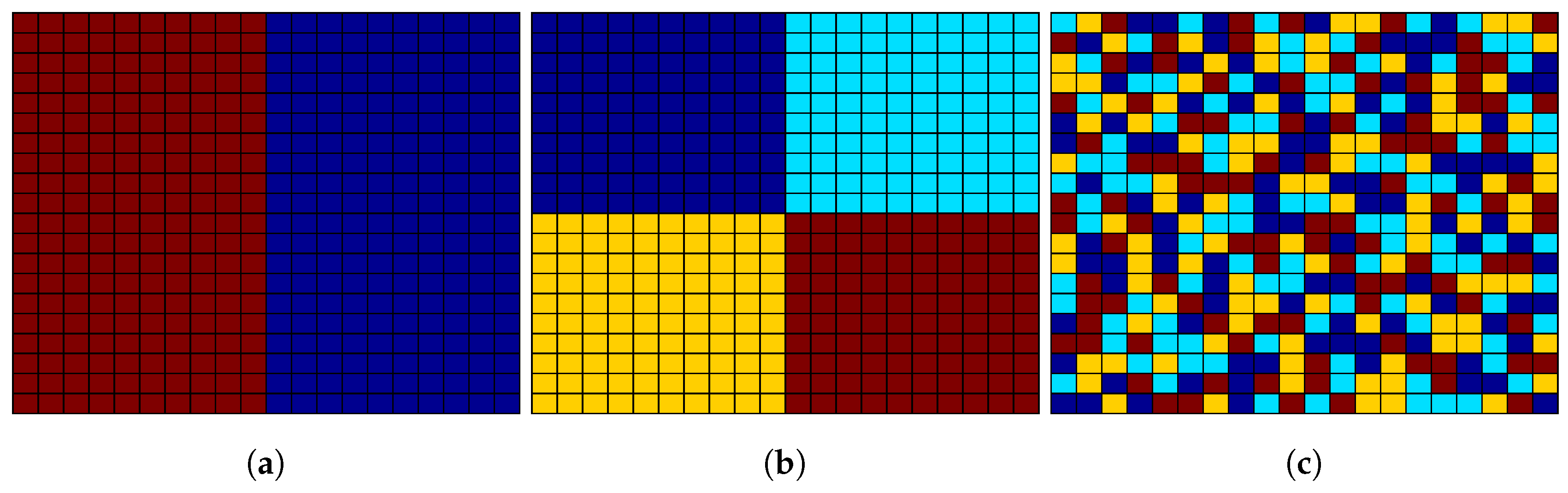
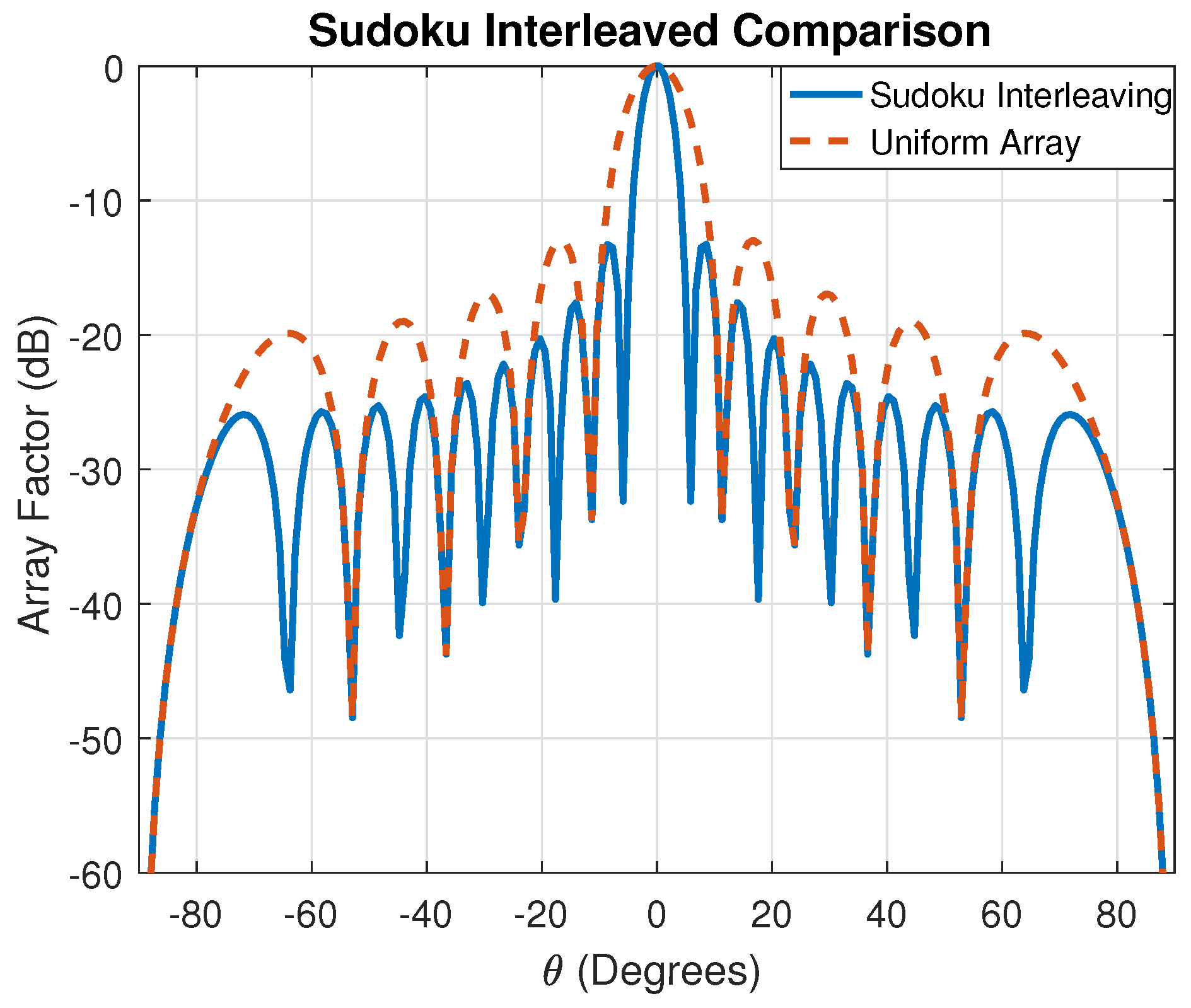
4.1. Sudoku Interleaved Arrays
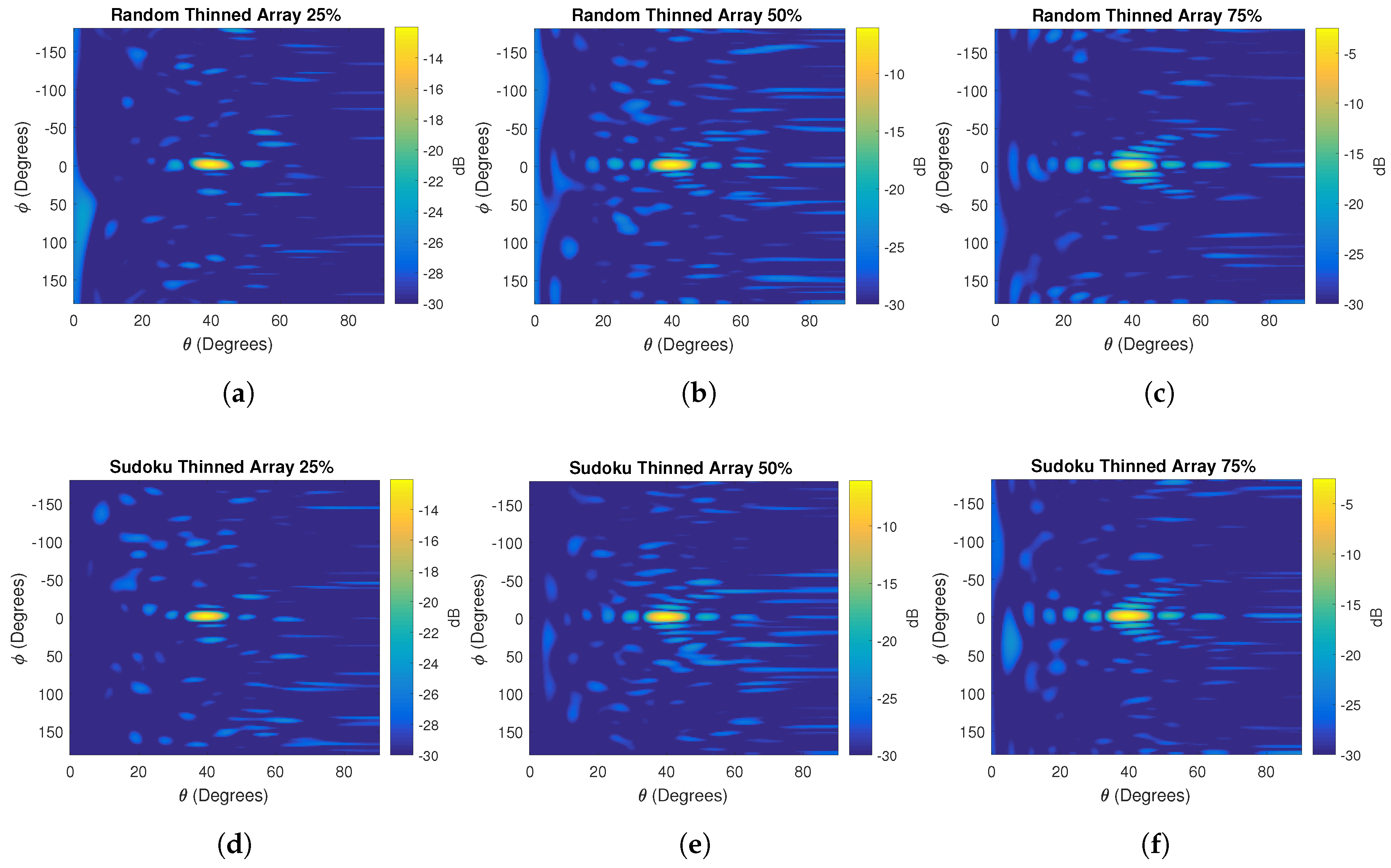
4.2. Array Thinning
4.3. Random Element Spacing
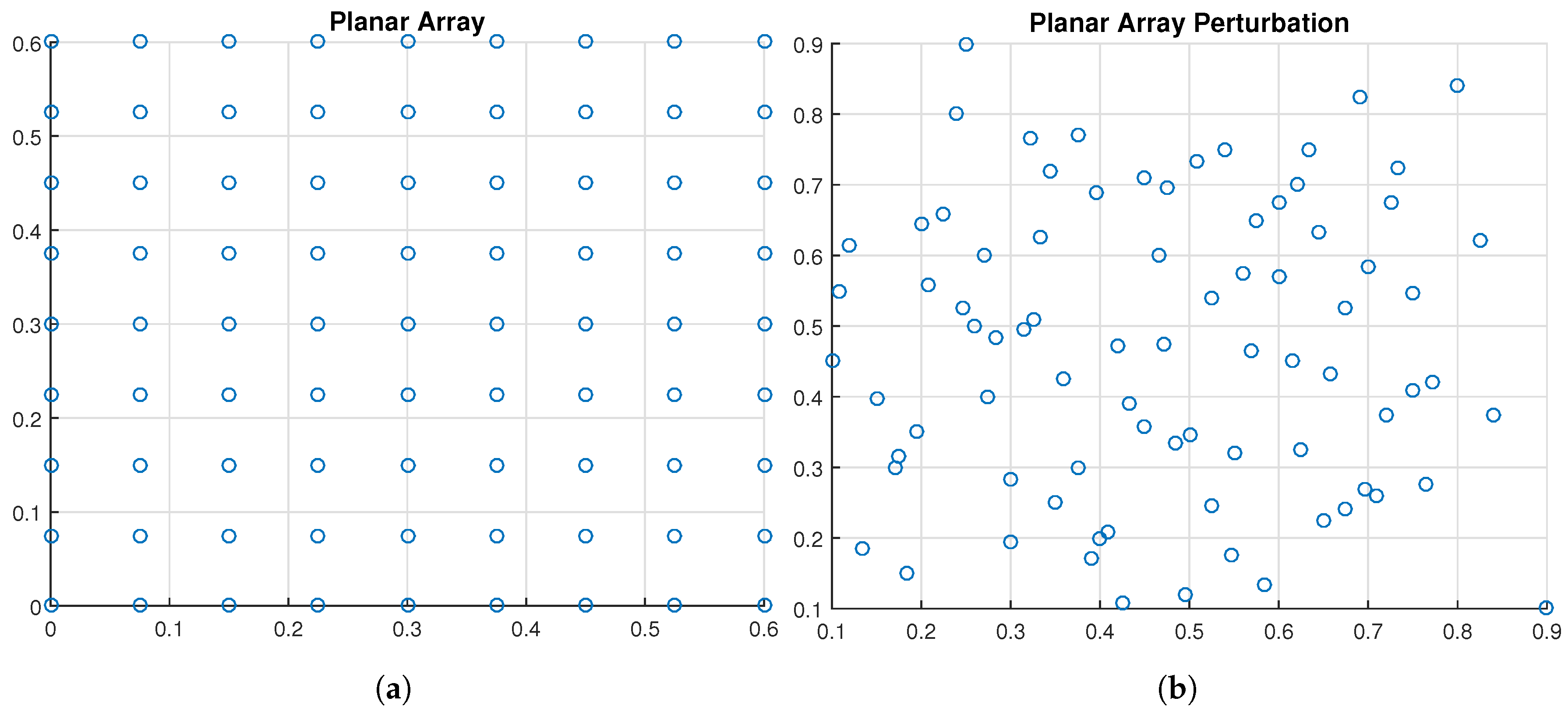
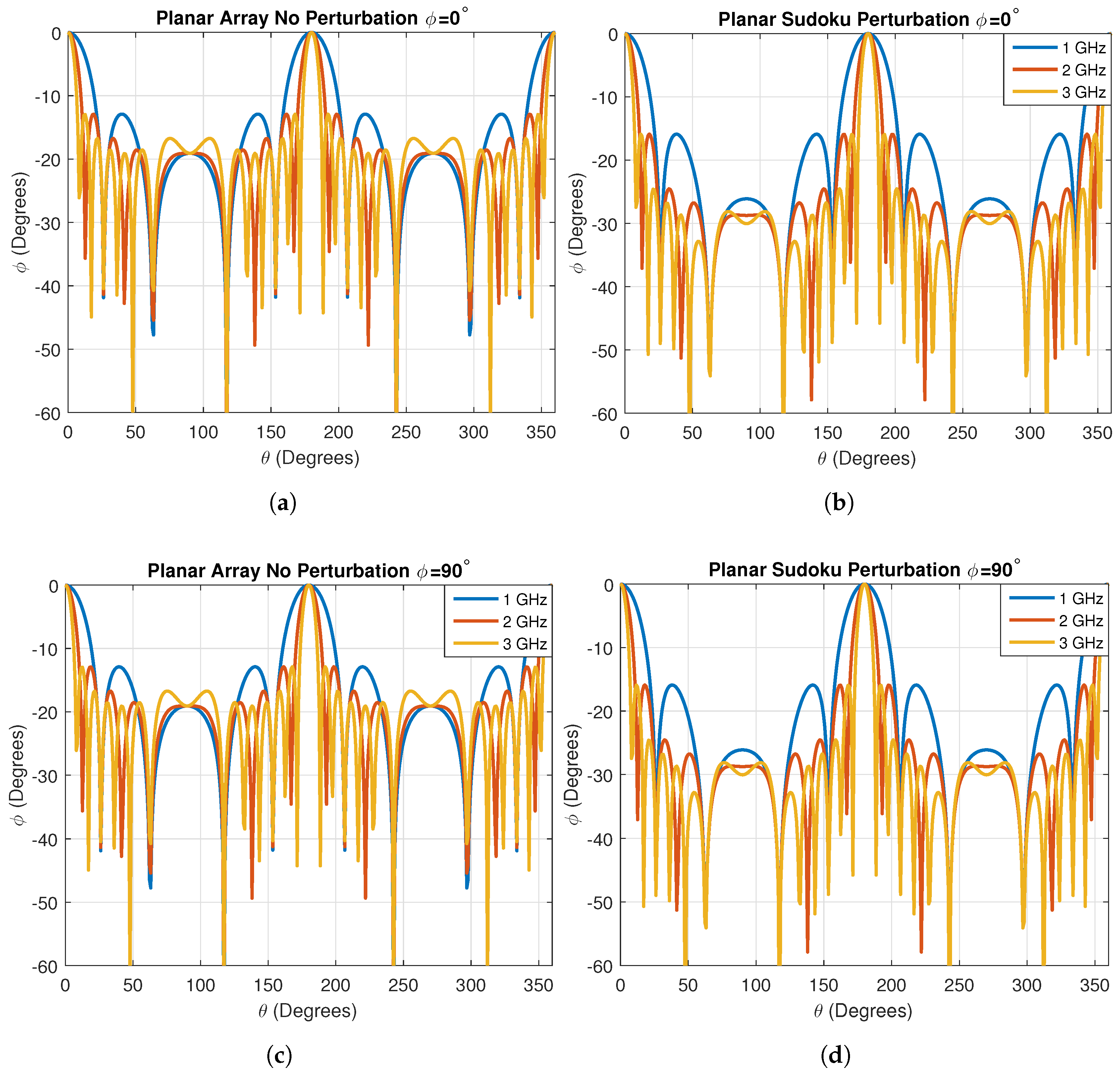
4.4. Perturbed Planar Arrays
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Keedwell, A.D.; Dénes, J. Latin Squares and their Applications; North Holland: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Newton, P.K.; DeSalvo, S.A. The Shannon entropy of Sudoku matrices. Proc. R. Soc. A 2010, 466, 1957–1975. [Google Scholar] [CrossRef]
- Sarkar, J.; Sinha, B.K. Sudoku squares as experimental designs. Resonance 2015, 20, 788–802. [Google Scholar] [CrossRef]
- Pedersen, R.M.; Vis, T.L. Sets of mutually orthogonal Sudoku Latin squares. Coll. Math. J. 2009, 40, 174–181. [Google Scholar] [CrossRef]
- Keedwell, A.D. Constructions of complete sets of orthogonal diagonal Sudoku squares. Australas. J. Comb. 2010, 47, 227–238. [Google Scholar]
- Narayanan, R.M.; Bufler, T.D.; Leshchinskiy, B. Radar ambiguity functions and resolution characteristics of Sudoku-based waveforms. In Proceedings of the IEEE International Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 17–21.
- Costas, J.P. A study of a class of detection waveforms having nearly ideal range-Doppler ambiguity properties. Proc. IEEE 1984, 72, 996–1009. [Google Scholar] [CrossRef]
- Wehner, D.R. High Resolution Radar; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Levanon, N. Radar Principles; John Wiley: New York, NY, USA, 1988. [Google Scholar]
- Woodward, P.M. Probability and Information Theory with Applications to Radar; Pergamon: New York, NY, USA, 1953. [Google Scholar]
- Golomb, S.W.; Taylor, H. Constructions and properties of Costas arrays. Proc. IEEE 1984, 72, 1143–1163. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J. Design of frequency-hopping waveforms based on ambiguity function. In Proceedings of the 2nd International Congress on Image and Signal Processing, Tianjin, China, 17–19 October 2009.
- Chang, W.; Scarbrough, K. Costas arrays with small number of cross-coincidences. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 109–112. [Google Scholar] [CrossRef]
- Kang, E.W. Radar System Analysis, Design and Simulation; Artech House: Norwood, MA, USA, 2008. [Google Scholar]
- Levanon, N.; Mozeson, E. Radar Signals; John Wiley: New York, NY, USA, 2004. [Google Scholar]
- Haupt, R.L. Antenna Arrays: A Computational Approach; John Wiley: New York, NY, USA, 2010. [Google Scholar]
- Stutzman, W.L.; Thiele, G.A. Antenna Theory and Design; John Wiley: New York, NY, USA, 2012. [Google Scholar]
- Haupt, R.L. Thinned arrays using genetic algorithms. IEEE Trans. Antennas Propag. 1994, 42, 993–999. [Google Scholar] [CrossRef]
- Felgenhauer, B.; Jarvis, F. Enumerating possible Sudoku Grids. Available online: http://www.afjarvis.staff.shef.ac.uk/sudoku/sudoku.pdf (accessed on 1 October 2015).


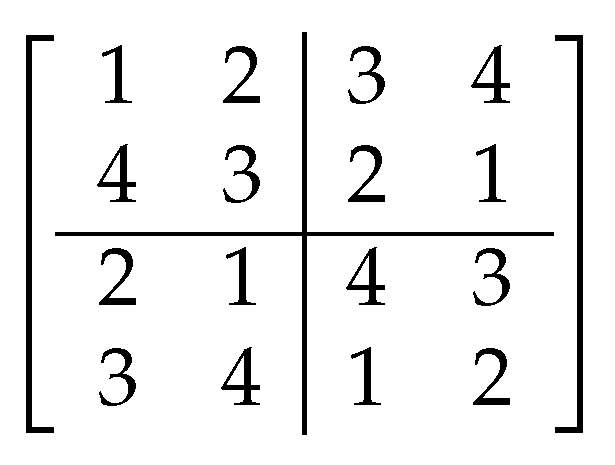
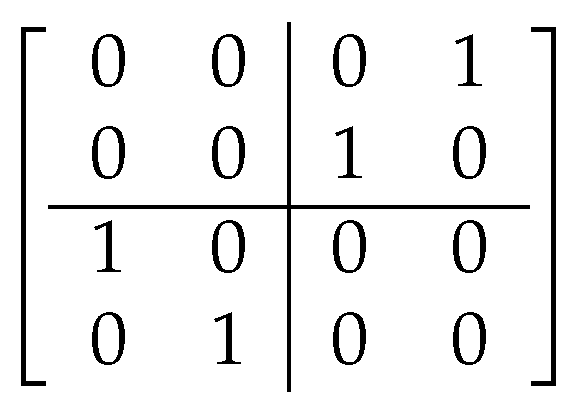
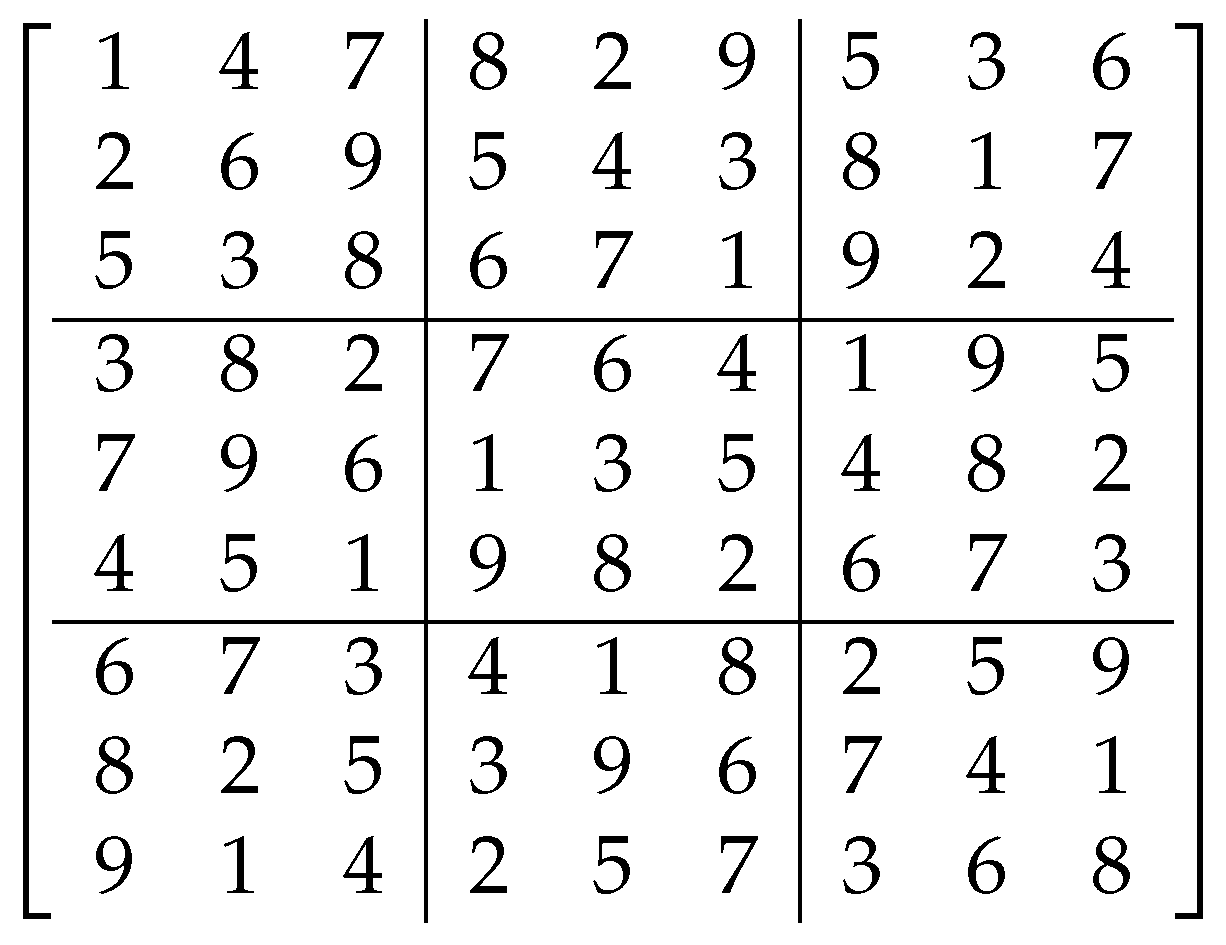
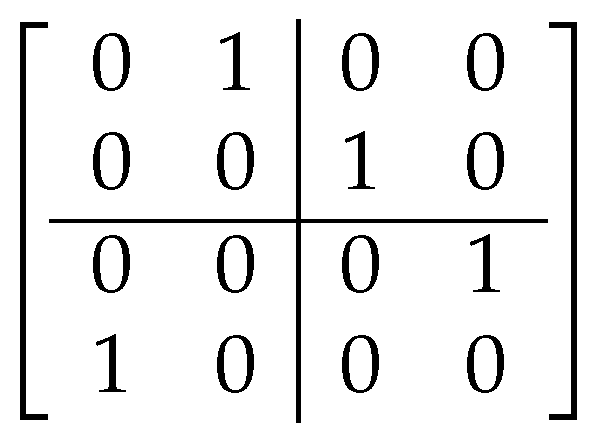
| Collisions | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Sudoku | 50% | 50% | 0% | 0% | 0% | 0% | 0% | 0% |
| Latin Square | 50% | 50% | 0% | 0% | 0% | 0% | 0% | 0% |
| Sudoku | 22.21% | 55.8% | 19.93% | 2.04% | 0% | 0% | 0% | 0% |
| Latin Square | 15.15% | 59.5% | 21.93% | 2.88% | 0.50% | 0% | 0% | 0% |
| Sudoku | 0.20% | 50.24% | 42.02% | 6.56% | 0.88% | 0% | 0% | 0% |
| Latin Square | 0.20% | 45.54% | 44.15% | 8.75% | 1.15% | 0.17% | 0.01% | 0.0044% |
| Sudoku | 0% | 24.51% | 58.44% | 15.16% | 1.97% | 0.22% | 0% | 0% |
| Latin Square | 0.0025% | 22.67% | 58.34% | 16.24% | 2.54% | 0.30% | 0.033% | 0.0042% |
| Collisions | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Sudoku | 0.20% | 41.31% | 44.6% | 12.7% | 1.08% | 0% | 0% |
| Latin Square | 0.36% | 41.1% | 48.6% | 8.69% | 1.79% | 0% | 0% |
| Sudoku | 0% | 10.4% | 63.2% | 22.2% | 3.5% | 0.5% | 0% |
| Latin Square | 0% | 11.95% | 64.6% | 20.2% | 2.9% | 0.31% | 0.02% |
| Sudoku | 0% | 1.66% | 56.28% | 34.96% | 6.15% | 0.8% | 0.1% |
| Latin Square | 0% | 1.97% | 59.00% | 33.07% | 5.24% | 0.6% | 0.06% |
| Radar Parameter | Values |
|---|---|
| Code Lengths | 9 and 81 |
| 10 GHz | |
| Bandwidths | 9 MHz and 81 MHz |
| Target Range | 2 km |
| Radar Cross Section (RCS) | 10 |
| Group Number | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Numbers | 1,2,3,4,5 | 6,7,8,9,10 | 11,12,13,14,15 | 16,17,18,19,20 |
| Scan Angle |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bufler, T.D.; Narayanan, R.M.; Sherbondy, K.D. Sudoku Inspired Designs for Radar Waveforms and Antenna Arrays. Electronics 2017, 6, 13. https://doi.org/10.3390/electronics6010013
Bufler TD, Narayanan RM, Sherbondy KD. Sudoku Inspired Designs for Radar Waveforms and Antenna Arrays. Electronics. 2017; 6(1):13. https://doi.org/10.3390/electronics6010013
Chicago/Turabian StyleBufler, Travis D., Ram M. Narayanan, and Kelly D. Sherbondy. 2017. "Sudoku Inspired Designs for Radar Waveforms and Antenna Arrays" Electronics 6, no. 1: 13. https://doi.org/10.3390/electronics6010013
APA StyleBufler, T. D., Narayanan, R. M., & Sherbondy, K. D. (2017). Sudoku Inspired Designs for Radar Waveforms and Antenna Arrays. Electronics, 6(1), 13. https://doi.org/10.3390/electronics6010013







