1. Introduction
Unmanned aerial vehicles have rapidly gained in popularity in recent years [
1,
2,
3]. In particular, there has been significant interest in unmanned multirotor helicopters [
4,
5,
6,
7,
8,
9,
10,
11]. This is primarily due to the wide range of applications and to their mechanical simplicity and durability. However, the mechanical simplicity of multirotor helicopters does come at a cost: traditional multirotor helicopters are underactuated. In particular, only four of the six degrees-of-freedom are controllable. Multirotor helicopters are capable of tracking desired attitudes, headings and accelerations in the body-fixed vertical direction. Multirotor helicopters cannot achieve accelerations in the body-fixed horizontal plane. This results in a coupling between multirotor helicopters’ attitude and acceleration. This underactuation places fundamental restrictions on the ability to perform tasks requiring manipulation of the surrounding environment. It also necessitates the use of complex mechanical componentry if a payload is to remain at a given attitude independent of the desired movement of the multirotor helicopter.
In an effort to overcome this limitation, several approaches have been proposed. An aerial vehicle with three ducted fans mounted on gimbals is under investigation by Jayakody [
12] and Yuan [
13]. The gimbals allow the thrust produced by the ducted fans to be directed with respect to the body of the aircraft, allowing for horizontal accelerations independent of attitude. Another approach has been presented by Cetinsoy et al. [
14]. Their platform consists of a multirotor helicopter with sub-rotor control surfaces. The control surfaces allow the down-wash from the rotors to be directed, thus producing a lateral component in the resultant force. Further, tilt-rotor actuation has been investigated by Kendoul et al. [
15] and Ryll et al. [
16]. Tilt-rotor actuation involves mounting the rotors of traditional multirotor helicopters on gimbals, thus allowing the resultant thrust to be vectored as in the approach by Jayakody and Yuan [
12,
13]. Finally, helicopters utilise swash-plates to allow cyclic-pitch rotor blade actuation [
17]. The cyclic-pitch of a rotor affects the moment produced by the rotor about axes perpendicular to the rotor’s axis of rotation. The cyclic-pitch further causes the thrust produced by the rotor to be vectored with respect to the body of the multirotor helicopter. Therefore, cyclic-pitch allows lateral accelerations to be achieved. However, changes to a rotor’s cyclic-pitch induce a secondary change in attitude towards the direction of thrust produced.
Drawing inspiration from research into tilt-rotor-equipped multirotor helicopters, in this paper, a minimal actuation concept that aims to achieve the same result is proposed. Rather than allowing all rotors to tilt, only a single tilting rotor is included on an otherwise traditional multirotor helicopter. The proposed aircraft is mechanically simpler than a tilt-rotor multirotor helicopter, as only a single additional actuator is required. The proposed multirotor helicopter can achieve control of five degrees-of-freedom; allowing for horizontal accelerations that are independent of attitude. To achieve this, a daisy chaining-based control allocation methodology is proposed. This control allocation methodology takes full advantage of the proposed multirotor helicopter by prioritising maintaining the desired attitude when manoeuvring and utilising changes in attitude only when absolutely necessary.
The remainder of this paper is structured as follows. In
Section 2, the dynamics model of the single tilt-rotor multirotor helicopter is developed. An analysis is conducted to determine the available control bandwidth in
Section 3. The proposed daisy chaining-based control allocation methodology is detailed in
Section 4. Computational and experimental analyses of the single tilt-rotor multirotor helicopter and control system architecture are presented in
Section 5 and
Section 6, respectively. Finally, concluding remarks are given in
Section 7.
2. Multirotor Helicopter Dynamics Model
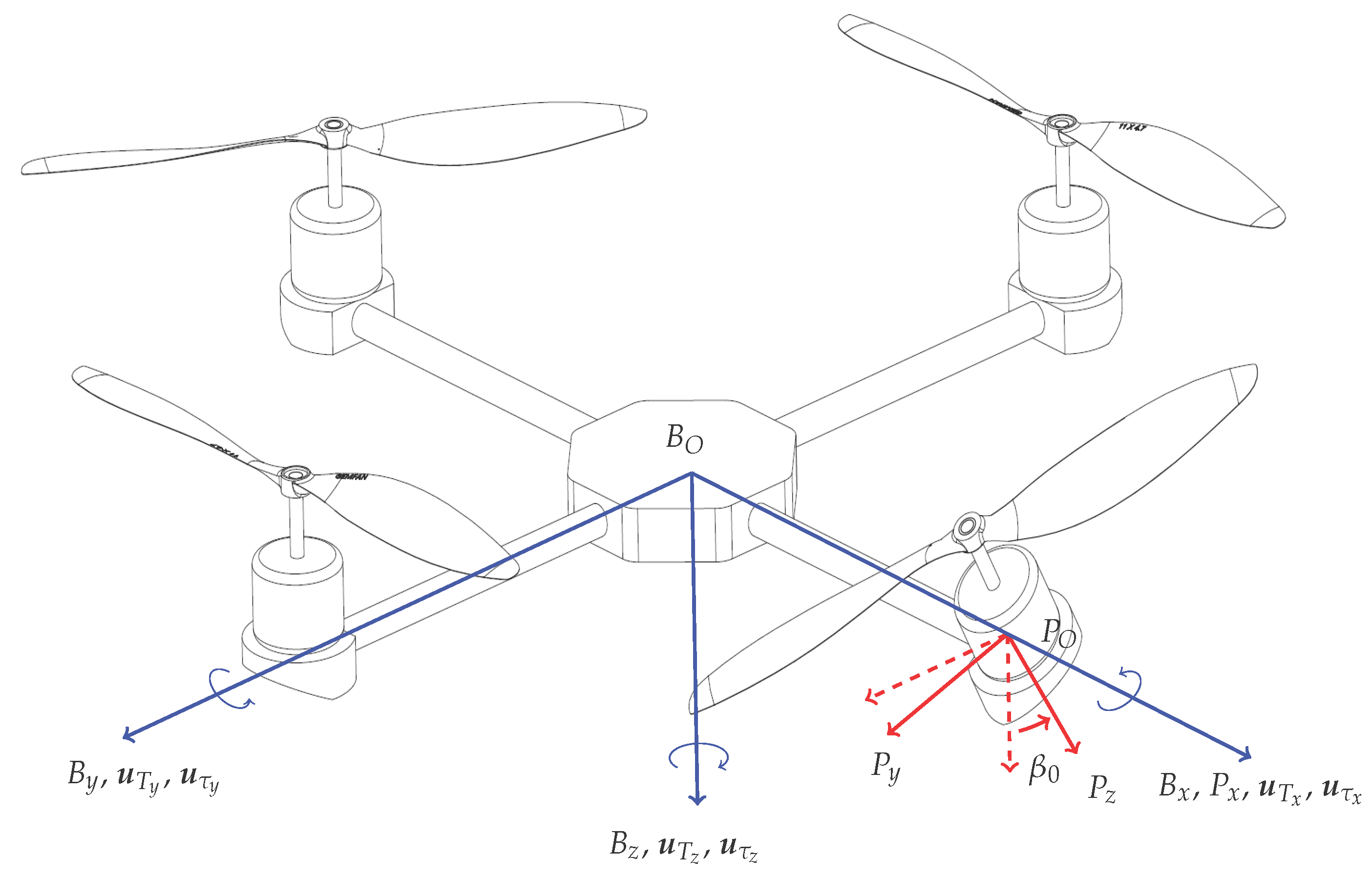
The multirotor helicopter proposed in this research consists of two rigid bodies: the multirotor helicopter body,
B, which includes the non-tilting rotor groups; and the tilting rotor group,
P. The tilting rotor group includes the gimbal, the motor driving the tilting rotor and the rotor itself. The tilting rotor is constrained to only rotate about the arm to which it is attached. A schematic of the proposed multirotor helicopter is presented in
Figure 1. In this section, the dynamics model of this multirotor helicopter is developed. The nomenclature utilised in this section is presented in
Table 1.
A right-hand coordinate frame
, with origin
, is attached to the centre of
B as in
Figure 1. Additionally, a coordinate frame
is attached to the tilting rotor group. The origin of
,
, is positioned at the intersection of the axis about which the rotor group rotates and the axis about which the rotor itself rotates. Without loss of generality, it is assumed that the tilting rotor is positioned along the
x axis of
. An inertial coordinate frame is defined as
. The orientation of
with respect to
is given by the attitude quaternion,
. Likewise, the orientation of
with respect to
is given by
.
The following assumptions are made:
The multirotor helicopter body is rigid and symmetrical
and the centre of mass of the multirotor helicopter coincide
The rotors are rigid
The multirotor helicopter is operating in the vicinity of the hover condition
The aerodynamic drag force on the multirotor helicopter body is negligible
Under these assumptions, the dynamics model of the multirotor helicopter can be derived using the Newton–Euler formalism.
The angular velocity of the tilting rotor in
,
, is given by:
where
indicates the conjugate of quaternion
q;
is the angular velocity of
with respect to
;
β is the angle between
and
(the subscript
z indicates the
z axis); and
is the angular velocity of the tilting rotor about
. Differentiating this expression results in the angular acceleration of the tilting rotor in
, which is given in the following equation.
In Equation (
2),
is the angular velocity of
with respect to
.
The torque produced by the tilting rotor,
, is given by:
where
is the external torque applied to the tilting rotor.
is primarily due to a counter-rotating torque about
caused by the air drag [
17] and is typically considered to be of the following form in normal operating conditions (see [
8,
18,
19], for example),
where the subscript
i indicates the rotor number; and
is a constant determined by the rotor size and profile.
Similarly, the torque produced by each of the non-tilting rotors can be expressed as:
where:
The torque on the multirotor helicopter in
,
, can be described as:
The torques produced by the multirotor helicopter are due to the thrusts produced by each of the rotors and are given by:
where
is the vector from
to
;
is the thrust of the tilting rotor in
;
is the vector from
along each of the arms of the multirotor helicopter to the axis of rotation of the
i-th rotor; and
is the thrust vector of the
i-th rotor in
. It should be noted that, as for Equation (
4), it is typical to assume
takes the following form for a fixed-pitch rotor in normal operating conditions,
where
is a constant determined by the rotor size and profile.
The translational dynamics of the multirotor helicopter are derived using a force balance and are presented in the following equation.
In Equation (
10),
m is the mass of the multirotor helicopter;
is the position vector of
relative to
; and
is the gravity vector in
.
The complete dynamics model of the multirotor helicopter with single tilting rotor is given by Equations (
1) to (
10).
3. Control Bandwidth Analysis
One of the primary constraints when implementing a single tilting rotor is that the lateral thrust produced by the tilting rotor cannot be balanced by vectoring thrust produced by another rotor. Instead, the resulting moment about must be balanced by torque produced by the non-tilting rotors. As the torque produced by the rotors is an order of magnitude less than the thrust produced, this constraint requires careful consideration.
To characterise the available control bandwidth, the multirotor helicopter dynamics developed in the previous section can be simplified into Equations (
11) to (
16).
In (
16),
l is the distance from
to the axis each rotor rotates about;
β and
are the control inputs, and
and
are the virtual control inputs to the dynamics system. The process for setting the control inputs given a set of virtual control inputs is referred to as control allocation. Adding the virtual control input abstraction allows for simpler outer loop controller design, as the details of control allocation do not have to be considered.
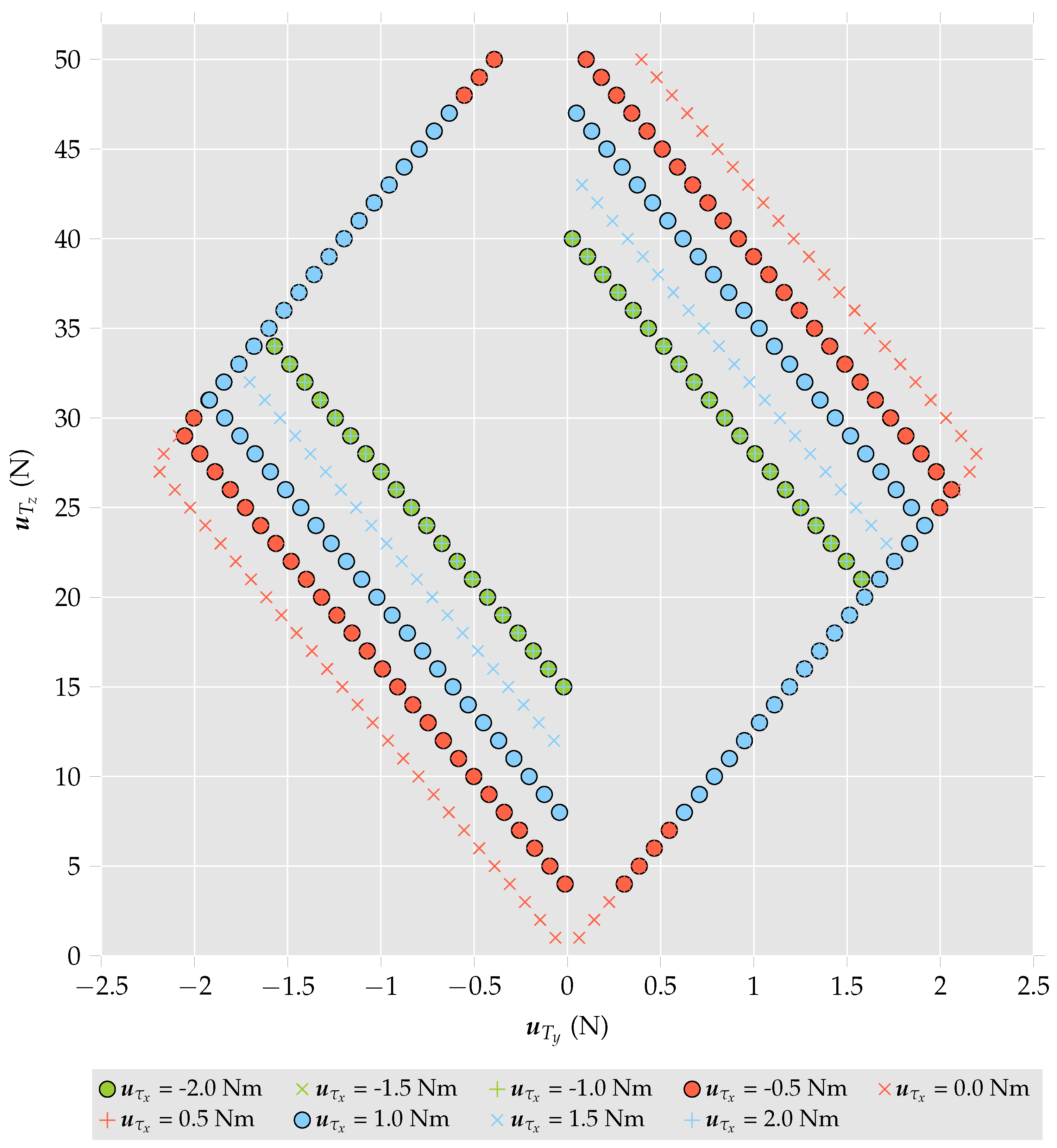
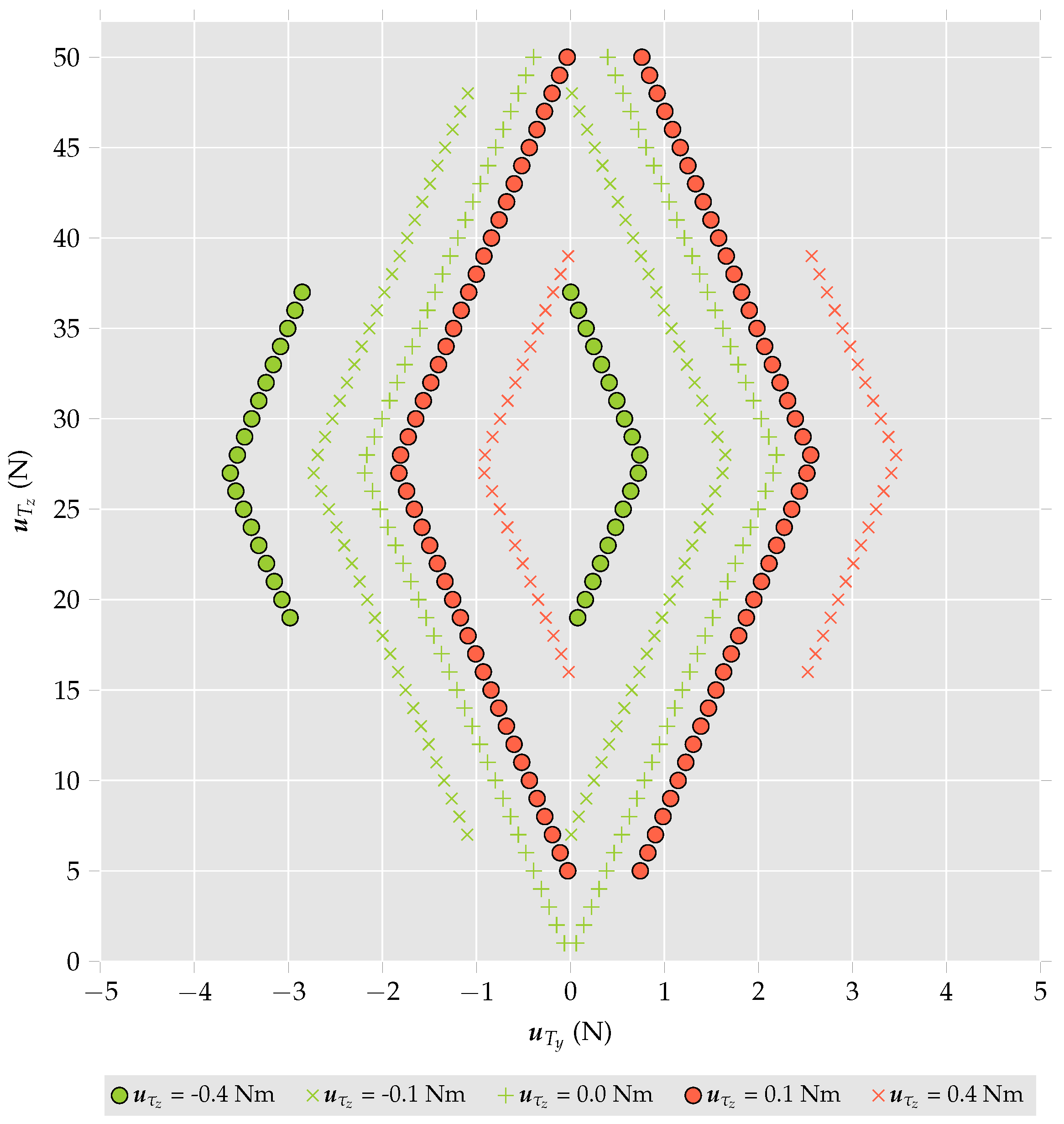
The control bandwidth can be characterised by an analysis of Equation (
16). In particular, given control input constraints, the maximum and minimum achievable lateral forces,
, that can be generated can be determined as a function of required vertical force,
, and torques,
. The results presented in
Figure 2,
Figure 3 and
Figure 4 were calculated by setting
and
and increasing or decreasing
until the system could no longer be solved to satisfy the control input constraints. The data points represent the maximum and minimum values of
for a given set of
and
. The parameters
,
and
l are presented in
Table 2, along with the control input constraints and additional multirotor helicopter parameters. It should further be noted that these results are valid for operating conditions sufficiently close to the hover condition where assumptions made in Equations (
4) and (
9) are valid.
To demonstrate how the addition of a single tilting rotor affects the control bandwidth of the multirotor helicopter, consider
Figure 2. In this case,
Nm. Consider a case where
and
are initially 40 N and 0 N, respectively. Referring to the figure, it is observed that under these conditions, the multirotor helicopter is able to generate ±2 Nm of torque about the
x axis. If the desired
is increased to 0.5 N and the other desired control inputs remain the same, the torque the multirotor helicopter can generate is reduced to ± 1 Nm. If the desired
is increased further to 1 N, the magnitude of torque the multirotor helicopter can generate is reduced to <0.5 Nm. If
continues to be increased, the system cannot be solved for any value of
once
reaches 1.3 N. In this case, to solve for the desired values
and
,
has to be decreased.
5. Computational Analysis
To characterise the performance of the single tilt-rotor multirotor helicopter, a computational model was developed. The parameters of the multirotor helicopter are presented in
Table 2. In this computational analysis the dynamics model is updated at a rate of 10 kHz, and the control is performed at 200 Hz.
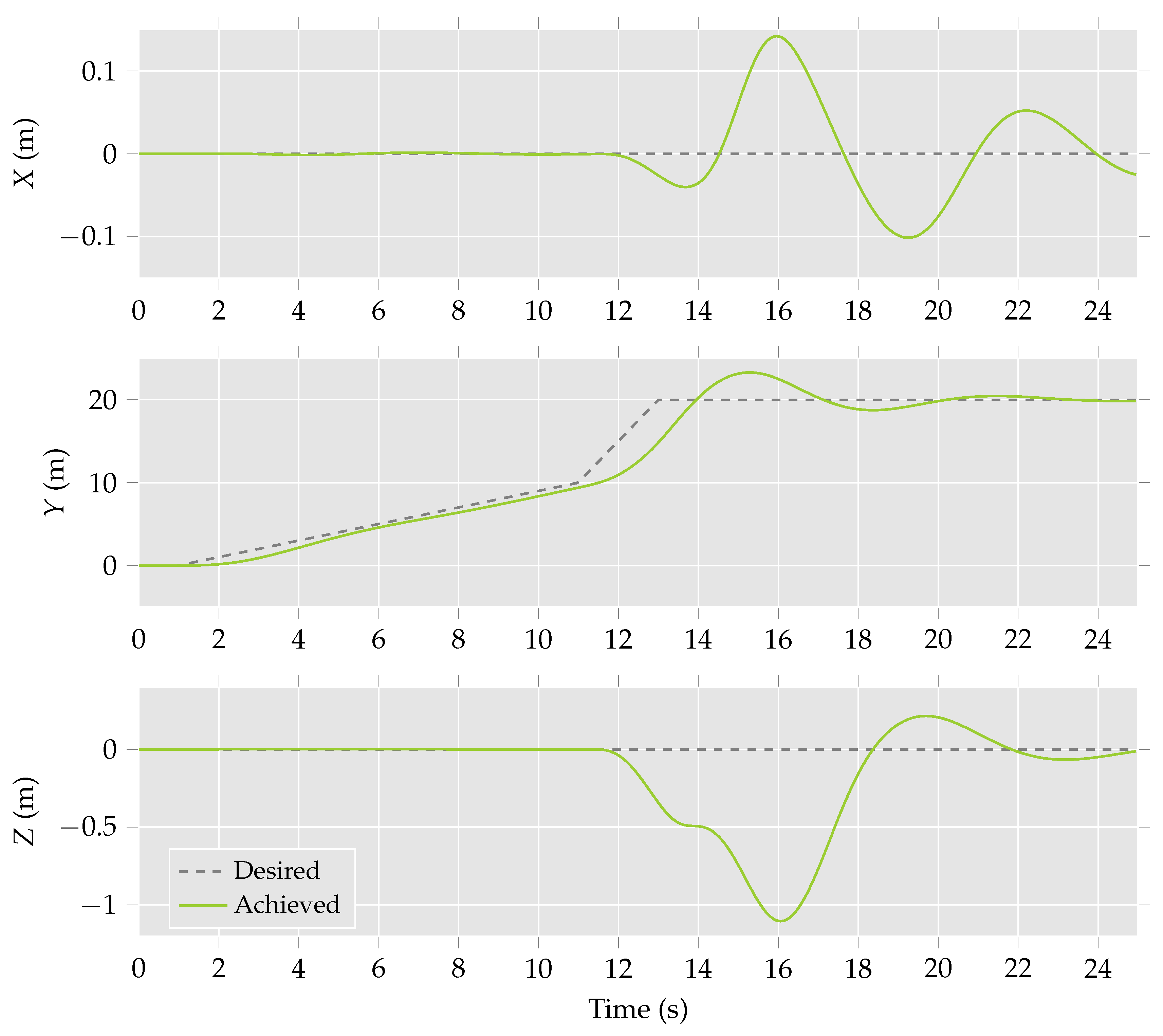
Initially, the multirotor helicopter is commanded to move in the
y-direction at a rate of 1 m/s. After a period of 10 s, the multirotor helicopter is commanded to increase its velocity to 5 m/s. The complete motion is presented in
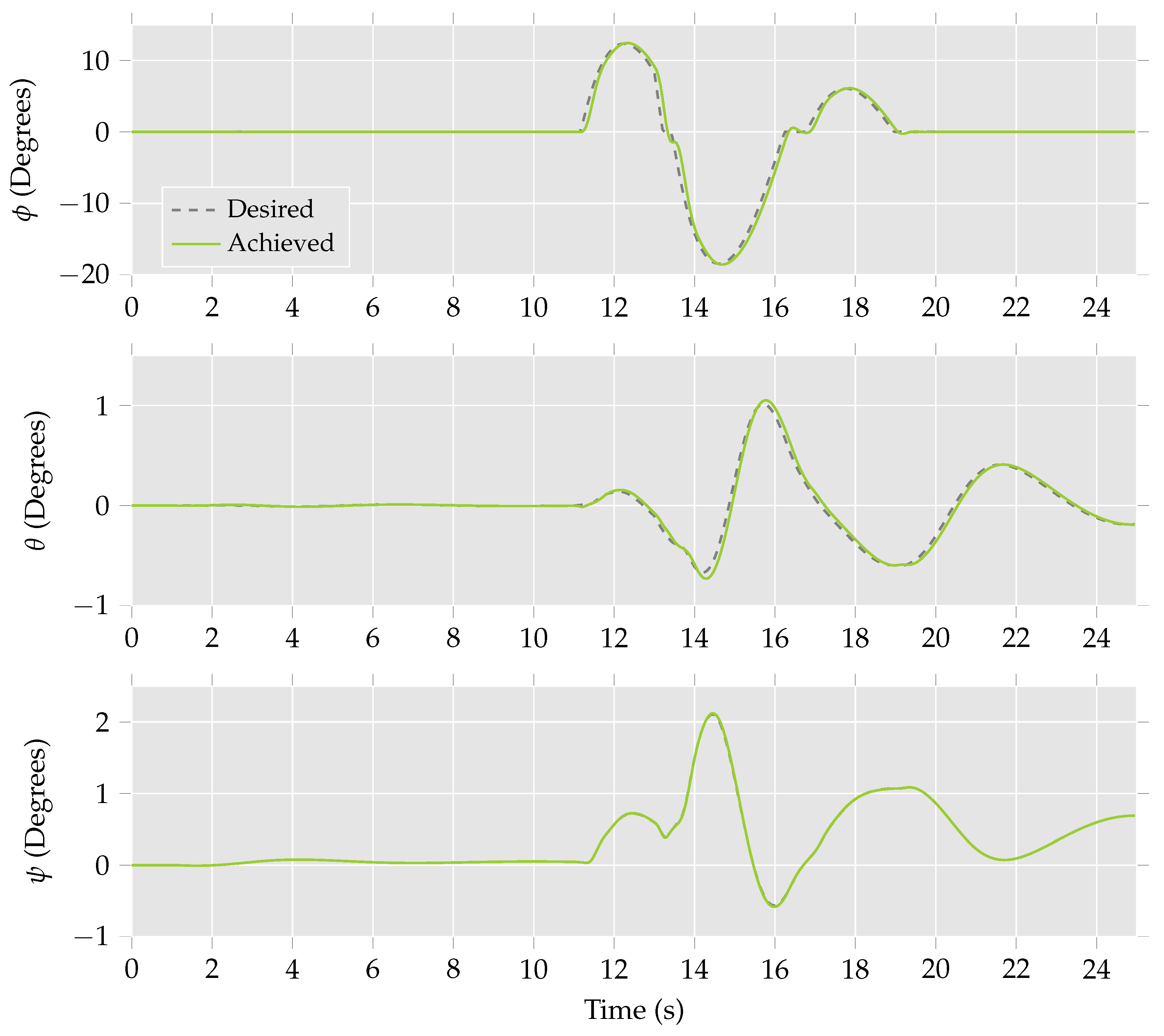
Figure 5. The attitude of the multirotor helicopter during the manoeuvre is presented in
Figure 6. Further,
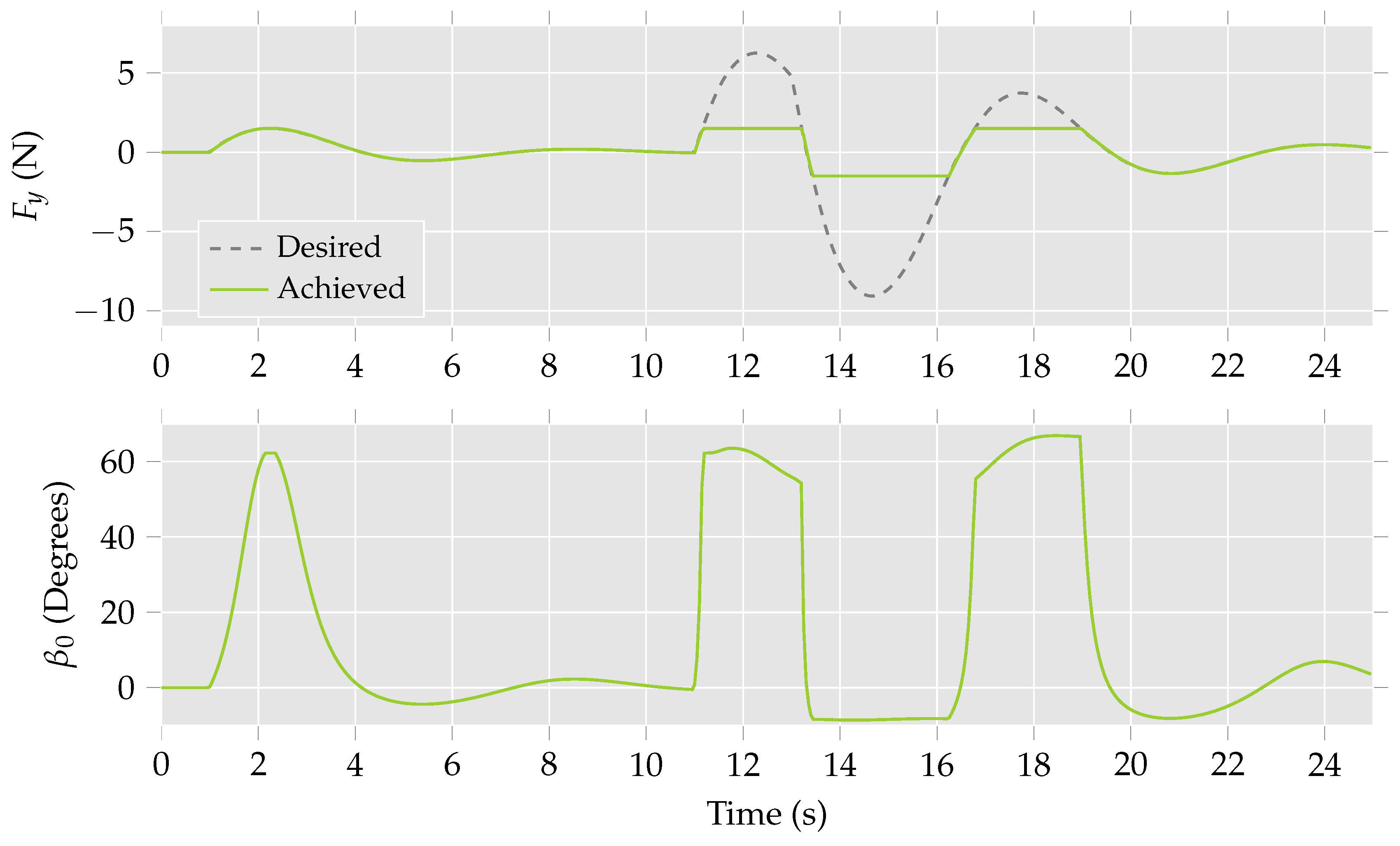
Figure 7 shows the achieved lateral force and the corresponding rotor tilt.
From
Figure 7, it is observed that the entire desired lateral force for the initial stage of the manoeuvre can be achieved through actuating the tilting rotor only. This is reflected in
Figure 6, as the roll remains unchanged despite the multirotor helicopter moving in the desired direction. During the second stage of the manoeuvre, it can be seen that actuating the only tilting rotor no longer produces the desired lateral force. Instead, the attitude of the multirotor helicopter must be utilised to achieve the desired motion. This is represented in
Figure 6 as a change in the roll,
ϕ, of the multirotor helicopter.
6. Experimental Analysis
To validate the results obtained from the computational analysis in the previous section, an experimental analysis has been undertaken. To this end, an experimental research facility has been established. The research facility incorporates a single tilt-rotor multirotor helicopter. The multirotor helicopter is presented in
Figure 8. The remainder of the research facility has been presented in previous work by the author [
22] and includes a laser interferometry-based sensing and measurement unit to precisely record the position of the multirotor helicopter at a rate of 1000 Hz. Measurements from accelerometers, gyroscopes and magnetometers mounted onboard the multirotor helicopter are recorded at a rate of 200 Hz. The algorithm proposed in [
23] is utilised to combine these sensor measurements to produce attitude estimates. The desired rotor angular velocities and rotor tilt angle are also updated a rate of 200 Hz. The PID and PD
2 controller gains in Equations (
17) and (
29), respectively, were calculated utilising the Ziegler–Nichols step-response tuning methodology [
24]. This methodology was chosen as the same set of tuning rules could be applied to multirotor helicopters with different rotor configurations, removing the effect of controller tunings from any comparisons drawn.
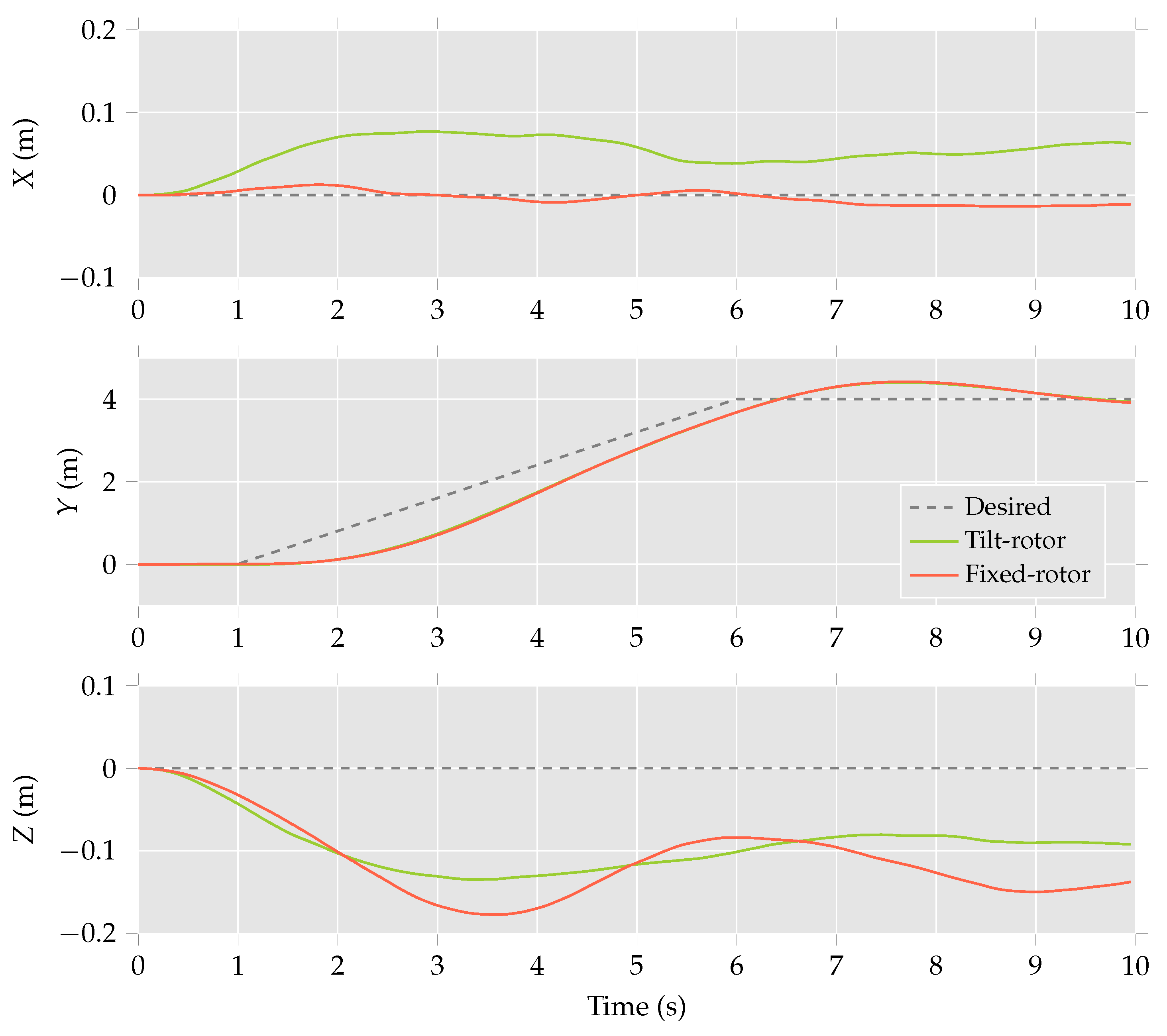
In the first experiment, the multirotor helicopter was commanded to move in the
y-direction at
m/s. The measured position and estimated attitude of the multirotor helicopter during this manoeuvre are presented in
Figure 9 and
Figure 10, respectively. The experiment was repeated with the same multirotor helicopter with all four rotors fixed in the traditional positions, the results of which are also presented in the figures.
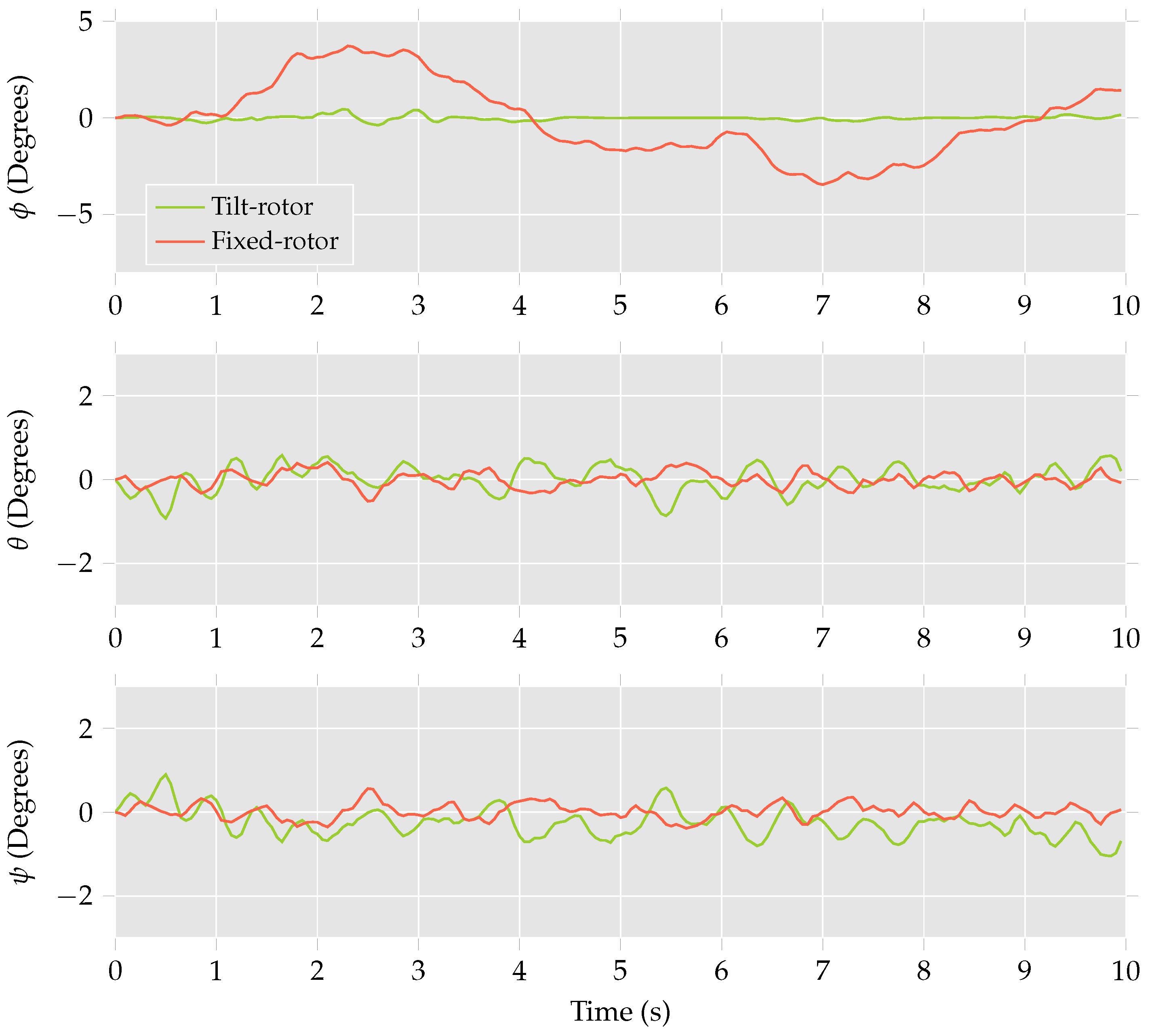
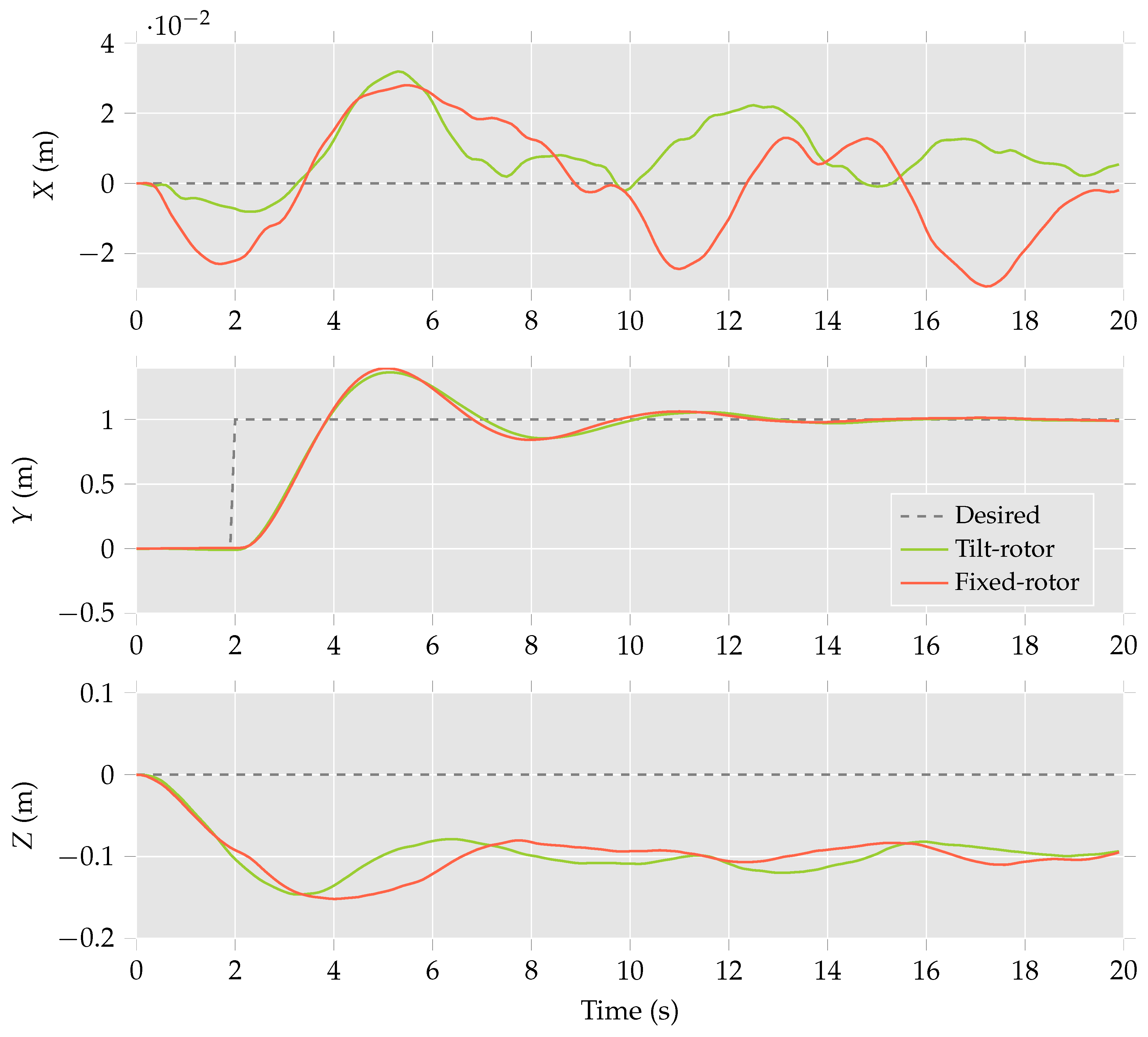
Referring to
Figure 9, it is observed that the differences between the trajectories for the multirotor helicopter with a single tilt-rotor configuration and the fixed-rotor configuration are minimal. The most notable difference is the drift in the
x-direction of the single tilt-rotor multirotor helicopter, which differs from the desired trajectory by
m. The corresponding drift of the fixed-rotor multirotor helicopter is only
m. The differences between the performance of the multirotor helicopter configurations is observed in
Figure 10. Here, the fixed-rotor multirotor helicopter is required to roll up to
to achieve the desired trajectory. The multirotor helicopter in the single tilt-rotor configuration exhibits a maximum roll of only
.
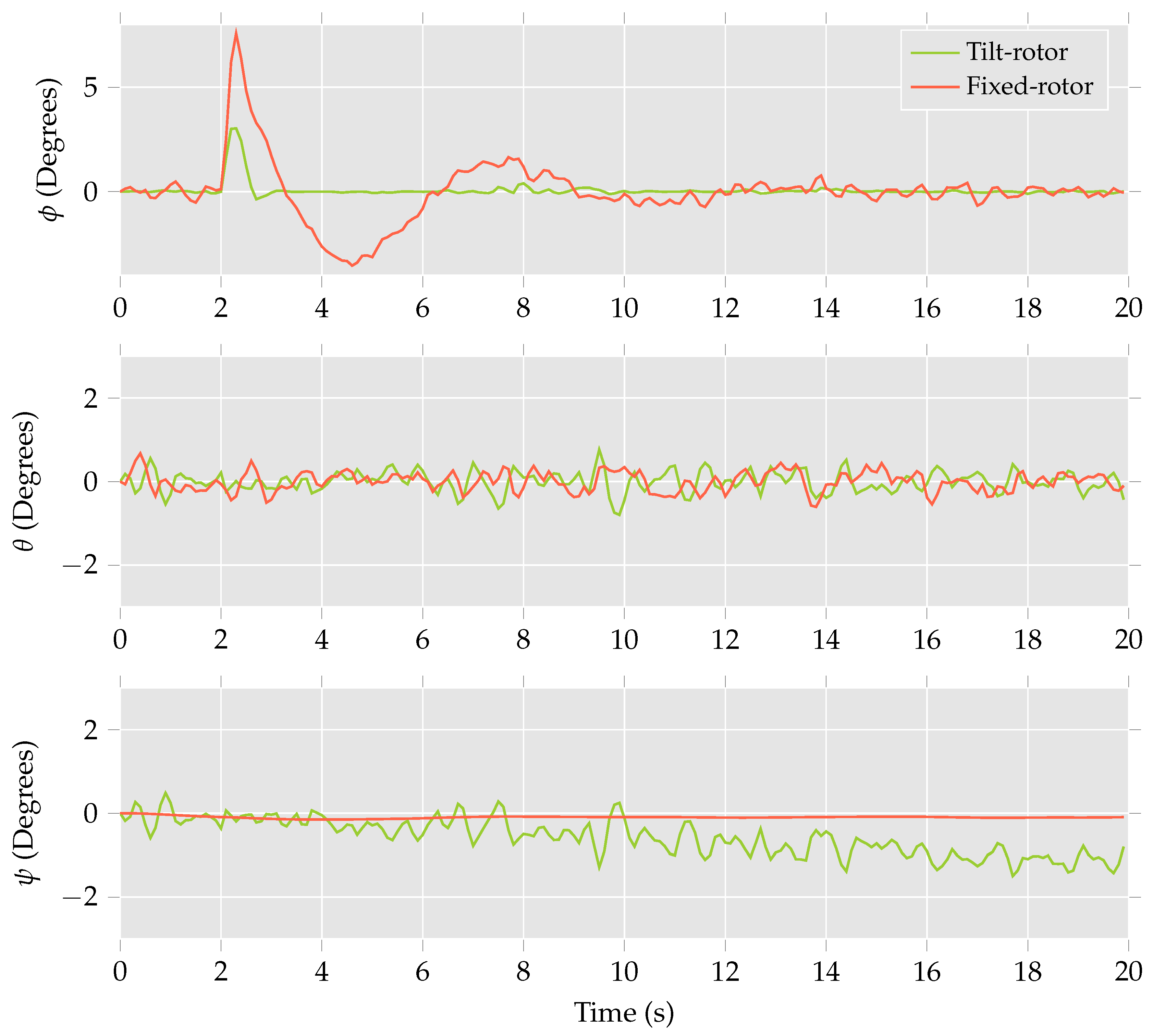
In the second experiment, the multirotor helicopter was commanded to track a step input of 1 m in the
y-direction. The position and attitude of the multirotor helicopter during the second manoeuvre are presented in
Figure 11 and
Figure 12, respectively. As in the previous case, the differences in trajectories for the fixed and tilt-rotor are minimal. Further, it is observed that both multirotor helicopters were required to perform roll manoeuvres to track the desired position trajectory. However, the maximum roll for the tilt-rotor configuration was approximately
, compared to
in the case of the fixed-rotor configuration.
These results are in line with those predicted by the computational analysis. Further, these results suggest that a single tilting-rotor multirotor helicopter can be utilised to track trajectories involving horizontal accelerations that are independent of attitude.
7. Concluding Remarks
This paper presents the development and implementation of a single tilting-rotor multirotor helicopter. The dynamics model of such a multirotor helicopter is developed and presented in detail.
The identified dynamics model allows for the establishment of a feedback control system for the proposed multirotor helicopter. The control system provisions the desired control effort to the actuators of the system with the aim of minimising the attitude of the aerial vehicle while maintaining the desired trajectory.
A characterisation of the available control bandwidth of the single tilting-rotor multirotor helicopter is presented and demonstrates the validity of the proposed concept. Further, a computational analysis of the control system and complete dynamics model of the multirotor helicopter demonstrates that the control system allows for effective trajectory tracking while simultaneously minimising the attitude of the multirotor helicopter. The computational analysis is supported by an experimental analysis that compares the performance of the proposed multirotor helicopter to a multirotor helicopter with no tilting rotors. The experimental analysis demonstrates that the single tilting rotor multirotor helicopter is able to achieve comparable trajectory tracking performance for low-speed manoeuvres without requiring a change in attitude. Thus, the attitude and horizontal accelerations have been decoupled for low-speed manoeuvres by the addition of a single tilting rotor.
Further research will be undertaken to explore the full capabilities of the proposed single tilting rotor multirotor helicopter.