Equilibrium Molecular Dynamics (MD) Simulation Study of Thermal Conductivity of Graphene Nanoribbon: A Comparative Study on MD Potentials
Abstract
:1. Introduction
2. Theory and Simulation
2.1. Interatomic MD Potentials
2.2. Equilibrium Molecular Dynamics Simulation: Green-Kubo Method
2.3. Quantum Correction
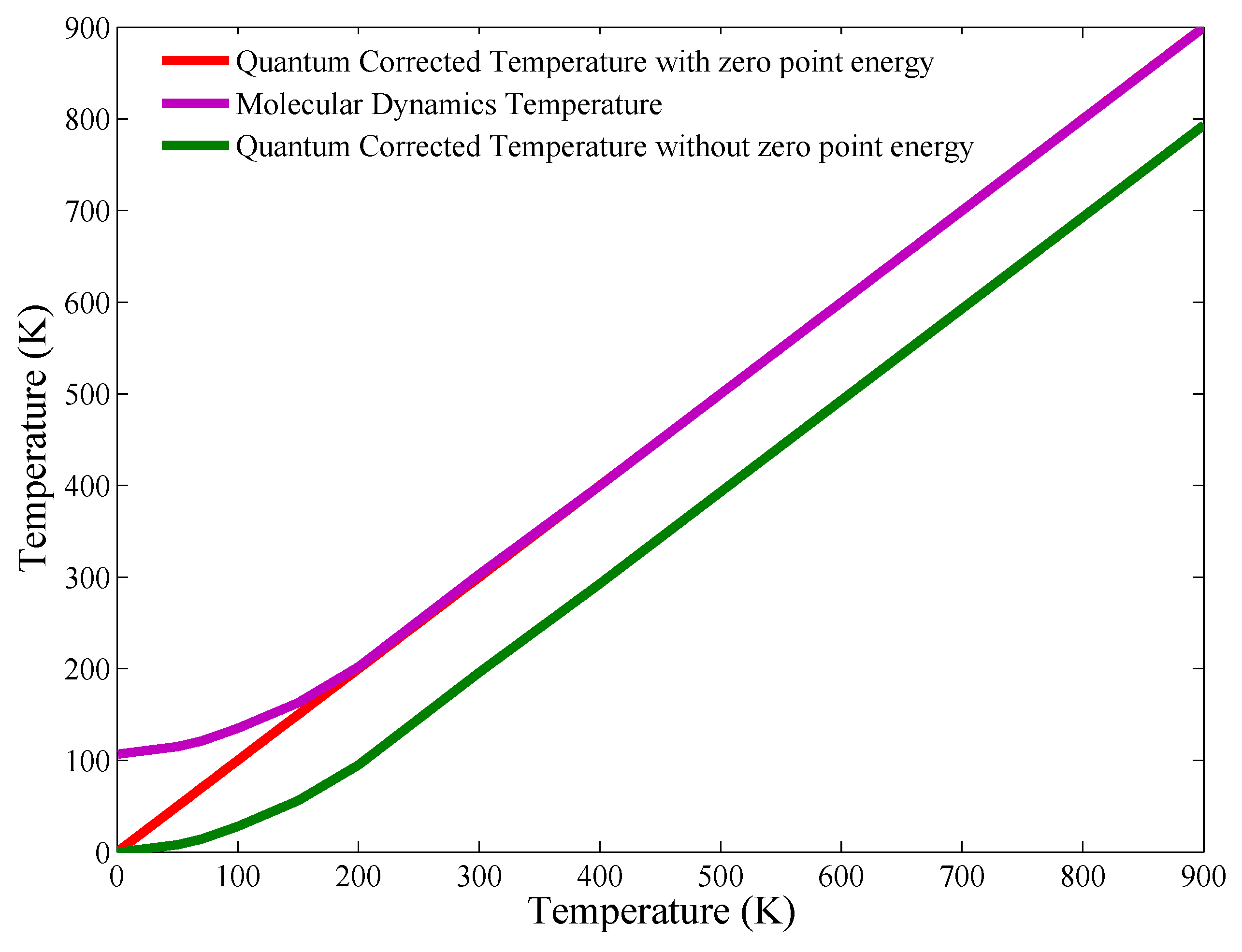
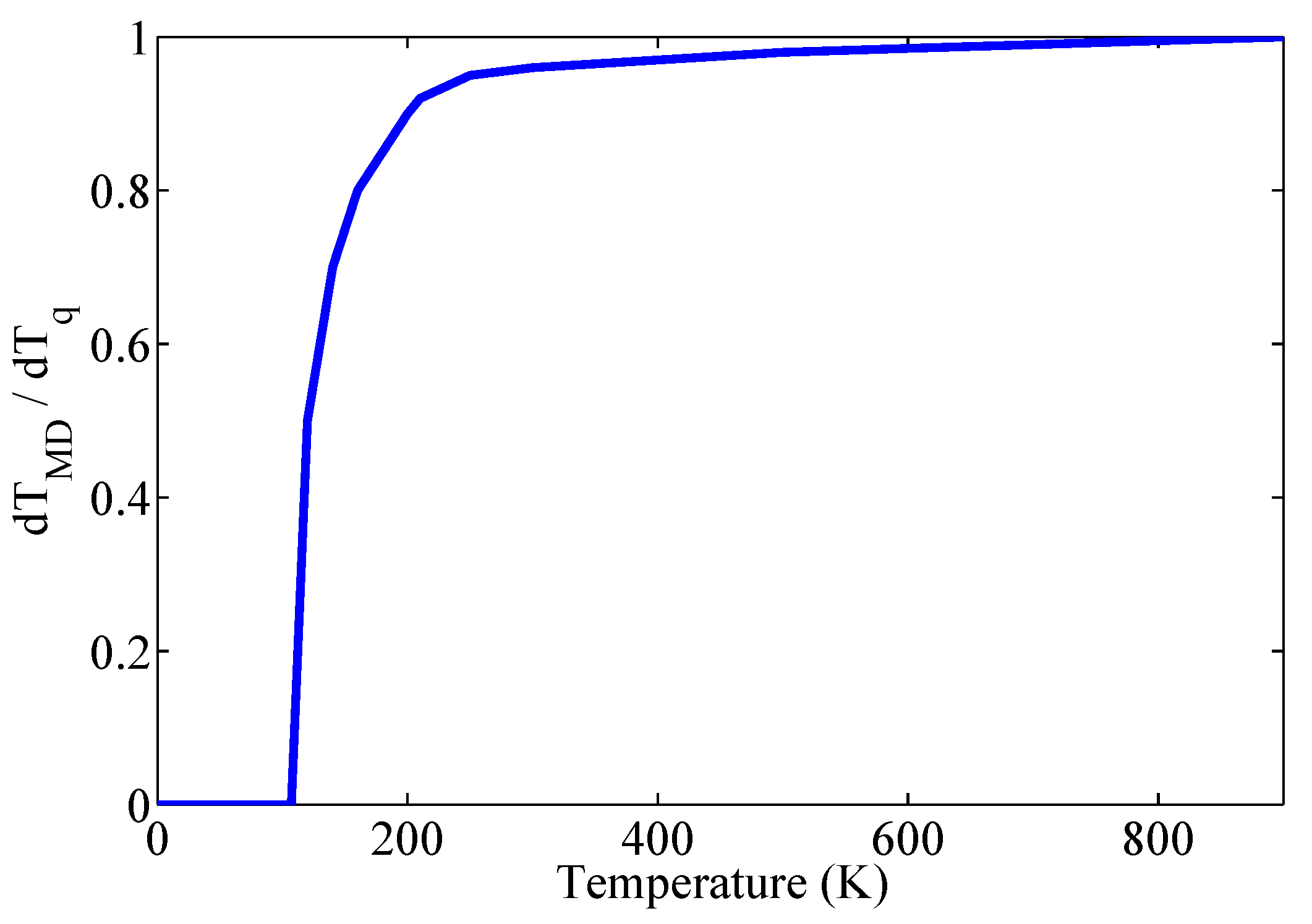
2.4. Simulation Details

3. Results and Discussion
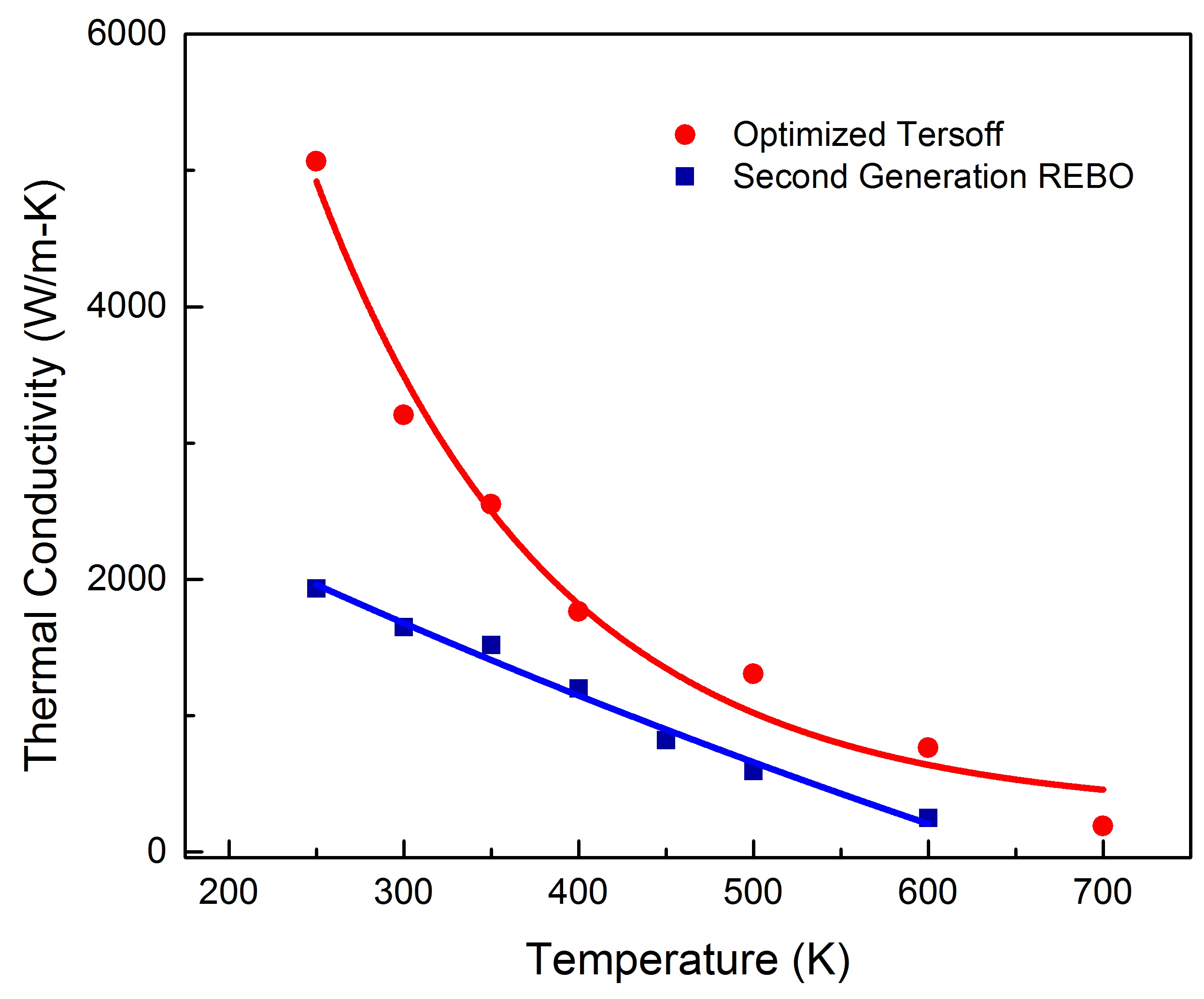
3.1. Potential Dependence of Thermal Conductivity
3.2. Temperature Dependence of Thermal Conductivity
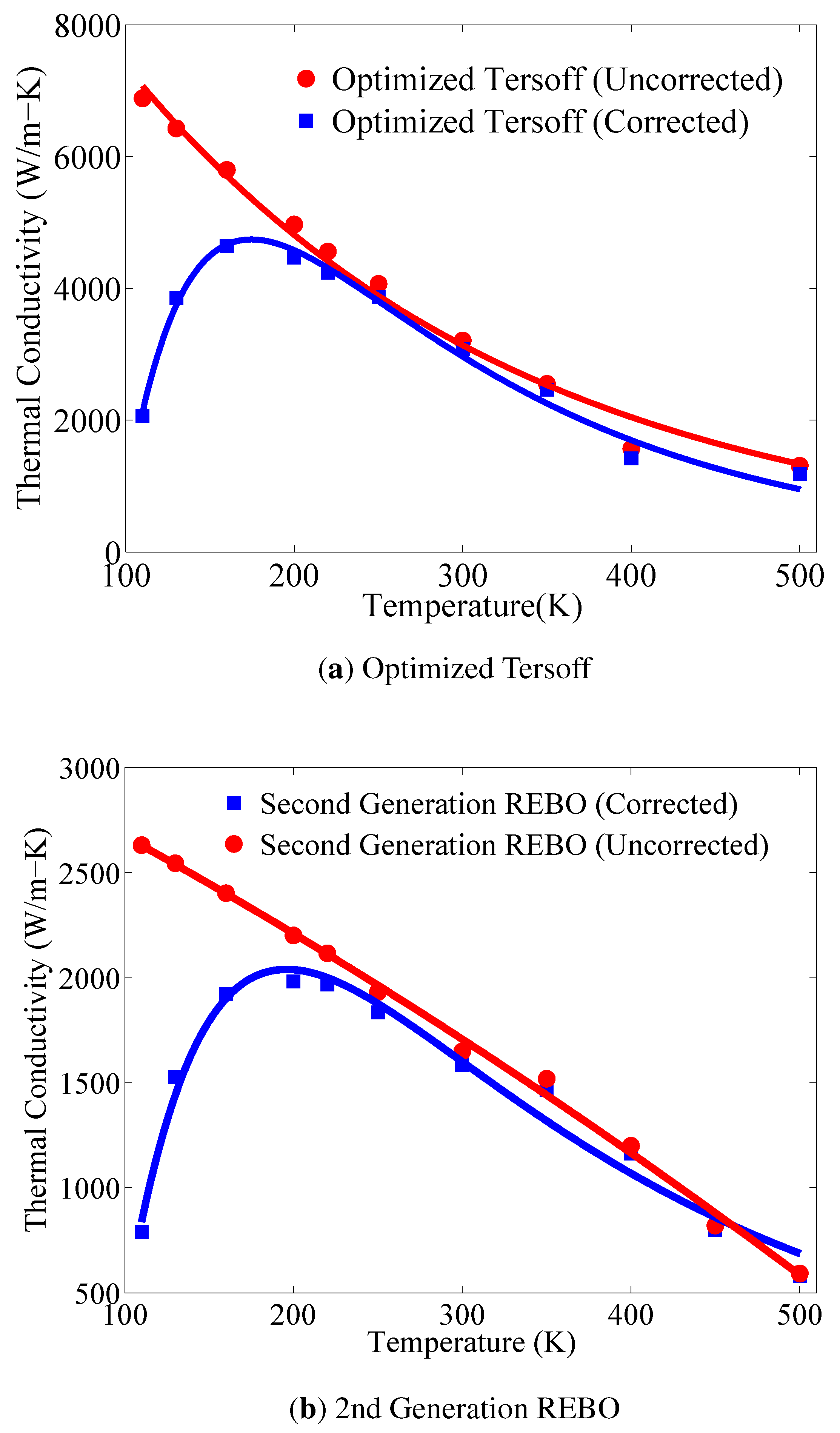
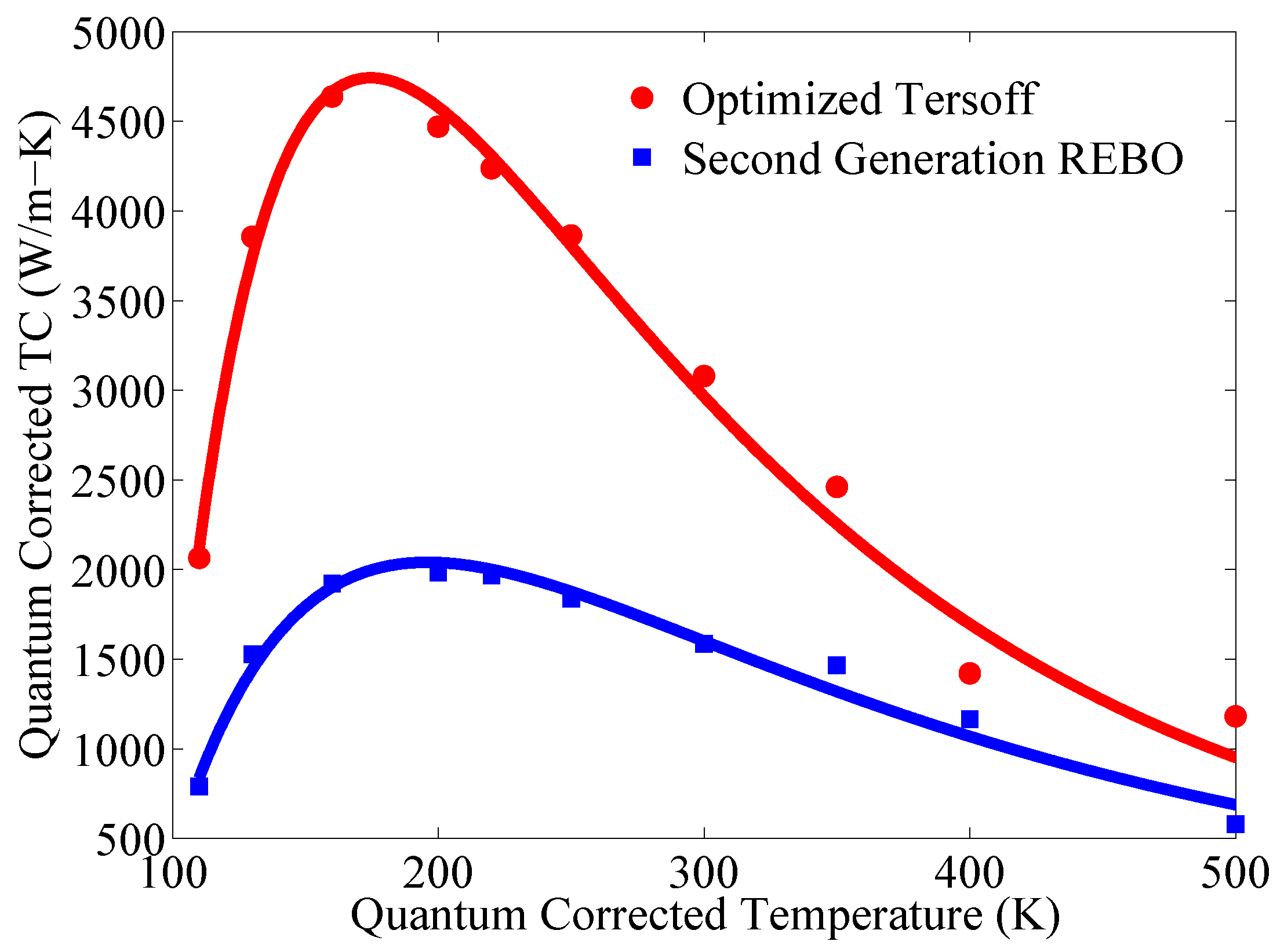
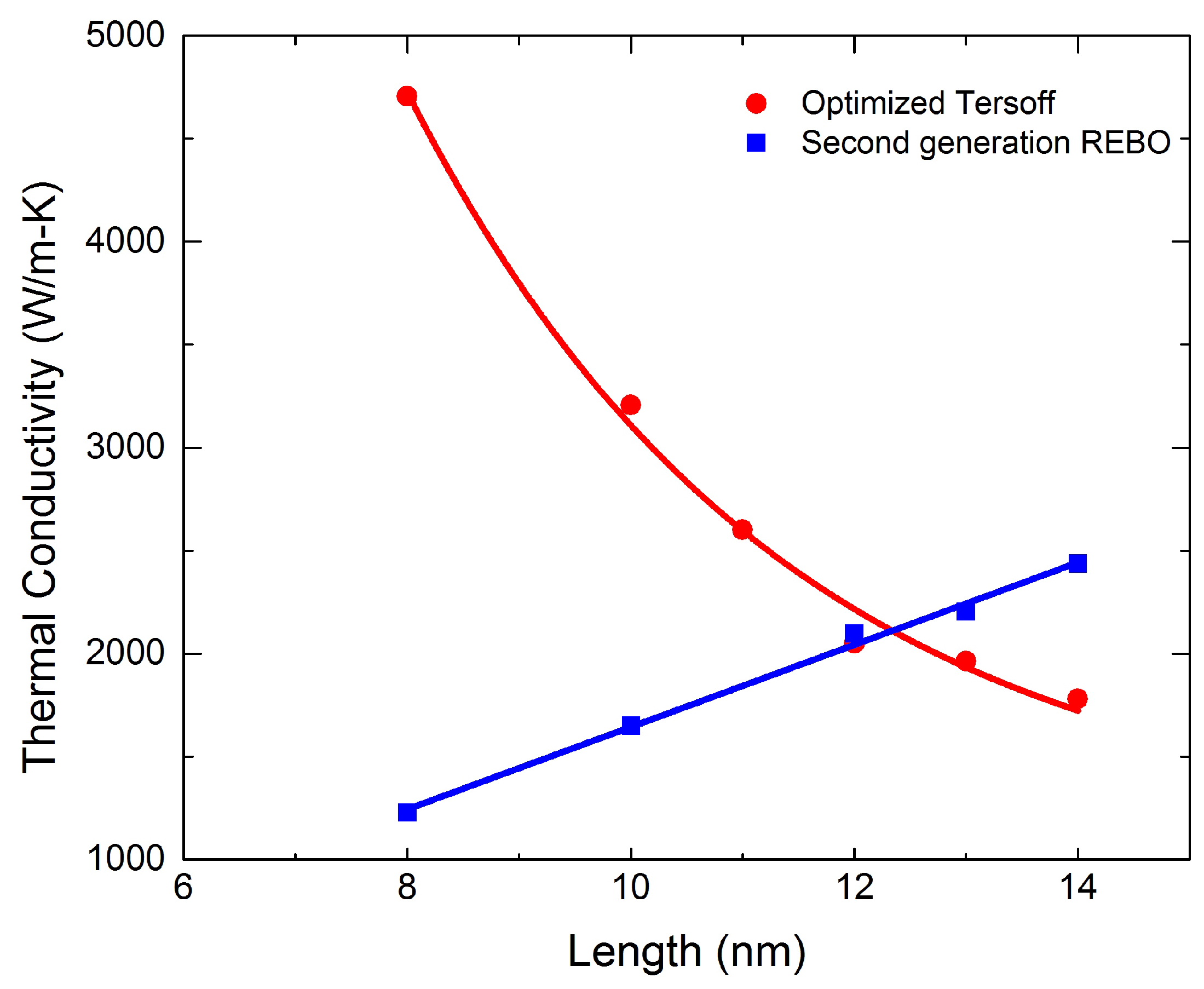
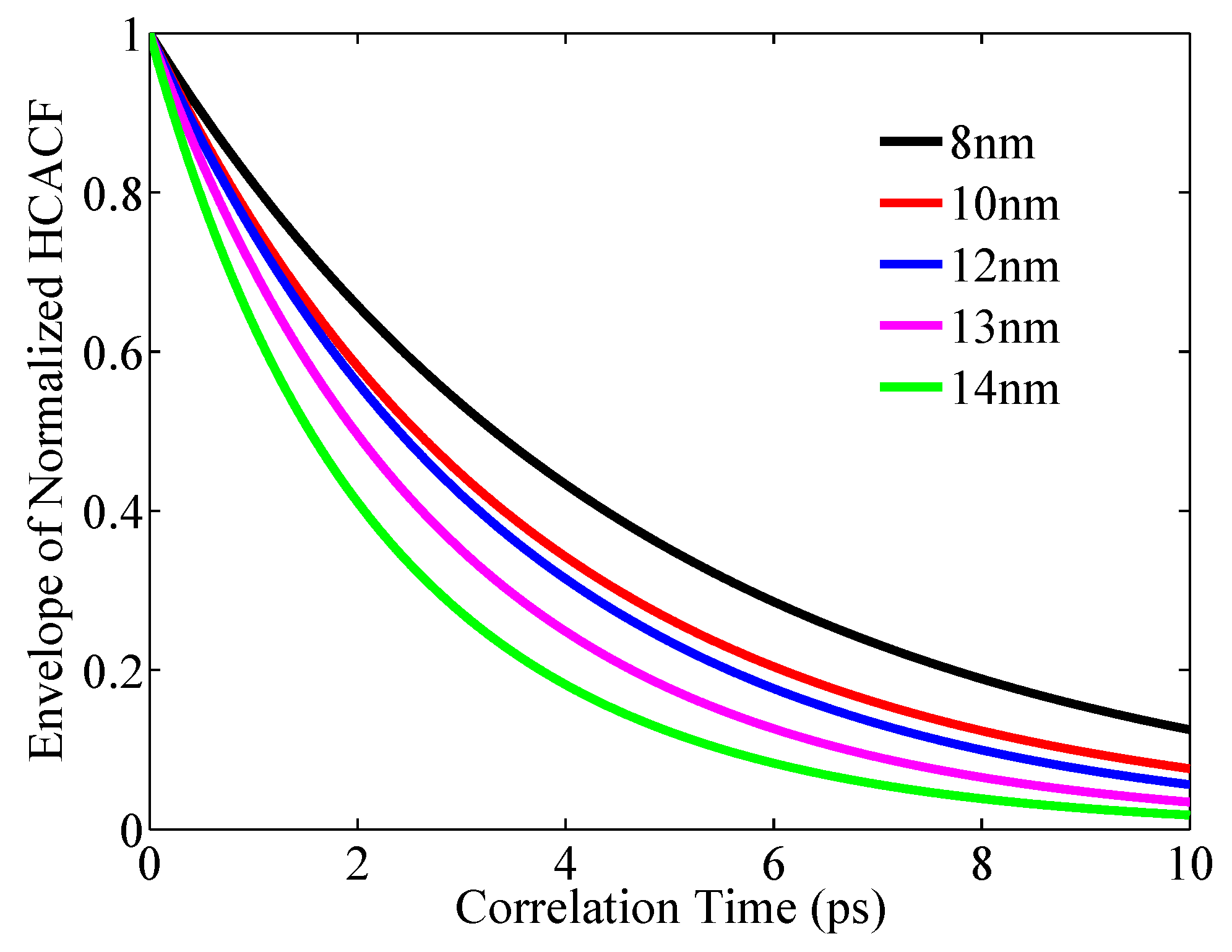
3.3. Length Dependence of Thermal Conductivity:
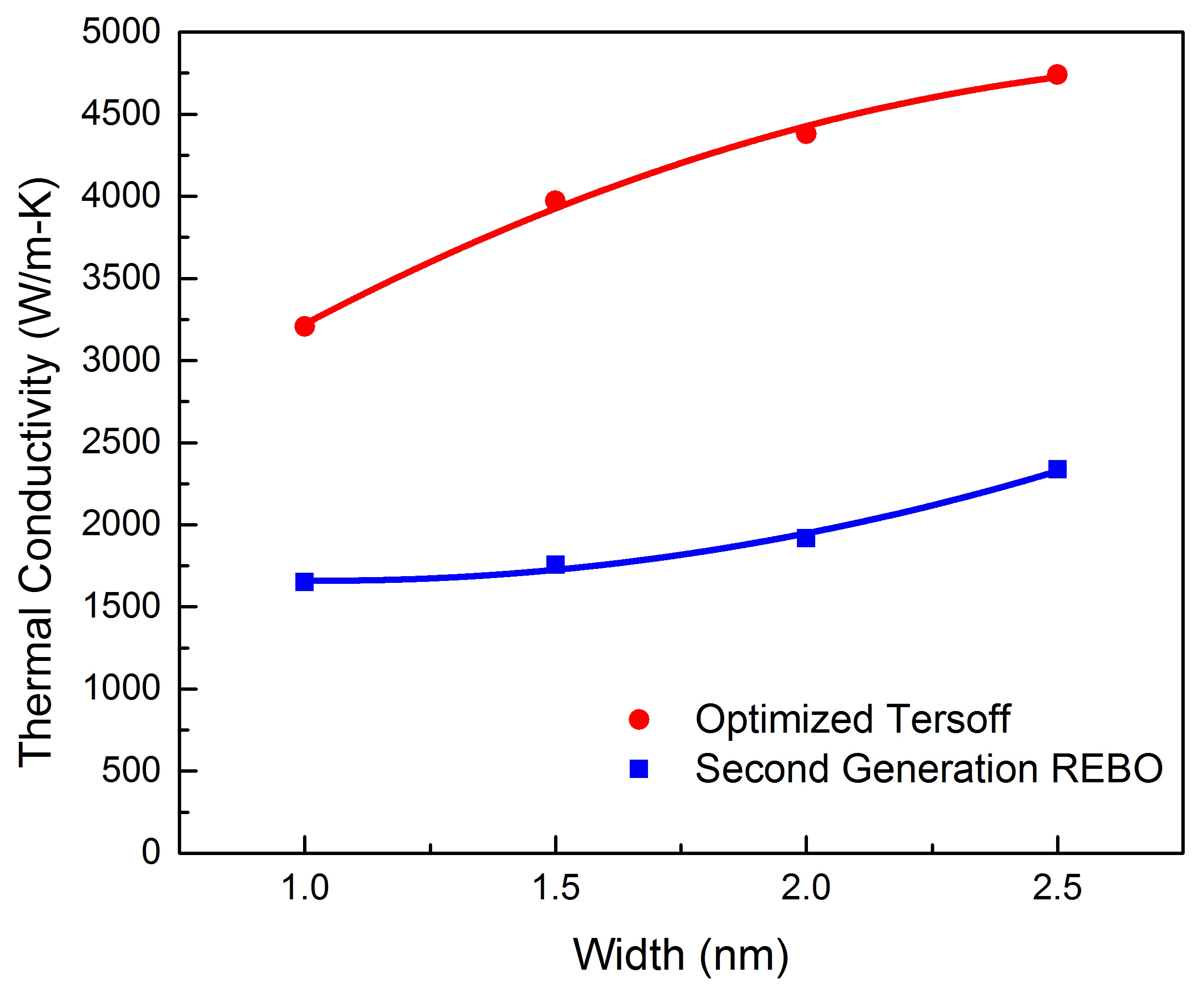
3.4. Width Dependence of Thermal Conductivity
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Novoselov, K.; Geim, A.; Morozov, S.; Jian, D.; Katsnelson, M.; Grigorieva, I.; Dubonos, S.; Firsov, A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seol, J.H.; Jo, I.; Moore, A.L.; Lindsay, L.; Aitken, Z.H.; Pettes, M.T.; Li, X.; Yao, Z.; Huang, R.; Broido, D.; et al. Two-Dimensional Phonon Transport in Supported Graphene. Science 2010, 328, 213–216. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Nakada, K.; Fujita, M. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 954–960. [Google Scholar] [CrossRef]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef] [PubMed]
- Han, M.Y.; Ozyilmaz, B.; Zhang, Y.; Kim, P. Energy Band-Gap Engineering of Graphene Nanoribbons. Phys. Rev. Lett. 2007, 98, 206805. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Ma, F.; Sun, Y.; Hu, T.; Xu, K. Influence of typical defects on thermal conductivity of graphene nanoribbons: An equilibrium molecular dynamics simulation. App. Surf. Sci. 2012, 258, 9926–9931. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior Thermal Conductivity of Single-Layer Graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Joung, D.; Zhai, L.; Das, S.; Khondaker, S.I.; Seal, S. Graphene based materials: Past, present and future. Prog. Mater. Sci. 2011, 56, 1178–1271. [Google Scholar] [CrossRef]
- Hone, J.; Whitney, M.; Piskoti, C.; Zettl, A. Thermal conductivity of single-walled carbon nanotubes. Phys. Rev. B 1999, 59, 2514–2516. [Google Scholar] [CrossRef]
- Cao, A. Molecular dynamics simulation study on heat transport in monolayer graphene sheet with various geometries. App. Phys. Lett. 2012, 111, 083528. [Google Scholar] [CrossRef]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. App. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Hu, J.; Ruan, X.; Chen, Y.P. Thermal Conductivity and Thermal Rectification in Graphene Nanoribbons: A Molecular Dynamics Study. Nano Lett. 2009, 9, 2730–2735. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Kumar, S. Thermal transport in graphene supported on copper. J. Appl. Phys. 2012, 112, 043502. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, Y.; Pei, Q.; Wang, C.; Xiang, Y. Thermal conductivity of defective graphene. Phys. Lett. A 2012, 376, 3668–3672. [Google Scholar] [CrossRef]
- Yu, C.; Zhang, G. Impacts of length and geometry deformation on thermal conductivity of graphene nanoribbons. J. App. Phys. 2013, 113. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Schelling, P.K.; Phillpot, S.R.; Keblinski, P. Comparison of atomic-level simulation methods for computing thermal conductivity. Phys. Rev. B 2001, 65, 144306. [Google Scholar] [CrossRef]
- Khadem, M.H.; Wemhoff, A.P. Comparison of Green-Kubo and NEMD heat flux formulations for thermal conductivity prediction using the Tersoff potential. Comp. Mater. Sci. 2013, 69, 428–434. [Google Scholar] [CrossRef]
- Mahdizadeh, S.J.; Goharshadi, E.K. Thermal conductivity and heat transport properties of graphene nanoribbons. Springer 2014, 16, 1–12. [Google Scholar] [CrossRef]
- Tersoff, J. Empirical Interatomic Potential for Carbon, with Applications to Amorphous Carbon. Phys. Rev. Lett. 1988, 61, 2879–2882. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.J.; Hu, L.; Keblinski, P. Thermal conductivity of graphene ribbons from equilibrium molecular dynamics: Effect of ribbon width, edge roughness, and hydrogen termination. Appl. Phys. Lett. 2010, 96, 203112. [Google Scholar] [CrossRef]
- Lindsay, L.; Broido, D.A. Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 2010, 81, 205441. [Google Scholar] [CrossRef]
- Brenner, D.W. Empirical potential for hydrocarbons for use in simulating the chemical vapor deposition of diamond films. Phys. Rev. B 1990, 42, 9458–9471. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Zhang, H.; Lee, G.; Fonseca, A.F.; Borders, T.L.; Cho, K. Isotope Effect on the Thermal Conductivity of Graphene. J. Nanomater 2010, 2010, 537657. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shenderova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter 2002, 14, 783–802. [Google Scholar] [CrossRef]
- Lee, Y.H.; Biswas, R.; Soukoulis, C.M.; Wang, C.Z.; Chan, C.T.; Ho, K.M. Molecular-Dynamics Simulation of Thermal Conductivity in Amorphous Silicon. Phys. Rev. B 1991, 43, 6573–6580. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thomas, J.A.; Iutzi, R.M.; McGaughey, A.J.H. Thermal conductivity and phonon transport in empty and water-filled carbon nanotubes. Phys. Rev. B 2010, 81, 045413. [Google Scholar] [CrossRef]
- Yu, C.; Shi, L.; Yao, Z.; Li, D.; Majumdar, A. Thermal Conductance and Thermopower of an Individual Single-Wall Carbon Nanotube. Nano Lett. 2005, 5, 1842–1846. [Google Scholar] [CrossRef] [PubMed]
- ZIMAN, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: Amen House, London, UK, 1960. [Google Scholar]
- Pereira, L.F.C.; Donadio, D. Divergence of the thermal conductivity in uniaxially strained graphene. Phys. Rev. B 2013, 87, 125424. [Google Scholar] [CrossRef]
- Ecsedy, D.J.; Klemens, P.G. Thermal resistivity of dielectric crystals due to four-phonon processes and optical modes. Phys. Rev. B 1977, 15, 5957–5962. [Google Scholar] [CrossRef]
- Steigmeier, E.F.; Kudman, I. Acoustical-Optical Phonon Scattering in Ge, Si, and III-V Compounds. J. Appl. Phys. 1966, 141, 767–774. [Google Scholar] [CrossRef]
- Pichanusakorn, P.; Bandaru, P. Nanostructured thermoelectrics. Mater. Sci. Eng. R 2010, 67, 19–63. [Google Scholar] [CrossRef]
- Sonvane, Y.; Gupta, S.K.; Raval, P.; Lukacevic, I.; Thakor, P. Length, Width and Roughness Dependent Thermal Conductivity of Graphene Nanoribbons. Chem. Phys. Lett. 2015, 634. [Google Scholar] [CrossRef]
- Nika, D.; Ghosh, S.; Pokatilov, E.; Balandin, A. Lattice Thermal conductivity of graphene flakes: Comparison with bulk graphite. App. Phys. Lett. 2009, 94, 203103. [Google Scholar] [CrossRef]
- Nissimagoudar, A.S.; Sankeshwar, N.S. Significant reduction of lattice thermal conductivity due to phonon confinement in graphene nanoribbons. Phys. Rev. B 2014, 89, 235422. [Google Scholar] [CrossRef]
- Klemens, P.G. Theory of the A-Plane Thermal Conductivity of Graphite. J. Wide Bandgap Mater. 2000, 7, 332–339. [Google Scholar] [CrossRef]
- Klemens, P.G.; Pedraza, D.F. Thermal Conductivity of Graphite in the Basal Plane. Carbon 1994, 32, 735–741. [Google Scholar] [CrossRef]
- Nika, D.L.; Askerov, A.S.; Balandin, A.A. Anomalous Size Dependence of the Thermal Conductivity of Graphene Ribbons. Nano Lett. 2012, 12, 3238–3244. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.Y.; Guo, Z.X.; Xiang, H.; Gong, X.G. Layer and size dependence of thermal conductivity in multilayer graphene nanoribbons. Phys. Lett. A 2012, 376, 525–528. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, A.I.; Navid, I.A.; Noshin, M.; Uddin, H.M.A.; Hossain, F.F.; Subrina, S. Equilibrium Molecular Dynamics (MD) Simulation Study of Thermal Conductivity of Graphene Nanoribbon: A Comparative Study on MD Potentials. Electronics 2015, 4, 1109-1124. https://doi.org/10.3390/electronics4041109
Khan AI, Navid IA, Noshin M, Uddin HMA, Hossain FF, Subrina S. Equilibrium Molecular Dynamics (MD) Simulation Study of Thermal Conductivity of Graphene Nanoribbon: A Comparative Study on MD Potentials. Electronics. 2015; 4(4):1109-1124. https://doi.org/10.3390/electronics4041109
Chicago/Turabian StyleKhan, Asir Intisar, Ishtiaque Ahmed Navid, Maliha Noshin, H. M. Ahsan Uddin, Fahim Ferdous Hossain, and Samia Subrina. 2015. "Equilibrium Molecular Dynamics (MD) Simulation Study of Thermal Conductivity of Graphene Nanoribbon: A Comparative Study on MD Potentials" Electronics 4, no. 4: 1109-1124. https://doi.org/10.3390/electronics4041109
APA StyleKhan, A. I., Navid, I. A., Noshin, M., Uddin, H. M. A., Hossain, F. F., & Subrina, S. (2015). Equilibrium Molecular Dynamics (MD) Simulation Study of Thermal Conductivity of Graphene Nanoribbon: A Comparative Study on MD Potentials. Electronics, 4(4), 1109-1124. https://doi.org/10.3390/electronics4041109




