Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey
Abstract
:1. Introduction
2. Overview of Resistive Switching Memory
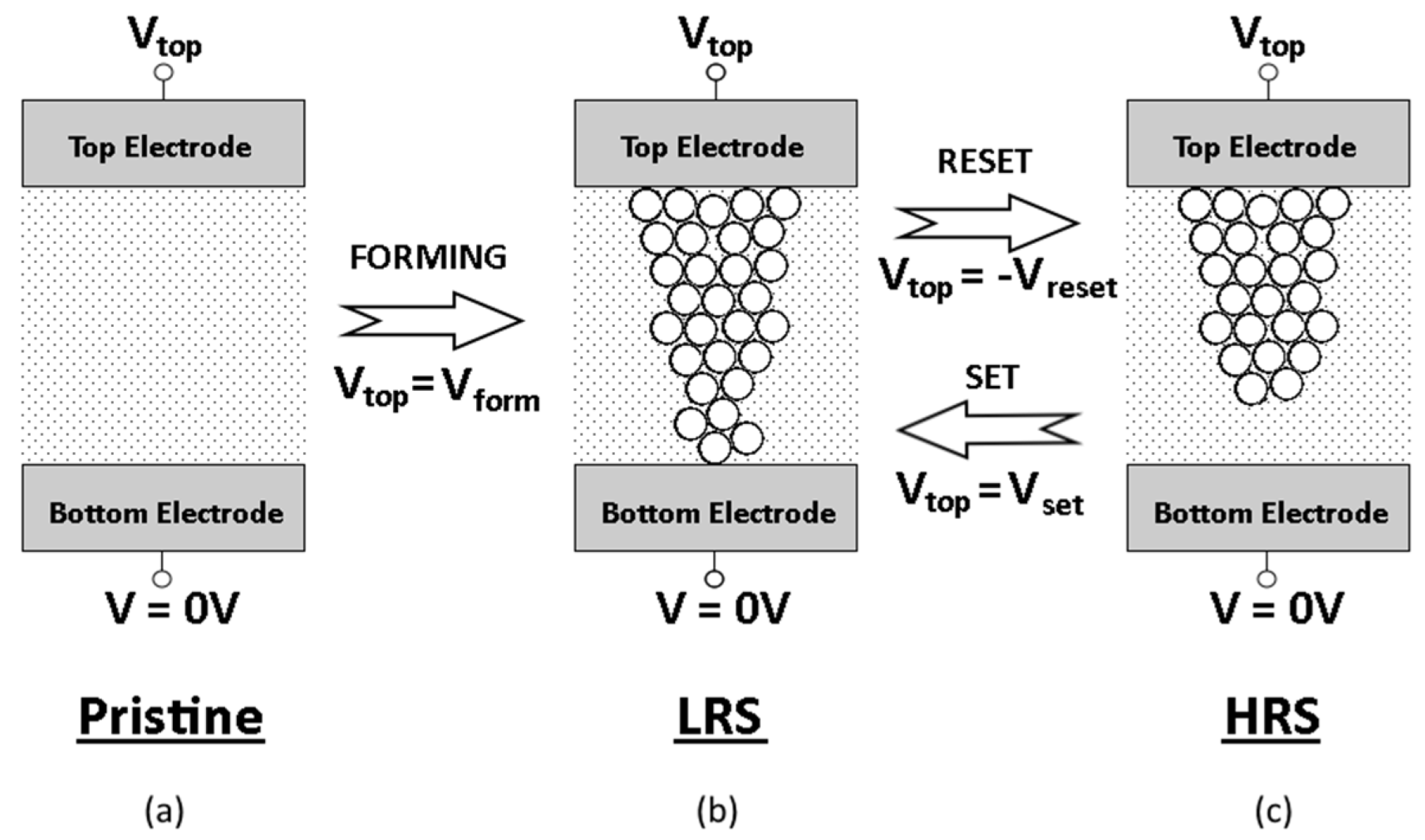
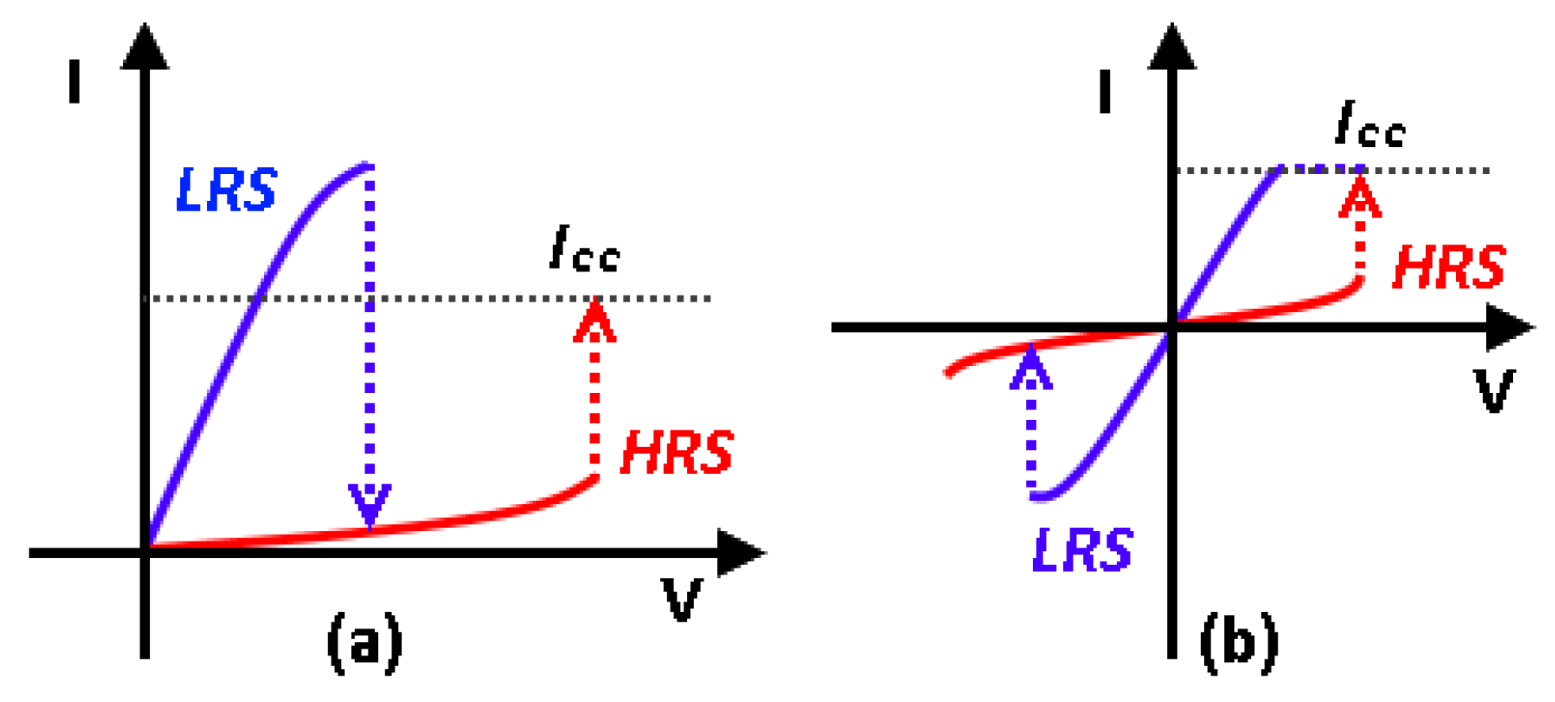
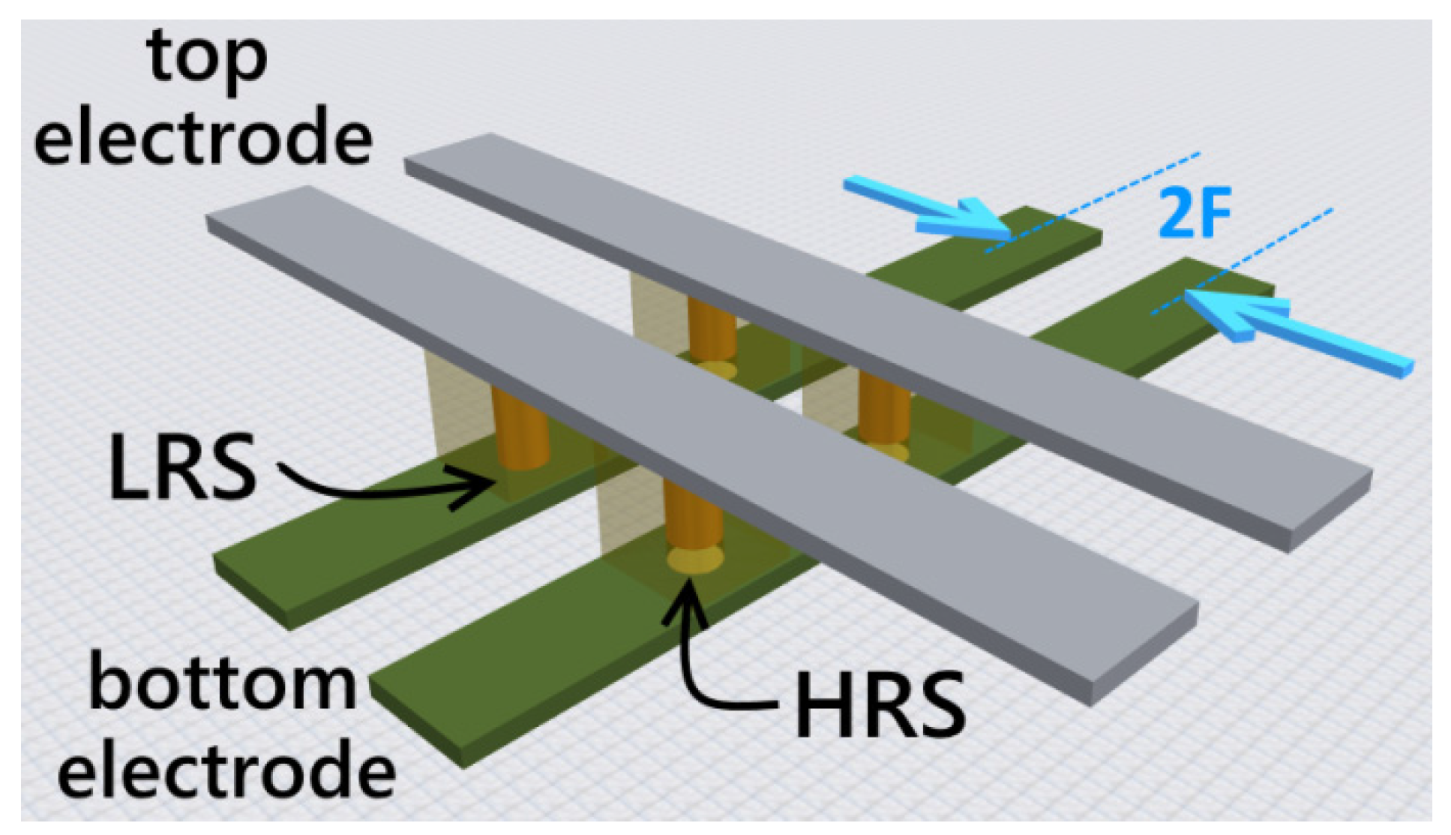
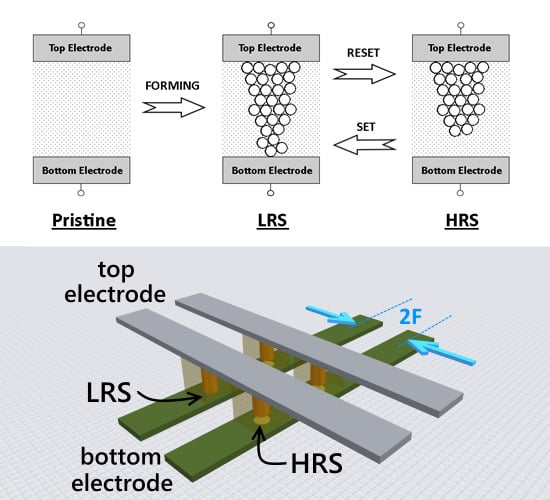
3. Typical Conduction Mechanism in Resistive Switching Memory
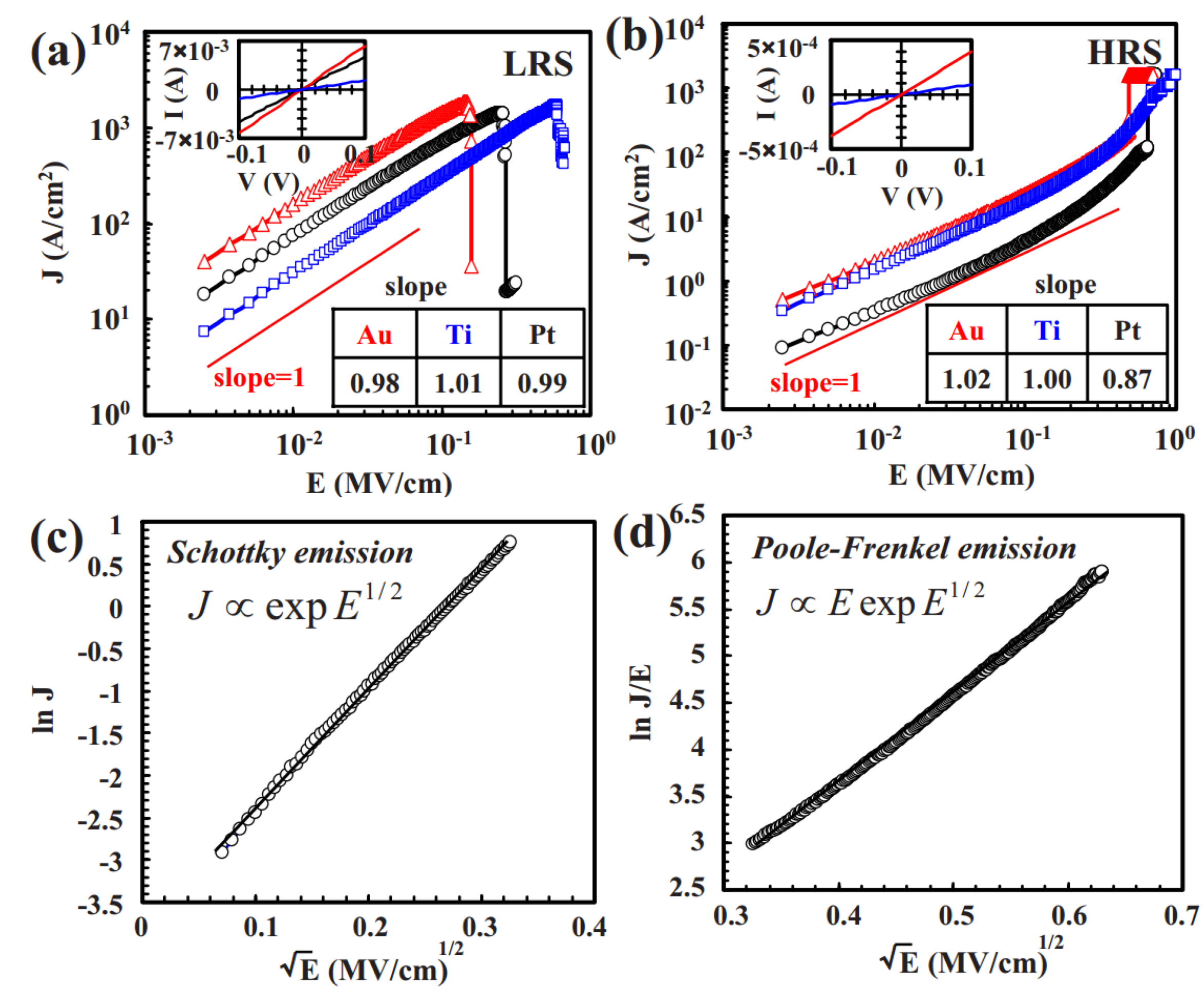
3.1. Schottky Emission
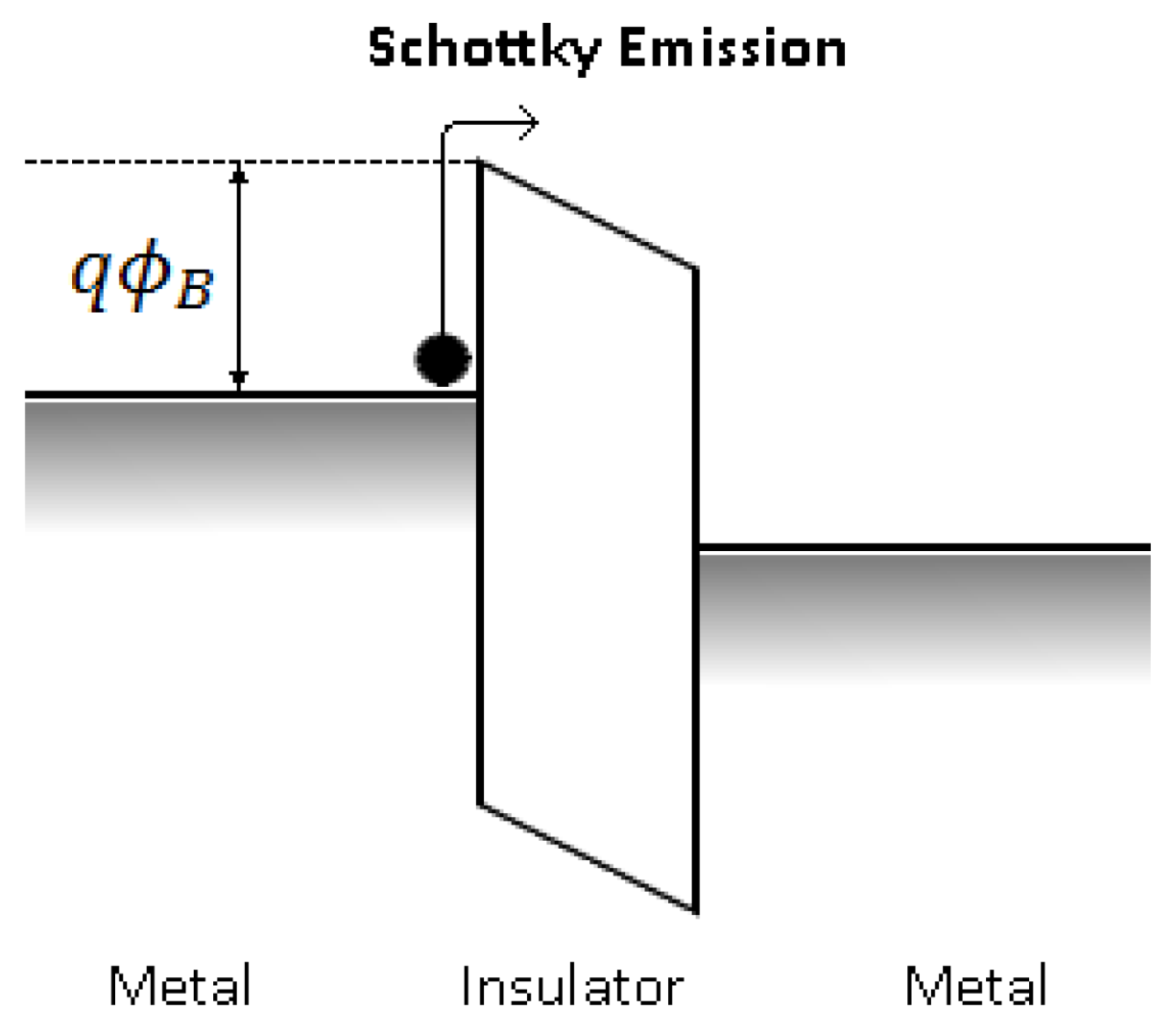
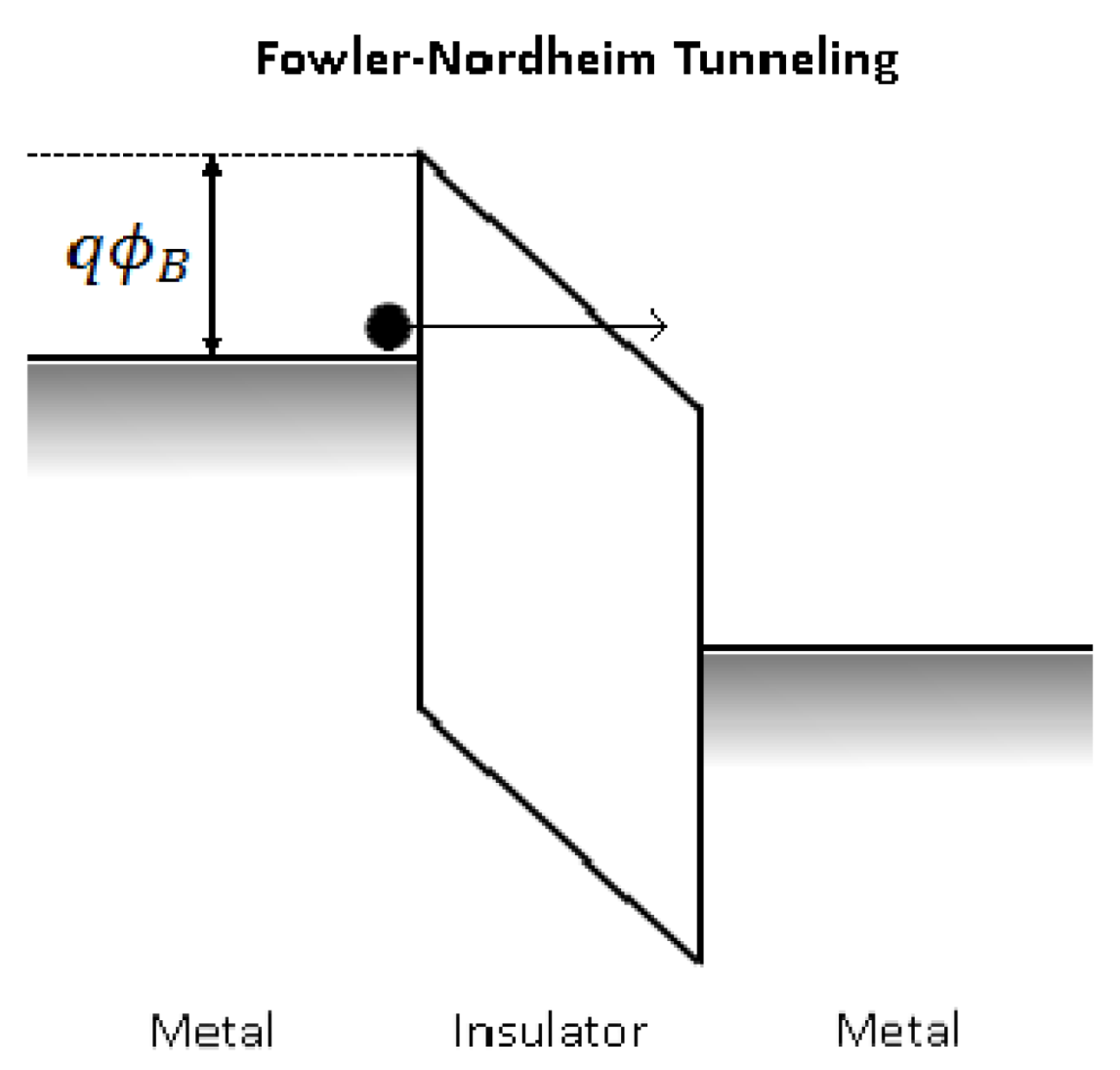
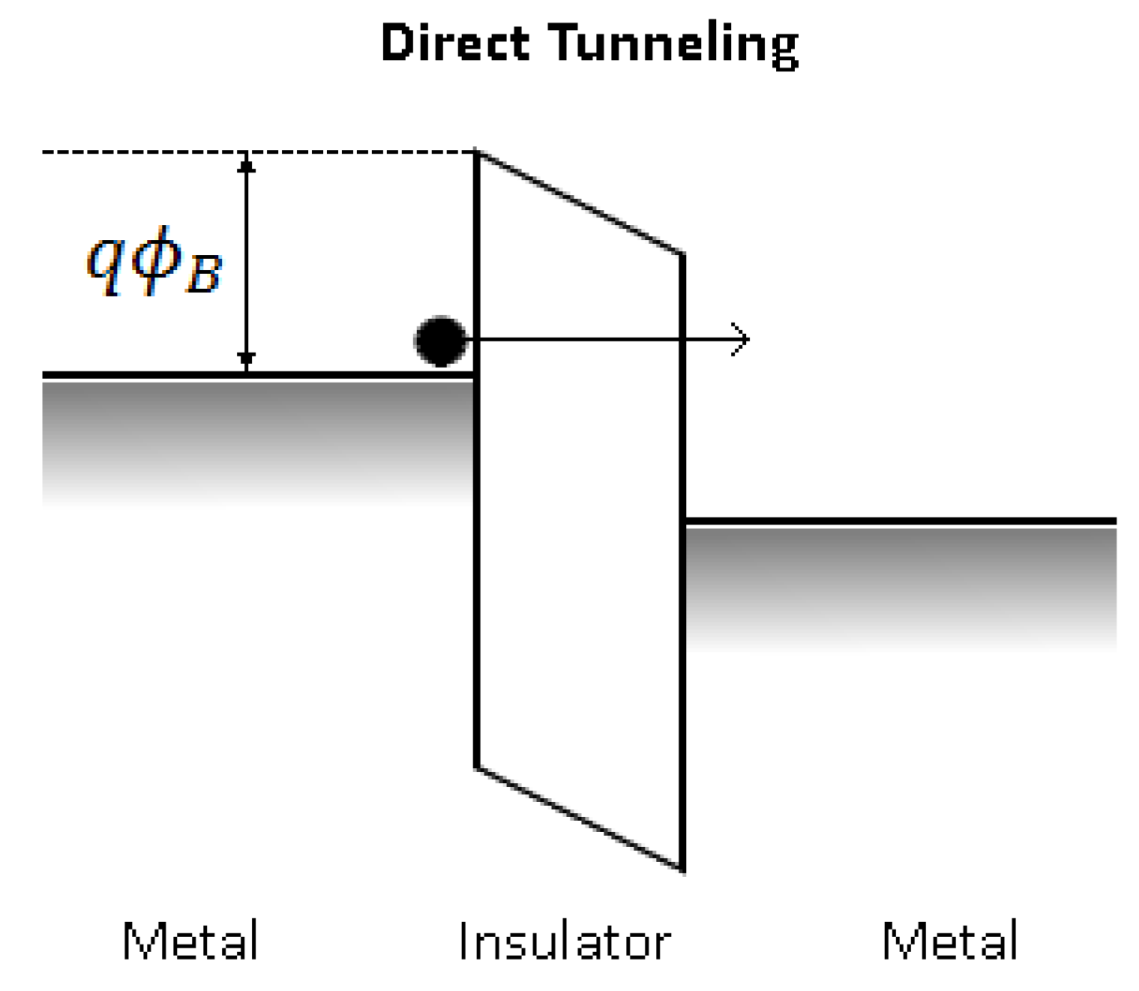
3.2. Fowler-Nordheim (F-N) and Direct Tunneling
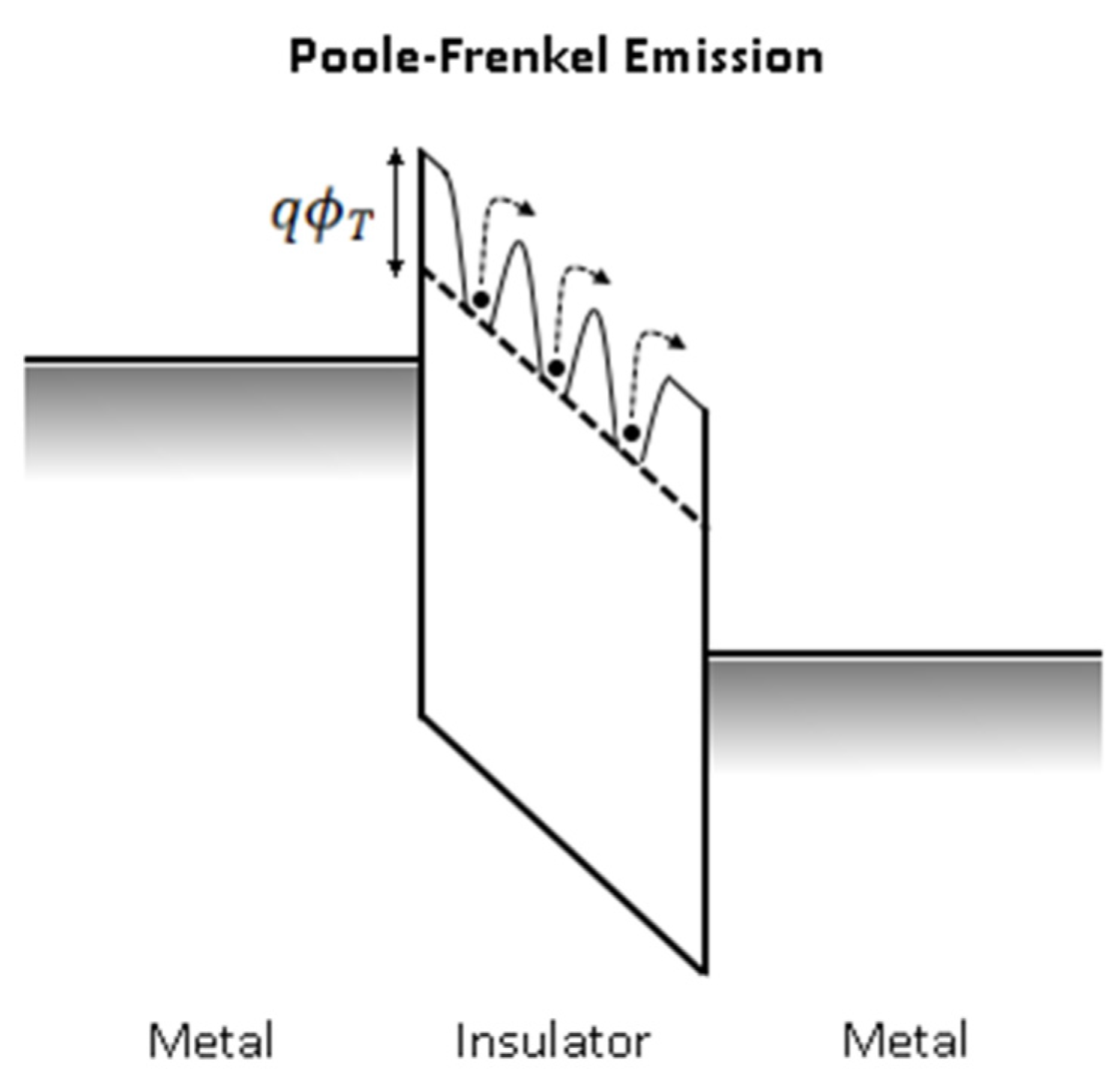
3.3. Poole-Frenkel (P-F) Emission
3.4. Space-Charge-Limited-Conduction (SCLC)
3.5. Ionic Conduction
3.6. Ohmic Conduction
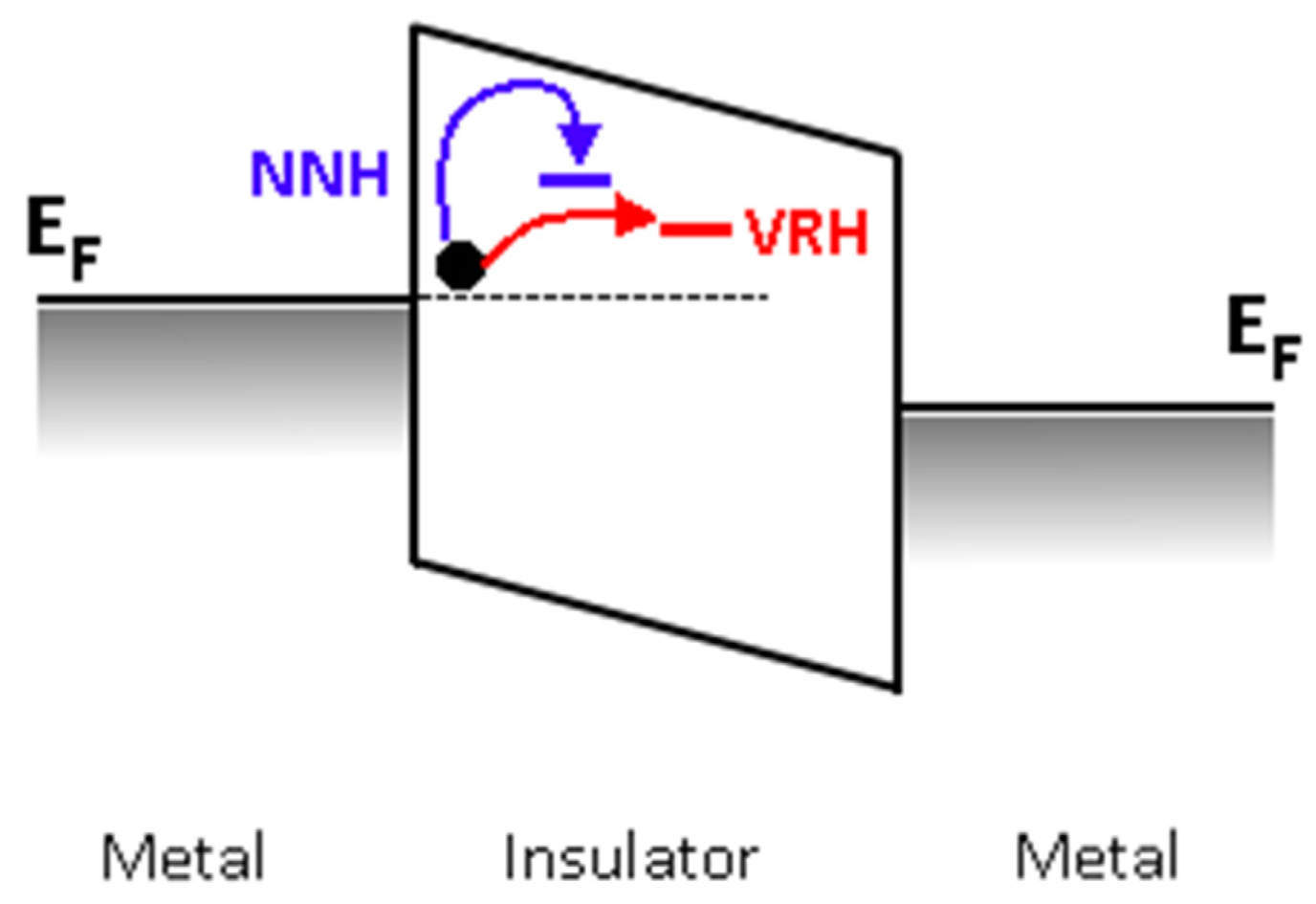
3.7. Nearest Neighbor Hopping (NNH)
3.8. Mott Variable Range Hopping (VRH)
3.9. Trap-Assisted Tunneling (TAT)
3.10. Summary
| Conduction Mechanism | Current Density Expression | Electric Field and Temperature Dependency b |
|---|---|---|
| Schottky Emission | ||
| Fowler-Nordheim (F-N) Tunneling | ||
| Direct Tunneling | ||
| Poole-Frenkel (P-F) Emission | ||
| Space-charge-limited Conduction (SCLC) a | ||
| Ionic Conduction | ||
| Ohmic Conduction | ||
| Nearest Neighbor Hopping (NNH) | ||
| Variable-range Hopping (VRH) | ||
| Trap-assisted Tunneling (TAT) |
4. Conduction Mechanism of Published Resistive Switching Memories
4.1. Poole-Frenkel (P-F) Emission
| Reference | Electrode/Material(s)/Electrode | Conduction Mechanism | ||
|---|---|---|---|---|
| LRS | HRS | |||
| Low V | High V | |||
| Nagashima et al., 2009 [24] | {Pt,Au,Ti}/SnO2/Pt | SE | P-F | |
| Lee et al., 2009 [25] | Au/ZnO/SS | Ohmic | Ohmic | P-F |
| Chan et al., 2012 [26] | Al/ZnO/Si | SCLC | P-F | |
| Kim et al., 2014 [27] | Al/N-AlOx/Al | P-F | P-F | |
| Sharma et al., 2014 [102] | Pt/SmGdO3/Pt | Ohmic | P-F | |
| Ismail et al., 2015 [28] | TaN/CeOx/Pt | Ohmic | P-F | |
| Hong et al., 2015 [29] | Ti/WOx/Pt | Ohmic | Ohmic | P-F |
| Sharma et al., 2015 [30] | Pt/LaHoO3/Pt | Ohmic | P-F | |
| Mahapatra et al., 2015 [31] | Au/HfOx/TiOx/HfOx/Pt | Ohmic | P-F | |
| Guo et al., 2015 [32] | Pt/Ga2O3−x/Pt | Ohmic | Ohmic | P-F |
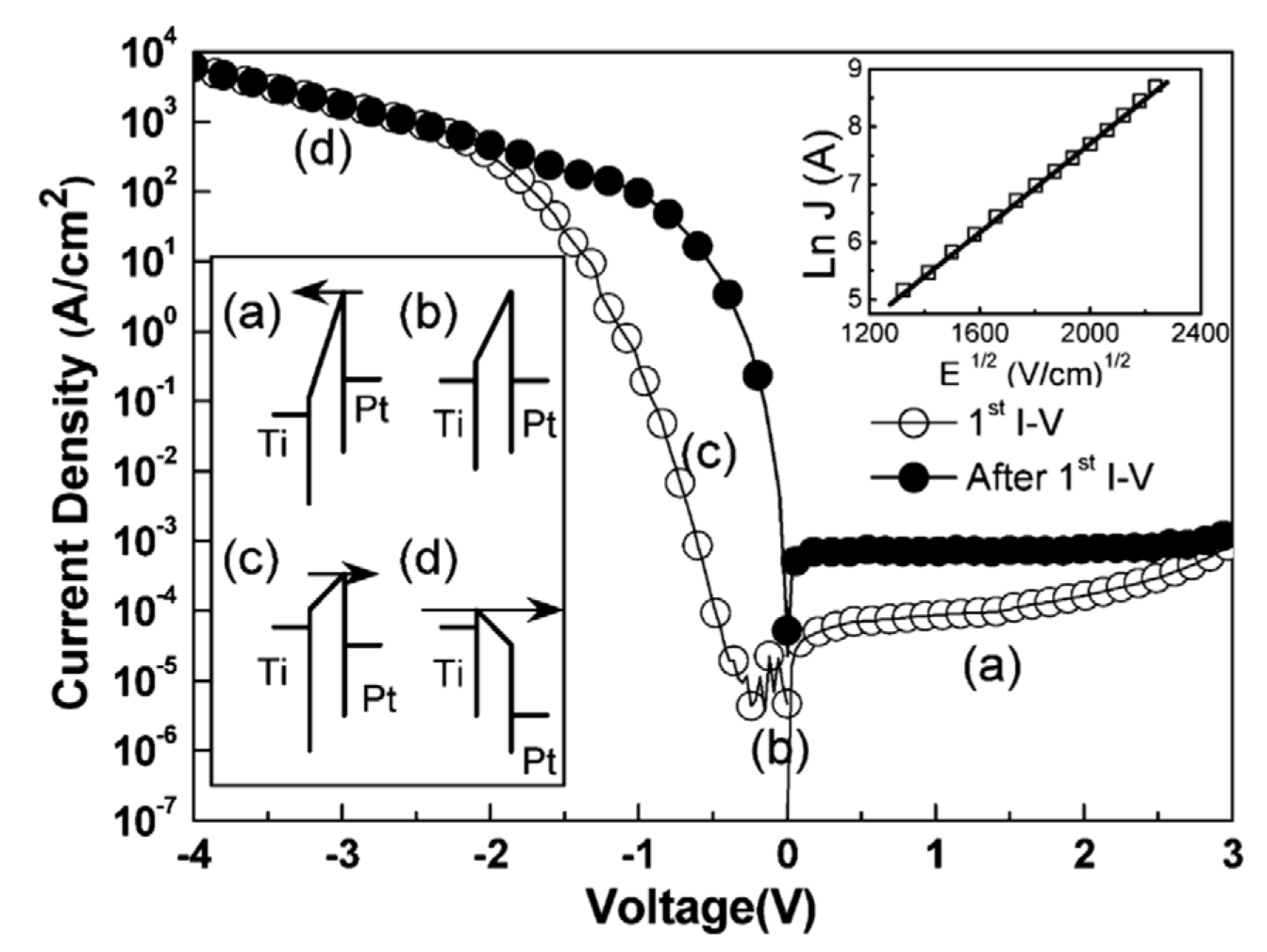
4.2. Schottky Emission
| Reference | Electrode/Material(s)/Electrode | Conduction Mechanism | ||
|---|---|---|---|---|
| LRS | HRS | |||
| Low V | High V | |||
| Cao et al., 2009 [33] | Pt/TiO2/Pt | Ohmic | Ohmic | |
| Huang et al., 2010 [34] | Ti/TiO2/Pt | SE | SE | |
| Lee et al., 2012 [35] | TiN/Ti/TiOx/HfOx/TiN | SE | SE | |
| Zhu et al. 2012 [36] | Al/anodic AlOx/Al | Ohmic | Both P-F and SE | |
| Syu et al., 2013 [37] | Ti/HfO/TiN | Ohmic | SE | |
| Kuo et al., 2014 [38] | Al/VOx/Cu | Ohmic | SE | |
| Zhang et al., 2014 [39] | ITO/Gd:SiO2/TiN | SE | SE | |
| Zhong et al., 2014 [40] | Cu/SiC/Au | Ohmic | SE | P-F |
| Mondal et al., 2014 [42] | Ni/Sm2O3/ITO | Ohmic | SE | |
| Hsieh et al., 2015 [41] | Ni/ZnO/HfO2/Ni | Ohmic | SE | |
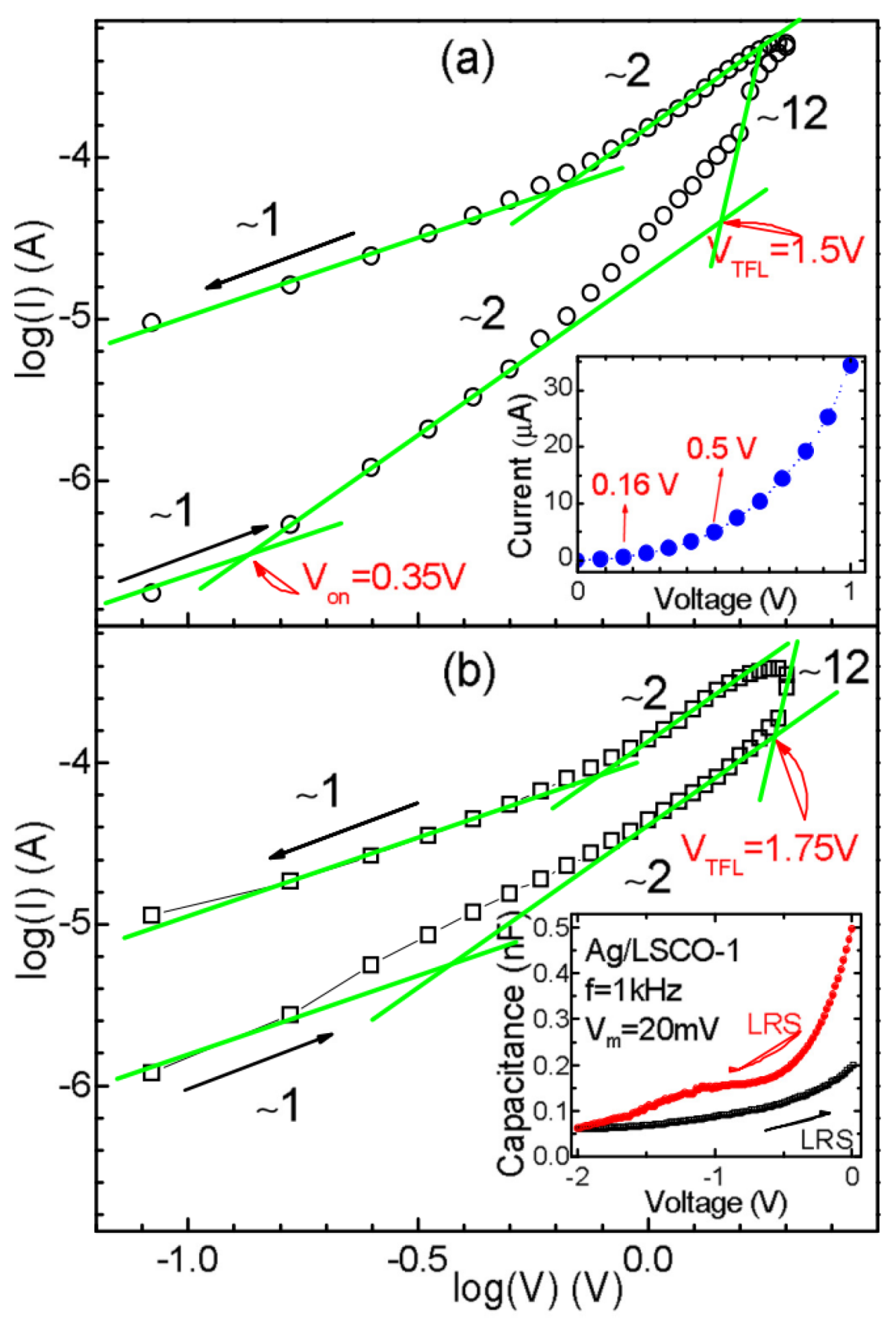
4.3. Space Charge Limited Conduction (SCLC)
| Reference | Electrode/Material(s)/Electrode | Conduction Mechanism | |
|---|---|---|---|
| LRS | HRS | ||
| Yu et al., 2008 [43] | Al/TiOx/Al | SCLC | SCLC |
| Liu et al., 2008 [44] | Au/Cr/Zr+ implanted ZrO2/Si | SCLC and Ohmic | SCLC |
| Peng et al., 2009 [45] | Au/ZnMn2O4/Pt Au/ZnMnO3/Pt | Ohmic | SCLC |
| Wang et al., 2010 [46] | Ti/CuxO/Pt | SCLC | SCLC |
| Kim et al., 2010 [47] | Al/TiOx/TiO2/Al | SCLC | SCLC |
| Lee et al., 2009 [48] | TiN/AlCu/HfOx/TiN | SCLC | SCLC |
| Lee et al., 2010 [49] | TiN/Ti/HfOx/TiN | SCLC | SCLC |
| Chen et al., 2010 [50] | Cu/AlN/Pt | Ohmic | SCLC |
| Mondel et al., 2014 [42] | Ni/Lu2O3/ITO | Ohmic | SCLC |
| Fu et al., 2014 [51] | Ag/La0.5Sr0.5CoO3/Pt | SCLC | SCLC |
| Ismail et al., 2014 [52] | Zr/CeOx/Pt | Ohmic | SCLC |
| Zeng et al., 2014 [53] | Pt/ZrO2/TiO2/Pt | Ohmic | SCLC |
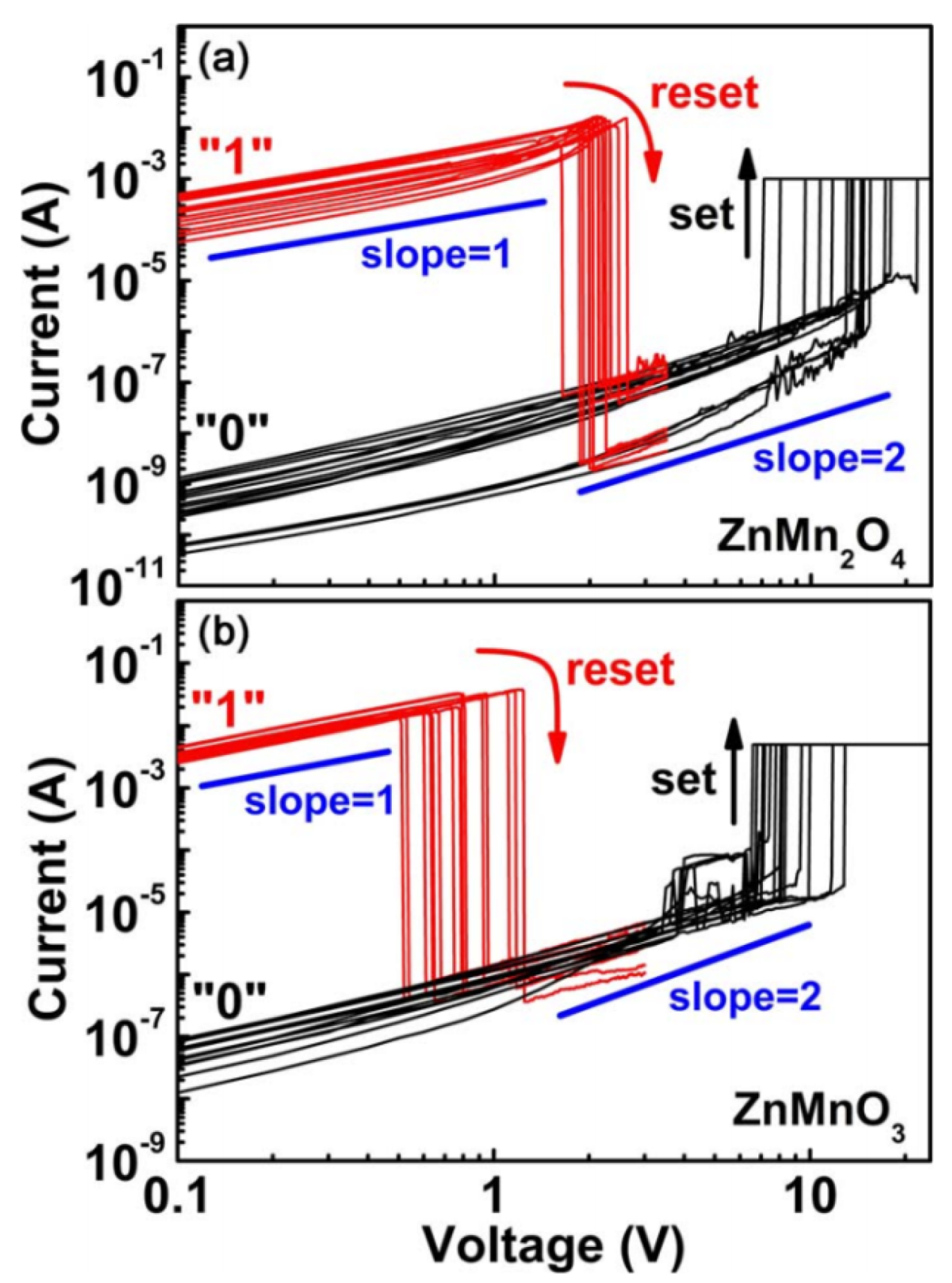
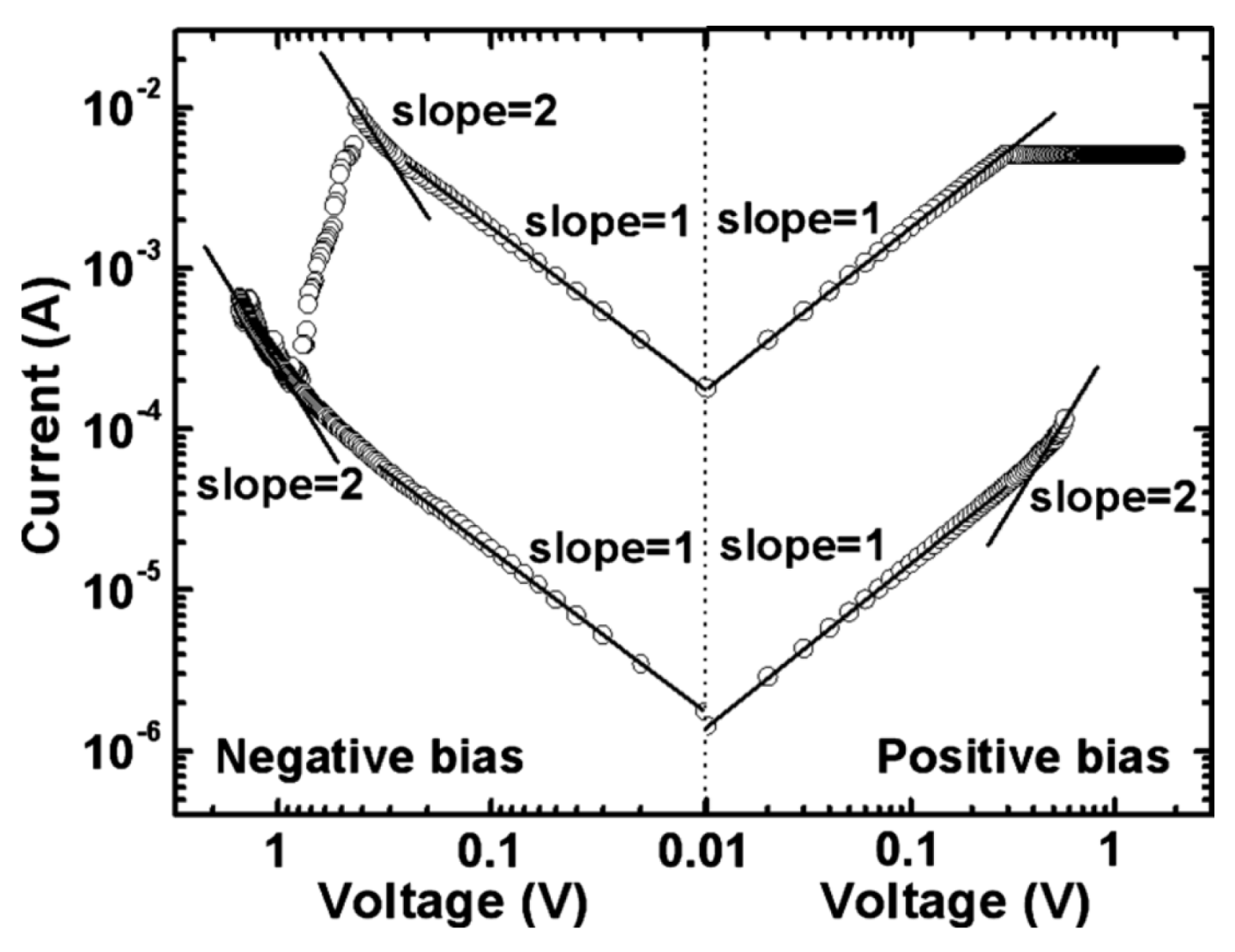
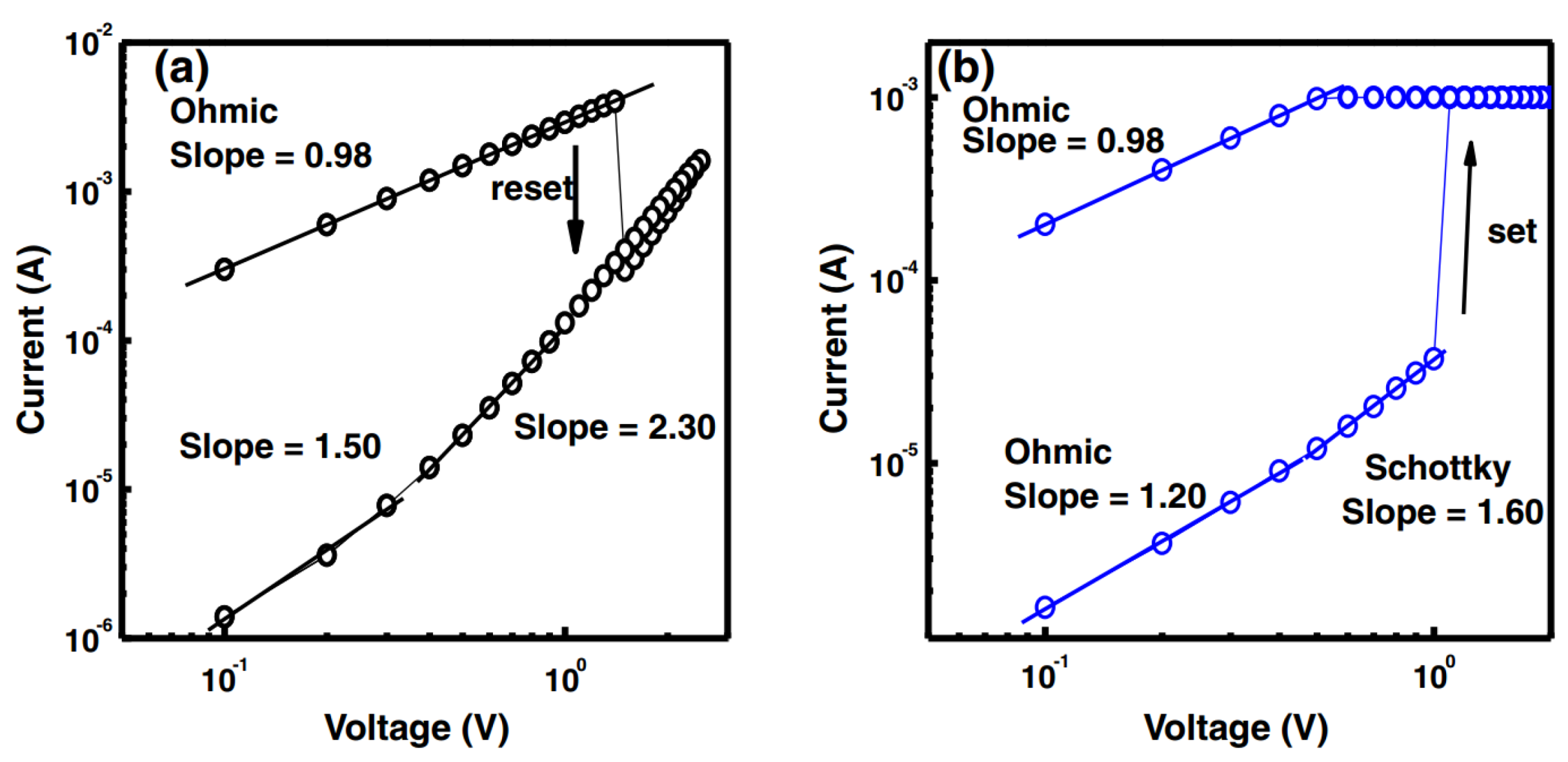
4.4. Trap-Assisted Tunneling (TAT)
| Reference | Electrode/Material(s)/Electrode | Conduction Mechanism | |
|---|---|---|---|
| LRS | HRS | ||
| Bersuker et al., 2011 [54] | TiN/HfO2/TiN | Ohmic | TAT |
| Yu et al., 2011 [55] | TiN/HfOx/Pt | TAT | TAT |
| Long et al., 2012 [56] | Ru/HfO2/TiOx/Ru | Ohmic | TAT(Low T), P-F(High T) |
| Jeon et al., 2014 [57] | Pt/TaOx/TaON/Pt | Ohmic | P-F and TAT |
| Mehonic et al., 2012 [58] | ITO/SiOx/p-type Si/Cr | TAT | F-N and TAT |
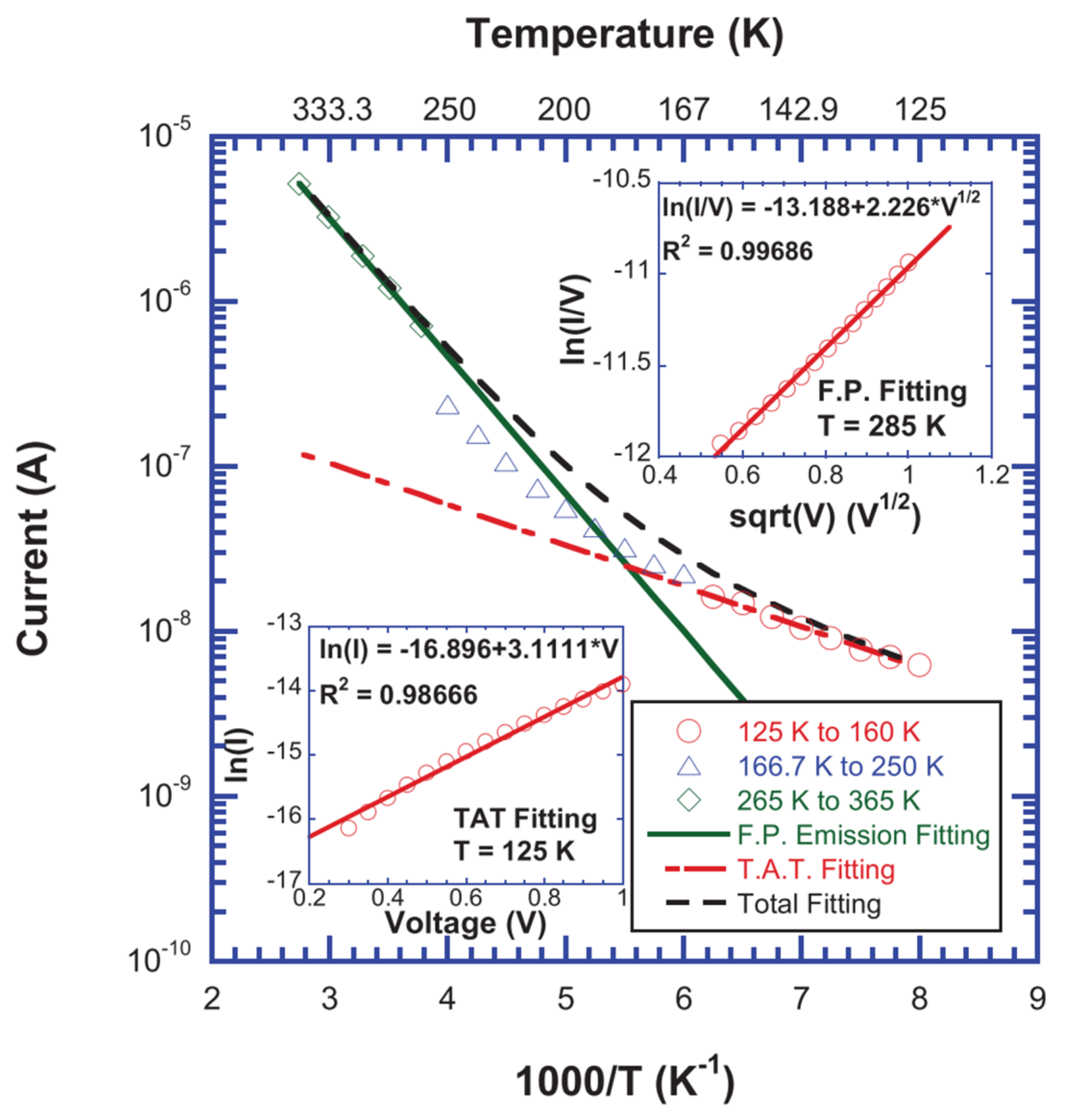
4.5. Hopping Conduction
| Reference | Electrode/Material(s)/Electrode | Conduction Mechanism | |
|---|---|---|---|
| LRS | HRS | ||
| Ho et al., 2007 [60] | TiN/WOx/W | Ohmic | VRH |
| Wei et al., 2011 [61] | Ir/Ta2O5−σ/TaOx/TaN | FRH(high T), VRH(low T) | |
| Phan et al., 2012 [62] | Pt/Cr-SrTiO3/La0.5Sr0.5CoO3 | VRH(V>0), SCLC(V | |
| Sekar et al., 2014 [63] | TiN/TaOx/HfO2/TiN | VRH | NNH |
| Zhang et al., 2014 [64] | Pt/TaOy/Ta2O5−x/Pt | NNH(high T), VRH(low T) | |
| Fang et al., 2015 [65] | Pt/HfOx/TiN | NNH(high T), VRH(low T) | |
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Pan, F.; Gao, S.; Chen, C.; Song, C.; Zeng, F. Recent progress in resistive random access memories: Materials, switching mechanisms, and performance. Mater. Sci. Eng. R. Rep. 2014, 83, 1–59. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Salahuddin, S. Memory leads the way to better computing. Nat. Nanotechnol. 2015, 10, 191–194. [Google Scholar] [CrossRef] [PubMed]
- Choi, B.J.; Torrezan, A.C.; Norris, K.J.; Miao, F.; Strachan, J.P.; Zhang, M.X.; Ohlberg, D.A.A.; Kobayashi, N.P.; Yang, J.J.; Williams, R.S. Electrical Performance and Scalability of Pt Dispersed SiO2 Nanometallic Resistance Switch. Nano Lett. 2013, 13, 3213–3217. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.J.; Lee, C.B.; Lee, D.; Lee, S.R.; Chang, M.; Hur, J.H.; Kim, Y.B.; Kim, C.J.; Seo, D.H.; Seo, S.; et al. A fast, high-endurance and scalable non-volatile memory device made from asymmetric Ta2O5−x/TaO2−x bilayer structures. Nat. Mater. 2011, 10, 625–630. [Google Scholar] [CrossRef] [PubMed]
- Wei, Z.; Kanzawa, Y.; Arita, K.; Katoh, Y.; Kawai, K.; Muraoka, S.; Mitani, S.; Fujii, S.; Katayama, K.; Iijima, M.; et al. Highly reliable TaOx ReRAM and direct evidence of redox reaction mechanism. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008.
- Chien, W.C.; Chen, Y.C.; Lee, F.M.; Lin, Y.Y.; Lai, E.K.; Yao, Y.; der Gong, J.; Horng, S.F.; Yeh, C.W.; Tsai, S.C.; et al. A novel Ni/WOx/W resistive random access memory with excellent retention and low switching current. Jpn. J. Appl. Phys. 2011. [Google Scholar] [CrossRef]
- Wang, X.P.; Fang, Z.; Li, X.; Chen, B.; Gao, B.; Kang, J.F.; Chen, Z.X.; Kamath, A.; Shen, N.S.; Singh, N.; et al. Highly compact 1T-1R architecture (4F2 footprint) involving fully CMOS compatible vertical GAA nano-pillar transistors and oxide-based RRAM cells exhibiting excellent NVM properties and ultra-low power operation. In Proceedings of the IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2008; Volume 6, pp. 493–496.
- Meng, Y.; Xue, X.Y.; Song, Y.L.; Yang, J.G.; Chen, B.A.; Lin, Y.Y.; Zou, Q.T.; Huang, R.; Wu, J.G. Fast Step-Down Set Algorithm of Resistive Switching Memory with Low Programming Energy and Significant Reliability Improvement. In Proceedings of the 2014 Symposium on VLSI Technology (VLSI-Technology): Digest of Technical Papers, Honolulu, HI, USA, 9–12 June 2014.
- Lee, S.; Sohn, J.; Chen, H.; Wong, H.P. Metal Oxide Resistive Memory using Graphene Edge Electrode. 2015. Available online: http://www.arxiv.org/abs/1502.02675 (accessed on 30 June 2015).
- Sharma, Y.; Misra, P.; Katiyar, R.S. Unipolar resistive switching behavior of amorphous YCrO3 films for nonvolatile memory applications. J. Appl. Phys. 2014. [Google Scholar] [CrossRef]
- Misra, P.; Pavunny, S.P.; Sharma, Y.; Katiyar, R.S. Resistive Switching and Current Conduction Mechanisms in Amorphous LaLuO3 Thin Films Grown by Pulsed Laser Deposition. Integr. Ferroelectr. 2014, 157, 47–56. [Google Scholar] [CrossRef]
- Lanza, M. A review on resistive switching in high-k dielectrics: A nanoscale point of view using conductive atomic force microscope. Materials 2014, 7, 2155–2182. [Google Scholar] [CrossRef]
- Dai, Y.; Zhao, Y.; Wang, J.; Xu, J.; Yang, F. First principle simulations on the effects of oxygen vacancy in HfO2-based RRAM. AIP Adv. 2015. [Google Scholar] [CrossRef]
- Waser, R. Redox-based resistive switching memories. J. Nanosci. Nanotechnol. 2012, 12, 7628–7640. [Google Scholar] [CrossRef] [PubMed]
- Yu, S. Overview of Resistive Switching Memory (RRAM) Switching Mechanism and Device Modeling. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne VIC, Australia, 1–5 June 2014; pp. 2017–2020.
- Guan, X.; Yu, S.; Wong, H.S.P. A SPICE compact model of metal oxide resistive switching memory with variations. IEEE Electron Device Lett. 2012, 33, 1405–1407. [Google Scholar] [CrossRef]
- Ielmini, D. Modeling the universal set/reset characteristics of bipolar RRAM by field- and temperature-driven filament growth. IEEE Trans. Electron Devices 2011, 58, 4309–4317. [Google Scholar] [CrossRef]
- Huang, P.; Member, S.; Wang, Y.; Li, H.; Member, S.; Gao, B.; Chen, B.; Member, S.; Zhang, F.; Zeng, L.; et al. Analysis of the Voltage—Time Dilemma of Metal Oxide-Based RRAM and Solution Exploration of High Speed and Low Voltage AC Switching. Nanotechnol. IEEE Trans. 2014, 13, 1127–1132. [Google Scholar] [CrossRef]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833–840. [Google Scholar] [CrossRef] [PubMed]
- Waser, R.; Menzel, S.; Rana, V. Recent progress in redox-based resistive switching. In Proceedings of the 2012 IEEE International Symposium on Circuits and Systems (ISCAS), Seoul, Korea, 20–23 May 2012; pp. 1596–1599.
- Blasco, J.; Ghenzi, N.; Suñé, J.; Levy, P.; Miranda, E. Equivalent circuit modeling of the bistable conduction characteristics in electroformed thin dielectric films. Microelectron. Reliab. 2015, 55, 1–14. [Google Scholar] [CrossRef]
- Yu, S.; Lee, B.; Wong, H.S.P. Metal Oxide Resistve Switching Memory. In Functional Metal Oxide Nanostructures; Wu, J., Cao, J., Han, W.-Q., Janotti, A., Kim, H.-C., Eds.; Springer: Berlin, Germany, 2012; Volume 149, pp. 269–302. [Google Scholar]
- Wang, L.; Yang, C.H.; Wen, J. Physical principles and current status of emerging non-volatile solid state memories. Electron. Mater. Lett. 2015, 11, 505–543. [Google Scholar] [CrossRef]
- Nagashima, K.; Yanagida, T.; Oka, K.; Kawai, T. Unipolar resistive switching characteristics of room temperature grown SnO2 thin films. Appl. Phys. Lett. 2009, 94, 1–4. [Google Scholar] [CrossRef]
- Lee, S.; Kim, H.; Yun, D.J.; Rhee, S.W.; Yong, K. Resistive switching characteristics of ZnO thin film grown on stainless steel for flexible nonvolatile memory devices. Appl. Phys. Lett. 2009. [Google Scholar] [CrossRef]
- Chen, C.; Pan, F.; Wang, Z.S.; Yang, J.; Zeng, F. Bipolar resistive switching with self-rectifying effects in Al/ZnO/Si structure. J. Appl. Phys. 2012. [Google Scholar] [CrossRef]
- Kim, W.; Park, S.I.L.; Zhang, Z.; Wong, S. Current Conduction Mechanism of Nitrogen-Doped AlOx RRAM. IEEE Trans. Electron Devices 2014, 61, 2158–2163. [Google Scholar] [CrossRef]
- Ismail, M.; Ahmed, E.; Rana, A.M.; Talib, I.; Khan, T.; Iqbal, K.; Nadeem, M.Y. Role of tantalum nitride as active top electrode in electroforming-free bipolar resistive switching behavior of cerium oxide-based memory cells. Thin Solid Films 2015, 583, 95–101. [Google Scholar] [CrossRef]
- Hong, S.M.; Kim, H.D.; Yun, M.J.; Park, J.H.; Jeon, D.S.; Kim, T.G. Improved resistive switching properties by nitrogen doping in tungsten oxide thin films. Thin Solid Films 2015, 583, 81–85. [Google Scholar] [CrossRef]
- Sharma, Y.; Misra, P.; Pavunny, S.P.; Katiyar, R.S. Unipolar resistive switching behavior of high-k ternary rare-earth oxide LaHoO 3 thin films for non-volatile memory applications. In Proceedings of the MRS, Boston, MA, USA, 30 November–5 December 2014; Volume 1729.
- Mahapatra, R.; Maji, S.; Horsfall, A.B.; Wright, N.G. Temperature impact on switching characteristics of resistive memory devices with HfOx/TiOx/HfOx stack dielectric. Microelectron. Eng. 2015, 138, 118–121. [Google Scholar] [CrossRef]
- Guo, D.Y.; Wu, Z.P.; An, Y.H.; Li, P.G.; Wang, P.C.; Chu, X.L.; Guo, X.C.; Zhi, Y.S.; Lei, M.; Li, L.H.; et al. Unipolar resistive switching behavior of amorphous gallium oxide thin films for nonvolatile memory applications. Appl. Phys. Lett. 2015. [Google Scholar] [CrossRef]
- Cao, X.; Li, X.M.; Gao, X.D.; Zhang, Y.W.; Liu, X.J.; Wang, Q.; Chen, L.D. Effects of the compliance current on the resistive switching behavior of TiO2 thin films. Appl. Phys. A Mater. Sci. Process. 2009, 97, 883–887. [Google Scholar] [CrossRef]
- Huang, J.J.; Kuo, C.W.; Chang, W.C.; Hou, T.H. Transition of stable rectification to resistive-switching in Ti/TiO2/Pt oxide diode. Appl. Phys. Lett. 2010. [Google Scholar] [CrossRef]
- Lee, J.; Jung, S.; Park, J.; Chung, S.; Sung, J.; Lee, J.; Jung, S.; Park, J.; Chung, S.; Roh, J.S. Accurate analysis of conduction and resistive-switching mechanisms in double-layered resistive-switching memory devices. Appl. Phys. Lett. 2012, 101, 1–5. [Google Scholar] [CrossRef]
- Zhu, W.; Chen, T.P.; Liu, Y.; Fung, S. Conduction mechanisms at low- and high-resistance states in aluminum/anodic aluminum oxide/aluminum thin film structure. J. Appl. Phys. 2012, 112, 9–14. [Google Scholar] [CrossRef]
- Syu, Y.; Chang, T.; Lou, J.; Tsai, T.; Chang, K.; Tsai, M.; Wang, L.; Liu, M.; Sze, S.M. Atomic-level quantized reaction of HfOx memristor. Appl. Phys. Lett. 2013. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, K.; Wang, F.; Sun, W.; Lu, T.; Wang, B.; Cheng, W. An Increasing High Resistance State Phenomenon in Al/VO. ECS Trans. 2014, 60, 1057–1062. [Google Scholar] [CrossRef]
- Zhang, R.; Chang, K.C.; Chang, T.C.; Tsai, T.M.; Huang, S.Y.; Chen, W.J.; Chen, K.H.; Lou, J.C.; Chen, J.H.; Young, T.F.; et al. Characterization of oxygen accumulation in indium-tin-oxide for resistance random access memory. IEEE Electron Device Lett. 2014, 35, 630–632. [Google Scholar]
- Zhong, L.; Reed, P.A.; Huang, R.; de Groot, C.H.; Jiang, L. Resistive switching of Cu/SiC/Au memory devices with a high ON/OFF ratio. Solid State Electron. 2014, 94, 98–102. [Google Scholar] [CrossRef]
- Hsieh, W.K.; Lam, K.T.; Chang, S.J. Bipolar Ni/ZnO/HfO2/Ni RRAM with multilevel characteristic by different reset bias. Mater. Sci. Semicond. Process. 2015, 35, 30–33. [Google Scholar] [CrossRef]
- Mondal, S.; Chueh, C.H.; Pan, T.M. Current conduction and resistive switching characteristics of Sm2O3 and Lu2O3 thin films for low-power flexible memory applications. J. Appl. Phys. 2014. [Google Scholar] [CrossRef]
- Yu, L.E.; Kim, S.; Ryu, M.K.; Choi, S.Y.; Choi, Y.L. Structure Effects on Resistive Switching of Al/TiOx/Al Device for RRAM Applications. IEEE Electron Device Lett. 2008, 29, 331–333. [Google Scholar]
- Liu, Q.; Guan, W.; Long, S.; Jia, R.; Liu, M.; Chen, J. Resistive switching memory effect of ZrO2 films with Zr+ implanted. Appl. Phys. Lett. 2008, 92, 4–6. [Google Scholar] [CrossRef]
- Peng, H.; Wu, T. Nonvolatile resistive switching in spinel ZnMn2O4 and ilmenite ZnMnO3. Appl. Phys. Lett. 2009, 95, 10–13. [Google Scholar] [CrossRef]
- Wang, S.Y.; Huang, C.W.; Lee, D.Y.; Tseng, T.Y.; Chang, T.C. Multilevel resistive switching in Ti/CuxO/Pt memory devices. J. Appl. Phys. 2010. [Google Scholar] [CrossRef]
- Kim, S.; Jeong, H.Y.; Choi, S.Y.; Choi, Y.K. Comprehensive modeling of resistive switching in the Al/TiOx/TiO2/Al heterostructure based on space-charge-limited conduction. Appl. Phys. Lett. 2010, 97, 2–4. [Google Scholar]
- Lee, H.Y.; Chen, P.S.; Wu, T.Y.; Chen, Y.S.; Chen, F.; Wang, C.C.; Tzeng, P.J.; Lin, C.H.; Tsai, M.J.; Lien, C. HfOx bipolar resistive memory with robust endurance using AlCu as buffer electrode. IEEE Electron Device Lett. 2009, 30, 703–705. [Google Scholar]
- Lee, H.Y.; Chen, Y.S.; Chen, P.S.; Wu, T.Y.; Chen, F.; Wang, C.C.; Tzeng, P.J.; Tsai, M.J.; Lien, C. Low-power and nanosecond switching in robust hafnium oxide resistive memory with a thin Ti cap. IEEE Electron Device Lett. 2010, 31, 44–46. [Google Scholar] [CrossRef]
- Chen, C.; Yang, Y.C.; Zeng, F.; Pan, F. Bipolar resistive switching in Cu/AlN/Pt nonvolatile memory device. Appl. Phys. Lett. 2010, 97, 8–10. [Google Scholar] [CrossRef]
- Fu, Y.J.; Xia, F.J.; Jia, Y.L.; Jia, C.J.; Li, J.Y.; Dai, X.H.; Fu, G.S.; Zhu, B.Y.; Liu, B.T. Bipolar resistive switching behavior of La0.5Sr0.5CoO3−σ films for nonvolatile memory applications. Appl. Phys. Lett. 2014. [Google Scholar] [CrossRef]
- Ismail, M.; Huang, C.Y.; Panda, D.; Hung, C.J.; Tsai, T.L.; Jieng, J.H.; Lin, C.A.; Chand, U.; Rana, A.M.; Ahmed, E.; et al. Forming-free bipolar resistive switching in nonstoichiometric ceria films. Nanoscale Res. Lett. 2014. [Google Scholar] [CrossRef] [PubMed]
- Zeng, B.; Xu, D.; Tang, M.; Xiao, Y.; Zhou, Y.; Xiong, R.; Li, Z.; Zhou, Y. Improvement of resistive switching performances via an amorphous ZrO2 layer formation in TiO2-based forming-free resistive random access memory. J. Appl. Phys. 2014, 116, 124514. [Google Scholar] [CrossRef]
- Bersuker, G.; Yum, J.; Vandelli, L.; Padovani, A.; Larcher, L.; Iglesias, V.; Porti, M.; Nafría, M.; McKenna, K.; Shluger, A.; et al. Grain boundary-driven leakage path formation in HfO2 dielectrics. Solid State Electron. 2011, 65–66, 146–150. [Google Scholar] [CrossRef]
- Yu, S.M.; Guan, X.M.; Wong, H.S.P. Conduction mechanism of TiN/HfOx/Pt resistive switching memory: A trap-assisted-tunneling model. Appl. Phys. Lett. 2011. [Google Scholar] [CrossRef]
- Long, B.; Li, Y.; Mandal, S.; Jha, R.; Leedy, K. Switching dynamics and charge transport studies of resistive random access memory devices. Appl. Phys. Lett. 2012. [Google Scholar] [CrossRef]
- Jeon, H.; Park, J.; Jang, W.; Kim, H.; Kang, C.; Song, H.; Seo, H.; Jeon, H.; Park, J.; Jang, W.; et al. Resistive switching of a TaOx/TaON double layer via ionic control of carrier tunneling. Appl. Phys. Lett. 2014. [Google Scholar] [CrossRef]
- Mehonic, A.; Cueff, S.; Wojdak, M.; Hudziak, S.; Jambois, O.; Labbé, C.; Garrido, B.; Rizk, R.; Kenyon, A.J. Resistive switching in silicon suboxide films. J. Appl. Phys. 2012. [Google Scholar] [CrossRef]
- Mehonic, A.; Cueff, S.; Wojdak, M.; Hudziak, S.; Labbé, C.; Rizk, R.; Kenyon, A.J. Electrically tailored resistance switching in silicon oxide. Nanotechnology 2012. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.; Lai, E.K.; Lee, M.D.; Pan, C.L.; Yao, Y.D.; Hsieh, K.Y.; Liu, R.; Lu, C.Y. A highly reliable self-aligned graded oxide WOx resistance memory: Conduction mechanisms and reliability. In Proceedings of the 2007 IEEE Symposium on VLSI Technology, Kyoto, Japan, 12–14 June 2007; pp. 228–229.
- Wei, Z.; Takagi, T.; Kanzawa, Y.; Katoh, Y.; Ninomiya, T.; Kawai, K.; Muraoka, S.; Mitani, S.; Katayama, K.; Fujii, S.; et al. Demonstration of high-density ReRAM ensuring 10-year retention at 85 °C based on a newly developed reliability model. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 721–724.
- Phan, B.T.; Choi, T.; Romanenko, A.; Lee, J. Hopping and trap controlled conduction in Cr-doped SrTiO3 thin films. Solid State Electron. 2012, 75, 43–47. [Google Scholar] [CrossRef]
- Sekar, D.C.; Bateman, B.; Raghuram, U.; Bowyer, S.; Bai, Y.; Calarrudo, M.; Swab, P.; Wu, J.; Nguyen, S.; Mishra, N.; et al. Technology and Circuit Optimization of Resistive RAM for Low-Power , Reproducible Operation. In Proceedings of the 2014 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 15–17 December 2014; pp. 657–660.
- Zhang, Y.; Deng, N.; Wu, H.; Yu, Z.; Zhang, J.; Qian, H. Metallic to hopping conduction transition in Ta2O5−x/TaOy resistive switching device. Appl. Phys. Lett. 2014, 105, 063508. [Google Scholar] [CrossRef]
- Fang, R.; Chen, W.; Gao, L.; Yu, W.; Yu, S. Low Temperature Characteristics of HfOx-Based Resistive Random Access Memory. IEEE Electron Device Lett. 2015, 36, 567–569. [Google Scholar] [CrossRef]
- Valov, I. Redox-Based Resistive Switching Memories (ReRAMs): Electrochemical Systems at the Atomic Scale. ChemElectroChem 2014, 1, 26–36. [Google Scholar] [CrossRef]
- Lee, M. Emerging Oxide Resistance Change Memories. In Emerging Non-Volatile Memories; Hong, S., Ed.; Springer: Berlin, Germany, 2014; pp. 195–218. [Google Scholar]
- Chen, Y.C.; Li, H.H.; Zhang, W.; Pino, R.E. The 3-D stacking bipolar RRAM for high density. IEEE Trans. Nanotechnol. 2012, 11, 948–956. [Google Scholar] [CrossRef]
- Yang, J.J.; Zhang, M.X.; Pickett, M.D.; Miao, F.; Strachan, P.J.; Li, W.; di Yi, W.; Ohlberg, D.A.A.; Choi, J.B.; Wu, W.; et al. Engineering nonlinearity into memristors for passive crossbar applications. Appl. Phys. Lett. 2012, 100, 98–102. [Google Scholar]
- Chiu, F.C.; Mondal, S.; Pan, T.M. Structural and Electrical Characteristics of Alternative High-k Dielectric for CMOS Application. In High-k Gate Dielectrics for CMOS Technology; He, G., Sun, Z., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 111–172. [Google Scholar]
- Chiu, F.C. A Review on Conduction Mechanisms in Dielectric Films. Adv. Mater. Sci. Eng. 2014. [Google Scholar] [CrossRef]
- Sharma, Y.; Pavunny, S.P.; Fachini, E.; Scott, J.F.; Katiyar, R.S. Nonpolar resistive memory switching with all four possible resistive switching modes in amorphous ternary rare-earth LaHoO3 thin films. 2015, arXiv: 1505.04690. arXiv.org e-Print archive. Available online: http://www.arxiv.org/abs/1505.04690 (accessed on 30 June 2015).
- Simmons, J.G. Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef]
- Majkusiak, B.; Palestri, P.; Schenk, A.; Spinelli, A.S.; Compagnoni, C.M.; Luisier, M. Modeling and Simulation Approaches for Gate Current Computation. In Nanoscale CMOS; Balestra, F., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 213–257. [Google Scholar]
- Zhu, Y.Q.; Qian, H.; Wang, L.F.; Wang, L.; Tang, J.Y. Measurement and analysis of substrate leakage current of RF mems capacitive switches. Microelectron. Reliab. 2014, 54, 152–159. [Google Scholar] [CrossRef]
- Perera, R.; Ikeda, A.; Hattori, R.; Kuroki, Y. Trap assisted leakage current conduction in thin silicon oxynitride films grown by rapid thermal oxidation combined microwave excited plasma nitridation. Microelectron. Eng. 2003, 65, 357–370. [Google Scholar] [CrossRef]
- Yeo, Y.C.; King, T.J.; Hu, C. Direct tunneling leakage current and scalability of alternative gate dielectrics. Appl. Phys. Lett. 2002, 81, 2091–2093. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lau, W.S. An Extended Unified Schottky-Poole-Frenkel Theory to Explain the Current-Voltage Characteristics of Thin Film Metal-Insulator-Metal Capacitors with Examples for Various High-k Dielectric Materials. ECS J. Solid State Sci. Technol. 2012, 1, N139–N148. [Google Scholar] [CrossRef]
- Rose, A. Space-Charge-Limited Currents in Solids. Phys. Rev. 1955, 97, 1538–1544. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, S.; An, I.; Song, C.; Jeong, H. Conduction mechanism of leakage current due to the traps in ZrO2 thin film. Semicond. Sci. Technol. 2009. [Google Scholar] [CrossRef]
- Zheng, K.; Zhao, J.L.; Leck, K.S.; Teo, K.L.; Yeo, E.G.; Sun, X.W. A ZnTaOx Based Resistive Switching Random Access Memory. ECS Solid State Lett. 2014, 3, Q36–Q39. [Google Scholar] [CrossRef]
- Lampert, M.A.; Mark, P. Current Injection in Solids; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Murgatroyd, P.N. Theory of space-charge-limited current enhanced by Frenkel effect. J. Phys. D Appl. Phys. 1970. [Google Scholar] [CrossRef]
- Valov, I.; Kozicki, M.N. Cation-based resistance change memory. J. Phys. D Appl. Phys. 2013. [Google Scholar] [CrossRef]
- Valov, I.; Waser, R.; Jameson, J.R.; Kozicki, M.N. Electrochemical metallization memories—Fundamentals, applications, prospects. Nanotechnology 2011. [Google Scholar] [CrossRef]
- Mott, N.F.; Davis, E.A. Electronic Processes in Non-Crystalline Materials; Clarendon Press: Oxford, UK, 1971. [Google Scholar]
- Ricco, B.; Gozzi, G.; Lanzoni, M. Modeling and simulation of stress-induced leakage current in ultrathin SiO2 films. Electron Devices IEEE Trans. 1998, 45, 1554–1560. [Google Scholar] [CrossRef]
- Moazzami, R.; Hu, C. Stress-Insuced Current in Thin Silicon Dioxide. In Proceedings of the Technical Digest. International Electron Devices Meeting, San Francisco, CA, USA, 13–16 December 1992; pp. 139–142.
- Gehring, A. Simulation of Tunneling in Semiconductor Devices. Ph.D. Dissertation, Technische Universität Wien, Austria, 2003. [Google Scholar]
- Entner, R. Modeling and Simulation of Negative Bias Temperature Instability. Ph.D. Dissertation, Technische Universität Wien, 2007. [Google Scholar]
- Houng, M.P.; Wang, Y.H.; Chang, W.J. Current transport mechanism in trapped oxides: A generalized trap-assisted tunneling model. J. Appl. Phys. 1999. [Google Scholar] [CrossRef]
- Menzel, S.; Waters, M.; Marchewka, A.; Böttger, U.; Dittmann, R.; Waser, R. Origin of the Ultra-nonlinear Switching Kinetics in Oxide-Based Resistive Switches. Adv. Funct. Mater. 2011, 21, 4487–4492. [Google Scholar] [CrossRef]
- Rozenberg, M.J.; Inoue, I.H.; Sánchez, M.J. Nonvolatile memory with multilevel switching: A basic model. Phys. Rev. Lett. 2004, 92, 178301–178302. [Google Scholar] [CrossRef]
- Rozenberg, M.J.; Inoue, I.H.; Sánchezll, M.J. Strong electron correlation effects in non-volatile electronic memory devices. Appl. Phys. Lett. 2006. [Google Scholar] [CrossRef]
- Larentis, S.; Nardi, F.; Balatti, S.; Gilmer, D.C.; Ielmini, D. Resistive switching by voltage-driven ion migration in bipolar RRAMPart II: Modeling. IEEE Trans. Electron Devices 2012, 59, 2468–2475. [Google Scholar] [CrossRef]
- Gao, B.; Kang, J.F.; Chen, Y.S.; Zhang, F.F.; Chen, B.; Huang, P.; Liu, L.F.; Liu, X.Y.; Wang, Y.Y.; Tran, X.A.; et al. Oxide-based RRAM: Unified microscopic principle for both unipolar and bipolar switching. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 417–420.
- Gao, B.; Yu, S.; Xu, N.; Liu, L.F.; Sun, B.; Liu, X.Y.; Han, R.Q.; Kang, J.F.; Yu, B.; Wang, Y.Y. Oxide-based RRAM switching mechanism: A new ion-transport-recombination model. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 15–17 December 2008.
- Gao, B.; Kang, J.; Liu, L.; Liu, X.; Yu, B. A physical model for bipolar oxide-based resistive switching memory based on ion-transport-recombination effect. Appl. Phys. Lett. 2011. [Google Scholar] [CrossRef]
- Degraeve, R.; Fantini, A.; Raghavan, N.; Goux, L.; Clima, S.; Chen, Y.Y.; Belmonte, A.; Cosemans, S.; Wouters, D.J.; Roussel, P.; et al. Hourglass concept for RRAM: A dynamic and statistical device model. In Proceedings of the International Symposium on the Physical and Failure Analysis of Integrated Circuits (IPFA), Marina Bay Sands, Singapore, 30 June–4 July 2014; pp. 245–249.
- Miranda, E.; Jimenez, D.; Sune, J. The quantum point-contact memristor. IEEE Electron Device Lett. 2012, 33, 1474–1476. [Google Scholar] [CrossRef]
- Sharma, Y.; Misra, P.; Pavunny, S.P.; Katiyar, R.S. Multilevel unipolar resistive memory switching in amorphous SmGdO3 thin film. Appl. Phys. Lett. 2014. [Google Scholar] [CrossRef]
- Haiyang, P. Nonvolatile Resistive Switching in Metal Oxides for the Application in Resistive Random Access Memory. Ph.D. Thesis, Nanyang Technological University, 2013. [Google Scholar]
- Larcher, L. Statistical simulation of leakage currents in MOS and flash memory devices with a new multiphonon trap-assisted tunneling model. IEEE Trans. Electron Devices 2003, 50, 1246–1253. [Google Scholar] [CrossRef]
- Vandelli, L.; Padovani, A.; Larcher, L.; Southwick, R.G.; Knowlton, W.B.; Bersuker, G. A physical model of the temperature dependence of the current through SiO2/HfO2 stacks. IEEE Trans. Electron Devices 2011, 58, 2878–2887. [Google Scholar] [CrossRef]
- Yu, S.; Wu, Y.; Chai, Y.; Provine, J.; Wong, H.S.P. Characterization of switching parameters and multilevel capability in HfOx/AlOx bi-layer RRAM devices. In Proceedings of the International Symposium on VLSI Technology, Systems and Applications—VLSI-TSA, Hsinchu, Taiwan, 25–27 April 2011; pp. 106–107.
- Yu, S.; Guan, X.; Wong, H.S.P. On the stochastic nature of resistive switching in metal oxide RRAM: Physical modeling, Monte Carlo simulation, and experimental characterization. In Proceedings of the 2011 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 5–7 December 2011; pp. 413–416.
- Yu, S.; Guan, X.; Wong, H.S.P. Understanding metal oxide RRAM current overshoot and reliability using Kinetic Monte Carlo simulation. In Proceedings of the 2013 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 10–13 December 2012.
- Padovani, A.; Larcher, L.; Bersuker, G.; Pavan, P. Charge transport and degradation in HfO2 and HfOx dielectrics. IEEE Electron Device Lett. 2013, 34, 680–682. [Google Scholar] [CrossRef]
- Zaima, S.; Furuta, T.; Koide, Y.; Yasuda, Y.; Lida, M. Conduction Mechanism of Leakage Current in Ta2O5 Films on Si Prepared by LPCVD. J. Electrochem. Soc. 1990. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, E.W.; Ismail, R. Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey. Electronics 2015, 4, 586-613. https://doi.org/10.3390/electronics4030586
Lim EW, Ismail R. Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey. Electronics. 2015; 4(3):586-613. https://doi.org/10.3390/electronics4030586
Chicago/Turabian StyleLim, Ee Wah, and Razali Ismail. 2015. "Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey" Electronics 4, no. 3: 586-613. https://doi.org/10.3390/electronics4030586
APA StyleLim, E. W., & Ismail, R. (2015). Conduction Mechanism of Valence Change Resistive Switching Memory: A Survey. Electronics, 4(3), 586-613. https://doi.org/10.3390/electronics4030586