A Theoretical Study on the Operation Principle of Hybrid Solar Cells
Abstract
:1. Introduction
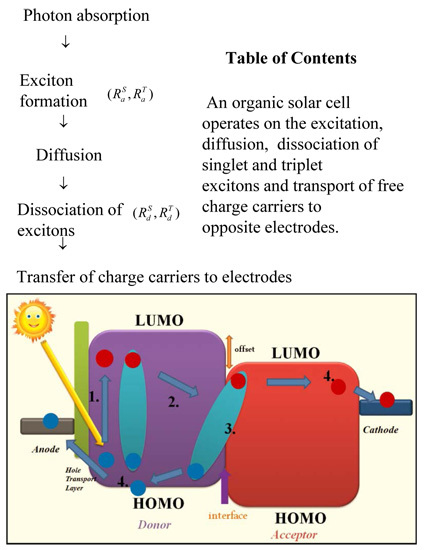
2. Operation Mechanism in Hybrid Solar Cells
2.1. Excitation of Singlet and Triplet Excitons
2.2. Exciton Diffusion to Organic-Inorganic Interface
2.3. Exciton Dissociation at the Organic-Inorganic Interface
3. Results and Discussion
| Mechanism | Parameter | Value |
|---|---|---|
| Excitation | 1.27 × 1010 s−1 | |
| 3.09 × 105 s−1 | ||
| Diffusion | DS | 1.99 cm2 s−1 |
| DT | 2.71 × 10−6 cm2·s−1 | |
| 2.82 × 102 nm | ||
| 1.17 nm | ||
| Dissociation | 2.60 × 1017 s−1 | |
| 2.98 × 1012 s−1 | ||
| Charge transport | F | 3.36 × 10−12 N |
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Wright, M.; Uddin, A. Organic—Inorganic hybrid solar cells: A comparative review. Sol. Energy Mater. Sol. Cells 2012, 107, 87–111. [Google Scholar] [CrossRef]
- Chandrasekaran, J.; Nithyaprakash, D.; Ajjan, K.B.; Maruthamuthu, S.; Manoharan, D.; Kumar, S. Hybrid solar cell based on blending of organic and inorganic materials—An overview. Renew. Sustain. Energy Rev. 2011, 15, 1228–1238. [Google Scholar] [CrossRef]
- Arici, E.; Sariciftci, N.S.; Meissner, D. Hybrid solar cells. Encycl. Nanosci. Nanotechnol. 2004, 3, 929–944. [Google Scholar]
- Narayan, M.R.; Singh, J. Roles of binding energy and diffusion length of singlet and triplet excitons in organic heterojunction solar cells. Phys. Status Solidi 2012, 9, 2386–2389. [Google Scholar] [CrossRef]
- Narayan, M.R.; Singh, J. Effect of exciton-spin-orbit-photon interaction in the performance of organic solar cells. Eur. Phys. J. B 2013, 86, 1–4. [Google Scholar] [CrossRef]
- Narayan, M.R.; Singh, J. Effect of simultaneous excitation of singlet and triplet excitons on the operation of organic solar cells. J. Appl. Phys. 2013, 114, 154515–154517. [Google Scholar] [CrossRef]
- Narayan, M.R.; Singh, J. Study of the mechanism and rate of exciton dissociation at the donor-acceptor interface in bulk-heterojunction organic solar cells. J. Appl. Phys. 2013, 114, 073510–073517. [Google Scholar] [CrossRef]
- Narayan, M.R.; Singh, J. Exciton dissociation and design optimization in p3ht:Pcbm bulk-heterojunction organic solar cell. Can. J. Phys. 2013, 92, 853–856. [Google Scholar] [CrossRef]
- Narayan, M.R.; Singh, J. Optimizing the design of flexible ptb7:Pc71bm bulk-heterojunction and p3ht:Sinw hybrid organic solar cells. J. Nanosci. Nanotechnol. 2013, 1, 8. [Google Scholar]
- Syu, H.; Shiu, S.; Lin, C. Silicon nanowire/organic hybrid solar cell with efficiency of 8.40%. Sol. Energy Mater. Sol. Cells 2012, 98, 267–272. [Google Scholar] [CrossRef]
- Plass, R.; Pelet, S.; Krueger, J.; Grätzel, M.; Bach, U. Quantum dot sensitization of organic-inorganic hybrid solar cells. J. Phys. Chem. B 2002, 106, 7578–7580. [Google Scholar] [CrossRef]
- Beek, W.J.; Wienk, M.M.; Janssen, R.A. Efficient hybrid solar cells from zinc oxide nanoparticles and a conjugated polymer. Adv. Mater. 2004, 16, 1009–1013. [Google Scholar] [CrossRef]
- Huynh, W.U.; Dittmer, J.J.; Alivisatos, A.P. Hybrid nanorod-polymer solar cells. Science 2002, 295, 2425–2427. [Google Scholar] [CrossRef] [PubMed]
- Roncali, J. Molecular bulk heterojunctions: An emerging approach to organic solar cells. Acc. Chem. Res. 2009, 42, 1719–1730. [Google Scholar] [CrossRef] [PubMed]
- Kippelen, B.; Brédas, J.L. Organic photovoltaics. Energy Environ. Sci. 2009, 2, 251–261. [Google Scholar] [CrossRef]
- Brédas, J.L.; Norton, J.E.; Cornil, J.; Coropceanu, V. Molecular understanding of organic solar cells: The challenges. Acc. Chem. Res. 2009, 42, 1691–1699. [Google Scholar] [CrossRef] [PubMed]
- Steinbacher, F.S.; Krause, R.; Hunze, A.; Winnacker, A. Triplet exciton transfer mechanism between phosphorescent organic dye molecules. Phys. Status Solidi 2012, 209, 340–346. [Google Scholar] [CrossRef]
- Lunt, R.R.; Giebink, N.C.; Belak, A.A.; Benziger, J.B.; Forrest, S.R. Exciton diffusion lengths of organic semiconductor thin films measured by spectrally resolved photoluminescence quenching. J. Appl. Phys. 2009, 105, 053711–053717. [Google Scholar] [CrossRef]
- Zhu, X.-Y.; Yang, Q.; Muntwiler, M. Charge-transfer excitons at organic semiconductor surfaces and interfaces. Acc. Chem. Res. 2009, 42, 1779–1787. [Google Scholar] [CrossRef] [PubMed]
- Scharber, M.C.; Mühlbacher, D.; Koppe, M.; Denk, P.; Waldauf, C.; Heeger, A.J.; Brabec, C.J. Design rules for donors in bulk-heterojunction solar cells—Towards 10% energy-conversion efficiency. Adv. Mater. 2006, 18, 789–794. [Google Scholar] [CrossRef]
- Kendrick, M.J.; Neunzert, A.; Payne, M.M.; Purushothaman, B.; Rose, B.D.; Anthony, J.E.; Haley, M.M.; Ostroverkhova, O. Formation of the donor-acceptor charge transfer exciton and its contribution to charge photogeneration and recombination in small-molecule bulk heterojunctions. J. Phys. Chem. C 2012, 116, 18108–18116. [Google Scholar] [CrossRef]
- Bruder, I. Organic Solar Cells: Correlation between Molecular Structure, Morphology and Device Performance; Max-Planck-Institut für Festkörperforschung: Stuttgart, Germany, 2010. [Google Scholar]
- Davenas, J.; Dkhil, S.B.; Cornu, D.; Rybak, A. Silicon nanowire/p3ht hybrid solar cells: Effect of the electron localization at wire nanodiameters. Energy Proced. 2012, 31, 136–143. [Google Scholar] [CrossRef]
- Liu, K.; Qu, S.; Zhang, X.; Tan, F.; Wang, Z. Improved photovoltaic performance of silicon nanowire/organic hybrid solar cells by incorporating silver nanoparticles. Nanoscale Res. Lett. 2013, 8, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Dang, M.T.; Hirsch, L.; Wantz, G. P3ht: Pcbm, best seller in polymer photovoltaic research. Adv. Mater. 2011, 23, 3597–3602. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Nakahara, A.; Wei, D.; Nordlund, D.; Russell, T.P. P3ht/pcbm bulk heterojunction organic photovoltaics: Correlating efficiency and morphology. Nano Lett. 2010, 11, 561–567. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.Y.; Gau, C. Arrangement of band structure for organic-inorganic photovoltaics embedded with silicon nanowire arrays grown on indium tin oxide glass. Appl. Phys. Lett. 2009, 95, 053302. [Google Scholar] [CrossRef]
- Huang, J.-S.; Goh, T.; Li, X.; Sfeir, M.Y.; Bielinski, E.A.; Tomasulo, S.; Lee, M.L.; Hazari, N.; Taylor, A.D. Polymer bulk heterojunction solar cells employing forster resonance energy transfer. Nat. Photonics 2013, 7, 479–485. [Google Scholar] [CrossRef]
- Mangold, H. Charge Separation and Recombination in Novel Polymeric Absorber Materials for Organic Solar Cells—A Photophysical Study. Ph.D. Thesis, Johannes Gutenberg-Universität Mainz, Mainz, Germany, 2013. [Google Scholar]
- Azizi, S.; Braik, M.; Dridi, C.; Ouada, H.B.; Ryback, A.; Davenas, J. Study of charge transport in p3ht: Sinw-based photovoltaic devices. Appl. Phys. A 2012, 108, 99–106. [Google Scholar] [CrossRef]
- Köhler, A.; Beljonne, D. The singlet-triplet exchange energy in conjugated polymers. Adv. Func. Mater. 2004, 14, 11–18. [Google Scholar] [CrossRef]
- Blom, P.W.M.; Mihailetchi, V.D.; Koster, L.J.A.; Markov, D.E. Device physics of polymer: Fullerene bulk heterojunction solar cells. Adv. Mater. 2007, 19, 1551–1566. [Google Scholar] [CrossRef]
- Huang, J.; Hsiao, C.; Syu, S.; Chao, J.; Lin, C. Well-aligned single-crystalline silicon nanowire hybrid solar cells on glass. Sol. Energy Mater. Sol. Cells 2009, 93, 621–624. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Narayan, M.; Singh, J. A Theoretical Study on the Operation Principle of Hybrid Solar Cells. Electronics 2015, 4, 303-310. https://doi.org/10.3390/electronics4020303
Narayan M, Singh J. A Theoretical Study on the Operation Principle of Hybrid Solar Cells. Electronics. 2015; 4(2):303-310. https://doi.org/10.3390/electronics4020303
Chicago/Turabian StyleNarayan, Monishka, and Jai Singh. 2015. "A Theoretical Study on the Operation Principle of Hybrid Solar Cells" Electronics 4, no. 2: 303-310. https://doi.org/10.3390/electronics4020303
APA StyleNarayan, M., & Singh, J. (2015). A Theoretical Study on the Operation Principle of Hybrid Solar Cells. Electronics, 4(2), 303-310. https://doi.org/10.3390/electronics4020303