Kronecker-Based Fusion Rule for Cooperative Spectrum Sensingwith Multi-Antenna Receivers

Abstract

This paper considers a novel fusion rule for spectrum sensing scheme for a cognitive radio network with multi-antenna receivers. The proposed scheme exploits the fact that when any primary signal is present, measurements are spatially correlated due to presence of inter-antenna and inter-receiver spatial correlation. In order to exploit this spatial structure, the generalized likelihood ratio test (GLRT) operates with the determinant of the sample covariance matrix. Therefore, it depends on the sample size N and the dimensionality of the received data (i.e., the number of receivers K and antennas L). However, when the dimensionality $\left\{K,L\right\}$ is on the order, or larger than the sample size N, the GLRT degenerates due to the ill-conditioning of the sample covariance matrix. In order to circumvent this issue, we propose two techniques that exploit the inner spatial structure of the received observations by using single pair and multi-pairs Kronecker products. The performance of the proposed detectors is evaluated by means of numerical simulations, showing important advantages with respect to the traditional (i.e., unstructured) GLRT approach.

1. Introduction

The field of radio communication has grown up with the emergence of new wireless devices and applications. Therefore, the demand for radio spectrum has increased, which is expected to increase further in the coming years [1]. On the other hand, most of the existing useful radio spectrum has been already allocated; therefore, it is becoming hard to find free spectrum for the deployment of new services or enhancement of the existing ones [1,2]. Moreover, the conventional approach to spectrum management is very rigid in the sense that each operator is allowed to operate in a certain frequency band. Similarly, studies show that assigned frequencies are not occupied all the time, resulting in under-utilization of the available spectrum. In that sense, cognitive radio has become one of the most important solutions to the spectrum under-utilization problem. Cognitive radio (CR) is defined by Federal Communications Commission (FCC) as: “A radio or system that senses its operational electromagnetic environment and can dynamically and autonomously adjust its radio operating parameters to modify system operation, such as maximize throughput, mitigate interference, facilitate interoperability, access secondary markets” [1]. Hence, the main concept behind CR is to exploit under-utilized spectral resources by reusing unused spectrum in an opportunistic manner. In other words, both license (primary) and unlicensed (secondary) users share same frequency band in such a way that the primary users are allowed to use the free spectrum spaces left by the secondary users in an opportunistic manner [3,4,5].

In order to exploit under-utilized spectral resources by reusing unused spectrum in an opportunistic manner, reliable sensing of the primary users (PU) spectrum is certainly of paramount importance. Such spectrum sensing is performed by secondary users (SU), either following a single-sensor or a multisensor approach. In a CR system, it is often difficult for a single receiver (sensor) (i.e., an unlicensed or secondary user) to meet the sensing requirements for detecting a primary signal when large-scale fading and other propagation disturbances are present. In this context, cooperation of multiple secondary users becomes a must choice, as already shown in several previous contributions [3,4].

The present literature for spectrum sensing is still in its early stages of development. Many algorithms have been proposed, including, e.g., likelihood ratio test (LRT), energy detection, matched-filter (MF) detection, and cyclostationarity based detection [6]. All of these techniques have been proposed for an individual secondary user or in a collaborative network of secondary users [1,3,4]. However, for all such schemes it is usually assumed that there is full or partial knowledge about primary signal such as primary signal characteristics, the channel between primary user and secondary user, and/or the noise power level at the secondary user. The LRT is optimal but it requires exact knowledge and distributions of the source signal and noise [7]. The MF-based method requires that the receiver has perfect knowledge about the channel responses from the primary user. In such method accurate synchronization is also required in order to achieve good performance [8,9]. However, this may not be possible as in most of the spectrum sensing applications, the primary users do not cooperate with the secondary users [4,8]. The cyclostationary detection method also requires information about the cyclic frequencies of the primary users, which may not be realistic for many spectrum sensing applications [4]. Energy detection does not need any information of the primary signal, however, it requires perfect knowledge of the noise power [4,7]. In most of the applications, the noise powers are unknown and these should be estimated. The estimated noise power could be quite inaccurate due to noise uncertainty. Inaccurate estimation of the noise power results in high probability of false alarm. Hence, the energy detection can not perform in the presence of noise power uncertainty [10,11]. Furthermore, energy detection is considered to be optimal for detecting an independent and identically distributed (i.i.d.) signal, it is not optimal for detecting a correlated signal, which is the case for most practical applications [4,9].

As mentioned above, in more realistic CR environments, the required assumptions may limit the applicability of the traditional algorithms [3,4,9]. Hence, there is need for spectrum sensing schemes that are blind and do not require such prior information. Recently, multi-antenna receivers have become an integral part of many cognitive radios [12,13], thus giving us the chance to consider multi-antenna techniques to improve the performance of cooperative spectrum sensing. Multiple antennas can offer spatial diversity and improve the spectrum sensing performance [3,4]. Intuitively, the presence of any primary signal should result in some spatial correlation in the observations received at the multi-antenna receivers [4,14]. One solution to overcome the above shortcomings of the traditional detection schemes is to exploit the statistical correlation of the received signals [4,9,14]. In this paper we consider the presence of the spatial correlation as a detection metric since the noise processes can be safely assumed statistically independent [3].

Based on the above discussion, we consider a detection problem that takes into account the presence of some unknown inter-antenna and inter-receiver spatial correlation. Because of that uncertainty in the spatial correlation, the problem is typically formulated through the GLRT, which is a simple test that just decides whether the estimated covariance matrix departs from the signal-absent covariance matrix or not ([15,16], Chapers 9 and 10). Since the GLRT involves estimation of the unknown covariance matrix, it depends on the sample size and the dimensionality [17]. In the case of a large wireless network, the dimensionality of the problem can be on the order of the available sample size and thus the GLRT degenerates due to the ill-conditioned sample covariance matrix [17]. Moreover, the GLRT assumes no structure for the covariance matrix, except for the fact that it is a symmetric matrix. To cope with the problem of small sample support we propose two techniques that exploit the embedded spatial structures. In these techniques we propose the decomposition of a large covariance matrix into small matrices by exploiting the inter-receiver and inter-antenna spatial structures in the received observations. To be more specific, the two detectors use single-pair Kronecker product (SPKP) [18] and multi-pairs Kronecker product (MKPK) [19] of the inter-receiver and inter-antenna covariance matrices. By doing so, the demand for large sample size reduces, and hence, this results in an enhanced robustness against the small sample support.

The remainder of the paper is organized as follows. Section 2 introduces the proposed methodology and the signal model. In Section 3, we solve the problem by using the traditional GLRT formulations. The proposed detection schemes are derived in Section 4. Numerical results are provided in Section 5. The conclusion is finally drawn in Section 6.

2. Problem Formulation

We consider a cognitive network that has K secondary users, in which the k-th SU is equipped with L antennas. In the presence of the primary signal (macrocell user signal), the received signal at the output of the L antennas of the k-th SU can be expressed as: ${\mathbf{x}}_k\left(n\right)={\mathbf{s}}_k\left(n\right)+{\mathbf{w}}_k\left(n\right),n=1,\cdots ,N$, where the ($L\times 1$) vector ${\mathbf{s}}_k\left(n\right)$ contains the samples of the primary signal and vector ${\mathbf{w}}_k\left(n\right)$ consists of the complex additive white Gaussian noise samples at time n. We assume that measurements from SUs ${\left\{{\mathbf{x}}_k\left(n\right)\right\}}_{k=1}^K$ are sent to the fusion center (i.e., the base station) via dedicated links. Which is in general a reasonable assumption, as in most of the cases SUs and the fusion center would have mutually agreed upon digital communication links. Moreover, the SUs will have better error correction schemes to overcome the impairments of their corresponding channels with the fusion center. One particular example where such assumption is completely applicable is the cognitive-enabled femtocell networks (network of base stations of femtocells). Femtocells are small cellular telecommunications base stations that can be installed in residential or business environments either as single stand-alone items or in clusters to provide improved cellular coverage within a building [20]. In most cognitive-enabled femtocell networks, there exists a wired back-haul connection between HeNBs (HeNB is the 3GPP’s term for a LTE femtocell or Small Cell) that can be considered as an ideal link between receivers and the fusion center [20], as shown in the Figure 1. The fusion center stacks the received signal vectors ${\left\{{\mathbf{x}}_k\left(n\right)\right\}}_{k=1}^K$ in the ($L\times K$) matrix $\mathbf{X}\left(n\right)$. By using the $vec$ operator as $\mathbf{x}\left(n\right)=vec\left\{\mathbf{X}\left(n\right)\right\}$, the two hypotheses can be represented as:

$$\begin{gathered} {\mathcal{H}}_0:\mathbf{x}\left(n\right)=\mathbf{w}\left(n\right),\mathrm{ }n=1,...,N \\ {\mathcal{H}}_1:\mathbf{x}\left(n\right)=\mathbf{s}\left(n\right)+\mathbf{w}\left(n\right), n=1,...,N \end{gathered}$$

(1)

where

$$\mathbf{x}\left(n\right)={\left[{\mathbf{x}}_1^T\left(n\right),{\mathbf{x}}_2^T\left(n\right),\cdots ,{\mathbf{x}}_K^T\left(n\right)\right]}^T$$

(2)

$$\mathbf{s}\left(n\right)={\left[{\mathbf{s}}_1^T\left(n\right),{\mathbf{s}}_2^T\left(n\right),\cdots ,{\mathbf{s}}_K^T\left(n\right)\right]}^T$$

(3)

$$\mathbf{w}\left(n\right)={\left[{\mathbf{w}}_1^T\left(n\right),{\mathbf{w}}_2^T\left(n\right),\cdots ,{\mathbf{w}}_K^T\left(n\right)\right]}^T$$

(4)

Therefore, we have the covariance matrix ${\Sigma }_1=\mathrm{E}\left[\mathbf{x}{\mathbf{x}}^H\right]$ as:

$${\Sigma }_1=\left[\begin{array}{cccc}{\Sigma }_{11}& {\Sigma }_{12}& \cdots & {\Sigma }_{1K}\\ {\Sigma }_{21}& {\Sigma }_{22}& \cdots & {\Sigma }_{1K}\\ ⋮& ⋮& \ddots & ⋮\\ {\Sigma }_{K1}& {\Sigma }_{K2}& \cdots & {\Sigma }_{KK}\end{array}\right]\in {\mathbb{C}}^{KL\times KL}$$

(5)

where the covariance matrices ${\Sigma }_{k,k}=E\left[{\mathbf{x}}_k{\mathbf{x}}_k^H\right]$, $k=1,\dots ,K$ capture the inter-antennas correlation present in the signal received at L antennas of the k-th SU. Similarly, non-zero off-diagonal blocks ${\Sigma }_{k,j}=E\left[{\mathbf{x}}_k{\mathbf{x}}_j^H\right]$ with $k\ne j$ indicate the presence of inter-receiver spatial correlation. Furthermore, in most practical working conditions, it seems reasonable to consider the ensemble vectors ${\left\{\mathbf{x}\left(n\right)\right\}}_{n=1}^N$ to be zero mean complex Gaussian distributed, a case that is particularly well-suited for orthogonal frequency division multiplexing (OFDM) [21]. It is to be noted that we begin with the complex baseband signal sampled at the specific Nyquist rate. Hence, the hypotheses become:

$$\begin{gathered} {\mathcal{H}}_0:\mathbf{x}\left(n\right)~C\mathcal{N}\left(\mathbf{0},{\Sigma }_0\right) \\ {\mathcal{H}}_1:\mathbf{x}\left(n\right)~C\mathcal{N}\left(\mathbf{0},{\Sigma }_1\right) \end{gathered}$$

(6)

where $C\mathcal{N}\left(\mathbf{0},{\Sigma }_h\right)$$h=\left\{0,1\right\}$, denotes the complex Gaussian distribution with zero mean and covariance ${\Sigma }_h$. Under ${\mathcal{H}}_0$, ${\Sigma }_0$ is an unknown diagonal matrix, since in the absence of the primary signal the observations are assumed to be white. Therefore, the detection problem (6) distinguishes a perfectly white noise from spatially correlated (i.e., inter-receiver and inter-antenna correlation) signal. For this problem, we will next present the traditional detector, and then derive the proposed improved detector by introducing the pair Kronecker product.

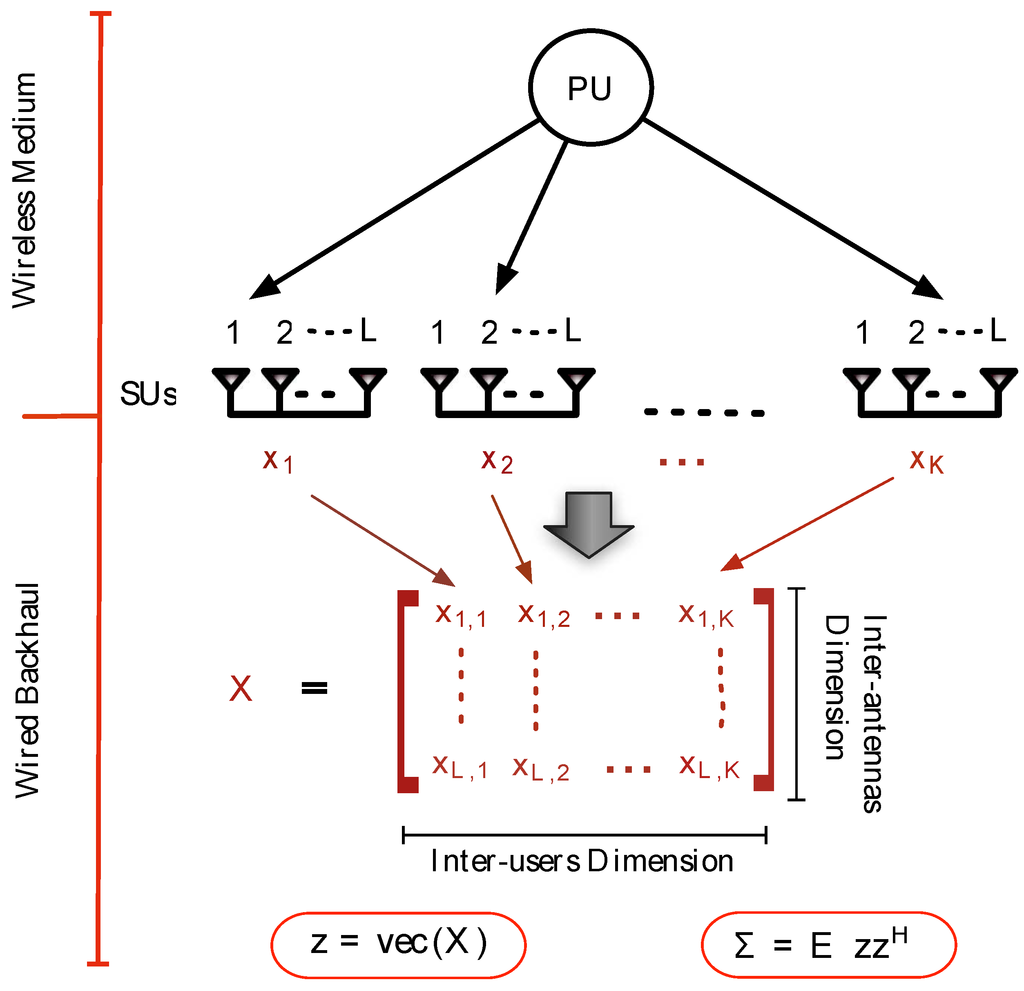
Figure 1. Multi-sensor with Multi-antenna (MAMS) methodology.

Figure 1. Multi-sensor with Multi-antenna (MAMS) methodology.

3. GLRT Based Detection Scheme

In this section, we adopt the GLRT for the detection problem introduced in Equation (6) since it is asymptotically an optimal detector and it is well-suited to the presence of unknown parameters. Later on, we will use it as a benchmark for the proposed techniques. For the detection problem (6), the GLRT statistic becomes:

$$\begin{array}{cc}\hfill {\Lambda }_{\mathrm{T}}\left({\mathbf{X}}_N\right)& =\frac{\underset{{\Sigma }_0}{\max }{f}_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_0\right)}{\underset{{\Sigma }_1}{\max }{f}_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_1\right)}\hfill \end{array}{\gtrless }_{{\mathcal{H}}_1}^{{\mathcal{H}}_0}\gamma ,$$

(7)

where γ is the threshold, $f_{\mathbf{x}}\left({\mathbf{X}}_N,{\Sigma }_0\right)$ and $f_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_1\right)$ are likelihood functions under hypothesis ${\mathcal{H}}_0$ and ${\mathcal{H}}_1$, respectively. Similarly, the ($KL\times 1$) matrix ${\mathbf{X}}_N=\left[\begin{array}{cccc}\mathbf{x}\left(1\right)& \mathbf{x}\left(2\right),& \cdots ,& \mathbf{x}\left(N\right)\end{array}\right]$ contains all of the available samples of $\mathbf{x}$$\left(n\right)$, $n=1,\dots ,N$. Solving Equation (7) we get the final expression of the GLRT as:

$$\begin{array}{cc}\hfill {\Lambda }_{\mathrm{T}}\left({\mathbf{X}}_N\right)& =\frac{\left|{\widehat{\Sigma }}_1\right|}{\left|{\widehat{\Sigma }}_0\right|}{\gtrless }_{{\mathcal{H}}_1}^{{\mathcal{H}}_0}\gamma ,\hfill \end{array}$$

(8)

where ${\widehat{\Sigma }}_1=\frac{1}{N}{\sum }_{n=1}^N\mathbf{x}\left(n\right){\mathbf{x}}^H\left(n\right)$ is the maximum likelihood estimator (MLE) of ${\Sigma }_1$. Similarly, under the alternate hypothesis, we assume that only noise is present and ${\Sigma }_0$ is diagonal matrix, then ${\widehat{\Sigma }}_0=\mathrm{diag}\left(\frac{1}{N}{\sum }_{n=1}^N\mathbf{x}\left(n\right){\mathbf{x}}^H\left(n\right)\right)$. In practice, the GLRT is used based on the assumption that the sample size N is large while the sample dimensions $\left\{K,L\right\}$ are small. However, when the sample support is limited (in particular, when $N\le KL$) , the GLRT degenerates due to the ill-conditioning of the estimated covariance matrix [22]. A way to reduce these limitations will be presented next.

4. GLRT Based on Kronecker Product

The GLRT-based detection scheme in Equation (7) assumes no structure for the covariance matrix, except that it is symmetric. In order to improve the conditioning for small sample support, in this section we exploit an a-priori suitable structure for the covariance matrix based on the underlying physical topology [22]. Taking this into effect, we propose two detection techniques in Section 4.1 and Section 4.2 that exploit the embedded correlation structure based on the SPKP and MPKP, respectively.

4.1. SPKP-GLRT

In Section 2, we have discussed that the ($KL\times 1$) vector $\mathbf{x}$(n) contains K sub-vectors of dimension ($L\times 1$) corresponding to the arrays at the K different SUs. Consequently, we see that the covariance matrix ${\Sigma }_1$ has mainly two types of spatial correlation structures. Inter-receiver correlation structure appears between the SUs due to their proximity, and inter-antenna correlation appears between samples from the antenna elements of the same SU. Moreover, by assuming that the spatial correlation structure of arrays at different SUs is similar, the observation matrix $\mathbf{X}$ can be assumed as a matrix normal with separable structure [23,24].

Keeping the above facts and discussion in [22,24] into considerations, the overall (inter-antenna plus inter-receiver) spatial covariance ${\Sigma }_1$ can be represented with the help of the SPKP model as:

$${\Sigma }_1={\Sigma }_{\mathrm{A}}\otimes {\Sigma }_{\mathrm{S}}$$

(9)

where ${\Sigma }_{\mathrm{S}}\in {\mathbb{C}}^{K\times K}$ and ${\Sigma }_{\mathrm{A}}\in {\mathbb{C}}^{L\times L}$ capture the inter-receiver and inter-antenna spatial correlation, respectively. By using Equation (9) the SPKP-GLRT is [17]:

$${\Lambda }_{\mathrm{SPKP}}\left({\mathbf{X}}_N\right)=\frac{\underset{{\Sigma }_0}{\max }{f}_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_0\right)}{\underset{{\Sigma }_{\mathrm{S}},{\Sigma }_{\mathrm{A}}}{\max }{f}_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_{\mathrm{A}}\otimes {\Sigma }_{\mathrm{S}}\right)}{\gtrless }_{{\mathcal{H}}_1}^{{\mathcal{H}}_0}\gamma .$$

(10)

Solving Equation (10), under the hypothesis ${\mathcal{H}}_1$, we need to estimate covariance matrices ${\Sigma }_{\mathrm{S}}$ and ${\Sigma }_{\mathrm{A}}$ by using the MLE paradigm. The MLEs under the hypothesis ${\mathcal{H}}_1$, can be written as [17,23,25]:

$${\widehat{\Sigma }}_{\mathrm{A}}=\frac{1}{KN}\sum _{n=1}^N\mathbf{X}\left(n\right){\widehat{\Sigma }}_{\mathrm{S}}^{-1}{\mathbf{X}}^H\left(n\right),$$

(11)

$${\widehat{\Sigma }}_{\mathrm{S}}=\frac{1}{LN}\sum _{n=1}^N{\mathbf{X}}^H\left(n\right){\widehat{\Sigma }}_{\mathrm{A}}^{-1}\mathbf{X}\left(n\right).$$

(12)

Expressions Equations (11) and (12) suggest that ${\widehat{\Sigma }}_{\mathrm{A}}$ and ${\widehat{\Sigma }}_{\mathrm{S}}$ can be achieved using an iterative method such as the Flip-Flop algorithm [23,25]. The Flip-Flop algorithm is obtained by alternately maximizing $\log f_{\mathbf{x}}\left({\mathbf{X}}_N;{\Sigma }_{\mathrm{S}}\otimes {\Sigma }_{\mathrm{A}}\right)$ w.r.t. ${\Sigma }_{\mathrm{S}}$ keeping the last available estimate of ${\Sigma }_{\mathrm{A}}$ fixed and vice versa. In [23], it has been proved that for the case of large enough N, asymptotic efficiency of the ML approach can be achieved by only performing steps 1 to 3, without iterating. Taking into account this fact, in order to get positive definite ${\widehat{\Sigma }}_1$ we adopt a non-iterative Flip-Flop approach and only perform the steps given in Algorithm 1 with an initial value of ${\widehat{\Sigma }}_{\mathrm{S}}^0={\mathbf{I}}_{K\times K}$. Finally, solving Equation (10), we get the expression:

Algorithm 1 ML based Non-Iterative Flip-Flop

$$\begin{array}{cc}\hfill {\Lambda }_{\mathrm{SPKP}}\left({\mathbf{X}}_N\right)& =\frac{{\left|{\widehat{\Sigma }}_{\mathrm{A}}\right|}^K{\left|{\widehat{\Sigma }}_{\mathrm{S}}\right|}^L}{\left|{\widehat{\Sigma }}_0\right|}\hfill \end{array}{\gtrless }_{{\mathcal{H}}_1}^{{\mathcal{H}}_0}\gamma .$$

(13)

The main advantage of the SPKP-GLRT in Equation (13) over the traditional GLRT in Equation (8) is that under ${\mathcal{H}}_1$, instead of $\frac{1}{2}KL(KL+1)$ parameters, it has only $\frac{1}{2}K\left(K+1\right)+\frac{1}{2}L\left(L+1\right)$ parameters to estimate. Therefore, the dimensions of ${\Sigma }_{\mathrm{A}}$ and ${\Sigma }_{\mathrm{S}}$ are much smaller than the dimension of the full covariance matrix ${\Sigma }_1$, thus allowing a relaxation on the sample size that is required to avoid ill-conditioning of the ML estimate ${\widehat{\Sigma }}_1$. Hence, the SPKP model is a good approximation that captures important information about the correlations and ${\widehat{\Sigma }}_1$ found under Equation (9) is generally positive definite for $N>\max (\frac{K}{L},\frac{L}{K})$ [25].

4.2. MPKP-GLRT

In Section 4.1, we have approximated ${\Sigma }_1$ in the form of two smaller covariance matrices through the SPKP model (9). The aforementioned SPKP model can also be written as:

$${\Sigma }_1={\Sigma }_{\mathrm{A}}\otimes \sum _{k=1}^K{\lambda }_k{\mathbf{S}}_k,$$

(14)

where ${\mathcal{S}}_k\triangleq {\mathbf{v}}_k{\mathbf{v}}_k^H$ is an orthonormal basis component represented as a singular matrix [19]. Furthermore, by using the identity $\mathbf{B}\otimes \left(\mathbf{O}+\mathbf{D}\right)=\mathbf{B}\otimes \mathbf{O}+\mathbf{B}\otimes \mathbf{D}$, we can write

$${\Sigma }_1=\sum _{k=1}^K{\Sigma }_{\mathrm{A}}\otimes {\lambda }_k{\mathcal{S}}_k=\sum _{k=1}^K{\lambda }_k{\Sigma }_{\mathrm{A}}\otimes {\mathcal{S}}_k.$$

(15)

The expression makes it obvious that each spatial component ${\mathcal{S}}_k$ has the same inter-antenna covariance matrix. Hence, the SPKP covariance model is based on a very rigid assumption since it assumes similar inter-antenna spatial covariance structures at different SUs. However, in a more realistic case, different SUs are likely to have different inter-antenna spatial covariance. Therefore, to relax this rigid assumption and better explain the separation of inter-receiver and inter-antenna correlation, we consider a more general multi-pair Kronecker product (MPKP) model as:

$$\begin{array}{cc}\hfill {\Sigma }_1& =\sum _{k=1}^K{\mathbf{A}}_k\otimes {\mathcal{S}}_k.\hfill \end{array}$$

(16)

Note that by setting ${\mathbf{A}}_k={\lambda }_k{\Sigma }_{\mathrm{A}}$ we can see how Equation (16) subsumes the SPKP model. Moreover, it is to be noted that the inter-receiver correlation components ${\left\{{\mathcal{S}}_k\right\}}_{k=1}^K$ are ($K\times K$) rank-1 matrices and their corresponding inter-antenna correlation matrices ${\mathbf{A}}_k$ are full rank ($L\times L$) matrices. The estimate of ${\mathcal{S}}_k$ or the spatial orthogonal components the ${\left\{{\mathbf{v}}_k\right\}}_{k=1}^K$ can be found by singular value decomposition (SVD) of ${\mathbf{X}}_V={\left[{\mathbf{X}}^T\left(1\right),{\mathbf{X}}^T\left(2\right),\cdots ,{\mathbf{X}}^T\left(N\right)\right]}^T\in {\mathbb{C}}^{LN\times K}$ as: ${\mathbf{X}}_V=\mathbf{U}\Psi {\mathbf{V}}^H$[19]. Where $\mathbf{U}$ is a ($LN\times K$) orthogonal matrix, Ψ is a ($K\times K$) diagonal matrix with singular values ${\left\{{\eta }_k\right\}}_{k=1}^K$ of ${\mathbf{X}}_V$ as diagonal elements and $\mathbf{V}$ is a ($K\times K$) orthogonal matrix of the spatial components. Each row of ${\mathbf{V}}^H$ is ${\mathbf{v}}_k$ that forms ${\mathcal{S}}_k$ as: ${\mathcal{S}}_k={\mathbf{v}}_k{\mathbf{v}}_k^H$ for the model (16). Similarly, the estimate of ${\mathbf{A}}_k$ can be found based on the MLE paradigm as [19]:

$${\widehat{\mathbf{A}}}_k=\frac{1}{N}\sum _{n=1}^N\mathbf{X}\left(n\right){\widehat{\mathcal{S}}}_k{\mathbf{X}}^H\left(n\right),$$

(17)

and ${\widehat{\mathcal{S}}}_k={\mathbf{v}}_k{\mathbf{v}}_k^H$. Hence, we can write ${\widehat{\Sigma }}_1={\sum }_{k=1}^K{\widehat{\mathbf{A}}}_k\otimes {\widehat{\mathcal{S}}}_k$ and the MPKP-GLRT becomes:

$$\begin{array}{cc}\hfill {\Lambda }_{\mathrm{MPKP}}\left({\mathbf{X}}_N\right)& =\frac{\left|{\sum }_{k=1}^K{\widehat{\mathbf{A}}}_k\otimes {\widehat{\mathcal{S}}}_k\right|}{\left|{\widehat{\Sigma }}_0\right|}\hfill \end{array}{\gtrless }_{{\mathcal{H}}_1}^{{\mathcal{H}}_0}\gamma .$$

(18)

Compared to the SPKP-GLRT in Equation (13), the MPKP-GLRT in Equation (18) can better account for the different inter-antenna structures, since it is not constrained to the assumption of identical inter-antenna correlation at different SUs. However, the computational cost of the detection scheme Equation (18) is slightly higher than that of Equation (13). This is because the number of free parameters in the covariance matrix to be estimated under hypothesis ${\mathcal{H}}_1$ has increased to $L^2+LK\left(K-1\right)/2$ [19].

5. Numerical Results

For the analysis to be conducted herein, we consider a wireless network with a total of $K=10$ multi-antenna SUs randomly deployed to detect a PU that appears at an unknown position. The spatial correlation between the antennas of a SU is modeled herein as $c_{i,j}={\rho }^{\left|i-j\right|}$, with $\left\{i,j\right\}=1,\cdots ,L$. Moreover, $0<\rho <1$ with $\rho =e^{-23{\kappa }^2{\left(d{\lambda }_c\right)}^2}$, which is called correlation coefficient between two adjacent antennas, and it relies on the angular spread κ, the wavelength ${\lambda }_c$ and the distance d between two adjacent antennas [12]. Finally, the spatial correlation between SUs due to the correlated shadowing effects is modeled based on the model given in [26].

In order to analyze the performance of the proposed detectors, we use receiver operating characteristic curve (ROC) and area under the ROC curve (AUC), which varies between 0.5 (poor performance) and 1 (good performance). Moreover, we define the average signal-to-noise ratio (SNR) of all SUs as: $\overline{\kappa }=\frac{1}{K}{\sum }_{i=1}^K{\kappa }_i$ and the SNR of i-th SU is ${\kappa }_i={\zeta }^{i-1}{\kappa }_{\min }$ where ${\kappa }_{\min }$ is the minimum SNR among those of the SUs [13]. For a given average SNR $\overline{\kappa }$ and SNR gap ζ, we can generate the random SNRs of the SUs. Similarly, in order to analyze the effect of noise power uncertainty we generate the noise power at k-th SU as ${\sigma }_{w,k}^2\sim \mathcal{U}\left(\frac{{\sigma }_{n,k}^2}{{\alpha }_{nu}},{\alpha }_{nu}{\sigma }_{n,k}^2\right)$, where ${\alpha }_{nu}\ge 1$, and ${\alpha }_{nu}=1$ means no noise uncertainty.

In Figure 2 we plot ROC curves to compare the performance of our proposed spectrum sensing schemes with the optimal likelihood ratio test (LRT) and the energy detection schemes. For the the optimal LRT, to solve Equation (6) we assume that the covariance matrices under both hypothesis are known. On the other hand the energy detector is given as:

$${\Lambda }_{\mathrm{ENG}}\left({\mathbf{X}}_N\right)=\sum _{n=1}^N\sum _{k=1}^K\sum _{l=1}^L{\left|x_{k,l}\left(n\right)\right|}^2{\gtrless }_{{\mathcal{H}}_0}^{{\mathcal{H}}_1}\gamma .$$

(19)

Note that dashed lines represent the plots for ${\alpha }_{nu}=2$ and solid lines represent the case when ${\alpha }_{nu}=1$. In Figure 3, we show the AUC plots to analyze the effects of the sample size N in the presence of noise power uncertainty. With these considerations, the results clearly show that ${\Lambda }_{\mathrm{MPKP}}$ and ${\Lambda }_{\mathrm{SPKP}}$ outperform the traditional GLRT${\Lambda }_{\mathrm{T}}$ with a smaller sample support. Moreover, we can see that the energy detector performs better in the absence of the noise power uncertainty, however, it has poor performance in the presence of noise power uncertainty. Interestingly, we can also observe that in the presence of noise power uncertainty, the increase of sample size has very negligible impact on the performance of the energy based detection scheme ${\Lambda }_{\mathrm{ENG}}$ due to the phenomena of SNR-Wall [4]. In Figure 4, we show the AUC plots to further analyze the effects of noise power uncertainty. Once again, we can see that ${\Lambda }_{\mathrm{MPKP}}$ and ${\Lambda }_{\mathrm{SPKP}}$ have superior performance than ${\Lambda }_{\mathrm{T}}$ and ${\Lambda }_{\mathrm{ENG}}$. Moreover, we can observe the proposed schemes are robust against the noise power uncertainty compared to ${\Lambda }_{\mathrm{ENG}}$. It because the proposed schemes estimate the noise power in real time.

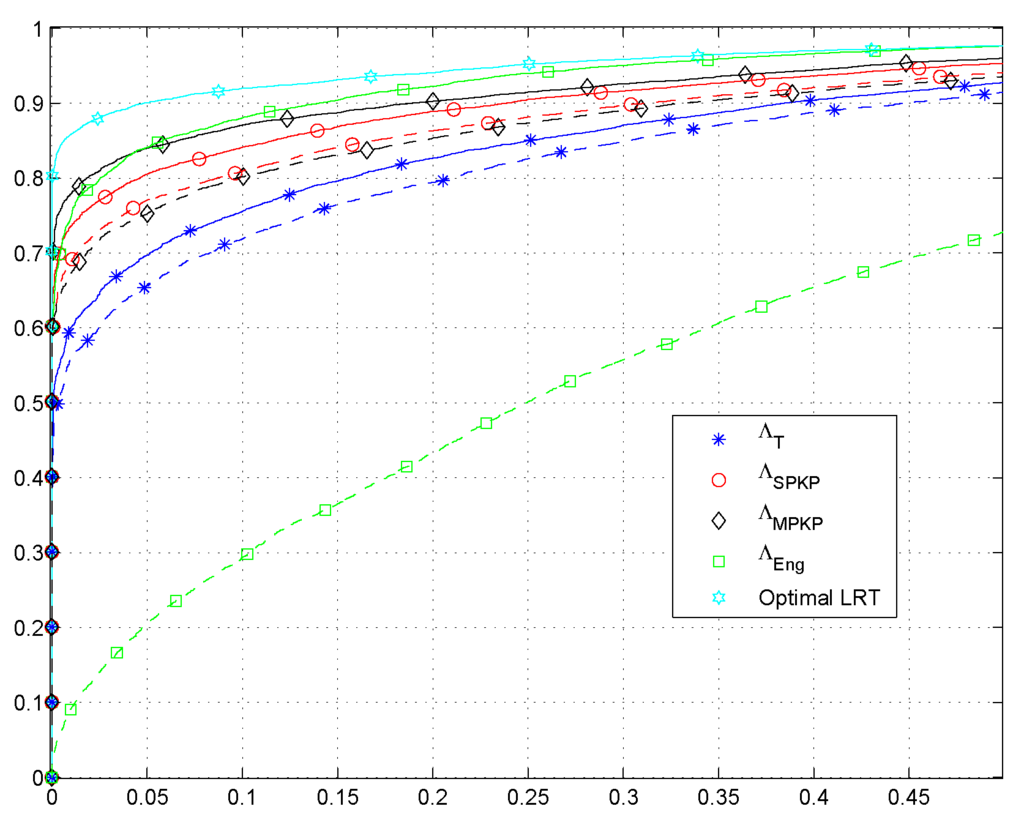
Figure 2. Receiver operating characteristic (ROC) curves: L = 4, K = 10, N = 70, κ = −15 dB. Solid Lines and Dashed Lines α_nu = 2.

Figure 2. Receiver operating characteristic (ROC) curves: L = 4, K = 10, N = 70, κ = −15 dB. Solid Lines and Dashed Lines α_nu = 2.

Figure 3. Area under the ROC curve to asses the effects of the sample size N, using, κ = −15 dB. Solid Lines α_nu = 1, Dashed lines α_nu = 2.

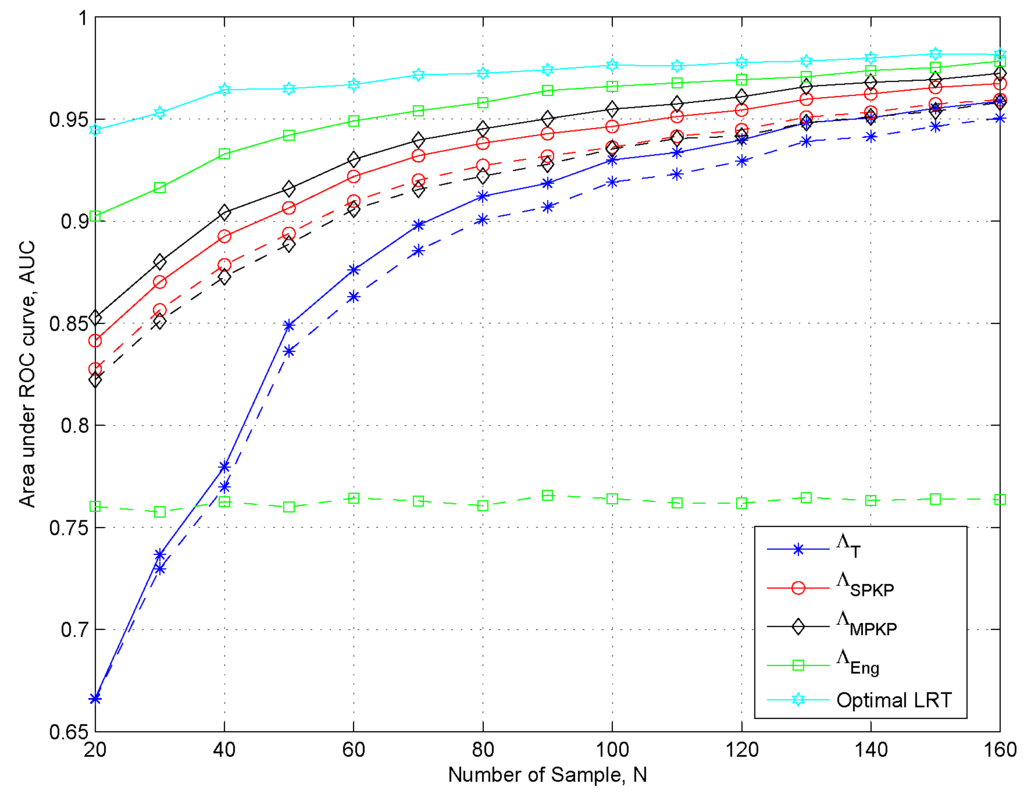
Figure 3. Area under the ROC curve to asses the effects of the sample size N, using, κ = −15 dB. Solid Lines α_nu = 1, Dashed lines α_nu = 2.

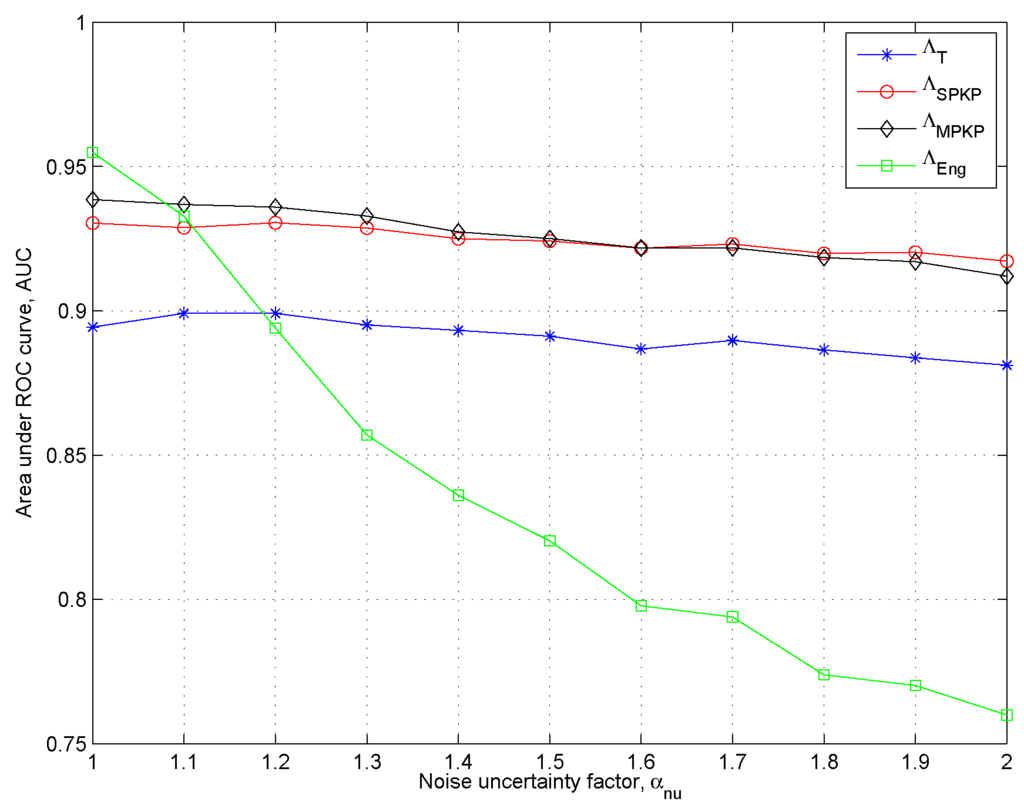
Figure 4. Area under the ROC curve to asses the effects of Noise uncertainty α_nu = 2, N = 70, κ = −15 dB.

Figure 4. Area under the ROC curve to asses the effects of Noise uncertainty α_nu = 2, N = 70, κ = −15 dB.

In Figure 5, we show the AUC plots to analyze the effect of shadowing (i.e., ${\sigma }_{\mathrm{dB}-\mathrm{Spread}}$). From the result we can see that the effect of the shadowing is very small over the detection performance of the detection schemes as the presented spectrum sensing schemes are cooperative. However, in the case of ${\Lambda }_{\mathrm{ENG}}$, the detection performance slightly increases with the increase in the ${\sigma }_{\mathrm{dB}-\mathrm{Spread}}$. The most obvious reason for this can be the heavy-tailed distribution of the primary signal strength due to the log-normally-distributed shadow fading that behave in such a way at lower SNR [27].

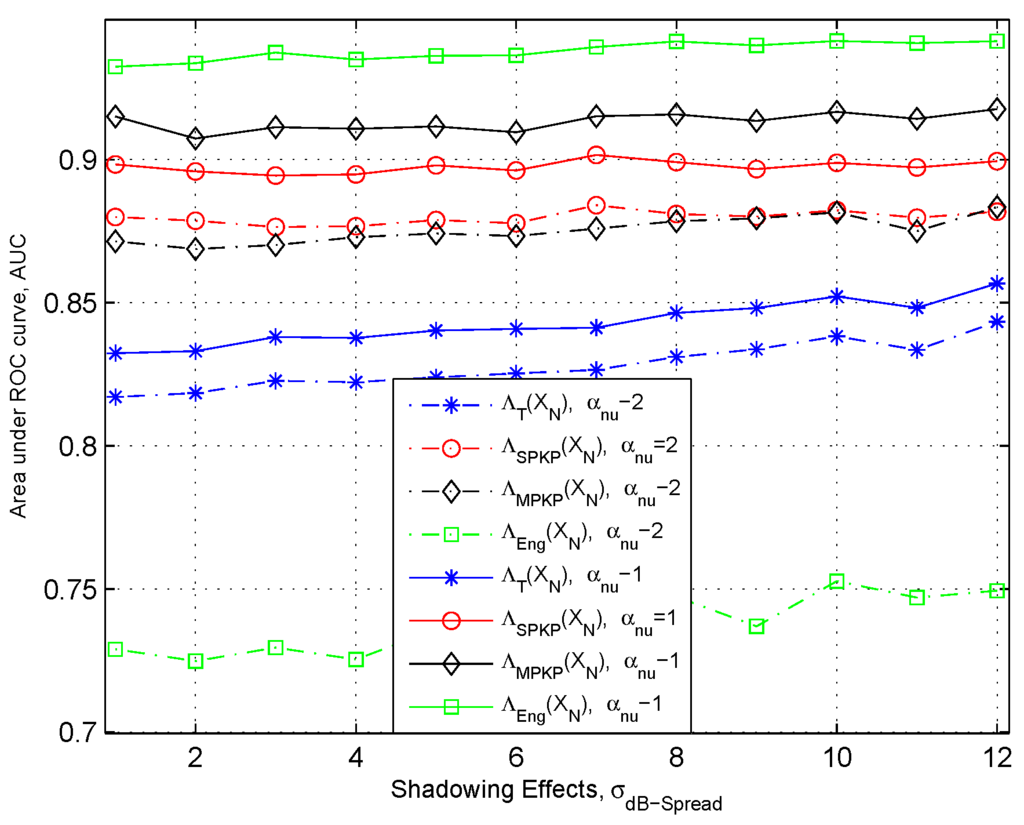
Figure 5. Area under the ROC curve to asses the effect of Shadowing, σ_dB–Spread: N = 60, κ = −15 dB and Solid Lines α_nu = 1, Dashed lines α_nu = 2.

Figure 5. Area under the ROC curve to asses the effect of Shadowing, σ_dB–Spread: N = 60, κ = −15 dB and Solid Lines α_nu = 1, Dashed lines α_nu = 2.

In Figure 6 and Figure 7, we show the AUC plots to analyze the effect of number of antennas (i.e., L) for a fixed number of users K. The results clearly show that the performances of the two proposed schemes are consistently better than the traditional schemes that confirm result in previous plots. However, we can see that the traditional GLRT ${\Lambda }_{\mathrm{T}}$ performance degrades by increasing L (i.e., $L=2$ to $L=8$). It is because for fixed $N=60$ when $L=8$, we have $KL=80>N=60$ and we get ill-conditioned sample covariance matrix needed for implementation of GLRT. One the other hand, once again the results in these figures prove that ${\Lambda }_{\mathrm{MPKP}}$ and ${\Lambda }_{\mathrm{SPKP}}$ are robust against the issue of large dimensional data and small sample support.

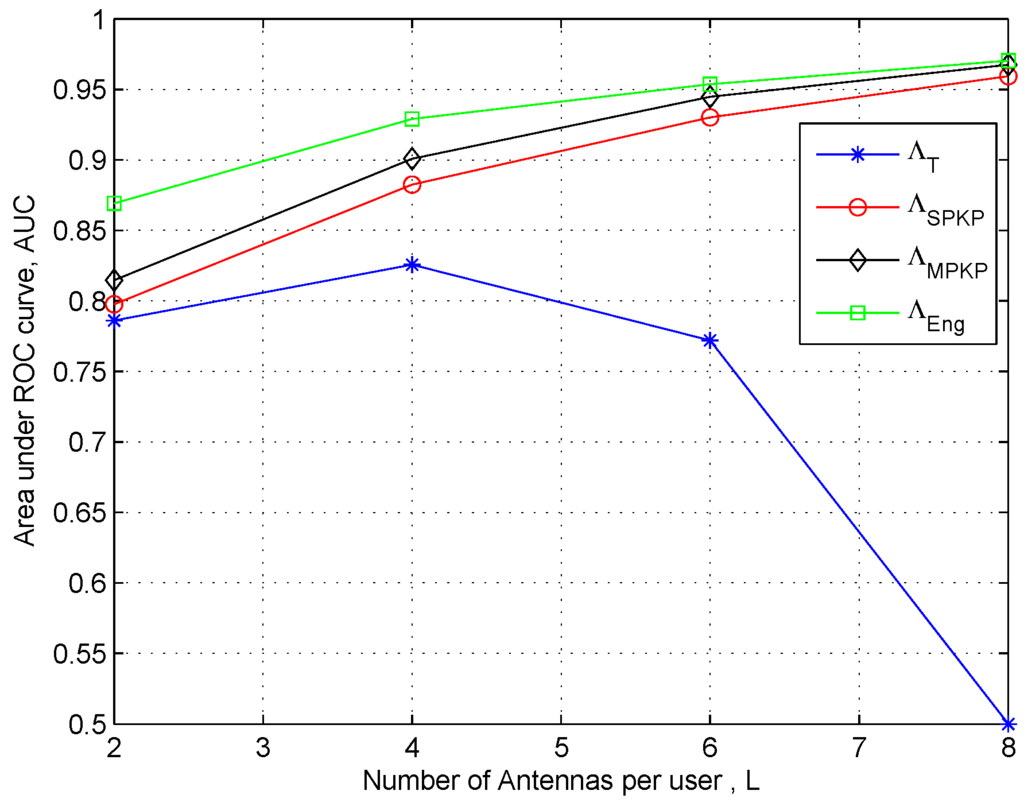
Figure 6. Area under the ROC curve to asses the effect of number of antennas: N = 60, κ = −15 dB and α_nu = 1.

Figure 6. Area under the ROC curve to asses the effect of number of antennas: N = 60, κ = −15 dB and α_nu = 1.

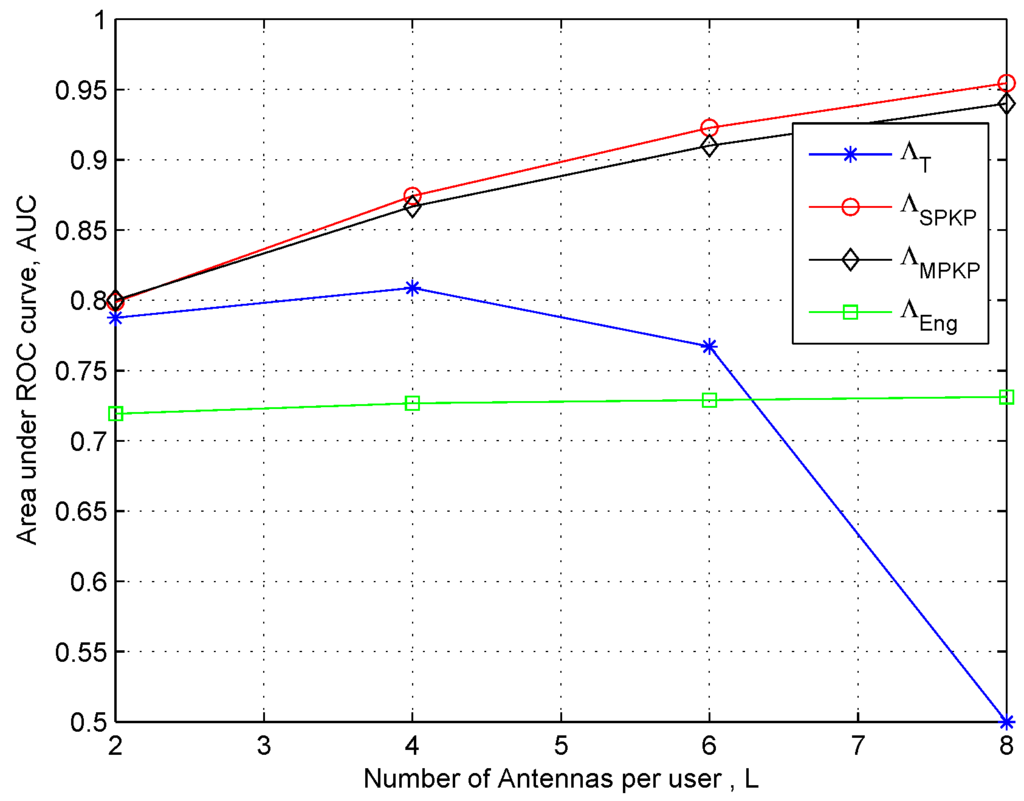
Figure 7. Area under the ROC curve to asses the effect of number of antennas: N = 60, κ = −15 dB and α_nu = 2.

Figure 7. Area under the ROC curve to asses the effect of number of antennas: N = 60, κ = −15 dB and α_nu = 2.

Finally, in order to further analyze the detection performance of the proposed schemes, for a fixed value of probability of false alarm ($P_{FA}$), in Figure 8 we compare the results by plotting probability of detection $P_D$ vs. average SNR. Once again, we can observe that the proposed schemes ${\Lambda }_{\mathrm{MPKP}}$ and ${\Lambda }_{\mathrm{SPKP}}$ outperform the remaining detection schemes presented in this paper.

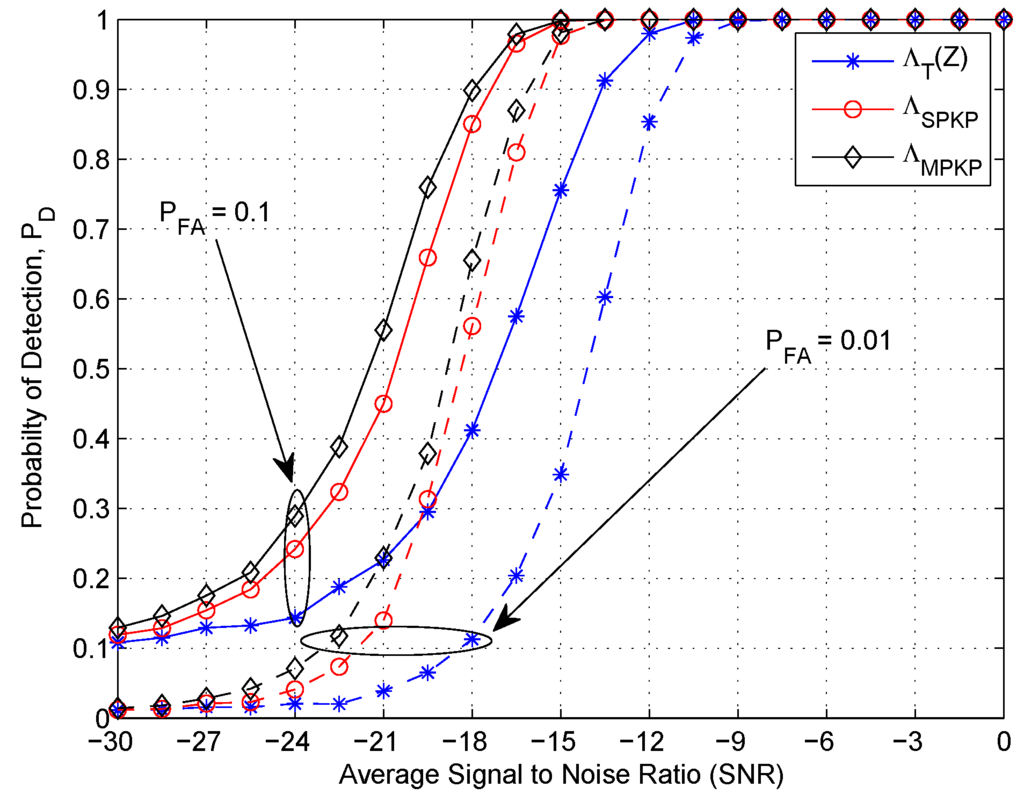
Figure 8. P_D vs average signal-to-noise ratio (SNR): Number of sensors K = 10, number of antennas L = 4, N = 100 and α_nu = 1.

Figure 8. P_D vs average signal-to-noise ratio (SNR): Number of sensors K = 10, number of antennas L = 4, N = 100 and α_nu = 1.

6. Conclusions

In this work we presented three spectrum sensing schemes that exploit the spatial correlation present in the received observations at distributed SUs, each of them equipped with multiple antennas. Even though the traditional GLRT is asymptotically an optimal detector, it performs poorly when the sample support is small. To cope with this problem we have proposed two detectors by exploring the properties of Kronecker product of matrices. The performance of the proposed detectors has been evaluated in presence of uncertain additive noise and shadowing with the help of numerical simulations, where important improvements have been shown.