Multicarrier Spread Spectrum Modulation Schemes and Efficient FFT Algorithms for Cognitive Radio Systems
Abstract
:1. Introduction
2. OFDM Based Multicarrier Modulation Schemes
2.1. Non-Contiguous OFDM
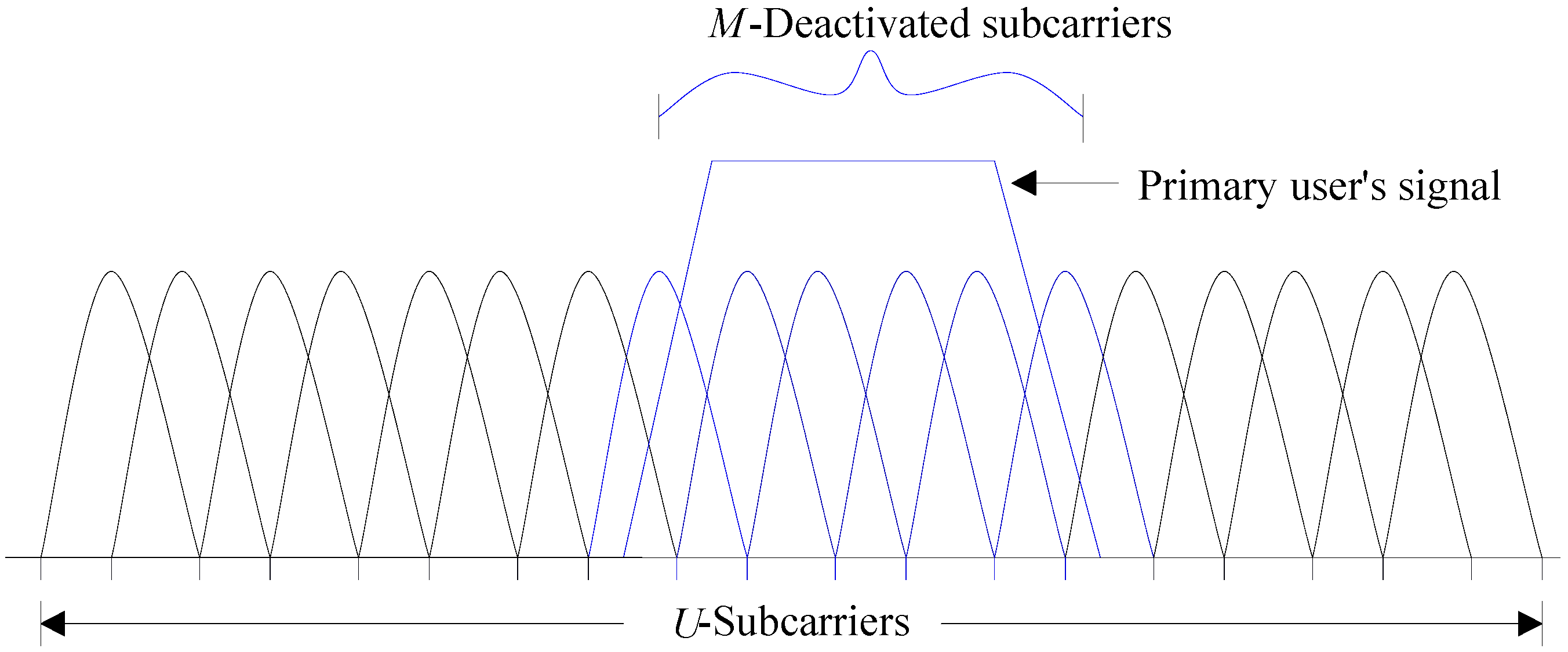

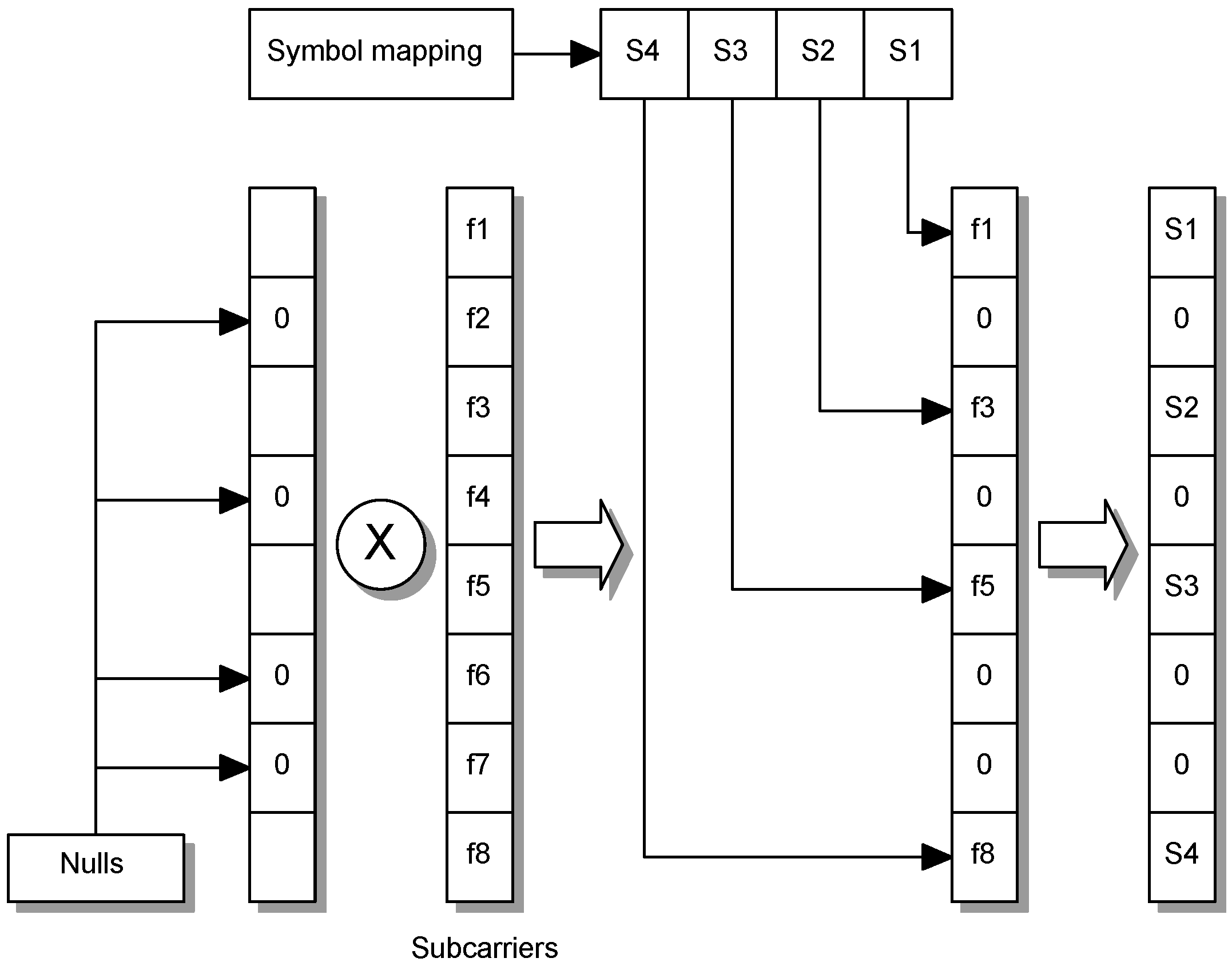
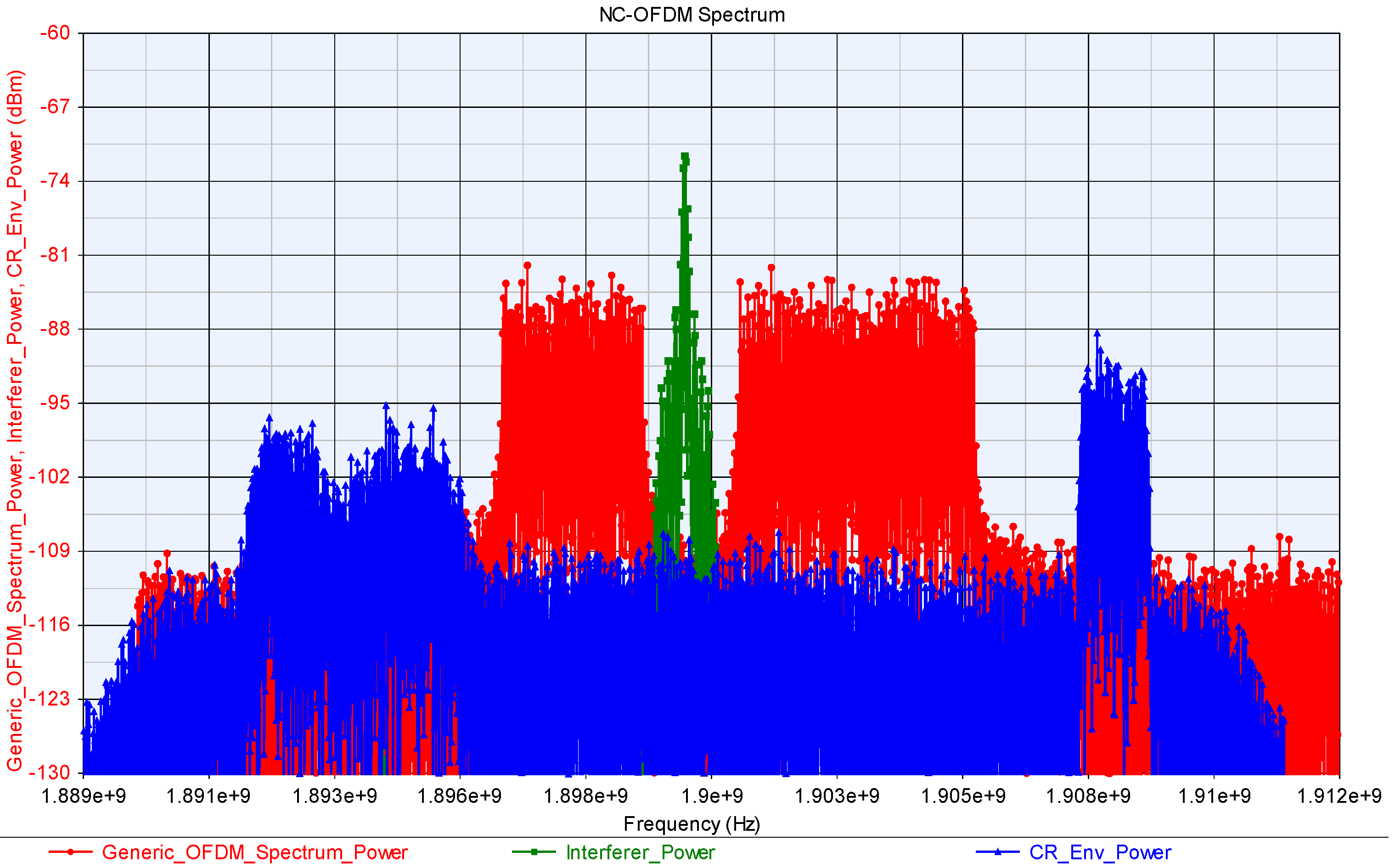
2.2. Spread OFDM
2.3. Filter Bank Multicarrier Modulation
3. Multicarrier CDMA Based Modulation Schemes
3.1. MC-CDMA
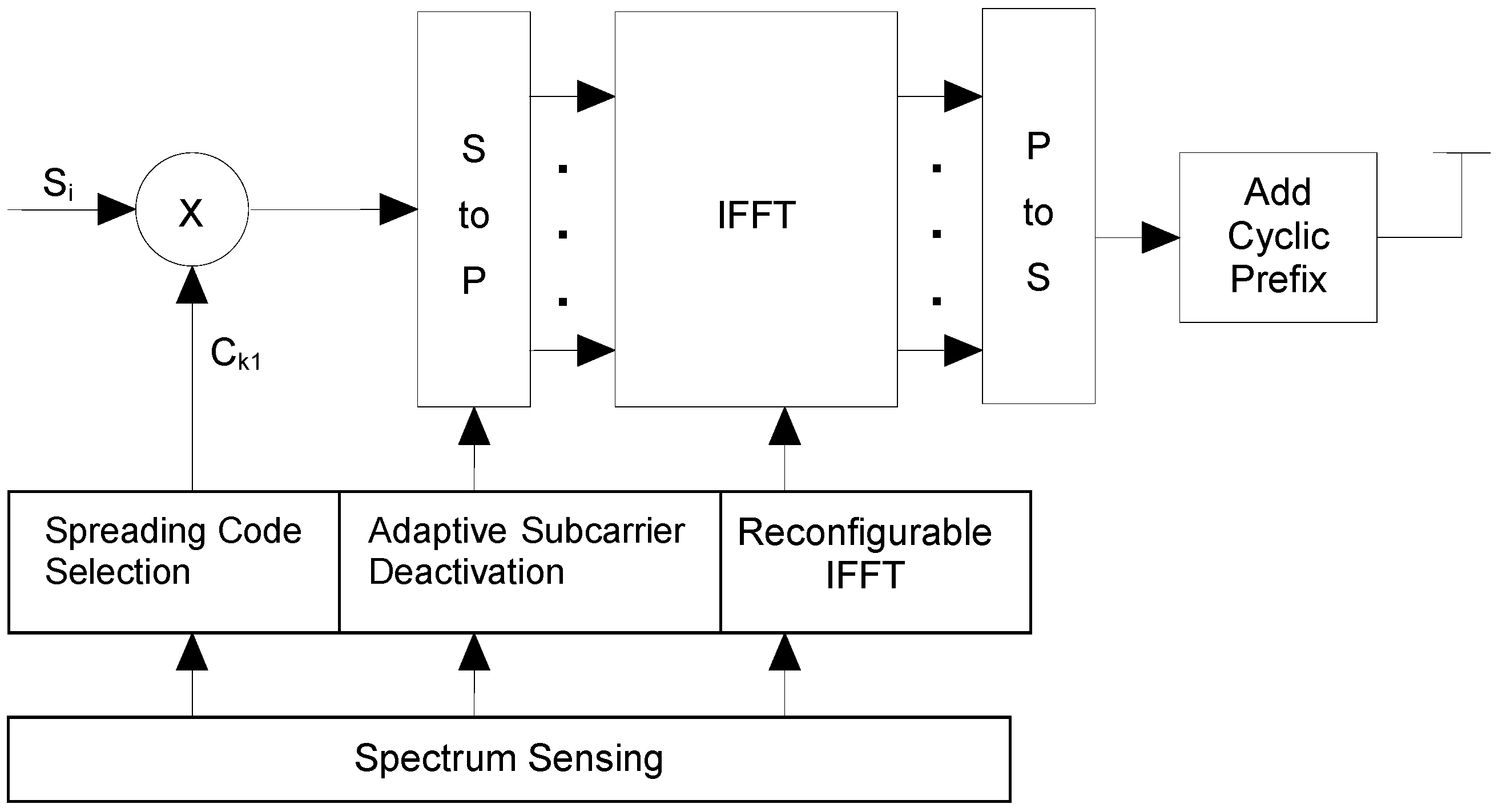
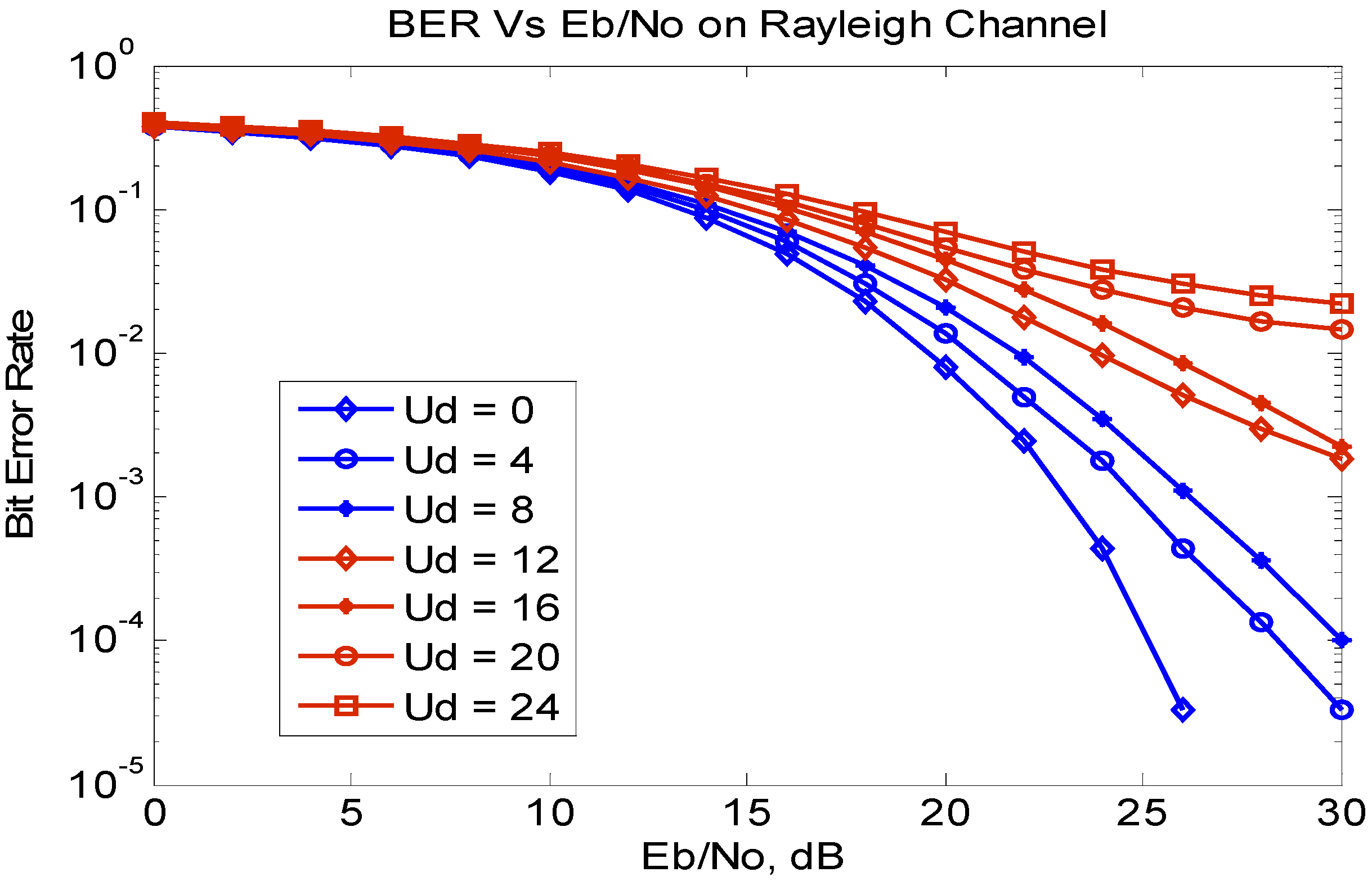
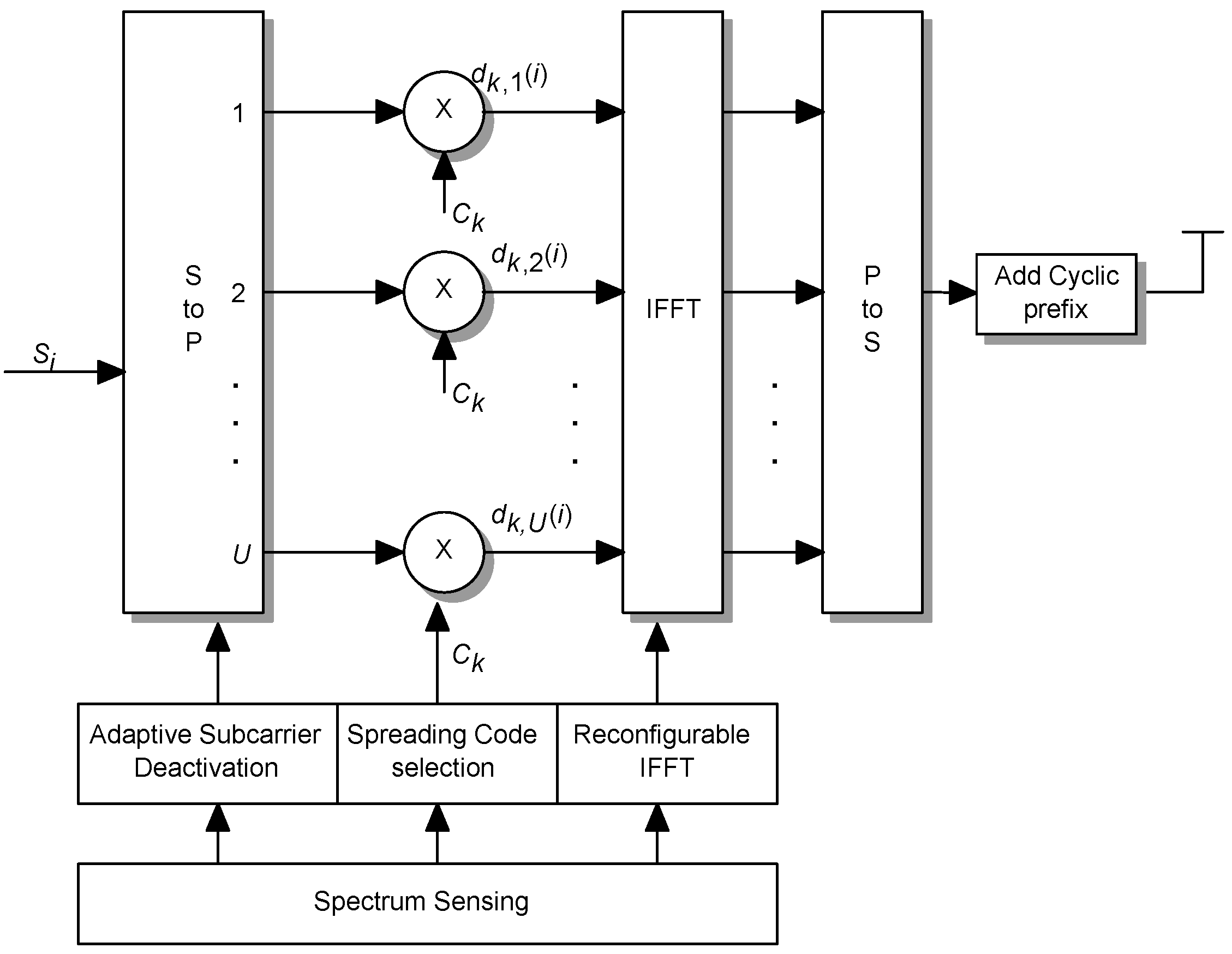
3.2. SS-MC-CDMA
3.3. CI/MC-CDMA
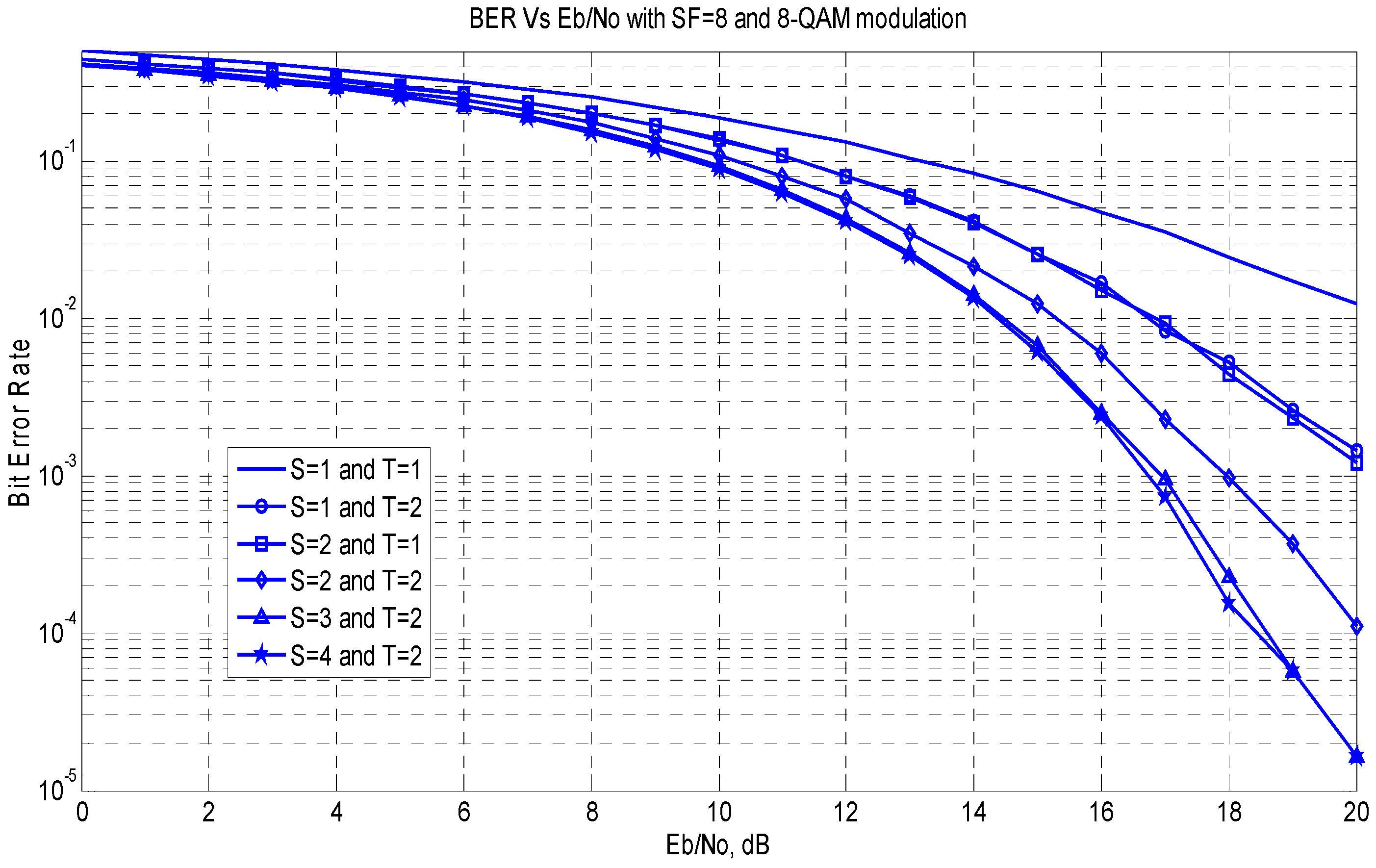
3.4. MC-DS-CDMA
| Technique | Advantages | Limitations |
|---|---|---|
| OFDM and its variants |
|
|
| FBMC and its variants |
|
|
| MC-CDMA and its variants |
|
|
4. Efficient FFT Algorithms
4.1. FFT Pruning
4.2. Modified FFT Pruning
4.3. Partial FFT Pruning
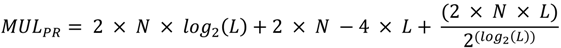

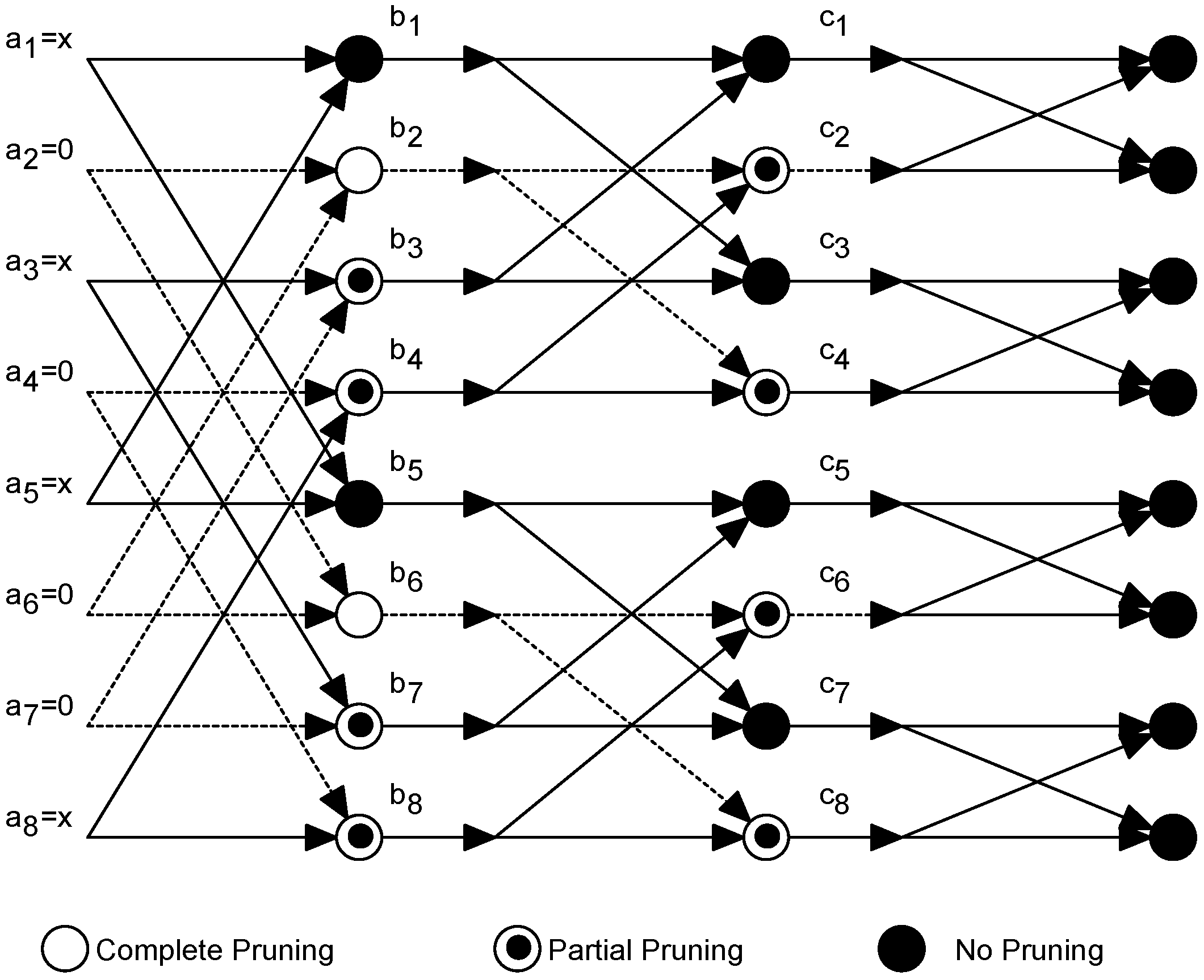
4.4. Traced FFT Pruning
4.5. Transform Decomposition

4.6. Split-radix FFT Pruning
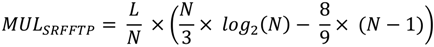
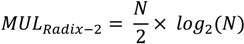
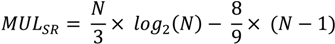
4.7. Fast Walsh-Hadamard-Fourier Transform
4.8. T-Transform
4.9. Sparse FFT
5. Summary of Efficient FFT Algorithms
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Mitola, J., III. Cognitive radio for flexible mobile multimedia communications. In Proceedings of the International Workshop on Mobile Multimedia Communications, San Diego, CA, USA, 15–17 November 1999; pp. 3–10.
- Haykin, S. Cognitive Radio: Brain-empowered Wireless Communications. IEEE J. Sel. Areas Commun. 2005, 23, 201–220. [Google Scholar] [CrossRef]
- Benmammar, B.; Amraoui, A.; Krief, F. A Survey on Dynamic Spectrum Access Techniques in Cognitive Radio Networks. Int. J. Commun. Netw. Inf. Security 2013, 5, 68–79. [Google Scholar]
- Hu, S.; Yao, Y.-D.; Yang, Z. MAC protocol identification using support vector machines for cognitive radio networks. IEEE Wireless Commun. 2014, 21, 52–60. [Google Scholar]
- Yucek, T.; Arslan, H. A Survey of Spectrum Sensing Algorithms for Cognitive Radio Applications. IEEE Commun. Surveys Tuts. 2009, 11, 116–130. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B.; Kempter, R. Multicarrier Communication Techniques for Spectrum Sensing and Communication in Cognitive Radios. IEEE Commun. Mag. 2008, 46, 80–85. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Lee, W.Y.; Vuran, M.C.; Mohanty, S. Next Generation Dynamic Spectrum Access Cognitive Radio Wireless Networks: A Survey. Elsevier J. Comput. Netw. 2006, 50, 2127–2159. [Google Scholar] [CrossRef]
- Luo, T.; Jiang, T.; Xiang, W.; Chen, H.H. A Subcarriers Allocation Scheme for Cognitive Radio Systems Based on Multi-carrier Modulation. IEEE Trans. Wireless Commun. 2008, 7, 3335–3340. [Google Scholar] [CrossRef]
- Weiss, T.A.; Jondral, F.K. Spectrum pooling: An innovative strategy for the enhancement of spectrum efficiency. IEEE Commun. Mag. 2004, 42, S8–S14. [Google Scholar] [CrossRef]
- Mahmoud, H.A.; Yucek, T.; Arslan, H. OFDM for Cognitive Radio: Merits and Challenges. IEEE Trans. Wireless Commun. 2009, 16, 6–15. [Google Scholar] [CrossRef]
- Cheng, P.; Zhang, Z.Y.; Huang, H.; Qiu, P. A distributed algorithm for optimal resource allocation in cognitive OFDMA systems. In Proceedings of IEEE International Conference on Communications, Beijing, China, 19–23 May 2008; pp. 4718–4723.
- Zhang, Y.; Leung, C. Resource Allocation in an OFDM-Based Cognitive Radio System. IEEE Trans. Commun. 2009, 57, 1928–1931. [Google Scholar] [CrossRef]
- Xu, X.; Yao, Y.-D.; Hu, S.; Yao, Y. Joint subcarrier and bit allocation for secondary user with primary users’ cooperation. KSII Trans. Int. Inf. Syst. 2013, 7, 3037–3054. [Google Scholar]
- Pagadarai, S.; Wyglinski, A.M.; Rajbanshi, R. A Novel Sidelobe Suppression Technique for OFDM-Based Cognitive Radio Transmission. In Proceedings of IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks, Chicago, IL, USA, 14–17 October 2008; pp. 1–7.
- Fu, X.; Wang, J.; Li, S.Q. Sidelobe suppression for OFDM based cognitive radio systems. In Proceedings of the International Conference on Communications and Networking in China, Xian, China, 26–28 August 2009; pp. 1–5.
- Brandes, S.; Cosovic, I.; Schnell, M. Reduction of out-of-band radiation in OFDM systems by insertion of cancellation carriers. IEEE Commun. Lett. 2006, 10, 420–422. [Google Scholar] [CrossRef]
- Mahmoud, H.A.; Arslan, H. Sidelobe suppression in OFDM based spectrum sharing systems using adaptive symbol transition. IEEE Commun. Lett. 2008, 12, 133–135. [Google Scholar] [CrossRef]
- Ghassemi, A.; Gulliver, T.A. PAPR reduction in OFDM based cognitive radio with blockwise-subcarrier activation. In Proceedings of IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 5598–5602.
- Rajbanshi, R.; Wyglinski, A.M.; Minden, G.J. Adaptive-Mode Peak-to-Average Power Ratio Reduction Algorithm for OFDM-Based Cognitive Radio. In Proceedings of IEEE Vehicular Technology Conference, Montreal, Canada, 25–28 September 2006; pp. 1–5.
- Poston, J.D.; Horne, W.D. Discontiguous OFDM considerations for dynamic spectrum access in idle TV channels. In Proceedings of IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 607–610.
- Wylie-Green, M.P. Dynamic spectrum sensing by multiband OFDM radio for interference mitigation. In Proceedings of IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 619–625.
- Tang, H. Some physical layer issues of wide-band cognitive radio systems. In Proceedings of IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks, Baltimore, MD, USA, 8–11 November 2005; pp. 151–159.
- Park, M.; Jun, H.; Cho, J.; Cho, N.; Hong, D.; Kang, C. PAPR reduction in OFDM transmission using Hadamard transform. In Proceedings of IEEE International Conference on Communications, New Orleans, LA, USA, 18–22 June 2000; pp. 430–433.
- Dlugaszewski, Z.; Wesolowski, K. WHT/OFDM—An improved OFDM transmission method for selective fading channels. In Proceedings of IEEE Symposium on Communications and Vehicular Technology, Leuven, Belgium, 19 October 2000; pp. 144–149.
- Wu, Y.; Ho, C.K.; Sun, S. On some properties of Walsh-Hadamard transformed OFDM. In Proceedings of IEEE Vehicular Technology Conference-Fall, Vancouver, BC, Canada, 24–28 September 2002; pp. 2096–2100.
- Shaopeng, W.; Shihua, Z.; Guomei, Z. A Walsh-Hadamard coded spectral efficient full frequency diversity OFDM system. IEEE Trans. Commun. 2010, 58, 28–34. [Google Scholar] [CrossRef]
- Li, X.; Chakravarthy, V.D.; Wang, B.; Wu, Z. Spreading Code Design of Adaptive Non-Contiguous SOFDM for Dynamic Spectrum Access. IEEE J. Sel. Topics Signal Process. 2011, 5, 190–196. [Google Scholar] [CrossRef]
- Zhang, C. Non-continuous carrier-interferometry codes. In Proceedings of International Workshop on Signal Design and its Application in Communications, Fukuoka, Japan, 19–23 October 2009; pp. 134–137.
- Wiegandt, D.A.; Wu, Z.-Q.; Nassar, C.R. High-throughput, high performance OFDM via pseudo-orthogonal carrier interferometry spreading codes. IEEE Trans. Commun. 2003, 51, 1123–1134. [Google Scholar] [CrossRef]
- Kollar, Z.; Horvath, P. Physical Layer Considerations for Cognitive Radio: Modulation Techniques. In Proceedings of IEEE Vehicular Technology Conference (VTC Spring), Yokohama, Japan, 15–18 May 2011; pp. 1–5.
- Myung, H.G.; Lim, J.; Goodman, D.J. Single Carrier FDMA for Uplink Wireless Transmission. IEEE Veh. Technol. Mag. 2006, 1, 30–38. [Google Scholar] [CrossRef]
- Farhang-Boroujeny, B. Ofdm versus filter bank multicarrier. IEEE Signal Process. Mag. 2011, 28, 92–112. [Google Scholar] [CrossRef]
- Elezabi, A.; Kashef, M.; Abdallah, M.; Khairy, M.M. Cognitive interference-minimizing code assignment for underlay CDMA networks in asynchronous multipath fading channels. In Proceedings of the 2009 International Conference on Wireless Communications and Mobile Computing (IWCMC ’09), Leipzig, Germany, 21–24 June 2009; pp. 1279–1283.
- Elezabi, A.; Kashef, M.; Abdallah, M.; Khairy, M. CDMA underlay network with cognitive interference-minimizing code assignment and semi-blind interference suppression. Wirel. Commun. Mob. Comput. 2009, 9, 1460–1471. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, D. Performance analysis in CDMA-based cognitive wireless networks with spectrum underlay. In Proceedings of IEEE Global Telecommunication conference (GLOBECOM), New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6.
- Hoang, A.T.; Liang, Y.-C. A two-phase channel and power allocation scheme for cognitive radio networks. In Proceedings of the IEEE 17th International conference on PersonalIndoor and Mobile Radio Communications, Helsinki, Finland, 11–14 September 2006; pp. 1–5.
- Zhang, X.; Su, H. Opportunistic spectrum sharing schemes for CDMA-based uplink MAC in cognitive radio networks. IEEE J. Sel. Areas Commun. 2011, 29, 716–730. [Google Scholar] [CrossRef]
- Li, M.; Batalama, S.N.; Pados, D.A.; Melodia, T.; Medley, M.J.; Matyjas, J.D. Cognitive code-division links with blind primary-system identification. IEEE Trans. Wireless Commun. 2011, 10, 3743–3753. [Google Scholar] [CrossRef]
- Yang, B.; Feng, G.; Shen, Y.; Long, C.; Guan, X. Channel-aware access for cognitive radio networks. IEEE Trans. Veh. Technol. 2009, 58, 3726–3737. [Google Scholar] [CrossRef]
- Dashti, M.; Azmi, P. Joint power and rate allocation in CDMA-based underlay cognitive radio networks for a mixture of streaming and elastic traffic. EURASIP J. Wirel. Commun. Netw. 2012, 2012, 262–272. [Google Scholar] [CrossRef]
- Roy, S.D.; Upadhayay, N.K.; Kundu, S. Performance of Joint Admission and Power Control Algorithms for Cognitive Radio CDMA Networks in Shadowed Environment. Int. J. of Comm. Net. Sec. 2011, 1, 1–6. [Google Scholar] [CrossRef]
- Roy, S.D.; Kundu, S.; Ferrari, G.; Raheli, R. Cognitive radio CDMA networking with spectrum sensing. Int. J. Commun. Syst. 2012. [Google Scholar] [CrossRef]
- Roy, S.D.; Kundu, S.; Ferrari, G.; Raheli, R. On spectrum sensing in cognitive radio CDMA networks with beamforming. Elsevier Phys. Commun. 2013, 9, 73–87. [Google Scholar]
- Hussein, N.M. Modified Greedy Algorithm for Cognitive DS-CDMA System. Int. J. Adv. Res. Comput. Commun. Eng. 2013, 2, 2321–2326. [Google Scholar]
- Sarath, D.; Nolan, K.E.; Sutton, P.D.; Doyle, L.E. Exploring The Reconfigurability Options of Multi-Carrier CDMA in Cognitive Radio Systems. In Proceedings of IEEE International Symposium on PersonalIndoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007; pp. 1–5.
- Prasad, R.; Hara, S. Overview of multicarrier CDMA. IEEE Commun. Mag. 1997, 35, 126–133. [Google Scholar]
- Rajbanshi, R.; Chen, Q.; Wyglinski, A.M.; Minden, G.J.; Evans, J.B. Quantitative comparison of agile modulation techniques for cognitive radio transceivers. In Proceedings of IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 11–13 January 2007; pp. 1144–1148.
- Mohandass, S.; Umamaheswari, G. Modelling and Simulation of Interference Cancellation Receiver for MIMO Multicarrier CDMA based Cognitive Radio. Int. Rev. Mod. Sim. 2014, 7, 196–205. [Google Scholar]
- Attar, A.; Nakhai, M.R.; Aghvami, A.H. Cognitive Radio Transmission Based on Direct Sequence MC-CDMA. IEEE Trans. Wirel. Commun. 2008, 7, 1157–1162. [Google Scholar] [CrossRef]
- Luo, T.; Lin, F.; Jiang, T.; Guizani, M.; Chen, W. Multicarrier modulation and cooperative communication in multihop cognitive radio networks. IEEE Wireless Commun. 2011, 18, 38–45. [Google Scholar] [CrossRef]
- Sarath, D.; Nolan, K.E.; Sutton, P.D.; Doyle, L.E. Enabling Dynamic Spectrum Access using SS-MC-CDMA. In Proceedings of International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Orlando, FL, USA, 1–3 August 2007; pp. 193–198.
- Natarajan, B.; Nassar, C.R.; Shattil, S.; Michelini, M.; Wu, Z. High-Performance MC-CDMA via Carrier Interferometry Codes. IEEE Trans. Veh. Technol. 2001, 50, 1344–1353. [Google Scholar] [CrossRef]
- Natarajan, B.; Wu, Z.; Nassar, C.R.; Shattil, S. Large Set of CI Spreading Codes for High-Capacity MC-CDMA. IEEE Trans. Commun. 2004, 52, 1862–1866. [Google Scholar] [CrossRef]
- Mukherjee, M.; Kumar, P. Design and performance of WH-spread CI/MC-CDMA with iterative interference cancellation receiver. Elsevier Phys. Commun. 2012, 5, 217–229. [Google Scholar] [CrossRef]
- Chang, C.W. An Interference-Avoidance Code Assignment Strategy for the Hierarchical Two-Dimensional-Spread MC-DS-CDMA System: A Prototype of Cognitive Radio Femtocell System. IEEE Trans. Veh. Technol. 2012, 61, 166–184. [Google Scholar] [CrossRef]
- Chang, C.W.; Kuo, C.C. An Interweave Cognitive Radio System Based on the Hierarchical 2D-Spread MC-DS-CDMA. In Proceedings of IEEE Vehicular Technology Conference Fall, Ottawa, ON, Canada, 6–9 September 2010; pp. 1–5.
- Yang, L.L.; Wang, L.C. Zero-forcing and minimum mean-square error multiuser detection in generalized multicarrier DS-CDMA systems for cognitive radio. EURASIP J. Wirel. Commun. Netw. 2008, 2008, 1–13. [Google Scholar]
- Markel, J. FFT Pruning. IEEE Trans. Audio Electroacoust. 1971, 19, 305–311. [Google Scholar] [CrossRef]
- Skinner, D.P. Pruning the decimation-in-time FFT algorithm. IEEE Trans. Acoust. Speech Signal Process. 1976, 24, 193–194. [Google Scholar] [CrossRef]
- Sreenivas, T.V.; Rao, P.V.S. FFT algorithm for both input and output pruning. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 291–292. [Google Scholar] [CrossRef]
- Jaroslavski, L.P. Comments on FFT algorithm for both input and output pruning. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 448–449. [Google Scholar] [CrossRef]
- Holm, S. FFT pruning applied to time domain interpolation and peak localization. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1776–1778. [Google Scholar] [CrossRef]
- He, S.; Torkelson, M. Computing Partial DFT for Comb Spectrum Evaluation. IEEE Signal Process. Lett. 1996, 3, 173–175. [Google Scholar] [CrossRef]
- Alves, R.G.; Osorio, P.L.; Swamy, M.N.S. General FFT Pruning Algorithm. In Proceedings of IEEE Midwest Symposium on Circuits and Systems, Lansing, MI, USA, 8–11 August 2000; pp. 1192–1195.
- Rajbanshi, R.; Wyglinski, A.M.; Minden, G.J. An Efficient Implementation of NC-OFDM Transceivers for Cognitive Radios. In Proceedings of International Conference on Cognitive Radio Oriented Wireless Networks and Communications, Mykonos Island, Greece, 8–10 June 2006; pp. 1–5.
- Cooley, J.W.; Tukey, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Airoldi, R.; Anjum, O.; Garzia, F.; Nurmi, J.; Wyglinski, M. Energy-efficient Fast Fourier Transforms for Cognitive Radio Systems. IEEE Micro 2010, 30, 66–76. [Google Scholar]
- Hu, Z.; Wan, H. A Novel Generic Fast Fourier Transform Pruning Technique and Complexity Analysis. IEEE Trans. Signal Process. 2005, 53, 274–282. [Google Scholar] [CrossRef]
- Sorensen, H.V.; Burrus, S. Efficient Computation of the DFT with Only a Subset of Input or Output Points. IEEE Trans. Signal Process. 1993, 41, 1184–1200. [Google Scholar] [CrossRef]
- Zhang, Q.; Kokkeler, A.B.J.; Smit, G.J.M. An Efficient FFT for OFDM Based Cognitive Radio on a Reconfigurable Architecture. In Proceedings of the IEEE International Conference on Communication, Glasgow, 24–28 June 2007; pp. 6522–6526.
- Zhang, Q.; Kokkeler, A.B.J.; Smit, G.J.M. An efficient multi-resolution spectrum sensing method for cognitive radio. In Proceedings of the International Conference on Communications and Networking in China, Hangzhou, China, 25–27 August 2008; pp. 1226–1229.
- Cui, Y.; Zhao, Z.; Zhang, H. An efficient transform decomposition method for sparse input points DFT in multiple-carriers cognitive radio system. In Proceedings of the International Symposium on Communications and Information Technologies, Tokyo, Japan, 26–29 October 2010; pp. 1200–1204.
- Chen, Z.; Lee, M.H.; Kim, C.J. Fast Hybrid DFT/DCT Architecture for OFDM in Cognitive Radio System. In Proceedings of the International Conference on Future Generation Communication and Networking, Jeju Island, Korea, 6–8 December 2007; pp. 301–306.
- Xu, Y.; Lim, M.S. Split-Radix FFT pruning for the reduction of computational complexity in OFDM based Cognitive Radio system. In Proceedings of the International Symposium on Communications and Information Technology, Icheon, Korea, 28–30 September 2009; pp. 421–424.
- Duhamel, P.; Hollmann, H. Split-radix FFT algorithm. Electron. Lett. 1984, 20, 14–16. [Google Scholar] [CrossRef]
- Hamood, M.T.; Boussakta, S. Fast Walsh Hadamard Fourier Transform Algorithm. IEEE Trans. Signal Process. 2011, 59, 5627–5631. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Boussakta, S.; Sharif, B.S.; Tsimenidis, C.C. OFDM Based on Low Complexity Transform to Increase Multipath Resilience and Reduce PAPR. IEEE Trans. Signal Process. 2011, 59, 5994–6007. [Google Scholar] [CrossRef]
- Schneider, D. A Faster Fast Fourier Transform: New algorithm crunches sparse data with speed. IEEE Spectr. 2012, 49, 12–13. [Google Scholar] [CrossRef]
- Hassanieh, H.; Indyk, P.; Katabi, D.; Price, E. Simple and Practical Algorithm for Sparse Fourier Transform. In Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, Kyoto, Japan, 17–19 January 2012; pp. 1183–1194.
- Hsieh, S.H.; Lu, C.S.; Pei, S.C. Sparse Fast Fourier Transform by downsampling. In Proceedings of the IEEE International Conference on AcousticsSpeech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 5637–5641.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sundararajan, M.; Govindaswamy, U. Multicarrier Spread Spectrum Modulation Schemes and Efficient FFT Algorithms for Cognitive Radio Systems. Electronics 2014, 3, 419-443. https://doi.org/10.3390/electronics3030419
Sundararajan M, Govindaswamy U. Multicarrier Spread Spectrum Modulation Schemes and Efficient FFT Algorithms for Cognitive Radio Systems. Electronics. 2014; 3(3):419-443. https://doi.org/10.3390/electronics3030419
Chicago/Turabian StyleSundararajan, Mohandass, and Umamaheswari Govindaswamy. 2014. "Multicarrier Spread Spectrum Modulation Schemes and Efficient FFT Algorithms for Cognitive Radio Systems" Electronics 3, no. 3: 419-443. https://doi.org/10.3390/electronics3030419
APA StyleSundararajan, M., & Govindaswamy, U. (2014). Multicarrier Spread Spectrum Modulation Schemes and Efficient FFT Algorithms for Cognitive Radio Systems. Electronics, 3(3), 419-443. https://doi.org/10.3390/electronics3030419




