High-Feedback Operation of Power Electronic Converters
Abstract
:1. Introduction
1.1. Power Electronic Converter Systems
1.2. Bifurcations in a Piecewise-Smooth System
1.3. Purpose and Content of the Review
2. Border-Collision Bifurcations in Piecewise-Linear Systems
2.1. The Sewing Approach
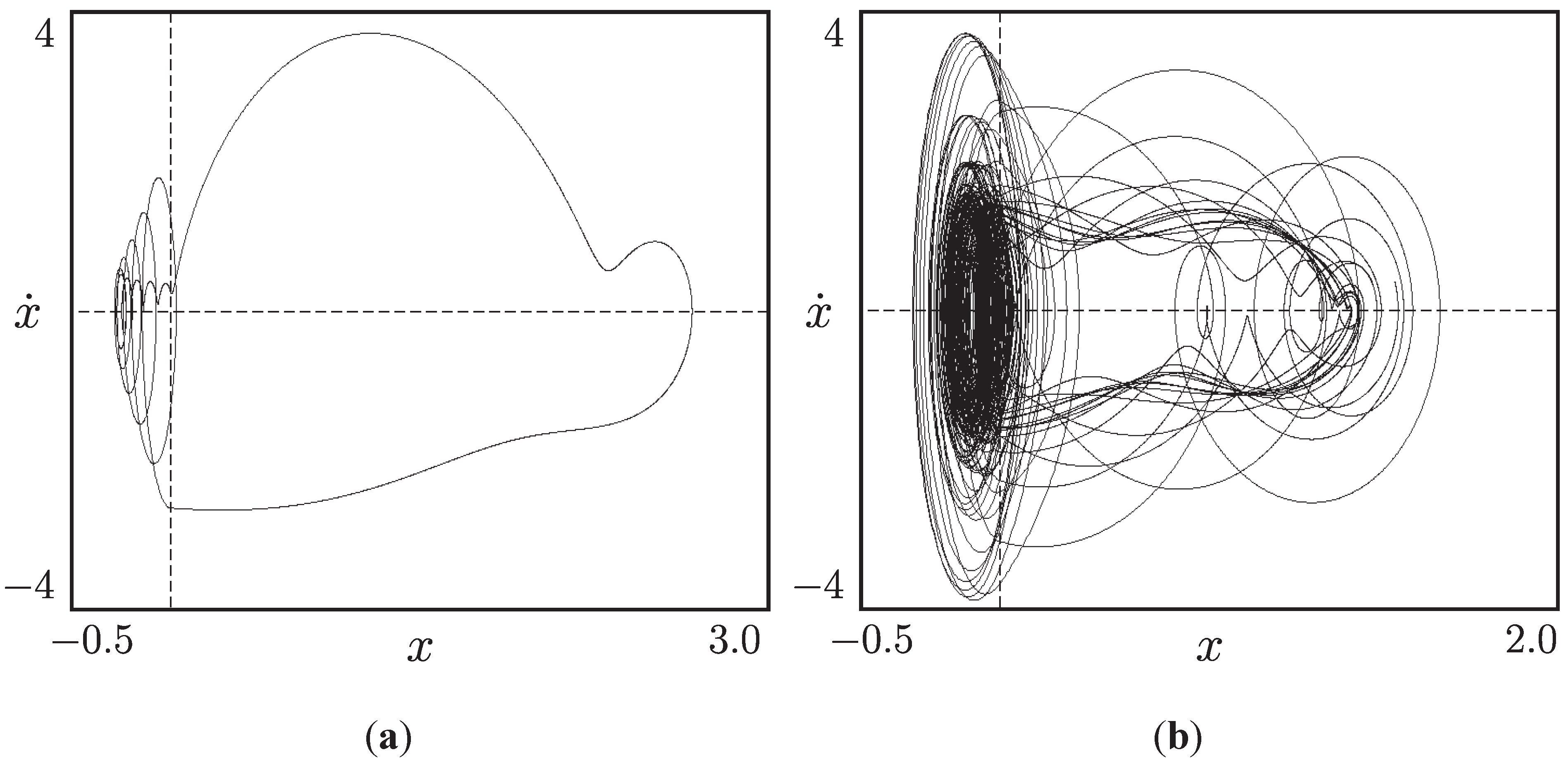
2.2. Modification of the Period-Doubling Bifurcations


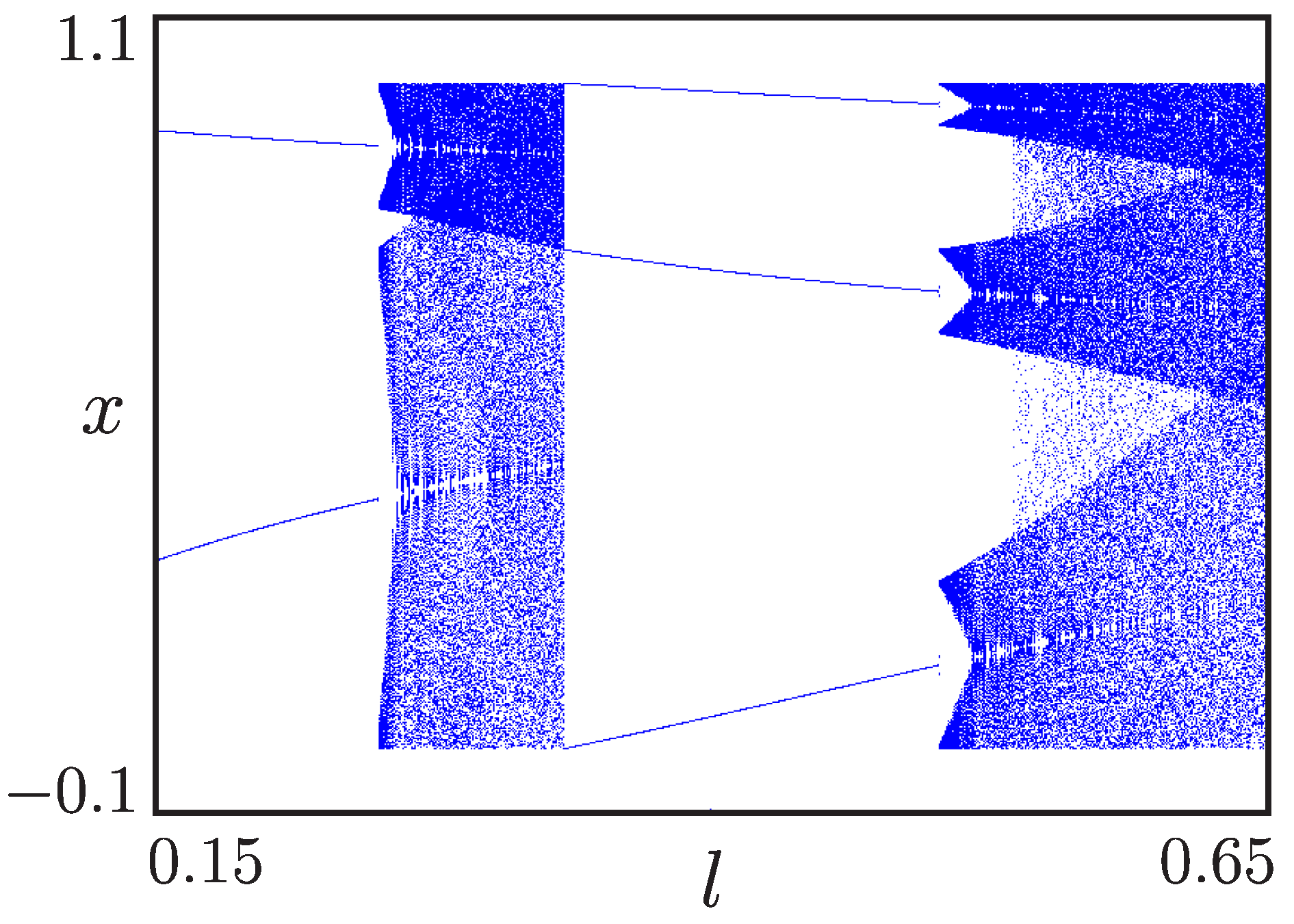
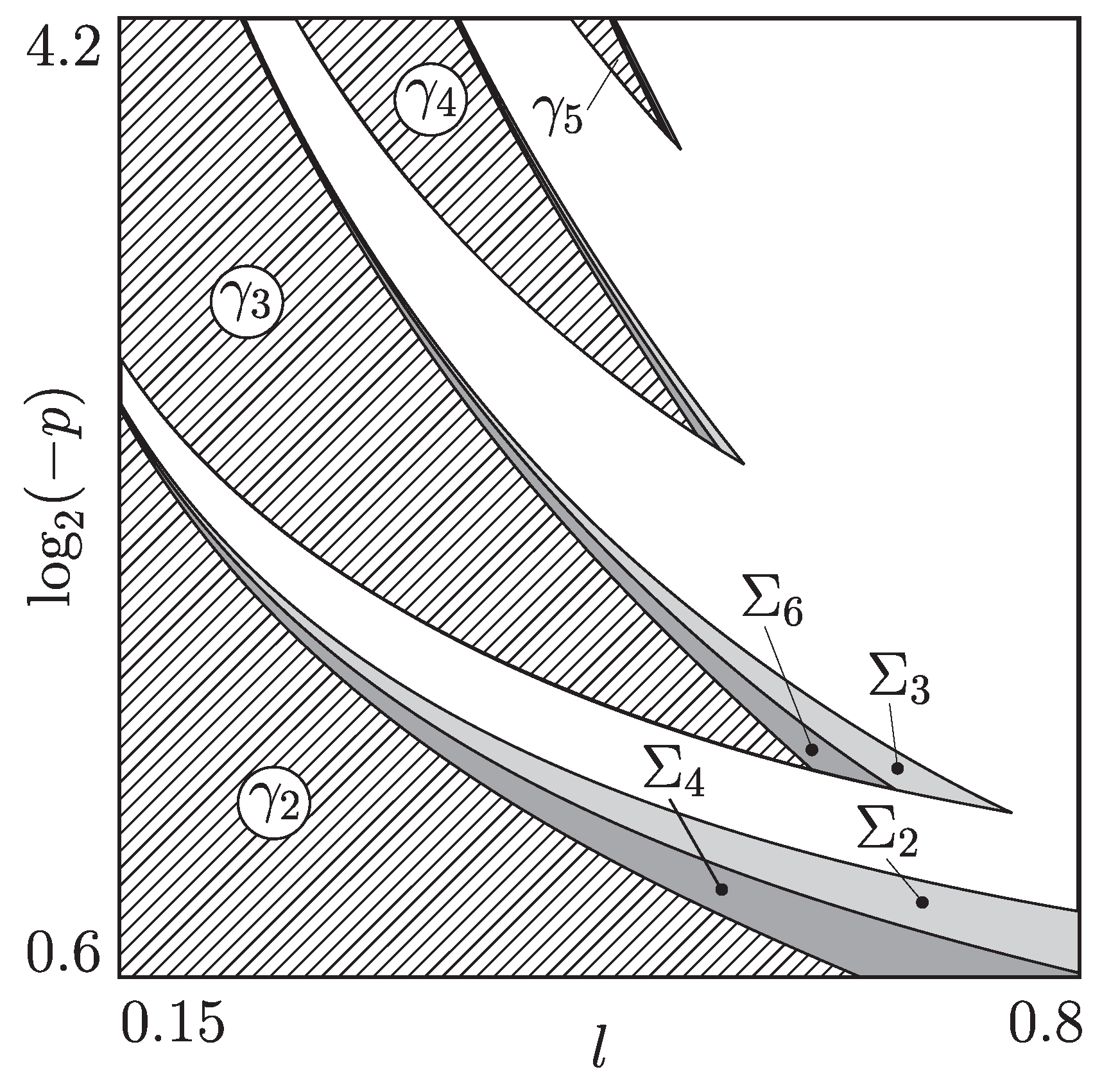
2.3. Border-Collision Bifurcations
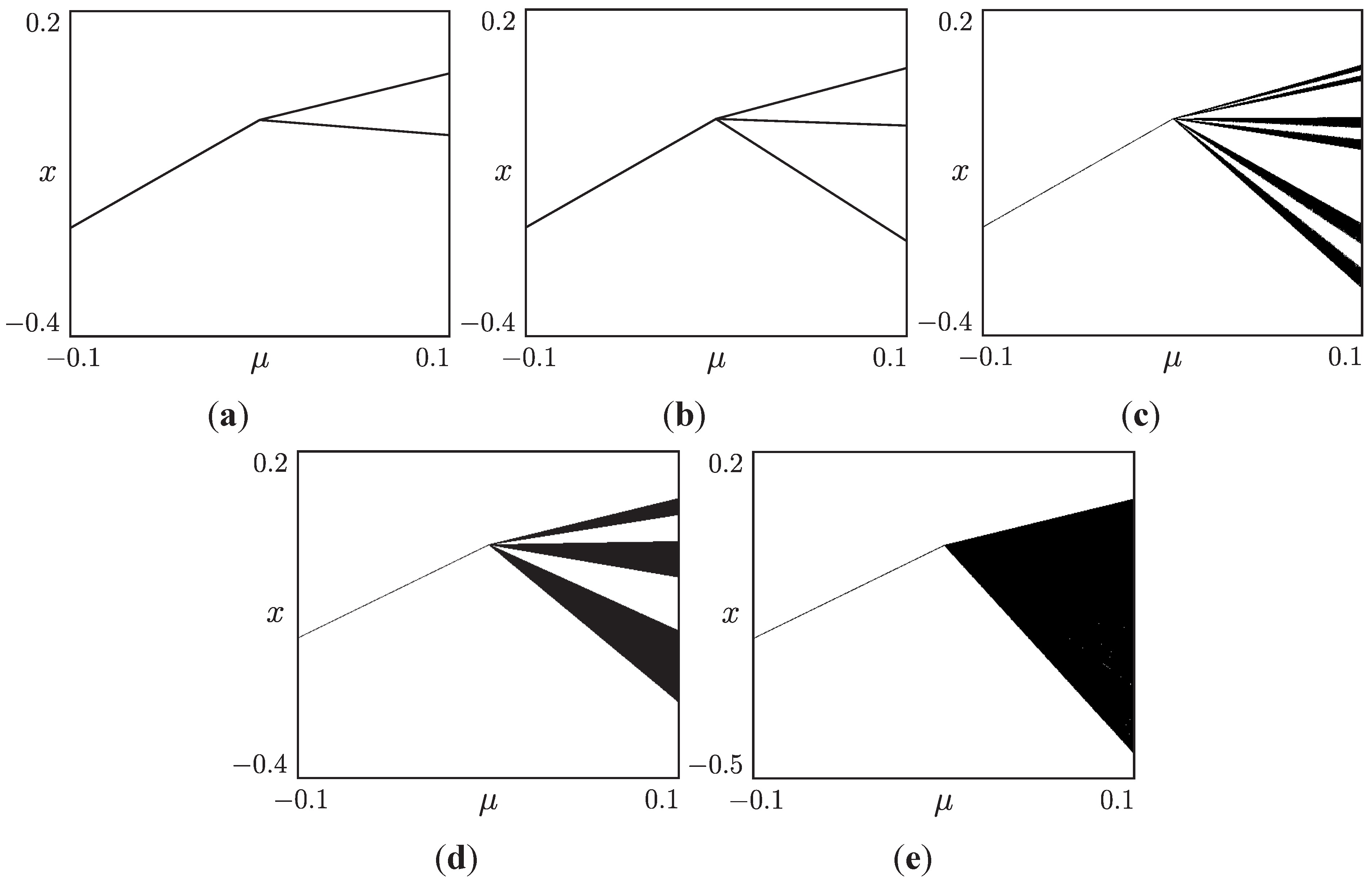
2.4. Synchronization Phenomena in Piecewise-Linear Systems
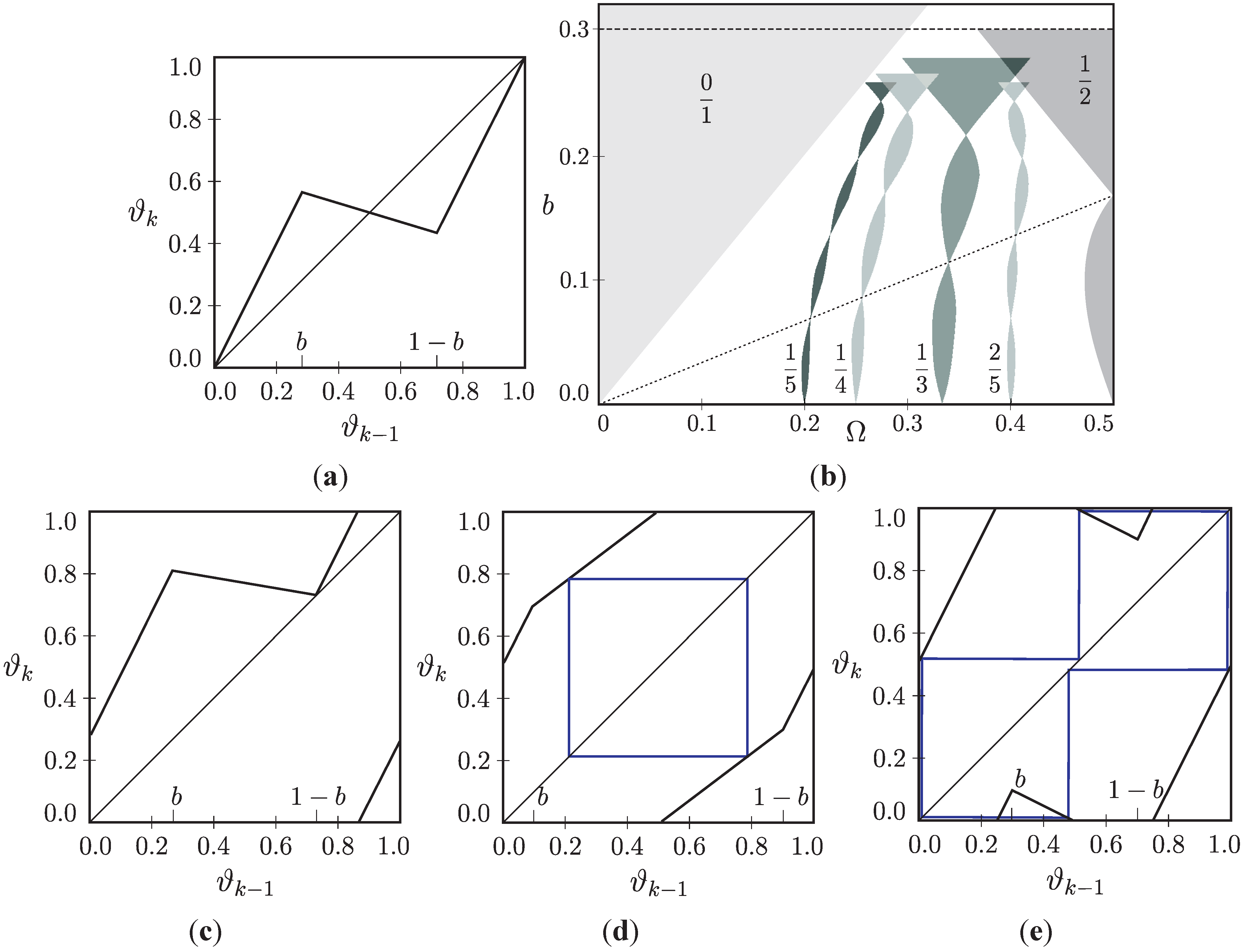
3. DC/DC Converter System
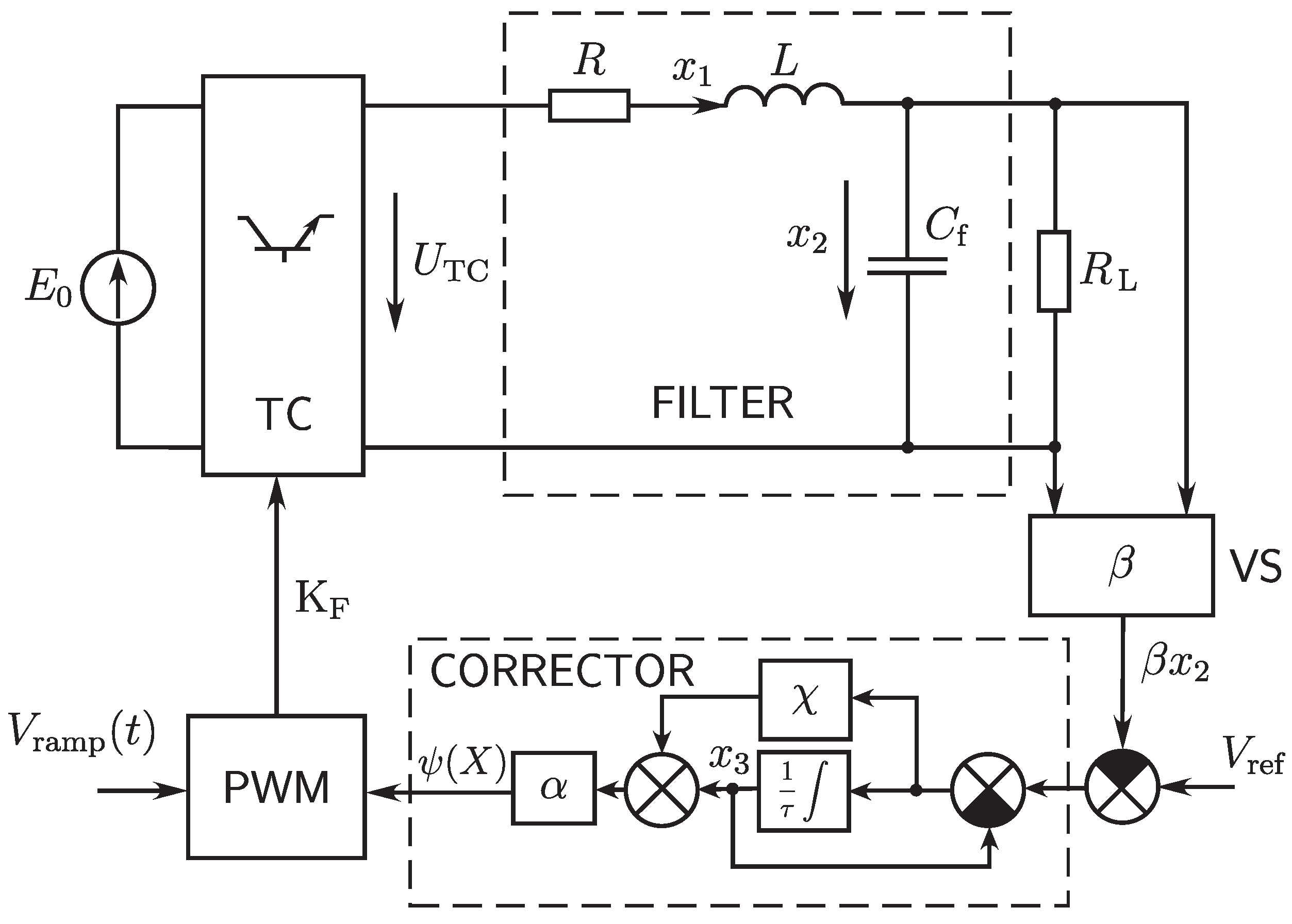
3.1. Model of a DC/DC Converter

3.2. Piecewise-Smooth Map
3.3. Methods of Bifurcation Analysis
3.4. Subcritical Torus-Birth Bifurcation
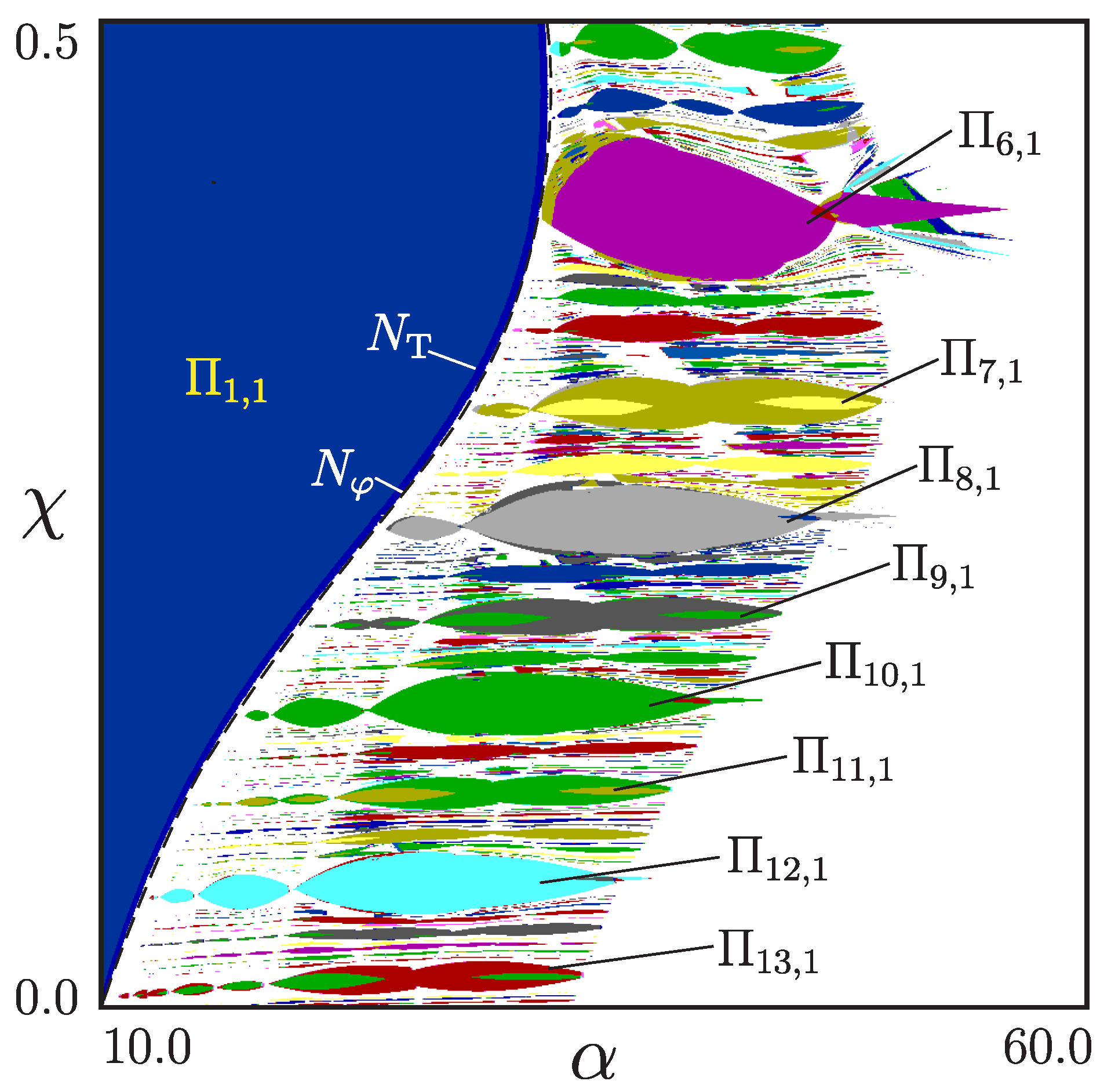
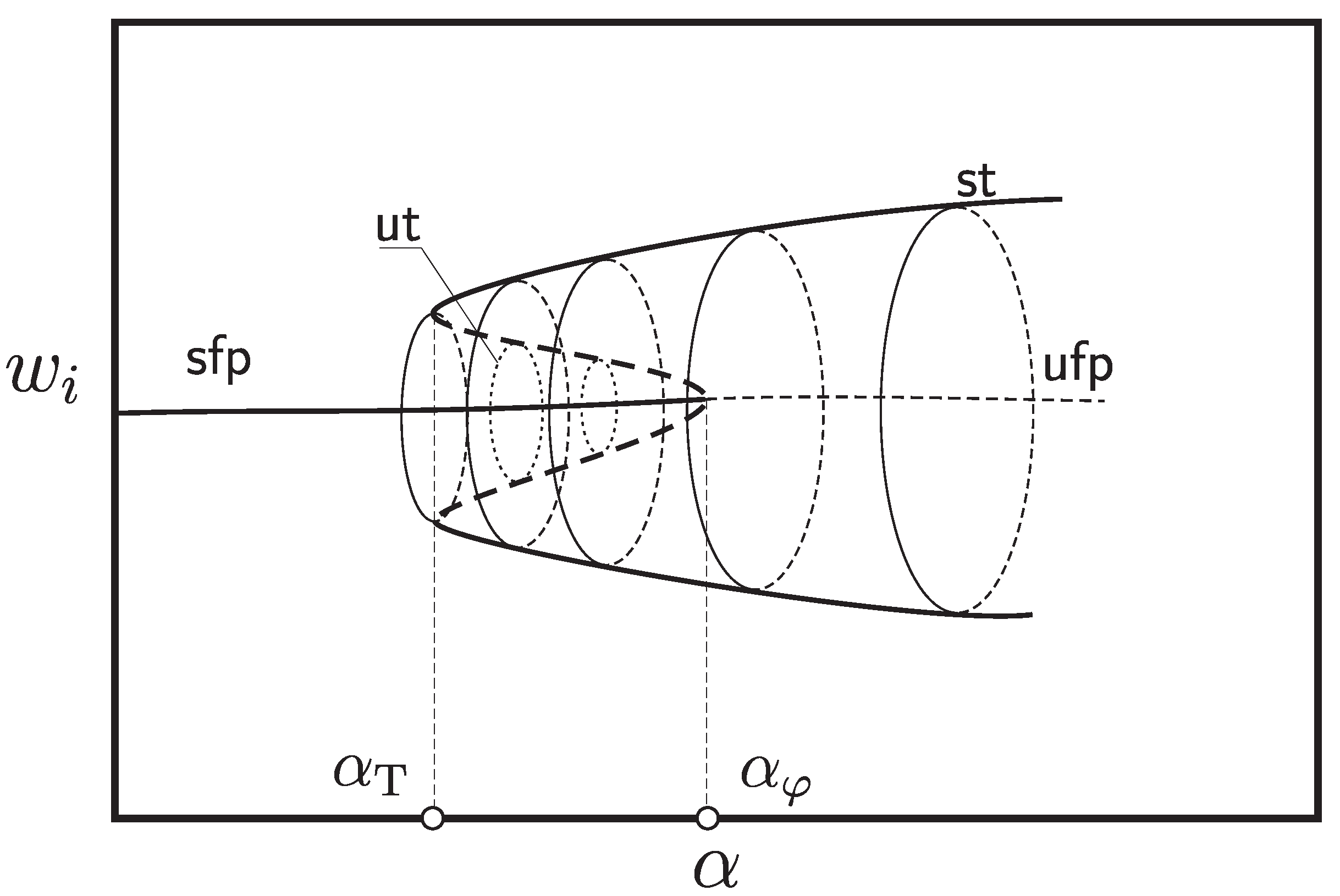
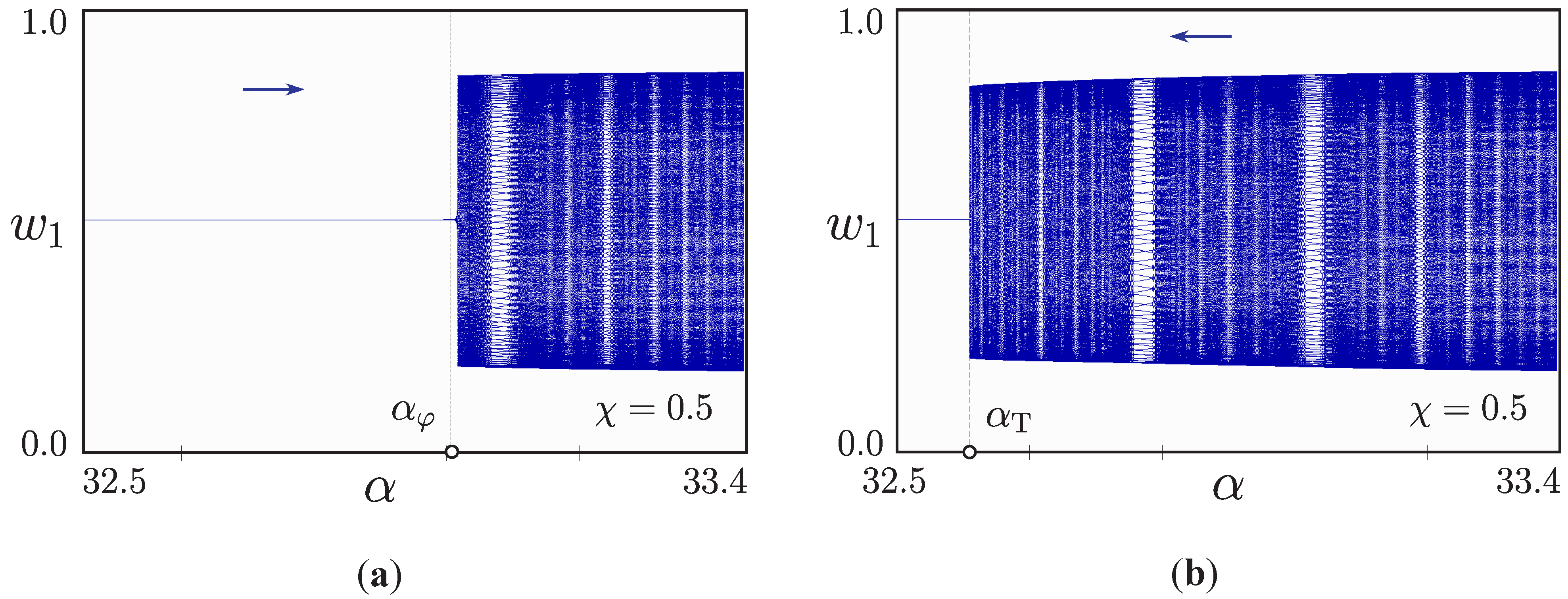
3.5. Internal Structure of the Resonance Zones
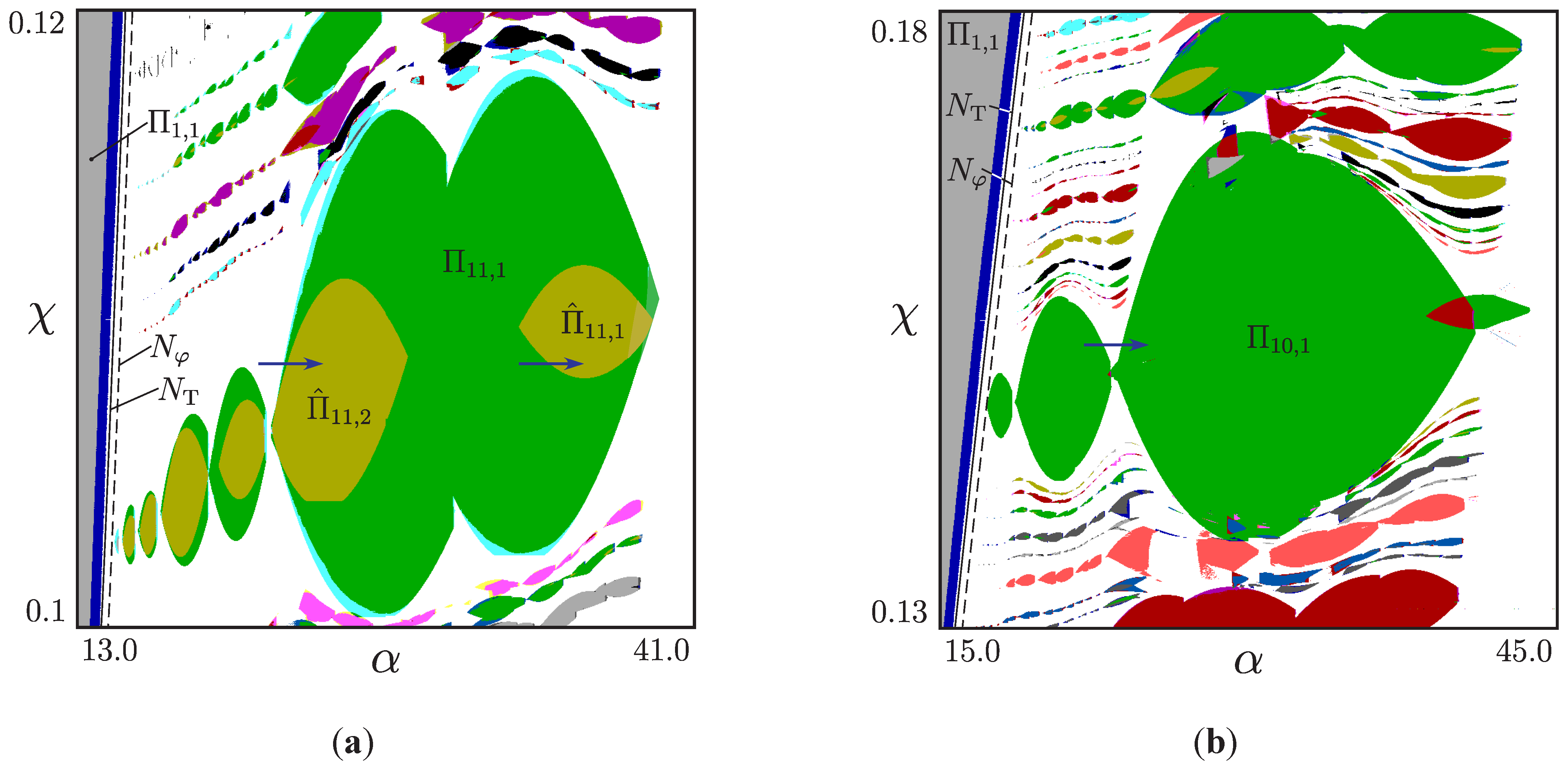
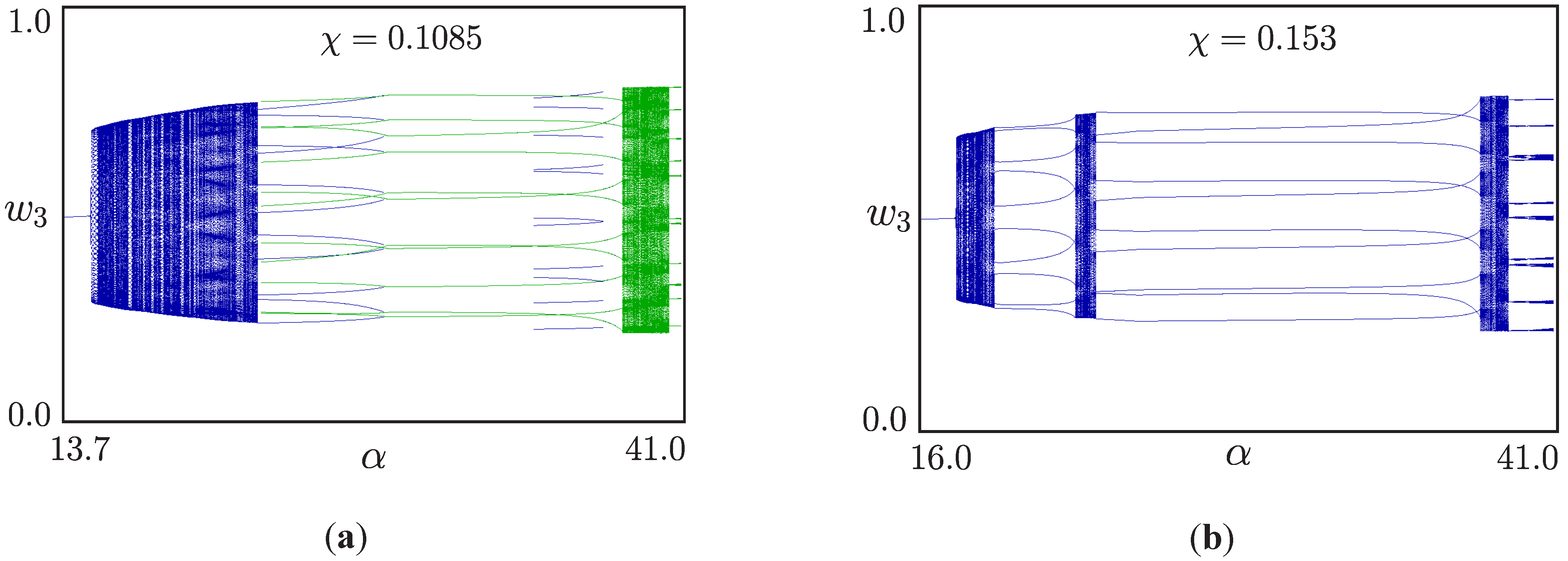
4. Torus Bifurcations in a Multilevel DC/DC Converter
4.1. Power-Electronic DC/DC Converter with Multilevel Control
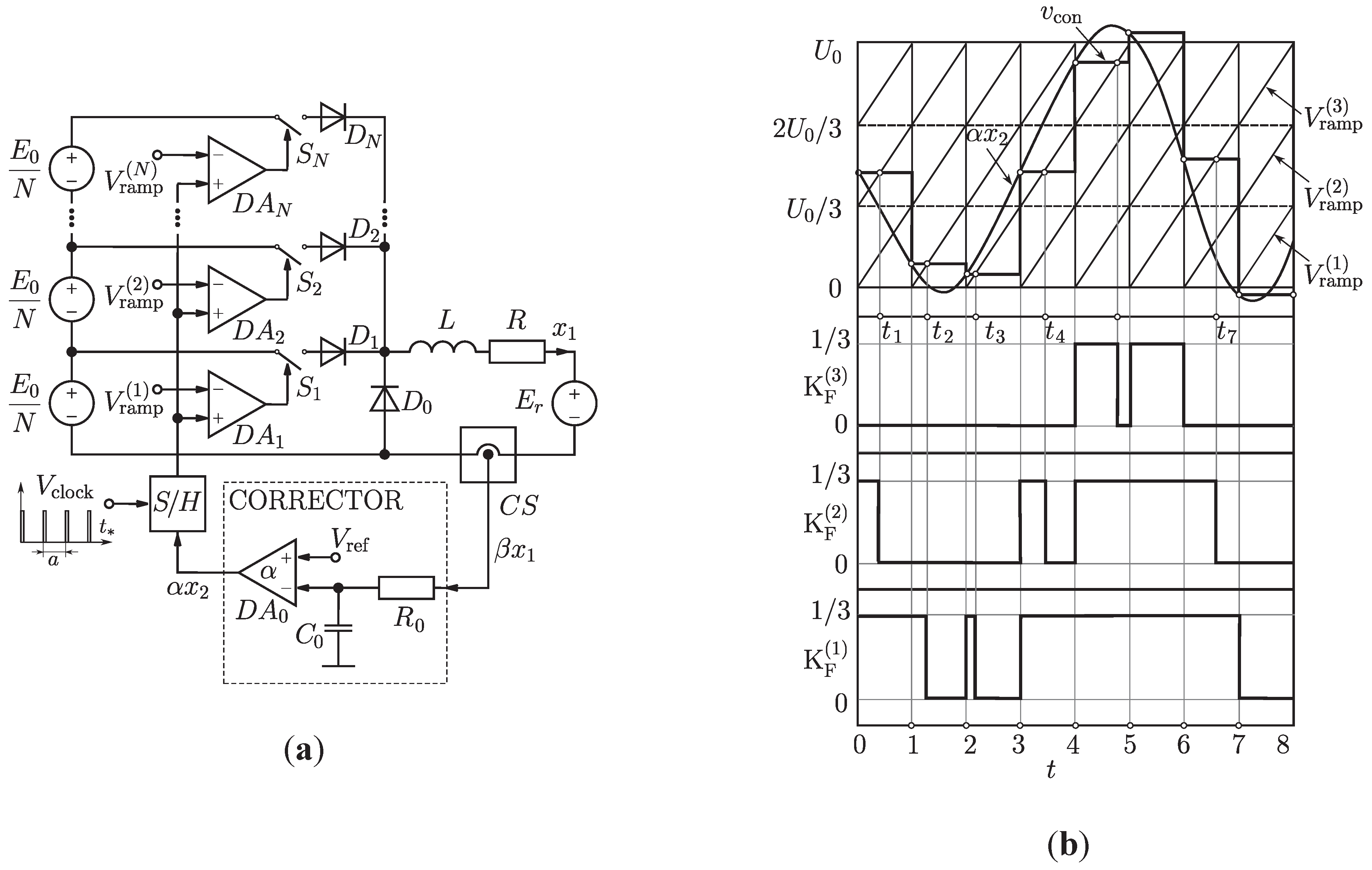
4.2. Chart of Dynamical Modes
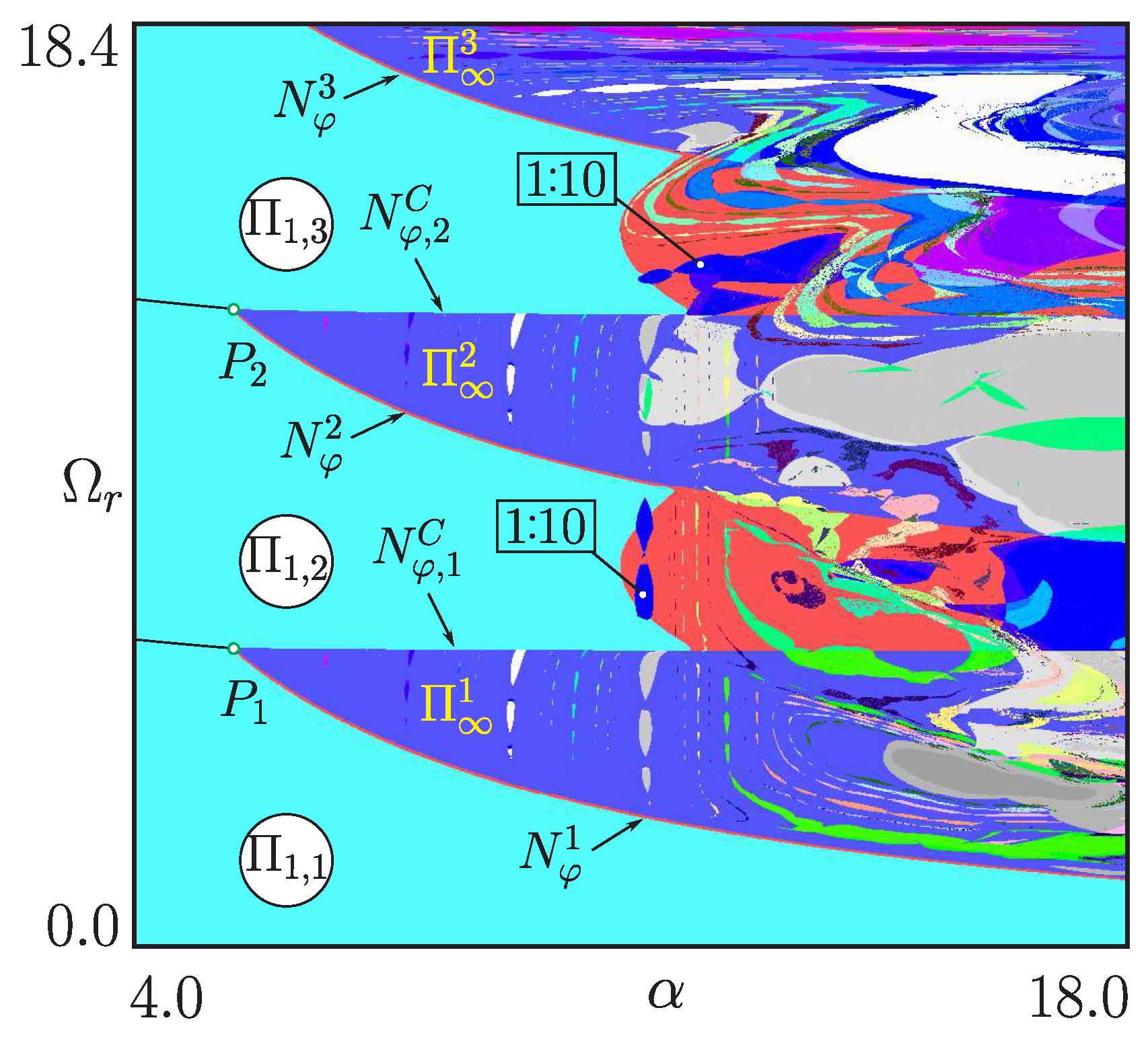
4.3. Embedded Tori
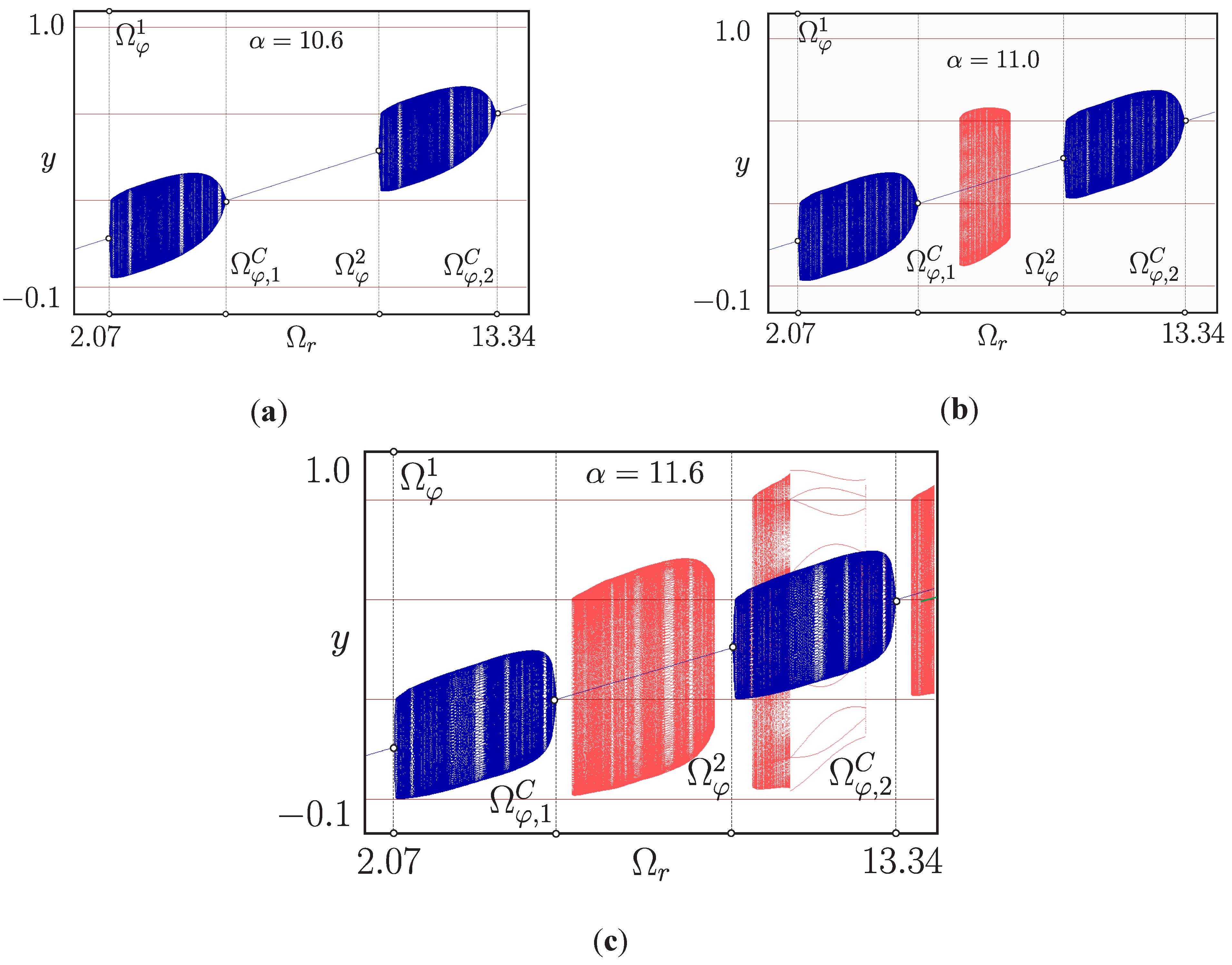

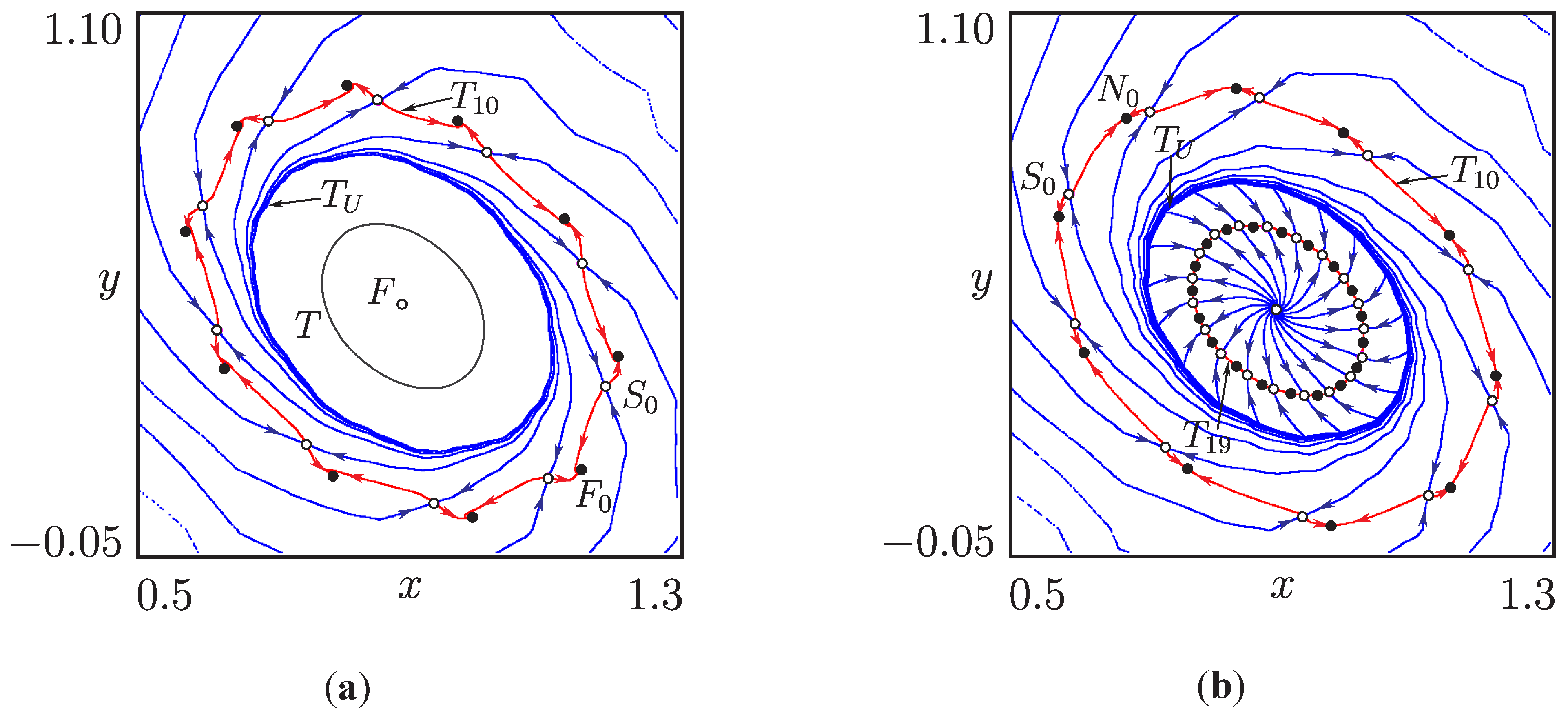
4.4. Torus Merging Processes
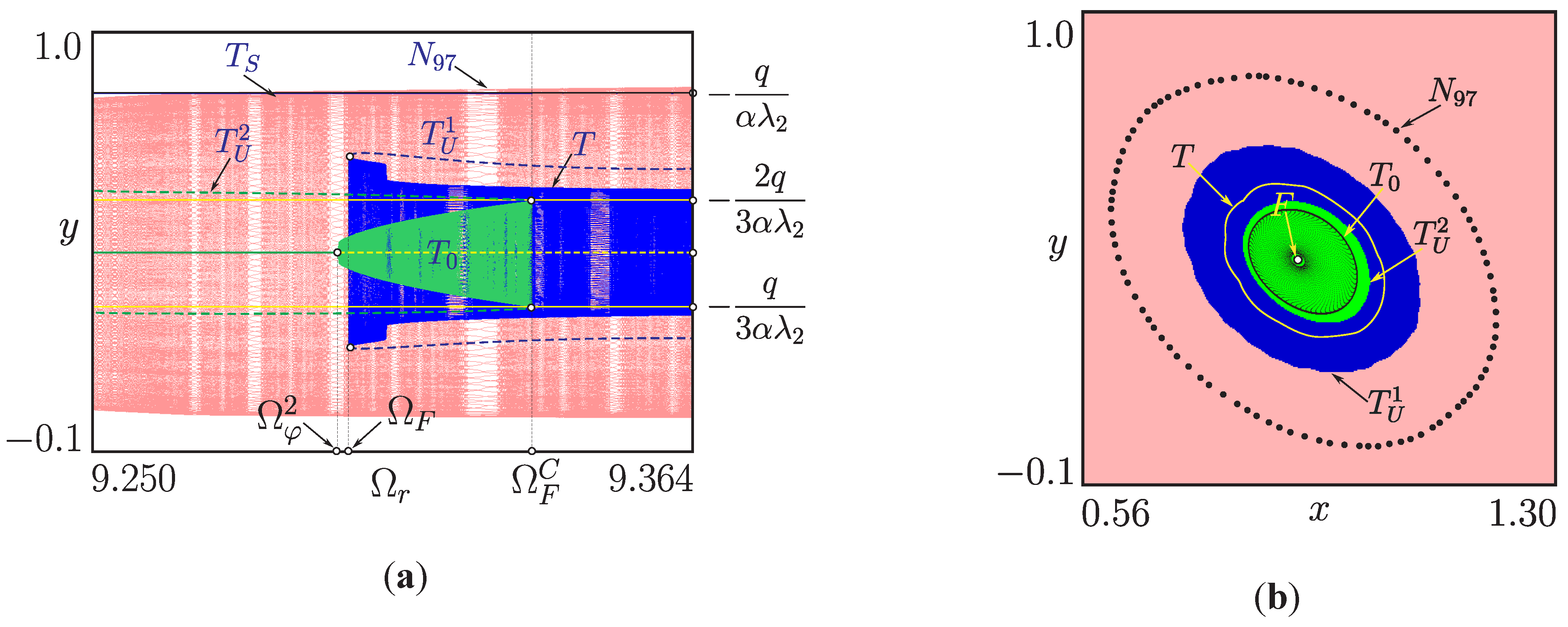
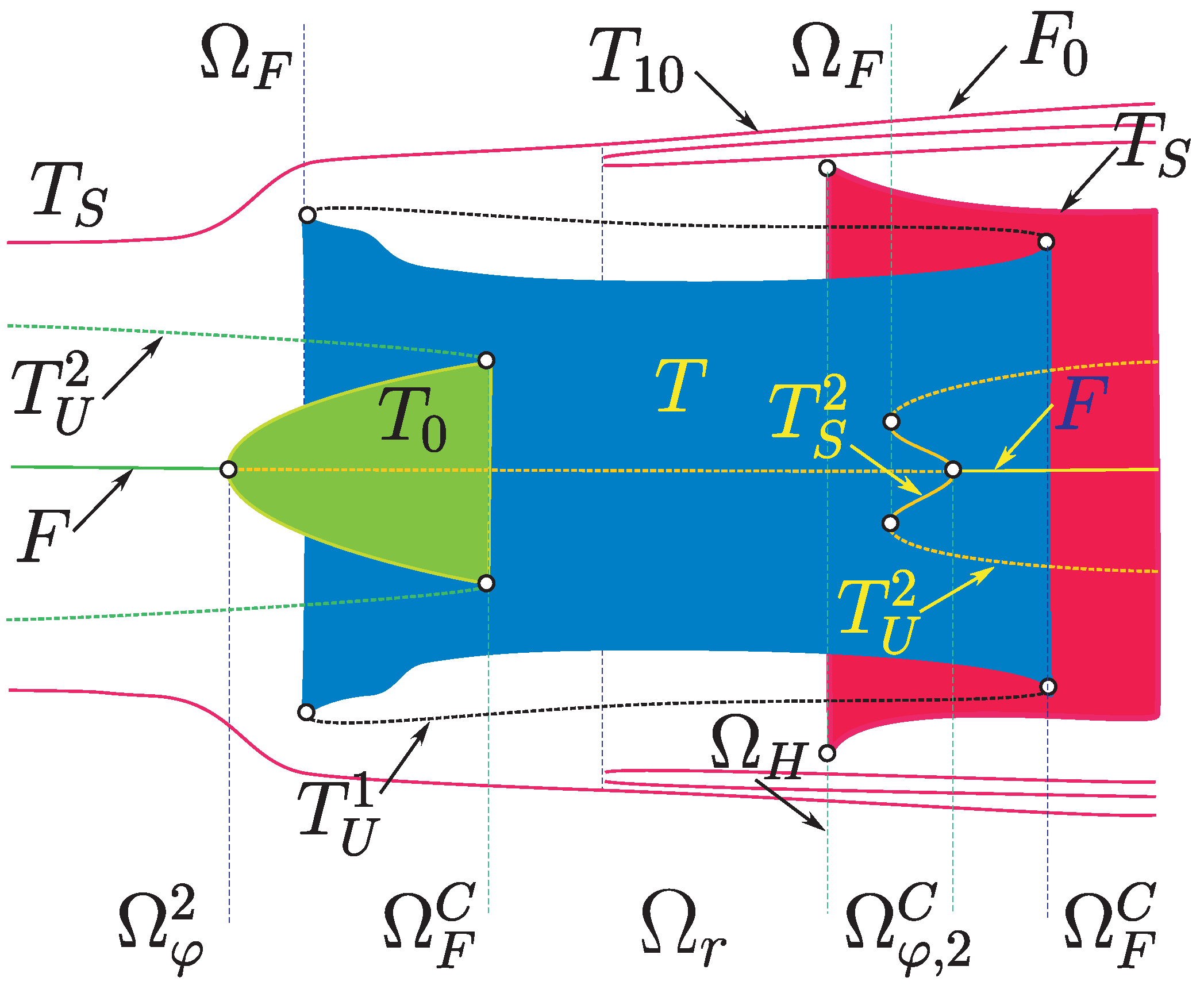
4.5. Behavioral Complexity of the Multilevel DC/DC Converter
5. Single-Phase Pulse-Width Modulated H-Bridge Inverter
5.1. Model of the Single Phase PWM H-Bridge Inverter

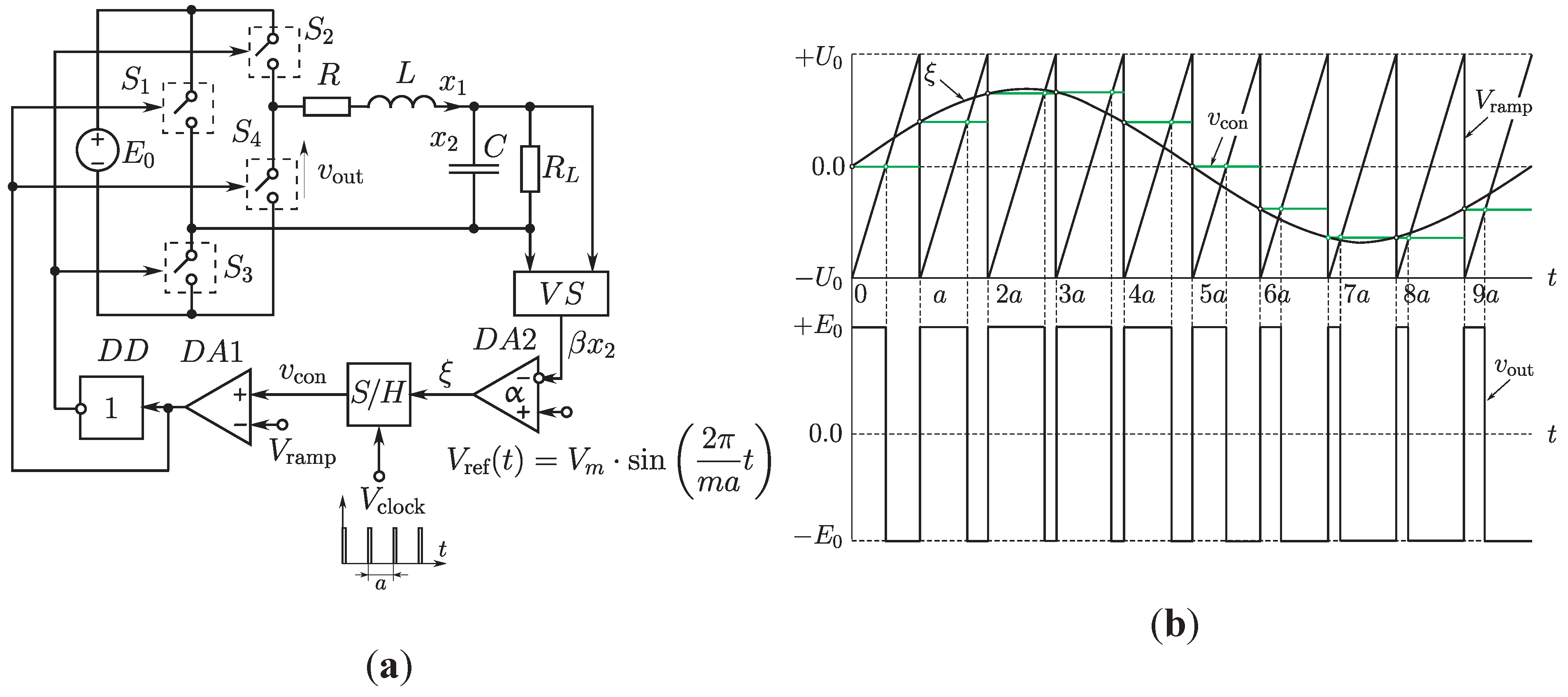
5.2. Torus-Birth Bifurcations
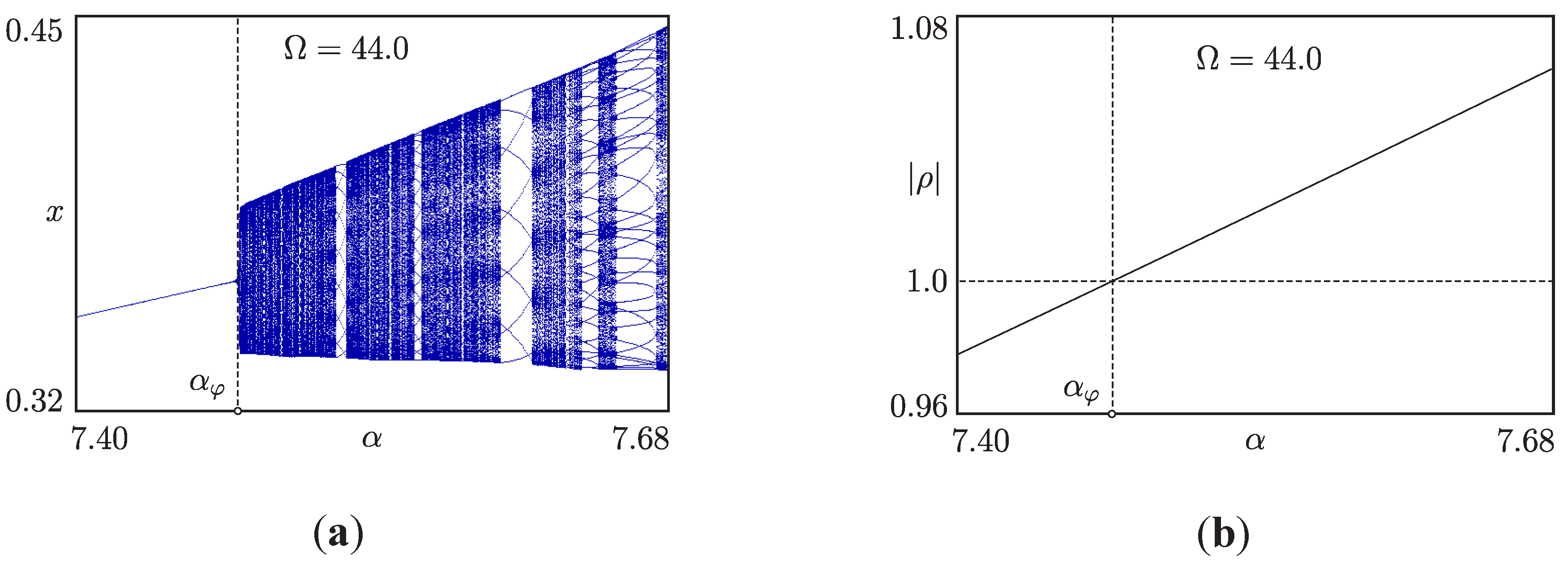
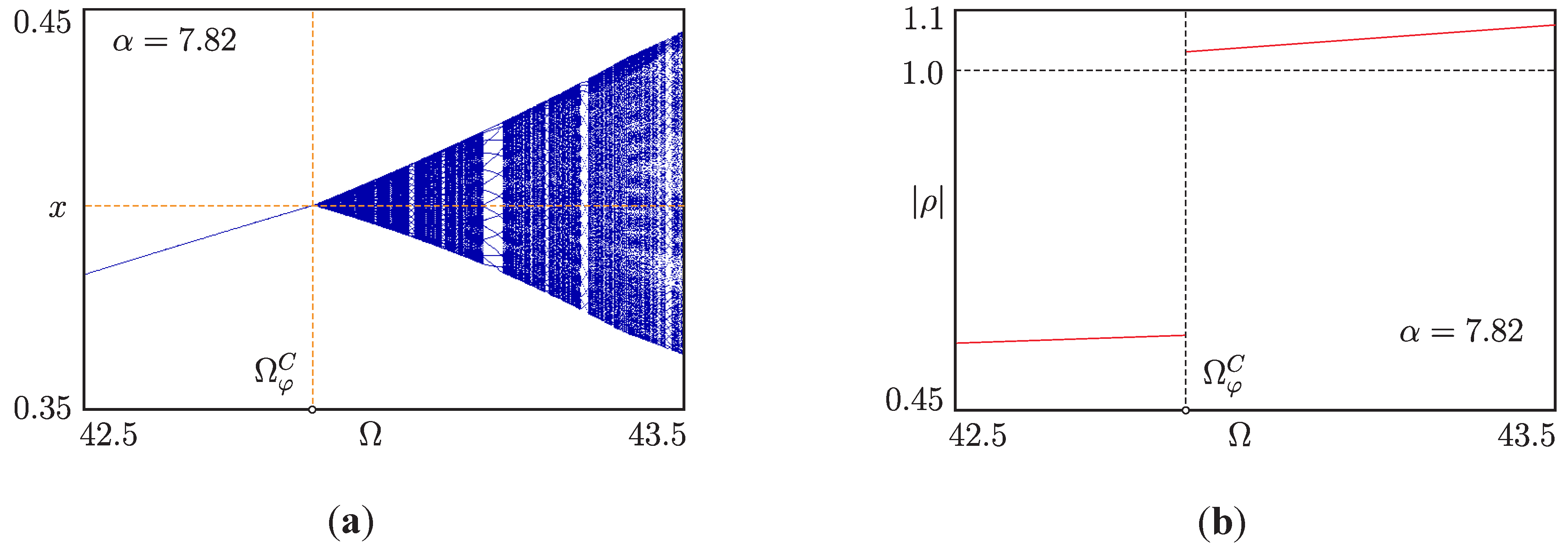

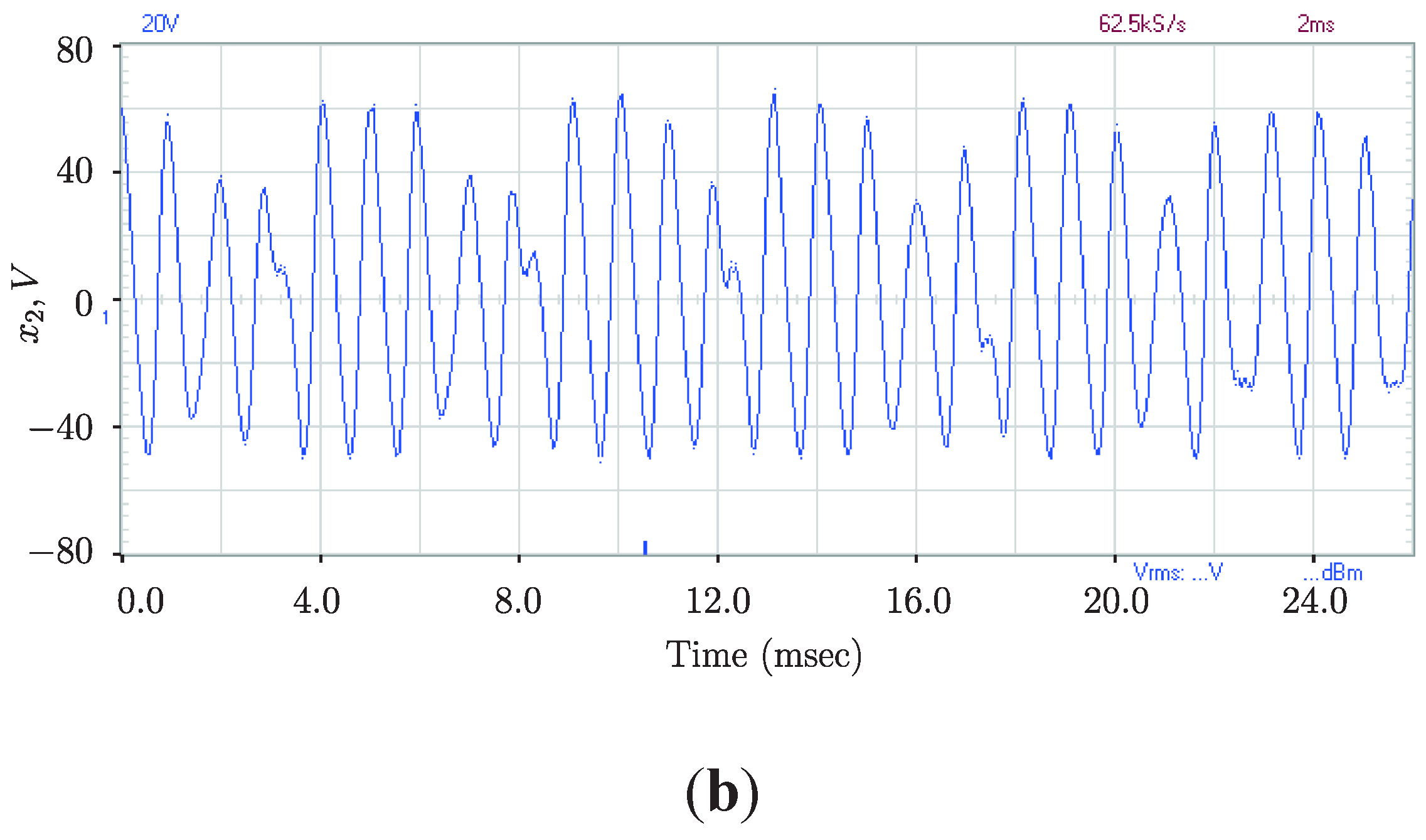
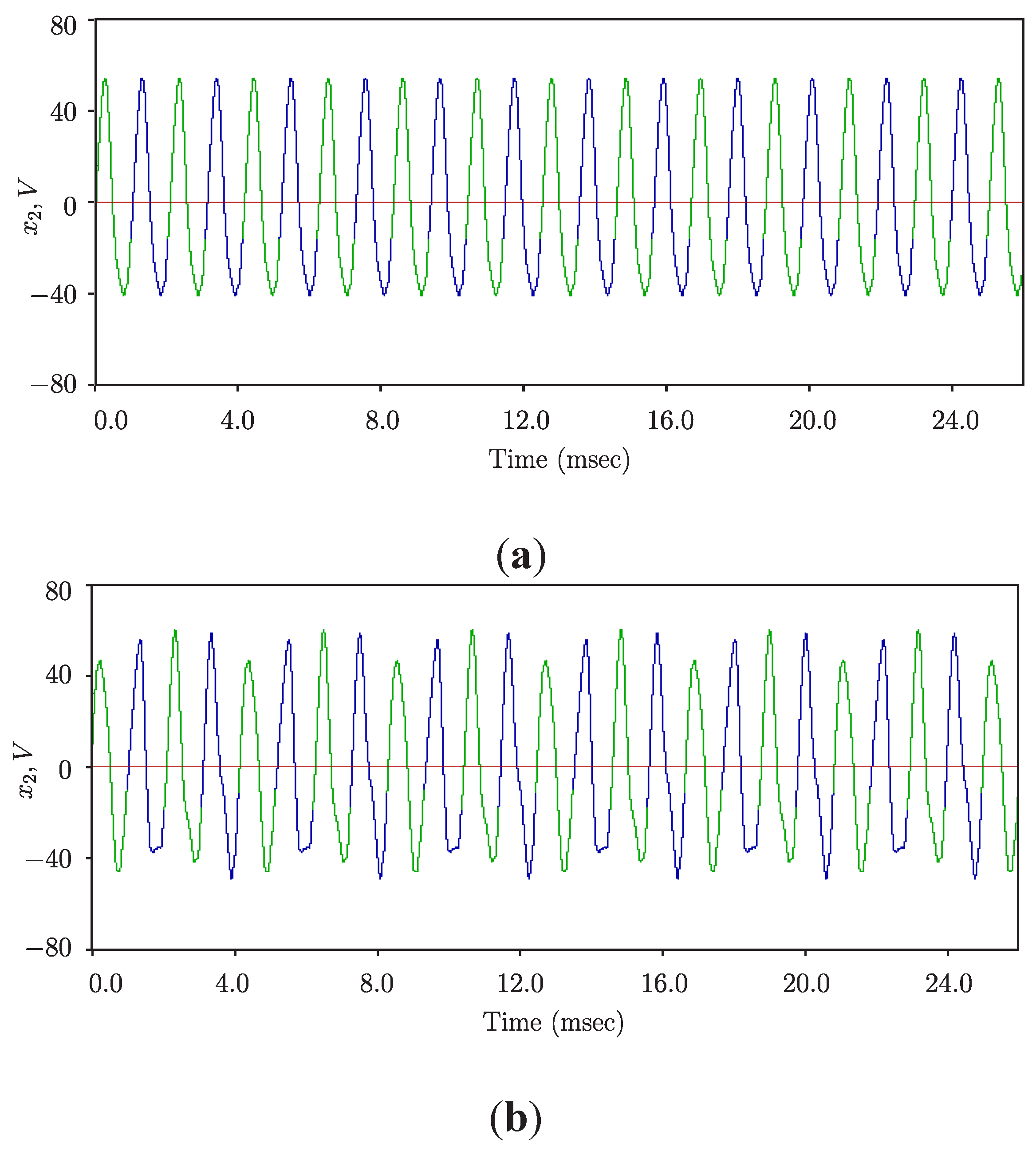
5.3. Phase Synchronized Quasiperiodicity
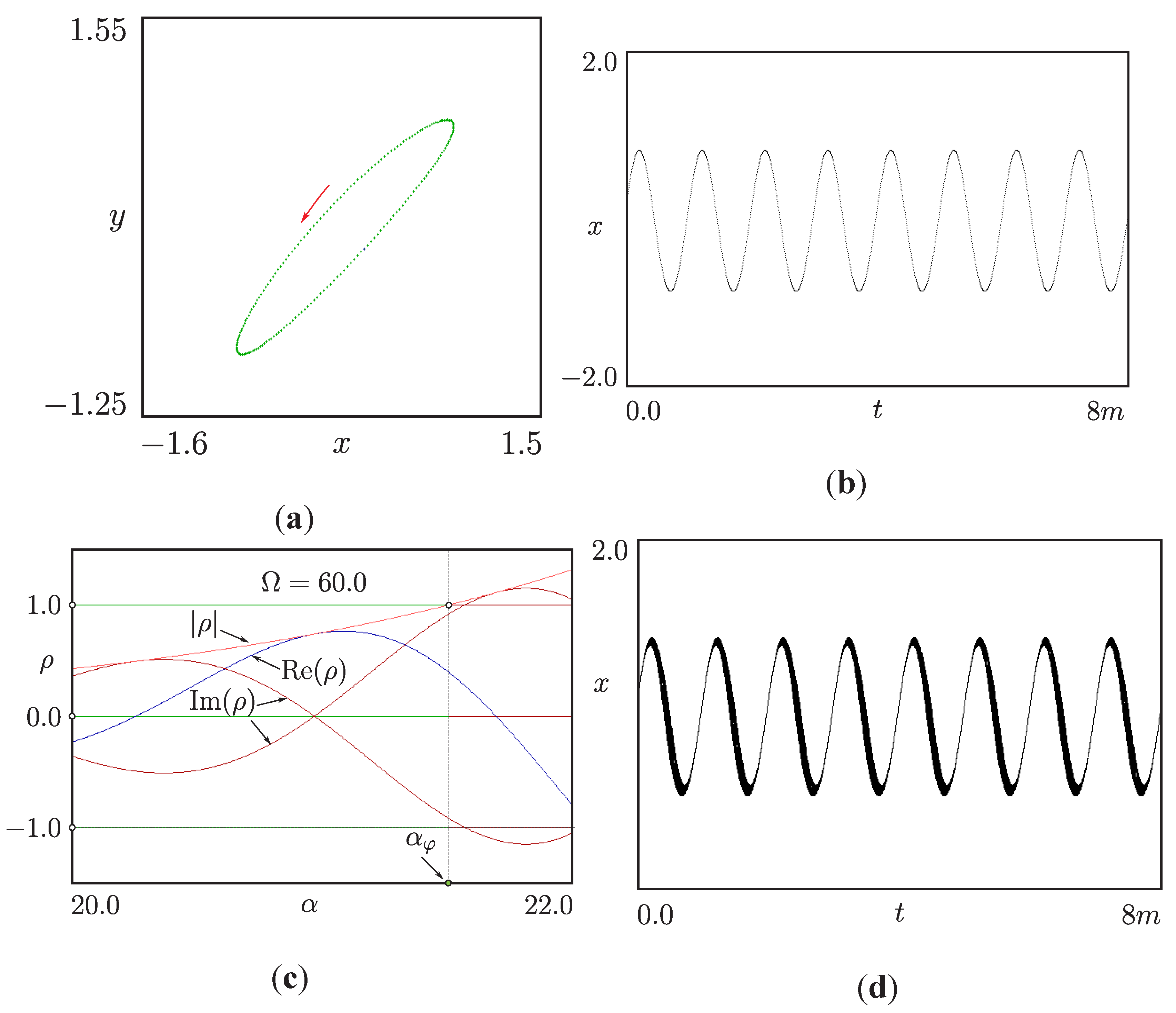

5.4. Signal Distortion
6. Conclusions and Perspectives
Acknowledgements
References
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Rashid, M.H.; Luo, F.L. Power Electronics Handbook; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kazmierkowski, M.; Krishnan, R.; Blaaberg, F. Control in Power Electronics-Selected Problems; Elsevier Science: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Meynard, T.A.; Foch, H.; Thomas, P.; Courault, J.; Jakob, R.; Nahrstaedt, M. Multilevel converters-A new breed of power converters. IEEE Trans. Ind. Electron. 1996, 32, 509–517. [Google Scholar]
- Meynard, T.A.; Foch, H.; Thomas, P.; Courault, J.; Jakob, R.; Nahrstaedt, M. Multicell converters: Basic concepts and industry applications. IEEE Trans. Ind. Electron. 2002, 49, 955–964. [Google Scholar] [CrossRef]
- Kouro, S.; Malinowski, M.; Gopakumar, K.; Pou, J.; Franquelo, L.G.; Wu, B.; Rodriguez, J.; Pérez, M.A.; Leon, J.I. Recent advances in industrial applications of multilevel converters. IEEE Trans. Ind. Electron. 2010, 57, 2553–2580. [Google Scholar] [CrossRef]
- Xiao, J.; Peterchev, A.V.; Zhang, J.; Sanders, S. A 4-µA quiescent-current dual-mode digitally controlled buck converter IC for cellular phone applications. IEEE J. Solid-State Circ. 2004, 39, 2342–2348. [Google Scholar] [CrossRef]
- Lee, Y.J.; Khaligh, A.; Emadi, A. Advanced integrated bidirectional AC-DC and DC-DC converter for plug-in hybrid electrical vehicles. IEEE Trans. Veh. Technol. 2009, 58, 3970–3980. [Google Scholar]
- Banerjee, S.; Verghese, G.C. Nonlinear Phenomena in Power Electronics; IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- Villanueva, E.; Correa, P.; Rodriguez, J.; Pacas, M. Control of a single-phase cascaded H-bridge multilevel inverter for grid-connected photovoltaic systems. IEEE Trans. Ind. Electron. 2009, 56, 4399–4406. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–737. [Google Scholar] [CrossRef]
- Xinbo, R.; Bin, L.; Qianhong, C.; Siew-Chong, T.; Tse, C.K. Fundamental considerations of three-level DC-DC converters: Topologies, Analyses, and Control. IEEE Trans. Circ. Syst. I 2008, 55, 3733–3743. [Google Scholar] [CrossRef]
- Moreno-Font, V.; Aroudi, A.E.; Calvente, J.; Giral, R.; Benadero, L. Dynamics and stability issues of a single-inductor dual-switching DC-DC converter. IEEE Trans. Circ. Syst. I 2010, 57, 415–426. [Google Scholar] [CrossRef] [Green Version]
- Kazmierkowski, M.P.; Jasinski, M.; Wrona, G. DSP-based control of grid-connected power converters operating under grid distortions. IEEE Trans. Ind. Inform. 2011, 7, 204–211. [Google Scholar] [CrossRef]
- Kousaka, T.; Ueta, T.; Kawakami, H. Bifurcation of switched nonlinear dynamical systems. IEEE Trans. Circ. Syst. II 1999, 46, 878–885. [Google Scholar] [CrossRef]
- Tse, C.K. Complex Behavior of Switching Power Converters; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zhusubaliyev, Z.T.; Mosekilde, E. Bifurcations and Chaos in Piecewise-Smooth Dynamical Systems; World Scientific: Singapore, 2003. [Google Scholar]
- Feigin, M.I. Doubling of the oscillation period with C-bifurcations in piecewise continuous systems. PMM J. Appl. Math. Mech. 1970, 34, 861–869. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Feigin, M.I.; Hogan, S.J.; Homer, M.E. Local analysis of C-bifurcations in n-dimensional piecewise-smooth dynamical systems. Chaos Solitons Fractals 1999, 10, 1881–1908. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer-Verlag: New York, NY, USA, 2004. [Google Scholar]
- Nusse, H.E.; Yorke, J.A. Border-collision bifurcations including “period two to period three” for piecewise smooth systems. Physica D 1992, 57, 39–57. [Google Scholar] [CrossRef]
- Nusse, H.E.; Ott, E.; Yorke, J.A. Border-collision bifurcations: An explanation for observed bifurcation phenomena. Phys. Rev. E 1994, 49, 1073–1076. [Google Scholar] [CrossRef]
- Nusse, H.E.; Yorke, J.A. Border-collision bifurcation for piecewise smooth one-dimensional maps. Int. J. Bifurcat. Chaos 1995, 5, 189–207. [Google Scholar] [CrossRef]
- Banerjee, S.; Grebogi, C. Border collision bifurcations in two-dimensional piecewise smooth maps. Phys. Rev. E 1999, 59, 4052–4061. [Google Scholar] [CrossRef]
- Banerjee, S.; Ranjan, P.; Grebogi, C. Bifurcations in two-dimensional piecewise smooth maps—Theory and applications in switching circuits. IEEE Trans. Circ. Syst. I 2000, 47, 633–643. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E. Direct transition from a stable equilibrium to quasiperiodicity in non-smooth systems. Phys. Lett. A 2008, 372, 2237–2246. [Google Scholar] [CrossRef]
- Brogliato, B. Nonsmooth Mechanics—Models, Dynamics and Control; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar]
- Leine, R.I.; Nijmeijer, H. Dynamics and Bifurcations of Non-Smooth Mechanical Systems; Springer-Verlag: Berlin, Germany, 2004. [Google Scholar]
- Nordmark, A. Nonperiodic motion caused by grazing incidence in an impact oscillator. J. Sound Vib. 1991, 145, 279–297. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Budd, C.J.; Champneys, A.R. Grazing and border-collision in piecewise-smooth systems: A unified analytical framework. Phys. Rev. Lett. 2001, 86, 2553–2556. [Google Scholar] [CrossRef] [PubMed]
- Nordmark, A.B.; Kowalczyk, P. A codimension-two scenario of sliding solutions in grazing-sliding bifurcations. Nonlinearity 2006, 19, 1–26. [Google Scholar] [CrossRef]
- Wiercigroch, M. Chaotic vibration of a simple model of the machine tool-cutting process system. ASME J. Vib. Acoust. 1997, 119, 468–475. [Google Scholar] [CrossRef]
- Knudsen, C.; Feldberg, R.; True, H. Bifurcations and chaos in a model of a rolling railway wheelset. Phil. Trans. R. Soc. Lond. A 1992, 338, 455–469. [Google Scholar] [CrossRef]
- Thompson, J.M.T. Complex dynamics of compliant off-shore structures. Proc. Roy. Soc. Lond. A 1983, 387, 407–428. [Google Scholar] [CrossRef]
- Choi, S.K.; Noah, S. Mode locking and chaos in a Jeffcott rotor with bearing clearances. J. Appl. Mech. 1994, 61, 131–138. [Google Scholar] [CrossRef]
- Natsiavas, S. Regular and chaotic response of vibration absorbers with elastic stops. Nonl. Vib. 1992, 144, 15–20. [Google Scholar]
- Thomsen, J.S.; Mosekilde, E.; Sterman, J.D. Hyperchaotic phenomena in dynamic decision making. J. Syst. Anal. Mod. Sim. 1992, 9, 137–156. [Google Scholar]
- Mosekilde, E.; Laugesen, J.L. Nonlinear dynamic phenomena in the beer model. Syst. Dyn. Rev. 2007, 23, 229–252. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Soukhoterin, E.A.; Mosekilde, E. Border-collision bifurcations on a two-dimensional torus. Chaos Solitons Fractals 2002, 13, 1889–1915. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Soukhoterin, E.A.; Mosekilde, E. Quasi-periodicity and border-collision bifurcations in a DC/DC converter with pulsewidth modulation. IEEE Trans. Circ. Syst. I 2003, 50, 1047–1057. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E. Torus birth bifurcation in a DC/DC converter. IEEE Trans. Circ. Syst. I 2006, 53, 1839–1850. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E. Birth of bilayered torus and torus breakdown in a piecewise-smooth dynamical system. Phys. Lett. A 2006, 351, 167–174. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Maity, S.M.; Mohanan, S.; Banerjee, S. Border collision route to quasiperiodicity: Numerical investigation and experimental confirmation. Chaos 2006, 16. [Google Scholar] [CrossRef] [PubMed]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Yanochkina, O.O. Torus-bifurcation mechanisms in a DC/DC converter with pulse-width modulated control. IEEE Trans. Power Electron. 2011, 26, 1270–1279. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Yanochkina, O.O. Torus bifurcations in multilevel converter systems. Int. J. Bifurcat. Chaos 2011, 21, 2343–2356. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Pavlova, E.V. Multistability and torus reconstruction in a DC/DC converter with multilevel control. IEEE Trans. Ind. Inform. 2012. [Google Scholar] [CrossRef]
- Aroudi, A.E.; Benadero, L.; Toribio, E.; Olivar, G. Hopf bifurcation and chaos from torus breakdown in a PWM voltage-controlled DC-DC boost converter. IEEE Trans. Circ. Syst. I 1999, 46, 1374–1382. [Google Scholar] [CrossRef]
- Mazumder, S.K.; Nayfeh, A.H.; Boroyevich, D. An investigation into the fast- and slow-scale instabilities of a single phase bidirectional boost converter. IEEE Trans. Power Electron. 2003, 18, 1063–1069. [Google Scholar] [CrossRef]
- Dai, D.; Li, S.; Ma, X.; Tse, C. Slow-scale instability of single-stage power-factor-correction power supplies. IEEE Trans. Circ. Syst. I 2007, 54, 1724–1735. [Google Scholar] [CrossRef]
- Aroudi, A.E.; Orabi, M.; Haroun, R.; Martinez-Salamero, L. Asymptotic slow-scale stability boundary of PFC AC-DC power converters: Theoretical prediction and experimental validation. IEEE Trans. Ind. Electron. 2011, 58, 3448–3460. [Google Scholar] [CrossRef]
- Rodriguez, E.; Aroudi, A.E.; Guinjoan, F.; Alarcon, E. A ripple-based design-oriented approach for predicting fast-scale instability in DC-DC switching power supplies. IEEE Trans. Circ. Syst. I 2012, 59, 215–227. [Google Scholar] [CrossRef]
- Feldberg, R.; Szymkat, M.; Knudsen, C.; Mosekilde, E. Iterated-map approach to die tossing. Phys. Rev. A 1990, 42, 4493–4502. [Google Scholar] [CrossRef] [PubMed]
- Hansen, L.U.W.; Christensen, M.; Mosekilde, E. Deterministic analysis of the probability machine. Phys. Scr. 1995, 51, 35–45. [Google Scholar] [CrossRef]
- Galiaz, Z.; Ogorzalek, M.J. Bifurcation phenomena in second order digital filters with saturation-type adder overflow characteristics. IEEE Trans. Circ. Syst. 1990, 37, 1068–1070. [Google Scholar] [CrossRef]
- Thompson, J.M.T.; Stewart, H.B. Nonlinear Dynamics and Chaos; Wiley: Chichester, UK, 1986. [Google Scholar]
- Feigenbaum, M.J. The universal metric properties of nonlinear transformations. J. Stat. Phys. 1979, 21, 669–706. [Google Scholar] [CrossRef]
- Landford, O.E. A computer-assisted proof of the Feigenbaum conjectures. Am. Math. Soc. 1982, 6, 427–434. [Google Scholar] [CrossRef]
- Devany, R.L. An Introduction to Chaotic Systems; Addison-Wesley: Redwood City, CA, USA, 1989. [Google Scholar]
- Maistrenko, Y.L.; Maistrenko, V.L.; Vikul, S.I.; Chua, L.O. Bifurcations of attracting cycles from time-delayed Chua’s circuit. Int. J. Bifurcat. Chaos 1995, 5, 653–671. [Google Scholar] [CrossRef]
- Metropolis, N.; Stein, M.L.; Stein, P.R. On finite limit sets for transformations on the unit interval. J. Combin. Theor. A 1973, 15, 25–44. [Google Scholar] [CrossRef]
- Feigin, M.I. On the generation of sets of subharmonic modes in piecewise continuous systems. Prikl. Mat. Mekh. 1974, 38, 810–818, in Russian. [Google Scholar]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Banerjee, S. Multiple-attractor bifurcations and quasiperiodicity in piecewise-smooth maps. Int. J. Bifurcat. Chaos 2008, 18, 1775–1789. [Google Scholar] [CrossRef]
- Gardini, L.; Tramontana, F. Snap-back repellers and chaotic attractors. Phys. Rev. E 2010, 81. [Google Scholar] [CrossRef]
- Arnol’d, V.I. Small denominators, I: Mappings of the circumference into itself. AMS Trans. Series 2 1965, 46, 213–284. [Google Scholar]
- Rand, D.; Ostlund, S.; Sethna, J.; Siggia, E. Universal transition from quasiperiodicity to chaos in dissipative systems. Phys. Rev. Lett. 1982, 49, 132–135. [Google Scholar] [CrossRef]
- Pikovsky, A.; Rosenblum, M.; Kurths, J. Synchronization: A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Balanov, A.; Janson, N.; Postnov, D.; Sosnovtseva, O. Synchronization: From Simple to Complex; Springer: Berlin, Germany, 2009. [Google Scholar]
- Mosekilde, E. Topics in Nonlinear Dynamics: Applications to Physics, Biology and Economic; World Scientific: Singapore, 1996. [Google Scholar]
- Uherka, D. Tongue art. CNLS Newsl. 1992, 78, 1–23. [Google Scholar]
- Yang, W.M.; Hao, B.L. How the Arnol’d tongues become sausages in a piecewise linear circle map. Commun. Theor. Phys. 1987, 8, 1–15. [Google Scholar]
- Simpson, D.J.W.; Meiss, J.D. Shrinking point bifurcations of resonance tongues for piecewise-smooth, continuous maps. Nonlinearity 2009, 22, 1123–1144. [Google Scholar] [CrossRef]
- Plante, J.; Shue, J.; Liu, D.; Wang, B.; Shaw, H. Advanced DC/DC Converters towards Higher Volumetric Efficiencies for Space Applications; NASA Goddard Space Flight Center, USA, 2005; NASA Technical Reports Server (NTRS). Available online: http://ntrs.nasa.gov/search.jsp (accessed 25 July 2009).
- Zhusubaliyev, Z.T.; Soukhoterin, E.A.; Rudakov, V.; Mosekilde, E.; Kolokolov, Y.V. Bifurcations and chaotic oscillations in an automatic control relay system with hysteresis. Int. J. Bifurcat. Chaos 2001, 11, 1193–1231. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Soukhoterin, E.A.; Mosekilde, E. Border-collision bifurcations and chaotic oscillations in a piecewise-smooth dynamical system. Int. J. Bifurcat. Chaos 2001, 11, 2977–3001. [Google Scholar] [CrossRef]
- Hamill, D.C.; Deane, J.H.B.; Jefferies, D.J. Modeling of chaotic DC-DC converters by iterated nonlinear mappings. IEEE Trans. Power Eletron. 1992, 7, 25–36. [Google Scholar] [CrossRef]
- Baushev, V.S.; Zhusubaliyev, Z.T. Indeterminable states of a voltage regulator with pulsewidth control. Electr. Technol. 1992, 3, 85–88. [Google Scholar]
- di Bernardo, M.; Vasca, F. Discrete-time maps for the analysis of bifurcations in dc-dc converters. IEEE Trans. Circ. Syst. I 2000, 47, 130–143. [Google Scholar] [CrossRef]
- Hamill, D.C.; Jeffries, D.J. Subharmonics and chaos in a controlled switched-mode power converter. IEEE Trans. Circ. Syst. 1988, 35, 1059–1061. [Google Scholar] [CrossRef]
- Yuan, G.H.; Banerjee, S.; Ott, E.; Yorke, J.A. Border-collision bifurcations in the buck converter. IEEE Trans. Circ. Syst. I Fund. Theory Appl. 1998, 45, 707–716. [Google Scholar] [CrossRef]
- Aroudi, A.E.; Benadero, L.; Toribio, E.; Machiche, S. Quasiperiodicity and chaos in DC-DC buck-boost converter. Int. J. Bifurcat. Chaos 2000, 10, 359–371. [Google Scholar] [CrossRef]
- Aroudi, A.; Leyva, R. Quasiperiodic route to chaos in a PWM voltage-controlled DC-DC boost converter. IEEE Trans. Circ. Syst. I 2001, 48, 967–978. [Google Scholar] [CrossRef]
- Di Bernardo, M.; Tse, C. Chaos in Power Electronics: An Overview. In Chaos in Circuits and Systems; Chen, G., Ueta, T., Eds.; World Scientific: Singapore, 2002; pp. 317–340. [Google Scholar]
- Hao, B.L. Elementary Symbolic Dynamics and Chaos in Dissipative Systems; World Scientific: Singapore, 1989. [Google Scholar]
- Zhusubaliyev, Z.T.; Yanochkina, O.O.; Mosekilde, E. Coexisting tori and torus bubbling in non-smooth systems. Physica D 2011, 240, 397–405. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Yanochkina, O.O.; Mosekilde, E.; Banerjee, S. Two-mode dynamics in pulse-modulated control systems. Ann. Rev. Control 2010, 34, 60–70. [Google Scholar] [CrossRef]
- Postnov, D.; Balanov, A.; Sosnovtseva, O.; Mosekilde, E. Chaotic hierarchy in high dimensions. Int. J. Mod. Phys. B 2000, 14, 2511–2527. [Google Scholar]
- Anishchenko, V.; Nikolaev, S.; Kurths, J. Winding number locking on a two-dimensional torus: Synchronization of quasiperiodic motions. Phys. Rev. E 2006, 73. [Google Scholar] [CrossRef]
- Loose, A.; Wuensche, H.J.; Henneberger, F. Synchronization of quasiperiodic oscillations to a periodic force studied with semiconductor lasers. Phys. Rev. E 2010, 82. [Google Scholar] [CrossRef]
- Giaouris, D.; Banerjee, S.; Imrayed, O.; Mandal, K.; Zahawi, B.; Pickert, V. Complex interaction between tori and onset of three-frequency quasi-periodicity in a current mode controlled boost converter. IEEE Trans. Circ. Syst. I 2012, 59, 207–214. [Google Scholar] [CrossRef]
- Buccella, C.; Cecati, C.; Latafat, H. Digital control of power converters-A survey. IEEE Trans. Ind. Inform. 2012, 8, 437–447. [Google Scholar] [CrossRef]
- Xia, C.; Wang, M.; Song, Z.; Liu, T. Robust model predictive current control of three-phase voltage source PWM rectifier with online disturbance observation. IEEE Trans. Ind. Inform. 2012, 8, 459–471. [Google Scholar] [CrossRef]
- Li, B.; Lin-Shi, X.; Allard, B.; Rétif, J.M. A digital dual-state-variable predictive controller for high switching frequency buck converter with improved Σ-Δ DPWM. IEEE Trans. Ind. Inform. 2012, 8, 472–481. [Google Scholar] [CrossRef]
- Rivera, M.; Rodriguez, J.; Espinoza, J.R.; Abu-Rub, H. Instantaneous reactive power minimization and current control for an indirect matrix converter under a distorted AC supply. IEEE Trans. Ind. Inform. 2012, 8, 482–490. [Google Scholar] [CrossRef]
- Buticchi, G.; Barater, D.; Lorenzani, E.; Franceshini, G. Digital control of actual grid-connected converters for ground leakage current reduction in PV transformerless systems. IEEE Trans. Ind. Inform. 2012, 8, 563–572. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhusubaliyev, Z.T.; Mosekilde, E.; Andriyanov, A.I.; Mikhal'chenko, G.Y. High-Feedback Operation of Power Electronic Converters. Electronics 2013, 2, 113-167. https://doi.org/10.3390/electronics2020113
Zhusubaliyev ZT, Mosekilde E, Andriyanov AI, Mikhal'chenko GY. High-Feedback Operation of Power Electronic Converters. Electronics. 2013; 2(2):113-167. https://doi.org/10.3390/electronics2020113
Chicago/Turabian StyleZhusubaliyev, Zhanybai T., Erik Mosekilde, Alexey I. Andriyanov, and Gennady Y. Mikhal'chenko. 2013. "High-Feedback Operation of Power Electronic Converters" Electronics 2, no. 2: 113-167. https://doi.org/10.3390/electronics2020113
APA StyleZhusubaliyev, Z. T., Mosekilde, E., Andriyanov, A. I., & Mikhal'chenko, G. Y. (2013). High-Feedback Operation of Power Electronic Converters. Electronics, 2(2), 113-167. https://doi.org/10.3390/electronics2020113




