A Detection Method for Frequency-Hopping Signals in Complex Environments Using Time–Frequency Cancellation and the Hough Transform

Abstract

Frequency-hopping (FH) communication is widely employed in modern wireless communication systems due to its strong resistance to interference. Accurate detection of FH signals is therefore essential for effective spectrum monitoring and reliable communication in complex electromagnetic environments. However, real-world electromagnetic environments are highly complex and dynamic, with substantial noise and multiple interfering signals coexisting. These conditions pose significant challenges to frequency-hopping signal detection, particularly in terms of low signal-to-noise ratios and co-channel interference. To address these challenges, this paper proposes a frequency-hopping signal detection method based on time–frequency cancellation and the Hough transform. The received signals are first preprocessed using time–frequency cancellation and singular value decomposition to suppress noise and fixed-frequency interference. Subsequently, the time–frequency characteristics of the preprocessed signals are extracted, and the time–frequency cancellation ratio is computed to perform an initial determination of the presence of frequency-hopping signals. To further reduce false detections caused by multiple interference sources, the Hough transform is applied to analyze the time–frequency spectrum in greater detail. By jointly exploiting the geometric and statistical characteristics of the signals, accurate detection of frequency-hopping signals is achieved. Experimental results demonstrate that the proposed method enables precise detection of frequency-hopping signals under challenging electromagnetic conditions.

1. Introduction

Frequency-hopping communication is a spread-spectrum method that uses pseudo-random sequences to periodically change the carrier frequency. Due to its advantages in combating multipath fading, resisting narrowband interference, and achieving a low intercept probability, it has found widespread application in the communications sector [1,2]. Its inherent time-varying, non-stationary characteristics effectively enhance the security of communication link transmission by pseudo-randomizing the signal carrier frequency [3,4]. Meanwhile, in the civilian sector, frequency-hopping technology is widely used in applications such as Bluetooth communication and drone remote control [5]. By dynamically avoiding congested frequency points, frequency-hopping technology effectively mitigates co-channel interference, ensuring stable data transmission in complex electromagnetic environments [6]. However, its exceptional anti-jamming and anti-detection capabilities not only enhance the security of communications but also present a significant challenge to signal detection by non-cooperative parties.

In frequency-hopping signal reconnaissance missions, the main goal is to detect the presence of these signals. However, the carrier frequency of frequency-hopping signals undergoes rapid changes over time, which presents significant challenges for signal detection. Concurrently, the inherent complexity of real-world electromagnetic environments further exacerbates detection difficulties, primarily manifested through signal fading induced by channel multipath effects and the severe impact of background noise within densely populated frequency bands [7,8]. Moreover, the simultaneous presence of fixed-frequency and frequency-sweeping signals within the target band creates an overlapping electromagnetic environment, leading to severe co-channel interference that degrades the performance of conventional detection algorithms [9,10]. Therefore, there is an urgent need for a detection method with high detection probability, strong robustness, and good environmental adaptability to ensure the successful completion of reconnaissance missions.

Currently, detection methods for frequency-hopping signals can be broadly divided into traditional approaches and deep learning-based approaches. Traditional methods are further divided into those based on time-domain or frequency-domain features, and those that utilize time–frequency domain features. Among detection methods based on time-domain or frequency-domain features, representative approaches include energy-threshold detection, channelized detection, and compression-sensing detection. Fan [11] employed an atomic decomposition-based approach to analyze frequency-hopping signals. Zhang [12] employed a method based on a channelized receiver to detect frequency-hopping signals in complex environments. Hu [13] used spectral kurtosis and residual signal compression for frequency-hopping signal detection. Lee [14] achieved rapid frequency-hopping signal detection by employing a Dirty template in the frequency domain. Wang [15] analyzed frequency-hopping signals using Bayesian compressed sensing enhanced by hidden Markov models (HMMs). Li [16] achieved detection of frequency-hopping signals through compressed spectrum sensing and maximum likelihood estimation. Zhu [17] analyzed frequency-hopping signals in the compressed domain based on an improved atomic dictionary. Yang [18] analyzed frequency-hopping signals using compressed sensing methods to achieve detection. However, the aforementioned detection methods rely on certain prior knowledge and may have limitations in practical application.

Compared to one-dimensional detection methods based on time-domain or frequency-domain features, detection methods used time–frequency domain features are better suited to characterizing the time-varying properties of frequency-hopping signals. Zheng [19] achieved detection of frequency-hopping signals through wavelet decomposition and the Hilbert-Huang transform. Guo [20] employed MWC-MSBL reconstruction for frequency-hopping signal detection. Kang [21] proposed a detection method targeting the radio frequency fingerprint of frequency-hopping signals. Xu [22] proposed a detection algorithm based on multi-segment signal spectrum clustering, achieving detection through differences in the time–frequency characteristics between frequency-hopping signals and interference signals. Zhou et al. [23,24,25,26] transformed signals into the time–frequency domain via the short-time Fourier transform, detecting frequency-hopping signals by analyzing their characteristics in this domain. Mao et al. [27,28,29] transformed signals into the time–frequency domain, extracted their image information, and separated frequency-hopping signals from interference signals using clustering methods. Zhang et al. [30,31] analyzed the time–frequency matrix by leveraging the inherent data processing capability of atomic norm soft thresholding. Although time–frequency analysis methods are superior to one-dimensional methods in terms of performance, their effectiveness still relies heavily on manually designed feature extraction rules. More importantly, the existing methods are mostly optimized for Gaussian background noise or a single type of interference, and in complex electromagnetic environments where multiple interferences and noises coexist, such as fixed-frequency, swept-frequency, and burst, the time–frequency map features are prone to be mixed, and the preset rules are prone to be invalidated, resulting in the insufficient generalization ability and robustness of the methods.

In recent years, deep learning techniques have provided a novel research paradigm for frequency-hopping signal detection. Ye et al. [32,33] and colleagues employed contrastive learning and self-supervised signal segmentation methods to extract signal parameters, used clustering to achieve frequency-hopping signal detection. Li [34] proposed a method based on residual networks and an optimized generalized S-transform for frequency-hopping signal detection. Chen [35] adopted an image analysis perspective, introducing a lightweight neural network approach combining time–frequency analysis with deep learning image processing algorithms to detect frequency-hopping signals. Liu et al. [36,37,38] employed the time–frequency map of frequency-hopping signals as input for deep neural network models to conduct label learning and training, used the trained models for frequency-hopping signal detection. Jiang et al. [39,40,41,42] combined time–frequency analysis with deep learning to overcome the challenge of identifying multiple frequency-hopping signals amidst complex electromagnetic interference. Li [43] achieved frequency-hopping signal detection through time–frequency analysis, wavelet detection, and the construction of a long short-term memory (LSTM) neural network model. Wang et al. [44,45] achieved detection of frequency-hopping signals through a deep learning-based temporal-spatial detection and feature generation framework. Li [46] obtained a time–frequency map via time–frequency analysis and employed an enhanced YOLOv5-7.0 object detection model to detect frequency-hopping signals. However, deep learning methods still face inherent limitations such as the contradiction between high data dependency and scarcity of actual data, as well as poor model interpretability.

In summary, traditional detection methods lack sufficient robustness under conditions involving multiple types of interference, whereas deep learning-based approaches generally suffer from high computational complexity and a strong dependence on large-scale training data. To address these limitations, this paper proposes a frequency-hopping signal detection method that combines time–frequency pair cancellation with the Hough transform. The proposed method fully exploits the differences in time–frequency characteristics between frequency-hopping signals and various interfering signals. Background interference is first suppressed and preliminary discriminative features are constructed through time–frequency cancellation. Subsequently, the geometric and statistical characteristics of frequency-hopping signals in the time–frequency plane are further extracted using the Hough transform, enabling effective detection of frequency-hopping signals. Without requiring large amounts of prior training data, the proposed method maintains stable detection performance in complex environments with multiple interfering sources. Compared with traditional detection methods that rely on empirically defined thresholds and deep learning-based methods that are heavily data-driven, the proposed approach achieves lower computational complexity while retaining strong physical interpretability. Moreover, it exhibits superior robustness under low signal-to-noise ratio conditions and in scenarios involving the coexistence of multiple interferences, effectively bridging the gap between interpretability and interference resistance that exists in current methods. These advantages demonstrate the novelty and effectiveness of the proposed method for frequency-hopping signal detection in complex electromagnetic environments. The principal contributions of this paper are as follows:

1. To address the limitations of conventional detection methods in handling multiple coexisting interference signals, this paper proposes a detection approach based on time–frequency cancellation and the Hough transform. By analyzing the time–frequency characteristics of both frequency-hopping signals and interference signals, the time–frequency cancellation ratio is employed as a discriminative feature. Combined with the Hough transform for extracting the geometric and statistical characteristics of the signal, the proposed approach enables reliable detection of frequency-hopping signals in environments with multiple coexisting interferences. Moreover, by fully exploiting time–frequency characteristics, the method maintains robust detection performance even under low signal-to-noise ratio conditions.

2. By analyzing the time–frequency characteristics of different signal components, time–frequency cancellation is applied to suppress fixed-frequency interference. Meanwhile, singular value decomposition is used to separate the useful signal from background noise. By jointly exploiting these preprocessing techniques, the proposed method effectively enhances the time–frequency representation of frequency-hopping signals, thereby improving detection performance in complex electromagnetic environments. Compared with deep learning-based approaches, the proposed method achieves significantly lower computational complexity.

3. In this paper, we propose a FH signal detection method that achieves a balance among physical interpretability, low computational complexity, and robustness against complex interference. To address the limitations of traditional detection methods, which typically rely on a single decision criterion and exhibit insufficient robustness in the presence of multiple types of interference, the proposed approach introduces a multicriteria joint decision-making mechanism for frequency-hopping signal detection. This mechanism effectively overcomes the shortcomings of conventional methods in complex electromagnetic environments. Furthermore, without requiring large-scale training data, the proposed method achieves a favorable trade-off between computational efficiency and detection robustness by combining the efficiency of traditional signal processing techniques with the strong interference resistance of deep learning-based methods. As a result, this work fills an important research gap in the development of efficient and physically interpretable frequency-hopping signal detection methods for complex electromagnetic environments.

The remainder of this paper is organized as follows. Section 2 establishes the mathematical model of the frequency-hopping signal and provides a brief introduction to the time–frequency analysis methods. Section 3 details the fundamental principles and implementation of the proposed method. Section 4 evaluates the detection performance of the proposed method through experimental results and comparative analyses. Section 5 discusses the applicability and potential limitations of the proposed method and outlines possible directions for future research. Finally, Section 6 summarizes the paper.

2. Signal Model and Time–Frequency Analysis

2.1. Signal Model

In the detection of frequency-hopping signals within complex electromagnetic environments, common interference signals can generally be classified into three categories: fixed-frequency signals, frequency-swept signals, and burst signals. For example, voice broadcasts and television transmissions are typical fixed-frequency signals whose carrier frequencies remain relatively constant over time. Frequency-swept signals exhibit linear or periodic frequency variations, as observed in many radar systems. Burst signals, in contrast, are characterized by high randomness and short durations [35]. Consequently, in practical detection scenarios, the received signal can be modeled as a superposition of frequency-hopping signals, fixed-frequency signals, frequency-swept signals, burst signals, and Gaussian background noise. Let the total observation time be denoted by $T_0$. The received signal $r\left(t\right)$ can then be expressed as follows:

$$r\left(t\right)=\sum _{k=1}^K{c}_k\left(t\right)+\sum _{w=1}^W{f}_w\left(t\right)+\sum _{h=1}^H{g}_h\left(t\right)+\sum _{q=1}^Q{j}_q\left(t\right)+v\left(t\right)$$

(1)

where $\nu \left(t\right)$ denotes additive Gaussian white noise, and $K,W,H,Q$ represent the quantities of the four signal types, respectively.

If $T_h$ denotes the frequency-hopping period, $A_i$ denotes the signal amplitude within each hop, I denotes the frequency-hopping frequency, $t_0$ denotes the starting time of the first hop, and $f_i$ denotes the frequency-hopping frequency [23], then the frequency-hopping signal can be expressed as

$$c\left(t\right)=A_i\sum _{i=1}^{I}rect(t-i{T}_h-t_0)e^{j2\pi f_i(t-i{T}_h-t_0)}$$

(2)

Among these, $rect(•)$ is the unit of the rectangular pulse function.

In practical scenarios, FH signals may occasionally collide with interference frequencies at certain hopping instants. However, because FH signals hop pseudo-randomly across a wide bandwidth, the probability of such collisions is very low. Even when collisions occur, their effects are limited to small localized regions in the time–frequency plane and do not affect the overall sparsity or structural characteristics of FH signals in the time–frequency domain [24]. Therefore, all non-target components other than the FH signal—including various types of interference and background noise—can be uniformly modeled as an equivalent interference–noise composite term, denoted by $n\left(t\right)$, and defined as follows:

$$\begin{array}{c}\hfill n\left(t\right)={\displaystyle \sum _{w=1}^W}{f}_w\left(t\right)+{\displaystyle \sum _{h=1}^H}{g}_h\left(t\right)+{\displaystyle \sum _{q=1}^Q}{j}_q\left(t\right)+\nu \left(t\right)\end{array}$$

(3)

In signal detection theory, a binary hypothesis testing model is typically employed for the statistical modeling of signals. Let $H_0$ denote a scenario where the signal contains only noise and interference components, and $H_1$ denote a scenario where, in addition to noise and interference, a frequency-hopping signal is present. Combining Equations (1) and (3), the signal $r\left(t\right)$ can be expressed as

$$r\left(t\right)=\left\{\begin{array}{cc}n\left(t\right)\hfill & H_0\hfill \\ c\left(t\right)+n\left(t\right)\hfill & H_1\hfill \end{array}\right.$$

(4)

2.2. Signal Time–Frequency Analysis

FH signals are typical non-stationary signals whose carrier frequency changes rapidly over time, resulting in pronounced transient energy jumps in the frequency domain. Traditional one-dimensional analysis methods, such as the Fourier transform, can only represent the global spectral characteristics of a signal and have difficulty describing the dynamic process of frequency evolution over time. As a result, these methods cannot effectively capture the instantaneous frequency and hopping patterns of FH signals [26]. Time–frequency analysis provides an effective approach for analyzing non-stationary signals by jointly representing signals in the time and frequency domains, thereby revealing both local time-varying characteristics and spectral structures. The short-time Fourier transform achieves localized spectral analysis by introducing a window function, enabling a controllable trade-off between time resolution and frequency resolution. Consequently, the STFT can intuitively characterize the segmented energy distribution and hopping trajectories of frequency-hopping signals in the time–frequency plane. Therefore, time–frequency analysis is selected as the core signal representation in this paper. The STFT of the signal $r\left(t\right)$ is defined as $R(t,f)$

$$R(t,f)={\int }_{-\infty }^{\infty }r\left(t\right)h(\tau -t)e^{-j2\pi f\tau }d\tau$$

(5)

where $h\left(t\right)$ denotes the window function, and combining this with Equation (4), the STFT of the signal can be expressed as

$$R(t,f)=\left\{\begin{array}{cc}N(t,f)\hfill & H_0\hfill \\ C(t,f)+N(t,f)\hfill & H_1\hfill \end{array}\right.$$

(6)

where $H_0$ denotes a scenario where the signal contains only noise and interference components, and $H_1$ denotes a scenario where, in addition to noise and interference, frequency-hopping signals are also present within the signal.

In time–frequency analysis, the choice of window function has a significant impact on the analysis results. Different window functions involve distinct trade-offs between time–frequency resolution and spectral leakage. Among them, the Hanning window offers a favorable balance between main-lobe width and side-lobe suppression, making it well suited for extracting the characteristics of frequency-hopping signals. In addition, the selection of window length directly affects the achievable time–frequency resolution. According to Heisenberg’s uncertainty principle,

$$\Delta t\times \Delta f\ge {\displaystyle \frac{1}{4\pi }}$$

(7)

Time resolution $\Delta t$ and frequency resolution $\Delta f$ are mutually constrained and cannot be simultaneously optimized. Selecting a shorter window improves time resolution but degrades frequency resolution, whereas choosing a longer window enhances frequency resolution at the expense of time resolution. In practical signal analysis, the sampling rate is typically fixed, making the window function the primary factor influencing detection performance. The window length directly determines the trade-off between time and frequency resolution, while the sliding step size mainly affects the sampling density, smoothness, and computational efficiency of the time–frequency representation, with only a limited impact on detection performance itself. To further enhance time–frequency resolution and emphasize regions of concentrated energy, the time–frequency representation $R(t,f)$ obtained from the STFT of the signal $r\left(t\right)$ is squared in magnitude. This operation yields the time–frequency spectrogram of the signal. The expression for $SPEC(t,f)$ is given as follows:

$$SPEC(t,f)={\left|R(t,f)\right|}^2$$

(8)

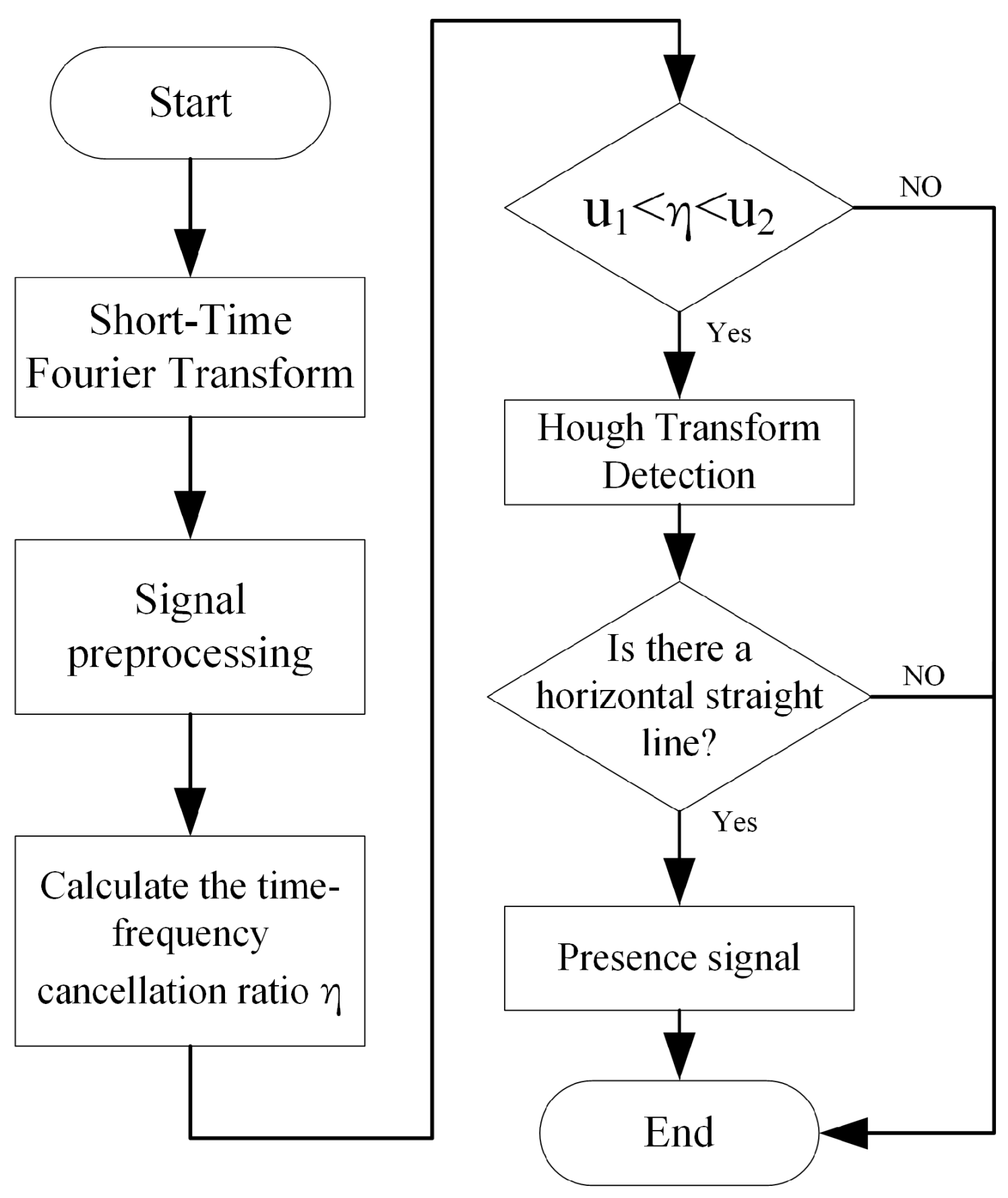
3. Frequency-Hopping Signal Detection Method

3.1. Signal Preprocessing

(1)

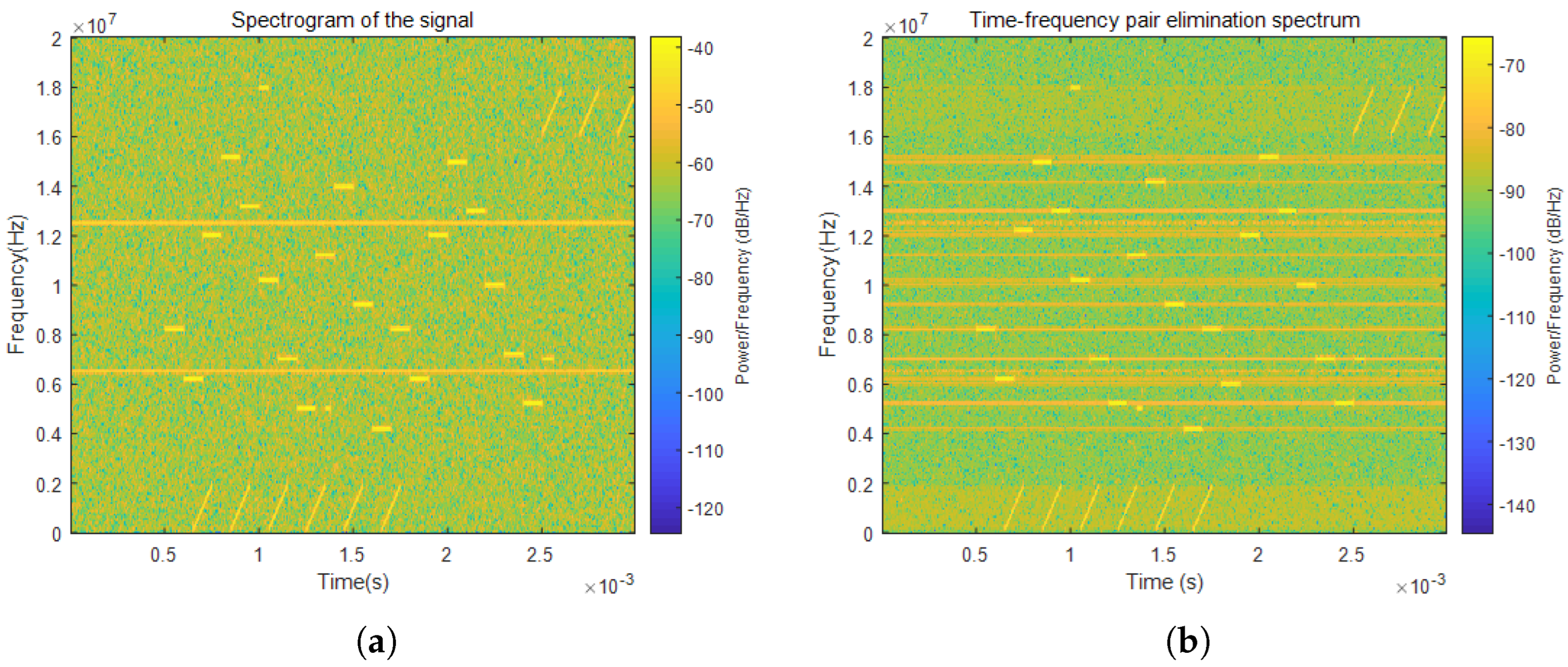
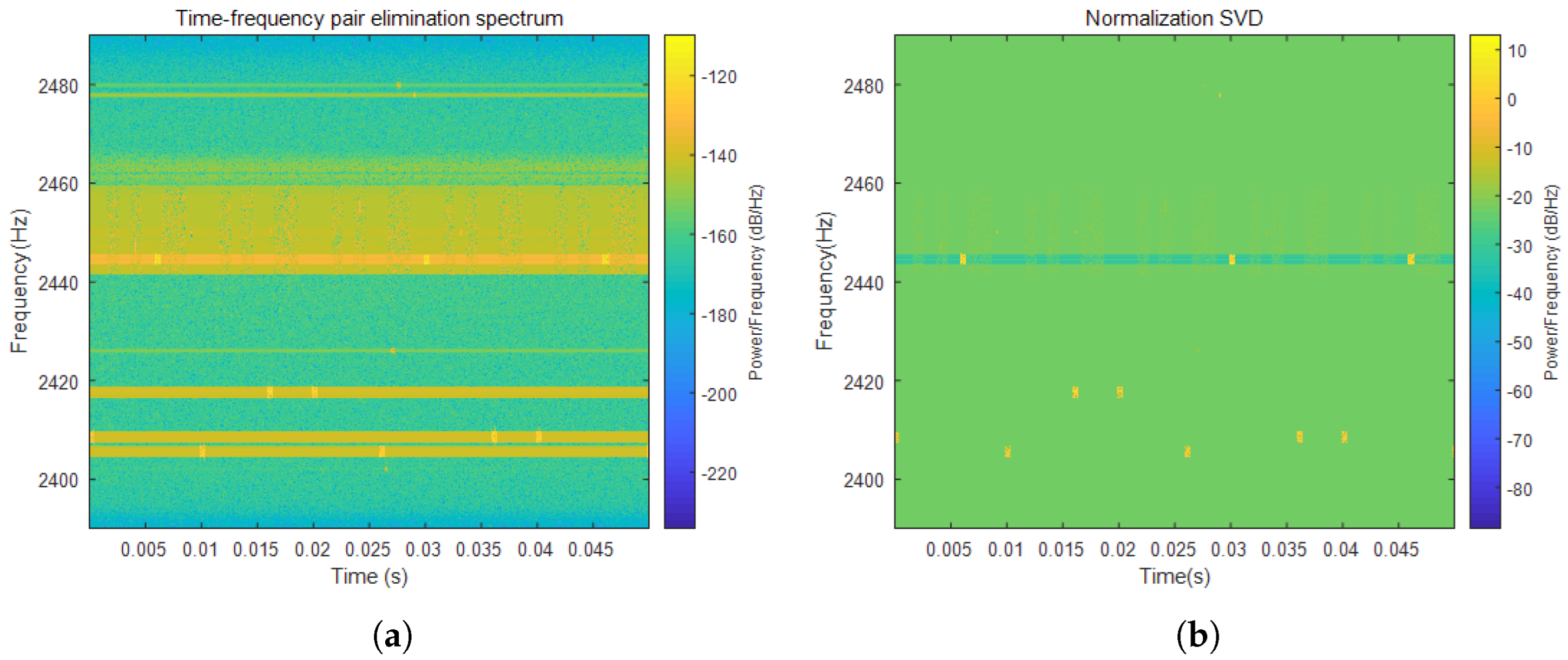
Time–frequency cancellation processing

In a time–frequency diagram, the energy of a fixed-frequency signal is concentrated at a single frequency and extends continuously along the time axis. In contrast, the energy of a frequency-hopping signal shifts across the frequency domain over time. By exploiting this difference, time–frequency cancellation processing can effectively remove the fixed-frequency components from the signal. From Equation (8), we obtain the time–frequency spectrum of the signal $r\left(t\right)$. To reduce the effect of absolute energy values, the time–frequency spectrum $SPEC(m,n)$ is normalized to produce the normalized time–frequency spectrum $P_x(m,n)$ as follows:

$$P_x(m,n)={\displaystyle \frac{1}{L}}\left|SPEC(m,n)\right|$$

(9)

where L denotes the length of the window function, $m=1,2,3,\cdots ,M$ represents the discrete frequency points, and $n=1,2,3,\cdots ,N$ signifies the discrete time points.

To address the time-varying nature of random noise, a cumulative averaging operation is applied to the time–frequency spectrum $P_x(m,n)$ along the time axis. This produces an average power spectrum $\overline{P_x}\left(m\right)$, which reflects only the frequency-dependent components. This method not only effectively suppresses noise but also preserves the time-invariant characteristics of fixed-frequency disturbances. The expression for $\overline{P_x}\left(m\right)$ is given by

$$\overline{P_x}\left(m\right)={\displaystyle \frac{1}{N}}\sum _{n=1}^N{P}_x(m,n)$$

(10)

To remove fixed-frequency interference and improve the detection of frequency-hopping signals, a subtraction operation is performed along the time axis of the time–frequency spectrum. This operation eliminates fixed-frequency components at specific frequencies, yielding the processed time–frequency cancellation spectrum $P_{sub}(m,n)$. The expression is given by

$$P_{sub}=P_x(m,n)-\overline{P_x}\left(m\right)$$

(11)

(2)

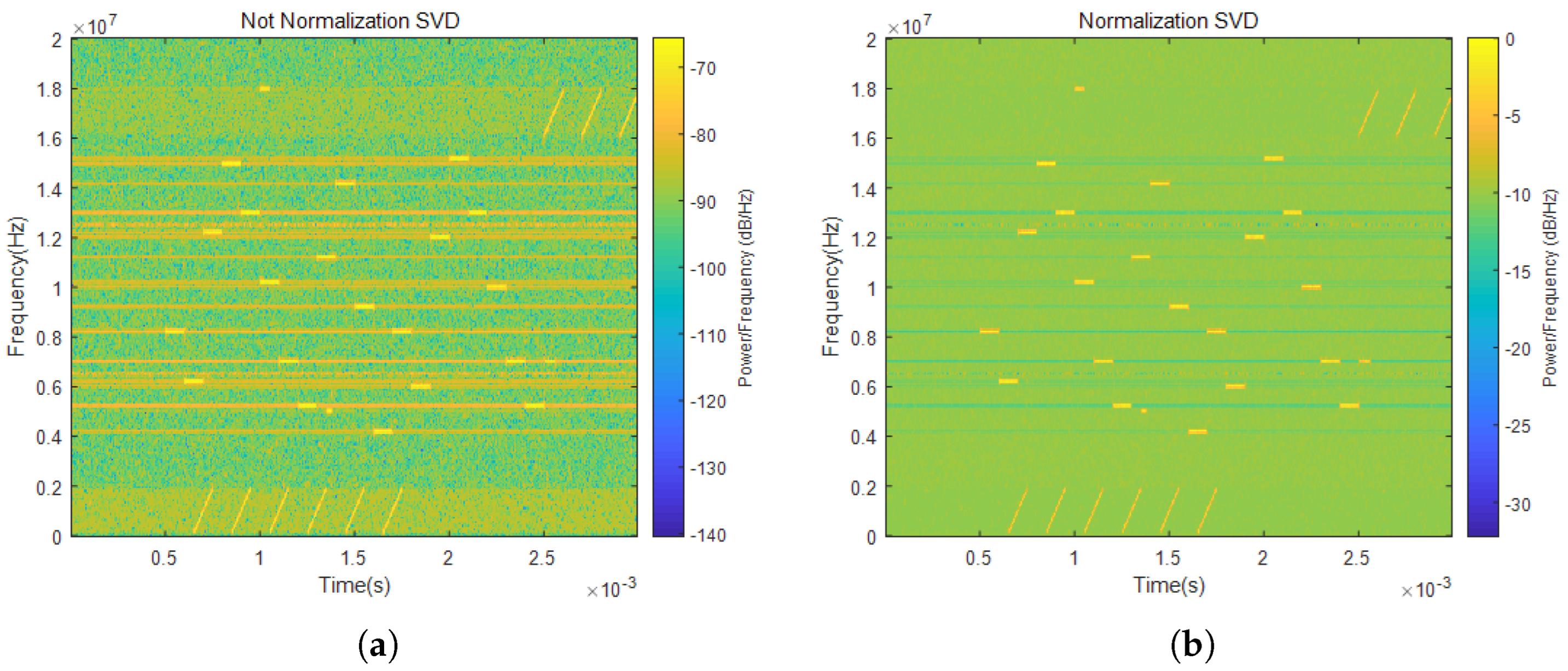
Singular value decomposition for noise reduction.

Due to the randomness of background noise and fluctuations in the noise floor, residual components can remain after time–frequency cancellation because of energy leakage, making further denoising necessary. After performing the subtraction operation on the time–frequency spectrum, the resulting time–frequency matrix contains both positive and negative values, resulting in an ambiguous energy distribution. Directly applying singular value decomposition (SVD) to this matrix produces singular values that do not accurately represent the original signal’s time–frequency energy distribution, which can degrade subsequent denoising performance. To achieve more effective noise reduction, a normalization method is applied to process the time–frequency cancellation matrix:

$$P_{sub}^{\prime }(m,n)={\displaystyle \frac{P_{sub}(m,n)-a}{d-a}}$$

(12)

Among these, d and a represent the maximum and minimum values of the time–frequency cancellation spectrum $P_{sub}(m,n)$, respectively.

SVD is a method of matrix factorization in linear algebra. For real matrices, the SVD takes the form:

$$A_{m\times n}=U_{m\times m}{D}_{m\times n}{V}_{n\times n}^{\mathrm{T}}$$

(13)

In the formula, $U_{m\times m}$ and $V_{n\times n}$ denote orthogonal matrices; the eigenvector matrix $D_{m\times n}$ of $A{A}^T$ is a diagonal matrix; the non-zero values on the diagonal of $\mathrm{D}$ are the square roots of the non-zero eigenvalues of matrix $A{A}^T$, arranged in descending order, also known as singular values. Based on the above formula, the time–frequency cancellation matrix P can be expressed as

$$\begin{array}{cc}\hfill \mathrm{P}& =\left[\begin{array}{c}{u}_1,u_2,\dots ,u_m\end{array}\right]\left[\begin{array}{ccccc}{\sigma }_1& 0& \dots & 0& 0\\ 0& {\sigma }_2& \dots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& 0\\ 0& 0& \dots & {\sigma }_m& 0\end{array}\right]\left[\begin{array}{c}{\nu }_1^T\\ {\nu }_2^T\\ ⋮\\ {\nu }_n^T\end{array}\right]\hfill \\ \hfill & ={\sigma }_1{u}_1{v}_1^T+{\sigma }_2{u}_2{v}_2^T+\cdots +{\sigma }_m{u}_m{v}_m^T\hfill \\ \hfill & =P_1+P_2+\cdots +P_m\hfill \end{array}$$

(14)

Among these, $u_i\in R^{m\times 1}$ denotes the $\mathrm{i}$ column vector of the left singular matrix $\mathrm{U}$, referred to as the left singular vector; $v_i\in R^{n\times 1}$ denotes the $\mathrm{i}$ column vector of the right singular matrix $\mathrm{V}$, referred to as the right singular vector.

Therefore, each submatrix $P_i(i=1,2,\dots ,m)$ in the formula above corresponds to a singular component of the original time–frequency cancellation matrix. The singular values associated with background noise and the signal differ, with the matrix’s essential information primarily contained in the singular components having larger singular values. Accordingly, by setting thresholds based on these singular value differences, redundant information can be effectively removed.

3.2. Signal Feature Analysis Based on Time–Frequency Cancellation

Due to differences in the time–frequency cancellation ratio among frequency-hopping signals, other interference sources, and background noise, this ratio serves as an effective feature for rapid detection of frequency-hopping signals. Using the powers of the original time–frequency spectrum and the time–frequency cancellation spectrum, we define the signal time–frequency cancellation ratio $\eta$ as follows:

$$\eta ={\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{P}_x(m,n)}{{\sum }_{m=1}^M{\sum }_{n=1}^N\left|P_{sub}(m,n)\right|}}$$

(15)

(1)

Time–frequency cancellation ratio of frequency-hopping signals

A fundamental property of frequency-hopping signals is the temporal variation in the carrier frequency. Given that the frequency-hopping period $T_h$ is significantly shorter than the total observation time $T_0$ of the received signal ($T_h\ll T_0$), the dwell time at any individual hopping frequency is much shorter than the overall observation interval. The dwell time is defined as the duration during which the signal remains at a specific hopping frequency. Accordingly, as shown in the following equation, the power at each frequency point is averaged over the time dimension to mitigate temporal fluctuations.

$$\overline{P_x}\left(m\right)={\displaystyle \frac{1}{N}}\sum _{n=1}^N{P}_x(m,n)$$

(16)

Suppose that the hopping period of the frequency-hopping signal is points in the time domain, and the total observation time is $N_T$ points $(N_t<N_T)$. When frequency $\mathrm{m}$ is the frequency-hopping point and time $\mathrm{n}$ falls within the cycle, the power magnitude at this point is $P_x(m,n)=A_p$. When outside the cycle, the power is $P_x(m,n)=0$, persisting until the commencement of the next hopping cycle. Combining Equations (14) and (15) yields the time–frequency cancellation ratio $\eta$ for the frequency-hopping signal as follows:

$$\eta ={\displaystyle \frac{m·N_t·A_p}{m·2·A_p·N_t(1-\frac{N_t}{N_T})}}={\displaystyle \frac{1}{2\left((1-\frac{N_t}{N_T})\right)}}$$

(17)

According to the above equation, the time–frequency cancellation ratio $\eta$ for a frequency-hopping signal is determined exclusively by the ratio between the dwell time $N_t$ and the total observation time $N_T$, and is independent of the number of frequency-hopping points $\mathrm{m}$. In practical scenarios, the dwell time $N_t$ is smaller than $N_T$, and the signal exhibits no fewer than two distinct hopping frequencies. Therefore, the corresponding time–frequency cancellation ratio satisfies $1/2<\eta <1$.

(2)

Time–frequency cancellation ratio of fixed-frequency signals

A fixed-frequency signal occupies a constant frequency over the full observation interval, resulting in a nearly uniform energy distribution in the time–frequency domain. Accordingly, the average power spectrum closely matches the original time–frequency power spectrum, such that $P_x(m,n)\approx {\overline{P}}_x\left(m\right)$. Following time–frequency cancellation as defined in Equation (11), the resulting cancellation spectrum satisfies $P_{sub}(m,n)\approx 0$. For fixed-frequency signals, the denominator of the time–frequency cancellation ratio therefore approaches zero, whereas the numerator corresponds to the total power of the original spectrum. Hence, in the ideal case, the cancellation ratio tends to infinity, i.e., $\eta \approx \infty$.

(3)

Time–frequency cancellation ratio of Gaussian white noise

Since Gaussian white noise $\nu \left(n\right)$ follows a normal distribution degrees, the received signal’s time–frequency spectrum $P_x(m,n)$ follows a chi-squared distribution with 2 degrees of freedom, i.e., $P_x(m,n)\sim {\displaystyle \frac{{\sigma }_{\nu }^2}{2}}{x}^2\left(2\right)$. Furthermore, the average time–frequency spectrum ${\overline{P}}_x\left(m\right)$ follows a chi-squared distribution with $2N$ degrees of freedom, i.e., ${\overline{P}}_x\left(m\right)\sim {\displaystyle \frac{{\sigma }_{\nu }^2}{2N}}{x}^2\left(2N\right)$. Consequently, the time–frequency cancellation for Gaussian white noise may be constructed as follows:

$$\eta \ge {\displaystyle \frac{{\sum }_{m=1}^M{\sum }_{n=1}^N{P}_x(m,n)}{{\sum }_{m=1}^M{\sum }_{n=1}^N[P_x(m,n)+\overline{P_x}\left(m\right)]}}$$

(18)

Let $q_1={\sum }_{m=1}^M{\sum }_{n=1}^N{P}_x(m,n)$, $q_2={\sum }_{m=1}^M{\sum }_{n=1}^N[P_x(m,n)+\overline{P_x}\left(m\right)]$, $r_1={\displaystyle \frac{q_1}{q_2}}$. Combining the above analysis, it follows that $q_1$ obeys a chi-squared distribution with $2MN$ degrees of freedom, while $q_2$ approximates a central chi-squared distribution with $2(N+1)MN$ degrees of freedom. Consequently, $r_1$ obeys an $F(2MN,2(N+1\left)MN\right)$ distribution, where M and N are discrete frequency points of the signal associated with discrete time points. whose mean time–frequency cancellation ratio is

$$E\left\{r_1\right\}={\displaystyle \frac{2(N+1)MN}{2(N+1)MN-2}}\approx 1(N\gg 1)$$

(19)

Since $P_{sub}(m,n)=P_x(m,n)-{\overline{P}}_x\left(m\right)$, the expected value of its absolute value satisfies

$$E\{\mid P_{\mathrm{sub}}(m,n)\mid \}<E\left\{P_x(m,n)\right\}$$

(20)

Therefore, the expected value of the denominator is less than that of the numerator, resulting in the following:

$$E\left\{\eta \right\}={\displaystyle \frac{E\left\{q_1\right\}}{E\{\sum \mid P_{sub}\mid \}}}>1$$

(21)

Therefore, when M and N are large, the statistical mean $E\left\{\eta \right\}$ of $\eta$ is a finite value greater than 1.

(4)

Time–frequency cancellation ratio between impulse signals and swept-frequency signals

For burst signals, they appear randomly at any frequency and at any time within the observation period, and their duration $N_q$ is extremely short. Hence, $N_q\ll N_T$ is satisfied, and thus the time–frequency cancellation ratio of burst signals can be expressed as

$$\eta ={\displaystyle \frac{1}{2(1-\frac{N_q}{N_T})}}$$

(22)

From the above equation, it can be seen that when $N_q\ll N_T$, and if the burst signal occurs at multiple frequency points, its time–frequency cancellation ratio $\eta$ is approximately 0.5.

In the case of swept-frequency signals, the instantaneous frequency varies linearly with time, and the dwell time at each frequency point is significantly shorter than the frequency-hopping period. Consequently, their time–frequency characteristics are analogous to those of burst signals with short temporal duration. As a result, the time–frequency cancellation ratio $\eta$ for swept-frequency signals is approximately 0.5.

According to the theoretical analysis, the time–frequency pair cancellation ratio $\eta$ exhibits clear differences between FH signals, various types of interference, and Gaussian white noise. These differences can be exploited for fast and reliable FH signal detection. To systematically determine whether an unknown signal contains an FH component, the problem can be categorized into the following typical scenarios: a pure noise environment; an environment where FH signals coexist with Gaussian noise; a complex environment in which FH signals coexist with noise and multiple interference sources; and a complex environment that contains no FH signals. The detailed analysis is as follows:

(1) If only Gaussian white noise is present in the signal, the resulting time–frequency cancellation ratio will be a finite value greater than 1, indicating that no frequency-hopping signal is present in the signal.

(2) For fixed-frequency signals, following time–frequency cancellation processing, the time–frequency cancellation spectrum yields $P_{sub}(m,n)\approx 0$. Consequently, the theoretical value of the time–frequency cancellation ratio $\eta$ approaches infinity. However, as time–frequency cancellation effectively eliminates interference from fixed-frequency signals, this factor is disregarded during signal analysis.

(3) When both frequency-hopping signals and Gaussian white noise coexist within a signal, the time–frequency cancellation ratio exhibits dynamic characteristics as the signal-to-noise ratio varies. However, the overall numerical value remains within the cancellation ratio range observed when either signal is present alone. This characteristic may serve as a basis for discerning the presence of frequency-hopping signals.

(4) When the signal contains frequency-hopping signals, background noise, and swept or burst interference, the time–frequency cancellation ratio of the mixed signal will be distributed between 0.5 and 1.

(5) When only swept or burst interference and background noise are present in the signal, the time–frequency cancellation ratio will similarly fall between 0.5 and 1. This scenario could lead to misclassification, requiring the incorporation of additional feature parameters to mitigate the interference effects of burst and swept signals.

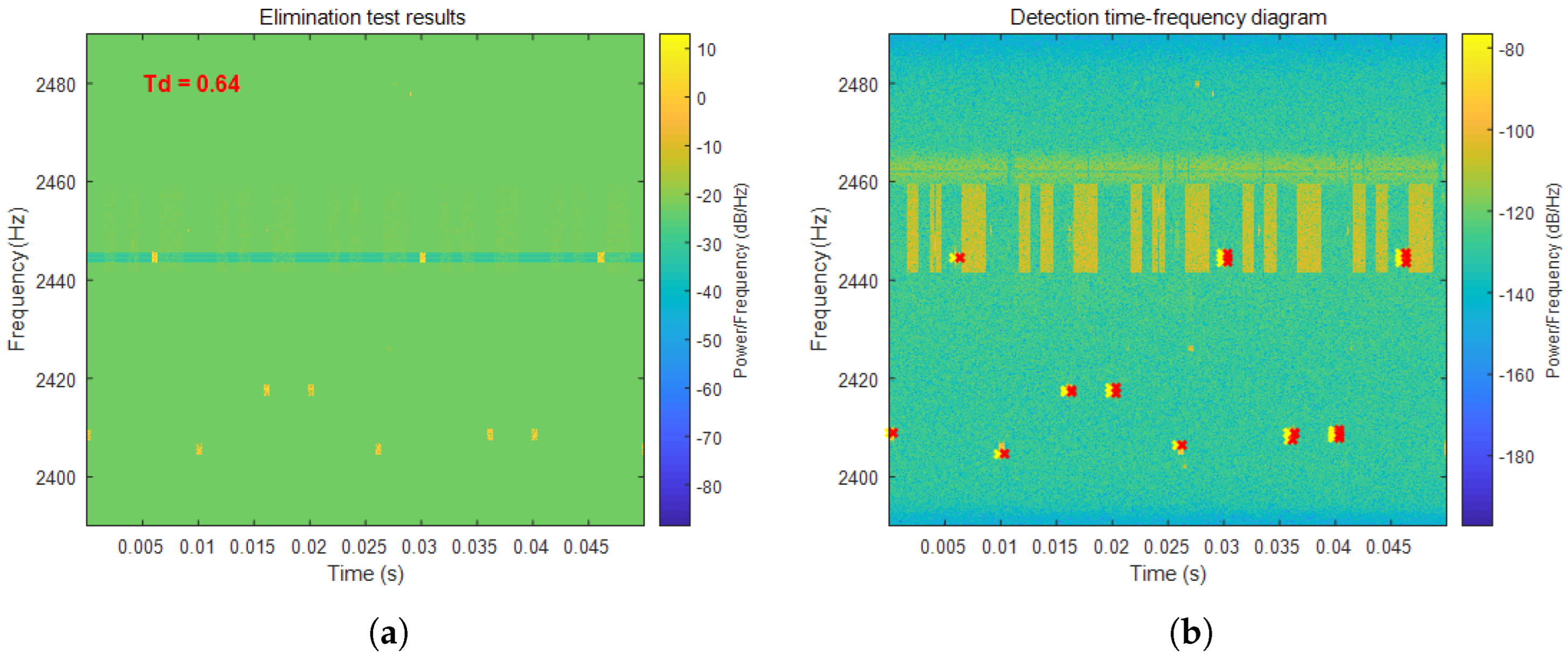
3.3. Frequency-Hopping Signal Detection Based on the Hough Transform

To address the deterioration in detection performance resulting from sudden and swept-frequency interference signals with time–frequency cancellation characteristics similar to those of frequency-hopping signals in complex electromagnetic environments, a detection framework based on the Hough transform is introduced. The proposed method extracts geometric and morphological features in the time–frequency domain, where frequency-hopping signals manifest as regular horizontal line segments, swept-frequency signals as diagonal trajectories with fixed slopes, and burst signals as irregular distributions. By integrating these geometric features with statistical characteristics and leveraging differences in time–frequency continuity between frequency-hopping signals and interference sources, a multidimensional detection criterion is established, enabling precise and robust frequency-hopping signal detection.

The Hough transform for line detection is based on point–line duality, whereby the problem of line detection in the image domain is transformed into a point detection problem in the corresponding parameter space. This approach exhibits strong robustness in noisy image environments. The equation of a straight line in Cartesian coordinates is expressed as

$$y=kx+b$$

(23)

Here, k and b are parameters representing the slope and y-intercept of the line.

In the Cartesian coordinate system, the original image space contains a line perpendicular to the X-axis with an infinite slope, which cannot be correctly represented by Cartesian coordinates. Therefore, in practical applications, to circumvent this issue, the Hough transform typically employs polar coordinates as its parameter space. In polar coordinates, a straight line in the image can be represented by the parameters $\gamma$ and $\theta$, where $\gamma$ denotes the shortest distance from the line to the origin and $\theta$ represents the angle between the line’s normal vector and the X-axis. Therefore, Equation (23) can be expressed as

$$\gamma =xcos\theta +ysin\theta$$

(24)

To visualize the time–frequency characteristics of different signal types, a hybrid time–frequency distribution containing frequency-hopping, fixed-frequency, swept-frequency, and burst signals is generated using simulated data, as shown in Figure 1. The following features can be observed:

• Frequency-hopping signals appear as periodic horizontal segments.
• Swept-frequency signals exhibit diagonal traces due to linear frequency variation.
• Burst signals appear as randomly distributed short segments with limited temporal duration.

Figure 1. Mixed-signal time–frequency spectrum (SNR = 0 dB).

Figure 1. Mixed-signal time–frequency spectrum (SNR = 0 dB).

Given these significant structural differences in the time–frequency representations, this paper employs the Hough transform to detect linear features within the time–frequency image, enabling accurate identification of frequency-hopping signals. The specific implementation steps are as follows:

(1) Binarization processing: If the conditions for time–frequency cancellation detection are met, binarize the time–frequency plot to enhance the signal features

(2) Parameter space quantization: Discretize $\theta$ within the range $[0,{180}^{\circ }]$ and quantize $\gamma$ according to the image dimensions.

(3) Accumulator Construction: Establish a two-dimensional accumulator array $A(\theta ,\gamma )$ to record parameter space votes. Iterate through each foreground point in the binary image, compute its trajectory within the parameter space, and accumulate the results.

(4) Peak detection: Locating local maxima within the parameter space, corresponding to linear features in the image space;

(5) Feature classification: Frequency-hopping signals exhibit multiple peaks with differing $\gamma$ values near $\theta ={90}^{\circ }$; frequency-sweeping signals display distinct peaks at specific angles; burst signals show no significant peak clustering within the parameter space. To mitigate interference from multiple burst signals, the classification process incorporates the length information of the corresponding straight line when $\theta ={90}^{\circ }$ as an auxiliary criterion.

3.4. Algorithm Summary

To address the challenges posed by low signal-to-noise ratios and the coexistence of multiple interference types in complex electromagnetic environments, this paper proposes a detection method that integrates time–frequency pair cancellation with the Hough transform. As shown in Figure 2, the overall framework of the proposed method consists of three main stages. First, the STFT is applied to the received signal to obtain a two-dimensional time–frequency representation. Background noise and fixed-frequency interference are then suppressed through preprocessing, providing a clean basis for subsequent feature extraction. Second, the time–frequency pair cancellation ratio of the signal is computed, and a preliminary decision regarding the presence of potential frequency-hopping components is made using a predefined threshold. Finally, for signals that satisfy this criterion, the Hough transform is applied to the time–frequency representation. By identifying horizontal line structures, the method achieves the final detection of frequency-hopping signals.

3.5. Calculation Complexity Analysis

To evaluate the theoretical advantages of the proposed algorithm in terms of computational complexity, this paper analyzes its time complexity in the temporal domain. The overall complexity is determined by the number of operations required in the algorithm’s core steps. Let N denote the length of the input discrete signal, L the length of the STFT window, S the sliding step, $M_f=L/2+1$ the number of frequency points, and $N_{Tt}\approx N/S$ the umber of time frames. In the time–frequency analysis stage, the STFT is performed by computing the fast Fourier transform (FFT) for each of the $N_{Tt}$ frames. If the computational complexity of the FFT for a single frame is $O(LlogL)$, then the total complexity of this stage is

$$O_{\mathit{STFT}}=O\left({\displaystyle \frac{N}{S}}·LlogL\right)$$

(25)

Second, during the time–frequency cancellation and interference suppression stage, statistical feature calculations and SVD are performed on the time–frequency matrix to separate the structured signal from background noise. The computational complexity is dominated by the SVD of the $M_f\times N_{Tt}$ time–frequency matrix. For a standard SVD, the computational complexity is $O\left(\min \right(M_f^2{N}_{Tt},M_f{N}_{Tt}^2\left)\right)$. Therefore, the complexity of this step can be expressed as

$$O_{SVD}=O({\displaystyle \frac{M_f^{2}N}{S}})$$

(26)

Finally, in the Hough transform stage, parameter-space accumulation is performed on the thresholded set of time–frequency points. The computational complexity of this step depends on the number of foreground pixels P and the number of angular quantization levels $K_{\theta }$ in the time–frequency map. Therefore, the complexity can be expressed as $O\left(P{K}_{\theta }\right)$.

In the frequency-hopping signal detection method based on OpGST-ResNet proposed in the literature [34], the parameters $\lambda$ and p of the generalized S-transform are optimized using a multi-population genetic algorithm to generate an optimized time–frequency representation, which is subsequently processed by a residual neural network for frequency-hopping signal detection. From a computational complexity perspective, the optimization stage of the generalized S-transform has a complexity of $O\left(N^2\right)$, while the detection stage based on the residual network has a complexity of $O(K\times N)$, Where K is the dimension. Since the length of the discrete signal N is typically much larger than the number of frequency points $M_f$, the overall computational complexity of this method is dominated by the OpGST transformation step, resulting in an overall complexity on the order of $O\left(N^2\right)$, which is significantly higher than that of the method proposed in this paper.

This higher complexity arises primarily because deep learning-based frequency-hopping signal detection methods generally involve a large number of convolutional kernel parameters and multi-layer network architectures. As a result, both the computational complexity and storage overhead during training and inference increase substantially with network depth and input size, leading to high demands on computational and memory resources. In contrast, from both theoretical complexity and engineering implementation perspectives, the proposed method achieves comparable detection performance while maintaining significantly lower computational complexity, thereby demonstrating greater potential for real-time applications.

4. Experimental Results and Analysis

To evaluate the effectiveness and robustness of the proposed FH signal detection method—based on time–frequency pair cancellation and the Hough transform—under complex electromagnetic conditions, simulated signals are constructed to reflect representative signal characteristics for experimental validation. The parameters listed in

Table 1. Signal parameter settings.

Signal Type	Parameter Description	Key Parameter Settings
FH signal	Frequency, period	4–15 MHz, 0.1 ms
Burst signal	Frequency, duration	5, 7, 18 MHz, 0.03 ms
Chirp signal 1	Frequency, period	0.1–1 MHz, 0.1 ms
Chirp signal 2	Frequency, period	16.1–17 MHz, 0.1 ms
Fixed-frequency signal	Frequency	6.5 MHz, 12.5 MHz

are chosen to emulate a typical complex signal environment, containing multiple signal types with partially overlapping parameter configurations. In the simulations, the sampling frequency is set to 40 MHz, the total sampling duration is 3 ms, and the corresponding number of sampling points is 120,000. The detailed parameter configurations for the frequency-hopping, burst, swept-frequency, and fixed-frequency signals in a Gaussian noise background are provided in Table 1.

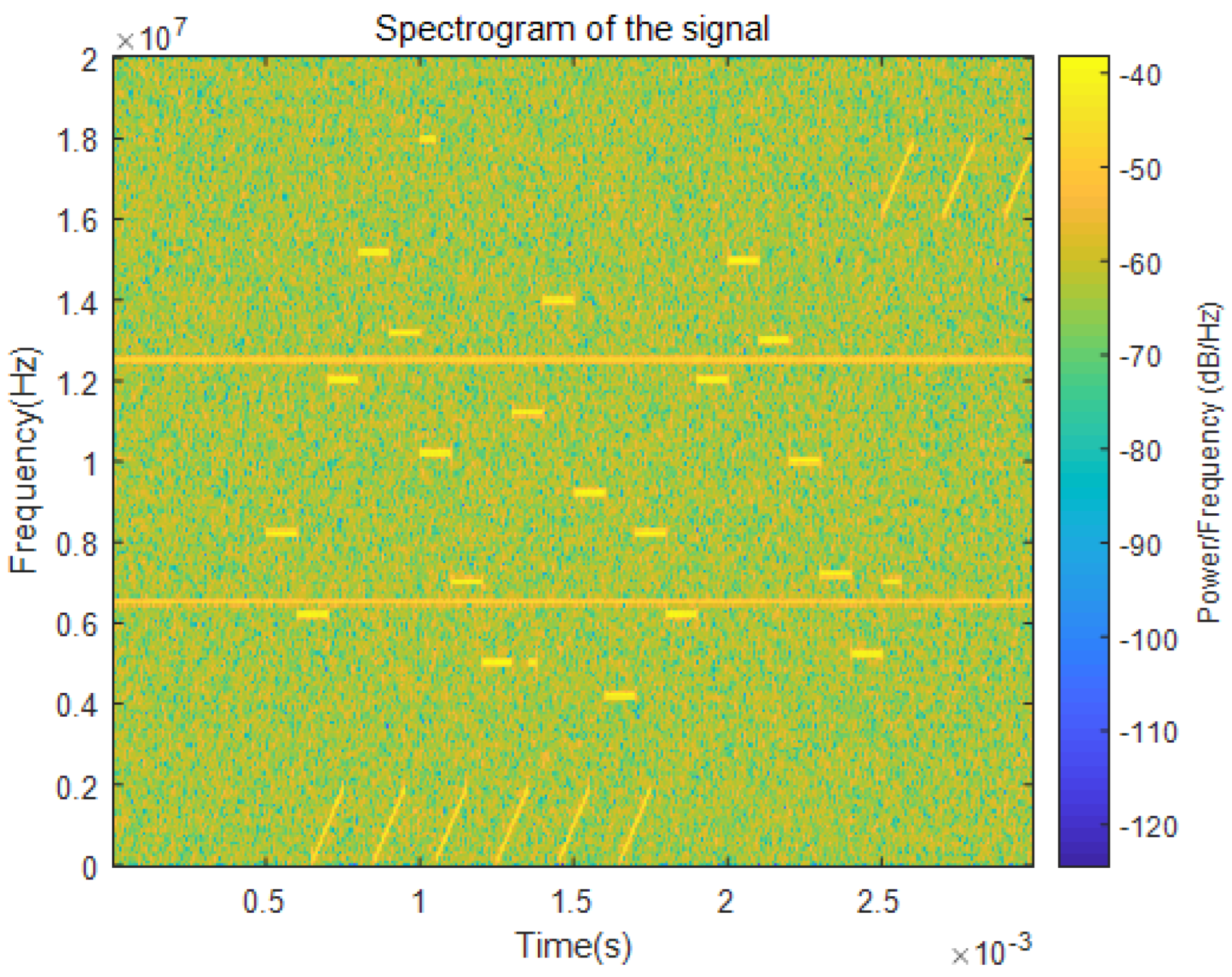
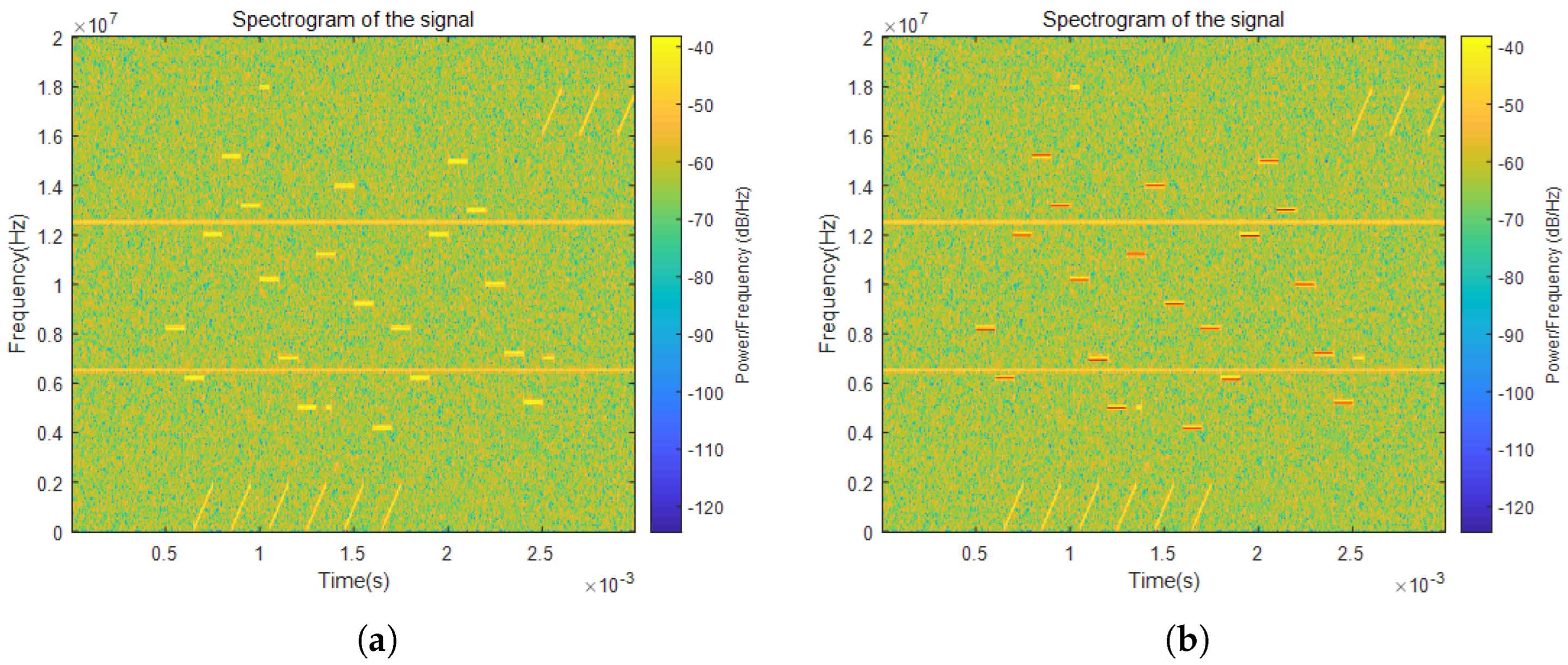
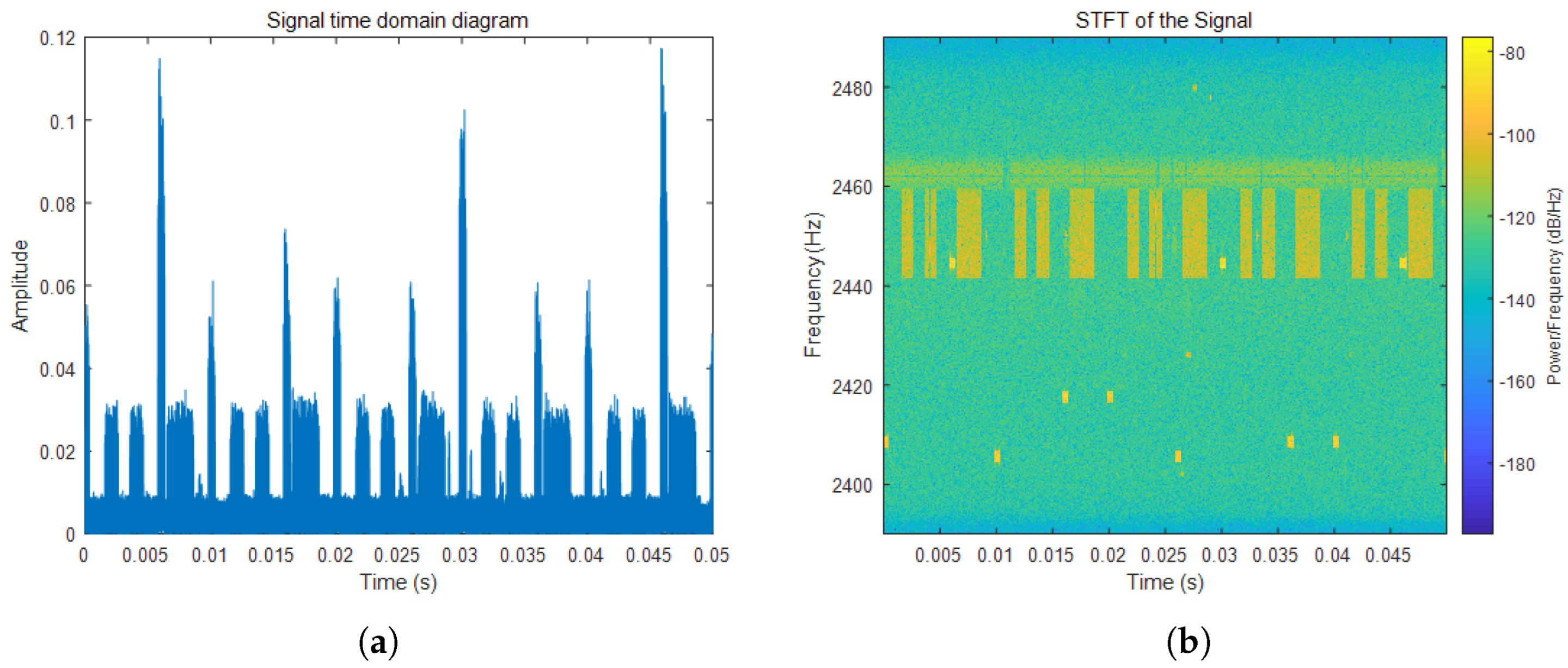
4.1. Data Preprocessing

To evaluate the effectiveness of the time–frequency cancellation method in suppressing fixed-frequency interference, time–frequency analysis was performed on the signal described above using a Hann window of length 512. The results are shown in Figure 3. Figure 3a illustrates the original time–frequency plot, clearly revealing the fixed-frequency interference components. Figure 3b shows the time–frequency plot after cancellation, where the elongated lines correspond to the residual portions of the signal’s time-averaged power. Comparison with Figure 3a demonstrates that the time–frequency cancellation method effectively suppresses fixed-frequency interference.

After time–frequency cancellation, residual components remain due to background noise, requiring further processing. Figure 4 illustrates the denoising results obtained by applying SVD to the time–frequency spectrum after cancellation. In Figure 4a, the data are not normalized, which limits the ability of the singular values to accurately represent the original time–frequency energy distribution. In contrast, Figure 4b, which incorporates normalization, more clearly highlights the relative differences in energy across the time–frequency spectrum.

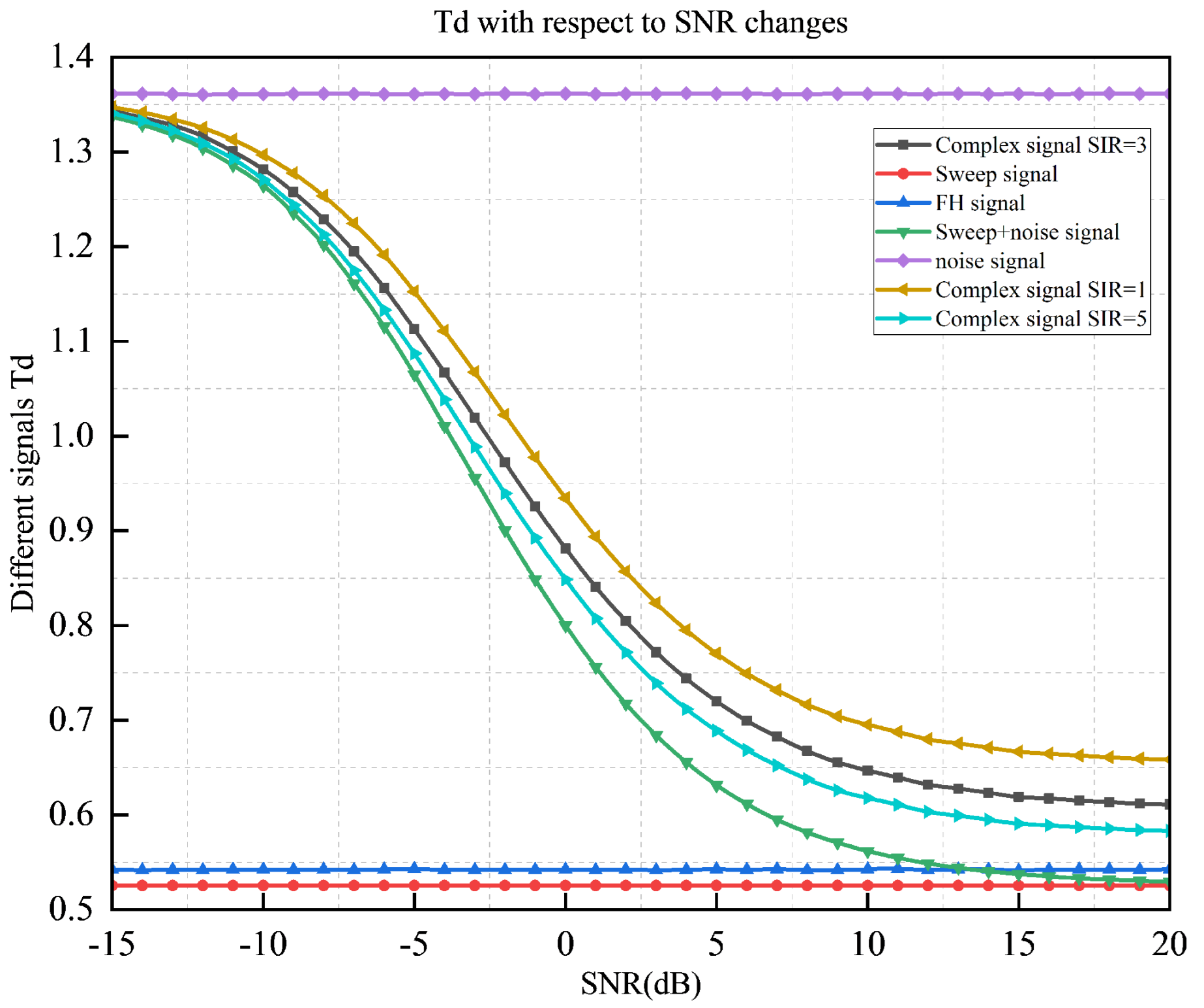
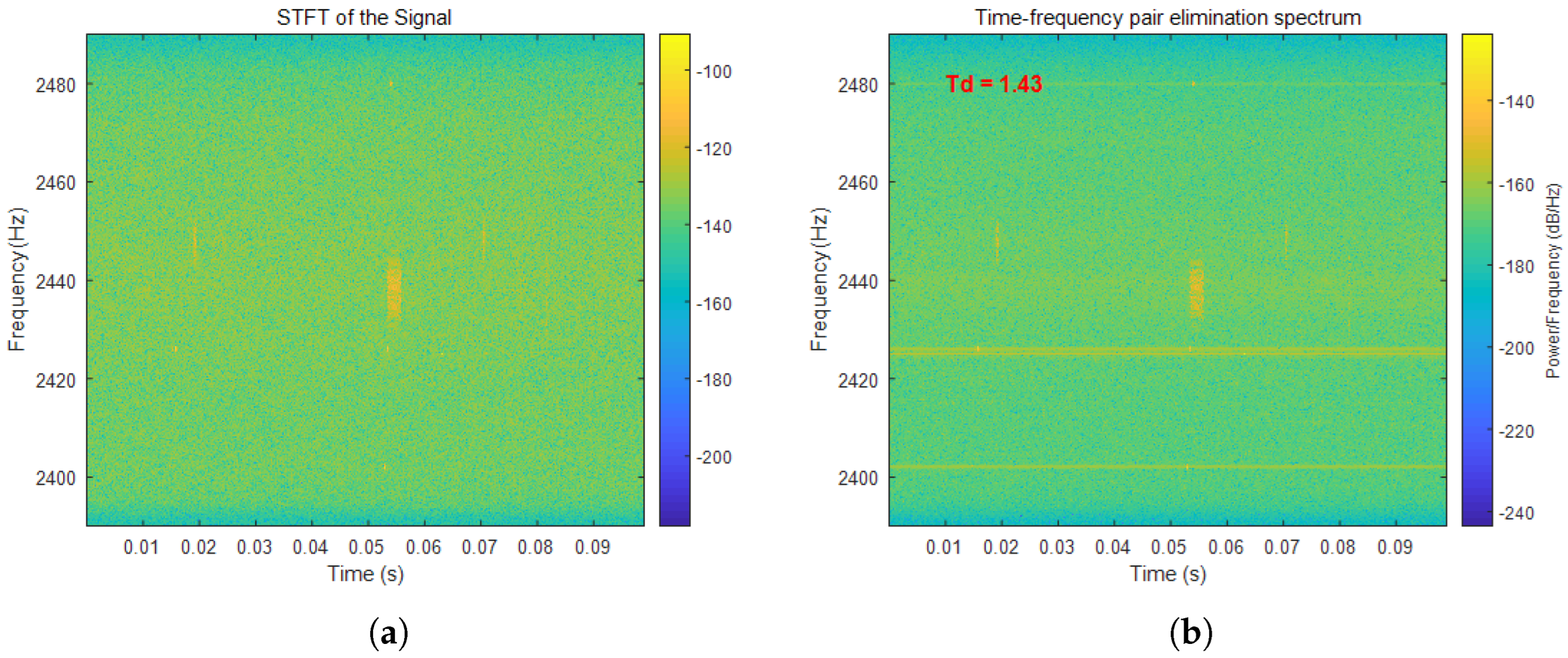
4.2. Analysis of Time–Frequency Cancellation Ratio and Hough Transform Results

In complex electromagnetic environments, the signals under test typically include frequency-hopping signals, fixed-frequency signals, swept-frequency signals, burst signals, and mixed signals combined with Gaussian white noise. As shown in the preprocessing results, time–frequency cancellation effectively suppresses the influence of fixed-frequency interference. The signal-to-interference ratio (SIR) is defined as the ratio of the power of the frequency-hopping signal to the combined power of the swept-frequency and burst signals. Based on this definition, simulations were conducted under various scenarios, including frequency-hopping signals, swept-frequency signals, Gaussian white noise, mixed signals with different SIR values, and mixed signals without frequency-hopping components. The resulting time–frequency cancellation ratio as a function of signal-to-noise ratio (SNR) is shown in Figure 5.

As shown in Figure 5, the time–frequency cancellation ratio of frequency-hopping signals ranges between 0.5 and 1.0. For Gaussian white noise, the ratio assumes a finite value greater than 1, while for swept-frequency and burst signals it approaches 0.5. These statistical observations are consistent with the theoretical analysis. However, the presence of swept-frequency and burst signals can adversely affect detection accuracy. To mitigate false detections, the Hough transform is applied to impose constraints on the detection process. The results of Hough transform-based detection are also shown in Figure 6. In comparison, swept-frequency signals form diagonal lines at specific angles in the time–frequency plot, whereas burst signals occur sporadically and have very short durations. By leveraging both morphological features and statistical properties, the method can reliably detect frequency-hopping signals.

4.3. Comparative Analysis of Algorithm Detection Performance

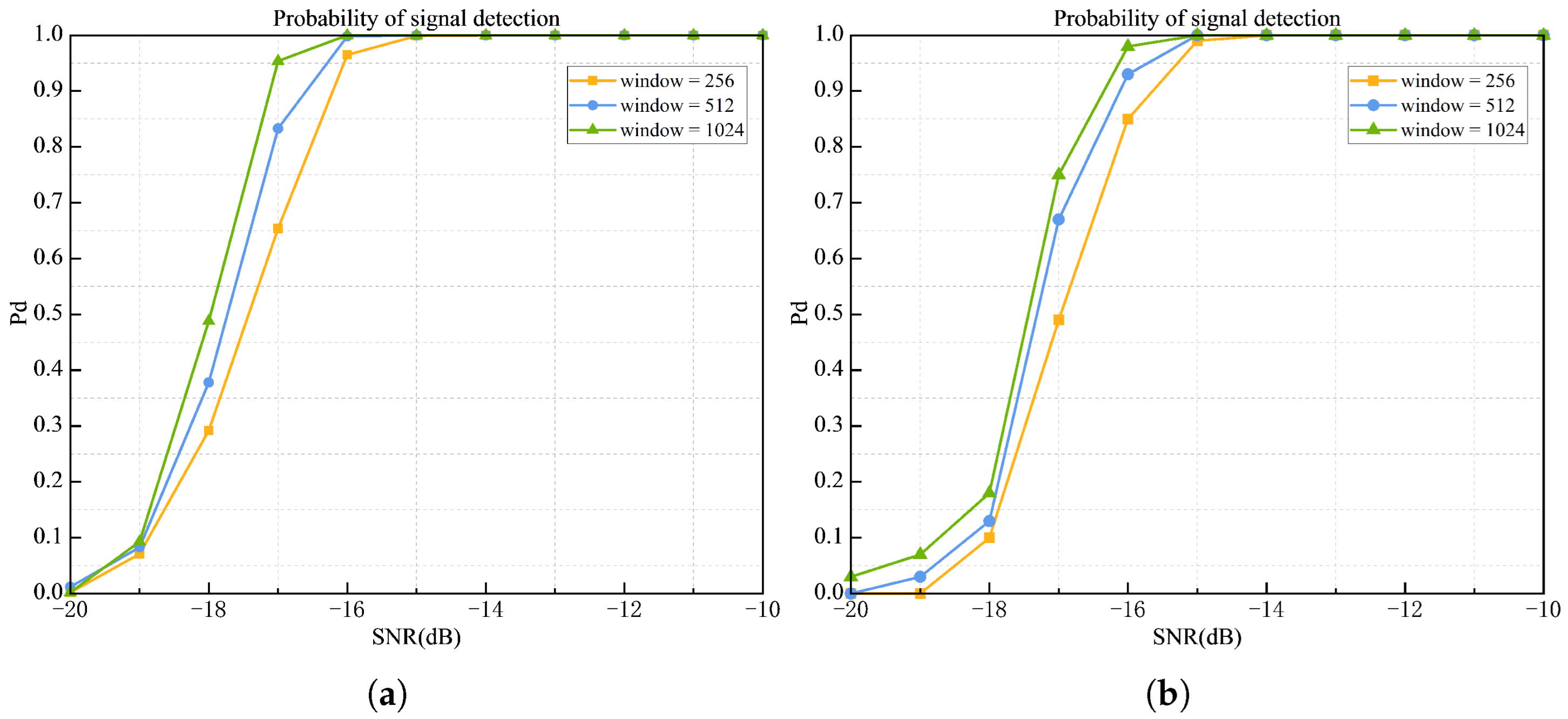
(1)

The effect of different STFT window lengths on detection performance

To analyze the impact of the STFT window length on detection performance, the STFT window length L was set to 256, 512, and 1024, respectively, with the sliding length fixed at $L/4$. The algorithm’s performance was validated under both Gaussian background noise and complex electromagnetic environments. Figure 7a and Figure 7b, respectively, illustrate the variation curves of detection probability with signal-to-noise ratio (SNR) under these two different environments. In complex electromagnetic environments, the detection probability of the algorithm for frequency-hopping signals increases as the window length grows. The algorithm has good detection performance for different window lengths, and the probability of the algorithm detecting the signal in complex environments is 100% for SNR greater than −15 dB. When the SNR is −16 dB, the detection probabilities for frequency-hopping signals with window lengths of 1024, 512, and 256 are 98%, 94%, and 85%, respectively.

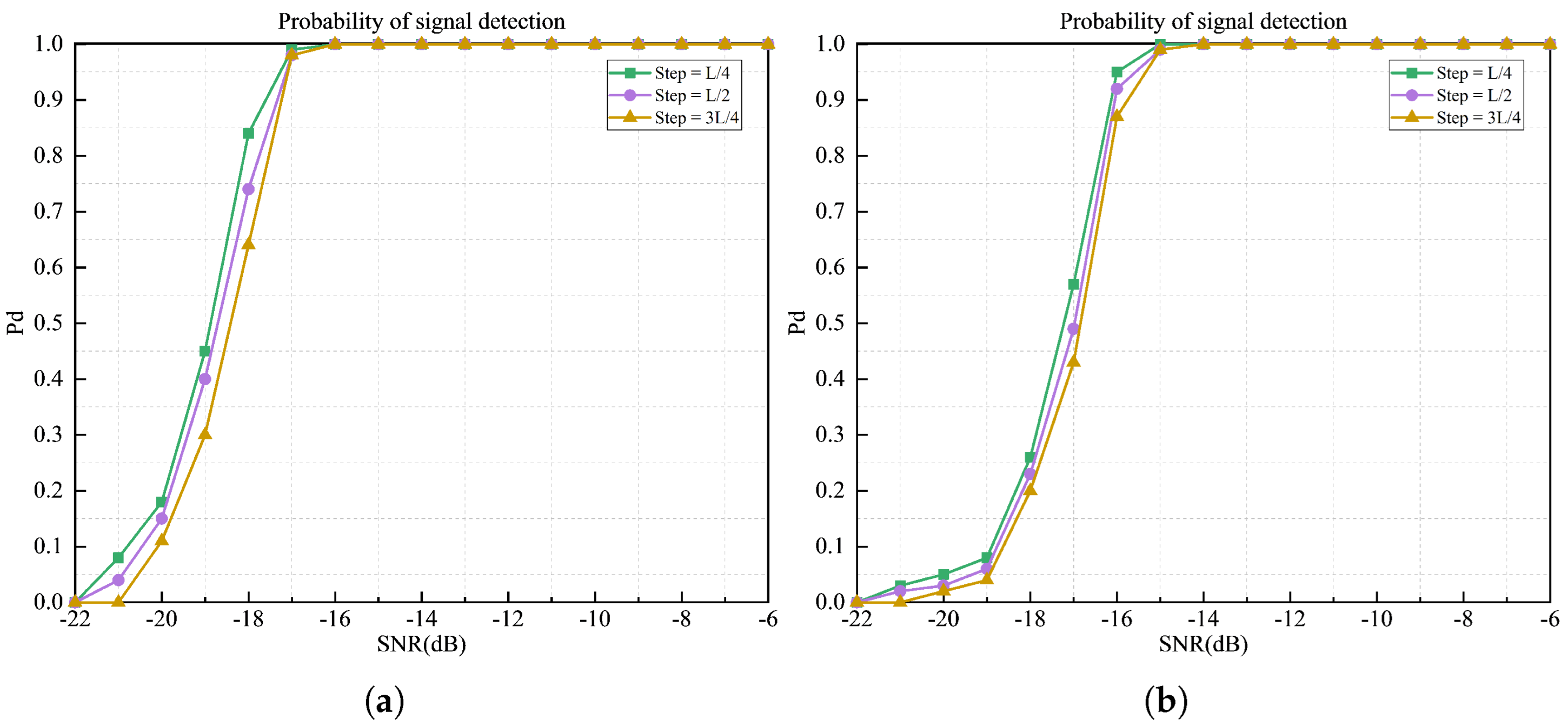
(2)

The effect of different STFT window sliding lengths on detection performance

The STFT window length L was fixed at 512, with window sliding increments set $L/4$, $2L/4$, and $3L/4$, respectively. The effect of the window sliding step size on detection performance under Gaussian background noise is illustrated in Figure 8a, which reflects the variation in detection probability with SNR. Simultaneously, in complex electromagnetic environments containing both burst and sweep-frequency interference, the relationship between the algorithm’s detection performance and the STFT sliding window size is illustrated in Figure 8a. A comprehensive analysis reveals that, whether in Gaussian background noise or complex electromagnetic environments, the impact of varying sliding window sizes on detection performance is relatively minor. Moreover, as the sliding window size decreases, detection performance exhibits a slight upward trend.

(3)

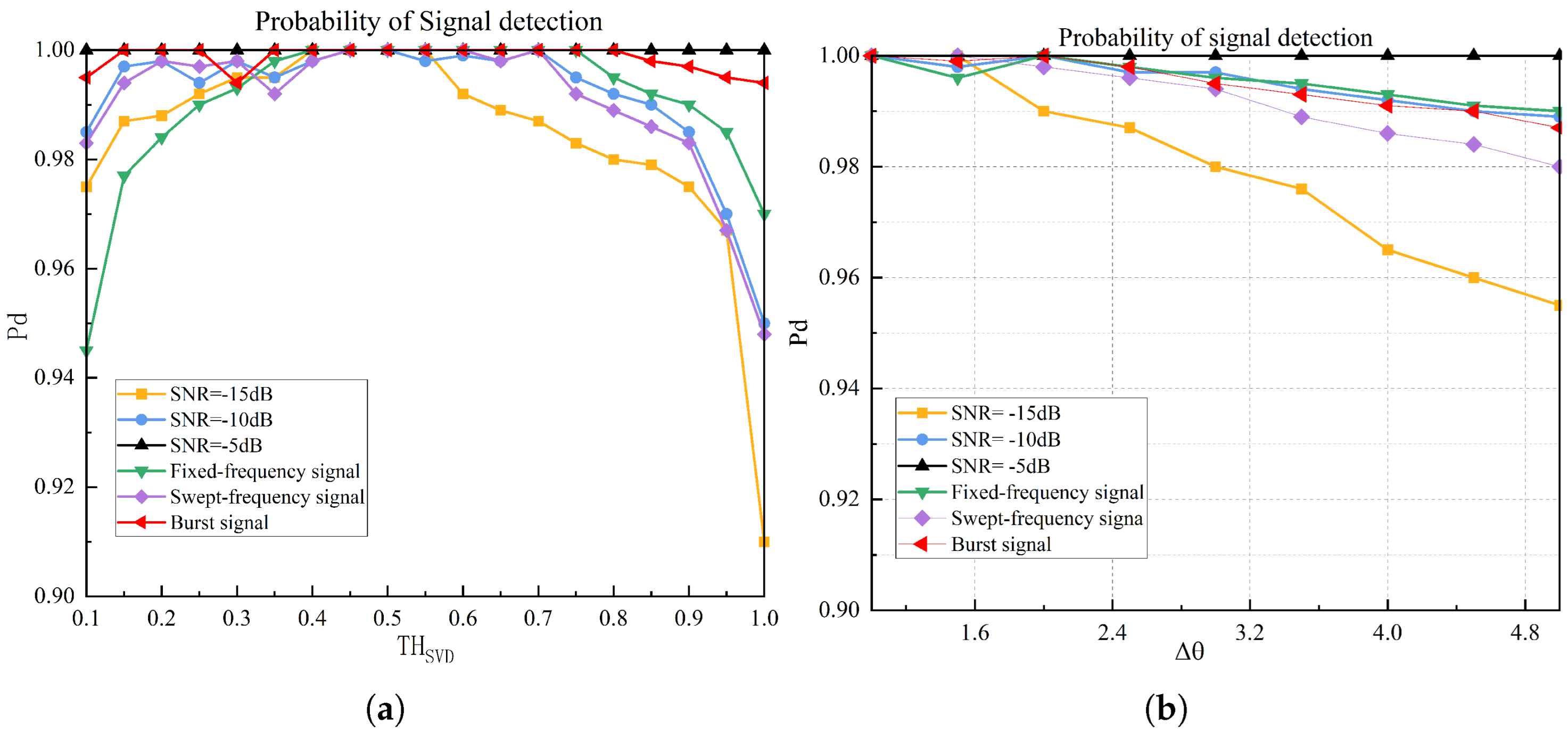
Effect of singular value threshold and Hough transform quantization interval on detection performance.

Figure 9 illustrates the impact of the singular value threshold and the Hough transform quantization interval on detection performance. In Figure 9a, the effect of varying the singular value threshold is shown under different signal-to-noise ratio (SNR) conditions. When the SNR is −5 dB, changes in the singular value threshold have little effect, and the detection probability remains essentially stable. As the SNR decreases further, variations in the threshold begin to influence detection performance, but the overall decrease is limited, indicating that the proposed method is robust to changes in the singular value threshold. Figure 9b shows the effect of the Hough transform quantization interval on detection performance. At an SNR of −5 dB, the quantization interval has a negligible effect. As the SNR decreases, the detection probability gradually declines with increasing quantization interval; however, the algorithm still maintains a high detection probability over a wide range of parameter values.

Meanwhile, to further investigate the relationship between key parameters and detection probability under varying electromagnetic environments, this paper adjusts the proportions of different interference signals based on the signal parameters listed in Table 1 to create three types of interference-dominant environments: fixed-frequency interference dominant, frequency-sweeping interference dominant, and burst interference dominant. The results show that when fixed-frequency interference dominates, detection performance is primarily influenced by the singular value threshold, and appropriately increasing this threshold enhances the suppression of fixed-frequency interference. When frequency-sweeping interference dominates, the quantization interval of the Hough transform has the greatest impact on performance, and reducing this interval improves the distinguishability of different trajectories. In a burst interference-dominant environment, changes in key parameters have relatively limited effects on detection performance. This demonstrates the stability of the proposed method with respect to parameter selection and its strong noise immunity.

(4)

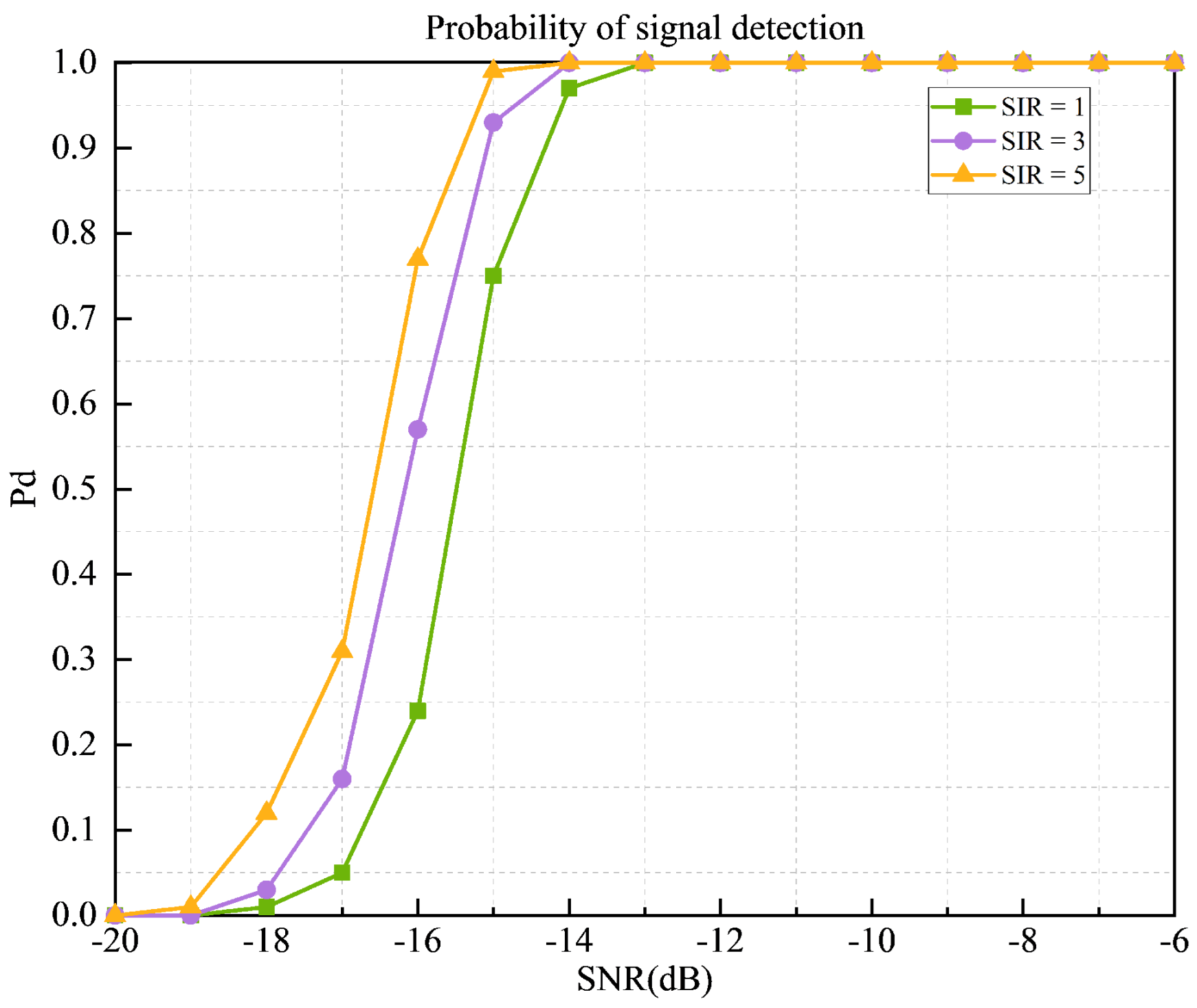
Signal detection performance under varying interference levels.

The fixed STFT window length L is set to 512, with a sliding step size of $L/4$. The signal-to-interference ratio is configured at 1 dB, 3 dB, and 5 dB, respectively. The signal detection probability curves under varying interference intensities are illustrated in Figure 10. As shown in the figure, when the signal-to-noise ratio exceeds −14 dB, the detection probability of frequency-hopping signals under all three signal-to-interference ratios reaches 100%. When the signal-to-noise ratio falls below −14 dB, the detection probability increases to a certain extent as the signal-to-interference ratio rises. The reason is that under low signal-to-noise ratio conditions, the time–frequency characteristics of frequency-hopping signals are easily overwhelmed by noise and interference, leading to reduced distinguishability and consequently affecting detection performance.

(5)

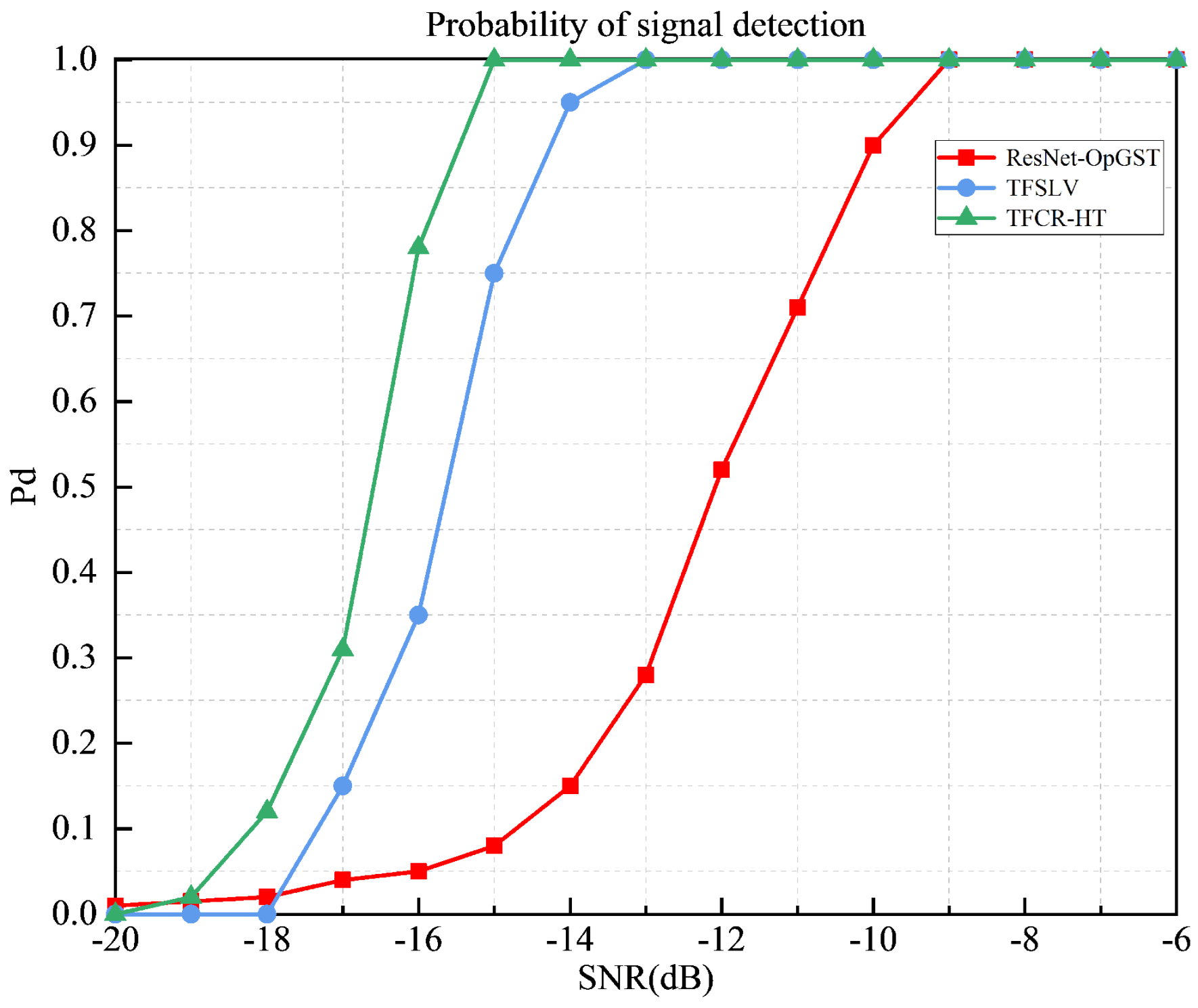
Performance comparison between different detection algorithms

Setting the STFT window length L to 512 and the window sliding step size to $L/4$, the detection performance curves of the time–frequency cancellation and Hough transform-based detection algorithm (TFCR-HT), The time–frequency spectrum local variance detection algorithm (TFSLV) and the residual network with optimized generalized S-transform-based detection algorithm (ResNet-OpGST) [34] for frequency-hopping signals are shown in Figure 11. As illustrated in the figure, the proposed detection algorithm demonstrates a distinct advantage over the other two algorithms. At a signal-to-noise ratio of −15 dB, the proposed algorithm achieves a detection probability of 100% for frequency-hopping signals, whereas the TFSLV algorithm achieves a detection probability of 75%. The ResNet-OpGST algorithm obtains a 100% detection probability only at −1 dB, and its detection performance at low SNR is insufficient. Therefore, from the experimental results, it can be seen that the algorithm in this paper has better detection performance at low SNR, and it can still realize the accurate detection of frequency-hopping signals when the SNR is −15 dB.

4.4. Algorithm Validation Based on Measured Signals

To validate the algorithm’s effectiveness, the publicly available large-scale drone radio frequency signal dataset DroneRFa [47] was selected for testing. Taking DJI drone models such as the Phantom series, Matrice series, and Inspire series—which support the second-generation BigZee communication protocol—as examples, their uplink control signals employ frequency-hopping spread spectrum technology. Consequently, the drones’ uplink control signals can be regarded as frequency-hopping signals. This dataset captures radio frequency signals from communications between unmanned aerial vehicles and remote controllers via the USRP-2955 software-defined radio device, controlled by LabVIEW 2024 Q1 with the NI-USRP Hardware Driver Suite version 21.8.0, encompassing multiple drone signals alongside background noise.

To validate the algorithm’s detection performance under background noise conditions, the background noise portions of the dataset were selected for verification, representing scenarios where no frequency-hopping signals were present. The results are shown in Figure 12, where Figure 12a depicts the raw time–frequency plot of the signal, and Figure 12b presents the time–frequency cancellation spectrum of the signal. As shown in the figure, the time–frequency cancellation ratio obtained after processing is 1.43, exceeding the preset detection threshold. This confirms that no frequency-hopping signals are present in the current signal, thereby validating the algorithm’s correctness in a pure noise environment.

To validate the detection performance of the proposed algorithm under actual signal acquisition conditions, the publicly available DroneRFa radio frequency signal dataset was employed for testing. A segment of typical signals was selected for analysis, with the results presented in Figure 13. Figure 13a presents the time-domain waveform of the signal, illustrating the amplitude variation over time; Figure 13b depicts the time–frequency spectrum of the signal, revealing the characteristic distribution of frequency transitions over time. The analysis of the actual acquired signal effectively validates the algorithm’s detection performance and applicability in real-world conditions.

Analysis of the above diagram reveals that, in addition to frequency-hopping signals, the signal contains various forms of interference, including drone video transmission signals and random burst signals. These interfering signals significantly compromise the accuracy of signal detection. Therefore, preprocessing of the received signal is required prior to implementing signal detection. First, the signal undergoes time–frequency cancellation processing, with the result shown in Figure 14a. Subsequently, SVD is applied to the time–frequency matrix of the received signal, yielding the final processed result depicted in Figure 14b.

Analysis of the pre-processed signal yielded the time–frequency cancellation ratio results shown in Figure 15a. The calculated time–frequency cancellation ratio value for the signal was 0.64, consistent with the 0.5–1 range observed for the frequency-hopping signals analyzed above and below the preset detection threshold. Figure 15b displays the detection results of the Hough transform. As can be seen from the figure, even in complex electromagnetic environments with interfering signals, the frequency-hopping signal can still be effectively detected. Experimental results demonstrate that the proposed algorithm can reliably detect frequency-hopping signals in complex electromagnetic environments, validating the effectiveness of this method.

5. Discussion and Future Work

The proposed algorithm enables rapid detection of frequency-hopping signals by leveraging their time–frequency characteristics and morphological features. Experimental results indicate that the method maintains high detection accuracy even under low-SNR conditions. Moreover, it demonstrates robust performance in environments with multiple types of coexisting interference, and its effectiveness has been further confirmed using measured data.

Despite these promising results, several limitations remain. First, the current study focuses primarily on UAV remote control signals, and although representative, other communication systems may differ in modulation schemes, frequency-hopping strategies, and channel conditions. Therefore, the method’s adaptability and generalization to other typical communication scenarios—such as tactical communications or civilian frequency-hopping systems—require systematic validation using more extensive measured data. Second, frequency-hopping communications are often associated with secure or covert communication models. In such scenarios, the deliberate weakening of time–frequency features through randomized modulation and power shaping may reduce feature discriminability. To address this, future work should explore time–frequency feature enhancement strategies and adaptive decision mechanisms tailored to covert signals. Third, the current method has been validated primarily in offline signal processing; its real-time implementation on embedded or resource-constrained platforms, including assessments of power consumption, stability, and latency, remains to be investigated. Finally, the inherent trade-off between time and frequency resolution in STFT analysis necessitates careful parameter selection, particularly for ultra-wideband signals or high-speed frequency-hopping scenarios.

Future research will focus on optimizing computational complexity, developing adaptive parameter selection mechanisms, and validating the method in diverse channel conditions and broadband applications. These efforts aim to further improve detection robustness, enhance practical applicability, and expand deployment potential in both conventional and covert communication environments.

6. Conclusions

Complex electromagnetic environments, combined with the inherently non-stationary characteristics of FH signals, pose significant challenges for accurate detection. Existing methods often struggle, particularly in scenarios where multiple types of interference coexist. To address these challenges, this paper proposes a frequency-hopping signal detection method based on time–frequency pair cancellation and the Hough transform. The method comprises three main modules: data preprocessing, detection based on time–frequency pair elimination, and joint detection using the Hough transform.In the first module, background noise and fixed-frequency interference are suppressed through preprocessing, significantly enhancing the system’s anti-interference capability. In the second module, the distinct time–frequency distribution characteristics of FH signals are exploited, and the time–frequency pair cancellation ratio is used to effectively distinguish FH signals from interference. In the final module, the Hough transform resolves feature ambiguities, further improving detection reliability. Simulation results demonstrate that the proposed method achieves strong detection performance under low-SNR conditions (SNR > −15 dB) and in environments with multiple interference sources, outperforming existing comparison algorithms. Validation using measured data confirms that the method can reliably detect FH signals even in the presence of complex noise and interference.