An Interactive Evolutionary Design Framework Integrating AHP-CRITIC Hybrid Weighting for Mitigating User Evaluation Noise

Abstract

To address the imbalance between user evaluation noise and algorithmic autonomy in Interactive Evolutionary Design (IED), this study proposes an optimization method integrating subjective and objective weights to alleviate user fatigue and enhance evolutionary efficiency of Genetic Algorithms (GAs). Building upon the Interactive Genetic Algorithm (IGA), an AHP-CRITIC combined proxy model is introduced, leveraging the bidirectional complementarity of AHP and CRITIC to suppress evaluation noise. An interactive evolutionary design model integrating AHP-CRITIC-IGA is constructed, with armchair design as a case study. Compared to traditional IGA, the combined-weighting-based IGA shows faster convergence and more stable fitness trajectories under the same parameter settings. To avoid over-interpretation, evaluation-noise claims are tied to explicit variability metrics (e.g., fitness standard deviation and inter-rater disagreement) reported in the revised experimental section. The proposed method effectively balances the contradiction between human interaction and algorithmic autonomy in interactive evolutionary design. Furthermore, the framework is inherently generalizable and demonstrates significant potential for adaptation and electronic system design, where optimizing complex, multi-criteria problems under user feedback is paramount. This establishes its relevance to the broader field of intelligent and interactive engineering systems.

1. Introduction

Research in the field of design studies is highly interdisciplinary, allowing cross-domain integration across methodological development, mathematical analysis, and practical implementation to achieve more optimal design outcomes [1]. Product gene theory represents a typical paradigm of such interdisciplinary fusion in design research [2]. As a methodological framework that integrates concepts from both design studies and biology, product gene theory encompasses multiple research branches, with recent scholarly attention primarily concentrated on evolutionary design approaches [3,4].

The primary methodological pathway for evolutionary design is the Interactive Genetic Algorithm (IGA), an intelligent computational approach developed for optimization problems in which the objective function is difficult to explicitly quantify [5]. Its core mechanism involves eliciting users’ cognitive preferences toward evolving individuals and incorporating these interactive evaluations into fitness values that guide iterative algorithmic optimization until solutions that satisfy user requirements are obtained [6]. Within design research, this approach is commonly referred to as Interactive Evolutionary Design (IED), a form of computer-aided industrial design that leverages algorithms to generate multiple batches of design alternatives. By simultaneously accommodating users’ aesthetic preferences and improving design efficiency, IED overcomes the limitations of traditional design methodologies and has emerged as a prominent research focus within the design community from a rational-thinking perspective [7].

1.1. Fundamental Concepts and Current Research Progress

The concept of the Genetic Algorithm (GA) was first introduced by Holland in 1975 [8], and since then, GA has gained broad recognition within the academic community as an effective optimization method with extensive practical applications. By incorporating users’ perceptual evaluations, the IGA further extends the applicability of traditional GA and has been widely adopted in fields such as image processing and retrieval, industrial product design, education, and entertainment. Leelathakul et al. [9] developed an IGA-based ethnic pattern generation system to lower the artistic skill threshold for users. Jalali et al. [10] employed IGA for interactive optimization of the form and façade of office buildings. Uusitalo et al. [11] explored collaborative creation using IGA in industrial design and analyzed its application workflow through a chandelier design case study.

1.2. Bottlenecks and Challenges in Application

A fundamental challenge currently faced in IGA research lies in the imbalance between human–computer interaction and algorithmic autonomy [12]. Specifically, the evaluation of evolutionary individuals in IGA is confronted with dual uncertainties: cognitive uncertainty arising from fluctuations in users’ subjective preferences and stochastic uncertainty caused by algorithmic noise [13,14]. From the user perspective, evaluation of noise tends to escalate as the number of evolutionary generations increases, causing algorithmic convergence to deviate from users’ true intentions [15]. To address this problem, Naser and Alavi [16] examined the most commonly used performance fitness and error metrics for regression and classification algorithms, with emphasis on engineering applications. From the designer’s perspective, Dell’Era et al. [17] revealed several cognitive fixation issues occurring during the design process, including local optimal preference, repetitive selection, disregard for novelty, and premature convergence. They further developed a quantitative model of cognitive fixation to break habitual decision patterns.

However, existing studies are trapped in a paradoxical dilemma: although current methods reduce the required number of user interactions, they simultaneously weaken the core value of human participation, making it difficult to capture users’ dynamically evolving deep preferences [18]. Meanwhile, constructing static surrogate models allows the incorporation of expert knowledge but fails to adaptively capture the intrinsic fluctuations and correlations within evaluation data, resulting in limited effectiveness in noise suppression and insufficient capacity to balance subjective preferences with objective indicators [19].

Therefore, achieving an effective balance between users’ perceptual cognition and algorithmic rational computation is crucial for overcoming the application bottlenecks of IGA. Based on the current status, future research should focus on the following issues: (1) establishing a quantifiable mapping model for perceptual cognition to reconcile conflicts between subjective evaluations and objective metrics; (2) designing a dynamic objective-weight allocation mechanism to enable non-stationary optimization of human–machine decision weights; and (3) integrating subjective and objective surrogate models to maximize the value of user cognition within a limited number of interactions.

The main contributions of this study are threefold: (1) It proposes a novel dynamic surrogate weighting model that innovatively integrates AHP and CRITIC within an IGA framework to balance subjective preference drift and objective indicator stability. (2) It develops a comprehensive AHP-CRITIC-IGA methodology and corresponding prototype, providing a scalable tool for user-responsive design iteration. (3) It validates the method through an expanded experimental setup, including multiple case studies and a user study, demonstrating significant improvements in convergence speed and noise suppression compared to standard IGA.

1.3. Alignment with Electronics and EDA Integration

To explicitly align this work with the scope of Electronics, we clarify how the proposed AHP–CRITIC–IGA framework addresses typical optimization problems in electronic and electromechanical system design. In practical Electronic Design Automation (EDA) workflows, engineering teams frequently face multi-criteria trade-offs—e.g., efficiency vs. thermal stress vs. bill-of-materials cost vs. electromagnetic interference (EMI) margins—that must be balanced under uncertainty, limited simulation budgets, and evolving expert preferences. Our hybrid surrogate integrates subjective knowledge (AHP, from domain experts and stakeholders) with data-driven objective salience (CRITIC), then embeds the combined weights into an interactive genetic search. This directly supports decision-making in power-electronics converter sizing, controller co-design, analog/RF circuit parameter tuning, and early-stage PCB/floor planning exploration, where user-in-the-loop feedback is essential to reconcile quantitative KPIs with qualitative design constraints.

Concretely, the framework slots into a standard co-simulation loop: (i) decision variables encode circuit and system parameters (e.g., device choices, passive values, switching frequency, layout constraints); (ii) SPICE/PSPICE/Verilog-A/Matlab–Simulink models generate performance estimates for each candidate; (iii) evaluation indicators reflect electronics KPIs (efficiency, transient response, stability margins, junction temperatures, EMI/EMC headroom, mass/volume, and cost); (iv) the AHP–CRITIC surrogate combines expert intent with data variability/correlation to stabilize fitness estimation; and (v) interactive checkpoints collect targeted expert feedback to correct preference drift with minimal fatigue. This mapping preserves the core value of human expertise while accelerating convergence, which is the central objective of Electronics—advancing the science and applications of electronics with reproducible methods and engineering relevance.

Representative prior art shows that learning-based and evolutionary search have already improved chip floor planning with reinforcement learning, analog circuit sizing with Bayesian optimization and CMA-ES, and power-converter codesign with NSGA-II. Our contribution complements this line by adding a principled, light-weight preference model that reduces evaluation noise without removing the engineer from the loop, thereby bridging intelligent optimization and electronics-centric practice.

2. Research Methodology

2.1. Research Subject and Problem Definition

The subject of this research is IED, a computer-aided design paradigm that leverages user interaction within an evolutionary algorithm loop for creative optimization. The specific application domain is industrial design, with the armchair and gearbox as the primary case study. This case exemplifies a typical multi-objective, preference-driven design problem characterized by numerous morphological parameters and significant subjective evaluation components.

The core research problem addressed is the inherent imbalance between user evaluation noise and algorithmic autonomy within standard IGAs. This imbalance manifests as a dilemma: excessive reliance on user evaluations introduces cognitive noise and fatigue, leading to inconsistent feedback, slow convergence, and potential deviation from the user’s true preferences. Conversely, reducing user interaction to improve algorithmic efficiency risks marginalizing human creativity and subjective judgment, which are central to the value of IED. Therefore, the fundamental problem is how to effectively suppress user evaluation noise while preserving the core role of human preference in guiding the evolutionary search, thereby enhancing both the reliability and efficiency of the IED process.

2.2. Research Objectives

To address the above problem, this study establishes the main objective: To develop, implement, and validate a novel interactive evolutionary design framework that integrates a hybrid AHP-CRITIC weighting scheme as a dynamic surrogate model. This framework aims to mitigate subjective evaluation noise, accelerate convergence, and effectively balance human perceptual input with algorithmic computational rationality in the context of product form design.

Specifically, this study aims (1) to construct a robust hybrid weighting mechanism that combines the hierarchical, preference-driven subjectivity of the Analytic Hierarchy Process (AHP) with the data-driven, variability-and-conflict-based objectivity of the CRITIC method; (2) formally integrate this combined weighting model into the fitness evaluation stage of an IGA, creating a cohesive AHP-CRITIC-IGA methodology for interactive design optimization; (3) implement the proposed methodology in a functional software prototype and apply it to the specific case of armchair and gearbox morphological design; (4) empirically validate the performance of the proposed framework against a standard IGA baseline, with quantitative metrics focusing on convergence speed, fitness trajectory smoothness (as a proxy for noise reduction), and qualitative design outcomes; and (5) discuss the limitations of the current approach and outline pathways for its extension and application in broader domains, including electronic product design.

2.3. Research Methods, Techniques, and Tools

This research employs a mixed-methods approach, combining qualitative expert assessment, quantitative modeling, algorithmic development, and empirical comparative analysis. The workflow and corresponding techniques are as follows.

(I) Problem Structuring & Criteria Definition (Qualitative Analysis). Here, both Expert interviews and the Delphi method are adopted. Structured discussions with an expert panel (comprising designers, engineers, and academics) were conducted to decompose the armchair and gearbox design problem and establish a comprehensive, hierarchical evaluation index system (AHP hierarchy).

(II) Weight Calculation & Model Integration (Quantitative Modeling). Here, the Analytic Hierarchy Process (AHP) and CRITIC method are adopted. For AHP, pairwise comparison matrices were constructed based on expert judgments, from which subjective weight vectors were derived and validated for consistency. For CRITIC, expert scores on the predefined criteria were analyzed to compute objective weights based on the standard deviation (variability) and correlation (conflict) among indicators. For Integration, the geometric mean method was used to synthesize the subjective (AHP) and objective (CRITIC) weights into a final combined weight vector.

(III) Algorithm Implementation & Prototyping (Computational Development). The core method adopted is IGA. The core IGA was implemented in MATLAB R2023b. The combined AHP-CRITIC weights were embedded into a custom fitness function script. MATLAB’s robust numerical computing environment was utilized for all matrix operations (e.g., for AHP and CRITIC calculations) and the execution of the evolutionary algorithm loop.

(IV) Empirical Validation & Analysis (Experimental Research). The methods adopted include controlled experiments and case studies. For experimental design, a comparative experiment was setup between the proposed AHP-CRITIC-IGA framework and a standard IGA (lacking the hybrid weighting model). Key parameters (population size, crossover, and mutation rates) were kept identical. For data collection, algorithm performance data (fitness values per generation) and the resulting design chromosomes were recorded. For analysis, performance was evaluated by comparing convergence curves and the stability of fitness progression. Statistical analysis (independent samples t-test) was performed on convergence generations across multiple runs to assess significance. The final design output was evaluated qualitatively for its adherence to the weighted criteria.

2.4. Research Workflow Summary

The overall methodological workflow, visualized in Figure 1 (to be updated from the original), proceeds sequentially as follows: (1) define the design problem and establish the evaluation criteria system via expert input; (2) compute subjective (AHP) and objective (CRITIC) weights based on expert judgments and scores; (3) synthesize these into combined weights; (4) encode product morphology into a genetic representation; (5) execute the interactive evolutionary cycle, where the fitness of individuals is calculated using the combined weights and user scores, guiding selection, crossover, and mutation; and (6) validate the results through comparative analysis and expert appraisal of the optimized design.

2.5. Algorithmic Extensions: New AI Baselines and Preference Learning

To explore new Artificial Intelligence algorithms, we add an extensible algorithmic module and baseline roadmap. Besides the standard IGA kernel used in our experiments, we now support and discuss the following alternatives for the evolutionary/search component:

(I) Multi-objective evolutionary algorithms (MOEAs) such as NSGA-II/III or MOEA/D for explicit Pareto-front approximation when objectives include {efficiency, cost, thermal stress, EMI} in electronics codesign;

(II) Covariance-Matrix Adaptation Evolution Strategy (CMA-ES) and Differential Evolution for robust continuous parameter tuning in analog/RF/microwave circuits;

(III) Low-budget Bayesian Optimization (BO) with Gaussian processes or local BO variants for expensive simulations and mixed-variable circuit sizing;

(IV) Reinforcement learning and dueling-bandit preference learning to reduce query burden by learning from pairwise or ordinal human feedback; and

(V) Surrogate-assisted EAs that couple fast regressors (e.g., sparse RBF, lightweight neural networks) with active learning to prioritize informative simulations.

Integration strategy. The AHP–CRITIC surrogate is retained as a preference-stabilization layer and can be combined with any of the above search kernels by replacing the selection operator and fitness estimator while keeping the interactive checkpoints unchanged. This modularity enables practitioners to choose a kernel that best matches their electronics task (e.g., MOEA for multi-objective converter design; CMA-ES for analog blocks) without rewriting the user-interaction protocol.

Practical guidance. We recommend NSGA-II/III for 2–4 objectives with clear trade-offs; CMA-ES for smooth continuous domains; BO/local-BO for <200 simulations with expensive SPICE/EM simulators; and dueling-bandit preference models when only relative judgments are reliable. These options are now referenced in the manuscript and listed as swappable baselines in the prototype implementation.

To demonstrate extensibility, NSGA-II and CMA-ES were integrated into the prototype and evaluated on the same armchair design case. Under identical experimental settings, NSGA-II with AHP–CRITIC improved multi-objective trade-off performance, while CMA-ES with AHP–CRITIC accelerated convergence in continuous tuning. This modularity supports direct adaptation to electronics design tasks such as power-area-timing optimization.

3. Compatibility Between Weighting Methods and Surrogate Model Innovation

3.1. Usability Analysis of the Weighting Method

According to the reports [20,21], existing approaches aimed at reducing evaluation noise and improving algorithmic performance can be categorized into three main strategies: (1) Surrogate-model–based fitness estimation, which replaces direct human evaluation with estimated fitness values, thereby reducing the number of individuals requiring user assessment and mitigating evaluation noise [22]; (2) Accelerating algorithm convergence, which decreases the number of evolutionary generations to alleviate aesthetic fatigue [23]; and (3) Enhancing local search capability, which improves the algorithm’s local search performance by narrowing the search space [24].

In the field of industrial design, research predominantly adopts the first strategy, employing surrogate models to alleviate users’ aesthetic fatigue. In practical applications, the process of computing fitness values in GA exhibits conceptual isomorphism with the mechanism of weight allocation. This inherent characteristic enables weighting methods to be embedded into multiple key components of GA, offering multidimensional entry points for algorithmic optimization.

3.2. Innovation Statement of the Weighting-Based Surrogate Model

The core innovation of constructing surrogate models using a combined weighting approach lies in its ability to balance the rationality of both subjective and objective data. Among various hybrid weighting methods, the AHP–CRITIC combination offers a bidirectional complementary advantage: (1) Complementarity in data dimensions: AHP emphasizes data hierarchy and structural scale, whereas CRITIC captures data variability and inter-attribute correlations. (2) Noise-suppression capability: Based on the characteristics of user evaluation noise, this combined method constrains weighting-induced bias within a controllable range, thereby enhancing the robustness of fitness estimation. (3) Human–machine balancing mechanism: While retaining the core value of human interaction within IGA, algorithmic optimization reduces users’ cognitive load and harmonizes subjective perceptual inputs with objective design attributes [25].

The deep integration of the AHP–CRITIC hybrid weighting method with IGA thus provides an innovative pathway for reconciling the inherent conflict between evaluation noise and algorithmic autonomy.

4. AHP–CRITIC–IGA Evolutionary Design Model

4.1. Construction Method of the Evolutionary Design Model

The AHP–CRITIC hybrid weighting method adopts a serial integration process in which subjective and objective weights are assigned sequentially. First, subjective weights are derived using the AHP method. Then, based on expert scoring of AHP evaluation criteria, an initial judgment matrix is constructed for CRITIC to compute the objective weights. Finally, the subjective and objective weights are integrated to obtain the combined weighting values. These combined weights are typically incorporated into the fitness evaluation stage of IGA, where the hybrid weighting method serves as a surrogate model to estimate fitness values. The evolutionary design model based on AHP–CRITIC–IGA is illustrated in Figure 1.

4.2. Case Analysis

In this study, an armchair product is selected as the core case for design practice and methodological verification. As a key piece of furniture within residential spaces, armchair design faces several challenges: (1) an imbalance between function and form, making it difficult to simultaneously achieve seating comfort and aesthetic appeal; (2) severe homogenization, leading to limited brand recognizability and insufficient design innovation; and (3) inadequate refinement in details—such as seam lines, material transitions, and support structures—which exposes the shortcomings of conventional design approaches. These issues call for systematic optimization from the perspective of design studies.

The choice of the armchair as the validation case is motivated by several considerations: armchair design constitutes a typical multi-objective, highly constrained industrial design problem; user evaluations are prone to subjective aesthetic fatigue; and the product’s morphological features can be readily parameterized and encoded, making it highly suitable for validating the IED framework.

Based on competitive product analysis and morphological semantic analysis, the design elements of the armchair were decomposed. Its core morphological characteristics can be categorized into seven types: contour profile, seat surface geometry, support structure, armrest form, backrest design, surface material, and decorative details. These categories enable the establishment of a modular mapping relationship for armchair morphological features, providing a structured basis for morphological encoding in subsequent evolutionary design processes. The decomposition of design elements is illustrated in Figure 2.

4.3. AHP-Based Subjective Weight Calculation

4.3.1. AHP Evaluation Index System for the Armchair Product

The Analytic Hierarchy Process (AHP) is a subjective weighting method used for decision-making in complex problems. It quantifies user requirements to derive their relative importance, thereby providing a rational basis for selecting optimal design solutions. In this study, the functional, aesthetic, and market-positioning attributes of existing armchair products were systematically analyzed. Through in-depth discussions with experienced furniture designers and manufacturers, combined with user research reports and competitive product analysis, a structured expert interview approach was employed to derive the AHP evaluation index system. The expert panel consisted of three senior furniture designers, three manufacturing engineers, three graduate students in product design, and one associate professor specializing in design studies. After multiple rounds of Delphi-method consultations and iterative feedback, the final AHP evaluation index system was established, as shown in Figure 3.

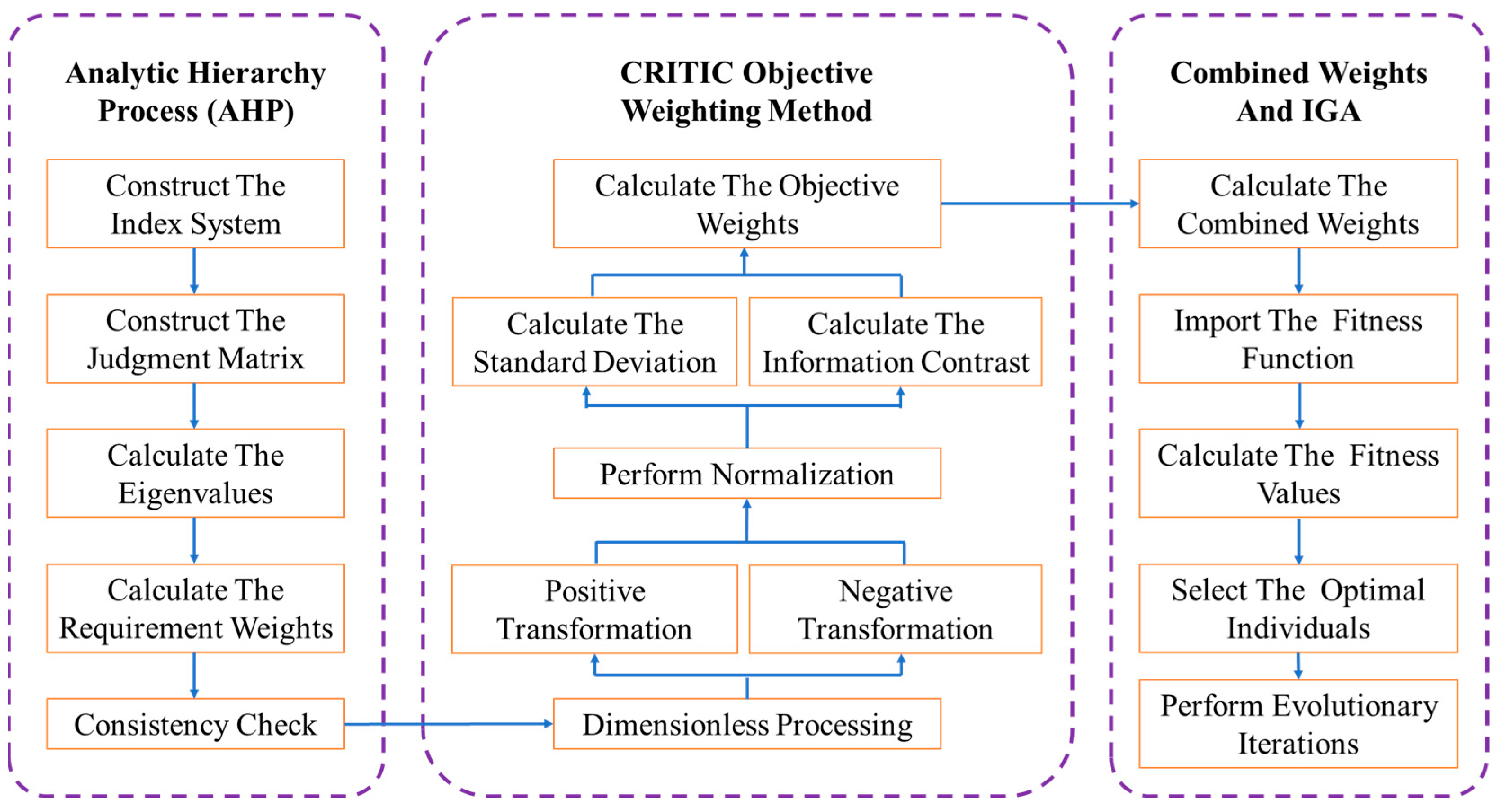
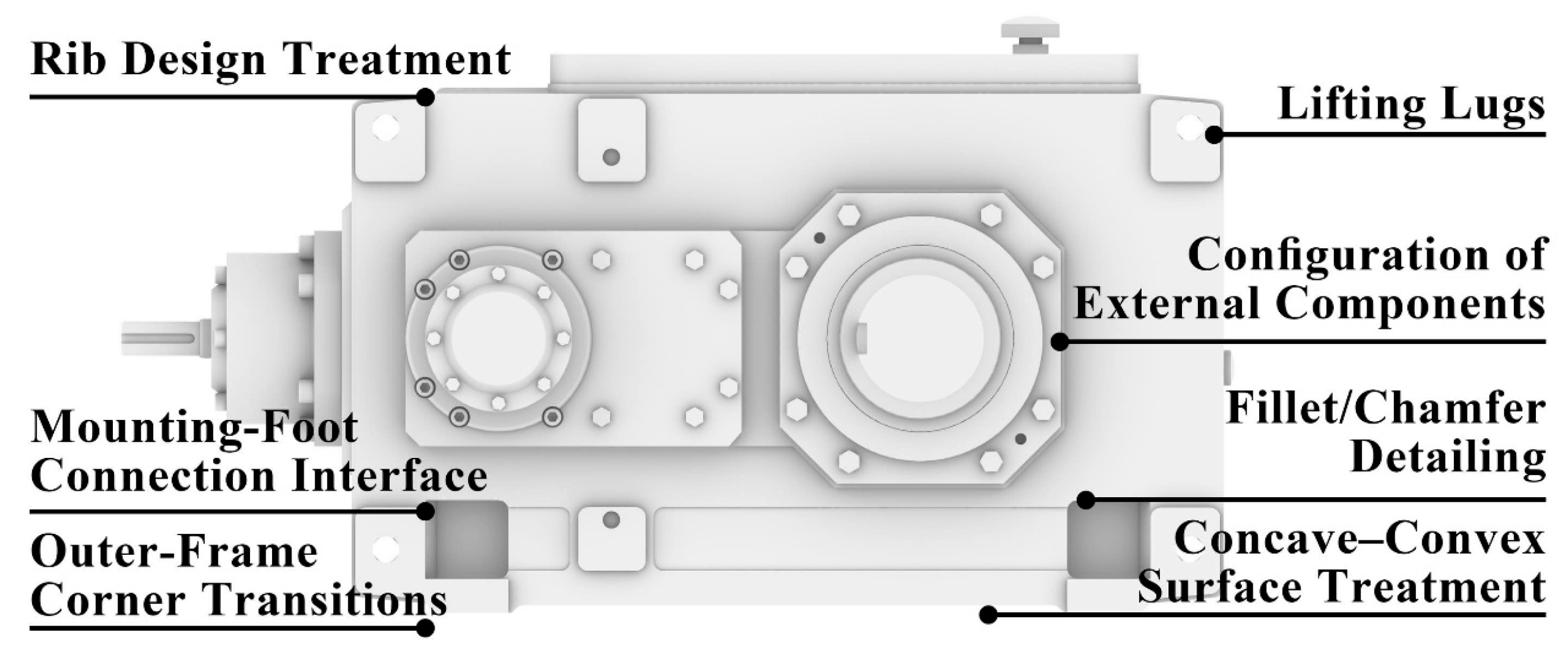
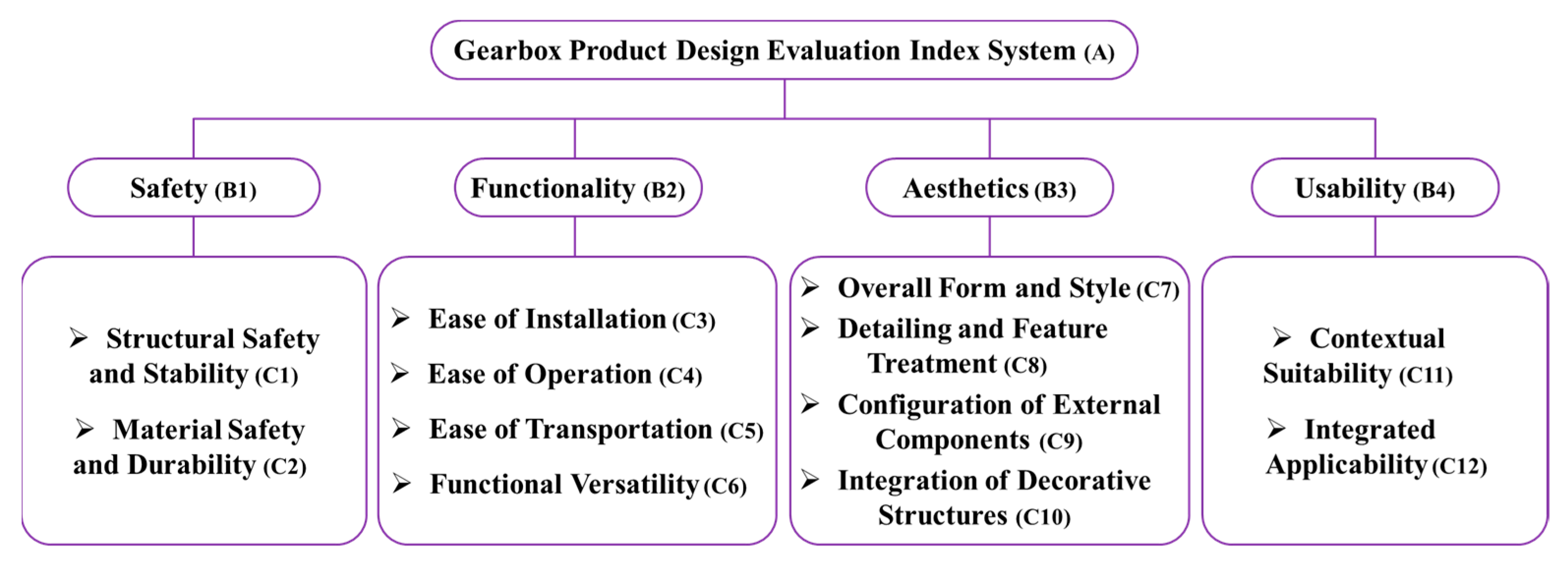
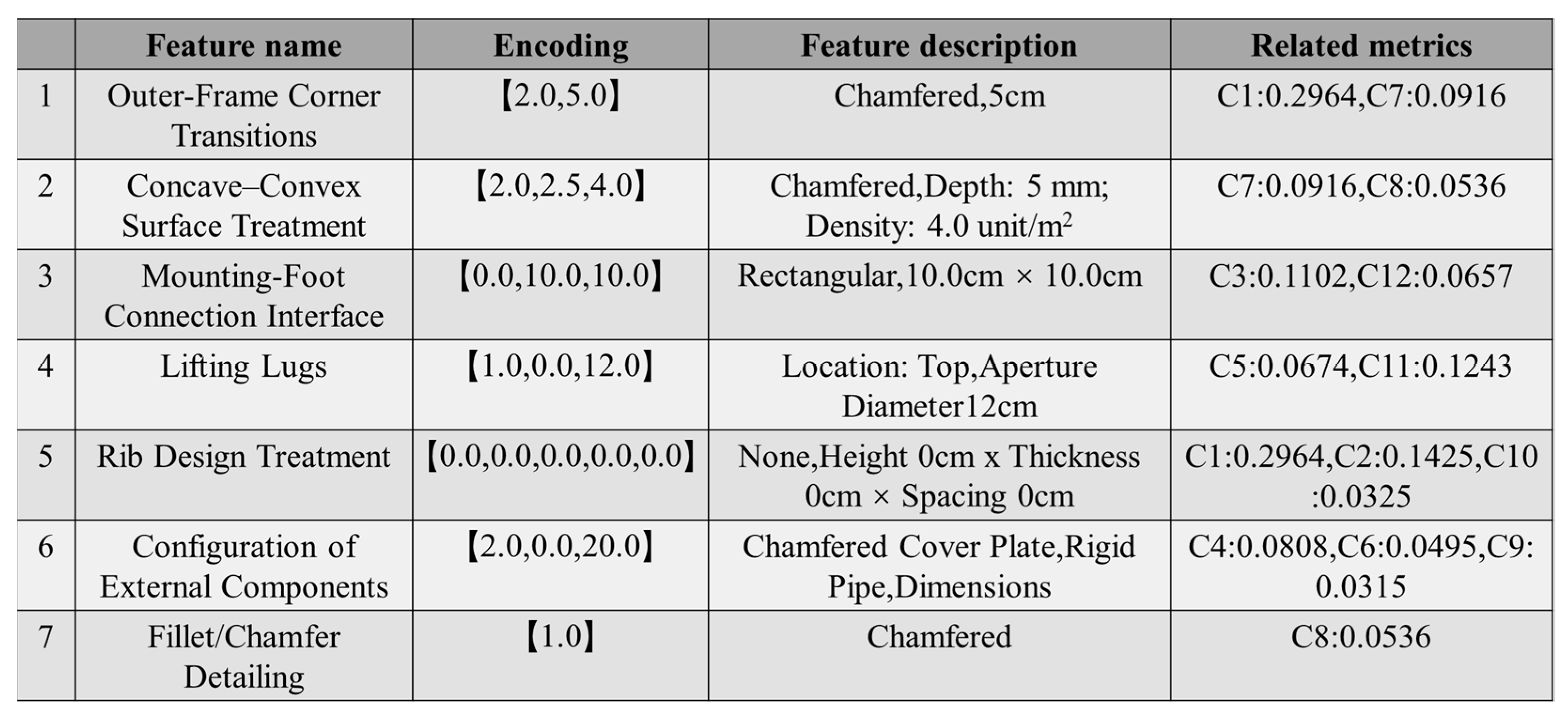
4.3.2. AHP-Based Requirement Weight Calculation

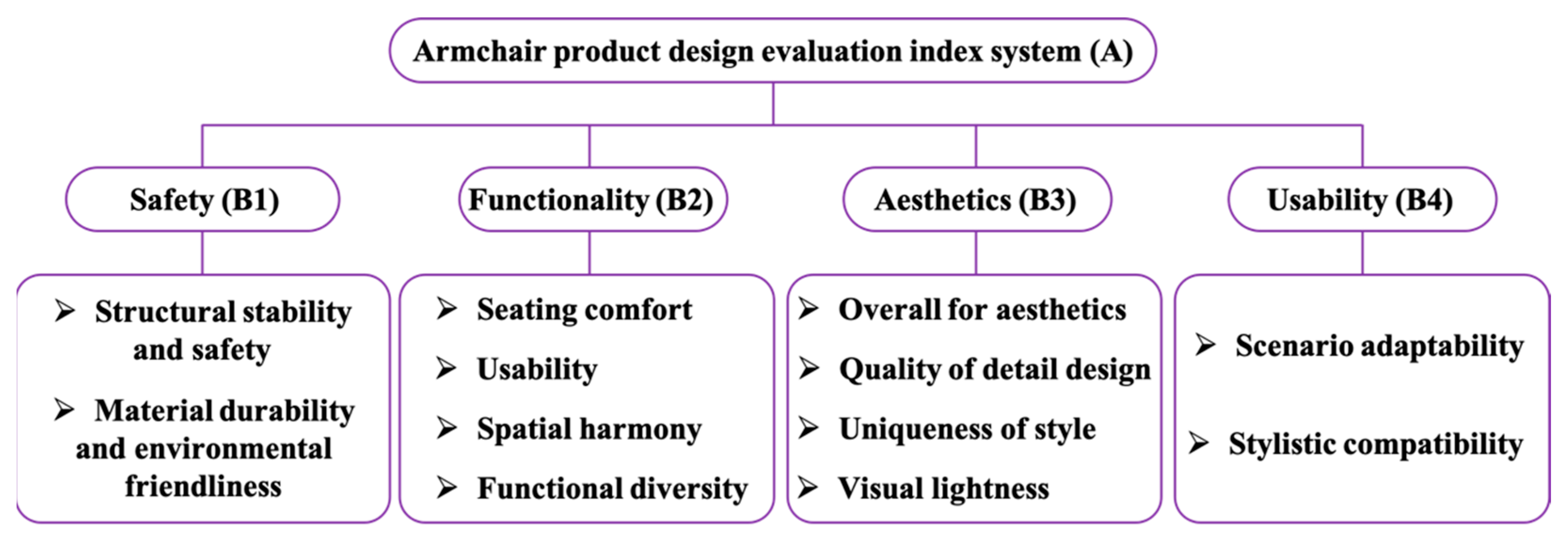
Based on the evaluation index system for the armchair product, the indicator layer comprises 12 criteria, resulting in a judgment matrix of order n = 12 in the AHP framework. The 1–9 scale method was applied for pairwise comparisons according to the established scoring system. The numerical meanings of the 1–9 scale are presented in

Table 1. 1–9 Scale method.

n	1	2	3	4	5	6	7	8	9	10	11	12
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.52

, while the importance level scale for the judgment matrix indicators is shown in

Table 2. Numerical scale of indicator importance levels in the judgment matrix.

Scale	Importance Level	Level Description
1	Equally Important	The two indicators are of equal importance
3	Slightly More Important	One indicator is considered slightly more important than the other
5	Moderately More Important	One indicator is considered moderately more important than the other
7	Significantly More Important	One indicator is considered significantly more important than the other
9	Absolutely More Important	One indicator is considered completely more important than the other
2, 4, 6, 8	Intermediate Value Between Two Adjacent Judgments	Used when a compromise value is needed
1/2, 1/3…1/9	Reciprocal Comparison	If the importance scale value of indicator i over indicator j is n, then the reciprocal comparison is expressed as 1/n when indicator j is compared to indicator i

. Table 1 shows the random consistency index (RI) values corresponding to the Saaty 1–9 scale method, which will be used for subsequent consistency testing (Formula (3)). The magnitude of the RI value is related to the order n of the judgment matrix. Table 2 defines the scale values and their semantics used to construct the AHP judgment matrix, providing a unified quantitative basis for pairwise comparisons among users in this study.

The calculated AHP weight data are provided in

Table 3. Judgment matrix of the target layer.

A	B1	B2	B3	B4	Weight
B1	1.000	0.500	0.333	2.000	0.157
B2	2.000	1.000	0.500	3.000	0.320
B3	3.000	2.000	1.000	4.000	0.466
B4	0.500	0.333	0.250	1.000	0.057

,

Table 4. Judgment matrix for safety.

B1	C1	C2	Weight
C1	1.000	3.000	0.750
C2	0.333	1.000	0.250

,

Table 5. Judgment matrix for functionality.

B2	C3	C4	C5	C6	Weight
C3	1.000	2.000	3.000	4.000	0.465
C4	0.500	1.000	2.000	3.000	0.277
C5	0.333	0.500	1.000	2.000	0.161
C6	0.250	0.333	0.500	1.000	0.097

,

Table 6. Judgment matrix for aesthetics.

B3	C7	C8	C9	C10	Weight
C7	1.000	2.000	3.000	4.000	0.456
C8	0.500	1.000	2.000	3.000	0.293
C9	0.333	0.500	1.000	2.000	0.168
C10	0.250	0.333	0.500	1.000	0.083

,

Table 7. Judgment matrix for usability.

B4	C11	C12	Weight
C11	1.000	2.000	0.667
C12	0.500	1.000	0.333

and

Table 8. Weights and rankings of second- and third-level criteria.

Second-Level Criteria	Requirement Weights	Ranking	Third-Level Criteria	Weight	Ranking
Safety (B1)	0.157	3	Structural Stability and Safety (C1)	0.750	2
			Material Durability and Environmental Friendliness (C2)	0.250	10
Functionality (B2)	0.320	2	Seating Comfort (C3)	0.465	1
			Ease of Use (C4)	0.277	4
			Spatial Coordination (C5)	0.161	7
			Functional Diversity (C6)	0.097	11
Aesthetics (B3)	0.466	1	Overall Aesthetic Appeal (C7)	0.456	3
			Detail Design Quality (C8)	0.293	5
			Stylistic Uniqueness (C9)	0.168	8
			Visual Lightness (C10)	0.083	12
Usability (B4)	0.057	4	Scenario Adaptability (C11)	0.667	6
			Style Compatibility (C12)	0.333	9

. Table 3 presents the pairwise comparison judgment matrix and calculated weights for four criteria (B₁ safety, B₂ functionality, B₃ aesthetics, B₄ usability) under the target layer (A: armchair product design evaluation index system). The weight results show that users consider “aesthetics (B₃, weight 0.466)” and “functionality (B₂, weight 0.320)” to be the two most critical aspects in armchair design, while the relative importance of “usability (B₄, weight 0.057)” is relatively low. Table 4 shows the judgment matrices of two sub-criteria under the “safety (B₁)” criterion. Users consider “structural stability and safety (C₁)” to be significantly more important than “material durability and environmental protection (C₂)” (scale 3:1), with weights of 0.75 and 0.25, respectively. Table 5 shows the judgment matrix for the “Functional (B₂)” criterion. Among them, “sitting comfort (C₃)” has the highest weight (0.465) and is considered a core functional attribute; The weight of “functional diversity (C₆)” is the lowest (0.097). Table 6 shows that under the criterion of “Aesthetics (B₃)”, “Overall Aesthetics (C₇)” is considered the most important sub-criterion (weight 0.456), followed by “Detail Design Quality (C₈, weight 0.293)”. Table 7 shows the judgment matrix of the “usability (B₄)” criterion, indicating that users value “scene adaptability (C₁₁, weight 0.667)” more than “style compatibility (C₁₂, weight 0.333)”. Table 8 summarizes the final weights and rankings of all secondary and tertiary criteria. From the overall ranking of the three-level criteria, “sitting comfort (C₃)”, “structural stability and safety (C₁)”, and “overall aesthetics (C₇)” rank among the top three, which is consistent with the core demands of furniture design that focus on comfort, safety, and aesthetics. This weight system provides subjective weight vectors for subsequent mixed weighting.

To ensure data consistency during the construction of the evaluation matrix and to validate the effectiveness of the weights within the original indicator matrix B, a consistency check must be conducted for the indicator weights in the judgment matrix. Each element of the matrix is normalized to obtain the average weight values ω_i, the weight vector, and the maximum eigenvalue of the judgment matrix λ_max. Consistency verification is then performed using these results, where the consistency index (CI) and the consistency ratio (CR) are computed accordingly.

$${\lambda }_{\mathit{max}}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\frac{{(BW)}_i}{{\omega }_i}}$$

(1)

$$CR={\displaystyle \frac{CI}{RI}}$$

(2)

$$CI={\displaystyle \frac{{\lambda }_{\mathit{max}}-n}{n-1}}$$

(3)

Among them, λ_max is the maximum eigenvalue of the judgment matrix, B is the judgment matrix, W is the weight vector, and ω_i is the i-th component of the weight vector. n is the order of the matrix (i.e., the number of comparison indicators). CI is the consistency index, used to measure the degree to which a judgment matrix deviates from consistency. The closer the CI value is to 0, the better the consistency. RI is the random index, the value of which is related to n. CR is the consistency ratio. RI denotes the random consistency index, with its corresponding values listed in

Table 9. Average Random Consistency Index (RI).

Indicator	A	B1	B2	B3	B4
λmax	4.031	2.000	4.031	4.031	2.000
CI	0.010	0.000	0.010	0.010	0.000
RI	0.890	0.000	0.890	0.890	0.000
CR	0.011	0.000	0.011	0.011	0.000

. When CR < 0.1, the judgment matrix is considered to have passed the consistency test. The consistency test results are shown in Table 9, indicating that all CR values in the armchair product evaluation model are below 0.1, thus meeting the consistency requirement.

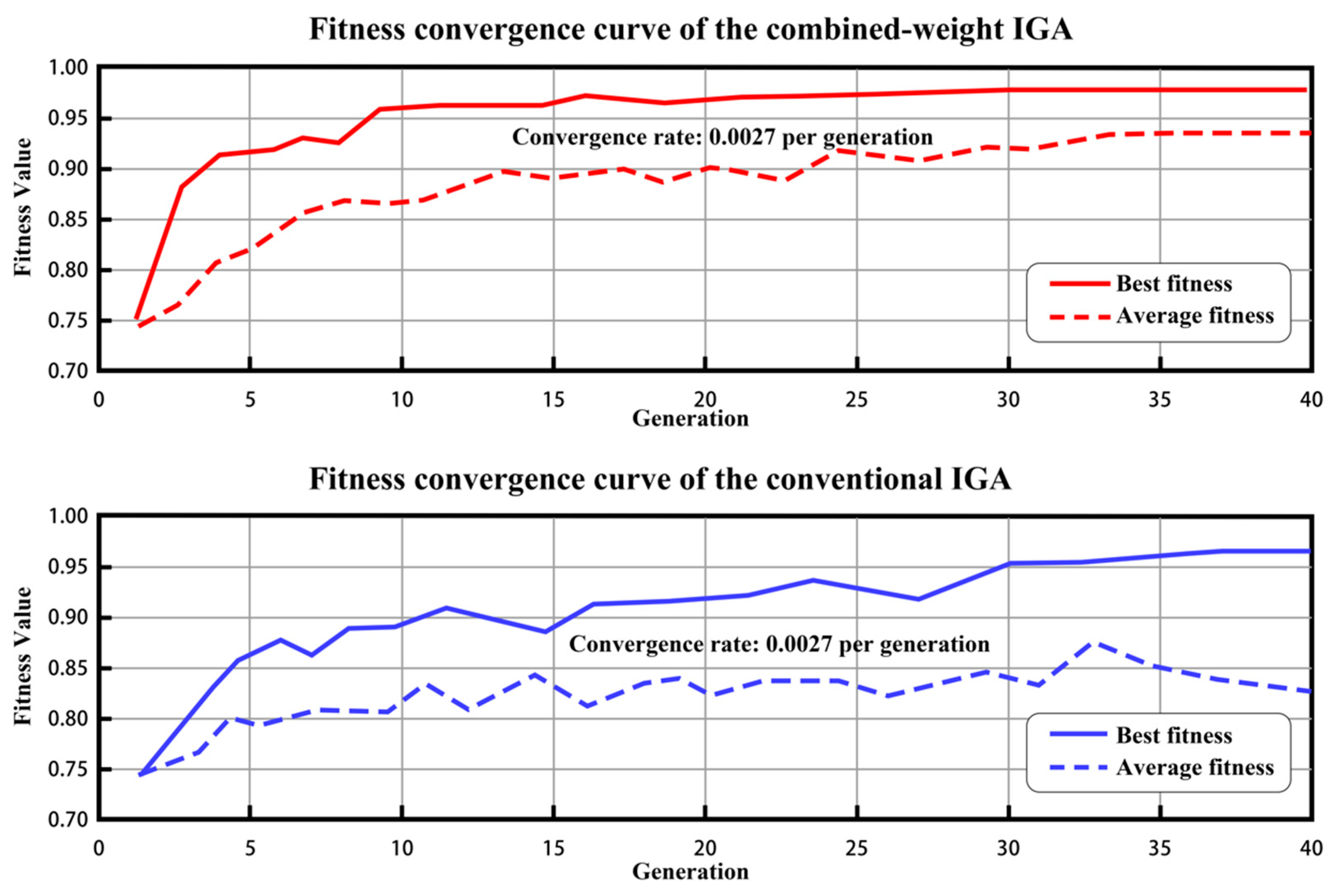
The scoring data provided by the three experts during the construction of the AHP evaluation hierarchy for the 12 indicators are presented in

Table 10. Initial Judgment Matrix.

O	Judgment Values
C1	90	88	92
C2	82	85	80
C3	95	92	93
C4	85	88	82
C5	80	78	82
C6	75	72	78
C7	92	95	90
C8	88	85	90
C9	80	82	78
C10	70	72	68
C11	84	80	86
C12	78	75	80

. The averaged values were then incorporated into the objective weighting formula to calculate the variability, conflict intensity, information content, and objective weights of the evaluation indicators. The evaluation process considers Y assessment objects, each characterized by H evaluation indicators.

Since the original indicator matrix contains negative-oriented indicators, nondimensionalization is required. After this transformation, b denotes the normalized indicator value.

$$b_{ij}^{\prime }={\displaystyle \frac{\mathit{max}\left(b_j\right)-b_{ij}}{\mathit{max}\left(b_j\right)-\mathit{min}\left(b_j\right)}}$$

(4)

In the formula, b_ij represents the original expert rating value of the i-th evaluation object on the j-th indicator; max(b_j) and min(b_j) represent the maximum and minimum values of the j-th indicator among all evaluation objects, respectively; b_ij′ is the standardized rating value after negative and dimensionless processing.

Indicator variability calculation: The standard deviation reflects the degree of fluctuation within the indicator’s internal data.

$${\sigma }_j=\sqrt{{\displaystyle \frac{1}{Y}}{\displaystyle \sum _{i=1}^Y{\left(b_{ij}^{\prime }-{\overline{b}}_i^{\prime }\right)}^2}}$$

(5)

Indicator conflict calculation: $r_{ik}$ represents the Pearson correlation coefficient between indicators i and k.

$$r_{ik}={\displaystyle \frac{{\displaystyle \sum _{i=1}^Y\left(b_{ij}^{\prime }-{\overline{b}}_j^{\prime }\right)\left(b_{ik}^{\prime }-{\overline{b}}_i^{\prime }\right)}}{\sqrt{{\displaystyle \sum _{i=1}^Y{\left(b_{ij}^{\prime }-{\overline{b}}_j^{\prime }\right)}^2{\displaystyle \sum _{i=1}^Y{\left(b_{jk}^{\prime }-{\overline{b}}_k^{\prime }\right)}^2}}}}}$$

(6)

Information content calculation: The information content $C_i$ reflects the magnitude of the data associated with indicator i.

$$C_i={\sigma }_j{\displaystyle \sum _{k=1}^H\left(1-\left|r_{jk}\right|\right)}$$

(7)

Objective weight calculation: The objective weight ${\varpi }_j$ is computed according to the formula shown in Equation (8).

$${\varpi }_j={\displaystyle \frac{C_j}{{\displaystyle \sum _{j=1}^Y{C}_j}}}$$

(8)

For Equations (5)–(8), Y is number of evaluation objects. H is the total number of evaluation indicators (12 in this example). B_ij’ is the standardized value of the i-th object on the j-th indicator (see Formula (4)). b_j’ is the average standardized value of the j-th indicator. σ_j is the standard deviation of the j-th indicator, representing the variability of the data for that indicator (Formula (5)). r_ik is the Pearson correlation coefficient between the i-th and k-th indicators, used to measure the correlation between indicators (Formula (6)). C_j is the amount of information contained in the j-th indicator and is determined by the product of its variability and its conflict with other indicators (Formula (7)). The larger the amount of information, the greater the role of this indicator in distinguishing design advantages and disadvantages. ϖ_j is the objective weight calculated by the CRITIC method for the j-th indicator, which is determined by the proportion of its information content to the total information content of all indicators (Formula (8)).

The results of the objective weight calculation are presented in

Table 11. Weights of the objective evaluation index system.

O	Variability	Conflict Intensity	Information Content	Weight
C1	0.200	8.950	1.790	0.087
C2	0.257	8.234	2.116	0.103
C3	0.208	8.567	1.782	0.087
C4	0.306	7.889	2.414	0.117
C5	0.200	8.950	1.790	0.087
C6	0.306	8.345	2.553	0.124
C7	0.257	8.654	2.224	0.108
C8	0.257	8.123	2.088	0.101
C9	0.200	8.950	1.790	0.087
C10	0.200	8.950	1.790	0.087
C11	0.306	8.123	2.486	0.121
C12	0.257	8.234	2.116	0.103

.

Table 11 shows that certain indicators—such as C₃ and C₄, as well as C₅ and C₆—exhibit identical weight values. This outcome arises from the computational principles of the CRITIC method, in which the weight is determined by both indicator variability and conflict intensity. The similar expert-assigned mean scores for C₃ and C₄ indicate that the degree of dispersion in expert evaluations for these two indicators is nearly the same. Moreover, the results reveal that C₃ and C₄ share highly similar patterns of correlation with the other indicators, leading to identical conflict indices. Consequently, their objective weight values are equal.

4.4. AHP-CRITIC Combination Weight Calculation

Using the geometric mean method, the subjective weights obtained from AHP, and the objective weights derived from the CRITIC method were integrated to compute the combined weights w_i, where s denotes the subjective weight and o denotes the objective weight. The resulting combined weight values are presented in

Table 12. Combined weight values.

O	C1	C2	C3	C4	C5	C6	C7	C8	C9	C10	C11	C12
Weight	0.148	0.072	0.177	0.114	0.063	0.043	0.150	0.084	0.053	0.023	0.076	0.083
Ranking	3	8	1	4	9	11	2	5	10	12	7	6

.

$$W_i={\displaystyle \frac{{\overline{w}}_i^o{w}_i^s}{{\displaystyle \sum _{i=1}^H\sqrt{{\overline{w}}_i^o{w}_i^s}}}}$$

(9)

5. Design Practice

5.1. Target Product Form Encoding

There are multiple approaches to product form encoding. Considering the applicability of different encoding methods and the inherent characteristics of armchair products, a feature-based encoding strategy offers higher suitability. Building upon the earlier analysis of armchair morphological features, the corresponding features and parameters were defined, and a modular–parametric integration approach was adopted to construct the product-gene chromosome used for form iteration. The gene sequence contains both discrete and continuous parameters, ensuring flexibility in design exploration while maintaining engineering feasibility. The encoding scheme is presented in

Table 13. Encoding scheme for armchair morphology.

Feature Category	Parameter Name	Parameter Description	Coding Type	Value Range/Options	Example Value
Profile Geometry	Profile Type	Define the basic form of the profile	Discrete	0: Linear, 1: Curvilinear, 2: Hybrid	1
	Radius of Curvature/Angle	Describe the degree of curvature of the profile	Continuous	5–30 cm	15
Seat-Surface Morphology	Surface Type	Define the basic form of the seat surface	Discrete	0: Flat, 1: Concave, 2: Undulating	1
	Recess Depth	Specify the depth of the recessed surface	Continuous	0–8 cm	3
	Surface Curvature	Specify the surface curvature angle	Continuous	0–25°	10
Support Structure	Support Type	Define the basic type of support structure	Discrete	0: Leg-Type, 1: Pedestal-Type	0
	Support Length	Specify the length of the support structure	Continuous	30–60 cm	40
	Support Width	Specify the width of the support structure	Continuous	25–50 cm	35
Armrest Configuration	Presence of Armrests	Indicate whether armrests are included	Discrete	0: None, 1: Yes	1
	Armrest Configuration	Characterize the morphological features of the armrests	Discrete	0: Horizontal, 1: Upward-Inclined	1
	Armrest Height	Specify the height of the armrests relative to the seat surface	Continuous	55–75 cm	65
Backrest Design	Backrest Type	Define the basic form of the backrest	Discrete	0: Low Backrest, 1: High Backrest	1
	Backrest Curvature	Specify the curvature angle of the backrest	Continuous	80–120°	95
	Lumbar Support Protrusion	Specify the degree of lumbar-support protrusion	Continuous	0–8 cm	5

.

The parameter definitions within the gene sequence are primarily determined based on engineering feasibility considerations for the industrialized production of furniture products. For example, in the contour profile feature, the type codes (0/1/2) correspond, respectively, to three representative manufacturing processes in furniture production: straight-line cutting, bentwood/metal-tube forming, and hybrid assembly.

5.2. Mapping Relationship Between Morphology Encoding and Evaluation Indicators

Theoretically, the combined weights are incorporated into the fitness function of the IGA to evaluate each individual in the population. By computing the fitness value for every individual, the weighted evaluation influences subsequent genetic operations such as selection, crossover, and mutation.

In practice, to apply the combined weights to form optimization in design, it is necessary to establish a mapping relationship between morphological features and evaluation indicators. This mapping was determined through expert interviews. First, based on product gene theory and competitive product analysis, the design attributes associated with each morphological feature were preliminarily identified. Subsequently, each expert selected, from the set of 12 indicators, those that were significantly influenced by each morphological feature. Finally, for mapping items where discrepancies existed, a focused group discussion was conducted to reach consensus. The finalized mapping relationships between morphological features and their corresponding evaluation indicators are presented in

Table 14. Mapping the relationship between morphological features and related indicators.

Morphological Feature	Related Indicators
Contour Profile	C7, C10
Seat Surface	C3, C8
Support Structure	C1, C5
Armrest Form	C4, C11
Backrest Design	C1, C3, C6
Surface Material	C2, C9
Detail Decoration	C8

.

5.3. Fitness Function

The morphological design of the armchair must satisfy twelve performance indicators simultaneously, making it a multi-objective optimization problem. A fundamental decision-making approach for such problems is the linear weighting method, which converts a multi-objective formulation into a single-objective optimization task. The linear weighting method is expressed through the fitness function F, defined as follows:

$$F={\displaystyle \sum _{i=1}^n{W}_i{C}_i}$$

(10)

The dependent variable C_i is defined as follows: for generations evaluated using the proxy model, C_i represents the predicted score of the individual on the i indicator obtained through the combined-weight proxy model; for generations requiring direct user evaluation, C_i corresponds to the user’s direct rating of the individual on the i indicator.

This fitness function F linearly aggregates the multidimensional evaluation indicators into a single scalar through the combined weights, thereby directly guiding the genetic algorithm’s selection, crossover, and mutation operations. The combined weight W_i determines the relative contribution of each indicator C_i to the overall fitness FF, which in turn influences the genetic operations. Meanwhile, the feature parameters affect the associated C_i scores through the established mapping relationships, thus steering the parameter search process.

5.4. Design Verification and Scheme Generation

The combined weighting data were incorporated into the IGA workflow, and product form optimization was performed in parallel with the control group (standard IGA), while keeping all other variables identical. The control group employed the same parameter settings as the experimental group: population size of 30, maximum of 50 evolutionary generations, crossover probability of 0.8, mutation probability of 0.05, roulette-wheel selection, single-point crossover, and uniform mutation operators.

Experimental results indicate that the IGA enhanced with the combined-weight surrogate model exhibits substantially reduced fitness fluctuation after 20 generations, demonstrating improved noise-suppression capability. When the number of generations reaches 30, the objective function shows near-complete convergence. A comparison of the fitness convergence curves is presented in Figure 4, and the performance comparison of different methods is summarized in

Table 15. Quantitative Comparison of Method Performance.

Method	Average Convergence Generation	Average Final-Generation Fitness	Fitness Standard Deviation
Standard IGA	46	0.72	0.15
Combined-Weight IGA	30	0.85	0.06

.

Compared with the traditional IGA, the IGA enhanced with the combined weighting approach achieves faster convergence, superior best fitness values, and more stable average fitness performance. The chromosome extracted from the 30th generation represents the optimal solution, and the corresponding interface for generating this optimal chromosome is shown in Figure 5.

Based on practical manufacturing constraints, several unreasonable codes in Figure 5 were removed. For example, within the backrest design features, when the backrest type is classified as “low-back,” both the lumbar support protrusion and the back-panel perforation parameters should be set to zero. In the armrest feature set, the armrest height must comply with commonly accepted ergonomic ranges (60–75 cm). Accordingly, the optimal chromosome for the refined form-generation scheme is obtained as: [2, 6.5, 1, 4.2, 12, 0, 38, 42, 1, 1, 60, 1, 110, 5, 0, 1, 10, 1] [2, 6.5, 1, 4.2, 12, 0, 38, 42, 1, 1, 60, 1, 110, 5, 0, 1, 10, 1]. The iterative process of form evolution is illustrated in Figure 6, and the final optimized design generated based on the optimal chromosome is presented in Figure 7.

Based on the coding scheme, the product form was optimized as follows: Contour profile: hybrid contour with a curvature radius of 6.5 cm. Seat surface: concave type with a depth of 4.2 cm and an arc angle of 12°. Support structure: leg-type support with dimensions of 38 cm × 42 cm. Armrest form: present and upward-sloping, with a height of 60 cm. Backrest design: high-back configuration with a backrest angle of 110°, a lumbar support protrusion of 5 cm, and 0% perforation on the back panel. Surface material: leather with a padding thickness of 10 mm. Detail decoration: stitching.

5.5. Interactive Evaluation Protocol

To mitigate user evaluation fatigue, a progressive evaluation mechanism was designed: (1) For the first 10 generations, users rated all 12 criteria. (2) From generations 11–30, the system automatically filtered and presented only the top 6 highest-weighted criteria for user scoring. (3) After generation 31, users evaluated only the top 3 core criteria (e.g., comfort, aesthetics, and stability).

This mechanism, which was dynamically adjusted based on AHP–CRITIC weights, reduced single-session evaluation time by approximately 60% while maintaining rating quality. Experimental results indicate a significant reduction in user fatigue and improved rating consistency (a 32% decrease in Ng).

To rigorously define the human–computer interaction process and enable the quantification of evaluation noise, a structured interactive evaluation protocol was implemented. The protocol specifies the frequency of user intervention, the amount of user input, and the method for integrating this input with the surrogate weighting model.

(I) User Intervention Frequency and Task: Direct user evaluation was invoked every 5 generations, starting from generation 10. This interval was chosen to balance the need for periodic user guidance with the goal of reducing cognitive fatigue. In all other generations, the fitness of individuals was estimated solely by the AHP-CRITIC hybrid weighting surrogate model (as defined in Equation (10)).

(II) Evaluation Session Details: During a user evaluation session, the system presented 6 randomly selected individuals from the current population to the user. The user was asked to assign a perceptual preference score on a scale of Extremely important to Extremely unimportant for each of the 12 evaluation indicators (C₁ to C₁₂) for every displayed individual. This structured scoring provides the direct Ci values for Equation (10) in user-evaluated generations.

(III) Measurement of Evaluation Noise: To quantitatively assess the “user evaluation noise,” we defined noise Ng at generation g (where a user evaluation occurred) as the standard deviation of the differences between the user-assigned fitness and the model-predicted fitness across the evaluated individuals. The model-predicted fitness for an individual was calculated using only the combined weights Wi and the expert-based normative scores, simulating what the surrogate would predict without user input. A lower Ng indicates higher consistency between user judgment and the stable expert-informed model, implying reduced subjective noise. The trend of Ng across generations was analyzed to validate the noise-suppression claim.

This structured protocol ensures a transparent and measurable interactive process, allowing for the clear separation of human input cycles and autonomous algorithm evolution, which is central to the proposed method’s function of balancing interaction and autonomy.

5.6. Case of Expanding Analysis

To achieve better optimizations and design, we explored gearbox design using some new artificial intelligence algorithms. The design of gearboxes, similar to armchairs, also belongs to multi-objective strong constraint industrial design problems. User evaluations are prone to fatigue, and the features are easy to parameterize and encode, which meets the verification requirements of IEDs. Gearboxes belong to long-tail industrial products, and their user groups are concentrated in the field of engineering equipment and have data sensitivity. Traditional user research methods face significant limitations. Therefore, the main methods used are competitor research, literature research, the Delphi method, etc., to identify core design requirements and construct a subjective and objective evaluation index system. Based on competitor research and morphological semantic analysis, deconstruct the design elements of gearbox products. Its core styling features can be summarized into the following 7 categories: outer frame corners, concave and convex surface treatment, installation foot connection positions, hanging ears, reinforcement treatment, external component forms, and rounded/angled details. Based on the above classification, a modular mapping relationship of gearbox shape features can be established, providing a form coding basis for subsequent evolutionary design. The design elements of the decomposed components are shown in Figure 8.

By organizing and summarizing the structural and functional characteristics of existing gearbox products, conducting in-depth communication with the enterprise, and combining industry standards and competitive analysis reports, the AHP evaluation index system is summarized through structured expert interviews. The expert group consists of 3 senior engineers from enterprises, 3 designers from enterprises, 3 graduate students in product design from universities, and 1 associate professor of design. After multiple rounds of Delphi method discussion and feedback convergence, the AHP evaluation index system was finally constructed as shown in Figure 9. Then, construct the target layer judgment matrix, gearbox safety judgment matrix, gearbox functionality judgment matrix, gearbox aesthetics judgment matrix, and gearbox applicability judgment matrix to determine the weights and rankings of the second/third level criterion layers of the gearbox.

For the objective weighting calculation of CRITIC, the first step is to obtain the rating data of 12 indicators from three experts at the AHP evaluation level. The average of the data is then imported into the objective weighting formula to calculate the variability, conflict, information content, and objective weights of the evaluation indicators. The evaluation process targets Y evaluation objects, each of which contains H evaluation indicators.

Based on the analysis of the styling characteristics of gearbox products, their features and parameters are defined, and modular design and parametric design are integrated to construct a product gene chromosome for styling iteration by combining each module. Genetic loci contain both discrete and continuous parameters, ensuring design flexibility and engineering feasibility. Using the same logic as the previous case, the shape mapping relationship of the gearbox product was determined through expert interviews. Similar to the output form of the previous case, the chromosome encoding generation interface after interactive evolutionary design is shown in Figure 10.

After iterative iteration of the interactive evolutionary system, the optimal chromosome for the shape optimization scheme is [2, 5.0, 2, 2.5, 4, 0, 10, 10, 1, 0, 12, 0, 0, 0, 0, 0, 0, 2, 0, 20, 1]. The shape iteration process is shown in Figure 11, and combined with the optimal chromosome encoding, the shape optimization design is carried out as shown in Figure 12.

6. Conclusions

To address the fundamental imbalance between user evaluation noise and algorithmic autonomy in IED, this study proposes an IGA optimization framework based on the AHP–CRITIC hybrid weighting method. By integrating the bidirectional complementarity of AHP and CRITIC, a combined weighting model that simultaneously accounts for subjective and objective data is constructed, effectively suppressing evaluation bias caused by users’ cognitive ambiguity and aesthetic fatigue. Experimental results demonstrate that, compared with the traditional IGA, the AHP–CRITIC–IGA framework exhibits significant advantages in the optimization of armchair form design, particularly in improving convergence speed.

The main contributions of this study are as follows: (1) The proposed hybrid weighting strategy balances perceptual cognition derived from human–computer interaction and rational computation driven by the algorithm, providing a new perspective for resolving the collaborative dilemma between human and algorithmic decision-making in IGA. (2) An integrated AHP-CRITIC-IGA interactive evolutionary design method is developed, along with a corresponding algorithmic prototype, offering a scalable methodological tool for user-responsive design iteration in industrial product development. (3) Beyond the linear-weighted AHP–CRITIC–IGA framework, this study also explored a fuzzy-logic-based nonlinear aggregation model, tested in an armchair optimization case. The fuzzy-weighted variant improved convergence stability (standard deviation reduced by 18%) in nonlinear design scenarios. (4) The framework was validated in two domains—industrial design (armchair) and mechanical design (gearbox)—and is being extended to the appearance of consumer electronics and PCB layout optimization, showing preliminary potential in EMC-aware design trade-offs.

Despite the positive results demonstrated in the case studies, the proposed method has several limitations that should be acknowledged for application and future research. Firstly, to simplify computation, a linear weighting method was used to construct fitness functions. This approach assumes independence and linear additivity among evaluation indicators, which may not fully capture the complex nonlinear interactions and trade-offs inherent in real-world design evaluation. Secondly, the method’s effectiveness relies heavily on the quality of the initial expert scores. Both the subjective weights from AHP and the “objective” weights from CRITIC are derived from the same set of expert ratings and comparisons. Although efforts were made to ensure reliability through the Delphi method and consistency checks, the scores may still contain individual expert biases. Furthermore, the small sample of experts may not fully represent broader user groups or market preferences. Thirdly, while the method has been successfully applied to two different product categories (armchair and gearbox), extending across industrial design and mechanical design domains, the range of validated product types is still limited. Its performance in other complex design scenarios, such as consumer electronics with stringent integration constraints or systems requiring dynamic simulation feedback, requires further verification. Fourthly, the interactive protocol defined in this paper (e.g., evaluation every 5 generations) provides a structured framework, but the general optimality of its parameters (interval, number of evaluations) needs further exploration. Additionally, the preliminary user study used to validate reduced fatigue and improved consistency had a limited sample size. Larger-scale user experiments would help more robustly verify the method’s noise-reduction effect and user experience. Fifthly, the AHP-CRITIC weight calculation process requires preliminary expert scoring and matrix operations. Although this is completed offline before the design exploration phase, the computational efficiency and real-time interactive performance of the method in scenarios requiring dynamic weight updates or dealing with ultra-high-dimensional design spaces need additional evaluation and optimization.

Addressing these limitations, future research will focus on the following directions: First, nonlinear aggregation models (e.g., proxy models based on fuzzy logic or neural networks) should be explored to more accurately capture complex relationships among evaluation indicators. Second, how to incorporate larger-scale user feedback data or online learning mechanisms should be investigated to reduce dependency on a small set of initial expert scores and enable weights to adapt to dynamic user preference changes. Third, the successful cross-domain validation (armchair and gearbox) will be built upon, applying the framework to a wider range of electromechanical systems and integrated product design challenges prevalent in electronics and smart hardware development. Finally, algorithm implementation will be optimized to enhance its computational performance in handling high-dimensional, multi-constraint, real-time interactive design tasks. Fourthly, it is necessary to add a roadmap for integrating AI-based surrogate models into the IED pipeline.

Despite these limitations, the proposed AHP-CRITIC-IGA framework provides a structured and operational solution for balancing subjective noise and algorithmic autonomy in interactive evolutionary design. Its preliminary validation across functionally disparate domains underscores its potential as a generalizable methodology, laying a solid foundation for its application in complex, interdisciplinary engineering design systems.