1. Introduction
To exploit existing satellites’ non-cooperative signals for Positioning, Navigation, and Timing (PNT), the National Time Service Center proposed a non-cooperative passive PNT method using very-long-baseline interferometry and passive radar technology [
1,
2,
3]. The time difference between the reference station and the user is measured to obtain indirect distance measurements. Unlike conventional GNSS receivers, the proposed system operates without demodulation, which means that despreading gain and signal characteristic information cannot be obtained. Link-budget analyses and recorded data indicate that an omnidirectional user antenna yields SNRs down to −36 dB, leaving the signal buried. Classical detection/estimation therefore fails, and SNR enhancement is essential for sub-nanosecond time-difference measurement and robust PNT.
Existing weak-signal denoising methods remain deficient in low-SNR regimes. Low-pass filters remove high-frequency details [
4,
5]. Median filtering is incapable of processing complex signals [
6]. The Kalman filter demands substantial prior information [
7,
8]. The LMS adaptive filtering algorithm is trapped in a step-size dilemma: large μ diverges, and small μ crawls [
9,
10,
11]. Empirical mode decomposition (EMD) has endpoint effects and mode-mixing [
12,
13,
14,
15,
16,
17]. The denoising performance of the empirical wavelet transform relies on the model parameters [
18,
19,
20]. The cross-correlation method has poor denoising performance when the SNR is low [
21]. In 1995, Donoho proposed the wavelet threshold denoising method [
22]. Donoho’s work inspired extensive research on the characteristics of multiresolution analysis and the significance of the threshold setting in wavelet denoising [
23,
24,
25,
26,
27]. It has been shown that wavelet threshold denoising effectively suppresses random noise but suffers from discontinuity [
28], whereas soft thresholding outperforms traditional filters for satellite signals yet introduces a constant bias [
29].
To overcome the above limitations, we propose an improved wavelet-threshold denoising correlation (IWTDC) algorithm for weak non-cooperative satellite signals. Lip-index-driven threshold optimisation is performed scale-by-scale by exploiting the wavelet-coefficient correlation of the raw data, preventing both over- and under-filtering while preserving satellite-related coefficients. An improved threshold function simultaneously eliminates the discontinuity of hard thresholding and the bias of soft thresholding. Residual noise is further suppressed by a subsequent cross-correlation stage. IWTDC requires no prior state-space model or training data, and its efficacy is demonstrated down to −36 dB SNR on real recorded passes.
2. IWTDC Method
2.1. Wavelet Threshold Denoising
According to the concept of wavelet threshold denoising proposed by Donoho [
22], the user observation signal is given by
where
represents the noisy signal,
denotes the pure sampling signal,
is the noise, and
denotes the signal length. To recover
from
, the wavelet threshold method is also utilized.
The hard and soft threshold functions are commonly used in wavelet threshold denoising [
30]. The hard threshold function is defined as
The soft threshold function is defined as
The threshold [
31] is defined as
where
is the coefficient,
is the estimated coefficient,
is the selected threshold,
is the scale of wavelet decomposition,
is a positive integer, and
is a constant,
.
According to Equation (2), when , the function is discontinuous. Discontinuities exist between λ and −λ, resulting in abrupt oscillations in the denoised signal as the hard threshold function only processes wavelet coefficients below the threshold. However, in the observation signal, noise also exists in wavelet coefficients above the threshold. The estimated wavelet coefficients in Equation (3) consistently deviate from the actual values, causing the reconstructed signal to poorly approximate the real signal and introducing errors. In Equation (4), parameter β remains constant for all detail coefficients and cannot be dynamically adjusted based on their magnitude, resulting in a loss of signal energy. Therefore, to effectively preserve useful signals, reformulating this function is essential.
2.2. Wavelet Improved Threshold
According to wavelet analysis, a discrete transform is applied to Equation (1) to obtain the wavelet coefficient
of
, which still consists of two parts: the coefficient corresponding to the signal, denoted as
, and the coefficient corresponding to the noise, denoted as
.
A fixed deviation is observed in Equation (3) that needs to be reduced in the newly designed threshold function. Combined with Equation (5), the estimated wavelet coefficients of Equation (2) contain the wavelet coefficients of noise.
To overcome the shortcoming of soft and hard thresholding, it is necessary to minimize the value of
. Therefore, setting the values of
between
and
can result in the estimated wavelet coefficient
being closer to
. Based on this idea, the threshold function is constructed:
Observing this function, when
is set to 0 and 1, it becomes equivalent to the hard threshold and soft threshold functions, respectively. When
, as
increases,
gradually decreases to
. This considerably reduces the bias generated in the soft thresholding method and improves reconstruction accuracy. It can be seen that compared to hard and soft threshold functions, the new threshold function can achieve better denoising results as long as an appropriate
value is selected.
Figure 1 shows the curves of various threshold functions.
In addition, the new threshold function has infinite continuous derivatives, which facilitates mathematical processing and more efficiently leverages the advantages of threshold denoising. Compared with traditional hard and soft threshold functions, the new threshold function has significant advantages and broad application prospects.
2.3. Threshold Function
After the wavelet transform, as
increases,
of the original signal increases and
of noise decreases. Hence, different thresholds can be selected for the different decomposition layers. According to Lipschitz analysis [
32,
33,
34], the
-layer wavelet coefficients satisfy
where
is a coefficient,
is the Lipschitz exponent and
is a constant.
The
layer wavelet coefficients can be expressed as
For noise,
because
, so
Equation (8) can be written as
Equations (8) and (9) indicate that appropriate thresholds should be selected at different layers to effectively remove noise. The threshold selection formula can be expressed as
2.4. Performance Analysis
This section focuses on analysis of algorithm complexity and SNR of the IWTDC method.
- (1)
Algorithm Complexity
In the IWTDC algorithm, its algorithm complexity is represented as O(N), where N represents the sample length. This method performs the following steps:
Wavelet decomposition: Perform wavelet decomposition on the signal to obtain wavelet coefficients, with a complexity of O(N).
Threshold selection: The complexity of threshold selection is based on the Lipschitz index that involves constant operations, usually O(1).
Threshold function processing: Perform threshold processing on each according to Equation (5). This step involves simple addition and multiplication operations with a time complexity of O(1). The total complexity of threshold processing for N wavelet coefficients is O(N).
Wavelet reconstruction: Reconstruct the denoised signal to restore the original signal. with a complexity of O(N).
Based on the above steps, the total computational complexity of the IWTDC algorithm is O(N), which is proportional to the length of the signal. This complexity indicates that the method has high efficiency in processing large-scale data. Therefore, the IWTDC algorithm provides an effective solution for practical applications.
- (2)
SNR
The signal denoised using this algorithm is correlated with the reference signal. The SNR is calculated based on the values of the correlation peak and noise floor using Equation (11).
where
is the correlation peak (the maximum correlation coefficient between the denoised signal and the reference signal) and
is the noise floor value (the mean or median of the correlation coefficients). The higher the correlation peak and the lower the noise floor value, the higher the SNR, indicating a denoised signal closer to the reference signal and better denoising effect.
3. Simulation Results
We conducted simulations on the MATLAB R2014a platform to evaluate the effectiveness of the IWTDC method. Two radiating satellite signals were used to simulate various algorithms. The denoising performance of the IWTDC algorithm was verified by analyzing the correlation peak, assuming that station A is the reference station and station B is the user.
3.1. Radiation Signal: Navigation Satellite Signal
In the simulation, we constructed a navigation satellite signal
with a bandwidth of 4.092 MHz. In accordance with the bandpass sampling theorem, the sampling frequency was set to 80 MHz. Noise was uncorrelated by considering additive white noise. Considering the actual reception of a weak navigation signal, the SNR was set to 10 dB for station A and −35 dB for station B for signals received using an omnidirectional antenna. The cross-correlation, adaptive filtering, wavelet threshold, and the proposed IWTDC methods were simulated and analyzed. To select an appropriate wavelet, candidate bases (db2–db6, sym4–sym6) were evaluated over 500 Monte-Carlo runs at an input SNR of −35 dB, according to signal-analysis and link-budget considerations. The db4 was selected.
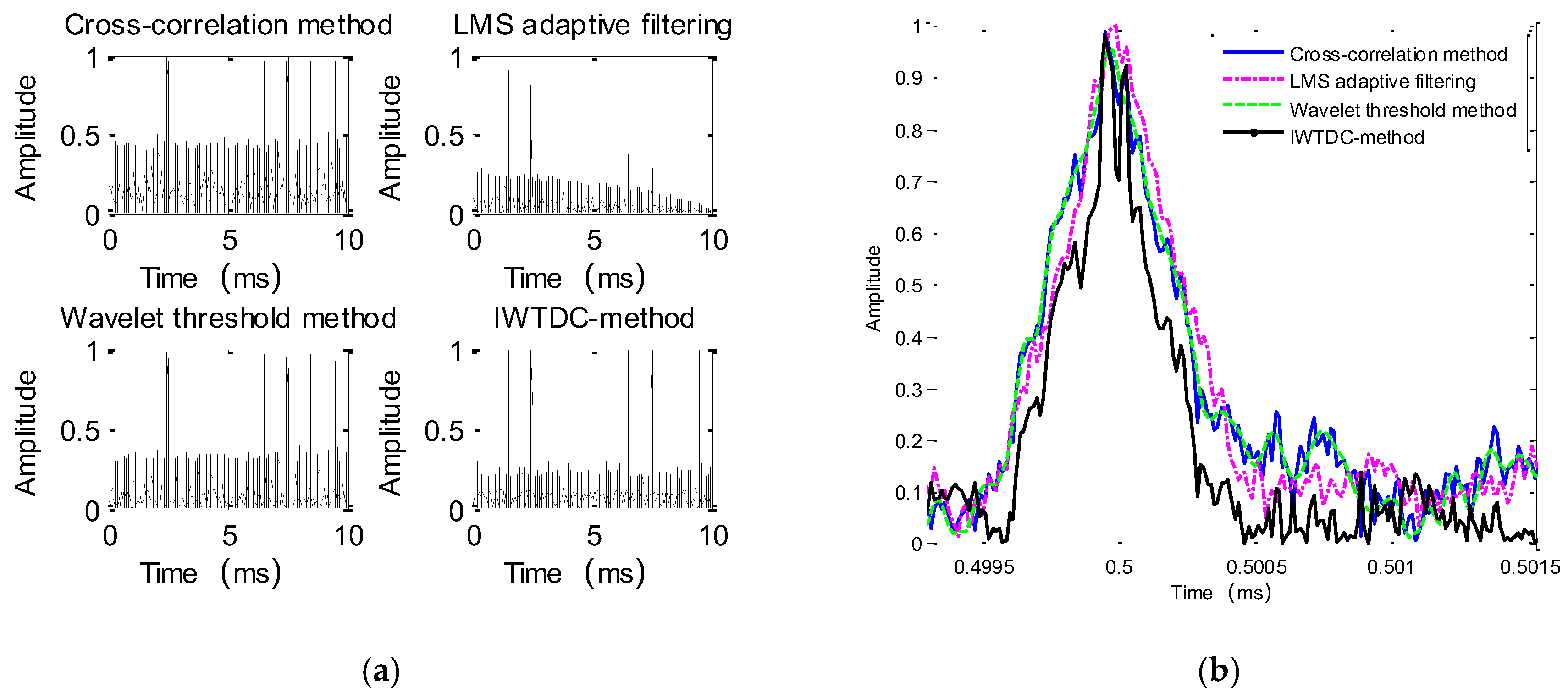
Figure 2 shows the correlation results of the evaluated algorithms for a correlation time of 10 ms.
Figure 2a shows the correlation results for each evaluated algorithm over a correlation time of 10 ms. Notably, the noise amplitude of the cross-correlation method was approximately 0.5. The correlation peak amplitude of the adaptive filtering method was attenuated relative to the code period of the navigation signal, indicating a slightly poorer correlation peak detection performance. The noise amplitude of the wavelet threshold method was close to 0.4. The noise amplitude of the proposed IWTDC method was close to 0.3, being substantially smaller than those of the other methods. Compared with the other methods, IWTDC provided an improvement of 2–5 dB. Owing to the characteristics of the navigation signal, the correlation peak was affected by the modulated carrier. To enhance the detection performance of the correlation peak, enveloping using the Hilbert change was required.
Figure 2b shows the enlarged results after obtaining the envelope. Notably, the correlation peak of the IWTDC method was narrower than that of the comparison methods. Additionally, the noise amplitude near the correlation peak was lower, indicating efficient denoising performance of the proposed method.
3.2. Radiated Signal: Communication Satellite Signal
We constructed the communication satellite signal
with a signal bandwidth of 30 MHz. Additive white noise was used to ensure noise was uncorrelated. The SNR was set to 10 dB for station A and −35 dB for station B. Based on the analysis of the signal and 500 Monte Carlo simulations, the db3 was selected.
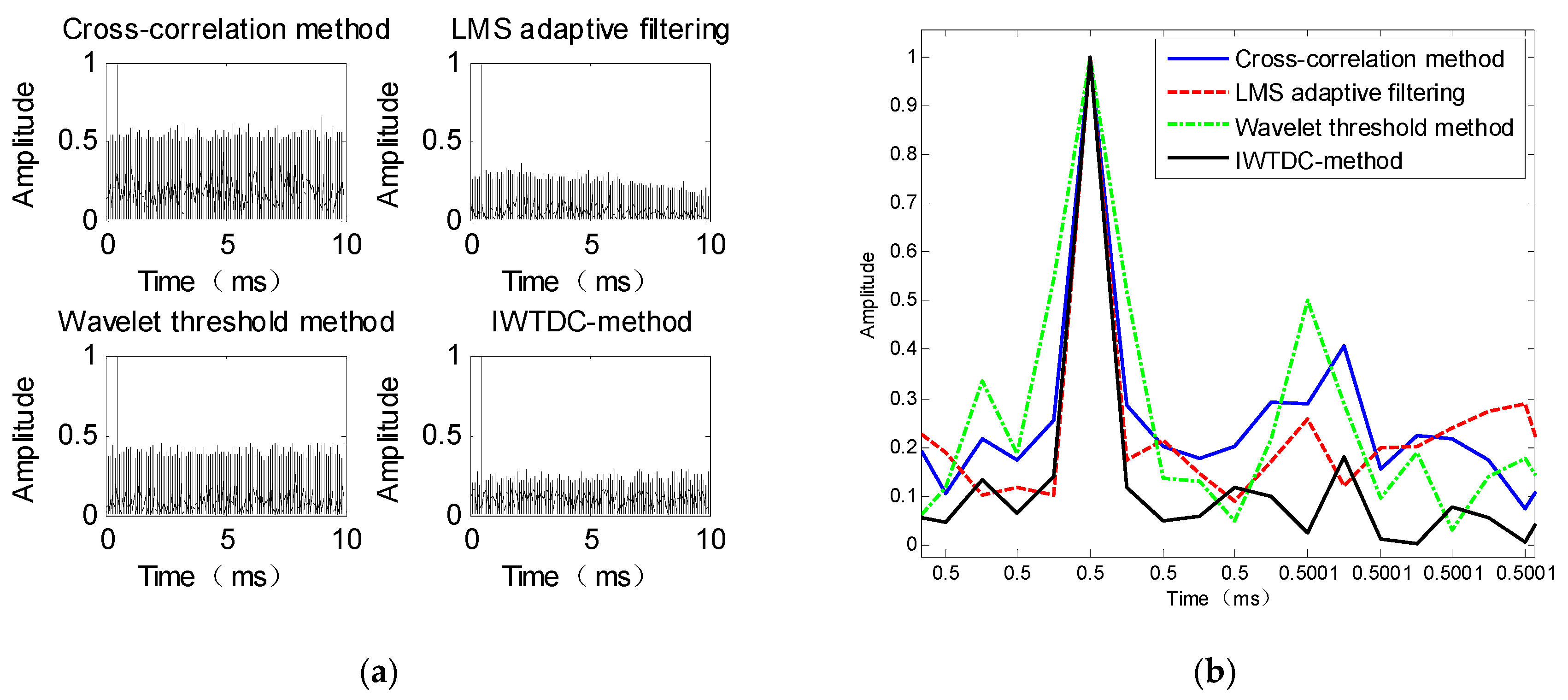
Figure 3 shows the correlation results for each algorithm with a correlation time of 10 ms.
Figure 3a shows that the noise amplitude of the cross-correlation method approached 0.6, while that of the adaptive filtering method was close to 0.4. The wavelet threshold method was close to 0.5, whereas the IWTDC method achieved a substantially lower noise amplitude of approximately 0.3. Compared with other methods, our method provided an improvement of approximately 2–5 dB. As shown in
Figure 3b, the correlation peak of the IWTDC method was narrower than that of the wavelet threshold algorithm and close to those of the cross-correlation and LMS adaptive filtering methods, thus facilitating detection through our method.
Table 1 lists the denoising performances of the four evaluated methods.
As shown in
Table 1, when the SNR of signals received by users was low (i.e., −35 and −40 dB), the traditional cross-correlation method exhibited the poorest denoising performance, followed by the wavelet threshold method. The denoising performance of the adaptive filtering method was improved, while that of the proposed algorithm was the best. At an SNR of −35 dB, all algorithms exhibited a correlation peak, whereas at −40 dB, only the IWTDC method retained a correlation peak.
Overall, when the SNR was −35 dB, the SNR of the signals processed by the IWTDC method was better by approximately 5 dB compared with that obtained using the traditional correlation method. The SNR of the IWTDC method was 2 dB higher than that of the adaptive filtering method. However, the convergence speed of the adaptive filtering method was slow, and its implementation was relatively complex, making it less convenient for subsequent data collection experiments. Compared with the wavelet threshold method, the SNR improved by approximately 4 dB using the proposed method. When the SNR was −40 dB, the signal processed by the IWTDC method showed a higher SNR of approximately 5 dB compared with the other methods. Moreover, only the proposed IWTDC method produced a correlation peak. Notably, our method demonstrated superior denoising performance and ensured a stronger correlation between the processed and reference station signals.
4. Results from Actual Data
We used a test platform generated by the National Time Service Center to collect data to validate the proposed IWTDC method and evaluate its performance. From 15 July to 16 July 2018, the reference station and users simultaneously observed the Asia Pacific 7 satellite, receiving C-band signals at the frequencies of 3826 and 3780 MHz, respectively. The frequency of the navigation satellite signal was 3826 MHz, and the signal bandwidth was 20.46 MHz. The frequency of the unknown communication signal was 3780 MHz, with an effective bandwidth of the signal observed from the analyzer being approximately 27 MHz. According to the bandpass sampling theorem, the data sampling frequency was 100 MHz. The collected signals were processed, and the correlation measurement results for the two signals were analyzed and compared.
4.1. Radiation Signal: Navigation Satellite Signal
A navigation satellite signal was collected from 09:40 to 15:30 on 15 July 2018. The navigation signal system observed in this study is based on CDMA with pseudo-random code spreading. It operates at a carrier frequency of 3826 MHz and has a signal bandwidth of 20.46 MHz.
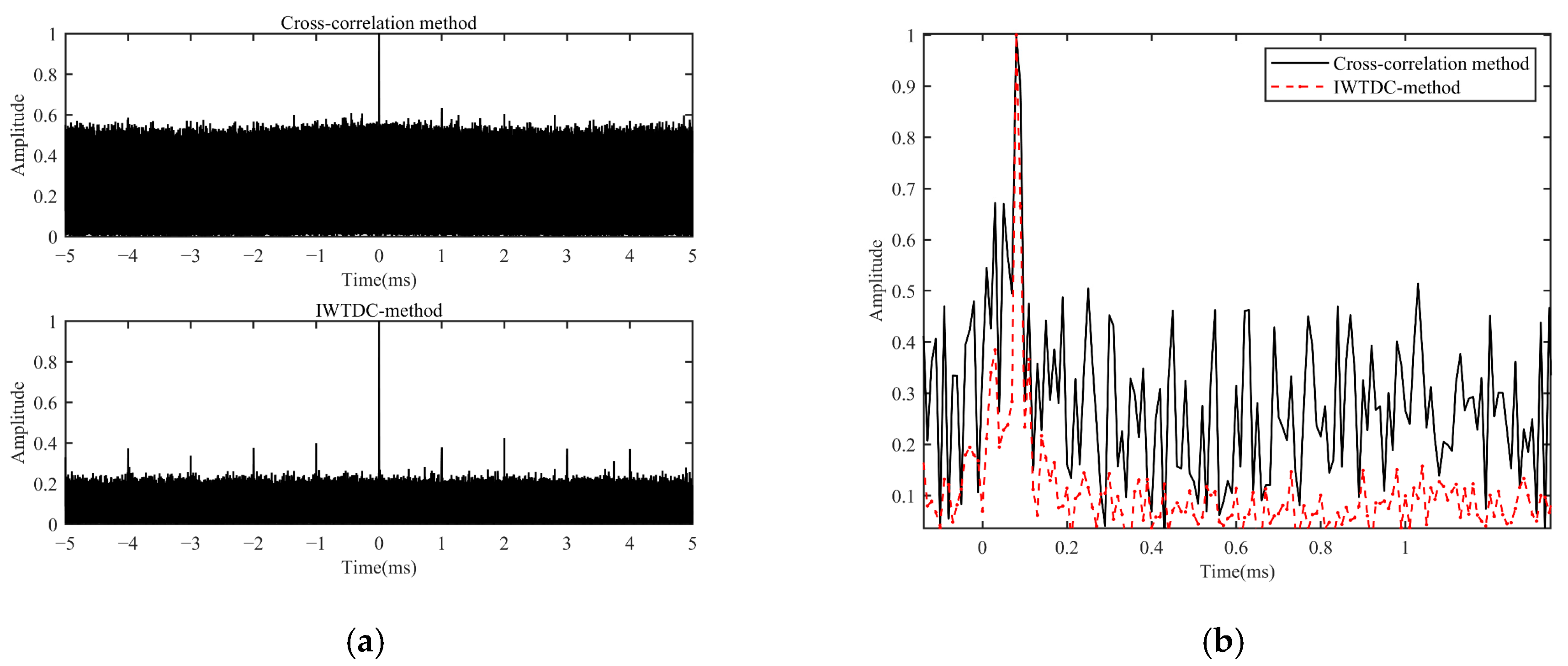
Figure 4 shows the correlation measurement results for the cross-correlation and IWTDC methods.
Figure 4a shows the collected signal processed by the proposed IWTDC method in an actual receiving environment. Compared with the cross-correlation method, the noise amplitude of our proposal was substantially lower, with an improvement of 6 dB.
Figure 4b shows that the correlation peak detection performance of the IWTDC method was higher, achieving an improved denoising performance.
4.2. Radiated Signal: Communication Satellite Signal
A communication satellite signal was collected from 14:00 to 16:30 (Beijing time) on 16 July 2018. This is a multi-channel television multiplexed signal originating from the Apstar-7 satellite’s C-band payload. It is transmitted at a center frequency of 3780 MHz with a bandwidth of 27 MHz. The one-dimensional time cross-correlation was obtained from the collected signal.
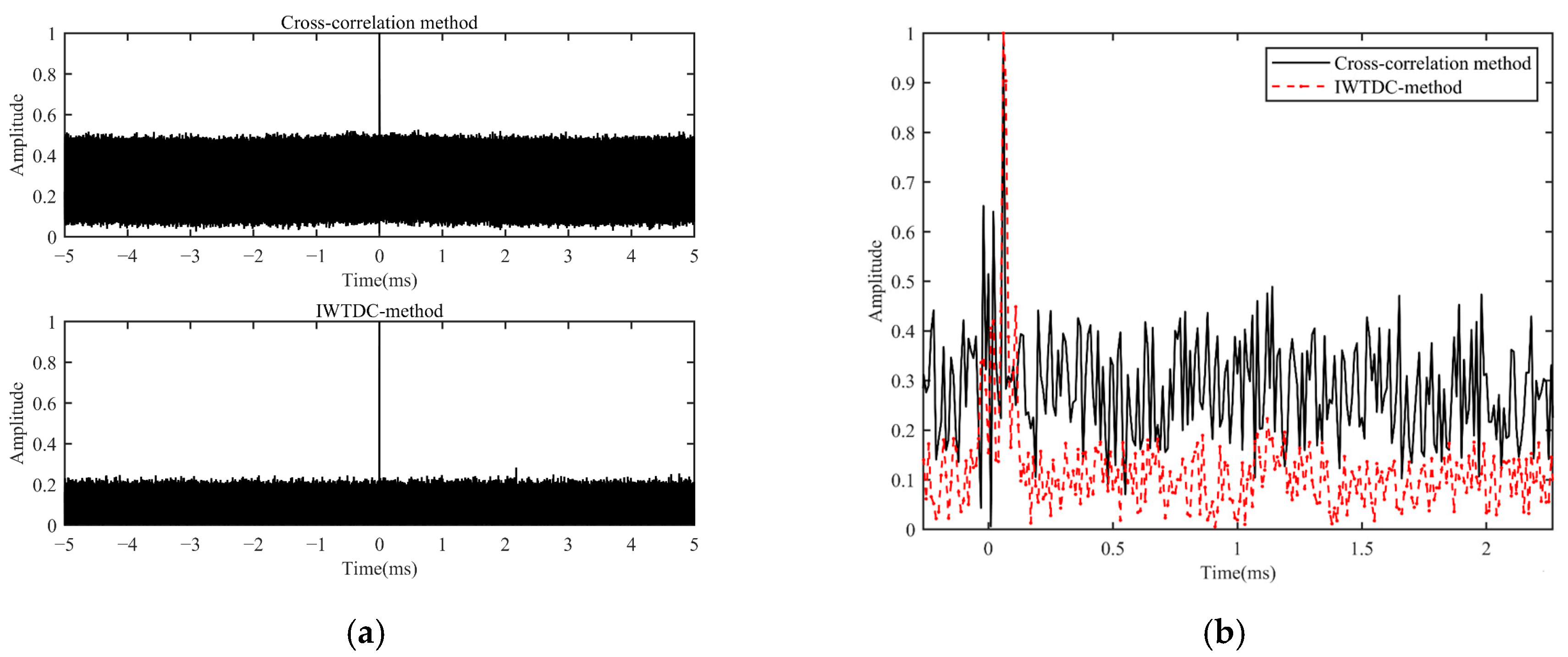
Figure 5 shows the single-correlation measurement results.
Figure 5 shows that the noise floor amplitude of the IWTDC method was drastically lower than the cross-correlation noise, which increased by approximately 7 dB. Similarly to the navigation signal correlation measurement test, the IWTDC algorithm effectively removed noise, thereby improving the SNR. The method enhanced the SNR, thereby significantly improving the accuracy of subsequent time-difference measurements and positioning.
5. Conclusions
In this paper, we propose the IWTDC method to address the limitations of the wavelet threshold denoising algorithm by constructing a new threshold function and adopting a new threshold determination method. At −35 dB input SNR, navigation and communication satellite signals were simulated to analyze the denoising performance of the IWTDC method. Simulations show that the IWTDC method significantly outperforms other algorithms at extremely low SNR, suppressing noise while preserving correlation peaks of satellite signals. The SNR was improved by about 2–6 dB.
Moreover, real-time testing further confirms its robustness, yielding an SNR enhancement of 7–8 dB with clearly discernible correlation peaks.
In summary, the IWTDC method exhibits strong performance in both theoretical simulations and practical implementations. When spreading gain is unavailable, IWTDC delivers high-SNR data for passive PNT systems, thereby establishing a reliable foundation for nanosecond-level time-difference estimation. Validation on a zero-baseline platform is currently underway, with subsequent campaigns planned across baselines ranging from 50 to 500 km to further optimize the method.
Author Contributions
All authors have made valuable contributions to this paper. Conceptualization: X.Z.; methodology: X.Z. and Y.G.; software: C.H.; validation: X.Z. and S.W.; formal analysis: X.Z. and Y.X.; investigation: Y.G.; resources: Y.H.; data curation: Y.G.; writing—original draft preparation: X.Z.; writing—review and editing: X.Z. and Y.G.; visualization: Y.X.; supervision: C.H.; project administration: Y.H.; funding acquisition: Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Basic Research Program of Natural Sciences of Shaanxi Province, grant number 2024JC-DXWT-01.
Data Availability Statement
The original contributions presented in the study are included in the article, and any inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Symbol | Term |
| Lipschitz exponent (α > 0 for signal, α < 0 for noise) |
| Threshold tuning factor in Equation (4) |
| Selected threshold value |
| Threshold tuning factor in IWTDC method |
| Estimated wavelet coefficient |
| Noisy observation signal |
| Scale of wavelet decomposition |
| A positive integer |
| Signal length |
| Additive noise |
| Noise floor value |
| Correlation peak |
| Pure sampling signal |
| Wavelet coefficient corresponding to signal |
| Wavelet coefficient corresponding to noise |
| the -layer wavelet coefficients |
| Wavelet coefficient (original) |
References
- Gao, Y.; Zhao, X.; Wang, S.; Xiang, Y.; Huang, C.; Hua, Y. Positioning via GEO communication satellites’ signals of opportunity. IET Radar Sonar Navig. 2021, 15, 1472–1482. [Google Scholar] [CrossRef]
- Gao, Y.; Hua, Y.; Xiang, Y.; Huang, C.; Wang, S.; Zhao, X. Ranging technology using signals of opportunity of non-cooperative communication satellites. J. Navig. 2021, 74, 488–500. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, Y.; Gao, Y.; Hua, Y.; Huang, C.; Zhao, X. The Time Difference of Arrival Estimation Method Utilizing an Inexact Reconstruction Within the Framework of Compressed Sensing. Remote Sens. 2024, 16, 4039. [Google Scholar] [CrossRef]
- Srivastava, G.; Bhatt, D. A High SFDR Wide-Bandwidth Third-Order Low-Pass Elliptic Filter in 180 nm CMOS Technology. IEEE Microw. Wirel. Technol. Lett. 2025, 35, 1688–1691. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Beyond low-pass filtering: Graph convolutional networks with automatic filtering. IEEE Trans. Knowl. Data Eng. 2022, 35, 6687–6697. [Google Scholar] [CrossRef]
- Wang, W.; Du, W.; Li, Y.; Jia, Z. Advanced Adaptive Median Filter for Reducing Salt-and-Pepper Noise in GPR Data. IEEE Geosci. Remote Sens. Lett. 2025, 22, 1–5. [Google Scholar] [CrossRef]
- Gao, S.; Hong, S.; Gao, C.; Zhang, D.; Huang, Z.; Wang, H. The high-accuracy ionosphere correcting algorithm for GNSS signals based on kalman filter. IEICE Electron. Express 2011, 8, 266–272. [Google Scholar] [CrossRef]
- Li, Y.; Shi, J.; Xu, K. Equivalent Loop Bandwidth of Kalman Filter-Based Tracking Method. Electronics 2025, 14, 2588. [Google Scholar] [CrossRef]
- Youn, D.; Ahmed, N.; Carter, G. On using the LMS algorithm for time delay estimation. IEEE Trans. Acoust. Speech Signal Process. 1982, 30, 798–801. [Google Scholar] [CrossRef]
- Liu, Q.; Huo, X.; Liu, K.Z.; Zhao, H. A parallelized input matching LMS adaptive filter for the rejection of spatially cyclic disturbances. IEEE Trans. Ind. Electron. 2022, 70, 10536–10545. [Google Scholar] [CrossRef]
- Somefun, C.T.; Daramola, S.A.; Somefun, T.E. Advancements and Applications of Adaptive Filters in Signal Processing. J. Eur. Des Systèmes Autom. 2024, 57, 1259–1272. [Google Scholar] [CrossRef]
- Yang, J.; Fu, Z.; Zou, Y.; He, X.; Wei, X.; Wang, T. A response reconstruction method based on empirical mode decomposition and modal synthesis method. Mech. Syst. Signal Process. 2023, 184, 109716. [Google Scholar] [CrossRef]
- Huang, Y.; Hasan, N.; Deng, C.; Bao, Y. Multivariate empirical mode decomposition based hybrid model for day-ahead peak load forecasting. Energy 2022, 239, 122245. [Google Scholar] [CrossRef]
- Van Jaarsveldt, C.; Peters, G.W.; Ames, M.; Chantler, M. Tutorial on empirical mode decomposition: Basis decomposition and frequency adaptive graduation in non-stationary time series. IEEE Access 2023, 11, 94442–94478. [Google Scholar] [CrossRef]
- Thirumalaisamy, M.R.; Ansell, P.J. Fast and adaptive empirical mode decomposition for multidimensional, multivariate signals. IEEE Signal Process. Lett. 2018, 25, 1550–1554. [Google Scholar] [CrossRef]
- Usman, M.; Zubair, M.; Hussein, H.S.; Wajid, M. Empirical mode decomposition for analysis and filtering of speech signals. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 343–349. [Google Scholar] [CrossRef]
- Wu, Y.C.; Lan, Y.P.; Liu, W.R.; Lin, J.H.; Lin, B.H.; Hsieh, W.F. Analyzing random lasing spectra of the zinc oxide bulk and the multiple quantum wells by empirical mode decomposition and fast Fourier transform. Appl. Phys. Lett. 2021, 119, 131110. [Google Scholar] [CrossRef]
- Qin, S.; Tang, J.; Feng, J.; Zhou, Y.; Yang, F.; Wahab, M.A. Modal parameter identification in civil structures via Hilbert transform ensemble with improved empirical wavelet transform. J. Vib. Control 2024, 30, 1621–1634. [Google Scholar] [CrossRef]
- Ni, C.; Peng, W. An integrated approach using empirical wavelet transform and a convolutional neural network for wave power prediction. Ocean Eng. 2023, 276, 114231. [Google Scholar] [CrossRef]
- Geetha, K.; Hota, M.K. Seismic random noise attenuation using optimal empirical wavelet transform with a new wavelet thresholding technique. IEEE Sens. J. 2023, 24, 596–606. [Google Scholar] [CrossRef]
- Pang, Z.; Wang, G.; Wang, B.; Wang, L. Comparison between time shifting deviation and cross-correlation methods. J. Light. Technol. 2022, 40, 3003–3009. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theor. 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Chen, C.; Luo, Y.; Liu, J.; Yi, Y.; Zeng, W.; Wang, S.; Yao, G. Joint sound denoising with EEMD and improved wavelet threshold for real-time drilling lithology identification. Measurement 2024, 238, 115363. [Google Scholar] [CrossRef]
- Dong, H.; Liu, S.; Liu, D.; Tao, Z.; Fang, L.; Pang, L.; Zhang, Z. Enhanced infrasound denoising for debris flow analysis: Integrating empirical mode decomposition with an improved wavelet threshold algorithm. Measurement 2024, 235, 114961. [Google Scholar] [CrossRef]
- Rao, D.; Huang, M.; Shi, X.; Yu, Z.; He, Z. A Microseismic Signal Denoising Algorithm Combining VMD and Wavelet Threshold Denoising Optimized by BWOA. CMES-Comput. Model. Eng. Sci. 2024, 141, 187–217. [Google Scholar] [CrossRef]
- Du, S.; Chen, S. Study on optical fiber gas-holdup meter signal denoising using improved threshold wavelet transform. IEEE Access 2023, 11, 18794–18804. [Google Scholar] [CrossRef]
- Ouyang, C.; Cai, L.; Liu, B.; Zhang, T. An improved wavelet threshold denoising approach for surface electromyography signal. EURASIP J. Adv. Signal Process. 2023, 2023, 108. [Google Scholar] [CrossRef]
- Liu, S. Research on Disturbance Noise an Analysis and Wavelet Denoising Algorithm of Magnetic Measurement. Ph.D. Thesis, North China University of Technology, Beijing, China, 2022. [Google Scholar]
- Zhou, T.; Deng, X. Analysis of Positioning Error and De-Noising Characteristic of Beidou Single Epoch. J. Geomat. Sci. Technol. 2018, 6, 174–181. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, S.; Qi, Z.; Wang, X.; Chen, Y.; Feng, P. Research on eLoran Weak Signal Extraction Based on Wavelet Hard Thresholding Processing. Remote Sens. 2024, 16, 3012. [Google Scholar] [CrossRef]
- Zhu, Y.; Cao, K.; Cui, G.; Hu, D. Improved joint denoise method for Loran-C signal. Electron. Meas. Technol. 2008, 11, 21–24. [Google Scholar]
- Kamienski, E.A.; Bonato, P.; Asada, H.H. Time-Critical Fall Prediction Based on Lipschitz Data Analysis and Design of a Reconfigurable Walker for Preventing Fall Injuries. IEEE Access 2024, 12, 1822–1838. [Google Scholar] [CrossRef]
- Patel, V.; Berahas, A.S. Gradient descent in the absence of global lipschitz continuity of the gradients. SIAM J. Math. Data Sci. 2024, 6, 602–626. [Google Scholar] [CrossRef]
- Iiduka, H. Theoretical analysis of Adam using hyperparameters close to one without Lipschitz smoothness. Numer. Algorithms 2024, 95, 383–421. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |