Robust Voltage Control in Distribution Networks via CVaR-Based Bayesian Optimization

Abstract

The rapid proliferation of distributed solar photovoltaic systems has intensified voltage fluctuations and uncertainty in distribution networks. Traditional Volt/VAR control strategies often struggle with robustness against extreme scenarios and impose high communication overheads. To address these challenges, this paper proposes a Bayesian Evolutionary Optimization with Conditional Value at Risk (BEO-CVaR) framework for optimizing Volt/VAR control rules. This novel approach integrates Conditional Value at Risk (CVaR) into the objective function to explicitly mitigate tail risks arising from grid uncertainties. Furthermore, it employs Bayesian Evolutionary Optimization (BEO) utilizing Gaussian process surrogate modeling to efficiently solve the computationally expensive, black-box optimization problem. Validation on a standard IEEE test feeder demonstrates that BEO-CVaR achieves superior voltage regulation, strict adherence to safety standards, and significantly reduced communication requirements compared to conventional decentralized strategies. Additionally, the framework’s scalability and robustness are verified through extensive experiments across varying dimensions of decision spaces, confirming its effectiveness in complex multi-inverter coordination scenarios.

1. Introduction

The global energy landscape is experiencing a profound transformation, driven by the urgent need to combat climate change and the volatility of fossil fuel prices. This transition has spurred a worldwide effort to integrate substantial amounts of renewable energy sources, particularly distributed energy resources (DERs) [1]. The rapid growth of DERs, exemplified by the significant increase in distributed photovoltaic (PV) inverters in China’s southern power grid, highlights the broader challenges and opportunities in modern power systems. As of September 2024, the total grid-connected installed capacity of distributed solar PV in the Southern China region reached 36.72 gigawatts, accounting for 34.2% of the total installed PV capacity in the entire grid. This represents a year-on-year increase of 114%, with an average growth rate of 104% over the past two years. From January to September 2024, the entire grid added 15.89 gigawatts of new distributed PV capacity, constituting 45.6% of the total newly installed PV capacity during this period. Consequently, the high penetration of DERs has introduced significant variability and uncertainty into the distribution grid, necessitating research into effective Volt/VAR power control rules [2,3]. To address the uncertainty from high DER penetration, recent studies have begun to explore advanced optimization and risk-aware approaches. For instance, hybrid policy-based reinforcement learning has been applied to adaptive energy management in constrained environments [4], while the chance-constrained optimization framework proposed in [5] provides probabilistic guarantees for voltage compliance.

This necessity arises because the inherent variability of renewable generation frequently drives distribution feeders away from their nominal operating states [6].

Maintaining bus voltages within their safety bounds (e.g., $\pm 5\%$ of the rated value) is critical, as operation outside these limits entails detrimental consequences for both utility assets and end-user equipment. Specifically, undervoltage conditions can cause induction motors to stall or draw excessive current, leading to thermal damage and potentially triggering localized voltage collapse due to the lack of reactive power support. Conversely, overvoltage accelerates the aging of equipment insulation, increases transformer core losses, and often forces the curtailment of distributed PV inverters to protect the grid, thereby reducing economic benefits. In severe scenarios, sustained voltage violations may even evolve into cascading failures, jeopardizing the stability of the entire power system.

To address these issues, effective voltage regulation through Volt/VAR control strategies has become essential. By utilizing inverters equipped with advanced power electronics to provide reactive power compensation, it is possible to dynamically stabilize voltage levels, provided these inverters are appropriately controlled. The IEEE 1547 standard [2], a set of technical specifications governing the interconnection of DERs to the grid, recommends various Volt/VAR control strategies that involve adjusting inverter setpoints to maintain grid stability and optimize voltage profiles.

Traditionally, inverter-based voltage regulation strategies can be categorized into three approaches: centralized, distributed, and localized methods. Centralized approaches are capable of determining optimal reactive power setpoints through optimal power flow solutions. However, they often encounter challenges related to high computational and communication overheads. Additionally, optimal power flow only identifies optimal reactive power setpoints. It cannot directly define the essential Volt/VAR control rules necessary for dynamic and adaptive voltage regulation [7]. Distributed strategies, on the other hand, allow limited communication between neighboring stations to enhance coordination. An example is the distributed voltage control approach, where stations exchange information locally to achieve a more balanced and optimized voltage profile, as introduced in [8]. Nevertheless, they can suffer from convergence delays. Localized control strategies rely solely on local data to adjust reactive power injections based on immediate voltage measurements. For example, local static feedback laws, such as those described in [9,10], directly link reactive power adjustments to local voltage levels, achieving fast response times but often lacking global optimality.

To address the challenges mentioned above, this study proposes Bayesian Evolutionary Optimization with Conditional Value at Risk (BEO-CVaR) for Volt/VAR control rule optimization. The contributions of this paper are summarized as follows:

• This paper enhances the objective function with Conditional Value at Risk (CVaR). In our voltage regulation process, the regulation results are affected by uncertainties (environmental variables, noise, model errors, etc.). In the event of communication failures, applying decision variables derived from a specific load scenario to other scenarios may expose the system to extreme tail risks, resulting in insufficient robustness and vulnerability under high uncertainty. CVaR quantifies the risk measure of the average worst-case loss when the loss exceeds the Value at Risk (VaR) at a given confidence level [11].
• This paper employs Bayesian Evolutionary Optimization (BEO) to address this issue. For Volt/VAR power control issues, the BEO framework dynamically optimizes decision vectors. By constructing a Gaussian process (GP) surrogate model to approximate computationally expensive multi-load-scenario power flow calculations, and actively selecting the most promising parameter points for evaluation based on acquisition functions such as Expected Improvement (EI), this approach significantly reduces the number of simulations required to accurately estimate the CVaR risk value. The method ensures optimization accuracy while substantially enhancing search efficiency, ultimately enabling effective solutions to high-dimensional, non-convex CVaR optimization problems with uncertain constraints under a limited computational budget.

The rest of this paper is organized as follows: In Section 2, the detailed power grid model is defined. In Section 3, the proposed BEO-CVaR is elaborated. In Section 4, this paper shows the details of the experiment. The conclusions are presented in Section 5.

2. The Formulation of Volt/VAR Control Rules Optimization

2.1. System Modeling

Consider a radial distribution network with $N+1$ buses, where bus 0 denotes the slack bus (substation) with a fixed voltage magnitude $v_0=1$ p.u. The remaining N buses are modeled as $PQ$ nodes.

The exact AC power flow equations are non-convex and computationally expensive, posing a significant challenge for iterative optimization frameworks like BEO. To balance computational efficiency and modeling accuracy, this paper adopts the linearized power flow model proposed in [12]. This model provides a reliable approximation of voltage magnitudes under nominal operating conditions by exploiting the structural characteristics of distribution grids.

It is important to note that, while this linearized model serves as the theoretical basis for deriving the stability constraints (Section 2.2), the proposed BEO framework employs exact nonlinear AC power flow calculations (via MATPOWER) for the objective function evaluation. This ensures that the optimization accuracy is not compromised by linearization errors, and the solver interacts with the true physical model of the grid.

Let $\mathbf{v}\in {\mathbb{R}}^N$ denote the vector of squared voltage magnitudes, while $\mathbf{p},\mathbf{q}\in {\mathbb{R}}^N$ represent the vectors of active and reactive power injections, respectively. The relationship between nodal voltages and power injections is approximated as follows:

$$\mathbf{v}\approx \mathbf{1}+\mathbf{R}\mathbf{p}+\mathbf{X}\mathbf{q}$$

(1)

where $\mathbf{1}$ is a vector of all ones.

The sensitivity matrices $\mathbf{R},\mathbf{X}\in {\mathbb{R}}^{N\times N}$ are strictly positive definite and are determined solely by the network topology and line impedances. Specifically, the element $X_{ij}$ corresponds to the common reactance path shared by nodes i and j from the substation. This formulation effectively decouples the voltage deviation into active and reactive components, allowing us to explicitly quantify the impact of inverter reactive power support ($\mathbf{q}$) on the voltage profiles. For the rigorous derivation of the sensitivity matrices and the error bound analysis of this linearization, we refer the readers to [12].

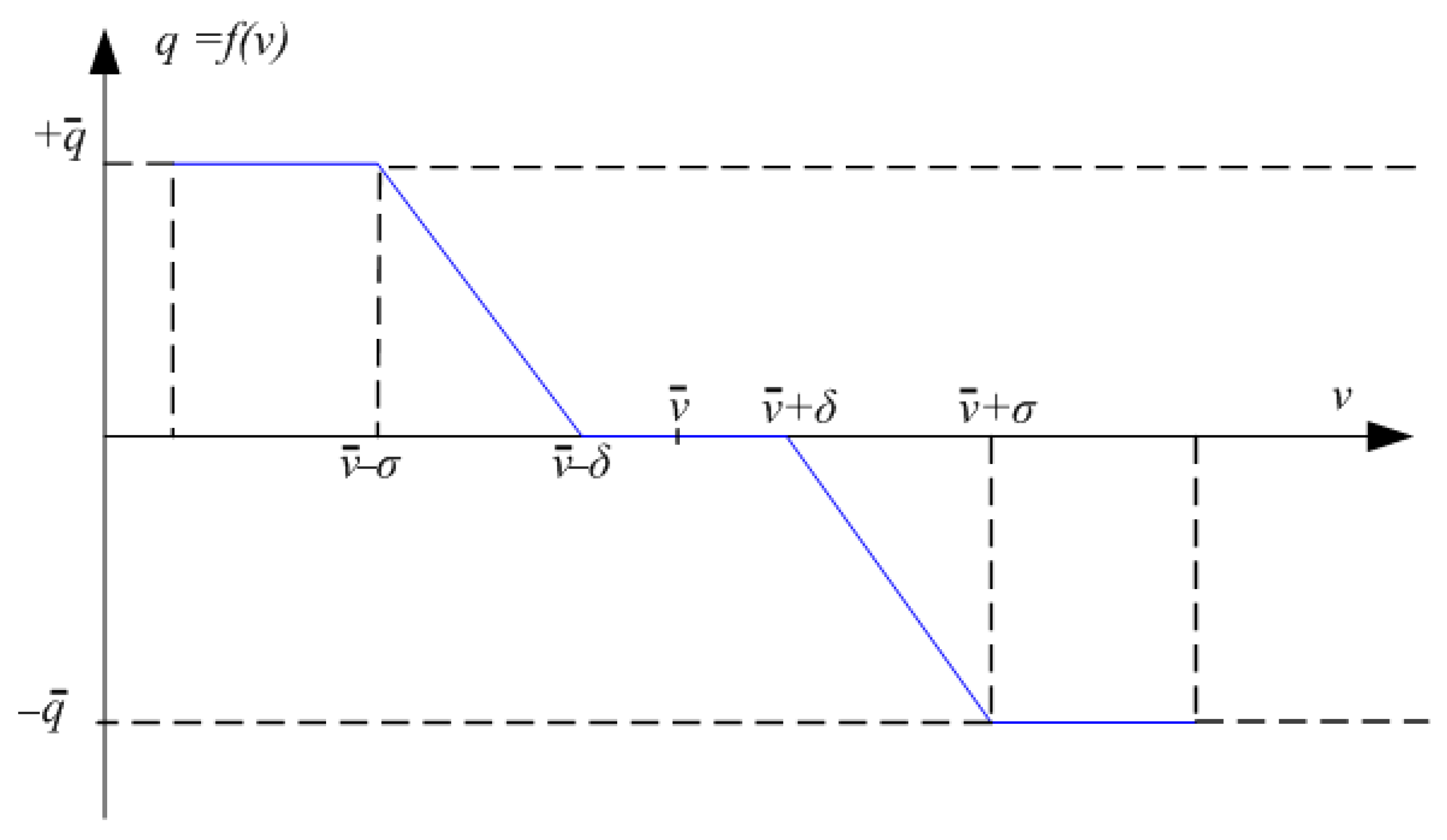
2.2. Volt/VAR Control Rule

The IEEE 1547 standard [13] allows DERs to regulate voltage by adjusting reactive power output based on local voltage measurements. This feedback mechanism creates a dynamical system where the inverter at node h updates its reactive power injection $q_h$ at time step $t+1$ based on the local voltage $v_h$ at time t:

$$q_h(t+1)=g_h\left(v_h\left(t\right)\right)$$

(2)

where $g_h(·)$ is the Volt/VAR control function.

As illustrated in Figure 1, this paper adopts the standard piecewise linear characteristic defined by four tunable parameters: reference voltage $\overline{v}$, deadband $\delta$, saturation voltage $\sigma$, and maximum reactive power capacity $\overline{q}$. The control function $g_h\left(v\right)$ dictates that the inverter injects reactive power to counteract voltage deviations. Specifically, in the linear regulation region (where the voltage deviation is between $\delta$ and $\sigma$), the control law is defined as follows:

$$q=-\beta (v-\overline{v}-\delta ·\mathrm{sgn}(v-\overline{v}))$$

(3)

where $\mathrm{sgn}(·)$ is the sign function. The slope $\beta =\overline{q}/(\sigma -\delta )$ represents the control gain.

While a steeper slope $\beta$ (high gain) provides stronger voltage support, it may lead to control loop instability. Therefore, the optimization of these parameters must strictly satisfy stability constraints.

The primary objective is to minimize voltage deviations across the network while satisfying operational constraints. The optimization problem is formulated as follows:

$$\underset{z\in Z}{min}F\left(z\right)=\sum _{n=1}^N{[v_n\left(z\right)-1]}^2$$

(4)

where $z=[\overline{v},\delta ,\sigma ,\overline{q}]$ is the parameter vector defining the Volt/VAR control rules.

Stability constraints must be incorporated to prevent oscillations. Let $\mathit{\beta }$ be the vector collecting all slope parameters, and define the diagonal control matrix $\mathbf{A}:=\mathrm{diag}\left(\mathit{\beta }\right)$. Theoretically, the system dynamics are stable if the spectral radius of the interaction matrix $\mathbf{AX}$ is strictly less than 1. To ensure robustness against modeling errors, this paper enforces a stricter condition with a safety margin $\epsilon$:

$${\parallel \mathbf{AX}\parallel }_2\le 1-\epsilon$$

(5)

Although the stability condition is derived based on the linearized approximation in Equation (1), the inherent modeling errors and higher-order terms neglected by linearization are compensated for by enforcing this stricter inequality with a safety margin $\epsilon$. This margin acts as a buffer, ensuring that the control rules remain robust even when the actual grid dynamics deviates slightly from the linear approximation.

This condition is equivalently expressed as a Linear Matrix Inequality (LMI):

$$\left[\begin{array}{cc}(1-\epsilon )\mathbf{I}& \mathbf{A}\mathbf{X}\\ \mathbf{X}\mathbf{A}& (1-\epsilon )\mathbf{I}\end{array}\right]⪰0$$

(6)

where $\mathbf{X}$ represents the grid topology matrix described in Section 2.

To ensure that the Volt/VAR control decision variables are robust against grid fluctuations, they must be screened using CVaR [14,15]. CVaR optimizes against severe tail risks and safeguards against system instability under worst-case scenarios.

At a given confidence level $\alpha$ (e.g., $\alpha =95\%$ or $\alpha =99\%$), the Value at Risk (VaR) represents the maximum possible loss. In other words, we have $\alpha$ certainty that the loss will not be greater than ${\mathrm{VaR}}_{\alpha }$. The standard definition of VaR at confidence level $\alpha$ is

$${\mathrm{VaR}}_{\alpha }\left(\mathcal{L}\right)=inf\left\{l\in \mathbb{R}\mid F_{\mathcal{L}}\left(l\right)\ge \alpha \right\}$$

(7)

where $\mathcal{L}$ is a random variable representing the loss (voltage deviation), $F_{\mathcal{L}}\left(l\right)=P(\mathcal{L}\le l)$ is the Cumulative Distribution Function (CDF) of the loss, and inf denotes the lower bound.

CVaR measures the average expected loss faced in a worst-case, small-probability, extreme loss scenario. It provides a more complete picture of the extent of tail risk than (7). Mathematically, ${\mathrm{CVaR}}_{\alpha }$ is the conditional expectation that loss $\mathcal{L}$ exceeds ${\mathrm{VaR}}_{\alpha }$ ($\mathcal{L}\ge {\mathrm{VaR}}_{\alpha }$):

$${\mathrm{CVaR}}_{\alpha }\left(\mathcal{L}\right)=\mathbb{E}\left[\mathcal{L}\mid \mathcal{L}\ge {\mathrm{VaR}}_{\alpha }\left(\mathcal{L}\right)\right]$$

(8)

Expressed in integral form, we can write CVaR as follows:

$${\mathrm{CVaR}}_{\alpha }\left(\mathcal{L}\right)={\displaystyle \frac{1}{1-\alpha }}{\int }_{\alpha }^1{\mathrm{VaR}}_{\gamma }\left(\mathcal{L}\right)d\gamma$$

(9)

Thus, the true objective function is the CVaR-robustified sum of squared voltage deviation:

$$\underset{z\in Z}{min}{\mathrm{CVaR}}_{\alpha }\left(F(z,\xi )\right)=\underset{z\in Z}{min}{\mathrm{CVaR}}_{\alpha }\left(\sum _{n=1}^N{\left[v_n(z,\xi )-1\right]}^2\right)$$

(10)

By integrating active/reactive power profiles from historical/simulated data, applying stability constraints (5), and modeling voltage and reactive power through power flow equations, a baseline performance metric (4) can be calculated. However, optimizing this metric alone ignores extreme risks arising from grid uncertainties. Thus, the proposed CVaR-based objective function explicitly minimizes the average worst-case voltage deviations beyond a specified risk threshold ($\alpha$), thereby ensuring robust voltage regulation under high uncertainty while preserving all operational constraints and the physical model.

3. The Proposed BEO-CVaR

3.1. BEO

Traditional BEO directly models the risk measure objective function (4), which requires numerous repeated evaluations of the expensive black-box function to estimate the risk value. If a single evaluation takes 30 min, accurately estimating the risk value may require several days. In contrast, the BEO-CVaR algorithm proposed in this paper directly models the underlying function and leverages a GP to capture its structure, thereby avoiding the prohibitively expensive direct evaluation of the risk measure.

Since the computation of voltage deviation is prohibitively expensive, this paper deems the voltage deviation calculation function as a black-box function. For such costly black-box functions, BEO can efficiently perform optimization within a limited number of computational iterations. It iterates through three core steps [16,17].

3.1.1. Training a GP Surrogate Model

Using a GP Surrogate Model, which is defined as

$$f\left(\mathbf{x}\right)\sim \mathcal{GP}(m\left(\mathbf{x}\right),k(\mathbf{x},{\mathbf{x}}^{\prime })),$$

(11)

the joint distribution of the observed data y follows a multivariate Gaussian distribution:

$$y\sim \mathcal{N}(0,K_{\theta }+{\sigma }_n^{2}I)$$

(12)

where $\mu \left(\mathbf{x}\right)$ is the mean function, typically set to zero; $k({\mathbf{x}}_i,{\mathbf{x}}_j)$ is the RBF kernel function/covariance function, used to define the similarity between points; and $K_{\theta }$ is the kernel matrix, and its elements are defined as $K_{ij}=k_{\theta }({\mathbf{x}}_i,{\mathbf{x}}_j)$.

The RBF kernel function is given by

$$k_{\theta }({\mathbf{x}}_i,{\mathbf{x}}_j)={\sigma }_f^{2}exp\left(-{\displaystyle \frac{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j{\parallel }^2}{2l^2}}\right)$$

(13)

Here, the hyperparameter vector $\theta$ contains three parameters: the length scale l, the output scale ${\sigma }_f^2$, and the observation noise variance ${\sigma }_n^2$; l controls the smoothness of the function. The influence of a point ${\mathbf{x}}_i$ on another point ${\mathbf{x}}_j$ decays rapidly as the normalized distance ${\displaystyle \frac{\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel }{l}}$ increases. ${\sigma }_f^2$ controls the amplitude (vertical scale) of the function. A larger ${\sigma }_f^2$ allows for a larger possible range of function values. ${\sigma }_n^2$ measures the average magnitude of the deviation of the observed values from the true function values. A larger ${\sigma }_n^2$ indicates more noise in the observations and higher uncertainty; a smaller ${\sigma }_n^2$ indicates more precise observations and lower uncertainty.

The goal of training is to find the hyperparameters $\theta$ that best explain the current observed data D. The objective function used in this paper is the marginal log-likelihood (MLL):

$$logp\left(\mathbf{y}\right|\mathbf{X},\theta )=-{\displaystyle \frac{1}{2}}{\mathbf{y}}^T{({\mathbf{K}}_{\theta }+{\sigma }_n^2\mathbf{I})}^{-1}\mathbf{y}-{\displaystyle \frac{1}{2}}log|{\mathbf{K}}_{\theta }+{\sigma }_n^2\mathbf{I}|-{\displaystyle \frac{n}{2}}log\left(2\pi \right)$$

(14)

This formula consists of three components: The data-fitting term ($-{\displaystyle \frac{1}{2}}{\mathbf{y}}^T{\mathbf{K}}^{-1}\mathbf{y}$) measures how well the model matches the observed data. The complexity penalty term ($-{\displaystyle \frac{1}{2}}log\left|\mathbf{K}\right|$) acts as a regularizer for the model complexity. The determinant $\left|\mathbf{K}\right|$ of the kernel matrix measures the model’s flexibility in a certain sense. A more complex model typically has a larger $\left|\mathbf{K}\right|$, resulting in a smaller value for this term (i.e., a larger penalty). The constant term ($-{\displaystyle \frac{n}{2}}log\left(2\pi \right)$) can be ignored during optimization.

This structure resembles the classic bias–variance trade-off in machine learning. Equation (14) automatically balances data fitting and model complexity.

Therefore, the goal of GP optimization is to find the optimal hyperparameters ${\theta }^{*}$ that maximize Equation (14).

The optimal hyperparameters ${\theta }^{*}$ are found by maximizing the MLL:

$${\theta }^{*}=arg\underset{\theta }{max}logp(\mathbf{y}\mid \mathbf{X},\theta )$$

(15)

This is inherently a non-convex optimization problem with continuous variables. Although it cannot be solved analytically, iterative methods based on the gradient descent principle—such as gradient descent itself, conjugate gradient, or L-BFGS—can be employed to find the optimal solution. This work derives the gradient of the objective function (14) with respect to the hyperparameters $\theta =(l,{\sigma }_f^2,{\sigma }_n^2)$:

$${\displaystyle \frac{\partial logp(\mathbf{y}\mid \mathbf{X},\theta )}{\partial l}}={\displaystyle \frac{1}{2}}{\mathbf{y}}^T{\mathbf{K}}^{-1}{\displaystyle \frac{\partial \mathbf{K}}{\partial l}}{\mathbf{K}}^{-1}\mathbf{y}-{\displaystyle \frac{1}{2}}tr\left({\mathbf{K}}^{-1}{\displaystyle \frac{\partial \mathbf{K}}{\partial l}}\right)$$

(16)

The term ${\displaystyle \frac{\partial \mathbf{K}}{\partial l}}$ can be computed based on the definition of the RBF kernel function given in (13).

The parameters are then updated iteratively, where the “loss” refers to the negative MLL (the negative of (14), i.e., $-logp(\mathbf{y}\mid \mathbf{X},\theta )$):

$${\theta }_{\mathrm{new}}={\theta }_{\mathrm{old}}-\eta {\displaystyle \frac{\partial \mathrm{loss}}{\partial \theta }}$$

(17)

In summary, the training procedure for a GP is as follows:

• Initialize the hyperparameters $\theta =\{l,{\sigma }_f^2,{\sigma }_n^2\}$.
• Construct the kernel matrix $\mathbf{K}$ using the current $\theta$.
• Compute the current negative marginal log-likelihood (loss).
• Compute the gradients of the loss with respect to $\theta$ in (16).
• Update the hyperparameters $\theta$ using an optimizer (e.g., gradient descent as in (17)).
• Repeat Steps 2–5 until a convergence criterion is met (e.g., the gradient norm is sufficiently small, the maximum number of iterations is reached, or the change in the loss function is negligible).

3.1.2. Constructing and Optimizing the Acquisition Function

Based on the mean ${\mu }_t\left(x\right)$ and standard deviation ${\sigma }_t\left(x\right)$ provided by the current GP model, an acquisition function is defined to measure the expected utility of performing the next evaluation at point x. This function balances exploration (of regions with high uncertainty) and exploitation (of regions with a high predicted mean). The point $x_t$ that corresponds to the maximum value of the acquisition function is considered to be the most promising candidate for locating a better solution in the next iteration.

This paper compares four distinct acquisition function strategies: EI, upper confidence bound (UCB), Max-Value Entropy Search (MES), and Thompson Sampling (TS). The acquisition function can be formally expressed as $a(x;D_{1:t})$, where $D_{1:t}$ denotes the set of all observed data accumulated from the first to the t-th iteration. For acquisition functions in medium-to-high dimensions that are differentiable, multi-start gradient-based methods are commonly employed to efficiently obtain high-quality local maxima, which are then selected as the next sampling points.

• EI: Measures the expected value of improvement of x over $y_{\mathrm{best}}$ (improvement amount weighted by probability).

  $$a_{\mathrm{EI}}(x;D_{1:t})=\mathbb{E}\left[max(f\left(x\right)-f_{\mathrm{best}},0)\right]$$

  (18)
• UCB: Selects the next point based on the upper confidence bound.

  $$a_{\mathrm{UCB}}(x;D_{1:t})={\mu }_t\left(x\right)+{\lambda }_t{\sigma }_t\left(x\right)$$

  (19)

  where ${\lambda }_t\ge 0$ is a parameter controlling the degree of exploration (which can be time-varying or fixed).
• MES: Aims to select an evaluation point x such that, after observing the function value y at this point, the uncertainty about the global maximum $f^{*}$ is maximally reduced, which can be expressed using conditional entropy as $H\left(f^{*}\right|D)$. This reduction in uncertainty is the information gain:

  $$a_{\mathrm{MES}}\left(x\right|D_{1:t})=I(f^{*};y|D_{1:t},x)$$

  (20)

  $$a_{\mathrm{MES}}\left(x\right|D_{1:t})=H\left(f^{*}\right|D_{1:t})-{\mathbb{E}}_{p\left(y\right|x)}\left[H\left(f^{*}\right|D_{1:t}\cup \left\{(x,y)\right\})\right]$$

  (21)

  where ${\mathbb{E}}_{p\left(y\right|x)}\left[H\left(f^{*}\right|D_{1:t}\cup \left\{(x,y)\right\})\right]$ represents the remaining uncertainty about $f^{*}$ after sampling at candidate point x and obtaining observation y. This expectation is taken over possible values of y (which follows the predictive distribution $p\left(y\right|D_{1:t},x)$ of the current GP model at point x).
• TS: Samples a function $f_{\mathrm{sample}}\sim \mathrm{gp}({\mu }_t,k_t)$ from the GP posterior distribution, and then takes the maximum point on $f_{\mathrm{sample}}$ as $x_{t+1}$. No explicit calculation of $a\left(x\right)$ is required.

3.1.3. Evaluation and Update

Evaluate the computationally expensive objective function at the selected point. Add the new (input, output) data pairs to the existing training dataset. Repeat this process until the evaluation budget is exhausted or a convergence criterion is met.

3.2. BEO-CVaR Algorithm Framework

The black-box function of the BEO-CVaR algorithm is used to solve for voltage deviation values. Figure 2 illustrates the framework of BEO-CVaR. It consists of two parts: (1) BEO-CVaR optimization and (2) computation of the voltage deviation via (4).

We refer to the second part of the function used to solve for the voltage deviation values as a black-box function for the BEO-CVaR algorithm. Algorithm 1 is the pseudo-code.

Algorithm 1: BEO-CVaR Framework

Input: Variable boundaries $B\in {\mathbb{R}}^{s\times 2}$, initial sample size $N_{\mathrm{init}}$, optimization iteration count T, environmental sample count K, risk level $\alpha$ Output: Optimal parameters $z_{best}$, minimum CVaR $y_{best}$    1: Normalize the training data to the range $[0,1]$    2: for iteration = 1 to max_iterations T do    3:       Normalize training data to the range [0,1]    4:       Train a GP model: Use the RBF kernel function from (13); train the model hyperparameters using MLL (neural network gradient method)    5:       Construct the acquisition function: Use the acquisition function strategy from Section 3.1, calculate the current optimum as the reference point, and construct the acquisition function    6:       Optimize the acquisition function: Acquisition function optimization is performed via multi-start random restarts and random sampling points, using gradient-based optimization methods within the 8-dimensional standardized parameter space, while employing boundary handling and convergence checks to ensure numerical stability    7:       Denormalize the candidate point to the original parameter space    8:       Evaluate the black-box function at the candidate point:    9:       for environment sample = 1 to K do    10:           Randomly select a load scenario    11:           Calculate power system voltage deviation cost    12:       end for    13:       Calculate CVaR at $\alpha$ risk level    14:       Update the training dataset with the new candidate point and its CVaR value    15:       Periodically save the optimization progress    16: end for

Figure 3 is the flowchart of the voltage deviation calculation function. This function is computationally expensive. This paper computes it based on (4).

The input is an 8-dimensional control decision vector to be evaluated, which defines the Volt/VAR power control rules for two inverters (including decision variables such as reference voltage, deadband voltage, saturation voltage, and maximum reactive power).

To fully capture grid uncertainties (such as fluctuations in load and photovoltaic output), the algorithm randomly selects K different operating scenarios. For each scenario, the following detailed calculation process is executed: (1) Initialize the grid model by loading the topology and initial parameters of the IEEE 123-bus test system using MATPOWER’s loadcase function. (2) Inject the load and photovoltaic data for the current scenario, modifying the active load, reactive load, and photovoltaic active power output in the model. (3) Call MATPOWER’s runpf function to perform a complete AC power flow calculation. This function iteratively solves the power balance equations using the Newton–Raphson method, directly outputting the precise voltage magnitudes for each node. (4) Based on the power flow results, calculate the sum of squared deviations between all node voltages and the nominal voltage for that scenario.

After iterating through all K scenarios, the process collects a set of voltage deviation samples and finally computes the CVaR at a given risk level $\alpha$ as the output. This process ensures the accuracy of performance evaluation through expensive multi-scenario power flow calculations, while also highlighting the necessity of employing the BEO algorithm for efficient optimization.

4. Experiment and Result Analysis

To comprehensively evaluate the effectiveness and robustness of the proposed BEO-CVaR framework, this section presents a series of numerical simulations on the IEEE 123-node test feeder. The experimental validation is organized as follows: First, the test system setup and algorithmic parameter configurations are detailed in Section 4.1 and Section 4.2. Subsequently, Section 4.3 analyzes the algorithm’s internal characteristics, including sensitivity to the risk confidence level ($\alpha$) and convergence behavior. Following this, comparative studies against traditional decentralized strategies and meta-heuristic optimization (PSO) are presented in Section 4.4, while the performance of different acquisition functions is evaluated in Section 4.5. Finally, the framework’s scalability, communication efficiency, and robustness under extreme physical constraints are rigorously verified in Section 4.6, Section 4.7, and Section 4.8, respectively.

4.1. Test Case

The backbone network of the standard IEEE 123-node test grid proposed in [18] was adopted as the grid infrastructure, with a schematic diagram shown in Figure 4. To simulate realistic load conditions, the power demand profiles were derived from the DiSC simulation framework, which aggregates anonymized residential electricity consumption data from approximately 1200 households near Horsens, Denmark, provided by the local distribution system operator NRGi.

Two PV units were integrated into the grid model as micro-generators. Figure 5a illustrates the total load demand profiles across all nodes over a 12 h period (6:00–18:00), with one representative curve highlighted.

Figure 5b simultaneously displays the power generation curves of the two newly added PV units, exhibiting time-varying output patterns influenced by factors such as solar irradiance.

To validate the practical value of the BEO-CVaR algorithm in setting Volt/VAR control decision vectors, the optimization process was simulated and verified using MATPOWER on a quasi-steady-state nonlinear AC power flow model.

4.2. Experimental Setting

For the architecture in Section 3.2, its key parameters are shown in

Table 1. BEO-CVaR parameters and their values.

Parameter	Value	Parameter	Value
Dimensions	8	Restarts	50
Initial samples	20	Raw samples	200
Optimization iterations	68	Risk level ($\alpha$)	See Section 4.3.1

. This table defines the key algorithm parameters for BEO-CVaR optimization. While most parameters are determined by the physical constraints and computational budget, the risk confidence level $\alpha$ is a critical hyperparameter that dictates the trade-off between average efficiency and tail risk robustness. Its specific selection process and the resulting impact on system performance are investigated in detail in Section 4.3.1. There exists an 8-dimensional decision vector representing the Volt/VAR power control rule settings ($\overline{v}$, $\delta$, $\sigma$, $\overline{q}$) of 2 inverters. Subsequently, 68 optimization iterations are carried out. In each iteration, the GP and an acquisition function are used to select the next most promising point for evaluation. The EI strategy is employed in this subsection, while the remainder of this paper will compare the results produced by different strategies. Unless otherwise stated, all computations were performed on a hardware platform equipped with an AMD64 Family 25 Model 97 processor and 16 GB of RAM.

To address the computationally expensive CVaR objective and ensure the robustness of local optima, a multi-restart strategy with a large number (50) of restarts was employed during the acquisition function optimization step. The 200 original samples represent the number of unique load/PV scenarios (K) used in each evaluation of the black-box function to compute the CVaR at the specified risk level. The risk confidence level $\alpha$ represents the proportion of the loss distribution that the optimizer accounts for when calculating risk. In this study, we explore a range of candidates $\alpha \in \{0.5,0.6,0.7,0.8,0.9\}$ to empirically identify the optimal operating point for the IEEE 123-node feeder. This ensures that the chosen control rules are not only robust against extreme scenarios but also maintain high performance under normal operating conditions.

Table 2. Feasible search space for Volt/VAR control vector.

Parameter	Min	Max	Parameter	Min	Max
${\overline{v}}_1$	0.95	1.05	${\overline{v}}_2$	0.95	1.05
${\delta }_1$	0.00	0.03	${\delta }_2$	0.00	0.03
${\sigma }_1$	0.03	0.180	${\sigma }_2$	0.03	0.180
${\overline{q}}_1$	−1.0	1.0	${\overline{q}}_2$	−0.2	0.2

defines the feasible search space for the Volt/VAR power control decision vector and imposes physical and operational constraints on the two inverters.

To ensure reproducibility, the specific algorithmic settings and convergence strategies are defined as follows:

• Hyperparameter Optimization: The GP kernel hyperparameters are optimized by maximizing the MLL using the L-BFGS-B algorithm. As a quasi-Newton method, this approximates the Hessian matrix to automatically adapt step sizes, eliminating the need for manual tuning of the learning rate and terminating the update when the gradient norm satisfies the convergence tolerance.
• Convergence Strategy: The outer optimization loop employs a fixed evaluation budget ($T=68$ iterations) rather than an asymptotic convergence threshold. Given the computationally expensive nature of the CVaR objective, this budget strategy ensures a strictly bounded and predictable execution time (approx. 31 min) while sufficiently exploring the design space.
• Acquisition Maximization: To address the non-convexity of the acquisition function, we employ a multi-start optimization strategy. The algorithm generates $N_{raw}=200$ random samples to identify high-potential regions, which are then used to initialize $N_{restarts}=50$ local gradient-based searches (via L-BFGS-B) to precisely locate the next sampling point.

4.3. Results and Analysis

4.3.1. Sensitivity Analysis and Selection of Risk Parameter $\alpha$

THe CVaR confidence level, $\alpha$, serves as a critical hyperparameter in the BEO-CVaR framework, determining the algorithm’s degree of risk aversion. A generic choice of $\alpha$ may not yield the optimal trade-off between operational efficiency (average performance) and grid safety (robustness against extreme events). To scientifically determine the optimal $\alpha$ for the IEEE 123-node test feeder, we conducted a sensitivity analysis by varying $\alpha$ across the set $\{0.5,0.6,0.7,0.8,0.9\}$.

Figure 6 illustrates the impact of $\alpha$ on two key performance metrics: the average voltage deviation (representing normal operating efficiency) and the extreme tail risk (quantified as the 99.9% worst-case voltage deviation). The results reveal a convex, “U-shaped” relationship, indicating that neither risk-neutral nor excessively risk-averse strategies are ideal:

• Under-Protection Region ($\alpha <0.7$): At $\alpha =0.5$, the algorithm behaves similarly to a risk-neutral expectation minimization. While it achieves a moderate average deviation ($0.0122$ p.u.), it fails to sufficiently penalize extreme violations. Consequently, the system exhibits the highest tail risk ($0.0520$ p.u.), indicating vulnerability to rare but severe load fluctuations.
• Over-Conservatism Region ($\alpha >0.7$): As $\alpha$ increases to $0.9$, the optimizer focuses exclusively on the worst $10\%$ of scenarios. This excessive risk aversion leads to “over-regulation,” where inverters adopt aggressive control rules that are suboptimal for the majority of normal scenarios. As a result, the average voltage deviation degrades to $0.0115$ p.u. Furthermore, estimating the extreme tail with finite samples introduces higher variance into the GP surrogate, resulting in a slight increase in the measured risk ($0.0510$ p.u.) compared to $\alpha =0.7$.
• Optimal Balance ($\alpha =0.7$): The value of $\alpha =0.7$ is identified as the optimal trade-off point. It achieves the global minimum for the average voltage deviation (0.0102 p.u.), which prioritizes and guarantees the highest efficiency under day-to-day nominal conditions. While a marginally lower extreme tail risk is observed at $\alpha =0.8$, this gain is minimal and comes at the cost of a significant degradation in average performance. Therefore, $\alpha =0.7$ is the superior choice, as it robustly constrains the tail risk (0.0478 p.u.) without sacrificing crucial operational efficiency. This indicates that focusing on the worst $30\%$ of scenarios provides sufficient data for the BEO algorithm to learn robust control boundaries without sacrificing performance in nominal states.

Based on these empirical findings, $\alpha =0.7$ was identified as the optimal operating point for this specific network topology. Therefore, this value is adopted for all subsequent performance comparisons and scalability analyses in this study.

4.3.2. Optimization Process and Convergence Analysis

Figure 7 shows the step-by-step evaluation of the CVaR objective (blue dots) and the progression of the historical best CVaR (red line). Some points with high CVaR values represent exploratory samples evaluated by the BEO process. These high values originate from the algorithm intentionally testing potentially high-risk regions (decision vectors that could lead to system instability, e.g., load curtailment, in some scenarios). The graph demonstrates the progressive improvement in risk control during the BEO process, highlighted by the continuous downward trend of the historical best CVaR, which clearly indicates the algorithm’s convergence.

Figure 8 visualizes the evolution of all eight optimized decision variables throughout the evaluation process, revealing the search trajectory and convergence behavior of each variable during BEO. All of the parameters spend most of their time in stable “exploitation” phases, conducting local fine searches. The occasional abrupt changes represent crucial “exploration” behaviors, where the algorithm actively jumps out of the current region to probe new areas of the search space, avoiding local optima and seeking the global best solution.

Figure 9 tracks the dynamic changes of the noise variance (${\sigma }_n^2$) and output scale (${\sigma }_f^2$) hyperparameters of the GP model throughout the iterations, demonstrating the enhancement of the model’s stability in capturing the behavior of the objective function.

• ${\sigma }_n^2$ reaches its peak around the 35th iteration, and then declines rapidly and stabilizes at a low value, indicating early active exploration of high-uncertainty regions and improved model reliability. The delayed convergence of ${\sigma }_n^2$ underscores its role as a key parameter requiring careful calibration.
• ${\sigma }_f^2$ undergoes a sharp drop around the 10th iteration and quickly converges to a stable value, reflecting the algorithm’s rapid calibration of the overall variation amplitude of the target function in the initial phase (with early emphasis on exploring extreme regions), ultimately determining an appropriate scale.

Both parameters evolve independently but stabilize after their respective transitions, marking the shift of the BEO algorithm from exploration to exploitation.

Figure 10 displays the length scales l for the eight Volt/VAR power control decision variables defined in Table 2. In the early stages of optimization (when the number of iterations is low), the length scales across all dimensions typically undergo significant fluctuations and exploration. This occurs because the GP model has limited knowledge of the function’s structure initially and must explore different length scale configurations to identify the optimal model structure. The early peaks observed in some dimensions in the figure confirm this behavior. As the iterations progress (with increasing number of iterations), the BEO algorithm collects more data, and the GP model gains a clearer understanding of the target function. As a result, the length scales in all dimensions gradually stabilize, with reduced fluctuations, eventually converging to a relatively stable and very small value. This indicates that the target function being optimized is complex and finely detailed (highly nonlinear with intricate physical relationships), and that its output is highly sensitive to minor changes in the input decision variables. Through learning and modeling, the BEO algorithm successfully identifies this characteristic. It ultimately selects a high-resolution, high-precision model (with a small l value) to characterize the target function, enabling a detailed search within this complex function and accurately locating the global optimum or its vicinity.

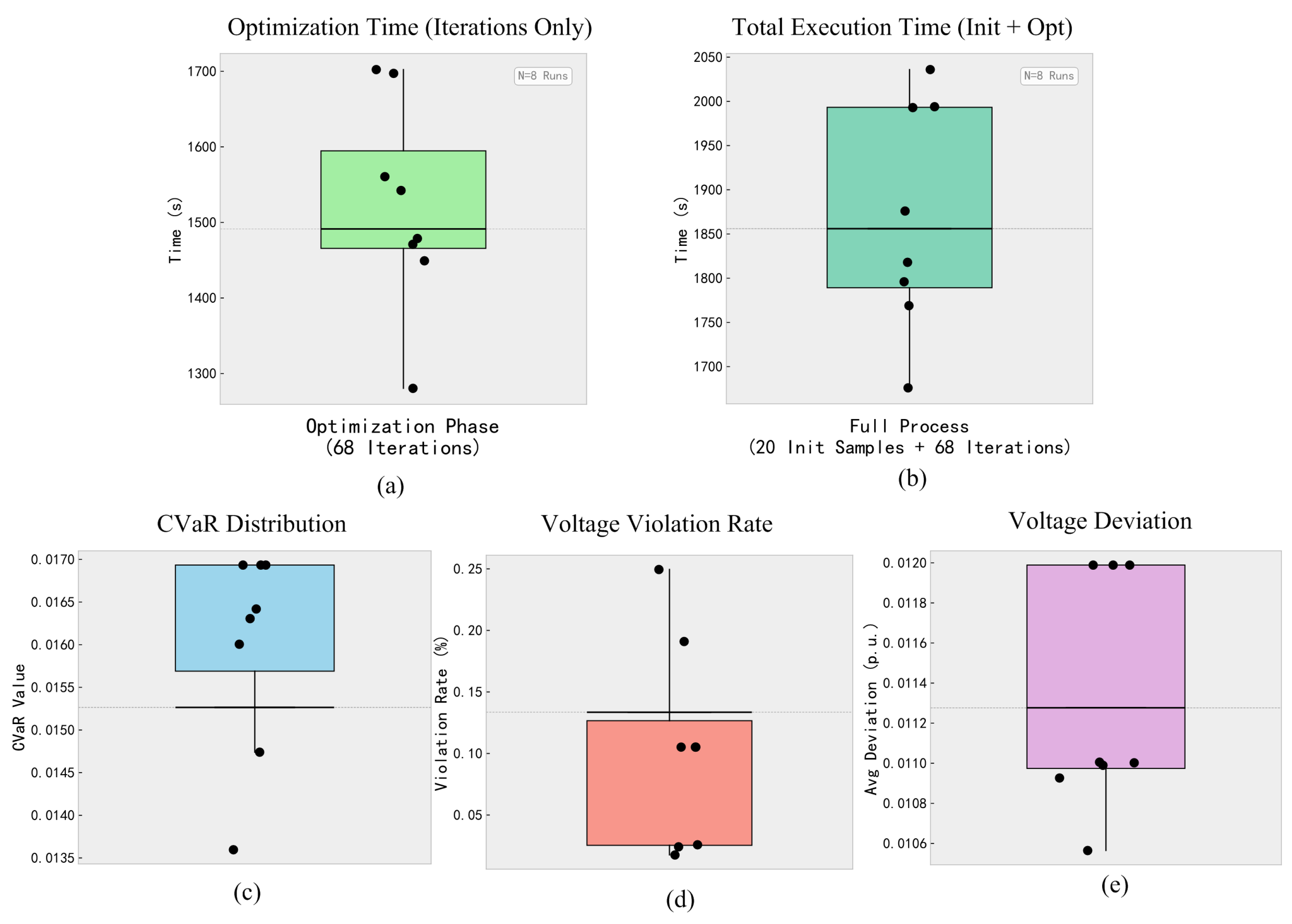
4.3.3. Statistical Reproducibility and Computational Efficiency

To strictly evaluate the reproducibility and robustness of the proposed method, we conducted eight independent trials with different random seeds. The statistical distribution of key performance metrics and computational costs is illustrated in Figure 11.

Figure 11c–e display the distribution of the final optimized objectives. As detailed in

Table 3. Statistical performance metrics over 8 independent runs.

Metrics	Mean ± Std	Unit
CVaR	$0.0160\pm 0.0012$	-
Voltage Violation Rate	$0.1030\pm 0.0834$	%
Avg. Voltage Deviation	$0.0113\pm 0.0006$	p.u.

, the BEO-CVaR framework demonstrates high stability. The standard deviation of the CVaR objective is extremely low (0.0012), indicating that the algorithm consistently converges to high-quality solutions regardless of the initial random sampling. Notably, the voltage violation rate remains minimal at $0.1030\%\pm 0.0834\%$, and the average voltage deviation is stable at $0.0113\pm 0.0006$ p.u. These results confirm the statistical significance of the method’s performance, proving that the optimization capability is robust against the randomness inherent in the BEO process.

Furthermore, to quantify the computational overhead, we recorded the execution time for both the initialization phase (20 samples) and the optimization phase (68 iterations), as shown in Figure 11a,b. The specific time consumption statistics are summarized in

Table 4. Computational time breakdown (Hardware: AMD64 Family 25 Model 97).

Metric	Mean ± Std	Unit
Optimization Time (68 Iterations)	$1522.74\pm 138.00$	s
Initialization Time (20 Samples)	$347.01\pm 45.00$	s
Total Execution Time	1869.75 ± 127.68	s

.

The average total execution time is approximately 31 min ($1869.75$ s). Considering that the optimized control rules are intended for long-term operation (e.g., updated every 12 h, as discussed in Section 4.3.4) and eliminate the need for real-time communication, this offline training cost is highly acceptable for practical engineering applications.

4.3.4. Performance Validation on Standard Test Scenarios

Following the statistical analysis, we selected the representative decision vector to validate the control efficacy across the full set of test scenarios. We sampled every 5 s over 12 h (6 a.m. to 6 p.m.) to obtain the 8640 scenarios. When deployed across these 8640 scenarios, the results are as shown in Figure 12:

The simulation results can be summarized as follows:

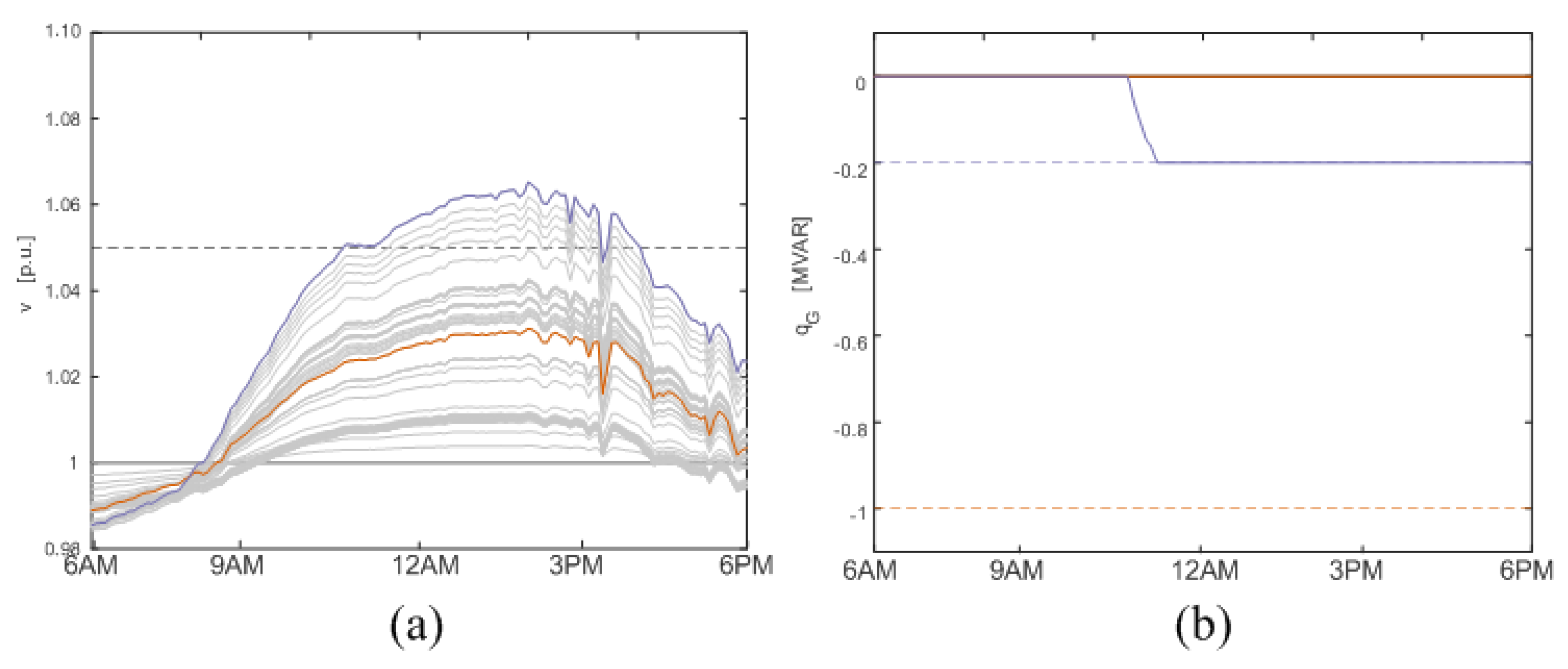
• Strict Safety Compliance: The proposed BEO-CVaR method achieved a remarkably low voltage violation rate of 0.026% (violations occurred in only a negligible fraction of the 8640 scenarios). This demonstrates that the algorithm effectively learned to mitigate tail risks, ensuring that the grid operates within the IEEE 1547 safety limits (≤1.05 p.u.) under almost all uncertainty realizations.
• Coordinated Inverter Response: As shown in the bottom panel of Figure 12, the inverters exhibit a distinct coordinated behavior. The smaller Inverter 2 (Green) operates near its saturation limit to provide baseload reactive support, while the larger Inverter 1 (Orange) dynamically adjusts its output, reaching full saturation only during peak solar generation periods (scenario indices 4000–6000).

In contrast to the method in [1], which requires communication every two hours to update the control rules, the proposed approach relies on a robust, fixed decision vector derived from offline training. The results confirm that this fixed strategy can autonomously maintain grid stability over a 12 h period using only locally measured voltages, significantly reducing communication dependency.

4.4. Comparison with Traditional and Meta-Heuristic Strategies

4.4.1. Comparison with Traditional Decentralized Methods

There are three traditional methods:

• Uncontrolled Scenario: In the uncontrolled case, the two PV inverters inject active power at a unitary power factor (i.e., zero reactive power). This results in voltage violations, with the magnitude exceeding the 1.05 p.u. upper limit at multiple buses (Figure 13, uncontrolled panel). These overvoltage issues highlight the necessity of reactive power control strategies to maintain grid voltage stability.
• Fully Decentralized Control (Static Feedback): This scenario evaluates the static local feedback law proposed in [2,9,10,19]. The control law relies on purely local measurements. It adjusts reactive power injection based on a predefined control strategy with a reference voltage $\overline{v}$ of 1.0 p.u., a deadband voltage $\delta$ of ±0.01 p.u., a saturation voltage $\sigma$ of ±0.04 p.u., and maximum reactive power injections $\overline{q}$ of 1.0 p.u. for one PV inverter and 0.2 p.u. for the other. As shown in Figure 14 (Fully decentralized control (static)), while some buses exhibit improved voltage profiles, violations persist at certain nodes, including generator buses. This indicates that static decentralized control strategies are insufficient for effectively mitigating overvoltage in all cases.
• Fully Decentralized Control (Incremental Feedback): This paper also implements the incremental feedback strategy, which adjusts reactive power iteratively based on local voltage deviation [20,21,22]. The results, depicted in Figure 15, demonstrate that while incremental feedback offers some improvements, it fails to strictly regulate voltages below the 1.05 p.u. threshold. The persistent overvoltage issues at certain nodes underscore the limitations of purely decentralized strategies.

The experimental results of these three traditional methods are compared with those of the BEO-CVaR framework in

Table 5. Comparison of different strategies based on various performance metrics.

Strategy	Overall Compliance	Non-Compliant Bus Count	High-Risk Violation Rate	Comm. Frequency
Uncontrolled	95.75%	6	10.71%	–
Static Feedback	98.61%	4	5.21%	Real-time
Incremental Feedback	97.17%	5	8.64%	Real-time
PSO (Meta-heuristic)	99.47%	2	2.34%	12 h
BEO-CVaR (Proposed)	99.90%	1	0.50%	12 h

. In summary, the comparative analysis clearly demonstrates the superiority of the proposed BEO-CVaR framework over traditional Volt/VAR power control strategies.

Specifically, to evaluate robustness under extreme conditions, we analyzed a high-risk operational interval (scenarios 4500–6000) characterized by high load or generation volatility. As shown in the “High-Risk Violation Rate” column of Table 5, traditional methods fail significantly in this interval, with violation rates soaring to 10.71% (uncontrolled), 8.64% (incremental), and 5.21% (static). This indicates that decentralized methods lack the coordination required to handle system stress.

In contrast, BEO-CVaR achieves consistent and robust voltage regulation. Crucially, across all 8640 real-world load scenarios, BEO-CVaR effectively maintains voltage deviation within safe margins, achieving near-perfect compliance (99.90%) with the IEEE 1547 safety standard. Furthermore, this enhanced stability and robustness are achieved with significantly reduced operational overhead: BEO-CVaR only requires infrequent decision vector updates (once every 12 h in the experiment), greatly diminishing reliance on communication reliability. This stands in sharp contrast to traditional decentralized methods, which necessitate continuous real-time communication or frequent updates to maintain their own relatively ineffective control, thereby imposing a substantial communication burden. The results demonstrate that BEO-CVaR effectively addresses the inherent key limitations of existing decentralized methods—namely, robustness, optimality, and communication efficiency—in managing distribution networks with DERs.

4.4.2. Comparison with Meta-Heuristic Optimization (PSO)

To rigorously evaluate the advanced nature of BEO-CVaR in handling black-box optimization problems, in addition to the aforementioned traditional methods, this study benchmarks the proposed framework against a classic meta-heuristic algorithm: Particle Swarm Optimization (PSO). PSO is widely recognized for its simplicity and effectiveness and has been extensively utilized in optimal power flow and Volt/VAR optimization tasks within power systems [23,24]

Under the exact same experimental environment, the PSO was configured with a population size of 30 and 50 iterations, targeting the minimization of the average voltage deviation. The comparative results are presented in Table 5 and Figure 16. The analysis reveals two key insights:

• Superior Robustness in High-Risk Scenarios: While PSO achieves a reasonable overall compliance rate, it struggles significantly under stress. In the high-risk interval (scenarios 4500–6000), PSO exhibits a violation rate of 2.34%. This reveals a critical limitation: standard PSO optimizes for average performance (expectation minimization) and ignores tail risks. In sharp contrast, BEO-CVaR maintains a violation rate of only 0.50% in the same high-stress window—an improvement of nearly 80% over PSO. This demonstrates the effectiveness of the CVaR component, which explicitly penalizes voltage violations in worst-case scenarios, ensuring grid safety even during peak volatility.
• Computational Efficiency: Regarding computational cost, the optimization process for PSO required approximately 54.5 min, whereas BEO-CVaR required only about 31 min. PSO relies on stochastic exploration of the search space by a population, necessitating a large number of function evaluations. Conversely, BEO-CVaR leverages a GP surrogate model to efficiently “learn” the grid behavior, achieving superior convergence with significantly fewer samples. This demonstrates the superior sample efficiency of the Bayesian optimization framework.

4.5. Comparison of Four Acquisition Function Strategies

Figure 17 illustrates the performance of four different acquisition strategies (EI, UCB, MES, and TS) in minimizing the objective function CVaR. The EI strategy, represented by the blue curve, demonstrates the fastest initial convergence speed. It shows extremely rapid performance improvement within the first few iterations, quickly catching up with and surpassing other strategies. This is a strategy that is biased towards exploitation, as it greedily searches near the currently known optimal point, enabling it to rapidly find local improvements. The UCB strategy, depicted by the red curve, exhibits very robust performance. From early to late stages, it maintains a steady declining trend without significant performance fluctuations. This indicates that it is a reliable and robust choice requiring minimal parameter tuning, with strong performance predictability. The MES strategy, shown by the purple curve, starts from the best initial point (the point most informative about the global optimum). However, it progresses slowly in the early stages, even with slight fluctuations. Nevertheless, during the mid-to-late iterations (after approximately 10 iterations), it demonstrates sustained optimization capability, ultimately achieving slightly leading or comparable performance relative to other strategies. The TS strategy, represented by the green curve, performs similarly to MES but possesses inherent randomness and a strong exploratory nature. The selection of its initial point highly depends on the form of the randomly sampled function, allowing it to explore any uncertain regions within the search space. It shows more pronounced fluctuations in the early stages before eventually converging to a good solution. The semi-transparent region surrounding each curve represents the average fluctuation range across multiple runs (95% confidence interval). The narrowest region observed for EI indicates very stable and highly reproducible performance. In contrast, MES and TS show wider regions, reflecting greater variability in results across different runs due to their more random, exploration-focused nature. This further confirms their core characteristic of being exploration-oriented.

4.6. Scalability Analysis in Multi-Inverter Scenarios

To rigorously evaluate the scalability of the proposed BEO-CVaR framework, a series of experiments were conducted on a standard distribution test system modified to incorporate a varying number of controllable inverters. Three distinct scenarios were established: a 2-inverter base case, a 5-inverter case, and a 10-inverter case. The inverters were progressively added to different buses to simulate increasing penetration of DERs. A large-scale inverter, rated at 1.0 Mvar, was situated at a designated node, while the remaining inverters, each with a 0.2 Mvar capacity, were deployed in a decentralized manner at remote locations within the network to provide fine-grained local voltage regulation. This configuration was consistently maintained across all test scenarios. For all scenarios, the risk-aversion parameter for the CVaR objective was set to $\alpha =0.95$, creating a stringent test condition that forces the algorithm to optimize against the worst 5% of potential outcomes, thereby providing a rigorous benchmark for system robustness under extreme uncertainty.

The performance was evaluated based on the voltage violation rate across 8640 load scenarios. The results are summarized in

Table 6. Performance violation rates vs. number of inverters (CVaR = 0.95).

Number of Inverters	Voltage Violation Rate (%)
2	0.3121%
5	0.0062%
10	0.1007%

.

As illustrated in Table 6, the voltage violation rate remains exceptionally low (below 0.32%) across all cases, demonstrating the robust scalability of the BEO-CVaR method. The 5-inverter case achieved the lowest violation rate of 0.0062%, indicating an optimal balance between control authority and optimization complexity. At this moderate scale, the BEO effectively navigates the search space to find a coordination strategy that leverages the additional control points to near-perfect effect.

In the 2-inverter case (Figure 18), the dark blue curve represents a large-scale 1.0 Mvar inverter. In the majority of high-risk scenarios, it operates almost continuously at its full capacity of −1.0 Mvar. This indicates that the system relies heavily on this single inverter to maintain grid voltage, shouldering the vast majority of the voltage regulation task. The light blue curve, representing a small-scale 0.2 Mvar inverter, also actively absorbs reactive power, but its output is constrained by its 0.2 Mvar capacity.

In the 5-inverter case (Figure 19), the voltage profiles exhibit significant convergence. The maximum nodal voltage is effectively suppressed, establishing a safer margin from the 1.05 p.u. upper limit, which demonstrates a notable improvement in overall voltage quality. The operational saturation of the 1.0 Mvar primary inverter (dark blue curve) increases compared to the 2-inverter scenario, reaching full capacity in approximately half of the scenarios. Concurrently, the other four distributed inverters actively participate in voltage regulation. This case strikes an optimal balance between control degrees of freedom and optimization tractability. The 20-dimensional decision space is sufficiently rich to enable effective coordinated control. The BEO-CVaR algorithm successfully explores this space and identifies a high-quality solution approaching the global optimum within a finite computational budget. This solution is characterized by assigning the core task to the most capable unit (the primary inverter) while mobilizing all distributed units for auxiliary support and local optimization, ultimately achieving near-perfect risk mitigation. The high saturation level of the primary inverter is, in fact, an integral part of this efficient, coordinated strategy.

In the 10-inverter case (Figure 20), the 1.0 Mvar primary inverter operates at its full −1.0 Mvar capacity for over 80% of its operational time, a saturation level far exceeding the previous two cases. Among the remaining nine 0.2 Mvar inverters, only one operates in a relatively saturated state, while the other eight provide almost no reactive power output. Although the Voltage Violation Rate (0.1007%) remains at a favorable level, it is higher than in the 5-inverter case. This performance degradation in the 40-dimensional case (10 inverters) can be theoretically attributed to the “curse of dimensionality” inherent in non-parametric BEO. As the dimension D of the decision space increases, the volume of the search space grows exponentially, leading to extreme data sparsity when the sample size N (computation budget) remains fixed. From the perspective of the GP surrogate model, this sparsity specifically impacts the efficacy of the RBF kernel (13). The kernel relies on the Euclidean distance $\parallel {\mathbf{x}}_i-{\mathbf{x}}_j\parallel$ to measure similarity. In high-dimensional spaces, the distance between any two randomly sampled points tends to converge, making it difficult for the GP to distinguish between ‘nearby’ and ‘distant’ points effectively. Consequently, the predictive variance ${\sigma }_t\left(\mathbf{x}\right)$ becomes less informative, and the acquisition function struggles to balance exploration and exploitation efficiently. The optimizer requires significantly more samples to cover the latent structure of the objective function, confirming that standard BO faces theoretical bottlenecks when $D>20$ without dimensionality reduction techniques.

In summary, the scalability analysis confirms that the BEO-CVaR framework is highly effective for systems with 2 to 10 inverters, consistently ensuring robust voltage regulation under a strict risk-aversion setting. The results clearly demonstrate that the method’s performance is subject to the curse of dimensionality, as evidenced by the non-monotonic trend in violation rates. The optimal performance at 5 inverters suggests a practical limit for the current setup under the given computational budget.

Nevertheless, it is crucial to emphasize that, even in the challenging 10-inverter case, the framework maintains a remarkably low violation rate (0.1007%), which drastically outperforms traditional decentralized methods (as shown in Table 5). This demonstrates that BEO-CVaR possesses significant robustness to the degradation effects of high dimensionality, making it a practical and powerful solution for real-world distribution grids. Future work will address the identified curse of dimensionality by incorporating high-dimensional BEO techniques. Potential strategies include using additive GPs (which decompose the objective function into lower-dimensional sub-problems) or embedding the search space into a lower-dimensional manifold (e.g., via random embeddings or autoencoders) to further enhance performance in very large-scale systems.

4.7. Quantitative Analysis of Communication Efficiency and Robustness

To evaluate the communication burden, we distinguish between the monitoring uplink (data collection) and the critical control downlink (dispatching commands). While the BEO-CVaR framework maintains a standard 3 min uplink for SCADA data acquisition, it fundamentally decouples voltage stability from real-time control instructions.

4.7.1. Reduction in Mandatory Control Updates

Traditional real-time strategies require continuous dispatching of reactive power setpoints ($Q_{set}$) to handle PV variability. While our simulations evaluate performance against grid dynamics evolving every 5 s, traditional centralized control is often constrained by communication bandwidth and computational latency, typically allowing for a 3 min control cycle. Under this common operational constraint, the number of mandatory control updates for a standard 12 h window is

$$N_{traditional}={\displaystyle \frac{12\times 60\min }{3\min }}=240\mathrm{updates}$$

(22)

In contrast, BEO-CVaR optimizes control rules rather than specific setpoints. Although the communication channel supports frequent data exchange, the necessity of transmitting new decisions is minimized to a single initial update:

$$N_{BEO-CVaR}=1\mathrm{update}$$

(23)

Consequently, the frequency of critical control interventions is reduced by approximately 99.6%. While the monitoring link remains active, the control bandwidth remains effectively idle for the vast majority of operation, significantly lowering the operational burden.

4.7.2. Robustness Against Communication Failures

The most critical advantage is the system’s resilience during outages.

• Traditional Methods (High Real-Time Dependency): A downlink failure causes the loss of crucial 3 min optimal setpoint dispatches ($N_{traditional}$ updates missed). Inverters, unable to receive these updates, must revert to unoptimized fallback modes.
• BEO-CVaR (Asynchronous Robustness): In contrast, BEO-CVaR transmits a robust Volt/VAR curve, enabling local control execution. Even if communication is severed immediately after the single initial update (losing all subsequent monitoring data), inverters autonomously adjust reactive power based on local voltage.

In summary, BEO-CVaR converts communication from a synchronous, critical constraint to an asynchronous support function, greatly enhancing grid resilience.

4.8. Stress Testing Under Extreme Physical Conditions

While the previous sections have validated the scalability and communication robustness, it is equally critical to assess the control generality under complex grid characteristics and off-nominal operating states (e.g., weak grids). To this end, a rigorous stress test was conducted on the IEEE 123-node test feeder by introducing three simultaneous physical constraints that drastically compress the feasible solution space:

• High Impedance (Weak Grid): All line impedances (Z) are scaled by a factor of $2.0$, significantly exacerbating voltage sensitivity to power injections.
• Heavy Loading: The active and reactive load demands are scaled by $1.5$, pushing the system far beyond its nominal operating point.
• Limited Capacity: The reactive power capacity ($Q_{max}$) of all inverters is reduced to $50\%$ of the nominal value.

Furthermore, the high-impedance (weak grid) scenario serves as a scenario-based sensitivity analysis regarding the linearization assumption used in Section 2. Since linearization errors typically increase with grid impedance, the robust performance observed in this scenario validates that the stability constraints derived from the linear model remain effective even when the grid characteristics challenge the modeling assumptions.

Despite the severe degradation of the physical environment, statistical analysis across 10 independent experiments confirms that the BEO-CVaR framework maintains extremely high robustness. For the vast majority of time steps, nodal voltages were effectively maintained confined within safety bounds (0.95–1.05 p.u.), with the Voltage Violation Rate limited to $1.722\%$ and an average voltage deviation of $0.145$ p.u.

Figure 21 presents the results of the most representative trial among these 10 experiments, revealing the control mechanism under limit states in detail:

• Voltage Profile (Top Panel): It can be observed that, despite severe physical constraints, the vast majority of voltage curves remain within the safety band. Only during the middle period with the most intense PV and load fluctuations (approximately scenarios 3500 to 7500) did a few specific nodes exhibit voltage violations.
• Inverter Response (Bottom Panel): The bottom panel clearly explains the cause of these violations. During the violation periods, both the large-capacity Inverter 1 (orange line) and the small-capacity Inverter 2 (green line) demonstrated coordinated stress response behavior; both reached and sustained their physical output lower limits (saturation state) for extended periods.

This phenomenon indicates that the rare voltage violations do not stem from the algorithm’s failure to find an optimal solution, but rather that the algorithm accurately identified the risk and commanded all inverters to release their full available capacity. The residual violations can thus be attributed to the physical scarcity of hardware regulation resources. This result robustly proves that, even on the verge of physical infeasibility, BEO-CVaR can maximize the utilization of existing resources to maintain system stability through “best-effort” saturation control.

5. Conclusions

This paper presents BEO-CVaR, a robust data-driven framework for optimizing Volt/VAR control rules in distribution grids with high DER penetration. The key innovations are the integration of CVaR for risk-averse optimization against severe uncertainty-driven voltage deviation and the use of BEO for efficient global optimization of the non-convex, computation-heavy CVaR objective. BEO-CVaR dynamically tailors control parameters by learning grid behavior through GP regression and strategically exploring the parameter space via BEO.

Experimental results on the IEEE 123-node test system confirm that BEO-CVaR achieves the following:

• Ensures Robust Voltage Stability: Maintains voltage deviation within strict safety limits under diverse uncertainty scenarios, achieving near-perfect voltage compliance across standard and high-risk tested conditions.
• Mitigates Extreme Risks: Explicitly minimizes the impact of worst-case uncertainty realizations through CVaR, enhancing grid resilience.
• Reduces Operational Burden: The framework requires only infrequent updates of decision variables (once every 12 h), reducing the critical control downlink frequency by 99.3% compared to standard 3 min real-time control cycles. This significantly lowers the communication overhead and ensures high robustness against communication outages.
• Outperforms Comparative Baselines: Significantly improves voltage profiles compared to traditional decentralized strategies and achieves superior sample efficiency and risk control compared to the meta-heuristic benchmark (i.e., PSO).

In an evolving energy landscape with increasing renewable integration, BEO-CVaR provides a practical and risk-aware solution for optimizing voltage control and enhancing grid stability.