Abstract
In order to achieve precise vector control of permanent magnet synchronous motors and maintain reliability during operation, it is necessary to obtain more accurate rotor position and rotor angular velocity. However, the installation of sensors can lead to increased motor volume and cost, so it is necessary to use sensorless estimation of rotor position and angular velocity. The switching function of traditional sliding mode observers is a discontinuous sign function, which can lead to serious chattering problems and phase lag problems caused by low-pass filters. Therefore, this article proposes an improved fuzzy hyper spiral sliding mode observer based on the traditional sliding mode observer. Firstly, the observer takes the current as the observation object and uses the difference between the actual current and the observed current and its derivative as the fuzzy input. The sliding mode gain is used as the fuzzy output to tune the parameters of the sliding mode gain. Secondly, in response to the chattering problem caused by traditional sliding mode control methods, the hyper spiral algorithm is adopted and a ) nonlinear function is introduced instead of the sign function as the switching function to achieve switch continuous sliding mode control, thereby suppressing the system’s chattering. Finally, the rotor position information is extracted through an orthogonal normalized phase-locked loop to improve observation accuracy. For time-varying nonlinear permanent magnet synchronous motor control systems, fractional order PID can improve the control accuracy of the system and adjust the dynamic performance of the system more quickly compared to traditional PID control algorithms. Therefore, fractional order PID is used instead of traditional PID controllers. By comparing simulation experiments with traditional sliding mode observers and fuzzy improved adaptive sliding mode observers, it was proven that the improved fuzzy super spiral sliding mode observer can effectively suppress chattering and extract rotor position with higher accuracy, a faster response rate, and better dynamic performance. This provides a new approach for the sensorless control strategy of permanent magnet synchronous motors.
1. Introduction
Permanent Magnet Synchronous Machines are extensively utilized in aerospace, intelligent vehicles, and engineering equipment owing to their compact structure, high efficiency, superior power factor, and rapid dynamic response [1,2,3,4]. Consequently, stringent demands are placed on their control performance. Sensorless control technology for PMSMs offers advantages such as reduced algorithm complexity, faster dynamic response, enhanced control precision, and lower costs compared to sensor-based control methods. In recent years, control strategies like sliding mode control (SMC) and adaptive control have gained significant attention for addressing issues such as system chattering, limited robustness, and parameter perturbations associated with sensorless control algorithms [5,6,7].
Among various sensorless control techniques, the sliding mode control algorithm stands out for its rapid response, low sensitivity to internal parameter disturbances, and excellent dynamic performance [8,9,10]. The sliding mode observer (SMO), designed based on SMC, has attracted considerable interest from researchers. However, traditional SMO systems often suffer from reduced control accuracy, increased chattering, and degraded dynamic response due to the use of discontinuous switching functions and inappropriate selection of reaching laws [11,12]. According to the Lyapunov stability theorem, the stability condition for conventional SMOs requires the sliding mode gain to exceed the maximum back electromotive force (EMF) [13,14]. Since the back EMF of PMSMs is proportional to the motor speed during constant flux speed regulation, the fixed sliding mode gain in traditional SMOs is unsuitable for low-speed operations with wide speed ranges. Additionally, the discontinuous sign function in traditional SMOs introduces high-frequency oscillations and position estimation errors [15], necessitating further research to address these limitations.
The sliding mode observer proposed in reference [16] introduces a low-pass filter and estimates the angular velocity and speed position through an inverse tangent function. Although this method is easy to calculate and implement, it may have the following effects: (1) The introduction of this method can cause phase lag, resulting in deviations between the observed rotor position and speed signals and the actual values. (2) Low-pass filters attenuate signal amplitude, resulting in significant rotor position errors. (3) Their switching function is a discontinuous sign function, leading to severe high-frequency jitter. In order to address the problem of high-frequency chattering caused by switching functions, the sliding mode observer based on a new smooth continuous function proposed in reference [17] replaces the sign function with a continuous switching function and adds angle compensation to reduce the rotor position error. Even though this method is easy to implement and can effectively reduce high-frequency chattering phenomena, the use of arctangent function to extract rotor position information amplifies noise at low speeds, leading to rotor position jitter, and the arctangent function is sensitive to harmonics, resulting in periodic fluctuations in the calculated position. In response to the above issues, based on the smooth continuous function used in reference [17], reference [18] proposes a method combined with phase-locked loop. Although this method can improve the accuracy of extracting rotor position and the dynamic performance of the system to a certain extent, it will increase the complexity of the system, and temperature drift will also cause estimation errors in the phase-locked loop. Reference [19] proposed a non-singular terminal sliding mode control strategy, based on which the observer can achieve convergence of state variables in a finite time and effectively suppress chattering to improve the tracking effect of position information. However, the sliding mode gain in reference [19] is set based on human experience, and in reality, the parameters of the motor change in real-time with the speed. The selection of sliding mode gain in this strategy has randomness and limitations. Reference [20] adopts a super spiral sliding mode observer and a dual sliding mode control system, which not only weakens chattering and improves response speed, but also improves the accuracy and robustness of rotor position observation. However, its parameter tuning is too complex and the computational complexity is too large, which is not conducive to its application in engineering practice. Reference [21] proposed a full order sliding mode observer using current back electromotive force as the observation object. The sliding mode observer designed by this method has the characteristics of a low-pass filter, which can filter out high-order harmonics and effectively suppress chattering. However, the fixed sliding mode gain and discontinuity of the switching function may also result in high-frequency chattering. Reference [22] adopted fuzzy control algorithm, combining fuzzy control with sliding mode observer, effectively adjusting sliding mode gain, achieving parameter tuning and adaptability, but affecting the control accuracy and dynamic performance of speed.
In order to solve the above problems, this paper proposes an improved fuzzy hyper spiral sliding mode observer based on fractional order PI. A fractional order PI controller is introduced in the speed loop to reduce high-frequency chattering phenomenon and improve speed control accuracy and dynamic response characteristics by utilizing the slow energy transfer characteristic of fractional calculus in engineering practice. In order to compensate for the large rotor position error and insufficient estimation accuracy, a hyper spiral control algorithm is proposed. The fuzzy control method is used to tune the parameters of the sliding mode fixed gain problem. A new switching function, , is introduced into the hyper spiral sliding mode observer to further reduce system chattering and improve control accuracy. This article first establishes the mathematical model of PMSM. Secondly, a sliding mode observer was designed and a new switching function, , was used to replace the traditional sign function. The stability conditions of the sliding mode observer were obtained through Lyapunov stability analysis. Then, a fuzzy controller that can adaptively adjust the sliding mode gain was designed. Then, a super spiral sliding mode observer was designed to incorporate a novel switching function, and the sliding mode gain is adjusted through a fuzzy controller for parameter tuning. Then, by normalizing the orthogonal phase-locked loop to calculate the position information, this method further improves the accuracy of rotor position estimation. Finally, a fractional order PI controller is designed in the speed loop to improve the accuracy of speed control and dynamic response characteristics. Through experimental comparison, it can be concluded that compared with traditional sliding mode observers and improved fuzzy adaptive sliding mode observers, the improved fuzzy hyper spiral sliding mode observer based on fractional order PI controller designed in this paper has the advantages of high control accuracy and fast dynamic response.
2. Mathematical Model of Permanent Magnet Synchronous Motor
The permanent magnet synchronous motor is a surface mounted permanent magnet synchronous motor (). And as an idealized model, the mathematical model of PMSM in a two-phase stationary coordinate system is as follows:
In the above equation, represent the stator currents of the and axes, respectively; extended back electromotive force in a two-phase stationary coordinate system; stator phase resistance; and phase inductance, of which the following occurs:
In the above equation, separate the permanent magnet magnetic flux; rotor electrical angular velocity; and rotor electrical angle.
Further transforming (1) can obtain the equation of state for current
For the IPMSM voltage equation and torque equation, the motion equation is as follows:
In the above equation, are inductors on the d-q axis.
The electromagnetic torque equation is as follows:
The equation of motion is as follows:
In the above equation, is the moment of inertia; is the mechanical angular velocity; is the load torque; and is the damping coefficient.
3. Design of Improved Fuzzy Sliding Mode Observer
3.1. Mathematical Model of New Sliding Mode Observer
According to Equations (2) and (3), the state equation of the new sliding mode observer with two-phase current and back electromotive force in two-phase stationary coordinate system as observation objects is as follows:
In the above equation, represent the stator currents of the and axes, respectively; extended back electromotive force in two stationary coordinate systems; stator phase resistance; phase inductance; and rotor electrical angular velocity.
The further improved sliding mode observer is as follows:
In the above equation, are the switching gain for the sliding mode observer.
In the equation, and are the switching gains of the sliding mode observer.
3.2. Design of Novel Sliding Mode Observer Based on Sin (Arctan(nx)) Function
In order to overcome the chattering caused by the discontinuity of traditional sign functions as switch functions at the origin, this paper designs a function with smooth continuity near the far point to replace the traditional sign function. Its expression is as follows, The function graph is shown in the Figure 1:
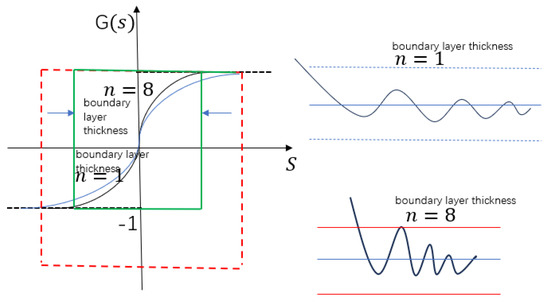
Figure 1.
New switching function.
In the above equation, is to adjust the boundary layer thickness coefficient. This function has a continuous characteristic at the origin, which can effectively suppress the generation of chattering, and the slope of this function is larger near the far point, which can make the system have a faster response rate. When s is large enough, the function always approaches 1.
When the velocity error is minimal, reducing the boundary layer thickness coefficient is recommended. For instance, setting it to 8 can narrow the boundary layer, thereby lowering both the amplitude and frequency of chattering. This adjustment helps the current error converge toward the sliding surface, effectively suppressing system chattering. On the other hand, when the velocity error is substantial, increasing the boundary layer thickness coefficient is advantageous. A thicker boundary layer raises the frequency of crossing the sliding surface, which diminishes the chattering amplitude. Additionally, as the current error approaches the sliding surface with increasing speed, the chattering effect is further alleviated. By dynamically adjusting the boundary layer thickness coefficient based on the velocity error, the system can achieve faster error convergence to the sliding surface, significantly reducing chattering. Table 1 compares the mathematical properties of with other switching functions.

Table 1.
Mathematical properties and comparison.
In addition, has a smoother slope near the origin (compared to ), which can further reduce high-frequency switching. Compared to sigmoid, which involves exponential operations, this function only requires trigonometric operations, making it more suitable for embedded real-time systems.
When is used as the switching function, the improved sliding mode observer state equation is as follows:
In the above equation:
Subtract Equation (7) from Equation (10) to obtain the error state equation of current and back electromotive force:
In the above equation:
According to Laplace transform, Equation (10) can be used to obtain:
By substituting (15) into (14), we can obtain:
Organizing can lead to the following:
Further organizing Equation (13) yields:
By combining Equations (14) and (15), we can obtain:
In the equation, is the Laplacian operator.
From Equation (19), it can be seen that the back electromotive force at this time has the characteristics of a second-order low-pass filter, which can filter out high-order harmonics. Therefore, there is no need to add an additional low-pass filter, which can avoid the phase delay and amplitude attenuation caused by the low-pass filter and effectively improve the accuracy of estimating the rotor position.
3.3. Stability Analysis
According to Lyapunov’s stability theorem, when , the sliding mode observer system is stable, assuming that the sliding surface of the current is . Construct Lyapunov function:
In the equation, , and γ is the adaptive gain.
According to the Lyapunov stability theorem, as long as , to ensure system stability, take the derivative of Equation (20):
Accordingly, :
Substitute Equation (3) into Equation (22):
In the equation, , is the estimation error of the back electromotive force; the uncertainty of the parameters in the .
Similarly, the expression for can be obtained:
The estimation error of back electromotive force is as follows:
In the equation, .
Substitute Equations (23)–(25) into Equation (21):
The property of switching function :
- (1)
- The boundedness of functions: (that is because ).
- (2)
- The monotonicity of functions: take the derivative of :
It can be seen that is strictly monotonic.
- (3)
- Can be approximated:
When , .
When , (linearization).
Using its properties for inequality scaling, utilizing its properties
, when .
Design a sufficiently large gain to meet:
The following can be obtained:
Design speed adaptive law:
According to Lyapunov’s second stability theorem, the designed observer is asymptotically stable, and the speed error is also asymptotically stable.
For the back electromotive force, let the sliding surface of the back electromotive force be . The selected Lyapunov function is as follows:
By taking the derivative of Equation (31), we can obtain:
By substituting Equation (25) into Equation (32) and organizing it, we can obtain:
Further simplification can lead to the following:
To ensure , it is necessary to utilize the following:
From Equation (33), it can be seen that needs to be sufficiently large to cancel out the interference of .
So should:
Similarly, for :
Comprehensively obtained:
When satisfies the above conditions, the system stability error is bounded.
3.4. Design of Fuzzy Controller
According to the constraint of , the sliding mode gain needs to be designed large enough to meet the stability condition. In general, the sliding mode gain is a fixed value designed based on the designer’s experience, but the current error varies with time. If an inappropriate sliding mode gain is selected, the chattering phenomenon will become more severe. So, it is necessary to dynamically adjust the gain to adapt to different states of the system. This article adopts fuzzy control to dynamically adjust the sliding mode gain of the current sliding surface, improving the convergence speed and suppressing the generation of chattering while ensuring stability.
The input of the fuzzy controller is the error of the current and the derivative of the current error. The output variable is the sliding mode gain factor . Thus, achieving adaptive adjustment of sliding mode gain. Equal , the sliding mode gain factor should be reduced, which will make the state smoother when crossing the sliding mode surface, thereby weakening the system’s chattering. When , the sliding mode gain factor should be increased to enable the state to reach the sliding mode surface more quickly. According to the analysis above, the optimized sliding mode gain factor is as follows:
In the above equation, is the observed angular velocity of the motor; is the back electromotive force coefficient of the motor; and is the back electromotive force coefficient of the motor.
When the motor’s observed angular velocity falls below the critical threshold, the sliding mode factor K output by the fuzzy controller is set to . Conversely, when the angular velocity meets or exceeds the critical value, the sliding mode gain factor K is dynamically adjusted in accordance with fuzzy rules. The schematic diagram of the improved fuzzy sliding mode observer is illustrated in Figure 2.
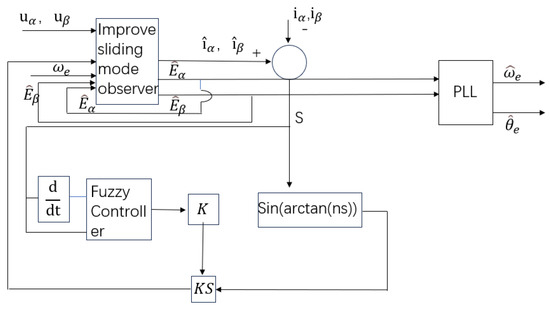
Figure 2.
Schematic diagram of improved fuzzy sliding mode observer.
The domain of the input variables of the fuzzy controller is [−1, 1]. The domain of the output variable is [0, 1], and the fuzzy languages of the input variables are {positive large (PB), positive medium (PM), positive small (PS), zero (ZO), negative large (NB), negative medium (NM), negative small (NS)}. The fuzzy languages for output variables are {Greater Big (PB), Medium Small (PS), Zero (ZO)}. Under the condition of satisfying (14), the fuzzy rule table involved is shown in Table 2.

Table 2.
Fuzzy control rules.
The input and output functions both use triangular membership functions, and the membership degree of the input and output functions of the fuzzy controller are shown in Figure 3.
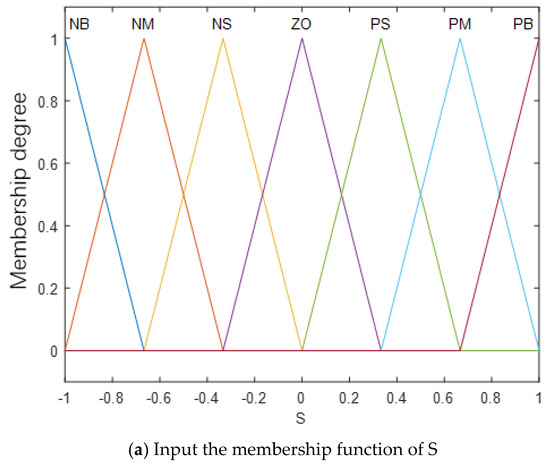
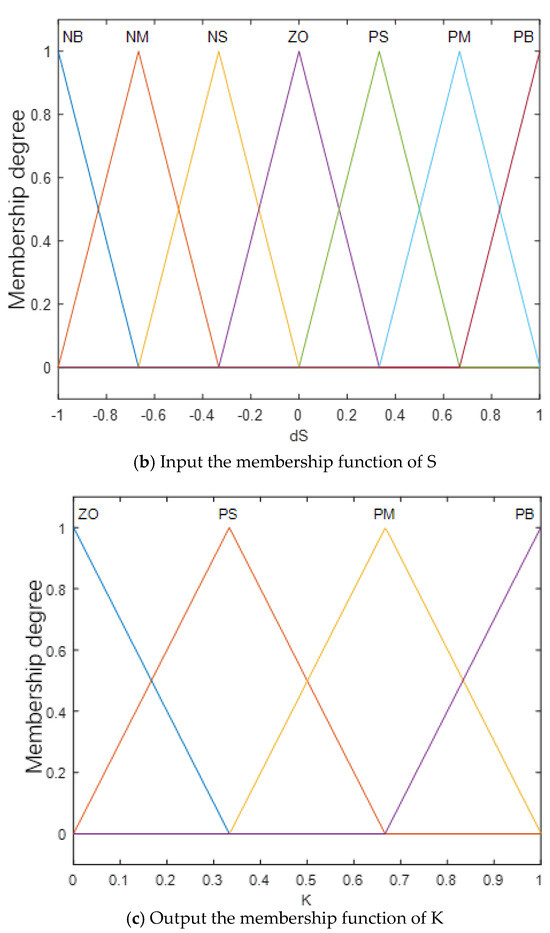
Figure 3.
Membership function diagram of input and output of fuzzy controller.
The improved fuzzy adaptive sliding mode observer proposed in this article has the following advantages compared to traditional fuzzy sliding mode observers:
In terms of academic contributions:
A Stability enhancement:
The fixed gain or empirical fuzzy rules of traditional methods may lead to high-frequency oscillations near the sliding surface, affecting the stability of the system. The improved fuzzy adaptive sliding mode observer designed in this article adjusts the gain K through fuzzy logic. When , is reduced to suppress chattering, and when , is increased to accelerate convergence. Combined with Lyapunov theory (stability has been proven in the article), the system can ensure global stability under adaptive gain.
B Speed optimization:
The traditional method of sliding mode gain requires balancing speed and chattering, resulting in slow response at low speeds or large overshoot at high speeds. The improved fuzzy adaptive sliding mode observer designed in the text has segmented the adjustment of angular velocity (where takes and achieves adaptive adjustment), which can achieve full speed domain adaptive adjustment. In addition, the output domain of the design is more streamlined, further enhancing the dynamic response.
C Robustness improvement:
Traditional methods are sensitive to parameter perturbations (changes in the back electromotive force coefficient ). The controller in this article adjusts in a timely manner based on current error and its derivative, automatically compensating for load disturbances and parameter uncertainties.
In terms of actual contributions:
A Improving computational efficiency:
The traditional method of establishing a high-dimensional fuzzy rule library in the input–output domain increases the computational burden. The method designed in this article simplifies the domain language variables and reduces the number of rules. The proposal of segmented gain formula further reduces online computational complexity.
B Vibration suppression:
Traditional methods rely on fixed boundary filtering, which leads to a decrease in tracking accuracy. The fuzzy logic in the method designed in this article adjusts K smoothly based on the distance of the image, significantly reducing vibration.
C Usability:
Traditional methods require manual parameter tuning. The adaptive mechanism of the method designed in this article reduces human involvement ( and can be initialized through motor parameters).
Although the performance of the proposed fuzzy adaptive sliding mode observer in stability and chattering suppression is still limited by empirical fuzzy rules and segmented gain fixed thresholds due to traditional methods, in order to further improve observation accuracy and suppress chattering, it is necessary to introduce a higher-order sliding mode algorithm called the super spiral sliding mode algorithm. However, fixed gain cannot meet the requirements of the motor under all operating conditions. Therefore, this paper proposes an improved fuzzy super spiral algorithm that adjusts the global optimal observation through dynamic gain adjustment.
3.5. Fuzzy Improved Hyper Spiral Sliding Mode Observer
The traditional hyper spiral algorithm equation is as follows:
In the equation, are state variables, are the differences between the actual and estimated values, are both greater than 0, which is the sliding mode gain, and are disturbance terms. is a sign function.
According to the mathematical model of PMSM, the sliding mode control theory of hyper spiral algorithm, and the current observer of the new switching function PMSM can be calculated as follows:
In the above equation, “”, “-” represent estimated values separately; the difference between the estimated value and the actual value.
Moreno et al. [23] demonstrated the stability condition of the hyper spiral sliding mode observer, where the sliding mode coefficient should satisfy the following:
The disturbance term should satisfy the following:
where is a positive number.
Furthermore, when reach the sliding surface, the estimated back electromotive force of the improved hyper spiral sliding mode observer is as follows:
3.6. Sliding Mode Gain Fuzzy Design
Fuzzy parameter tuning enables adaptive adjustment of the sliding mode gain according to the system’s operating state. Compared to traditional control methods, fuzzy control simplifies the design process of the system controller, reduces complexity, and ensures system stability to a certain extent. Therefore, fuzzy control is integrated into the improved super-twisting sliding mode observer. The control principle diagram of the improved super-twisting sliding mode observer is illustrated in Figure 4.
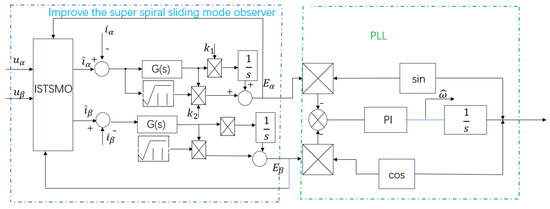
Figure 4.
Schematic diagram based on improved super spiral sliding mode observer.
Due to the fact that the traditional sliding mode gain is fixed and too large or too small can affect the stability of the system, it is necessary to set reasonable sliding mode parameters. Fuzzy control has good nonlinear adaptability and robustness, so this paper adopts fuzzy control for parameter tuning.
The input of the fuzzy controller is the error S and the derivative S ∴ of the error, and the domain is set to be the same as in the previous text. The sliding mode gain is used as the output, and its domain is set to be the same as in the previous text. The fuzzy language and control rules are shown in Table 2. The triangular membership function is used for fuzzification, and the centroid method is used for deblurring.
The conventional sliding mode observer, when combined with a low-pass filter, often introduces phase lag and amplitude attenuation. Additionally, extracting rotor position information through inverse tangent operations tends to generate noise. To address these issues, this paper employs an orthogonal normalized phase-locked loop (PLL) for calculation. PLL technology operates as a feedback system capable of maintaining frequency synchronization with the input signal, ensuring accurate frequency tracking of the output signal. The working principle of the phase-locked loop is depicted in Figure 5.
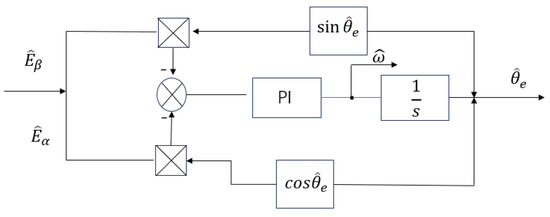
Figure 5.
Principle block of phase-locked loop.
4. Design of Fractional Order PID Controller
4.1. Fractional Calculus Theory
Fractional calculus is different from integer calculus in that it has a wider range of adjustability and introduces the slow energy transfer characteristic of fractional calculus into engineering practice, which can weaken the chattering problem caused by nonlinear control methods. So far, there are multiple definitions for fractional calculus, with the most commonly used being the R-L definition, which is as follows:
In the above equation, are differential operators; , are the upper and lower limits of the differential operator, where n is the order of the fractional order and ; and is the Gamma function.
The PMSM stator voltage equation is as follows:
In the above equation, are the stator voltages of the d and q axes, respectively. are the d and q axis currents, respectively. are the and axis inductors, respectively. is the flux linkage.
The motion equation of PMSM is as follows:
In the above equation, is the moment of inertia; is the moment of inertia; is the moment of inertia; is the electromagnetic torque; is the load torque; and is the number of pole pairs.
4.2. Controller Design
The fractional PID controller extends traditional PID control into the fractional order domain. By adjusting the parameters of fractional order differentiation and integration, it enables more precise tuning of the system’s dynamic response. The fractional order integration and differentiation terms offer a broader and more flexible adjustment range, making fractional PID particularly suitable for complex nonlinear systems like permanent magnet synchronous motors. Additionally, fractional PID enhances system robustness and anti-interference capabilities through its fractional order integral and derivative adjustments. It can also improve system response speed, reduce steady-state error, and minimize overshoot. In summary, fractional PID outperforms traditional PID controllers in dynamic performance and is better suited for complex, nonlinear systems. Therefore, fractional PID is employed for speed loop control.
The transfer function of fractional order PID is as follows:
In the above equation, , , are the proportional, integral, and derivative parameters, respectively; are the proportional, integral, and derivative parameters, respectively; is generally [0, 1]. We can obtain a discrete form of fractional order PID controller similar to incremental PID controller, whose discrete expression is as follows:
In the above equation, is an integer with a number of operations greater than or equal to 3; .
The time-domain equation corresponding to fractional order PID is as follows:
In the above equation, are the approximate integral order and differential order operators defined by G-L, expressed as follows:
In the above equation, is the forensic operation factor, and h is the calculation step size. The smaller the value, the higher the accuracy. is the quadratic coefficient of the function .
4.3. Parameter Tuning
The performance of high-precision motion control systems is highly dependent on the tuning quality of controller parameters. This paper uses an online parameter tuning method based on fuzzy inference, which dynamically adjusts the sliding mode gain K to suppress chattering and improve the accuracy of rotor position estimation. By adjusting various parameters in fractional order PID, the fast response of speed can be achieved, and the control accuracy of speed can be improved. The following are the specific steps for parameter tuning.
For improving the fuzzy adaptive sliding mode gain parameters: ① Fixed mechanical parameters. Calibrate and , where is measured through motor data manuals or experiments, and can generally be set to 10–30% of the rated speed. ② Initialize the gain of the sliding mode observer. Assuming , achieve real-time updates of observation error convergence through fuzzy rules. Adjust fuzzy rules. Fixed input membership function, adjust output gain rules. Compared with traditional fixed gain sliding mode observers that require repeated trial and error parameter tuning, the proposed method converts manual parameter tuning into linguistic variable design through fuzzy rules, reducing dependence on precise parameters. Table 3 summarizes the tuning methods for the above parameters.

Table 3.
Parameter tuning method.
The tuning method for fractional order PID is as follows:
- (1)
- Initialize PID parameters. First, use traditional methods to tune , , as a fundamental value.
- (2)
- Introduce fractional order , . For integral order , if the system requires a softer integration effect (such as eliminating overshoot), let . To quickly eliminate static errors, take (close to traditional integration). Differential order , if the system is sensitive to high-frequency noise, let to smooth the differential action. If damping is required to suppress oscillation, take .
- (3)
- Fine tune the gain parameters. After fixing and , readjust . Increasing accelerates the response, but may cause overshoot. Increasing reduces stability error, but may decrease stability. Increase , suppress oscillations, and amplify noise effects.
For the above tuning parameters, : Take 80–120% of traditional PID. : If decreases, it is necessary to increase appropriately to compensate for the weakening of the integral.: If decreases, it is necessary to increase to maintain the damping effect.
The fractional order PID parameters selected in this article are ; ; ; ; .
5. Simulation and Result Analysis
This article uses Matlab/Simulink R2018b software to build a simulation model based on an improved fuzzy sliding mode observer. The sensorless control block diagram of the improved fuzzy hyper spiral sliding mode observer based on fractional order PI is shown in Figure 6. The parameters of the motor are shown in Table 4. This article will conduct simulation experiments comparing three control algorithms for sudden load changes in the full speed domain under acceleration and deceleration states. Key performance indicators such as speed waveform, speed error, rotor position error, and rotor position estimation waveform will be detected in real-time to evaluate the control performance of the proposed control algorithm.
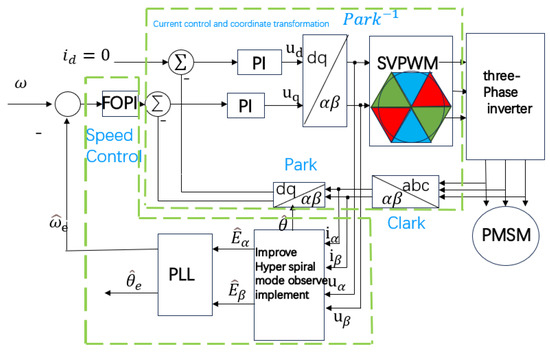
Figure 6.
Improved sensorless control diagram of fuzzy hyper spiral sliding mode observer based on fractional order PI.

Table 4.
Motor parameters.
5.1. Sudden Load Changes During Acceleration
The numerical solver in this article adopts the Bocgacki Shampine fixed step algorithm. The simulation time is set to , and the motor is started under no load with a given speed of . The speed changes abruptly at and , accelerating to and and a load torque of is suddenly applied at , , and , respectively. The simulation results are shown in Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14.
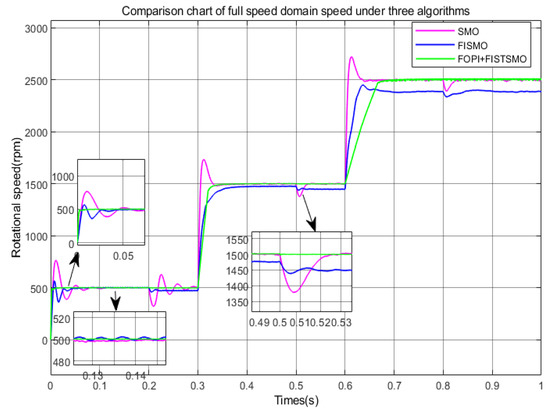
Figure 7.
Comparison chart of full speed domain speed under three algorithms. (Under acceleration conditions).
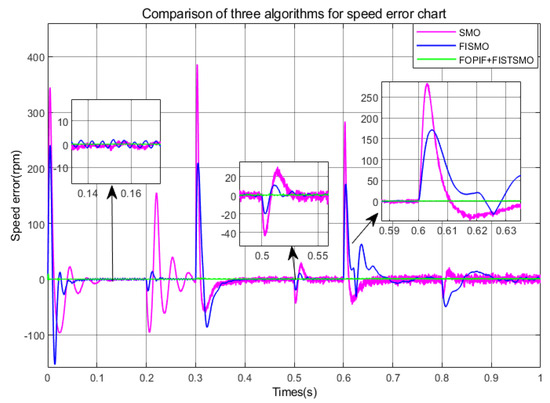
Figure 8.
Comparison of algorithms for speed error chat (Under acceleration conditions).
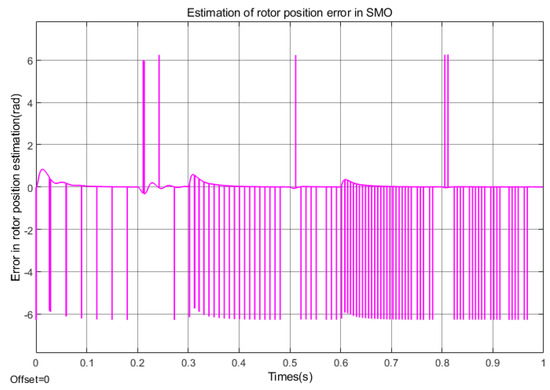
Figure 9.
Estimation of rotor position error in SMO (Under acceleration conditions).
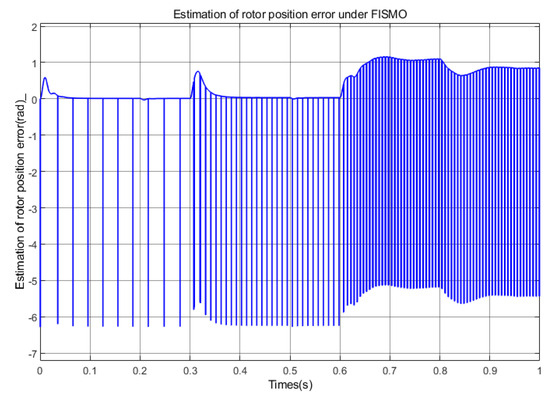
Figure 10.
Estimation of rotor position error under FISMO (Under acceleration conditions).
Figure 11.
FOPI + FISTSMO rotor position error (Under acceleration conditions).
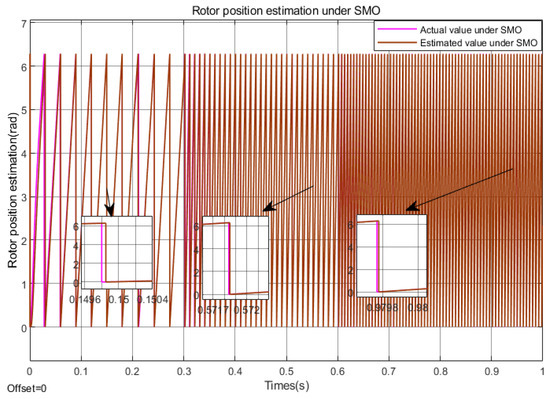
Figure 12.
Rotor position estimation under SMO (Under acceleration conditions).
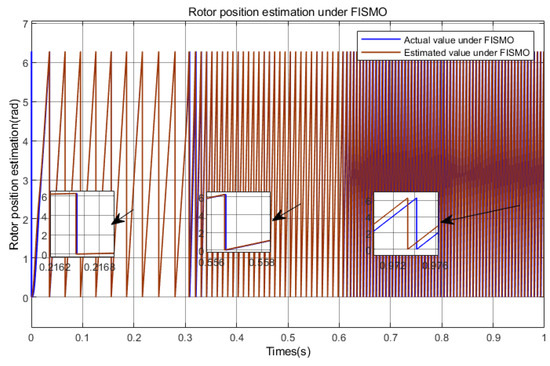
Figure 13.
Rotor position estimation under FISMO (Under acceleration conditions).
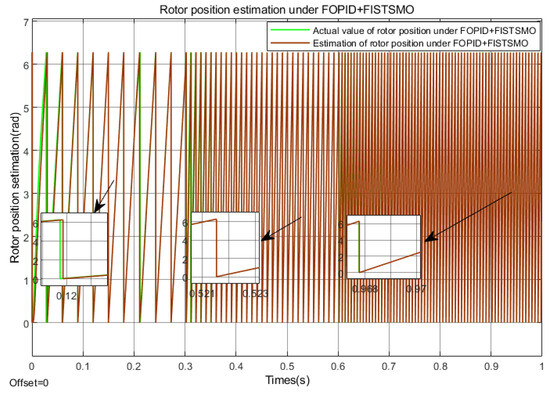
Figure 14.
Rotor position estimation under FOPI + FISTSMO (Under acceleration conditions).
As shown in Figure 7, the improved fuzzy hyper spiral sliding mode observer based on fractional order PI (FOPI + FISTSMO) proposed in this paper has the fastest dynamic response and shortest adjustment time in the low-speed, medium speed, and high-speed domains, with almost no overshoot. Although the speed drops slightly after a sudden load of 5 N·m, it can return to the given speed in almost 0.001 s. It has the best effect in suppressing chattering in the full speed domain, fast dynamic response, high control accuracy, and strong robustness. Compared with traditional sliding mode observers (SMOs), the improved fuzzy adaptive sliding mode observer (FISMO) takes about 0.02 s less to adjust in both the low and medium speed domains. The overshoot of SMO in the low and medium speed domains is about 40% and 16.7%, respectively, while the overshoot of FISMO in the low and medium speed domains is about 2% and 5%, respectively. The overshoot of FISMO in the low and medium speed domains is much smaller than that of SMO, and the effect of suppressing chattering is also better than that of SMO. Under a sudden load torque of 5 N·m in the low and medium speed range, although the speed of FISMO drops, it can recover to the given value in about 0.02 s with minimal fluctuations. Its performance is also better than SMO, but in the high-speed domain, FISMO’s speed tracking effect is not ideal.
The overall performance algorithm efficiency is FOPI + FISTSMO > FISMO > SMO.
As shown in Figure 8, the error of FOPI + FISTSMO proposed in this paper is very small in the full speed domain. After sudden load changes, the fluctuation is also very small, and the control speed accuracy is the highest. At the moment of sudden change in speed, FISMO has speed errors that are 100 rpm, 170 rpm, and 90 rpm smaller than SMO, followed by control speed accuracy; SMO speed error maximum.
According to Figure 12, Figure 13 and Figure 14, the FOPI+FISMO proposed in this paper has good tracking performance in the speed and position within the full speed range, with the smallest tracking error and the best tracking effect. Compared with the other two algorithms, FISMO has the largest error in the high-speed domain, about 0.9 rad, which is about 0.7 rad larger than the other two algorithms.
5.2. Sudden Load Change During Deceleration State
The numerical solver and motor parameters used in this section are the same as those in the previous section. The simulation time is set to , and the motor is set to a given speed of under no-load starting. The speed is suddenly reduced at and , and then slowed down to and At , , and load torque is suddenly applied. The simulation results are shown in Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21 and Figure 22.
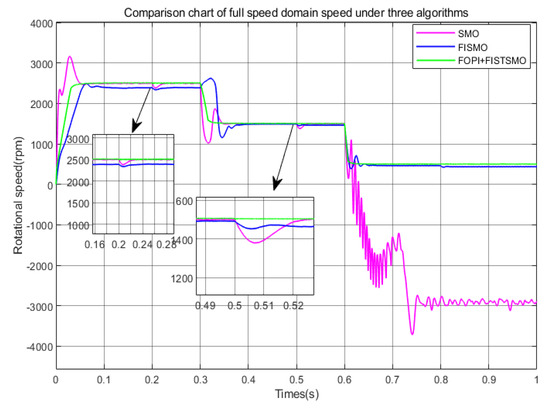
Figure 15.
Comparison chart of full speed domain speed under three algorithms (Under deceleration conditions).
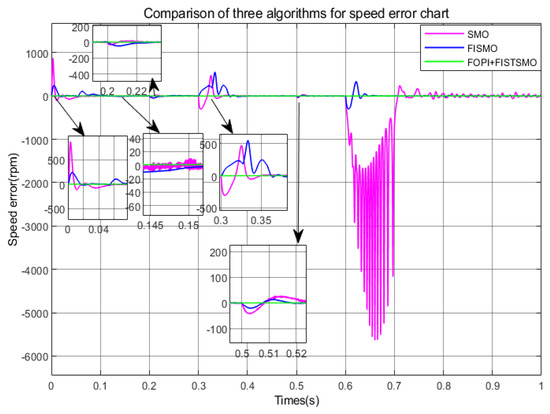
Figure 16.
Comparison of algorithms for speed error chat (Under deceleration conditions).
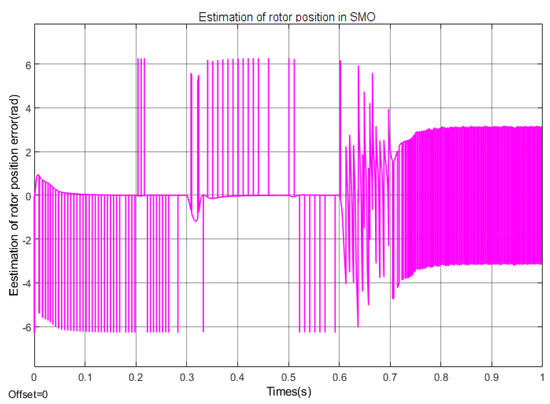
Figure 17.
Estimation of rotor position error in SMO (Under deceleration conditions).
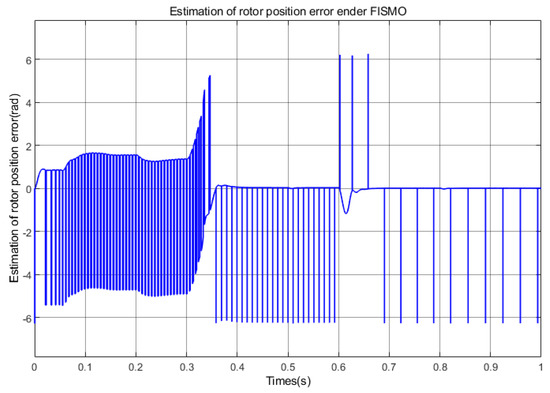
Figure 18.
Estimation of rotor position error under FISMO (Under deceleration conditions).
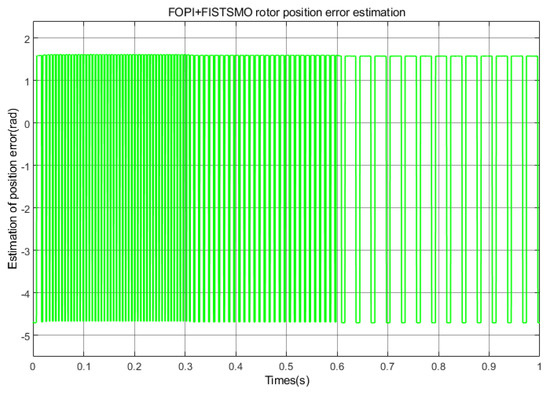
Figure 19.
FOPI + FISTSMO rotor position error estimation (Under deceleration conditions).
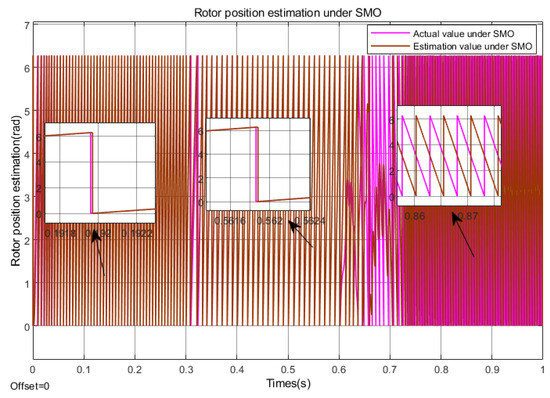
Figure 20.
Rotor position estimation under SMO (Under deceleration conditions).
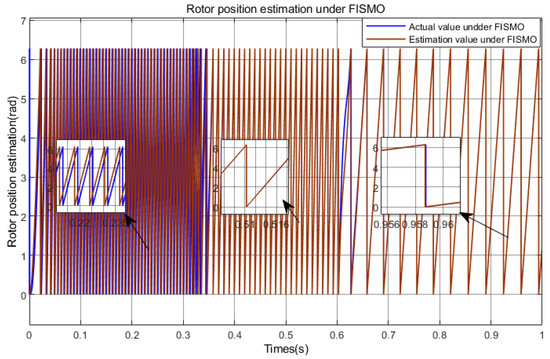
Figure 21.
Rotor position estimation under FISMO (Under deceleration conditions).
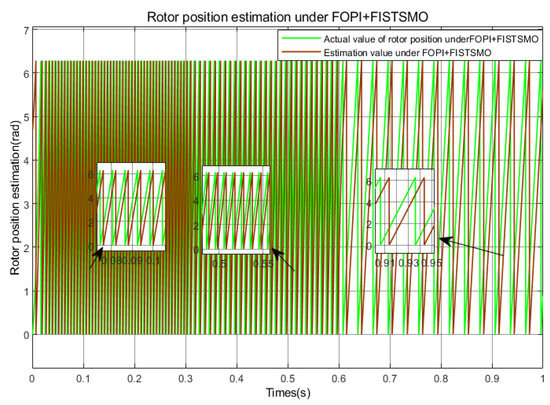
Figure 22.
Rotor position estimation under FOPI + FISTSMO (Under deceleration conditions).
As shown in Figure 15, the FOPI + FISTSMO proposed in this paper has the fastest dynamic response and shortest adjustment time in the low-speed, medium speed, and high-speed domains, with almost no overshoot. Although the speed drops slightly after a sudden load of, it can almost return to the given speed in . It has the best vibration suppression effect in the full speed range, along with fast dynamic response, high control accuracy, and strong robustness. The speed tracking performance of FISMO in the high-speed domain is still not ideal, but its vibration suppression effect is better than SMO. In the high-speed domain, the overshoot of SMO is about 24%, with maximum overshoot. After a sudden load change, FISMO recovers to the given speed faster than SMO and takes less time. In the medium speed domain, at the moment of sudden load changes, FISMO has a significantly faster recovery speed and smaller waveform than SMO. However, in low-speed regions, SMO loses its effectiveness under the interference of high-frequency noise and parameter perturbations; FISMO can maintain its stable state and suppress chattering phenomenon.
As shown in Figure 16, the error of FOPI + FISTSMO proposed in this paper is very small in the full speed domain. After sudden load changes, the fluctuation is also very small, and the control speed accuracy is the highest. At the time of no-load start-up, FISMO is about 700 rpm smaller than SMO, with higher control accuracy and consistently better performance than SMO. In the medium speed range, when the load undergoes a sudden change, FISMO recovers to the given speed faster than SMO, with a smaller waveform. In the low-speed range, due to SMO losing its function under high-frequency noise and parameter perturbations, the maximum error is caused, and the speed control accuracy is poor.
As shown in Figure 17, Figure 18 and Figure 19, SMO has an error of about in the high-speed and medium speed domains and tends to stabilize, while FISMO maintains a maximum error of about in the high-speed domain. Therefore, compared to SMO, SMO has better estimation accuracy in the high-speed domain and FISMO has better estimation accuracy in the medium speed domain. SMO is basically ineffective in the low-speed domain, and the estimation error is the largest. The FOPI + FISTSMO designed in this paper will have a certain estimation error of about in the deceleration state, but it can still stably track.
According to Figure 20, Figure 21 and Figure 22, it can be seen that in the deceleration state, SMO has better tracking accuracy in the high-speed domain; FISMO has poor estimation accuracy in the high-speed domain and the best tracking performance in the medium speed domain; SMO basically loses its tracking function in the low-speed domain, while FOPI + FISTSMO has a certain tracking error, which is smaller than the other two algorithms, but it can still be tracked stably.
5.3. Applicability and Universality Analysis
The simulation results for the surface mounted permanent magnet synchronous motor ( demonstrate that the proposed control strategy meets the design requirements in terms of current tracking accuracy error and dynamic response. However, the built-in permanent magnet synchronous motor (IPMSM,) may introduce reluctance torque and cross coupling effects due to the asymmetry of its orthogonal magnetic circuit, which may significantly affect the closed-loop performance. In order to verify the universality of the algorithm, this section will further analyze the impact of the salient rate () on the system.
Based on the simulation framework model of SPMSM mentioned above, this section adapts to IPMSM operating conditions by modifying the following: keeping all other parameters unchanged, setting the inductance parameter in the motor model to, ; and to analyze the current harmonic distortion and speed error. The simulation results are shown in Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30 and Figure 31.
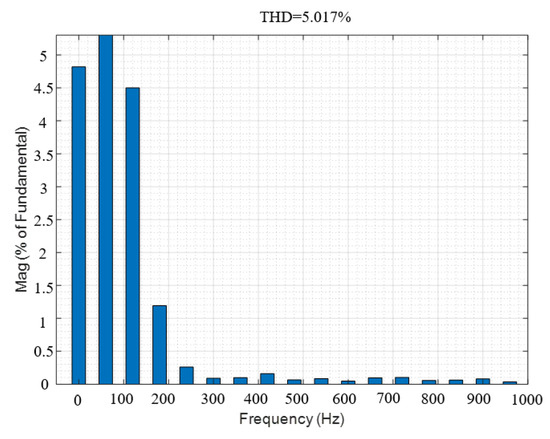
Figure 23.
Current THD with .
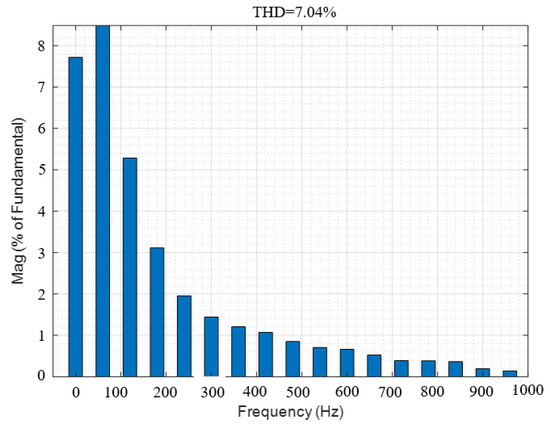
Figure 24.
Current THD with .
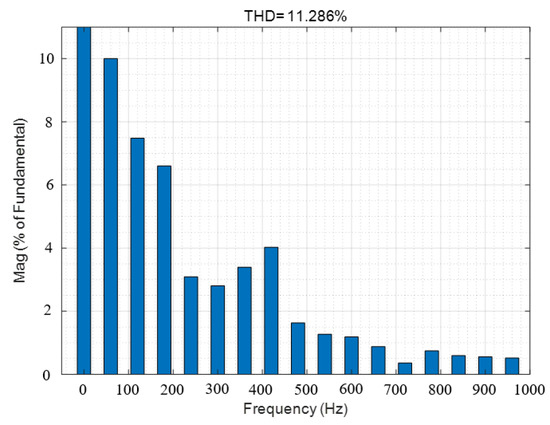
Figure 25.
Current THD with .
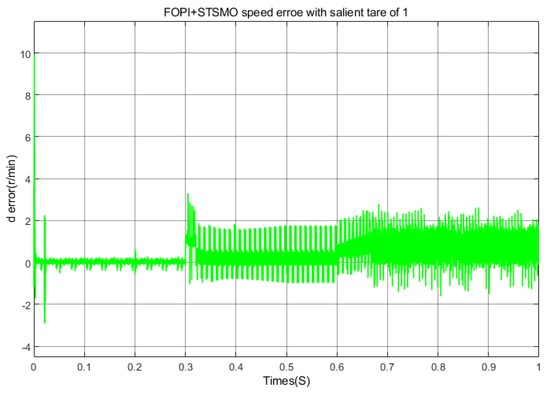
Figure 26.
Speed error in acceleration state with .
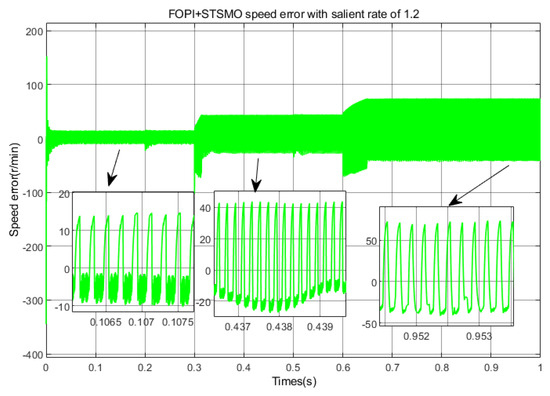
Figure 27.
Speed error in acceleration state with .
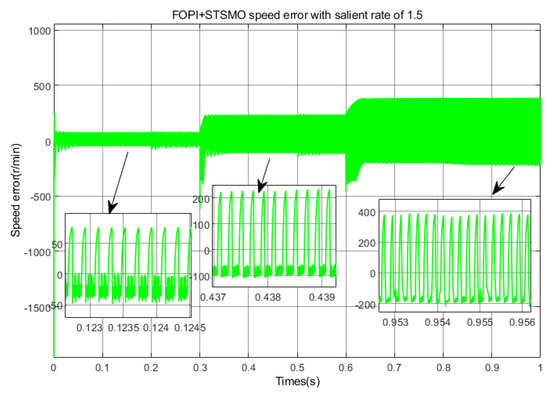
Figure 28.
Speed error in acceleration state with .
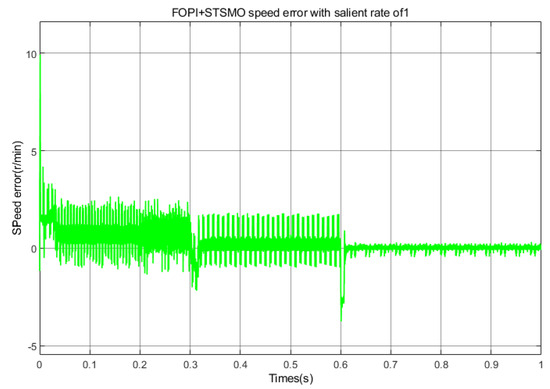
Figure 29.
Speed error in deceleration state with .
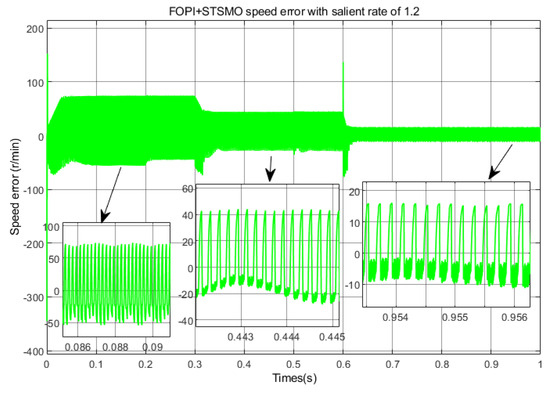
Figure 30.
Speed error in deceleration state with .
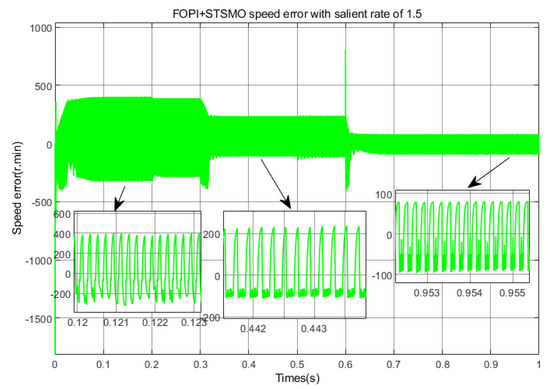
Figure 31.
Speed error in deceleration state with .
Figure 26, Figure 27 andFigure 28 correspond to the speed errors in the full speed range under acceleration states of , , and, respectively. As shown in the figure, when the average speed error of is around 1%, there is almost no error, and the average overshoot is around 1%. When , the average speed error in the full speed range is about 5.7%, and the average overshoot is about 5.72%. When , the average speed error in the full speed range is about 12.4%; the average overshoot is about 12.73%.
Figure 29, Figure 30 and Figure 31 correspond to the full speed domain speed error under deceleration states of ,, and , respectively. As shown in the figure, when , the average speed error and average overshoot are both around 1%. When , the remaining average speed error at full speed is about 4.7%, and the average overshoot is about 4.76%. When , the average speed error in the full speed range is about 12.1%, and the average overshoot is 12.21%.
Figure 23, Figure 24 and Figure 25 correspond to the current THD of , , and , respectively. From the figure, it can be seen that when , the current THD reaches as high as 11.2886%, and the high-order harmonics in the current increase, which will affect the dynamic performance of the system and is not conducive to the steady-state operation of the system.
Therefore, the improved fuzzy hyper spiral sliding mode observer based on fractional order PI proposed in this article is fully applicable under the condition of the salient rate () and has the best control effect and dynamic performance. However, when the salient rate exceeds 1.5, the current THD can reach as high as 11.2886%. An increase in high-order harmonic content will affect the steady-state accuracy of the system. Table 5 shows the relationship between saliency and performance.

Table 5.
Relationship between salient rate and performance.
In summary, the FOPI + FISTSMO proposed in this article is fully applicable under the condition of the salient rate , has good control effects in the full speed range under acceleration and deceleration states, and is the best among the three control effects. It has the best suppression of chattering, fast dynamic response, short adjustment time, small overshoot, strong robustness, and high estimation accuracy. FISMO has poor control performance in the high-speed domain and cannot accurately track in both acceleration and deceleration states, while it has better control performance in the medium and low-speed domains. Although SMO can achieve stable control and good rotor position estimation performance during acceleration, compared to other algorithms, it has the largest overshoot and the worst sliding mode chattering suppression effect. During deceleration, the system’s dynamic changes are severe due to noise interference and parameter perturbations, and the control function is basically lost in the low-speed region, resulting in an unsatisfactory control effect. Table 6 provides a specific summary of the three control methods.

Table 6.
Algorithm comparison.
6. Conclusions
This article takes PMSM as the research object and designs an improved super spiral control algorithm sliding mode observer based on a permanent magnet synchronous motor sensorless control system to address the problems of high-frequency chattering and phase delay in traditional sliding mode observers. Fuzzy control is used to adjust the sliding mode gain parameters to improve the dynamic performance of the system. And by introducing a new function ), orthogonal normalized phase-locked loop, and designing a fractional order PI controller, the overshoot is further reduced and the stability and control accuracy of the system are improved. By introducing a fractional order PI controller and an improved fuzzy hyper spiral sliding mode observer, the rotor position and speed with higher accuracy are obtained. Finally, simulation experiments are compared with the PI controller improved fuzzy adaptive sliding mode observer and traditional PI controller sliding mode observer. The experimental results show that the control strategy proposed in this paper has the fastest dynamic response, high control accuracy, best suppression of chattering effect, and the highest rotor position accuracy in the full speed domain, providing a new idea for sensorless control of permanent magnet synchronous motors.
Author Contributions
Conceptualization, methodology, and writing—original draft, H.J.; formal analysis and investigation, H.J. and X.L.; validation and writing—review and editing, X.F.; supervision and project administration, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge financial support from the Guoneng Shuohuang Railway Project, (SHTL-22-17).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Xiaoqi Fan was employed by the company Guoneng Shuohuang Railway Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Boussak, M. Implementation and experimental investigation of sensorless speed control with initial rotor position estimation for interior permanent magnet synchronous motor drive. IEEE Trans. Power Electron. 2005, 20, 1413–1422. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Khanh, P.Q.; Van Kien, C. Advanced PMSM Machine Parameter Identification Using Modified Jaya Algorithm. In Proceedings of the 2019 International Conference on System Science and Engineering (ICSSE), Dong Hoi, Vietnam, 20–21 July 2019; pp. 445–450. [Google Scholar]
- Termizi, M.S.; Lazi, J.M.; Ibrahim, Z.; Talib, M.H.N.; Aziz, M.J.A.; Ayob, S.M. Sensorless PMSM drives using Extended Kalman Filter (EKF). In Proceedings of the 2017 IEEE Conference on Energy Conversion (CENCON), Kuala Lumpur, Malaysia, 30–31 October 2017; pp. 145–150. [Google Scholar]
- Dai, S.; Wang, J.; Sun, Z.; Chong, E. An Improved Gradient-Based Optimization Algorithm for Synchronous Optimal Modulation of High-Speed PMSM Drives. In Proceedings of the 2021 IEEE International Electric Machines & Drives Conference (IEMDC), Hartford, CT, USA, 17–20 May 2021; pp. 1–8. [Google Scholar]
- Carter, S.R.; Praveen, P.; Varadhan, N.V.; Kowshik, S.; Gopinath, G. Field-Oriented Control (FOC) for Permanent Magnet Synchronous Motors (PMSM) in Electric Vehicle. In Proceedings of the 2023 International Conference on Next Generation Electronics (NEleX), Vellore, India, 14–16 December 2023; pp. 1–5. [Google Scholar]
- Cui, M.; Zhang, C.; Zhu, J. Realization of PMSM adjustable speed system based on sliding mode control. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012; pp. 435–438. [Google Scholar]
- Teymoori, V.; Ghalebani, P.; Kamper, M.J.; Wang, R.-J. Sensorless Adaptive PI Control of High-Power Propulsion PMSM Based on Sliding-mode Extremum Seeking Algorithm. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 5158–5163. [Google Scholar]
- Liu, J. Fuchun Research and Progress on Sliding Mode Variable Structure Control Theory and Its Algorithms. Control. Theory Appl. 2007, 3, 407–418. [Google Scholar]
- Zhao, Y.; Liu, X. Speed Control for PMSM Based on Sliding Mode Control with a Nonlinear Disturbance Observer. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 634–639. [Google Scholar]
- Nicola, M.; Nicola, C.-I. Sensorless Control of PMSM using SMC and Sensor Fault Detection Observer. In Proceedings of the 2021 18th International Multi-Conference on Systems, Signals & Devices (SSD), Monastir, Tunisia, 22–25 March 2021; pp. 518–525. [Google Scholar]
- Bo, Y.; Lu, Q.; Xue, Y.; Zhou, X.; Zhang, G. Research on Adaptive PMSM Control Based on Novel Exponential Reaching Law. In Proceedings of the 2023 10th International Forum on Electrical Engineering and Automation (IFEEA), Nanjing, China, 3–5 November 2023; pp. 932–936. [Google Scholar]
- Xing, X.; Sheng, H. PMSM Sliding Mode Control Based on A New Exponential Reaching Law. In Proceedings of the 2021 3rd International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 10–12 December 2021; pp. 199–203. [Google Scholar]
- Li, J.; Gao, Y.; Wang, L.; Yuan, H. A Sensorless Control System of PMSM Based on LADRC and SMO. In Proceedings of the 2020 International Conference on Artificial Intelligence and Electromechanical Automation (AIEA), Tianjin, China, 26–28 June 2020; pp. 66–71. [Google Scholar]
- Saadaoui, O.; Khlaief, A.; Abassi, M.; Chaari, A.; Boussak, M. Position sensorless vector control of PMSM drives based on SMO. In Proceedings of the 2015 16th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Monastir, Tunisia, 21–23 December 2015; pp. 545–550. [Google Scholar]
- Shi, J.; Liu, J.; Xu, J. Hybrid Position Sensorless Control Based on Estimation Position Error Switching for PMSM in Full Speed Range. In Proceedings of the IECON 2023—49th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 16–19 October 2023; pp. 1–6. [Google Scholar]
- Chu, D. Research on Sensorless Vector Control of Permanent Magnet Synchronous Motor Based on Sliding Mode Observer; Harbin Institute of Technology: Harbin, China, 2015. [Google Scholar]
- Xinyu, S.; Xin, J. Research on position sensorless control of PMSM based on new SMO. In Proceedings of the 2024 39th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Dalian, China, 7–9 June 2024; pp. 1508–1513. [Google Scholar]
- Amina Hasna, T.A.; Vijayasree, G. Sensorless Speed Control of PMSM Based on SMO with Traditional PLL and Tangent Function PLL. In Proceedings of the 2024 IEEE International Conference on Smart Power Control and Renewable Energy (ICSPCRE), Rourkela, India, 19–21 July 2024; pp. 1–5. [Google Scholar]
- Wu, B.; Yuan, Y. Research on PMSM Vector Control Based on Nonsingular Terminal Sliding Mode Observer. In Proceedings of the 2019 IEEE 3rd Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 11–13 October 2019; pp. 1773–1777. [Google Scholar]
- Yan, L.; Mao, Y. Position sensorless control of synchronous reluctance motor based on super spiral sliding mode observer. Softw. Guide 2024, 23, 105–113. [Google Scholar]
- Saadaoui, O.; Khlaief, A.; Abassi, M.; Chaari, A.; Boussak, M. Sensorless FOC of PMSM drives based on full order SMO. In Proceedings of the 2016 17th International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2016; pp. 663–668. [Google Scholar]
- Zhang, X.; Jiang, Q. Research on Sensorless Control of PMSM Based on Fuzzy Sliding Mode Observer. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; pp. 213–218. [Google Scholar]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 2008 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).