Current-Adaptive Control for Efficiency Enhancement in Interleaved Converters for Battery Energy Storage Systems
Abstract
1. Introduction and Motivation
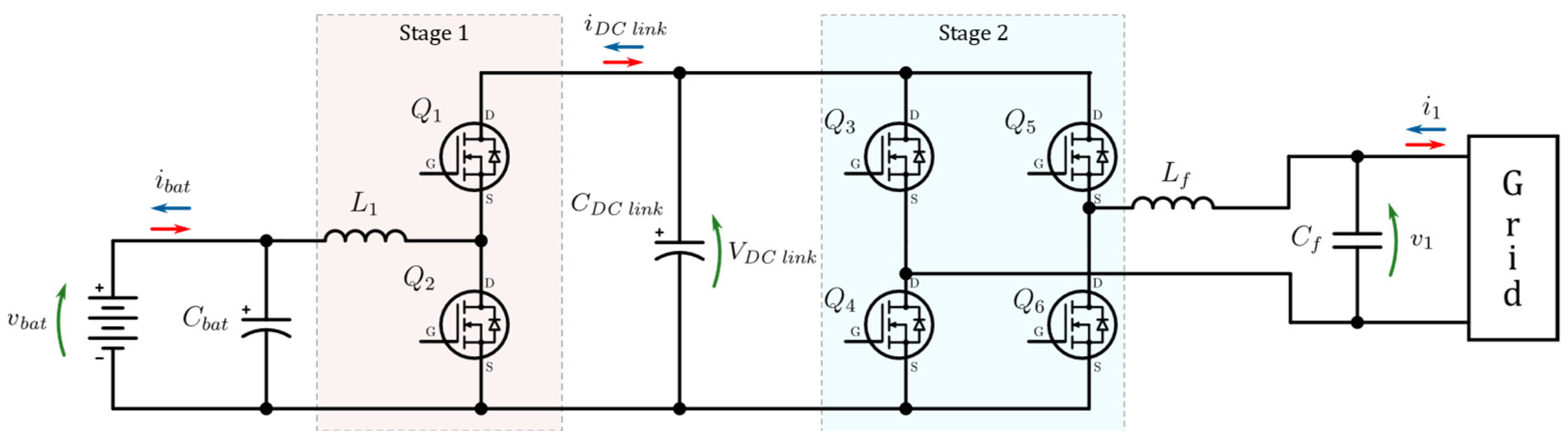
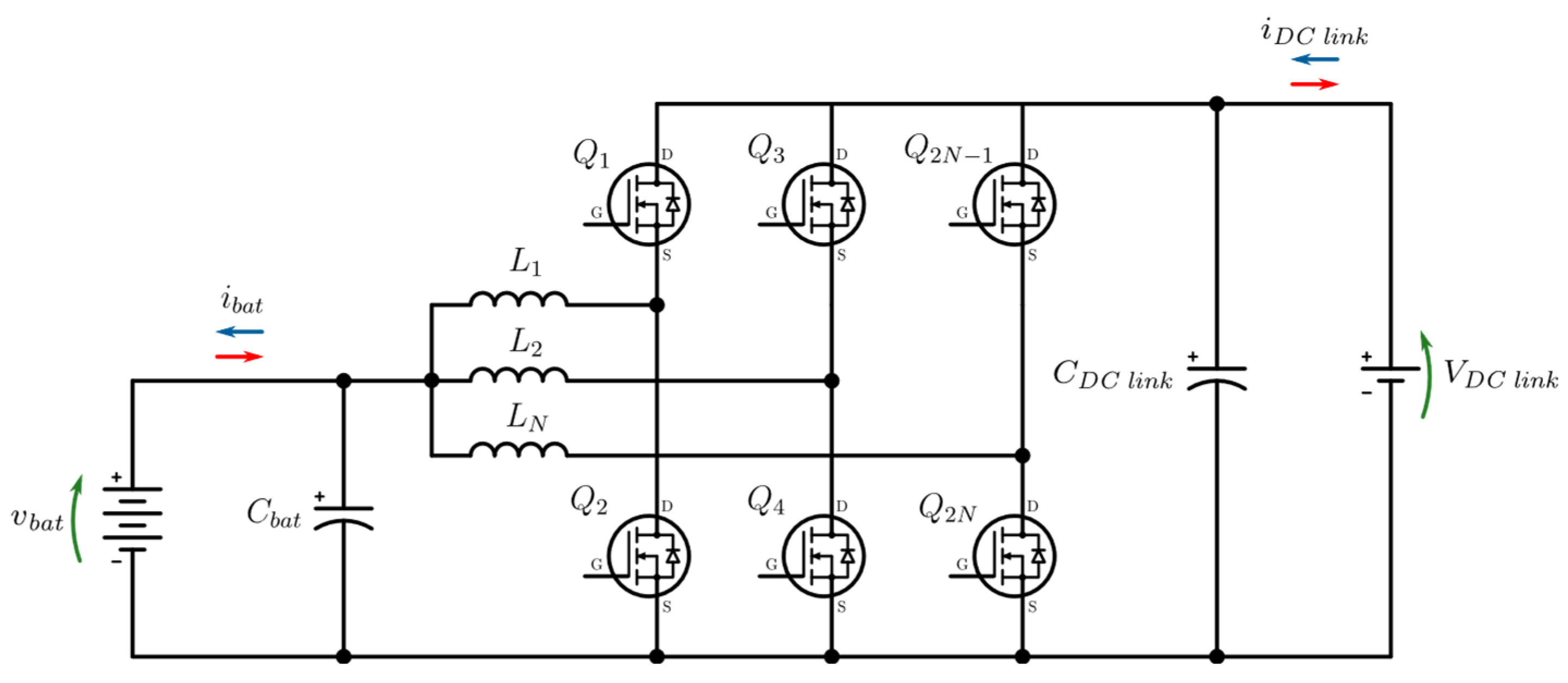
1.1. Interleaved Half-Bridge DC-DC Converter
- Increased Power Capability—A higher number of branches allows for the distribution of power across multiple branches, thereby enabling higher power transfer.
- Reduction in Current Ripple—With a proper control strategy, a multi-branch DVC can reduce inductor current ripple, thereby minimizing the need for additional filtering components.
- Enhanced Efficiency—For the same rated power, increasing the number of branches leads to smaller component sizes, which in turn reduces power losses.
1.2. Overview of Existing Methods for Efficiency Optimization via Branch Control in BIC
1.3. Research Scope and Main Contributions
- Development of a current-adaptive control algorithm for dynamically adjusting the number of active branches in a bidirectional interleaved converter (BIC) based on the battery operating curve, thereby enhancing the converter’s efficiency.
- Integration of a temperature-based control mechanism within the current-adaptive control strategy, incorporating a real-time thermal model to ensure operational reliability and mitigate thermal stress on semiconductor components.
- Design and implementation of a real-time simulation model with integrated electro-thermal modeling, developed using the Typhoon HIL 402 system. This model enables a realistic evaluation of the proposed control strategy under various operating conditions and confirms its applicability in practical scenarios.
- Provision of an open-access Typhoon HIL model, ensuring full reproducibility of the experimental setup and results, serving as a foundation for further research in adaptive control strategies for power electronic converters.
1.4. Paper Structure
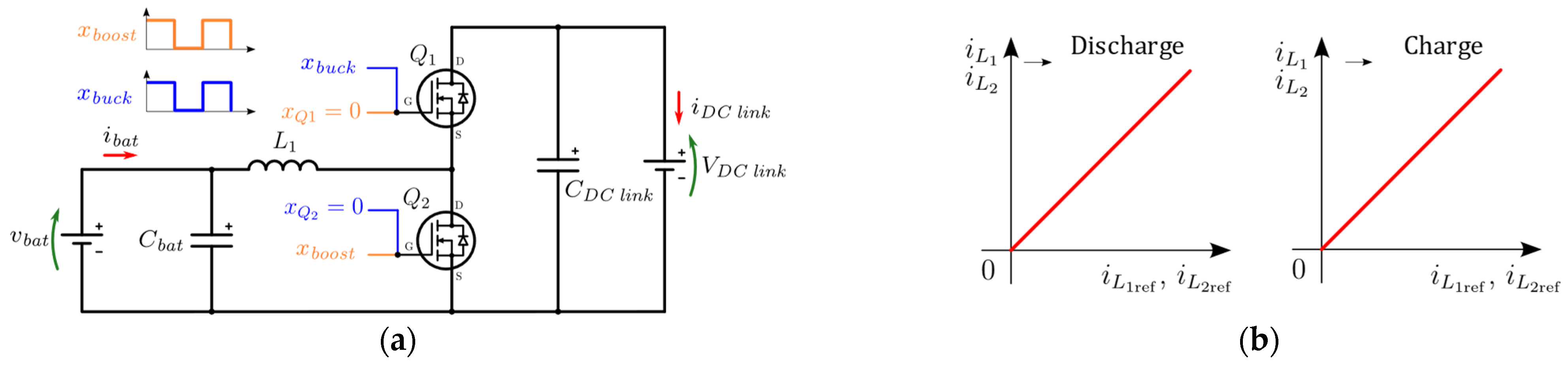
2. Two-Branch Interleaved Bidirectional DC-DC Converter Modeling
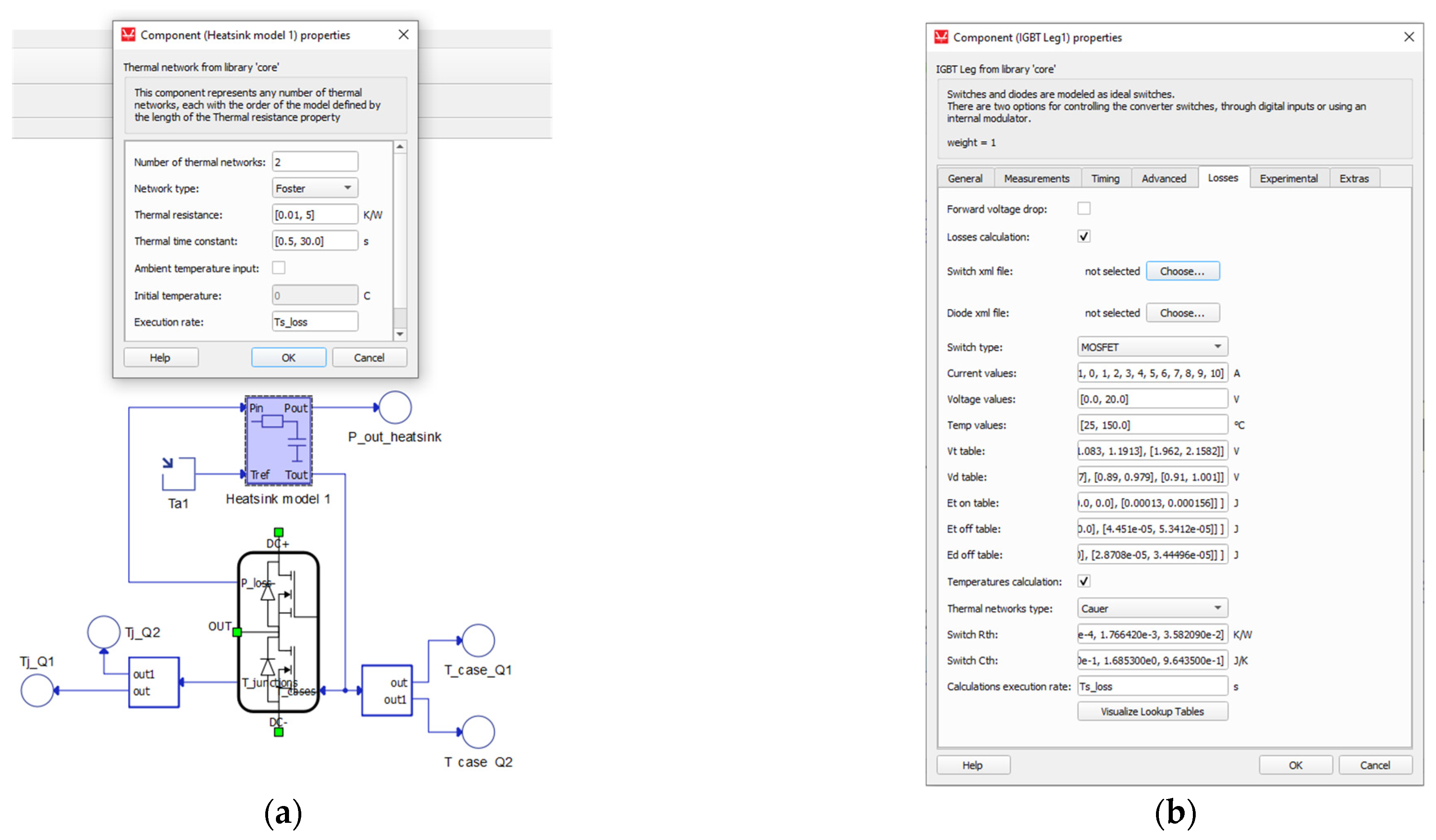
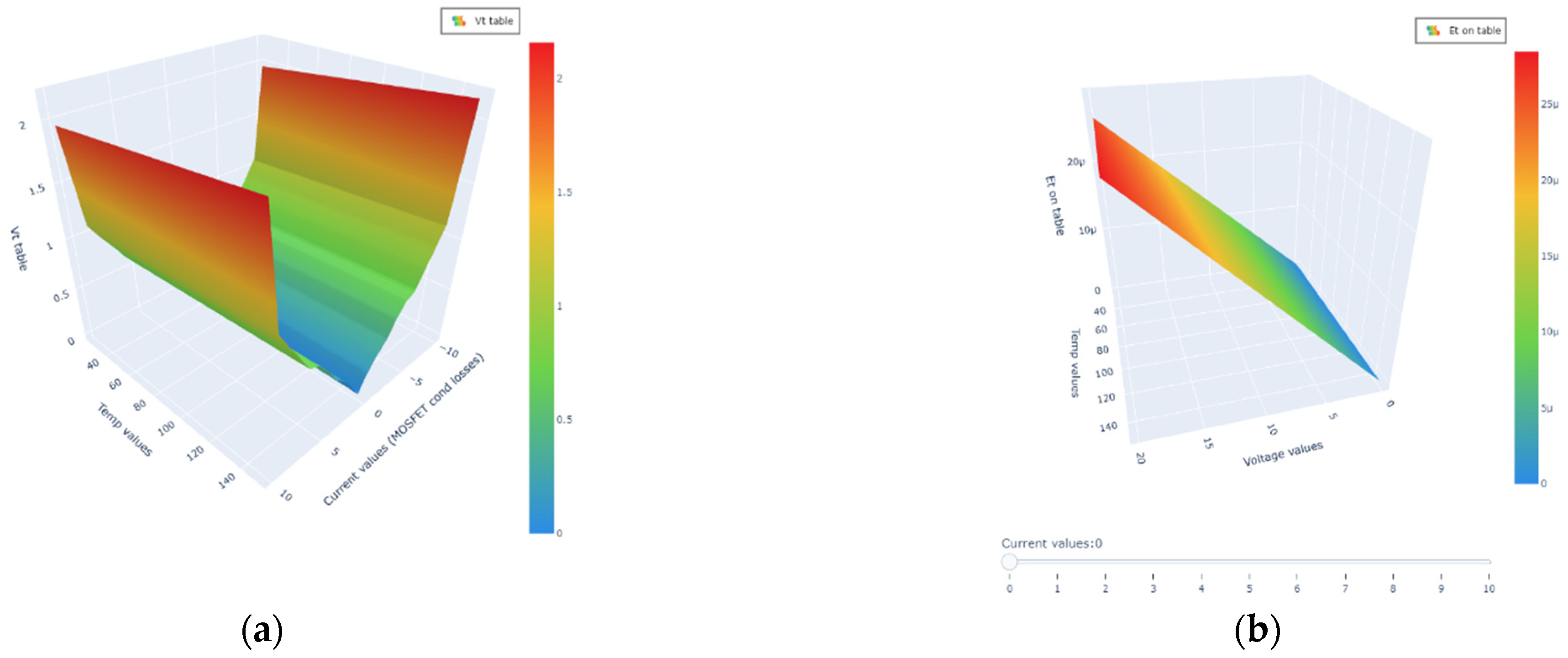
Thermal Modeling
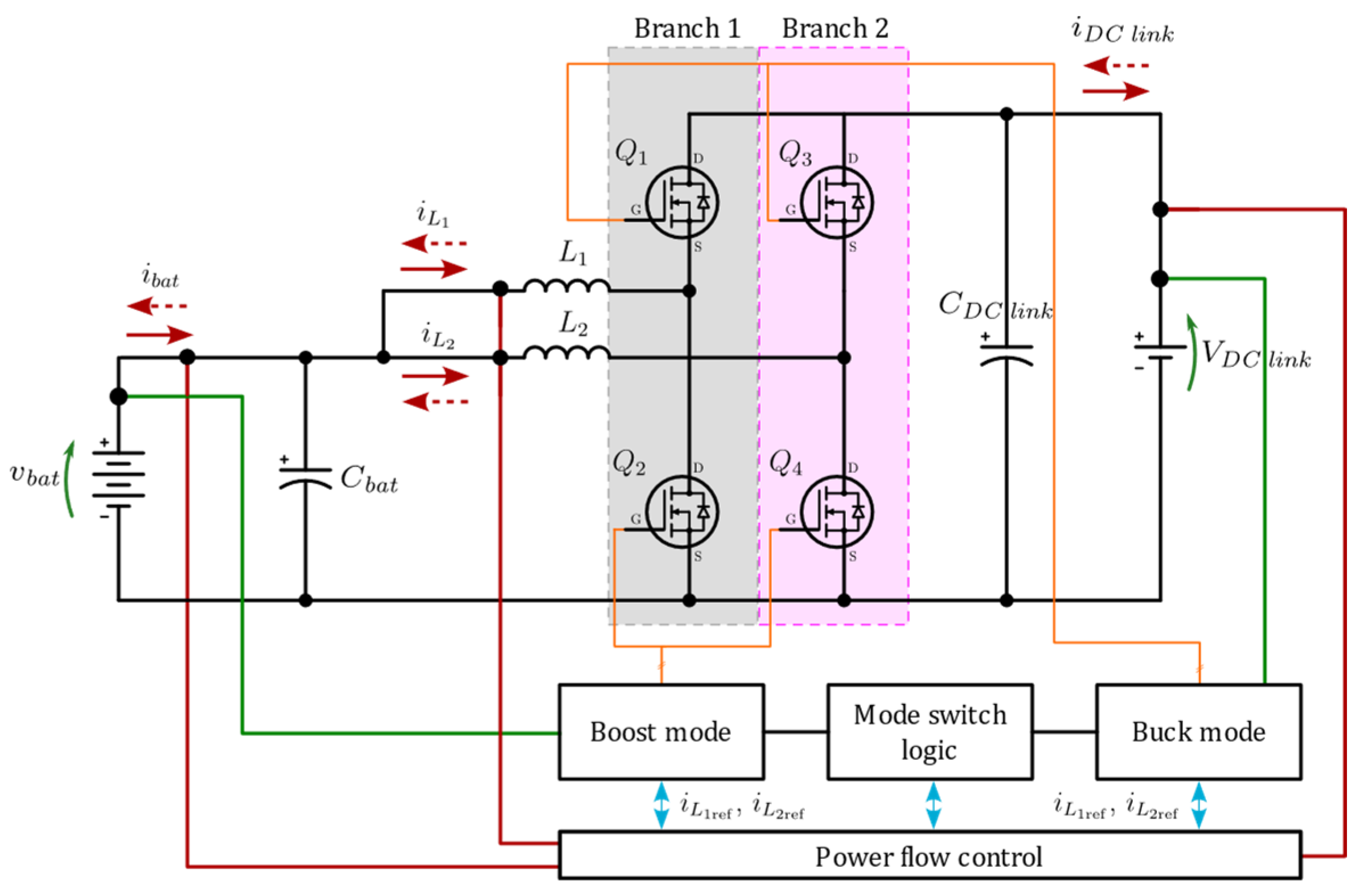
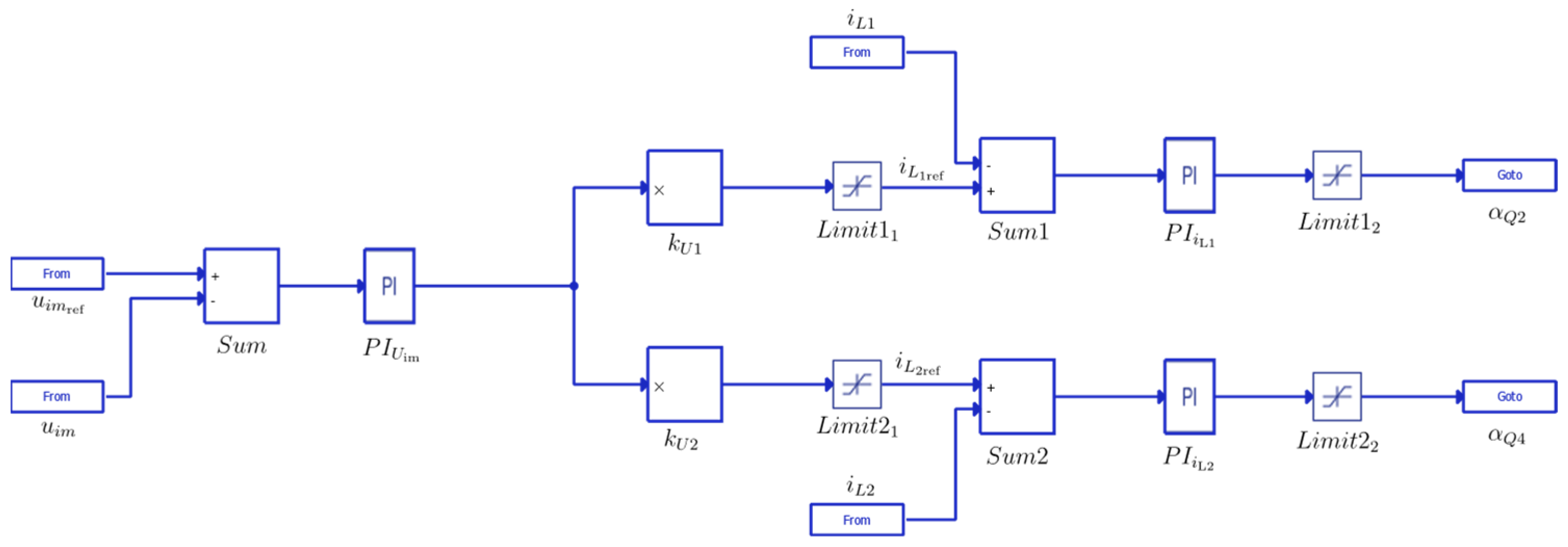
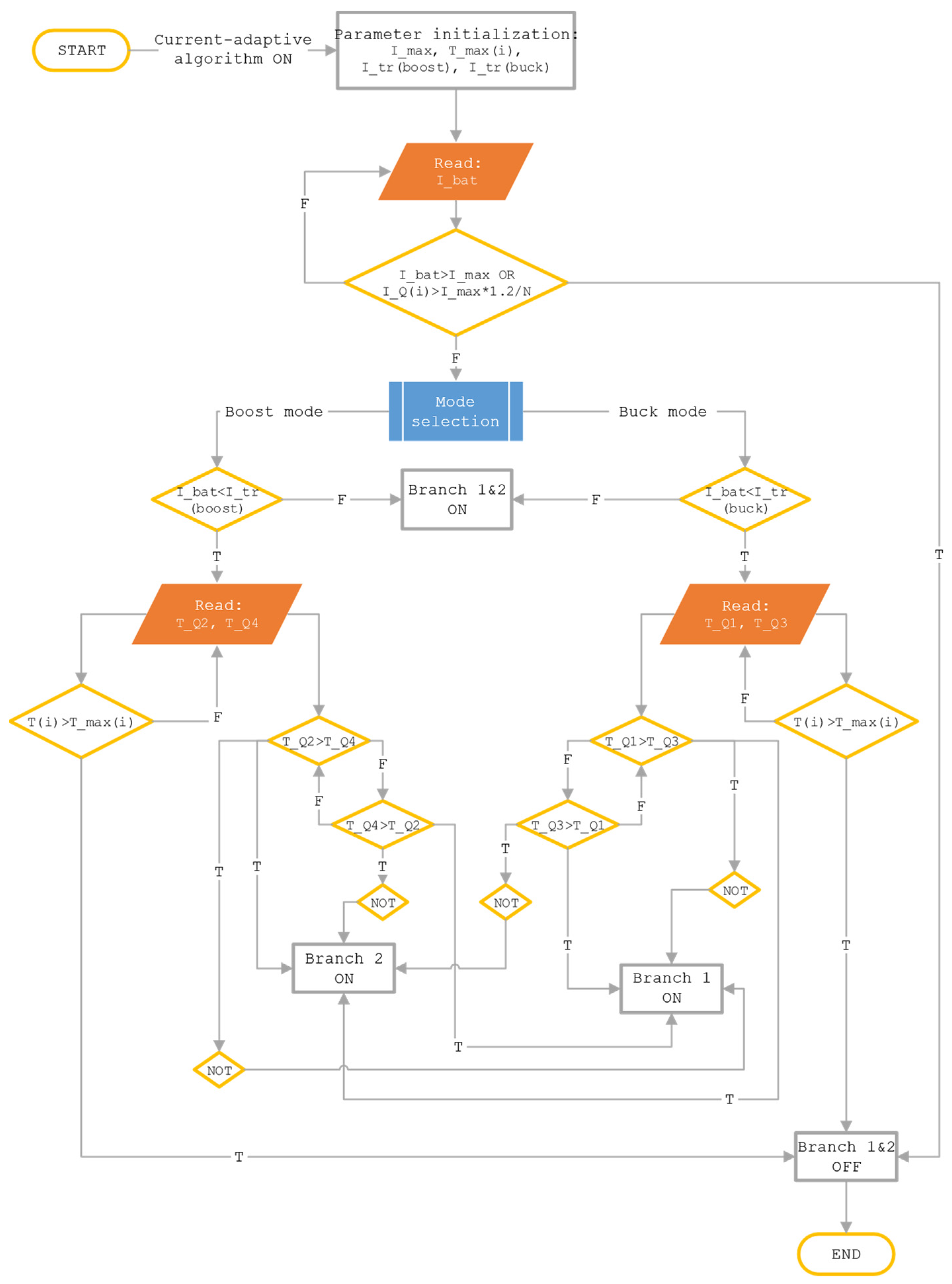
3. Current-Adaptive Control Strategy
Current-Adaptive Control Strategy Algorithm
- I_max: The maximum allowable current in the system.
- T_max(i): The maximum allowable temperature for each transistor.
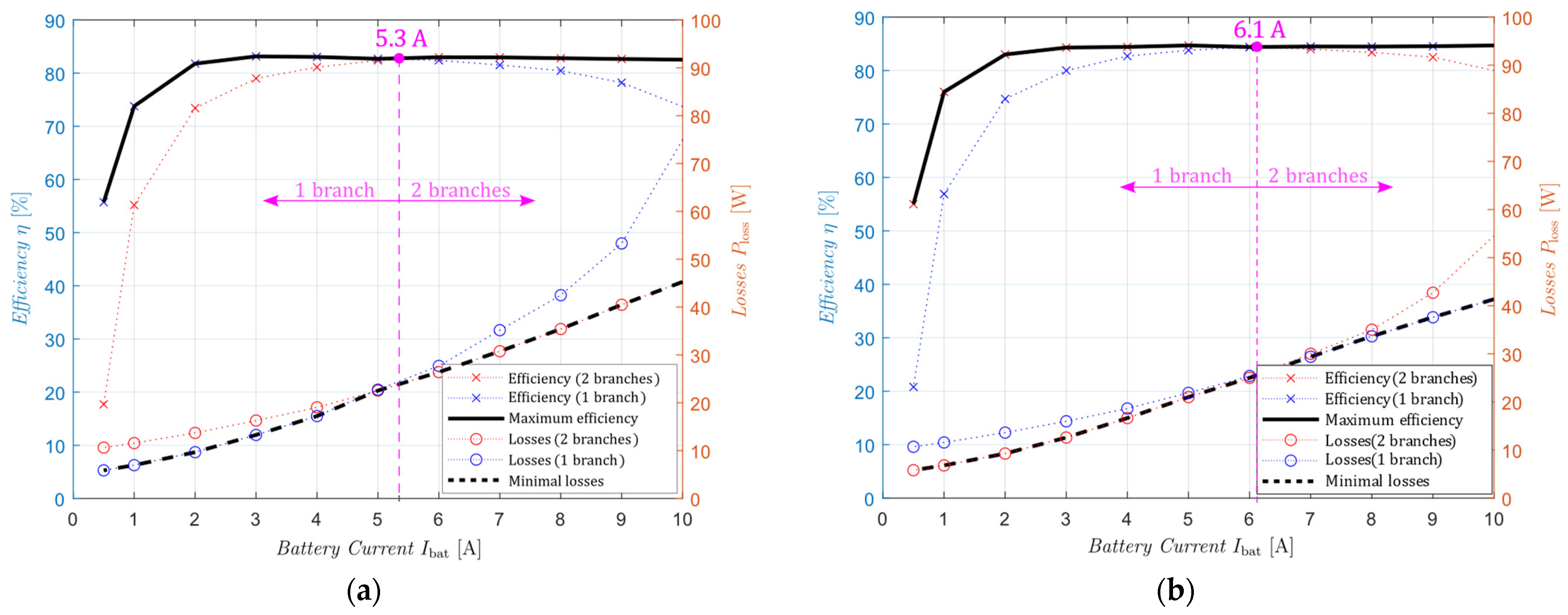
- I_tr(boost): The threshold current triggering the transition from two branches to one, and vice versa, in the boost (ascending) mode.
- I_tr(buck): The threshold current triggering the transition from two branches to one, and vice versa, in the buck (descending) mode.
4. Real-Time Hardware-in-the-Loop Simulation
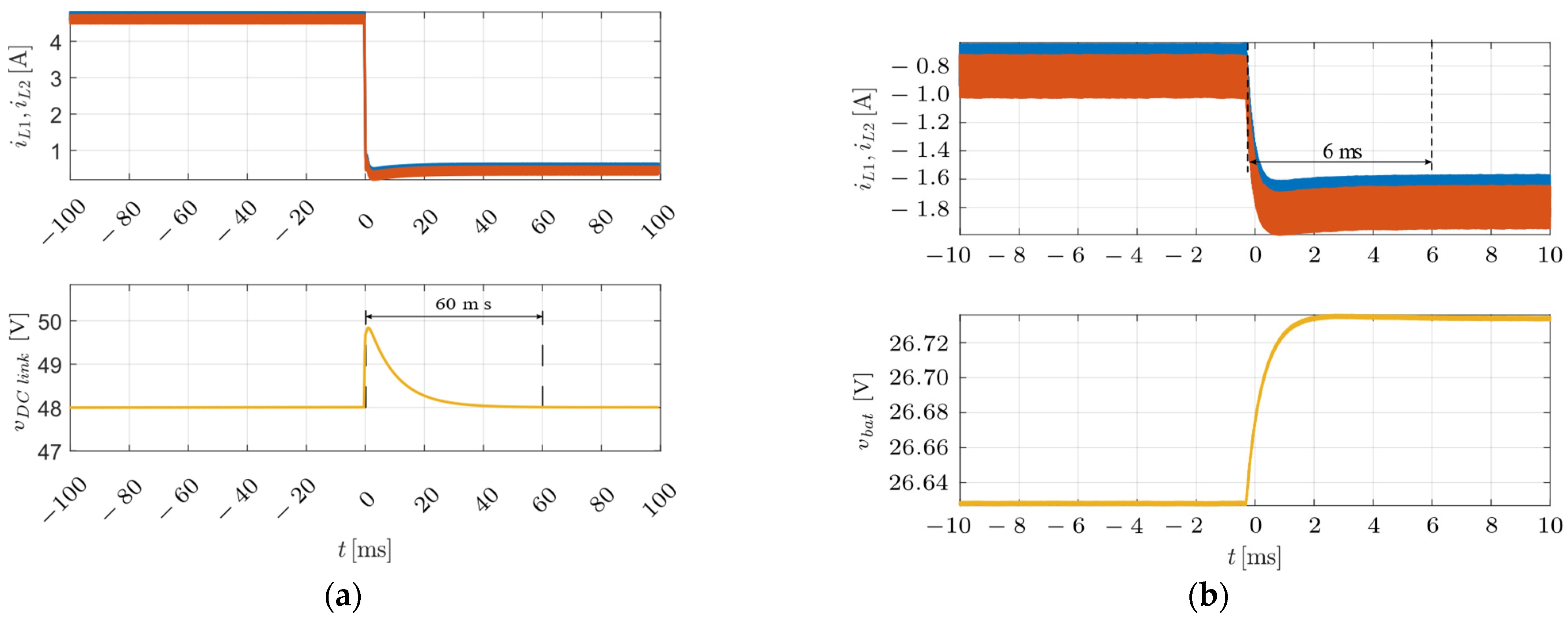
4.1. Converter Simulation Model Validation
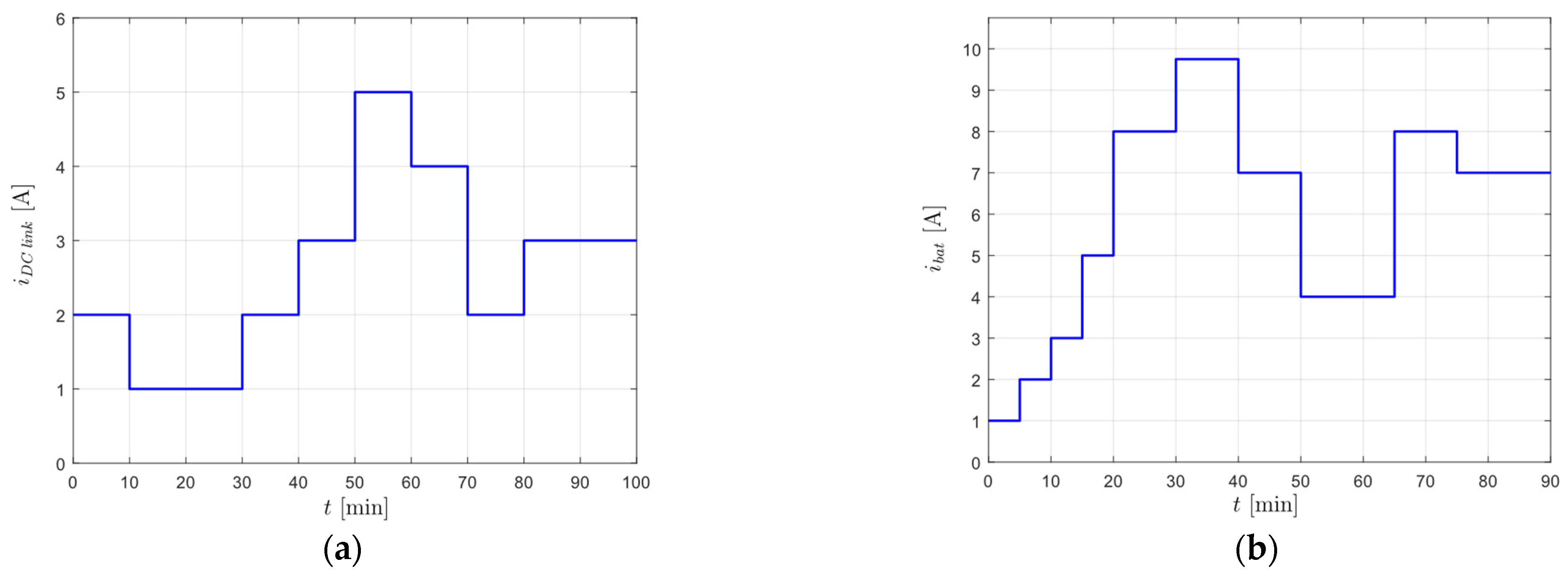
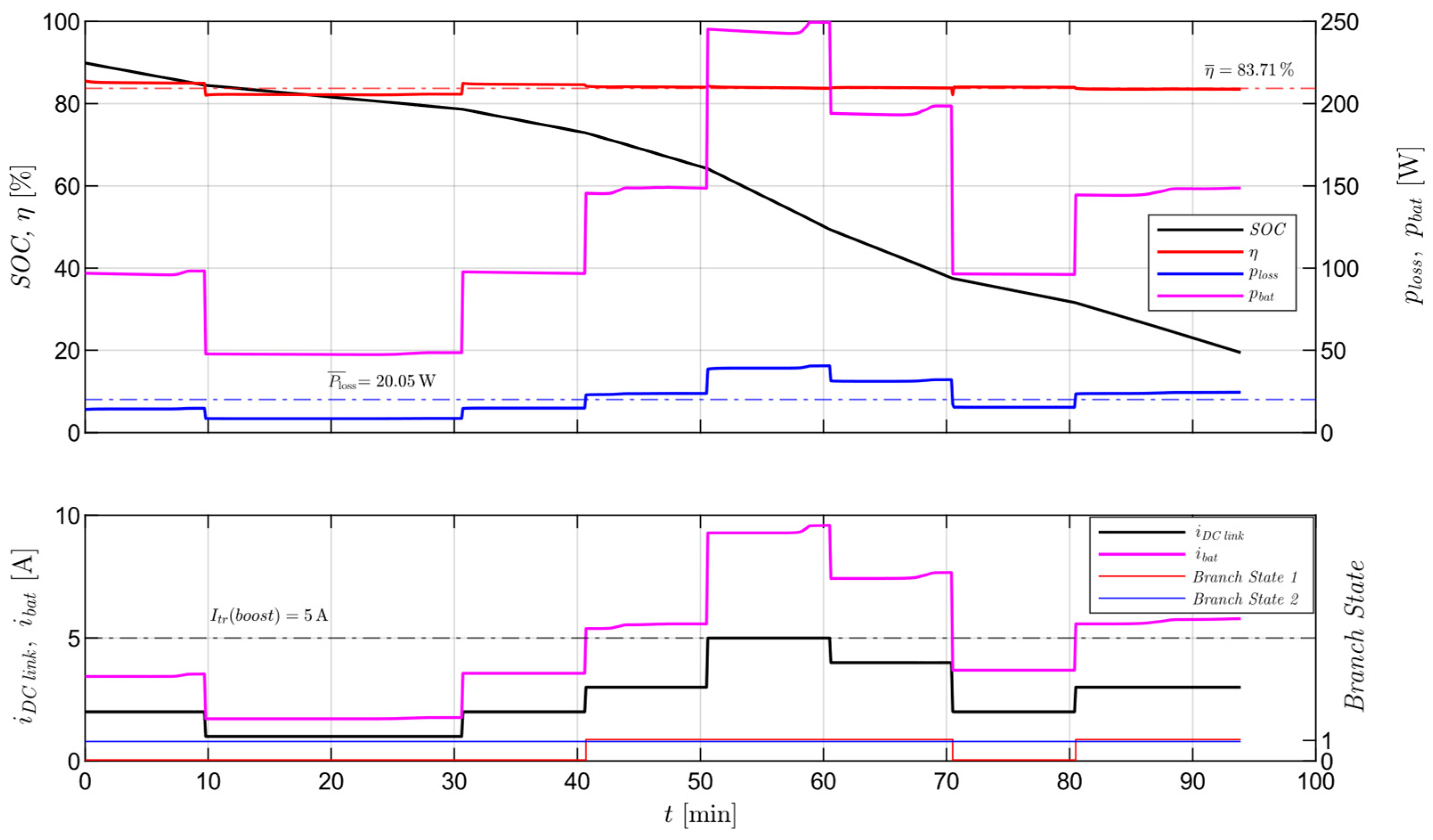
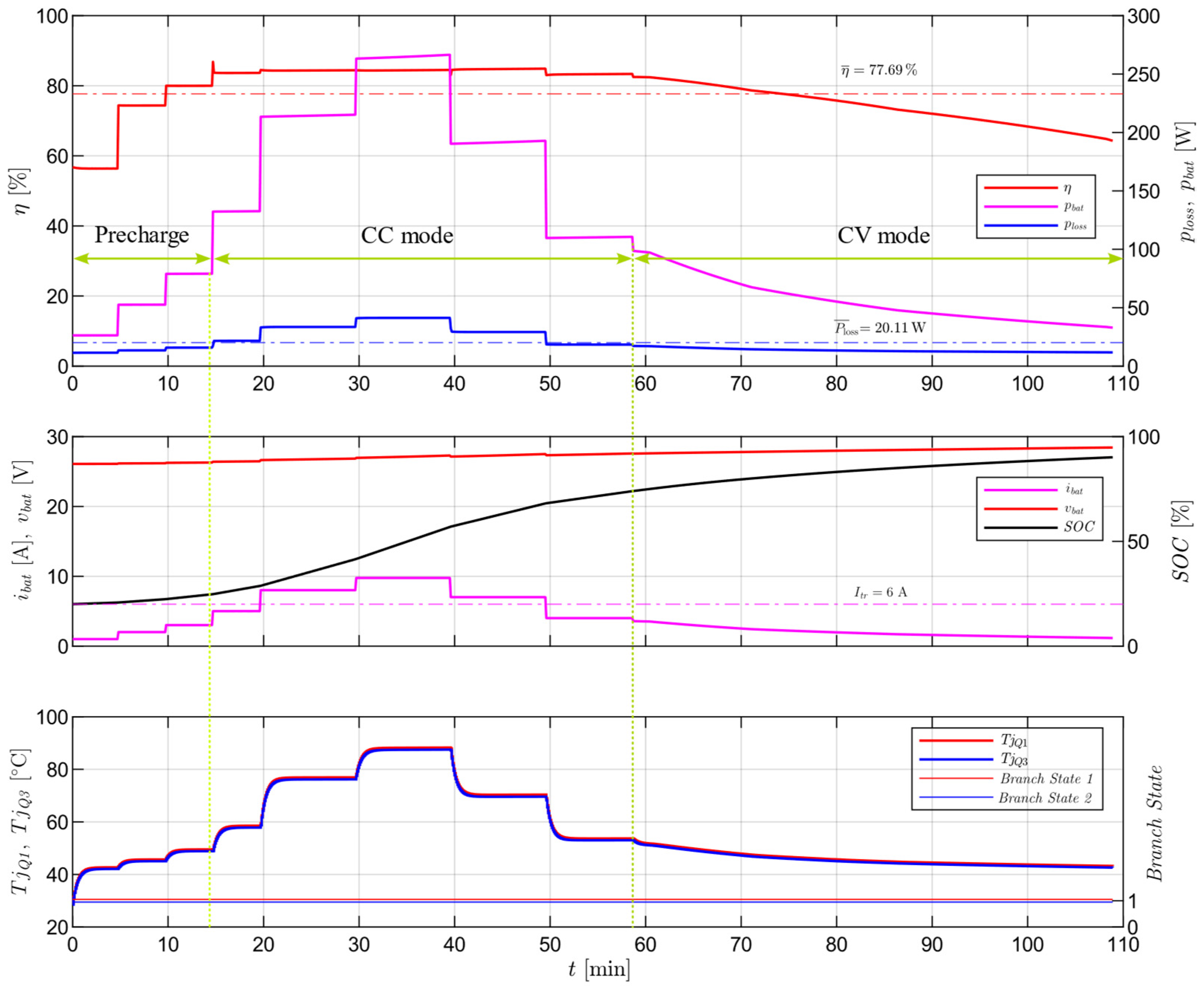
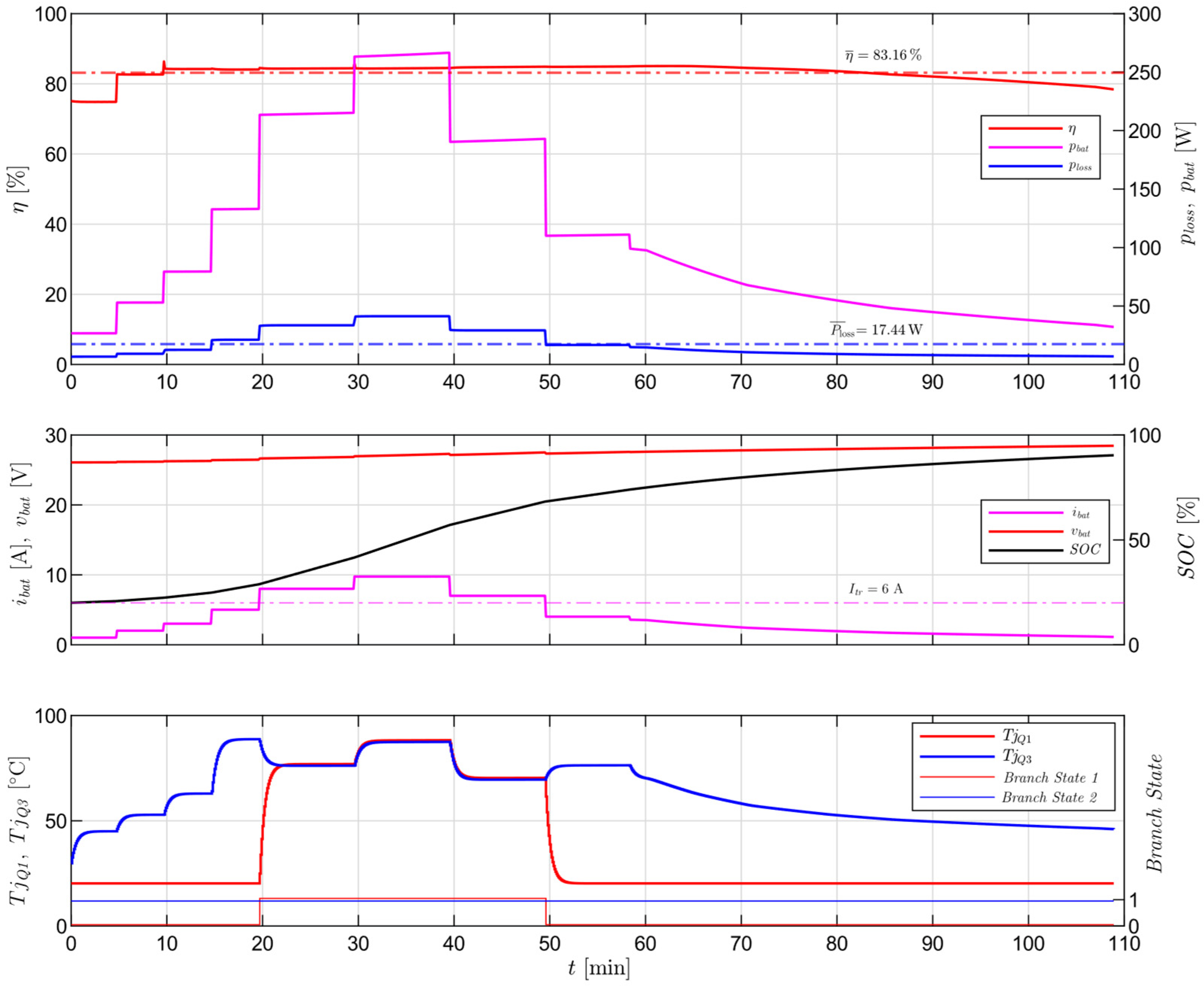
4.2. Current-Adaptive Control Algorithm Validation
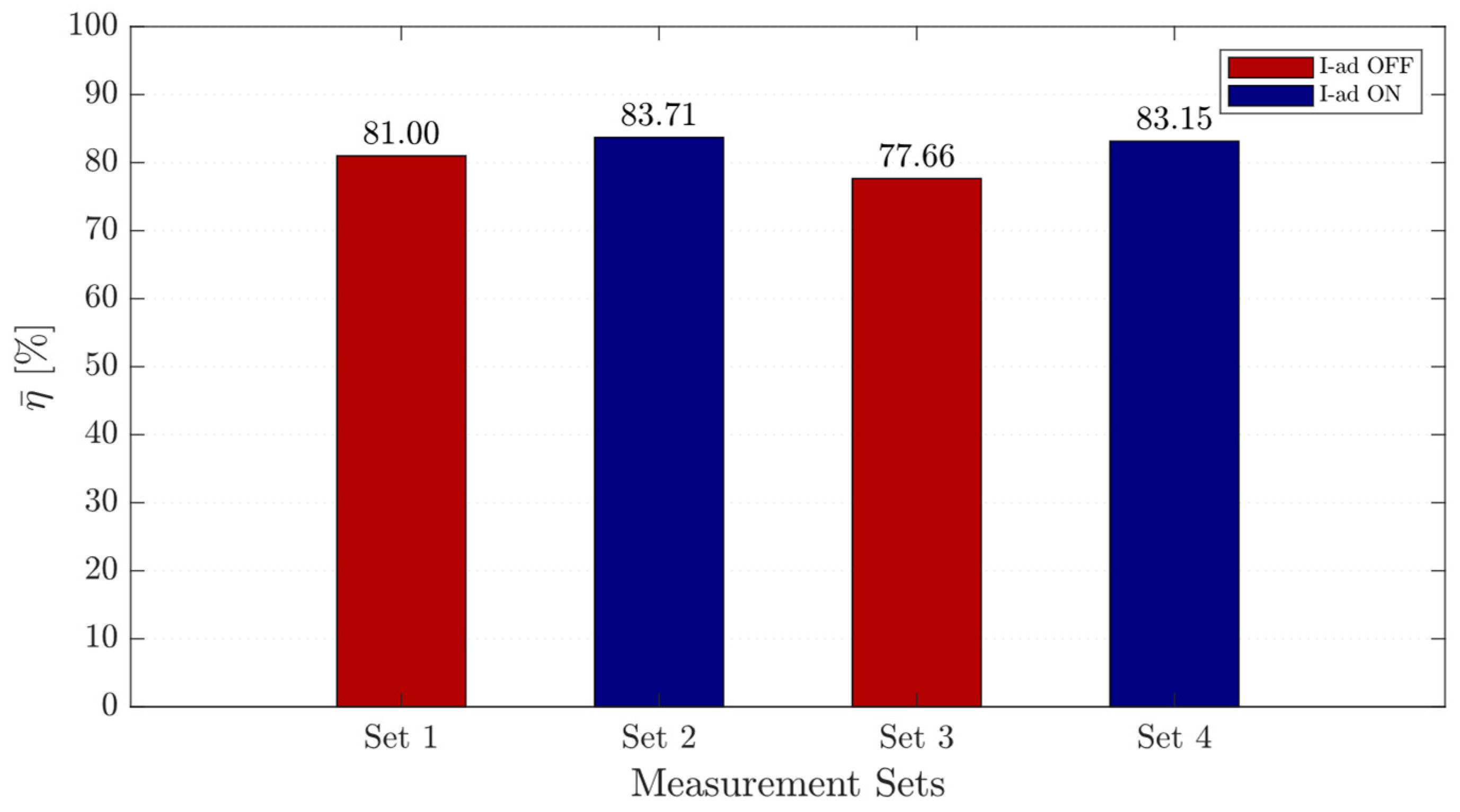
5. Discussion
6. Conclusions
- Average efficiency is increased from to in charging (buck) mode and from to in discharging (boost) mode.
- Minimum power losses were reduced by and in Boost and Buck modes, respectively.
- Testing the algorithm on a real prototype to compare the simulation results with real-world performance.
- Developing a temperature-based control system to regulate transistor temperatures in real time.
- Using machine learning to fine-tune control parameters dynamically during operation.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Vedhanarayanan, B.; Seetha Lakshmi, K.C. Beyond lithium-ion: Emerging frontiers in next-generation battery technologies. Front. Batter. Electrochem. 2024, 3, 1377192. [Google Scholar] [CrossRef]
- Padullaparti, H.; Pratt, A.; Mendoza, I.; Tiwari, S.; Baggu, M.; Bilby, C.; Ngo, Y. Peak Demand Management and Voltage Regulation Using Coordinated Virtual Power Plant Controls. IEEE Access 2023, 11, 130674–130687. [Google Scholar] [CrossRef]
- Precedence Research Stationary Energy Storage Market Size, Share, and Trends 2025 to 2034. Available online: https://www.precedenceresearch.com/stationary-energy-storage-market (accessed on 2 January 2025).
- Kroics, K.; Husev, O.; Tytelmaier, K.; Zakis, J.; Veligorskyi, O. An Overview of Bidirectional AC-DC Grid Connected Converter Topologies for Low Voltage Battery Integration. Int. J. Power Electron. Drive Syst. 2018, 9, 1223. [Google Scholar] [CrossRef]
- Panchanathan, S.; Vishnuram, P.; Rajamanickam, N.; Bajaj, M.; Blazek, V.; Prokop, L.; Misak, S. A Comprehensive Review of the Bidirectional Converter Topologies for the Vehicle-to-Grid System. Energies 2023, 16, 2503. [Google Scholar] [CrossRef]
- Sutikno, T.; Aprilianto, R.A.; Purnama, H.S. Application of non-isolated bidirectional DC–DC converters for renewable and sustainable energy systems: A review. Clean Energy 2023, 7, 293–311. [Google Scholar] [CrossRef]
- Lai, C.-M.; Lin, W.-H.; Liu, H.-E.; Liu, S.; Mishima, T.; Teh, J. A Two-Phase Interleaved Bidirectional DC-DC Converter with Asymmetrical Duty Limit Control for Wide-Range DC-Bus Voltage Applications. IEEE Trans. Ind. Applicat. 2024, 60, 3306–3321. [Google Scholar] [CrossRef]
- Ni, L.; Patterson, D.J.; Hudgins, J.L. High Power Current Sensorless Bidirectional 16-Phase Interleaved DC-DC Converter for Hybrid Vehicle Application. IEEE Trans. Power Electron. 2012, 27, 1141–1151. [Google Scholar] [CrossRef]
- Qiu, W.; Cheung, C.; Xiao, S.; Miller, G. Power Loss Analyses for Dynamic Phase Number Control in Multiphase Voltage Regulators. In Proceedings of the Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; IEEE: New York, NY, USA, 2009; pp. 102–108. [Google Scholar]
- Su, J.-T.; Liu, C.-W. A Novel Phase-Shedding Control Scheme for Improved Light Load Efficiency of Multiphase Interleaved DC–DC Converters. IEEE Trans. Power Electron. 2013, 28, 4742–4752. [Google Scholar] [CrossRef]
- Costabeber, A.; Mattavelli, P.; Saggini, S. Digital Time-Optimal Phase Shedding in Multiphase Buck Converters. IEEE Trans. Power Electron. 2010, 25, 2242–2247. [Google Scholar] [CrossRef]
- Zumel, P.; Fernández, C.; De Castro, A.; García, O. Efficiency improvement in multiphase converter by changing dynamically the number of phases. In Proceedings of the 37th IEEE Power Electronics Specialists Conference, Jeju, Republic of Korea, 18–22 June 2006; IEEE: New York, NY, USA, 2006; pp. 1–6. [Google Scholar]
- Alharbi, M.A.; Dahidah, M.; Ethni, S.; Ali, S.; Kadandani, N.B.; Pickert, V. A Phase Shedding Control Technique for Ripple Minimisation for EV Fast DC Charging Applications. In Proceedings of the 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021; IEEE: New York, NY, USA, 2021; pp. 1–10. [Google Scholar]
- Lim, H.; Jang, M.; Agelidis, V. A Phase Shedding Technique for PV System Based on Interleaved Boost Converter. In Proceedings of the IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Lee, J.-S.; Huang, C.-Y.; Liang, T.-J.; Chen, K.-H. Design of control IC for multiphase interleaved buck converter with alternate phase-shedding. In Proceedings of the 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Republic of Korea, 1–5 June 2015; IEEE: New York, NY, USA, 2015; pp. 1025–1032. [Google Scholar]
- Lin, J.-T.; Hu, K.; Tsai, C.-H. Digital Multiphase Buck Converter with Current Balance/Phase Shedding Control. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; IEEE: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Alharbi, M.A.; Alcaide, A.M.; Dahidah, M.; Ethni, S.; Pickert, V.; Leon, J.I. Rotating Phase Shedding for Interleaved DC–DC Converter-Based EVs Fast DC Chargers. IEEE Trans. Power Electron. 2023, 38, 1901–1909. [Google Scholar] [CrossRef]
- Yedukondalu, G.; Samanta, S. Effective phase utilization and efficiency improvement of high power interleaved DC–DC converter using modified rotating phase shedding control. Comput. Electr. Eng. 2023, 110, 108837. [Google Scholar] [CrossRef]
- Typhoon HIL HIL402 Hardware User Guide. Available online: https://www.typhoon-hil.com/documentation/typhoon-hil-hardware-manual/hil402_user_guide/topics/hil402_abstract.html (accessed on 18 February 2025).
- EVAL-1ED020I12-BT; Infineon: Munich, Germany, 2013.
- Tony, R. Kuphaldt Lessons in Industrial Automation. Available online: https://control.com/textbook/closed-loop-control/analog-electronic-pid-controllers/?utm_source=chatgpt.com (accessed on 15 January 2025).
- Ma, D.; Niculescu, S.; Guo, L.; Chen, J. Special issue on PID control in the information age: Theoretical advances and applications. Int. J. Robust. Nonlinear 2022, 32, 9384–9388. [Google Scholar] [CrossRef]
- Solsona, J.A.; Gomez Jorge, S.; Busada, C.A. Modeling and Nonlinear Control of DC–DC Converters for Microgrid Applications. Sustainability 2022, 14, 16889. [Google Scholar] [CrossRef]
- Etxeberria, A.; Vechiu, I.; Camblong, H.; Vinassa, J.-M. Comparison of Sliding Mode and PI Control of a Hybrid Energy Storage System in a Microgrid Application. Energy Procedia 2011, 12, 966–974. [Google Scholar] [CrossRef]
- Laoprom, I.; Tunyasrirut, S. Design of PI Controller for Voltage Controller of Four-Phase Interleaved Boost Converter Using Particle Swarm Optimization. J. Control Sci. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Rachmad, R.W.; Abuzairi, T. Efficiency Comparison of Asynchronous and Synchronous Buck Converter with Variation in Duty Cycle and Output Current. Bul. Ilm. Sarj. Tek. Elektro 2023, 5, 41–55. [Google Scholar] [CrossRef]
- Setiawan, I.; Facta, M.; Andromeda, T.; Hermawan, H.; Syakur, A. Unified and Separated Buck/Boost Averaged Current Control Strategies of Bidirectional DC-DC Converter for DC Microgrid Systems. IREACO 2022, 15, 204. [Google Scholar] [CrossRef]
- Zhang, J.; Lai, J.S.; Yu, W. Bidirectional DC-DC converter modeling and unified controller with digital implementation. In Proceedings of the Twenty-Third Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 24–28 February 2008; IEEE: New York, NY, USA, 2008; pp. 1747–1753. [Google Scholar]
- Codecasa, L.; Rencz, M. Thermal and Electro-Thermal System Simulation; MDPI: Basel, Switzerland, 2019; ISBN 978-3-03921-736-6. [Google Scholar]
- Typhoon HIL Thermal Modeling of Power Electronic Devices. Available online: https://www.typhoon-hil.com/documentation/typhoon-hil-software-manual/concepts/thermal_modeling_pe.html (accessed on 18 February 2025).
- Lagonotte, P.; Soulier, F.; Thomas, A.; Martemianov, S. The Differences Between Equivalent Foster and Cauer Circuits and Factorised Impedance. Adv. Theor. Comput. Phys. 2022, 5, 314–323. [Google Scholar]
- VNP10N07 Omnifet; STMicroelectronics: Geneva, Switzerland, 2013.
- Tripathi, S.M.; Gonzalez-Longatt, F.M. (Eds.) Real-Time Simulation and Hardware-in-the-Loop Testing Using Typhoon HIL; Transactions on Computer Systems and Networks; Springer Nature: Singapore, 2023; ISBN 978-981-99-0223-1. [Google Scholar]
- Chen, G.-J.; Chung, W.-H. Evaluation of Charging Methods for Lithium-Ion Batteries. Electronics 2023, 12, 4095. [Google Scholar] [CrossRef]
- Xiaoyan, S.; Leilei, M.; Jiantao, W. Effects of Pre-Charge Temperatures on Gas Production and Electrochemical Performances of Lithium-Ion Batteries. In Proceedings of the 3rd International Conference on Civil Architecture and Energy Science (CAES 2021), Hangzhou, China, 19–21 March 2021; Volume 248, p. 1040. [Google Scholar] [CrossRef]
- Bandara, T.G.T.A.; Viera, J.C.; González, M. The next generation of fast charging methods for Lithium-ion batteries: The natural current-absorption methods. Renew. Sustain. Energy Rev. 2022, 162, 112338. [Google Scholar] [CrossRef]
- Alldatasheet NCR18650B Datasheet. Available online: https://www.alldatasheet.com/datasheet-pdf/pdf/597043/PANASONICBATTERY/NCR18650B.html (accessed on 6 May 2023).
- iCharger 4010 Manual; Shenzhen Junsi Electronic: Shenzhen, China, 2012.





| Parameter | Symbol | Value |
|---|---|---|
| Number of converter branches | ||
| Maximum system power | ||
| Maximum power per branch | ||
| Converter switching frequency | ||
| Nominal DC-link voltage | ||
| Nominal battery voltage 1 | ||
| Maximum battery current | ||
| Maximum current per converter branch |
| Measurement Sets | Set 1 | Set 2 |
|---|---|---|
| Parameter | Boost Mode | Buck Mode |
| ) | ||
| ) | depending) | |
| ) | ||
| Reference current (Load) | ||
| Control signals | ||
| Recorded waveforms | ||
| Measurement Set | 1. | 2. | 3. | 4. |
|---|---|---|---|---|
| Mode of Operation | Boost (Discharging) | Buck (Charging) | ||
| Current-adaptive (I-ad) mode | OFF | ON | OFF | ON |
| Auto | Auto | |||
| I-ad algorithm current activation | - | - | ||
| According to the load curve | ||||
| Sampled quantity 1 | ||||
| [W] | |||||||
|---|---|---|---|---|---|---|---|
| Set 1 | |||||||
| Set 2 | |||||||
| Set 3 | 109.4 | ||||||
| Set 4 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandis, A.; Knol, K.; Pelin, D. Current-Adaptive Control for Efficiency Enhancement in Interleaved Converters for Battery Energy Storage Systems. Electronics 2025, 14, 1862. https://doi.org/10.3390/electronics14091862
Brandis A, Knol K, Pelin D. Current-Adaptive Control for Efficiency Enhancement in Interleaved Converters for Battery Energy Storage Systems. Electronics. 2025; 14(9):1862. https://doi.org/10.3390/electronics14091862
Chicago/Turabian StyleBrandis, Andrej, Kristian Knol, and Denis Pelin. 2025. "Current-Adaptive Control for Efficiency Enhancement in Interleaved Converters for Battery Energy Storage Systems" Electronics 14, no. 9: 1862. https://doi.org/10.3390/electronics14091862
APA StyleBrandis, A., Knol, K., & Pelin, D. (2025). Current-Adaptive Control for Efficiency Enhancement in Interleaved Converters for Battery Energy Storage Systems. Electronics, 14(9), 1862. https://doi.org/10.3390/electronics14091862







