Abstract
Subspace clustering has emerged as a prominent research focus, demonstrating remarkable potential in handling multi-view data by effectively harnessing their diverse and information-rich features. In this study, we present a novel framework for multi-view subspace clustering that addresses several critical aspects of the problem. Our approach introduces three key innovations: First, we propose a dual-component representation model that simultaneously considers both consistent and inconsistent elements across different views. The consistent component is designed to capture shared structural patterns with robust commonality, while the inconsistent component effectively models view-specific variations through sparsity constraints across multiple modes. Second, we implement cross-mode sparsity constraints that enable the inconsistent component to efficiently extract high-order information from the data. This design not only enhances the representation capability of the inconsistent component but also facilitates the consistent component in revealing high-order structural relationships within the data. Third, we develop an adaptive loss function that offers greater flexibility in handling noise and outliers, thereby significantly improving the model’s robustness in real-world applications. Through extensive experimentation, we demonstrate that our proposed method consistently outperforms existing approaches, achieving superior clustering performance across various benchmark datasets. The experimental results comprehensively validate the effectiveness and advantages of our approach in terms of clustering accuracy, robustness, and computational efficiency.
1. Introduction
As a basic approach in machine learning, clustering has proven to be highly effective in diverse areas, including image segmentation [1], face clustering [2], community detection [3], cancer biology [4], text mining [5], etc. High-dimensional data often contain redundant or irrelevant features that can obscure meaningful patterns, making traditional clustering methods less effective. By reducing dimensionality, innovative techniques help to reveal the underlying structure of the data, improving both the efficiency and accuracy of clustering algorithms. Thus, there has been an ongoing requirement to develop innovative techniques, such as low-dimensional representations [6,7,8], for clustering that can elucidate the latent structures within high-dimensional data.
Subspace clustering has been well studied during the last decades with great success in constructing low-dimensional representations for efficient clustering [1,7,9,10,11]. Among them, the subspace clustering methods built upon spectral clustering principles have attracted considerable interest and become the focus of recent developments in subspace clustering methods [6,7,12]. The sparse subspace clustering [13] and low-rank representation [7] approaches are among the most typical methods. Various algorithms have been developed with improved clustering performance [12,14]. However, in practical applications, data often originate from various sources [15]. As an example, we can utilize various features such as texts, images, or other types of characteristics to depict an object [15]. These features are considered as multi-view representations of the object, providing a comprehensive and diverse perspective on the data and resulting in multi-view data. Although multi-view data offer richer and more informative information than single-view data, single-view methods are unable to effectively utilize the features available across multiple views and thus they may have suboptimal learning performance.
To tackle this challenge, multi-view clustering techniques have been thoroughly investigated over the past decade, yielding promising clustering performance [16,17,18,19,20]. Existing methods can be broadly categorized into two types based on their approach to constructing the affinity matrix [21], which are briefly summarized in Figure 1. The first type constructs the affinity matrix directly from similarity matrices [16,17,18,22], while the second type, known as multi-view subspace clustering, builds on spectral clustering-based subspace clustering techniques [15,19,23]. For instance, LT-MSC extends the traditional low-rank representation framework by incorporating a tensor nuclear norm constraint to explore cross-view correlations and global structures [24]. Similarly, CSMSC emphasizes both consistency and specificity in representations, enabling the identification of shared and view-specific characteristics [25]. Another notable method, MLRR, improves low-rank representation by applying symmetry constraints and diversity regularization to preserve angular consistency and capture view-specific information [26]. MVCIL tackles catastrophic forgetting and concept interference in open-ended incremental learning via random representation, orthogonal fusion, and selective weight consolidation [27]. The EOMSC-CA method integrates anchor learning and graph construction, and by imposing graph connectivity constraints, it directly outputs clustering labels [28].
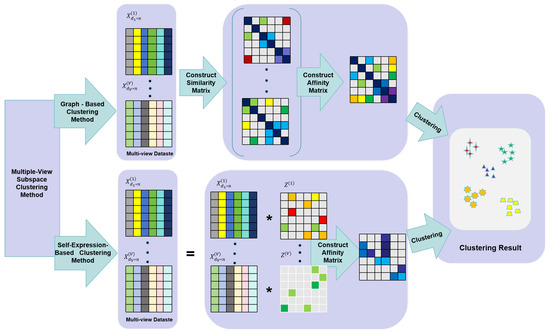
Figure 1.
Flowdiagram illustrating graph-based and subspace clustering-based algorithms in the field of multi-view clustering. * denotes multiplication.
Despite these advancements, existing methods still face several critical limitations. First, many approaches fail to effectively exploit the cross-view high-order information and spatial structure of the data, resulting in incomplete representations that do not well capture the underlying relationships across views. Second, while consistency and diversity across views are crucial for multi-view clustering, current methods often struggle to balance these aspects, leading to either over-emphasis on shared structures or neglect of view-specific characteristics. Third, the robustness of existing methods to noise and outliers remains a challenge, as many approaches rely on rigid loss functions that are sensitive to data imperfections.
To address these limitations, we propose a novel multi-view clustering method that integrates consistency and diversity across views while capturing high-order information and enhancing robustness. Our approach introduces the following key innovations: (1) We adopt an adaptive loss function that combines the benefits of various matrix norms. This strategy effectively mitigates the effects of noise and outliers, and thus makes the proposed model more robust. (2) We separate the representation matrix of each view into two parts that correspond to consistency and inconsistency of the data, respectively. In particular, the consistency part exhibits the desired structural property with strict commonality and block diagonal structural constraints, which enhances the affinity matrix to explicitly identify the grouping pattern of the data. Meanwhile, the inconsistency part captures high-order information of the data through sparsity constraints imposed on different modes. This strategy effectively helps reveal latent cross-view structures of the data. (3) The proposed model involves several terms, which are complicated and not straightforward to solve. We design an effective optimization algorithm for the proposed method, which generalizes the practical applicability of the proposed techniques. (4) Through extensive experimental results, the effectiveness and superiority of our method have been effectively demonstrated, which further improves the learning performance of the MVC algorithms.
The rest of this paper is organized as follows: Section 2 introduces the essential background information. In Section 3, we introduce the proposed method, followed by the development of an optimization algorithm in Section 4. In Section 5, we perform comprehensive experiments to confirm the efficacy of the proposed method. Finally, we summarize the findings and conclude the paper in Section 6.
2. Background Knowledge
Herein, we introduce the required notations and offer a concise review of related methods. Given multi-view data , we denote its number of samples by n, number of views by V, number of clusters by k, dimension of each view by with , and the largest dimension is . We represent the feature matrix for each view as . For ease of notation, the superscript is also used to denote the v-th frontal slice of the tensors. Subsequently, a self-expression-based multi-view subspace clustering model can be universally formulated as follows:
where tensor consists of representation matrices in each frontal slice, serves as the loss function of , serves as a balancing parameter, and functions as a regularizer of . When , the aforementioned model simplifies to a traditional single-view subspace clustering method like the tensor nuclear norm and low-rank representation, while employing their respective regularizers.
3. Proposed Method
In general, utilizing the self-expressive property allows us to formulate the multi-view clustering model as
where denotes a proper regularizer for the affinity tensor. This regularizer enforces constraints on the structural characteristics of the low-dimensional representation within each individual view. Generally, when a model is fitted using the samples, most of the samples lead to a small loss while a big loss is generated by only a few samples [29].
To alleviate the loss function’s sensitivity to outliers, as well as to marry the advantages of different norms, for enhanced robustness and accurate information preservation from the data, we adopt an adaptive loss function [29]. In particular, for an arbitrary matrix , the adaptive loss function can be formulated as follows:
where the i-th row of the matrix is denoted by and is a parameter. The adaptive loss function is closely related to various matrix norms, of which the properties are summarized in lemmaadaptive.
Lemma 1
([29]). For matrix , the following are the characteristics of the adaptive loss function:
- 1.
- The norm is nonnegative and convex.
- 2.
- The norm is twice differentiable.
- 3.
- If , , then .
- 4.
- If , , then , where .
- 5.
- .
- 6.
- .
Thus, with the adaptive loss function, we may develop Equation (2) into
In general, different views of the data exhibit both consistency and inconsistency, where the consistency reflects the shared information across all views, while the inconsistency captures the unique diversity information of each view. To effectively capture the consistency and inconsistency information of the representation matrices among different views, we follow and decompose the representation tensor into consistent and inconsistent parts as [30], which are captured by and , respectively. In this paper, we aim to assist in capturing the strong commonalities among different views, and we propose to extract a common part from the multiple representation matrices, which is denoted as . Thus, each view’s representation matrix can be factorized as with a hard commonness constraint. Therefore, we may further develop Equation (4) into
where serves as an appropriate regularizer to enforce the desired structural properties of both and . In general, it is expected that the inconsistency of different views should not be significantly large since different views have close connections, which suggests that is sparse. To enhance the sparse structures of the inconsistency part, we consider the following two cases. First, the sample-wise sparsity has been widely considered, which leads to mode-2 sparsity of . Second, for each sample, the representation vectors in different views should be similar, which leads to a mode-3 sparse structure of . Thus, to ensure that has a joint mode-2 and mode-3 sparse structure, we further develop Equation (5) into
where is a balancing parameter. Although the sparsity of helps capture the commonness across different views to construct , we still need to exploit the structural constraint for for the desired structural properties of the common representation. First, it is natural to impose structural constraints on the consensus affinity matrix, which gives rise to
where extracts the diagonal elements of the input matrix and arranges them into a column vector. The constraints imposed in Equation (7) require that is nonnegative and symmetric and avoid a trivial interpretation of that the coefficient of a sample itself is the largest by restricting , which enforces the natural and desired property for an affinity matrix. To further exploit the local and nonlinear structures inherent in the data, we introduce the graph Laplacian to our model, which leads to
where serves the role of a balancing parameter and denotes a tensor that consists of graph Laplacian matrices of different views in frontal slices. It is seen that the manifold learning embedded in the third term of Equation (8) provides a consensus local geometric structure of across different views, which is important in revealing the structures of the data [31]. The structural constraints naturally treat as a graph matrix, which measures neighbor relationships of the data. For such data, the connected components are k, each corresponding to a distinct cluster.
To guarantee such property, we refer to the theorem stated below.
Theorem 1
([32]). For any and , let be its Laplacian matrix. The number of connected components present in is reflected by the multiplicity k of the eigenvalue 0 of .
Theorem 1 inspires us to restrict that has exactly k zero eigenvalues for the desired connectivity property of . It is straightforward to impose constraint into Equation (7) to restrict the rank of , with being the rank operator. However, it is widely recognized that this problem, which involves rank minimization, is NP-hard [32], making it challenging to solve. Thus, we refer to the following k-block diagonal regularizer for a relaxed rank constraint.
Definition 1
([14]). Given an affinity matrix , a k-block diagonal regularizer can be defined as
where denotes the matrix singular value of the input and is the i-th largest.
It is seen that the k-block diagonal regularizer can be treated as a relaxed rank constraint, by minimizing which we may ideally restrict the desired rank for the target graph Laplacian matrix. Then, ideally contains k connected sub-graphs, which correspond to the k clusters of the data and thus reveal the group structure of the data. Thus, with the connectivity constraint of , we further develop our model as
where is a balancing parameter. The aforementioned model is named Commonness and Inconsistency Learning with Structure Constrained Adaptive Loss Minimization for Multi-view Clustering (CISCAL-MVC). We summarize the flow diagram of the CISCAL-MVC in Figure 2. We will present an effective optimization algorithm to address Equation (10) in the next section.
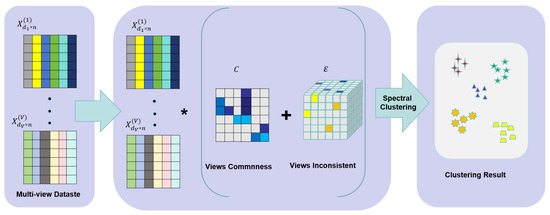
Figure 2.
Flow diagram of the proposed method. * denotes multiplication.
4. Optimization
In this section, we will develop an effective optimization algorithm for Equation (10) by employing the augmented Lagrange multiplier method (ALM). First, we introduce several auxiliary variables to facilitate the optimization and construct the augmented Lagrange function. Then, our algorithm efficiently solves the optimization problem by decomposing it into several manageable subproblems. For all the subproblems, we provide their corresponding closed-form solutions using various techniques, such as the Sylvester equation, shrinkage operator, etc. We update each of the variables while fixing the others till convergence. The detailed optimization procedure is presented as follows:
Since the fourth term is highly nonlinear and difficult to solve, we convert it to an equivalent form to facilitate the optimization. First, we may refer to the following Theorem 2 as a useful tool.
Theorem 2
([33]). ∀ and the following equality holds:
where denotes the inner product of matrices.
Then, according to Definition 1 and Theorem 2, we may rewrite as the following convex programming problem:
Thus, we may convert the original objective into an equivalent form as follows:
where denotes an operator that transforms the input vector into a diagonal matrix. To solve Equation (13), we first introduce auxiliary variables and . Then, the augmented Lagrange function of equation Equation (13) can be expressed as
where the Lagrange multipliers are given by , , and , and the penalty parameter of the ALM is given by , respectively.
4.1. -Subproblem
The subproblem connected with J is
Define and with then Equation (15) can be restructured as:
The above problem appears complicated in J and is not straightforward to solve. To
facilitate the optimization, we first reformulate the above problem into the following form:
To ensure that the above problem has a minimizer, we need to show that the above
problem is convex. For the first term, it is seen that the following
inequality holds:
which confirms the convexity of the first term of Equation (17). Since is the graph Laplacian matrix constructed from
we have
and thus
as well [31]. Moreover, it is clear that the second term of Equation (17) is linear while the last term
is quadratic. Then, it is clear that Equation (16) is quadratic and convex, which can be
solved by the first-order optimality condition:
The above equation is essentially a Sylvester equation. To be clearer, we define:
Then, by plugging Equation (20) into Equation (19), we obtain a standard Sylvester
equation as follows:
For the Sylvester equation in Equation (21), we may adopt various algorithms such as the Bartels–Stewart [34] or the Hessenberg–Schur [35] algorithm to efficiently resolve the problem, which generally requires complexity. It is noted that we may also apply other algorithms, such as the gradient descent, to the original optimization problem of Equation (17). By using the gradient, we need to obtain the gradient of the objective at each iteration, which requires complexity. The Sylvester equation solver directly addresses the first-order optimality conditions, typically achieving an exact solution in a finite number of steps, making it highly efficient and numerically stable for small to medium-scale problems. In contrast, gradient descent relies on iterative updates, often exhibiting slower convergence, particularly for ill-conditioned problems, leading to potential robustness issues. Without loss of generality, we adopt the Sylvester equation solver and summarize the above steps as the following operator:
4.2. -Subproblem
The subproblem for is presented as follows:
With straightforward algebra, the aforementioned problem can be reformulated equivalently as
For ease of notation, we define
Then, according to [14], Equation (24) admits a closed-form solution:
where denotes the nonnegative projection.
4.3. -Subproblem
The subproblem of is as follows:
According to [36], Equation (26) admits a closed-form solution:
where the eigenvectors of corresponding to the smallest k eigenvalues are represented by .
4.4. -Subproblem
The subproblem associated with is as follows:
In a way similar to Equation (16), we may rewrite the above problem into:
It is evident that Equation (29) can be solved by slice. For each , it is clear that the corresponding problem is quadratic and convex, and a closed-form solution can be obtained by the first-order optimality condition:
Thus, can be obtained by slice as
4.5. -Subproblem
For , the subproblem is:
The above problem is essentially a -shrinkage problem of along the mode-3 fiber, which can be clearly seen by a simplified standard form in the following:
Then, according to [37], Equation (33) admits a closed-form solution along the mode-3 fiber as follows:
where , and is a function that returns 0 if it does not satisfy the condition in the subscript and returns 0 if it does.
4.6. -Subproblem
For , the subproblem is
Similarly to Equation (32), the aforementioned problem can be solved using the -shrinkage operator; so, we have the following closed-form solution:
where .
4.7. Updating of ,, , and μ
We update the Lagrange multiplier and penalty parameters using classical methods, as outlined below:
where keeps that is increasing. We iterate the above steps until convergence is achieved, then we may obtain a unified view-commonness matrix . Finally, we apply standard spectral clustering techniques to to achieve the final clustering result.
4.8. Time Complexity
We analyze the time complexity of our method as follows. In particular, we analyze the dominant operations that determine the complexity of our algorithm at each iteration. For the J-subproblem, it needs to solve a Sylvester equation, which requires a time complexity of by utilizing the Bartels–Stewart algorithm [34]. For the C-subproblem, it
requires a time complexity . The time complexity for constructing graph Laplacian matrices is . Similarly to J, the W-subproblem requires a time complexity of for calculating the matrix multiplications and solving the Sylvester equations. For the -subproblem, it has a similar structure to J and requires a time complexity of . Regarding the subproblems of and , both entail l2,1 norm contraction
operations, leading to a time complexity of for each. In summary, it requires a
total time complexity of .
5. Experiments
In this section, experiments are carried out to validate the effectiveness of our method. Especially, we compare our method with nine baseline methods, which will be introduced in the following subsection. Six datasets are utilized, including the 3Sources [38], ORL [39], WebKB-Texas [40], COIL-20 [41], Caltech-7 [42], and Yale [43] datasets. We adopt four evaluation metrics—the clustering accuracy (ACC) as a measure of cluster assignment correctness, normalized mutual information (NMI) as an indication of clustering quality, purity (PUR) as a metric for cluster homogeneity, and the adjusted rand index (ARI) as a measure of clustering agreement—whose details can be found in [44,45,46,47,48]. Basically, the first three metrics values range within [0, 1] while the last one is within [−1, 1], where the larger value indicates better performance. All experiments in this paper are conducted using MATLAB 2018a on a workstation equipped with a 6-core Intel i5-8500T CPU running at 2.10 GHz and 16 GB of memory. The detailed experimental setup, along with the corresponding results, is presented in the subsequent parts of this section. The code for our method can be accessed on 28 March 2025, at https://www.researchgate.net/profile/Chong-Peng-8/publications.
5.1. Methods in Comparison
In the experiment, we conduct a comparison between our approach and nine other baseline methods: (1) SC [49] is a traditional clustering technique for single-view data. In our experiment, we execute SC independently on each view and present the optimal results; (2) MVSpec [50] extends the SC for multi-view data, which uses a weighted combination of kernel matrices of different views for clustering; (3) RMSC [22] constructs probability matrices from different views and learns a unified probability matrix with low-rank constraint for multi-view clustering; (4) MVGL [17] creates a unified graph by integrating affinity graphs from various views under a low-rank constraint, which is utilized for multi-view clustering; (5) BMVC [46] performs binary learning for representation and clustering; (6) SMVSC [11] performs anchor learning collaboratively and builds a unified graph to represent the underlying structures of the data; (7) MVSC [51] constructs a unified bipartite graph for clustering based on cross-view sample-anchor bipartite graphs; (8) FPMVS-CAG [52] introduces a parameter-free method that aims to obtain an anchor representation by combining anchor selection with graph construction for clustering; (9) JSMC [30] concurrently integrates the cross-view commonness and inconsistencies into the learning of subspace representations. (10) MvDSCN [53] learns a multi-view self-representation matrix in an end-to-end manner by integrating multiple backbones and combining convolutional autoencoders with self-representation.
5.2. Datasets
In our experiment, we utilize six benchmark datasets. The main features of these datasets are outlined in Table 1, and we briefly introduce them as follows: (1) 3Sources [38] comprises data from 948 news articles. Each article presents multiple points of view and is drawn from three online news platforms: BBC, Reuters, and the Guardian. We only select the instances that have complete information across all views. The feature dimensions of the three news platforms are 3068d, 3631d, and 3560d, respectively. (2) ORL [39] contains 400 facial images of 40 individuals. The images were captured under various lighting conditions, showcasing a variety of facial expressions and intricate details. Three types of features, including the 4096d intensity, 6750d Gabor, and 3304d LBP, are preserved in this dataset. (3) WebKB-Texas [40] consists of 187 documents from the University of Texas Department of Computer Science homepage. These documents belong to five categories, including student, project, course, staff, and faculty. Each document has two types of features, including 187d citation and 1703d content. (4) COIL-20 [41] consists of 1440 grayscale images of 20 objects. For each object, 72 images are captured from different angles. Three types of features are preserved in this dataset, including the 1024d intensity, 3304d LBP, and 6750d Gabor. (5) Caltech-7 [42] selects 7 out of a total number of 101 classes from the Caltech-101 dataset, including Faces, Garfield, Snoopy, StopSign, Windsor-Chair, Dollar Bill, and Motorbikes. This dataset contains three types of features, including 512d GIST, 1984d HOG, and 928d LBP. (6) Yale [43] consists of 165 facial images of 15 persons. These images are captured with varying facial expressions under different lighting conditions. There are three types of features in this dataset, including 4096d intensity, 6750d Gabor, and 3304d LBP. We visually show some examples of the image datasets in Figure 3.

Table 1.
Overview of benchmark datasets.

Figure 3.
Visual examples of the image datasets. From top to bottom are ten samples selected from the ORL, COIL-20, Yale, and Caltech-7 datasets, respectively.
5.3. Clustering Performance
For all methods in the comparison, we utilize a grid search strategy for parameter tuning in the experiment. For our method, we adjust the balancing parameters , , and from the set , with the parameter within the set , respectively. For the baseline methods, if not otherwise clarified in the original paper, we tune the balancing parameters within as well. For each method, we enumerate all possible combinations of parameter values on each dataset and record the highest result for each evaluation metric, respectively. The clustering results are presented in detail in Table 2.

Table 2.
Comparison of clustering performance across various methods on benchmark datasets.
The experimental results demonstrate that the proposed CISCAL-MVC consistently achieves the best clustering performance across all benchmark datasets. In general, it secures the first-place results in 21 out of 24 cases and the second-best results in 3 cases, which is highly promising. Among the baseline methods, the JSMC and MvDSCN emerge as the most competitive, achieving at least the top three results in 24 and 14 out of 24 cases, respectively. Compared to other baseline methods, JSMC demonstrates substantial improvements. Based on the results, the following key observations can be made:
(1) On the 3Sources dataset, the CISCAL-MVC achieves the highest scores in all metrics, improving the second-best performance by 1.46% in ACC, 2.54% in NMI, 0.73% in ARI, and 2.96% in PUR, respectively. Notably, the MvDSCN, JSMC, and CISCAL-MVC are the only three methods that achieve results higher than 60% across all metrics, highlighting their robustness in handling multi-view data.
(2) On the ORL dataset, the CISCAL-MVC dominates with 89.25% ACC, 93.59% NMI, 83.58% ARI, and 90.50% PUR, which is highly promising. Among the baseline methods, the MvDSCN and JSMC are the most competitive, securing the second and third-best results, respectively. This demonstrates CISCAL-MVC’s ability to effectively capture both consistency and diversity across views.
(3) On the WebKB-Texas dataset, the CISCAL-MVC again achieves the best performance, with 77.83% ACC, 42.24% NMI, 44.84% ARI, and 77.83% PUR. While the MvDSCN shows competitive performance on the 3Sources and ORL datasets, it fails to rank among the top three on this dataset. This observation further emphasizes the robustness of CISCAL-MVC in handling diverse and challenging data structures. Moreover, the WebKB-Texas and 3Sources datasets are collected from a real-world news platform and academic website, thus the effectiveness of the proposed method on these datasets demonstrates the potential applicability in real-world scenarios.
(4) On the COIL-20 dataset, the CISCAL-MVC achieves perfect scores (100%) across all metrics, demonstrating its exceptional ability to effectively capture the underlying data structure. Among the baseline methods, the JSMC and MVGL are the most competitive, but their results are lower than CISCAL-MVC by approximately 16.04% in ACC, 6.20% in NMI, 18.72% in ARI, and 11.32% in PUR. Although MvDSCN is inferior to MVGL on this dataset, it is among the only three methods that consistently achieve results higher than 80%, showcasing the potential of deep learning approaches.
(5) On the Caltech-7 dataset, the CISCAL-MVC achieves the highest results, improving the second-best performance by 9.79% in ACC and 8.60% in ARI. While the JSMC and MvDSCN show competitive performance in certain metrics, they lack consistency across all metrics. For instance, the third-best results are obtained by different methods, such as the MvDSCN and MVGL, indicating their instability. In contrast, the CISCAL-MVC demonstrates superior stability and performance, making it a more reliable choice.
(6) On the Yale dataset, the CISCAL-MVC achieves the best result in purity (74.72%) and the second-best results in the other metrics. On this dataset, the CISCAL-MVC, MvDSCN, and JSMC show comparable performance, with at least 10.81% improvement in ACC, 8.73% in NMI, and 10.71% in ARI compared to other baseline methods. This further highlights the effectiveness of the CISCAL-MVC in leveraging high-order information and cross-view relationships.
To further validate the superiority of the proposed method from a statistical perspective, we apply the Wilcoxon signed-rank test to compare the clustering performance of the proposed method against baseline methods. Specifically, we aggregate the results across multiple datasets and evaluation metrics for each method. The Wilcoxon signed-rank test is then conducted on the combined results, with the statistical outcomes presented in Table 3. The results reveal that the p-value is consistently less than 0.001 in all cases, providing strong statistical evidence that the proposed method significantly outperforms the baseline methods.

Table 3.
Comparison results of Wilcoxon signed rank tests on a baseline dataset.
In summary, the CISCAL-MVC consistently outperforms all baseline methods across different datasets and metrics. While the MvDSCN and JSMC show competitive performance in certain cases, they are unable to match the overall superiority of CISCAL-MVC. Notably, the JSMC demonstrates robustness across datasets, but other baseline methods fail to achieve consistent performance. Compared to individual baseline methods, the improvements achieved by the CISCAL-MVC are more significant. These observations confirm the effectiveness, as well as the potential real-world applicapability, of the proposed method.
5.4. Ablation Study
To assess the importance of incorporating various components in our model, we conduct an ablation study for evaluation. We conduct experiments comparing our model with three of its variants. In particular, these variants are developed by removing a specific term from our model, which is obtained by setting the corresponding parameter, i.e., , , or to zero, respectively. For the variant, we adhere to the experimental settings detailed in Section 5.3 to adjust the remaining parameters. We report the results of the CISCAL-MVC, as well as its variants, in Table 4.

Table 4.
Comparison of the CISCAL-MVC and its variants.
Based on the results we obtained, it can be observed that the overall model always generates superior performance to the variants. For example, compared with these variants, the CISCAL-MVC shows about 20.98–65.74%, 9.26–41.88%, and 8.19–30.23% improvements across all datasets in purity, respectively, which is quite notable. In other metrics, we consistently observe that the performance of the model is significantly degraded when any single component is removed from the overall architecture. This consistent pattern across multiple evaluations underscores the critical role each component plays in the model’s functionality and overall effectiveness. Thus, it becomes evident that the various components used in our model are not only essential but also synergistically contribute to its robustness and superior performance.
5.5. Visual Illustration of Data Distribution
In this test, we visually show how the consistent and inconsistent parts of the representation behave in the learning process by showing the distribution of the data. Without loss of generality, we show the results using the ORL dataset from two perspectives.
First, we visually present and the different views of in Figure 4. The results demonstrate that the consistent part effectively preserves the strong group structure of the data, while the inconsistent part captures cross-view inconsistencies without exhibiting clear structural patterns. Furthermore, we visualize the distributions of the features recovered by the consistent and inconsistent representations using t-SNE in Figure 5. The results reveal that the features derived from the consistent representation exhibit distinct cluster patterns, whereas those from the inconsistent representation lack any discernible clustering structure. These observations provide a clear visual illustration of how the consistent and inconsistent components of the representation behave during the clustering process. They also validate the effectiveness of CISCAL-MVC in uncovering meaningful cluster patterns within the data.

Figure 4.
Visual illustration of the overall, consistent, and inconsistent representation matrices of different views of the ORL dataset. In particular, we show the results of the second and third views. On the diagonal of the figures, clear group structures can be observed in the consistent representation.
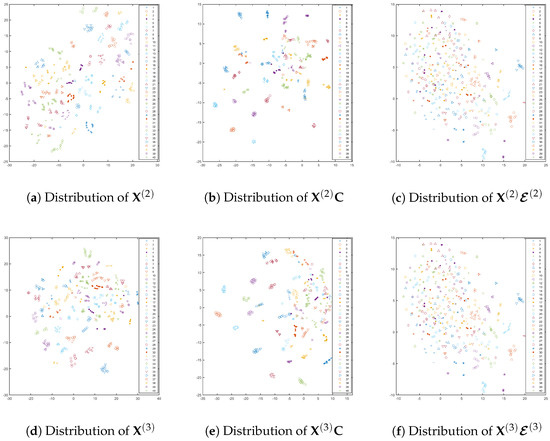
Figure 5.
T−SNE illustration of the distributions of the original and recovered features of the ORL dataset. In particular, we show the results of the second and third views. The features recovered by the consistent representation have a clearer cluster structure than the original features of the data with t−SNE visualization.
5.6. Convergence Analysis
In this convergence analysis test, we carry out experiments to provide empirical evidence of the convergence behavior exhibited by the proposed method. Through these experiments, we aim to provide robust empirical evidence that substantiates the efficiency and reliability of the method’s convergence properties. Without compromising generality, we plot the error curves of the 3Sources, ORL, and COIL-20 datasets, where the parameters are fixed at , , , and . For ease of representation, we use in the subscript to denote the number of iterations. Since is used for the final clustering, we focus on the convergent behavior of . In this test, we cancel the other termination conditions and run our algorithm for 200 iterations. Then, we plot the first 200 values of the sequence that are generated on the 3Sources, ORL, and COIL-20 datasets in Figure 6. Based on the experimental results, we find that the CISCAL-MVC converges in approximately 50 iterations, which is quite significant.
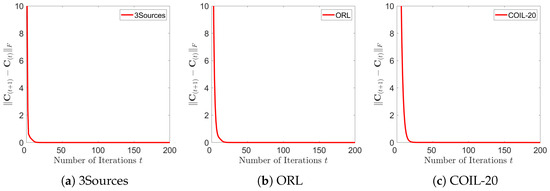
Figure 6.
Plot of the first 200 values of the sequence generated by the CISCAL-MVC on 3Sources, ORL, and COIL-20 datasets, respectively. represents the absolute difference of two consecutive updates, which measures the convergent behavior of the proposed algorithm. As observed, the sequences generally converge within about 50 iterations, which shows the fast convergent property of the CISCAL-MVC.
Next, we undertake additional experiments to delve deeper into the convergent behavior of the CISCAL-MVC. In particular, we treat as the convergent solution, which is denoted as for clarity. Then, we plot the first 50 values of the sequence that are generated on the 3Sources, ORL, and COIL-20 datasets in Figure 7, respectively. From the results, we may observe that the values of are in the range of ; this means that CISCAL-MVC has about a linear convergent rate.
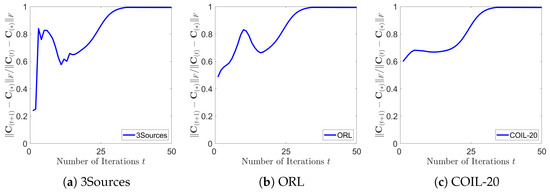
Figure 7.
Plot of the first 50 values of the sequence generated by the CISCAL-MVC on the 3Sources, ORL, and COIL-20 datasets, respectively. represents the relative difference of two consecutive updates, which measures the convergent rate of the proposed algorithm. As observed, the values are generally within (0, 1), which empirically suggests that the CISCAL-MVC has a linear convergence rate on these datasets.
These observations confirm the convergent behavior of the CISCAL-MVC, as well as its efficiency, that is essentially important for learning algorithms for guaranteed performance.
5.7. Comparison of Time Cost
In this test, we compare the time cost of our method with the baselines. Among the baseline methods, the MvDSCN and JSMC show the second and third best performance. Among the remaining baseline methods, the RMSC shows relatively better performance. Since the clustering result is essential, for clarity of presentation, we only compare our method with the above three baseline methods that show superior performance among these methods.
First, we compare the time complexity of these methods. In particular, the MvDSCN, RMSC and JSMC have time complexity of , , , respectively, Where M represents the spatial dimension of the input data, l represents the l-th convolutional layer, Q represents the number of convolutional kernels in that layer, and K represents the size of each convolutional kernel. It can be seen that the non-deep learning methods generally require complexity, which are comparable. Next, we empirically compare the time cost of these methods in Figure 8. From the results, it can be seen that the CISCAL-MVC is several times faster than the RMSC and JMSC on the COIL-20 and Caltech-7 datasets. On other datasets, such as the 3Sources, WebKB-Texas, and Yale, all methods terminate within a few seconds. These observations confirm that the CISCAL-MVC is at least comparable to, if not faster than, the baseline methods from both theoretical time complexity and empirical time cost perspectives. Considering the superiority of the CISCAL-MVC in clustering performance, such time cost is acceptable.
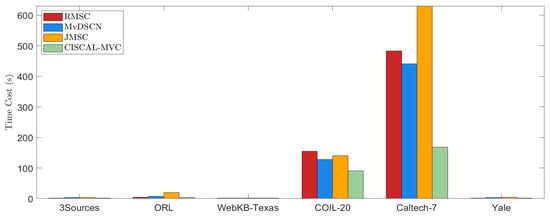
Figure 8.
Time cost of different methods for comparison. These methods are selected for comparison due to their superior clustering performance as reported in Section 5.3.
5.8. Parametric Sensitivity
In this experiment, we empirically investigate the impact of key parameters on the learning performance of the proposed method. Without loss of generality, we use the ORL dataset to present the results in Figure 9, with fixed values of and . To systematically evaluate parameter sensitivity, we vary the parameters over the following ranges: , , , and . For each parameter, we analyze its individual impact on the performance of CISCAL-MVC while keeping the other parameters optimized. The experimental results reveal that the performance of CISCAL-MVC exhibits minimal variation across different values of and , indicating robustness to these parameters. Furthermore, CISCAL-MVC achieves superior performance when smaller values are selected for and . Notably, the method demonstrates competitive performance across a wide range of small values for and These findings suggest that CISCAL-MVC is generally insensitive to its parameter settings. For practical implementation, we recommend selecting small values for and , while adopting moderate values for and .
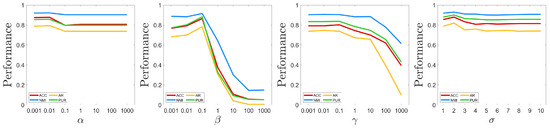
Figure 9.
Performance changes of the CISCAL-MVC with respect to different values of the parameters on the ORL dataset. In particular, in each figure, the other parameters are tuned to the best. As can be seen, the CISCAL-MVC is insensitive to and and achieves superior results with a broad selection of small values for and .
5.9. Data Reconstruction
In this test, we conduct experiments to empirically showcase how the consistency and inconsistency parts of the representation capture features from the data. For illustrative purposes, and without compromising generality, we use the Yale and ORL datasets. Since the Yale dataset does not contain pixel features, we additionally introduce the original pixel features to the dataset as the 4-th view and use the augmented data to learn and , which provides a clearer visualization of the learning effects. Then, we visually show some of the original and reconstructed features in Figure 10, respectively. Based on the results, we make the following key observations: First, the features reconstructed by the overall representation matrix capture well the information from the original data, where the recovered features are visually close to the original ones. Second, the features reconstructed by the consistency part well capture the key features of the data, and the reconstructed features of different samples within the same group are visually similar with strong commonness. Third, the features captured by the inconsistency part show the diversity of the samples. These findings highlight the importance of both the consistency and inconsistency components of the representation in capturing different types of features.

Figure 10.
Visualization of original and reconstructed features on the Yale dataset, where we use the pixel features for illustration. As observed from the figures, the recovered features well capture the information from the original features. Moreover, the consistent features well capture the key features of the data, where the features from the same cluster have high visual similarities. In contrast, the inconsistent features are sparse and capture diverse features from the data.
6. Conclusions
In this paper, a novel approach for multi-view subspace clustering, named CISCAL-MVC, is presented. First, the novel method utilizes an adaptive loss function, which is more flexible to account for noise effects. Moreover, both the consistency and inconsistency parts of the representation matrices are exploited across different views. In particular, the consistency part exhibits hard commonness with the desired structural property, while the inconsistency part captures cross-mode sparsity to account for cross-mode differences. Then, the cross-mode sparsity constraints promote the inconsistency part to effectively exploit high-order information, thereby enhancing the consistency part to reveal high-order information of the data as well. The effectiveness and superiority of the proposed method are confirmed by extensive experiments.
Despite the effectiveness of CISCAL-MVC, there are still several aspects that could be further improved. First, the high time complexity of CISCAL-MVC limits its scalability to large-scale datasets. One potential solution to enhance efficiency is to adopt the anchor-based strategy, which approximates the representation of samples using a selected set of anchor points. This approach can be formulated as: , where are the anchors, m is the number of anchor points, denotes the consistency representation, and is the inconsistent part of the representation. Since , the approach may significantly reduce the time complexity of the CISCAL-MVC. Second, while the current formulation of CISCAL-MVC incorporates the local geometric structure of the data on a manifold, it may not effectively capture the complex high-order neighbor relationships inherent in the data [54]. To address this limitation, inspired by recent advancements in graph-based learning [55], a high-order neighbor graph could be constructed to better preserve the intricate relationships among samples. This would allow the method to leverage more sophisticated structural information, potentially leading to improved clustering performance. Third, the proposed method requires that the dataset contains complete entries. For incomplete multi-view data, we present a potential approach as follows. We may first learn incomplete affinity matrices of the data using the observed entries. Then, we may adopt a low-rank tensor recovery technique to complete the affinity tensor for the subsequent learning procedure. However, since incomplete multi-view clustering is often considered as a different task from the general multi-view clustering [56], we do not fully expand this line of research in our current work.
The primary objective of this work is to develop a novel multi-view clustering framework that effectively utilizes cross-view high-order information, spatial structure, and both consistency and diversity across views. While the aforementioned improvements, such as anchor-based efficiency enhancement and high-order graph construction, could further advance the performance and scalability of CISCAL-MVC, they are beyond the scope of this paper. These directions, however, present promising avenues for future research.
Author Contributions
Conceptualization, K.Z., K.K. and C.P.; methodology, K.Z., K.K. and C.P.; software, K.Z.; validation, Y.B. and C.P.; formal analysis, K.Z. and K.K.; investigation, Y.B.; resources, K.Z. and K.K.; data curation, K.Z. and K.K.; writing—original draft preparation, K.Z. and K.K.; writing—review and editing, C.P.; visualization, K.Z. and K.K.; supervision K.Z., K.K., Y.B. and C.P.; project administration, K.Z., K.K., Y.B. and C.P.; funding acquisition, C.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Shandong Province Colleges and Universities Youth Innovation Technology Plan Innovation Team Project under Grant 2022KJ149 and the National Natural Science Foundation of China (NSFC) under Grant 62276147.
Data Availability Statement
We did not create new data, and the data sets we used were all existing mainstream data. However, due to privacy, we have chosen not to make the dataset public.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviation
The following abbreviation is used in this manuscript:
| CISCAL-MVC | Commonness and Inconsistency Learning with Structure Constrained Adaptive Loss Minimization for Multi-view Clustering |
References
- Lei, T.; Liu, P.; Jia, X.; Zhang, X.; Meng, H.; Nandi, A.K. Automatic fuzzy clustering framework for image segmentation. IEEE Trans. Fuzzy Syst. 2019, 28, 2078–2092. [Google Scholar]
- Peng, C.; Zhang, J.; Chen, Y.; Xing, X.; Chen, C.; Kang, Z.; Guo, L.; Cheng, Q. Preserving bilateral view structural information for subspace clustering. Knowl.-Based Syst. 2022, 258, 109915. [Google Scholar] [CrossRef]
- Park, N.; Rossi, R.; Koh, E.; Burhanuddin, I.A.; Kim, S.; Du, F.; Ahmed, N.; Faloutsos, C. Cgc: Contrastive graph clustering forcommunity detection and tracking. In Proceedings of the ACM Web Conference 2022, Lyon, France, 25–29 April 2022; pp. 1115–1126. [Google Scholar]
- Gönen, M.; Margolin, A.A. Localized data fusion for kernel k-means clustering with application to cancer biology. In Proceedings of the Advances in Neural Information Processing Systems, Quebec, QC, Canada, 8–13 December 2014; pp. 1305–1313. [Google Scholar]
- Guan, R.; Zhang, H.; Liang, Y.; Giunchiglia, F.; Huang, L.; Feng, X. Deep feature-based text clustering and its explanation. IEEE Trans. Knowl. Data Eng. 2020, 34, 3669–3680. [Google Scholar]
- Peng, C.; Kang, Z.; Li, H.; Cheng, Q. Subspace clustering using logdeterminant rank approximation. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 925–934. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar]
- Peng, C.; Zhang, Y.; Chen, Y.; Kang, Z.; Chen, C.; Cheng, Q. Log-based sparse nonnegative matrix factorization for data representation. Knowl.-Based Syst. 2022, 251, 109127. [Google Scholar]
- Vidal, R.; Ma, Y.; Sastry, S. Generalized principal component analysis (gpca). IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1945–1959. [Google Scholar] [CrossRef]
- Rao, S.; Tron, R.; Vidal, R.; Ma, Y. Motion segmentation in the presence of outlying, incomplete, or corrupted trajectories. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1832–1845. [Google Scholar]
- Sun, M.; Zhang, P.; Wang, S.; Zhou, S.; Tu, W.; Liu, X.; Zhu, E.; Wang, C. Scalable multi-view subspace clustering with unified anchors. In Proceedings of the 29th ACM International Conference on Multimedia, Chengdu, China, 20–24 October 2021; pp. 3528–3536. [Google Scholar]
- Peng, C.; Kang, Z.; Cheng, Q. Subspace clustering via variance regularized ridge regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2931–2940. [Google Scholar]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar]
- Wang, F.; Chen, C.; Peng, C. Essential low-rank sample learning for group-Aware subspace clustering. IEEE Signal Process. Lett. 2023, 30, 1537–1541. [Google Scholar]
- Zhang, C.; Fu, H.; Hu, Q.; Cao, X.; Xie, Y.; Tao, D.; Xu, D. Generalized latent multi-view subspace clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 86–99. [Google Scholar]
- Wang, H.; Yang, Y.; Liu, B. Gmc: Graph-based multi-view clustering. IEEE Trans. Knowl. Data Eng. 2019, 32, 1116–1129. [Google Scholar] [CrossRef]
- Zhan, K.; Zhang, C.; Guan, J.; Wang, J. Graph learning for multiview clustering. IEEE Trans. Cybern. 2017, 48, 288–2895. [Google Scholar] [CrossRef]
- Kumar, A.; Rai, P.; Daume, H. Co-regularized multi-view spectral clustering. In Proceedings of the Advances in Neural Information Processing Systems, Granada, Spain, 12–17 December 2011; pp. 1413–1421. [Google Scholar]
- Wang, X.; Guo, X.; Lei, Z.; Zhang, C.; Li, S.Z. Exclusivity-consistency regularized multi-view subspace clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 923–931. [Google Scholar]
- Bai, R.; Huang, R.; Qin, Y.; Chen, Y.; Xu, Y. A structural consensus representation learning framework for multi-view clustering. Knowl.-Based Syst. 2024, 283, 111132. [Google Scholar] [CrossRef]
- Wu, J.; Lin, Z.; Zha, H. Essential tensor learning for multi-view spectral clustering. IEEE Trans. Image Process. 2019, 28, 5910–5922. [Google Scholar] [PubMed]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec, QC, Canada, 27–31 July 2014; pp. 2149–2155. [Google Scholar]
- Li, R.; Zhang, C.; Fu, H.; Peng, X.; Zhou, T.; Hu, Q. Reciprocal multi-layer subspace learning for multi-view clustering. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 8172–8180. [Google Scholar]
- Zhang, C.; Fu, H.; Liu, S.; Liu, G.; Cao, X. Low-rank tensor constrained multiview subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1582–1590. [Google Scholar]
- Luo, S.; Zhang, C.; Zhang, W.; Cao, X. Consistent and specific multi-view subspace clustering. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; pp. 3730–3737. [Google Scholar]
- Chen, J.; Yang, S.; Mao, H.; Fahy, C. Multiview subspace clustering using low-rank representation. IEEE Trans. Cybern. 2021, 52, 12364–12378. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Chen, J.; Lian, C.; Zeng, Z. Multi-view class incremental learning. Inf. Fusion 2024, 102, 102021. [Google Scholar] [CrossRef]
- Liu, S.; Wang, S.; Zhang, P.; Xu, K.; Liu, X.; Zhang, C.; Gao, F. Efficient One-Pass Multi-View Subspace Clustering with Consensus Anchors. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 22 February–1 March 2022; pp. 7576–7584. [Google Scholar]
- Nie, F.; Wang, H.; Huang, H.; Ding, C. Adaptive loss minimization for semisupervised elastic embedding. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–9 August 2013; pp. 1565–1571. [Google Scholar]
- Cai, X.; Huang, D.; Zhang, G.Y.; Wang, C.D. Seeking commonness and inconsistencies: A jointly smoothed approach to multi-view subspace clustering. Inf. Fusion. 2023, 91, 364–375. [Google Scholar]
- Cai, D.; He, X.; Han, J. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 1548–1560. [Google Scholar]
- Lu, C.; Feng, J.; Lin, Z.; Mei, T.; Yan, S. Subspace clustering by block diagonal representation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 48–501. [Google Scholar] [CrossRef]
- Dattorro, J. Convex Optimization & Euclidean Distance Geometry, 2nd ed.; Meboo Publishing: Palo Alto, CA, USA, 2018. [Google Scholar]
- Bartels, R.H.; Stewart, G.W. Solution of the matrix equation AX + XB = C. Commun. ACM 1972, 15, 820–826. [Google Scholar] [CrossRef]
- Golub, G.; Nash, S.; Van, C. A Hessenberg-Schur method for the problem AX + XB= C. IEEE Trans. Autom. Control. 1979, 24, 909–913. [Google Scholar]
- Xie, X.; Guo, X.; Liu, G.; Wang, J. Implicit block diagonal low-rank representation. IEEE Trans. Image Process. 2017, 27, 477–489. [Google Scholar] [CrossRef] [PubMed]
- McCoy, M.B.; Tropp, J.A. Two proposals for robust pca using semidefinite programming. Electron. J. Stat. 2010, 5, 1123–1160. [Google Scholar] [CrossRef]
- Wang, H.; Li, H.; Fu, X. Auto-weighted mutli-view sparse reconstructive embedding. Multimed. Tools Appl. 2019, 78, 30959–30973. [Google Scholar] [CrossRef]
- Hu, Z.; Nie, F.; Wang, R.; Li, X. Multi-view spectral clustering via integrating nonnegative embedding and spectral embedding. Inf. Fusion 2020, 55, 251–259. [Google Scholar] [CrossRef]
- Craven, M.; DiPasquo, D.; Freitag, D.; McCallum, A.; Mitchell, T.; Nigam, K.; Slattery, S. Learning to extract symbolic knowledge from the world wide web. In Proceedings of the AAAI Conference on Artificial Intelligence, Madison, WI, USA, 26–30 July 1998; pp. 509–516. [Google Scholar]
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (Coil-20); Department of Computer Science, Columbia University: New York, NY, USA, 1996. [Google Scholar]
- Li, F.-F.; Fergus, R.; Perona, P. Learning generative visual models from few training examples: An incremental bayesian approach tested on 101 object categories. In Proceedings of the 2004 Conference on Computer Vision and Pattern Recognition Workshop, Washington, DC, USA, 27 June–2 July 2004; p. 178. [Google Scholar]
- Chen, M.S.; Huang, L.; Wang, C.D.; Huang, D.; Lai, J.H. Relaxed multiview clustering in latent embedding space. Inf. Fusion 2021, 68, 8–21. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Li, M.; Wang, L.; Tang, C.; Yin, J.; Shen, D.; Wang, H.; Gao, W. Late fusion incomplete multi-view clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2410–2423. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Zhang, Z.; Liu, L.; Shen, F.; Shen, H.T.; Shao, L. Binary multi-view clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1774–1782. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.D.; Peng, H.; Lai, J.; Kwoh, C.K. Enhanced ensemble clustering via fast propagation of cluster-wise similarities. IEEE Trans. Syst. Man. Cybern. Syst. 2018, 51, 508–520. [Google Scholar] [CrossRef]
- Sharma, K.; Seal, A.; Yazidi, A.; Krejcar, O. S-Divergence-Based Internal Clustering Validation Index. Int. J. Interact. Multimedia Artif. Intell. 2023, 8, 127–139. [Google Scholar]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 849–856. [Google Scholar]
- Tzortzis, G.; Likas, A. Kernel-based weighted multi-view clustering. In Proceedings of the 2012 IEEE 12th international conference on data mining, Brussels, Belgium, 10–13 December 2012; pp. 675–684. [Google Scholar]
- Li, Y.; Nie, F.; Huang, H.; Huang, J. Large-scale multi-view spectral clustering via bipartite graph. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 2750–2756. [Google Scholar]
- Wang, S.; Liu, X.; Zhu, X.; Zhang, P.; Zhang, Y.; Gao, F.; Zhu, E. Fast parameter-free multi-view subspace clustering with consensus anchor guidance. IEEE Trans. Image Process. 2021, 31, 556–568. [Google Scholar] [CrossRef] [PubMed]
- Zhu, P.; Yao, X.; Wang, Y.; Hui, B.; Du, D.; Hu, Q. Multiview deep subspace clustering networks. IEEE Trans. Cybern. 2024, 54, 4280–4293. [Google Scholar]
- Peng, C.; Kang, K.; Chen, Y. Fine-grained essential tensor learning for robust multi-view spectral clustering. IEEE Trans. Image Process. 2024, 33, 3145–3160. [Google Scholar]
- Peng, C.; Zhang, K.; Chen, Y. Cross-view diversity embedded consensus learning for multi-view clustering. In Proceedings of the the Thirty-Third International Joint Conference on Artificial Intelligence, Jeju Island, Republic of Korea, 3–9 August 2024; pp. 4788–4796. [Google Scholar]
- Wen, J.; Zhang, Z.; Zhang, B.; Xu, Y.; Zhang, Z. A Survey on Incomplete Multiview Clustering. IEEE Trans. Cybern. 2023, 53, 1136–1149. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).