Abstract
Hierarchical Federated Learning (HFL) for the Internet of Vehicles (IoV) leverages roadside units (RSU) to construct a low-latency, highly scalable multilayer cooperative training framework. However, with the rapid growth in the number of vehicle nodes, this framework faces two major challenges: (i) communication inefficiency under bandwidth-constrained conditions, where uplink congestion imposes significant burden on intra-framework communication; and (ii) interference from untrustworthy vehicle nodes, which disrupts model training and affects convergence. Therefore, in order to achieve secure aggregation while alleviating the communication bottleneck problem, we design a hierarchical three-layer federated learning framework with Gradient Quantization (GQ) and secure aggregation, called FedHSQA, which further integrates anomaly scoring to enhance robustness against untrustworthy vehicle nodes. Specifically, FedHSQA organizes IoV devices into three layers based on their respective roles: the cloud service layer, the RSU layer, and the vehicle node layer. During each non-initial communication round, the cloud server at the cloud layer computes anomaly scores for vehicle nodes using a Kullback–Leibler (KL) divergence-based multilayer perceptron (MLP) model. These anomaly scores are used to design a secure aggregation algorithm (ASA) that is robust to anomalous behavior. The anomaly scores and the aggregated global model are then transmitted to the RSU. To further reduce communication overhead and maintain model utility, FedHSQA introduces an adaptive GQ method based on the anomaly scores (ASQ). Unlike conventional vehicle node-side quantization, ASQ is performed at the RSU layer. It calculates the Jensen–Shannon (JS) distance between each vehicle node’s anomaly distribution and the target distribution, and adaptively adjusts the quantization level to minimize redundant gradient transmission. We validate the robustness of FedHSQA against anomalous nodes through extensive experiments on three real-world datasets. Compared to classical aggregation algorithms and GQ methods, FedHSQA reduced the average network traffic consumption by approximately 30 times while improving the average accuracy of the aggregation model by about 5.3%.
1. Introduction
With the rapid advancement of Intelligent Transport Systems (ITS), the Internet of Vehicles (IoV) emerges as the critical system for enabling efficient communication, collaborative sensing, and intelligent decision-making among vehicle nodes by improving traffic flow prediction and accelerating the deployment of autonomous driving and related applications [1,2,3,4,5]. In the IoV system, vehicle nodes collect and process large volumes of local data continuously by being equipped with sensors and onboard computing units. These data carry significant value and computational potential for training high-performance machine learning models. However, concerns over privacy protection, communication overhead, and bandwidth limitations discourage vehicle nodes from sharing raw data, resulting in data silos that constrain the scalability of IoV systems. To enable data fusion and knowledge sharing without compromising privacy, recent studies introduce Hierarchical Federated Learning (HFL) into the IoV system [6,7,8,9,10]. The HFL framework divides IoV devices into multiple layers based on their geographic location and functional roles. Under the HFL framework, each vehicle node trains machine learning models locally and transmits model updates to the roadside unit (RSU), which forwards aggregated updates to the cloud-based cloud server. This process facilitates efficient and privacy-preserving collaborative learning, helps overcome the problem of data silos, and supports the practical deployment of intelligent IoV applications. However, as the HFL framework scales across large IoV systems, the frequent transmission of model updates from numerous vehicle nodes significantly increases uplink communication overhead, introduces latency, and slows global model convergence [11,12,13,14,15]. Therefore, reducing the communication burden of the HFL framework for IoV while maintaining model performance becomes a critical challenge that demands urgent attention. To this end, some studies introduce the Gradient Quantization (GQ) method into the HFL framework for IoV, aiming to reduce uplink data transmission and alleviate bandwidth bottlenecks by compressing local model gradients and discarding redundant information [16,17,18,19,20]. GQ method effectively reduces the volume of data uploaded in each communication round, thereby improving the overall system efficiency to a certain extent. However, existing GQ methods still face a key limitation: most adopt undifferentiated quantization strategies during compression, which may discard critical gradient information and ultimately affect the accuracy of the aggregated model. To address this issue, recent works explore mechanisms such as clustering and head node communication to enhance the adaptability and robustness of quantization strategies [21,22,23]. Nevertheless, these approaches typically overlook the heterogeneity in data distribution across vehicle nodes, especially in the presence of anomalous nodes (e.g., due to malicious attacks) [24,25,26]. As a result, they fail to effectively identify and handle anomalous model updates, thereby degrading the performance of the aggregated model in complex traffic environments with heterogeneous data distributions. As a result, these methods fall short of fully addressing the key challenges faced by the HFL framework in IoV scenarios.
Therefore, in order to achieve secure aggregation while alleviating the communication bottleneck problem, we design a hierarchical three-layer federated learning framework with gradient compression and secure aggregation based on anomalous vehicle node scores, called FedHSQA. FedHSQA enhances the aggregation model’s ability to identify and defend against anomalous vehicle nodes by integrating anomaly detection mechanisms while ensuring communication efficiency, providing a new solution for achieving an efficient and reliable HFL framework for IoV. Specifically, during non-initial communication rounds, the cloud server in FedHSQA performs anomaly scoring on vehicle nodes using an MLP model before aggregating the model updates uploaded by RSUs. It uses Kullback–Leibler (KL) divergence as the loss function to measure anomaly severity and applies the resulting scores to weighted aggregation [27], the secure aggregation algorithm of FedHSQA, called ASA. Once the scores are generated, the cloud server sends the score vector to the RSU along with the updated aggregated model parameters. To address limited communication resources and client heterogeneity, FedHSQA designs an adaptive GQ method based on anomaly scoring, called ASQ. Each vehicle node constructs a single-node distribution from its own score, computes the Jensen–Shannon (JS) distance to the target distribution [28], and maps the result to its adaptive quantization level. A larger distance indicates a higher probability of anomaly and results in a lower quantization level; a smaller distance preserves more information. ASQ enables adaptive adjusted communication compression, effectively reducing communication costs while increasing the robustness to the abnormal vehicle nodes in the IoV system. The main contributions of this paper are as follows:
- We propose a three-layer HFL framework for IoV, called FedHSQA, which integrates GQ and anomaly detection for vehicle nodes.
- We propose a secure aggregation algorithm based on anomaly scoring, called ASA, which adopts KL divergence as the loss function to improve the robustness of the aggregation process against anomalous vehicle nodes.
- We propose an anomaly score-based GQ method, called ASQ, which resolves the impact of anomalous data on the global model by calculating the JS distance and mapping it to adaptive quantization levels.
- We validate the effectiveness of FedHSQA under various parameter settings on several datasets. Experimental results show that compared to the classical aggregation algorithms and quantization methods, FedHSQA exhibits strong robustness to anomalous vehicle nodes under the HFL framework for IoV.
2. Related Work
2.1. Hierarchical Federated Learning
Federated learning (FL) typically assumes a direct connection between clients and the server in theoretical designs [29]. However, in practical deployments, training devices often adopt a layered framework. To bridge this gap, existing studies have proposed the HFL framework, which introduce intermediate layers (e.g., clusters or RSU) to coordinate devices across different layers and enhance system scalability. Although the layered framework offers structural advantages, it still encounters several challenges. These include model synchronization across multiple layers, convergence difficulties caused by data heterogeneity, and the trade-off between communication efficiency and privacy protection.
Considering that non-independent and identically distributed (non-IID) data on clients can lead to asynchronous model bias across multiple levels and degrade global convergence, MTGC [30] introduces a multi-timescale gradient correction mechanism. This method incorporates two control variables to correct gradient bias from clients to clusters and from clusters to the global model, respectively. Theoretical analysis proves that its convergence upper bound is independent of data heterogeneity, thereby improving convergence stability in heterogeneous environments. However, MTGC overlooks practical issues such as communication delays and system asynchrony, which limits its adaptability in complex network settings. To alleviate network congestion caused by large-scale client participation, IKC [31] optimizes the traditional K-center algorithm by introducing a device scheduling mechanism and designing a lightweight mini-model with only one convolutional layer to reduce communication cost. Although IKC maintains stable performance under varying client participation ratios, its scheduling policy remains static and lacks adaptive responsiveness to changes in client states. To achieve dynamic resource allocation and client scheduling, TP-DDPG [32] constructs a two-stage reinforcement learning framework that combines client selection via the DDPG algorithm with bandwidth allocation using SCABA. This approach effectively reduces training delay and mitigates the impact of dropped clients, demonstrating strong scheduling capability in dynamic scenarios. Beyond scheduling, some studies focus on aggregation strategies to improve system adaptability to non-IID data. FedGau [33] introduces Gaussian modeling to compute aggregation weights and employs the Bhattacharyya distance to measure data distribution differences between clients and clusters, as well as between clusters and the cloud. This enables dynamic adjustment of aggregation weights to address slow convergence caused by data heterogeneity. However, the need to solve a nonlinear optimization problem in each round increases the computational burden on clients. Incentive mechanisms have also been explored. HiFi-Gas [34] combines HFL with reward design, dividing total rewards into data quality and model contribution components to encourage clients to upload high-quality data and improve global model accuracy. However, the method does not address the risk of malicious clients forging data to manipulate rewards, posing potential security threats. To enhance privacy protection, HDP [35] introduces a super-node layer and applies a Gaussian mechanism for differential privacy on uploaded gradients. It also allows clients in different regions to adopt customized privacy levels, improving the flexibility of the privacy strategy. Nevertheless, the method lacks a detailed analysis of system robustness under dynamic and heterogeneous conditions, such as client dropouts and bandwidth fluctuations. Addressing the impact of client dynamics on training stability, HIST [36] proposes partitioning the global model into several non-overlapping sub-models, which are independently trained using edge servers (cells). The method employs AirComp to accelerate intra-cell aggregation and decouple communication latency from fluctuations in client numbers, thereby enhancing system scalability and stability.
2.2. Gradient Quantization
With the development of AI technology, the increasing scale of models deployed by clients in FL has significantly raised the number of gradients generated during local training. The frequent transmission of massive gradients not only consumes substantial bandwidth but also causes severe communication delays. To address this issue, existing studies propose GQ methods that compress gradient representations and reduce transmission bit counts by mapping high-precision floating-point values to predefined fixed-point levels, thereby alleviating uplink bandwidth pressure. Among these methods, QSGD [37]—which is a stochastic quantization method with convergence guarantees—combines normalization, segmentation, and stochastic rounding strategies to effectively reduce communication overhead in distributed SGD. It also enables a tunable trade-off between communication cost and training efficiency via an adjustable quantization level s. Building on this, DQN-GradQ [38] introduces a reinforcement learning framework that jointly optimize training time and quantization error. By leveraging a DDQN network, the method accelerates convergence and allows clients to dynamically select quantization bit levels based on their local states, thus, enabling more flexible communication control strategies. TTM [39] proposes an optimization strategy at the system level that jointly adjusts quantization levels and bandwidth allocation, aiming to minimize total training time. The method also characterizes the trade-off between the number of communication rounds and the delay of a single round. To address device heterogeneity, AdaGQ [18] extends QSGD by introducing a dynamic quantization strategy based on gradient variation. It assigns lower quantization levels to slower devices and higher levels to faster ones, thereby mitigating the straggler effect. Unlike the aforementioned approaches, FedDQ [40] builds on stochastic uniform quantization and adopts a reverse design perspective. It introduces an adaptive mechanism in which the quantization level decreases with the number of training rounds, effectively reducing redundant high-precision communication in later stages and improving overall training efficiency. In addition, LGC [40] breaks the single-node compression paradigm by introducing a lightweight self-encoder that learns shared structural information across multiple client nodes, thereby further improving compression efficiency without compromising model accuracy.
2.3. Secure Aggregation for IoV
In the HFL scenarios for the IoV, vehicle nodes collect large volumes of environmental and driving data through onboard sensors to support various intelligent tasks such as object detection and traffic flow prediction. These data often contain sensitive and private information, making them prime targets for potential attackers. Although FL avoids centralized sharing of raw data to a certain extent, malicious participants can still infer private information from model updates through techniques such as inference attacks.
To defend against such threats, SAFELearn [41] proposes a secure aggregation scheme that eliminates the need for a trusted third party. The cloud server can access only the aggregated values of vehicle node model updates, not the individual updates themselves, effectively mitigating active inference attacks. To improve aggregation efficiency, LightSecAgg [42] designs a lightweight secure aggregation protocol that combines a novel key exchange mechanism with a mask calculation and elimination strategy. This approach significantly reduces communication cost while ensuring security and maintains strong robustness against dynamic changes in vehicle node participation. To address the issue of limited communication resources in IoV, PEDA [43] integrates Additive Secret Sharing (ASS), Homomorphic Encryption (HE), and asymmetric encryption (e.g., RSA) to construct a privacy-enhanced federated aggregation framework. It further reduces communication overhead and enhances the defense of vehicle nodes against malicious participants through the Randomized Group Participation (RPGP) policy applied in the RSU layer. Considering the trustworthiness of aggregation nodes in layered frameworks, SADA [44] introduces the Schnorr multi-signature mechanism to ensure the verifiability of local aggregation updates uploaded by RSUs. This approach enhances the reliability of local aggregation results without incurring high computational overhead. To counter intelligent jamming attacks, RA-FRL [45] proposes a secure communication mechanism based on federated reinforcement learning. It trains an intelligent policy to dynamically select secure communication channels for vehicle nodes, effectively avoiding communication risks caused by intelligent jammers. In addition, to address the difficulty traditional intrusion detection systems (IDS) face in identifying unknown (zero-day) attacks, Zero-X [46] constructs a novel security detection framework for IoV by combining blockchain with Open-Set FL (Open-Set FL). This framework enables the joint identification and classification of both known (N-day) and unknown (zero-day) attacks.
3. Model System
In the presence of abnormal vehicle nodes participating in HFL, we designed a hierarchical three-layer framework for the IoV, called FedHSQA, to alleviate the communication bottleneck while achieving secure aggregation, as shown in Figure 1. FedHSQA incorporates gradient compression and secure aggregation across three layers: the vehicle node layer, the RSU layer, and the cloud service layer. In the vehicle node layer, each vehicle node , , performs local model training by collecting traffic information. In the RSU layer, each RSU , , serves as an intermediate device that receives model updates from vehicle nodes within its service domain, performs anomaly scoring, applies GQ, and uploads the quantized updates to the cloud. In the cloud service layer, the cloud server C conducts anomaly scores for all participating vehicle nodes and performs weighted aggregation of the global model based on these scores. The server then distributes both the anomaly scores and the aggregated global model to each RSU. Each vehicle node maintains a local dataset , which consists of a set of input–output pairs:
where denotes the k-th input sample and denotes its corresponding class label. Communication rounds are indexed by t, and the cloud server maintains the global model parameters at each round. The specific training process of FedHSQA is detailed in Section 3.1, Section 3.2, Section 3.3 and Section 3.4.
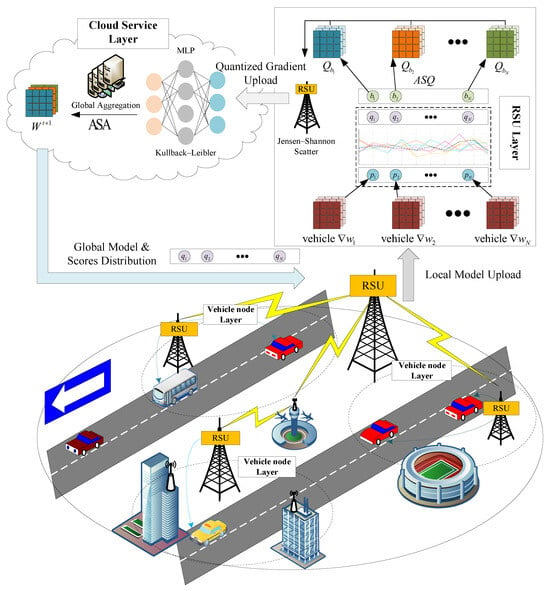
Figure 1.
Architecture of FedHSQA: A hierarchical three-layer federated learning framework for Internet of Vehicles.
3.1. Global Models Distribution
Before each communication round, the cloud server C determines whether it is the first round. If , it broadcasts the initialized model parameters to all RSUs , which then forward the model to their associated vehicle nodes . If , the cloud server first uses the model updates uploaded by clients from the previous round to compute anomaly scores for each vehicle node using the anomaly detection model MLP. The scores are normalized into a distribution vector:
Subsequently, the target distribution p is constructed, and the KL dispersion is computed to optimize the MLP model and derive aggregation weights for each vehicle node. The cloud server then sends the updated global model parameters along with the anomaly scores q to the RSUs. Each RSU stores the scores vector locally and forwards only the model parameters to its connected vehicle nodes.
3.2. Local Model Training
Each vehicle node performs local training on its dataset after receiving the global model, and obtains the local model update:
Considering the potential presence of untrustworthy or anomalous clients in IoV, all vehicle nodes transmit their model updates in full precision to ensure the accuracy of anomaly detection in the cloud server. In other words, is not subjected to any local compression. These updates are then transmitted to the corresponding RSUs .
3.3. Adaptive Gradient Quantization
In the proposed quantization method based on anomaly scoring (ASQ), the RSU adopts different compression strategies depending on whether the current communication round is the first. If it is the first round, the RSU applies the QSGD method to compress the model updates of all vehicle nodes using a fixed, uniform quantization level. In subsequent rounds, the RSU determines an adaptive quantization level b for each vehicle node based on its anomaly score , which is computed by the MLP model in the cloud server in the previous round. The score is projected onto the interval using a JS dispersion-based mapping function. The ASQ method is then applied to compress the model update . The compressed gradients are uploaded to the cloud server for global aggregation.
3.4. Model Secure Aggregation
In the proposed aggregation algorithm based on anomaly scores, the cloud server first receives the quantized gradients uploaded by all RSUs and downscales them into fixed-dimensional feature vectors. These features serve as input to the MLP model, which generates a new round of anomaly scores s for each vehicle node. Next, the cloud server constructs a probability distribution q from the anomaly scores s and derives a dispersion metric with respect to a target distribution p. The resulting loss value is used to update the parameters of the MLP model. Simultaneously, the aggregation weight for vehicle node is redefined based on its’ anomaly score. The cloud server then performs weighted aggregation to update the global model. The objective of federated aggregation is to minimize the following global loss function:
where denotes the local objective function of the vehicle node on its dataset. This communication and aggregation process is iterated in each training round until the global model reaches a predefined aggregation accuracy.
4. Scheme Design
4.1. Anomaly Scoring-Based Security Aggregation
To enhance the robustness of HFL for the IoV against abnormal vehicle nodes, FedHSQA introduces an anomaly-scoring-based secure aggregation (ASA) approach. This method conducts anomaly scores on the gradient updates uploaded by RSUs using an MLP model deployed in the cloud service layer. Based on the anomaly scoring results, it assigns adaptive aggregation weights to different gradients to reduce the influence of anomalous vehicle nodes on the aggregation process. The detailed procedures are presented in Section 4.1.1, Section 4.1.2, Section 4.1.3, Section 4.1.4 and Section 4.1.5.
4.1.1. Calculating Anomaly Score
In each communication round, the cloud server deployed in the cloud service layer uses a MLP model to define a scoring function that extracts potential anomalies from each gradient update. The output anomaly scores vector is shown as:
where , , denotes the model update from vehicle node uploaded via RSU , and s,, represents the anomaly score of the corresponding vehicle node. A higher score indicates a greater likelihood that vehicle node is anomalous. To help the MLP capture anomaly-relevant features, the function applies Layer-wise Mean Pooling (LMAP) to , , averaging gradients at each layer to produce a low-dimensional feature vector , shown as:
Z-score normalization is then applied to to obtain the normalized vector , shown as:
where denotes the mean and the standard deviation across all vehicle nodes. Therefore, the function is shown as:
It should be noted that the scoring function is not initialized during the first round of communication, as the MLP model has to learn gradually based on historical communication data. Therefore, in the first round, the system uniformly performs a standard weighted average aggregation without any intervention from the scoring mechanism. After the first communication round is completed, the parameter server collects the gradient updates uploaded by all RSUs. It performs LMAP to apply dimensionality reduction, thereby constructing the input feature space for the MLP-based anomaly scorer. The scorer is initialized using the Kaiming Uniform initialization strategy and updated once after each communication round to compute anomaly scores for the next round.
4.1.2. Anomaly Probability Distribution
ASA applies SoftMax normalization to the anomaly scores vector s, transforming it into an anomaly probability distribution vector q, shown as:
This distribution reflects the scoring function’s estimation of the likelihood of each vehicle node being anomalous. It serves as the output distribution for the supervised signal during training.
4.1.3. Designing Target Distribution
Vehicle nodes may conceal their anomaly status to gain more computational resources. To address this, ASA allows RSUs to infer anomaly labels and transmit them to the cloud server. Specifically, let the label vector be , where each element indicates whether vehicle node is judged as anomalous.
Considering that the label information may be incomplete or delayed, ASA employs a smoothing strategy to construct a pseudo-label distribution, shown as:
where denotes the set of vehicle nodes judged as anomalous by the RSU, is the smoothing coefficient, is the indicator function that returns 1 if node is marked anomalous and 0 otherwise, and N is the total number of vehicle nodes. This smoothing strategy assigns non-zero probability to all vehicle nodes while preserving the guidance provided by the anomaly labels. It improves the generalization ability of the scoring function in weakly supervised scenarios. To evaluate the impact of the smoothing coefficient on the aggregation model, we design a corresponding set of ablation experiments in the Section 5.5.
4.1.4. Training the MLP Model
ASA uses the pseudo-label distribution p as the supervised target and trains the MLP model by minimizing the KL divergence between the predicted anomaly distribution and the target distribution of vehicle node , shown as:
KL-based training encourages the MLP model to assign higher probabilities of anomalies to vehicle nodes labeled anomalous, thus, improving the ability of ASA to accurately identify them.
4.1.5. Calculating Aggregation Weight
ASA inverts the aggregation weight of vehicle node based on the output distribution . Meanwhile, in order to reduce the influence of anomalous vehicle nodes, the inverse anomaly weight is defined as:
Therefore, the aggregation weight of vehicle node is:
Finally, ASA aggregates and updates the global model at the communication round according to the weighted average within the cloud server based on the weights of different vehicle nodes:
4.2. Anomaly Scoring-Based Adaptive Quantization
In the HFL framework for IoV, to reduce uplink bandwidth pressure while preserving the utility of the aggregation model, FedHSQA designs an anomaly scoring-based GQ method (ASQ). Specifically, considering the risk of tampering or injection attacks on vehicle nodes, performing quantization directly at the client side may be bypassed by malicious participants. To address this, FedHSQA adopts a two-stage communication compression strategy. Each vehicle node uploads its locally trained gradient update in full precision to the corresponding RSU , which then performs adaptive quantization based on the anomaly score feedback from the MLP model deployed in the cloud service layer. Considering that the MLP model is not yet initialized in the first communication round, the system defaults to using the QSGD method with the 8-bit uniform quantization in the round. The detailed procedure is shown in Section 4.2.1, Section 4.2.2, Section 4.2.3 and Section 4.2.4.
4.2.1. Designing Anomaly Distribution
The RSU receives the anomaly probability distribution vector q from the cloud service layer, shown as:
where, indicates that vehicle node is determined to be anomalous. This distribution is generated by the MLP model based on the full-precision gradient updates uploaded in each communication round.
4.2.2. Calculating Anomaly Metric
To characterize the deviation between each vehicle node’s uploaded gradient update and the expected distribution, the RSU computes the scatter as an anomaly indicator, shown as:
where , and p denotes the target distribution constructed in the same manner as in the cloud service layer. A higher scatter indicates a greater deviation of vehicle node from the expected anomaly distribution. Accordingly, the RSU assigns a higher quantization degree, i.e., fewer bits are used for gradient representation.
4.2.3. Calculating Quantization Level
After receiving the scatter value, the RSU applies a linear scaling function to map it to the quantization bit level b for vehicle node v, where . This value defines the quantization level used by the vehicle node . The function is shown as:
where the lower and upper quantization bounds are and , respectively. In practice, 8-bit decentralized training is generally sufficient to achieve minimal accuracy loss [47]. To evaluate the specific impact of the quantization range on the aggregated model, we also design a corresponding ablation experiment in the Section 5.5.
4.2.4. Adaptive Gradient Quantization
At the t-th communication round, the RSU quantized the full-precision gradient uploaded by each vehicle node using the quantization level b obtained in the previous step. The quantization function is shown as:
where denotes the quantized gradient value obtained by applying quantization level to . The quantization result is further shown as:
where denotes the sign function, and is a stochastic scaling factor determined by a random variable that follows a Bernoulli distribution:
the probability that the gradient of vehicle node is quantized to value is shown as:
and the probability of quantization to value is:
where denote the normalized coordinate of the gradient value, shown as:
This quantization process adaptively adjusts the compression level for each vehicle node based on its anomaly score, enabling more efficient and robust communication. The specific flow of the FedHSQA framework is shown in Algorithm 1.
| Algorithm 1 FedHSQA—The Hierarchical Three-Layer Federated Learning Framework for IoV |
|
5. Experiment
In this section, we analyze the key components of the FedHSQA framework in terms of framework feasibility, aggregation performance, and compression effectiveness. First, for feasibility validation, we evaluate the anomaly detection performance of FedHSQA in the presence of anomalous vehicle nodes using AUC-ROC and AUC-PR as metrics. Then, to assess the effectiveness of the ASA aggregation strategy, we compare its performance in terms of average test accuracy and training loss against three mainstream aggregation algorithms: FedAvg, FedProx, and FedMOON. Finally, we introduce three classical gradient compression methods—QSGD, SignSGD, and TernGrad—as baselines to compare the performance of the ASQ method across different datasets and summarize its overall compression effectiveness in terms of communication overhead, using AUC-ROC and AUC-PR as evaluation measures.
5.1. Experimental Setup
Simulation Scenario: We built an HFL framework for IoV in the PyCharm environment. The overall system consists of a cloud server, 5 RSUs, and 50 vehicle nodes. Each RSU manages 10 vehicle clients, including 7 normal nodes and 3 anomalous nodes, simulating an environment with abnormal interference. Datasets: We adopt three widely used image classification datasets: MNIST [48], CIFAR10 [49], and SVHN [50]. These correspond to tasks involving low-dimensional grayscale images, natural color images, and street-view house number recognition, respectively, covering diverse sensing environments from simple to complex. Aggregation Algorithms: To evaluate the performance of the ASA aggregation strategy under the FedHSQA framework, we used three mainstream FL aggregation algorithms—FedAvg, FedProX, and FedMOON—as baselines for comparison [29,51,52]. Quantization methods: In communication compression experiments, we selected three classical gradient compression methods—QSGD, SignSGD, and TernGrad—as baseline methods to assess the effectiveness of the proposed ASQ quantization method [37,53,54].
5.2. Framework Feasibility Analysis
To evaluate the impact of anomalous vehicle nodes on the FedHSQA framework for IoV, we assessed anomaly detection performance on three datasets—MNIST, CIFAR10, and SVHN—using AUC-ROC and AUC-PR as evaluation metrics. The experimental results are shown in Figure 2.
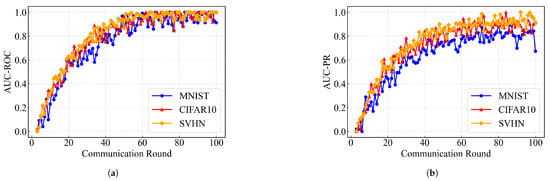
Figure 2.
Anomaly detection performance over communication rounds: (a) AUC-ROC; (b) AUC-PR.
As shown above, all three datasets exhibit an overall upward trend in both metrics, indicating that FedHSQA continuously improves the identification of anomalous nodes as communication rounds progress. In particular, SVHN and CIFAR10 show faster rises with lower fluctuations, reflecting strong convergence and stability. In contrast, MNIST displays slightly more volatility, suggesting slower performance improvement in tasks with relatively simple feature structures. By the 100th communication round, the SVHN dataset achieves approximately 0.99 in AUC-ROC and 0.95 in AUC-PR, while CIFAR10 reaches about 0.98 and 0.92, respectively. In comparison, MNIST attains an AUC-PR of around 0.85, which is slightly lower than the other two datasets. Overall, the comparison of final scores and convergence rates indicates that the FedHSQA framework exhibits stronger robustness when handling perceptual tasks with more complex and feature-rich inputs. Detailed results are presented in Table 1, where “Peak” indicates the earliest round achieving maximum precision.

Table 1.
Anomaly detection performance of the FedHSQA framework over communication rounds.
5.3. Model Performance Analysis
To further evaluate the robustness of the ASA aggregation algorithm under the FedHSQA framework in the presence of anomalous nodes, we introduced 30% anomalous vehicle nodes in each training round and uniformly adopt QSGD as the quantization method. The global model performance of different aggregation algorithms is tested on three public datasets. The corresponding test accuracy and training loss curves are shown in Figure 3.
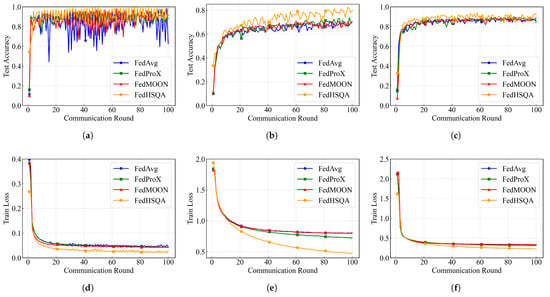
Figure 3.
FedHSQA performance on three datasets using different aggregation algorithms: (a) Test accuracy on MNIST. (b) Test accuracy on CIFAR10. (c) Test accuracy on SVHN. (d) Training loss on MNIST. (e) Training loss on CIFAR10. (f) Training loss on SVHN.
Overall, FedHSQA outperforms the baseline methods across all datasets. Its test accuracy curve exhibits lower fluctuation and faster convergence, indicating enhanced training stability. Meanwhile, its training loss declines rapidly in the early rounds and stabilizes at the lowest level in the later rounds, demonstrating good convergence behavior. Taking CIFAR10 as an example, FedHSQA consistently maintains over 75% test accuracy after the 30th round, whereas FedAvg and FedProX hover around 68–70% with slower convergence. Notably, on the MNIST dataset, the test accuracy curves of all aggregation algorithms show frequent fluctuations. The accuracy of FedAvg drops below 50% at one point, indicating its vulnerability to anomalous client interference. In contrast, FedHSQA maintains accuracy between 90% and 95%, with fluctuations within ±5%, and significantly lower training loss, which eventually stabilizes at 0.03. On the SVHN dataset, the test accuracy of FedHSQA remains significantly higher than that of other methods, consistently fluctuating around 90%, while its training loss converges rapidly. These results highlight FedHSQA strong capability for anomaly isolation and resistance to adversarial interference. Thus, FedHSQA not only achieves faster convergence in the initial communication rounds but also maintains higher accuracy and lower training error during long-term training, fully demonstrating the robustness and practicality of its aggregation mechanism in IoV scenarios with anomalous vehicle nodes. Detailed results are summarized in Table 2.

Table 2.
Test accuracy and training loss over communication rounds.
5.4. Quantization Effectiveness Analysis
(1) To evaluate the effectiveness of the ASQ GQ method under the FedHSQA framework, we compare its performance with three classical GQ methods—QSGD, TernGrad, and SignSGD—under the ASA aggregation algorithm across three datasets: MNIST, CIFAR10, and SVHN. AUC-ROC and AUC-PR are used as evaluation metrics for anomaly detection performance. The results are shown in Figure 4.
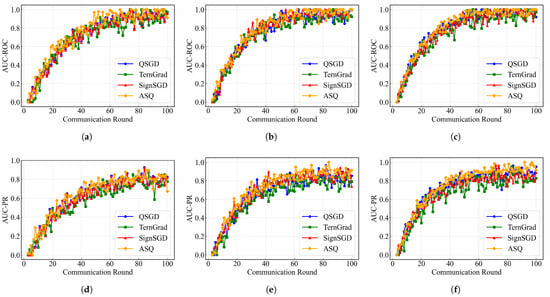
Figure 4.
Anomaly detection performance of different compression methods: (a) AUC-ROC on MNIST. (b) AUC-ROC on CIFAR10. (c) AUC-ROC on SVHN. (d) AUC-PR on MNIST. (e) AUC-PR on CIFAR10. (f) AUC-PR on SVHN.
The results show that ASQ outperforms the baseline methods in most communication rounds. Particularly during the mid-to-late training stages (rounds 40–100), ASQ achieves higher AUC-ROC and AUC-PR values than the other methods, indicating that it maintains strong anomaly detection capabilities even after model convergence. Additionally, ASQ exhibits smoother and more stable curves compared to TernGrad and SignSGD, suggesting that its compression process is more effective in preserving anomaly-relevant information. On the MNIST and SVHN datasets, ASQ maintains an AUC-ROC consistently above 0.95 and an AUC-PR around 0.85, surpassing QSGD and the other comparative methods. For CIFAR10, although all four methods produce similar final results, ASQ demonstrates a faster improvement during the first 60 rounds, indicating its advantage in convergence acceleration. Overall, ASQ demonstrates strong capability in filtering anomalous gradients and maintains high detection performance even under low-bit compression. These results validate its practical value in communication-constrained HFL scenarios. Detailed results are presented in Table 3.

Table 3.
Anomaly detection performance of different quantization methods over communication rounds.
(2) To further evaluate the compression capability of ASQ under the FedHSQA framework, we record the communication overhead on the MNIST, CIFAR10, and SVHN datasets over the first 100 communication rounds. Figure 5a shows the communication volume in the uncompressed setting, while Figure 5b shows the communication volume with ASQ compression applied.
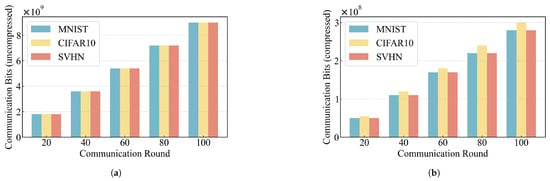
Figure 5.
Comparison of communication overhead in compressed and uncompressed states: (a) Uncompressed; (b) Compressed.
As shown in the histograms, ASQ significantly reduces the number of bits transmitted in each communication round, and this reduction remains consistent across all datasets. While the original communication volume increases linearly with the number of rounds, the growth in compressed communication volume slows down substantially, indicating that ASQ maintains a stable compression advantage over long-term training. Furthermore, the compression patterns across all three datasets are similar, confirming the generality and robustness of ASQ under different input distributions. By comparing specific values at the 100th communication round, we observe that ASQ reduces the raw communication volume to approximately bits for MNIST, bits for CIFAR10, and bits for SVHN. Aggregating statistics across all rounds, ASQ achieves an average compression rate of approximately 30× on all three datasets. Detailed results are presented in Table 4.

Table 4.
Model performance across communication rounds.
5.5. Ablation Experiments
(1) In order to investigate the effect of the hyperparameter smoothing coefficient on the weight distribution of the ASA aggregation, we set , respectively, and compare the Test Accuracy and Training Loss of the FedHSQA framework on the MNIST dataset. The experimental results are shown in Figure 6.
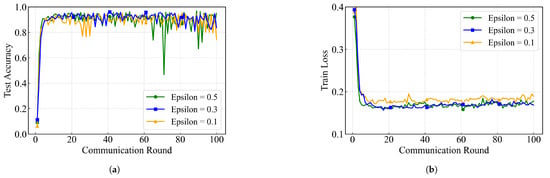
Figure 6.
Impact of smoothing coefficient on aggregation models: (a) Test Accuracy; (b) Train Loss.
The experimental results show that at the early stage of training (within the first 10 rounds), all three sets of smoothing coefficient settings can converge quickly, with the test accuracy exceeding 85% and the training loss dropping to less than 0.2, indicating that the ASA algorithm has a good convergence potential under different settings. However, in the middle and late stages (rounds 20–100), the model performance diverges: when = 0.3, the test accuracy is maintained in the range of 90–95%, and the training loss stabilizes below 0.15, which shows the best convergence and stability; when = 0.5, although the overall accuracy is relatively high, there is a large fluctuation in rounds 60–90, with the accuracy dropping below 60%, and the fluctuation of the training loss is obvious. This shows that the large smoothing factor weakens the ability to respond to abnormal scoring differences and is prone to cause aggregation bias; when = 0.1, although the early convergence is faster, the late accuracy fluctuates sharply, and the training loss is always higher than that of the other two groups, showing that the aggregation weights are skewed to the extremes and are susceptible to abnormal perturbations. Finally, among the three settings, = 0.3 has the highest test accuracy and the lowest training loss; = 0.5 has the most significant fluctuation in accuracy; and = 0.1 has the weakest robustness. Therefore, the setting of the smoothing coefficient has a significant effect on the convergence speed and stability of the model.
(2) To further evaluate the impact of the upper and lower bounds settings of the JS mapping function, which is the range of quantization levels , on the global model performance in the ASQ method, we set to be , , , and , respectively, and conducted experiments on MNIST, CIFAR10, and SVHN datasets. The focus was on analyzing the metrics of compression degree, communication overhead and average quantization bit. The average quantization bits represent the average number of bits used for each floating-point model parameter after compression; the communication overhead refers to the total number of bits transmitted by each vehicle node to upload the gradient in each communication round; and the compression degree is defined as the “number of uncompressed bits/number of transmitted bits”, where smaller values indicate higher compression ratios. The experimental results are shown in Table 5.

Table 5.
Impact of quantization level ranges on aggregation models.
The experimental data show that as increases, the mapping output of ASQ tends to be more centralized, and the regulation space of anomaly scoring at the quantization level is reduced, making the number of bits allocated to each client more stable. Taking SVHN as an example, when the quantization range is increased from to , the average quantization bit increases from 7 to 8, and the communication overhead increases slightly, but the compression degree increases to 0.40, indicating that the high-starting point compression strategy effectively mitigates the information loss caused by the low bit quantization, and reduces the client-side differences caused by the large span of the levels. A similar trend is observed on MNIST and CIFAR10, where the model accuracy increases with , further confirming the judgment that too few quantization bits, while improving the compression rate, can limit the model performance. Furthermore, the control experiment of our setup achieves the optimal accuracy across datasets, but the average quantization bit is as high as 13, almost doubling the communication overhead. Due to the large level span in this setting, the ASQ mapping tends to average the bit allocation, which weakens the adaptive compression capability and significantly increases the communication overhead. Therefore, under the premise of fixing , moderately increasing helps to improve the robustness of the model while taking into account the communication efficiency, which is a better strategy for setting the compression level.
6. Conclusions and Future Work
In this paper, we propose a three-layer HFL framework for IoV, called FedHSQA, which integrates a secure aggregation algorithm (ASA) and an adaptive level quantization method (ASQ). Experimental results on three public datasets demonstrated that FedHSQA effectively reduces communication overhead while enhancing the robustness of the global model against untrusted vehicle nodes. Despite its promising experimental performance, FedHSQA still presents several directions for future exploration:
First, its scalability requires further investigation. As the number of vehicle nodes and RSUs increases, the cloud server must process more model updates and scoring computations, leading to increased aggregation overhead. Future work will explore the introduction of multi-level hierarchical aggregation trees and cluster-based group aggregation strategies to improve computational efficiency and support large-scale deployment.
Second, in computation resource-constrained environments, FedHSQA may encounter challenges such as the high computational cost of the anomaly scoring model and the additional computation burden introduced by using ASQ-based communication compression. To alleviate the pressure on IoV devices, our future work will consider integrating lightweight anomaly scorers with asynchronous communication mechanisms, enabling delayed local updates to reduce real-time computational demands.
Finally, due to the highly dynamic connectivity of IoV environments, unstable communication links may impair model synchronization and aggregation. To enhance system robustness, future efforts will focus on designing asynchronous or delay-tolerant aggregation mechanisms and deploying FedHSQA on more realistic simulation platforms to obtain results with higher practical relevance.
Author Contributions
Conceptualization, L.X. and K.D.; methodology, L.X., Z.L., and K.D.; software, Z.L.; validation, Z.L. and K.D.; formal analysis, H.W., H.M., K.D., and X.L.; investigation, Z.L. and X.L.; resources, H.W., H.M., and X.L.; data curation, Z.L. and X.L.; writing—original draft preparation, Z.L. and K.D.; writing—review and editing, L.X., K.D., H.W., H.M., and X.L.; supervision, L.X., H.W., and H.M.; project administration, L.X., H.W., and K.D.; funding acquisition, L.X., H.W., and K.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Henan Province (252300421237), Key Research and Development Special projects of Henan Province (251111210900), and the Science and Technology Research Project of Henan Province (252102211014).
Data Availability Statement
The data can be shared up on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Khezri, E.; Hassanzadeh, H.; Yahya, R.O.; Mir, M. Security challenges in internet of vehicles (IoV) for ITS: A survey. Tsinghua Sci. Technol. 2025, 30, 1700–1723. [Google Scholar] [CrossRef]
- Ali, E.S.; Hasan, M.K.; Hassan, R.; Saeed, R.A.; Hassan, M.B.; Islam, S.; Nafi, N.S.; Bevinakoppa, S. Machine learning technologies for secure vehicular communication in internet of vehicles: Recent advances and applications. Secur. Commun. Networks 2021, 2021, 8868355. [Google Scholar] [CrossRef]
- Taslimasa, H.; Dadkhah, S.; Neto, E.C.P.; Xiong, P.; Ray, S.; Ghorbani, A.A. Security issues in Internet of Vehicles (IoV): A comprehensive survey. Internet Things 2023, 22, 100809. [Google Scholar] [CrossRef]
- Sharma, S.; Kaushik, B. A survey on internet of vehicles: Applications, security issues & solutions. Veh. Commun. 2019, 20, 100182. [Google Scholar]
- Agbaje, P.; Anjum, A.; Mitra, A.; Oseghale, E.; Bloom, G.; Olufowobi, H. Survey of interoperability challenges in the internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 22838–22861. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, J.; Song, S.; Letaief, K.B. Client-edge-cloud hierarchical federated learning. In Proceedings of the ICC 2020–2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Abad, M.S.H.; Ozfatura, E.; Gunduz, D.; Ercetin, O. Hierarchical federated learning across heterogeneous cellular networks. In Proceedings of the ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 8866–8870. [Google Scholar]
- Zhou, H.; Zheng, Y.; Huang, H.; Shu, J.; Jia, X. Toward robust hierarchical federated learning in internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5600–5614. [Google Scholar] [CrossRef]
- Chai, H.; Leng, S.; Chen, Y.; Zhang, K. A hierarchical blockchain-enabled federated learning algorithm for knowledge sharing in internet of vehicles. IEEE Trans. Intell. Transp. Syst. 2020, 22, 3975–3986. [Google Scholar] [CrossRef]
- Hammoud, A.; Otrok, H.; Mourad, A.; Dziong, Z. On demand fog federations for horizontal federated learning in IoV. IEEE Trans. Netw. Serv. Manag. 2022, 19, 3062–3075. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, X.; Wu, D.; Wang, R.; Zhang, P.; Wu, Y. Efficient asynchronous federated learning research in the internet of vehicles. IEEE Internet Things J. 2022, 10, 7737–7748. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Z.; Xu, Z.; Liu, W.; Tian, J. Hierarchical decentralized federated learning framework with adaptive clustering: Bloom-filter-based companions choice for learning non-iid data in iov. Electronics 2023, 12, 3811. [Google Scholar] [CrossRef]
- Yu, X.; Cherkasova, L.; Vardhan, H.; Zhao, Q.; Ekaireb, E.; Zhang, X.; Mazumdar, A.; Rosing, T. Async-HFL: Efficient and robust asynchronous federated learning in hierarchical IoT networks. In Proceedings of the 8th ACM/IEEE Conference on Internet of Things Design and Implementation, San Antonio, TX, USA, 9–12 May 2023; pp. 236–248. [Google Scholar]
- Khan, L.U.; Guizani, M.; Al-Fuqaha, A.; Hong, C.S.; Niyato, D.; Han, Z. A joint communication and learning framework for hierarchical split federated learning. IEEE Internet Things J. 2023, 11, 268–282. [Google Scholar] [CrossRef]
- Lim, W.Y.B.; Ng, J.S.; Xiong, Z.; Niyato, D.; Miao, C.; Kim, D.I. Dynamic edge association and resource allocation in self-organizing hierarchical federated learning networks. IEEE J. Sel. Areas Commun. 2021, 39, 3640–3653. [Google Scholar] [CrossRef]
- Xing, L.; Zhao, P.; Gao, J.; Wu, H.; Ma, H.; Zhang, X. Federated Learning for IoV Adaptive Vehicle Clusters: A Dynamic Gradient Compression Strategy. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Liang, Z.; Yang, P.; Zhang, C.; Lyu, X. Secure and efficient hierarchical Decentralized learning for Internet of Vehicles. IEEE Open J. Commun. Soc. 2023, 4, 1417–1429. [Google Scholar] [CrossRef]
- Liu, S.; Yu, G.; Yin, R.; Yuan, J.; Qu, F. Communication and computation efficient federated learning for Internet of vehicles with a constrained latency. IEEE Trans. Veh. Technol. 2023, 73, 1038–1052. [Google Scholar] [CrossRef]
- Luo, P.; Yu, F.R.; Chen, J.; Li, J.; Leung, V.C. A novel adaptive gradient compression scheme: Reducing the communication overhead for distributed deep learning in the Internet of Things. IEEE Internet Things J. 2021, 8, 11476–11486. [Google Scholar] [CrossRef]
- Xue, Y.; Su, L.; Lau, V.K. FedOComp: Two-timescale online gradient compression for over-the-air federated learning. IEEE Internet Things J. 2022, 9, 19330–19345. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, C.; Zhang, T.; Zhang, J.; Piao, M. A new algorithm of clustering AODV based on edge computing strategy in IOV. Wirel. Netw. 2021, 27, 2891–2908. [Google Scholar] [CrossRef]
- Scott, C.; Khan, M.S.; Paranjothi, A.; Li, J.Q. Decentralized cluster head selection in iov using federated deep reinforcement learning. In Proceedings of the 2024 IEEE 21st Consumer Communications & Networking Conference (CCNC), Las Vegas, NV, USA, 6–9 January 2024; pp. 1–7. [Google Scholar]
- Hu, Z.; Li, Y.; Tang, S. Efficient Caching and Spreading of Traffic Videos by Optimized Topology in IoV. IEEE Trans. Veh. Technol. 2024, 73, 11821–11833. [Google Scholar] [CrossRef]
- Mahmood, A.; Siddiqui, S.A.; Sheng, Q.Z.; Zhang, W.E.; Suzuki, H.; Ni, W. Trust on wheels: Towards secure and resource efficient IoV networks. Computing 2022, 104, 1337–1358. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, L.; Wu, S.; Li, S.; Zhang, T.; Zhang, L.; Xu, J.; Xiong, Y.; Cui, X. Attacks and countermeasures in the internet of vehicles. Ann. Telecommun. 2017, 72, 283–295. [Google Scholar] [CrossRef]
- Sakiz, F.; Sen, S. A survey of attacks and detection mechanisms on intelligent transportation systems: VANETs and IoV. Ad Hoc Netw. 2017, 61, 33–50. [Google Scholar] [CrossRef]
- Hershey, J.R.; Olsen, P.A. Approximating the Kullback Leibler divergence between Gaussian mixture models. In Proceedings of the 2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP’07, Honolulu, HI, USA, 15–20 April 2007; Volume 4, p. IV-317. [Google Scholar]
- Nielsen, F. On the Jensen–Shannon symmetrization of distances relying on abstract means. Entropy 2019, 21, 485. [Google Scholar] [CrossRef] [PubMed]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Fang, W.; Han, D.J.; Chen, E.; Wang, S.; Brinton, C. Hierarchical federated learning with multi-timescale gradient correction. Adv. Neural Inf. Process. Syst. 2024, 37, 78863–78904. [Google Scholar]
- Zhang, T.; Lam, K.Y.; Zhao, J. Device scheduling and assignment in hierarchical federated learning for internet of things. IEEE Internet Things J. 2024, 11, 18449–18462. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Ni, W.; Wang, X.; Zhang, S.; Sun, Y.; Xu, S.; Pei, Q. Towards dynamic resource allocation and client scheduling in hierarchical federated learning: A two-phase deep reinforcement learning approach. IEEE Trans. Commun. 2024, 72, 7798–7813. [Google Scholar] [CrossRef]
- Kou, W.B.; Lin, Q.; Tang, M.; Ye, R.; Wang, S.; Zhu, G.; Wu, Y.C. Fast-convergent and communication-alleviated heterogeneous hierarchical federated learning in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2025, 1–16. [Google Scholar] [CrossRef]
- Sun, H.; Tang, X.; Yang, C.; Yu, Z.; Wang, X.; Ding, Q.; Li, Z.; Yu, H. HiFi-Gas: Hierarchical federated learning incentive mechanism enhanced gas usage estimation. In Proceedings of the Proceedings of the AAAI Conference on Artificial Intelligence; Vancouver, BC, Canada, 26–27 February 2024, Volume 38, pp. 22824–22832.
- Chandrasekaran, V.; Banerjee, S.; Perino, D.; Kourtellis, N. Hierarchical federated learning with privacy. In Proceedings of the 2024 IEEE International Conference on Big Data (BigData), Washington, DC, USA, 15–18 December 2024; pp. 1516–1525. [Google Scholar]
- Fang, W.; Han, D.J.; Brinton, C.G. Federated Learning Over Hierarchical Wireless Networks: Training Latency Minimization via Submodel Partitioning. IEEE Trans. Netw. 2025, 1–16. [Google Scholar] [CrossRef]
- Alistarh, D.; Grubic, D.; Li, J.; Tomioka, R.; Vojnovic, M. QSGD: Communication-efficient SGD via gradient quantization and encoding. Adv. Neural Inf. Process. Syst. 2017, 30, 1707–1718. [Google Scholar]
- Zhang, C.; Zhang, W.; Wu, Q.; Fan, P.; Fan, Q.; Wang, J.; Letaief, K.B. Distributed deep reinforcement learning based gradient quantization for federated learning enabled vehicle edge computing. IEEE Internet Things J. 2024, 12, 4899–4913. [Google Scholar] [CrossRef]
- Liu, P.; Jiang, J.; Zhu, G.; Cheng, L.; Jiang, W.; Luo, W.; Du, Y.; Wang, Z. Training time minimization for federated edge learning with optimized gradient quantization and bandwidth allocation. Front. Inf. Technol. Electron. Eng. 2022, 23, 1247–1263. [Google Scholar] [CrossRef]
- Qu, L.; Song, S.; Tsui, C.Y. FedDQ: Communication-efficient federated learning with descending quantization. In Proceedings of the GLOBECOM 2022–2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 4–8 December 2022; pp. 281–286. [Google Scholar]
- Fereidooni, H.; Marchal, S.; Miettinen, M.; Mirhoseini, A.; Möllering, H.; Nguyen, T.D.; Rieger, P.; Sadeghi, A.R.; Schneider, T.; Yalame, H.; et al. SAFELearn: Secure aggregation for private federated learning. In Proceedings of the 2021 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 27 May 2021; pp. 56–62. [Google Scholar]
- So, J.; He, C.; Yang, C.S.; Li, S.; Yu, Q.; E Ali, R.; Guler, B.; Avestimehr, S. Lightsecagg: A lightweight and versatile design for secure aggregation in federated learning. Proc. Mach. Learn. Syst. 2022, 4, 694–720. [Google Scholar]
- Mun, H.; Han, K.; Damiani, E.; Kim, T.Y.; Yeun, H.K.; Puthal, D.; Yeun, C.Y. Privacy enhanced data aggregation based on federated learning in internet of vehicles (IoV). Comput. Commun. 2024, 223, 15–25. [Google Scholar] [CrossRef]
- Liu, R.; Pan, J. Schnorr Approval-Based Secure and Privacy-Preserving IoV Data Aggregation. IEEE Trans. Veh. Technol. 2025, 1–15. [Google Scholar] [CrossRef]
- Lu, X.; Xiao, L.; Xiao, Y.; Wang, W.; Qi, N.; Wang, Q. Risk-Aware Federated Reinforcement Learning-Based Secure IoV Communications. IEEE Trans. Mob. Comput. 2024, 23, 14656–14671. [Google Scholar] [CrossRef]
- Boualouache, A.; Ghamri-Doudane, Y. Zero-x: A blockchain-enabled open-set federated learning framework for zero-day attack detection in iov. IEEE Trans. Veh. Technol. 2024, 73, 12399–12414. [Google Scholar]
- Aketi, S.A.; Kodge, S.; Roy, K. Low precision decentralized distributed training over IID and non-IID data. Neural Networks 2022, 155, 451–460. [Google Scholar] [CrossRef]
- Deng, L. The mnist database of handwritten digit images for machine learning research [best of the web]. IEEE Signal Process. Mag. 2012, 29, 141–142. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1106–1114. [Google Scholar] [CrossRef]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading digits in natural images with unsupervised feature learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning, Granada, Spain, 12–15 December 2011; Volume 2011, p. 4. [Google Scholar]
- Li, T.; Sahu, A.K.; Zaheer, M.; Sanjabi, M.; Talwalkar, A.; Smith, V. Federated optimization in heterogeneous networks. Proc. Mach. Learn. Syst. 2020, 2, 429–450. [Google Scholar]
- Li, Q.; He, B.; Song, D. Model-contrastive federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 10713–10722. [Google Scholar]
- Bernstein, J.; Wang, Y.X.; Azizzadenesheli, K.; Anandkumar, A. signSGD: Compressed optimisation for non-convex problems. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 560–569. [Google Scholar]
- Wen, W.; Xu, C.; Yan, F.; Wu, C.; Wang, Y.; Chen, Y.; Li, H. Terngrad: Ternary gradients to reduce communication in distributed deep learning. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).