Multi-Objective Day-Ahead Scheduling for Air Conditioning Load Considering Dynamic Carbon Emission Factor
Abstract
1. Introduction
- (1)
- Integrating carbon-emission costs and electricity-consumption costs based on dynamic carbon emission factors into comprehensive electricity costs, while considering user comfort, establishes a multi-objective optimization model for day-ahead scheduling of air conditioning loads;
- (2)
- Obtaining the optimal compromise solution through the NSGA-II algorithm combined with GTD, which ensures user comfort while minimizing comprehensive electricity costs, overcoming the limitations of conventional single-objective optimization and preference decision-making, thereby providing scientific decision-making for day-ahead scheduling of air conditioning loads.
2. Characteristics Related to Day-Ahead Scheduling of Air Conditioning Systems
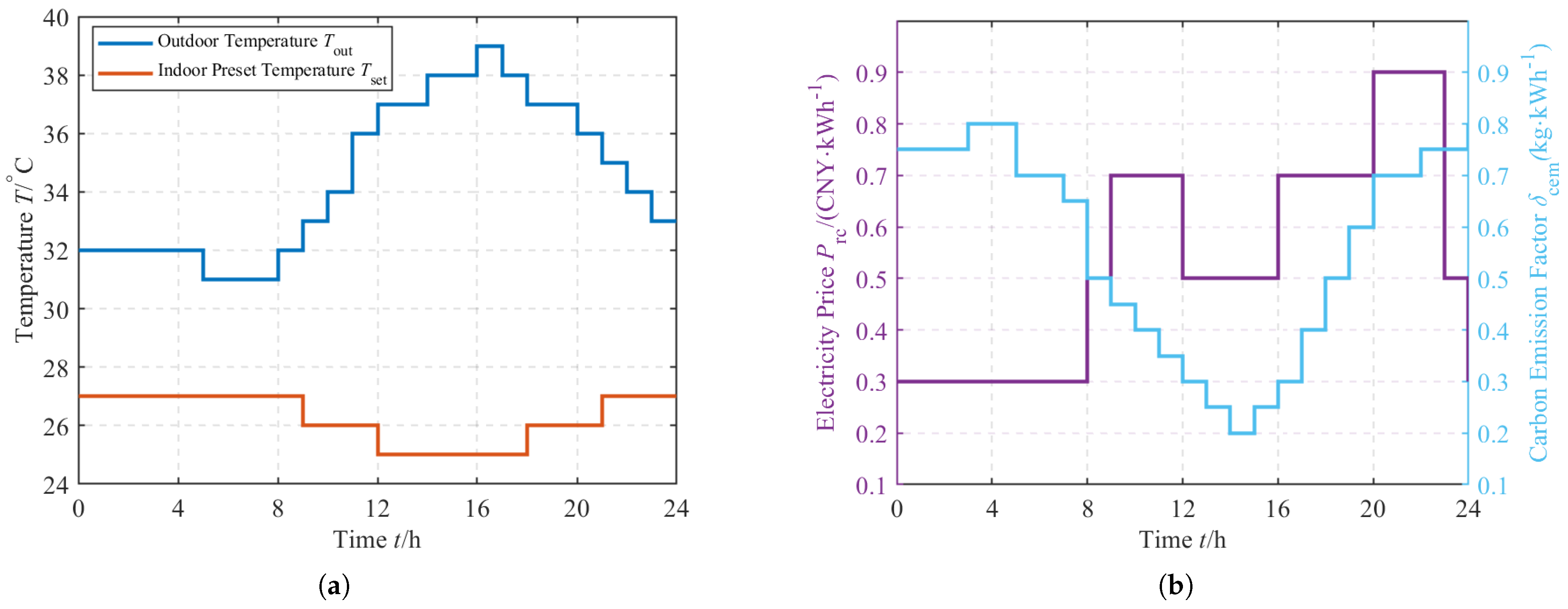
2.1. Dynamic Carbon Emission Factor
2.2. Air Conditioning Load-Regulation Characteristics
3. Optimization Objectives and Constraints for Air Conditioning Day-Ahead Scheduling
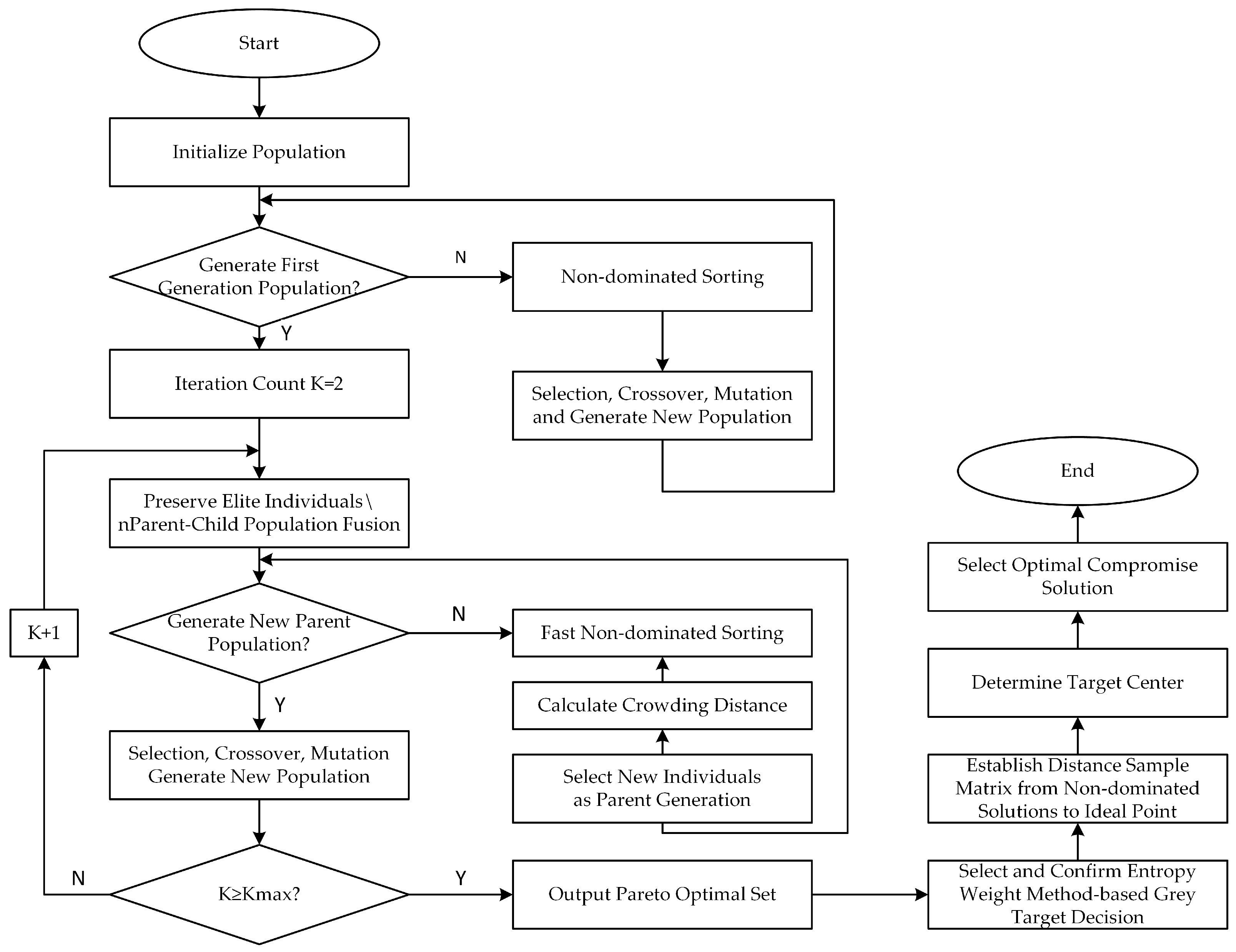
4. NSGA-II and Grey Target Decision-Making Combined Optimal Day-Ahead Scheduling of Air Conditioning Loads
4.1. NSGA-II
4.1.1. Non-Dominated Sorting
4.1.2. Crowding Distanceg
- (1)
- Suppose there is a population . First, use the selection, crossover and mutation operators of the GA algorithm to obtain the offspring with the same number of individuals as the population , then combine the two to get a new group, denoted as . Then, carry out non-dominated sorting for to obtain each domination level, such as
- (2)
- According to the obtained domination level order, sequentially add individuals from the high domination level to the low domination level into the next population .
- (3)
- When the number of optimal solutions in a certain domination level is too large and exceeds the capacity of , sort all individuals of this level according to the crowding distance, retain the individuals with larger crowding distances and add them to the population first, until the population is full.
4.2. Grey Target Decision-Making
- (1)
- Based on the normalized pareto solution set and the distances from each non-dominated solution to the ideal point, establish the sample matrix.
- (2)
- Normalize the sample matrix to obtain the decision matrix, and determine the bullseye within the grey decision region formed by the decision matrix.
- (3)
- Calculate all distances to the bullseye.
4.2.1. Establish Sample Matrix
4.2.2. Determine the Bullseye
4.2.3. Select the Best Compromise Solution
- (1)
- Calculate the weight value of the j-th objective for the i-th decision alternative
- (2)
- Calculate the entropy value of the j-th objective value for the i-th decision alternative
- (3)
- Calculate the entropy weight of the j-th objective value
- (4)
- Calculate the distance from each solution to the bullseye, and select the solution closest to the bullseye as the optimal decision-making solution.
4.3. Mathematical Expressions
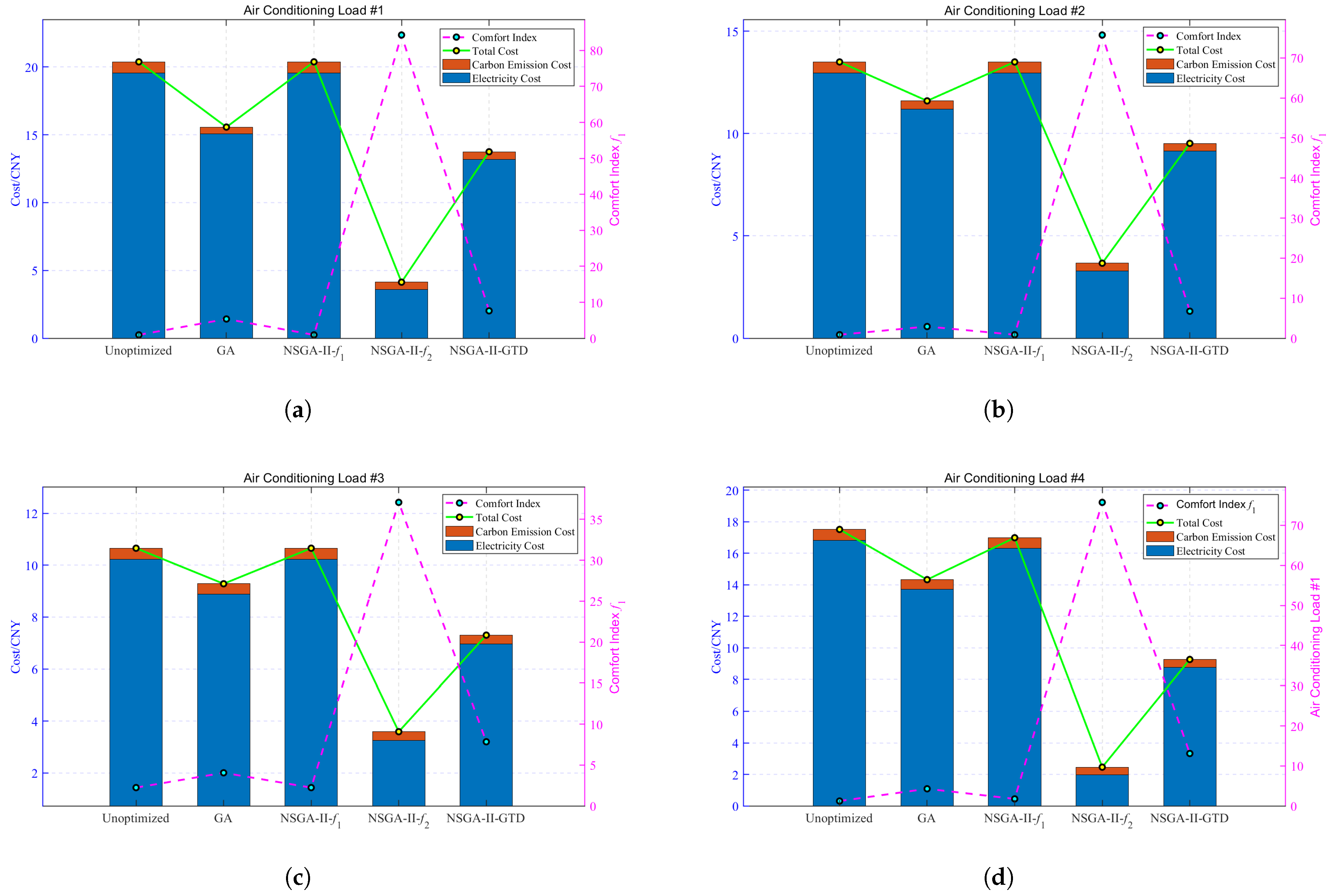
5. Case Study
6. Conclusions
- (1)
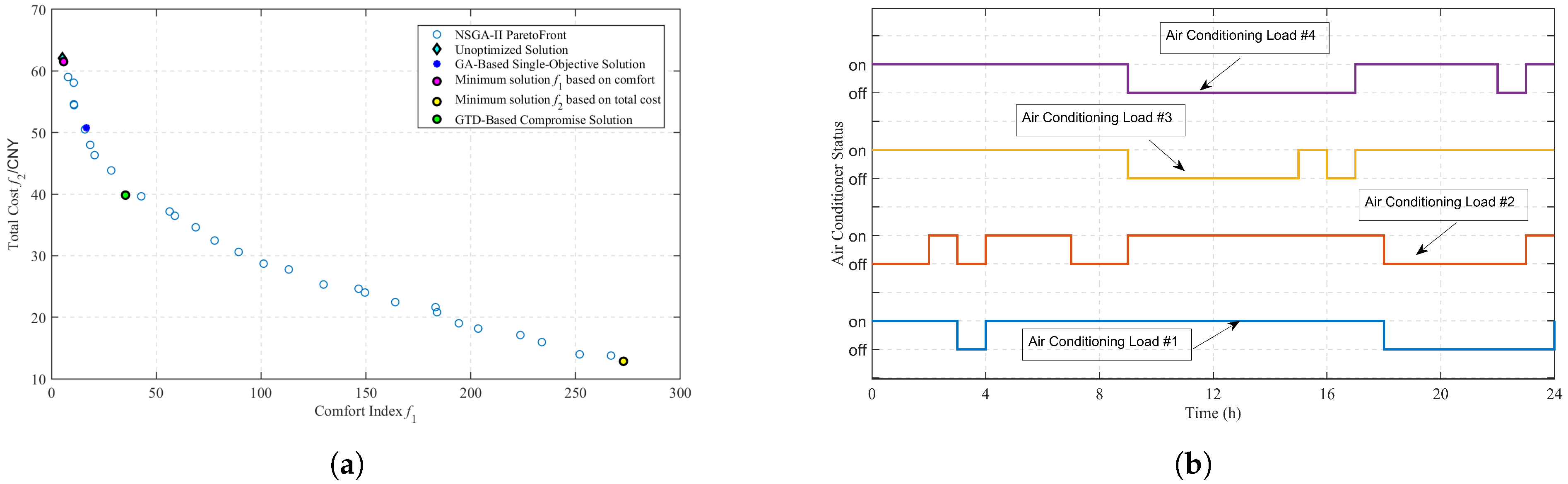
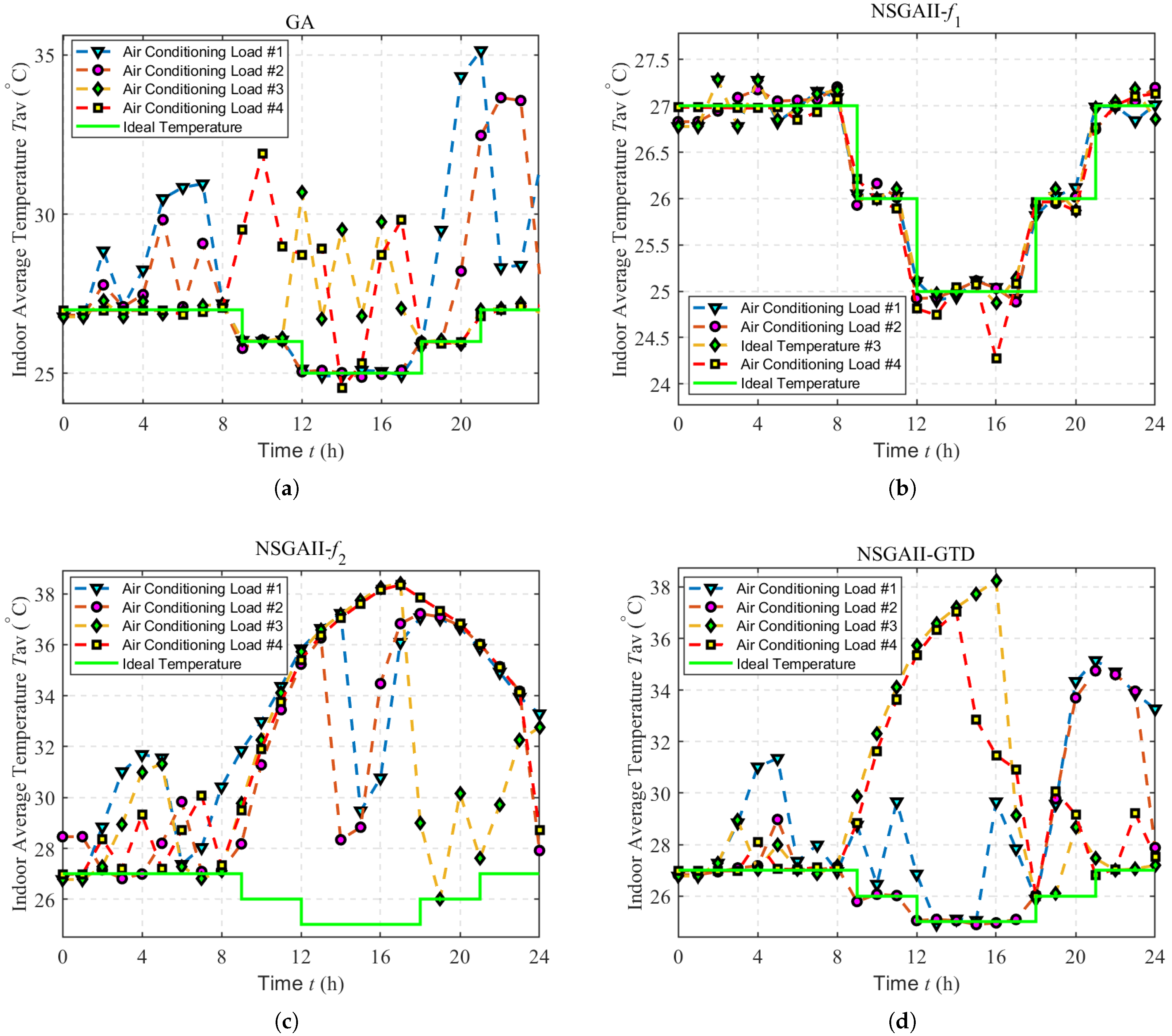
- User costs and comfort exhibit inherent conflict. The pareto frontier obtained by NSGA-II shows that when prioritizing comfort entirely, the temperature deviation remains below 1.5 °C, but the cost reaches 62 CNY. Conversely, when focusing solely on cost reduction, the maximum temperature deviation exceeds 13 °C. These results demonstrate that the two objectives cannot be minimized simultaneously, adhering to the "no free lunch" theorem.
- (2)
- NSGA-II-GTD proves operationally effective. Compared to competitive strategies (GA, NSGA-II-, or NSGA-II-), the proposed NSGA-II-GTD method achieves a balanced solution, reducing electricity costs by 36.09% (from 59.57 to 38.07 CNY) and carbon-emission costs by 28.05% (from 2.46 to 1.77 CNY) while maintaining comfort deviations below 15 for all users (vs. 272.85 for NSGA-II-).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Möller, T.; Högner, A.E.; Schleussner, C.F.; Bien, S.; Kitzmann, N.H.; Lamboll, R.D.; Rogelj, J.; Donges, J.F.; Rockström, J.; Wunderling, N. Achieving net zero greenhouse gas emissions critical to limit climate tipping risks. Nat. Commun. 2024, 15, 6192. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Dai, H.; Li, S.; Guo, C.; Ho, M.; Cai, W.; He, J.; Huang, H.; Li, J.; Liu, Y.; et al. The general equilibrium impacts of carbon tax policy in China: A multi-model comparison. Energy Econ. 2021, 99, 105284. [Google Scholar] [CrossRef]
- Mengesha, I.; Roy, D. Carbon pricing drives critical transition to green growth. Nat. Commun. 2025, 16, 1321. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Mao, C.; Tian, F. Influencing Factors of CO2 Emissions in Chinese Power Industry: A Study from the Production and Consumption Perspectives. Comput. Intell. Neurosci. 2022, 2022, 3615492. [Google Scholar] [CrossRef]
- Guo, Y.; Li, H.; Pan, M. Colocation Data Center Demand Response Using Nash Bargaining Theory. IEEE Trans. Smart Grid 2018, 9, 4017–4026. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, Y.; Guo, B.; Huang, L.; Li, C. Optimal Day-Ahead Dispatch of Air-Conditioning Load under Dynamic Carbon Emission Factors. In Proceedings of the 2023 5th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 23–26 March 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Algarni, A.S.; Suryanarayanan, S.; Siegel, H.J.; Maciejewski, A.A. Combined Impact of Demand Response Aggregators and Carbon Taxation on Emissions Reduction in Electric Power Systems. IEEE Trans. Smart Grid 2021, 12, 1825–1827. [Google Scholar] [CrossRef]
- Fleschutz, M.; Bohlayer, M.; Braun, M.; Henze, G.; Murphy, M.D. The Effect of Price-Based Demand Response on Carbon Emissions in European Electricity Markets: The Importance of Adequate Carbon Prices. Appl. Energy 2021, 295, 117040. [Google Scholar] [CrossRef]
- Wang, Y.; Qiu, J.; Tao, Y. Robust Energy Systems Scheduling Considering Uncertainties and Demand Side Emission Impacts. Energy 2022, 239, 122317. [Google Scholar] [CrossRef]
- Agrawal, K.K.; Jain, S.; Jain, A.K.; Dahiya, S. Assessment of Greenhouse Gas Emissions from Coal and Natural Gas Thermal Power Plants Using Life Cycle Approach. Int. J. Environ. Sci. Technol. 2014, 11, 1157–1164. [Google Scholar] [CrossRef]
- Ma, W.; Cai, D.; Wan, L.; Chen, R.; Liu, H.; Cao, K. A Calculation Method of Dynamic Carbon Emission Factors for Different Regions in a Province Based on Time Division. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 963–967. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, E.; Han, S.; Ji, H. Optimal Scheduling of Combined Heat and Power Systems Integrating Hydropower-Wind-Photovoltaic-Thermal-Battery Considering Carbon Trading. IEEE Access 2024, 12, 98393–98406. [Google Scholar] [CrossRef]
- Li, J.; Wenjing, C.; Ying, X.; Miao, B.; Na, M. The Calculation Method of User-Level Dynamic Carbon Emission Factor Based on Electric Energy Trading Flow. In Proceedings of the 2023 IEEE 5th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 14–16 July 2023; pp. 374–379. [Google Scholar] [CrossRef]
- Tan, H.; Yu, H.; Chen, T.; Qiao, W. Research on Carbon Emission Monitoring Indicator System of Power Users. In Proceedings of the 2023 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chongqing, China, 7–9 July 2023; pp. 613–619. [Google Scholar] [CrossRef]
- Zhang, S.; Li, Y.; Du, E.; Wang, W.; Wang, M.; Feng, H.; Xie, Y.; Chen, Q. Research on Carbon-Reduction-Oriented Demand Response Technology Based on Generalized Nodal Carbon Emission Flow Theory. Energies 2024, 17, 4672. [Google Scholar] [CrossRef]
- Zhang, Q.; Qiao, K.; Hu, C.; Su, P.; Cheng, O.; Yan, N.; Yan, L. Study on Life-Cycle Carbon Emission Factors of Electricity in China. Int. J. Low-Carbon Technol. 2024, 19, 2287–2298. [Google Scholar] [CrossRef]
- Gao, P.; Li, B.; Yan, C.; Li, D.; Huang, Y.; Yang, X.; Li, K.; Wu, D. Multi-Objective Coordinated Optimal Scheduling Considering Electric Vehicles and Air-conditioning Loads (CICED 2024). In Proceedings of the 2024 China International Conference on Electricity Distribution (CICED), Hangzhou, China, 12–13 September 2024; pp. 235–240. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, R.; Jiang, Z.; Ji, C.; Li, A.; Yu, S. An Improved Risk-Benefit Collaborative Grey Target Decision Model and Its Application in the Decision Making of Load Adjustment Schemes. Energy 2018, 156, 387–400. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, Y.; Zhang, K.; Li, P.; Li, M.; He, Q.; Chao, H. Time-of-Use Pricing Model Considering Wind Power Uncertainty. CSEE J. Power Energy Syst. 2022, 8, 1039–1047. [Google Scholar] [CrossRef]
- Guo, S.; Kurban, A.; He, Y.; Wu, F.; Pei, H.; Song, G. Multi-Objective Sizing of Solar-Wind-Hydro Hybrid Power System with Doubled Energy Storages Under Optimal Coordinated Operational Strategy. CSEE J. Power Energy Syst. 2023, 9, 2144–2155. [Google Scholar] [CrossRef]
- Mahdi, B.S.; Sulaiman, N.; Shehab, M.A.; Shafie, S.; Hizam, H.; Hassan, S.L.B.M. Optimization of Operating Cost and Energy Consumption in a Smart Grid. IEEE Access 2024, 12, 18837–18850. [Google Scholar] [CrossRef]
- Elenes, A.G.N.; Williams, E.; Hittinger, E.; Goteti, N.S. How Well Do Emission Factors Approximate Emission Changes from Electricity System Models? Environ. Sci. Technol. 2022, 56, 14701–14712. [Google Scholar] [CrossRef]
- Xiong, T.; Liu, Y.; Yang, C.; Cheng, Q.; Lin, S. Research Overview of Urban Carbon Emission Measurement and Future Prospect for GHG Monitoring Network. Energy Rep. 2023, 9, 231–242. [Google Scholar] [CrossRef]
- Yang, C.; Liu, J.; Liao, H.; Liang, G.; Zhao, J. An Improved Carbon Emission Flow Method for the Power Grid with Prosumers. Energy Rep. 2023, 9, 114–121. [Google Scholar] [CrossRef]
- Zhu, G.X.; Bao, Y.Q.; Yu, Q.Q. A Control Strategy for Air-Conditioning Loads Participating in Frequency Regulation Based on Model Predictive Control. Sustain. Energy Grids Netw. 2024, 38, 101369. [Google Scholar] [CrossRef]
- Callaway, D.S.; Hiskens, I.A. Achieving Controllability of Electric Loads. Proc. IEEE 2011, 99, 184–199. [Google Scholar] [CrossRef]
- Li, W.; Wu, H.; Zhao, Y.; Jiang, C.; Zhang, J. Study on Indoor Temperature Optimal Control of Air-Conditioning Based on Twin Delayed Deep Deterministic Policy Gradient Algorithm. Energy Build. 2024, 317, 114420. [Google Scholar] [CrossRef]
- Duan, L.; Guo, Z.; Taylor, G.; Lai, C.S. Multi-Objective Optimization for Solar-Hydrogen-Battery-Integrated Electric Vehicle Charging Stations with Energy Exchange. Electronics 2023, 12, 4149. [Google Scholar] [CrossRef]
- Shojae Chaeikar, S.; Mirzaei Asl, F.; Yazdanpanah, S.; Zamani, M.; Manaf, A.A.; Khodadadi, T. Secure CAPTCHA by Genetic Algorithm (GA) and Multi-Layer Perceptron (MLP). Electronics 2023, 12, 4084. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.; Sun, S.; Liu, T.; Shan, Y. A Comprehensive Survey on NSGA-II for Multi-Objective Optimization and Applications. Artif. Intell. Rev. 2023, 56, 15217–15270. [Google Scholar] [CrossRef]
- Zu, X.; Yang, C.; Wang, H.; Wang, Y. An EGR Performance Evaluation and Decision-Making Approach Based on Grey Theory and Grey Entropy Analysis. PLoS ONE 2018, 13, e0191626. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, Z.; Pan, F.; Yang, Y.; Li, C. Dynamic Carbon Emission Factor Based Interactive Control of Distribution Network by a Generalized Regression Neural Network Assisted Optimization. Energy 2023, 283, 129132. [Google Scholar] [CrossRef]
- Wang, J.; Jin, X.; Jia, H.; Tostado-Véliz, M.; Mu, Y.; Yu, X.; Liang, S. Joint Electricity and Carbon Sharing With PV and Energy Storage: A Low-Carbon DR-Based Game Theoretic Approach. IEEE Trans. Sustain. Energy 2024, 15, 2703–2717. [Google Scholar] [CrossRef]

| Air Conditioning Load Number | R (°C/kW) | C (kWh/°C) | P (kW) | Temperature Control Period | |
|---|---|---|---|---|---|
| #1 | 5.36 | 0.16 | 4.0 | 1.1 | 09:00–18:00 |
| #2 | 6.00 | 0.19 | 3.5 | 1.5 | 09:00–18:00 |
| #3 | 5.60 | 0.16 | 2.5 | 2.0 | 00:00–08:00, 18:00–24:00 |
| #4 | 5.76 | 0.19 | 2.3 | 1.2 | 00:00–08:00, 18:00–24:00 |
| Cases | Time (hours) | Dynamic CEF (kgCO2/kWh) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 00:00–12:00 | 0.75 | 0.75 | 0.80 | 0.80 | 0.70 | 0.70 | 0.65 | 0.50 | 0.45 | 0.40 | 0.35 | 0.30 |
| 12:00–24:00 | 0.25 | 0.20 | 0.25 | 0.30 | 0.40 | 0.50 | 0.60 | 0.70 | 0.70 | 0.75 | 0.75 | 0.80 | |
| #2 | 00:00–12:00 | 0.99 | 1.00 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.97 | 0.97 | 0.96 | 0.93 | 0.96 |
| 12:00–24:00 | 0.96 | 0.96 | 0.97 | 0.98 | 0.96 | 0.96 | 0.97 | 0.97 | 0.97 | 0.97 | 1.00 | 0.99 | |
| AC Load No. | Index | Optimization Strategy | |||||
|---|---|---|---|---|---|---|---|
| Unoptimized | GA | NSGAII- | NSGAII- | MOEA/D-GTD | NSGAII-GTD | ||
| #1 | Electricity Cost (dynamic CEF) | 19.5599 | 15.0625 | 20.0199 | 3.5798 | 11.6337 | 13.1902 |
| Carbon Cost (dynamic CEF) | 0.8161 | 0.5039 | 0.8461 | 0.5565 | 0.3916 | 0.5565 | |
| Carbon Cost (average CEF) | 1.0303 | 0.6774 | 1.0303 | 0.5840 | 0.6439 | 0.5840 | |
| Total Cost (dynamic CEF) | 20.3760 | 15.5664 | 20.8660 | 4.1363 | 12.0253 | 13.7467 | |
| Comfort Index (dynamic CEF) | 0.9453 | 5.3550 | 0.9554 | 84.2978 | 12.3692 | 7.6286 | |
| #2 | Electricity Cost (dynamic CEF) | 12.9610 | 11.1824 | 12.9732 | 3.2835 | 8.3983 | 9.1371 |
| Carbon Cost (dynamic CEF) | 0.5356 | 0.4127 | 0.5424 | 0.3830 | 0.3122 | 0.3830 | |
| Carbon Cost (average CEF) | 0.6774 | 0.5624 | 0.6774 | 0.4550 | 0.4697 | 0.4552 | |
| Total Cost (dynamic CEF) | 13.4966 | 11.5951 | 13.5156 | 3.6665 | 8.7106 | 9.5201 | |
| Comfort Index (dynamic CEF) | 0.8877 | 2.9321 | 0.8912 | 75.7282 | 9.3734 | 6.7590 | |
| #3 | Electricity Cost (dynamic CEF) | 10.2313 | 8.8882 | 10.4920 | 3.2523 | 8.1771 | 6.9628 |
| Carbon Cost (dynamic CEF) | 0.4233 | 0.3953 | 0.5216 | 0.3402 | 0.3409 | 0.3402 | |
| Carbon Cost (average CEF) | 0.5374 | 0.4767 | 0.5286 | 0.4376 | 0.4215 | 0.4376 | |
| Total Cost (dynamic CEF) | 10.6546 | 9.2835 | 11.0136 | 3.5925 | 8.5180 | 7.3030 | |
| Comfort Index (dynamic CEF) | 2.2436 | 4.0547 | 2.3766 | 37.0784 | 9.3383 | 7.8487 | |
| #4 | Electricity Cost (dynamic CEF) | 16.8213 | 13.7174 | 16.3060 | 1.9716 | 12.0848 | 8.7775 |
| Carbon Cost (dynamic CEF) | 0.6859 | 0.6076 | 0.6763 | 0.4877 | 0.5314 | 0.4877 | |
| Carbon Cost (average CEF) | 0.8804 | 0.6949 | 0.8804 | 0.4526 | 0.5926 | 0.4526 | |
| Total Cost (dynamic CEF) | 17.5072 | 14.3250 | 16.9823 | 2.4593 | 12.6163 | 9.2652 | |
| Comfort Index (dynamic CEF) | 1.2312 | 4.2892 | 1.7640 | 75.7444 | 10.0666 | 13.1019 | |
| Total Load | Electricity Cost (dynamic CEF) | 59.5735 | 48.8505 | 59.7911 | 12.0872 | 40.2939 | 38.0676 |
| Carbon Cost (dynamic CEF) | 2.4609 | 1.9195 | 2.5864 | 1.7674 | 1.5761 | 1.7674 | |
| Carbon Cost (average CEF) | 3.1255 | 2.4114 | 3.1167 | 1.9292 | 2.1277 | 1.9294 | |
| Total Cost (dynamic CEF) | 62.0344 | 50.7700 | 62.3775 | 13.8546 | 41.8701 | 39.8350 | |
| Comfort Index (dynamic CEF) | 5.3078 | 16.6310 | 5.9872 | 272.8488 | 41.1475 | 35.3382 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Guo, Z.; Wang, J.; Tang, J.; Zhang, X. Multi-Objective Day-Ahead Scheduling for Air Conditioning Load Considering Dynamic Carbon Emission Factor. Electronics 2025, 14, 1550. https://doi.org/10.3390/electronics14081550
Zhang K, Guo Z, Wang J, Tang J, Zhang X. Multi-Objective Day-Ahead Scheduling for Air Conditioning Load Considering Dynamic Carbon Emission Factor. Electronics. 2025; 14(8):1550. https://doi.org/10.3390/electronics14081550
Chicago/Turabian StyleZhang, Kun, Zhengxun Guo, Ji Wang, Jianlin Tang, and Xiaoshun Zhang. 2025. "Multi-Objective Day-Ahead Scheduling for Air Conditioning Load Considering Dynamic Carbon Emission Factor" Electronics 14, no. 8: 1550. https://doi.org/10.3390/electronics14081550
APA StyleZhang, K., Guo, Z., Wang, J., Tang, J., & Zhang, X. (2025). Multi-Objective Day-Ahead Scheduling for Air Conditioning Load Considering Dynamic Carbon Emission Factor. Electronics, 14(8), 1550. https://doi.org/10.3390/electronics14081550






