A Novel Optimization Method of the DS-LCC Compensation Topology to Reduce the Sensitivity of the Load-Independent Constant Current Output Characteristics to the Component Parametric Deviation

Abstract

For the double-sided inductor–capacitor–capacitor (DS-LCC) compensation topology, the parametric deviation of compensation elements results in the mismatch between the resonant frequency and operating frequency. Furthermore, this mismatch leads to the loss of the load-independent constant output characteristics. Therefore, an innovative design approach based on the reduction in the capacitance ratio is proposed to attain the load-independent constant current under the parametric deviation. With the presented method, simply by reducing the compensation capacitor ratio, the load-independent constant current output characteristics can be preserved, and fluctuations in the transmission gain caused by the parametric deviation are minimized. This implies that when the constant transmission gain is achieved by the frequency modulation (FM) control, the required FM range can be reduced. Finally, from the experimental results, in the load range of 3 Ω to 33 Ω, compared to the high capacitance ratio, the load-independent constant current characteristics can be maintained at the low capacitance ratio. In addition, without parametric deviation, the transmission efficiencies at different capacitance ratios are basically the same at 93.5% and 94.2%, respectively. However, the transmission efficiencies under different parametric deviations at the low capacitance ratio are 87.4% and 84.9%, but only 73.9% and 68.2% at the high capacitance ratio.

1. Introduction

Inductive power transfer (IPT) technology is capable of transmitting energy through the high-frequency magnetic field without physical contact. This indicates that IPT technology, adopted in a variety of applications, such as implantable medical devices and electric vehicles, is promising, due to its advantages of weather proofing, higher convenience, and low maintenance [1,2,3]. The IPT system generally requires separate compensation circuits at the transmitter and receiver, respectively, to compensate for the leakage inductance and achieve the high-performance operation of the system. Figure 1 shows the DS-LCC compensation topology, in which there is an LCC circuit on both the transmitter and receiver. L₁, C₁, and C_s1 make up compensation elements of the transmitter. L₂, C₂, and C_s2 make up compensation elements of the receiver. L_s and L_p are the self-inductances of the transmitting coil and receiving coil. M depicts the mutual inductance. Switching devices S₁–S₄ compose the inverter at the transmitting side, while diodes D₁–D₄ compose the rectifier at the receiving side. Compared to lower order compensation networks such as SS compensation topology, this compensation topology offers greater design flexibility, multiple resonant points, a stable resonant frequency independent of the mutual inductance, and enhanced tolerance to the misalignment [4,5,6]. Its ability to maintain the load-independent constant output at the resonant frequency simplifies the control system design, making it a preferred choice in recent research [7,8]. However, due to a number of factors, such as the variation in the internal heat and ambient temperature, aging effect, and industrial error, the parameter of elements can deviate from their ideal values with the ±10% fluctuation [9]. The parametric deviation can cause the system to be detuned and further leads to the loss of the load-independent constant output characteristic. Therefore, for the DS-LCC compensation topology, it is of great significance that under the parametric deviation, the load-independent constant output characteristics can be implemented.

Several methodologies are proposed to analyze parametric sensitivity and reduce the influence of the parametric deviation in compensation components. On the one hand, it is very effective to compensate for the output fluctuation resulting from the parametric deviation through different control strategies [10,11,12,13,14]. The constant output current of the S-LCC compensation topology can be achieved by employing the frequency tracking [10]. However, for the DS-LCC compensation topology, frequency tracking techniques may lead to the loss of the load-independent constant current characteristics and increase the complexity of the control system. Based on the SS compensation topology, a fractional-order IPT system is proposed to achieve the constant output [11]. Nevertheless, since there are many components, it is hardly possible to establish a fractional-order equivalent model of the DS-LCC compensation topology. Alternatively, the variable inductor and switched controllable capacitor (SCC) can also be adopted to compensate for the parametric deviation [12,13,14]. However, due to the larger number of components in the DS-LCC compensation topology, these methods will increase the complexity of the control system and also lead to a reduction in efficiency.

On the other hand, the optimal design of the compensation network seems to be another effective strategy [15,16,17,18,19,20]. The parametric sensitivity of the DS-LCC compensation topology is analyzed and it is noted that the parametric deviation of the primary series compensation capacitor and secondary compensation inductor have the least effect on the load-independent constant output characteristics [15,16]. Nevertheless, solutions for the parametric deviation of other components are not presented. Based on the parametric sensitivity analysis of the S-S-P network, the selection of higher precision compensation capacitors is proposed [17]. This method will undoubtedly increase the cost of the system. The optimally resonant mode can be selected by the comparison of the frequency sensitivity in different constant current modes of the DS-LCC compensation topology [18]. However, the correlation between the parametric deviation and resonant frequency variations has yet to be fully established. A combination of exhaustive and Monte Carlo stochastic analysis can be utilized to design the DS-LCC compensation circuit and the fluctuation of the output power is less than 10% over the ±10% range of the parametric deviation [19]. For implementing the constant voltage output of the LCC-S network under the parametric deviation in compensation capacitors, Sobol sensitivity analysis is employed to obtain the optimal parameter [20]. However, in both parameter optimization methods, the load-independent constant output characteristics cannot be attained.

Therefore, a distinctive design method is proposed to implement the load-independent constant current output characteristics under ±10% parametric deviations. In the proposed methodology, only through the reduction in the capacitance ratio, the load-independent constant current output characteristics can be maintained and transmission gain fluctuations caused by the parametric deviation are also reduced. This suggests that the constant transmission gain can be achieved through FM control alone, and the frequency adjustment range can be effectively reduced. In addition, for the IPT system, the imaginary part of the input impedance is generally required to be greater than 0 to realize zero voltage switching (ZVS) for efficiency enhancement. However, parametric deviation may also lead to fluctuations in the input impedance of the system, resulting in the loss of ZVS. Therefore, the ZVS realization condition of the proposed method is further investigated.

The following sections make up the rest of this paper: Section 2 analyzes the output characteristics of the equivalent π-circuit and the L-circuit under the parametric deviation in the load range is analyzed. Furthermore, the method based on the reduction in the capacitance ratio is proposed to reduce the output deviation caused by the parametric deviation. The ZVS condition is also deduced. The design procedure and construction of the proposed IPT system are presented in Section 3. In Section 4, simulation and experimental results are revealed and analyzed to validate the accuracy of the proposed method. Lastly, the paper is conclusively summarized in Section 5.

2. Realization of Load-Independent Constant Output Characteristics Under Component Parameter Deviations

The leakage equivalent circuit of the DS-LCC compensation topology is illustrated in Figure 2. Where the leakage inductance of the corresponding coil and equivalent load are represented as L′_s, L′_p, and R′_L, and can be expressed as (1).

$$R_{\mathrm{L}}^{\prime }={\displaystyle \frac{8R_{\mathrm{L}}}{{\pi }^2}} \hspace{1em}{L}_{\mathrm{p}}^{\prime }=L_{\mathrm{p}}-M \hspace{1em}{L}_{\mathrm{s}}^{\prime }=L_{\mathrm{s}}-M$$

(1)

From the leakage inductance model, the KVL equation can be derived as

$$\begin{array}{l}{\mathit{U}}_{\mathbf{i}\mathbf{n}}=j{Z}_1{I}_{\mathbf{i}\mathbf{n}}-{\displaystyle \frac{I_{\mathbf{1}}}{j\omega C_1}} \hspace{1em}{Z}_{\mathrm{s}1}{I}_{\mathbf{1}}=\omega M{I}_{\mathbf{2}}-{\displaystyle \frac{I_{\mathbf{i}\mathbf{n}}}{\omega C_1}}\\ Z_{\mathrm{s}2}{I}_{\mathbf{2}}=\omega M{I}_{\mathbf{1}\mathbf{c}}-{\displaystyle \frac{I_{\mathbf{o}}}{\omega C_2}} \hspace{1em}{\displaystyle \frac{I_{\mathbf{2}}}{j\omega C_2}}=\left(j{Z}_2+R_{\mathrm{L}}^{\prime }\right)I_{\mathbf{o}}\end{array}.$$

(2)

where

$$\begin{array}{l}{Z}_1=\omega L_1-{\displaystyle \frac{1}{\omega C_1}} \hspace{1em}{Z}_{\mathrm{s}1}=\omega L_{\mathrm{s}}-{\displaystyle \frac{1}{\omega C_1}}-{\displaystyle \frac{1}{\omega C_{\mathrm{s}1}}}\\ Z_2=\omega L_2-{\displaystyle \frac{1}{\omega C_2}} \hspace{1em}{Z}_{\mathrm{s}2}=\omega L_{\mathrm{p}}-{\displaystyle \frac{1}{\omega C_2}}-{\displaystyle \frac{1}{\omega C_{\mathrm{s}2}}}\end{array}$$

(3)

It can be easily deduced from (2) that the transmission gain g, i.e., the ratio of the output current I_o to the input voltage U_in, can be expressed as

$$g={\displaystyle \frac{I_{\mathbf{o}}}{U_{\mathbf{i}\mathbf{n}}}}={\displaystyle \frac{\omega M{C}_2}{\omega {C_2}^2\left(j{Z}_2+R_{\mathrm{L}}^{\prime }\right)a+j\left(\frac{1}{{\omega }^2{C}_1}-C_1{Z}_{\mathrm{s}1}{Z}_1\right)}}$$

(4)

where

$$a=\omega C_1{Z}_{\mathrm{s}1}{Z}_{\mathrm{s}2}{Z}_1-{\omega }^3{M}^2{C}_1{Z}_1-{\displaystyle \frac{Z_{\mathrm{s}2}}{\omega C_1}}$$

(5)

In the conventional design method of the DS-LCC compensation topology [21,22], it can be deduced from (4) that the resonant frequency ω₀ is generally designed to satisfy the condition in (6). Further, substituting (6) into (4), the output current I_o is further deduced as (7), and from (7) the load-independent constant current output characteristics can be achieved.

$${{\omega }_0}^2={\displaystyle \frac{1}{L_1{C}_1}}={\displaystyle \frac{1}{L_{\mathrm{p}}}}\left({\displaystyle \frac{1}{C_{\mathrm{s}2}}}+{\displaystyle \frac{1}{C_2}}\right)$$

(6)

$$I_{\mathbf{o}}=U_{\mathbf{in}}\cdot {\displaystyle \frac{1}{j{\omega }_0{L}_1}}\cdot {{\omega }_0}^{2}M{C}_2$$

(7)

However, due to the internal heat, ambient temperature, aging effects, and industrial errors, there is usually a ±10% parametric deviation from the nominal value for each component. The parametric deviation can make it difficult for the DS-LCC compensation topology to maintain resonance and, furthermore, cause the loss of the load-independent constant current output characteristics. Therefore, it is of great interest to reduce the effect of the parametric deviation on the load-independent constant current output characteristics of the DS-LCC compensation topology.

2.1. Effect of the Parametric Deviation on the Load-Independent Constant Current Output Characteristics

An analysis of (6), (7), and Figure 2 indicates that for the DS-LCC compensation topology, the first-stage L-circuit and the second-stage π-circuit are required to be in resonance at the same time for implementing the load-independent constant current output. However, the parametric deviation of the compensation elements may lead to different resonant frequencies for the L-circuit and π-circuit. This implies that it is difficult to compensate for the parametric deviation through the frequency-tracking technique alone. Therefore, the optimal design method of the compensating element needs to be further investigated in order to reduce the effect of the parametric deviation on the load-independent constant output characteristics for the L-circuit and π-circuit.

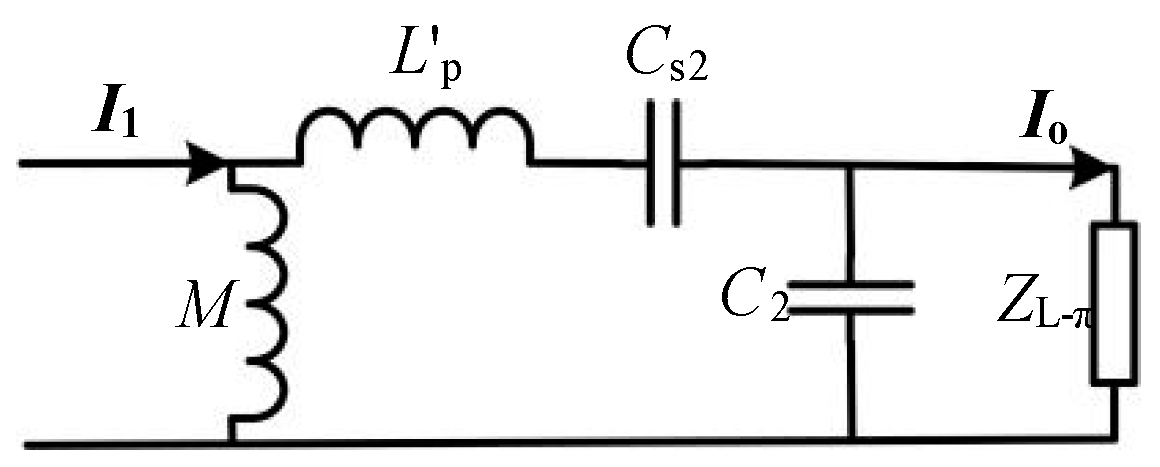
In accordance with Figure 2, the π-circuit consisting of L′_p, M, C_s2, and C₂ can further be represented, as in Figure 3, where the equivalent load Z_L-π, consisting of the compensation inductor L₂ and load R′_L, can be expressed as (8).

$$Z_{\mathrm{L}\text{-}\mathsf{\pi }}=j\omega L_2+R_{\mathrm{L}}^{\prime }$$

(8)

On the basis of Figure 3 and (1), the current gain g_π can be deduced as

$$g_{\mathsf{\pi }}={\displaystyle \frac{I_{\mathbf{o}}}{I_{\mathbf{1}}}}={\displaystyle \frac{M}{j\omega C_2{Z}_{\mathrm{L}\text{-}\mathsf{\pi }}\left(L_{\mathrm{p}}-\frac{1}{{\omega }^2{C}_{\mathrm{s}2}}-\frac{1}{{\omega }^2{C}_2}\right)+L_{\mathrm{p}}-\frac{1}{{\omega }^2{C}_{\mathrm{s}2}}}}.$$

(9)

As can be gathered from (9), if the operating frequency ω, and the compensation elements L_p, C_s2, and C₂ are designed to satisfy the condition in (6), the load-independent constant output characteristics of the π-circuit can be realized. This indicates that if there is the parametric deviation in the element L_p, C_s2, or C₂, the resonant frequency ω₀ is bound to fluctuate, which causes the π-circuit to be detuned. Consequently, there must be a deviation factor λ_p1, presented as (10), between the operating frequency ω and the resonant frequency ω₀.

$${\lambda }_{\mathrm{p}1}={\displaystyle \frac{\omega }{{\omega }_0}}=\sqrt{{\displaystyle \frac{L_{\mathrm{p}0}{C}_{\mathrm{s}20}{C}_{20}\left(C_{\mathrm{s}2}+C_2\right)}{L_{\mathrm{p}}{C}_{\mathrm{s}2}{C}_2\left(C_{\mathrm{s}20}+C_{20}\right)}}}$$

(10)

where L_p0, C_s20, and C₂₀ are the ideal value of corresponding components.

From (10), when there is the ±10% parametric deviation in compensation elements L_p, C_s2, and C₂, the fluctuation range of the deviation factor λ_p1 is ±10%. This suggests that the parametric deviation of components L_p, C_s2, and C₂ can be equated to the fluctuation of the deviation factor λ_p1. Hence, to analyze the effect of deviation factor λ_p1 fluctuations on the load-independent output characteristics of the π-circuit, Figure 3 can be further equated to Figure 4, where the series connection of L′_p and C_s2 is equated to the series connection of equivalent inductance L_eq and capacitance C_eq, and their relation can be represented as

$$L_{\mathrm{p}}^{\prime }-{\displaystyle \frac{1}{{\omega }^2{C}_{\mathrm{s}2}}}=L_{\mathrm{eq}}-{\displaystyle \frac{1}{{\omega }^2{C}_{\mathrm{eq}}}}.$$

(11)

Substituting (11) into (9), the current gain can further be derived as

$$g_{\mathsf{\pi }}={\displaystyle \frac{M}{j\omega C_2{Z}_{\mathrm{L}\text{-}\mathsf{\pi }}\left(M-\frac{1}{{\omega }^2{C}_{\mathrm{eq}}}+L_{\mathrm{eq}}-\frac{1}{{\omega }^2{C}_2}\right)+M-\frac{1}{{\omega }^2{C}_{\mathrm{eq}}}+L_{\mathrm{eq}}}}$$

(12)

Based on (12), there always exists a set of L_eq and C_eq, regardless of the parametric deviation of the components, in which the capacitance C_eq enables the condition in (13) to be satisfied. This demonstrates that in this equivalent model, the circuit consisting of M and C_eq remains resonant at all times.

$$C_{\mathrm{eq}}={\displaystyle \frac{1}{{\omega }^{2}M}}$$

(13)

From (10), (12), and (13), the current gain can be simplified as

$$g_{\mathsf{\pi }}={\displaystyle \frac{M}{L_{\mathrm{p}}\left(1-\frac{1}{{{\lambda }_{\mathrm{p}1}}^2\left(1+\frac{1}{n}\right)}\right)\left(\frac{j{\lambda }_{\mathrm{p}2}}{Q_{\mathsf{\pi }}}\left(1-\frac{1}{{{\lambda }_{\mathrm{p}2}}^2}\right)+1\right)}}.$$

(14)

where

$$n={\displaystyle \frac{C_{20}}{C_{\mathrm{s}20}}} \hspace{1em}{\lambda }_{\mathrm{p}2}={\lambda }_{\mathrm{p}1}\sqrt{1+\left(1-{\displaystyle \frac{1}{{{\lambda }_{\mathrm{p}1}}^2}}\right)n} \hspace{1em}\mathsf{\hspace{1em}}{Q}_{\pi }={\displaystyle \frac{\omega L_{\mathrm{eq}}}{{\lambda }_{\mathrm{p}2}{Z}_{\mathrm{L}\text{-}\mathsf{\pi }}}}={\displaystyle \frac{{\lambda }_{\mathrm{p}2}}{\omega C_2{Z}_{\mathrm{L}\text{-}\mathsf{\pi }}}}$$

(15)

From (15), the variation in the load R′_L can be equated to the fluctuation of Q_π. According to (14), when λ_p1 ≠ 1, the current gain must vary with fluctuations in Q_π, i.e., the load-independent constant current characteristic is lost. Therefore, it is necessary to investigate how to design the capacitance ratio n to enable the π-circuit to equivalently maintain the load-independent constant current characteristics.

Based on (14), it is difficult to directly analyze the design method of the capacitance ratio. Therefore, the deviation rate η_π of the current gain is defined as

$${\eta }_{\pi }={\displaystyle \frac{\left|g_{\pi }\left({\lambda }_{\mathrm{p}1}=1\right)\right|}{\left|g_{\pi }\left({\lambda }_{\mathrm{p}1}\ne 1\right)\right|}}$$

(16)

Based on (16), the deviation rate η_π of the current gain as the function of capacitance ratios n can be expressed in Figure 5 under different tolerance factors λ_p1 and Q_π. It can be observed from Figure 5 that when λ_p1 ≠ 1, the deviation η_π gradually increases with the increase in capacitance ratio n. In addition, in comparison with Figure 5a–d, under the same capacitance ratio n, the larger Q_π is, the smaller the deviation η_π is. As a result, for the π-circuit, reducing the capacitance ratio n and increasing Q_π by the parameter optimization can effectively minimize the deviation rate η_π of the current gain when λ_p1 ≠ 1.

Further, it can be noted from (8) and (15) that the variation in the load R′_L can be equated to the fluctuation of Q_π. The comparison of Figure 5c,d indicates that when Q_π = 0.8 and Q_π = 1.6, the deviation η_π of the output current remains basically the same at the capacitance ratio n < 0.5, i.e., the load-independent output characteristics can still be implemented. However, from Figure 5a,b, when Q_π = 0.2 and Q_π = 0.4, the deviation η_π of the output current fluctuates significantly at n < 0.5. This suggests that a larger Q_π in the load range is better. From (6) and (15), an increase in Q_π can be achieved by decreasing the capacitance ratio n without changing the resonant frequency and equivalent load of the system. Therefore, for the π-circuit, lowering the capacitance ratio n not only reduces the effect of the parametric deviation on the load-independent constant current, but also reduces the fluctuation of the output current.

Furthermore, the analysis of (15) reveals that the parametric deviation of the compensation capacitors C₂ and C_s2 lead to fluctuations in the capacitance ratio. Thus, the fluctuation range D of the capacitance ratio can be further represented as

$$D={\displaystyle \frac{a_1}{b_1}}$$

(17)

where a₁ and b₁ are the ratios of the actual to ideal values for the compensation capacitors C₂ and C_s2.

$$a_1={\displaystyle \frac{C_2}{C_{20}}}\hspace{1em}{b}_1={\displaystyle \frac{C_{\mathrm{s}2}}{C_{\mathrm{s}20}}}$$

(18)

From (18), when parameter deviations of compensation capacitors are C_s2 and C₂, i.e., a₁, b₁ ∈ [0.9, 1.1], the fluctuation range is D ∈ (0.82, 1.22). From Figure 5, when λ_p1 ≠ 1, the smaller the capacitance ratio n, the smaller the output current deviation η_π under D ∈ (0.82, 1.22). Consequently, at the low capacitance ratio, capacitance ratio fluctuations caused by the parametric deviation of compensation capacitors C_s2 and C₂ have little effect on the load-independent output characteristics.

Then, in order to analyze the load-independent constant output characteristics of the L-circuit under the parametric deviation, Figure 2 can be further equated to Figure 6, where equivalent impedance Z_p of the secondary side can be expressed as (19).

$$Z_{\mathrm{p}}={\displaystyle \frac{\omega M^2\left(1+n\right)\left[j\left(1-{\omega }^2{L}_2{C}_2\right)-\omega C_2{R}_{\mathrm{L}}^{\prime }\right]}{L_2\left[j\omega C_2{R}_{\mathrm{L}}^{\prime }\left(1-{\omega }^2{L}_{\mathrm{p}}{C}_2+n\right)-{\omega }^2{L}_2{C}_2+\left(n-{\omega }^2{L}_{\mathrm{p}}{C}_2\right)\left(1-{\omega }^2{L}_2{C}_2\right)\right]}}$$

(19)

From Figure 6, the output current I₁ and output voltage U_c1 of the L-circuit can be expressed as (20) and (21).

$$I_{\mathbf{1}}={\displaystyle \frac{U_{\mathbf{i}\mathbf{n}}}{Z_{\mathrm{L}\text{-}\mathrm{L}}\left(1-{\omega }^2{L}_1{C}_1\right)+j\omega L_1}}$$

(20)

$$U_{\mathbf{c}\mathbf{1}}={\displaystyle \frac{U_{\mathbf{i}\mathbf{n}}}{\left(1-{{\lambda }_1}^2\right)+j{\lambda }_1{Q}_{\mathrm{L}}}}$$

(21)

where

$$Z_{\mathrm{L}\text{-}\mathrm{L}}=j\omega L_{\mathrm{s}}+{\displaystyle \frac{1}{j\omega C_{\mathrm{s}1}}}+Z_{\mathrm{p}} \hspace{1em}{\lambda }_1={\displaystyle \frac{\omega }{{\omega }_0}} \hspace{1em}{Q}_{\mathrm{L}}={\displaystyle \frac{{\omega }_0{L}_1}{Z_{\mathrm{L}\text{-}\mathrm{L}}}}$$

(22)

From (20), if compensating elements L₁ and C₁ are designed to satisfy the condition in (6), the current I₁ remains constant and is unaffected by variations in the equivalent load Z_L-L of the L-circuit. Similarly, the ±10% parametric deviation in the compensating elements L₁ and C₁ inevitably leads to λ₁ ≠ 1, and the loss of the load-independent constant output characteristics.

To still maintain the load-independent constant output characteristics of the L-circuit, from (21), the output voltage deviation rate η_L = |U_c1(λ₁≠1)|/|U_c1(λ₁ = 1)| as the function of Q_L can be shown in Figure 7 under different λ₁. As illustrated in Figure 7, the deviation rate η_L remains essentially constant over the larger range of Q_L. Consequently, Q_L should be designed to be as large as possible during the load R_L range.

In order to investigate the method for increasing Q_L, through the parameter optimization, based on (6), (19), and (22), it can be further denoted as

$$Q_{\mathrm{L}}={\displaystyle \frac{{\omega }_0{L}_1}{j\omega L_{\mathrm{s}}+\frac{1}{j\omega C_{\mathrm{s}1}}+\frac{M^2{\left(1+n\right)}^2{R}_{\mathrm{L}}^{\prime }}{{L_{\mathrm{p}}}^2}-jn\left(1-\frac{L_2\left(1+n\right)}{L_{\mathrm{p}}}\right)}}$$

(23)

From (23), the reduction in the capacitance ratio n can not only lead to an increase in Q_L at the same load R′_L but also reduce the fluctuation in Q_L caused by load variations. This means that Q_L remains almost constant over the load range. As a result, the load-independent constant output of L-circuit can be equivalently implemented by reducing the capacitance ratio.

Based on the above analysis, it can be concluded that reducing the capacitance ratio can enable the DS-LCC compensation network to maintain the load-independent constant output characteristics under the parametric deviation of the compensation element. However, from [23], when the rectifier is not operated in continuous mode, the system could still lose the load-independent constant output. Therefore, the boundary condition between the continuous and discontinuous mode needs to be derived and always keep the rectifier in the continuous mode under the parametric deviation.

The load current I_R depends on the average value of the current i₀ and can be expressed as (24).

$$I_{\mathrm{R}}={\displaystyle \frac{U_{\mathrm{R}}}{R_{\mathrm{L}}}}={\displaystyle \frac{1}{\pi }}{\displaystyle \underset{0}{\overset{\pi }{\int }}{i}_0\left(t\right)}d\left(\omega t\right)$$

(24)

According to Figure 1, furthermore, the load voltage U_R can be derived as

$$U_{\mathrm{R}}={\displaystyle \frac{2R_{\mathrm{L}}{U}_{\mathrm{C}2}\left[2\mathbf{sin}\left(\theta \right)+\pi \mathbf{cos}\left(\theta \right)\right]}{{\pi }^2{R}_{\mathrm{L}}+2\pi \omega L_2}}.$$

(25)

where

$$\mathbf{tan}\left(\theta \right)={\displaystyle \frac{\omega L_2}{R_{\mathrm{L}}}}$$

(26)

For the rectifier, the voltage U_C2 should be greater than the load voltage U_R for operation in the continuous mode. Therefore, based on (24) and (25), the boundary condition for the continuous mode can be deduced as

$$L_2\ge {\displaystyle \frac{2R_{\mathrm{L}}}{{\omega }_0\pi }}.$$

(27)

It can be observed from (27) that the compensation inductance L₂ should be slightly larger than the ideal value to ensure that the rectifier operates in the continuous mode.

From (4) and (7), the parametric deviation not only affects the load-independent constant output characteristics, but also cause fluctuations in the transmission gain g. Based on (14) and Figure 5, under the parametric deviation, the current gain of the π-circuit can be maintained as a constant also through reducing the capacitance ratio. However, according to (20), for the L-circuit, the current I₁ fluctuations caused by the parametric deviation are unavoidable. Hence, the conventional FM control can be adopted to achieve the constant current I₁, and the current I₁ can be further deduced as

$$I_{\mathbf{1}}={\displaystyle \frac{U_{\mathbf{i}\mathbf{n}}}{Z_{\mathrm{L}\text{-}\mathrm{L}}\left(1-{\omega }^2{a}_1{b}_1{L}_{10}{C}_{10}\right)+j\omega a_1{L}_{10}}}.$$

(28)

where a₁ and b₁ are the deviation coefficients of L₁ and C₁, and can be denoted as

$$a_1={\displaystyle \frac{L_1}{L_{10}}}\hspace{1em}{b}_1={\displaystyle \frac{C_1}{C_{10}}}.$$

(29)

It can be observed from (28) that under the parametric deviation of L₁ and C₁, the constant output current I₁ can be achieved by the FM control.

2.2. Implementation of the Soft Switching

For an IPT system, it is essential to implement the soft switching over the load range to improve efficiency. Since the IPT system generally operates at a higher frequency, the inverter is generally composed of MOSFETs. Hence, ZVS is more conducive to minimizing losses than the zero current switching. For the MOSFET, if the turn-off current I_off satisfies the condition in (30), ZVS can be implemented [24].

$$I_{\mathrm{off}}\ge {\displaystyle \frac{2U_{\mathrm{d}}{C}_{\mathrm{j}}}{t_{\mathrm{d}}}}$$

(30)

where C_j and t_d denote the junction capacitance and dead time.

For an IPT system, the imaginary part of the input impedance is required to be greater than zero for implementing ZVS. Therefore, on the basis of (2) and (6), the input impedance of the system can be deduced as

$$Z_{\mathrm{in}\text{-}\mathrm{c}}={\displaystyle \frac{L_1\left({{\omega }_0}^4{M}^2{C_2}^2{R}_{\mathrm{L}}^{\prime }+jb\right)}{C_1\left({{\omega }_0}^8{M}^4{C_2}^4{R_{\mathrm{L}}^{\prime }}^2+b^2\right)}}.$$

(31)

where

$$b={\displaystyle \frac{1}{{\omega }_0{C}_1}}+{\displaystyle \frac{1}{{\omega }_0{C}_{\mathrm{s}1}}}-{\omega }_0{L}_{\mathrm{s}}+{{\omega }_0}^3{M}^2{C}_2\left(1-{{\omega }_0}^2{C}_2{L}_2\right)$$

(32)

It can be observed from (31) that the parametric deviation of the compensation elements L₂, C₂, C₁, and C_s1 may cause the imaginary part of the input impedance to be less than zero. However, from (6) and (15), with the constant resonant frequency, the compensation capacitance C₂ decreases with the reduction in the capacitance ratio. Based on (32), the smaller the compensation capacitor C₂ is, the smaller the impedance fluctuation caused by the parametric deviation of compensation elements L₂ and C₂.

Moreover, based on the above analysis of the L-circuit, FM control is employed to achieve the constant current I₁. From (28), the impedance fluctuation of compensation capacitor C₁ is small with the FM. Therefore, the parametric deviation of C_s1 should be the primary consideration to ensure the realization of ZVS.

In order to investigate the design constraints of the compensation capacitor C_s1, the input current should be further investigated. From (31), the fundamental harmonic I_in-1st of the input current can be expressed as

$$I_{\mathbf{in}\text{-}\mathbf{c}\text{-}\mathbf{1}\mathbf{s}\mathbf{t}}={\displaystyle \frac{C_1{U}_{\mathbf{in}}}{L_1}}\left({{\omega }_0}^4{M}^2{C_2}^2{R}_{\mathrm{L}}^{\prime }-jb\right).$$

(33)

In addition, L₁ and C₁ compose an LC filter on the primary side, which causes the input current to contain high harmonic currents. The (2m + 1)th harmonics I_in-(2m+1)th of the input current can be expressed as

$$I_{\mathbf{i}\mathbf{n}\text{-}\left(\mathbf{2}\mathbf{m}+\mathbf{1}\right)\mathbf{t}\mathbf{h}}\approx {\displaystyle \frac{U_{\mathbf{in}\text{-}\left(\mathbf{2}\mathbf{m}+\mathbf{1}\right)\mathbf{t}\mathbf{h}}}{j\left(2\mathrm{m}+1\right){\omega }_0{L}_1+\frac{1}{j\left(2\mathrm{m}+1\right){\omega }_0{C}_1}}}.$$

(34)

Further, the input current for all higher harmonics can be derived as (35).

$${\displaystyle \sum I_{\mathbf{in}\text{-}\mathbf{m}\mathbf{t}\mathbf{h}}}\approx {\displaystyle \frac{U_{\mathbf{i}\mathbf{n}}}{j4{\omega }_0{L}_1}}$$

(35)

Based on (30) and (35), under the ±10% parametric deviation, for the realization of ZVS, the compensation capacitor C_s1 should satisfy the condition in (36).

$$C_{\mathrm{s}1}\le {\displaystyle \frac{11\left(t_{\mathrm{d}}-2\pi {\omega }_0{L}_1{C}_{\mathrm{j}}\right)}{40{{\omega }_0}^2{t}_{\mathrm{d}}{C}_1\left[{{\omega }_0}^4{k}^2{L}_{\mathrm{p}}{L}_{\mathrm{s}}{C_2}^2\left({{\omega }_0}^2{L}_2{C}_2-1\right)+{{\omega }_0}^2{L}_{\mathrm{s}}-\frac{1}{C_{\mathrm{f}1}}\right]}}.$$

(36)

3. Design of the DS-LCC Compensated IPT Converter with the Proposed Method

3.1. Design Procedure with Proposed Method

On the basis of the above analysis, it can be concluded that under the parametric deviation of components, the load-independent constant current output of the DS-LCC compensation topology can be implemented by reducing the capacitance ratio n. However, the reduction in the capacitance ratio n may affect the transmission gain and transmission efficiency without the parametric deviation.

From (7), for the DS-LCC compensation topology, the transmission gain in resonance can be expressed as

$$g={\displaystyle \frac{I_{\mathbf{o}}}{U_{\mathbf{in}}}}={\displaystyle \frac{M\left(1+n\right)}{j{\omega }_0{L}_1{L}_{\mathrm{p}}}}$$

(37)

Based on (37), the transmission gain g decreases as the capacitance ratio n decreases. Therefore, in order to achieve the same transmission gain at the low capacitance ratio, the compensation inductance L₁ should be reduced.

From (35), the decrease in compensation inductance L₁ leads to an increase in the harmonic current, and the harmonic current can be further expressed as

$${\displaystyle \sum I_{\mathbf{in}\text{-}\mathbf{c}\text{-}\mathbf{m}\mathbf{t}\mathbf{h}}}\approx {\displaystyle \frac{U_{\mathbf{in}}g{L}_{\mathrm{p}}}{j4M\left(1+n\right)}}$$

(38)

According to (38), with the decrease in capacitance ratio n, the harmonic current will further increase. This leads to the variation in the input impedance angle, consequently increasing the reactive power loss and switching loss of the system.

To further investigate the effect of reducing the capacitance ratio n on the system transmission efficiency, the input impedance angle α can be represented as

$$\alpha =\mathbf{arctan}\left({\displaystyle \frac{\left({\omega }_0{C}_{1}b+1\right)L_{\mathrm{p}}g}{{{\omega }_0}^6{M}^3{C_1}^2{C_2}^2{R}_{\mathrm{L}}^{\prime }\left(1+n\right)}}\right)$$

(39)

From (39), the input impedance angle increases as the capacitance ratio decreases, which can lead to an increase in reactive losses. Therefore, the minimum capacitance ratio n_min should be determined according to the maximum input impedance angle α_max, where the transmission efficiency can meet the requirements of the system.

Moreover, from (15), the reduction in the capacitance ratio n leads to an increase in the compensation capacitance C_s2 and a decrease in the compensation capacitance C₂. However, for capacitance, the value that is too large or too small can increase the cost and difficulty of the manufacture. Therefore, the compensation capacitance C_s2 and C₂ can be further expressed as

$$C_2={\displaystyle \frac{1+n}{{{\omega }_0}^2{L}_{\mathrm{p}}}}{C}_{\mathrm{s}2}={\displaystyle \frac{1+n}{n{{\omega }_0}^2{L}_{\mathrm{p}}}}$$

(40)

From (40), it can be seen that at a constant capacitance ratio, the compensation capacitance C_s2 and C₂ can be adjusted by a reasonable choice of the resonant frequency, thus, reducing the cost of the system.

On the basis of the above analysis, it can be concluded that under the parametric deviation of components, the load-independent constant current output of the DS-LCC compensation topology can be implemented by reducing the capacitance ratio n, and the constant transmission gain can be achieved by the FM control. However, the reduction in the capacitance ratio n not only leads to a decrease in the transmission efficiency in resonance but also causes compensation capacitances C_s2 and C₂ to become excessively large or small. In addition, the parasitic resistance of the compensating element is ignored in all of the above analysis, which may also affect the implementation of the load-independent constant current output. As a result, for the purpose of implementing the load-independent constant current and constant transmission gain under the parametric deviation, the proposed design approach is illustrated in Figure 8 and as follows:

Step 1: Depending on the practical application, the self-inductance of the transmitter coil L_s and receiver coil L_p, mutual inductance M, input voltage U_d, output current I_o, resonant frequency f₀, and load range must be estimated.

Step 2: According to the ±10% parameter fluctuation, the capacitance ratio n can be selected. Furthermore, according to the receiver coil L_p, resonant frequency f₀, and capacitance ratio n_c, the compensation capacitance C_s2 and C₂ can be calculated by (40).

Step 3: At this point, in order to reduce the cost and manufacturing difficulty of the system, C_s2 and C₂ should be checked to see whether they are too large or too small. If C_s2 or C₂ is too large, the resonant frequency f₀ needs to be increased, i.e., f₀ = f₀ + Δf₀. If C_s2 or C₂ is too small, the resonant frequency f₀ needs to be increased, i.e., f₀ = f₀ − Δf₀.

Step 4: In accordance with (27), the larger the compensation inductance L₂ is, the easier the rectifier operates in the continuous mode. However, a large L₂ could increase the size of the receiving LCC network, which is not conducive to the lightweight design of the receiving side. Therefore, the minimum compensation inductance L₂ for the continuous mode operation of the rectifier should be designed according to the load and ±10% parameter fluctuation range and can be calculated by (41).

$$L_2={\displaystyle \frac{20R_{\mathrm{L}\text{-}\max }}{9{\omega }_0\pi }}$$

(41)

Step 5: At this point, to meet the transmission gain of the system, based on the input voltage U_d, output current I_o, mutual inductance M, and resonant frequency f₀, the compensation inductance L₁ and the compensation capacitance C₁ can be calculated by (6) and (7).

Step 6: With the purpose of implementing the ZVS, the compensation capacitance C_s1 can be calculated by (36).

Step 7: At this time, within the FM range and ±10% parametric deviation, the load-independent constant current output characteristics can be implemented. If the results are not satisfied, reduce the compensation capacitance ratio n and recalculate the parameter of this compensation topology.

Step 8: Based on the above analysis, decreasing the capacitance ratio can lead to an increase in the harmonic current, and result in a decrease in the transmission efficiency of the system. For the IPT system, the transmission efficiency η = U_RI_R/U_dI_d should be greater than 90% according to [25,26,27]. Therefore, it is necessary to verify whether η > 90%. If the efficiency is not achieved, the entire parametric design process needs to be repeated.

3.2. Design of the Proposed IPT System

When the design of the compensation network is completed, the proposed IPT system still requires the FM to achieve the constant current output. Consequently, the schematic diagram of the DS-LCC compensation IPT converter can be represented as in Figure 9. As can be gathered from Figure 9, the output current I₁ of the L-circuit is detected and conveyed to the FM controller. Then, switching signals can be generated by comparing I₁ with I_ref. This demonstrates that the suggested methodology is able to eliminate the communication module between the transmitter and receiver.

4. Experimental and Simulation Verification

Based on the preceding analysis, it is evident that the DS-LCC compensation topology can maintain the load-independent constant current output despite the parametric deviation of components by decreasing the capacitance ratio n. Additionally, the constant transmission gain can be attained through the FM control. In order to validate the effectiveness and feasibility of the proposed method, under the same electrical parameters illustrated in

Table 1. Electrical parameter.

Symbols	Parameters	Value
ud	Input Voltage	80 V
i0	Output Current	1.5 A
f0	Resonant Frequency	90 kHz
RL	Load Range	3Ω–33Ω
Ls	Transmitter Coil	128 μH
Lp	Receiver Coil	128 μH
k	Coupling Coefficient	0.38

, the parameters of the DS-LCC compensation network with the capacitance ratio n = 1 shown in

Table 2. Parameters of the double-sided LCC compensation network at n = 1.

Symbols	Parameters	Ideal	Actual
L1	Primary Series Inductor (μH)	55	54.3
C1	Primary Parallel Capacitor (nF)	57	56.6
Cs1	Primary Series Capacitor (nF)	50	49.6
L2	Secondary Series Inductor (μH)	48	47.3
C2	Secondary Parallel Capacitor (nF)	49	48.6
Cs2	Secondary Series Capacitor (nF)	49	49.2

are optimized. According to the parameter design procedure illustrated in Figure 8, the optimization result is shown in

Table 3. Parameters of the double-sided LCC compensation network at n = 0.15.

Symbols	Parameters	Ideal	Actual
L1	Primary Series Inductor (μH)	31	31.3
C1	Primary Parallel Capacitor (nF)	98	97.5
Cs1	Primary Series Capacitor (nF)	30	30.4
L2	Secondary Series Inductor (μH)	48	47.3
C2	Secondary Parallel Capacitor (nF)	28	27.8
Cs2	Secondary Series Capacitor (nF)	187	187.9

, in which the capacitance ratio n = 0.15.

4.1. Simulation Verification

In practice, for the DS-LCC compensation network, it is often the case that the parametric deviation of multiple components exists simultaneously. Therefore, in order to validate the effectiveness of the proposed method, a random numerical statistical simulation based on the Monte Carlo analysis is further adopted. Within the ±10% parametric deviation range and an accuracy of 0.0001, 100,000 combinations of random parametric deviation are generated through MATLAB 2018b under n = 0.15 and n = 1, respectively. In this paper, for the convenience of counting and analyzing the influence of each combination on the output current, the output current deviation η_DS-LCC is further defined as the output current under each combination divided by the output current without the parametric deviation. Furthermore, the different ranges of the output current deviation η_DS-LCC, as indicated in

Table 4. Different deviation ranges of the output current deviation.

Symbols	Deviation Range	Symbols	Deviation Range
A1	0.83 ≤ ηDS-LCC < 0.85	A9	0.99 < ηDS-LCC ≤ 1.01
A2	0.85 ≤ ηDS-LCC < 0.87	A10	1.01 < ηDS-LCC < 1.03
A3	0.87 ≤ ηDS-LCC < 0.89	A11	1.03 ≤ ηDS-LCC < 1.05
A4	0.89 ≤ ηDS-LCC < 0.91	A12	1.05 ≤ ηDS-LCC < 1.07
A5	0.91 ≤ ηDS-LCC < 0.93	A13	1.07 ≤ ηDS-LCC < 1.09
A6	0.93 ≤ ηDS-LCC < 0.95	A14	1.09 < ηDS-LCC ≤ 1.11
A7	0.95 ≤ ηDS-LCC < 0.97	A15	1.11 < ηDS-LCC ≤ 1.13
A8	0.97 ≤ ηDS-LCC < 0.99	A16	1.13 < ηDS-LCC ≤ 1.15

, are established. Based on Table 4, the Gaussian distribution of combinations at different deviation ranges is represented in Figure 10. From Figure 10, at the capacitance ratio n = 0.15, the probability that output current deviation is within ±10% is 93.1%, while at the capacitance ratio n = 1, the probability that output current deviation is within ±10% is only 73.4%. Therefore, under the parametric deviation, the range of the output current deviation at n = 0.15 is significantly smaller than at n = 1. This means that the reduction in the capacitance ratio effectively reduces the output fluctuation, thus reducing the FM range to achieve constant transmission gain. Therefore, the parameters of the DS-LCC compensation network can be optimized by the design procedure shown in Figure 8.

As analyzed in Section 2, for the L-circuit, the deviation factor λ₁ reaches the minimum when both L₁ and C₁ have +10% parametric deviations, and the maximum when both L₁ and C₁ have −10% parametric deviations. For the π-circuit, the output characteristics can be affected by fluctuations in the capacitance ratio n and deviation factor λ_p1. The values of both n and λ_p1 would vary in the following two cases: (1) C₂ has a +10% deviation while C_s2 has −10%, (2) C₂ has a −10% deviation while C_s2 has +10%. Therefore, the combination of the parametric deviation shown in

Table 5. Parametric deviation at n = 0.15 and n = 1.

Symbols	Parameters	Case 1	Case 2
L1	Primary Series Inductor	+10%	−10%
C1	Primary Parallel Capacitor	+10%	−10%
Cs1	Primary Series Capacitor	+10%	−10%
L2	Secondary Series Inductor	−10%	−10%
C2	Secondary Parallel Capacitor	+10%	−10%
Cs2	Secondary Series Capacitor	−10%	+10%

is chosen for the comparative validation.

The output current, as the function of the operating frequency under different parametric deviation combinations, is represented in Figure 11 and Figure 12, when n = 0.15 and n = 1. From Figure 11a and Figure 12a, without the parametric deviation, the FM range for implementing the load-independent constant current output characteristics is 85 kHz to 95 kHz for n = 0.15, while the FM range is only 88 to 92 kHz for n = 1. Likewise, it can be observed from the comparison of Figure 11b and Figure 12b that when the parametric deviation is Case 1, the FM range with the load-independent constant output is 80 kHz to 92 kHz for n = 0.15, and the FM range is 85 kHz to 90 kHz for n = 1. From Figure 11c and Figure 12c, when the parametric deviation is Case 2, the FM range for n = 0.15 is also wider than that for n = 1. Therefore, through the reduction in the capacitance ratio n, the load-independent constant output characteristics can be maintained under the parametric deviation and FM.

4.2. Experimental Verification

Based on Table 1, Table 2 and Table 4, a prototype of the DS-LCC compensation topology is shown in Figure 13. The main DC-AC full-bridge inverter comprises four MOSFETs with the manufacturer part number SPW47N60C3, and the secondary rectifier comprises four fast-recovery diodes with manufacturer part number MUR860T. The main electrical parameters of the MOSFET and fast recovery diode are shown in

Table 6. Main electrical parameters of the MOSFET and fast recovery diode.

Device	Parameter	Symbol	Values
MOSFET	Output capacitance	Coss	2200 pF
	Input capacitance	Ciss	6800 pF
	Reverse transfer capacitance	Crss	145 pF
	Turn-on delay time	td(on)	18 ns
	Rise time	tr	27 ns
	Turn-off delay time	td(off)	111 ns
	Fall time	tf	8 ns
Fast-recovery diode	Reverse recovery time	trr	25 ns

. The load is substituted by a variable resistor. Coupling coils are designed as the conventional round.

Without the parametric deviation, experimental waveforms of input current i_in, input voltage u_in, load current i_R, and load voltage u_R under different loads and capacitance ratios are shown in Figure 14. It can be observed from Figure 14 that regardless of n = 0.15 or n = 1, the load current is almost constant at 1.5 A at 90 kHZ when the load is increased from 3 Ω to 33 Ω. This indicates that without the parametric deviation, the load-independent constant output characteristics can be maintained at different capacitance ratios. Moreover, ZVS can be implemented over the load range at different capacitance ratios. When R_L = 33 Ω, i.e., at the rated output power, the efficiency is 93.5% and 94.2% for n = 0.15 and n = 1, respectively. Based on (37), to obtain the same transmission gain under different capacitance ratios, a smaller compensating inductance L₁ is required at the lower capacitance ratio. From (38), the harmonic input current would be increased at the smaller L₁. Therefore, it can be noticed that the efficiency with the capacitance ratio n = 0.15 is slightly lower than that with the capacitance ratio n = 1.

Figure 15 illustrates experimental waveforms of input current i_in, input voltage u_in, load current i_R, and load voltage u_R under different capacitance ratio when the parametric deviation is Case 1 and R_L = 33 Ω. It can be observed from Figure 15a that when n = 1, the output current can be sustained at 1.5 A by adjusting the operating frequency from 90 kHz to 80 kHz. According to Figure 15b, when n = 0.15, the operating frequency only needs to be regulated from 90 kHz to 85 kHz to maintain the output current at 1.5 A. Due to the increase in the reactive power caused by the FM, the efficiency at n = 1 and n = 0.15 drops to 73.9% and 87.4%. A comparison of Figure 15a,b shows that the higher efficiency can be obtained at n = 0.15, since the FM range is smaller.

Figure 16 demonstrates the experimental waveforms of load switching under different capacitance ratios when the parametric deviation is Case 1. Based on Figure 16a, under n = 1, when the load is changed from 3 Ω to 33 Ω, the output current varies from 1.77 A to 1.5 A, and the fluctuation of the output current is +18%. This indicates that the load-independent constant current characteristic at n = 1 is lost. From Figure 16b, under n = 0.15, the output current is briefly lowered and remains at 1.52 A after 40 ms. The maximum fluctuation of the output current is only +3.33%. Comparing Figure 16a,b, when the parametric deviation is Case 1, the load-independent constant current characteristic can also be realized at n = 0.15. Moreover, at n = 0.15, ZVS can be implemented over the load range.

Figure 17 illustrates experimental waveforms of input current i_in, input voltage u_in, load current i_R, and load voltage u_R under different capacitance ratio when the parametric deviation is Case 2 and R_L = 33 Ω. As can be noticed from Figure 17a, when n = 1, the output current can be sustained at 1.5 A by adjusting the operating frequency to 100 kHz. Based on Figure 17b, when n = 0.15, the operating frequency only needs to be regulated to 95 kHz to maintain the output current at 1.5 A. Similarly, because of the smaller FM range, the transmission efficiency is higher at 84.9% for n = 0.15, while it is lower at 68.2% for n = 1.

Figure 18 shows the experimental waveforms of load switching under different capacitance ratios when the parametric deviation is Case 2. Based on Figure 18a, under n = 1, when the load is changed from 3 Ω to 33 Ω, the output current varies from 1.47 A to 1.61 A at the constant operating frequency, the fluctuation of the output current is +7.3%. From Figure 18b, under n = 0.15, the output current can also be maintained at approximately 1.5 A within 40 ms, and the fluctuation is less than 5%. Likewise, from Figure 18, when the parametric deviation is Case 2, the load-independent constant current characteristic can also be realized under n = 0.15. In addition, at n = 0.15, ZVS can also be implemented over the load range.

It can be observed from

Table 7. Comparison with the previous method.

	Topology	Varying Parameter	Solution	Efficiency	Power Range
This work	DS-LCC	Inductance, capacitance, laod	Reduction in capacitance ratio, FM	93.5%	10–100% of the rated power
[28]	DS-LCC	Load	None	92.1%	10–100% of the rated power
[29]	S-SP, LCC-S, LCC-P, DS-LCC	Load, coupling coefficient, frequency	None	91.8%	Rated power
[30]	LCC-S	Inductance, capacitance	Phase shift control, SCC	93.7%	Rated power
[19]	DS-LCC	Inductance, capacitance	Monte Carlo design, frequency tuning	96.3%	Rated power
[20]	LCC-S	Capacitance	Sobol sensitivity analysis	94.8%	Rated power

that, compared with the previous methods, under multi-parametric deviation of the DS-LCC compensation network, load-independent constant-current output characteristics and constant transmission gain can be implemented through the suggested method. Compared to the methods presented in [28,29], the proposed design method can achieve load-independent constant current despite the parametric deviation of the compensating inductor and compensating capacitor. Compared with [30], the proposed method does not require SCC and simplifies the control system. From [19,20], the influence of parameter deviations can be minimized under the rated power, which means that the load-independent constant current output characteristics cannot be realized. With the proposed method, the load-independent constant current output can be maintained over the 10–100% of the rated output power.

5. Conclusions

From the experimental results, the maximum fluctuation of the output current at n = 0.15 is +3.33%, while that at n = 1 is +18%. This means that through reducing the capacitance ratio n, the load-independent constant output characteristics of the DS-LCC compensation topology can be maintained under the ±10% parametric deviation. Moreover, the constant transmission gain can be realized by FM. The frequency modulation range is 85 kHz–95 kHz at n = 0.15, while that is 80 kHz–100 kHz at n = 1. The smaller the frequency adjustment range, the lower the reactive power loss caused by FM. Therefore, the transmission efficiencies at n = 0.15 are 87.4% and 84.9% under different parametric deviations, which are significantly higher than those at n = 1. Finally, reducing the capacitance ratio will lead to an increase in the harmonic content of the input current, resulting in an increase in the imaginary part of the input impedance, so further research should be carried out to reduce harmonics.