Comprehensive Investigation of Security and Quality Metrics for Lightweight Double Arbiter PUF on FPGAs: Design and Analysis ^†

Abstract

Protecting IoT (Internet of Things) devices against attacks is essential due to the rapid increase in connected devices. This is particularly challenging for lightweight devices with limited hardware capacity, making computationally intensive encryption inefficient. To address this issue, PUF-based security applications can enhance security while reducing resource requirements. The PUF must meet key criteria such as unclonability, unpredictability, and uniqueness throughout its operational lifetime. To achieve this, it is important to minimize unwanted offsets in signal propagation delays caused by unbalanced design strategies and ensure that the PUF responds robustly to physical influences. This paper presents the development and an extensive investigation of a novel 56-bit 2-4 Double Arbiter PUF. Its performance is evaluated on 110 FPGAs with a dataset of 3 million challenge–response pairs (CRPs) under temperature variations in a range from 0 to 50 °C. This study also examines the identification of bit positions with high offsets in order to detect and eliminate potential weaknesses. Furthermore, we extend the 2-4 DAPUF with a lightweight XOR layer to create a 2-4 XOR-DAPUF and improve performance. Our results demonstrate robust and efficient hardware architecture. The optimized 2-4 XOR-DAPUF delivers outstanding performance with 95.85% reliability, 48.09% randomness, and 48.79% uniqueness.

1. Introduction

The security of critical infrastructures is becoming increasingly important due to the rapid development and number of connected devices in networks [1]. It is estimated that by 2027 there will be around 30 billion [2] networked devices, which represents a major challenge for the chip industry and the protection of critical data [2,3]. Networked IoT (Internet of Things) devices are being used in a wide variety of areas such as industry, smart cities [4,5], vehicles [6] and smart home systems [7,8]. In particular, the security of lightweight IoT devices is an important factor due to their limited memory, resources, and thus computing power. Due to these factors, the implementation of modern cryptographic functions, e.g., for authentication on low-cost devices, can pose a significant challenge [9]. It must be considered that memory-based cryptographic algorithms are subject to invasive and side-channel attacks [10]. An attack can have considerable economic consequences and even lead to a life-threatening situation [11]. Unfortunately, low-cost IoT devices are often powered by batteries [11], making computationally intensive operations inefficient or impossible.

As a solution to this, physical unclonable functions (PUFs) can be used to enhance the security of connected devices with limited hardware resources. PUFs are specialized hardware architectures that generate an individual and device-specific output signal (called the response) for a given input signal (called the challenge), similar to fingerprints or watermarks. In delay-based PUFs, unique signals are generated due to variations in the manufacturing process of the integrated circuit (IC), leading to different processing times for each individual component. These output signals can be used in PUF-based authentication protocols [12,13,14,15] to prevent data transmission and processing on cloned or tampered devices. A key advantage of PUFs is that, depending on their architecture, hundreds, thousands, or even millions of unique CRPs can be generated without requiring memory components such as block RAMs (BRAM). In addition, PUFs are particularly energy-efficient due to their lightweight structure. This makes PUFs an attractive alternative security component for small IoT devices [16] with limited storage. Additionally, this property prevents key extraction, for example, in symmetric or asymmetric encryption, as the output signal is generated directly on-chip by the circuit. However, to generate device-unique keys with high reliability, delay-based PUFs must have a fixed and well-balanced structure and should fulfill several security criteria [16]. Otherwise, unwanted effects such as offsets in the signal propagation delay can occur, which compromise security as described in our previous work [11]. Moreover, like any hardware, PUFs are susceptible to physical influences such as on-chip temperature, electromagnetic signals, or aging processes, which can affect their uniqueness and reliability [17]. These effects must be considered during development and implementation to ensure the robustness and security of PUFs, which presents a significant challenge [11] in recent research.

This paper presents the development of a novel, robust, and lightweight delay-based PUF called 2-4 Double Arbiter PUF (2-4 DAPUF). The evaluation of the PUF is based on extensive measurements performed on 110 FPGAs using a large dataset of 3 million challenges under different ambient temperatures and conditions. The analysis focuses on the effects of ambient temperature in the range from 0 to 50 °C and internal noise circuits on the performance of the PUF. As part of the performance analysis, key quality metrics such as reliability, randomness, and uniqueness as well as detailed investigations of bit-level offsets are evaluated. The aim is to identify potential bit errors to improve the overall performance of the PUF. In addition, a statistical model of the implemented design is also presented. Our results demonstrate overall good values for the evaluated quality metrics. Across the entire temperature range, the average reliability is 97.25%, the randomness 43.65%, and the uniqueness amounts to 41.75%. Additionally, the results indicate temperature-resistant behavior. When analyzing the effects of internal disturbance circuits, the implemented PUF also shows robust performance. The reliability decreases by only 0.02%, the randomness by 0.24%, and the uniqueness 0.07% across the entire temperature range, which highlights the resilience of the PUF against disturbances caused by internal circuits. In addition to the performance analysis, the presented PUF features a lightweight architecture, requiring only 13 slices to generate a single response bit. By extending the PUF with an XOR layer, the quality metrics are significantly improved. The extended PUF achieves a randomness of 48.09% and a uniqueness of 48.79%, with a slight reduction in reliability to 95.85%.

The aim of this paper is to present the implementation and analysis of a robust and temperature-resistant DAPUF, identify and optimize vulnerabilities and limitations of PUFs, and provide results and investigations that will support future research in the field of PUF-based security applications. This investigation is based on the 2-4 DAPUF introduced in our previous work [18] and expands previous research by implementing the design on 110 FPGAs and providing comprehensive performance evaluations and statistical analysis.

This work is structured as follows: Section 2 introduces delay-based PUFs, with a particular focus on APUFs and their optimization into a double arbiter PUF. Additionally, this section also presents and compares various APUF architectures from different works. Furthermore, PUF-based security applications from recent research are also presented in this section. Section 3 describes the quality metrics—reliability, randomness, and uniqueness. Section 4 introduces the modeling of MUX-based PUFs and presents the statistical models for simulating APUFs. The structure of the proposed 2-4 DAPUF is presented in Section 5. Section 6 describes the experimental setup, while the comprehensive analysis of the implemented PUF is presented in Section 7. In Section 8, the experimental results and findings are discussed and ideas for further research are presented. Finally, Section 9 summarizes the findings of the work and outlines our next steps in research.

2. Background and Related Work

This section describes the structure and functionality of an APUF (Arbiter PUF). It discusses the challenges associated with implementing APUFs on FPGAs and presents their characteristics as well as optimizations to improve performance and resource utilization. In addition, current approaches and solutions for various APUF implementations from recent research are presented and analyzed in detail. Finally, the use of PUFs for enhancing the security of a device is also briefly described in this section.

2.1. Delay-Based Physical Unclonable Functions

Delay-based PUFs generate device-specific signals that can be used in various security applications. Here, the propagation delay of two identical circuits that differ in processing time due to variations in the manufacturing process, aging effects, or internal and external influences are analyzed. In contrast to ring oscillator PUFs (RO-PUF) [19,20,21], APUFs generate unique output signals by passing a trigger signal through parallel paths and analyzing which path has the fastest propagation delay (Figure 1a). The path can be changed by the challenge bits c, which modify the routing of the path and thus impact propagation delay. Path changes are performed by switching units (SUs), which consist of two multiplexers (MUXs) as shown in Figure 1a. At the end of an APUF chain, a register (FF) is used to generate the response bit. In this case, a ‘1’ is generated if the signal at the D input arrives before the signal at the C (CLK) input, while a ‘0’ is generated when the signal at the C input arrives first. In the following, a series of SUs is referred to as an arbiter block.

A major disadvantage of this APUF is that a complete symmetrical implementation of the paths on FPGAs is extremely difficult or even impossible due to their specific and fixed architecture. The main problem arises from asymmetries in the connection of two SUs, which are caused by other FPGA components such as digital signal processors (DSPs) or block RAMs (BRAMs), as these components enable further connections and thus disrupt the routing of an arbiter chain. In addition, the parallel routing of two paths through a switching matrix is either very difficult or not feasible due to the fixed routing options. An additional asymmetry arises at the connection between the last SU and the register responsible for generating a response bit, as the routing to the D and C inputs of the register cannot be done symmetrically. However, this offset can be minimized through targeted routing adjustments, which help reduce the negative impact on the generation of the response bit. Furthermore, the uneven distribution of FPGA components, such as DSBs, BRAMs, and others, can cause fixed offsets in propagation delay that are uniform across all individual FPGA devices of the same type. This uneven architecture can affect the randomness and uniqueness of the output signal [11]. As described in our previous works [11,18,22], conventional APUFs as in [23,24] show high reliability and low uniqueness, which can be attributed to an asymmetric design strategy. These PUFs are therefore not suitable for use in security applications. For this reason, the implementation of the APUF in Figure 1a is better suited for ASICs (Application-Specific Integrated Circuits).

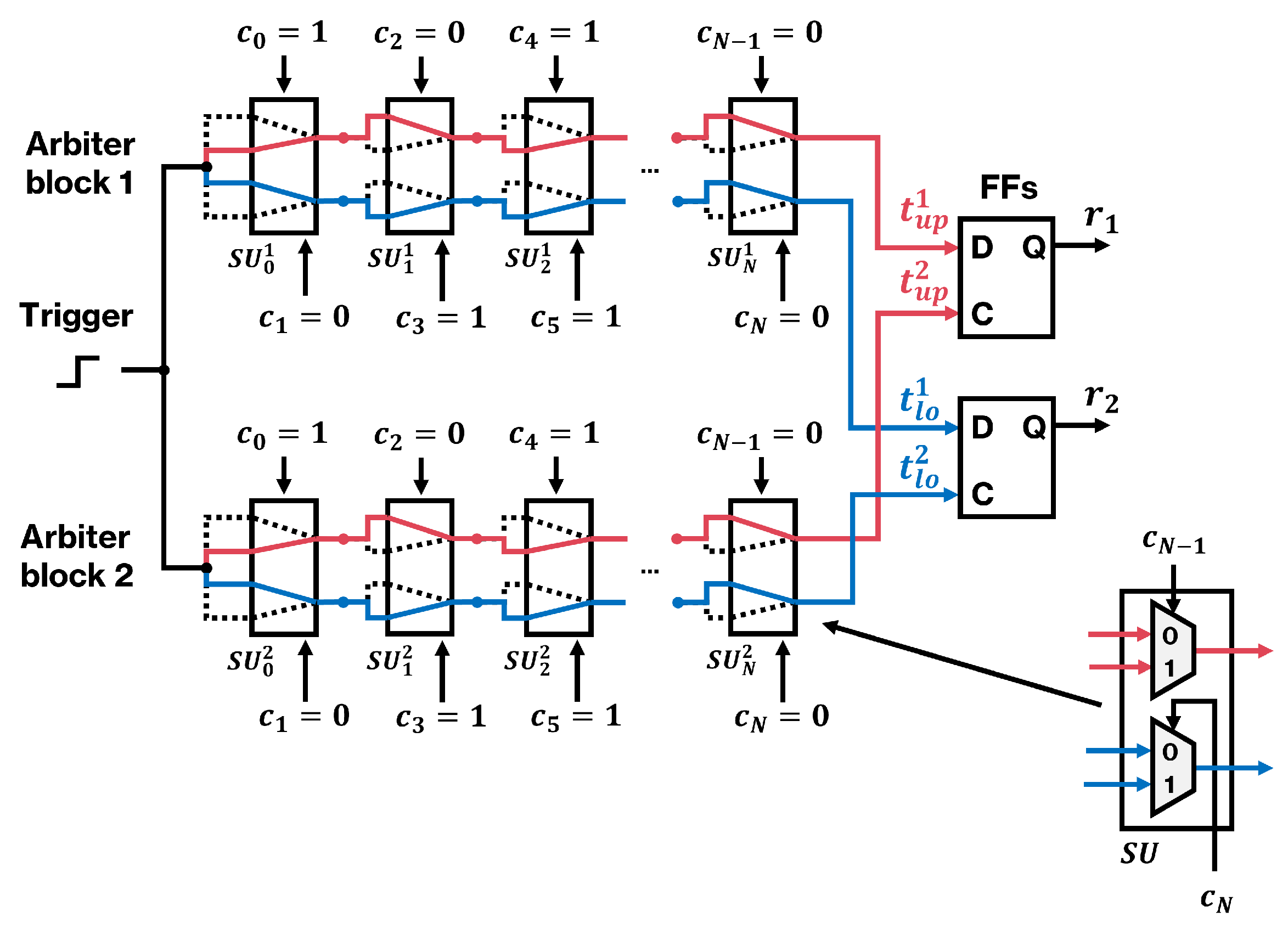
To reduce offsets in propagation delay, the paths are implemented in two separate arbiter blocks as shown in Figure 1b. By using the same challenge bits for the respective SUs of the two arbiter blocks, the paths (red and blue) can be implemented in parallel, resulting in a DAPUF block. Due to the two-dimensional structure of FPGAs, an arbiter block consists of a chain of CLBs (Configurable Logic Blocks) connected in series. For the symmetry, the second arbiter block is implemented with the same routing configuration (e.g., through the hard macro function) under the first arbiter block, so that the SUs in each stage ($S{U}_x^1,S{U}_x^2$) are implemented directly below one another. Due to the identical routing configuration and the identical structure of the CLBs within an FPGA, symmetrical paths can be established between two arbiter blocks. This approach enables the implementability of APUFs on FPGAs by using specific constraints or the hard macro function of the EDA tool. For this purpose, it should be noted that the chain of CLBs should not be disturbed by other FPGA components. Therefore, resource efficiency and reducing SU-SU connections are essential, as further described in Section 5 in detail. This extended PUF structure is called 2-1 double arbiter PUF (2-1 DAPUF), as a single response bit is generated for two arbiter blocks. Due to this optimization, DAPUFs as in [25,26] show improved uniqueness compared to APUFs. The disadvantage of this structure is that it features double the number of arbiter blocks and thus hardware resources are required for the generation of a single response bit.

To address this problem, the structure of the 2-1 DAPUF (Figure 1b) can be further optimized to generate individual signals with reduced resource consumption. The optimized DAPUF from our previous implementation [22] is shown in Figure 2. Compared to Figure 1b, it can be observed that the arbiter blocks contain two independent paths (red and blue), each of which can be configured separately. For this purpose, the SUs include two MUXs, one for each path, and they can also be implemented into a single slice. At the output of the PUF, both paths can be evaluated independently using an FF for each response bit as shown in Figure 2. This PUF is referred to as a 2-2 DAPUF, as two arbiter blocks are used to generate two response bits.

In [27], a flip-flop-based APUF (FF-APUF) design on FPGAs is presented with the aim of improving the weaknesses of conventional APUFs and achieving high uniqueness (Figure 3). The structure of this PUF is similar to the 2-1 DAPUF in Figure 1b. The difference is that in this work, the propagation delays of FFs instead of LUTs are investigated. Therefore, an SU consists of four FFs, which are loaded with an initial value of ‘1’, and three MUXs, whereby one of four output signals of the FFs can be selected ($e_i,f_i,g_i,h_i$) by the challenge. The output signal of an SU is thus connected to the CLK signal of the subsequent SU, which is used to activate the next stage. An RS latch is then used to generate a response bit. This design was implemented on 11 FPGAs boards and tested with different ambient temperature and supply voltage variations. The average uniqueness was 41.53% and the reliability was 97.10%.

In [28], a feed-forward XOR PUF (called FFXOR PUF) is presented. A simple feed-forward PUF is an extended version of an APUF into which one or more intermediate arbiter(s) are inserted. Instead of a direct signal race through all SUs, an intermediate arbiter captures a partial output at a specific point and uses it as additional input (as hidden challenge) for other stages. This leads to non-linearity, making the PUF more resistant to machine learning attacks, but also reduces the reliability of the responses. In order to generate a single response bit in [28], several feed-forward PUFs are implemented in parallel, where the outputs are XORed. Therefore, two main variants are presented in this work: homogeneous FFXOR PUF, where all components have the same structure, and heterogeneous FFXOR PUF, where the components have different designs. The results from the paper show that the heterogeneous FFXOR PUF provides high security against modeling attacks. However, the designs show low reliability and are less resistant against physical influences. To solve this problem, a method called soft-response thresholding is used. Here, CRPs are generated several times to determine which challenge generates constant and stable responses. For this purpose, stable challenges can be used in security applications, while unstable challenges are discarded in this approach.

A priority arbiter PUF (called PA-PUF) is presented in [29]. The architecture is based on a triple-input arbiter (top, center, bottom) combined with two multiplexers and XOR logic (priority arbiter). This results in a higher non-linearity compared to classic APUFs. In addition, feed-forward arbiters are integrated to increase the number of CRPs and improve security. The PA-PUF was implemented on an AMD-Xilinx Artix-7 FPGA. This design shows a randomness of 49.45% and a uniqueness of 49.63%, which are close to the ideal value of 50%. The reliability amounts to 94.5%, which is increased to 100% by using Bose–Chaudhuri–Hocquenghem (BCH) error-correcting codes (ECCs) [30]. The architecture is also configurable so that more CRPs can be generated using an additional feed-forward arbiter.

2.2. PUF-Based Application Scenarios

One of the best-known areas of application for PUFs is PUF-based authentication protocols. The aim here is to identify attackers or unauthenticated devices in a network and to block data transmission to these devices. Authentication is basically carried out in two processes, the enrollment and the authentication phases between two nodes (device and a secure instance). In the first phase, the CPRs are exchanged. To achieve this, the server sends a random challenge to the device, receives the corresponding response, and saves the CRP in a database. In the second phase (Figure 4a), a previously registered device is authenticated. During this process, the server fetches a CRP ($C_i,R_i$) from the database and sends the challenge to the device again. The device generates a response using the PUF ($R_i=PUF\left(C_i\right)$) and sends it back to the server. The server checks whether the response received matches with the entry in the database ($R_i^{\prime }=R_i$). If this is the case, it can be assumed that the device has already been registered. If not, the connection is aborted. In research, PUF-based authentication protocols are used particularly in critical areas such as IoT [31,32,33], IoMT (Internet of Medical Things) [34,35,36], or in smart agriculture [37,38].

The on-chip generation of unique and reliable keys is also a PUF-based application used in research [39,40] (Figure 4b). The main advantage here is that the generated keys do not need to be stored in a memory and can be regenerated through the corresponding challenge. On the other hand, PUFs are also used as TRNGs (True Random Number Generators) as shown in Figure 4c. The main difference is that PUFs for generating random numbers are usually based on memory-based PUFs [41,42,43,44,45]. In this case, the random number is generated by the random state of SRAM cells after power-up.

Another PUF-based application is the obfuscation of IP (Intellectual Property) cores (Figure 4d) and the use of PUFs as know-how protection and to prevent counterfeiting [46,47,48]. Manufacturers can provide the developed IP core with a locking mechanism that hides the functionality of the developed IP core. The output of the IP core is only enabled if a previously registered PUF generates the desired signal. This means that the IP core cannot generate the desired output by copying the hardware configuration to another device.

The PUF-based applications presented can be implemented both on FPGAs and on ASICs. The implementation on ASICs performs better in terms of resources and energy efficiency than on FPGAs, as only the resources that are required are used. Unlike ASICs, FPGAs have other components that are additionally supplied. On the other hand, the implementation of PUFs on ASICs is very time-consuming compared to FPGAs. However, the most important factor is security. Due to the limited number of CRPs that can be produced with a delay-based PUF, security cannot be guaranteed if the CRPs have been read by a third party. With an FPGA, the PUF can be reconfigured and implemented in a different area, generating new CRPs, which would not work with an ASIC. In research, memory-based PUFs are therefore implemented on ASICs, which are used for the generation of random numbers [41,42,43,44,45]. Compared to other PUF structures, they show lower reliability and improved uniqueness performance.

3. Quality Metrics of PUFs

The performance analysis of PUFs is crucial for their use in security applications. In particular, asymmetric architectures in delay-based PUFs can potentially compromise important properties and fail to meet the required specifications. Quality metrics can identify potential factors that may negatively affect the performance of the PUF. This work focuses on the quality metrics of reliability, randomness, and uniqueness, which are described in this section.

3.1. Reliability

The reliability is calculated individually for each IC and describes the stability of a response under different conditions for the same challenge C. For this, a reference response $R_{ref}\left(C\right)$ is obtained under normal conditions ($T=20$ °C). Then, the PUF is subjected to various physical factors and generates s additional responses $R_y\left(C\right)$ by using the same challenge C. Next, the intra-hamming distance ($H{D}_{intra,C}$) between the reference response and the generated one-bit responses $R_y\left(C\right)$ is calculated. Finally, the reliability can be calculated using Equation (2). The ideal value for $H{D}_{intra,C}$ is 0, which corresponds to a reliability of 100%. The reliability is calculated for each challenge in the dataset, and the mean value is then determined.

$$H{D}_{intra,C}={\displaystyle \frac{1}{s}}\sum _{y=1}^s{\displaystyle \frac{HD(R_{ref}\left(C\right),R_y\left(C\right))}{l}}$$

(1)

$$Rel{.}_C=100\%-(H{D}_{intra,C}·100\%)$$

(2)

3.2. Randomness

The randomness is calculated for each IC individually and describes the distribution of 0 s and 1 s of a l-bit response for a given challenge C. For this purpose, the mean value of 1 s in a l-bit response is determined according to Equation (3). This metric helps identify unbalanced deviations caused by factors such as asymmetric design strategies. The ideal value is 50%, which means that the number of 0 s and 1 s is equal on average. However, a deviation of 10% indicates that 10% of the response bits are ‘1’ and 90% are ‘0’. This offset represents a vulnerability and increases susceptibility to brute-force attacks. The randomness is calculated separately for each challenge C. Finally, the average value across all challenges is calculated.

$$Rand{.}_C={\displaystyle \frac{1}{l}}\sum _{x=1}^l{r}_x·100\%$$

(3)

3.3. Uniqueness

Uniqueness measures how different the responses generated by k devices with the same PUF structure and challenge C are. To assess this, the inter-hamming distance ($H{D}_{inter,C}$) between the responses of two devices ($R_i\left(C\right)$, $R_j\left(C\right)$) under identical conditions is calculated. This calculation is performed pairwise for all k devices. An ideal uniqueness value of 50% is achieved if half of the generated response bits differ. Conversely, a uniqueness value of 10% would mean that only 10% of the generated bits are different and therefore unique, which makes the PUF unsuitable for use in safety-critical applications. The uniqueness is calculated using Equations (4) and (5).

$$H{D}_{inter,C}=HD(R_i\left(C\right),R_j\left(C\right))$$

(4)

$$Uniq{.}_C={\displaystyle \frac{2}{k·(k-1)}}\sum _{i=1}^{k-1}\sum _{j=i+1}^k{\displaystyle \frac{H{D}_{inter,C}}{l}}·100\%$$

(5)

4. Simulation of Delay-Based PUFs

The statistical analysis of delay-based PUFs is an important aspect for security. For this purpose, the behavior of the PUF and the effects of various factors and influences such as temperature, supply voltage, external influences, or processing time of individual components are described using a mathematical model. Especially for delay-based PUFs, statistical analysis can also be used to investigate the impact of an unbalanced design strategy on the performance of PUFs. In addition, prior analysis can help to identify important parameters and weaknesses of the PUF in order to increase security and reduce high development costs.

This section briefly presents the statistical analysis of APUFs with regard to the calculation of reliability, randomness, and uniqueness. Here, it should be noted that the presented models are suitable for MUX-based APUFs and are partly adopted from [49,50]. Subsequently, the statistical models are used in Section 7 to model the proposed design presented in this work.

As already described, an APUF (Figure 1) compares the signal propagation delay between two parallel paths in order to generate unique signals. Therefore, each response bit depends on the difference between the signal propagation delays of the upper ($t_1$) and lower ($t_2$) path and can be modeled by a Gaussian distribution $N(0,2{\sigma }^2)$. Considering the successively connected SUs, the total delay time is described by the Equation (6).

$$\Delta t=t_{up}-t_{lo}\sim N(0,2N{\sigma }^2)$$

(6)

Due to the occurrence of asymmetries when implementing APUFs on FPGAs, this undesirable effect should also be considered. This is modeled by a threshold value ${\Delta }_{Arb}$, which shifts the probability of generating a 0 and therefore 1 (Figure 5). With a real PUF, depending on the design or FPGA technology, the threshold value ${\Delta }_{Arb}$ may be different for each bit. On the other hand, for an ideal APUF without any asymmetries in the design strategy, the threshold would be equal to 0. The response bit for an APUF by considering ${\Delta }_{Arb}$ can be calculated using Equation (7).

$$R=sign(\Delta t)==\left\{\begin{array}{ccc}\hfill 1& ,& {\Delta }_t\ge {\Delta }_{Arb}\hfill \\ \hfill 0& ,& {\Delta }_t<{\Delta }_{Arb}\hfill \end{array}\right.$$

(7)

The probability that the generated response bit is 1 ($P(R=1)$) can be calculated using Equation (8) [49]. This probability depends on the number of SUs N, the offset ${\Delta }_{Arb}$, and the variation in signal propagation delays ${\sigma }_s$.

$$P(R=1)=P(\Delta t\ge {\Delta }_{Arb})={\int }_{{\Delta }_{Arb}}^{\infty }{\displaystyle \frac{1}{\sqrt{2\pi N{\sigma }_s^2}}}exp({\displaystyle \frac{-x^2}{2N{\sigma }_s^2}})dx={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{2}}erf({\displaystyle \frac{{\Delta }_{Arb}}{\sqrt{2N{\sigma }_s^2}}})$$

(8)

This equation shows that $P(R=1)$ is equal to 0.5 for an ideal APUF (${\Delta }_{Arb}=0$). In addition, it can be observed that the probability approaches the ideal value with increasing N or ${\sigma }_s$, while it deteriorates at higher ${\Delta }_{Arb}$.

As already described in Section 3, the reliability describes how stably the PUF can generate the same response for a specific challenge under varying conditions. In addition to various parameters (N, ${\sigma }_s$, ${\Delta }_{Arb}$), the impact of interference factors such as ambient temperature or electromagnetic interference signals should also be considered in the model. In the simulation, the noise signal can also be represented as a Gaussian distribution $z\sim N(0,{\sigma }_z^2)$. For each stage, a random number for the signal propagation delay $\Delta t_i$ is generated, along with two random numbers $z,z^{\prime }$ for the noise signal, which are then added together. By summing over all N stages and considering the constant offset value ${\Delta }_{Arb}$, the response bit is determined. The calculation of $P_{intra}$ represents the probability that the addition of a noise signal causes a sign change, resulting in a bit flip. $P_{intra}$ can be calculated using Equation (9) [49].

$$\begin{array}{c}\hfill P_{intra}=P\left[sign(\sum _{i=1}^N(\Delta t_i+z_i)-{\Delta }_{Arb})\ne sign(\sum _{i=i}^N(\Delta t_i+z_i^{\prime })-{\Delta }_{Arb})\right]\\ \hfill ={\displaystyle \frac{1}{2}}-{\displaystyle \frac{1}{\pi }}arctan(\sqrt{{\displaystyle \frac{{\sigma }_s^4}{2{\sigma }_s^2{\sigma }_z^2+{\sigma }_z^4}}})+{\displaystyle \frac{{\Delta }_{Arb}}{\sqrt{2\pi N{\sigma }_s^2}}}\left(1-{\displaystyle \frac{2}{\pi }}\sqrt{{\displaystyle \frac{{\sigma }_s^2}{{\sigma }_s^2+{\sigma }_z^2}}}arctan(\sqrt{{\displaystyle \frac{{\sigma }_s^2}{{\sigma }_s^2+{\sigma }_z^2}}})\right)\end{array}$$

(9)

The reliability is therefore defined as $Rel.=1-P_{intra}$ and can be calculated using Equation (10) [49].

$$Rel.={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{\pi }}arctan(\sqrt{{\displaystyle \frac{{\sigma }_s^4}{2{\sigma }_s^2{\sigma }_z^2+{\sigma }_z^4}}})+{\displaystyle \frac{{\Delta }_{Arb}}{\sqrt{2\pi N{\sigma }_s^2}}}\left(1-{\displaystyle \frac{2}{\pi }}\sqrt{{\displaystyle \frac{{\sigma }_s^2}{{\sigma }_s^2+{\sigma }_z^2}}}arctan(\sqrt{{\displaystyle \frac{{\sigma }_s^2}{{\sigma }_s^2+{\sigma }_z^2}}})\right)$$

(10)

Based on the probability value ($P(R=1)$), the randomness can be modeled as a function of ${\Delta }_{Arb}$, N, and ${\sigma }_s$ using Equation (11) [49]. Here, it should be ensured that the ideal value is 1 rather than 0.5.

$$Rand.=1-\left|2P(R=1)-1\right|=1-erf\left({\displaystyle \frac{{\Delta }_{Arb}}{\sqrt{2N{\sigma }_s^2}}}\right)$$

(11)

The modeling of uniqueness is based on the $P_{inter}$ probability. This describes the probability that two responses differ, which is calculated using Equation (12) [49].

$$P_{inter}=2P(R=1)(1-P(R=1))$$

(12)

Finally, uniqueness is defined as follows [49]:

$$Uniq.=1-\left|2P_{inter}-1\right|=4P(R=1)(1-P(R=1))=1-er{f}^2\left({\displaystyle \frac{{\Delta }_{Arb}}{\sqrt{2N{\sigma }_s^2}}}\right)$$

(13)

The presented equations are used in Section 7 to perform a statistical analysis of the proposed design and calculate the parameters, ${\Delta }_{Arb}$, ${\sigma }_s$, and ${\sigma }_z$.

5. Proposed 2-4 Double Arbiter PUF

This section outlines the structure of the proposed design. First, the architecture of an SU of the proposed design is described, highlighting the optimizations and improvements compared to conventional DAPUFs. Then, the structure of the proposed 2-4 DAPUF is presented in detail. Finally, the implementation of the design on an AMD-Xilinx Spartan-6 FPGA is discussed.

The proposed design is based on the structure of the 2-1 DAPUF (Figure 1b) and 2-2 DAPUF (Figure 2). The main difference is the structure of the SUs. Figure 6 illustrates the improved SUs of the proposed design, including the wiring and the implementation of the arbiter blocks (red and blue) on an AMD-Xilinx Spartan-6 FPGA. As shown in Figure 6, each SU is implemented on a single CLB, which consists of two slices. In contrast to the 2-1 DAPUF, where only one of two inputs is active, the proposed SU has a total of four inputs. This enables a total of four independent propagation delay times at the output of an SU. In the first slice, the inputs are each connected to an LUT, which acts as a delay element. Due to variations in the manufacturing process of the IC, the processing times of the individual LUTs are different. Next, the signals are paired and connected to two MUXs, allowing one of two signals to pass into the next slice. In this case, the connection from slice 1 to slice 2 introduces varying delay times because of different wiring configurations of each multiplexer. In the second slice, the signals are paired and connected to four MUXs. As a result, four different propagation delay times (A, B, C, and D) are generated at the output of each SU, which can be configured using six challenge bits. This means that a total of $2·⌈{\displaystyle \frac{56}{6}}⌉=20$ CLBs (2 × 10) are required to implement a single 2-4 DAPUF block with two arbiter blocks (Figure 6) for 56-bit challenge. Additionally, a total of $⌈{\displaystyle \frac{56}{4}}⌉=14$ 2-4 DAPUF blocks are utilized to generate 56 response bits. The required area on the FPGA for implementing the proposed design is therefore 14x2x10 CLBs.

The structure of the SUs enables two significant improvements that considerably reduce resource consumption as well as energy requirements.

Table 1. Number of CLBs for single response bit and for generation of 64-bit CRPs.

PUF	CLB Count for Single PUF Block	CLB Count for Processing 64-Bit CRPs
APUF	1 × 32	64 × 1 × 32
2-1 DAPUF	2 × 32	64 × 2 × 32
2-2 DAPUF	2 × 16	32 × 2 × 16
Proposed Design	2 × 11	16 × 2 × 11

compares resource consumption for the implementation of a single PUF block and for the generation of 64 bit CRPs. Here, it should be noted that the number of slices required for the FF, which are used to generate the response bit, was not considered. To achieve this, an FF must be added for each response bit.

By increasing the number of challenge bits per SU to six, the number of SU-to-SU connections within a 2-4 DAPUF block can be reduced. For example, a 2-2 DAPUF block (Figure 2) with 64 challenge bits consists of a total of 2x32 SUs connected in series. Each SU handles two challenge bits and can be implemented on a single slice. This means that a single CLB can be used for the implementation of two SUs. To this end, a total of 32 CLBs (2x16 CLBs) are required to implement a 2-2 DAPUF block for 64 challenge bits. Since the 2-2 DAPUF generates at least two response bits, the resource consumption per response bit is therefore 16 CLBs. On the other hand, the proposed design assigns one CLB to each SU, allowing each to process six challenge bits. This reduces the number of CLBs required for 64 challenge bits to only 22 (2x11 CLBs). In addition, a single 2-4 DAPUF block generates a total of four response bits, which improves the resource consumption per response bit to approx. 6 CLBs (12 slices). This can improve the FPGA utilization and the implementability of the PUF on a small FPGAs. The second optimization involves increasing the number of generated response bits from two to four by using a single 2-4 DAPUF block. This optimization reduces the total number of DAPUF blocks needed to generate the required response bits as shown in Table 1.

The proposed design can also be implemented on newer FPGA technologies that contain two slices per CLB. The implementation on Spartan-6 FPGAs is based on the availability and thus the comprehensive investigation with 110 FPGA boards.

6. Experimental Setup

The proposed DAPUF design was implemented on 110 Digilent Nexys-3 boards equipped with an AMD-Xilinx Spartan-6 FPGA (XC6SLX16). The design was tested under different conditions and temperature ranges. In addition to examining the temperature resistance, the influence of a targeted interference circuit was also analyzed. For this purpose, three 256-bit shift registers (SRs) were implemented alongside the PUF, which are clocked at high a frequency and generate an alternating signal of 0 and 1. For each measurement, a total of 3 million 56-bit challenges were processed on each FPGA, with each challenge going through 10 iterations. This results in a dataset of 30 million CRPs per FPGA for each measurement (

Table 2. Overview of the performed measurements and the number of FPGAs used.

Measurement	SR	Temperature Range	Number FPGAs
Normal measurement	no	0–50 °C	110
Active shift registers	yes	0–50 °C	35

). The proposed design was developed using the Xilinx ISE Design Suite 14.7.

The architecture of the experimental setup is shown in Figure 7. To investigate the influence of ambient temperature on the PUF, a climate chamber is used in which up to five FPGAs can be measured simultaneously. Each FPGA is connected to a Raspberry Pi (RPi 1-5), which sends and receives the CRPs and stores them on a USB stick. Another Raspberry Pi (RP0) monitors the climate chamber and starts/stops the measurement depending on the temperature. A computing unit (monitoring) is used to monitor the measurement.

7. Experimental Results

This section discusses the experimental results of the implemented 56-bit 2-4 DAPUF under the different conditions described in Section 6. In addition to the quality metrics presented in Section 3, other aspects are also analyzed as part of the investigation. This includes the identification of particularly stable and unstable bit positions when generating responses. Furthermore, a statistical analysis of the implemented 2-4 DAPUF design is also presented in this section. In our previous works [18,22], it was shown that a slight extension of the PUF by using XOR gates at the output of the PUF significantly improves the quality metrics of randomness and uniqueness, which also applied in this study. Finally, the results of the implementation are compared with other PUF implementations from recent research.

7.1. Performance Evaluation of Normal Measurement

In this section, the performance of the presented design is examined depending on the ambient temperature in a range from 0 to 50 °C.

Figure 8 compares the presented quality metrics, i.e., reliability (top), randomness (middle), and uniqueness (bottom), of the proposed 2-4 DAPUF implemented on 110 FPGAs and a total of 30 million 56-bit CRPs per FPGA with our previous 2-2 DAPUF design to illustrate the improvements in performance as well as temperature resistance.

The proposed PUF shows a high reliability over the entire temperature range. Since the reference response is considered under normal conditions ($T=20$ °C), the maximum reliability is therefore achieved at a temperature value of 20 °C. Here, the maximum reliability is 97.88% ($\sigma =0.13)$ and the minimum is 96.73% ($\sigma =0.2)$ on average, resulting in a difference of approx. 1.15%. Compared to our previous design, reliability shows improved performance. The difference between the maximum and minimum is approx. 3.33%, which is a factor of two higher than the proposed 2-4 DAPUF. Assuming randomness and uniqueness, the results indicate that performance decreases with increasing temperature. The average randomness reaches a maximum of 43.81% ($\sigma =5.44)$ and a minimum of 43.49% ($\sigma =5.37)$. A difference of 0.32% clearly indicates that the 2-4 DAPUF exhibits very temperature-resistant behavior compared to 7.09% for our previous design. In contrast, the uniqueness exhibits a difference of 0.11% between the maximum (41.8%, $\sigma =2.57$) and the minimum (41.69%, $\sigma =2.61$), which also indicates a high resistance to temperature fluctuations. In our previous design, the uniqueness demonstrates a difference of 4.21%, which is also higher compared to the proposed design.

The temperature resistance of the implemented 2-4 DAPUF compared to our previous design can be attributed to several factors. These include the FPGA technology used, the specific area of the FPGA where the PUF is implemented, and the structure and number of SUs in an arbiter block.

In our previous 2-2 DAPUF implementation (Figure 2) on an AMD-Xilinx Artix-7 FPGA (28nm technology), each SU contains two independent paths (red and blue), each controlled by a MUX. Additionally, due to the structure of the SUs, which requires two challenge bits per SU, more SU-SU connections are necessary. In contrast, the 2-4 DAPUF design is implemented on an AMD-Xilinx Spartan-6 FPGA (45nm technology). The SUs of the proposed design are controlled by six challenge bits, reducing the total number of SU-SU connections (Figure 6). Minor distortions in the signal propagation delay of individual SUs, caused by temperature influences, electromagnetic interferences, or aging, are passed on to the next stage (SU). As a result, the probability of errors propagating along the chain and affecting the stability of the PUF response increases. Furthermore, the paths between two slices within an SU are interconnected (Figure 6), further minimizing the risk of bit errors across four response bit per arbiter block instead of one response bit in our previous design.

Overall, the mean reliability of the proposed 2-4 DAPUF is 97.25%, the randomness is 43.65%, and the uniqueness is 41.75%.

7.2. Identification of Unstable Bits

The identification of unstable or reliable bit locations when generating individual signals is an essential aspect for the security of PUF-based applications and should therefore be protected against attacks. This information can be exploited by an attacker to increase the probability of success in a brute force attack. On the other hand, this information can be used to identify and thus reduce offsets in the arbiter blocks of the respective bit locations caused by asymmetric routing. This can improve the randomness and uniqueness of the generated responses. In addition, the performance in terms of randomness and uniqueness can be further enhanced by filtering and concealing response bits with a high offset.

The investigation of the stability of the generated response bits on 110 FPGAs is illustrated in Figure 9 and Figure 10.

To achieve this, the offset values ${\Delta }_{Arb}$ shown in Figure 9 were determined individually for each bit using a timing analysis with the EDA tool. This offset value occurs at the connection between the last SU and FF, since symmetrical routing of the D and CLK input of an FF is not possible. In addition, further FPGA components such as DSPs or BRAMs would make a symmetrical connection even more difficult. Furthermore, in the upper plot of Figure 10, the mean intra-hamming distance ($H{D}_{intra}$), as defined by Equation (1), is analyzed for individual bit locations at different temperatures. The goal is to determine which bit positions are stable or unstable. The ideal value of the intra-hamming distance is 0 and is achieved when the respective bit location has 100% stability. In addition, the next plot (middle) shows the average probability with which the respective response bits generate a ‘1’ ($P(R=1)$). This means that $H{D}_{intra}$ and the probability values can be used to determine which bits have high stability and which output signal (0 or 1) is to be expected at the respective bit positions. Finally, the mean inter-hamming distance ($H{D}_{inter}$) is calculated from the responses of two different FPGAs and describes which bit positions are different. The ideal value for both $P(R=1)$ and $H{D}_{inter}$ is 0.5. Figure 10 also clearly illustrates that the proposed design shows temperature-resistant behavior.

The offset values in Figure 9 clearly show an increased asymmetry at bit positions 20, 22, 25, 27, 30, 47, 53, and 55. The value at positions 20, 22, and 30 is positive, which occurs when the upper path $t_{up}$ has a higher propagation delay than the lower path $t_{lo}$ ($t_{up}>t_{lo}$). A comparison of these bit positions in Figure 10 shows that a high level of reliability is achieved. The probability curve also shows reduced values at these bit positions, which means that the inter-distance and therefore the uniqueness is also low. In contrast, the bit positions 25, 27, 47, 53, and 55 show a negative offset, which means that the lower path has a higher signal propagation delay than the upper path ($t_{up}<t_{lo}$). These bit positions also show a high reliability. When examining the probability curve, it is noticeable that bits 25, 27, 47, and 55 have a high probability $P(R=1)$, which corresponds to a low inter-distance. In contrast, bits 17, 29, 33, and 49 exhibit low offset values, indicating that their performance relies solely on variations in the signal propagation delay and the effects of external influences. The remaining bits show a repeated pattern, which can be explained by the identical routing strategy using the hard macro function. The average offset value ${\Delta }_{Arb}$ for all 56 bits is $1·{10}^{-11}$ s.

Due to the high number of FPGAs tested, Figure 11 shows the probability values of eight randomly selected FPGAs at a temperature of 20 °C and calculated using the same 30 million CRPs. By comparing the probability values for each FPGA, it becomes clear that each FPGA exhibits different probability values for the respective bit positions. This can be explained by the variations of the signal propagation delay of the IC. In addition to the probabilities, the stable and unstable bit positions can also be identified for each FPGA individually. An example of this includes bit positions 17–20 and 53–55 for FPGAs 0 and 1. Here, FPGA 0 generates a ‘0’ at bits 17–20 with high probability, while FPGA 1 produces a ‘1’. In contrast, FPGA 0 generates a ‘1’ at bits 53–55, while FPGA 1 achieves better results at bits 53 and 55. Using this information, certain response bits can be predicted regardless of the challenge, which constitutes a vulnerability. Moreover, FPGAs 2, 3, and 7 display a high offset at bits 35–42, whereas FPGA 6 shows values that are close to the ideal value of 0.5. The examination of additional FPGAs also shows different probability values.

From these results, it can be concluded that the implemented design reacts differently to various FPGAs. When examining the selected FPGAs, offsets occur at different locations, depending on both the asymmetrical implementation strategy (Figure 9) and minor variations in the processing times of the FPGAs.

These bit-level offset values can pose a potential vulnerability to various attack vectors. One of the most effective attack vectors against delay-based PUFs are ML-based modeling attacks [11]. In an insecure sensor network, an attacker can receive the CRPs from the PUF during a fake authentication process and train a neural network using the CRPs to predict the response to a particular challenge. Depending on the number of CRPs, high accuracies of >90% [51,52,53] can be achieved. With bit-level offset values, the amount of training data can be reduced and thus a modeling attack can be generated quickly and with less training data. In PUF-based application scenarios (Figure 4), a modeled PUF can masquerade as an authenticated device and compromise the security of a sensor network by performing other attack vectors such as spoofing or delaying data packets or DoS attacks. In addition, bit-level offset values also represent an increased vulnerability to brute-force attacks. The offset values also make it possible to carry out brute force attacks quickly and efficiently by not changing bit positions with a high offset and thus reducing the possible combinations.

7.3. Statistical Analysis of the Proposed Design

In this section, the statistical models are used to model the proposed design based on the results of the performance analysis in order to calculate the variations in the signal propagation delay ${\sigma }_s$ and the impact of temperature variations ${\sigma }_z$. This enables the simulation of the implemented DAPUF under different conditions.

Table 3. Calculated parameters for modeling the proposed design.

Calculated Parameter	Value
$P(R=1)$	43.65%
${\sigma }_s$	$1.9889·{10}^{-11}$ s
${\sigma }_z$	$2.6·{10}^{-12}$ s
$P_{intra}$	2.6%
$P_{inter}$	49.19%

illustrates the parameters determined from the equations presented in Section 4. For the analysis, the number of stages is $N=10$, since each arbiter consists of 10 consecutively connected CLBs (Section 5). Additionally, the model uses an average delay time of ${\Delta }_{Arb}=1·{10}^{-11}$ s.

First, the probability $P(R=1)$ is calculated using Equation (8). Then, by rearranging Equation (11), ${\sigma }_s$ can be calculated using the given values. Subsequently, the equation for the intra-distance (Equation (9)) can be used to calculate ${\sigma }_z$. Finally, the calculated parameters are used to determine $P_{inter}$.

From these parameters, the quality metrics of the modeled PUF can now be calculated. As mentioned in Section 4, the ideal value for randomness and uniqueness is 100%. To account for this, the results were divided by two.

Table 4. Quality metrics of the implemented and modeled design.

Design	Rel./%	Rand./%	Uniq./%
Implemented	97.25	43.65	41.75
Modeled	97.38	43.66	49.2

presents the quality metrics of the implemented and modeled design.

As expected, the reliability and randomness of the modeled design closely align with the results of the implemented design. However, the uniqueness shows a difference of 7.45%. This discrepancy between the simulated and implemented design can be attributed to various factors. One possibility is the assumption that each bit has a constant probability $P(R=1)$ (Table 3) and an offset ${\Delta }_{Arb}$, which is not the case, as illustrated in Figure 9 and Figure 11. Real measurements are additionally affected by various interference factors, such as aging effects, fluctuations in the suppy voltage of the FPGA, and EMC (Electromagnetic Compatibility) influences, which are not considered in the simulation.

7.4. Performance Analysis of the Improved 2-4 XOR-DAPUF

Optimizing the PUF by applying an XOR layer at the output influences the distribution of the response bits and, consequently, the quality metrics. Figure 12 shows the architecture of the extended XOR-DAPUF. The initial step involves rotating the response of the 2-4 DAPUF m positions to the left, followed by the XOR operation on neighboring bits in the second step. As a result, bit positions that generate ‘0’ or ‘1’ with a high probability can be influenced by neighboring bits and thus improved. In research, XOR-based PUFs are primarily used for three reasons: optimizing the PUF’s performance in terms of randomness and uniqueness, obfuscating the PUF response, and protecting against modeling attacks. However, studies such as [51,54,55,56] show that the CRPs of an XOR-PUF can be predicted through an ML-based modeling attack and are thus not a viable alternative for increasing security.

In our experiment, we use the XOR layer to optimize the performance of the implemented 2-4 DAPUF. For this purpose, we perform measurements on 20 FPGAs with different bit rotations (ROTs) to identify the best configuration before performing measurements on 110 FPGAs.

In

Table 5. Performance analysis of the improved 2-4 XOR-DAPUF depending on the bit rotation.

ROT	Reliability/ %	Randomness/ %	Uniqueness/ %
0	97.83	45.11	42.33
4	95.76	49.36	49.04
8	95.76	48.54	48.68
12	95.76	49.62	48.98
16	95.76	49.77	48.48
20	95.76	48.93	49.2
24	95.76	49.16	48.47
28	95.76	47.04	48.7
32	95.76	49.16	48.47
36	95.76	48.93	49.2
40	95.76	49.77	48.48
44	95.76	49.62	48.98
48	95.76	48.54	48.68
52	95.76	49.36	49.04

, the quality metrics for different bit rotations (ROTs) in steps of four are presented. A rotation of 0 means that the XOR layer has no influence on the response. The table clearly illustrates that the use of the XOR layer increases randomness by approximately 3–4% and uniqueness by about 6%, while reliability decreases by around 2%. In addition, the proposed DAPUF shows the best performance for $ROT=20$ and 30.

Based on these findings,

Table 6. Comparison of the quality metrics between 2-4 DAPUF and 2-4 XOR-DAPUF.

Design	Reliability/ %	Randomness/ %	Uniqueness/ %
2-4 DAPUF	97.25	43.65	41.75
2-4 XOR-DAPUF (ROT 20)	95.85	48.09	48.79

shows the quality metrics of the proposed and improved 2-4 XOR-DAPUF for a bit rotation of 20. These metrics were examined using the CRPs of 110 FPGAs and 30 million CRPs per FPGA.

Figure 13 illustrates the improvements in the probability value for the enhanced 2-4 XOR-DAPUF, using the same selected FPGAs as shown in Figure 11. When comparing $P(R=1)$ for both designs, it is evident that some bit positions with a high offset were attenuated by the extension of the design. These include, for example, bit positions 17–20 for FPGA 0 and 1; 36-38 for FPGA 2, 3, and 4; 8-10 for FPGA 5; and 25, 27, and 46 for FPGA 6 and 7. The improvement of the probability values can be described by the fact that the rotation and XORing of neighboring bit positions leads to an adjustment of the probability values. This becomes particularly clear when XORing an unstable (e.g., for $P(R=1)\approx 0.5$) and stable (e.g., for $P(R=1)<0.15$ or >0.85) bit position. The probability value of the stable bit is reduced and thus become more unstable. This increases the randomness and uniqueness of the generated response, while the reliability decreases due to the unstable bits as clearly shown in Figure 13. On the other hand, reliability can be significantly improved by using ECC algorithms as in [29]. By improving performance, the proposed 2-4 XOR-DAPUF can enhance the security of PUF-based applications and is suitable for small IoT devices due to its lightweight structure.

Overall, randomness and uniqueness are improved compared to 2-4 DAPUF. Reliability is slightly decreased to 95.85% as clearly shown in Table 6.

7.5. Performance Evaluation with Active Shift Registers

As described in Section 6, the behavior of the proposed PUF in relation to interference circuits is analyzed as part of the performance evaluation. For this purpose, the quality metrics of the PUF are calculated and compared with and without SRs to simulate the impact of additional circuits on the PUF’s performance.

The performance comparison is shown in Figure 14. The results indicate that the performance of PUFs with active SRs does not exhibit any significant changes. Reliability varies by a maximum of 0.02% at both 10 °C and 20 °C. The impact of the shift registers on randomness and uniqueness is also limited. The maximum change in randomness is 0.24% at 0 °C, while the maximum change in uniqueness is 0.07%, occurring at both 0 °C and 5 °C. This suggests that the design remains robust against the influence of internal circuits.

7.6. Comparison

This section compares the quality metrics of different PUF implementations from related works. Due to the implementation on different FPGA technologies, the number of slices per response bit is also considered in this comparison in order to examine the efficiency of the PUF.

The average quality metrics and resource consumption of different works are presented in

Table 7. Comparison of the quality metrics and resource consumption for generating a 1-bit response of different APUF implementations from related studies.

Design	Rel./ %	Rand./ %	Uniq./ %	# Slices	FPGA
APUF [57]	98.97	-	15.15	-	Artix-7
APUF [23]	99.5	88.9	9.42	129	Artix-7
APUF [24]	99.76	55.69	18.37	-	Virtex-5
2-1 DAPUF [25]	90.32	45.74	46.37	303	Virtex-5
3-1 DAPUF [25]	88.2	53.93	50.24	436	Virtex-5
4-1 DAPUF [26]	73.4	55	50.03	577	Virtex-5
4:1MUXAPUF [58]	98	49	49.1	-	Zynq7000
FF-APUF [27]	97.10	-	41.53	128	Artix-7
FF-APUF [59]	97.10	-	40	44	Artix-7
PA-PUF [29]	94.5	49.45	49.63	47	Artix-7
PCS-based APUF [60]	98.19	49.77	49.81	196	Spartan-3E
PCS-based APUF [60]	97.57	57.64	51.34	132	Artix-7
2-2 DAPUF [22]	95.16	39.84	42.65	72	Artix-7
2-2 XOR-DAPUF [22]	90.91	47.51	50.72	73	-
2-4 DAPUF	97.25	43.65	41.75	13	Spartan-6
2-4 XOR-DAPUF	95.85	48.09	48.79	14	Spartan-6

. Comparing the implementations in [23,24,57], it is evident that these approaches show high reliability and low uniqueness. As already described in Section 2, these results are typical characteristics of an asymmetric implementation strategy. The uniqueness is significantly improved by the use of parallel arbiter blocks as in [25,26,58] and is close to the ideal value of 50%. On the other hand, these designs also show high resource consumption, which makes implementation on small IoT devices difficult. This becomes apparent when comparing the number of slices for generating a response bit between the APUF in [23] and 4-1 DAPUF in [26], which is approximately 4.5 times higher. The FF-based APUFs [27,59] also demonstrate good performance; however, they exhibit lower uniqueness compared to the DAPUFs. Conversely, the FF-APUFs are significantly more resource-efficient. The PCS-based (Path-Changing Switch) APUF [60] shows improved performance. This approach also implements parallel arbiter paths, which can be configured by challenge bits, similar to DAPUFs. This PUF is implemented on two different FPGAs (Spartan-3E and Artix-7), which show different performance and resource consumption. The implementation on Spartan-3E FPGAs shows an average reliability of 98.19%, which is 0.62% higher than the implementation on an Artix-7 FPGA. The randomness and uniqueness are also improved with the Spartan-3E implementation. In terms of resource consumption, the implementation on an Artix-7 FPGA performs better. These differences in performance and hardware consumption result from the different technology of the FPGAs used. In our previous work [22], we also showed improved performance by using an XOR layer at the output of the PUF. With the presented 2-2 XOR-DAPUF, we increased the randomness by 7.67% and the uniqueness by 8.07%. Reliability decreased by about 4.25% due to the XOR operations. The design also had a resource efficient architecture with 72 slices per response bit. Compared to the proposed and improved 2-4 XOR-DAPUF design, the performance in terms of randomness and uniqueness were significantly enhanced and close to the ideal value of 50%. In addition, a high reliability of 95.85% was achieved, compared to 90.91% for the 2-2 XOR-DAPUF, resulting in an improvement of approx. 4.94%. Furthermore, the design showed very good results in terms of resource consumption, with approx. 14 slices per response bit. The PA-PUF design [29] shows improved performance in terms of randomness and uniqueness. Moreover, with 47 slices per PUF, this architecture shows overall good performance compared to other designs in terms of quality metrics and resource efficiency. In comparison to the proposed 2-4 XOR-DAPUF, randomness is slightly higher by 1.36% and uniqueness by 0.84%, while reliability (without ECC algorithm) is lower by 1.35%. In terms of resource consumption, the proposed 2-4 XOR-DAPUF is more resource-efficient than the PA-PUF by a factor of approx. 3.4, which enables, in particular, the implementation of lightweight PUF-based security applications on small IoT devices with limited hardware resources. Overall, the proposed design shows good performance that is robust to temperature fluctuations as well as interference signals from internal circuits.

8. Discussion

In this section, we discuss the results and findings of our study, addressing the limitations of PUFs and PUF-based applications, as well as their impacts. Additionally, we suggest key points and ideas for further research.

Our investigations show that a delay-based PUF exhibits vulnerabilities to various attack vectors on PUF-based applications despite good quality metrics. The vulnerabilities arise from the offsets caused by unbalanced connections within an arbiter block (Figure 9), which can be reduced by manually rerouting of the connections, as well as from unavoidable process variations that can lead to further offsets, which are different for each FPGA as shown in Figure 11. Based on these offsets, the response bits of a PUF can be derived regardless of the challenge. This contradicts the basic idea of PUFs, which was described in Section 1. To address this problem, we presented an approach with an ROT-XOR layer, which reduces the effect of offsets, but does not eliminate it completely (Figure 13). For this reason, these factors must be taken into account when evaluating PUFs, in addition to the examination of quality metrics. Other influences such as voltage fluctuations or EMC influences on the PUF must also be considered. This will allow PUFs to be tested and evaluated with more real-world scenarios. As described in Section 2, a successful attack on PUFs implemented on FPGAs may require reconfiguring the PUF in a different physical area on the chip in order to generate new CRPs. In the case of an ASIC implementation, reconfiguration is impossible and thus security can no longer be guaranteed. The investigation of energy consumption is also an important point for future research in the area of lightweight security.

9. Conclusions and Outlook

In the literature, there are many studies in the area of PUF-based security applications. Due to their lightweight nature and ability to generate millions of device-specific signals without using memory components, PUFs are an interesting alternative for increasing the security of small devices with limited resources. In particular, the use of PUF-based applications can also circumvent the need for computationally intensive encryption mechanisms, which is an important aspect.

In this paper, a novel and resource-efficient DAPUF was presented. To this end, the use of PUFs in security applications was initially motivated and approaches from related studies were introduced. Additionally, quality metrics for PUFs were outlined for performance analysis. The statistical analysis of MUX-based PUFs was also included in this work. Furthermore, an in-depth investigation of the proposed PUF was conducted. Besides the quality metrics, the stability of the individual response bits was examined to identify potential weaknesses. To enhance performance, a lightweight method involving rotation and XORing of the response bits was presented. Finally, the quality metrics and resource consumption of the implemented design were compared to other works.

Our experimental results show that the proposed 2-4 DAPUF performs well and is robust against temperature variations as well as noise signals caused by other on-chip circuits. The performance was additionally improved by a simple extension using XOR gates in terms of randomness and uniqueness, where the reliability was slightly compromised. Here, the average uniqueness of the proposed 2-4 XOR-DAPUF was 48.79%, the randomness 48.09%, and the reliability 95.85%. Furthermore, the proposed PUF is well suited for use as a security component in small IoT devices with limited hardware resources.

Our next research steps focus on further investigations into PUFs regarding security and the identification of potential vulnerabilities. Since delay-based PUFs are particularly susceptible to modeling attacks, we will focus on developing robust and lightweight PUF designs. Additionally, we will develop lightweight PUF-based security applications suitable for small IoT devices while identifying and mitigating potential vulnerabilities.