Turbo Channel Covariance Conversion in Massive MIMO Frequency Division Duplex Systems
Abstract
1. Introduction
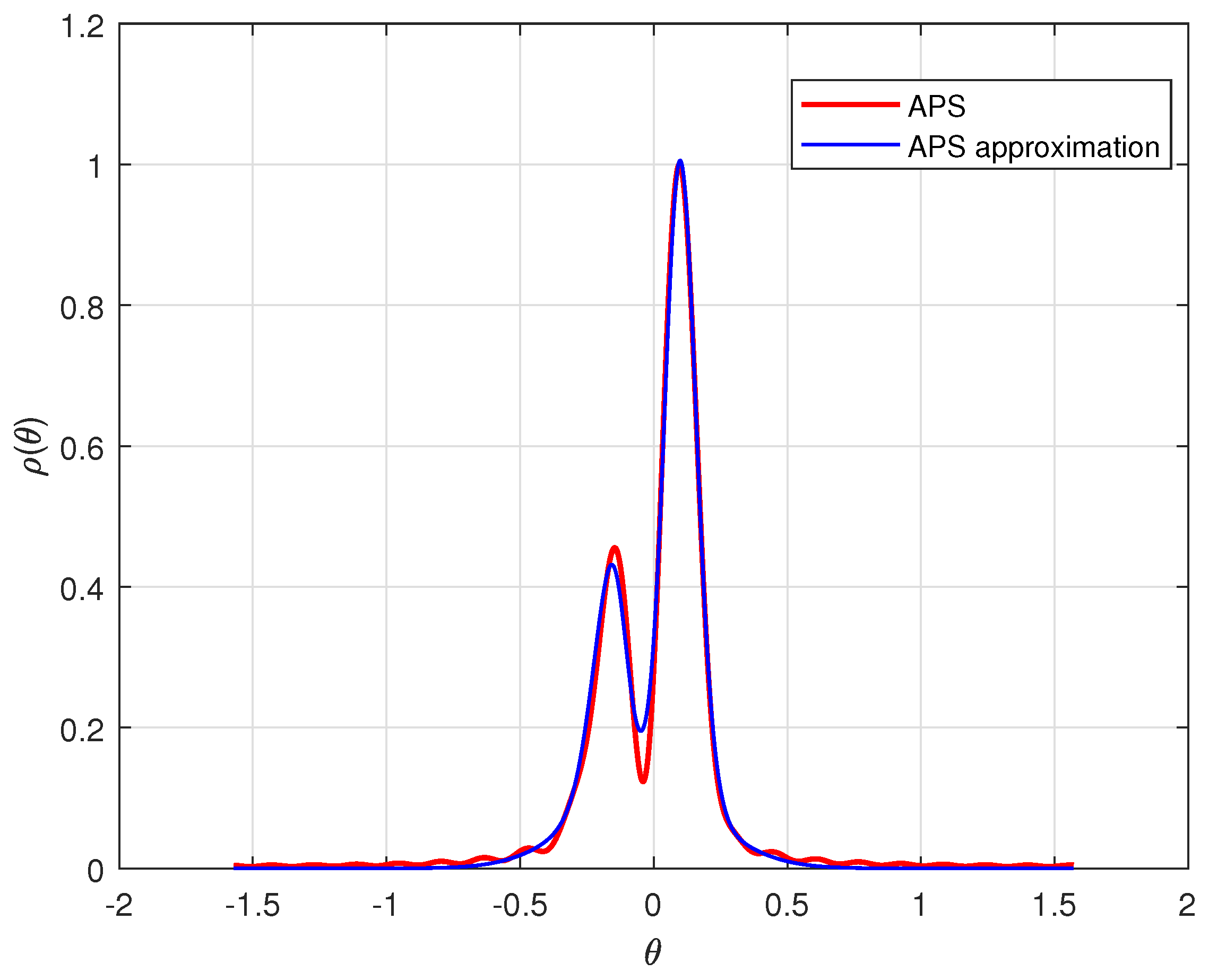
- In a multipath propagation environment, the signal undergoes multiple reflections, scattering, and diffraction, resulting in different propagation paths and arrival angles. The APS exhibits a concentrated distribution in these directions, resembling multiple peaks. Therefore, we model the APS using multiple Gaussian functions, with each Gaussian function representing the signal energy distribution in a specific direction.
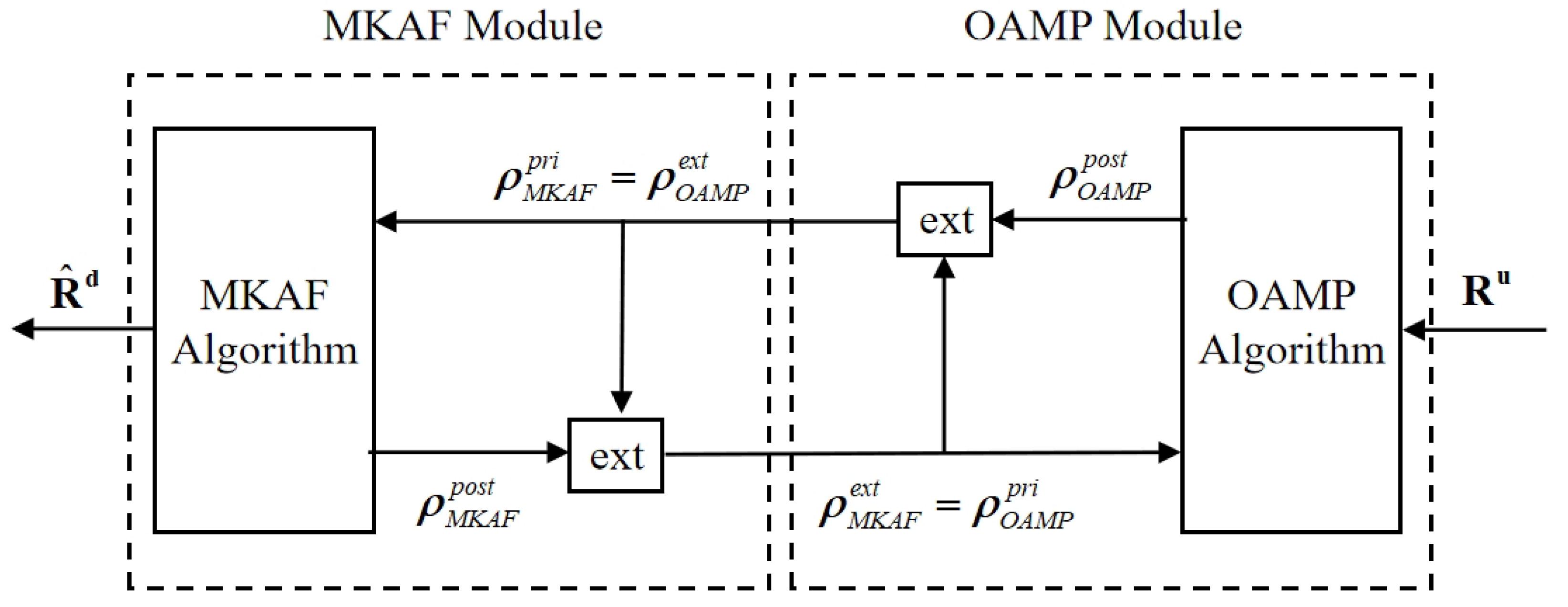
- Based on the APS reciprocity, we propose a turbo channel covariance conversion (Turbo-CCC) algorithm composed of two modules: the OAMP module and the MKAF module. The OAMP module estimates the APS based on the UL CCM, while the MKAF module extracts relevant information from the structural characteristics of the APS to refine the APS estimation. These two modules operate iteratively, progressively improving the accuracy of the DL CCM estimation.
- Our numerical results demonstrate that the proposed algorithm achieves higher accuracy and robustness in DL CCM estimation compared to conventional methods. It is applicable to most practical scenarios, making it an effective solution for DL CCM estimation in FDD massive MIMO systems.
2. System Model and Problem Formulation
2.1. System Model
2.2. Problem Formulation
3. Proposed Algorithm
3.1. Extended Probability Model and Algorithm Structure
- OAMP Module: The OAMP module leverages the UL CCM and the prior information fed back from the MKAF module to estimate the APS from UL CCM. Subsequently, it passes the messages to the MKAF module. We formulate the APS estimation problem as a CS problem, which will be addressed using the OAMP algorithm. For details, see Section 3.2.
- MKAF Module: This module first utilizes the messages to estimate the parameters of Gaussian functions , which is solved based on the MKAF algorithm. Subsequently, this module derives the extrinsic information of the APS based on Bayesian inference, which is defined as , and then passes it to the OAMP module for iterative refinement. In the final iteration, DL CCM estimation is generated based on the posterior mean of the APS. For details, see Section 3.3.
3.2. Orthogonal Approximate Message Passing Module
| Algorithm 1 OAMP algorithm. |
| Input: |
| Initialization: |
| for |
| end |
| Output: APS estimate . |
3.3. Multikernel Adaptive Filtering Module
| Algorithm 2 MKAF algorithm. |
| Input: , . |
| for do |
| Screen suitable variances by (34) and (35). |
| Update the kernel parameters by (37), (38) and (41). |
| end for |
| Update the extrinsic information of by (43)–(47); |
| Output: Extrinsic information . |
3.4. Overall Algorithm
| Algorithm 3 Turbo-CCC algorithm. |
| Input: . |
| Repeat |
| //OAMP Module |
| for do |
| Update APS estimate by Algorithm 1. |
| end for |
| Pass message to MKAF module. |
| //MKAF Module |
| for do |
| Update extrinsic information by Algorithm 2. |
| end for |
| Pass message to OAMP module. |
| Until: The convergence condition (48) is satisfied. |
| Generate DL CCM estimate based on the posterior mean from MKAF module in the final iteration by (2). |
| Output: DL CCM estimate . |
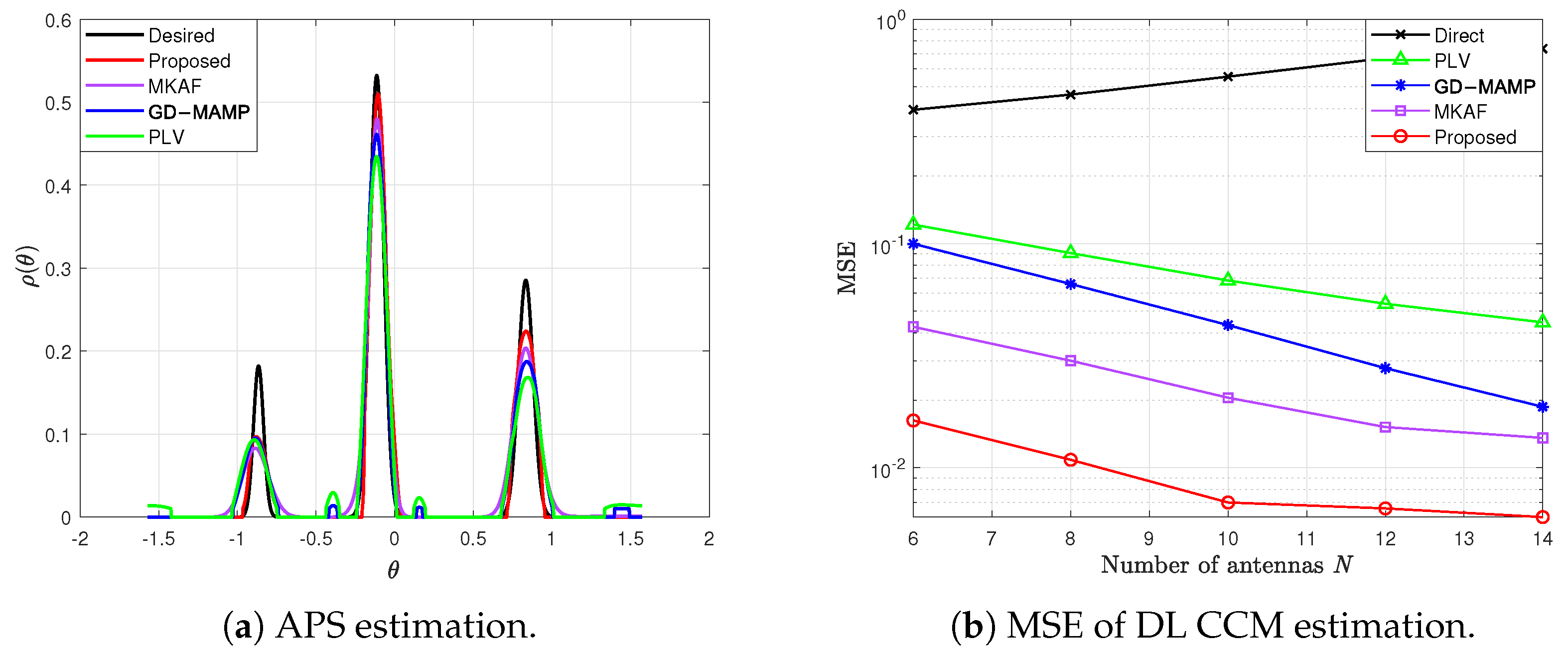
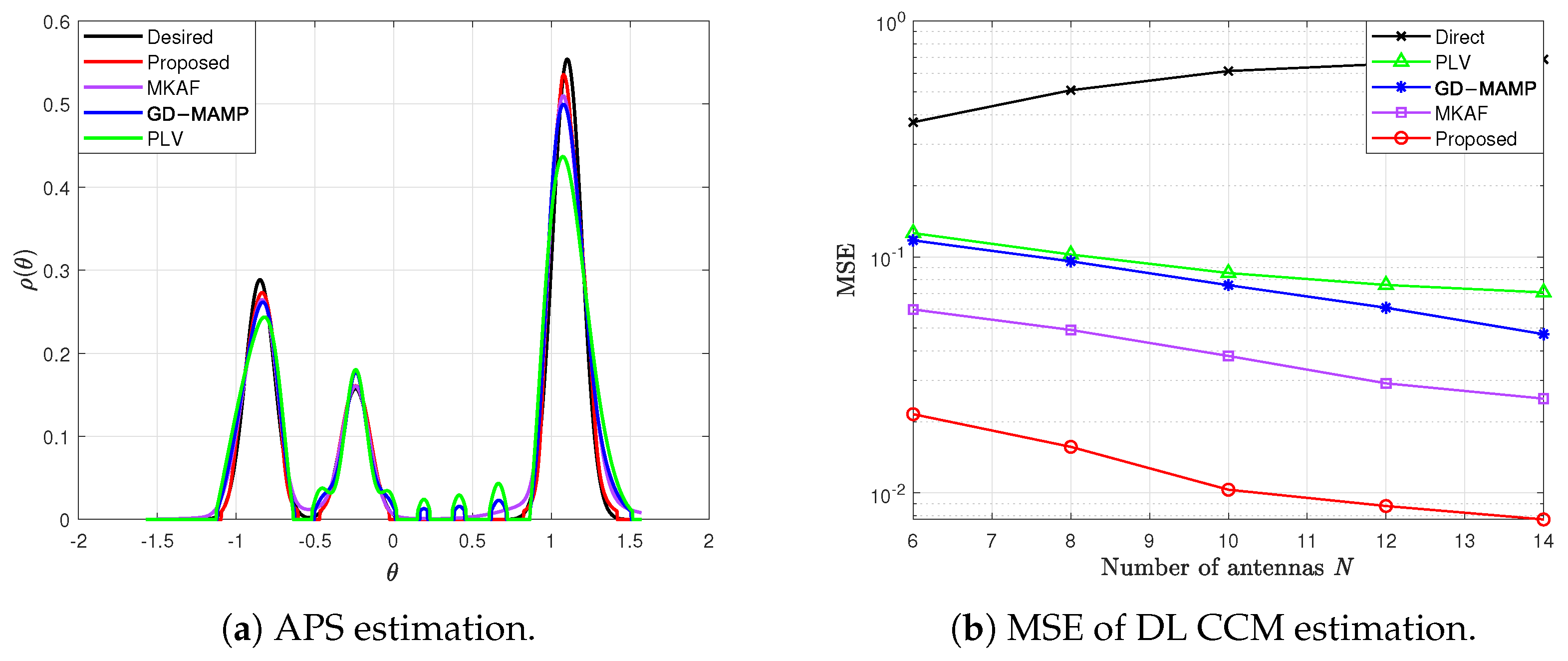
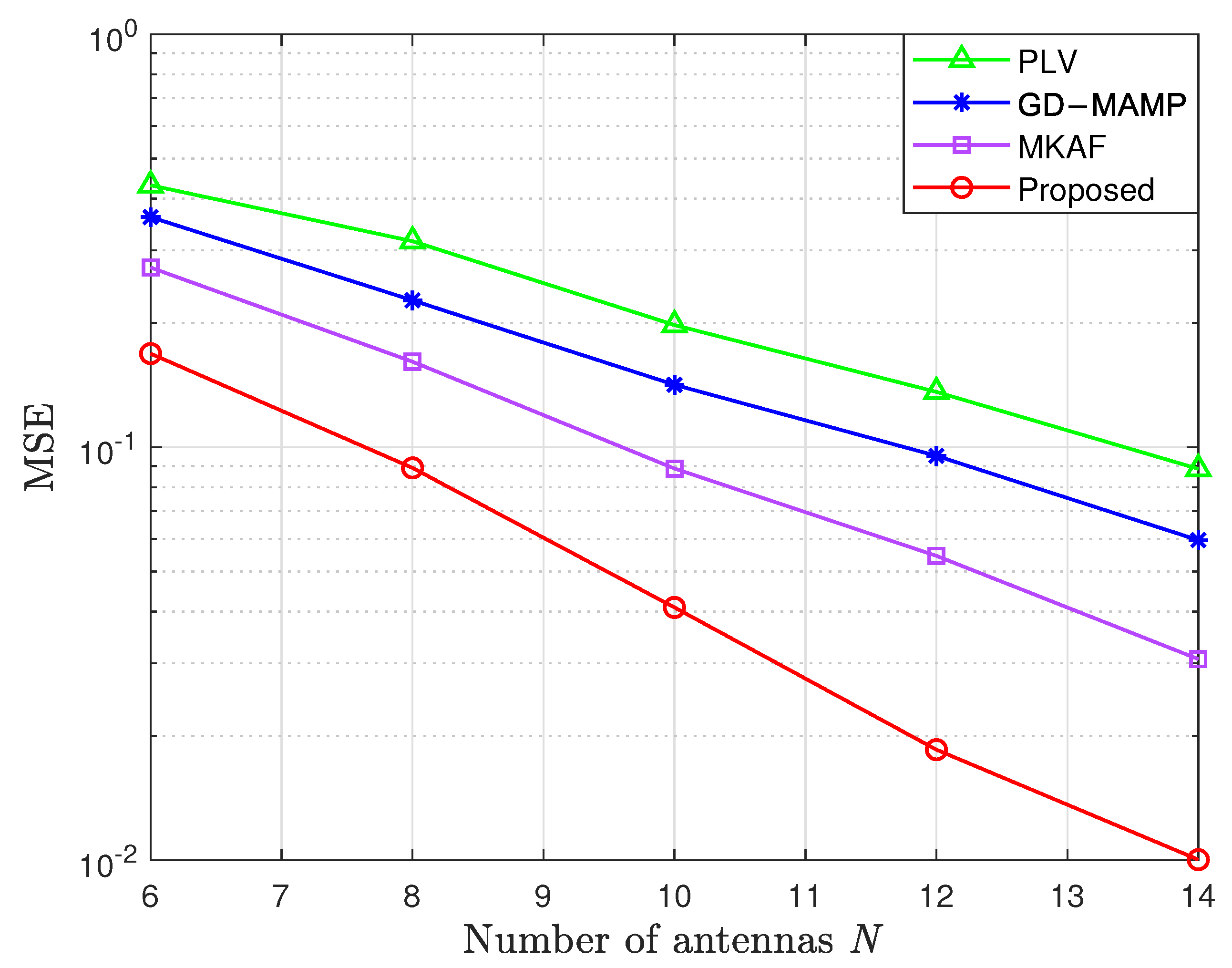
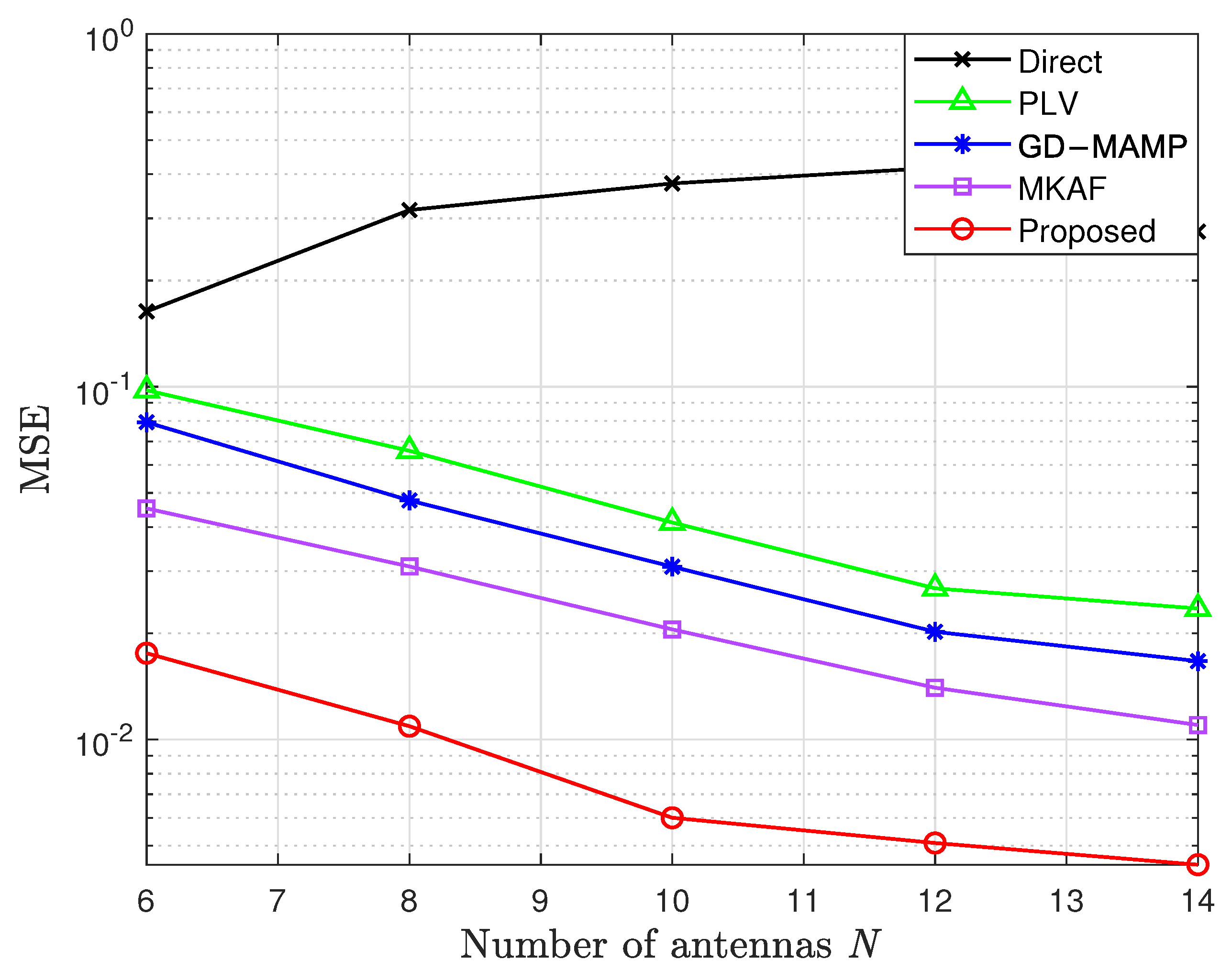
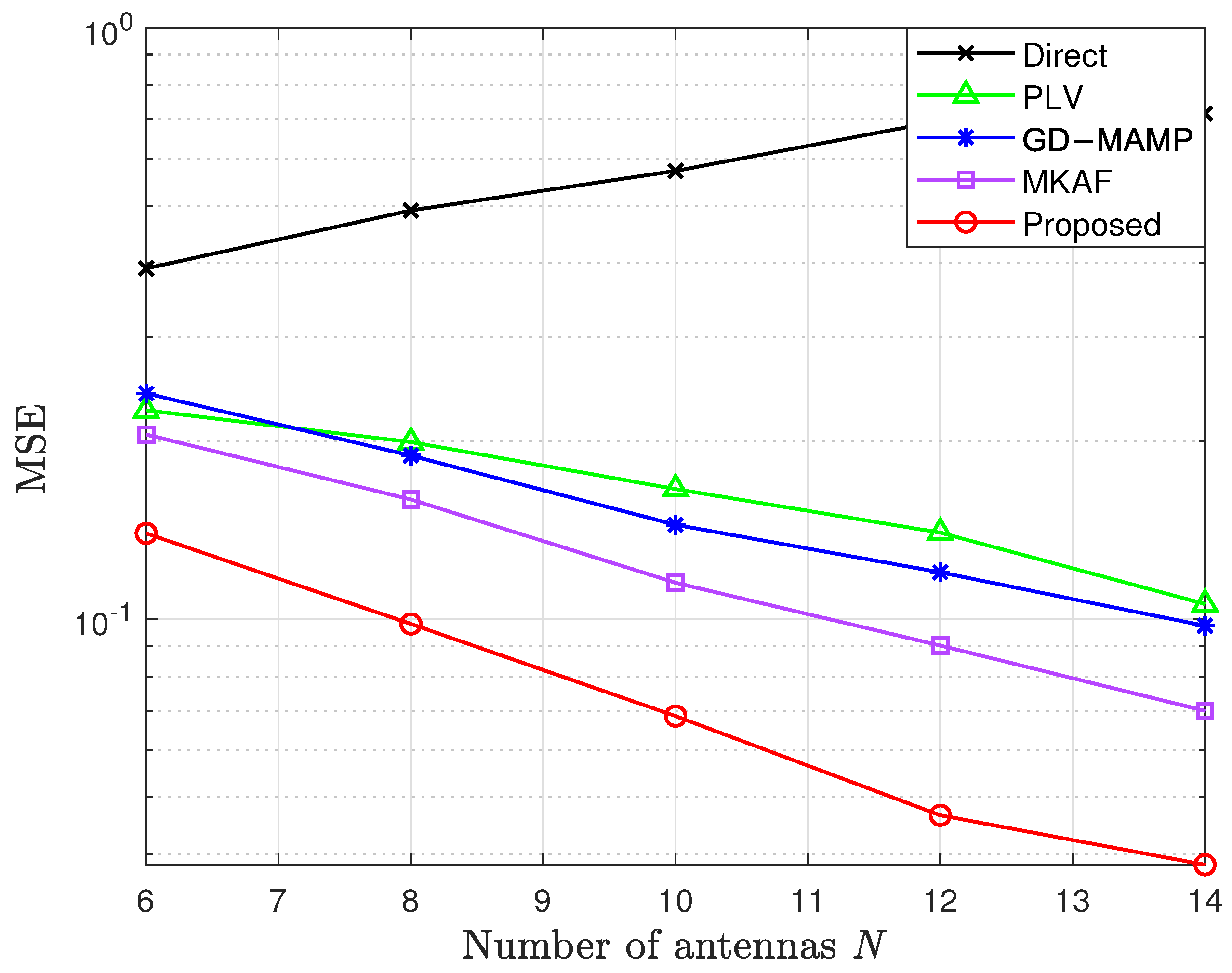
4. Numerical Results
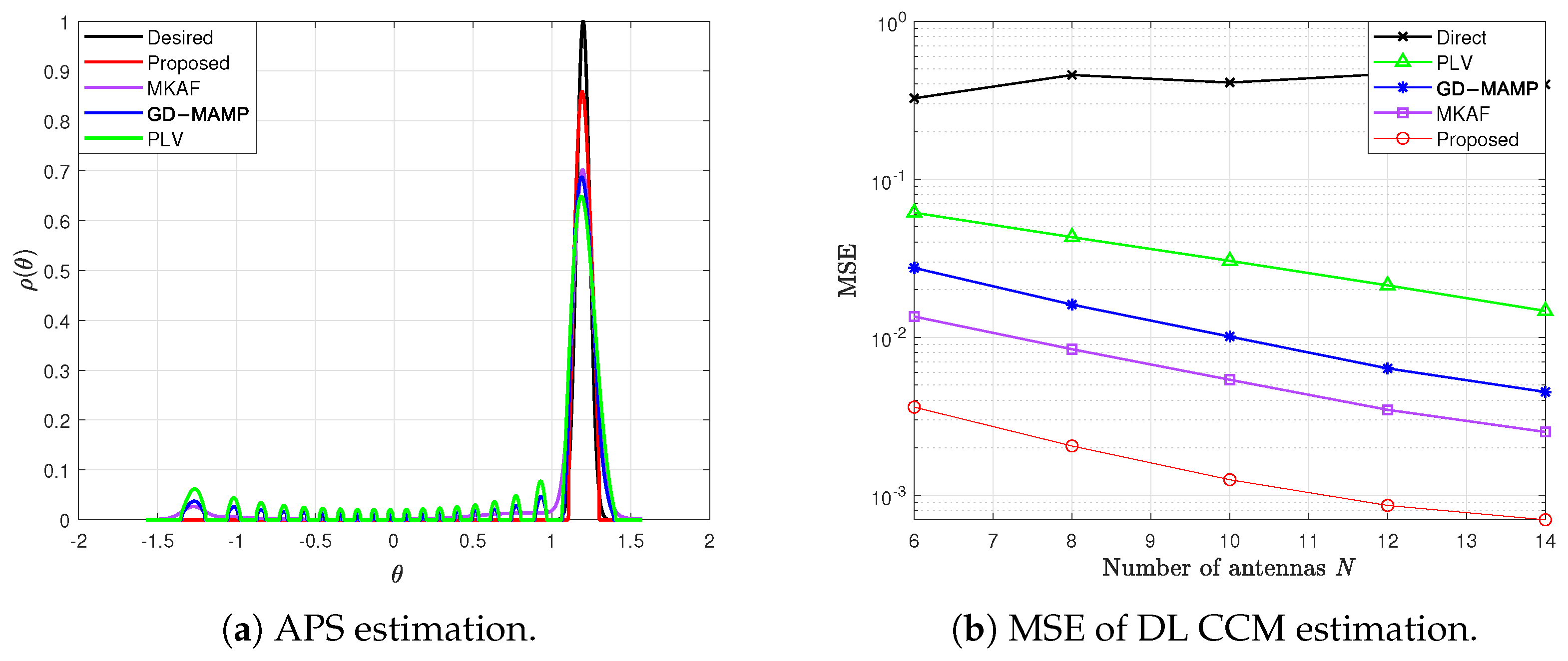
4.1. Simulation Performance Under an Ideal Channel Model
- PLV algorithm in [20]: Based on optimization theory, this algorithm estimates the APS from the UL CCM and achieves the CCM conversion by employing projection methods in an infinite-dimensional Hilbert space.
- Gradient Descent Memory AMP (GD-MAMP) in [34]: This algorithm is designed to address CS problems by integrating gradient descent with an AMP framework. It efficiently estimates the APS from the UL CCM, thereby deriving an accurate estimate of the DL CCM.
- MKAF algorithm in [35]: This algorithm models the APS using Gaussian kernels, directly updating the parameters of the kernels based on the UL CCM, and reconstructs the DL CCM according to the estimated APS.
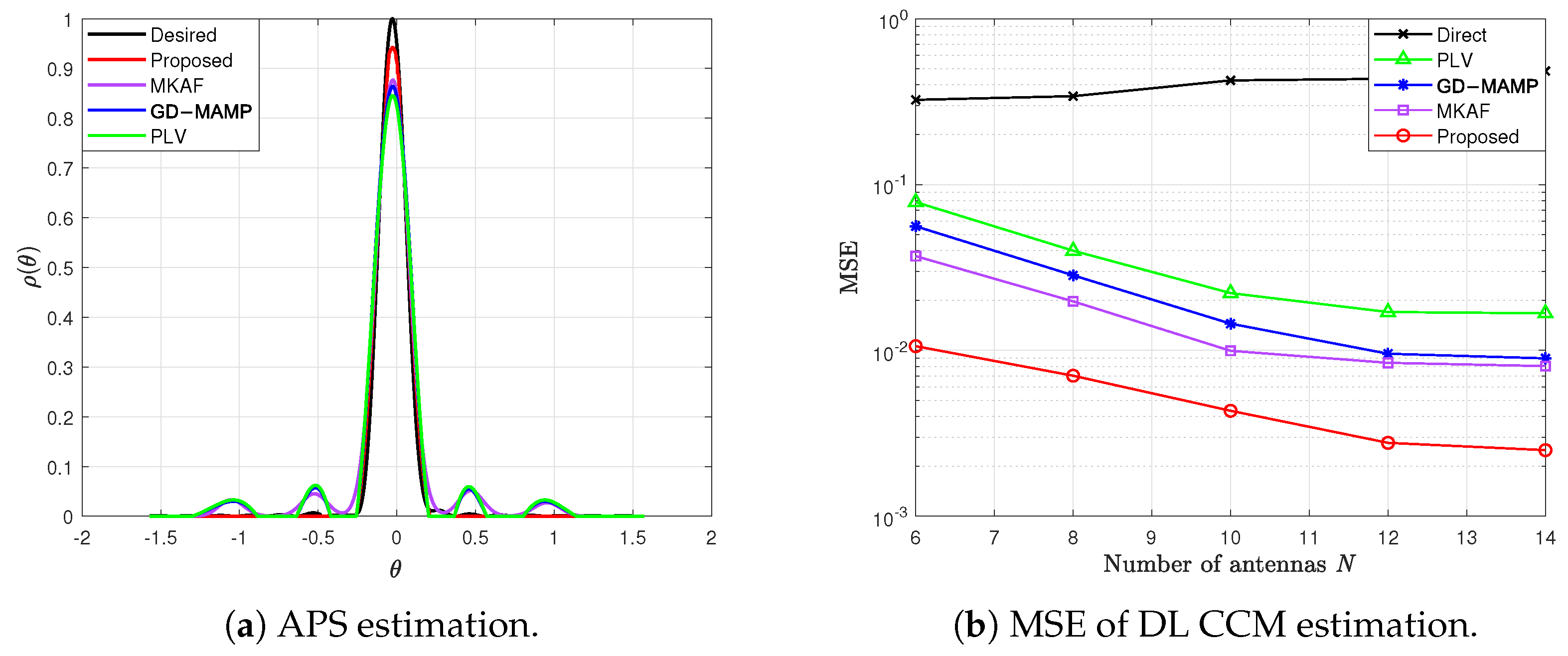
4.2. Simulation Performance Under a CDL Channel Model
- Delay Spread = 100 ns: A delay spread of 100 ns is assumed, representing the temporal dispersion of multipath components.
- DopplerShift = 30 Hz: Doppler shifts are calculated based on the relative velocity between the transmitter and the receiver.
- AngularSpread = 3°–10°: The angular spread is set to 3°–10° to represent the angular dispersion of multipath components, typical in urban scenarios where reflections from buildings and other obstacles cause multi-pathing.
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO networks: Spectral, energy, and hardware efficiency. Found. Trends® Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative cellular wireless with unlimited numbers of base station antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Process. Mag. 2012, 30, 40–60. [Google Scholar] [CrossRef]
- Kocian, A.; Badiu, M.A.; Fleury, B.H.; Martelli, F.; Santi, P. A unified message-passing algorithm for MIMO-SDMA in software-defined radio. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 4. [Google Scholar] [CrossRef]
- He, H.; Yu, X.; Zhang, J.; Song, S.; Letaief, K.B. Message passing meets graph neural networks: A new paradigm for massive MIMO systems. IEEE Trans. Wirel. Commun. 2023, 23, 4709–4723. [Google Scholar] [CrossRef]
- Bellili, F.; Sohrabi, F.; Yu, W. Generalized approximate message passing for massive MIMO mmWave channel estimation with Laplacian prior. IEEE Trans. Commun. 2019, 67, 3205–3219. [Google Scholar] [CrossRef]
- Wang, H.; Xu, L.; Yan, Z.; Gulliver, T.A. Low-complexity MIMO-FBMC sparse channel parameter estimation for industrial big data communications. IEEE Trans. Ind. Inform. 2020, 17, 3422–3430. [Google Scholar] [CrossRef]
- Peng, Q.; Huang, Y.; Zhou, W. Graph Neural Network-Based Low-Complexity Channel Estimation for Massive MU-MIMO Systems. In Proceedings of the 2024 9th International Conference on Computer and Communication Systems (ICCCS), Xi’an, China, 19–22 April 2024; pp. 623–628. [Google Scholar]
- Ma, Y.; He, H.; Song, S.; Zhang, J.; Letaief, K.B. Low-complexity CSI feedback for FDD massive MIMO systems via learning to optimize. IEEE Trans. Wirel. Commun. 2025. [Google Scholar] [CrossRef]
- Xie, H.; Gao, F.; Jin, S.; Fang, J.; Liang, Y.C. Channel estimation for TDD/FDD massive MIMO systems with channel covariance computing. IEEE Trans. Wirel. Commun. 2018, 17, 4206–4218. [Google Scholar] [CrossRef]
- De Figueiredo, F.A.; Cardoso, F.A.; Moerman, I.; Fraidenraich, G. Channel estimation for massive MIMO TDD systems assuming pilot contamination and frequency selective fading. IEEE Access 2017, 5, 17733–17741. [Google Scholar] [CrossRef]
- Chan, P.W.; Lo, E.S.; Wang, R.R.; Au, E.K.; Lau, V.K.; Cheng, R.S.; Mow, W.H.; Murch, R.D.; Letaief, K.B. The evolution path of 4G networks: FDD or TDD? IEEE Commun. Mag. 2006, 44, 42–50. [Google Scholar] [CrossRef]
- Jordan, M.; Dimofte, A.; Gong, X.; Ascheid, G. Conversion from uplink to downlink spatio-temporal correlation with cubic splines. In Proceedings of the VTC Spring 2009-IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; pp. 1–5. [Google Scholar]
- Haghighatshoar, S.; Khalilsarai, M.B.; Caire, G. Multi-band covariance interpolation with applications in massive MIMO. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 386–390. [Google Scholar]
- Decurninge, A.; Guillaud, M.; Slock, D. Riemannian coding for covariance interpolation in massive MIMO frequency division duplex systems. In Proceedings of the 2016 IEEE Sensor Array and Multichannel Signal Processing Workshop (SAM), Rio de Janeiro, Brazil, 10–13 July 2016; pp. 1–5. [Google Scholar]
- Zou, L.; Pan, Z.; Jiang, H.; Liu, N.; You, X. Deep learning based downlink channel covariance estimation for FDD massive MIMO systems. IEEE Commun. Lett. 2021, 25, 2275–2279. [Google Scholar]
- Hugl, K.; Kalliola, K.; Laurila, J. Spatial reciprocity of uplink and downlink radio channels in FDD systems. In Proceedings of the COST 273 Meeting, Espoo, Finland, 30–31 May 2002; Volume 273, p. 066. [Google Scholar]
- Zhong, Z.; Fan, L.; Ge, S. FDD massive MIMO uplink and downlink channel reciprocity properties: Full or partial reciprocity? In Proceedings of the GLOBECOM 2020-2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; pp. 1–5. [Google Scholar]
- Park, S.; Heath, R.W. Spatial channel covariance estimation for the hybrid MIMO architecture: A compressive sensing-based approach. IEEE Trans. Wirel. Commun. 2018, 17, 8047–8062. [Google Scholar] [CrossRef]
- Miretti, L.; Cavalcante, R.L.G.; Stańczak, S. Channel covariance conversion and modelling using infinite dimensional Hilbert spaces. IEEE Trans. Signal Process. 2021, 69, 3145–3159. [Google Scholar] [CrossRef]
- Vesperinas, M.N. Scattering and Diffraction in Physical Optics; World Scientific Publishing Company: Singapore, 2006. [Google Scholar]
- Burr, A. The multipath problem: An overview. In Proceedings of the IEE Colloquium on Multipath Countermeasures, London, UK, 23–23 May 1996; p. 1. [Google Scholar]
- Ninomiya, E.; Yukawa, M.; Cavalcante, R.L.; Miretti, L. Estimation of angular power spectrum using multikernel adaptive filtering. In Proceedings of the 2022 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Chiang Mai, Thailand, 7–10 November 2022; pp. 1996–2000. [Google Scholar]
- Elshirkasi, A.M.; Al-Hadi, A.A.; Mansor, M.F.; Khan, R.; Soh, P.J. Envelope correlation coefficient of a two-port MIMO terminal antenna under uniform and Gaussian angular power spectrum with user’s hand effect. Prog. Electromagn. Res. C 2019, 92, 123–136. [Google Scholar]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Björnson, E.; Larsson, E.G.; Marzetta, T.L. Massive MIMO: Ten myths and one critical question. IEEE Commun. Mag. 2016, 54, 114–123. [Google Scholar]
- Takizawa, M.A.; Yukawa, M. Online learning with self-tuned Gaussian kernels: Good kernel-initialization by multiscale screening. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4863–4867. [Google Scholar]
- Ma, J.; Ping, L. Orthogonal AMP. IEEE Access 2017, 5, 2020–2033. [Google Scholar]
- Yamamoto, T.; Yamagishi, M.; Yamada, I. Adaptive proximal forward-backward splitting for sparse system identification under impulsive noise. In Proceedings of the 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 2620–2624. [Google Scholar]
- Beck, A.; Teboulle, M. Mirror descent and nonlinear projected subgradient methods for convex optimization. Oper. Res. Lett. 2003, 31, 167–175. [Google Scholar] [CrossRef]
- Amari, S.i. Backpropagation and stochastic gradient descent method. Neurocomputing 1993, 5, 185–196. [Google Scholar] [CrossRef]
- Mimura, K.; Takeuchi, J. Dynamics of damped approximate message passing algorithms. In Proceedings of the 2019 IEEE Information Theory Workshop (ITW), Visby, Sweden, 25–28 August 2019; pp. 1–5. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Huang, S.; Liu, L.; Kurkoski, B.M. Overflow-avoiding memory AMP. In Proceedings of the 2024 IEEE International Symposium on Information Theory (ISIT), Athens, Greece, 7–12 July 2024; pp. 3516–3521. [Google Scholar]
- Kaneko, N.; Yukawa, M.; Cavalcante, R.L.; Miretti, L. Robust estimation of angular power spectrum in massive MIMO under covariance estimation errors: Learning centers and scales of Gaussians. In Proceedings of the 2024 IEEE 25th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Lucca, Italy, 10–13 September 2024; pp. 576–580. [Google Scholar]
- Cademartori, C.; Rush, C. A non-asymptotic analysis of generalized vector approximate message passing algorithms with rotationally invariant designs. IEEE Trans. Inf. Theory 2024, 70, 5811–5856. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Luo, S.; Xu, C. Turbo Channel Covariance Conversion in Massive MIMO Frequency Division Duplex Systems. Electronics 2025, 14, 1490. https://doi.org/10.3390/electronics14081490
Yu Z, Luo S, Xu C. Turbo Channel Covariance Conversion in Massive MIMO Frequency Division Duplex Systems. Electronics. 2025; 14(8):1490. https://doi.org/10.3390/electronics14081490
Chicago/Turabian StyleYu, Zhuying, Shengsong Luo, and Chongbin Xu. 2025. "Turbo Channel Covariance Conversion in Massive MIMO Frequency Division Duplex Systems" Electronics 14, no. 8: 1490. https://doi.org/10.3390/electronics14081490
APA StyleYu, Z., Luo, S., & Xu, C. (2025). Turbo Channel Covariance Conversion in Massive MIMO Frequency Division Duplex Systems. Electronics, 14(8), 1490. https://doi.org/10.3390/electronics14081490




