Data Throughput-Oriented Site Selection: Integrated Downlink Scheduling with Elastic Laser Communication Terminal Deployment
Abstract
1. Introduction
- We propose a tightly-coupled optimization model that holistically integrates geographic site selection with downlink scheduling, enabling quantitative evaluation of end-to-end data throughput performance across different candidate GS configurations.
- The proposed model incorporates an integer decision variable Q to characterize the LCT deployment scale at each GS, explicitly embedding equipment cost constraints and service capacity limitations for enhanced operational fidelity.
- A branch-and-bound algorithm is developed to solve the ILP problem, with numerical simulations demonstrating superior data throughput over existing solutions under equivalent installation cost constraints.
2. System Model and Problem Formulation
- Each LEO satellite carries a single LCT for space–ground links due to size, weight, and power constraints;
- The GEO satellite can be equipped with up to G LCTs, enabling potential connectivity with all candidate GSs;
- Availability probabilities and are considered statistically independent when GSs are sufficiently spaced, neglecting spatial weather correlations;
- To reduce the computational complexity of the problem, we assume that the link availability probabilities (for GEO-to-GS links) and (for LEO-to-GS links) remain fixed within each time slot;
- LEO satellites maintain fixed laser links with single GSs per time period, permitting dynamic link switching between periods.
- T, S, and G denote the total number of time periods, LEO satellites, and candidate GSs, respectively;
- quantifies the visible time window (measured in seconds) between the s-th LEO satellite and the g-th GS during period t, with representing the GEO-GS visibility duration;
- and indicate the data transfer rates for LEO-GS and GEO-GS links, respectively;
- Binary variables and activate LEO-GS and GEO-GS links when equal to 1 (downlink scheduling variables);
- Site selection variable determines the GS deployment at location g, and indicates the g-th candidate GS is selected (or, equivalently, a GS is installed at the g-th location).
2.1. Problem Formulation
2.2. Linearization of the Problem
3. Branch-and-Bound Algorithm
- : integer decision vector (dim: ) containing
- −
- Site selection ()
- −
- Scheduling variables ()
- −
- Scheduling variables ()
- −
- Auxiliary variables ()
- −
- Auxiliary variables ()
- −
- LCT variable ().
- : objective coefficient vector (dim: )
- : constraint matrix (dim: )
- : right-hand-side vector (dim: ).
- Variable dimension:
- Constraint dimension:
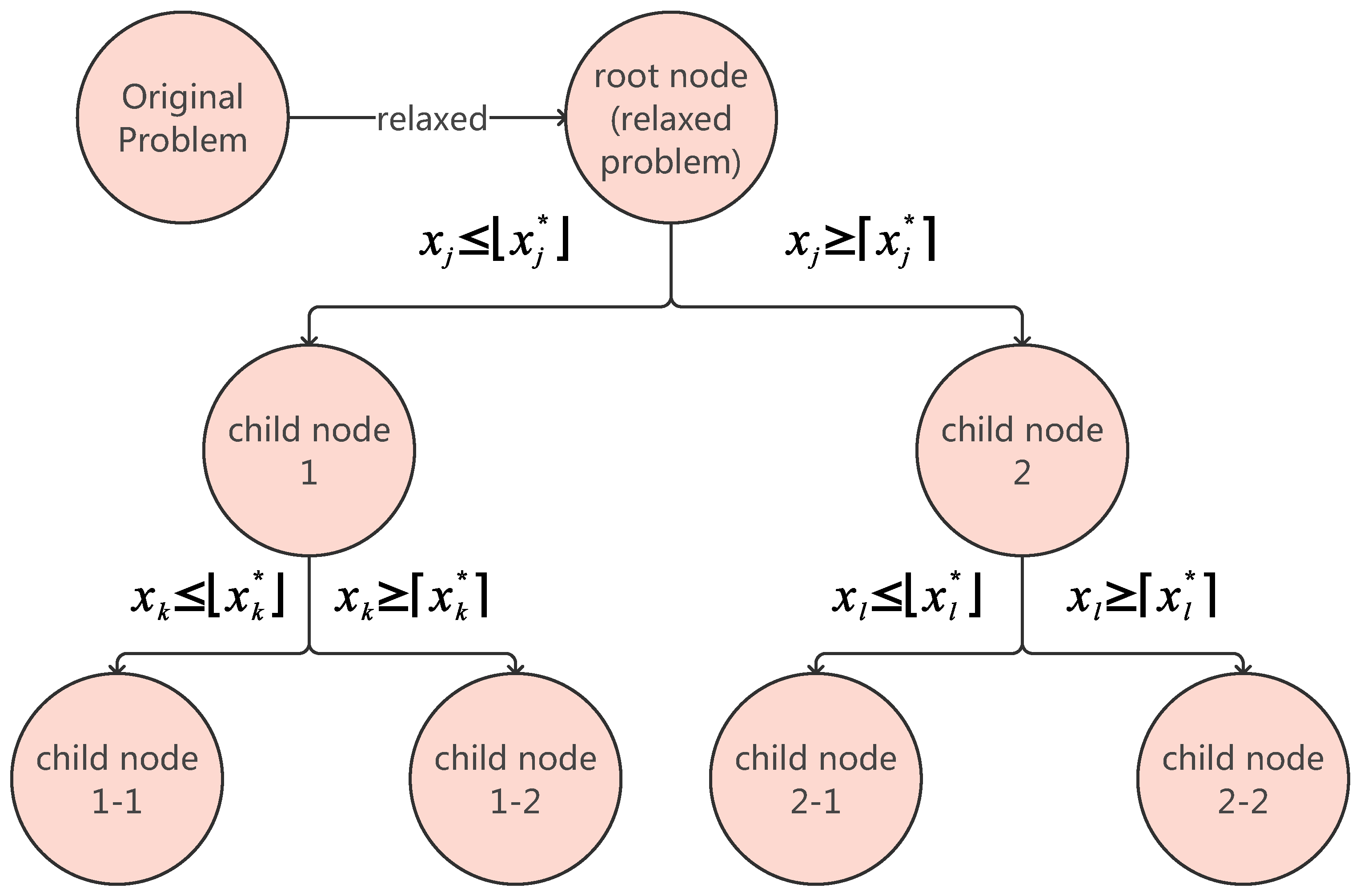
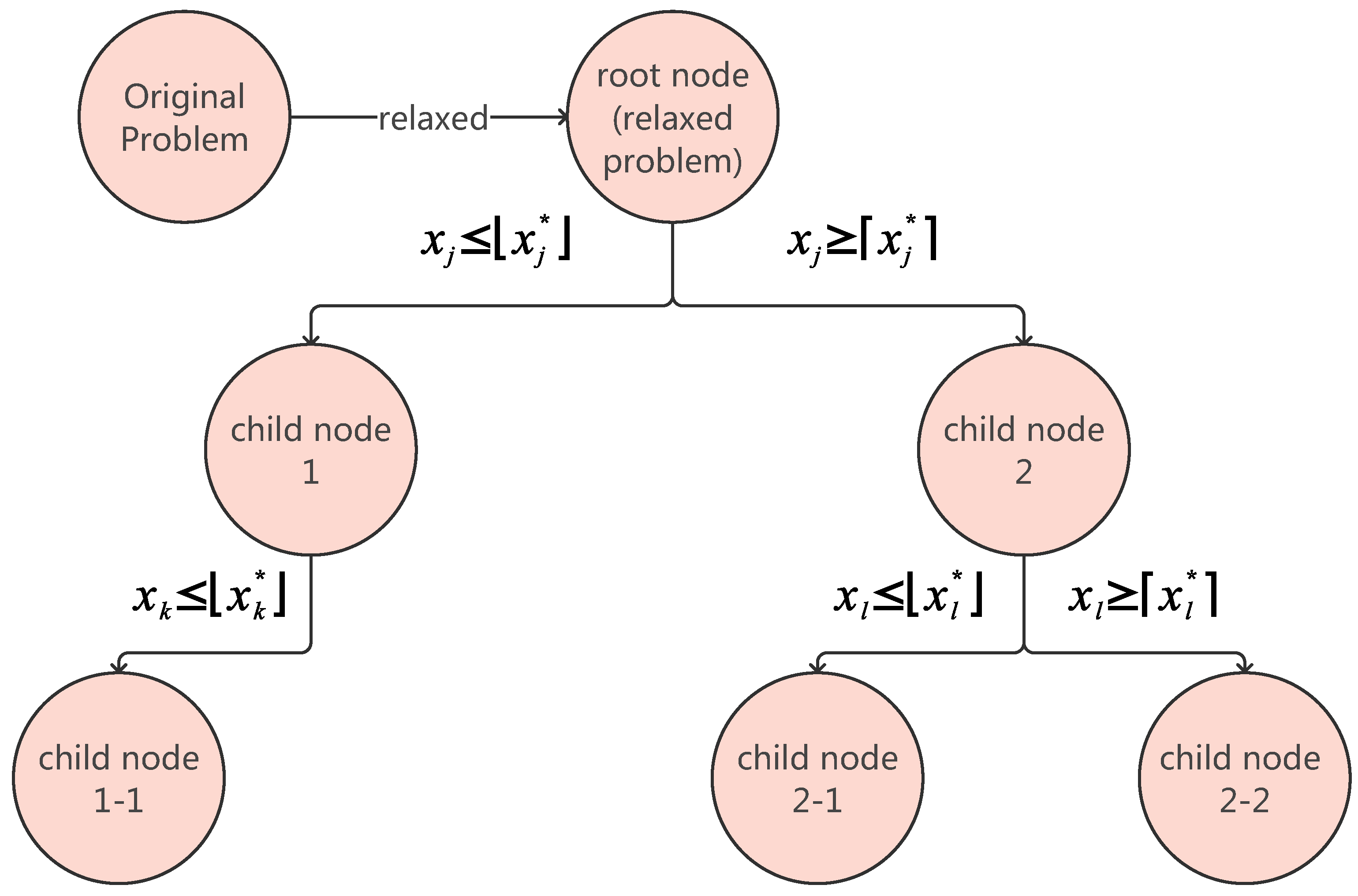
- Node: Based on the position of nodes in the search tree, they can be categorized into root nodes and child nodes. Based on the relationships between nodes, they are classified as parent nodes and child nodes. For example, child node 1 serves as the parent node for child nodes 1-1 and 1-2. Each node represents a constrained subproblem of the original problem, containing a constraint set, a relaxed solution, and status indicators. The constraint set inherits constraints from its parent node and adds new branching constraints. For instance, the constraint set of child node 1 includes constraints from the root node as well as the newly added constraint . Here, denotes the floor function of x, e.g., .
- Status indicators: These are used to denote the state of a node, categorized as unexplored or explored. Branching, pruning, or requiring no action will change the node’s status from unexplored to explored. Requiring no action indicates that the relaxed solution of the current node is an integer solution, and its objective value exceeds the current .
- Branching: Here, one selects a non-integer variable to partition the solution space into two branches: and . For example, the root node is divided into child node 1 and child node 2. Here, denotes the ceiling function of x, e.g., .
- Pruning: Subsequent branching operations are halted at the node. As illustrated in Figure 3, pruning removes child node 1-2 from the search tree. Pruning is justified under two conditions: (1) the relaxed solution is infeasible, or (2) the node’s upper bound satisfies (e.g., ). Here, represents the relaxed solution value of node i.
- Search Tree: This is hierarchical node collection with root–child relationships.
- First Branching Operation
- Branching Variable: (non-integer)
- Child Node Generation:
- −
- Node 1 (): Add constraint , relaxed solution with
- −
- Node 2 (): Add constraint , relaxed solution with
- Bound Update:
- −
- Upper Bound (UB):
- −
- Lower Bound (LB): Remains 0 (no integer solution found)
- Second Branching Operation
- Branching Variable: (non-integer)
- Child Node Generation:
- −
- Node 1-1 (): Add constraint , integer solution with
- −
- Node 1-2 (): Add constraint , infeasible solution with
- Bound Update:
- −
- Lower Bound (LB):
- −
- Upper Bound (UB):
- Pruning:
- −
- Node 1-2 pruned (Rule: Bound), since
- Third Branching Operation
- Branching Variable: (non-integer)
- Child Node Generation:
- −
- Node 2-1 (): Add constraint , solution with
- −
- Node 2-2 (): Infeasible
- Pruning:
- −
- Node 2-1 pruned (Rule: Bound), since
- −
- Node 2-2 pruned (Rule: Infeasibility)
- Algorithm Termination
- All active nodes processed
- Final Solution:
- −
- Optimal integer solution:
- −
- Objective value:
| Algorithm 1. Branch-and-Bound Algorithm for Site Selection Problem |
| Input: Integer linear programming problem: Output: Optimal solution , optimal value  |
4. Simulation Results
4.1. Data Throughput Comparison Under Different System Availability Constraints
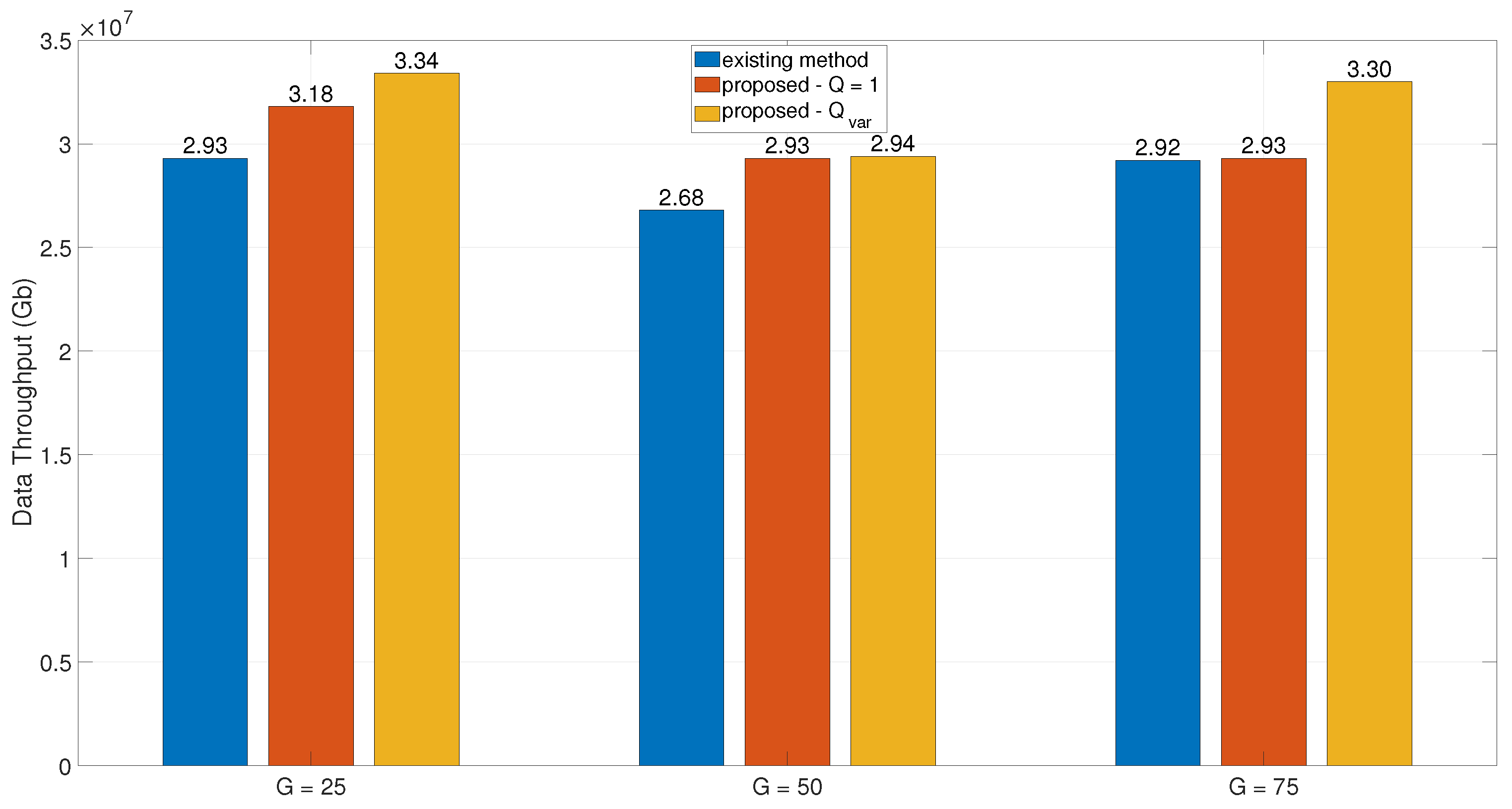
4.2. Data Throughput Comparison Under Different Number of Candidate GSs
4.3. Data Throughput Comparison Under Different Distributions of Link Availability Probability
4.4. Data Throughput Comparison Under Different Marginal Costs per Additional LCT
4.5. Impact of Cost Upper Limit on Data Throughput
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Fan, F.; Yu, H.; Wang, Y.; Dai, X.; Yang, Q.; Liu, R. A Bidirectional Multi-Format/Rate-Adjustable Integrated Laser Communication System for Satellite Communication. IEEE Photonics J. 2024, 16, 1–6. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Free-Space Optical (FSO) Satellite Networks Performance Analysis: Transmission Power, Latency, and Outage Probability. IEEE Open J. Veh. Technol. 2024, 5, 244–261. [Google Scholar] [CrossRef]
- Guelman, M.; Kogan, A.; Kazarian, A.; Livne, A.; Orenstein, M.; Michalik, H. Acquisition and pointing control for inter-satellite laser communications. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1239–1248. [Google Scholar] [CrossRef]
- Li, M.; Hong, Y.; Zeng, C.; Song, Y.; Zhang, X. Investigation on the UAV-To-Satellite Optical Communication Systems. IEEE J. Sel. Areas Commun. 2018, 36, 2128–2138. [Google Scholar] [CrossRef]
- Bushuev, D.; Kedar, D.; Arnon, S. Analyzing the performance of a nanosatellite cluster-detector array receiver for laser communication. J. Light. Technol. 2003, 21, 447–455. [Google Scholar] [CrossRef]
- Arnon, S.; Rotman, S.; Kopeika, N. Bandwidth maximization for satellite laser communication. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 675–682. [Google Scholar] [CrossRef]
- Al-Hraishawi, H.; Chougrani, H.; Kisseleff, S.; Lagunas, E.; Chatzinotas, S. A Survey on Nongeostationary Satellite Systems: The Communication Perspective. IEEE Commun. Surv. Tutor. 2023, 25, 101–132. [Google Scholar] [CrossRef]
- Xie, W.; Tan, L.; Ma, J. Received Signal Strength Reduction Analysis Based on the Wavelet Model in Intersatellite Laser Communications. J. Light. Technol. 2011, 29, 2327–2332. [Google Scholar] [CrossRef]
- Dang, K.D.; Le, H.D.; Nguyen, C.T.; Pham, A.T. Resource allocation for hybrid FSO/RF satellite-assisted multiple backhauled UAVs over Starlink networks. IEICE Commun. Express 2024, 13, 52–55. [Google Scholar] [CrossRef]
- Zedini, E.; Kammoun, A.; Alouini, M.S. Performance of Multibeam Very High Throughput Satellite Systems Based on FSO Feeder Links With HPA Nonlinearity. IEEE Trans. Wirel. Commun. 2020, 19, 5908–5923. [Google Scholar] [CrossRef]
- Samy, R.; Yang, H.C.; Rakia, T.; Alouini, M.S. Hybrid SAG-FSO/SH-FSO/RF Transmission for Next-Generation Satellite Communication Systems. IEEE Trans. Veh. Technol. 2023, 72, 14255–14267. [Google Scholar] [CrossRef]
- Le, H.D.; Trinh, P.V.; Pham, T.V.; Kolev, D.R.; Carrasco-Casado, A.; Kubo-Oka, T.; Toyoshima, M.; Pham, A.T. Throughput Analysis for TCP Over the FSO-Based Satellite-Assisted Internet of Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 1875–1890. [Google Scholar] [CrossRef]
- Spangelo, S.C.; Cutler, J.W.; Klesh, A.T.; Boone, D.R. Models and Tools to Evaluate Space Communication Network Capacity. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2387–2404. [Google Scholar] [CrossRef]
- Gong, S.; Shen, H.; Zhao, K.; Li, W.; Zhou, H.; Wang, R.; Sun, Z.; Zhang, X. Toward Optimized Network Capacity in Emerging Integrated Terrestrial-Satellite Networks. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 263–275. [Google Scholar] [CrossRef]
- Spangelo, S.; Cutler, J.; Gilson, K.; Cohn, A. Optimization-based scheduling for the single-satellite, multi-ground station communication problem. Comput. Oper. Res. 2015, 57, 1–16. [Google Scholar]
- Lyras, N.K.; Efrem, C.N.; Kourogiorgas, C.I.; Panagopoulos, A.D.; Arapoglou, P.D. Optimizing the Ground Network of Optical MEO Satellite Communication Systems. IEEE Syst. J. 2020, 14, 3968–3976. [Google Scholar] [CrossRef]
- Lyras, N.K.; Efrem, C.N.; Kourogiorgas, C.I.; Panagopoulos, A.D. Optimum Monthly Based Selection of Ground Stations for Optical Satellite Networks. IEEE Commun. Lett. 2018, 22, 1192–1195. [Google Scholar] [CrossRef]
- Fuchs, C.; Moll, F. Ground station network optimization for space-to-ground optical communication links. J. Opt. Commun. Netw. 2015, 7, 1148–1159. [Google Scholar] [CrossRef]
- Poulenard, S.; Crosnier, M.; Rissons, A. Ground segment design for broadband geostationary satellite with optical feeder link. J. Opt. Commun. Netw. 2015, 7, 325–336. [Google Scholar] [CrossRef]
- Gong, S.; Shen, H.; Zhao, K.; Wang, R.; Zhang, X.; De Cola, T.; Fraier, J.A. Network Availability Maximization for Free-Space Optical Satellite Communications. IEEE Wirel. Commun. Lett. 2020, 9, 411–415. [Google Scholar] [CrossRef]
- Efrem, C.N.; Panagopoulos, A.D. Globally Optimal Selection of Ground Stations in Satellite Systems With Site Diversity. IEEE Wirel. Commun. Lett. 2020, 9, 1101–1104. [Google Scholar] [CrossRef]
- Efrem, C.N.; Panagopoulos, A.D. Minimizing the Installation Cost of Ground Stations in Satellite Networks: Complexity, Dynamic Programming and Approximation Algorithm. IEEE Wirel. Commun. Lett. 2021, 10, 378–382. [Google Scholar] [CrossRef]
- Alfa, A.S.; Maharaj, B.T.; Lall, S.; Pal, S. Mixed-integer programming based techniques for resource allocation in underlay cognitive radio networks: A survey. J. Commun. Netw. 2016, 18, 744–761. [Google Scholar] [CrossRef]
- Jin, M.; Hu, R.Q.; Zhang, Z.; Hu, W. Integer linear programming models and performance evaluation on wavelength rearrangement in a mesh-restored all-optical network. IEEE Commun. Lett. 2006, 10, 111–113. [Google Scholar] [CrossRef]
- Garau-Luis, J.J.; Torrens, S.A.; Vila, G.C.; Pachler, N.; Crawley, E.F.; Cameron, B.G. Frequency Plan Design for Multibeam Satellite Constellations Using Integer Linear Programming. IEEE Trans. Wirel. Commun. 2024, 23, 3312–3327. [Google Scholar] [CrossRef]


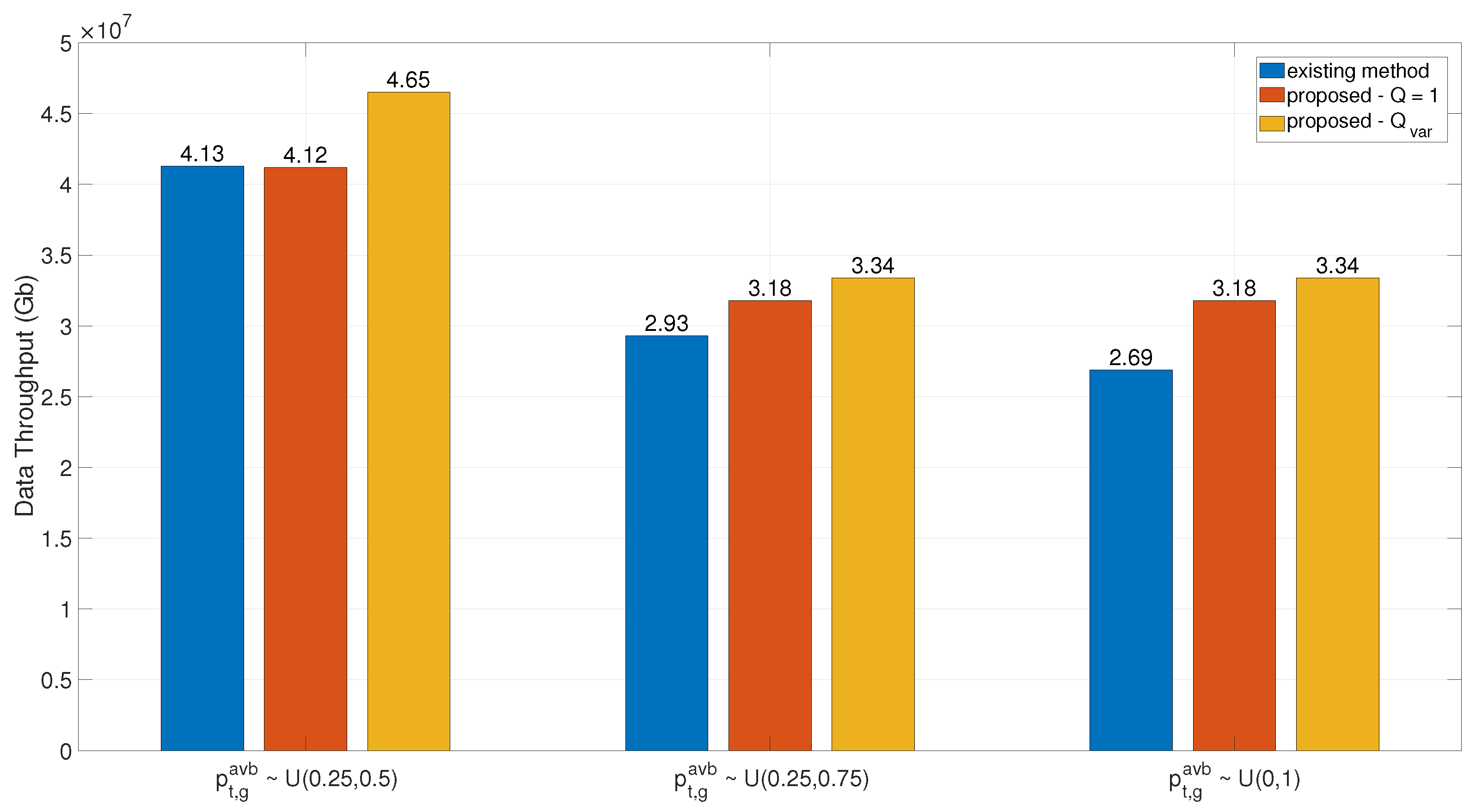
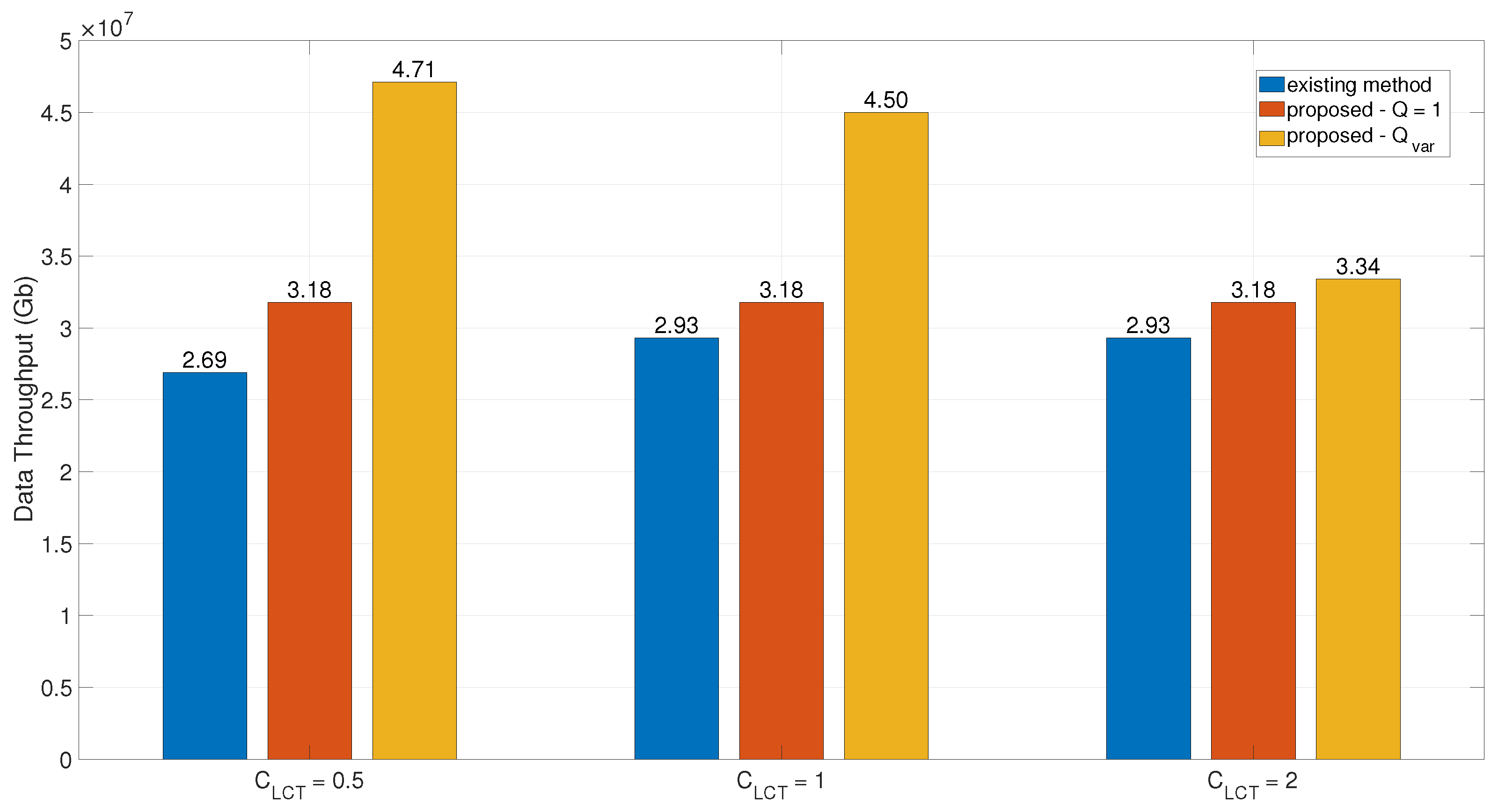
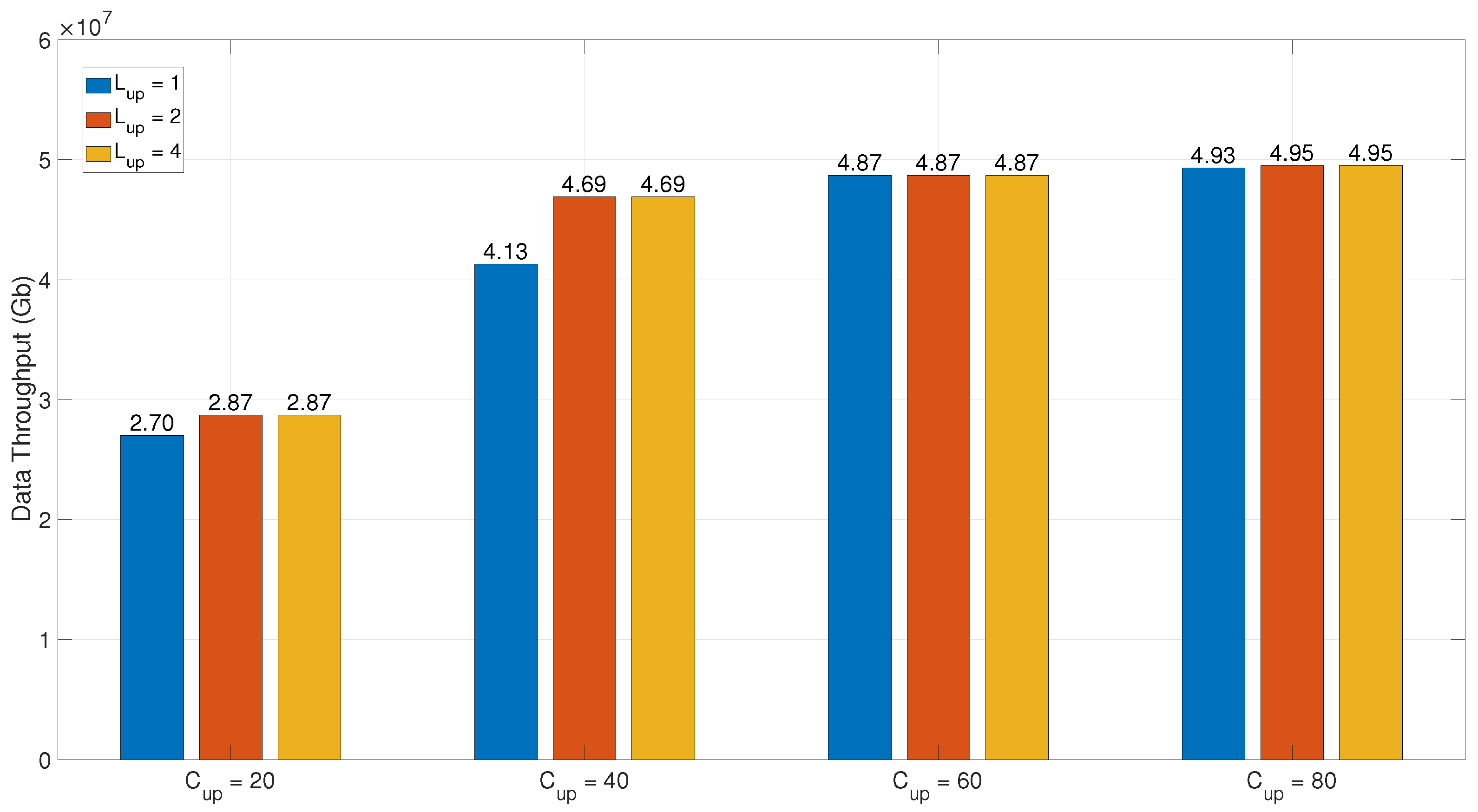
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, P.; Zhao, K.; Zhao, H. Data Throughput-Oriented Site Selection: Integrated Downlink Scheduling with Elastic Laser Communication Terminal Deployment. Electronics 2025, 14, 1479. https://doi.org/10.3390/electronics14071479
Lyu P, Zhao K, Zhao H. Data Throughput-Oriented Site Selection: Integrated Downlink Scheduling with Elastic Laser Communication Terminal Deployment. Electronics. 2025; 14(7):1479. https://doi.org/10.3390/electronics14071479
Chicago/Turabian StyleLyu, Pei, Kanglian Zhao, and Hangsheng Zhao. 2025. "Data Throughput-Oriented Site Selection: Integrated Downlink Scheduling with Elastic Laser Communication Terminal Deployment" Electronics 14, no. 7: 1479. https://doi.org/10.3390/electronics14071479
APA StyleLyu, P., Zhao, K., & Zhao, H. (2025). Data Throughput-Oriented Site Selection: Integrated Downlink Scheduling with Elastic Laser Communication Terminal Deployment. Electronics, 14(7), 1479. https://doi.org/10.3390/electronics14071479






