Low-Frequency Active Noise Control System Based on Feedback FXLMS

Abstract

The rise of industrial machinery and military training activities has significantly contributed to low-frequency noise pollution, which can penetrate traditional passive noise isolation methods and pose serious health risks, including irreversible hearing damage. To address this challenge, this study proposes a hybrid active noise control (HANC) system, integrating an adaptive active noise control (AANC) module based on the filtered-x least mean squares (FxLMS) algorithm and an audio-balance control circuit (ABCC). The AANC system actively generates anti-noise signals to mitigate low-frequency disturbances, while the ABCC module enhances voice clarity and protects users from excessive impulse noise. MATLAB R2023b simulations and hardware implementations validate the system’s effectiveness, achieving a noise reduction of up to 21.8 dB in controlled environments. Additionally, the proposed feedback active noise control architecture ensures robust performance under dynamic noise conditions, improving stability and response time. By integrating both software-based adaptive filtering and hardware circuit design, this study provides a comprehensive noise mitigation solution with potential applications in military, industrial, and vehicular environments.

1. Introduction

Low-frequency noise pollution, primarily generated by industrial machinery, military operations, and environmental sources, poses significant challenges in noise mitigation due to its imperceptibility and the ineffectiveness of passive noise isolation techniques. Traditional passive noise control methods, such as soundproofing and damping materials, struggle to attenuate low-frequency noise efficiently, necessitating the implementation of active noise control (ANC) systems. ANC leverages real-time adaptive algorithms to generate anti-noise signals, effectively canceling out unwanted noise through destructive interference. ANC technology has evolved significantly over the past decade, with a particular focus on linear system implementations. Lu et al. [1] conducted a comprehensive survey on active noise control in linear systems, detailing advancements in adaptive filtering techniques, stability considerations, and real-world applications. This foundational research highlights the critical role of adaptive algorithms in addressing low-frequency noise challenges, particularly in dynamic environments. Among various adaptive filtering techniques, the filtered-x least mean squares (FxLMS) algorithm remains the most widely adopted due to its real-time adaptability and robustness. The FxLMS algorithm is a modification of the standard LMS algorithm, incorporating secondary path modeling to ensure precise noise cancellation. Shi et al. [2] proposed an improved two-gradient direction FxLMS (TGDFxLMS) algorithm, which introduces an adaptive output constraint to enhance convergence speed and robustness in active noise control applications. This innovation significantly improves ANC system performance in complex acoustic environments. The effectiveness of ANC systems is heavily dependent on adaptive gain control, particularly in fixed-filter applications such as noise-canceling headphones. Shen et al. [3] introduced an adaptive-gain algorithm that dynamically adjusts the system’s gain based on real-time noise levels, ensuring optimal performance across varying acoustic conditions. Their study underscores the importance of balancing computational efficiency with real-time adaptability, a crucial factor for practical ANC implementations.

Several studies have sought to improve the FxLMS algorithm’s adaptability and convergence properties. Meng and Chen [4] proposed a particle swarm optimization (PSO)-based adaptive step-size FxLMS algorithm, which integrates a reference signal smoothing processor to improve noise reduction efficiency while minimizing computational overhead. This approach significantly enhances convergence rates, making it suitable for real-time ANC applications. To address the limitations of centralized ANC systems, researchers have explored decentralized and distributed ANC models. Karthik et al. [5] developed an FxLMS-based tap-decomposed adaptive filter for decentralized ANC systems, allowing for distributed processing across multiple noise control nodes. Similarly, Chen and Yang [6] introduced a distributed FxLMS algorithm for narrowband ANC, improving stability and computational efficiency while providing a detailed convergence analysis. A key limitation of ANC systems is their susceptibility to saturation nonlinearity, which can degrade noise cancellation performance. Tian et al. [7] addressed this issue by introducing an intermittent FxLMS algorithm designed to mitigate nonlinear distortion effects, thereby maintaining effective noise suppression in challenging environments.

While ANC is effective for continuous low-frequency noise, impulsive noise presents unique challenges due to its high-energy transient nature. Liu and Lei [8] reviewed recent advancements in active impulsive noise control (AINC), with a particular focus on adaptive algorithms that dynamically adjust to rapid noise changes. Their study highlights the role of hybrid adaptive filtering techniques in improving ANC performance against sudden, high-intensity noise events. To enhance ANC in impulsive noise environments, Wen et al. [9] developed a multi-reference adaptive gain FxLMS algorithm, capable of effectively suppressing impulsive noise disturbances. This innovation is particularly relevant in applications where unpredictable noise variations occur, such as industrial machinery operations and military environments. The stability of ANC systems is a critical factor in large-scale implementations, especially in distributed ANC networks. Ferrer et al. [10] conducted an extensive stability assessment of distributed FxLMS ANC systems, providing valuable insights into parameter selection and system behavior under real-world conditions. García-Mollá et al. [11] expanded on this work by proposing selective collaboration strategies, optimizing computational efficiency while maintaining high noise cancellation performance. In practical implementations, the design of hybrid active noise control (HANC) architectures has become increasingly important. Han and Chen [12] introduced a hybrid fixed-filter ANC system, integrating the FxLMS algorithm with feedforward and feedback control structures to improve noise suppression efficiency in real-time environments. The FxLMS algorithm has been widely adopted in consumer electronics, industrial noise control, and vehicular applications. Xie et al. [13] designed and simulated an active noise-canceling earphone system based on the FxLMS algorithm, demonstrating its feasibility in commercial ANC products. In the transportation sector, Zhang et al. [14] developed a four-channel ANC model utilizing dual FxLMS algorithms to enhance in-vehicle sound quality for electric buses. Their offline simulation results indicate significant noise reduction, reinforcing the practical benefits of ANC in automotive applications.

In HANC systems, long-term stability and experimental repeatability are critical. Therefore, this study adopts a comprehensive approach, integrating active noise cancellation (ANC) with precise circuit design. In the ANC segment, we implemented the filtered-x least mean squares (FXLMS) algorithm to generate a counter-phase signal, effectively reducing external noise. We validated the algorithm through both MATLAB simulations and hardware tests, confirming its efficacy in mitigating harmful noise exposure. For audio balancing control, we introduced precision rectifier diodes for analog signal processing. By combining software simulations with practical validation, we optimized electronic components to enhance processing speed and prevent overheating, ensuring system safety and reliability (an aspect rarely covered in the literature). The following points summarize the experimental contributions of this study:

1.

To prevent irreversible hearing damage caused by high-decibel impulse noises (e.g., artillery blasts), we designed a protection attenuation circuit that effectively reduces excessive noise to a safe hearing range.

2.

An amplification circuit was developed to enhance low-volume vocal signals in military environments, ensuring clear command transmission while preventing additional hearing damage. A bandpass filter was also integrated to eliminate non-human noise, maintaining speech clarity.

3.

To address signal distortion caused by switching circuit surge phenomena, we introduced a circuit-splitting approach that optimizes both attenuation and amplification circuits. This design enhances system stability and ensures reliable performance.

4.

Unlike conventional studies that focus solely on short-term experimental outcomes, this research prioritizes long-term system stability and response repeatability. Extensive simulation and hardware testing ensured optimal component selection, fast audio processing, and high operational safety.

5.

Each designed circuit and subsystem underwent multiple iterations of planning, simulation, and real-world testing to refine the selection of electronic components and ensure system robustness. The final active audio balance system delivers a low-distortion, fast-response output, making it reproducible and applicable for future developments in active noise control and audio signal processing.

2. System Design

2.1. Overview of the System

Active audio balancing system, integrating both adaptive active noise control (AANC) and adaptive bandwidth compensation control (ABCC) systems. This system uses ANC with the FXLMS algorithm to reduce intense background noise while preserving and enhancing human voice signals. The system flow is shown in Figure 1. Initially, both noise and speech are present in the input sound. The FXLMS module generates an anti-noise signal to cancel out much of the unwanted noise. The processed sound then passes through an attenuation circuit to further reduce noise, followed by a bandpass filter that isolates the human voice. Since the filtered voice may be too weak, an amplifier circuit boosts it to a clear and audible level. Finally, the ear receives a safe output with minimized noise and an enhanced voice, making communication easier in noisy environments. To achieve the design objectives of AANC and ABCC, we employed MATLAB and Cadence Orcad 17.4 for simulating and analyzing noise reduction and circuit balancing on the software side. On the hardware side, we developed an impulse noise test channel with a feedback structure and an audio balancing circuit capable of signal attenuation, protection, filtering, and amplification. By conducting both software simulations and hardware implementations of the AANC and ABCC systems, we successfully validated the effectiveness of the proposed HANC audio balancing system.

2.2. Active Noise Control

In this study, a closed-loop feedback architecture is adopted in the hardware design of the AANC system for active noise control. Generally, closed-loop acoustic processing hardware can be classified into three types: feedforward ANC, feedback ANC, and HANC [15]. Among them, feedforward noise control systems are susceptible to acoustic feedback due to the placement of microphones, which limits their effectiveness in periodic noise environments. While hybrid noise cancellation systems offer greater versatility, they often capture excessive unwanted noise, thereby increasing the development cost of the controller. Given that the acoustic spatial scale in this study is one-dimensional, the feedback architecture is particularly suitable for active noise control systems (as shown in Figure 2), providing enhanced noise reduction efficiency and system stability [16].

2.3. Controller and Adaptive Filtering

Designing an effective ANC controller requires accounting for the time-varying characteristics of the noise source signal. This study employs an adaptive controller that dynamically adjusts parameters in response to temporal noise variations. By integrating filters and controllers, the system continuously updates its parameters to minimize noise energy and mitigate interference [17]. To ensure robustness, the FIR filter has an all-zero structure, which not only ensures stability but also provides precise linear phase. In contrast, the IIR filter, composed of poles and zeros, presents stability challenges that need to be addressed. Moreover, when adjusting weight values, it is necessary to monitor whether the zeros move outside the unit circle, which increases processing time, making it relatively more complex in practical applications. Therefore, the selection of an FIR filter is crucial for the stable elimination of noise in the system.

2.4. Feedback Noise Cancellation and Secondary Path Modeling

In the feedback ANC system depicted in Figure 2, low-frequency impulse noise enters the system through the main path. It is then attenuated by the anti-noise signal generated by the ANC system before being effectively removed. However, an additional factor must be considered: the secondary path, which represents the route between the speaker and the error microphone. The concept of the secondary path was introduced by P. A. Nelson and S. J. Elliott, who demonstrated that compensating for the secondary path enhances the overall stability of the ANC system. In this study, we define the second path module in Figure 2 as S(n). Meanwhile, the noise source is defined as the target signal d(n), the ANC system’s output is termed the noise reduction signal y(n), and the signal captured by the error microphone is designated as the error signal e(n).

As shown in the signal flow diagram in Figure 3, we introduce an estimated secondary path filter $\widehat{S}\left(\mathrm{z}\right)$ between the reference signal $\widehat{d}\left(n\right)$ and the LMS algorithm. Through iterative updates, $\widehat{S}\left(\mathrm{z}\right)$ approximates the actual secondary path S(z), mitigating its impact on the system. However, since the feedback ANC architecture lacks an additional reference microphone for sampling external signals, the reference signal $\widehat{d}\left(n\right)$ must be synthesized from the error signal e(n), measured by the error microphone, and the control signal y(n), thereby establishing the input signal for the controller. The formula is as follows:

$$\widehat{d}\left(n\right)=\mathrm{e}\left(n\right)+{\sum }_{\mathrm{m}=0}^{\mathrm{M}-1}\widehat{s}\left(m\right)y\left(n-\mathrm{m}\right)$$

(1)

where ${\widehat{S}}_m$ is the m-th coefficient of the secondary path estimation filter $\widehat{S}\left(z\right)$, and M is the length of the filter S(z). The output y(n) of the control filter w(n) and the update of the control filter’s weights can be expressed by the following equations, where l is the order of the FIR filter.

$$\begin{gathered} y\left(n\right)=\sum _{l=0}^{L-1}{w}_l\left(n\right)\widehat{d}\left(n-l\right) \\ {w}_l\left(n+1\right)=w_l\left(n\right)+\mu \widehat{\mathit{d‘}}\left(n-l\right)e\left(n\right) \end{gathered}$$

(2)

where $\mathsf{\mu }$ is the convergence factor that controls stability and convergence rate.

2.5. Outdoor Noise Management and Decision-Making System

In outdoor environments, noise signals are superimposed, making it impractical to use a simple attenuation circuit to uniformly reduce all environmental noise. Some noises serve as warning signals or aid in situational awareness, drawing the user’s attention and supporting environmental analysis. Arbitrarily attenuating such warning-type noises could potentially put the user at risk. Therefore, a decision-making system is needed to selectively attenuate excessive noise while preserving important auditory cues, ensuring that the system protects the user’s ears without eliminating crucial sounds [18,19]. Considering that the attenuation system must evaluate whether the noise could pose a hazard to human health, this study designed both a switching circuit and a clipping circuit, which were incorporated into the attenuation system for signal processing and comparison. Figure 4 presents the simulation results using the switching circuit, where it is evident that the attenuation system exhibits a spiking phenomenon when determining whether the signal constitutes harmful noise. This phenomenon generates audio that could cause discomfort to the user. Therefore, this study selects the clipping circuit to process the signal, resulting in a smooth output, as shown in Figure 5, without any undesirable side effects.

2.6. Secondary Path Identification and Impact Noise Simulation

In previous discussions, it was noted that the secondary path (as shown in S(z) in Figure 2) can affect the system’s stability. Therefore, before applying the FXLMS algorithm, it is necessary to first identify the secondary path. We use an embedded system [20,21] to generate zero-mean white noise for identifying the secondary path of the system. With its uniform spectral characteristics, white noise enhances the adaptive filter’s ability to distinguish all frequency components of the secondary path. This not only improves noise reduction performance but also mitigates the occurrence of acoustic feedback. The simulation results in Figure 6 represent the frequency-domain identification results obtained from using white noise to identify the secondary path of the system. Based on these results, the signal flow simulation framework in Figure 7 can then be constructed.

Figure 8 presents the simulation results of the FXLMS-based active noise control system constructed in Figure 7 for suppressing artillery noise. By incorporating secondary path estimation and continuous algorithmic adaptation, the system effectively stabilizes and attenuates the noise energy.

2.7. Bandpass Filtering and Voice Signal Amplification

Due to the interference caused by environmental noise during calls, this study specifically designed a bandpass filter to capture voice information and effectively filter out non-voice audio interference. Additionally, small voice volumes from the audio source can be amplified to facilitate better understanding of call content by the receiver. The filtering circuit in this study prevents the inclusion of additional environmental noise and non-voice audio in the amplified signal, avoiding interference with intended call messages. The bandpass filter circuit (a fourth-order Butterworth bandpass filter) is shown in Figure 9, and its Bode plot is presented in Figure 10. Since the voice frequency range is primarily between 1 kHz and 3 kHz, Figure 10 clearly demonstrates that the designed filter effectively extracts voice signals. Building on the previously designed attenuation circuit, an amplification circuit was developed to enhance voice communication clarity in noisy environments (as shown in Figure 11). The simulation output results of the amplification circuit in Figure 11 are presented in Figure 12.

3. Results and Discussion

AANC systems play a crucial role in mitigating low-frequency impulsive noise. The implementation of such systems requires careful selection of system parameters and hardware components to achieve optimal noise reduction performance. This study explores the transition from software simulations to hardware implementation, examining the effects of system order, step size, and operational amplifier selection on the overall performance of an AANC system.

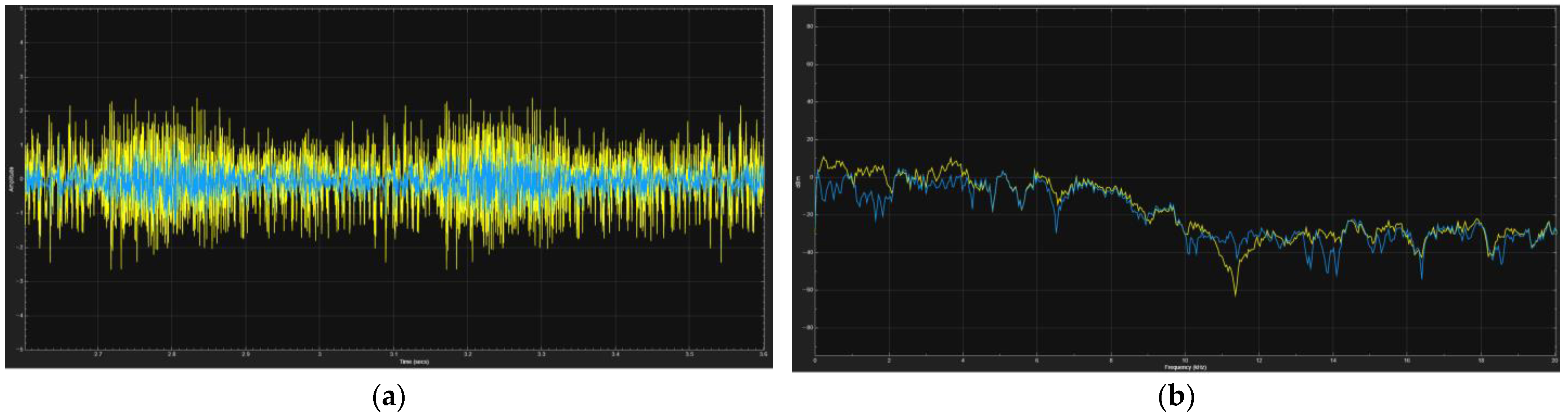
3.1. Software Simulation and Parameter Selection

According to the software simulation results presented in Figure 13 and

Table 1. Efficiency statistics on ANC order adjustment of the artillery system.

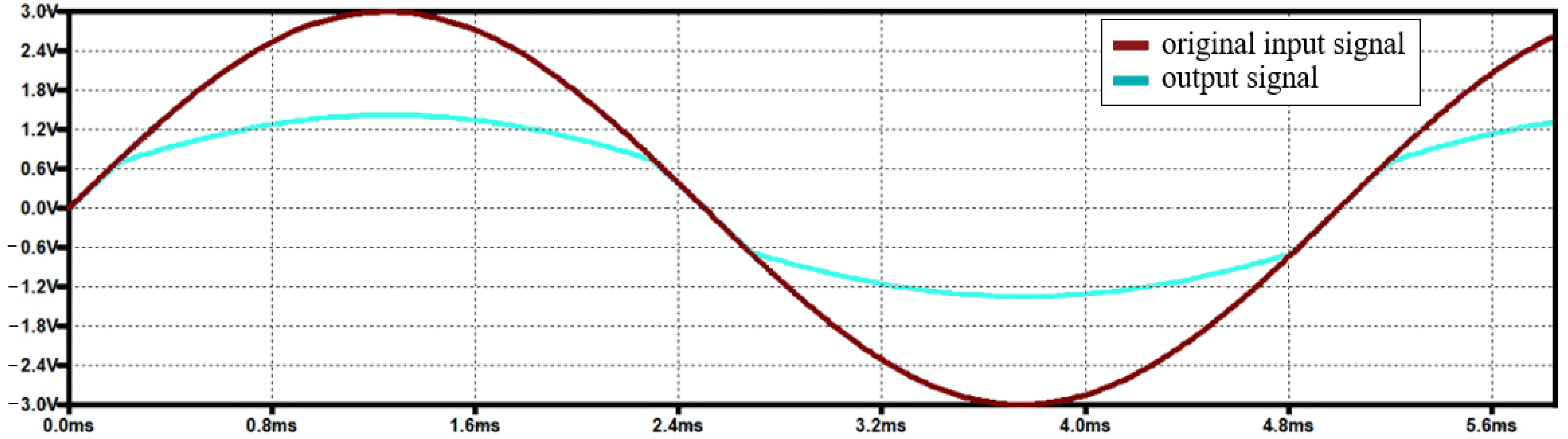
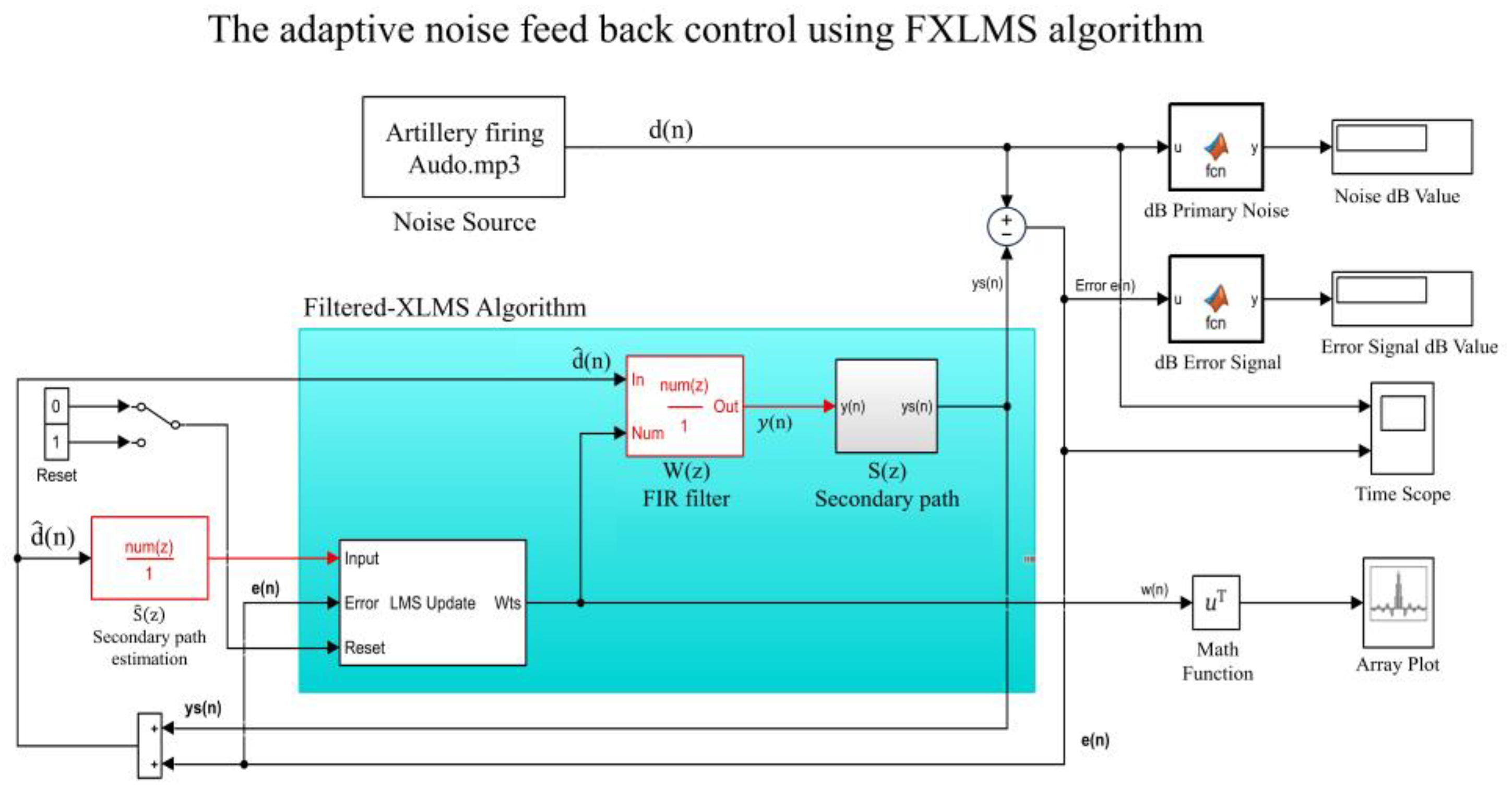
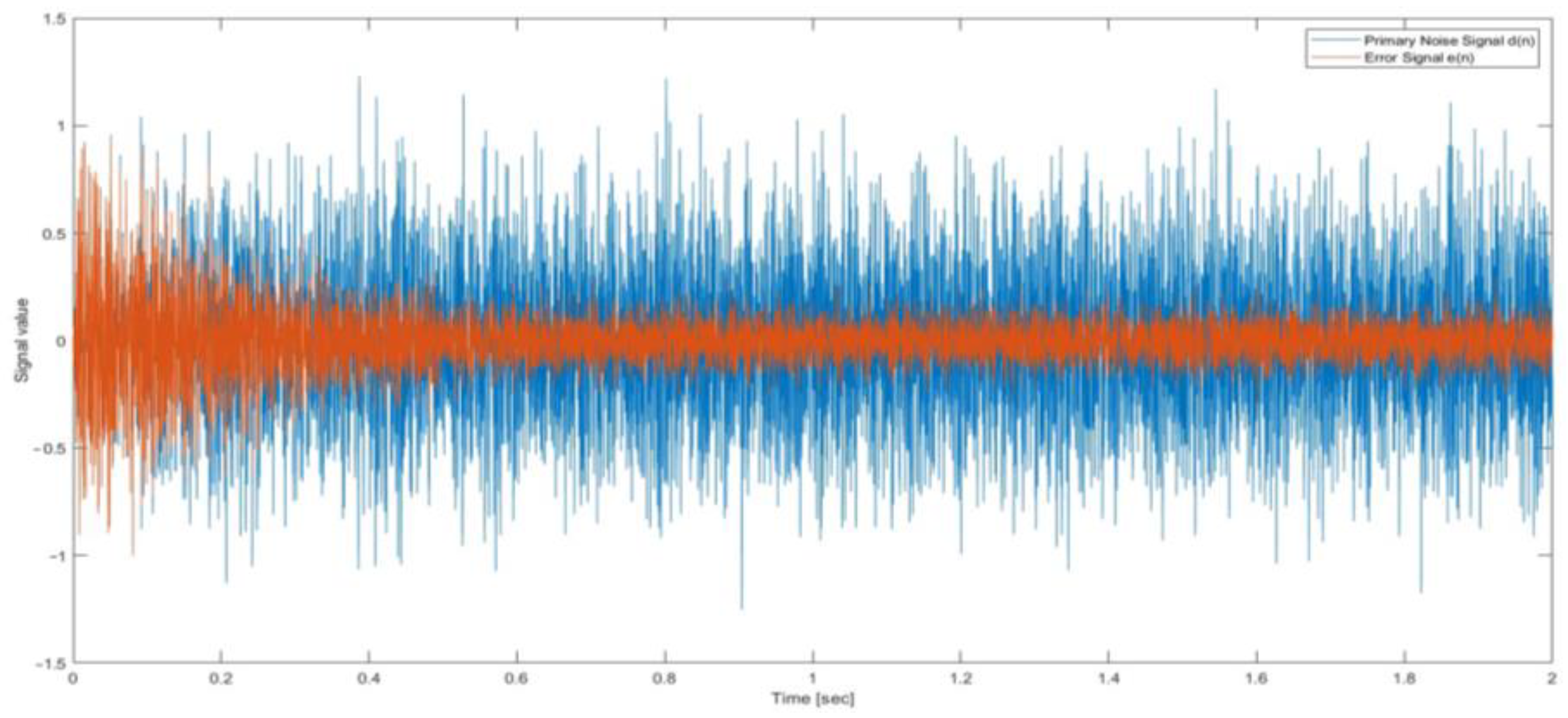
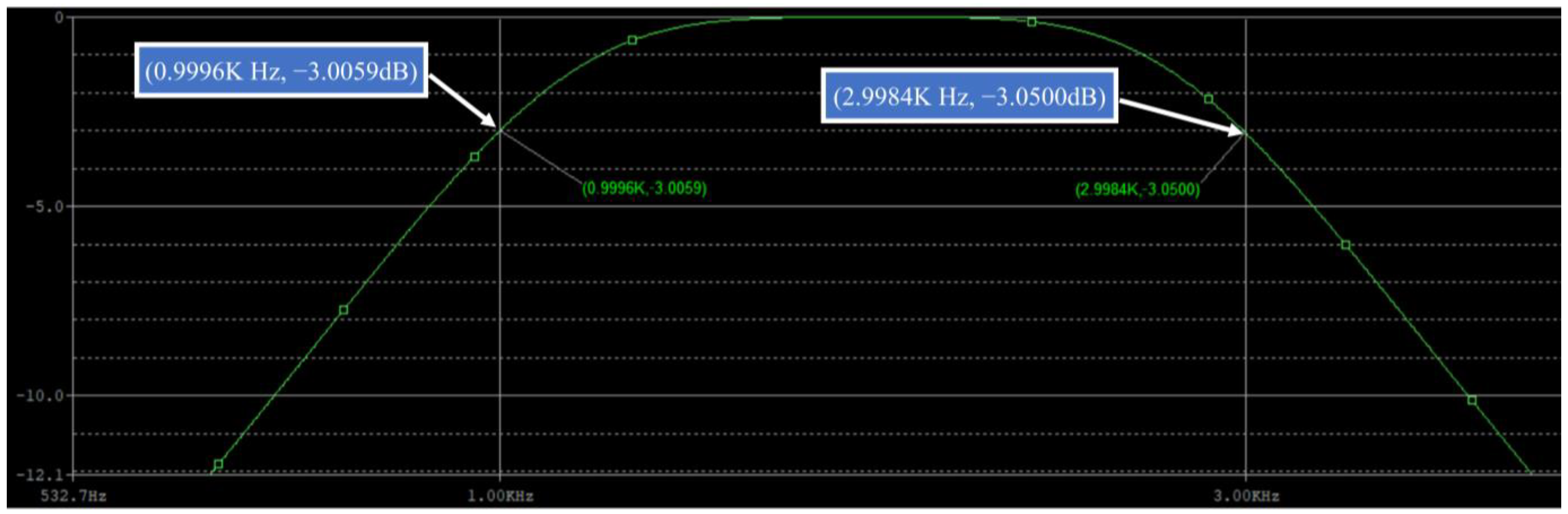
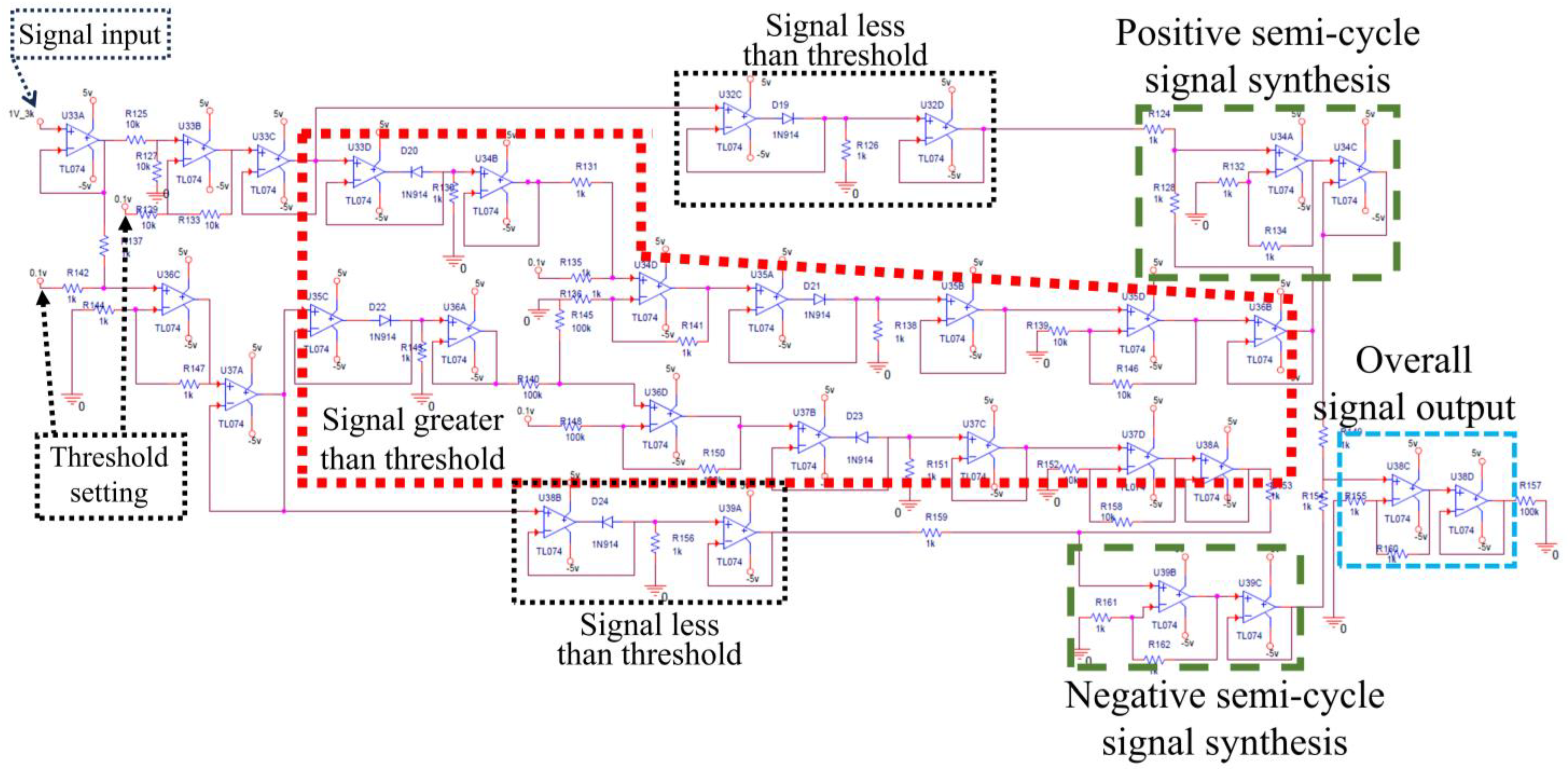
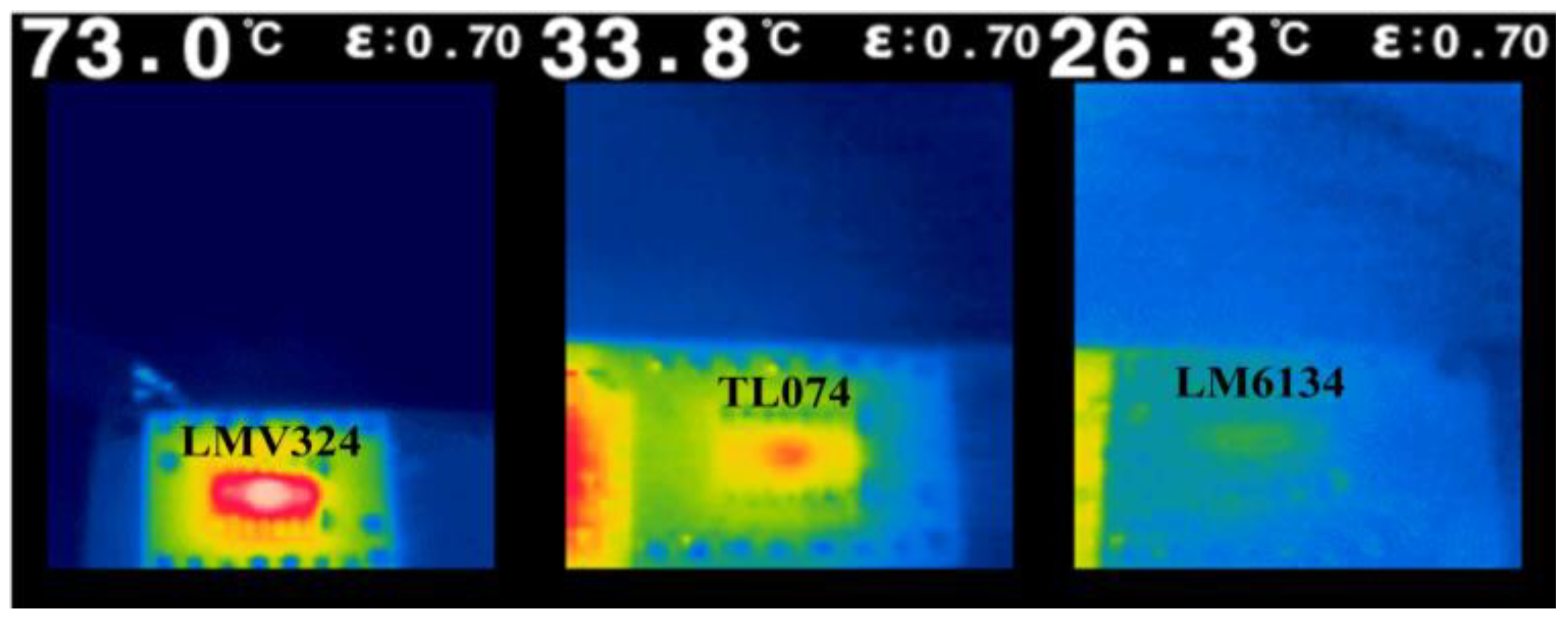
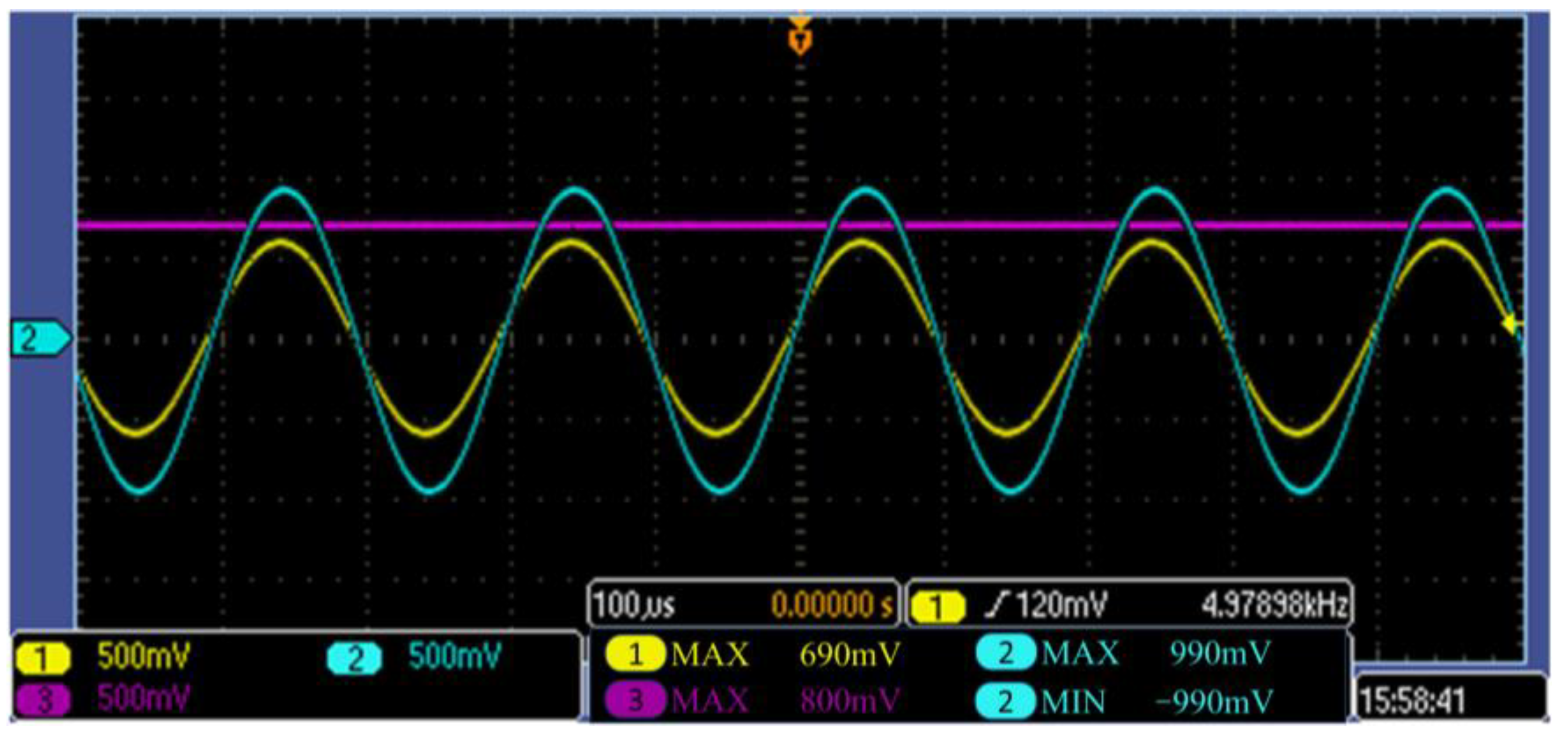
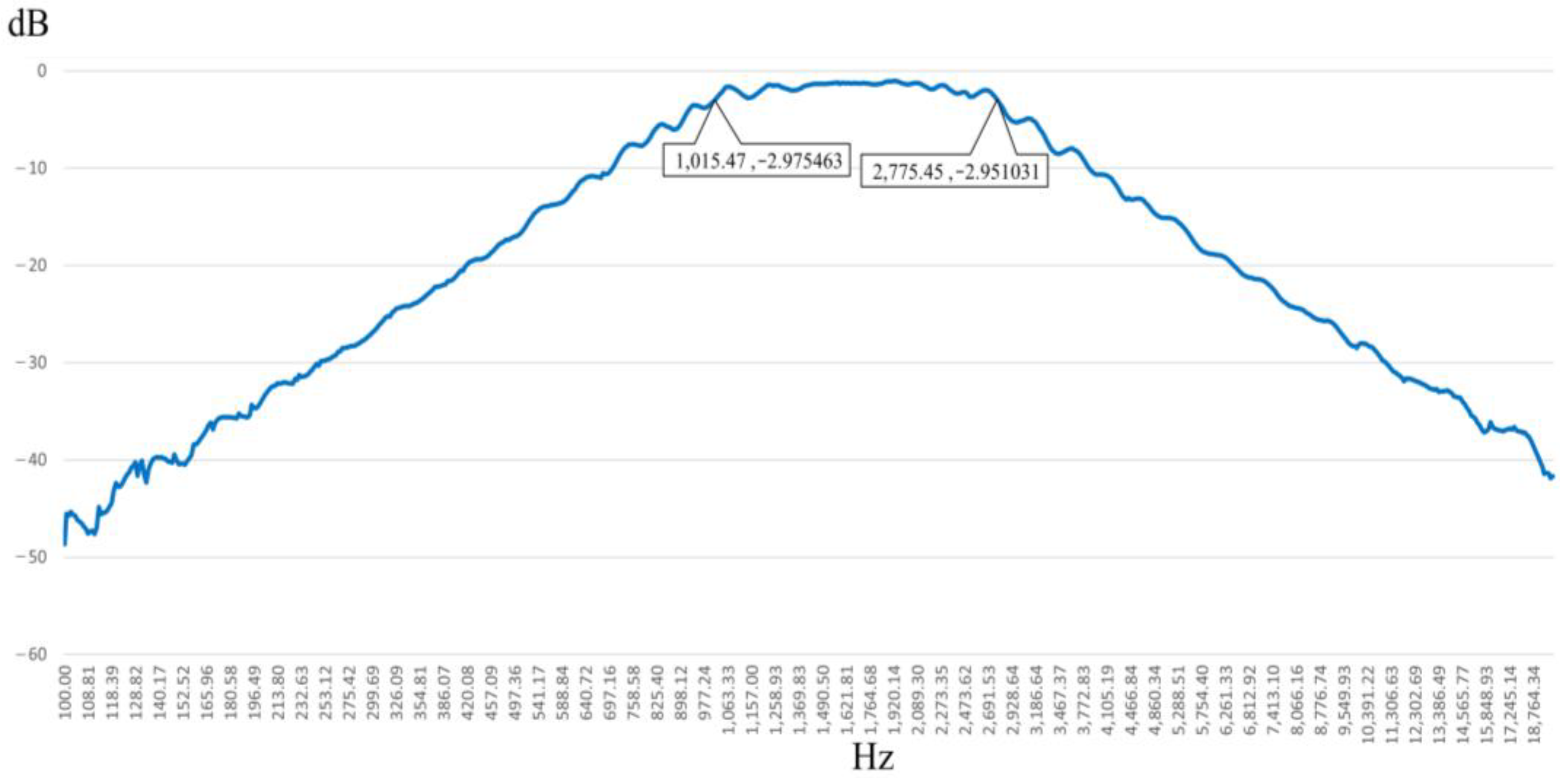
System Order	Before Control (dB)	After Control (dB)	Variation Amount (dB)
10	112.5	107.2	5.3
20	112.5	97.6	14.9
30	112.5	91.3	21.2
40	112.5	90.7	21.8
50	112.5	91.2	21.3
60	112.5	92.5	20
70	112.5	92.4	20.1
80	112.5	91.6	20.9
90	112.5	92.3	20.2
100	112.5	94.2	18.3

, the initial system design was configured with system orders ranging between 30 and 60 stages. The step size parameter was set between ${10}^{-3}$ and ${10}^{-2}$, as these values were expected to yield favorable results in noise reduction. These settings were determined through extensive simulations, ensuring a balance between convergence speed and stability.

3.2. Hardware Implementation and Experimental Analysis

The hardware implementation of the AANC system, depicted in Figure 14, was developed based on the insights gained from software simulations. The actual experimental results from the hardware setup are summarized in

Table 2. The AANC performance parameter adjustment table.

System Order	Step Size	Pre-Control (dB)	Post-Control (dB)	Difference (dB)
30	${10}^{-3}$	112	100.1	12.4
30	$5\times {10}^{-3}$	112	98.0	14.5
30	${10}^{-2}$	112	97.9	15.2
30	${5\times 10}^{-2}$	112	Unstable	Unstable
30	${10}^{-1}$	112	Unstable	Unstable
40	${10}^{-3}$	112	99.1	13.4
40	$5\times {10}^{-3}$	112	97.9	14.6
40	${10}^{-2}$	112	96.8	15.7
40	${5\times 10}^{-2}$	112	Unstable	Unstable
40	${10}^{-1}$	112	Unstable	Unstable
50	${10}^{-3}$	112	98.9	13.6
50	$5\times {10}^{-3}$	112	97.5	13.3
50	${10}^{-2}$	112	96.3	15
50	${5\times 10}^{-2}$	112	Unstable	Unstable
50	${10}^{-1}$	112	Unstable	Unstable
60	${10}^{-3}$	112	99.2	13.3
60	$5\times {10}^{-3}$	112	97.8	14.2
60	${10}^{-2}$	112	96.5	14.4
60	${5\times 10}^{-2}$	112	Unstable	Unstable
60	${10}^{-1}$	112	Unstable	Unstable
70	${10}^{-3}$	112	99.1	13.4
70	$5\times {10}^{-3}$	112	98.0	14.1
70	${10}^{-2}$	112	97.1	14
70	${5\times 10}^{-2}$	112	Unstable	Unstable
70	${10}^{-1}$	112	Unstable	Unstable
80	${10}^{-3}$	112	99.3	12.9
80	$5\times {10}^{-3}$	112	98.7	13.5
80	${10}^{-2}$	112	97.7	14.8
80	${5\times 10}^{-2}$	112	Unstable	Unstable
80	${10}^{-1}$	112	Unstable	Unstable
90	${10}^{-3}$	112	99.9	12.6
90	$5\times {10}^{-3}$	112	99.3	13.2
90	${10}^{-2}$	112	98.1	14.4
90	${5\times 10}^{-2}$	112	Unstable	Unstable
90	${10}^{-1}$	112	Unstable	Unstable

and visualized in Figure 15. These results allow for a comparative analysis between software predictions and real-world hardware performance. From

Table 3. Parameter comparisons of super diodes.

OPA	Slew Rate	Rail to Rail	Switch Diode	Load	Maximum Distortion of the 1/4 Cycle	Maximum Distortion of the 3/4 Cycle	Error (mv)
TL074	13 (V/us)	In to V+	1n914	100 Ω	351.957 mv	−0.6543 mv	352.6113
TL074	13 (V/us)	In to V+	1n914	1 KΩ	368.915 mv	−6.3288 mv	375.2438
TL074	13 (V/us)	In to V+	1n914	10 KΩ	382.506 mv	−56.507 mv	439.013
TL074	13 (V/us)	In to V+	1n4004	100 Ω	312.723 mv	−193.436 mv	506.159
TL074	13 (V/us)	In to V+	1n4004	1 KΩ	346.607 mv	−192.159 mv	538.766
TL074	13 (V/us)	In to V+	1n4004	10 KΩ	503.545 mv	−326.736 mv	830.281
Opa197	20 (V/us)	In, Out	1n914	100 Ω	148.652 mv	−1.3202 mv	149.9722
Opa197	20 (V/us)	In, Out	1n914	1 KΩ	229.230 mv	−12.371 mv	241.601
Opa197	20 (V/us)	In, Out	1n914	10 KΩ	281.818 mv	−95.559 mv	377.377
Opa197	20 (V/us)	In, Out	1n4004	100 Ω	150.952 mv	−203.511 mv	354.463
Opa197	20 (V/us)	In, Out	1n4004	1 KΩ	250.073 mv	−205.315 mv	455.388
Opa197	20 (V/us)	In, Out	1n4004	10 KΩ	123.796 mv	−420.276 mv	544.072
TLV9352	20 (V/us)	In to V−, Out	1n914	100 Ω	250.073 mv	−0.92112 mv	250.99412
TLV9352	20 (V/us)	In to V−, Out	1n914	1 KΩ	507.355 mv	−8.6397 mv	515.9947
TLV9352	20 (V/us)	In to V−, Out	1n914	10 KΩ	579.425 mv	−76.823 mv	656.248
TLV9352	20 (V/us)	In to V−, Out	1n4004	100 Ω	243.671 mv	−200.491 mv	444.162
TLV9352	20 (V/us)	In to V−, Out	1n4004	1 KΩ	467.421 mv	−196.289 mv	663.71
TLV9352	20 (V/us)	In to V−, Out	1n4004	10 KΩ	320.669 mv	−372.314 mv	692.983
Opa810	200 (V/us)	In to V−, Out	1n914	100 Ω	67.672 mv	−3.1010 mv	70.773
Opa810	200 (V/us)	In to V−, Out	1n914	1 KΩ	80.285 mv	−26.249 mv	106.534
Opa810	200 (V/us)	In to V−, Out	1n914	10 KΩ	165.539 mv	−126.372 mv	291.911
Opa810	200 (V/us)	In, Out	1n4004	100 Ω	73.264 mv	−213.165 mv	286.429
Opa810	200 (V/us)	In, Out	1n4004	1 KΩ	149.746 mv	−217.955 mv	367.701
Opa810	200 (V/us)	In, Out	1n4004	10 KΩ	409.660 mv	−458.050 mv	867.71
Opa820	240 (V/us)	No	1n914	100 Ω	221.196 mv	−6.8679 mv	228.0639
Opa820	240 (V/us)	No	1n914	1 KΩ	214.617 mv	−51.528 mv	266.145
Opa820	240 (V/us)	No	1n914	10 KΩ	145.079 mv	−275.602 mv	420.681
Opa820	240 (V/us)	No	1n4004	100 Ω	228.326 mv	−218.057 mv	446.383
Opa820	240 (V/us)	No	1n4004	1 KΩ	204.947 mv	−258.748 mv	463.695
Opa820	240 (V/us)	No	1n4004	10 KΩ	105.586 mv	−572.584 mv	678.17

, we observed that setting the system order to 30 stages and the step size to 10⁻³ provided the most effective noise reduction. Certain parameter settings led to suboptimal performance, emphasizing the importance of fine-tuning these values for hardware implementation. Moreover, Figure 15 demonstrates that when the system order is set to 30 stages, the noise reduction performance is significantly superior to other configurations, reaffirming the findings from the software simulations.

Since this study focuses on reducing impulsive noise, selecting appropriate operational amplifiers (op-amps) is essential to maintain signal integrity and minimize delays. High slew rate and stable performance are critical characteristics for effective noise signal processing. However, theoretical performance metrics of operational amplifiers often differ from practical results due to environmental factors, such as temperature variations, which software simulations do not account for. To address this discrepancy, we conducted practical performance tests using three different operational amplifiers: LMV324, TL074, and LM6134. The experimental results, as shown in Figure 16, indicate significant differences in processing speed and temperature stability among the selected op-amps. After multiple experiments, we determined that the TL074 operational amplifier provided the fastest processing speed within the permissible temperature range. Consequently, TL074 was chosen for signal processing in the final hardware implementation.

The signal attenuation results are shown as the CH3 (purple curve) in Figure 17. The oscilloscope results in Figure 17 represent the process of attenuating the input signal, exemplified by the positive half-cycle (the negative half-cycle yields similar results). In Figure 17, CH1 indicates the input signal, which, after passing through the attenuation system, becomes the output signal in CH3. However, both the experimental results and the simulation show a spiking phenomenon during signal processing. This indicates that this method is suboptimal. Therefore, to improve the attenuation system, this research opts to use a clipper circuit instead of a switch circuit. Before applying the clipping circuit to the attenuation system, it is essential to first design and analyze it. Unlike the previously discussed switch circuit, the clipping circuit is not as straightforward and requires careful consideration of electronic component selection to minimize signal distortion. Through theoretical design and software analysis, the component matching for the clipping circuit can be summarized as shown in Table 3. Based on the analysis results in Table 3, we constructed the hardware for the attenuation circuit system using the well-matched operational amplifier OPA810 and diode 1N914 to build a precision rectifier for clipping noise sources. The optimized output results of the attenuation circuit are illustrated in Figure 18. We used a signal generator to produce a signal of 3sin(2π3kt)V, which corresponds to a noise level of approximately 148 dB. This signal was input into the attenuation circuit, as shown in CH1 (yellow curve) in Figure 18. Under the operation of the attenuation circuit, the signal in CH1 was successfully attenuated to the output signal in CH2 (blue curve), with CH3 representing the audio threshold voltage (purple line). Signals exceeding the threshold voltage can cause harm to humans. Therefore, these exceeding signals are directed to the attenuation circuit, while signals below the threshold are not processed. Figure 18 shows that signals exceeding the threshold voltage were attenuated, reducing the original signal of 3sin(2π3kt)V to 1.14sin(2π3kt)V. The attenuated output signal corresponds to 57.1 dB, demonstrating the effectiveness of our designed attenuation circuit.

Since the clipping circuit in Figure 18 demonstrates effective signal clipping, we employed a similar approach for signal processing in the design of the amplification circuit. The amplification circuit features an adjustable gain setting to accommodate varying hearing abilities, enhancing user comfort. The signal output results are illustrated in Figure 19. In Figure 19, the CH1 (yellow curve) illustrates that the input signal is 690sin(2π5kt) mV, with a signal energy of approximately 34.6 dB, which is too faint to be easily heard. However, after processing through the amplification circuit, the originally insufficient signal is amplified to 690sin(2π5kt) mV, resulting in a signal energy of about 50 dB. This amplification corresponds to normal conversation levels, improving speech intelligibility. For further noise reduction, this study employs a fourth-order Butterworth filter in the bandpass filter circuit. The Butterworth filter was chosen for its smooth frequency response in the passband, maintaining voice volume without additional computation. The performance test results with different input signal frequencies are displayed in Figure 20. The designed fourth-order Butterworth filter has a passband range between 1000 Hz and 3000 Hz. As shown in Figure 20, within this range, the output amplitude closely approximates the input signal. At the center frequency of 2000 Hz, the amplitude remains nearly equal to the original input (Figure 20g). Conversely, when the signal frequency exceeds the 3000 Hz cutoff, the amplitude experiences increase attenuation, effectively suppressing unwanted noise signals. Moreover, the Bode plot in Figure 21 also demonstrates the effectiveness of the circuit. The circuit exhibits a bandpass characteristic in the frequency range of 1 kHz to 3 kHz. In Figure 22a,d, we have employed the fast Fourier transform to illustrate the attenuation characteristics beyond the 1 kHz to 3 kHz range, further verifying the circuit’s excellent performance. These results confirm the Butterworth filter’s effectiveness in removing non-speech signals, making it a crucial component in the overall noise reduction system.

This study bridges the gap between software simulation and hardware implementation in AANC systems by optimizing system parameters and selecting suitable hardware components. The experimental findings highlight the importance of parameter tuning, demonstrating that a system order of 30 stages and a step size of 10⁻³ yield the best noise reduction results. Additionally, the selection of the TL074 operational amplifier ensures optimal signal processing performance. Moreover, the implementation of a clipping circuit in the attenuation system and the use of an adjustable amplification circuit with a fourth-order Butterworth filter significantly enhance noise reduction efficiency. These insights contribute to the advancement of AANC systems, offering practical guidelines for future noise control circuit designs.

3.3. Comparison

ANC is currently recognized as the most effective method for eliminating low-frequency noise and can be implemented across various scenarios using different architectural designs. In this section, we compare our approach with recent studies. Paper [22] demonstrated a maximum noise reduction of 8.6 dB at 747 Hz, achieving an average reduction of 3.7 dB in a vehicle, with an effective noise suppression bandwidth of up to 1 kHz. However, mitigating high-frequency noise requires deploying a large number of monitoring microphones. Paper [23] proposed a cabin noise control method, which achieved a maximum processing bandwidth of 250 Hz, with noise attenuation exceeding 20 dB at 50 Hz and 100 Hz. However, its effectiveness diminished in higher frequency ranges, providing only ~4 dB attenuation at 250 Hz and even poorer performance at higher frequencies. Paper [24] introduced a noise control method for a free-field sound environment, achieving an average noise reduction of 5 dB within a 33° sector area at 100 Hz, 200 Hz, and 300 Hz. However, it exhibited limited tracking capabilities for mid- and high-frequency noise, with no noticeable reduction above 500 Hz. Paper [25] combined vibration and acoustic signals to compensate for ANC limitations between 100 Hz and 500 Hz, achieving an overall noise reduction of approximately 3.7 dB. However, this approach is highly sensitive to system latency, losing effectiveness if additional latency exceeds 20 ms. Paper [26] developed an ANC headrest system targeting a single 200 Hz frequency, achieving a 20 dB reduction. However, its evaluation was conducted under semi-anechoic conditions, neglecting real-world reflections within a cabin environment. Paper [27] proposed a feedback ANC system for tire-road noise suppression, achieving over 10 dB attenuation within 2 s. While effective for noise above 50 Hz, its feedback limitations prevent wideband noise suppression. Among these studies, paper [27] presents results most comparable to our work. However, to compensate for the limitations of AANC in high-frequency noise reduction, we introduce ABCC. As shown in Table 3, the OPA810 component configuration effectively handles high-power noise with minimal error. Additionally, a speech amplification system is integrated to enhance external voice reception in extreme noise conditions, ensuring clear voice frequency recording with adaptive magnification adjustments. The comparison with other methods is shown in

Table 4. Method comparison.

	Proposed Methods		Paper [22]	Paper [23]	Paper [24]	Paper [25]	Paper [26]	Paper [27]
	AANC	ABCC
Consider the second path impact	Yes	No	No	No	No	Yes	No	Yes
Maximum analysis frequency band	2 kHz	8 kHz	1 kHz	250 Hz	100 Hz, 200 Hz, 300 Hz, 400 Hz, 500 Hz	70–85 Hz, 100–500 Hz	200 Hz	300 Hz
Average noise reduction	10 dB	Attenuation ratio 1/10	3.7 dB	None	5 dB	3.7 dB	20 dB	10 dB
Maximum noise reduction	21.8 dB	Attenuation ratio 1/10	In 747 Hz, noise reduction 8.6 dB	In 50 Hz, noise reduction 23 dB	5 dB	3.7 dB	20 dB	30 dB

.

The proposed HANC system achieves stable noise suppression of 21.8 dB. Figure 23a illustrates that the complete audio duration of an artillery firing event is 2.7–3.15 s. As shown in the spectral analysis in Figure 23b, AANC reduces noise by 10–20 dB below 2 kHz. To maintain consistency with real-world conditions, no additional filtering was applied to the recorded artillery sounds. Figure 23b also includes frequency components above 2 kHz, as high-frequency energy is generated at the moment of firing. While ANC performs optimally in the low-frequency range, its primary function in high-frequency regions is to maintain system stability, providing 5–10 dB noise reduction in certain high-frequency bands.

4. Conclusions and Future Work

Mitigating the harmful effects of impact low-frequency noise on personnel is the primary motivation of this research. To address this, we developed an audio balancing control system integrating an AANC system and an ABCC system. The AANC system employs adaptive filtering to minimize external impact noise, while the ABCC system processes excessive noise and speech signals for improved communication. Through simulations and experiments, we optimized adaptive control parameters within the AANC system to enhance noise reduction. The ABCC system not only attenuates harmful noise to protect hearing, but also amplifies low-volume speech for clarity. Additionally, discrepancies in electronic component matching and circuit signal outputs are underexplored in the existing literature. This study bridges that gap by consolidating design principles, analysis, and empirical hardware testing, providing a valuable reference for future research. We successfully implemented the AANC system using the FXLMS algorithm, generating an inverse-phase signal to counteract noise effectively. MATLAB simulations and hardware tests confirmed its effectiveness. Given the risks of prolonged exposure to loud noise, we also developed a protective attenuation circuit to mitigate excessively high volumes, enhancing user safety. This research advances noise control technology and contributes to future innovations in hearing protection for noisy environments.

While this study has successfully demonstrated the feasibility of an AANC system for mitigating low-frequency impulsive noise, several areas remain for further investigation. Future work will focus on enhancing the real-time adaptability of the system by integrating machine learning algorithms to dynamically adjust noise cancellation parameters based on environmental variations. Additionally, expanding the system’s application to broader real-world scenarios, such as military training grounds, industrial machinery environments, and in-vehicle active noise control for electric vehicles, will be explored. Further optimization of the feedback ANC architecture and secondary path modeling will be conducted to improve noise reduction efficiency in non-stationary noise environments. Moreover, the system’s hardware will be refined to minimize power consumption and computational overhead, ensuring suitability for portable and embedded applications. Finally, additional human factor studies will be conducted to assess the long-term effects of noise reduction on auditory perception, user comfort, and hearing protection in high-noise environments.