Stacking Ensemble Learning-Assisted Simulation of Plasma-Catalyzed CO2 Reforming of Methane
Abstract
1. Introduction
2. Methodology
2.1. The Pulsed Discharge Plasma-Catalytic Kinetics Model
2.2. Stacking Ensemble Model
2.3. Data Preprocessing
2.4. Evaluation Metrics
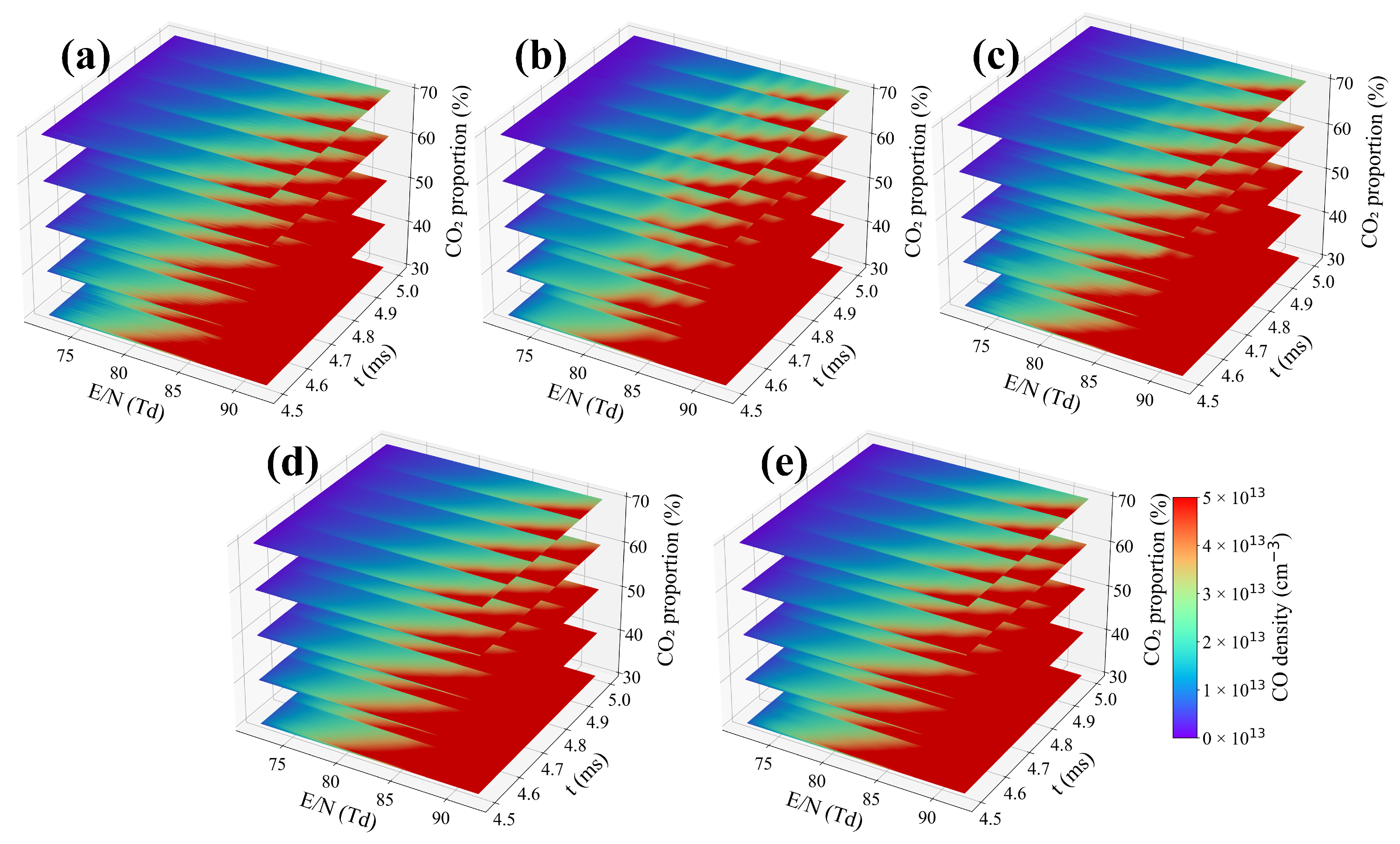
3. Results
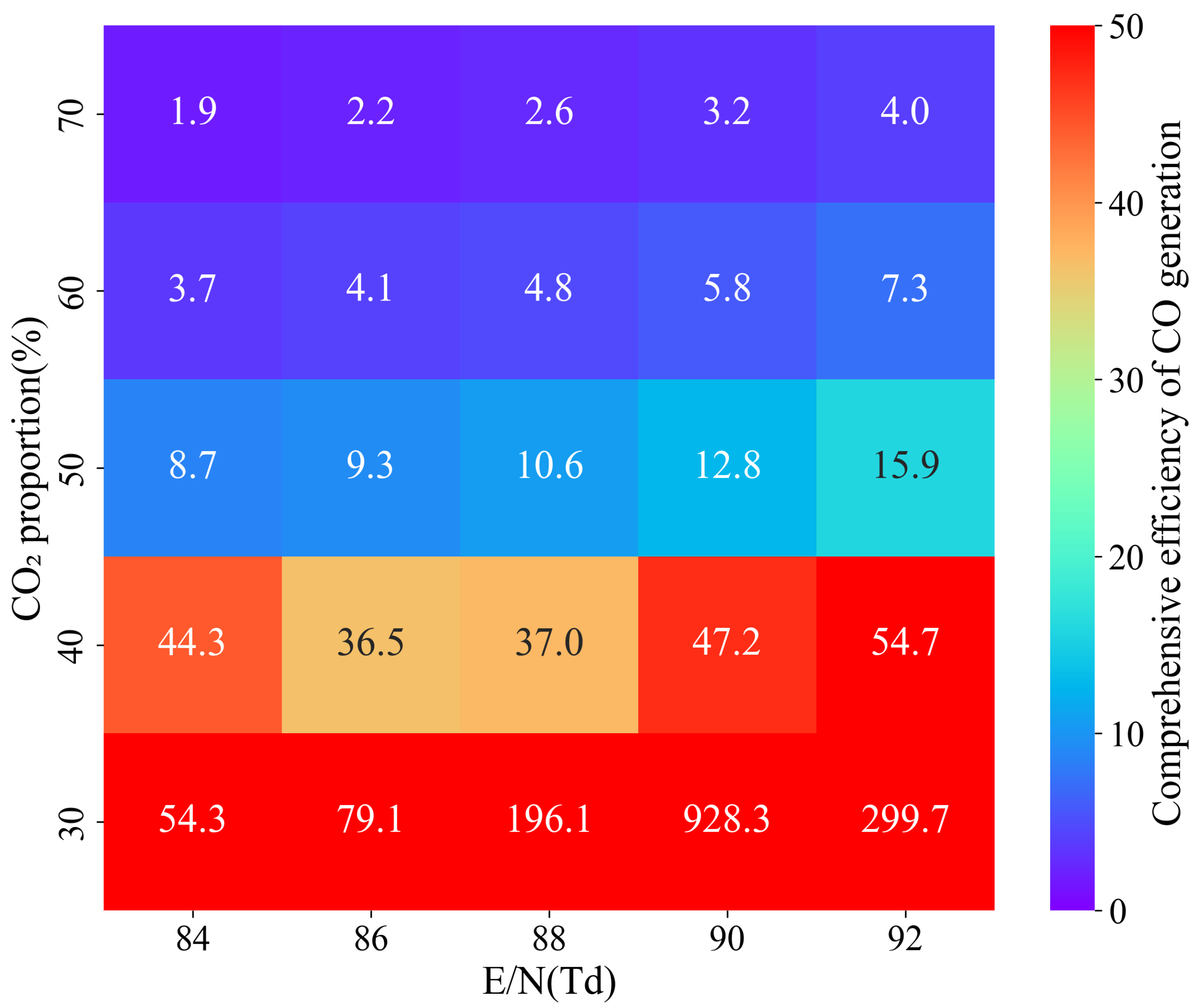
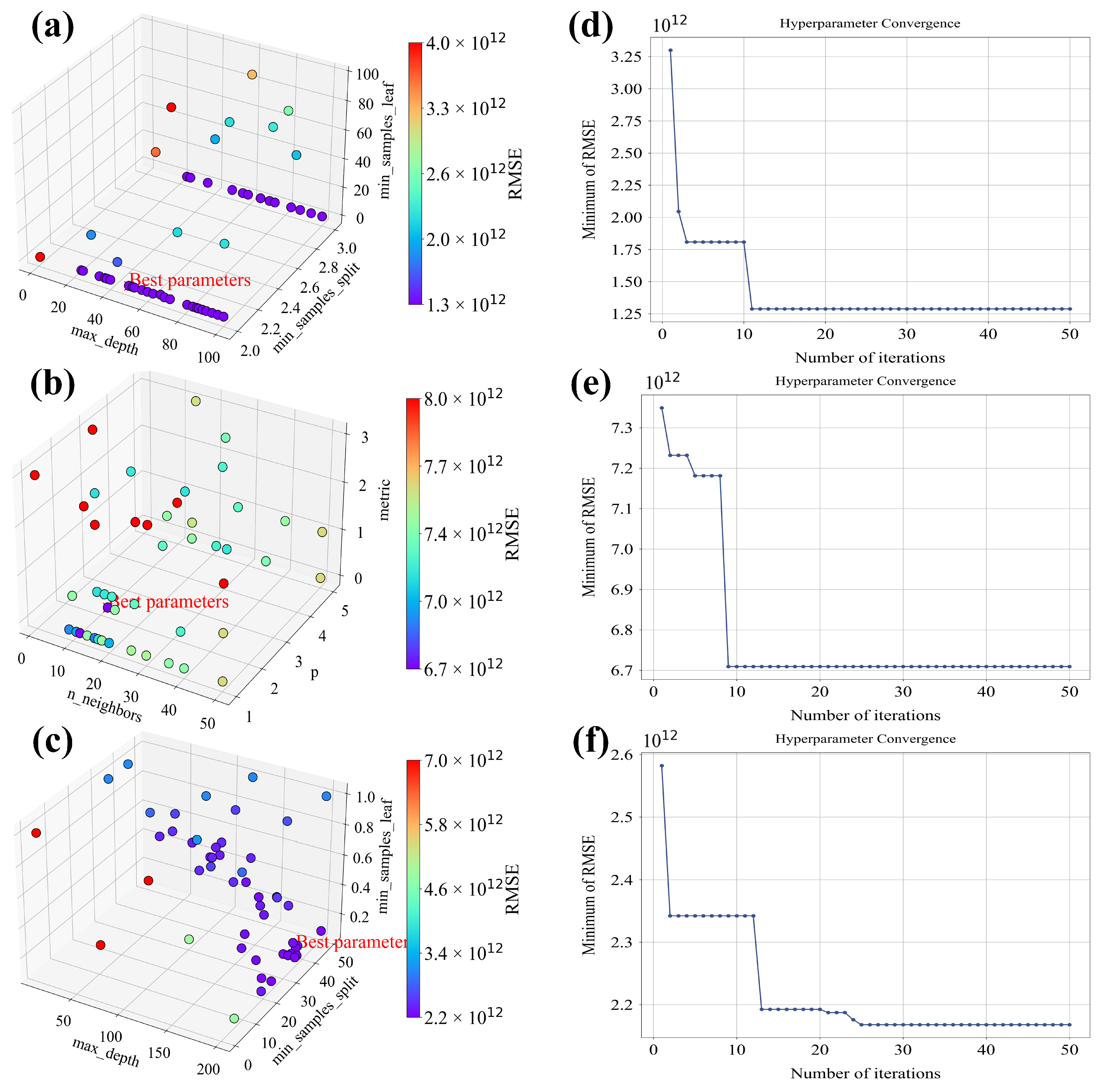
3.1. Hyperparameter Tuning with Bayesian Optimization
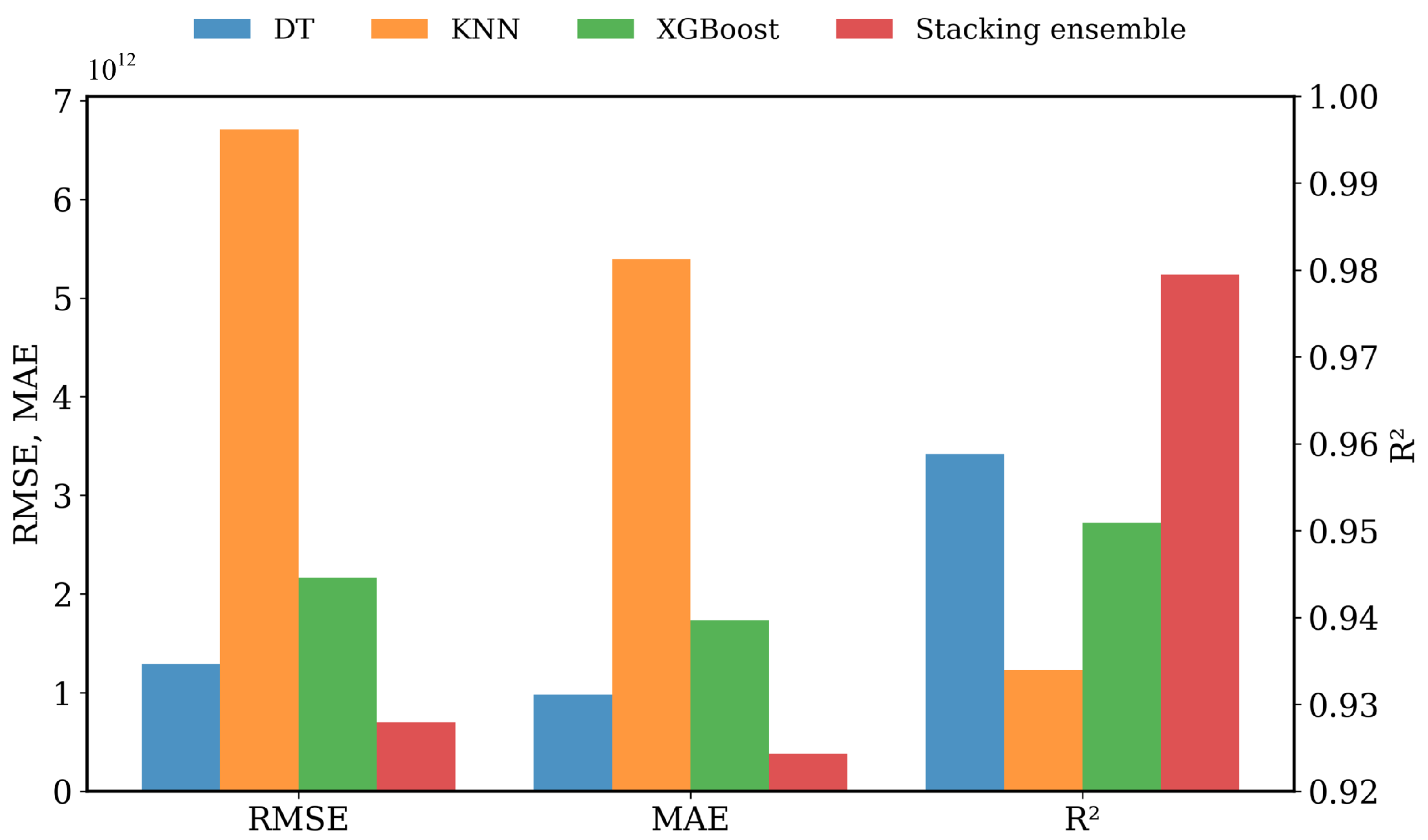
3.2. Performance of the Stacking Ensemble Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Dou, L.; Zhou, R.; Sun, H.; Fan, Z.; Zhang, C.; Ostrikov, K.K.; Shao, T. Liquid-phase methane bubble plasma discharge for heavy oil processing: Insights into free radicals-induced hydrogenation. Energy Convers. Manag. 2021, 250, 114896. [Google Scholar] [CrossRef]
- Osorio-Tejada, J.; van’t Veer, K.; Long, N.V.D.; Tran, N.N.; Fulcheri, L.; Patil, B.S.; Bogaerts, A.; Hessel, V. Sustainability analysis of methane-to-hydrogen-to-ammonia conversion by integration of high-temperature plasma and non-thermal plasma processes. Energy Convers. Manag. 2022, 269, 116095. [Google Scholar] [CrossRef]
- Liu, L.; Yang, K.; Li, L.; Liu, W.; Yuan, H.; Han, Y.; Zhang, E.; Zheng, Y.; Jia, Y. The aeration and dredging stimulate the reduction of pollution and carbon emissions in a sediment microcosm study. Sci. Rep. 2024, 14, 26172. [Google Scholar] [CrossRef]
- Gao, Y.; Dou, L.; Zhang, S.; Zong, L.; Pan, J.; Hu, X.; Sun, H.; Ostrikov, K.K.; Shao, T. Coupling bimetallic Ni-Fe catalysts and nanosecond pulsed plasma for synergistic low-temperature CO2 methanation. Chem. Eng. J. 2021, 420, 127693. [Google Scholar] [CrossRef]
- Du, J.; Zong, L.; Zhang, S.; Gao, Y.; Dou, L.; Pan, J.; Shao, T. Numerical investigation on the heterogeneous pulsed dielectric barrier discharge plasma catalysis for CO2 hydrogenation at atmospheric pressure: Effects of Ni and Cu catalysts on the selectivity conversions to CH4 and CH3OH. Plasma Process. Polym. 2022, 19, 2100111. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Y.; Zhang, S.; Sun, H.; Li, J.; Shao, T. Nanosecond pulsed plasma assisted dry reforming of CH4: The effect of plasma operating parameters. Appl. Energy 2019, 243, 132–144. [Google Scholar] [CrossRef]
- Alhemeiri, N.; Kosca, L.; Gacesa, M.; Polychronopoulou, K. Advancing in-situ resource utilization for earth and space applications through plasma CO2 catalysis. J. CO2 Util. 2024, 85, 102887. [Google Scholar] [CrossRef]
- Pan, J.; Li, L. Particle densities of the pulsed dielectric barrier discharges in nitrogen at atmospheric pressure. J. Phys. D Appl. Phys. 2015, 48, 055204. [Google Scholar] [CrossRef]
- Vakili, R.; Gholami, R.; Stere, C.E.; Chansai, S.; Chen, H.; Holmes, S.M.; Jiao, Y.; Hardacre, C.; Fan, X. Plasma-assisted catalytic dry reforming of methane (DRM) over metal-organic frameworks (MOFs)-based catalysts. Appl. Catal. B Environ. 2020, 260, 118195. [Google Scholar] [CrossRef]
- Khoja, A.H.; Tahir, M.; Amin, N.A.S. Recent developments in non-thermal catalytic DBD plasma reactor for dry reforming of methane. Energy Convers. Manag. 2019, 183, 529–560. [Google Scholar] [CrossRef]
- Mathews, A.; Francisquez, M.; Hughes, J.W.; Hatch, D.R.; Zhu, B.; Rogers, B.N. Uncovering turbulent plasma dynamics via deep learning from partial observations. Phys. Rev. E 2021, 104, 025205. [Google Scholar] [CrossRef] [PubMed]
- Zhong, L.; Gu, Q.; Wu, B. Deep learning for thermal plasma simulation: Solving 1-D arc model as an example. Comput. Phys. Commun. 2020, 257, 107496. [Google Scholar] [CrossRef]
- Zhu, Y.; Bo, Y.; Chen, X.; Wu, Y. Tailoring electric field signals of nonequilibrium discharges by the deep learning method and physical corrections. Plasma Process. Polym. 2022, 19, e2100155. [Google Scholar] [CrossRef]
- Li, H.; Fu, Y.; Li, J.; Wang, Z. Machine learning of turbulent transport in fusion plasmas with neural network. Plasma Sci. Technol. 2021, 23, 115102. [Google Scholar] [CrossRef]
- Pan, J.; Liu, Y.; Zhang, S.; Hu, X.; Liu, Y.; Shao, T. Deep learning-assisted pulsed discharge plasma catalysis modeling. Energy Convers. Manag. 2023, 277, 116620. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, S.; Hu, X.; Shao, T. Dielectric Barrier Discharge Plasma-Enabled Energy Conversion Under Multiple Operating Parameters: Machine Learning Optimization. Plasma Chem. Plasma Process. 2024, 44, 667–685. [Google Scholar] [CrossRef]
- Cai, Y.; Mei, D.; Chen, Y.; Bogaerts, A.; Tu, X. Machine learning-driven optimization of plasma-catalytic dry reforming of methane. J. Energy Chem. 2024, 96, 153–163. [Google Scholar] [CrossRef]
- Basha, S.S.; Vinakota, S.K.; Pulabaigari, V.; Mukherjee, S.; Dubey, S.R. Autotune: Automatically tuning convolutional neural networks for improved transfer learning. Neural Netw. 2021, 133, 112–122. [Google Scholar] [CrossRef]
- Mehrjerd, A.; Dehghani, T.; Jajroudi, M.; Eslami, S.; Rezaei, H.; Ghaebi, N.K. Ensemble machine learning models for sperm quality evaluation concerning success rate of clinical pregnancy in assisted reproductive techniques. Sci. Rep. 2024, 14, 24283. [Google Scholar] [CrossRef]
- Du, J.; Yang, S.; Zeng, Y.; Ye, C.; Chang, X.; Wu, S. Visualization obesity risk prediction system based on machine learning. Sci. Rep. 2024, 14, 22424. [Google Scholar] [CrossRef]
- Han, H.J.; Ji, H.; Choi, J.E.; Chung, Y.G.; Kim, H.; Choi, C.W.; Kim, K.; Jung, Y.H. Development of a machine learning model to identify intraventricular hemorrhage using time-series analysis in preterm infants. Sci. Rep. 2024, 14, 23740. [Google Scholar] [CrossRef]
- Alkhammash, A. Intelligence analysis of membrane distillation via machine learning models for pharmaceutical separation. Sci. Rep. 2024, 14, 22876. [Google Scholar] [CrossRef]
- Chen, H.; Zheng, Z.; Yang, C.; Tan, T.; Jiang, Y.; Xue, W. Machine learning based intratumor heterogeneity signature for predicting prognosis and immunotherapy benefit in stomach adenocarcinoma. Sci. Rep. 2024, 14, 23328. [Google Scholar] [CrossRef] [PubMed]
- Martinez-de Pison, F.; Gonzalez-Sendino, R.; Aldama, A.; Ferreiro-Cabello, J.; Fraile-Garcia, E. Hybrid methodology based on Bayesian optimization and GA-PARSIMONY to search for parsimony models by combining hyperparameter optimization and feature selection. Neurocomputing 2019, 354, 20–26. [Google Scholar] [CrossRef]
- Fernández-Sánchez, D.; Garrido-Merchán, E.C.; Hernández-Lobato, D. Improved max-value entropy search for multi-objective bayesian optimization with constraints. Neurocomputing 2023, 546, 126290. [Google Scholar] [CrossRef]
- Garrido-Merchán, E.C.; Hernández-Lobato, D. Predictive entropy search for multi-objective bayesian optimization with constraints. Neurocomputing 2019, 361, 50–68. [Google Scholar] [CrossRef]
- Phan-Trong, D.; Tran-The, H.; Gupta, S. NeuralBO: A black-box optimization algorithm using deep neural networks. Neurocomputing 2023, 559, 126776. [Google Scholar] [CrossRef]
- Mihaljević, B.; Bielza, C.; Larrañaga, P. Bayesian networks for interpretable machine learning and optimization. Neurocomputing 2021, 456, 648–665. [Google Scholar] [CrossRef]
- Nobile, M.S.; Cazzaniga, P.; Ramazzotti, D. Investigating the performance of multi-objective optimization when learning Bayesian Networks. Neurocomputing 2021, 461, 281–291. [Google Scholar] [CrossRef]
- Garrido-Merchán, E.C.; Hernández-Lobato, D. Dealing with categorical and integer-valued variables in bayesian optimization with gaussian processes. Neurocomputing 2020, 380, 20–35. [Google Scholar] [CrossRef]
- Song, C.; Ma, Y.; Xu, Y.; Chen, H. Multi-population evolutionary neural architecture search with stacked generalization. Neurocomputing 2024, 587, 127664. [Google Scholar] [CrossRef]
- Park, U.; Kang, Y.; Lee, H.; Yun, S. A stacking heterogeneous ensemble learning method for the prediction of building construction project costs. Appl. Sci. 2022, 12, 9729. [Google Scholar] [CrossRef]
- Huang, H.; Zhu, Q.; Zhu, X.; Zhang, J. An Adaptive, Data-Driven Stacking Ensemble Learning Framework for the Short-Term Forecasting of Renewable Energy Generation. Energies 2023, 16, 1963. [Google Scholar] [CrossRef]
- Sun, J.; Wu, S.; Zhang, H.; Zhang, X.; Wang, T. Based on multi-algorithm hybrid method to predict the slope safety factor–stacking ensemble learning with bayesian optimization. J. Comput. Sci. 2022, 59, 101587. [Google Scholar] [CrossRef]
- Shu, J.; Yu, H.; Liu, G.; Yang, H.; Chen, Y.; Duan, Y. BO-Stacking: A novel shear strength prediction model of RC beams with stirrups based on Bayesian Optimization and model stacking. Structures 2023, 58, 105593. [Google Scholar] [CrossRef]
- Shams, R.; Alimohammadi, S.; Yazdi, J. Optimized stacking, a new method for constructing ensemble surrogate models applied to DNAPL-contaminated aquifer remediation. J. Contam. Hydrol. 2021, 243, 103914. [Google Scholar] [CrossRef]
- Djarum, D.H.; Ahmad, Z.; Zhang, J. Reduced Bayesian Optimized Stacked Regressor (RBOSR): A highly efficient stacked approach for improved air pollution prediction. Appl. Soft Comput. 2023, 144, 110466. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Z.; Qu, Z.; Bell, A. Remaining useful life prediction for a catenary, utilizing Bayesian optimization of stacking. Electronics 2023, 12, 1744. [Google Scholar] [CrossRef]
- Cheng, H.; Ma, M.; Zhang, Y.; Liu, D.; Lu, X. The plasma enhanced surface reactions in a packed bed dielectric barrier discharge reactor. J. Phys. D Appl. Phys. 2020, 53, 144001. [Google Scholar] [CrossRef]
- Bai, C.; Wang, L.; Li, L.; Dong, X.; Xiao, Q.; Liu, Z.; Sun, J.; Pan, J. Numerical investigation on the CH4/CO2 nanosecond pulsed dielectric barrier discharge plasma at atmospheric pressure. AIP Adv. 2019, 9, 035023. [Google Scholar] [CrossRef]
- Cheng, H.; Fan, J.; Zhang, Y.; Liu, D.; Ostrikov, K.K. Nanosecond pulse plasma dry reforming of natural gas. Catal. Today 2020, 351, 103–112. [Google Scholar] [CrossRef]
- Li, S.; Bai, C.; Chen, X.; Meng, W.; Li, L.; Pan, J. Numerical investigation on plasma assisted ignition of methane/air mixture excited by the synergistic nanosecond repetitive pulsed and DC discharge. J. Phys. D Appl. Phys. 2020, 54, 015203. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Huang, B.; Dai, D.; Murphy, A.B.; Shao, T. Temporal evolution of electron energy distribution function and its correlation with hydrogen radical generation in atmospheric-pressure methane needle–plane discharge plasmas. J. Phys. D Appl. Phys. 2020, 54, 095202. [Google Scholar] [CrossRef]
- Hong, J.; Pancheshnyi, S.; Tam, E.; Lowke, J.J.; Prawer, S.; Murphy, A.B. Kinetic modelling of NH3 production in N2–H2 non-equilibrium atmospheric-pressure plasma catalysis. J. Phys. D Appl. Phys. 2017, 50, 154005. [Google Scholar] [CrossRef]
- Carrasco, E.; Jiménez-Redondo, M.; Tanarro, I.; Herrero, V.J. Neutral and ion chemistry in low pressure dc plasmas of H2/N2 mixtures: Routes for the efficient production of NH3 and NH4+. Phys. Chem. Chem. Phys. 2011, 13, 19561–19572. [Google Scholar] [CrossRef]
- van ’t Veer, K.; Reniers, F.; Bogaerts, A. Zero-dimensional modeling of unpacked and packed bed dielectric barrier discharges: The role of vibrational kinetics in ammonia synthesis. Plasma Sources Sci. Technol. 2020, 29, 045020. [Google Scholar] [CrossRef]
- Pan, J.; Chen, T.; Gao, Y.; Liu, Y.; Zhang, S.; Liu, Y.; Shao, T. Numerical modeling and mechanism investigation of nanosecond-pulsed DBD plasma-catalytic CH4 dry reforming. J. Phys. D Appl. Phys. 2021, 55, 035202. [Google Scholar] [CrossRef]
- Kardani, N.; Zhou, A.; Nazem, M.; Shen, S.L. Improved prediction of slope stability using a hybrid stacking ensemble method based on finite element analysis and field data. J. Rock Mech. Geotech. Eng. 2021, 13, 188–201. [Google Scholar] [CrossRef]


| Researcher | Reactant Gas | Plasma Generation Process | Conclusions |
|---|---|---|---|
| Xiaoling Wang [6] | CH4, CO2 | DBD | The short pulse rise/fall time can significantly improve the energy efficiency of CH4 and CO2. |
| Naama Alhemeiri [7] | CH4, CO2, H2O | DBD, microwave, sliding arc | Plasma catalysis has potential in CO2 conversion, where performance can be improved by optimizing catalysts and diagnostic methods. |
| Reza Vakilia [9] | CH4, CO2 | DBD | MOF-based catalysts significantly improve DRM efficiency by optimizing plasma catalyst synergy. |
| Asif Hussain Khoja [10] | CH4, CO2 | DBD | DBD has advantages in DRM; optimizing catalyst and reactor configurations can improve performance. |
| Type | Species |
|---|---|
| Molecules | , , , , , , , , , , CO, , CH2O, CH3OH, CH3CHO, CH2CO |
| Excited species | (), (), (), (), (), (), (), CO(), CO(), CO(), (a), (b), O(1D), O(1S), (), (), () |
| Radicals | , , CH, C, , , , , H, O, OH, CHO, CH2OH, CH3O, C2HO, CH3CO, CH2CHO, , , |
| Electron and ions | e, , , , , , , , , , , , , , , , , , , , , |
| Surface species | Surf, (s), CO(s), H(s), O(s), H2O(s), OH(s), C(s), (s), (s), CH(s), COOH(s), CH3OH(s), CH2OH(s), CHOH(s), COH(s), CH3O(s), CH2O(s), CHO(s) |
| Model | Hyperparameters | BO Range | Optimized Value |
|---|---|---|---|
| DT | max depth | 1–100 | 75 |
| p | 1–5 | 2 | |
| min samples leaf | 1–100 | 1 | |
| KNN | n neighbors | 1–50 | 12 |
| min samples split | 2–3 | 2 | |
| metric | Euclidean, Manhattan, Chebyshev, Minkowski | Euclidean | |
| XGBoost | learning rate | 0.01–1 | 0.1 |
| n estimators | 10–200 | 179 | |
| max depth | 1–50 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Qiao, X.; Zhang, C.; Li, B.; Li, L.; Li, G.; Qin, S. Stacking Ensemble Learning-Assisted Simulation of Plasma-Catalyzed CO2 Reforming of Methane. Electronics 2025, 14, 1329. https://doi.org/10.3390/electronics14071329
Pan J, Qiao X, Zhang C, Li B, Li L, Li G, Qin S. Stacking Ensemble Learning-Assisted Simulation of Plasma-Catalyzed CO2 Reforming of Methane. Electronics. 2025; 14(7):1329. https://doi.org/10.3390/electronics14071329
Chicago/Turabian StylePan, Jie, Xin Qiao, Chunlei Zhang, Bin Li, Lun Li, Guomeng Li, and Shaohua Qin. 2025. "Stacking Ensemble Learning-Assisted Simulation of Plasma-Catalyzed CO2 Reforming of Methane" Electronics 14, no. 7: 1329. https://doi.org/10.3390/electronics14071329
APA StylePan, J., Qiao, X., Zhang, C., Li, B., Li, L., Li, G., & Qin, S. (2025). Stacking Ensemble Learning-Assisted Simulation of Plasma-Catalyzed CO2 Reforming of Methane. Electronics, 14(7), 1329. https://doi.org/10.3390/electronics14071329






