Serving Cluster Design and Hybrid Precoding for Cell-Free-Assisted LEO Satellite Communications with Nonlinear Power Amplifiers
Abstract
1. Introduction
- We establish a comprehensive downlink transmission model for CF-mMIMO-assisted LEO SATCOM systems under the impact of NPAs. To quantify the distortion effects, the NPAs are modeled as finite-order memoryless polynomials, explicitly characterizing their in-band distortion. The formulation provides a tractable framework for analyzing and mitigating NPA-induced signal impairments.
- A user-centric SC strategy is proposed to optimize satellite–ground collaboration in CF-mMIMO LEO systems, where multiple satellites cooperatively serve multiple GUs. The strategy adaptively selects serving satellites for each GU by jointly considering the elevation angle and channel fading. Based on the proposed strategy, the link relationships between APs and GUs can be represented through a set of binary diagonal matrices, enabling low-complexity cluster management and resource allocation.
- A hybrid precoding problem for EE maximization is formulated by taking the product of tightly coupled analog and digital matrices as a single fully digital precoder. As for the fully digital precoding problem, we transform it into a linear programming problem by adopting an auxiliary variable and then use the WMMSE framework and a gradient descent method with Nesterov’s accelerated momentum to solve it. Additionally, we design the hybrid analog/digital precoders based on the principle of alternating minimization.
2. System Model
2.1. Channel Model
| Algorithm 1: Initial GU access and SC selection. |
|
2.2. Nonlinear PA Model
2.3. Downlink Transmission
2.4. Problem Formulation
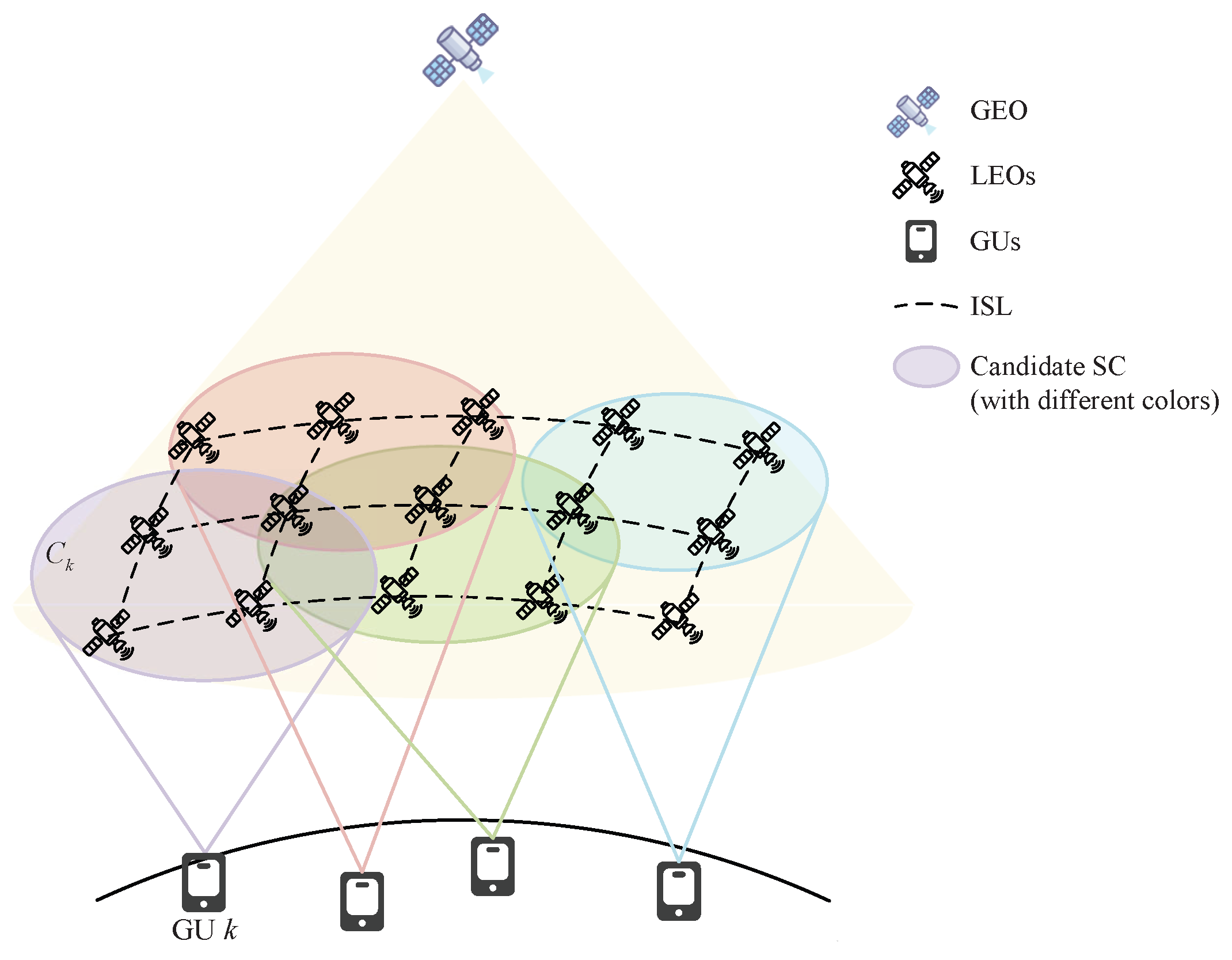
3. Cluster Formulation
- Step 1:
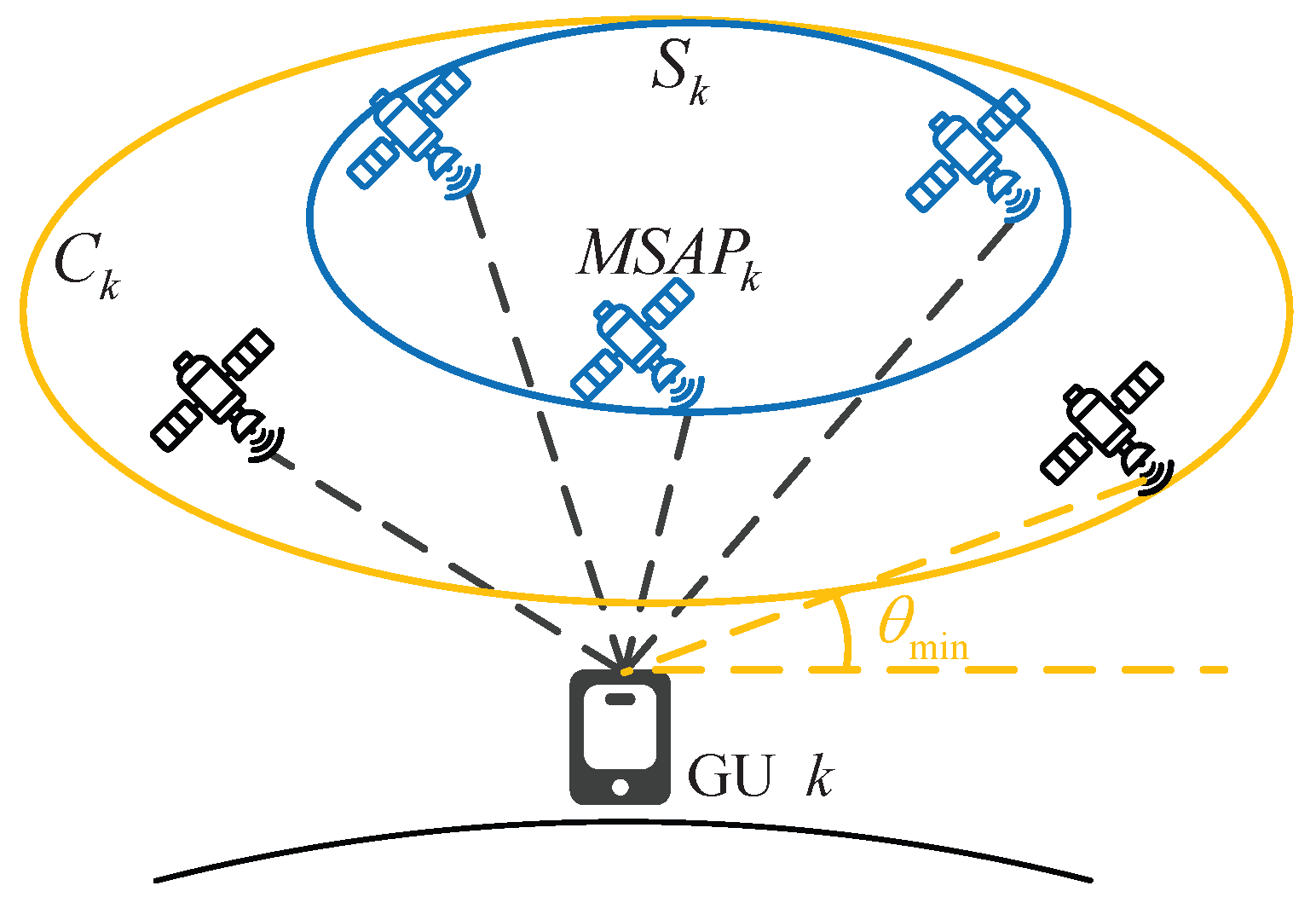
- According to the given minimum elevation angle , the candidate SCs are selected for each GU. The lth satellite is added to the kth GU’s set of candidate satellites when the elevation angle of the lth satellite relative to the kth GU satisfies .
- Step 2:
- For the kth GU, sequentially traverse the satellites in the set , and select the satellite corresponding to the maximum value of as the candidate MSAP. Determine whether the satellite is idle or not. If it is idle, then it is selected as the MSAP for the kth GU and denoted as . If it is not idle, traverse in order of value until is selected among the idle satellites. The K MSAPs of the K GUs are selected sequentially by this step, and the MSAPs are removed from the sets of candidate satellites and added to the sets of serving clusters.
- Step 3:
- Choose other accessible satellites to serve the GUs together with MSAPs. In order to ensure rational allocation of resources, the GUs are traversed to select the service satellites sequentially. Each round of traversal sequentially adds a service satellite to the candidate set of K GUs to the service cluster of the GU. The criteria for adding is that the large-scale fading coefficient between the satellite and the GU is maximum and the satellite is idle. The selected satellite is removed from sets of candidate satellites after successful addition until all the satellites in the candidate cluster are selected for all GUs.
4. Energy Efficiency
4.1. Optimization of Energy Efficiency
| Algorithm 2: WMMSE-based precoding algorithm for EE maximization. |
|
4.2. Hybrid Precoding for the Partially Connected Architectures
4.2.1. Analog Precoder Design
4.2.2. Digital Precoder Design
5. Simulation Results and Analysis
5.1. Setup and Parameters
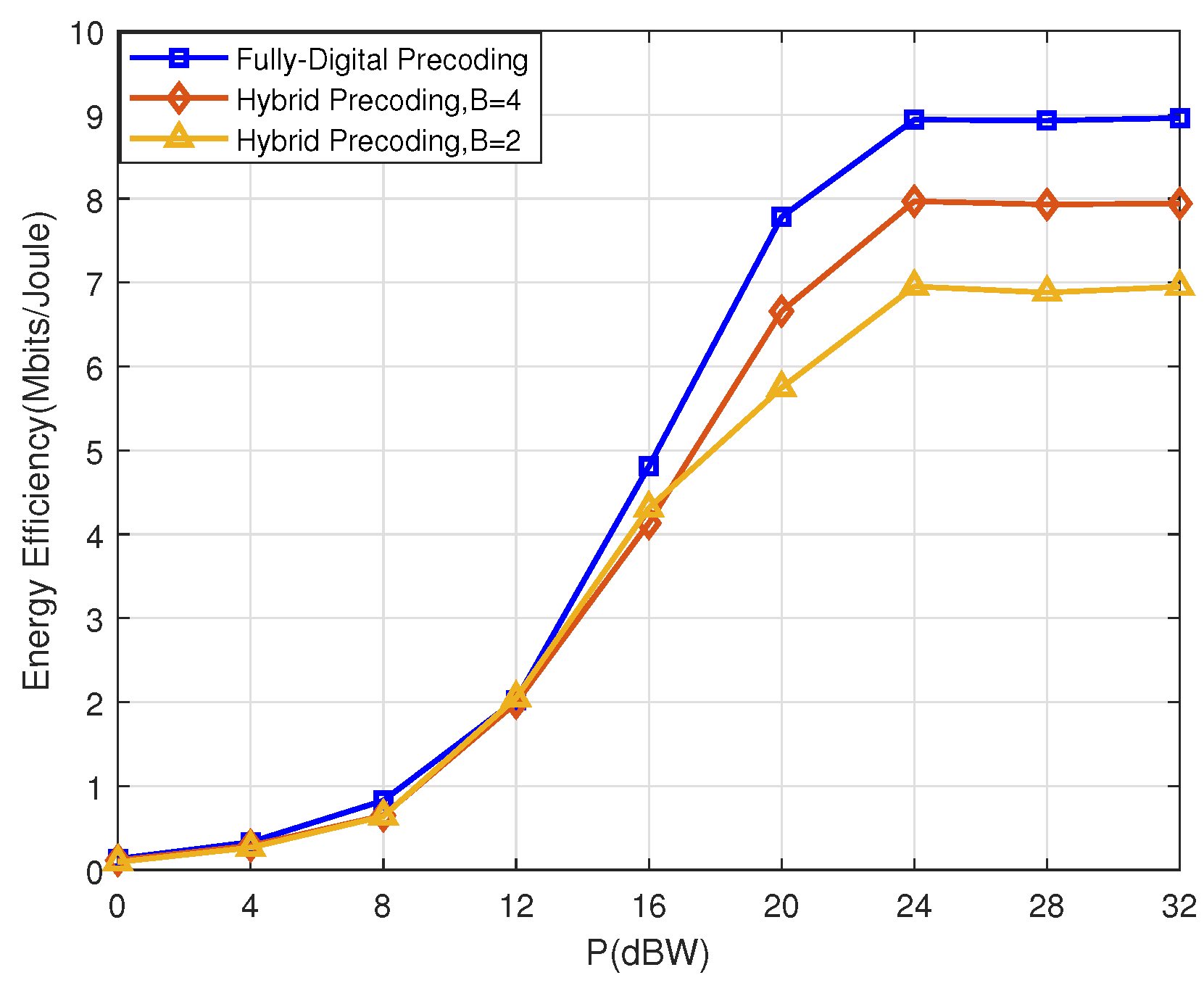
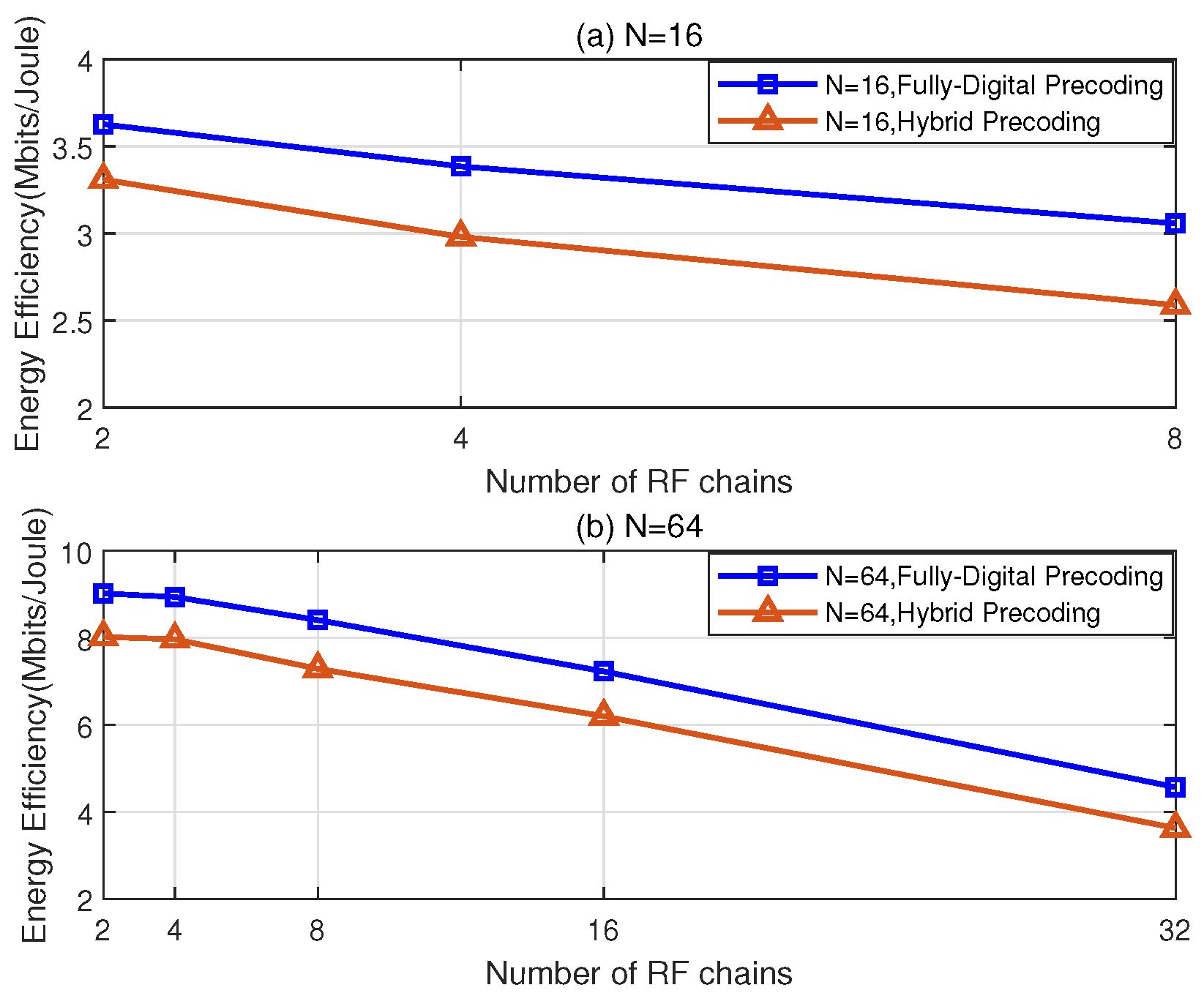
5.2. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Dakkak, M.R.; Riviello, D.G.; Guidotti, A.; Vanelli–Coralli, A. Federated Beamforming with Subarrayed Planar Arrays for B5G/6G LEO Non-Terrestrial Networks. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 01–06. [Google Scholar] [CrossRef]
- Abdelsadek, M.Y.; Yanikomeroglu, H.; Kurt, G.K. Future Ultra-Dense LEO Satellite Networks: A Cell-Free Massive MIMO Approach. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Virtual, 14–23 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, G.; Fernandez, R.; Gao, Y.; Tafazolli, R. Enhancement of Direct LEO Satellite-to-Smartphone Communications by Distributed Beamforming. IEEE Trans. Veh. Technol. 2024, 73, 11543–11555. [Google Scholar] [CrossRef]
- Riviello, D.G.; De Filippo, B.; Ahmad, B.; Guidotti, A.; Vanelli-Coralli, A. Location-based User Scheduling through Graph Coloring for Cell-Free MIMO NTN Systems. In Proceedings of the 2024 Joint European Conference on Networks and Communications & 6G Summit (EuCNC/6G Summit), Antwerp, Belgium, 3–6 June 2024; pp. 652–657. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Ashikhmin, A.; Yang, H.; Larsson, E.G.; Marzetta, T.L. Cell-Free Massive MIMO Versus Small Cells. IEEE Trans. Wirel. Commun. 2017, 16, 1834–1850. [Google Scholar] [CrossRef]
- Ammar, H.A.; Adve, R.; Shahbazpanahi, S.; Boudreau, G.; Srinivas, K.V. User-Centric Cell-Free Massive MIMO Networks: A Survey of Opportunities, Challenges and Solutions. IEEE Commun. Surv. Tutor. 2022, 24, 611–652. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Interdonato, G.; Larsson, E.G.; Caire, G.; Andrews, J.G. Ultradense Cell-Free Massive MIMO for 6G: Technical Overview and Open Questions. Proc. IEEE 2024, 112, 805–831. [Google Scholar] [CrossRef]
- Matthaiou, M.; Yurduseven, O.; Ngo, H.Q.; Morales-Jimenez, D.; Cotton, S.L.; Fusco, V.F. The Road to 6G: Ten Physical Layer Challenges for Communications Engineers. IEEE Commun. Mag. 2021, 59, 64–69. [Google Scholar] [CrossRef]
- Riera-Palou, F.; Femenias, G.; Caus, M.; Shaat, M.; García-Morales, J.; Pérez-Neira, A.I. Enhancing Cell-Free Massive MIMO networks through LEO Satellite Integration. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Nanjing, China, 29 March–1 April 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Riera-Palou, F.; Femenias, G.; Caus, M.; Shaat, M.; Pérez-Neira, A.I. Scalable Cell-Free Massive MIMO Networks with LEO Satellite Support. IEEE Access 2022, 10, 37557–37571. [Google Scholar] [CrossRef]
- Al-Hraishawi, H.; Rehman, J.u.; Chatzinotas, S. Quantum Optimization Algorithm for LEO Satellite Communications based on Cell-Free Massive MIMO. In Proceedings of the 2023 IEEE International Conference on Communications Workshops (ICC Workshops), Rome, Italy, 28 May–1 June 2023; pp. 1759–1764. [Google Scholar] [CrossRef]
- Humadi, K.; Kurt, G.K.; Yanikomeroglu, H. Distributed Massive MIMO System with Dynamic Clustering in LEO Satellite Networks. In Proceedings of the 2024 6th International Conference on Communications, Signal Processing, and Their Applications (ICCSPA), Istanbul, Turkiye, 8–11 July 2024; pp. 1–6. [Google Scholar] [CrossRef]
- You, L.; Qiang, X.; Li, K.X.; Tsinos, C.G.; Wang, W.; Gao, X.; Ottersten, B. Massive MIMO Hybrid Precoding for LEO Satellite Communications with Twin-Resolution Phase Shifters and Nonlinear Power Amplifiers. IEEE Trans. Commun. 2022, 70, 5543–5557. [Google Scholar] [CrossRef]
- Li, H.; Li, M.; Liu, Q. Hybrid Beamforming with Dynamic Subarrays and Low-Resolution PSs for mmWave MU-MISO Systems. IEEE Trans. Commun. 2020, 68, 602–614. [Google Scholar] [CrossRef]
- Vázquez, M.A.; Blanco, L.; Pérez-Neira, A.I. Hybrid Analog–Digital Transmit Beamforming for Spectrum Sharing Backhaul Networks. IEEE Trans. Signal Process. 2018, 66, 2273–2285. [Google Scholar] [CrossRef]
- Liu, Y.; Li, C.; Li, J.; Feng, L. Robust Energy-Efficient Hybrid Beamforming Design for Massive MIMO LEO Satellite Communication Systems. IEEE Access 2022, 10, 63085–63099. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, S.; Tao, M.; Huang, Q.; Tang, X. Multi-Satellite Cooperative Networks: Joint Hybrid Beamforming and User Scheduling Design. IEEE Trans. Wirel. Commun. 2024, 23, 7938–7952. [Google Scholar] [CrossRef]
- Ahmad, I.; Boukhedimi, I.; Nguyen, K.; Chan, T.; Karmokar, D.; Kodithuwakkuge, J.; Ramamurthy, B. On the performance of hybrid beamforming for massive-MIMO low earth orbit satellite systems. In Proceedings of the 39th International Communications Satellite Systems Conference (ICSSC 2022), Stresa, Italy, 18–21 October 2022; Volume 2022, pp. 186–191. [Google Scholar] [CrossRef]
- Wang, L.X.; Chen, Y.F. User Selection Algorithms and Hybrid Beamforming for Power Minimization in Multiuser Massive MIMO-OFDM LEO Satellite Communication Systems. In Proceedings of the 2024 10th International Conference on Applied System Innovation (ICASI), Kyoto, Japan, 17–21 April 2024; pp. 49–51. [Google Scholar] [CrossRef]
- Mollén, C.; Gustavsson, U.; Eriksson, T.; Larsson, E.G. Spatial Characteristics of Distortion Radiated From Antenna Arrays with Transceiver Nonlinearities. IEEE Trans. Wirel. Commun. 2018, 17, 6663–6679. [Google Scholar] [CrossRef]
- Moghadam, N.N.; Fodor, G.; Bengtsson, M.; Love, D.J. On the Energy Efficiency of MIMO Hybrid Beamforming for Millimeter-Wave Systems with Nonlinear Power Amplifiers. IEEE Trans. Wirel. Commun. 2018, 17, 7208–7221. [Google Scholar] [CrossRef]
- Wu, M.; Li, M.; Zhao, M.M.; Zhao, M. A WMMSE Approach to Distortion-Aware Beamforming Design for Millimeter-Wave Massive MIMO Downlink Communication. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Aghdam, S.R.; Jacobsson, S.; Eriksson, T. Distortion-Aware Linear Precoding for Millimeter-Wave Multiuser MISO Downlink. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Abdelsadek, M.Y.; Kurt, G.K.; Yanikomeroglu, H. Distributed Massive MIMO for LEO Satellite Networks. IEEE Open J. Commun. Soc. 2022, 3, 2162–2177. [Google Scholar] [CrossRef]
- You, L.; Li, K.X.; Wang, J.; Gao, X.; Xia, X.G.; Ottersten, B. Massive MIMO Transmission for LEO Satellite Communications. IEEE J. Sel. Areas Commun. 2020, 38, 1851–1865. [Google Scholar] [CrossRef]
- Benedetto, S.; Biglieri, E.; Daffara, R. Modeling and Performance Evaluation of Nonlinear Satellite Links-A Volterra Series Approach. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 494–507. [Google Scholar] [CrossRef]
- Schenk, T. Nonlinearities. In RF Imperfections in High-Rate Wireless Systems: Impact and Digital Compensation; Springer: Dordrecht, The Netherlands, 2008; pp. 185–243. [Google Scholar] [CrossRef]
- Arora, A.; Tsinos, C.G.; Shankar, B.; Chatzinotas, S.; Ottersten, B. Hybrid analog-digital precoding design for satellite systems. In Advances in Communications Satellite Systems. Proceedings of the 37th International Communications Satellite Systems Conference (ICSSC-2019), Okinawa, Japan, 29 October–1 November 2019; IEEE: Piscataway, NJ, USA; pp. 1–13. [CrossRef]
- He, S.; Huang, Y.; Jin, S.; Yang, L. Coordinated Beamforming for Energy Efficient Transmission in Multicell Multiuser Systems. IEEE Trans. Commun. 2013, 61, 4961–4971. [Google Scholar] [CrossRef]
- Shi, Q.; Razaviyayn, M.; Luo, Z.Q.; He, C. An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel. IEEE Trans. Signal Process. 2011, 59, 4331–4340. [Google Scholar] [CrossRef]
- Zhang, Y.; Huo, Y.; Wang, D.; Dong, X.; You, X. Channel Estimation and Hybrid Precoding for Distributed Phased Arrays Based MIMO Wireless Communications. IEEE Trans. Veh. Technol. 2020, 69, 12921–12937. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Huo, Y.; Dong, X.; You, X. Hybrid beamforming design for mmWave OFDM distributed antenna systems. Sci. China Inf. Sci. 2020, 63, 192301. [Google Scholar] [CrossRef]
- Yu, X.; Shen, J.C.; Zhang, J.; Letaief, K.B. Alternating Minimization Algorithms for Hybrid Precoding in Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 485–500. [Google Scholar] [CrossRef]
- Liang, L.; Xu, W.; Dong, X. Low-Complexity Hybrid Precoding in Massive Multiuser MIMO Systems. IEEE Wirel. Commun. Lett. 2014, 3, 653–656. [Google Scholar] [CrossRef]
- Lin, S.; An, J.; Gan, L.; Debbah, M.; Yuen, C. Stacked Intelligent Metasurface Enabled LEO Satellite Communications Relying on Statistical CSI. IEEE Wirel. Commun. Lett. 2024, 13, 1295–1299. [Google Scholar] [CrossRef]
- Zhi, K.; Pan, C.; Ren, H.; Wang, K.; Elkashlan, M.; Renzo, M.D.; Schober, R.; Poor, H.V.; Wang, J.; Hanzo, L. Two-Timescale Design for Reconfigurable Intelligent Surface-Aided Massive MIMO Systems with Imperfect CSI. IEEE Trans. Inf. Theory 2023, 69, 3001–3033. [Google Scholar] [CrossRef]



| Parameter (Each Satellite) | Value |
|---|---|
| Satellite orbital altitude | 600 km |
| Downlink carrier frequency | GHz |
| Bandwidth | GHz |
| Shadow fading variance | dB |
| Satellite antenna aperture radius | wavelengths |
| NPA efficiency | |
| Maximum output power per NPA | dBm |
| Satellite antenna gain | dBi |
| GU antenna gain | dBi |
| Transmit power constraint per satellite | dBW |
| Basic power consumption per satellite | mW |
| Power consumption per RF chain | mW |
| Power consumption per local oscillator | mW |
| Power consumption per baseband digital precoder | mW |
| Power consumption per phase shifter switch | mW |
| Power consumption per phase shifter | mW |
| Minimum elevation angle |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, X.; Zhang, Y.; Liu, L.; Zhang, Z. Serving Cluster Design and Hybrid Precoding for Cell-Free-Assisted LEO Satellite Communications with Nonlinear Power Amplifiers. Electronics 2025, 14, 1317. https://doi.org/10.3390/electronics14071317
Miao X, Zhang Y, Liu L, Zhang Z. Serving Cluster Design and Hybrid Precoding for Cell-Free-Assisted LEO Satellite Communications with Nonlinear Power Amplifiers. Electronics. 2025; 14(7):1317. https://doi.org/10.3390/electronics14071317
Chicago/Turabian StyleMiao, Xiaochen, Yu Zhang, Lilan Liu, and Zhizhong Zhang. 2025. "Serving Cluster Design and Hybrid Precoding for Cell-Free-Assisted LEO Satellite Communications with Nonlinear Power Amplifiers" Electronics 14, no. 7: 1317. https://doi.org/10.3390/electronics14071317
APA StyleMiao, X., Zhang, Y., Liu, L., & Zhang, Z. (2025). Serving Cluster Design and Hybrid Precoding for Cell-Free-Assisted LEO Satellite Communications with Nonlinear Power Amplifiers. Electronics, 14(7), 1317. https://doi.org/10.3390/electronics14071317






