Fast Coding Unit Partitioning Method for Video-Based Point Cloud Compression: Combining Convolutional Neural Networks and Bayesian Optimization

Abstract

As 5G technology and 3D capture techniques have been rapidly developing, there has been a remarkable increase in the demand for effectively compressing dynamic 3D point cloud data. Video-based point cloud compression (V-PCC), which is an innovative method for 3D point cloud compression, makes use of High-Efficiency Video Coding (HEVC) to carry out the compression of 3D point clouds. This is accomplished through the projection of the point clouds onto two-dimensional video frames. However, V-PCC faces significant coding complexity, particularly for dynamic 3D point clouds, which can be up to four times more complex to process than a conventional video. To address this challenge, we propose an adaptive coding unit (CU) partitioning method that integrates occupancy graphs, convolutional neural networks (CNNs), and Bayesian optimization. In this approach, the coding units (CUs) are first divided into dense regions, sparse regions, and complex composite regions by calculating the occupancy rate R of the CUs, and then an initial classification decision is made using a convolutional neural network (CNN) framework. For regions where the CNN outputs low-confidence classifications, Bayesian optimization is employed to refine the partitioning and enhance accuracy. The findings from the experiments show that the suggested method can efficiently decrease the coding complexity of V-PCC, all the while maintaining a high level of coding quality. Specifically, the average coding time of the geometric graph is reduced by 57.37%, the attribute graph by 54.43%, and the overall coding time by 54.75%. Although the BD rate slightly increases compared with that of the baseline V-PCC method, the impact on video quality is negligible. Additionally, the proposed algorithm outperforms existing methods in terms of geometric compression efficiency and computational time savings. This study’s innovation lies in combining deep learning with Bayesian optimization to deliver an efficient CU partitioning strategy for V-PCC, improving coding speed and reducing computational resource consumption, thereby advancing the practical application of V-PCC.

1. Introduction

As 5G technology has been developing rapidly, 3D capture techniques have made progress, and the utilization of 3D devices has been on the rise, real-world scenes can currently be digitized into 3D forms effectively by means of point clouds. These point clouds describe object shapes and properties through their 3D spatial topology, providing users with unprecedented visual experiences. Furthermore, 3D point clouds can be applied in a wide range of different fields, such as the preservation of cultural heritage, autonomous driving, robotics, and virtual reality, augmented reality, and mixed reality (VR/AR/MR) [1,2].

Three-dimensional point clouds are mainly classified into three types: static point clouds, dynamic point clouds, and dynamic collection point clouds  [3]. To achieve the effective compression of point cloud data, the Moving Picture Experts Group (MPEG) has formulated two standards regarding point cloud compression, namely geometry-based point cloud compression (G-PCC) and video-based point cloud compression (V-PCC). V-PCC, mainly concentrating on the compression of dynamic point clouds, maps 3D point clouds onto 2D video frames and makes use of the available video codecs to reduce the geometry and texture data of dynamic point clouds. This approach helps to reduce the development cycle [4]. Enhancing the 2D video coding process within V-PCC can significantly improve the overall performance of 3D point cloud compression [5]. Therefore, investigating fast coding techniques for 2D projection videos in combination with V-PCC is essential to further accelerate its implementation.

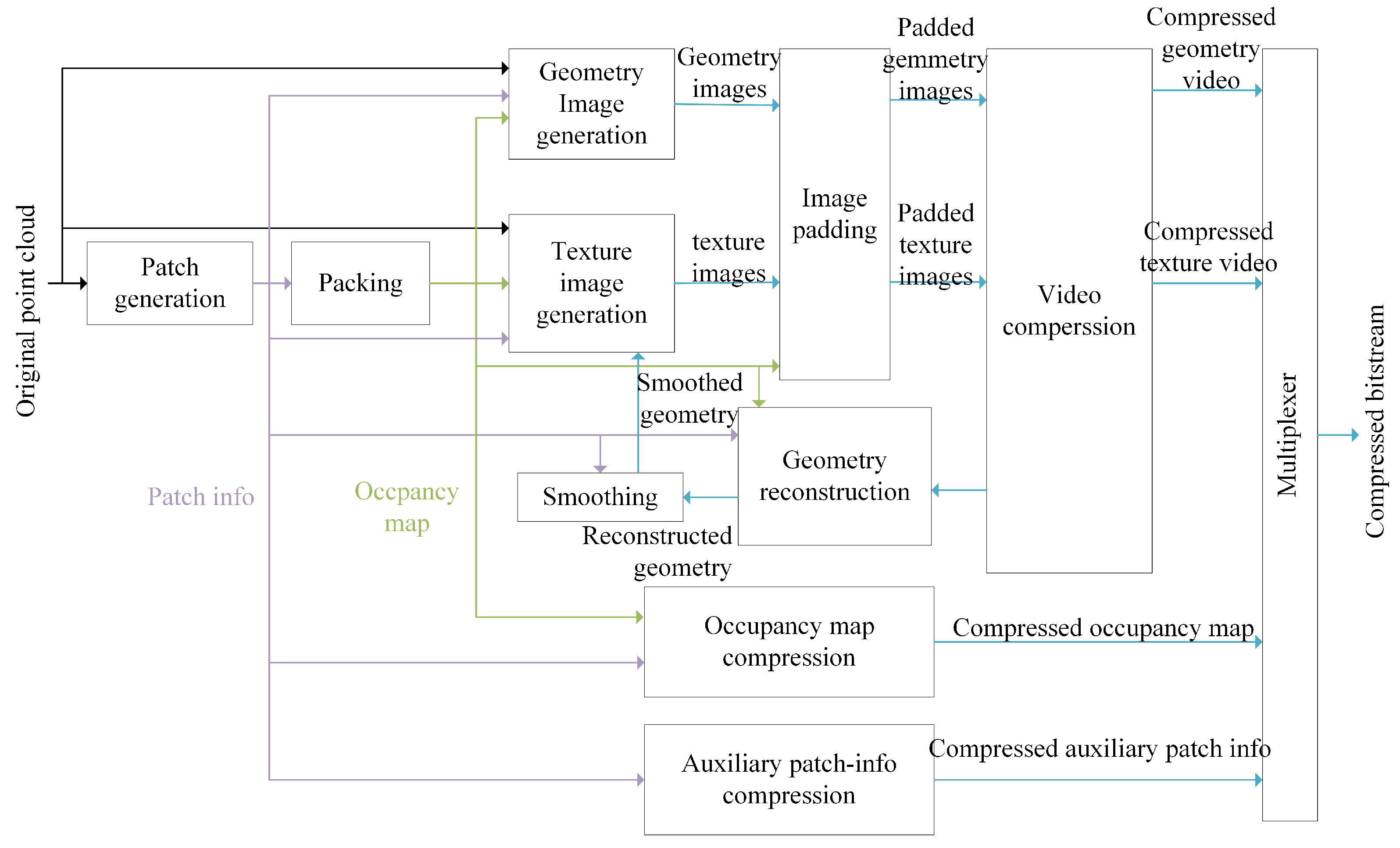
During the V-PCC procedure, the point cloud is initially split into small three-dimensional patches [6]. After that, these 3D patches are projected onto a two-dimensional surface and arranged to form geometry videos and attribute videos. Following this, the vacant areas in both the geometry videos and the attribute videos are filled up to guarantee spatial continuity and enhance the efficiency of video compression. Ultimately, High-Efficiency Video Coding (HEVC) is utilized to carry out the compression of the geometry and attribute videos [7]. Among them, the traditional sequential method follows a “prediction–transform” architecture, where the input frame is divided into blocks of equal size. The motion vector between the current frame and the previous reconstructed frame is calculated through motion estimation and compensation steps, thereby generating a prediction frame. Subsequently, the residual between the original frame and the prediction frame is transformed and quantized. The entire framework of the V-PCC encoding procedure is illustrated in Figure 1.

In the V-PCC reference software TMC2v18.0 [8,9], HEVC serves as the 2D video encoder, with coding unit (CU) partitioning as its initial stage. In the course of this process, every frame is split into coding tree units (CTUs) with a size of 64 × 64 [10]. Each CTU then recursively explores permitted partitioning patterns, including quadtree (QT) and non-split configurations; the procedure goes on until the smallest size of 8 × 8 is reached or the best partitioning plan is determined. The selection of segmentation modes is driven by the rate-distortion optimization (RDO) strategy [11]. This strategy necessitates that the encoder assesses all potential options and conducts subsequent operations, including prediction, quantization, and transformation, to identify the mode that has the minimum rate-distortion (RD) cost [12]. As a result, this process entails a high computational complexity. Predicting CU partitioning can reduce the RDO overhead in HEVC and accelerate V-PCC. However, although the CU partitioning method of HEVC performs well in natural video coding, it faces many challenges in V-PCC. First, V-PCC deals with data resulting from the projection of 3D point clouds onto 2D videos. When projected onto a 2D plane, point cloud data generate a large number of empty regions, which are rarely seen in natural videos. The CU partitioning method of HEVC typically attempts to encode these empty regions, leading to a waste of computational resources. Second, there are distinct sparse and dense regions in point cloud data. Sparse regions require fewer encoding resources, while dense regions need more refined encoding strategies. The CU partitioning method of HEVC lacks flexibility in handling such differences. Finally, V-PCC needs to encode both geometry and attribute information simultaneously, whereas the CU partitioning method of HEVC is mainly designed for single-type video content and is difficult to use in order to optimize the encoding efficiency of both geometry and attributes at the same time. Therefore, directly applying the CU partitioning method of HEVC in V-PCC may result in low encoding efficiency or degraded coding quality.

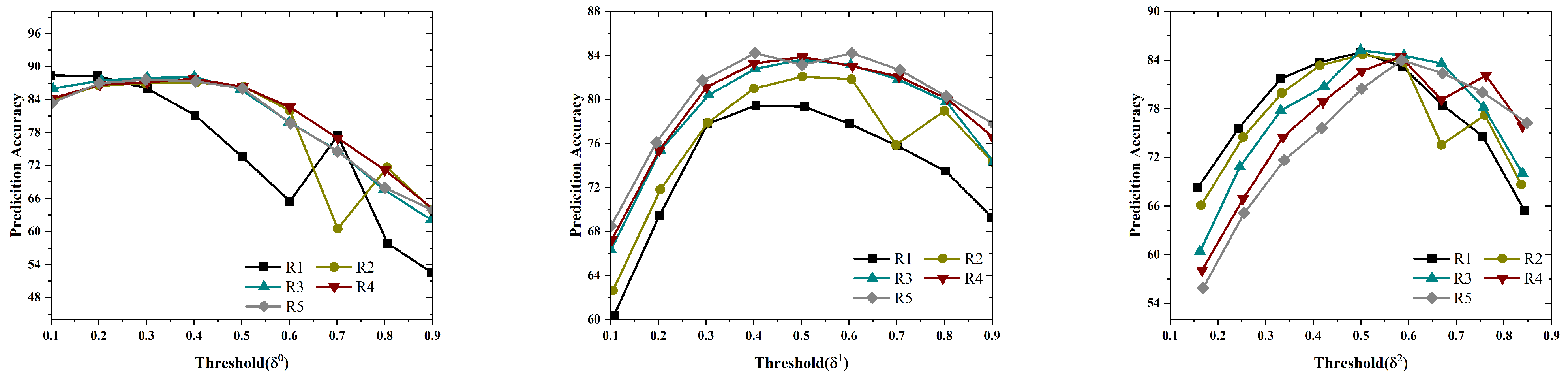
To meet the specific needs of V-PCC, this paper proposes an adaptive CU partitioning method combining occupancy maps, convolutional neural networks (CNNs), and Bayesian optimization [13], specifically targeting the coding complexity of dynamic 3D point clouds. The innovation of this paper lies in proposing an adaptive CU partitioning method that combines CNNs and Bayesian optimization, specifically targeting the coding complexity of dynamic 3D point clouds in V-PCC. This method introduces occupancy map information to classify coding units (CUs) into dense and sparse regions. It then uses CNNs for preliminary partitioning decisions and employs Bayesian optimization to fine-tune regions with low confidence. Compared with existing methods, this strategy, which integrates deep learning and Bayesian optimization, not only significantly reduces coding complexity but also maintains high coding quality, offering a new solution for the practical application of V-PCC.

The main contributions of this paper are as follows:

• Adaptive CU Partitioning Based on Occupancy Graph and CNN Framework: By calculating the occupancy rate R of the CUs, the regions are classified into dense areas, sparse areas, and complex composite areas. The partitioning is then adaptively adjusted according to the characteristics of each region.
• Bayesian Optimization to Improve Classification Accuracy in Low-Confidence Regions: In regions where the CNN outputs low confidence, Bayesian optimization is further employed to make adjustments, thereby improving the accuracy of partitioning and encoding efficiency.
• Adaptive Strategy for Optimizing Coding Efficiency and Quality: The proposed algorithm dynamically adjusts the partitioning depth based on the occupancy rate and spatial features of the CUs. It achieves adaptive partitioning for different regions, significantly enhancing the compression efficiency of V-PCC geometry image coding. Meanwhile, it ensures a low bit rate and high coding quality.

The structure of the paper is as follows. Section 2 reviews current research on CU partitioning, with a focus on existing algorithms developed to reduce video coding complexity. Section 3 details the proposed CU partitioning algorithm. The experimental results are presented in Section 4. Ultimately, Section 5 wraps up by summarizing the performance and contributions of the algorithm.

2. Research Background and Overview

This paper investigates the compression process of geometry videos, attribute videos, occupancy videos, and metadata generated by V-PCC via the default scheme of TMC2v18.0 reference software and HEVC.

2.1. Reducing the Coding Complexity of HEVC

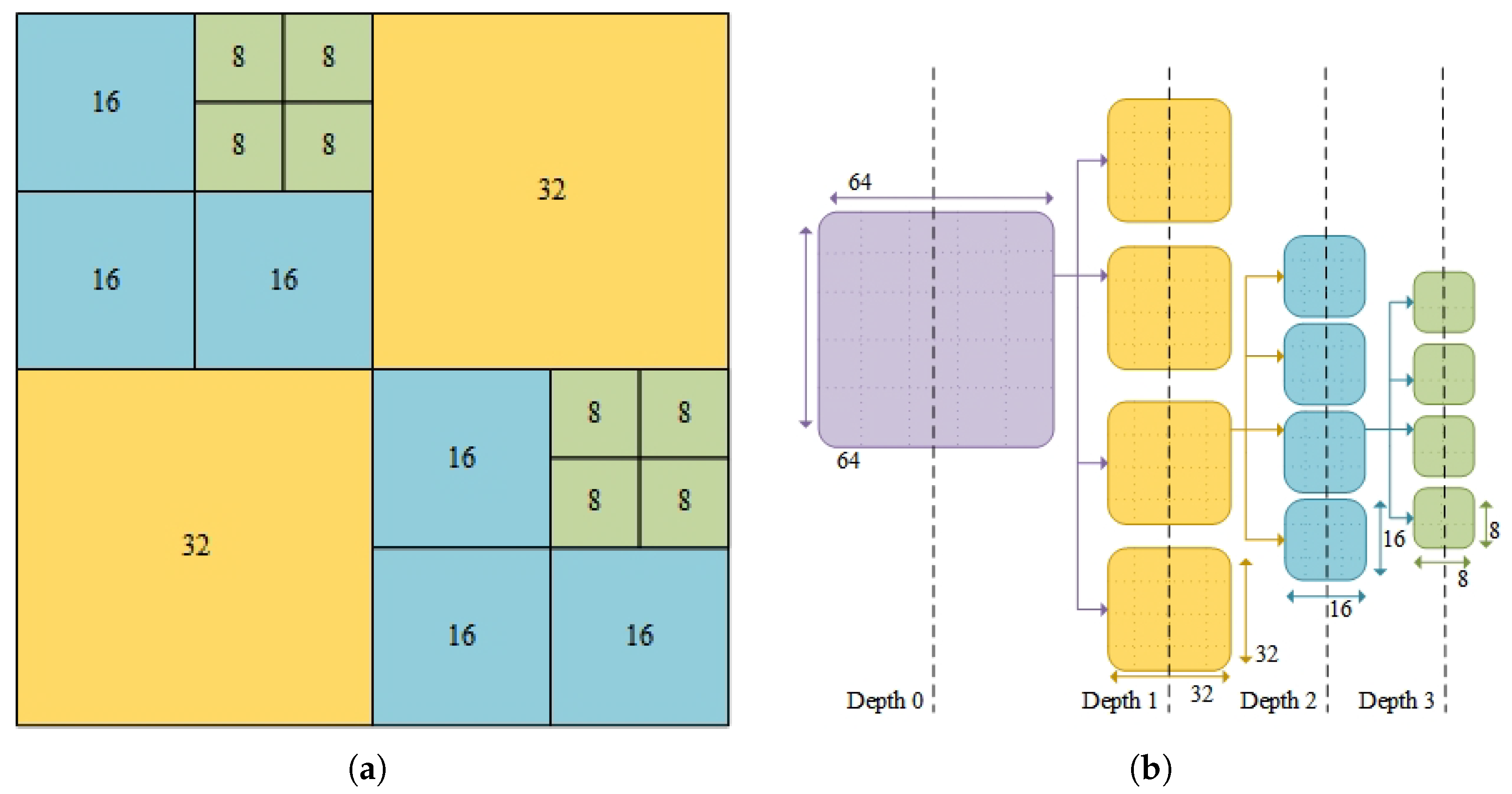
The CU partitioning process in HEVC involves significant computational complexity. It begins with a quadtree-based recursive partitioning structure that determines the size and depth of each CU based on the minimum RD cost. The procedure begins with a CTU 64 × 64 in size at depth 0 [14]. This CTU is successively divided in a recursive way into smaller CUs (with a size of 32 × 32 at depth 1 and 16 × 16 at depth 2), until the minimum CU size of 8 × 8 is achieved at depth 3 [15]. Finally, the minimum RD cost is calculated, and the partitioning is trimmed bottom-up based on the lowest RD cost. The process is illustrated in Figure 2.

When studying the CU division of HEVC, Xu et al. [16] proposed a deep learning-based method for reducing HEVC complexity by establishing a large-scale CU partitioning database and employing the ETH CNN and ETH LSTM networks to predict CU division. This approach replaces traditional brute-force search RDO, effectively reducing coding complexity. Li et al. [17] introduced a fast CU partitioning method that leverages spatial correlation and RD cost characteristics. By predicting the CU depth range and applying an adaptive threshold, they terminated partitioning early, reducing the coding time. Specifically, when the RD cost of a CU falls below the threshold, quadtree partitioning can be halted. Kuo et al. [18] developed a fast CU size decision algorithm based on spatiotemporal features, which reduces HEVC coding complexity through adaptive depth prediction, DBF boundary checking, and smooth region detection. Zhang et al. [19] utilized a CNN-based acceleration scheme for texture classification to predict division patterns in each CU layer of heterogeneous CTUs, thus reducing the complexity of internal coding in HEVC.

2.2. Reducing the V-PCC Coding Complexity

During the V-PCC encoding procedure, at the image generation phase, a 3D-to-2D mapping method is employed to encode the geometric and texture details of the point cloud into images [20], as illustrated in Figure 3.

Building upon the generated geometry and texture maps, the occupancy map is introduced. In V-PCC, the occupancy graph is a binary map that represents the distribution of point cloud data in 3D space on a 2D plane. Defined with a precision of B × B blocks, the occupancy graph distinguishes between occupied and non-occupied areas of the point cloud data (where B is a defined parameter). For lossless coding, B is set to 1. Each B × B block is classified as full or empty based on a binary value that indicates whether it contains at least one non-empty pixel. 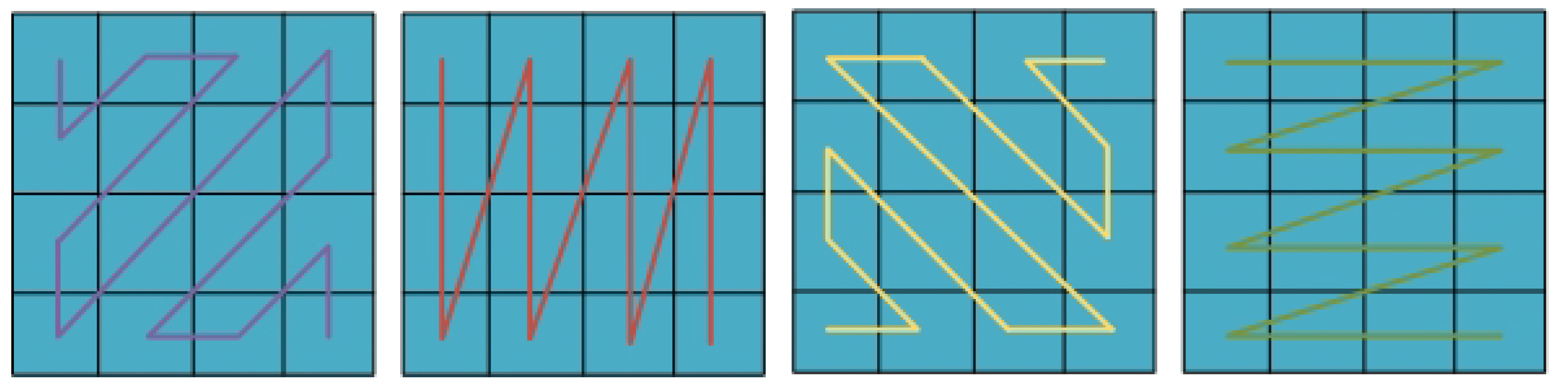During processing, each T × T block (Patch) is further subdivided into smaller B × B subblocks for more granular data management. The subblock traversal strategy involves the encoder selecting a specific order to traverse these B × B subblocks, with an explicit signal representing their index in the bitstream. This strategy enables the encoder to sort the binary values of the subblocks according to the selected traversal order and compress them using the stroke-length algorithm, thus optimizing the encoding process of the entire T × T block [21]. The subblock traversal is illustrated in Figure 4.

The existing research on V-PCC methods can be categorized into two main areas. First, the optimization of the process for converting point cloud data from 3D to 2D, which includes patch generation, packaging, efficient filling, and rate control, ensures that the generated images are better suited for 2D video encoders. Second, the 2D video encoder is optimized to handle the projected 2D images more effectively, involving coding unit division, quantization parameter selection, rate-distortion optimization, and image filling, among other techniques.

In addressing traditional fast CU partitioning algorithms for dynamic point cloud compression, Lin et al. [22] introduced the concept of block occupancy markers based on the occupancy graph and designed a fast CU decision method that leverages 2D/3D spatial homogeneity to terminate unnecessary CU partitioning early. Xiong et al. [23] investigated the relationship between predictive coding and block complexity using a local linear image gradient model, analyzed the complexity of different occupancy CU types, and proposed a fast coding approach guided by the occupancy graph. This method effectively reduced the computational complexity of V-PCC while maintaining coding quality. Liu et al. [24] proposed a coarse-to-fine rate control method that divides the 3D point cloud into distinct regions and applies different compression strategies to each, thereby improving compression efficiency and achieving better results. Yuan et al. [5] developed a rate-distortion-guided learning method based on cross-projection information. This approach determined the CU partitioning scheme by combining occupancy, geometry, and attribute characteristics, thereby reducing coding loss caused by CU partition misprediction.

With the widespread use of 3D point cloud data in various applications, high-quality point cloud data are crucial for fields such as cultural heritage preservation, autonomous driving, robotics, and virtual reality. In recent years, many studies have focused on developing effective point cloud quality assessment methods. For example, Zhou et al. [25] proposed a novel objective point cloud quality index with structure-guided resampling (SGR) to automatically evaluate the perceptual visual quality of dense 3D point clouds. This method leverages both geometric and attribute information of point clouds, achieving accurate quality assessments through regional preprocessing and quality-aware feature extraction. Additionally, Shan et al. [26] introduced a novel contrastive pre-training framework tailored for point cloud quality assessments (PCQAs), called CoPA. This framework combines contrastive pre-training with multi-view fusion, integrating deep learning and multi-view information to further enhance the performance of no-reference point cloud quality assessments. These methods provide new ideas and tools for the objective assessment of point cloud quality.

In this study, we integrate these advanced point cloud quality assessment methods with our encoding optimization strategies. By leveraging point cloud quality assessments to dynamically adjust the encoding parameters, we further enhance the encoding efficiency and quality, thereby achieving higher overall performance.

2.3. Application of Threshold-Based Partitioning in Video Coding

In video coding, threshold-based partitioning is a technique that determines the division of CUs based on specific decision criteria, aiming to reduce computational complexity and improve coding efficiency. Since different regions of a frame exhibit varying texture complexities, applying a uniform partitioning strategy across all regions can lead to redundant encoding and inefficient resource utilization. To address this issue, this study leverages occupancy maps and neural networks to analyze voxel distribution density, setting adaptive thresholds to determine whether finer CU partitioning is required. Furthermore, CNNs are combined with Bayesian optimization to fine-tune model hyperparameters, enhancing encoding decision accuracy and reducing redundant computations.

Several studies have explored threshold-based partitioning in video coding. Li et al. [3] proposed a fast CU size decision method for geometric video encoding, leveraging unsupervised learning. Considering that geometric videos are characterized by distinct sharp edges and multi-scale areas, the researchers devised a hierarchical clustering method to determine the most suitable CU size. Additionally, they integrated an adaptable linkage threshold within the clustering procedure, which makes adjustments based on the changing quantization parameters and CU dimensions. Tariq et al. [27] developed a novel early termination mechanism based on the duration problem, incorporating dynamic thresholds to minimize computational costs. Their model outperformed most existing approaches in computation efficiency and optimal decision adjustment. Bukit et al. [28] introduced an efficient depth decision algorithm utilizing spatial homogeneity and thresholding modification techniques. By utilizing uniform region characteristics and CU partitioning types, their approach effectively reduced the encoding time and overall computational complexity.

3. Research on Adaptive CU Partitioning for Efficient V-PCC Coding

This paper proposes a method for encoding geometric video using HEVC in V-PCC. While numerous fast CU partitioning methods exist for HEVC, these approaches are unable to take into consideration the distinctive features of point clouds. As a result, their efficiency diminishes when directly applied to V-PCC. Specifically, projecting a 3D point cloud onto a 2D image through patch generation often results in a significant number of empty pixels. Furthermore, the spatiotemporal correlation is lower than that of natural images. To address the complexity of geometry coding in V-PCC, we propose a fast coding method that integrates occupancy graphs, CNNs, and Bayesian optimization. By integrating deep learning techniques, improvements have been achieved in traditional sequential methods, and thus, this approach significantly enhances both coding efficiency and quality.

First, the occupancy rate R of every CU is computed according to the V-PCC occupancy graph, which indicates the ratio of the occupied voxels within the CU. Depending on the occupancy rate, the CUs are divided into three different types of regions: sparse regions, dense regions, and complex composite regions. Next, different CU sizes are input into the designed CNN framework to determine whether further division is necessary. The CNN generates partitioning decisions for each region by extracting features from the CU occupancy graph and other geometric information. For dense regions, the CNN generates deeper partitioning strategies to preserve more geometric details. For sparse regions, shallower division is employed to reduce the computation and bit rate. For the complex composite regions, we employ a hybrid strategy: First, we utilize a CNN framework to analyze the features within the region and identify the distribution of high-occupancy and low-occupancy pixels. Then, based on this distribution, we dynamically adjust the partitioning depth. Specifically, for the high-occupancy parts, we adopt the same partitioning strategy as for the dense regions; for the low-occupancy parts, we apply the same strategy as for the sparse regions. Through this hybrid approach, we are able to better handle the details of complex composite regions while maintaining coding efficiency.

The CNN’s output is the confidence value Conf(x), indicating whether further division is needed. If the confidence value exceeds a set threshold, the current partitioning result is finalized. Otherwise, the process moves to the next stage of Bayesian optimization. Finally, for low-confidence regions, Bayesian optimization adjusts the partitioning strategy by refining the proxy model based on the CNN’s partitioning results and the region’s occupancy information. This further optimization improves coding efficiency, reduces the bit rate, and maintains coding quality.

3.1. An Adaptive CU Partitioning Method Based on Occupancy Maps and CNN Framework

When coding is optimized via an occupancy graph, the first step is to divide it into occupied and unoccupied blocks. In V-PCC, the occupancy graph plays a crucial role in encoding the spatial distribution of 3D point cloud data. The 3D data are mapped to a 2D occupancy graph, where each pixel value represents whether the corresponding 3D voxel is occupied by a point cloud. Based on the binary values in the occupancy graph, the geometry is divided into occupied and unoccupied blocks, considering the equilibrium between the time efficiency and coding performance. To expedite CU partitioning, the occupancy graph is defined as O(x,y), where O(x,y) = 1 indicates that the corresponding area is occupied by the point cloud and O(x,y) = 0 indicates that it is not.

To increase coding efficiency, the occupancy graph is segmented into multiple CUs of uniform size, resulting in several subblocks. Each CU has a size of N × N. The occupancy rate R for each CU is then calculated using the following formula:

$$R={\displaystyle \frac{{\sum }_{x,y\in \mathrm{Block}}O(x,y)}{N^2}}$$

(1)

Herein, the occupancy rate R represents the proportion of occupied pixels within a sub-block, with a range of $[0,1]$. Based on the occupancy rate, CUs are classified into three categories: dense regions $(R>t_1)$, where the point cloud data are complex and rich in detail, potentially requiring deeper partitioning to preserve more details; sparse regions $(R\le t_2)$, where the point cloud data are sparse, allowing for reduced partitioning depth to enhance coding efficiency; and complex composite regions $(t_2<R\le t_1)$, which contain a mixture of high-occupancy and low-occupancy pixels, necessitating a specialized processing strategy. Among them, a higher CU occupancy rate indicates a denser point cloud and more complex geometric information, necessitating additional partitioning layers to retain the details. Conversely, CUs with low occupancy typically correspond to sparse regions, where the point cloud data are minimal and a shallower partition depth suffices, thereby improving compression efficiency.

This paper presents an adaptive CU partitioning strategy based on the binary index value and occupancy characteristics of the occupancy graph. In this study, ResNet-18 is selected as the backbone CNN network for CU partitioning decisions, aiming to minimize the computational complexity during the CU partitioning process. Specifically, three different CNN network structures are designed for CUs of various sizes, including 64 × 64, 32 × 32, 16 × 16, and 8 × 8. Each architecture comprises 17 convolutional layers, succeeded by a fully connected (FC) layer activated via the Softmax function, as illustrated in Figure 5.

To further enhance the generalization ability of ResNet-18 on occupancy maps, we employed dynamic point cloud data from the V-PCC reference software TMC2v18.0 as the training set to fine-tune ResNet-18. This process enabled the network to better adapt to the sparsity and binary structure of occupancy maps. To improve model robustness, data augmentation techniques were applied during training. Specifically, random cropping, rotation, and flipping operations were performed on the occupancy maps to generate more diverse training samples, thereby enhancing the model’s adaptability to different occupancy map structures. By continuing to train on occupancy map data and adjusting the network weights, the model was able to better capture local features and spatial relationships within the occupancy maps.

After the CU occupancy rate is calculated, the CU is input into the designed CNN framework, where the CNN extracts the features of the input CU. Each CNN network outputs a partition confidence value, denoted as $Conf\left(x\right)$, where $Conf\left(x\right)ϵ[0,1]$. If $Conf\left(x\right)>=\partial$ (the threshold for CNN confidence), the partition decision generated by the CNN is directly adopted. If $Conf\left(x\right)<\partial$, the CU enters the Bayesian optimization module for further evaluation.

Specifically, the frame that corresponds to the occupancy map is retrieved from the point cloud video sequence meant for encoding, and subsequently, it is split into 64 × 64 CTUs. Each CTU is initially treated as a CU with a depth of 0 and input into the first-level CNN of the CNN framework. Based on the occupancy rate and regional features, the first-level CNN outputs a confidence value, Conf64, to determine whether further partitioning is required for the current CU. If the model predicts no need for further division, the CU partitioning process is halted, and the RDO mechanism in V-PCC is utilized to finalize the encoding. If the prediction indicates the need for partitioning, the 64 × 64 CU is divided into four 32 × 32 child CUs, which are then input into the next-level CNN for further decision-making. This process is repeated for each 32 × 32 child CU, and, if partitioning is needed, it is further divided into four 16 × 16 child CUs and evaluated by the next-level CNN. Similarly, for each 16 × 16 child CU, the same decision process is applied, leading to further division into four 8 × 8 child CUs, followed by another CNN decision. When the CU attains the smallest partition size of 8 × 8, the CNN decision terminates, and the coding phase begins.

In this study, the CNN pipeline employs a multi-stage processing approach (64 × 64 → 32 × 32 → 16 × 16 → 8 × 8). This hierarchical structure may lead to the accumulation of errors in deeper layers. To mitigate the impact of error propagation, a feedback mechanism is introduced. Specifically, the output of each CNN stage is not only used for partitioning decisions at the current stage but is also fed back to the previous stage to correct errors. If the CNN output at a certain stage has low confidence, the output is fed back to the previous stage, where it is combined with the features from the previous stage to re-make partitioning decisions, as illustrated in the figure. Through this approach, errors can be corrected in a timely manner, reducing the accumulation of errors in subsequent stages. Additionally, the Bayesian optimization module further adjusts the partitioning strategy for low-confidence regions, thereby minimizing the impact of error accumulation, as illustrated in Figure 6.

In this paper, TMC2v18.0 with the HEVC encoder is employed to encode the generated video, and the proposed framework is developed in two stages: the training stage and the testing stage. During the training phase, the CNN determines whether to split each CU on the basis of the given dataset, which includes labeled data indicating whether a split is required for each CU. Upon the completion of the training process, the CNN model that has been trained is integrated into the V-PCC encoder, replacing the traditional recursive CU partitioning procedure.

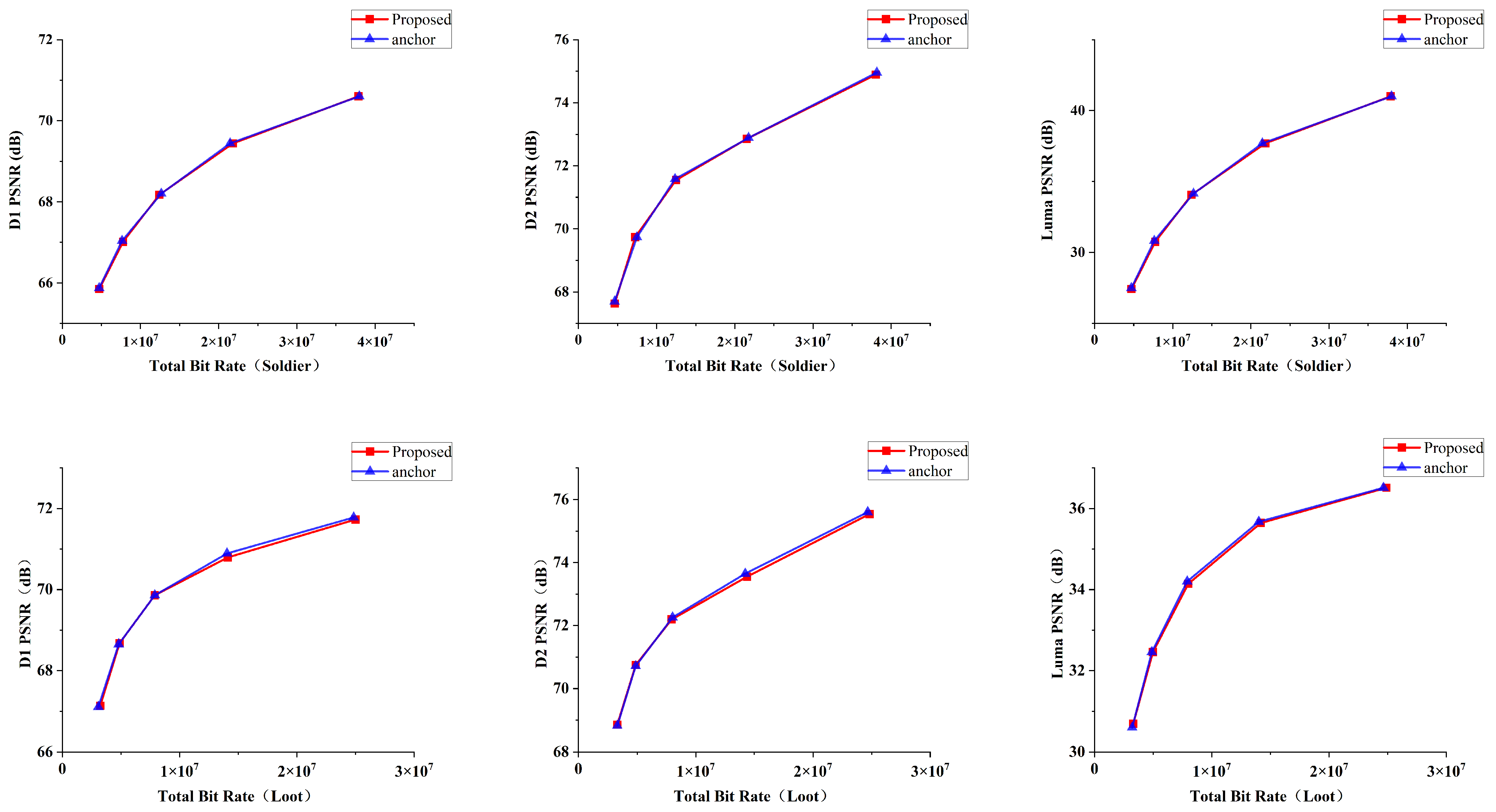
By incorporating the occupancy feature and the CNN framework, this partitioning strategy enables the adaptive partitioning of the occupancy graph area, allowing for the more detailed processing of dense and complex boundary regions. Simultaneously, it avoids redundant calculations in unoccupied and sparse areas, significantly improving encoding efficiency and compression performance. This method not only enhances the coding efficiency and shortens the encoding time, but also maintains high video quality and strengthens the robustness of the prediction.

3.2. Bayesian Optimization Improves the Accuracy of Low-Confidence Region Partitioning

In V-PCC, based on the definition of occupancy maps, this method combines occupancy rate R and a designed multi-stage CNN framework with Bayesian optimization (BO) for adaptive adjustment of geometric CU partitioning. In high-occupancy regions, the CNN framework directly determines the need for partitioning, followed by the fine-tuning of the partition strategy through Bayesian optimization. In low-occupancy regions, the CNN model may directly output a decision of no partitioning. The Bayesian optimization module will then further adjust the partitioning strategy. Through Gaussian process modeling and active sampling, it dynamically adjusts the partitioning parameters and optimizes the partitioning strategy, thereby reducing the impact of accumulated errors. Specifically, Bayesian optimization dynamically adjusts the partitioning strategy based on the current partitioning results from the CNN and the occupancy information of the region, ensuring minimal reconstruction distortion while maintaining a low bit rate.

For CU partition optimization in low-confidence regions, Bayesian optimization minimizes the rate-distortion cost by integrating Gaussian process (GP) modeling and active sampling. The objective is to minimize the following rate-distortion cost function:

$$J_{RD}\left(x\right)=R\left(x\right)+\lambda D\left(x\right)$$

(2)

where x represents the parameterized vector of CU partitioning modes, including quadtree depth, partition flags, and other discrete or continuous parameters. $R\left(x\right)$ is the encoding bitrate, $D\left(x\right)$ is the reconstruction distortion, and $\lambda$ is the Lagrange multiplier. Minimizing this objective function effectively reduces encoding redundancy and improves efficiency. The parameter space X for CU partitioning modes is defined by parameter vectors $x\in X$, such as the quadtree depth $x_1\in 0,1,2,3$ (0 for no partition and 1–3 for partition levels) and the partition direction $x_2\in 0,1$ (horizontal or vertical).

To make the objective function adaptable to different content complexities and point cloud densities, we propose a method for dynamically selecting the Lagrange multiplier $\lambda$, which is adjusted based on the occupancy rate R and texture complexity of the current CU. For regions with high occupancy rates, i.e., $R>t_1$, the point cloud data are complex and rich in detail, requiring higher encoding precision. Therefore, a smaller $\lambda$ value is chosen to focus more on optimizing the distortion $D\left(x\right)$. For regions with low occupancy rates, i.e., $R\le t_2$, the point cloud data are sparse, and it is possible to increase the bit rate to improve the encoding efficiency. Therefore, a larger $\lambda$ value is chosen to focus more on optimizing the bit rate $R\left(x\right)$. For boundary regions or regions with complex textures, we further adjust $\lambda$ by analyzing the spatial features T of the CU. If a region has high texture complexity, we appropriately reduce $\lambda$ to minimize reconstruction distortion. Conversely, if the texture complexity is low, we appropriately increase $\lambda$ to reduce the encoding bit rate. This dynamic selection mechanism allows $\lambda$ to be adaptively adjusted based on the occupancy rate and texture complexity of the CU. The formula for $\lambda$ is defined as follows:

$$\lambda ={\lambda }_0·e^{-\alpha R-\beta T}$$

(3)

Herein, ${\lambda }_0$ is the initial Lagrange multiplier, R is the occupancy rate of the current CU, T is the spatial feature complexity of the current CU, and $\alpha$ and $\beta$ are adjustment parameters.

Bayesian optimization uses a Gaussian process to probabilistically model the objective function $J_{RD}\left(x\right)$, capturing performance variations across different CU partitioning modes. Specifically, the objective function is modeled as a Gaussian process:

$$J_{RD}\sim GP(m\left(x\right),k(x,x^{\prime }))$$

(4)

where the mean function $m\left(x\right)$ is typically set to a constant and the covariance function $k(x,x^{\prime })$ uses the Squared Exponential (SE) Kernel:

$$k(x,x^{\prime })={\sigma }^{2}exp\left(-{\displaystyle \frac{{\left|\right|x-x^{\prime }\left|\right|}^2}{{2l}^2}}\right)$$

(5)

Here, ${\sigma }^2$ is the signal variance and l is the length scale parameter. Bayesian optimization approximates the objective function using the GP model and selects the optimal parameter combination based on the acquisition function. The acquisition function employs the Expected Improvement (EI) strategy:

$$EI\left(x\right)=\left(J_{RD}^{+}-\mu \left(x\right)\right)\mathsf{\Phi }\left(Z\right)+\sigma \left(x\right)\phi \left(Z\right)$$

(6)

where $J_{RD}^{+}$ is the current best objective value, $\mu \left(x\right)$ and $\sigma \left(x\right)$ are the predicted mean and standard deviation from the GP $model.Z={\displaystyle \frac{J_{RD}^{+}-\mu \left(x\right)}{\sigma \left(x\right)}}$, and $\mathsf{\Phi }\left(Z\right)$ and $\phi \left(Z\right)$ are the CDF and PDF of the standard normal distribution.

By maximizing the acquisition function, Bayesian optimization iteratively updates the parameter set, selecting the optimal solution as follows:

$$J_{RD}^{+}=argmaxEI\left(x\right)$$

(7)

Low-confidence regions benefit from BO by balancing exploration and exploitation through Gaussian process modeling and active sampling. This allows the approach to approximate the global optimum partition mode within a limited number of evaluations. In each iteration, parameters like $\lambda$ and the parameterized vector x are dynamically adjusted to optimize partitioning strategies for complex and uncertain regions, thus improving the balance between encoding efficiency and reconstruction quality.

During V-PCC encoding, Bayesian optimization continuously adjusts partition parameters (e.g., CU size, partition density) and gradually refines the partition strategy through a feedback mechanism, ensuring a balance between encoding efficiency and reconstruction quality. In each iteration, a new sampling point is selected based on the current surrogate model and the acquisition function, and the surrogate model is updated. The optimization is terminated when the predefined objective is achieved. The integration of Bayesian optimization with the CNN framework enables the system to flexibly adjust partition strategies based on the varying characteristics of point cloud data, further reducing redundant data encoding and optimizing computational overhead.

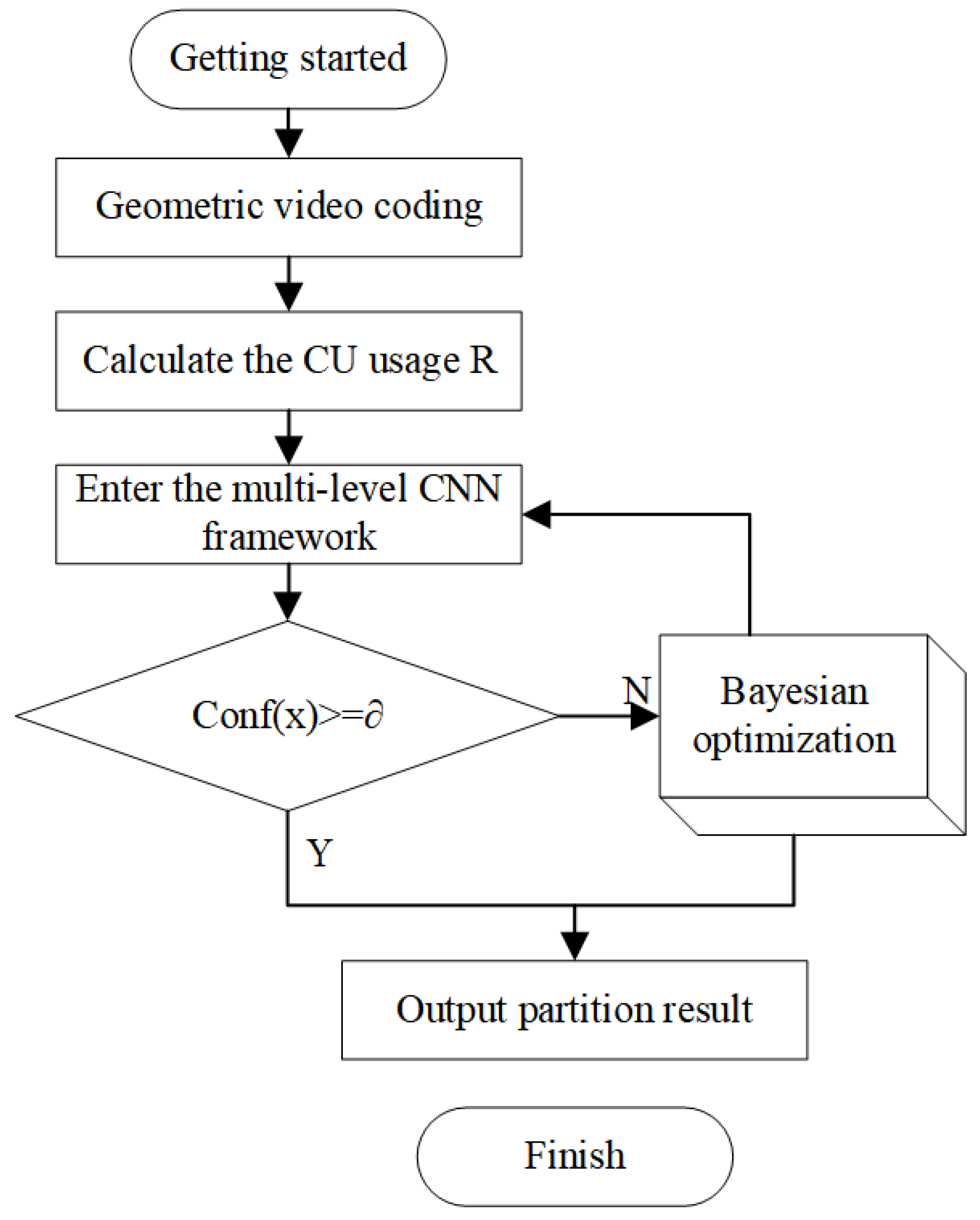
3.3. Algorithm Process

This algorithm integrates the definition of the V-PCC occupancy graph, occupancy information, CNN framework, and Bayesian optimization techniques to optimize the CU partitioning decision in point cloud video coding. This method effectively performs adaptive CU partitioning for different types of regions by combining multi-level recursive decisions based on occupancy information and the CNN framework with Bayesian optimization. For high-confidence regions, the partition results are directly output. For low-confidence regions, Bayesian optimization is applied to further increase the accuracy and efficiency of partitioning, ultimately optimizing the coding effect and improving both the compression performance and the quality of point cloud video coding. The specific algorithm flow is shown in Algorithm 1 below.

Algorithm 1: The proposed algorithm
1	Prepare the training data and preprocess the V-PCC data.
2	Calculate the occupancy rate R of each CU, which represents the proportion of occupied voxels in the CU. Based on the occupancy rate, divide the CU into three categories: dense regions, sparse regions, and complex composite regions.
3	Use the multilevel CNN framework to make partitioning decisions based on the regional occupancy information.
4	A multi-level recursive decision-making process is employed, where each CU is evaluated layer by layer through multiple stages of CNNs and outputs a confidence threshold. If the confidence output by the CNN is low, it is fed back to the previous stage.
5	For regions with low-confidence CNN outputs, apply Bayesian optimization to further refine the partitioning decision.
6	Output the partition results. For high-confidence regions, directly output the partitioning results and proceed to the subsequent coding stage. For low-confidence regions, after Bayesian optimization adjustments, output the final partitioning strategy and encode.

According to the above algorithm steps, the overall process of the two algorithms can be obtained as shown in Figure 7.

4. Experimental Results

4.1. Model Training and Hyperparameter Setting

At present, no comprehensive dataset is available for training the proposed method to effectively reduce the complexity of V-PCC coding. To support the training of the proposed network, the scheme is integrated into the V-PCC reference software TMC2v18.0 CTC, which uses the dynamic point cloud dataset provided by MPEG, specifically the 8i Voxelized Full Bodies (8iVFB) dataset. Under CTC lossy geometry conditions, we used the dynamic point cloud sequence named “Soldier” and other sequences from various scenes and types for training and validation. To enhance the diversity of the training data, we applied data augmentation techniques such as random cropping, rotation, and flipping. These techniques help generate more varied training samples, thereby improving the robustness and generalization ability of the model. Additionally, four dynamic point cloud sequences—Loot, Red and Black, Long Dress, and Thaidancer—were utilized for testing. The results were compared with the V-PCC anchor method. The performance of attribute videos was evaluated using the peak signal-to-noise ratio (PSNR) for Luma, Cb, and Cr components. Meanwhile, the geometric videos were assessed using point-to-point error (D1) and point-to-plane error (D2). The time savings were calculated as follows:

$$\Delta T={\displaystyle \frac{T_{\mathrm{method}}-T_{\mathrm{anchor}}}{T_{\mathrm{method}}}}\times 100\%$$

(8)

where $\Delta T$ represents the reduction in computational complexity; $T_{anchor}$ denotes the software coding time, which is the calculation time of the V-PCC anchor; and $T_{method}$ represents the computation time of the method proposed in this paper. The cross-entropy loss function is utilized to measure the difference between the predicted outcomes and the real results, and its formula is as follows:

$$Loss=-\sum _{i=1}^n\left(y_i{log(p}_i\right)+(1-y_i)log(1-p_i))$$

(9)

where $y_i$ represents the actual class label and $p_i$ denotes the probability that the model predicts for the i-th class.

To enhance training accuracy, this study employs Bayesian optimization to fine-tune the hyperparameters of low-confidence regions. The goal is to minimize encoding time and complexity while maintaining high encoding quality. By constructing a Gaussian process for the objective function and utilizing an acquisition function, the method efficiently searches for the optimal combination of hyperparameters. The defined hyperparameter space is shown in

Table 1. Bayesian optimization hyperparameters.

Parameter	Range
Signal variance	$[{10}^{-3},{10}^3]$
Rate-Distortion Trade-off Parameter $\lambda$	$[0,1]$
Maximum Partition Depth $d_{max}$	$[1,3]$
CNN Confidence Threshold	$[0.6,0.9]$
Exploitation Balance Parameter $\xi$	$[0.01,0.2]$
Number of Samples $n_{\mathrm{init}}$	$[5,50]$

.

The experimental results demonstrate that the Bayesian optimization employed in this study significantly enhances encoding efficiency and quality. However, its high computational complexity remains a limitation. In the future, we will continue to explore more efficient Bayesian optimization algorithms to further improve encoding efficiency and quality.

4.2. CNN Confidence Threshold Optimization

As discussed earlier, each CNN network outputs a partition confidence score, referred to as the CNN confidence threshold. If the confidence exceeds the threshold, the CNN’s partition decision is directly adopted. Otherwise, the decision proceeds to the Bayesian optimization module for further evaluation. The overall algorithm flow for threshold optimization is illustrated in the Figure 8.

The choice of threshold significantly impacts both computational complexity and RD performance. In this study, a higher confidence threshold indeed leads to an increase in computational time, as more regions require further optimization through the Bayesian optimization module. When the threshold is set too high, more regions enter the Bayesian optimization module, increasing computation time but reducing the risk of misclassification in low-confidence areas. Conversely, setting the threshold too low reduces the frequency of Bayesian optimization calls, saving encoding time, but may result in the misclassification of sparse regions as requiring partitioning, leading to increased bitrate and the accumulation of partitioning errors in low-confidence areas. Therefore, it is essential to find an optimal threshold that balances computational complexity with RD performance, ensuring lower computational cost while maintaining better RD performance.

To attain the optimal encoding performance and the greatest prediction accuracy, the trained model is assessed by making use of the entire dataset. Specifically, the output of the CNN model—namely the confidence threshold for various CU sizes—is compared against the optimized threshold to ascertain the predicted partitioning for the entire CTU. The threshold is predetermined. Subsequently, the prediction accuracy is determined on the basis of this threshold. To find the optimal threshold, its value is varied from 0 to 1, and the average prediction accuracy is calculated at each step. This process is repeated for three different CU sizes, yielding the relationship between the threshold and prediction accuracy. As shown in the Figure 9, the model’s training accuracy fluctuates with the threshold, as different thresholds affect the model’s CU partitioning decisions, leading to prediction errors and impacting accuracy. Therefore, the choice of threshold is crucial.

As shown in Figure 9, we found that there exists an optimal range for the confidence threshold (0.6–0.8), within which the increase in computational time can be offset by the improvement in encoding efficiency. Specifically, when the confidence threshold is set to 0.7, the encoding time savings reach the highest level (54.75%), while the increase in the BD rate is almost negligible. This indicates that by reasonably setting the confidence threshold, a good balance can be achieved between real-time performance and encoding quality.

4.3. Ablation Studies

To thoroughly analyze the impact of each module in the proposed method on overall performance, we designed three experimental settings for ablation studies. The original model containing both the CNN module and Bayesian optimization was used as the baseline. It was compared with models where either the CNN module or the Bayesian optimization module was removed. By comparing the performance differences between these settings and the complete model, we can clearly identify the role of the CNN module in feature extraction and information processing, as well as the contribution of Bayesian optimization in parameter adjustment and performance optimization. The ablation experiments revealed that the complete model achieved 11.25% and 5.75% savings in encoding time compared to the models without the CNN module and without the Bayesian optimization module, respectively, as shown in

Table 2. Performance comparison of different models.

Model	Geometry-T (%)	Attribute-T (%)	Total (%)	BD (%)
Complete Model	−57.37	−54.43	−54.75	0.42
Ablation CNN	−45.32	−42.15	−43.50	0.31
Ablation Bayesian	−50.12	−48.34	−49.00	0.56

and Figure 10.

These results demonstrate that both the CNN module and the Bayesian optimization module play crucial roles in accelerating the encoding process. The CNN module reduces redundant computations by efficiently extracting features and processing information, while the Bayesian optimization module further optimizes the model’s runtime efficiency through precise parameter adjustments and partitioning optimization in low-confidence regions. Regarding the changes in the BD rate, the complete model exhibited an increase of only 0.42%, whereas the models without the CNN module and without the Bayesian optimization module experienced BD rate increases of 0.31% and 0.56%, respectively. This indicates that these two modules effectively control the rise in the BD rate while maintaining encoding quality, ensuring that the model achieves high encoding efficiency without significantly compromising encoding quality. Through the detailed analysis of the ablation experiments, we have validated the significant contributions of the CNN module and the Bayesian optimization module to the model’s performance, providing a clear direction for the further optimization and improvement of the model.

4.4. Final Coding Performance

The overall performance of the proposed method is detailed in

Table 3. Reduced geometry and attribute video time.

Point Cloud	Geometry			Attribute			Total
	Unocc	Occ	Total-G	Unocc	Occ	Total-A
Loot	−32.83	−27.35	−60.18	−16.31	−51.97	−54.16	−56.11
RedandBlack	−34.96	−29.06	−62.02	−20.13	−56.32	−57.89	−58.09
Long Dress	−36.29	−31.84	−64.13	−18.33	−53.07	−56.19	−57.29
Thaidancer	−28.53	−22.91	−51.44	−15.71	−51.56	−53.27	−52.15
Soldier	−25.67	−21.39	−49.06	−12.34	−49.28	−50.62	−50.12
Average	−31.66	−26.51	−57.37	−16.56	−52.44	−54.43	−54.75

, offering a comparison of the coding time savings between the proposed approach and the reference method. Specifically, “Unocc” denotes the time savings for UNOCC block coding, while “Occ” indicates the time savings for OCC block coding. “Total-g” refers to the time savings for geometric graph coding, and “total-a” represents the time savings for attribute graph coding. “Total” signifies the overall time savings of the entire proposed method. As shown in Table 3, the subjective quality assessment indicates that, although the BD rate increased slightly in most test sequences, the visual quality did not degrade significantly. This trade-off has a minimal impact on perceptual quality. Disregarding the BD rate, the average time savings for geometric graph coding is 57.37%, and for attribute graph coding, it is 54.43%. The overall coding time savings amount to 54.75%. This demonstrates that our method is capable of maintaining perceptual quality while reducing encoding time. Moreover, by introducing a specialized processing strategy for complex composite regions, our method exhibits better adaptability and flexibility in handling areas with a mixture of high-occupancy and low-occupancy pixels. This hybrid approach not only enhances encoding efficiency but also further optimizes encoding quality, particularly in complex scenes, where it can better preserve detailed information. Additionally, for geometric graphs, the coding time for unoccupied blocks and occupied blocks is reduced by 31.66% and 26.51%, respectively. The time saved for unoccupied blocks in the attribute map is less than that in the geometry map. The reason for this phenomenon is that the percentage of unoccupied blocks in the attribute map is lower than that in the geometry map. Additionally, the texture complexity of the attribute map is higher, and its smoothness is lower compared to the geometry map.

Meanwhile, the results in Table 3 further illustrate that our proposed method can effectively identify sparse regions, dense regions, and complex composite regions and can specifically reduce redundant computations. In both the sparse point cloud Thaidancer and the dense point cloud Long Dress, this method demonstrates good applicability, with encoding time savings exceeding 50%. This indicates that our method can adapt to point cloud data of varying densities and complexities.

Additionally, each bit rate corresponds to a different quantization parameter (QPS) for the graphs of geometry and attributes.

Table 4. Time reduction at each bit rate.

Point Cloud	R1	R2	R3	R4	R5
Loot	−56.71	−57.01	−57.69	−56.46	−54.67
RedandBlack	−59.03	−58.45	−58.34	−57.91	−55.31
Long Dress	−58.69	−58.36	−57.31	−54.34	−52.17
Thaidancer	−54.77	−53.01	−53.88	−52.16	−50.11
Soldier	−55.09	−52.83	−56.74	−54.97	−53.29
Average	−56.86	−55.93	−56.79	−55.17	−53.11

presents the time savings at different bit rates, ranging from low to high (R1–R5). The average time saving of the proposed method is 54.75%. As shown in Table 4, the proposed method demonstrates effectiveness across all test sequences at various bit rates.

In the present study, the proposed approach is compared and evaluated against the benchmark method in TMC2v18.0 for V-PCC. The method proposed in this study demonstrates significant advantages in multiple aspects. First, an end-to-end optimization framework is employed, which enables the deep neural network to automatically learn motion and texture information from video sequences, thereby avoiding the complex manual design processes involved in traditional methods. Second, leveraging the nonlinear transformation capabilities of deep neural networks allows for the more efficient compression of video data. Finally, the adaptive motion modeling framework is capable of better handling complex motion scenarios, thus further enhancing encoding performance. The corresponding results are illustrated in

Table 5. Comparison of RD performance between the proposed global approach and the anchoring approach.

Point Cloud (%)	Geo. BD-GeomRate					Att. BD-AttrRate					Total
	D1	D2	Luma	Cb	Cr	D1	D2	Luma	Cb	Cr
Loot	0.08	0.07	−0.14	−1.39	−2.43	0.06	0.09	−0.17	−0.74	−1.56	−56.11
RedandBlack	0.38	0.79	0.23	0.11	−0.05	0.25	0.59	0.07	0.36	0.17	−58.09
Long Dress	0.77	0.91	1.13	−0.16	−0.53	0.63	0.87	0.53	−0.31	−0.23	−57.29
Thaidancer	0.56	0.65	−0.23	−0.37	−0.02	0.81	0.95	0.05	−0.11	0.13	−52.15
Soldier	0.31	0.37	−0.07	5.22	−2.19	0.31	0.41	0.11	2.21	−0.67	−50.12
Average	0.42	0.56	0.18	0.68	−1.04	0.41	0.58	0.12	0.28	−0.43	−54.75

and Figure 11. As for the geometric graph, the average BD rates of the D1 and D2 components have risen by 0.42% and 0.56% respectively. Concerning the attribute graph, the average BD rates of the Luma, Cb, and Cr components show an increase of 0.18% for the Luma component and 0.68% for the Cb component, whereas the Cr component experiences a decrease of 1.04%. These results indicate that the proposed approach is efficient in evaluating the geometric and attribute graphs of the sequences.

As illustrated in Figure 11, the proposed method in this study achieves R-D performance comparable to that of the anchor method. This finding further suggests that the proposed approach can substantially reduce computational complexity with a negligible increase in bit rate.

Under the same experimental conditions, our proposed method was compared with the approach of Que [14], which integrates handcrafted features with lightweight neural networks to pre-determine the optimal CU partitions, and with Xiong’s [23] placeholder map-guided fast V-PCC coding method, which leverages the rate-distortion characteristics of different block types, as shown in

Table 6. Comparison of relevant data among different methods.

Point Cloud (%)	Geo. BD-GeomRate					Att. BD-AttrRate					Total
	D1	D2	Luma	Cb	Cr	D1	D2	Luma	Cb	Cr
Xiong’s	0.31	0.47	0.21	0.19	−0.74	0.47	0.66	0.11	0.25	−0.46	−43.92
Que’s	0.12	0.15	0.27	−0.23	−0.97	0.38	1.15	0.19	−1.27	−0.61	−51.2
Our’s	0.42	0.56	0.18	0.68	−1.04	0.41	0.58	0.12	0.28	−0.43	−54.75

. The comparison results demonstrate that our algorithm outperforms the others in terms of compression efficiency for geometric diagrams. Additionally, it outperforms both Xiong’s and Que’s methods in terms of time savings. This confirms that the proposed algorithm enhances coding efficiency and quality while offering better compression performance, as illustrated in Figure 12.

5. Conclusions

In this paper, we propose a fast CU partitioning method based on deep learning for V-PCC, targeting the demand for efficient encoding in the context of 5G. By analyzing the V-PCC encoding process, we identify that the high dimensionality of dynamic 3D point cloud data and the large number of empty pixels generated during projection are the main sources of encoding complexity. To address these challenges, we design an adaptive partitioning strategy that leverages occupancy information. Specifically, we employ a CNN to perform adaptive partitioning for different regions and further optimize the partitioning strategy using Bayesian optimization when the CNN output has low confidence. The proposed algorithm, which combines a multi-level CNN framework and Bayesian optimization, reduces redundant computations and adopts flexible partitioning strategies for regions of varying complexities. This approach effectively enhances the compression efficiency and reconstruction quality of V-PCC geometry image encoding. Experimental results demonstrate that the proposed adaptive CU partitioning method based on CNN and Bayesian optimization achieves superior compression performance in both point cloud geometry and attribute image encoding, with encoding time savings of 57.37% and 54.43%, respectively. Moreover, compared with existing methods, our approach exhibits only a marginal increase in the BD rate, with negligible impact on video quality. Notably, it shows significant advantages in partitioning optimization for dense and low-confidence regions. In the future, we will continue to explore ways to improve the encoding performance of V-PCC, with a focus on power consumption reduction, and will further investigate other potential applications of deep learning in point cloud compression.