Application of Deep Dilated Convolutional Neural Network for Non-Flat Rough Surface
Abstract
:1. Introduction
- We present a DDCNN architecture designed for the reconstruction of periodic non-flattened surfaces. Notably, this approach is able to reconstruct the period, permittivity and shape of the rough surface simultaneously.
- Our numerical simulations demonstrate the robustness and precision of the proposed DDCNN architecture across varying noise conditions.
- The findings of this study highlight the pivotal role of AI in the reconstruction of surface coefficients. We delineate a hierarchy of reconstruction priorities during the training process: the primary focus is on achieving a surface period, followed by the secondary goal of estimating the dielectric constant, with the shape factor representing the final target. This prioritization arises from the varying sensitivities of each coefficient to the scattered field data, indicating an intricate interplay between these parameters in the reconstruction process.
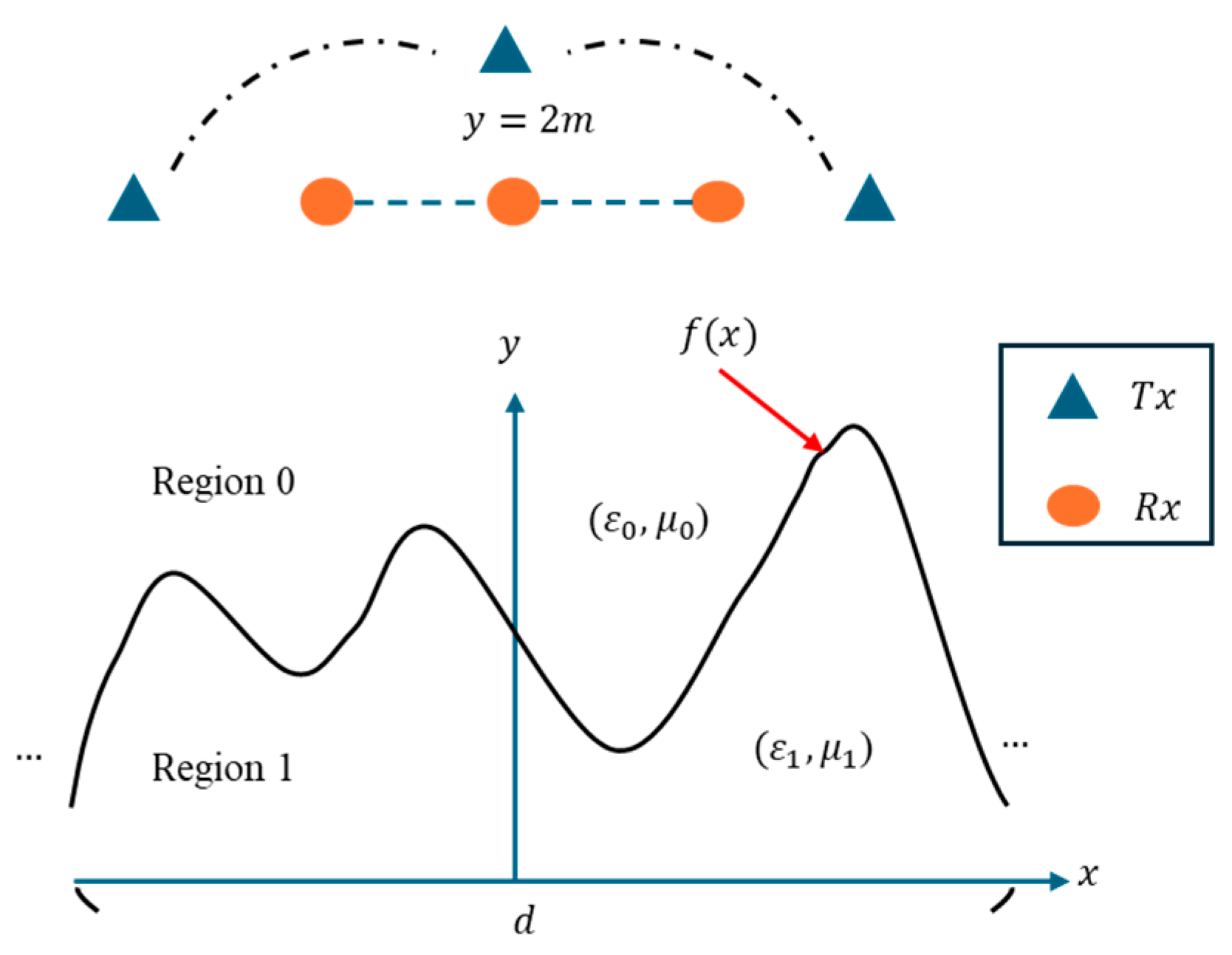
2. Formula and Theory
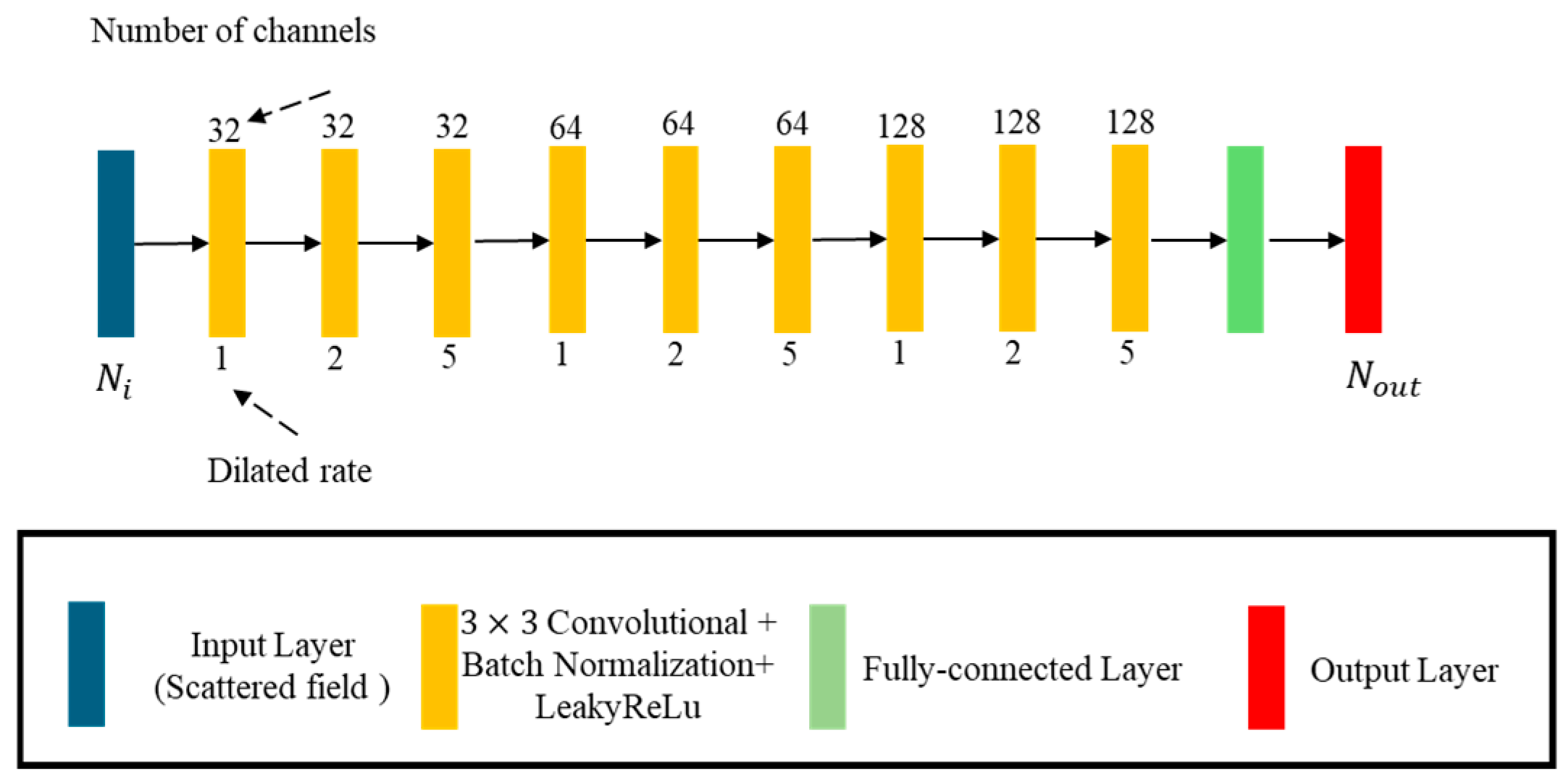
3. Deep Dilated Convolutional Neural Network
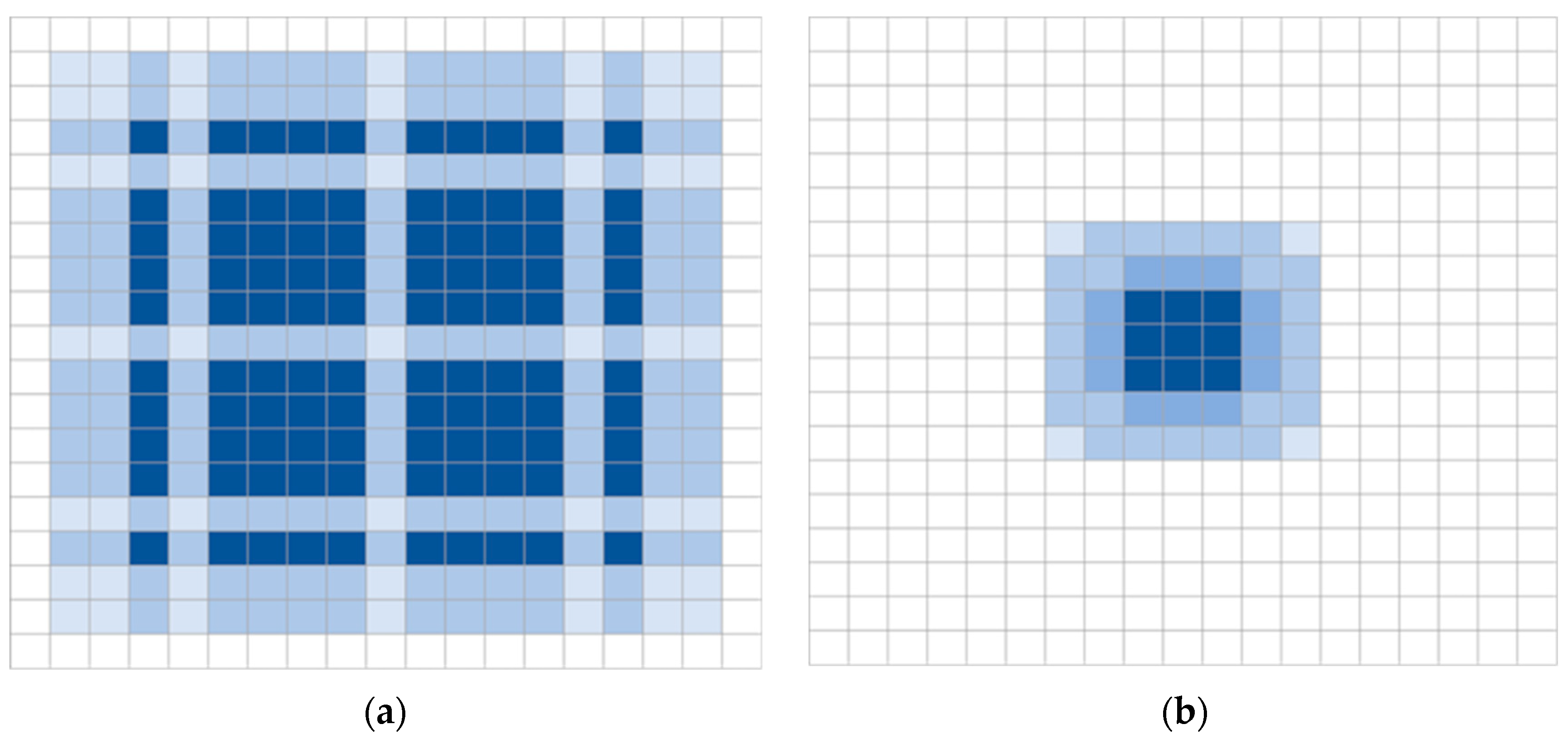
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- El-Shenawee, M.; Miller, E.L. Multiple-Incidence and Multifrequency for Profile Reconstruction of Random Rough Surfaces Using the 3-D Electromagnetic Fast Multipole Model. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2499–2510. [Google Scholar]
- Firoozabadi, R.; Miller, E.L.; Rappaport, C.M.; Morgenthaler, A.W. Subsurface Sensing of Buried Objects Under a Randomly Rough Surface Using Scattered Electromagnetic Field Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 104–117. [Google Scholar]
- Chen, Y.; Spivack, M. Rough Surface Reconstruction at Grazing Angles by an Iterated Marching Method. J. Opt. Soc. Am. A 2018, 35, 504–513. [Google Scholar]
- Chiu, C.C.; Chan, M.K. Microwave Imaging of Periodic Rough Surfaces. Microw. Opt. Technol. Lett. 2018, 60, 1719–1727. [Google Scholar]
- He, H.J.; Zhang, Y. An Effective Method for Electromagnetic Scattering from a Coated Object Partially Buried in a Dielectric Rough Surface. J. Electromagn. Waves Appl. 2020, 35, 754–765. [Google Scholar] [CrossRef]
- Sefer, A.; Yapar, A. An Iterative Algorithm for Imaging of Rough Surfaces Separating Two Dielectric Media. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1041–1051. [Google Scholar] [CrossRef]
- Sefer, A.; Yapar, A. Image Recovery of Inaccessible Rough Surfaces Profiles Having Impedance Boundary Condition. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3005105. [Google Scholar] [CrossRef]
- Özdemir, Ö.; Altuncu, Y. A Microwave Subsurface Imaging Technique for Rough Surfaces. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3003205. [Google Scholar]
- Sefer, A.; Yapar, A.; Yelkenci, T. Imaging of Rough Surfaces by RTM Method. IEEE Trans. Geosci. Remote Sens. 2024, 62, 2003312. [Google Scholar]
- Aydin, İ.; Budak, G.; Sefer, A.; Yapar, A. CNN-Based Deep Learning Architecture for Electromagnetic Imaging of Rough Surface Profiles. IEEE Trans. Antennas Propag. 2022, 70, 9752–9763. [Google Scholar] [CrossRef]
- Aydin, İ.; Budak, G.; Sefer, A.; Yapar, A. Recovery of Impenetrable Rough Surface Profiles via CNN-Based Deep Learning Architecture. Int. J. Remote Sens. 2022, 43, 658–5685. [Google Scholar] [CrossRef]
- Chiu, C.C.; Ho, C.S. Image Reconstruction of a Two-Dimensional Periodic Conductor by the Genetic Algorithm. J. Electromagn. Waves Appl. 2001, 15, 1175–1188. [Google Scholar] [CrossRef]
- Bourlier, C.; Pinel, N.; Kubicke, G. Method of Moments for 2D Scattering Problems: Basic Concepts and Applications, 1st ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
- Ishimaru, A. Electromagnetic Wave Propagation, Radiation, and Scattering; Prentice-Hall: Hoboken, NJ, USA, 1991. [Google Scholar]
- Yu, F.; Koltun, V. Multi-Scale Context Aggregation by Dilated Convolutions. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]


| Period | 0.04 | 0.06 | 0.083 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Noise | DP | DEPS | DF | DP | DEPS | DF | DP | DEPS | DF | |
| 5% | 0.09% | 0.01% | 10.45% | 0.12% | 0.1% | 10.65% | 0.1% | 0.01% | 7.32% | |
| 10% | 0.1% | 0.01% | 10.94% | 0.26% | 0.13% | 13.09% | 0.1% | 0.02% | 7.90% | |
| 15% | 0.12% | 0.02% | 12.06% | 0.33% | 0.19% | 16.58% | 0.13% | 0.02% | 9.45% | |
| 20% | 0.14% | 0.03% | 15.93% | 0.41% | 0.26% | 23.28% | 0.15% | 0.03% | 10.34% | |
| Period | DCNN | DDCNN | |||||
|---|---|---|---|---|---|---|---|
| Noise | DP | DEPS | DF | DP | DEPS | DF | |
| 5% | 0.18% | 0.32% | 13.9% | 0.1% | 0.01% | 7.32% | |
| Period | 0.083 | |||
|---|---|---|---|---|
| Noise | DP | DEPS | DF | |
| 10% | 0.1% | 0.02% | 8.80% | |
| 15% | 0.15% | 0.03% | 10.45% | |
| 20% | 0.21% | 0.04% | 11.34% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiu, C.-C.; Lee, Y.-H.; Chien, W.; Chen, P.-H.; Lim, E.H. Application of Deep Dilated Convolutional Neural Network for Non-Flat Rough Surface. Electronics 2025, 14, 1236. https://doi.org/10.3390/electronics14061236
Chiu C-C, Lee Y-H, Chien W, Chen P-H, Lim EH. Application of Deep Dilated Convolutional Neural Network for Non-Flat Rough Surface. Electronics. 2025; 14(6):1236. https://doi.org/10.3390/electronics14061236
Chicago/Turabian StyleChiu, Chien-Ching, Yang-Han Lee, Wei Chien, Po-Hsiang Chen, and Eng Hock Lim. 2025. "Application of Deep Dilated Convolutional Neural Network for Non-Flat Rough Surface" Electronics 14, no. 6: 1236. https://doi.org/10.3390/electronics14061236
APA StyleChiu, C.-C., Lee, Y.-H., Chien, W., Chen, P.-H., & Lim, E. H. (2025). Application of Deep Dilated Convolutional Neural Network for Non-Flat Rough Surface. Electronics, 14(6), 1236. https://doi.org/10.3390/electronics14061236








