An Effective Path Planning Method Based on VDWF-MOIA for Multi-Robot Patrolling in Expo Parks

Abstract

Expo parks are characterized by dense crowds and a high risk of accidents. A multi-robot patrolling system equipped with multiple sensors can provide personalized services to visitors and quickly locate emergencies, effectively accelerating response times. This study focuses on developing efficient patrolling strategies for multi-robot systems. In expo parks, this requires solving the multiple traveling salesman problem (MTSP) and addressing multi-robot obstacle avoidance in static environments. The main challenge is to plan paths and allocate tasks effectively while avoiding collisions and balancing workloads. Traditional methods often struggle to optimize task allocation and path planning at the same time. This can lead to an unbalanced distribution of patrol tasks. Some robots may have too much workload, while others are not fully utilized. In addition, poor path planning may increase the total patrol length and reduce overall efficiency. It can also affect the coordination of the multi-robot system, limiting its scalability and applicability. To solve these problems, this paper proposes a multi-objective immune optimization algorithm based on the Van der Waals force mechanism (VDWF-MOIA). It introduces an innovative double-antibody coding scheme that adapts well to environments with obstacles, making it easier to represent solutions more diversely. The algorithm has two levels. At the lower level, the path cost matrix based on vector rotation-angle-based obstacle avoidance (PCM-VRAOA) calculates path costs and detour nodes. It effectively reduces the total patrol path length and identifies optimal obstacle avoidance paths, facilitating collaborative optimization with subsequent task allocation. At the higher level, a crossover operator inspired by the Van der Waals force mechanism enhances solution diversity and convergence by enabling effective crossover between antibody segments, resulting in more effective offspring. The proposed algorithm improves performance by enhancing solution diversity, speeding up convergence, and reducing computational costs. Compared to other algorithms, experiments on test datasets in a static environment show that the VDWF-MOIA performs better in terms of total patrol path length, load balancing metrics, and the hypervolume (HV) indicator.

1. Introduction

Expo parks are important cultural and entertainment centers, characterized by complex layouts, high visitor density, and unpredictable events. Currently, they rely on human patrols and CCD positioning monitoring, but these approaches cannot meet the security requirements at night. Combining monitoring patrols with security robot patrols would be a better solution [1]. Compared to traditional wireless sensor networks, multi-robot systems offer greater flexibility, lower energy consumption, and enhanced security. Robots equipped with various sensors can autonomously perceive their surroundings. They effectively collect different types of information [2,3,4,5]. According to specific situational needs, patrol robots can provide diverse services. These include information consulting, interactive entertainment, and medical assistance [6]. This significantly enhances the intelligence level of the expo parks and enriches the visitor experience. When robots encounter abnormal situations, the central controller analyzes data transmitted by the sensors. It can quickly identify potential risks and direct the robots to respond promptly. This greatly improves the park’s risk prevention and control capabilities, ensuring its safety. Therefore, establishing a multi-robot patrolling system for real-time monitoring and environmental information collection is crucial for ensuring the safety of the park.

In recent years, multi-robot systems have become a popular research topic, with wide applications in ocean exploration, mining, and disaster rescue [7,8,9,10]. In large-scale scenarios, using a single robot to complete all tasks is very time-consuming. Compared to a single robot, multi-robot patrolling systems have clear advantages in handling complex tasks, as they can collaborate to improve both efficiency and coverage. Therefore, multi-robot collaboration to complete tasks is an inevitable trend [11]. Without considering the characteristics of the problem, randomly assigning tasks to robots or simply assigning tasks that are closer to each other to the same robot will result in low system efficiency [12]. Therefore, designing an effective patrolling strategy for the multi-robot patrolling system of expo parks is a worthwhile research topic.

Despite their advantages, implementing effective multi-robot patrolling systems in complex environments like expo parks still faces challenges. The multi-robot patrolling problem involves multiple robots continuously moving, reaching target points, and performing tasks in a given environment. Therefore, developing path planning algorithms to guide robots from start to end points without hitting obstacles is essential for patrolling robots in obstacle environments. As one of the core links of multi-robot systems, path planning technology has been widely applied [13]. Path planning studies typically define environments as either known or unknown, based on pre-identified maps. Additionally, environments are classified as static or dynamic, depending on whether obstacles change during robot movement [14]. The multi-robot patrolling problem in expo parks combines the MTSP with the obstacle avoidance path planning problem, making it NP-hard [15]. It involves assigning multiple patrol points to robots, optimizing their visiting order, and planning collision-free paths. Additionally, when finding the optimal patrol plan, two objectives are considered, rather than focusing on just one objective. The main objectives are to minimize the total patrol path length and balance workloads among robots. Therefore, the multi-robot patrolling problem is essentially a multi-objective optimization problem, making it more suitable to be solved using a multi-objective optimization algorithm [16]. The multi-objective nature makes the problem more complex. First, reducing the total patrol path may conflict with workload balance, as shorter paths can lead to uneven task distribution among robots. Second, optimizing both path planning and task allocation is a major challenge. Path planning must consider obstacle avoidance, while task allocation requires balanced workloads among robots. In obstacle environments, it is challenging for the algorithm to find the best patrol scheme in a short time. Advanced algorithms are needed to manage the trade-offs and balance path length with robot workloads.

The core challenge of the multi-robot system for the expo park is to achieve collaborative optimization between task allocation and path planning. For the multi-robot patrolling problem in an expo park, a simple and direct solution is to break it down into two steps: task allocation and path planning. First, tasks are assigned to multiple robots, and then the patrol path for each robot is optimized. Although the traditional step-by-step method is simple, it has several key issues. First, the partitioned solution space can lead to local optima. The task allocation stage does not consider the constraints of path planning, which restricts path optimization to a limited local space and prevents overcoming the suboptimal solution framework formed by task allocation. Second, the step-by-step approach limits global path optimization. The process is split into independent stages, which prevents larger improvements. Lastly, the static task allocation strategy does not consider the robots’ actual movement costs, leading to poor load balancing in complex environments. Some robots accumulate tasks while others remain idle. These problems arise because the step-by-step optimization cannot integrate task allocation and path planning.

Therefore, for the multi-robot patrolling problem in a static environment, which is essentially the MSTP with obstacles, this study aims to develop an efficient multi-objective optimization algorithm that integrates task allocation and path planning. The algorithm seeks to balance shorter paths with equitable workload distribution among multiple robots. To address these issues, we propose a multi-robot patrolling algorithm that uses a synchronized decision-making mechanism, incorporating both task allocation and path planning into a unified optimization model. This model calculates the impact of path costs on task allocation in real time, breaking through the limitations of traditional methods. Specifically, a wireless sensor network is deployed in the expo park to gather prior environmental information. Sensors transmit the collected data to the central processor. By processing the sensor data, the central processor identifies high-risk areas that require patrolling by robots. Each robot in the multi-robot patrolling system is equipped with multiple sensors, such as infrared sensors [17], image sensors, sound sensors [18], and gas sensors [4]. The sensors collect information from the surrounding area, helping robots to patrol safely and perform special tasks. The robots share the collected information with each other along their paths. The central processor uses the patrol algorithm to achieve efficient patrol path planning for the multi-robot system. The control architecture diagram of the multi-robot patrolling system, as shown in Figure 1, comprises the decision layer, path planning layer, perception layer, and execution layer. The main contributions of this work are as follows:

• A multi-objective multi-robot patrolling problem for the expo park is proposed. This problem combines the multiple traveling salesman problem (MTSP) and obstacle avoidance, simultaneously optimizing multi-robot task allocation and path planning. The objectives include minimizing the total patrol path length and achieving balanced task distribution among robots.
• A path cost matrix method based on vector rotation-angle obstacle avoidance (PCM-VRAOA) is introduced. Before path optimization, this method calculates all feasible paths between patrol points and stores the path length and detour information. By establishing a global path cost matrix in the early stage of path planning, this method provides more reasonable obstacle avoidance paths and ensures better integration between path planning and task allocation, improving patrol path quality.
• A new multi-objective immune optimization algorithm, VDWF-MOIA, is proposed. This algorithm is designed to enhance global search ability and path optimization in complex multi-robot patrolling problems. It adopts a dual-antibody encoding scheme to represent patrol paths and introduces a crossover operator inspired by the Van der Waals force mechanism. This operator improves solution diversity and convergence speed, effectively establishing a collaborative optimization mechanism between task allocation and path planning.

The remaining part of this paper consists of the following parts: Section 2 discusses related work, Section 3 states the multi-robot patrolling problem in the expo park, Section 4 describes our proposed optimization algorithm, and Section 5 presents simulation experiments and a comparison with other methods. The conclusion and a discussion of future work are finally presented in Section 6.

2. Related Work

Heuristic algorithms are effective methods for solving multi-robot path planning problems. Although they were initially designed for single-objective optimization, researchers have developed innovative mechanisms to adapt them for multi-objective optimization problems. As we aim to improve immune algorithms for solving the multi-robot patrolling problem, this section discusses the use of heuristic algorithms in addressing multi-robot path planning and multi-objective optimization.

2.1. Multi-Robot Path Planning Problem

In the past decades, various methods have been proposed to solve robot path planning problems. Broadly, traditional path planning methods can be divided into two categories: classical algorithms and heuristic algorithms. Classical methods, such as the cell decomposition scheme, potential field method, and sampling-based method, can guarantee optimal robot motion asymptotic. However, further studies have shown that these methods often lead to high computational costs and can easily be trapped in local minima values [19]. In order to overcome the defects of classical algorithms, heuristic algorithms have been developed, including neural networks, fuzzy logic, and nature-inspired algorithms (NIAs) [20].

As multi-robot systems are being increasingly applied in various fields, such as logistics delivery [21], environmental monitoring [22], counter-terrorism tasks [23], and disaster rescue [24,25,26], the requirements for different tasks are also expanding. Multi-robot systems now face increasingly complex scenarios. As a result, many researchers and engineers have focused on solving the multi-robot path planning problem in real-world environments, such as rugged terrain [27], underwater settings [28], and nuclear power stations [29]. In this paper, an important issue for the multi-robot patrolling system in expo parks is how to achieve effective multi-robot path planning. Researchers have made many efforts to address this problem.

According to whether prior map information is available, existing works can be divided into two types. One type is local path planning methods, which do not need any prior knowledge of the environment. Robots can use sensor data to plan their actions autonomously and respond to unexpected events. There are Simultaneous Localization and Mapping (SLAM) algorithms that allow robots to build maps of the environment. Combining SLAM with other navigation mechanisms can improve efficiency [30]. A widely used approach is the potential field method, which generates artificial attraction, repulsion, and alignment forces [31,32,33,34,35]. Multiple robots can share information and collaborate in navigation to jointly plan the optimal movement path [36,37]. The other type is the global path planning method. This method assumes that the robot receives environmental map information before path planning. This map can include all static obstacles and boundaries in the area. In this case, the optimal path is calculated based on prior map information. This paper mainly focuses on multi-robot path planning with known map information. The Dijkstra algorithm, popular in graph theory, is used to find the shortest path between nodes in an environment graph, making it effective for path planning problems [38]. Wu et al. used the Dijkstra algorithm to optimize path planning in urban traffic [39]. Compared to the Dijkstra algorithm, the A* algorithm has a notable heuristic function. It can predict the minimum cost between the current node and the goal, enabling A* to find more efficient paths. Ref. [40] proposes a path planning method that combines the A* algorithm with obstacle tangents for obstacle avoidance. Chen et al. uses the A* algorithm for global planning. Cubic spline functions are used to generate a set of candidate paths, ensuring path smoothness and obstacle avoidance. The optimal path is determined by adjusting the weight function [41]. Additionally, various alternative algorithms have been introduced: Collaborative A*, Hierarchical Collaborative A* (HCA*), Windowed HCA*, D*Lite [42], and M* [43,44]. However, graph-based methods have high computational complexity. Therefore, the need for intelligent algorithms increases when addressing more complex path planning problems. The genetic algorithm (GA) is a global search method. It optimizes paths through natural selection, crossover, and mutation [45]. Hao et al. optimizes the traditional genetic algorithm. They propose a global path planning method based on an adaptive genetic algorithm [46]. To improve exploration performance, Cui et al. introduces the teaching–learning-based optimization strategy to simultaneously determine the next position of all robots [47]. To enable robots to visit multiple target points and handle uncertainties in a known environment, ref. [48] further develops the Feedback-based Information Road Map (FIRM) to handle map uncertainties as a solvable Markov decision process. It achieves real-time replanning by combining offline and online algorithms.

Despite the emergence of various path planning algorithms, a single algorithm often struggles to meet practical requirements. Many scholars have found that combining multiple path planning methods can achieve better results [49,50,51,52,53]. Ref. [49] introduces logistic mapping in the immune algorithm (IA) to improve optimization. It combines the mutation and crossover operators of GA with the designed IA, enhancing antibody diversity during iterations. Ref. [50] uses an improved k-means clustering algorithm to divide the global map. Then, it uses a simulated annealing algorithm (SA) to compute the shortest patrol path for robots within the partitioned sub-maps. Ref. [51] presents a hybrid algorithm for global path planning of coal mine patrol robots, combining an improved artificial fish swarm algorithm with the dynamic window approach. However, these methods are not suitable for situations where robots have multiple target points. Ref. [52] adopts a centralized approach to task allocation and path planning. It uses GA for task allocation and A* for path planning. However, the A* algorithm requires storing all traversed paths, consuming significant memory and creating redundant paths. To improve the efficiency of iterative search, ref. [53] proposes the APF-IBRRT* algorithm, which integrates the Artificial Potential Field (APF) with an improved Bidirectional Rapidly-exploring Random Tree (B-RRT*). This algorithm addresses the local optima issue of traditional APF through potential field factor optimization and virtual obstacle introduction. It further designs a target threshold and an adaptive step size search strategy to improve tree search efficiency in narrow environments.

In recent years, reinforcement learning (RL) and deep learning (DL) have been used to improve multi-robot path planning. RL-based methods, such as signed-distance-field-based formation path planning (SDF-FPP), use rewards to learn better formation control and collision avoidance in static environments [54]. Deep Q-learning (DQN) helps optimize path planning by reducing redundant exploration with experience replay [55]. Hierarchical RL strategies, like TIHDP, enhance multi-robot cooperation by adapting to changing robot and object numbers. Its dynamic task priority layer optimizes resource allocation using global object data and inter-robot communication, ensuring efficient collaboration in dynamic environments [56]. However, reinforcement learning requires large training datasets and long training times. Deep learning models also have high inference delays, making real-time applications difficult. Beyond RL and DL, adaptive learning helps robots make better real-time decisions in dynamic environments. For example, an adaptive H_∞ control strategy was proposed for cruise control systems. It uses data-driven learning to estimate unknown system dynamics and update control strategies online [57]. This method shows how adaptive estimators and real-time learning can handle dynamic uncertainties well.

Table 1. Comparison of different types of multi-robot path planning algorithms.

Algorithm	Type	Advantage	Drawback
Dijkstra/A*	graph-based search	ensure the shortest path	high computational complexity
GA	metaheuristic algorithm	strong global search ability	complex parameter tuning
APF	local planning algorithm	strong dynamic real-time performance	prone to fall into local optimum
SDF-FPP	hierarchical reinforcement learning	suitable for unknown environments	limited dynamic obstacle avoidance capability
APF-IBRRT*	hybrid algorithm	improve the search efficiency in narrow environments	large memory consumption
Deep Q-learning	deep reinforcement learning	adapt to complex environments	long training time

provides a concise summary of several different types of path planning algorithms.

2.2. Multi-Objective Optimization Algorithm

The multi-robot patrolling problem we address involves multiple targets. To address this kind of problem, some researchers have proposed multi-objective optimization for robot paths. The most direct way to solve a multi-objective optimization problem is to transform it into multiple single-objective optimization problems [58]. In [59,60], this transformation is achieved using weighted coefficients. While this method is simple, determining the weights scientifically is challenging. The resulting path is often just a compromise among several objectives.

Another approach is heuristic algorithms based on the Pareto-optimal set. This method provides a good solution for multi-objective optimization problems (MOPs), as it requires minimal mathematical operations and can generate satisfactory solutions [61]. Ref. [62] proposes an improved NSGA-II-based multi-objective optimization method for path planning in static environments. It uses discrete encoding, and introduces total path length and turning count as dual objectives, optimizing energy consumption as well. This method produces a better, diversified set of solutions in obstacle environments. Ref. [63] presents a Pareto front approximation method based on “regret” sampling. It gradually adds weight vectors using a greedy algorithm, ensuring even coverage of the Pareto front while providing clear error bounds. This achieves more efficient and accurate solutions in multi-objective optimization problems. Ref. [64] proposes a multi-objective discrete artificial bee colony algorithm. It combines a heuristic allocation method based on load balancing and a multi-objective local search strategy for non-dominated solutions. This ensures diversity and effectiveness of the initial solutions, achieving faster convergence and greater stability.

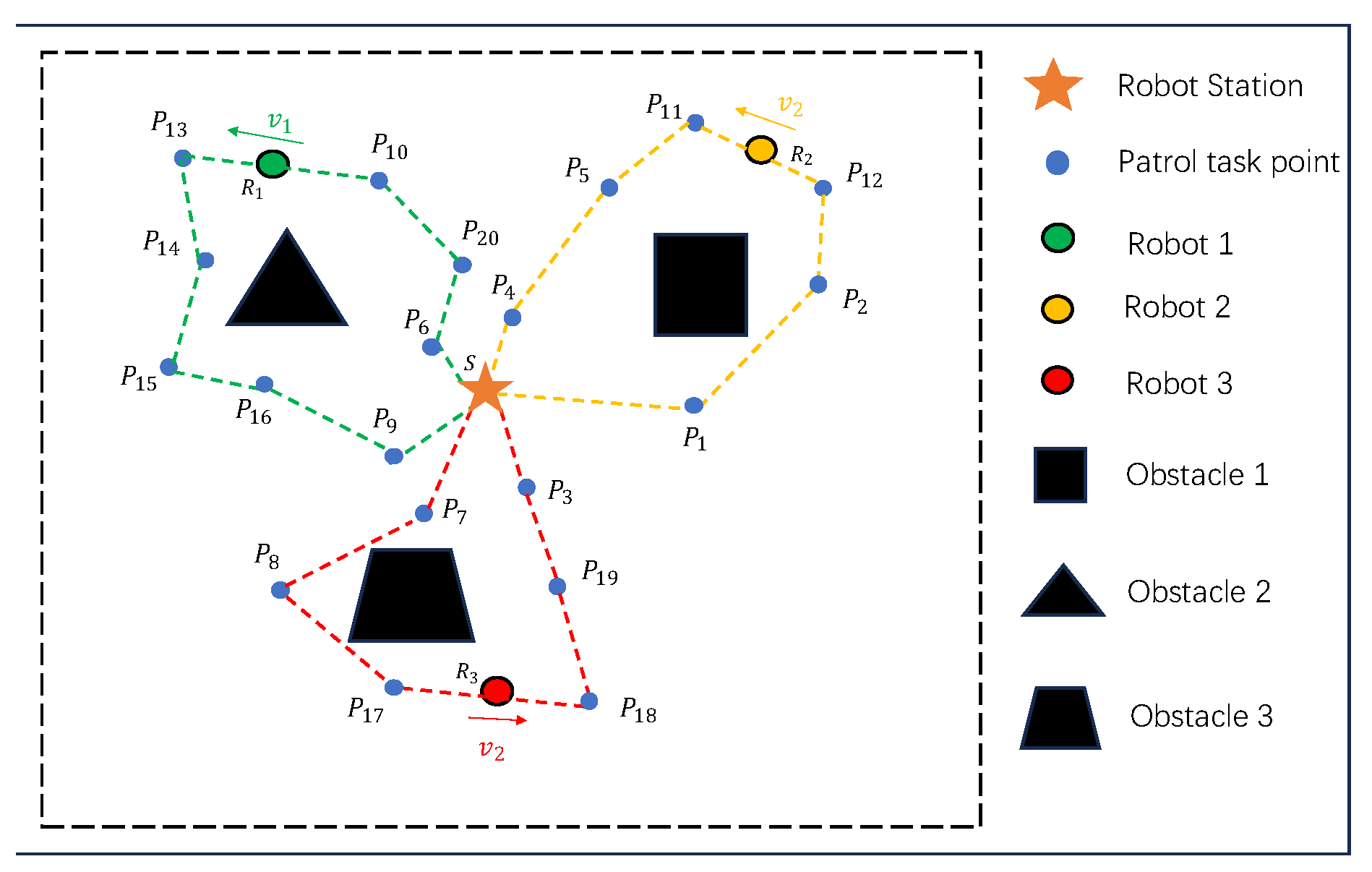
3. Multi-Robot Patrolling Problem

The multi-robot patrolling problem is one of the important components of studying multi-robot systems. This article mainly researches a multi-robot patrolling system for expo parks with multiple static obstacles.

3.1. Problem Statement

Firstly, construct a model of the expo park environment, where the exhibition halls are represented as convex polygonal obstacles. Then, install a set number of patrol points within the expo park as patrol tasks for the multi-robot system, and establish a robot station containing multiple operational robots. The environment modeling is illustrated in Figure 2. During a patrol cycle, each patrol point needs to be visited once by a robot without repetition. Robots depart from the robot station, execute all patrol tasks, and then return to the robot station.

In order to save energy costs, it is necessary to make the total patrol path length as short as possible. Here, the first objective function is introduced to minimize the total patrol path length of multiple robots. Additionally, to ensure balanced workload distribution among robots due to their limited energy capacity, the second optimization objective aims to minimize the standard deviation of patrol path lengths for each robot. In summary, this problem is a dual-objective optimization problem. The two objectives, namely minimizing the total patrol path length and minimizing the standard deviation of the patrol path length for each robot, are interconnected and mutually constraining.

3.2. Mathematical Model

First, we define all the variables that will be used:

$R=\{\mathrm{1,2},\dots ,m\}$: Set of robots.

$P=\{\mathrm{1,2},\dots ,n\}$: Set of patrol points.

$S$: Robot station (start/end point).

${\kappa }_{ijk}\in \left\{\mathrm{0,1}\right\}$: Binary variable where ${\kappa }_{ijk}=1$ if robot $k$ travels from $i$ to $j$ ($i,j\in P\cup \left\{S\right\}$), else 0.

$D=\left[d_{ij}\right]$: Distance matrix. $d_{ij}$ is the obstacle-avoiding shortest path between $i$ and $j$.

The calculation formula for $d_{ij}$, $L_k$ and $\overline{L}$ is as follows:

$$d_{ij}=\left\{\begin{array}{c}\sqrt{{(x_i-x_j)}^2-{(y_i-y_j)}^2},if no obstacles between i and j\\ avoidance obstacles distance between i and j\end{array}\right.$$

(1)

$$L_k={\sum }_{i=1}^n{\sum }_{j=1,j\ne i}^n{\kappa }_{ijk}·d_{ij}, \forall k\in R$$

(2)

$$\overline{L}={\displaystyle \frac{1}{m}}{\sum }_{k=1}^m{L}_k,\forall k\in R$$

(3)

In addition, we also need to set the maximum and minimum number of patrol tasks for a single robot, represented by the symbols $T_{min}$ and $T_{max}$, respectively.

Based on the definitions provided above, we can formulate our multi-robot patrolling problem as follows:

$$\min f_1={\sum }_{k=1}^m{\sum }_{i\in p\cup \left\{S\right\}}{\sum }_{j\in p\cup \left\{S\right\}}{d}_{ij}{\kappa }_{ijk}$$

(4)

$$min{f}_2=\sqrt{{\displaystyle \frac{1}{m}}{\sum }_{k=1}^m{(L_k-\overline{L})}^2}$$

(5)

s. t.

$${\sum }_{k=1}^m{\sum }_{j=1,j\ne i}^n{\kappa }_{ijk}=1, \forall i\in P$$

(6)

$${\sum }_{j=1}^n{\kappa }_{Sjk}=1, \forall k\in R$$

(7)

$${\sum }_{i=1}^n{\kappa }_{isk}=1, \forall k\in R$$

(8)

$$T_{min}\le {\sum }_{i\in P}{\sum }_{j\in P\cup \left\{S\right\},j\ne i}{\kappa }_{ijk}\le T_{max}, \forall k\in R$$

(9)

Expressions (4) and (5) represent two optimization objectives stated in the previous subsection, which stand for minimizing the total patrolling path length and minimizing the standard deviation of patrol path lengths for each robot. Constraint (6) ensures that each patrol point is visited once and not repeatedly accessed. Constraint (7) guarantees that each robot departs from the robot station. Constraint (8) restrains each robot returns to the robot station after completing the last patrol task. Constraint (9) means that the number of patrol tasks performed by a single robot is greater than $T_{min}$ but less than $T_{max}$.

3.3. Problem Complexity

The multi-robot patrolling problem for expo parks is classified as NP-hard due to its complexity, which comes from two main factors: the combinatorial nature of the MTSP and the presence of polygonal obstacles. The MTSP, even without obstacles, is NP-hard because the number of possible solutions grows exponentially as the number of patrol points increases. Obstacles make the problem even harder since calculating obstacle-avoiding paths between patrol points adds computation. The combination of task allocation and obstacle-aware path planning further increases complexity, making large-scale instances difficult to solve. Additionally, constraints like $T_{min}$ and $T_{max}$ limit the solution space, affecting both feasibility and solution quality. These constraints help balance the workload, but they need careful tuning. If the limits are too strict, optimal task assignments may be ruled out. If they are too loose, some robots may be overworked while others are underused. For example, a high $T_{min}$ might exceed a robot’s energy capacity, while a low $T_{max}$ could leave robots idle. These parameters should match the robots’ capabilities (e.g., battery life) to ensure both efficiency and feasibility.

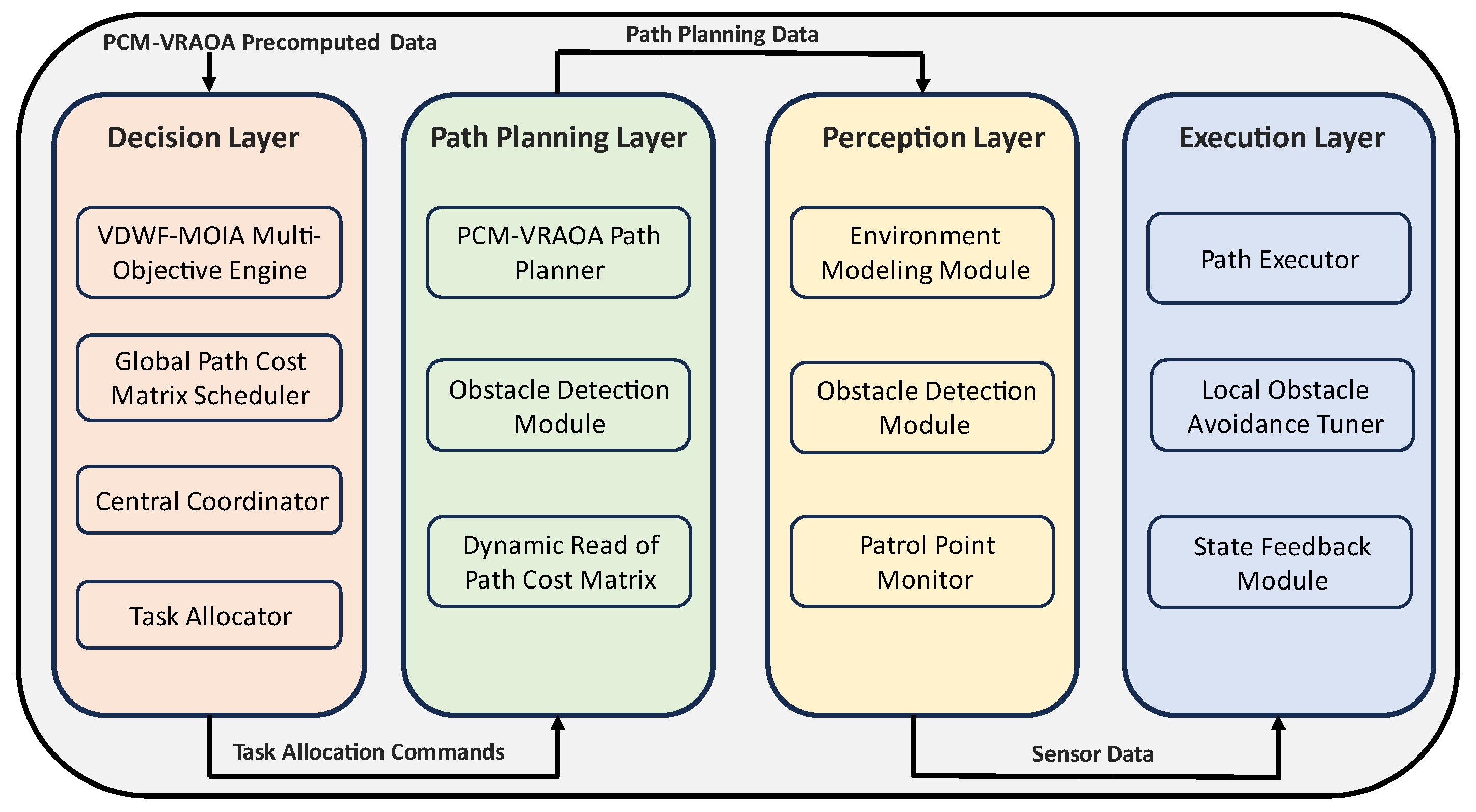
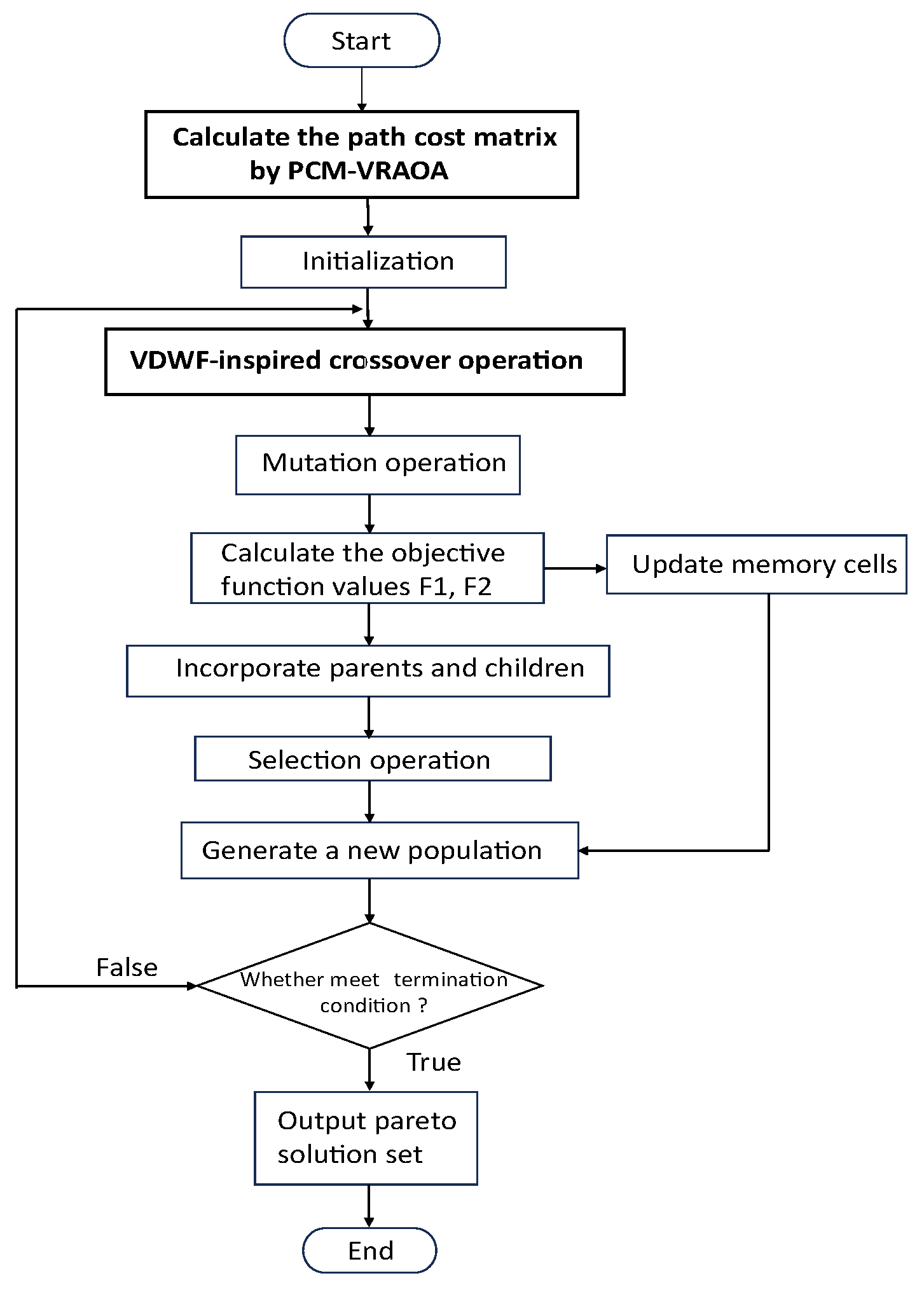
4. Multi-Objective Immune Algorithm with Van Der Waals Force Mechanism

The multi-robot patrolling problem in expo parks, as described in Section 3.1, involves two main tasks. The first task is to assign patrol points to each robot and determine the optimal patrol order. The second task is to plan collision-free paths for multiple robots to complete their patrol tasks efficiently. A traditional way to solve this problem is optimizing task allocation and path planning separately. However, this method is prone to getting trapped in a local optimum. The core problem is that it overlooks their interdependence. Treating them independently means optimizing one task can harm the other. Thus, the final solution is likely suboptimal, restricted to a less-than-ideal result within a limited search space. To address this limitation, we propose the VDWF-MOIA, a unified framework that simultaneously optimizes task allocation and path planning. It ensures their interdependence is fully considered, leading to a globally optimal solution. The VDWF-MOIA builds on the artificial immune optimization algorithm but overcomes its limitations. Traditional immune algorithms struggle to converge efficiently due to the large solution space, but the VDWF-MOIA incorporates a Van der Waals force mechanism to improve exploration and convergence. The complete flowchart is shown in Figure 3.

4.1. Antibody Encoding

In the immune optimization algorithm, antibodies represent solutions to the problem. Considering traditional binary coding has the problem of a long bit string when facing large-scale problems, this paper adopts real number coding [65]. To address the problem in this paper, a novel antibody coding scheme called double-antibody encoding with virtual points is devised. Figure 4 shows a pair of antibodies, which map to each other and represent a solution to the problem. The first antibody is divided into two parts. In the first part, each gene position represents a patrol point, and the sequence of genes determines the patrol point visit order. In the second part, each gene position indicates the number of patrol tasks assigned to the corresponding robot. The second antibody is mapped from the first antibody. Here, 0 marks a break point to separate different patrol task sequences for each robot. The floating-point number represents the virtual patrol point, which is actually an obstacle detour node. The real part represents the obstacle serial number, and the decimal part represents the obstacle detour node serial number. Thus, the second antibody can represent the final patrol path of each robot, which is a feasible solution.

4.2. Affinity Calculation and Pareto-Optimal Solutions

The affinity values are calculated according to (4) and (5). In a multi-objective problem, each objective conflicts with the others. Optimizing one objective may impact the performance of the others simultaneously. Thus, there is not a single optimal solution but rather a set of optimal solutions. Given this analysis, selecting the optimal solution directly based on affinity values is not feasible. Therefore, we introduce the concept of Pareto-optimal solutions [66] to identify promising individuals.

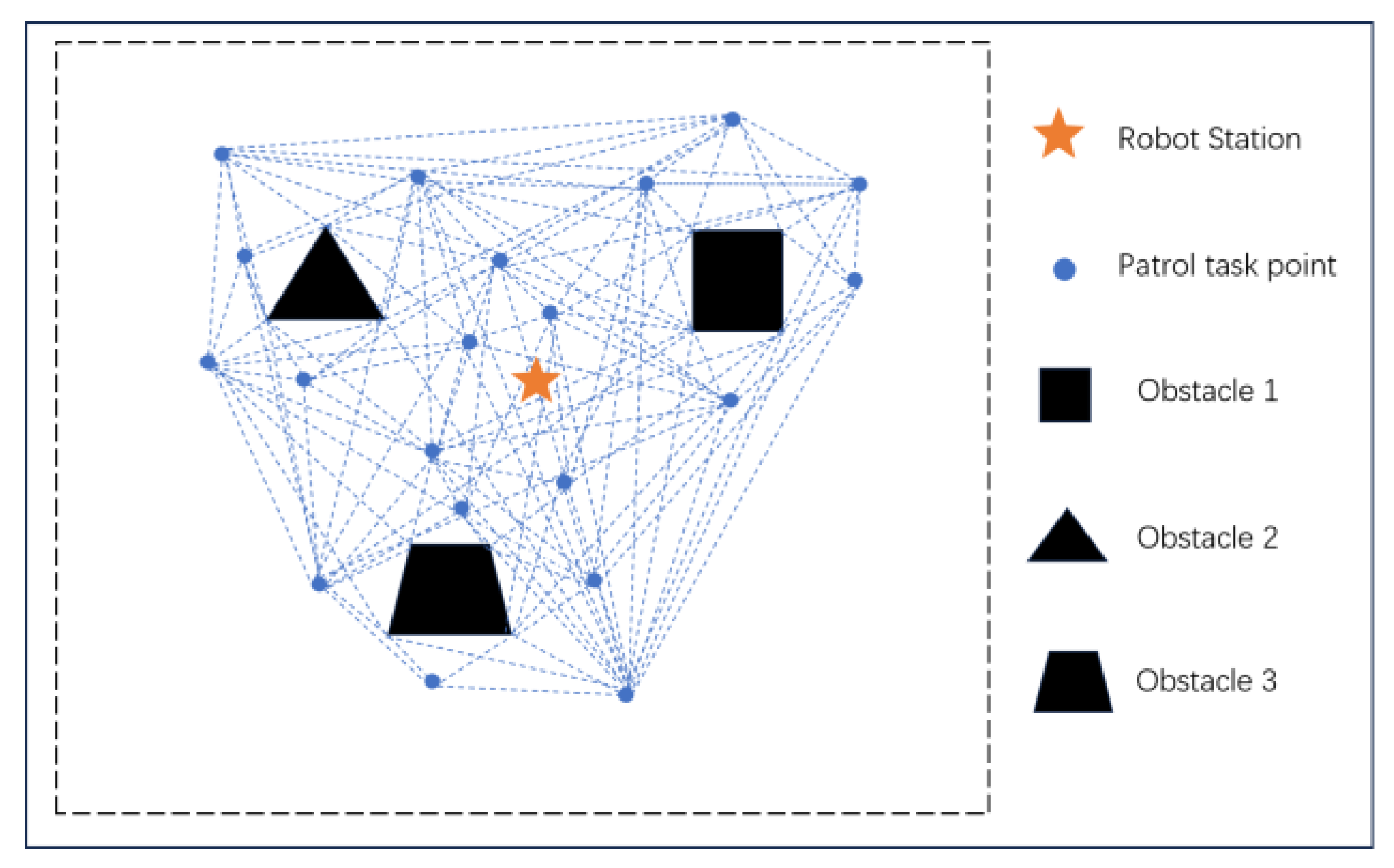
4.3. Path Cost Matrix Based on Vector Rotation-Angle-Based Obstacle Avoidance

We propose a path cost matrix based on vector rotation-angle obstacle avoidance algorithm (PCM-VRAOA) for multi-robot path planning. The implementation involves four key phases:

(1)

Vector Polar Angle Calculation: For each obstacle vertex $O_i=(x_i,y_i)$, the algorithm calculates the rotation angle $\theta$ relative to the robot’s current position $r=(x_r,y_r)$, using Formula (10):

$${\theta }_i=\arctan 2\left(y_i-y_r , x_i-x_r\right)$$

(10)

This formula computes the angle between the horizontal axis and the line connecting the robot to the vertex. These angles form an ordered sequence to identify critical detour nodes.

(2)

Bidirectional Search Strategy: The algorithm simultaneously explores two paths—one following maximum-angle vertices (clockwise) and another tracking minimum-angle vertices (counter-clockwise). This dual-path approach ensures comprehensive obstacle boundary coverage, as illustrated in Figure 5.

(3)

Path Cost Evaluation: The total length L of each candidate path is computed as shown in Formula (11):

$$L=‖r\to O_1‖+{\sum }_{i=1}^{n-1}‖O_i\to O_{i+1}‖+‖O_n\to g‖$$

(11)

Here, $‖r_1\to O_1‖$ is the distance from the robot’s start position $r$ to the first detour node $O_1$, $‖O_i\to O_{i+1}‖$ represents the distance between consecutive detour nodes, and $‖O_n\to g‖$ is the distance from the last detour node $O_n$ to the goal $g$.

(4)

Dynamic Path Selection: The shortest valid path is chosen based on Formula (12):

$$L_{final}=\mathrm{m}\mathrm{i}\mathrm{n}(L_1,L_2)$$

(12)

where $L_1$ and $L_2$ are the lengths of the maximum-angle and minimum-angle paths, respectively. This ensures efficient navigation through complex environments.

By iterating this process across all patrol points, PCM-VRAOA constructs an $n\times n$ path cost matrix containing optimized detour nodes and precomputed path lengths. This matrix serves as a global navigation knowledge base, enabling rapid task allocation decisions. The visualization result of this path construction is shown in Figure 6. The complete calculation process, as shown in Figure 7, accepts map inputs such as patrol points, convex polygons, and robot stations, and outputs both collision-free paths and the cost matrix for multi-robot coordination.

4.4. Van Der Waals Force Mechanism

The Van der Waals force [67], also known as intermolecular force, is a type of interaction that widely exists between molecules, or between molecules and rare gas atoms. The magnitude of Van der Waals forces varies between different molecules. Essentially, the force is an attraction or repulsion between positive and negative charges. This interaction allows most substances to exist in a condensed state. The Van der Waals force cannot change the internal structure of molecules; it can only order the arrangement of molecules.

Inspired by this fundamental physical phenomenon, this paper introduces the Van der Waals force mechanism into multi-objective immune optimization algorithms. The flow chart of the Van der Waals force mechanism is shown in Figure 8. Firstly, antibodies are segmented into a certain number of gene fragments. These fragments are considered as molecules or atoms in the physical world, and the Van der Waals forces between gene fragments are defined. Secondly, the Van der Waals forces between gene fragments are calculated. These forces are calculated to accurately distinguish the importance of different gene fragments in parental antibodies. Gene fragments with larger Van der Waals forces are more likely to aggregate together, forming gene fragment pairs. Finally, crossover operations are performed on the matched gene fragments to generate new antibodies.

Compared to existing immune algorithms and their crossover operators, the Van der Waals force mechanism has significant advantages in the following aspects: First, compared to traditional crossover operators (such as order crossover, OX, and partially mapped crossover, PMX), the Van der Waals force mechanism intelligently matches similar gene fragments, avoiding inefficient crossover caused by randomness while maintaining path continuity and diversity. OX can preserve path continuity but lacks consideration of the intrinsic relationships between fragments, making it prone to local optima. PMX, due to its high randomness, may lead to ineffective crossover, reducing algorithm efficiency. Second, compared to classical immune algorithms, the Van der Waals force mechanism introduces a physical model to better utilize the structural information of the solution space, improving search efficiency and solution quality. Traditional immune algorithms typically rely on random crossover and mutation operations, lacking in-depth exploration of the solution space structure, resulting in lower search efficiency.

4.4.1. The Definition of Van Der Waals Force

The basic idea of designing the Van der Waals force calculation formula between any two gene fragments is straightforward. It considers two main factors: the length and gene value of each gene fragment. These factors affect the distance and similarity between fragments. The Van der Waals force between gene fragments is inversely proportional to their distance, and directly proportional to their similarity. Thus, the Van der Waals force formula between gene fragments a and b is defined as (13):

$$F_v(a,b)={\displaystyle \frac{S(a,b)}{{\left[d\right(a,b\left)\right]}^2}}$$

(13)

where $S(a,b)$ represents the similarity between gene fragments $a$ and $b$, as shown in (14), assuming that $L_a$ represents the length of gene fragment $a$ and $L_b$ represents the length of gene fragment $b$, and $L_a\le L_b$; $d(a,b)$ represents the distance between gene fragments a and b, as shown in (15), where $N(a,b)$ represents the number of identical gene values in gene fragments $a$ and $b$.

$$S\left(a,b\right)=1-{\displaystyle \frac{d\left(a,b\right)}{L_b+1}}$$

(14)

$$d\left(a,b\right)=L_a-N(a,b)$$

(15)

4.4.2. Theoretical Basis and Formal Proof

The theoretical foundation of the Van der Waals force formula is based on the physical model of intermolecular interactions. Specifically, the similarity $S(a,b)$ and distance $d(a,b)$ in the formula simulate the attraction and repulsion between molecules. The similarity $S(a,b)$ is defined as the cosine similarity between gene fragments $a$ and $b$, with a range of $[-\mathrm{1,1}]$, accurately reflecting the correlation between fragments. The distance $d(a,b)$ is defined as the Euclidean distance between gene fragments $a$ and $b$, and its inverse-square relationship ensures strong attraction for closely located fragments. This design not only aligns with physical laws but also effectively captures the intrinsic relationships between gene fragments. To further validate the effectiveness of Formulas (13)–(15), we provide the following formal proofs:

• Similarity Measure: Cosine similarity measures the directional consistency between gene fragments. A value closer to 1 indicates higher similarity, while a value closer to −1 indicates lower similarity.
• Distance Measure: The inverse-square relationship of Euclidean distance ensures strong attraction for closely located fragments while avoiding excessive influence from distant fragments.
• Convergence Analysis: Using a Markov chain model, we prove that the Van der Waals force mechanism ensures the algorithm converges to the global optimal solution within a finite number of iterations. Specifically, the optimization process can be modeled as a Markov chain, where each state represents the current solution, and state transitions are driven by the crossover operations of the Van der Waals force mechanism. The transition probability $P_{ij}$ is proportional to $F_v(a,b)$, i.e.,$P_{ij}\propto F_v\left(a,b\right)={\displaystyle \frac{S(a,b)}{{\left[d\left(a,b\right)\right]}^2}}$. The monotonicity of transition probabilities ensures that the algorithm gradually approaches better solutions while maintaining solution diversity through intelligent matching of similar fragments, avoiding local optima.

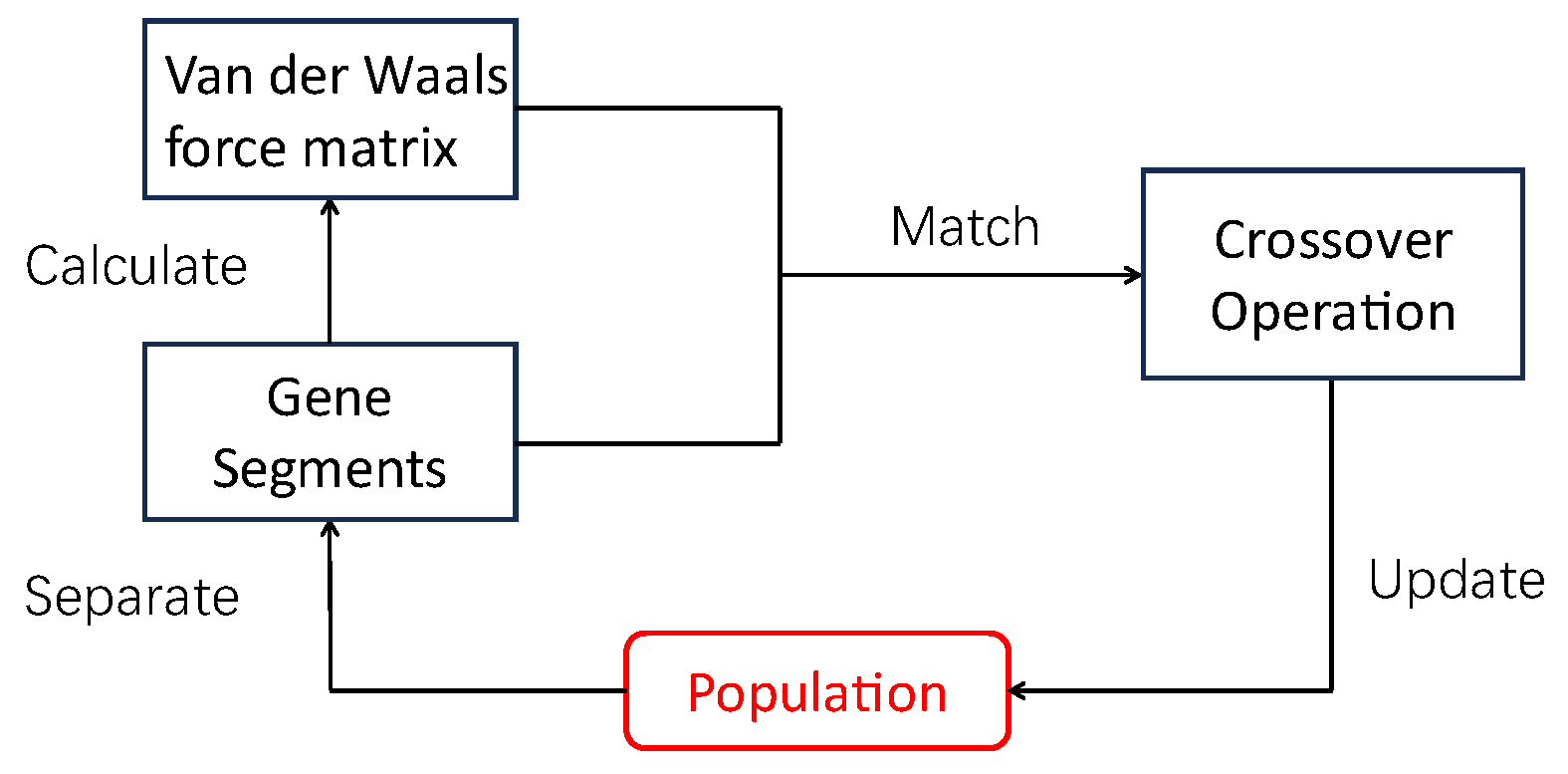
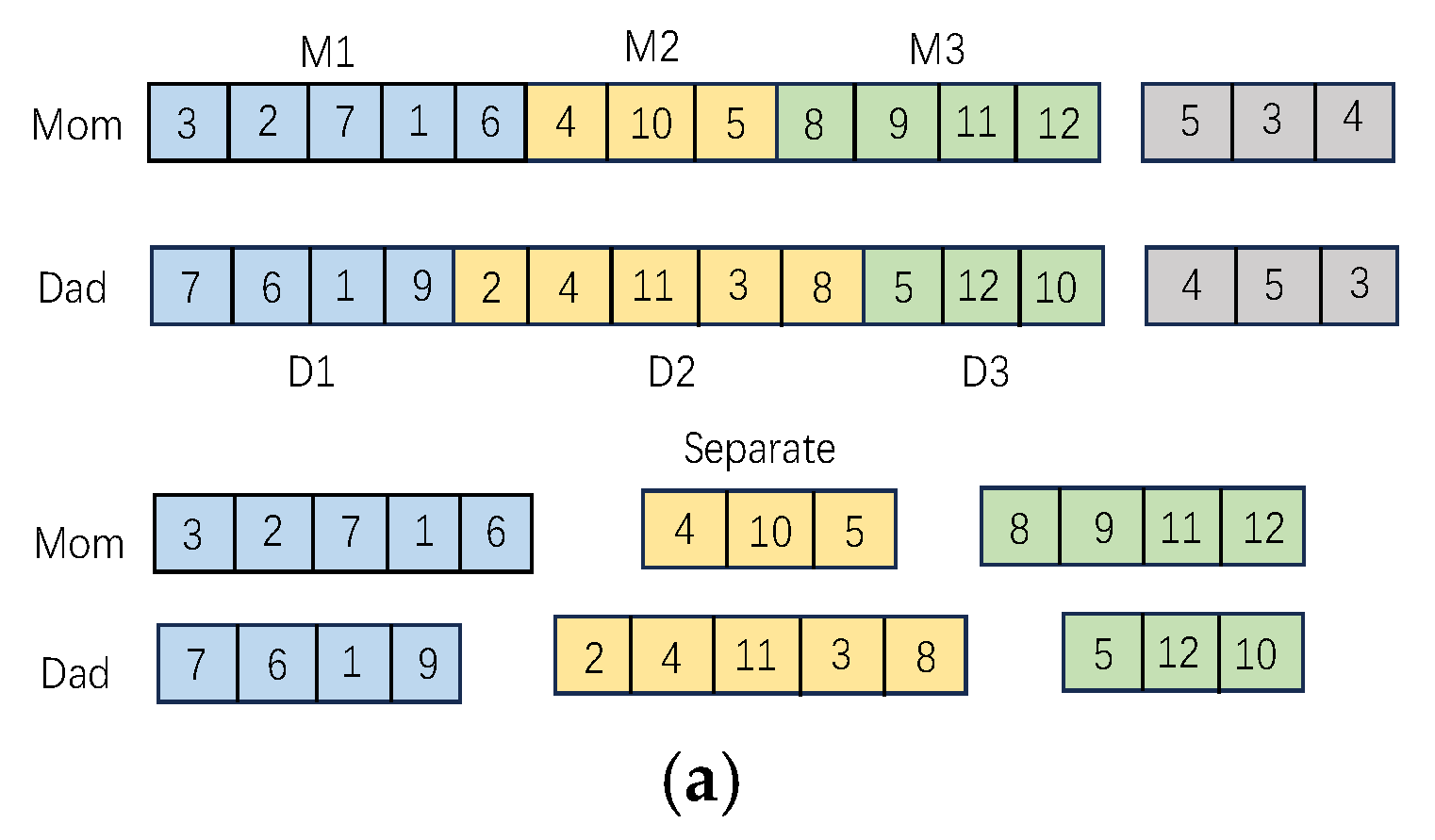
4.4.3. Gene Fragments Separating and Matching Process

This section explains in detail how to split and match the selected two parent antibodies. First, according to the gene representing the number of patrol points of each robot in the antibody, the gene representing the patrol point sequence is divided into different gene segments. Each gene segment represents the patrol point sequence of a robot. Then, according to (13)–(15), the Van der Waals forces between each gene fragment pair from two parent antibodies are calculated. These results are stored in the Van der Waals force matrix. Finally, the gene fragment pair corresponding to the largest Van der Waals force value in the Van der Waals force matrix is identified. These two gene fragments are matched together, laying the foundation for the subsequent crossover operation.

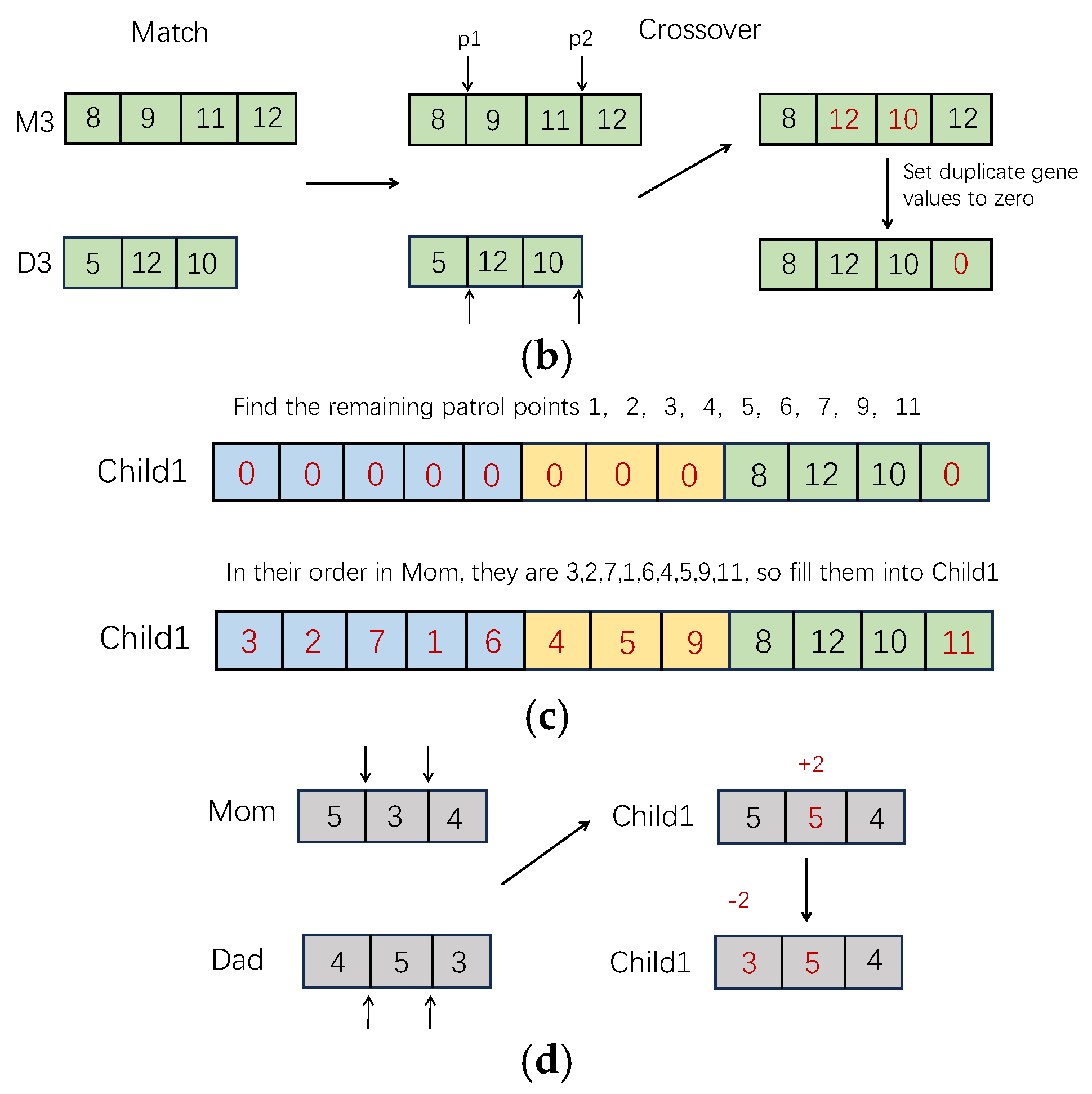
4.4.4. Gene Fragments Crossing Process

This section explains in detail how to perform a crossover operation on matched gene pairs. These gene pairs are generated from above process. For example, the antibody “Mom” is used as a benchmark. This benchmark is used to generate the offspring antibody “Child1”. Assume that “M3” and “D3” are gene pairs. These gene pairs are matched according to the Van der Waals force matrix.

Step1: Perform a crossover operation on the genes representing the patrol order in the antibody “Mom”. Two crossover points, denoted p1 and p2, are randomly generated. The length of the crossover fragment does not exceed the length of the shortest gene fragment. The gene fragments “M3” and “D3” are crossed at these two points. Then, check whether there are duplicate gene values in “M3” after crossing. If duplicates are found, the excess gene values are set to 0.

Step2: According to the position of gene fragment “M1” in antibody “Mom”, “M1” is inserted into the corresponding position in antibody “Child1”. Next, identify the remaining patrol points. These remaining patrol points are filled into the blank gene locations of “Child1,” according to their order in the antibody “Mom”.

Step3: Perform crossover operation on genes in antibody “Mom”. These genes represent the number of patrol points assigned to each robot. A gene is randomly selected to perform a single point crossover. After the crossover, the change amount of this gene location is calculated. If the change amount is positive, find the gene with the largest gene value among the remaining genes. Then subtract the change amount from the gene’ value. If the change amount is negative, find the gene with the smallest gene value among the remaining genes. Then add the change amount to the gene’s value. This ensures that the total number of all robot patrol points remains the same after crossover. It also creates more combinations of robot patrol points, which helps to improve antibody diversity. Meanwhile, employing the antibody “Dad” as a benchmark, the same operation as above is performed to generate the offspring antibody “Child2”. The schematic diagram of the separating, matching, and crossing process is shown in Figure 9.

5. Experiments

In this section, the effectiveness of PCM-VRAOA method is first verified. Then, the proposed VDWF-MOIA algorithm is compared and analyzed with various classic multi-objective optimization algorithms. Finally, the algorithm is applied to the path planning problem of the multi-robot patrolling system in the expo park, providing various patrol schemes for different scenarios.

5.1. Experimental Settings

Since the core of this study is path planning for the multi-robot patrolling system, all robots are simplified as particles, without considering their volume and specific actions. In order to verify the effectiveness of the proposed method, three simulation maps of the expo park, ranging from simple to complex, are set up.

Table 2. Parameter settings for maps.

Map	Patrol Point Number	Obstacle Number	Robot Number
Map 1	20	2	3
Map 2	30	3	4
Map 3	50	5	6

provides the parameters of the three simulation maps of the expo park, including the number of patrol points, obstacles, and robots. The obstacles are set as convex polygonal entities. The types, shapes, and quantities of obstacles in the map are different. The map size is uniformly 100 × 100.

To evaluate the advantages of the PCM-VRAOA method in terms of runtime, total path length, and load balancing, we compare the MOIA algorithm embedded with PCM-VRAOA (MOIA w/PCM-VRAOA) to the MOIA algorithms embedded with A* [68], BAS-A* [69], and RRT* [70] (MOIA w/A*, MOIA w/BAS-A*, and MOIA w/RRT*); To evaluate the improvements in convergence and search capability of VDWF-MOIA, we compared it with classic multi-objective optimization algorithms, including the non-dominated sorting genetic algorithm (NSGA) [71], non-dominated sorting genetic algorithm II (NSGA-II) [72], non-dominated neighbor immune algorithm (NNIA) [73], and a many-objective immune algorithm with a novel immune cloning operator (MaIA) [74]. These algorithms are considered state-of-the-art and widely used benchmarks in the field of multi-objective optimization. Additionally, NNIA and MaIA are both derived from immune algorithms. Therefore, we believe that comparing our proposed method with these algorithms convincingly demonstrates its advantages. Each algorithm is independently run 50 times on three simulation maps. Based on the pre-defined mathematical model of multi-robot patrolling path planning and simulation maps, all experiments were conducted using the software MATLAB R2023a on an Intel Core i7-12700H CPU at 2.30 GHz and with 16 GB RAM on a laptop computer.

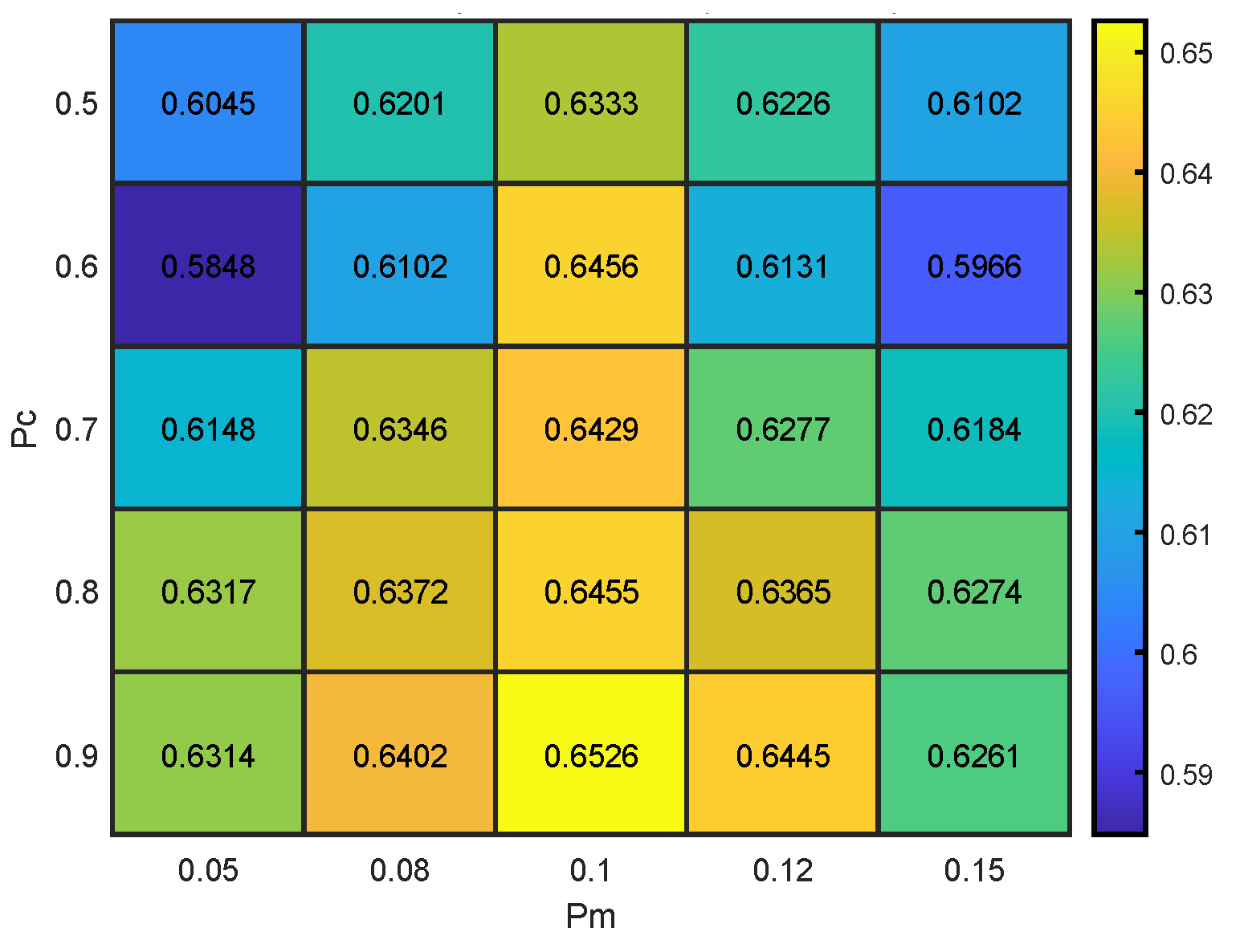
5.2. Parameter Sensitivity Analysis

To achieve the best optimization effect, we conduct sensitivity experiments on the parameters popsize, pc, and pm. In the first stage, we optimize the popsize by setting $pm=0.1$, $pc=0.9$, and popsize to 50, 100, 150, and 200, respectively. The performance indicators are HV and running time. The experimental results are shown in

Table 3. Analysis of the relationship between population size and running time. Fix pc = 0.9, pm = 0.1.

Popsize	HV	Running Time
50	0.6167	25.97
100	0.6526	48.75
150	0.6547	61.11
200	0.6625	77.46

. For the HV indicator, when the popsize goes from 50 to 100, the HV value goes up by about 5.82%. When the popsize increases from 100 to 200, the rise in the HV value is small, at around only 1.52%, but the running time increases by 58.89%. Therefore, this paper selects a popsize of 100. This is because this value can achieve a good balance between the HV value and the running time. In the second stage, a comprehensive tuning is conducted for the crossover probability and mutation probability. The popsize is fixed at 100. The tested crossover probabilities are 0.5, 0.6, 0.7, 0.8, and 0.9, and the tested mutation probabilities are 0.05, 0.08, 0.10, 0.12, and 0.15. The heatmap of pc and pm is shown in Figure 10. In the heatmap, the area with $pc=0.9$ and $pm=0.10$ is the brightest, meaning the HV value there is the highest. Thus, this paper determines the parameters $pc=0.9$ and $pm=0.10$.

5.3. Validation Experiment for the PCM-VRAOA

The comparative evaluation of MOIA combined with different path planning algorithms reveals performance differences in various test scenarios.

In terms of runtime, as shown in

Table 4. Comparison of the running times of the algorithms on different maps (in seconds).

Map	MOIA w/PCM-VRAOA	MOIA w/A*	MOIA w/BAS-A*	MOIA w/RRT*
Map 1	50.94 ± 2.40	16.61 ± 0.90	16.53 ± 1.52	66.39 ± 8.47
Map 2	265.70 ± 6.49	106.99 ± 5.24	95.85 ± 7.42	383.26 ± 31.65
Map 3	2302.03 ± 298.29	470.79 ± 46.46	437.56 ± 39.64	855.12 ± 50.31

, MOIA w/ BAS-A* achieves the shortest runtime on all maps, demonstrating its efficiency in online path computation. Notably, compared to sampling-based methods, MOIA w/PCM-VRAOA shows competitive runtime efficiency in small and medium-scale environments. For example, on Map 1, MOIA w/PCM-VRAOA completes tasks in 50.94 s, which is 23.27% faster than MOIA w/RRT* but slower than MOIA w/A* and MOIA w/BAS-A*. Similarly, on Map 2, MOIA w/PCM-VRAOA takes 265.70 s, which is 30.67% faster than MOIA w/RRT* but slower than MOIA w/A* and MOIA w/BAS-A*. However, this advantage diminishes in large-scale environments, where MOIA w/PCM-VRAOA has a higher runtime than other methods on Map 3. This performance difference is due to a strategic trade-off in MOIA w/PCM-VRAOA; by introducing an offline precomputation mechanism, it increases computational overhead during online task allocation but enables real-time collaborative optimization of path planning and task allocation. Although the runtime increases, it significantly improves the quality of patrol solutions, which is a critical requirement for multi-robot patrol systems. Therefore, while MOIA w/BAS-A* has the shortest runtime, MOIA w/PCM-VRAOA achieves a balanced trade-off between total path length and load balancing, making it more suitable for optimizing multi-robot coordination and overall system performance.

In terms of solution quality, the MOIA w/PCM-VRAOA algorithm offers significant advantages in both total path length and load balancing. It consistently outperforms baseline algorithms across different map environments. Its superior performance stems from its visibility reasoning framework and collaborative optimization mechanism, which enable more efficient path planning and balanced task allocation.

Regarding total path length, MOIA w/PCM-VRAOA effectively eliminates unnecessary detours by pre-connecting navigable obstacle vertices, resulting in shorter and more efficient paths. As shown in

Table 5. Comparison of the total path length of the algorithms on different maps.

Map	MOIA w/PCM-VRAOA	MOIA w/A*	MOIA w/BAS-A*	MOIA w/RRT*
Map 1	592.11 ± 87.35	781.23 ± 93.38	706.70 ± 90.51	824.83 ± 92.65
Map 2	773.93 ± 148.77	1136.80 ± 143.67	958.84 ± 135.71	1225.33 ± 136.31
Map 3	1193.24 ± 200.53	1390.96 ± 229.77	1287.47 ± 188.64	1446.53 ± 166.13

, MOIA w/PCM-VRAOA demonstrates clear advantages over other methods. Compared to MOIA w/A*, its paths are 24.21% shorter on Map 1, 31.92% shorter on Map 2, and 14.21% shorter on Map 3. This is because MOIA w/A* relies on a heuristic-based search strategy, which limits its ability to explore optimal routes and often leads to inefficient paths. Similarly, MOIA w/BAS-A* improves upon A* with a bidirectional search strategy but is still prone to getting stuck in local optima, causing its paths to be 16.21% longer on Map 1, 19.28% longer on Map 2, and 7.32% longer on Map 3 compared to MOIA w/PCM-VRAOA. MOIA w/RRT*, as a sampling-based method, lacks precise path refinement, resulting in excessive detours. Its paths are 28.21% longer on Map 1, 36.84% longer on Map 2, and 17.51% longer on Map 3 compared to MOIA w/PCM-VRAOA. These results illustrate the advanced path optimization capabilities of MOIA w/PCM-VRAOA, especially in structured environments.

Additionally, load balancing metrics further demonstrate MOIA w/PCM-VRAOA’s coordination capabilities in multi-robot systems. As shown in

Table 6. Comparison of the load balancing degree of the algorithms on different maps.

Map	MOIA w/PCM-VRAOA	MOIA w/A*	MOIA w/BAS-A*	MOIA w/RRT*
Map 1	12.34 ± 6.11	18.90 ± 6.58	16.04 ± 5.55	37.96 ± 8.53
Map 2	8.69 ± 4.97	16.56 ± 3.65	12.41 ± 5.62	40.88 ± 11.28
Map 3	9.28 ± 5.24	18.71 ± 4.93	17.26 ± 5.37	27.63 ± 10.34

, MOIA w/PCM-VRAOA maintains a low standard deviation in workload distribution. On Map 1–Map 3, this method improves by 23.07%, 29.89%, and 46.23% compared to the second-best method (MOIA w/BAS-A*). This advantage is mainly attributed to the dual optimization mechanism introduced by MOIA w/PCM-VRAOA, where collaborative optimization of task allocation and path planning is achieved through precomputation. Specifically, MOIA w/PCM-VRAOA reduces real-time computational burden by precomputing task allocation before path planning and optimizes load balancing during path planning to avoid spatial conflicts, enabling more efficient multi-robot coordination.

In summary, MOIA w/PCM-VRAOA successfully addresses the dual challenges of precise path planning and multi-robot coordination. While moderately increasing computational costs, the algorithm demonstrates excellent online performance in key areas such as solution quality and load balancing.

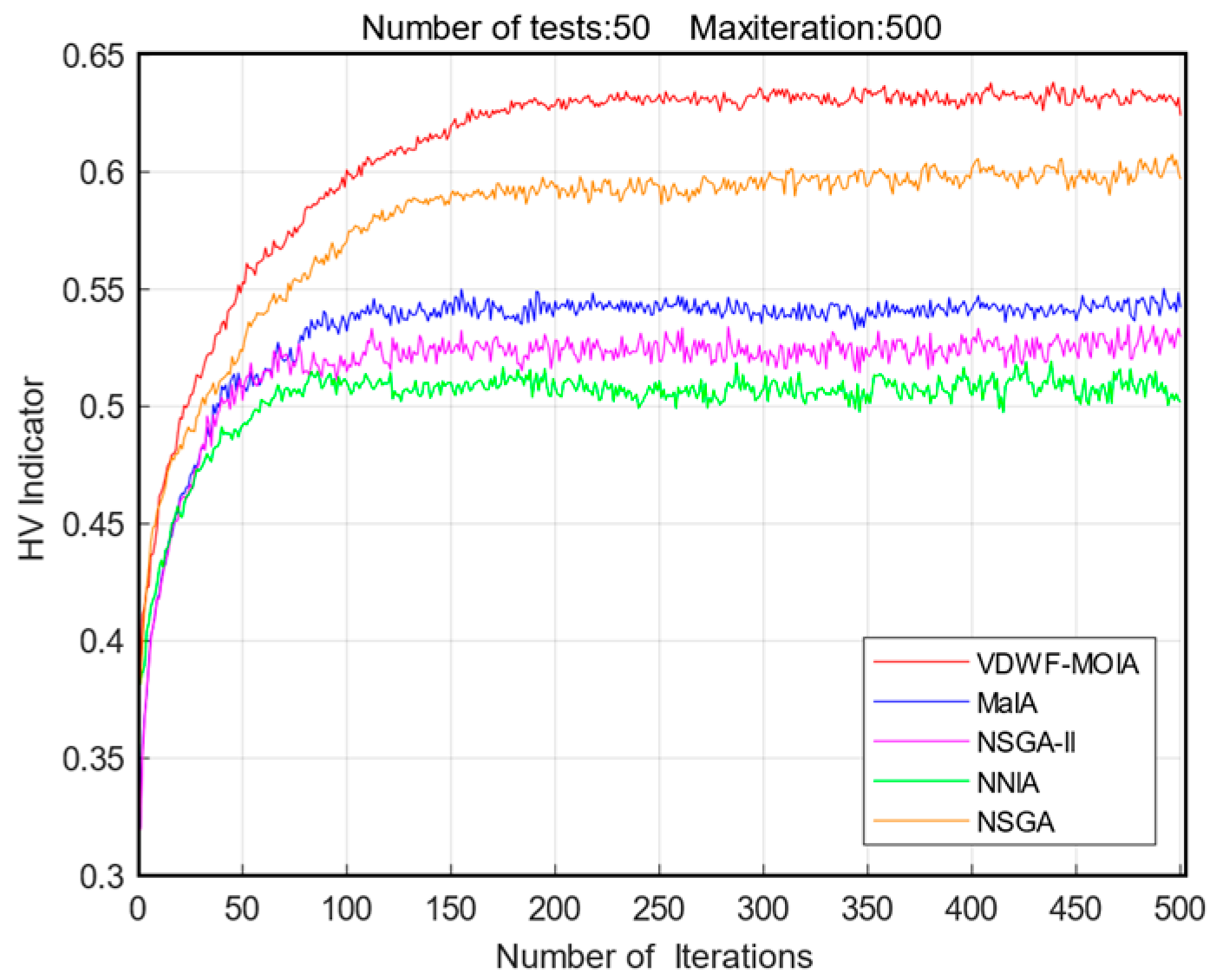
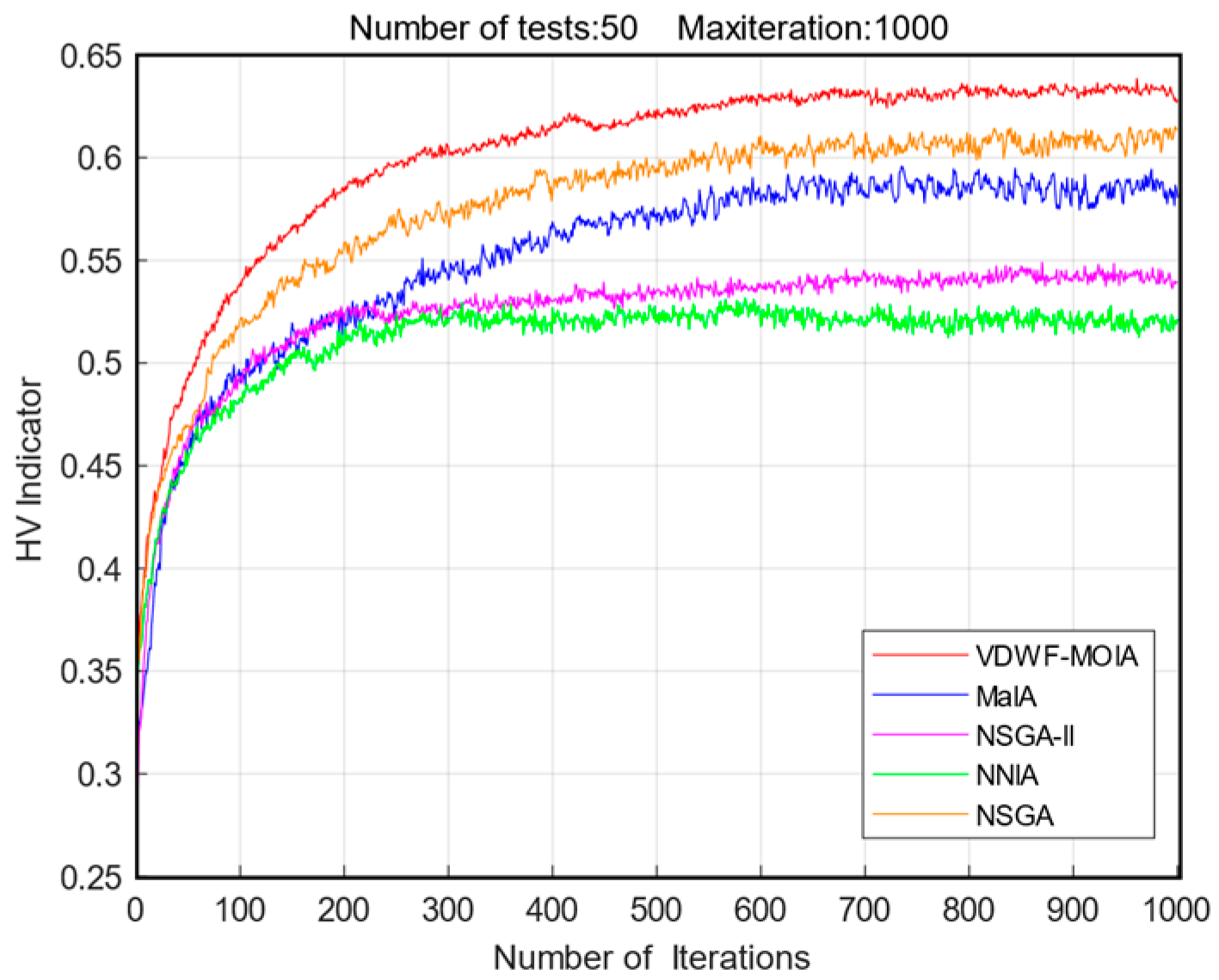
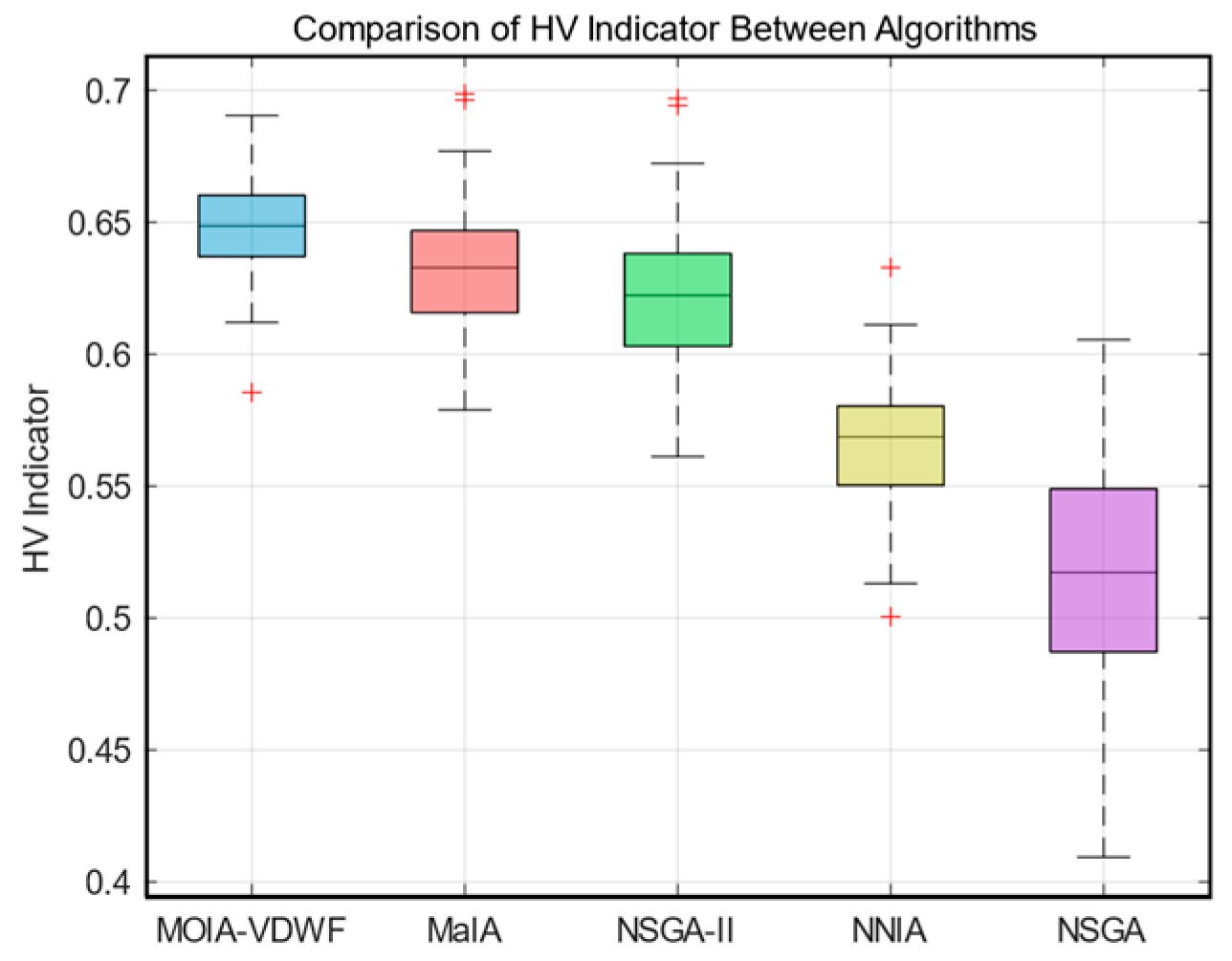
5.4. Comparison with Other Heuristic Algorithms

This paper selects the heuristic algorithms NSGA, NSGA-II, NNIA, and MaIA for comparison. They are all classic algorithms in the field of multi-objective optimization algorithms. Thus, they can serve as convincing competitors. To evaluate the improvements in convergence and search ability of our algorithm, we designed three maps of different sizes: small, medium, and large. To ensure effective optimization, we adjusted the population size and maximum iterations based on map scale. In the small-scale environment, we used a population of 100 and 500 iterations for efficient convergence. For the medium scale, we increased them to 200 and 1000 to balance exploration and efficiency. In the large-scale environment, we set them to 300 and 3000 for thorough optimization. These adjustments ensure effective performance across different scenarios while maintaining computational efficiency. The VDWF-MOIA algorithm presented in this study incorporates the PCM-VRAOA method for multi-robot path planning. To ensure consistency in the path planning method, the PCM-VRAOA method is also embedded in the NSGA, NSGA-II, NNIA, and MaIA algorithms when solving the problems in this study. To reduce randomness and more accurately assess the algorithms’ performance and stability, all algorithms were run independently 50 times. We provide the parameters of the compared algorithms and VDWF-MOIA in

Table 7. Parameters of applied algorithms.

Item	Value	Algorithm
Mutation probability	0.1	All
Crossover probability	0.9	All
Size of memory cell	20	VDWF-MOIA
Size of clone population	80	NNIA, MaIA
Maximum size of active population	20	NNIA
Maximum size of dominant population	30	NNIA

.

We introduce the hypervolume (HV) indicator [75] to comprehensively assess the convergence and diversity of the Pareto-optimal set, thereby evaluating the overall performance of these heuristic algorithms. A higher HV indicator indicates better overall performance of the algorithm. The calculation of the HV indicator is related to a reference point. Here we use the maximum value point of each group as the reference point. The HV convergence curves are shown in Figure 11, Figure 12 and Figure 13, clearly demonstrating the optimization performance of each algorithm in different scenarios. In the Map 1 scenario, VDWF-MOIA shows a strong initial convergence advantage. In the first 100 iterations, the HV indicator increases rapidly from 0.38 to 0.60, a growth of 57.89%, significantly outperforming other algorithms. By 500 iterations, the HV indicator stabilizes at 0.63, improving by 6.78%, 16.67%, 18.87%, and 23.53% compared to MaIA, NSGA-II, NNIA, and NSGA, respectively. In the Map 2 scenario, the convergence advantage of VDWF-MOIA is even more pronounced. In the first 300 iterations, the HV indicator increases by 66.67%, reaching 0.63 by 1000 iterations, with improvements of 2.28%, 8.28%, 16.54%, and 19.18% compared to MaIA, NSGA-II, NNIA and NSGA. In the Map 3 scenario, VDWF-MOIA achieves a 50% increase in HV indicator (from 0.30 to 0.60) within the first 1000 iterations. The HV metric eventually stabilized at about 0.65, representing improvements of 3.01%, 4.84%, 16.07%, and 24.81% compared to MaIA, NSGA-II, NNIA, and NSGA, respectively. The experimental results show that VDWF- MOIA exhibits fast convergence across scenarios of different scales, and its final solution quality is significantly better than that of the comparison algorithms. This verifies its excellent global search capability and resistance to premature convergence.

To further evaluate the stability and optimization effectiveness of VDWF-MOIA in multi-robot patrol tasks, this paper conducted boxplot analysis on the HV indicator. As shown in Figure 14, Figure 15 and Figure 16, VDWF-MOIA achieved the highest HV values across all test scenarios, demonstrating superior optimization performance. Additionally, its smaller interquartile range (IQR) indicates concentrated solution distribution and more stable optimization results. In contrast, NSGA and NNIA showed lower HV values with larger IQRs, revealing unstable optimization. While NSGA-II and MaIA showed improved HV values, they still underperformed compared to VDWF- MOIA. Overall, by optimizing task allocation and patrol sequence matching, VDWF-MOIA consistently maintains high-quality solution sets across various scale scenarios, exhibiting stronger global search capability and stability, effectively enhancing multi-robot system execution efficiency.

The two-tailed t-test compares mean differences between independent datasets to determine statistical significance. This study applied this method to verify whether VDWF-MOIA’s optimization effectiveness significantly outperforms other algorithms in repeated experiments. As shown in

Table 8. t-Test results on HV indicator.

Map	VDWF-MOIA vs. MaIA	VDWF-MOIA vs. NSGAII	VDWF-MOIA vs. NNIA	VDWF-MOIA vs. NSGA
Map 1	$7.1844\times {10}^{-20}$	$2.2223\times {10}^{-36}$	$2.8432\times {10}^{-42}$	$4.0165\times {10}^{-52}$
Map 2	$3.3609\times {10}^{-4}$	$6.6566\times {10}^{-14}$	$6.6312\times {10}^{-32}$	$7.9931\times {10}^{-25}$
Map 3	$1.3159\times {10}^{-3}$	$1.6494\times {10}^{-6}$	$2.2426\times {10}^{-31}$	$1.5262\times {10}^{-34}$

, VDWF-MOIA demonstrated statistically significant advantages with all p-values well below 0.05 across all maps. Particularly on small-scale maps (Map 1), p-values were far below 0.01, indicating strong optimization superiority. In medium- and large-scale maps (Map 2, Map 3), VDWF-MOIA maintained significant advantages (p < 0.05), further proving its stability and adaptability.

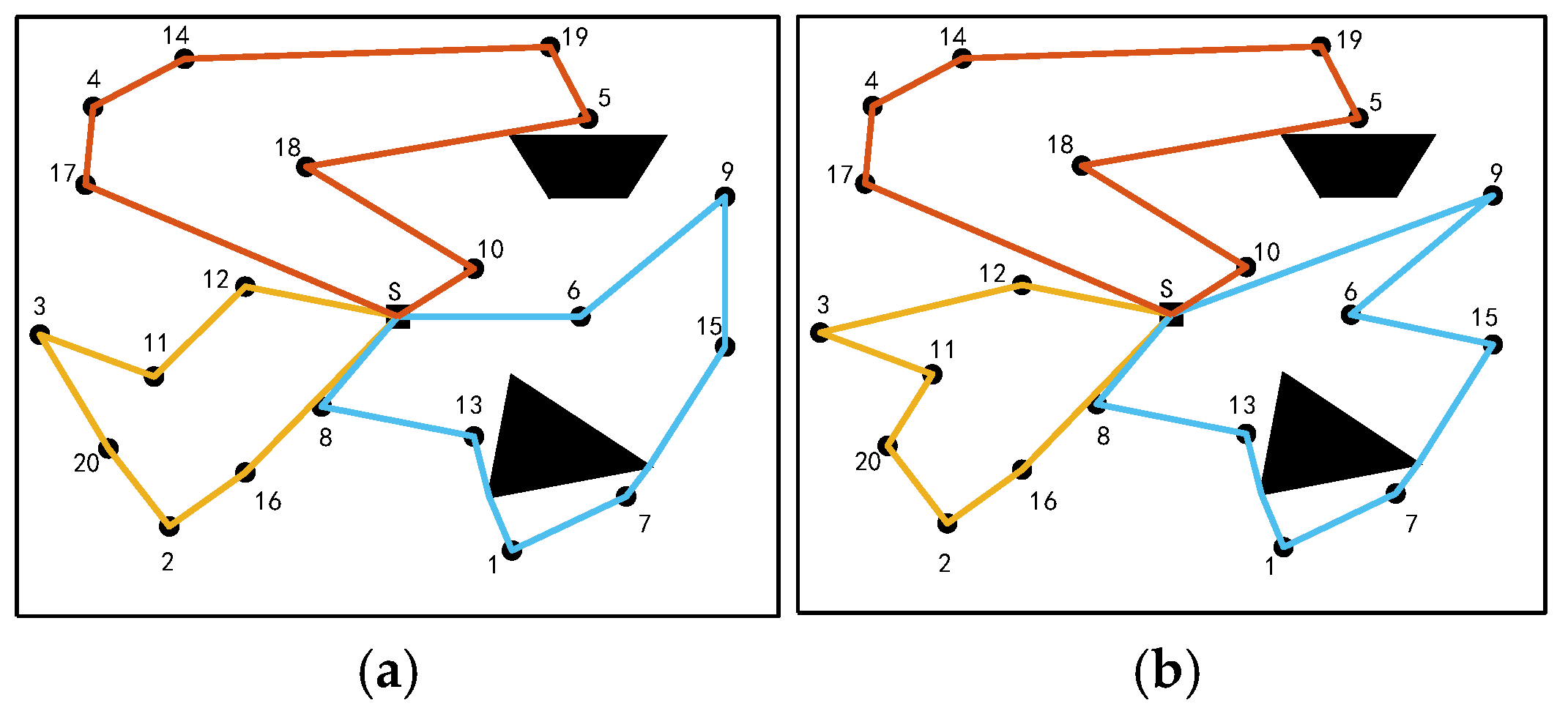
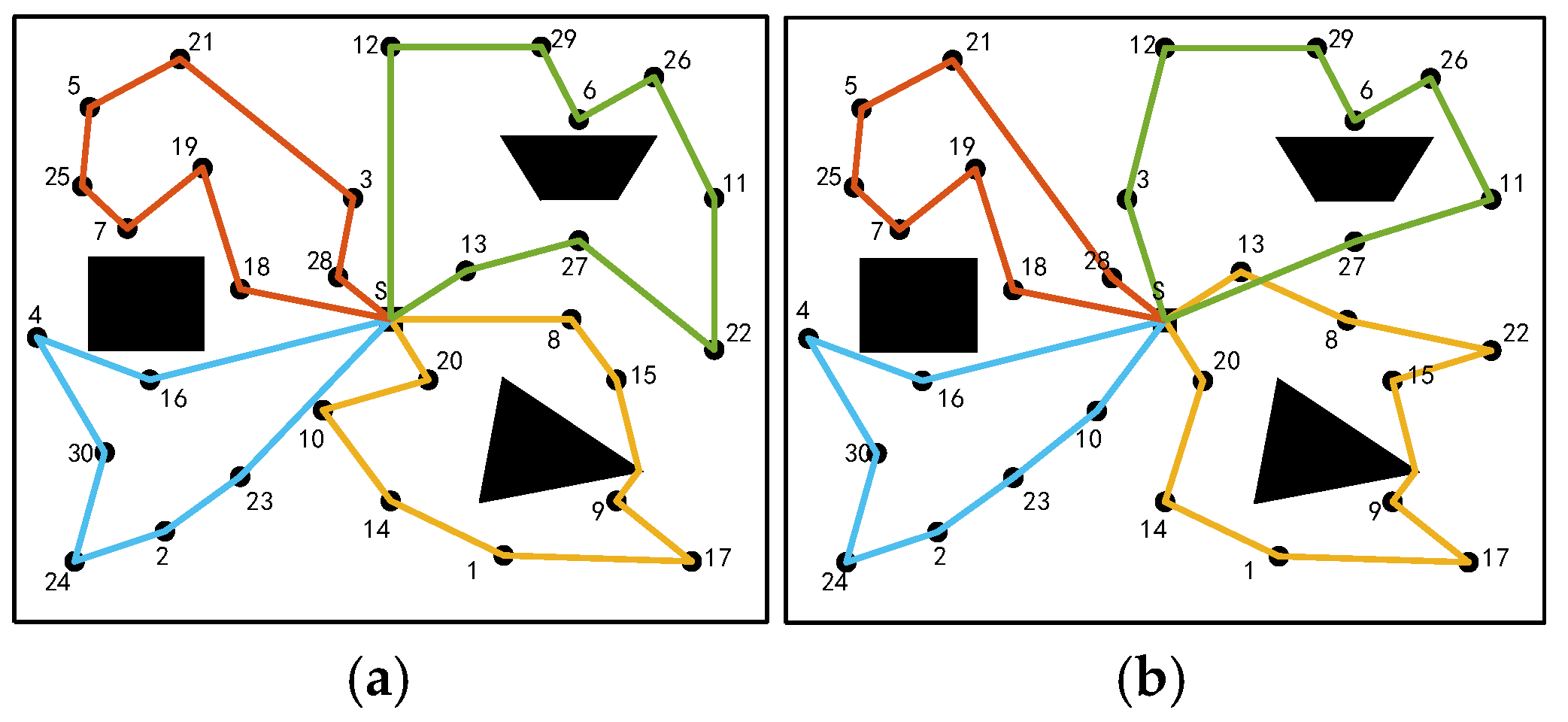
5.5. Simulation Patrol Scheme Diagram

As analyzed in Section 3, the multi-robot patrolling path planning problem concerned in this paper is a multi-objective optimization problem. Unlike general robot path planning problems, the scenarios we are concerned with require many different patrolling schemes. This is the main feature of this work, and it is also a realistic requirement that must be met.

We implemented and evaluated our VDWF-MOIA in the experimental environment described in Section 5.1. For the three simulation maps, the results of multi-robot patrolling path planning are shown in Figure 17, Figure 18 and Figure 19. Since the algorithm needs to optimize two objectives simultaneously, we select two representative Pareto solutions from the Pareto solution set as cases. Different Pareto solutions represent distinct multi-robot patrolling schemes. The objective function values for each scheme are shown in

Table 9. Application result of multi-objective patrolling executed by the multi-robot system.

Map		${\mathit{f}}_1$	${\mathit{f}}_2$
Map 1	(a)	485.350	2.742
	(b)	501.060	1.692
Map 2	(a)	646.696	8.777
	(b)	683.758	5.086
Map 3	(a)	902.713	15.178
	(b)	957.182	11.685

. For instance, in Map 3, for the first objective of minimizing the total patrolling path length, Figure 19a offers a satisfactory option for decision-makers. For the second objective of minimizing the standard deviation of path lengths between individual robots, Figure 19b provides a satisfactory choice. As can be seen from the results of Figure 17, Figure 18 and Figure 19, the VDWF-MOIA algorithm provides clear and rational path planning solutions for the multi-robot patrolling system in expo parks.

6. Conclusions and Future Work

In this research, we propose the VDWF-MOIA algorithm to address the multi-robot patrolling path planning problem in expo parks under a static environment. This problem is essentially equivalent to the MTSP with obstacles. The main contributions are as follows:

• This paper proposes a dual-antibody encoding scheme with virtual patrol points. Antibody 1 represents the robot task sequence. Antibody 2 represents the allocation of patrol points. Virtual patrol points expand the representation of the solution space. Traditional immune algorithms usually use a single encoding method. They struggle to represent both task allocation and path planning. This limits diversity and search ability. The proposed scheme makes antibody expressions more diverse. It optimizes task allocation and path planning at the same time, and provides a foundation for future collaborative optimization.
• This paper proposes the PCM-VRAOA method. The method precomputes path costs and obstacle avoidance nodes to ensure both feasibility and optimality. In multi-robot patrolling scenarios, the obstacle environment is complex. Traditional path planning methods struggle to balance obstacle avoidance and global optimization. The proposed method improves the coordination of multi-robot task allocation and path planning. It effectively enhances collaborative optimization, providing reliable support for multi-robot cooperative patrols.
• This paper proposes a crossover operator based on the Van der Waals mechanism. The operator intelligently matches gene segments to improve crossover efficiency and fully utilize the solution space structure. Traditional multi-objective immune optimization algorithms struggle to balance global search and convergence. They easily fall into local optima. Moreover, traditional crossover operators cannot effectively use the structural information of the solution space. In contrast, the proposed operator not only generates better Pareto solutions and significantly accelerates convergence, but also enhances search diversity, thus improving overall optimization performance.

In the experiment, three static simulation environments of different scales are established to verify the effectiveness of the VDWF-MOIA. Compared with NNIA, NSGA, NSGA-II, and MaIA, the experimental results show that in map scales ranging from small to large, VDWF-MOIA outperforms the comparison algorithms in terms of the HV indicator, total patrol path length, and load balancing metric.

Although VDWF-MOIA performs well in static environments, it has limitations that need to be addressed for broader practical applications. Future work will focus on two key directions:

• High Computational Cost: VDWF-MOIA requires significant computing resources due to the complexity of its fitness calculation and the Van der Waals force mechanism. In each iteration, the algorithm evaluates the fitness of all individuals, which relies on PCM-VRAOA to generate obstacle avoidance paths. Additionally, the Van der Waals force mechanism calculates the similarity and distance between all gene fragments, generating a Van der Waals force matrix. This process has a time complexity of $O\left(n^2\right)$, where $n$ is the number of gene fragments. As the number of patrol points and robots increases, the computational cost rises significantly. To reduce computational costs, future work will integrate deep learning and reinforcement learning (RL). A deep neural network (DNN) will replace traditional fitness calculations by learning path cost–task assignment mappings offline, significantly reducing online computation time. RL will dynamically adjust VDWF-MOIA parameters (e.g., crossover and mutation rates) to improve convergence speed and resource efficiency. Additionally, parallel computing and approximation techniques will be explored to optimize the Van der Waals force mechanism, further reducing computational overhead.
• Dynamic Environment Adaptability: While VDWF-MOIA excels in static environments, its functionality can be extended to handle dynamic obstacles and real-time patrol changes. To achieve this, a data-driven module will be introduced. This module will use real-time sensor data to detect dynamic obstacles and update the environment model. A data-driven task allocation mechanism will dynamically adjust patrol priorities based on risk levels, ensuring efficient responses to changing environments. Additionally, future work will address hardware and communication challenges by developing lightweight algorithms for resource-constrained robots and designing robust communication protocols to minimize delays and data loss, enhancing multi-robot coordination in dynamic scenarios.

These optimizations will build on VDWF-MOIA’s strengths, improving its efficiency and adaptability for real-world applications.