Electronic Artificial Intelligence–Digital Twin Model for Optimizing Electroencephalogram Signal Detection
Abstract
1. Introduction
- -
- -
- Results (Section 3): a discussion of the circuit simulations and the AI results by analyzing the algorithm performances and demonstrating the functioning of the DT ‘proof of concept’;
- -
- Discussion (Section 4): an explanation from the perspectives of DT implementation, including advantages, bottlenecks, limits, statistical analysis, and perspectives;
- -
2. Materials and Methods
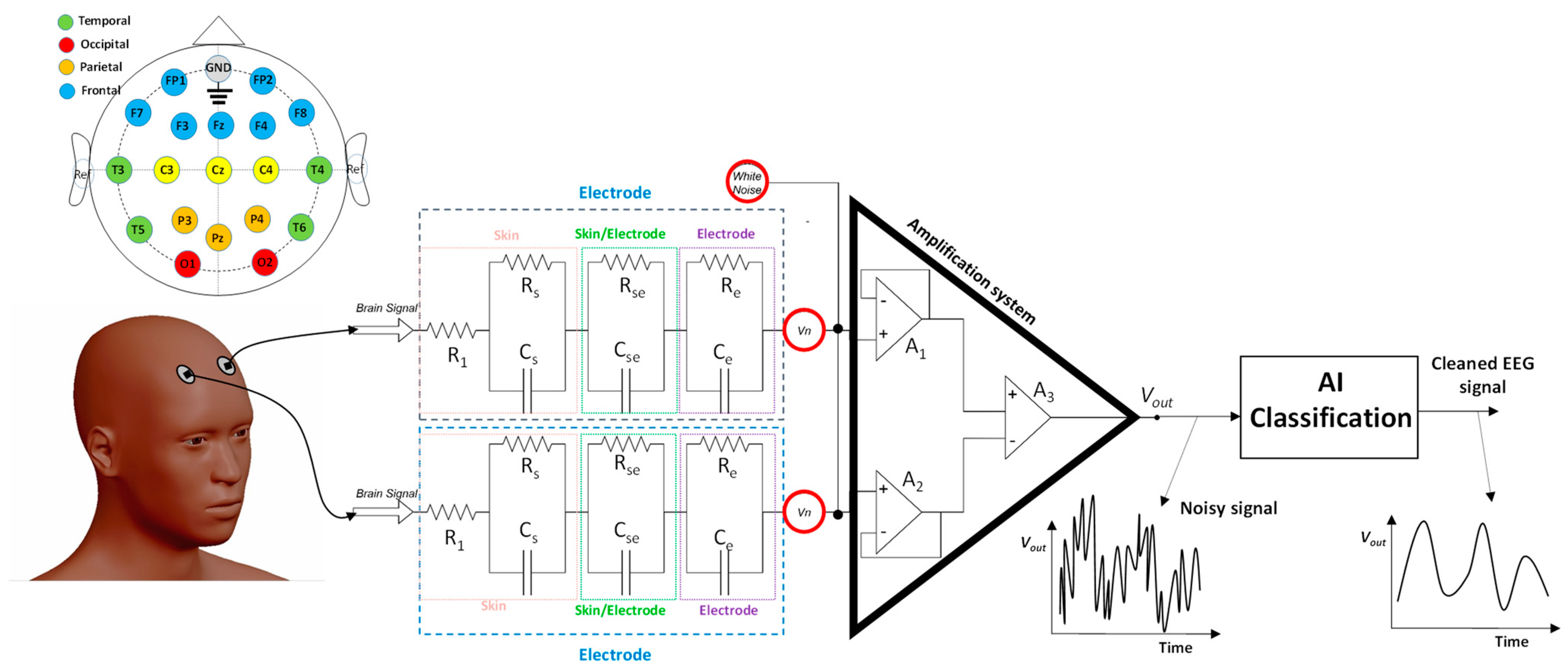
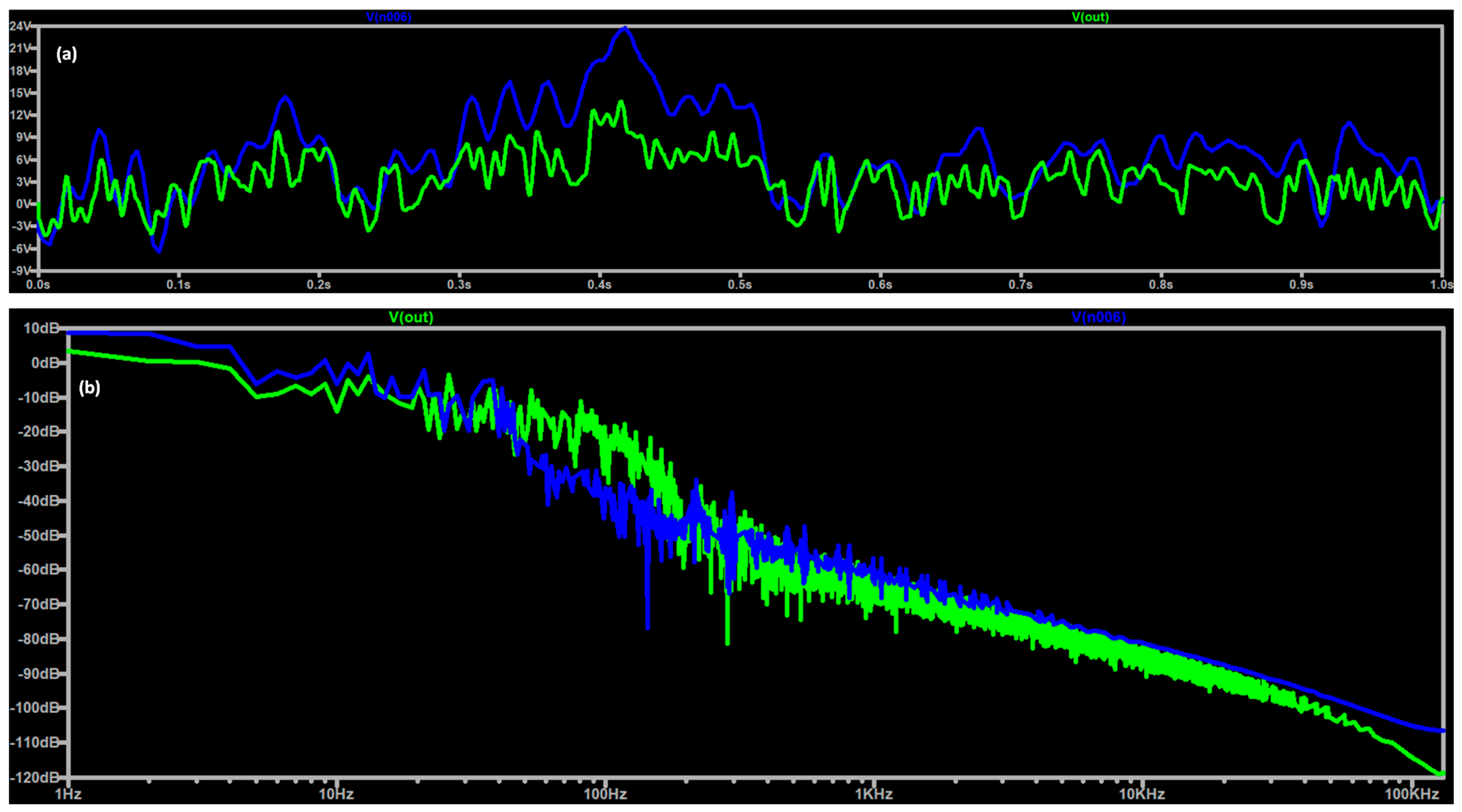
2.1. Electrodes and Related Electronic Noise
- F = frontal
- Fp = frontopolar
- T = temporal
- C = central
- P = parietal
- O = occipital
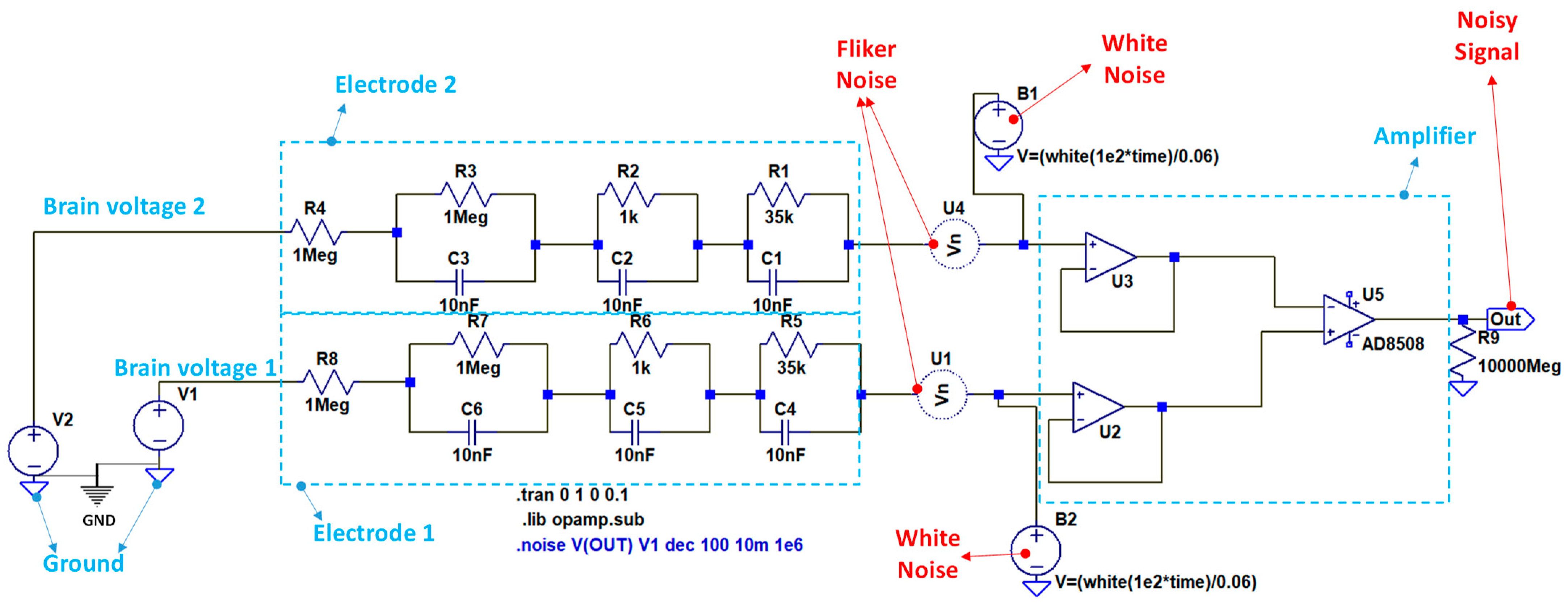
2.2. Circuit Modeling and Simulation
- -
- -
- -
- -
- Amplifier stage: it is composed of three operational amplifiers (A1 and A2 are in a non-inverting configuration and are connected with the A3 amplifier).
2.3. AI Brain Signal Classification
- −
- RF algorithm single EEG input signal: 100 tree models (number of trees to be learned); tree depth = 10 (limit number of levels); minimum node size = 5 (minimum number of records in child nodes); training dataset 80%; testing dataset 20%; linear sampling approach for the construction of the testing dataset;
- −
- RF algorithm double EEG input signals: 250 tree models; tree depth = 10; minimum node size = 5; linear sampling approach for the construction of the testing dataset;
- −
- ANN algorithm single EEG signal: 100 as the maximum number of iterations; 1 hidden layer; 10 neurons for the hidden layer; training dataset 80%; testing dataset 20%; linear sampling approach for the construction of the testing dataset;
- −
- ANN algorithm double EEG input signals: 400 as the maximum number of iterations; 5 hidden layers; 25 neurons for the hidden layer; linear sampling approach for the construction of the testing dataset.
3. Results
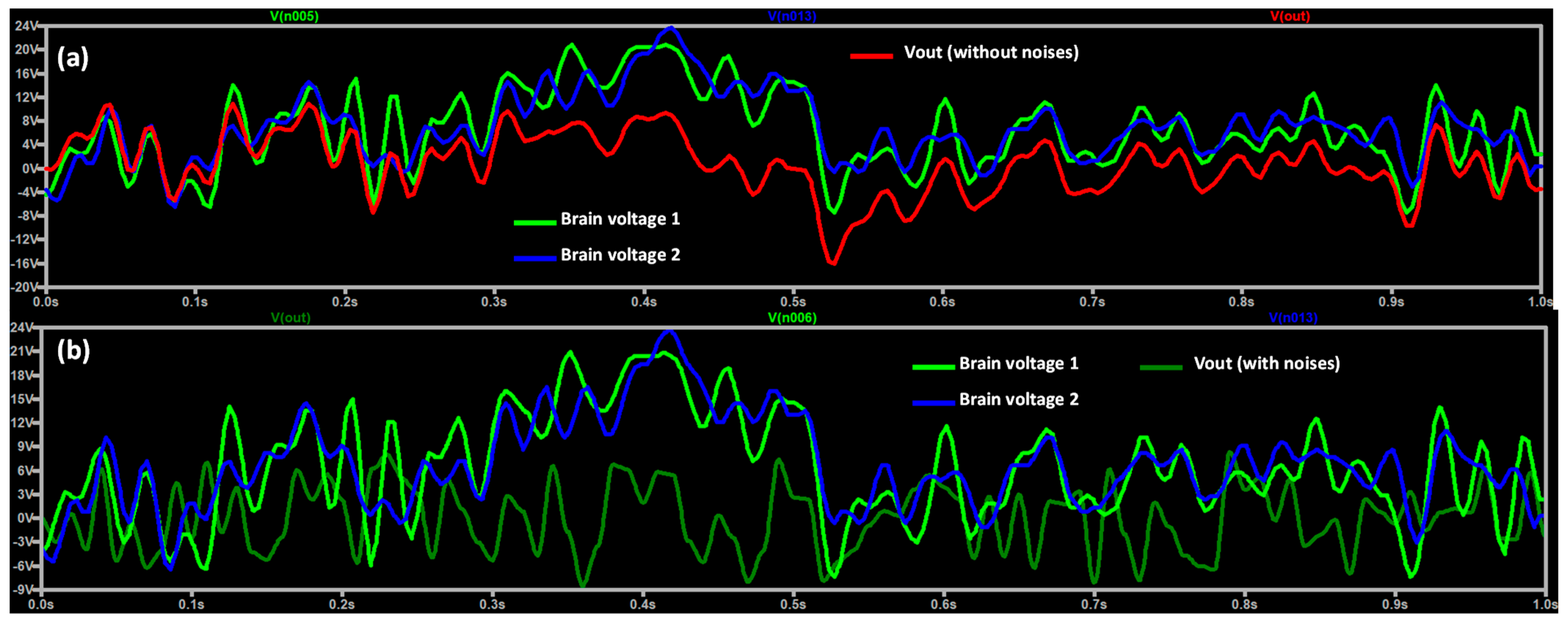
3.1. Noise Modeling and EEG DT Circuit Simulation
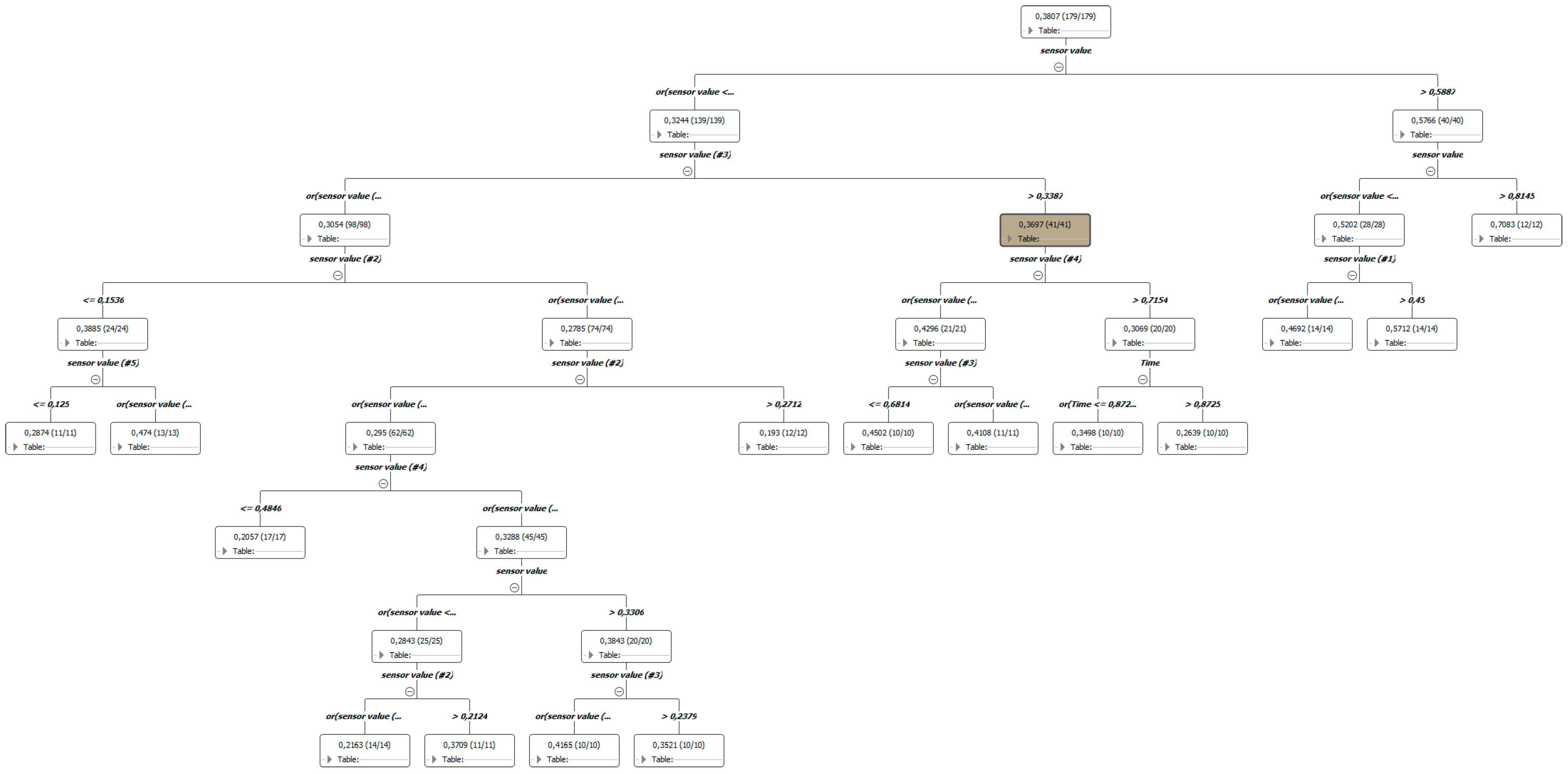
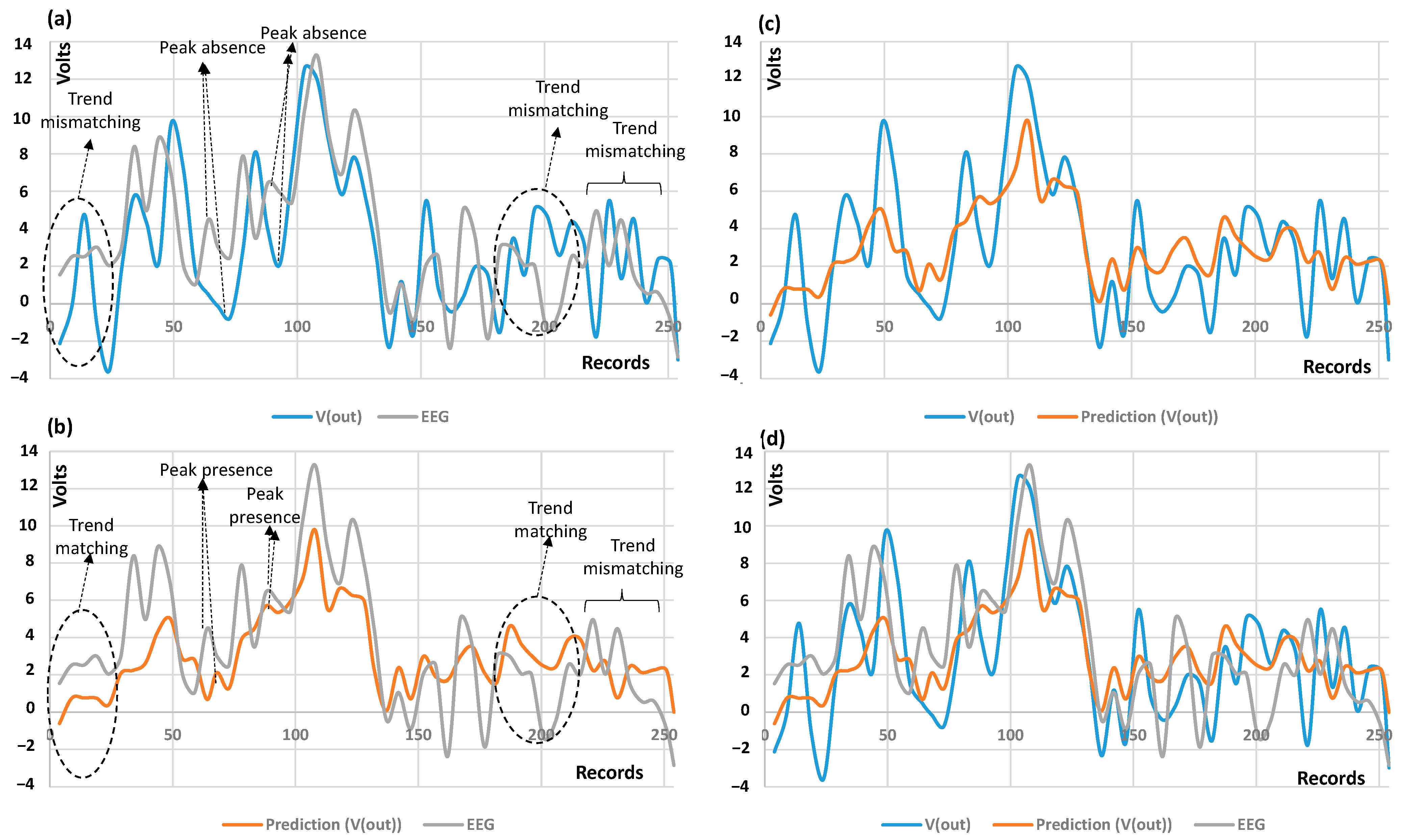
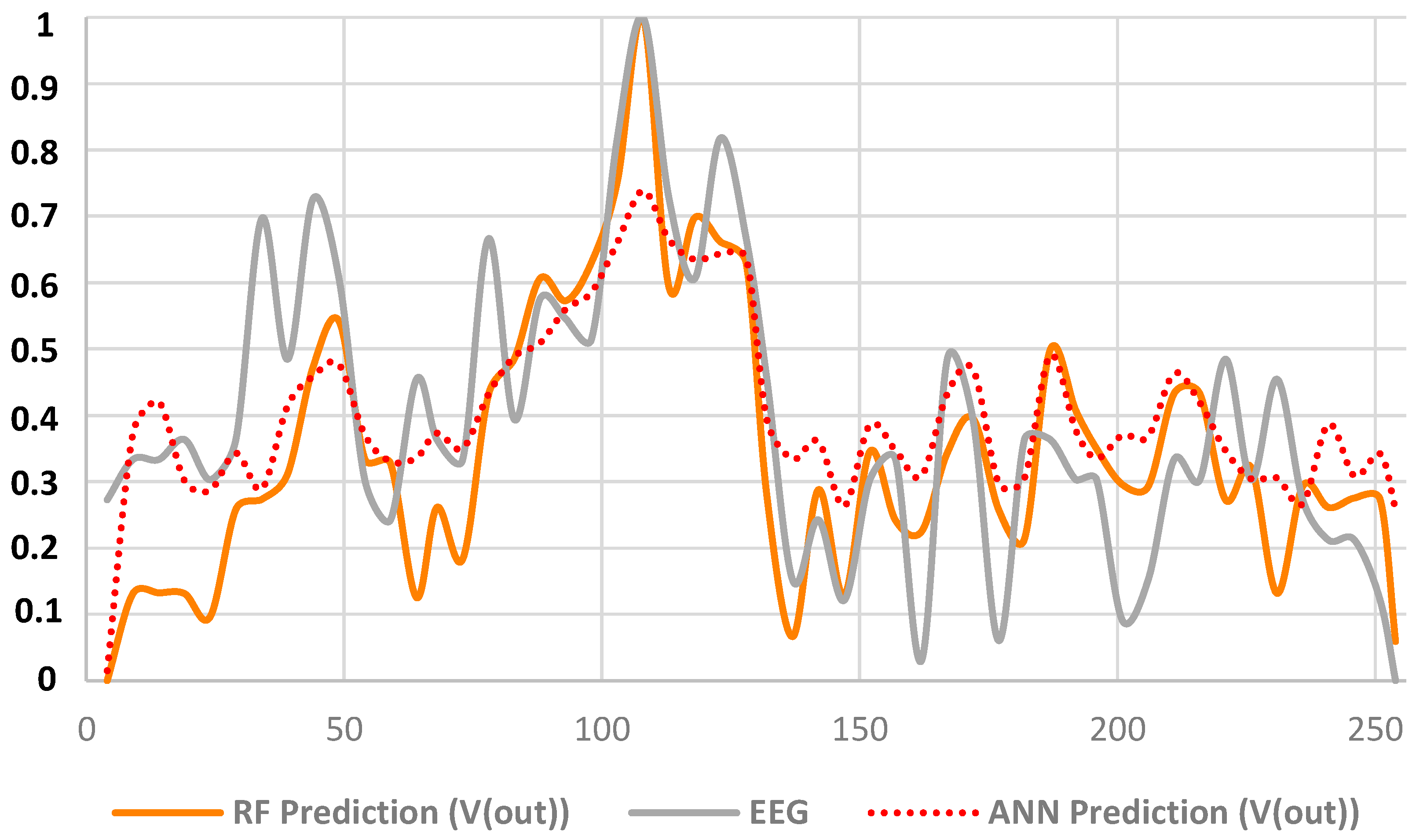
3.2. AI Results: RF and ANN Prediction and Performances
4. Discussion
4.1. Advantages, Disadvantages, Limits, Perspectives, and Innovative Aspects of the EEG DT Model
- A DT integrating a circuit simulator processing a real EEG signal to test the setting of the EEG DT to optimize the adjusting process;
- A DT able to select the most suitable AI algorithm using workflow implementation by checking the algorithm’s performance (rapid check of the performance and the possibility to use the same data pre-processing method to execute different AI algorithms in little time);
- A DT with configurable physical and physiological parameters (impedances of skin, gel, sweat, moisture, and hair);
- A DT usable for a real-time check of the detected EEG signal;
- A DT that is potentially usable for different EEG pathologies to construct a specific EEG training dataset to be processed by the AI-supervised algorithms.
4.2. EEG Hardware and Software Solutions
4.3. Bland–Altman Performance and MSE Metrics for ANN and RF Benchmark Comparison
4.4. Pseudocode Explaining EEG-DT Integration into a Unique Platform
| Algorithm 1: EEG DT pseudocode (integrated EEG platform, data detection, and data processing) |
|
4.5. Example of a BPMN Clinical Protocol Implementing EEG-DT
- Phase 1: Electrode setting and calibration according to the specific software and hardware technologies used for the EEG measurements;
- Phase 2: preliminary measurement check to avoid the superposition effect of more artifacts (muscular movements, electrode displacement, etc.);
- Phase 3 and Phase 4: real-time measurement checking using graphical dashboards, including, simultaneously, both the measurements and the AI-cleaned signal;
- Phase 5: if the measurement is performed correctly, the measurement is validated; otherwise, the process returns to phase 1;
- Phase 6: the validated measurement is stored into a database (DB) useful for the training of the specific pathology and supporting the AI cleaning process.
4.6. Main Statistical Characterization of the Proposed EEG DT System
4.6.1. Circuit Stability: Monte Carlo Tolerance Analysis
4.6.2. AI PCA
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
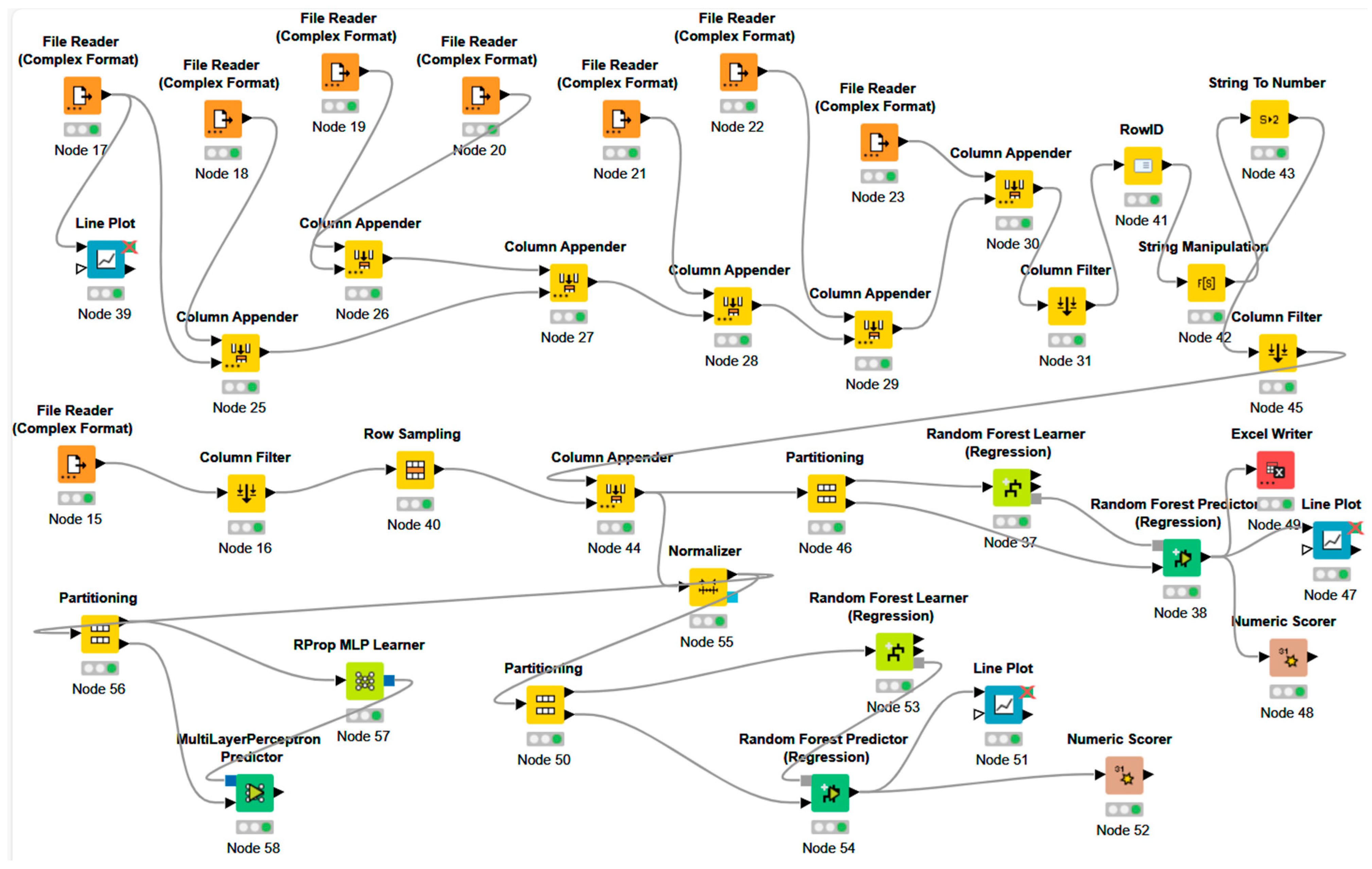
- -
- Input nodes importing the training dataset (seven tables) and the measured EEG signal (‘Excel Reader’);
- -
- Data pre-processing nodes: nodes merging tables (‘Column Appender’), nodes able to create the time variable (‘RowID’, ‘String Manipulation’, ‘String to Number’), nodes to clean unnecessary attributes (‘Column Filter’), node extracting a sample (a bunch of rows) from the input data to align the dataset dimensions of the testing dataset with the training dataset (‘Row Sampling’), and nodes splitting the dataset partition into training and testing AI nodes (‘Partitioning’);
- -
- AI training nodes (RF ‘Random Forest Learner’ and ANN ‘RProp MLP Learner’ nodes);
- -
- AI testing nodes (RF ‘Random Forest Predictor’ and ANN ‘Multilayer Perceptron Predictor’);
- -
- Error performance nodes (‘Numeric Score’);
- -
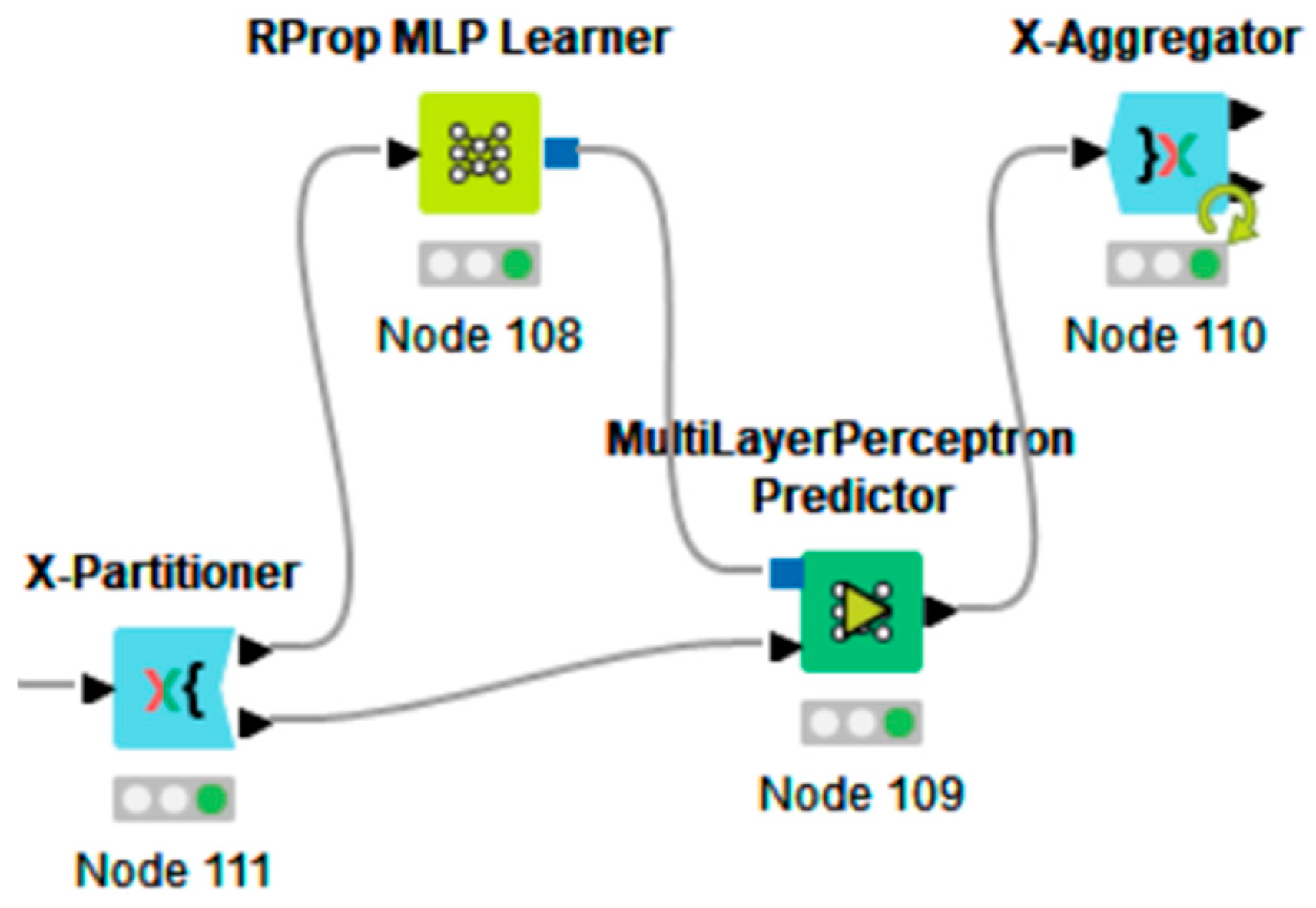
- Cross-validation nodes (‘X-Partitioner’ and ‘X-Aggregator’ nodes of Figure A2);
- -
- Graphical dashboards’ nodes (‘Line Plot’).

References
- Gajare, M.; Shedge, D.K. CMOS Trans Conductance Based Instrumentation Amplifier for Various Biomedical Signal Analysis. Neuroquantology 2022, 11, 63–71. [Google Scholar] [CrossRef]
- Saptono, D.; Wahyudi, B.; Irawan, B. Design of EEG Signal Acquisition System Using Arduino MEGA1280 and EEGAnalyzer. MATEC Web Conf. 2016, 75, 04003. [Google Scholar] [CrossRef]
- Habibzadeh Tonekabony Shad, E.; Molinas, M.; Ytterdal, T. Impedance and Noise of Passive and Active Dry EEG Electrodes: A Review. IEEE Sens. J. 2020, 20, 14565–14577. [Google Scholar] [CrossRef]
- Benda, M.; Volosyak, I. Peak Detection with Online Electroencephalography (EEG) Artifact Removal for Brain–Computer Interface (BCI) Purposes. Brain Sci. 2019, 9, 347. [Google Scholar] [CrossRef] [PubMed]
- Lay-Ekuakille, A.; Griffo, G.; Massaro, A.; Spano, F.; Gigli, G. Experimental Characterization of an Implantable Neuro-Packaging for EEG Signal Recording and Measurement. Measurement 2016, 79, 321–330. [Google Scholar] [CrossRef]
- Alonso, E.; Giannetti, R.; Rodríguez-Morcillo, C.; Matanza, J.; Muñoz-Frías, J.D. A Novel Passive Method for the Assessment of Skin-Electrode Contact Impedance in Intraoperative Neurophysiological Monitoring Systems. Sci. Rep. 2020, 10, 2819. [Google Scholar] [CrossRef]
- Su, S.; Zhu, Z.; Wan, S.; Sheng, F.; Xiong, T.; Shen, S.; Hou, Y.; Liu, C.; Li, Y.; Sun, X.; et al. An ECG Signal Acquisition and Analysis System Based on Machine Learning with Model Fusion. Sensors 2023, 23, 7643. [Google Scholar] [CrossRef]
- Heikenfeld, J.; Jajack, A.; Rogers, J.; Gutruf, P.; Tian, L.; Pan, T.; Li, R.; Khine, M.; Kim, J.; Wang, J.; et al. Wearable Sensors: Modalities, Challenges, and Prospects. Lab Chip 2018, 18, 217–248. [Google Scholar] [CrossRef] [PubMed]
- Lay-Ekuakille, A.; Griffo, G.; Vergallo, P.; Massaro, A.; Spano, F.; Gigli, G. Implantable Neurorecording Sensing System: Wireless Transmission of Measurements. IEEE Sens. J. 2015, 15, 2603–2613. [Google Scholar] [CrossRef]
- Zhang, K.; Xu, G.; Du, C.; Wu, Y.; Zheng, X.; Zhang, S.; Han, C.; Liang, R.; Chen, R. Weak Feature Extraction and Strong Noise Suppression for SSVEP-EEG Based on Chaotic Detection Technology. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 862–871. [Google Scholar] [CrossRef]
- Eltrass, A.S.; Ghanem, N.H. A New Automated Multi-Stage System of Non-Local Means and Multi-Kernel Adaptive Filtering Techniques for EEG Noise and Artifacts Suppression. J. Neural Eng. 2021, 18, 036023. [Google Scholar] [CrossRef]
- Kaur, C.; Bisht, A.; Singh, P.; Joshi, G. EEG Signal Denoising Using Hybrid Approach of Variational Mode Decomposition and Wavelets for Depression. Biomed. Signal Process. Control 2021, 65, 102337. [Google Scholar] [CrossRef]
- Jindal, K.; Upadhyay, R.; Singh, H.S. Application of Hybrid GLCT-PICA de-Noising Method in Automated EEG Artifact Removal. Biomed. Signal Process. Control 2020, 60, 101977. [Google Scholar] [CrossRef]
- Porr, B.; Daryanavard, S.; Bohollo, L.M.; Cowan, H.; Dahiya, R. Real-Time Noise Cancellation with Deep Learning. PLoS ONE 2022, 17, e0277974. [Google Scholar] [CrossRef] [PubMed]
- Amer, N.S.; Belhaouari, S.B. Exploring New Horizons in Neuroscience Disease Detection through Innovative Visual Signal Analysis. Sci. Rep. 2024, 14, 4217. [Google Scholar] [CrossRef]
- Lv, Z.; Qiao, L.; Lv, H. Cognitive Computing for Brain–Computer Interface-Based Computational Social Digital Twins Systems. IEEE Trans. Comput. Soc. Syst. 2022, 9, 1635–1643. [Google Scholar] [CrossRef]
- Takahashi, Y.; Idei, H.; Komatsu, M.; Tani, J.; Tomita, H.; Yamashita, Y. Digital Twin Brain Simulator: Harnessing Primate ECoG Data for Real-Time Consciousness Monitoring and Virtual Intervention. bioRxiv 2024. [Google Scholar] [CrossRef]
- Falkowski, P.; Osiak, T.; Wilk, J.; Prokopiuk, N.; Leczkowski, B.; Pilat, Z.; Rzymkowski, C. Study on the Applicability of Digital Twins for Home Remote Motor Rehabilitation. Sensors 2023, 23, 911. [Google Scholar] [CrossRef]
- Nishida, S.; Nakamura, M.; Ikeda, A.; Shibasaki, H. Signal Separation of Background EEG and Spike by Using Morphological Filter. Med. Eng. Phys. 1999, 21, 601–608. [Google Scholar] [CrossRef]
- Pyrzowski, J.; Siemiński, M.; Sarnowska, A.; Jedrzejczak, J.; Nyka, W.M. Interval Analysis of Interictal EEG: Pathology of the Alpha Rhythm in Focal Epilepsy. Sci. Rep. 2015, 5, 16230. [Google Scholar] [CrossRef]
- Ruiz de Miras, J.; Derchi, C.-C.; Atzori, T.; Mazza, A.; Arcuri, P.; Salvatore, A.; Navarro, J.; Saibene, F.L.; Meloni, M.; Comanducci, A. Spatio-Temporal Fractal Dimension Analysis from Resting State EEG Signals in Parkinson’s Disease. Entropy 2023, 25, 1017. [Google Scholar] [CrossRef] [PubMed]
- Olejarczyk, E.; Sobieszek, A.; Assenza, G. Automatic Detection of the EEG Spike–Wave Patterns in Epilepsy: Evaluation of the Effects of Transcranial Current Stimulation Therapy. Int. J. Mol. Sci. 2024, 25, 9122. [Google Scholar] [CrossRef] [PubMed]
- Gemein, L.A.W.; Schirrmeister, R.T.; Chrabąszcz, P.; Wilson, D.; Boedecker, J.; Schulze-Bonhage, A.; Hutter, F.; Ball, T. Machine-Learning-Based Diagnostics of EEG Pathology. Neuroimage 2020, 220, 117021. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hammad, A.; Ali, A.A. Human Emotion Recognition from EEG-Based Brain–Computer Interface Using Machine Learning: A Comprehensive Review. Neural Comput. Appl. 2022, 34, 12527–12557. [Google Scholar] [CrossRef]
- Attar, E.T. Review of Electroencephalography Signals Approaches for Mental Stress Assessment. Neurosciences 2022, 27, 209–215. [Google Scholar] [CrossRef]
- Shen, M.; Wen, P.; Song, B.; Li, Y. Detection of Alcoholic EEG Signals Based on Whole Brain Connectivity and Convolution Neural Networks. Biomed. Signal Process. Control 2023, 79, 104242. [Google Scholar] [CrossRef]
- Neeraj; Singhal, V.; Mathew, J.; Behera, R.K. Detection of Alcoholism Using EEG Signals and a CNN-LSTM-ATTN Network. Comput. Biol. Med. 2021, 138, 104940. [Google Scholar] [CrossRef]
- Agarwal, S.; Zubair, M. Classification of Alcoholic and Non-Alcoholic EEG Signals Based on Sliding-SSA and Independent Component Analysis. IEEE Sens. J. 2021, 21, 26198–26206. [Google Scholar] [CrossRef]
- Baijal, S.; Singh, S.; Rani, A.; Agarwal, S. Performance Evaluation of S-Golay and MA Filter on the Basis of White and Flicker Noise. In Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2016; pp. 245–255. [Google Scholar]
- Massaro, A. Artificial Intelligence Signal Control in Electronic Optocoupler Circuits Addressed on Industry 5.0 Digital Twin. Electronics 2024, 13, 4543. [Google Scholar] [CrossRef]
- Chi, Y.M.; Jung, T.-P.; Cauwenberghs, G. Dry-Contact and Noncontact Biopotential Electrodes: Methodological Review. IEEE Rev. Biomed. Eng. 2010, 3, 106–119. [Google Scholar] [CrossRef]
- Huigen, E.; Peper, A.; Grimbergen, I.C.A.; Samenvatting. Noise in Biopotential Recording Using Surface Electrodes; Technical Report; University of Amsterdam: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Voss, R.F.; Clarke, J. Flicker (1f) Noise: Equilibrium Temperature and Resistance Fluctuations. Phys. Rev. 1976, 13, 556–573. [Google Scholar] [CrossRef]
- LTspice. Available online: https://www.analog.com/en/resources/design-tools-and-calculators/ltspice-simulator.html (accessed on 17 December 2024).
- LTspiceNoiseSources. Available online: https://github.com/yildi1337/LTspiceNoiseSources (accessed on 17 December 2024).
- EEG-Alcohol. Available online: https://www.kaggle.com/datasets/nnair25/Alcoholics (accessed on 17 December 2024).
- KNIME. Available online: https://www.knime.com/ (accessed on 17 December 2024).
- Massaro, A. Electronics in Advanced Research Industries: Industry 4.0 to Industry 5.0 Advances; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Sabio, J.; Williams, N.S.; McArthur, G.M.; Badcock, N.A. A Scoping Review on the Use of Consumer-Grade EEG Devices for Research. PLoS ONE 2024, 19, e0291186. [Google Scholar] [CrossRef] [PubMed]
- LaRocco, J.; Le, M.D.; Paeng, D.-G. A Systemic Review of Available Low-Cost EEG Headsets Used for Drowsiness Detection. Front. Neuroinform. 2020, 14, 553352. [Google Scholar] [CrossRef]
- Jaros, R.; Barnova, K.; Vilimkova Kahankova, R.; Pelisek, J.; Litschmannova, M.; Martinek, R. Independent Component Analysis Algorithms for Non-Invasive Fetal Electrocardiography. PLoS ONE 2023, 18, e0286858. [Google Scholar] [CrossRef] [PubMed]
- Safieddine, D.; Kachenoura, A.; Albera, L.; Birot, G.; Karfoul, A.; Pasnicu, A.; Biraben, A.; Wendling, F.; Senhadji, L.; Merlet, I. Removal of Muscle Artifact from EEG Data: Comparison between Stochastic (ICA and CCA) and Deterministic (EMD and Wavelet-Based) Approaches. EURASIP J. Adv. Signal Process. 2012, 2012, 127. [Google Scholar] [CrossRef]
- Cataldo, A.; Criscuolo, S.; De Benedetto, E.; Masciullo, A.; Pesola, M.; Schiavoni, R.; Invitto, S. A Method for Optimizing the Artifact Subspace Reconstruction Performance in Low-Density EEG. IEEE Sens. J. 2022, 22, 21257–21265. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A.; Abasi, A.K.; Makhadmeh, S.N. EEG Signals Denoising Using Optimal Wavelet Transform Hybridized with Efficient Metaheuristic Methods. IEEE Access 2020, 8, 10584–10605. [Google Scholar] [CrossRef]
- Bajpai, B.K.; Zakelis, R.; Deimantavicius, M.; Imbrasiene, D. Comparative Study of Novel Noninvasive Cerebral Autoregulation Volumetric Reactivity Indices Reflected by Ultrasonic Speed and Attenuation as Dynamic Measurements in the Human Brain. Brain Sci. 2020, 10, 205. [Google Scholar] [CrossRef]
- Bastianini, S.; Alvente, S.; Berteotti, C.; Lo Martire, V.; Silvani, A.; Swoap, S.J.; Valli, A.; Zoccoli, G.; Cohen, G. Accurate Discrimination of the Wake-Sleep States of Mice Using Non-Invasive Whole-Body Plethysmography. Sci. Rep. 2017, 7, 41698. [Google Scholar] [CrossRef]
- Mariani, S.; Tarokh, L.; Djonlagic, I.; Cade, B.E.; Morrical, M.G.; Yaffe, K.; Stone, K.L.; Loparo, K.A.; Purcell, S.M.; Redline, S.; et al. Evaluation of an Automated Pipeline for Large-Scale EEG Spectral Analysis: The National Sleep Research Resource. Sleep Med. 2018, 47, 126–136. [Google Scholar] [CrossRef]
- Levendowski, D.J.; Popovic, D.; Berka, C.; Westbrook, P.R. Retrospective Cross-Validation of Automated Sleep Staging Using Electroocular Recording in Patients with and without Sleep Disordered Breathing. Int. Arch. Med. 2012, 5, 21. [Google Scholar] [CrossRef] [PubMed]
- Apicella, A.; Arpaia, P.; Mastrati, G.; Moccaldi, N. EEG-Based Detection of Emotional Valence towards a Reproducible Measurement of Emotions. Sci. Rep. 2021, 11, 21615. [Google Scholar] [CrossRef]
- Alyasseri, Z.A.A.; Khader, A.T.; Al-Betar, M.A. Electroencephalogram Signals Denoising Using Various Mother Wavelet Functions: A Comparative Analysis. In Proceedings of the International Conference on Imaging, Signal Processing and Communication, Penang, Malaysia, 26–28 July 2017; ACM: New York, NY, USA, 2017; pp. 100–105. [Google Scholar]
- St. Louis, E.K.; Frey, L.C.; Britton, J.W.; Hopp, J.L.; Korb, P.; Koubeissi, M.Z.; Lievens, W.E.; Pestana-Knight, E.M. EEG in the Epilepsies; American Epilepsy Society: Chicago, IL, USA, 2016. [Google Scholar]
- Gimenez-Aparisi, G.; Guijarro-Estelles, E.; Chornet-Lurbe, A.; Ballesta-Martinez, S.; Pardo-Hernandez, M.; Ye-Lin, Y. Early Detection of Parkinson’s Disease: Systematic Analysis of the Influence of the Eyes on Quantitative Biomarkers in Resting State Electroencephalography. Heliyon 2023, 9, e20625. [Google Scholar] [CrossRef]
- Hallett, M.; DelRosso, L.M.; Elble, R.; Ferri, R.; Horak, F.B.; Lehericy, S.; Mancini, M.; Matsuhashi, M.; Matsumoto, R.; Muthuraman, M.; et al. Evaluation of Movement and Brain Activity. Clin. Neurophysiol. 2021, 132, 2608–2638. [Google Scholar] [CrossRef] [PubMed]
- McDonald, C.; El Yaakoubi, N.A.; Lennon, O. Brain (EEG) and Muscle (EMG) Activity Related to 3D Sit-to-Stand Kinematics in Healthy Adults and in Central Neurological Pathology—A Systematic Review. Gait Posture 2024, 113, 374–397. [Google Scholar] [CrossRef] [PubMed]
- Gordleeva, S.Y.; Lobov, S.A.; Grigorev, N.A.; Savosenkov, A.O.; Shamshin, M.O.; Lukoyanov, M.V.; Khoruzhko, M.A.; Kazantsev, V.B. Real-Time EEG–EMG Human–Machine Interface-Based Control System for a Lower-Limb Exoskeleton. IEEE Access 2020, 8, 84070–84081. [Google Scholar] [CrossRef]
- Wang, Y.; Gotman, J. The Influence of Electrode Location Errors on EEG Dipole Source Localization with a Realistic Head Model. Clin. Neurophysiol. 2001, 112, 1777–1780. [Google Scholar] [CrossRef]
- Eye State Classification EEG Dataset. Available online: https://www.kaggle.com/datasets/robikscube/eye-state-classification-eeg-dataset/data (accessed on 26 February 2025).
- Massaro, A.; Lay-Ekuakille, A. Analysis of Magnetic Field Impact on Nanoparticles Used in Nanomedicine and a Measurement Approach. Measurement 2024, 226, 114167. [Google Scholar] [CrossRef]
- Massaro, A.; Cazzato, G.; Ingravallo, G.; Casatta, N.; Lupo, C.; Vacca, A.; Iannone, F.; Girolamo, F. Pre-Screening of Endomysial Microvessel Density by Fast Random Forest Image Processing Machine Learning Algorithm Accelerates Recognition of a Modified Vascular Network in Idiopathic Inflammatory Myopathies. Diagn. Pathol. 2025, 20, 13. [Google Scholar] [CrossRef]
- Knudtsen, S. How to Model Statistical Tolerance Analysis for Complex Circuits Using LTspice. Available online: https://www.analog.com/en/resources/technical-articles/how-to-model-statistical-tolerance-analysis.html (accessed on 4 March 2025).
- Adam, A.; Ibrahim, Z.; Mokhtar, N.; Shapiai, M.I.; Cumming, P.; Mubin, M. Evaluation of Different Time Domain Peak Models Using Extreme Learning Machine-Based Peak Detection for EEG Signal. Springerplus 2016, 5, 1036. [Google Scholar] [CrossRef]
- Krzysztof, P.; Kolodiy, Z.; Yatsyshyn, S.; Majewski, J.; Khoma, Y.; Petrovska, I.; Lasarenko, S.; Hut, T. Standard deviation in the simulation of statistical measurements. Metrol. Meas. Syst. 2023, 30, 17–30. [Google Scholar] [CrossRef]
- Kim, H.; Luo, J.; Chu, S.; Cannard, C.; Hoffmann, S.; Miyakoshi, M. ICA’s Bug: How Ghost ICs Emerge from Effective Rank Deficiency Caused by EEG Electrode Interpolation and Incorrect Re-Referencing. Front. Signal Process. 2023, 3, 1064138. [Google Scholar] [CrossRef]




| Stage | Value |
|---|---|
| Skin | R1 = 1 MΩ; RS = 1 MΩ; CS = 10 nF |
| Skin/electrode | RSe = 1 kΩ; CSe = 10 nF |
| Electrode | Re = 35 kΩ; CSe = 10 nF |
| Amplification | Ideal operational amplifier |
| Parameter | RF | ANN |
|---|---|---|
| R2 (coefficient of determination) | 0.378 | 0.344 |
| Mean Absolute Error (MAE) | 0.08 | 0.134 |
| Mean Squared Error (MSE) | 0.01 | 0.028 |
| Root Mean Squared Error (RMSE) | 0.0123 | 0.166 |
| Mean Signed Difference (MSD) | −0.005 | 0.037 |
| Fold | RF | ANN |
|---|---|---|
| 1 | 0.02 | 0.027 |
| 2 | 0.018 | 0.028 |
| 3 | 0.01 | 0.03 |
| 4 | 0.016 | 0.026 |
| 5 | 0.024 | 0.031 |
| 6 | 0.017 | 0.022 |
| 7 | 0.013 | 0.021 |
| 8 | 0.018 | 0.021 |
| 9 | 0.019 | 0.02 |
| 10 | 0.015 | 0.028 |
| Proposed Methodology | Advantages | Disadvantages |
|---|---|---|
| Circuit simulation | The circuit simulation provides the testing dataset to use for the classification process of the AI-supervised algorithm. The possibility to replicate real noise conditions allows the prediction of possible uncontrollable signal trend behaviors. | The circuital electrical and electronic parameters (resistances and capacitance of Table 1) could vary, consecutively changing the simulation output. In order to mitigate this effect, it is possible to perform a parametric simulation by studying the electrical parameters’ sensitivity versus the noisy trend of the voltage output. |
| Dataset sampling | Possibility to classify the sampled brain signal based on the region where the electrode is applied (F, Fp, T, C, P, O, A). The data sampling is a characteristic of the adopted technology. | The sampling of the circuit DT simulator should be aligned with the sampling of the adopted electrode technology to avoid losing significant data (important peak positions or significant trends). |
| Training dataset of the supervised AI algorithm | The preliminary selection of a dataset of a specific pathology or known EEG signal trends (as in the case of the paper related to EEG alcoholic signals) will optimize the training model to recognize the class of a specific EEG morphology. | The AI-supervised algorithms require a significant selection of training EEG datasets, including information regarding electrode application with reference to brain regions. |
| Quasi real-time EEG detection | The application of the DT model could correct in real time the EEG signal due to a wrong measurement affected by Flicker and white noises. | The model does not provide information about the origin of the noises to understand if the EEG technology is still suitable for measurements. |
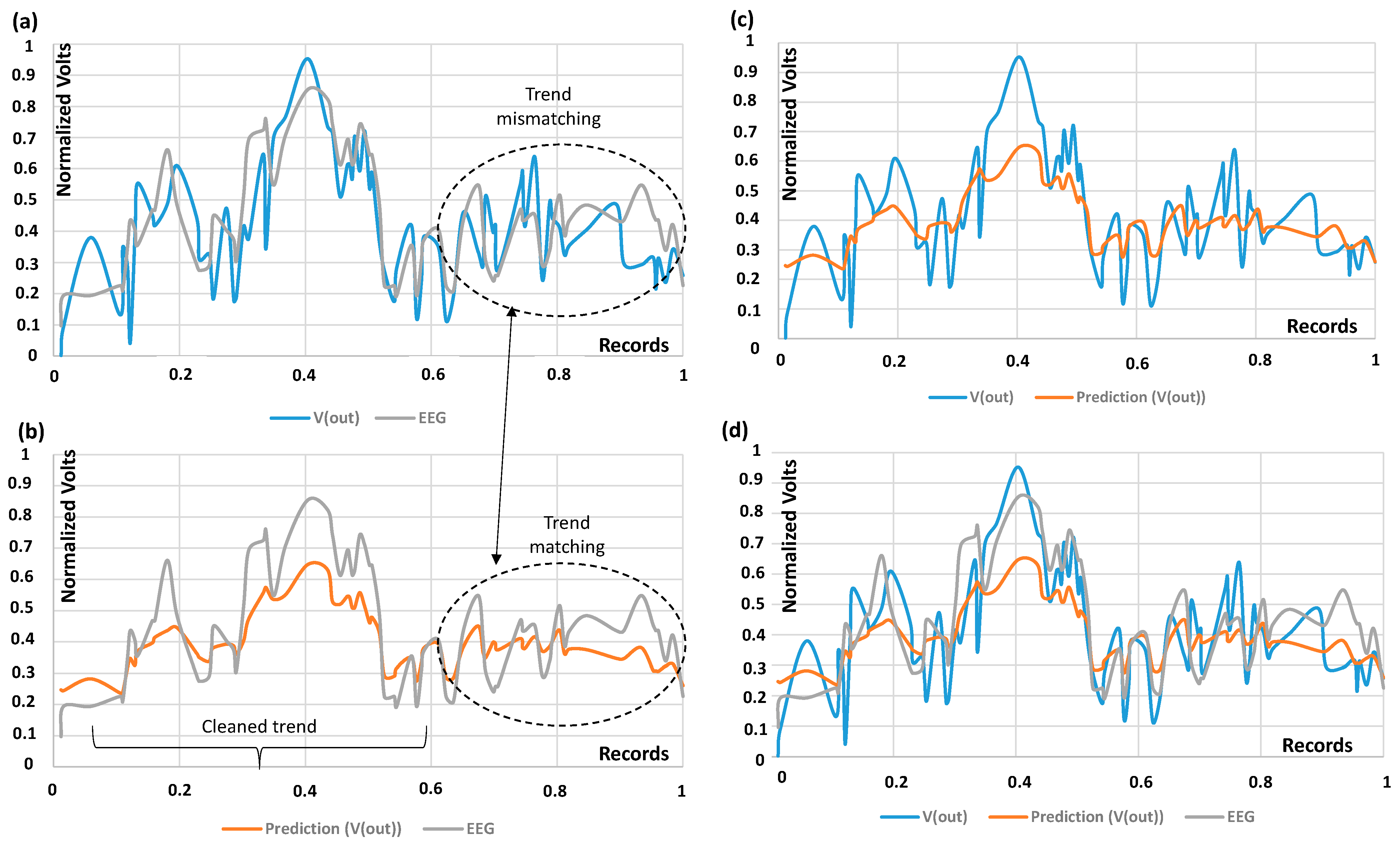
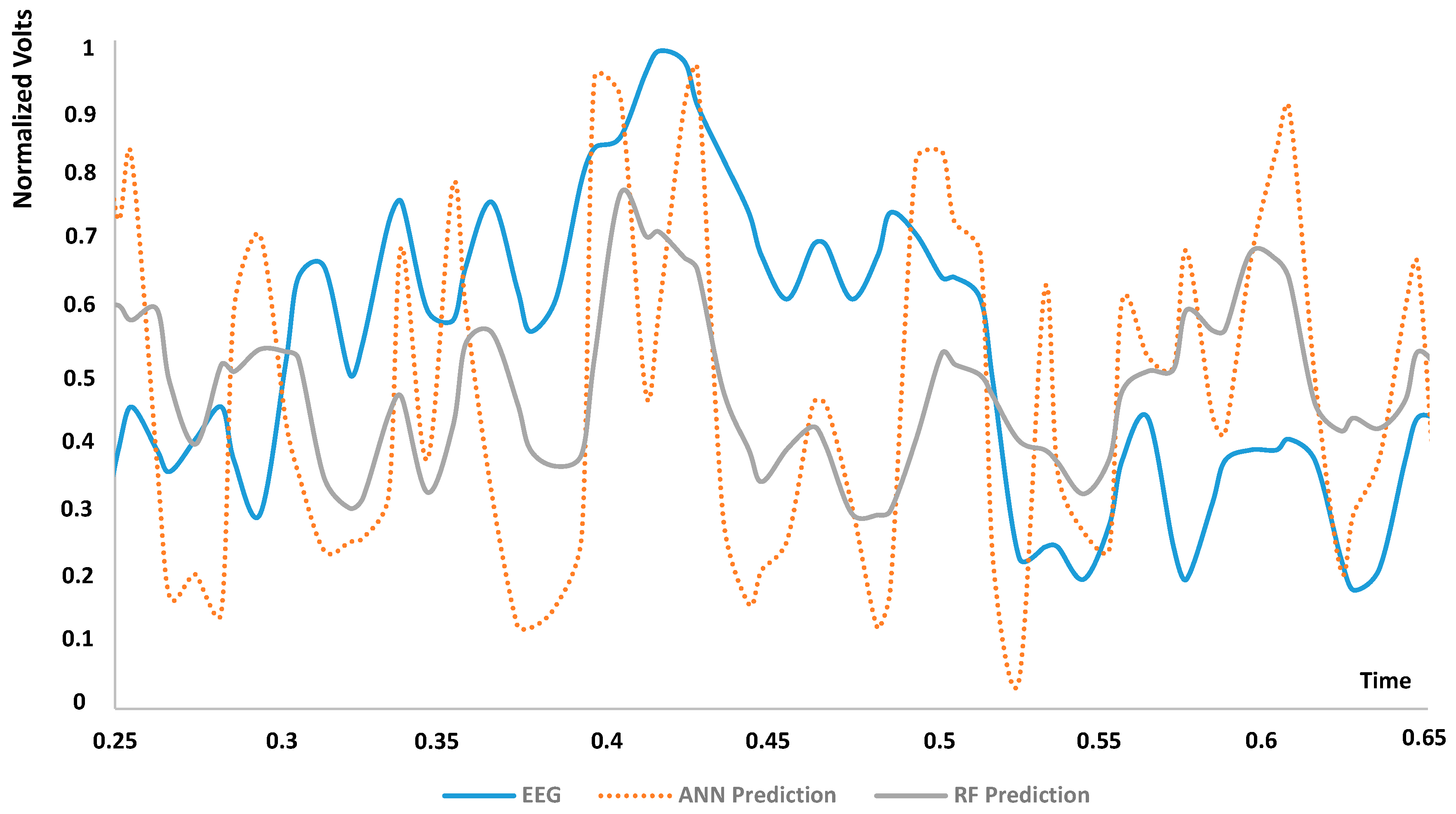
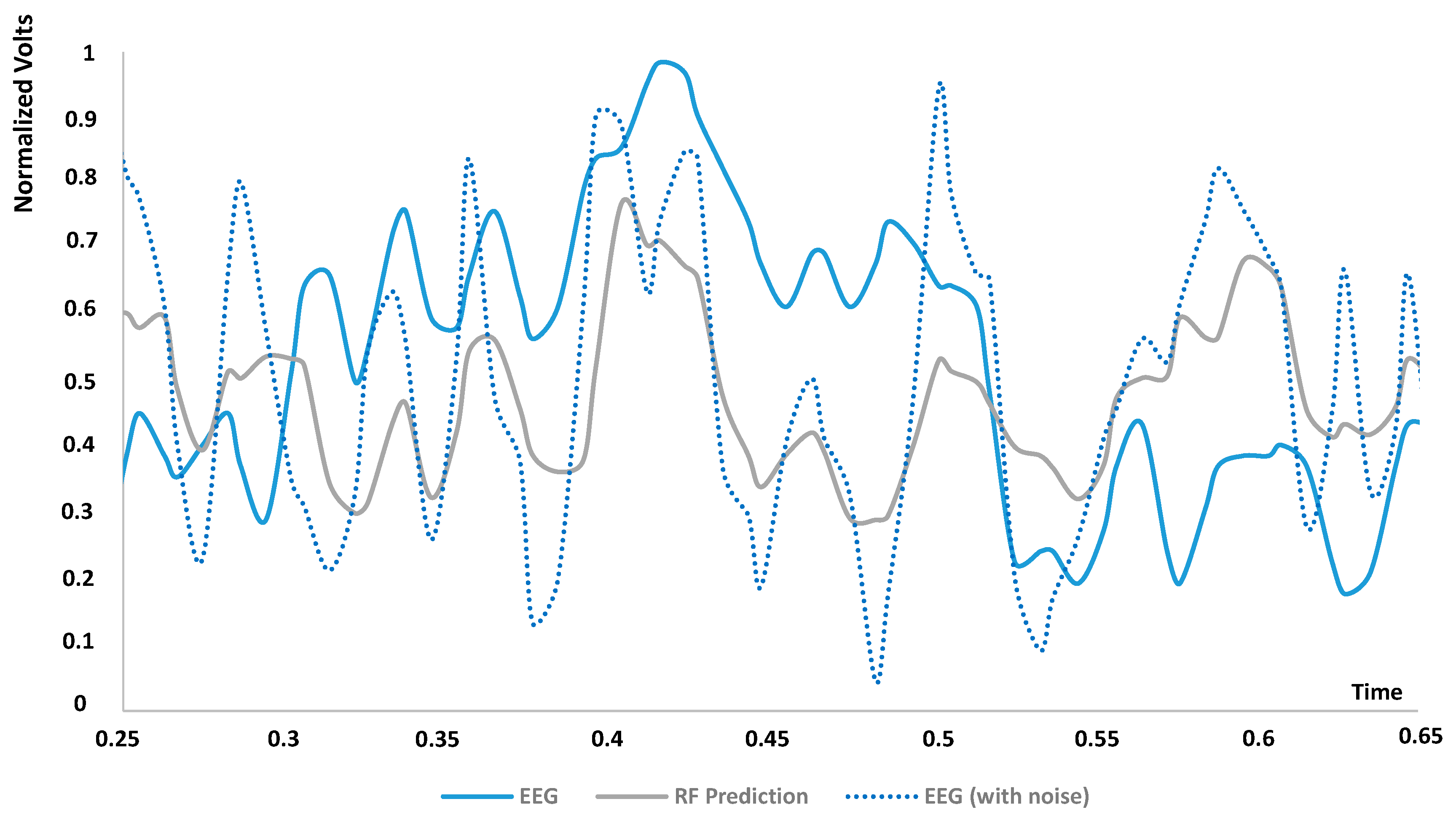
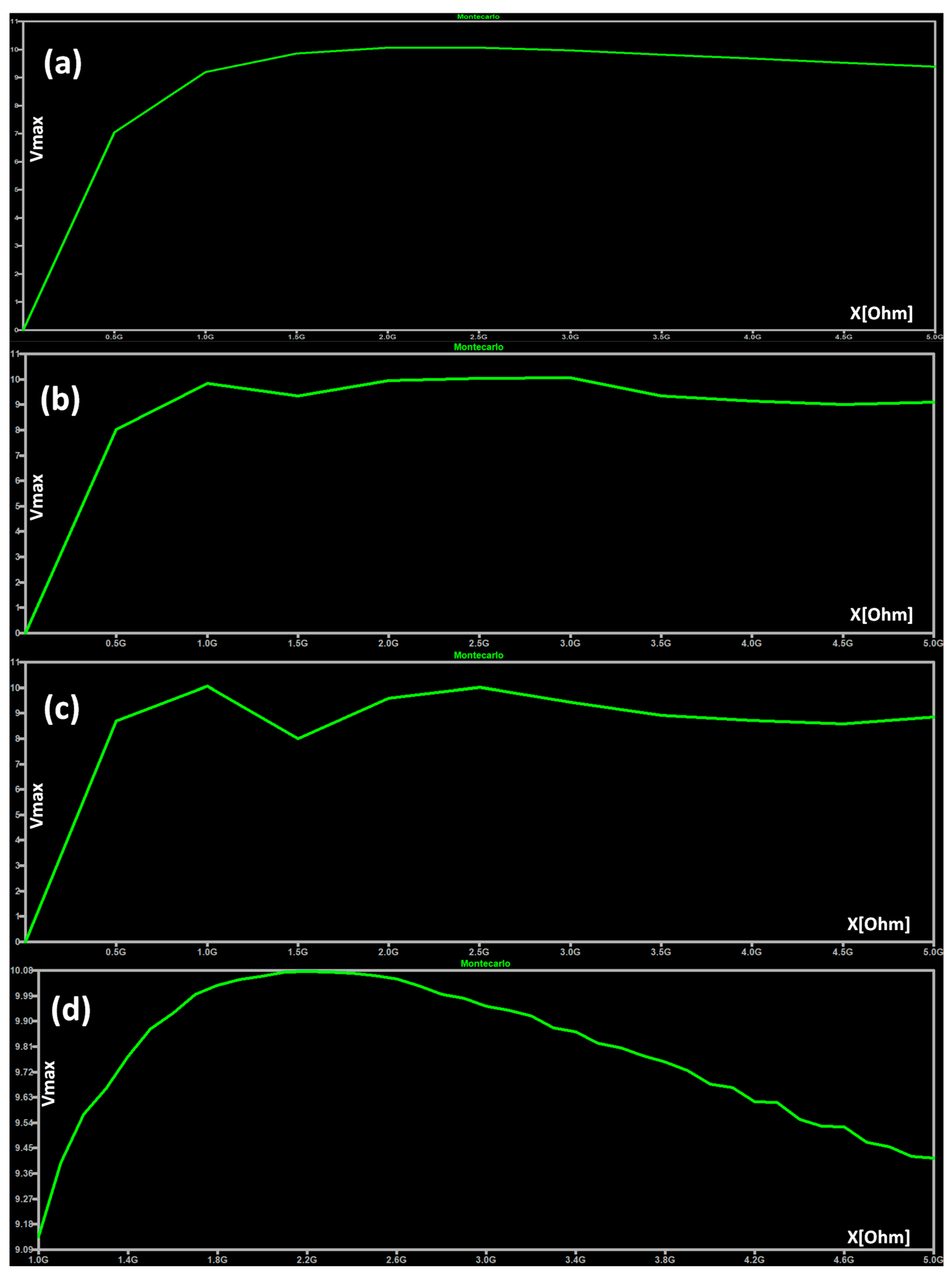
| DT dashboards and performance indicators | The dashboards of Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 and the error indicators of Table 2 (MAE, MSE, MSD, RMSE) are fundamental to checking the DT’s behavior and its performance during parameter setting. | The dashboards and the indicators refer to a specific supervised algorithm. It is not possible to decide a priori the best algorithm to apply, and this entails the need to compare different DT models (see Figure 6). |
| DT Property | Limits | Perspectives |
|---|---|---|
| Tools’ integration | A stable DT requires a fully integrated DT platform composed by the technology, the circuit simulator, and the AI engine. A limit of a non-integrated platform is the need to manipulate the dataset to align and balance the dataset homogeneously (for example, by fixing the number of records). This aspect could lead to the deletion of some records and, therefore, a lack of information to process (possible missed peaks or unseen trends). | A fully integrated DT platform, including hardware (electrode systems) and software (circuit simulator), allows for fixing the EEG sampling rate, thus facilitating the construction of a homogeneous dataset. |
| Application of the DT model to new measurements | The EEG model is applied in the proposed paper to an open dataset [35] to prove the DT ‘proof of concept’. The EEG DT should be set for a specific electrode technology which could lead to a significant change of the circuital parameters and of hyper-parameters according with new measurements. | The EEG DT could be applied to specific electrodes to customize the settings of the DT model. |
| Checks of EEG trend variations | The proposed DT model does not provide an automatic check of the comparison of the predicted results with the EEG input ones (the presence or absence of peaks, matching or mismatching of the voltage morphology). | An automatic check system could facilitate data interpretation and, in general, the reading of the output signal, thus accelerating EEG diagnosis. |
| Comparison between circuit simulation results and real measurements | The EEG DT model is applied to replicate and simulate a noisy signal. The simulation should be compared with the real noisy signal before to apply the ‘cleaning’ process by the AI-supervised algorithms. | Future work will address the definition of a procedure to compare the simulated EEG results with the detected EEG measurements. |
| Measurement | ANN | RF |
|---|---|---|
| 1 | Bias = −0.012 SD = 0.203 | Bias = −0.017 SD = 0.165 |
| 2 | Bias = 0.005 SD = 0.051 | Bias = −0.001 SD = 0.0545 |
| 3 | Bias = −0.004 SD = 0.063 | Bias = −0.001 SD = 0.074 |
| 4 | Bias = 0.004 SD = 0.0305 | Bias = −0.006 SD = 0.036 |
| 5 | Bias = 0.004 SD = 0.177 | Bias = 0.01 SD = 0.1385 |
| 6 | Bias = 0.02 SD = 0.144 | Bias = 0.012 SD = 0.137 |
| 7 | Bias = 0.016 SD = 0.0685 | Bias = 0.008 SD = 0.1005 |
| 8 | Bias = −0.012 SD = 0.054 | Bias = −0.009 SD = 0.0525 |
| Average SD (ANN) | Average SD (RF) | SD Bandpass Filtering [45] | SD FIR Filtering [45] |
|---|---|---|---|
| 0.0988 | 0.0947 | 0.1647 | 0.1382 |
| ANN (This Work) | RF (This Work) | Wavelet Functions Denoising PLN [50] | Wavelet Functions Denoising EMG [50] | Wavelet Functions Denoising 15 dB WGN [50] |
|---|---|---|---|---|
| 0.020 | 0.010 | ≅0.02 | ≅0.012 | ≅26.72 |
| Min | Max | Mean | St. Deviation (SD) | Variance | Skewness | Kurtosis |
|---|---|---|---|---|---|---|
| 9.137 | 10.075 | 9.787 | 0.243 | 0.059 | −0.611 | −0.432 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massaro, A. Electronic Artificial Intelligence–Digital Twin Model for Optimizing Electroencephalogram Signal Detection. Electronics 2025, 14, 1122. https://doi.org/10.3390/electronics14061122
Massaro A. Electronic Artificial Intelligence–Digital Twin Model for Optimizing Electroencephalogram Signal Detection. Electronics. 2025; 14(6):1122. https://doi.org/10.3390/electronics14061122
Chicago/Turabian StyleMassaro, Alessandro. 2025. "Electronic Artificial Intelligence–Digital Twin Model for Optimizing Electroencephalogram Signal Detection" Electronics 14, no. 6: 1122. https://doi.org/10.3390/electronics14061122
APA StyleMassaro, A. (2025). Electronic Artificial Intelligence–Digital Twin Model for Optimizing Electroencephalogram Signal Detection. Electronics, 14(6), 1122. https://doi.org/10.3390/electronics14061122








