HRRnet: A Parameter Estimation Method for Linear Frequency Modulation Signals Based on High-Resolution Spectral Line Representation
Abstract
1. Introduction
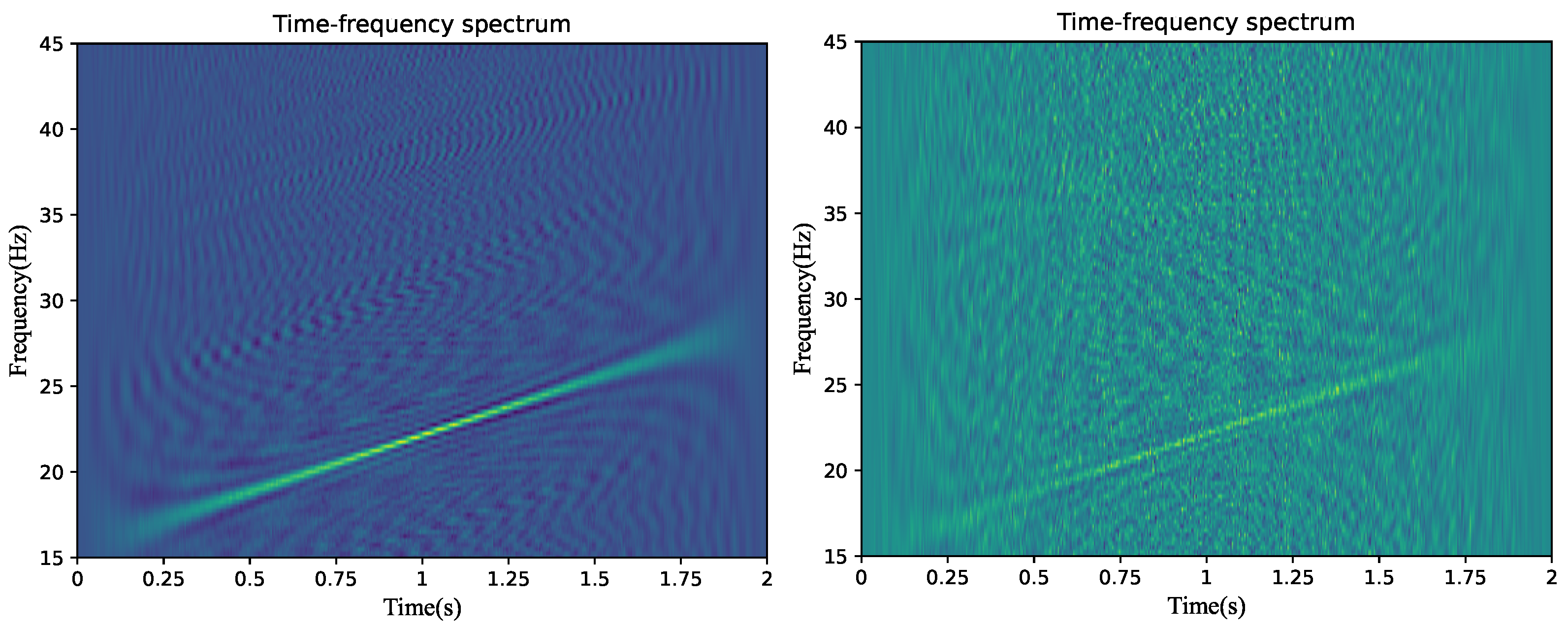
2. Signal Denoising and High-Resolution Representation of the Time–Frequency Spectrum
3. Design and Parameter Optimization of HRRnet
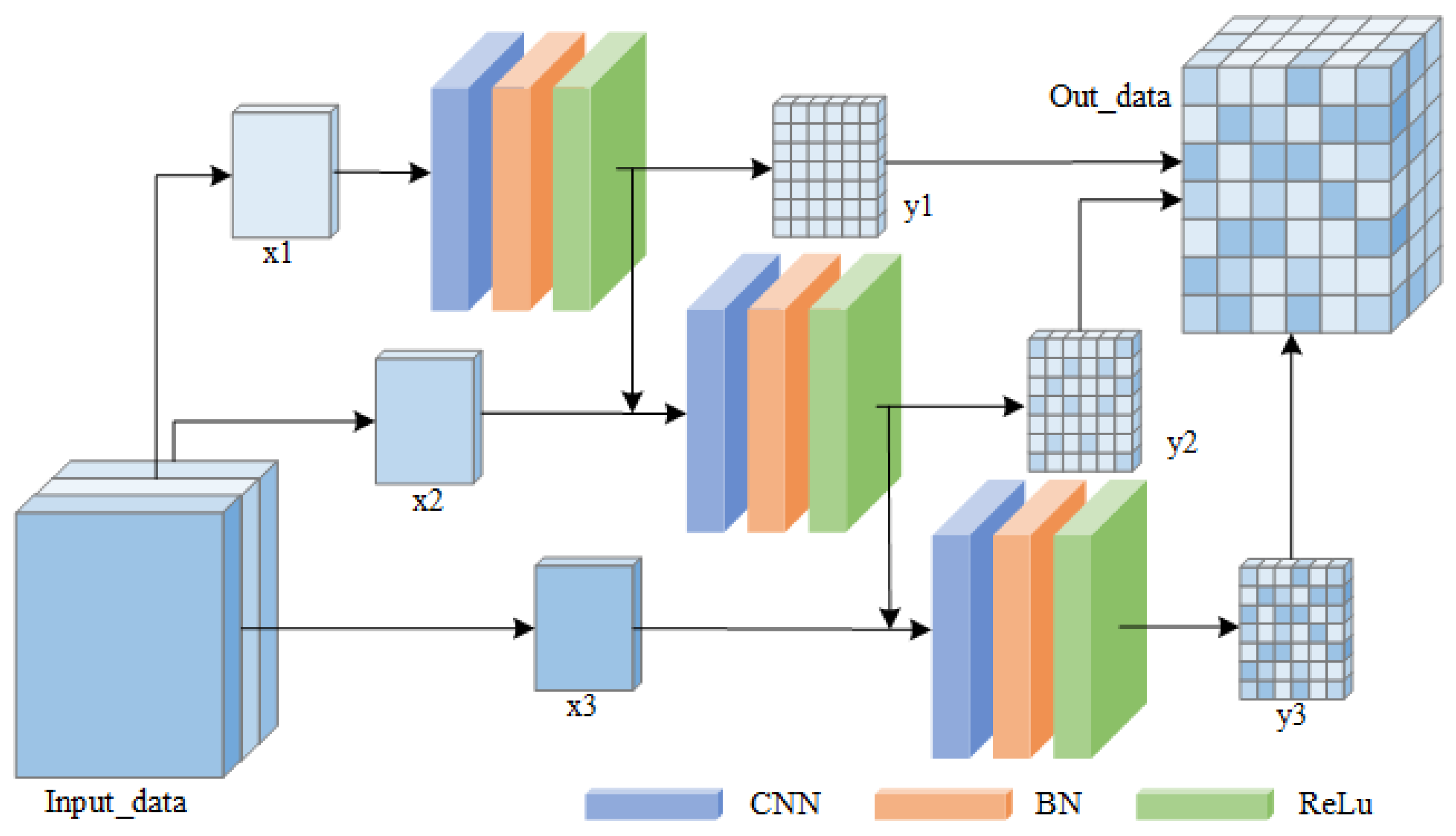
3.1. Design of HRRnet
3.2. Parameter Optimization Algorithms for HRRnet
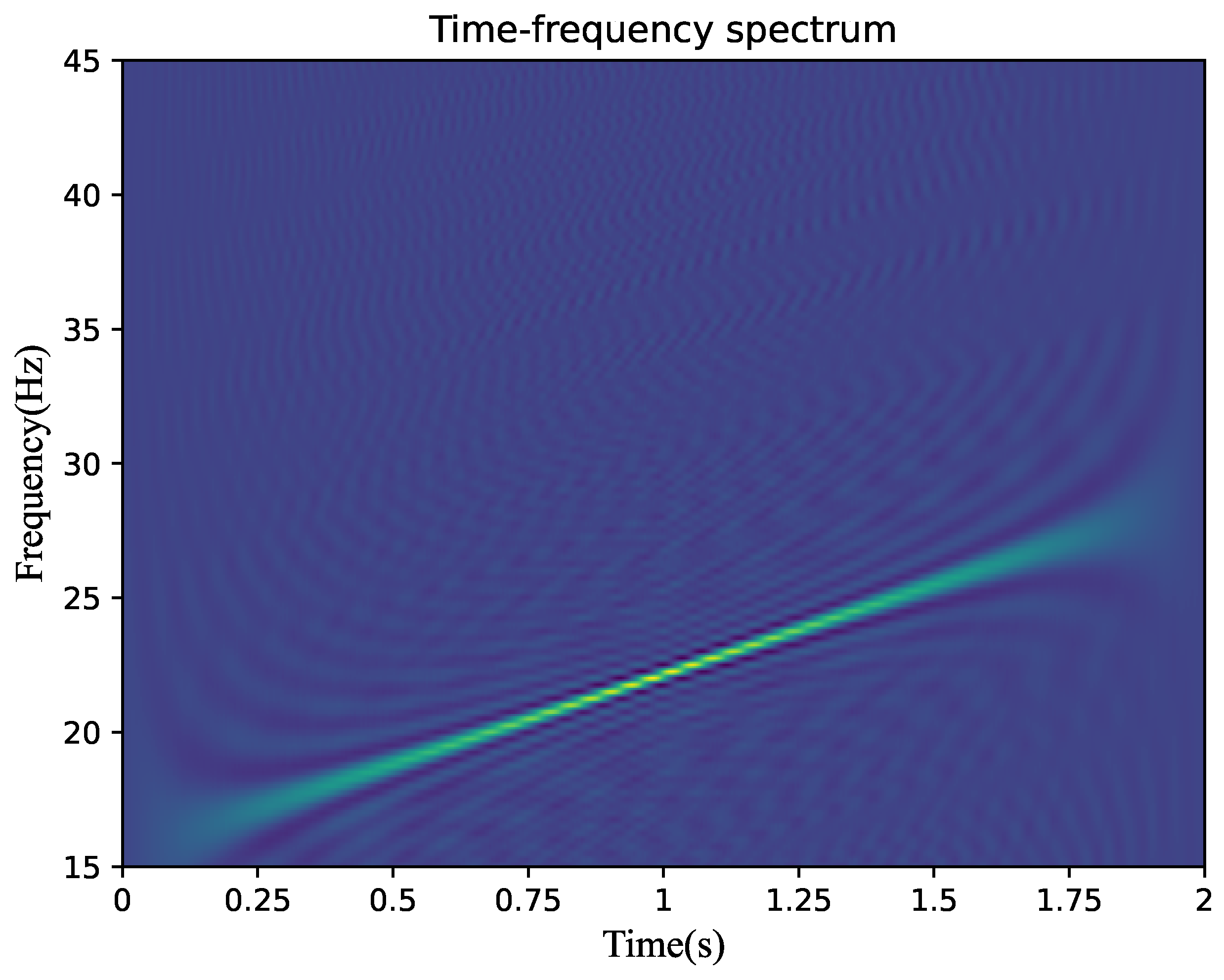
4. Simulation Verification and Analysis
4.1. Simulation Parameters
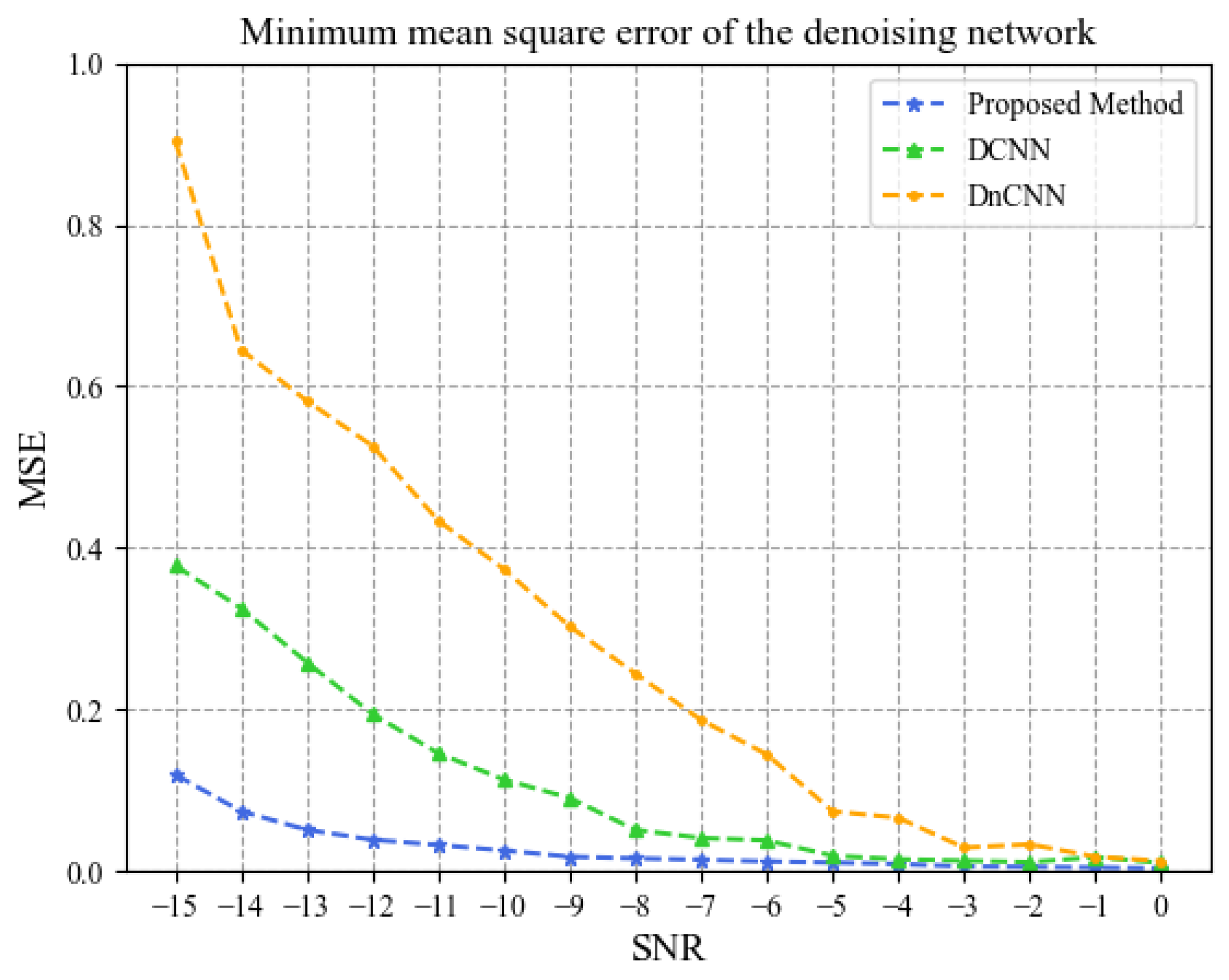
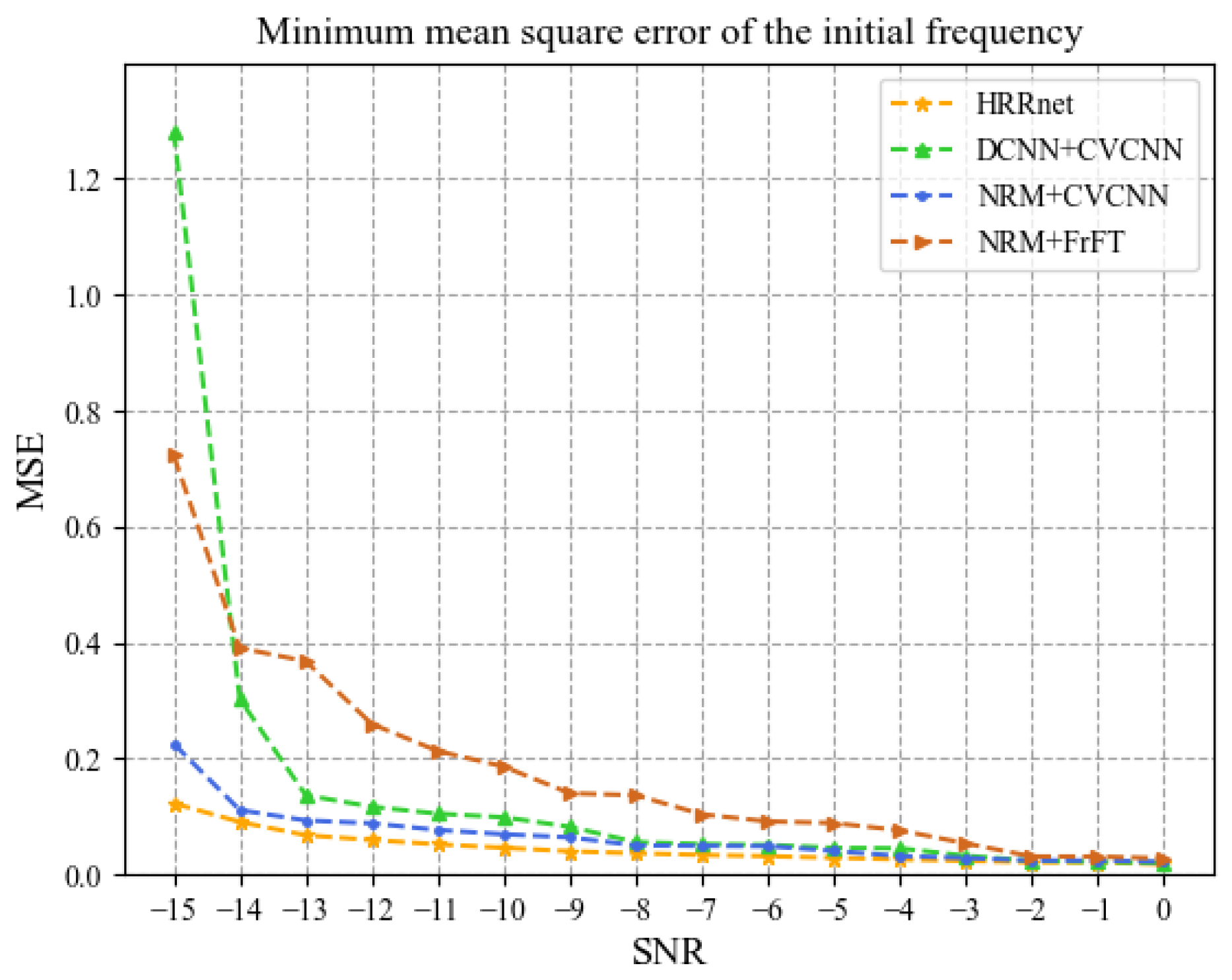
4.2. Analysis of Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Palmer, R.D.; Yeary, M.B.; Schvartzman, D.; Salazar-Cerreno, J.L.; Fulton, C.; McCord, M. Horus—A Fully Digital Polarimetric Phased Array Radar for Next-Generation Weather Observations. IEEE Trans. Radar Syst. 2023, 1, 96–117. [Google Scholar] [CrossRef]
- Johannes, W.; Caris, M.; Stanko, S. 94 GHz Radar Used for Perimeter Surveillance with Wide Target Clarification. In Proceedings of the 2020 21st International Radar Symposium (IRS), Warsaw, Poland, 5–8 October 2020; pp. 15–18. [Google Scholar] [CrossRef]
- Zhang, T.; Zeng, T.; Zhang, X. Synthetic Aperture Radar (SAR) Meets Deep Learning. Remote Sens. 2023, 15, 303. [Google Scholar] [CrossRef]
- Bullecks, B.; Suresh, R.; Rengaswamy, R. Rapid impedance measurement using chirp signals for electrochemical system analysis. Comput. Chem. Eng. 2017, 106, 421–436. [Google Scholar] [CrossRef]
- Czarnecki, K.; Moszynski, M. A novel method of local chirp-rate estimation of LFM chirp signals in the time-frequency domain. In Proceedings of the 2013 36th International Conference on Telecommunications and Signal Processing (TSP), Rome, Italy, 2–4 July 2013; pp. 704–708. [Google Scholar]
- Akan, A.; Karabiber Cura, O. Time–frequency signal processing: Today and future. Digit. Signal Process. 2021, 119, 103216. [Google Scholar] [CrossRef]
- Lu, L.; Ren, W.X.; Wang, S.D. Fractional Fourier transform: Time-frequency representation and structural instantaneous frequency identification. Mech. Syst. Signal Process. 2022, 178, 109305. [Google Scholar] [CrossRef]
- Shi, J.; Zheng, J.; Liu, X.; Xiang, W.; Zhang, Q. Novel Short-Time Fractional Fourier Transform: Theory, Implementation, and Applications. IEEE Trans. Signal Process. 2020, 68, 3280–3295. [Google Scholar] [CrossRef]
- Cao, W.; Yao, Z.; Xia, W.; Yan, S. Parameter Estimation of Linear Frequency Modulated Signals Based on Interpolated Short-Time Fractional Fourier Transform and Variable Weight Fitting. Acta Armam. 2020, 41, 9. [Google Scholar]
- Sejdi, E.; Djurovi, I.; Stankovi, L. Fractional Fourier transform as a signal processing tool: An overview of recent developments. Signal Process. 2011, 91, 1351–1369. [Google Scholar] [CrossRef]
- Wang, X.; Ying, T.; Tian, W. Spectrum Representation Based on STFT. In Proceedings of the 2020 13th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Chengdu, China, 17–19 October 2020; pp. 435–438. [Google Scholar] [CrossRef]
- Brynolfsson, J.; Sandsten, M. Classification of one-dimensional non-stationary signals using the Wigner–Ville distribution in convolutional neural networks. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 326–330. [Google Scholar]
- Chen, J.Y.; Li, B.Z. The short-time Wigner–Ville distribution. Signal Process. 2024, 219, 109402. [Google Scholar] [CrossRef]
- Guo, F.; Yang, L.; Zhang, Z. Fast algorithm for Radon-ambiguity transform. IET Radar Sonar Navig. 2015, 10, 553–559. [Google Scholar] [CrossRef]
- Liu, F.; Sun, D.P.; Huang, Y.; Tao, R.; Wang, Y. Fast Parameter-Estimation of LFM Signal Based on Improved Combined WVD and Randomized Hough Transform. Acta Armam. 2009, 30, 1642–1646. [Google Scholar]
- Feng, J.; Wu, Y.; Sun, H.; Zhang, S.; Liu, D. Panther: Practical Secure Two-Party Neural Network Inference. IEEE Trans. Inf. Forensics Secur. 2025, 20, 1149–1162. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, Q.; Su, N.; Chen, B.; Guan, J. LFM signal detection and estimation based on deep convolutional neural network. In Proceedings of the 2019 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, 18–21 November 2019; pp. 753–758. [Google Scholar]
- Ben, G.; Zheng, X.; Wang, Y.; Zhang, X.; Zhang, N. Chirp Signal Denoising Based on Convolution Neural Network. Circuits Syst. Signal Process. 2021, 40, 5468–5482. [Google Scholar] [CrossRef]
- Su, H.; Bao, Q. Deep Learning Enabled Parameters Estimation Using Time-Frequency Analysis of Chirp Signals. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 23–25 October 2020; IEEE: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, H.; Rangaswamy, M. Deep Learning Denoising Based Line Spectral Estimation. IEEE Signal Process. Lett. 2019, 26, 1573–1577. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2016, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Zou, H.; Lan, R.; Zhong, Y.; Liu, Z.; Luo, X. EDCNN: A novel network for image denoising. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1129–1133. [Google Scholar]
- Gao, S.H.; Cheng, M.M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Zhang, Z.; Zhu, X. Multitaper adaptive short-time Fourier transform with chirp-modulated Gaussian window and multitaper extracting transform. Digit. Signal Process. 2022, 126, 103472. [Google Scholar] [CrossRef]

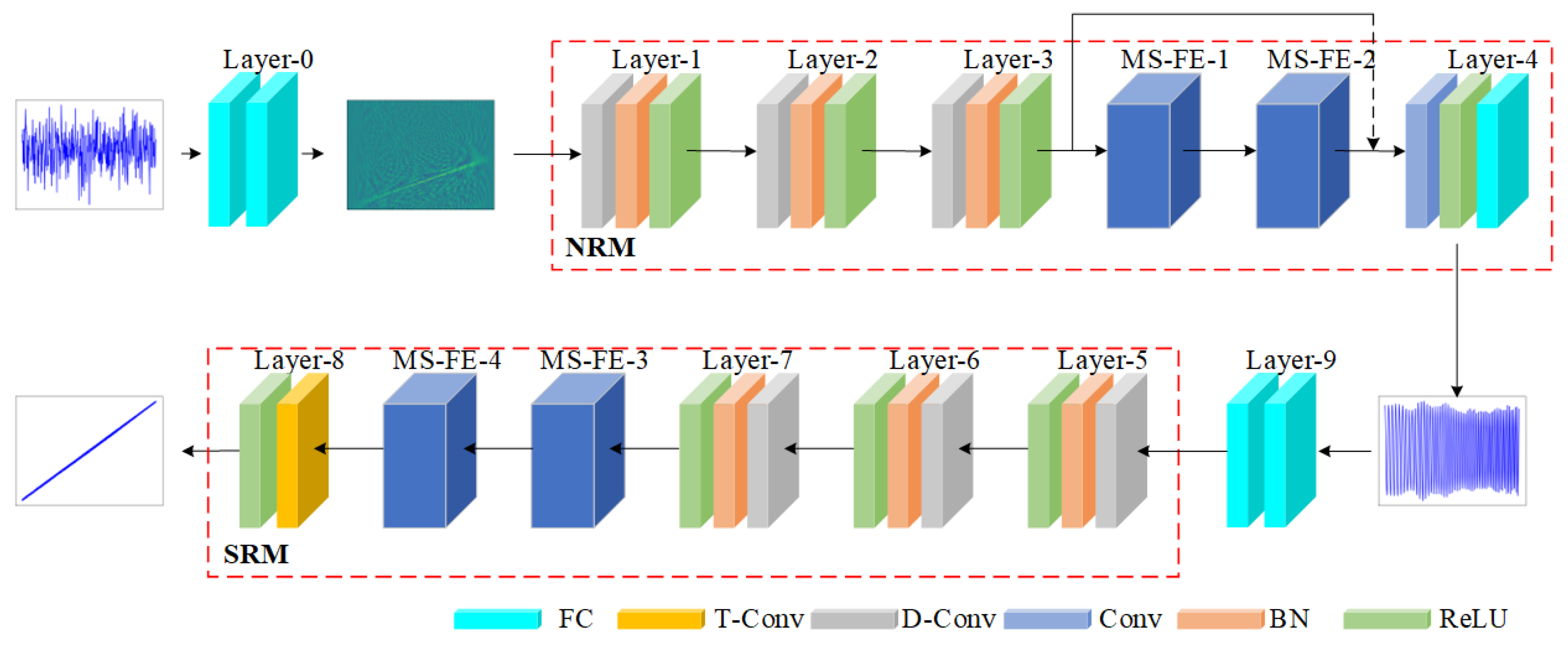






| Layer Name | Output Dimension | Convolution Kernel Size | Convolution Rate |
|---|---|---|---|
| Input | 2 × 512 | - | - |
| Layer-0 | 32 × 32 | - | - |
| Layer-1 | 32 × 32 × 32 | 3 × 3 | 1 |
| Layer-2 | 32 × 32 × 32 | 3 × 3 | 2 |
| Layer-3 | 64 × 32 × 32 | 3 × 3 | 5 |
| MS-FE-3 | 64 × 32 × 32 | 1 × 1/3 × 3 | 1 |
| MS-FE-4 | 64 × 32 × 32 | 1 × 1/3 × 3 | 1 |
| Layer-4 | 2 × 512 | 1 × 1 | 1 |
| Layer Name | Output Dimension | Convolution Kernel Size | Convolution Rate |
|---|---|---|---|
| Layer-9 | 32 × 32 × 32 | - | - |
| Layer-5 | 32 × 32 × 32 | 3 × 3 | 1 |
| Layer-6 | 32 × 32 × 32 | 3 × 3 | 2 |
| Layer-7 | 64 × 32 × 32 | 3 × 3 | 5 |
| MS-FE-3 | 64 × 32 × 32 | 1 × 1/3 × 3 | 1 |
| MS-FE-4 | 64 × 32 × 32 | 1 × 1/3 × 3 | 1 |
| Layer-8 | 1 × 5120 | 3 × 3 | 1 |
| The Number of Training/ Testing Samples | Initial Frequency (Hz) | Frequency Modulation Coefficient (Hz) | Sampling Point Count | Sampling Frequency (Hz) |
|---|---|---|---|---|
| 3000/500 | 15∼20 | 5∼10 | 256 |
| Optimizer | Learning Rate | Number of Training Epochs | Validation Method | Learning Rate Decay Strategy |
|---|---|---|---|---|
| Adam | 0.001 | 100 | 10-fold cross-validation | 0.8 |
| Network Name | NRM | DCNN | DnCNN |
|---|---|---|---|
| Number of Parameters | 4.21 M | 4.35 M | 4.37 M |
| Computational Complexity | 122.66 M | 183.9 M | 198.97 M |
| Network Name | HRRnet | NRM + CV-CNN | DCNN + CV-CNN |
|---|---|---|---|
| Number of Parameters | 56.81 M | 277.33 M | 277.47 M |
| Computational Complexity | 246.05 M | 1146.11 M | 1207.35 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fei, S.; Yan, M.; Zhou, F.; Wang, Y.; Zhang, P.; Wang, J.; Wang, W. HRRnet: A Parameter Estimation Method for Linear Frequency Modulation Signals Based on High-Resolution Spectral Line Representation. Electronics 2025, 14, 1121. https://doi.org/10.3390/electronics14061121
Fei S, Yan M, Zhou F, Wang Y, Zhang P, Wang J, Wang W. HRRnet: A Parameter Estimation Method for Linear Frequency Modulation Signals Based on High-Resolution Spectral Line Representation. Electronics. 2025; 14(6):1121. https://doi.org/10.3390/electronics14061121
Chicago/Turabian StyleFei, Shunchao, Mengqing Yan, Fan Zhou, Yang Wang, Peiying Zhang, Jian Wang, and Wei Wang. 2025. "HRRnet: A Parameter Estimation Method for Linear Frequency Modulation Signals Based on High-Resolution Spectral Line Representation" Electronics 14, no. 6: 1121. https://doi.org/10.3390/electronics14061121
APA StyleFei, S., Yan, M., Zhou, F., Wang, Y., Zhang, P., Wang, J., & Wang, W. (2025). HRRnet: A Parameter Estimation Method for Linear Frequency Modulation Signals Based on High-Resolution Spectral Line Representation. Electronics, 14(6), 1121. https://doi.org/10.3390/electronics14061121








