A Sparse Representation Classification Framework for Person Identification and Verification Using Neurophysiological Signals
Abstract
1. Introduction
2. Materials and Methods
2.1. SSVEP Datasets
2.2. Spatial Filtering and Filter-Bank Common Spatial Patterns
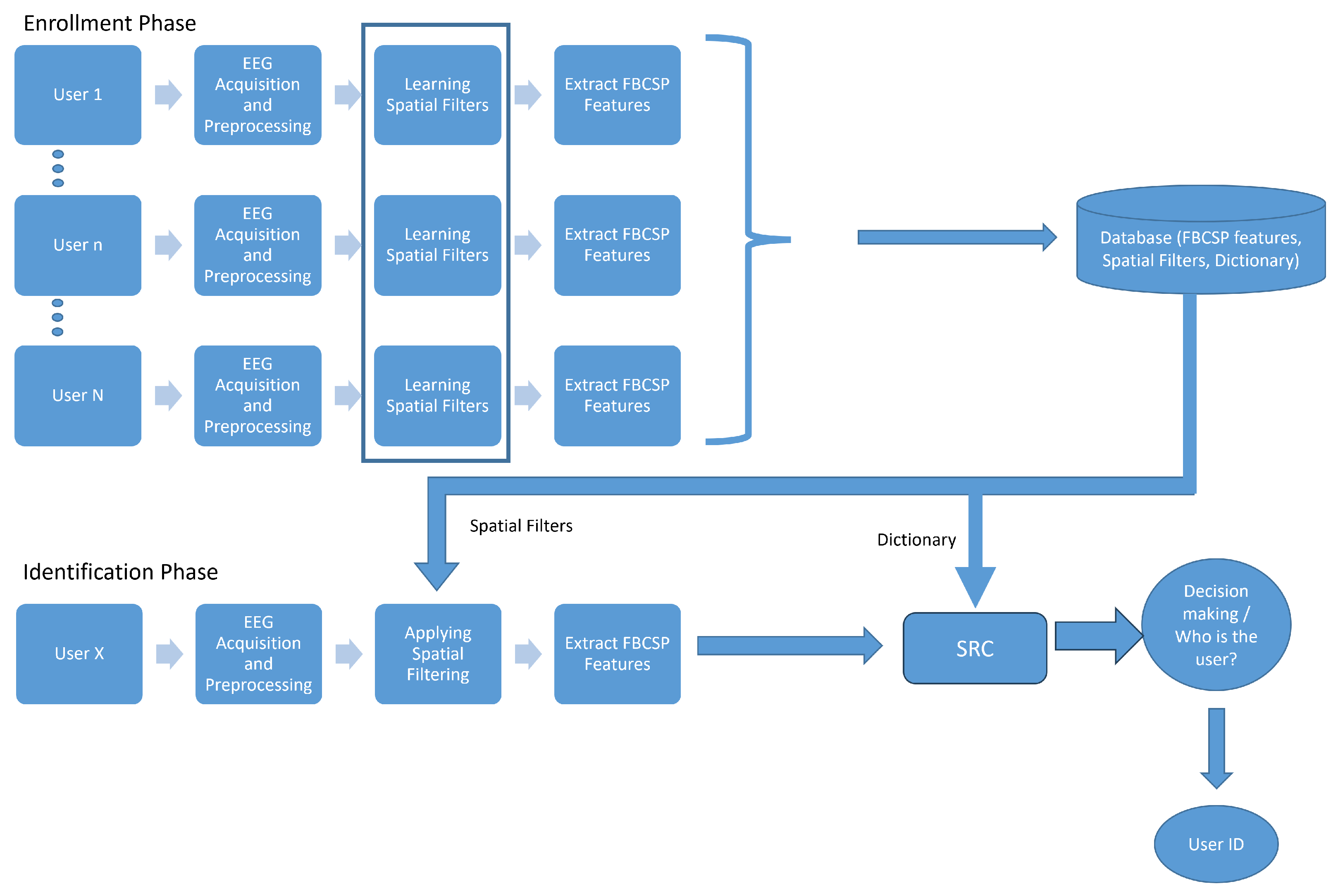
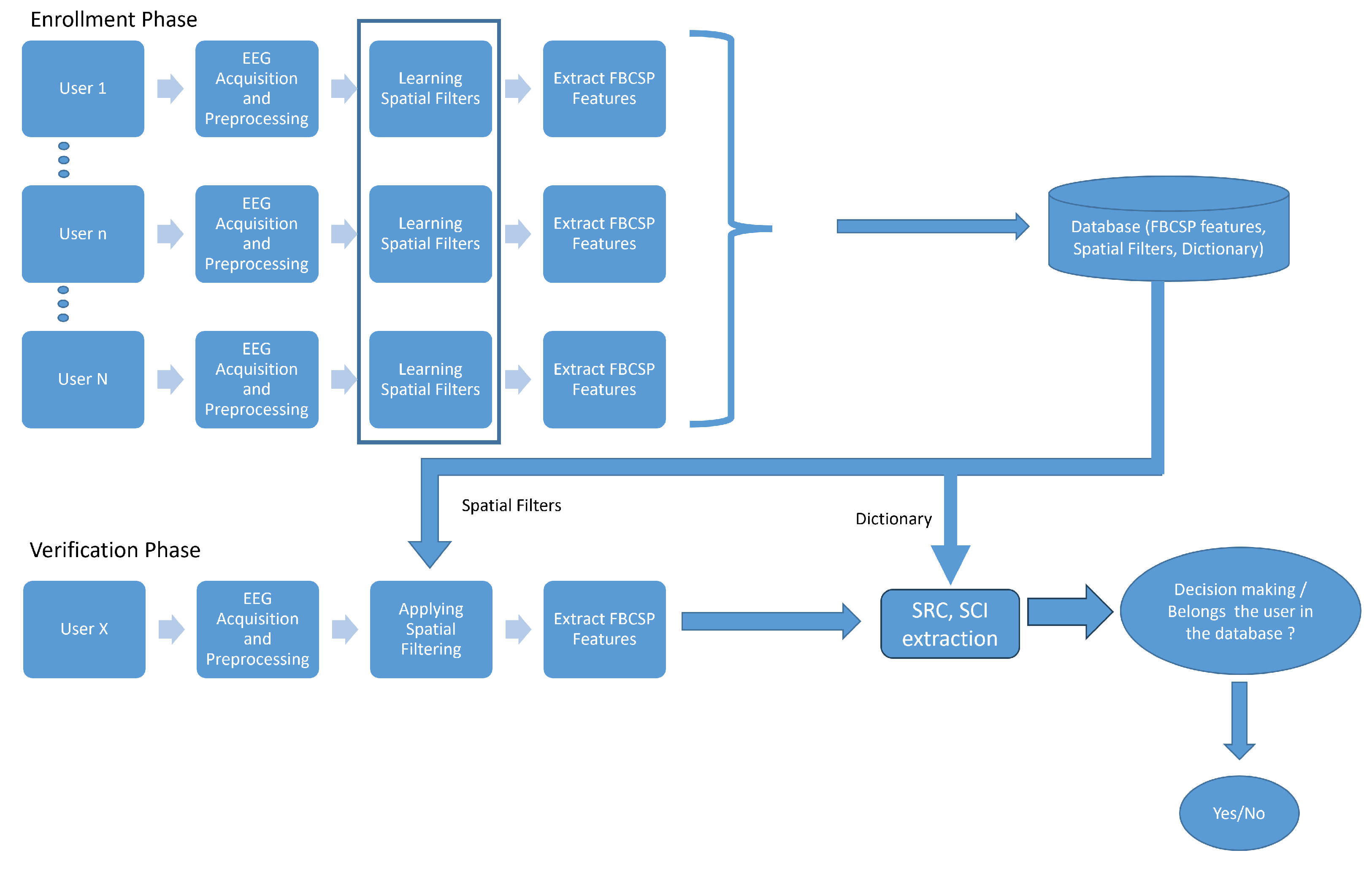
2.3. Sparse Representation Classification (SRC) Framework
2.3.1. Sparse Representation Classification (SRC) for Identification
| Algorithm 1 SRC for identification |
|
2.3.2. Sparse Representation Classification (SRC) for Verification
| Algorithm 2 SRC for verification |
|
3. Experimental Design
3.1. Performance Metrics
3.2. Experimental Settings
- : the number of subjects;
- : the number of blocks;
- : the number of stimulus frequencies;
- : the number of EEG channels;
- : the trial duration.
- SVM-FBCSP: The SVM classifier with a linear kernel, where FBCSP features are used to perform person identification;
- kNN-FBCSP: The kNN classifier with FBCSP features;
- Deep Feedforward Network (DFN) [27]: A deep neural network architecture based on a multilayer perceptron (MLP), specifically designed to use SSVEP responses for human recognition.
4. Results
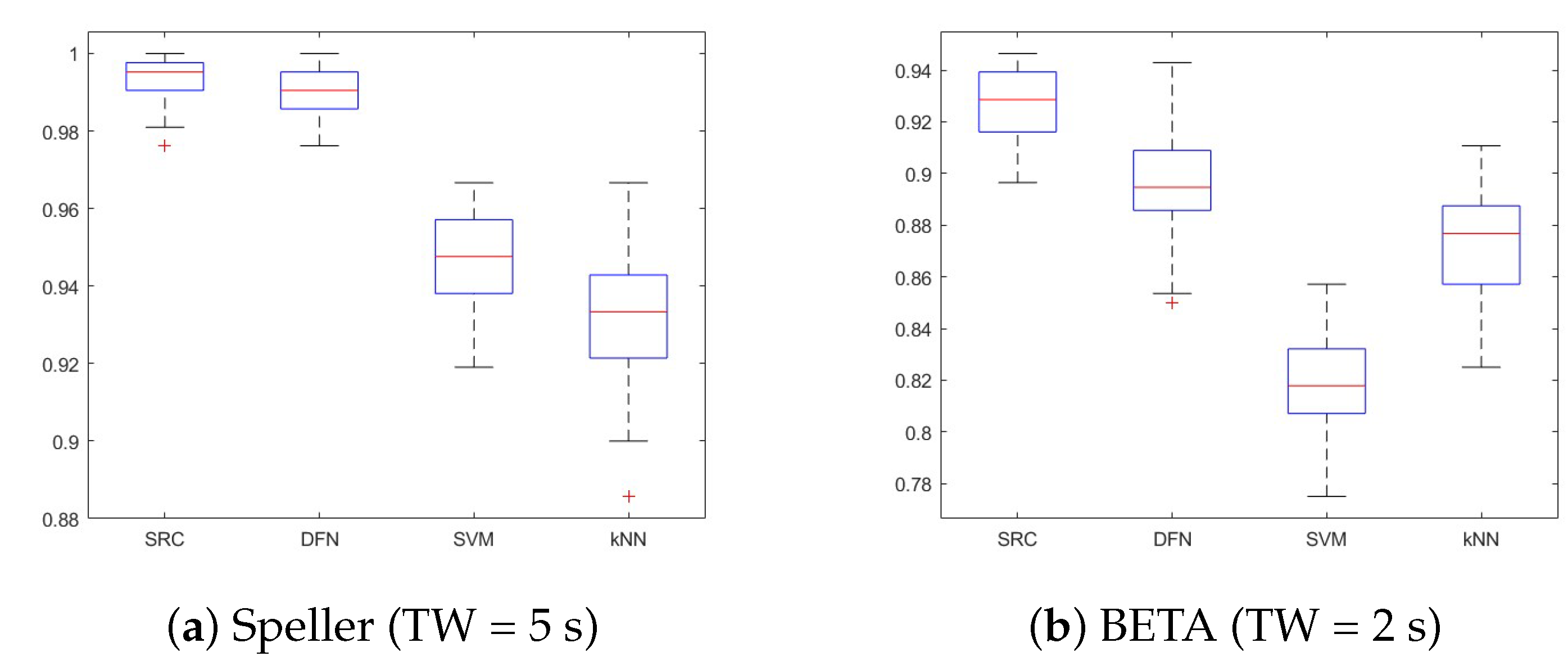
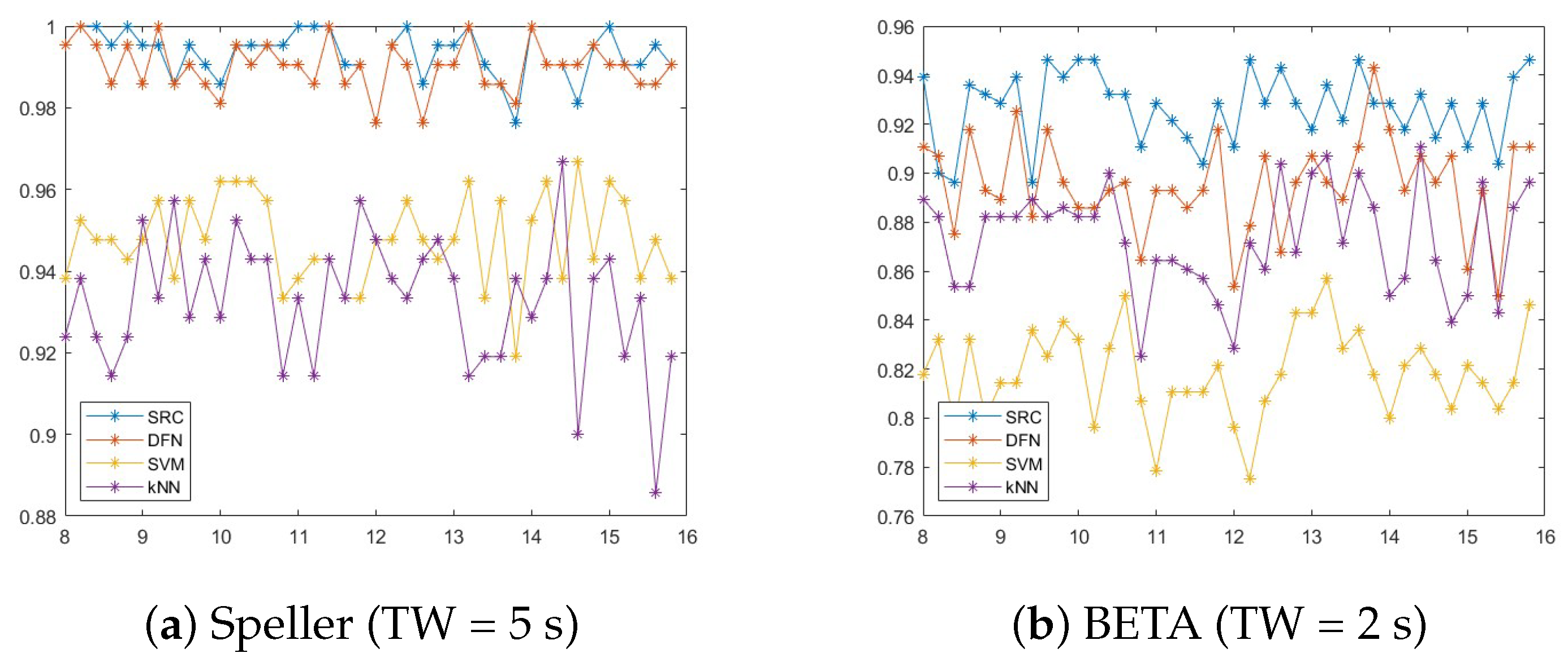
4.1. Identification Results
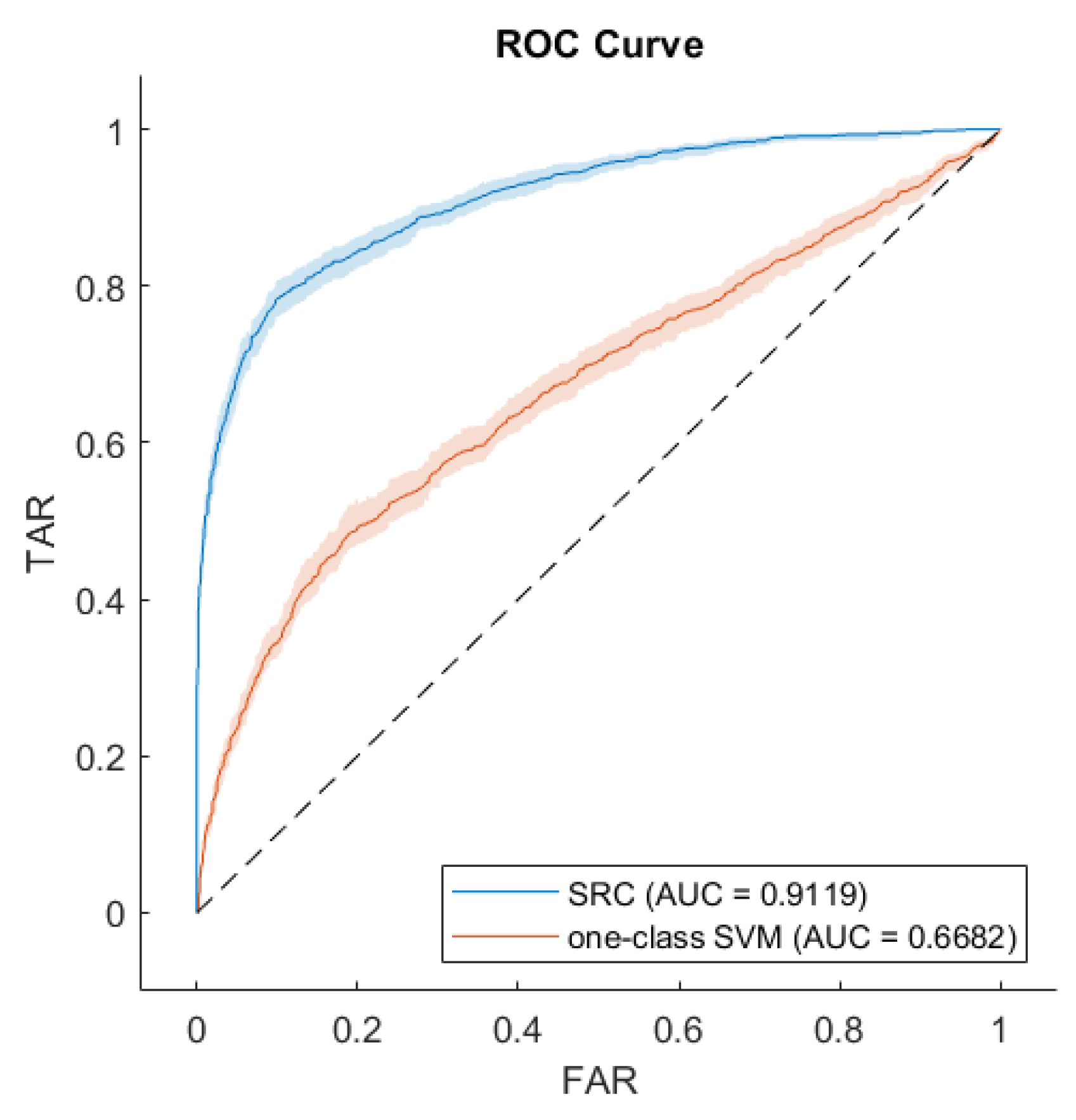
4.2. Verification Results
5. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, D.; Nijholt, A. Brain-Computer Interfaces: Applying Our Minds to Human-Computer Interaction; Springer: London, UK, 2010. [Google Scholar] [CrossRef]
- Jain, A.; Ross, A.; Nandakumar, K. Introduction to Biometrics; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Gui, Q.; Ruiz-Blondet, M.V.; Laszlo, S.; Jin, Z. A Survey on Brain Biometrics. ACM Comput. Surv. 2019, 51, 1–38. [Google Scholar] [CrossRef]
- Del Pozo-Banos, M.; Alonso, J.B.; Ticay-Rivas, J.R.; Travieso, C.M. Electroencephalogram subject identification: A review. Expert Syst. Appl. 2014, 41, 6537–6554. [Google Scholar] [CrossRef]
- Yang, S.; Deravi, F. On the Usability of Electroencephalographic Signals for Biometric Recognition: A Survey. IEEE Trans. Hum.-Mach. Syst. 2017, 47, 958–969. [Google Scholar] [CrossRef]
- Maiorana, E.; La Rocca, D.; Campisi, P. On the Permanence of EEG Signals for Biometric Recognition. IEEE Trans. Inf. Forensics Secur. 2016, 11, 163–175. [Google Scholar] [CrossRef]
- Das, R.; Maiorana, E.; Campisi, P. EEG Biometrics Using Visual Stimuli: A Longitudinal Study. IEEE Signal Process. Lett. 2016, 23, 341–345. [Google Scholar] [CrossRef]
- Jalaly Bidgoly, A.; Jalaly Bidgoly, H.; Arezoumand, Z. A survey on methods and challenges in EEG based authentication. Comput. Secur. 2020, 93, 101788. [Google Scholar] [CrossRef]
- Maiorana, E. Learning deep features for task-independent EEG-based biometric verification. Pattern Recognit. Lett. 2021, 143, 122–129. [Google Scholar] [CrossRef]
- El-Fiqi, H.; Wang, M.; Salimi, N.; Kasmarik, K.; Barlow, M.; Abbass, H. Convolution Neural Networks for Person Identification and Verification Using Steady State Visual Evoked Potential. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 1062–1069. [Google Scholar] [CrossRef]
- Wang, M.; El-Fiqi, H.; Hu, J.; Abbass, H.A. Convolutional Neural Networks Using Dynamic Functional Connectivity for EEG-Based Person Identification in Diverse Human State. IEEE Trans. Inf. Forensics Secur. 2019, 14, 3259–3272. [Google Scholar] [CrossRef]
- Abo-Zahhad, M.; Ahmed, S.M.; Abbas, S.N. State-of-the-art methods and future perspectives for personal recognition based on electroencephalogram signals. IET Biom. 2015, 4, 179–190. [Google Scholar] [CrossRef]
- Chen, Y.; Atnafu, A.D.; Schlattner, I.; Weldtsadik, W.T.; Roh, M.C.; Kim, H.J.; Lee, S.W.; Blankertz, B.; Fazli, S. A High-Security EEG-Based Login System with RSVP Stimuli and Dry Electrodes. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2635–2647. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, X.; Li, X.; Tan, Y. Sparse EEG compressive sensing for web-enabled person identification. Measurement 2015, 74, 11–20. [Google Scholar] [CrossRef]
- Maiorana, E.; Rocca, D.L.; Campisi, P. Eigenbrains and Eigentensorbrains: Parsimonious bases for EEG biometrics. Neurocomputing 2016, 171, 638–648. [Google Scholar] [CrossRef]
- Fraschini, M.; Hillebrand, A.; Demuru, M.; Didaci, L.; Marcialis, G.L. An EEG-Based Biometric System Using Eigenvector Centrality in Resting State Brain Networks. IEEE Signal Process. Lett. 2015, 22, 666–670. [Google Scholar] [CrossRef]
- Kang, J.H.; Jo, Y.C.; Kim, S.P. Electroencephalographic feature evaluation for improving personal authentication performance. Neurocomputing 2018, 287, 93–101. [Google Scholar] [CrossRef]
- Rocca, D.L.; Campisi, P.; Vegso, B.; Cserti, P.; Kozmann, G.; Babiloni, F.; Fallani, F.D.V. Human Brain Distinctiveness Based on EEG Spectral Coherence Connectivity. IEEE Trans. Biomed. Eng. 2014, 61, 2406–2412. [Google Scholar] [CrossRef]
- Zhang, R.; Yan, B.; Tong, L.; Shu, J.; Song, X.; Zeng, Y. Identity Authentication Using Portable Electroencephalography Signals in Resting States. IEEE Access 2019, 7, 160671–160682. [Google Scholar] [CrossRef]
- Nakamura, T.; Goverdovsky, V.; Mandic, D.P. In-Ear EEG Biometrics for Feasible and Readily Collectable Real-World Person Authentication. IEEE Trans. Inf. Forensics Secur. 2018, 13, 648–661. [Google Scholar] [CrossRef]
- Palaniappan, R.; Mandic, D.P. Biometrics from Brain Electrical Activity: A Machine Learning Approach. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 738–742. [Google Scholar] [CrossRef]
- Kong, W.; Wang, L.; Xu, S.; Babiloni, F.; Chen, H. EEG Fingerprints: Phase Synchronization of EEG Signals as Biomarker for Subject Identification. IEEE Access 2019, 7, 121165–121173. [Google Scholar] [CrossRef]
- Yang, S.; Deravi, F.; Hoque, S. Task sensitivity in EEG biometric recognition. Pattern Anal. Appl. 2018, 21, 105–117. [Google Scholar] [CrossRef]
- Phothisonothai, M. An investigation of using SSVEP for EEG-based user authentication system. In Proceedings of the 2015 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA), Hong Kong, China, 16–19 December 2015; pp. 923–926. [Google Scholar] [CrossRef]
- Abo-Zahhad, M.; Ahmed, S.M.; Abbas, S.N. A new multi-level approach to EEG based human authentication using eye blinking. Pattern Recognit. Lett. 2016, 82, 216–225. [Google Scholar] [CrossRef]
- Seha, S.N.A.; Hatzinakos, D. EEG-Based Human Recognition Using Steady-State AEPs and Subject-Unique Spatial Filters. IEEE Trans. Inf. Forensics Secur. 2020, 15, 3901–3910. [Google Scholar] [CrossRef]
- Oikonomou, V.P. Human Recognition Using Deep Neural Networks and Spatial Patterns of SSVEP Signals. Sensors 2023, 23, 2425. [Google Scholar] [CrossRef]
- Falzon, O.; Zerafa, R.; Camilleri, T.; Camilleri, K.P. EEG-based biometry using steady state visual evoked potentials. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju Island, Republic of Korea, 11–15 July 2017; pp. 4159–4162. [Google Scholar] [CrossRef]
- Piciucco, E.; Maiorana, E.; Falzon, O.; Camilleri, K.P.; Campisi, P. Steady-State Visual Evoked Potentials for EEG-Based Biometric Identification. In Proceedings of the 2017 International Conference of the Biometrics Special Interest Group (BIOSIG), Darmstadt, Germany, 20–22 September 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Shin, Y.; Lee, S.; Lee, J.; Lee, H.N. Sparse representation-based classification scheme for motor imagery-based brain–computer interface systems. J. Neural Eng. 2012, 9, 056002. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, Y.; Chen, X.; Yin, E.; Jin, J.; Wang, X.; Cichocki, A. Sparse Group Representation Model for Motor Imagery EEG Classification. IEEE J. Biomed. Health Inform. 2019, 23, 631–641. [Google Scholar] [CrossRef]
- Oikonomou, V.P.; Nikolopoulos, S.; Kompatsiaris, I. Robust Motor Imagery Classification Using Sparse Representations and Grouping Structures. IEEE Access 2020, 8, 98572–98583. [Google Scholar] [CrossRef]
- Oikonomou, V.P.; Georgiadis, K.; Kalaganis, F.; Nikolopoulos, S.; Kompatsiaris, I. A Sparse Representation Classification Scheme for the Recognition of Affective and Cognitive Brain Processes in Neuromarketing. Sensors 2023, 23, 2480. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust Face Recognition via Sparse Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, X.; Gao, X.; Gao, S. A Benchmark Dataset for SSVEP-Based Brain—Computer Interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1746–1752. [Google Scholar] [CrossRef]
- Liu, B.; Huang, X.; Wang, Y.; Chen, X.; Gao, X. BETA: A Large Benchmark Database Toward SSVEP-BCI Application. Front. Neurosci. 2020, 14, 627. [Google Scholar] [CrossRef]
- Oikonomou, V.P. An Adaptive Task-Related Component Analysis Method for SSVEP Recognition. Sensors 2022, 22, 7715. [Google Scholar] [CrossRef] [PubMed]
- Blankertz, B.; Tomioka, R.; Lemm, S.; Kawanabe, M.; Müller, K.R. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process. Mag. 2008, 25, 41–56. [Google Scholar] [CrossRef]
- Chin, Z.Y.; Ang, K.K.; Wang, C.; Guan, C.; Zhang, H. Multi-class filter bank common spatial pattern for four-class motor imagery BCI. In Proceedings of the 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Minneapolis, MN, USA, 3–6 September 2009; pp. 571–574. [Google Scholar] [CrossRef]
- Tipping, M.E. Sparse Bayesian Learning and the Relevance Vector Machine. J. Mach. Learn. Res. 2001, 1, 211–244. [Google Scholar]
- Jiang, B.; Chen, H.; Yuan, B.; Yao, X. Scalable Graph-Based Semi-Supervised Learning through Sparse Bayesian Model. IEEE Trans. Knowl. Data Eng. 2017, 29, 2758–2771. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the Support of a High-Dimensional Distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Noumir, Z.; Honeine, P.; Richard, C. On simple one-class classification methods. In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012; pp. 2022–2026. [Google Scholar] [CrossRef]
- Raza, H.; Rathee, D.; Zhou, S.M.; Cecotti, H.; Prasad, G. Covariate shift estimation based adaptive ensemble learning for handling non-stationarity in motor imagery related EEG-based brain-computer interface. Neurocomputing 2019, 343, 154–166. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2022. [Google Scholar]
- Oikonomou, V.P.; Geordiadis, K.; Kalaganis, F.P.; Nikolopoulos, S.; Kompatsiaris, I. Prediction of Successful Memory Formation during Audiovisual advertising using EEG signals. In Proceedings of the 2024 IEEE Conference on Artificial Intelligence (CAI), Singapore, 25–27 June 2024; pp. 1111–1116. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Wu, D.; Jiang, X.; Peng, R. Transfer learning for motor imagery based brain–computer interfaces: A tutorial. Neural Netw. 2022, 153, 235–253. [Google Scholar] [CrossRef]
- Zhao, Z.; Alzubaidi, L.; Zhang, J.; Duan, Y.; Gu, Y. A comparison review of transfer learning and self-supervised learning: Definitions, applications, advantages and limitations. Expert Syst. Appl. 2024, 242, 122807. [Google Scholar] [CrossRef]
- Wang, Y.; Chao, W.L.; Weinberger, K.Q.; van der Maaten, L. SimpleShot: Revisiting Nearest-Neighbor Classification for Few-Shot Learning. arXiv 2019, arXiv:1911.04623. [Google Scholar]
| Notation | Description |
|---|---|
| EEG | Electroencephalography |
| SSVEP | Steady-State Visual Evoked Potentials |
| SRC | Sparse Representation Classification |
| VR | virtual reality |
| AR | augmented reality |
| MR | mixed reality |
| PSD | power spectral density |
| PLV | phase locking values |
| TF | time frequency |
| SVM | Support Vector Machine |
| kNN | k-Nearest Neighborhood |
| LDA | Linear Discriminant Analysis |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| BCI | Brain–Computer Interface |
| MFCCs | Mel-frequency cepstral coefficients |
| AR | autoregressive |
| FBCSP | Filter-Bank Common Spatial Patterns |
| CCA | Canonical Correlation Analysis |
| TRCA | Task-Related Component Analysis |
| SCI | sparsity concentration index |
| CRR | correct recognition rate |
| Tr | duration of training set |
| Te | duration of test set |
| ROC | Receiver Operating Characteristic |
| TPR | true positive rate |
| FPR | false positive rate |
| TAR | true acceptance rate |
| FAR | false acceptance rate |
| DFN | Deep Feedforward Network |
| MLP | multilayer perceptron |
| TW | time window |
| PI | person identification |
| STFT | Short-Time Fourier Transform |
| SNR | signal-to-noise ratio |
| Parameter | Speller | BETA |
|---|---|---|
| 35 | 70 | |
| 6 | 4 | |
| 40 | 40 | |
| 9 | 9 | |
| 5 s | 2 s |
| Methods | ||||
|---|---|---|---|---|
| TW | SRC | DFN | SVM | kNN |
| Speller | ||||
| 1 s | 94.38 | 92.57 | 85.71 | 85.24 |
| 2 s | 97.81 | 97.52 | 91.33 | 90.86 |
| 3 s | 98.48 | 98.76 | 92.76 | 92.95 |
| 4 s | 98.95 | 98.19 | 94.38 | 93.05 |
| 5 s | 99.31 | 99.01 | 94.77 | 93.27 |
| BETA | ||||
| 1 s | 84.29 | 79.79 | 76.79 | 81.43 |
| 2 s | 92.69 | 89.54 | 81.87 | 87.31 |
| Methods | ||||
|---|---|---|---|---|
| TW | SRC | DFN | SVM | kNN |
| Speller | ||||
| 1 | 97.16 | 95.29 | 88.23 | 87.75 |
| 2 | 79.61 | 79.38 | 74.34 | 73.96 |
| 3 | 66.28 | 66.47 | 62.43 | 62.56 |
| 4 | 56.77 | 56.34 | 54.15 | 53.39 |
| 5 | 49.66 | 49.51 | 47.38 | 46.63 |
| BETA | ||||
| 1 | 393.35 | 372.35 | 358.35 | 380.01 |
| 2 | 270.35 | 261.16 | 238.79 | 254.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oikonomou, V.P. A Sparse Representation Classification Framework for Person Identification and Verification Using Neurophysiological Signals. Electronics 2025, 14, 1108. https://doi.org/10.3390/electronics14061108
Oikonomou VP. A Sparse Representation Classification Framework for Person Identification and Verification Using Neurophysiological Signals. Electronics. 2025; 14(6):1108. https://doi.org/10.3390/electronics14061108
Chicago/Turabian StyleOikonomou, Vangelis P. 2025. "A Sparse Representation Classification Framework for Person Identification and Verification Using Neurophysiological Signals" Electronics 14, no. 6: 1108. https://doi.org/10.3390/electronics14061108
APA StyleOikonomou, V. P. (2025). A Sparse Representation Classification Framework for Person Identification and Verification Using Neurophysiological Signals. Electronics, 14(6), 1108. https://doi.org/10.3390/electronics14061108






