Abstract
Multi-story path planning (MSPP) for indoor delivery robots presents unique challenges in modern logistics systems, particularly in efficiently handling multiple deliveries across different floors. This paper proposes a graph-based path planning algorithm that optimizes delivery routes in multi-story buildings while maintaining computational efficiency. The algorithm, with a complexity of O(|E|log|V|), integrates three key components: (1) a floor-based parcel grouping strategy, (2) an optimized Dijkstra-based path planning system, and (3) an efficient elevator selection mechanism. The modular design allows for adaptability to diverse building layouts and logistics scenarios. Evaluated in a 15-story simulation with varying parcel counts (n = 1 to 7), the algorithm demonstrated minimal runtime increase (1.28 s to 1.35 s) while ensuring optimal path selection. Delivery distances ranged from 48 m (single-parcel) to 126 m (seven parcels), demonstrating the system’s scalability and efficiency in complex multi-story environments. Unlike traditional methods such as A*, the proposed approach guarantees optimality while effectively addressing vertical navigation challenges. These results validate its practical applicability in smart building environments and modern logistics systems, offering a robust solution for real-world delivery challenges.
1. Introduction
The rapid growth of e-commerce has made last-mile delivery using mobile robots a crucial challenge in modern logistics [1,2]. Recent studies indicate that autonomous delivery robots can significantly improve efficiency and reduce operational costs [3,4]. However, the increasing complexity of indoor environments, particularly in multi-story buildings, presents unique challenges for autonomous navigation and delivery optimization [5].
Path planning algorithms have traditionally focused on single-floor navigation scenarios. While algorithms like A* [6] and Dijkstra [7] have proven effective for two-dimensional environments, they face significant limitations in multi-story buildings [8]. Recent surveys highlight that vertical navigation and elevator integration remain critical challenges in indoor robotics [9,10]. For example, A* algorithm’s heuristic-based approach faces fundamental challenges in multi-story environments, particularly when incorporating elevator selection. This limitation becomes even more pronounced when attempting to integrate elevator waiting times and floor transition costs into the heuristic function, often leading to suboptimal path selection and inefficient resource utilization in real-world scenarios.
The emergence of machine learning approaches, particularly deep reinforcement learning [11,12], has introduced new possibilities for robot navigation. However, these methods often require significant computational resources and may lack the reliability needed for commercial delivery applications [13]. Furthermore, they require direct communication between robots and elevator systems for state observation and action execution, which poses significant practical challenges. Such integration often demands proprietary access to elevator control systems, requirements that are often unfeasible due to security concerns and restricted access to elevator manufacturers’ systems in real-world deployments.
To address these challenges, we propose a graph-based Multi-Story Path Planning (MSPP) algorithm that introduces three key innovations:
- A memory-efficient weighted graph representation that simplifies multi-floor connectivity while maintaining computational scalability.
- A novel elevator function for effective vertical navigation, optimizing floor transitions and reducing waiting times.
- An intelligent parcel grouping strategy that streamlines delivery sequencing across multiple floors.
Unlike the traditional Dijkstra’s algorithm, which exhaustively explores all possible paths from the source to multiple destinations across floors, our grouping strategy allows for localized path calculations within each floor. This significantly reduces the computational complexity by eliminating the need to explore unnecessary inter-floor paths, while maintaining delivery optimization.
To illustrate our approach, Figure 1 shows an example of the underlying layer structure for a 15-floor building. Each node in the graph contains essential information including node ID, connectivity information, edge values, and coordinates. The graph uses destination nodes to represent customer doorsteps and elevator nodes to represent elevator locations, providing an efficient representation of the building’s structure. Figure 2 demonstrates how these underlying layers are stacked to create a complete multi-story representation. Instead of using vertical edges to connect elevator nodes directly, we introduce an elevator function , where a represents the current floor and b represents the destination floor. This approach provides more flexibility in handling elevator transitions while maintaining the graph’s structural clarity.
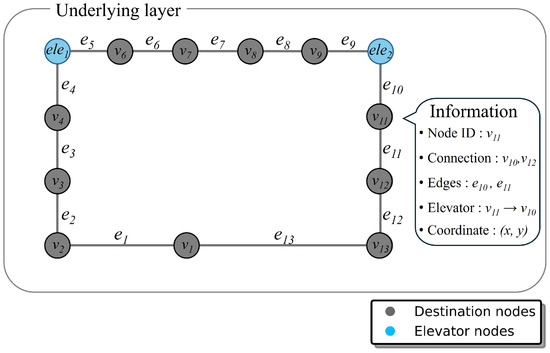
Figure 1.
Example of underlying layer for a 15-floor graph. The graph shows the basic structure of nodes and their connections, with destination nodes representing delivery points and elevator nodes enabling vertical transitions.
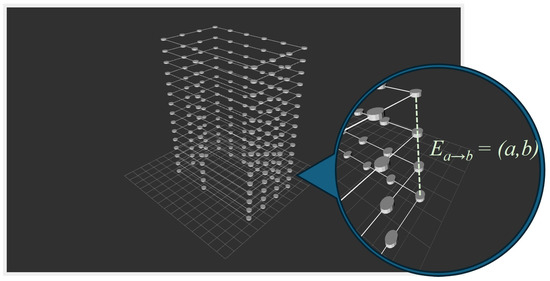
Figure 2.
Example of a 15-story building graph showing the stacked layer structure and elevator connections. The visualization demonstrates how individual layers are integrated while maintaining independent floor representations.
Our approach builds upon recent advances in hierarchical path planning [14] and graph-based navigation systems [15], while introducing novel solutions for elevator integration and delivery optimization. The proposed method has been evaluated in a 15-story building environment, demonstrating robust performance with varying numbers of parcels.
The remainder of this paper is organized as follows: Section 2 reviews related work in path planning and multi-story navigation. Section 3 formally defines the problem and outlines our key assumptions. Section 4 details the proposed Algorithm 1 and its implementation. Section 5 provides experimental results and a performance analysis. Finally, Section 6 concludes with a discussion of practical applications and future research directions.
2. Related Work
2.1. Path Planning Algorithms
Path planning algorithms are generally categorized into global path planning and local path planning approaches [16]. Global path planning, which is the focus of this paper, assumes complete environment knowledge beforehand [6,7], enabling comprehensive route optimization in known spaces such as indoor building layouts. In contrast, local planning relies on real-time sensor data for navigation [9,10,17] Traditional approaches like Dijkstra [7] and A* [6] have been fundamental in path planning, with their computational complexity thoroughly analyzed.
Building upon traditional path planning algorithms, hierarchical approaches [18] improve computational efficiency by grouping similar regions and allowing path planning algorithms to skip detailed explorations within these regions, effectively reducing the search space. These methods have shown significant performance improvements in complex environments by abstracting the search space into different levels of granularity [19]. Our approach similarly leverages this concept by treating each floor as a distinct region, avoiding the need for an exhaustive search across all possible inter-floor combinations.
Recent developments have focused on machine learning approaches [20], particularly deep reinforcement learning [12,13], which have shown promising results in handling dynamic environments [11]. However, as discussed in Section 1, these approaches face numerous challenges in real-world multi-story deployments due to elevator system integration requirements and security concerns. Graph-based methods have emerged as an efficient alternative for structured indoor environments [21], offering a more practical solution that can operate without requiring direct elevator system integration or real-time state predictions [22].
2.2. Multi-Story Delivery Systems
Multi-story delivery systems present unique operational challenges beyond traditional single-floor robotics applications. The integration of robots with the building infrastructure, particularly elevators, has emerged as a crucial research area [23]. Recent surveys [24,25] highlight several key challenges in autonomous delivery systems, including route optimization [26] and system integration [27]. The complexity of coordinating multiple robots in multi-floor environments [28] and optimizing delivery schedules [29] remains an active area of research.
Studies in robotic Mobile Fulfillment Systems (RMFS) have shown that heterogeneous robot fleets can significantly improve operational efficiency [30], particularly in scenarios involving elevator scheduling and multi-delivery coordination. Our graph-based path planning algorithm addresses these challenges while maintaining practical feasibility [31,32], offering a robust solution for complex multi-story delivery operations.
Current research trends indicate a move toward more integrated approaches that combine traditional path planning with learning-based methods [33]. These hybrid systems aim to leverage the reliability of classical algorithms while incorporating the adaptability needed for complex multi-story environments. However, challenges remain in developing truly efficient and scalable solutions for real-world applications [34].
3. Problem Definition
3.1. Multi-Dimensional Navigation Parameters
Traditional path planning algorithms such as A* and Dijkstra require two distinct positions as input data to identify the shortest path within a two-dimensional environment [6,7]. However, for multi-story path planning, it is necessary to add parameters representing vertical transitions between floors [8]. As the driving environment changes from a two-dimensional to three-dimensional structure, the absence of floor parameters results in distorted paths between floors [5]. Furthermore, recent studies have shown that optimizing paths based solely on two locations (start and goal positions) is insufficient for multi-story environments [35].
3.2. Start-Goal Position Constraints
In the context of last-mile delivery services [1,4], the mobile robot must return to a designated station point after completing deliveries to recharge or collect new parcels from staging areas. This return-to-start requirement creates a unique constraint where the start and goal positions are identical, contrary to the assumptions of traditional path planning algorithms [16]. While this return point could theoretically be positioned at any accessible location within the building (e.g., charging stations or staging areas on different floors), for systematic experimental validation of our 15-story test environment, we specifically consider scenarios where robots start from and return to nodes near the ground floor entrance. This experimental design choice enables a comprehensive testing of vertical navigation capabilities across the full range of floors (1st to 15th floor).
A key challenge in our approach is handling the identical start and goal positions, as illustrated in Figure 3. Unlike traditional path planning problems where the start and goal positions differ, our algorithm must efficiently handle these return trips while considering practical operational requirements such as battery management and parcel collection. The global planner receives information about each parcel’s destination (specifically, the destination floor and node) and the total number of parcels as input data.

Figure 3.
Illustration of the identical positions of the start and goal points for the Algorithm 1, showing how the robot must return to its initial position after completing deliveries.
3.3. Delivery Sequence Optimization
Prior to the commencement of the delivery service, the global planner must optimize the sequence of deliveries [36]. Recent research in delivery robotics [3] has shown that the efficiency of multi-story deliveries heavily depends on the following:
- The efficient grouping of deliveries by floor;
- Optimal elevator selection and scheduling;
- The minimization of unnecessary floor transitions.
The global planner must determine the optimal route considering these factors, as this initial path plan serves as the primary reference for the mobile robot’s navigation within the building [20]. The overall structure of our Algorithm 1 is shown in Figure 4. The algorithm takes parcel information as input and processes it through hierarchical layers, applying the Dijkstra algorithm at each level while maintaining elevator connectivity.
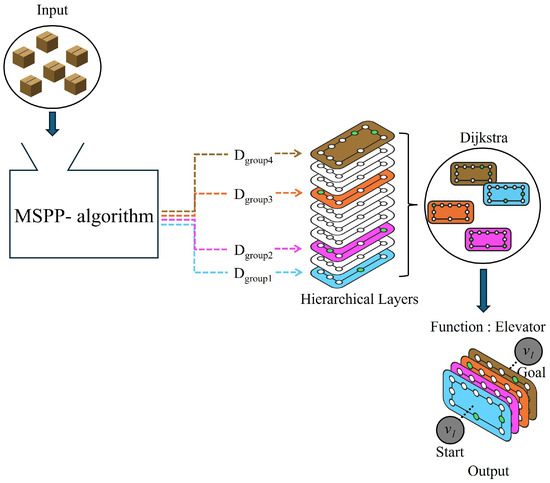
Figure 4.
Overall structure of Algorithm 1, demonstrating the hierarchical processing of parcel information and path planning across multiple floors.
3.4. Elevator Integration
The algorithm must determine which elevator to take at any given point and inform the robot of the necessary next steps [23]. Two specific challenges arise in this process:
- Buildings typically contain multiple elevators, requiring the mobile robot to identify and select the nearest elevator to optimize the path.
- The robot must determine the correct elevator selection based on both current location and delivery destinations.
To address these challenges, we introduce the elevator function , where a represents the current floor and b represents the destination floor. For example, when a robot on the 3rd floor needs to deliver parcels to the 7th floor, the function is invoked. This function considers several practical constraints, as follows:
- Elevator Availability: The function maintains a list of available elevators on the current floor a and evaluates their proximity to the robot’s current position.
- Floor Connectivity: Not all elevators may serve all floors, requiring the function to consider only elevators that connect both a and b floors.
- Path Optimization: When multiple elevators are available, the function selects the one that minimizes the total path length, considering both the distance to reach the elevator and the distance from the elevator to the delivery point on floor b.
3.5. Local–Global Planning Integration
The global planner must transmit the generated plan to the local planner in a format that enables real-time navigation [37]. Recent advances in robot navigation have emphasized the importance of seamless integration between global and local planning systems [38], particularly in dynamic indoor environments where obstacle avoidance and human interaction must be considered [34].
4. Solution
The proposed MSPP (Multi-Story Path Planning) algorithm introduces a novel integration of hierarchical Dijkstra’s algorithm with an elevator function to efficiently address path planning challenges in multi-story buildings. Our approach combines the computational efficiency of hierarchical path decomposition with an intelligent elevator selection mechanism, enabling optimal route planning across multiple floors while maintaining practical feasibility.
4.1. Graph-Design
4.1.1. Weighted Graph Representation
In graph theory [39], the shortest paths are typically calculated using directed and weighted graphs. Our approach utilizes weighted graphs to represent indoor environments, offering superior memory efficiency and computational performance compared to grid-based methods. In indoor environments, paths are not strictly governed by directional rules. Thus, the edges in the graph represent only traversable paths, and their weights correspond to the distances between nodes. Let represent the graph, where V is the set of vertices (nodes), and E is the set of edges. Each vertex represents a location the robot must visit, while edges represent the relative distances between these locations. This weighted graph significantly reduces memory usage, particularly in large, multi-story environments.
4.1.2. Parameters
To adapt Dijkstra’s algorithm for the Algorithm 1, several additional parameters are introduced. The floor parameter, denoted as , represents the destination floor and its hierarchical weight, where . This parameter is essential for coordinating vertical movements. The input parameter, , combines node and floor information, where is the node and is the floor. Parcel information encoded as QR codes stores this data, enabling efficient parcel sorting and route optimization. Additionally, elevator nodes, denoted as , are added to the graph to facilitate vertical movement. While and are both vertices, elevator nodes are distinguished by their role in inter-floor connectivity. These parameters collectively enable the algorithm to handle the complexities of multi-story environments effectively.
4.2. Hierarchical Dijkstra Implementation
4.2.1. Grouping Mechanism
The Algorithm 1 begins by processing multiple parcel inputs . Let I denote a set of parcel information . Initially, the input data are grouped into delivery groups based on their floor parameter , ensuring that nodes sharing the same floor are grouped together, as shown in Figure 5. For each delivery group, the algorithm applies Dijkstra’s algorithm to compute optimal paths. These delivery groups serve as hierarchical input layers for our modified Dijkstra’s algorithm. Each represents a distinct floor-level subgraph, allowing the hierarchical Dijkstra implementation to process path planning efficiently by decomposing the multi-story navigation problem into manageable floor-specific components.
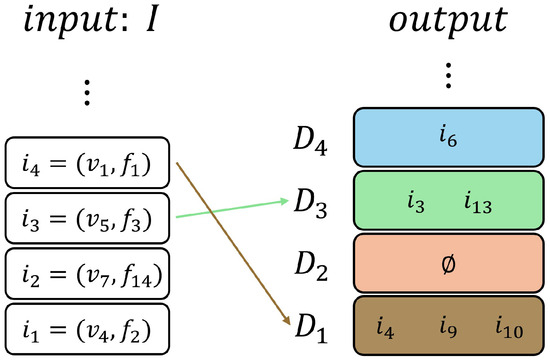
Figure 5.
Floor-based grouping process for hierarchical Dijkstra implementation.
4.2.2. Hierarchical Dijkstra
The hierarchical Dijkstra algorithm traditionally improves efficiency by grouping similar regions and skipping the detailed exploration within these regions. In our approach, we leverage this concept by treating each floor as a distinct region with shared characteristics. The algorithm divides the environment into distinct layers based on floors, treating each floor as an independent subgraph. Weight values are assigned to represent inter-floor transitions, allowing vertical movements to be managed as transitions between layers. This separation of horizontal and vertical movements reduces computational complexity and improves memory efficiency. The method allocates missions for each floor based on input data I. After exploring each floor, the optimized paths are stored in layers. By isolating vertical transitions and utilizing the floor-based hierarchical structure, the algorithm achieves significant efficiency improvements in handling multi-story environments, as it can skip unnecessary path calculations in regions (floors) that share similar characteristics.
4.3. Elevator Function Integration
Elevator Fuction Description
However, elevators operate in real-time with movements that are difficult to predict accurately. Rather than connecting floors directly with static edges, we introduce an elevator function to handle the dynamic nature of elevator transitions and their associated floor-specific weights. This approach enables our system to adapt to the varying states of elevators and their impact on inter-floor movement costs. Each node in our graph maintains information about elevator states, connectivity, and the location of the nearest elevator. When the elevator function identifies the optimal elevator for transition, MSPP can creates a path to the corresponding elevator node based on this stored information. Once the robot reaches the elevator node, the elevator function guarantees the transition to the target floor by coordinating with the building’s elevator system.
Figure 6 illustrates the hierarchical structure and the role of elevator nodes in connecting layers.The GetSuccessors function is a crucial component of the Algorithm 1. It processes delivery groups and computes shortest paths for each group using Dijkstra’s algorithm. This function begins by initializing the necessary data structures, including the distance and predecessor information for each node. For each delivery group , the function iterates through the nodes and calculates the shortest paths, storing the results in . Additionally, it integrates elevator nodes into the paths, ensuring seamless vertical transitions between floors. The function assigns weights to each path segment and appends the results to the corresponding hierarchical layer. At the final step, each path’s endpoint is connected to the nearest elevator node, preparing the data for subsequent processing by the GetSuccessors2 function.
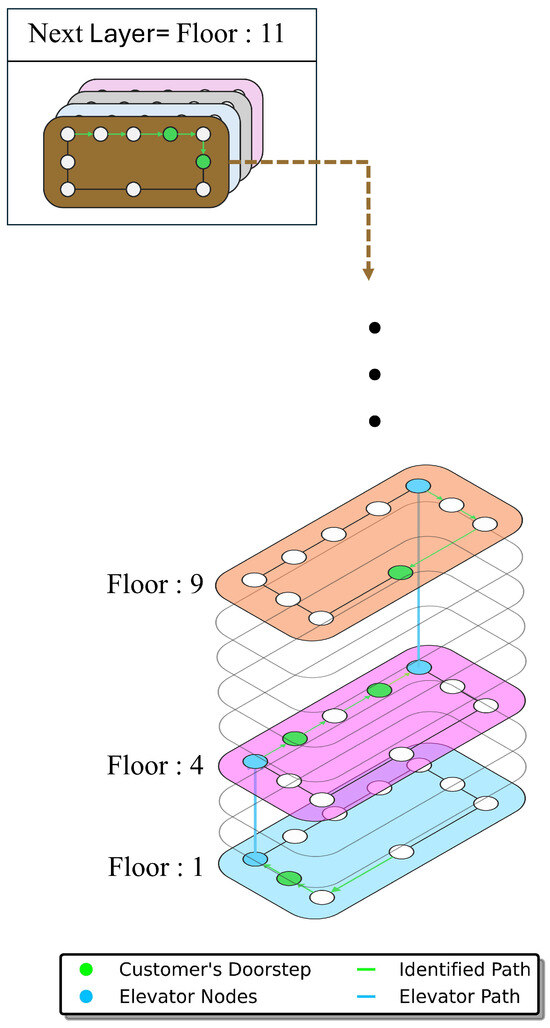
Figure 6.
Hierarchical structure of the Algorithm 1, showing layer separation and elevator node connectivity.
| Algorithm 1 MSPP |
|
4.4. Algorithm Complexity and Validation
The computational complexity of the Algorithm 1 is primarily determined by the hierarchical Dijkstra implementation. By isolating vertical transitions and using weighted graphs, the algorithm achieves significant improvements in scalability and memory usage. The hierarchical structure allows the algorithm to handle multi-dimensional path planning efficiently, even in complex environments. The use of elevator nodes and floor weights ensures that the algorithm maintains optimality in path computation. Compared to traditional methods, the Algorithm 1 demonstrates enhanced performance, particularly in large-scale multi-story environments.
5. Experiment
To evaluate the performance of the proposed Algorithm 1, we conducted experiments in a graph-based environment representing a 15-story building. The evaluation included scenarios with varying numbers of parcels, denoted as . For each scenario, the algorithm computed the shortest paths while optimizing delivery sequences and integrating elevator usage.
5.1. Evaluation Setup
The building environment was represented as a weighted graph with nodes corresponding to delivery destinations and edges indicating traversable paths. Input data, I, contained parcel information including node and floor numbers. The graph structure, weighted edges, and elevator nodes were tailored to the experiments to ensure realistic conditions.
5.2. Results and Analysis
Figure 7 illustrates the paths generated by the Algorithm 1 for varying numbers of parcels. Cases (a), (b), (c), and (d) represent scenarios with n = 1, 3, 5, 7. In these path visualizations, blue lines indicate upward paths from the starting position to delivery points, while red lines represent downward paths as the robot returns from the highest floor delivery point. This color-coded representation helps visualize the complete delivery sequence, from the initial ascent to the final descent.
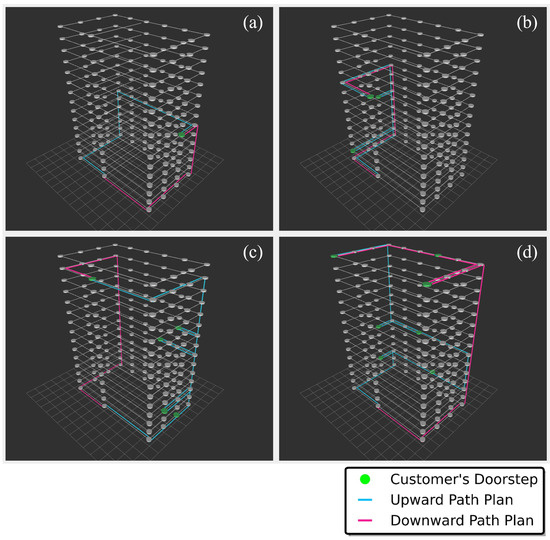
Figure 7.
Running example of an Algorithm 1 with a varying number of parcels in a graph-based environment. Each case (a–d) represents the mobile robot carrying a different number of parcels (n = 1, 3, 5, and 7).
The input data for these scenarios were as follows:
- (a): ;
- (b): ;
- (c): ;
- (d): .
These scenarios were designed to validate different aspects of the algorithm: Case (a) demonstrates the basic path planning capability with a single parcel, verifying optimal elevator selection and return path generation. Cases (b) and (c) test the algorithm’s performance with multiple parcels distributed across different floors, validating its ability to find the nearest elevators, optimize delivery sequences, and efficiently return to the starting position. Case (d) specifically evaluates the algorithm’s efficiency in handling multiple deliveries to the same floor, ensuring optimal path planning even when multiple parcels share destination floors.
The algorithm demonstrated its ability to efficiently group parcels by floor and optimize both horizontal and vertical movements. Elevator nodes were seamlessly integrated into the paths, as seen in the transitions between floors.
Figure 8 shows the potential range of total distances for scenarios with different numbers of parcels and the corresponding distances achieved by the Algorithm 1. For example, when , the total travel distance ranges from 0 m (when all five delivery points are at the starting position ) to 103 m (when deliveries must be made to consecutive highest floors with destinations , , , , ). Unlike traditional single-destination path planning, the optimal travel distance can vary significantly when multiple delivery points must be visited, and the black line in Figure 8 represents the actual travel distances achieved in the test cases shown in Figure 7. The results indicate that the algorithm consistently minimized travel distances, even with increasing delivery complexity.
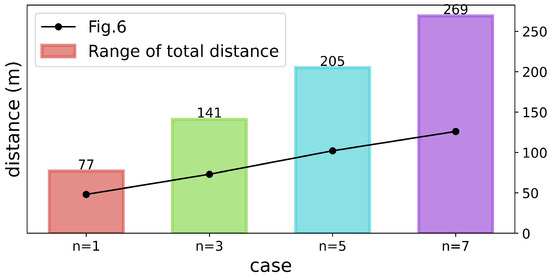
Figure 8.
The potential range of total distance when a mobile robot is delivering varying numbers of parcels and the resulting total distance from Figure 7.
Table 1 summarizes the runtime, stack size, total distance, and elevator usage for each case. Even with an increasing number of parcels, the runtime increased marginally, from 1.28 s for to 1.35 s for . The results validate the scalability of the algorithm in handling complex delivery scenarios. Table 2 compares the worst-case time complexity and properties of the proposed Algorithm 1, Dijkstra, and A*. The Algorithm 1 achieves optimal performance by leveraging hierarchical planning and efficient elevator integration. The results demonstrate that the Algorithm 1 maintains computational scalability and generates optimal paths for multi-story environments.

Table 1.
Comparison of result data for each case.

Table 2.
Comparison of time complexity and properties.
Figure 9 compares the average runtime of the proposed Algorithm 1 with the standard Dijkstra algorithm. For a controlled comparison, we manually configured the elevator function values to match each test scenario’s requirements. The Algorithm 1 achieved comparable runtimes to Dijkstra, demonstrating its computational efficiency despite the added complexity of multi-story navigation and delivery optimization.
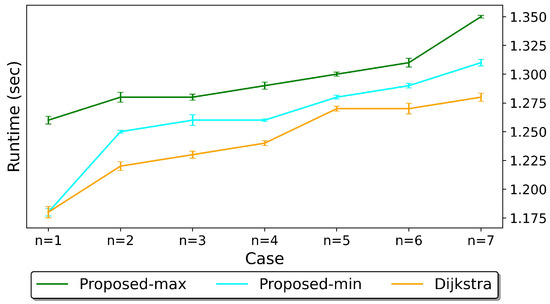
Figure 9.
Average runtime of proposed algorithm and Dijkstra.
5.3. Discussion
The experimental results highlight the effectiveness of the Algorithm 1 in addressing the unique challenges of multi-story delivery scenarios. The integration of elevator nodes and hierarchical planning enables efficient navigation, even in large and complex environments. The algorithm consistently achieves optimal performance in terms of path planning, runtime, and memory efficiency, making it a promising solution for autonomous delivery applications.
6. Conclusions
This paper presents a novel graph-based path planning algorithm, the MSPP, for multi-story buildings, addressing critical challenges in autonomous delivery systems. The research offers significant advancements in the field of indoor robotics and logistics automation. The proposed Algorithm 1 effectively handles multi-story navigation by employing a weighted graph representation that overcomes the limitations of traditional path planning methods. Our integration of elevator scheduling with path planning proves crucial, transforming the traditional vertical movement problem into a manageable graph traversal task while ensuring seamless transitions between floors. This integration, combined with our hierarchical approach, achieves an optimal computational complexity of O(|E|log|V|), matching the efficiency of the single-floor Dijkstra’s algorithm despite its handling the additional complexity of multi-story navigation.
The experimental results demonstrated the algorithm’s exceptional scalability, maintaining consistent performance even as the parcel counts increased from to with a minimal impact on runtime. This computational efficiency, coupled with optimal path selection, sets our approach apart from existing solutions. The findings of this study have practical implications for the deployment of autonomous delivery robots in complex indoor environments. The experimental evaluation confirms the algorithm’s consistent performance across various delivery scenarios, efficient resource utilization in terms of memory and computation, and applicability to real-world multi-story buildings. These achievements align with the industry demands for automation in logistics, as highlighted in recent studies on autonomous delivery systems.
While the proposed approach demonstrates promising results, it is not without limitations. Future work should address the adaptation of the algorithm to dynamic environments, particularly in diverse building settings such as healthcare facilities and residential complexes. In healthcare logistics, for example, the algorithm could be extended to handle priority-based deliveries in multi-story hospitals, where time-sensitive medical supplies require optimized routing. Similarly, for residential deliveries in apartment complexes, the system would need to account for varying access restrictions and resident-specific delivery preferences.
Future research should explore the integration of learning-based methods to enhance system resilience against elevator uncertainties. By incorporating reinforcement learning techniques, the algorithm could learn to predict and adapt to elevator failures, maintenance patterns, and traffic-based delays, moving beyond our current assumption of perfect elevator functionality. The development of more sophisticated elevator scheduling algorithms that account for real-world elevator conditions and historical performance data would enable robust path planning even under system faults. These advancements will further solidify the role of autonomous delivery robots in urban logistics, enabling efficient and sustainable solutions for complex indoor environments.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/electronics14050982/s1, Video S1: Multi-Story Path Planing for mobile robot last-mile delivery.
Author Contributions
Conceptualization, S.K. and Y.E.S.; methodology, S.K. and H.J.; software, S.K.; validation, J.H., D.L. and Y.H.; formal analysis, S.K.; investigation, S.K. and H.J.; resources, Y.E.S.; data curation, S.K. and J.H.; writing-original draft preparation, S.K.; writing—review and editing, Y.E.S.; visualization, S.K.; supervision, Y.E.S.; project administration, Y.E.S.; funding acquisition, Y.E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Technology Innovation Program (or Industrial Strategic Technology Development Program-Materials & Components Technology Development Program) (RS-2024-00433599, Development and verification of corner radar module based on metasurface lens) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea). This work was also financially supported by the Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) through the National Innovation Cluster R&D Program (P0025248, Development of cloud-based autonomous driving special automobile integrated control solution).
Data Availability Statement
The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Yeongho Ha was employed by the company FieldRo Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Boysen, N.; Fedtke, S.; Schwerdfeger, S. Last-mile delivery concepts: A survey from an operational research perspective. Or Spectr. 2021, 43, 1–58. [Google Scholar]
- Engesser, V.; Rombaut, E.; Vanhaverbeke, L.; Lebeau, P. Autonomous delivery solutions for last-mile logistics operations: A literature review and research agenda. Sustainability 2023, 15, 2774. [Google Scholar] [CrossRef]
- Srinivas, S.; Ramachandiran, S.; Rajendran, S. Autonomous robot-driven deliveries: A review of recent developments and future directions. Transp. Res. Part E Logist. Transp. Rev. 2022, 165, 102834. [Google Scholar]
- Alverhed, E.; Hellgren, S.; Isaksson, H.; Olsson, L.; Palmqvist, H.; Flodén, J. Autonomous last-mile delivery robots: A literature review. Eur. Transp. Res. Rev. 2024, 16, 4. [Google Scholar]
- El-Sheimy, N.; Li, Y. Indoor navigation: State of the art and future trends. Satell. Navig. 2021, 2, 7. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar]
- Dijkstra, E.W. A Note on Two problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar]
- Ivanov, R. An algorithm for on-the-fly K shortest paths finding in multi-storey buildings using a hierarchical topology model. Int. J. Geogr. Inf. Sci. 2018, 32, 2362–2385. [Google Scholar]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar]
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of autonomous path planning algorithms for mobile robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep reinforcement learning: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2022, 35, 5064–5078. [Google Scholar]
- Morales, E.F.; Murrieta-Cid, R.; Becerra, I.; Esquivel-Basaldua, M.A. A survey on deep learning and deep reinforcement learning in robotics with a tutorial on deep reinforcement learning. Intell. Serv. Robot. 2021, 14, 773–805. [Google Scholar]
- Singh, B.; Kumar, R.; Singh, V.P. Reinforcement learning in robotic applications: A comprehensive survey. Artif. Intell. Rev. 2022, 55, 945–990. [Google Scholar]
- Mac, T.T.; Copot, C.; Tran, D.T.; De Keyser, R. A hierarchical global path planning approach for mobile robots based on multi-objective particle swarm optimization. Appl. Soft Comput. 2017, 59, 68–76. [Google Scholar] [CrossRef]
- Gansner, E.R.; Koutsofios, E.; North, S.C.; Vo, K.P. A technique for drawing directed graphs. IEEE Trans. Softw. Eng. 1993, 19, 214–230. [Google Scholar]
- Sanchez-Ibanez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.W.; Lim, S.Y.; Ang, M.H., Jr. Hybrid of global path planning and local navigation implemented on a mobile robot in indoor environment. In Proceedings of the IEEE International Symposium on Intelligent Control, Vancouver, BC, Canada, 27–30 October 2002; IEEE: Piscataway, NJ, USA, 2002; pp. 821–826. [Google Scholar]
- Holte, R.C.; Perez, M.B.; Zimmer, R.M.; MacDonald, A.J. Hierarchical A*: Searching Abstraction Hierarchies Efficiently; AAAI/IAAI: Washington, DC, USA, 1996; Volume 1, pp. 530–535. [Google Scholar]
- van den Berg, J.; Shah, R.; Huang, A.; Goldberg, K. Anytime Nonparametric A*. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011; Volume 25, pp. 105–111. [Google Scholar]
- Xiao, X.; Liu, B.; Warnell, G.; Stone, P. Motion planning and control for mobile robot navigation using machine learning: A survey. Auton. Robot. 2022, 46, 569–597. [Google Scholar]
- Bachiller, P.; Rodriguez-Criado, D.; Jorvekar, R.R.; Bustos, P.; Faria, D.R.; Manso, L.J. A graph neural network to model disruption in human-aware robot navigation. Multimed. Tools Appl. 2022, 81, 3277–3295. [Google Scholar]
- Zivkovic, Z.; Bakker, B.; Krose, B. Hierarchical map building and planning based on graph partitioning. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, 15–19 May 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 803–809. [Google Scholar]
- Song, Z.; Tan, R.; Lou, S.; Lv, C. Robot-Elevator Interaction Through IoT Devices for Autonomous Robot Multi-Floor Transition. In Proceedings of the 2024 10th International Conference on Electrical Engineering, Control and Robotics (EECR), Guangzhou, China, 29–31 March 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 30–34. [Google Scholar]
- Sorooshian, S.; Khademi Sharifabad, S.; Parsaee, M.; Afshari, A.R. Toward a modern last-mile delivery: Consequences and obstacles of intelligent technology. Appl. Syst. Innov. 2022, 5, 82. [Google Scholar] [CrossRef]
- Ayyildiz, E.; Erdogan, M. Addressing the challenges of using autonomous robots for last-mile delivery. Comput. Ind. Eng. 2024, 190, 110096. [Google Scholar]
- Konstantakopoulos, G.D.; Gayialis, S.P.; Kechagias, E.P. Vehicle routing problem and related algorithms for logistics distribution: A literature review and classification. Oper. Res. 2022, 22, 2033–2062. [Google Scholar] [CrossRef]
- Chen, X.; Yang, P.; Shao, Z. Simulation-based time-efficient and energy-efficient performance analysis of an overhead robotic compact storage and retrieval system. Simul. Model. Pract. Theory 2022, 119, 102560. [Google Scholar] [CrossRef]
- Heuer, L.; Palmieri, L.; Mannucci, A.; Koenig, S.; Magnusson, M. Benchmarking Multi-robot coordination in realistic, unstructured human-shared environments. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 14541–14547. [Google Scholar]
- Correia, D.; Vagos, C.; Marques, J.L.; Teixeira, L. Fulfilment of last-mile urban logistics for sustainable and inclusive smart cities: A case study conducted in Portugal. Int. J. Logist. Res. Appl. 2024, 27, 931–958. [Google Scholar] [CrossRef]
- Rizk, Y.; Awad, M.; Tunstel, E.W. Cooperative heterogeneous multi-robot systems: A survey. ACM Comput. Surv. (CSUR) 2019, 52, 1–31. [Google Scholar] [CrossRef]
- Oliveira, G.S.; Röoning, J.; Carvalho, J.T.; Plentz, P.D. Efficient task allocation in smart warehouses with multi-delivery stations and heterogeneous robots. In Proceedings of the 2022 25th International Conference on Information Fusion (FUSION), Linköping, Sweden, 4–7 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–8. [Google Scholar]
- Ma, H. Graph-based multi-robot path finding and planning. Curr. Robot. Rep. 2022, 3, 77–84. [Google Scholar] [CrossRef]
- Al Mahmud, S.; Kamarulariffin, A.; Ibrahim, A.M.; Mohideen, A.J.H. Advancements and Challenges in Mobile Robot Navigation: A Comprehensive Review of Algorithms and Potential for Self-Learning Approaches. J. Intell. Robot. Syst. 2024, 110, 120. [Google Scholar] [CrossRef]
- Mavrogiannis, C.; Baldini, F.; Wang, A.; Zhao, D.; Trautman, P.; Steinfeld, A.; Oh, J. Core challenges of social robot navigation: A survey. ACM Trans. Hum.-Robot Interact. 2023, 12, 1–39. [Google Scholar]
- Mallik, M.; Panja, A.K.; Chowdhury, C. Paving the way with machine learning for seamless indoor–outdoor positioning: A survey. Inf. Fusion 2023, 94, 126–151. [Google Scholar] [CrossRef]
- Kim, J.; Jung, H. Robot routing problem of last-mile delivery in indoor environments. Appl. Sci. 2022, 12, 9111. [Google Scholar] [CrossRef]
- Garaffa, L.C.; Basso, M.; Konzen, A.A.; de Freitas, E.P. Reinforcement learning for mobile robotics exploration: A survey. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 3796–3810. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Mo, H. Reinforcement learning for robot research: A comprehensive review and open issues. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211007305. [Google Scholar] [CrossRef]
- West, D.B. Introduction to Graph Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2001; Volume 2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).