Picosecond-Level Synchronization over Optical Free Space Link Using White Rabbit
Abstract
1. Introduction
2. Principle of WR Time Synchronization
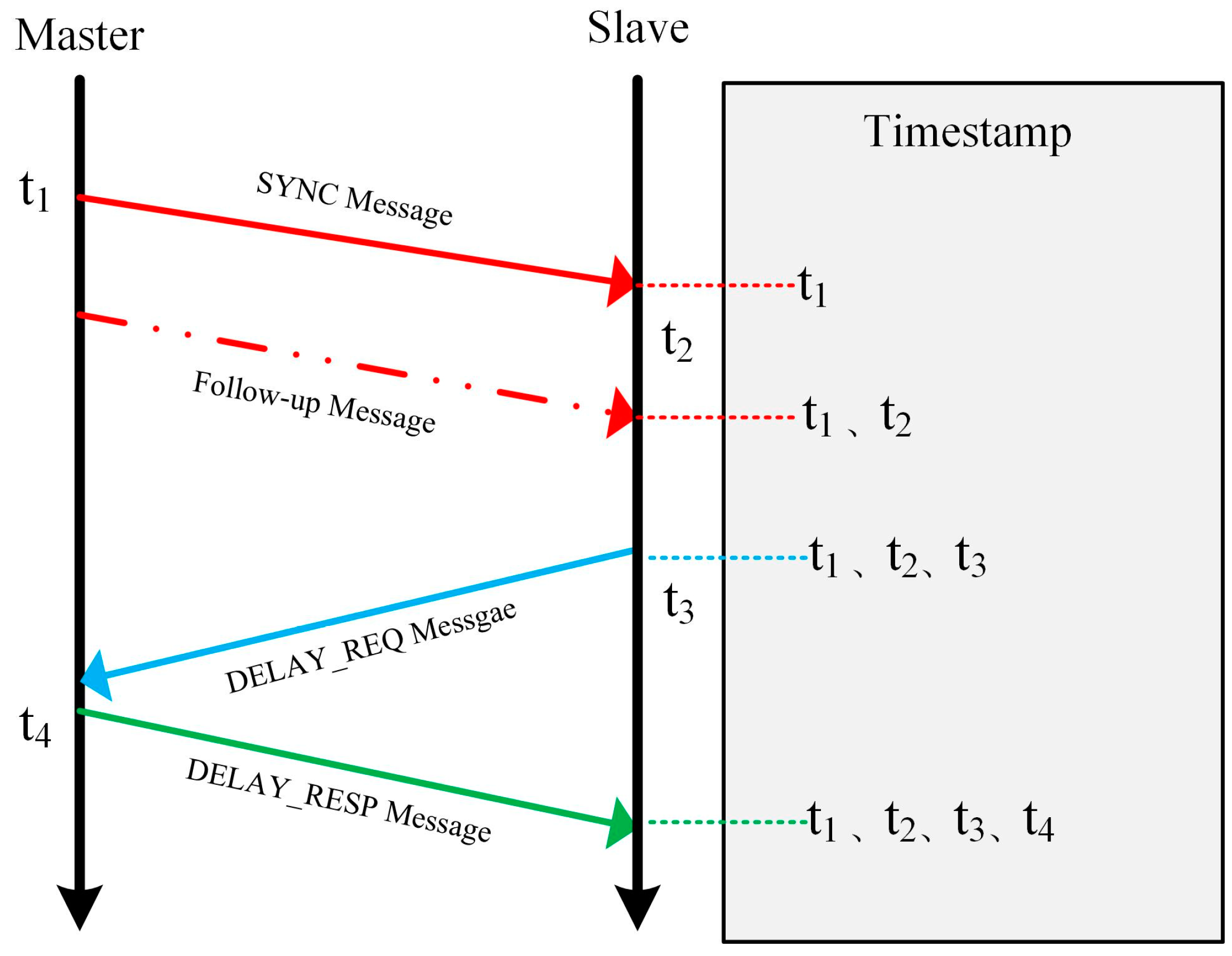
2.1. Precision Time Protocol
2.2. Digital Dual Mixer Time Difference (DDMTD)
2.3. WR Synchronization in Free Space
3. Scheme and Implementation of WR-Based Free Space Synchronization
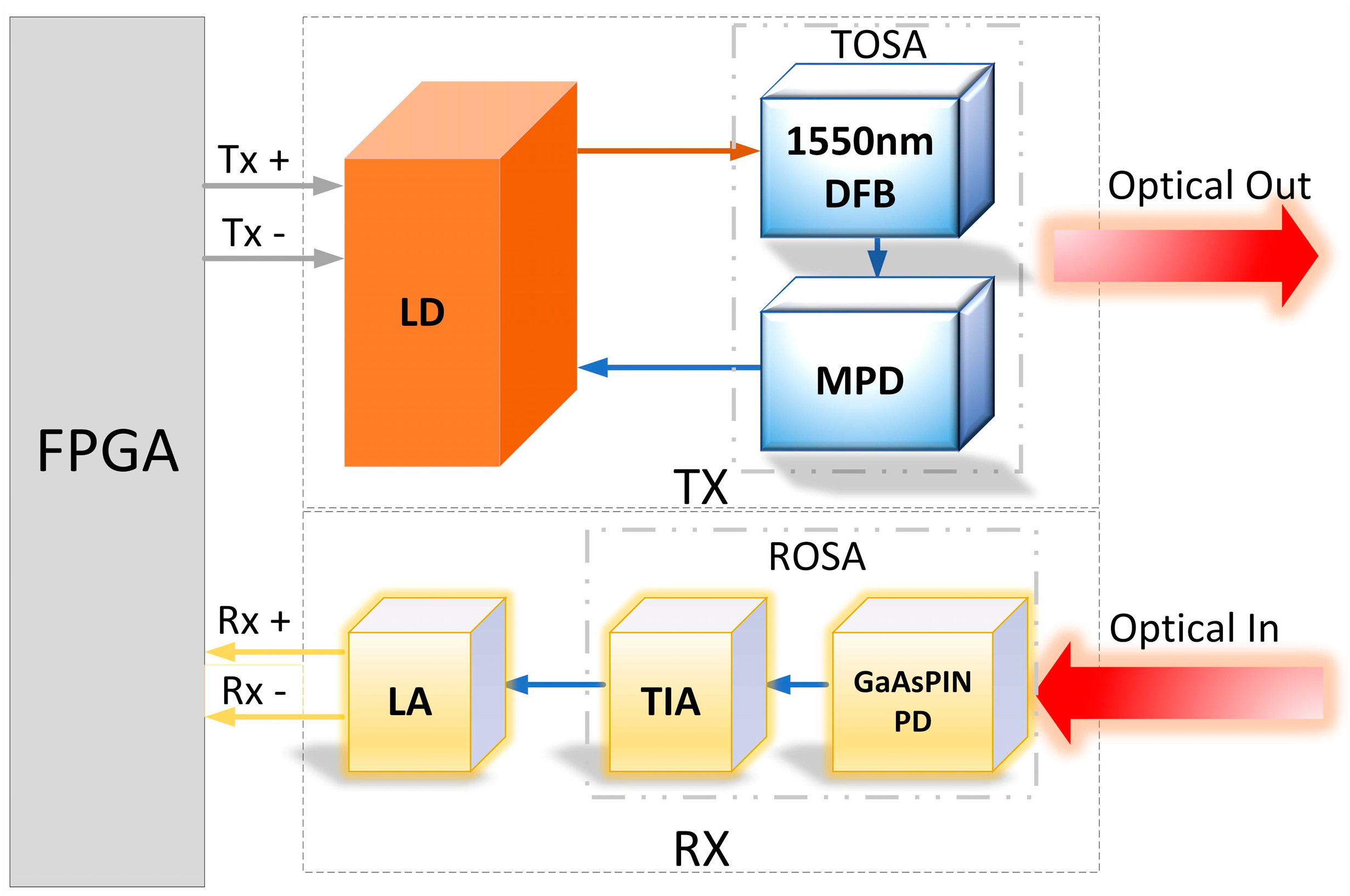
3.1. Optical Transceiver
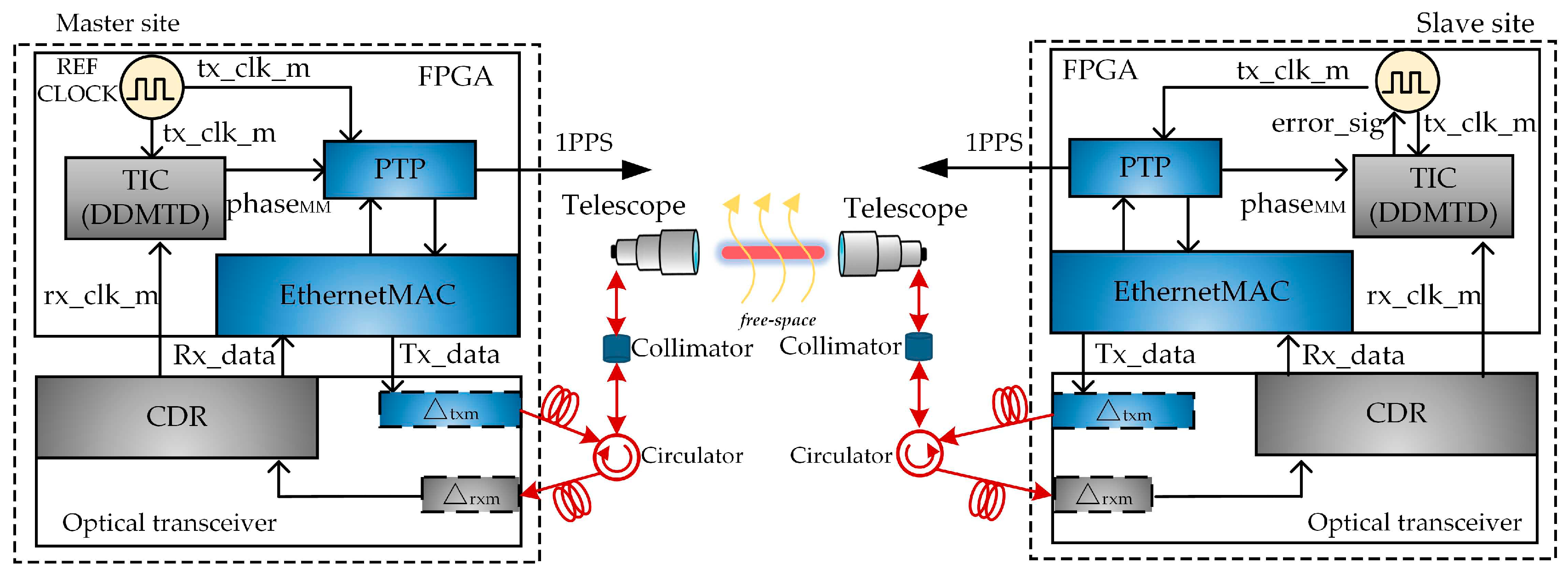
3.2. Schematic of WR Time Synchronization System
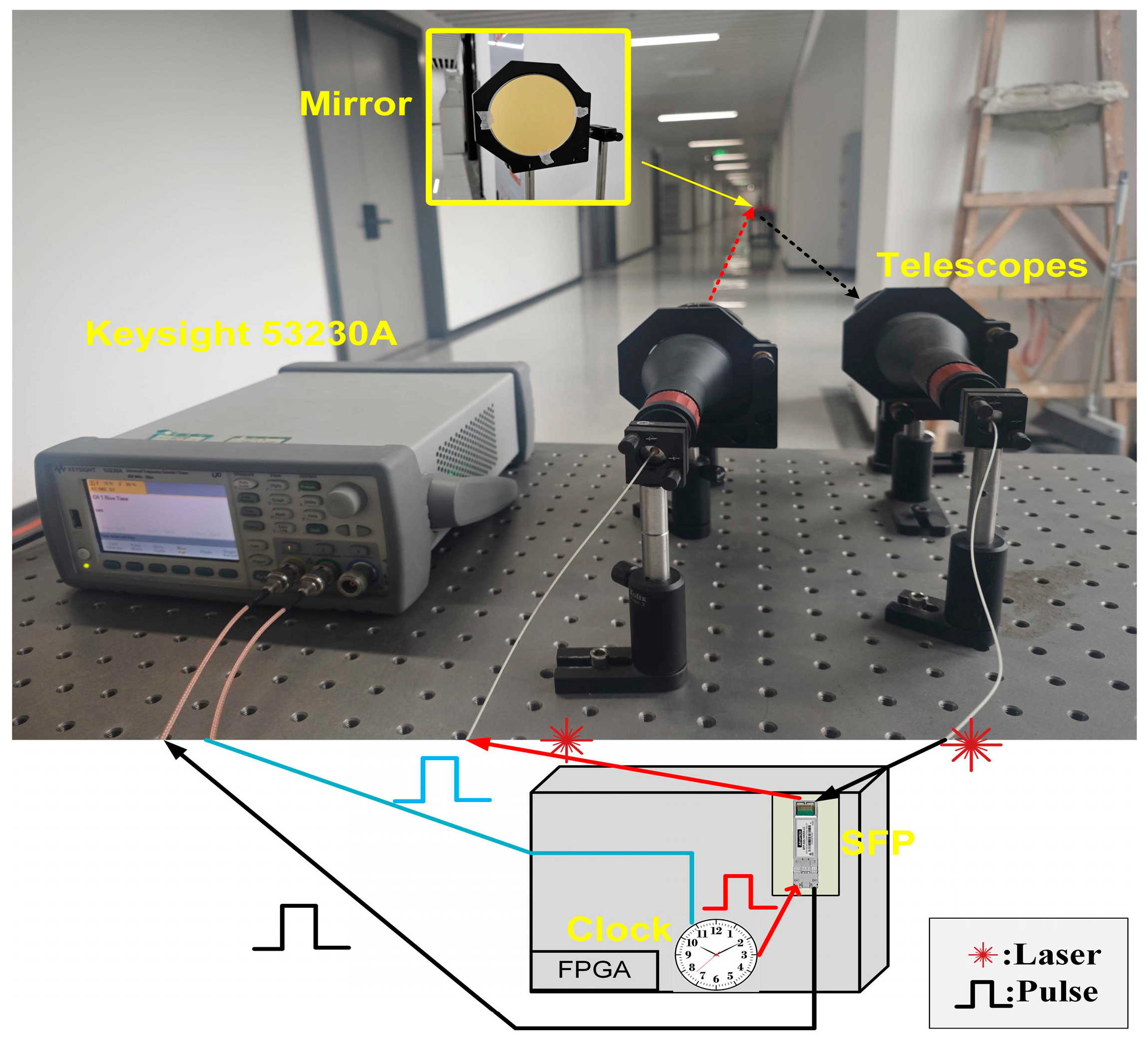
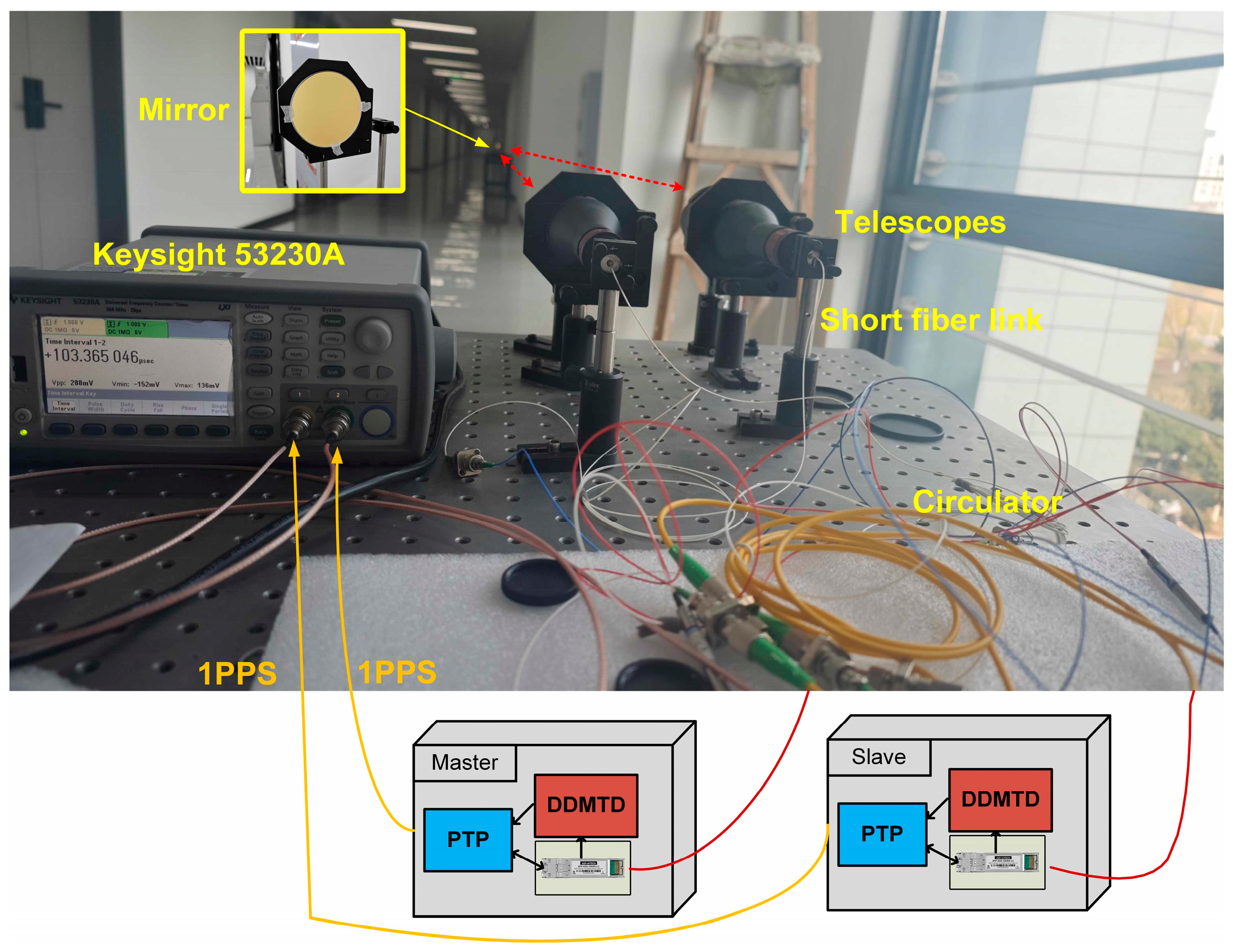
4. Experiment Setup and Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEEE Std 1588-2002; IEEE Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems. IEEE: New York, NY, USA, 2002; pp. 1–154.
- IEEE Std 1588-2008 (Revision of IEEE Std 1588-2002); IEEE Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems. IEEE: New York, NY, USA, 2008; pp. 1–269.
- Lipinski, M.; Wlostowski, T.; Serrano, J.; Alvarez, P.; Cobas, J.D.G.; Rubini, A. Performance results of the first White Rabbit installation for CNGS time transfer. In Proceedings of the 2012 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication Proceedings, San Francisco, CA, USA, 24–28 September 2012. [Google Scholar]
- Dierikx, E.F.; Wallin, A.E.; Fordell, T.; Myyry, J.; Koponen, P.; Merimaa, M. White Rabbit Precision Time Protocol on Long-Distance Fiber Links. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 945–952. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.; Sarihan, M.; Cheng, X.; Zhang, Z.; Wong, C. Large-alphabet time-bin quantum key distribution and Einstein–Podolsky–Rosen steering via dispersive optics. Quantum Sci. Technol. 2023, 9, 015018. [Google Scholar] [CrossRef]
- Gilligan, J.E.; Konitzer, E.M.; Siman-Tov, E.; Zobel, J.W.; Adles, E.J. White Rabbit Time and Frequency Transfer Over Wireless Millimeter-Wave Carriers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 1946–1952. [Google Scholar] [CrossRef] [PubMed]
- IEEE Std 1588-2019 (Revision of IEEE Std 1588-2008); IEEE Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems. IEEE: New York, NY, USA, 2019; pp. 1–499.
- Seijo, O.; Val, I.; Lopez-Fernandez, J.A.; Montalban, J.; Iradier, E. On the use of White Rabbit for Precise Time Transfer in 5G URLLC Networks for Factory Automation Applications. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; pp. 385–390. [Google Scholar]
- Lee, C.; Bunandar, D.; Zhang, Z.; Steinbrecher, G.R.; Dixon, P.B.; Wong, F.N.C.; Shapiro, J.H.; Hamilton, S.A.; Englund, D. Large-alphabet encoding for higher-rate quantum key distribution. Opt. Express 2019, 27, 17539–17549. [Google Scholar] [CrossRef] [PubMed]
- Kaur, N.; Frank, F.; Pottie, P.E.; Tuckey, P. Time and frequency transfer over a 500 km cascaded White Rabbit network. In Proceedings of the 2017 Joint Conference of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS), Besancon, France, 9–13 July 2017. [Google Scholar]
- Li, H.; Gong, G.; Pan, W.; Du, Q.; Li, J. Temperature Effect on White Rabbit Timing Link. IEEE Trans. Nucl. Sci. 2015, 62, 1021–1026. [Google Scholar] [CrossRef]
- Machnikowski, M.; Reddy, R.; Fodor, Z. Challenges with linuxptp on Telco RAN deployments. In Proceedings of the 2021 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control, and Communication (ISPCS), NA, FL, USA, 27–28 October 2021. [Google Scholar]
- Lan, Y.; Chen, Y.; Hou, T.; Wu, B.; Chu, Y. Development Board Implementation and Chip Design of IEEE 1588 Clock Synchronization System Applied to Computer Networking. Electronics 2023, 12, 2166. [Google Scholar] [CrossRef]
- Correll, K.; Barendt, N. Design Considerations for Software Only Implementations of the IEEE 1588 Precision Time Protocol. In Proceedings of the Conference on IEEE 1588 Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems, Winterhur, Switzerland, 10–12 October 2005. [Google Scholar]
- Khan, M.; Hayes, B. IEEE 1588 Time Synchronization in Power Distribution System Applications: Timestamping and Accuracy Requirements. IEEE Syst. J. 2023, 17, 2007–2017. [Google Scholar] [CrossRef]
- Rizzi, M.; Lipinski, M.; Ferrari, P.; Rinaldi, S.; Flammini, A. White Rabbit Clock Synchronization: Ultimate Limits on Close-In Phase Noise and Short-Term Stability Due to FPGA Implementation. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018, 65, 1726–1737. [Google Scholar] [CrossRef] [PubMed]
- Park, K.; Park, I.-C. Fast frequency acquisition phase frequency detectors with prediction-based edge blocking. In Proceedings of the 2009 IEEE International Symposium on Circuits and Systems, Taipei, Taiwan, 24–27 May 2009. [Google Scholar]
- Guo, G.; Li, C.; Hou, D.; Liu, K.; Sun, F.; Zhang, S. Analysis and Implementation of a Frequency Synthesizer Based on Dual Phase-Locked Loops in Cesium Atomic Clock. Appl. Sci. 2013, 13, 9155. [Google Scholar] [CrossRef]
- David, W.A.; Herman, D. Picosecond Time Difference Measurement System. In Proceedings of the 29th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 28–30 May 1975. [Google Scholar]
- Bloom, B.J.; Nicholson, T.L.; Williams, J.R.; Campbell, S.L.; Bishof, M.; Zhang, X.; Zhang, W.; Bromley, S.L.; Ye, J. An optical lattice clock with accuracy and stability at the 10–18 level. Nature 2014, 506, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Sprenger, B.; Zhang, J.; Lu, Z.; Wang, L. Atmospheric transfer of optical and radio frequency clock signals. Opt. Lett. 2009, 34, 965–967. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Hou, D.; Zhang, D.; Tian, J.; Hu, J.; Huang, X.; Chen, S. Femtosecond-level timing fluctuation suppression in atmospheric frequency transfer with passive phase conjunction correction. Opt. Exp. 2017, 25, 21312–21320. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Zhang, F.; Zhou, Y.; Ben, D.; Pan, S. Stable fiber delivery of radio-frequency signal based on passive phase correction. Opt. Lett. 2014, 39, 3360–3362. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Chen, C.; Hou, D. Analysis of Underwater Optical Transfer of Radio-Frequency Signal in Turbulence Water Environment. In Proceedings of the 2023 IEEE 6th International Conference on Electronics and Communication Engineering (ICECE), Xi’an, China, 15–17 December 2023. [Google Scholar]
- Nie, J.; Yang, L.; Duan, L. Atmospheric transfer of a radio-frequency clock signal with a diode laser. Appl. Opt. 2012, 51, 8190–8194. [Google Scholar] [CrossRef] [PubMed]
- Ivanov, E.N.; Diddams, S.A.; Hollberg, L. Analysis of noise mechanisms limiting the frequency stability of microwave signals generated with a femtosecond laser. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1059–1065. [Google Scholar] [CrossRef]
- Soboń, G.; Martynkien, T.; Tomaszewska, D.; Tarnowski, K.; Mergo, P.; Sotor, J. All-in-fiber amplification and com pression of coherent frequency-shifted solitons tunable in the 1800–2000 nm range. Photon. Res. 2018, 6, 368–372. [Google Scholar] [CrossRef]
- Riehle, F. Optical clock networks. Nature Photon. 2017, 11, 25–31. [Google Scholar] [CrossRef]
- Chen, S.; Sun, F.; Bai, Q.; Chen, D.; Chen, Q.; Hou, D. Sub-picosecond timing fluctuation suppression in laser-based atmospheric transfer of microwave signal using electronic phase compensation. Opt. Commun. 2017, 401, 18–22. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Optical Transmit Power | 3 dBm |
| Optical Center Wavelength | 1550 nm |
| Output Spectrum Width | 1 nm |
| Extinction Ratio | 12 dB |
| Parameter | Value |
|---|---|
| Sensitivity | −31 dBm |
| Wavelength of Operation | 1100~1610 nm |
| Signal Detect—Asserted | −34 dBm |
| Signal Detect—De-asserted | −45 dBm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Hou, D.; Liu, K.; Zhou, W.; Li, M.; Fang, L. Picosecond-Level Synchronization over Optical Free Space Link Using White Rabbit. Electronics 2025, 14, 970. https://doi.org/10.3390/electronics14050970
Zhang P, Hou D, Liu K, Zhou W, Li M, Fang L. Picosecond-Level Synchronization over Optical Free Space Link Using White Rabbit. Electronics. 2025; 14(5):970. https://doi.org/10.3390/electronics14050970
Chicago/Turabian StyleZhang, Peng, Dong Hou, Ke Liu, Wenjian Zhou, Minghong Li, and Lujun Fang. 2025. "Picosecond-Level Synchronization over Optical Free Space Link Using White Rabbit" Electronics 14, no. 5: 970. https://doi.org/10.3390/electronics14050970
APA StyleZhang, P., Hou, D., Liu, K., Zhou, W., Li, M., & Fang, L. (2025). Picosecond-Level Synchronization over Optical Free Space Link Using White Rabbit. Electronics, 14(5), 970. https://doi.org/10.3390/electronics14050970







