Towards Federated Robust Approximation of Nonlinear Systems with Differential Privacy Guarantee
Abstract
1. Introduction
- Federated learning framework for nonlinear systems: a decentralized training protocol tailored for nonlinear system modeling, enabling multiple clients to collaboratively train models without sharing raw data.
- Integration of differential privacy: The implementation of differential privacy mechanisms to protect sensitive data while maintaining the utility of the trained models. The privacy guarantees are achieved by introducing noise into model updates, preventing adversarial inference attacks.
- Our proposed framework efficiently scales to large numbers of clients, handling data heterogeneity and temporal variations, while maintaining privacy through the differential privacy mechanism, ensuring robust performance in distributed settings.
2. Related Work
2.1. Federated Learning for Nonlinear System Approximation
2.2. Differential Privacy in Federated Learning
2.3. Challenges in Handling Nonlinear Behaviors and Data Heterogeneity
2.4. Privacy-Preserving Techniques for Nonlinear System Models
3. Preliminaries
3.1. Federated Learning Framework for Nonlinear Systems
3.1.1. Local Training
3.1.2. Global Aggregation
3.2. Differential Privacy Mechanisms
Gradient Perturbation with Gaussian Noise
4. Methodology
4.1. Nonlinear System Modeling
| Algorithm 1 Federated Learning with Differential Privacy for Nonlinear System Modeling |
|
4.1.1. System Representation and Neural Network Architecture
- and are the weights and biases of the l-th layer.
- is a nonlinear activation function, such as ReLU (), tanh () or sigmoid ().
- L is the number of layers, and represents the number of neurons in layer l.
4.1.2. DP Guarantee
4.2. Handling Dynamic Nonlinear Behavior
4.3. Stability Analysis of Neural Network Approximation
5. Experiments
- The evaluation of the model’s ability to approximate nonlinear system dynamics.
- A comparison of privacy-preserving performance using differential privacy mechanisms.
- The computational efficiency and scalability of the federated learning framework.
- Robustness to data heterogeneity and dynamic nonlinear behavior.
5.1. Experimental Setup
5.1.1. Datasets
5.1.2. Federated Learning Setup
5.1.3. Evaluation Metrics
- Mean Squared Error (MSE) measures the approximation accuracy of the global model in predicting the outputs of the nonlinear system. The MSE is computed as , where is the predicted output, is the true output, and n is the number of test samples.
- Privacy loss () quantifies the privacy guarantee of the model, where a lower corresponds to stronger privacy.
- Computation time measures the total time taken for each communication round and the overall time required for training.
- Communication cost measures the total amount of data transmitted during the federated learning process.
5.2. Results
5.2.1. Nonlinear System Approximation Performance
- Lorenz dataset: The Federated Learning with DP model achieves an MSE of 0.0103 on the first segment (1–1000), 0.0116 on the second segment (1001–2000), 0.0108 on the third segment (2001–3000), and 0.0112 on the fourth segment (3001–4000). This is better than both the Centralized Model and Federated Learning without DP for all segments, particularly in the first segment, where FL with DP shows a clear advantage.
- Climate dataset: The Federated Learning with DP model achieves an MSE of 0.0174 on the first 5000 data points and 0.0181 on the next 5000 data points, which is significantly better than the Federated Learning without DP (0.0210 and 0.0221) and much closer to the Centralized Model’s result (0.0190 and 0.0202).
- Lorenz dataset: The score for FL with DP is 0.990 on the first segment, 0.992 on the second segment, 0.993 on the third segment, and 0.994 on the fourth segment, which are the highest values compared to both Centralized Model (0.988, 0.986, 0.987, 0.985) and Federated Learning without DP (0.983, 0.980, 0.982, 0.979).
- Climate dataset: For the Climate dataset, FL with DP achieves an score of 0.982 on the first 5000 data points and 0.986 on the next 5000 data points, outperforming Federated Learning without DP (0.968 and 0.963) and coming very close to the Centralized Model (0.977 and 0.974).
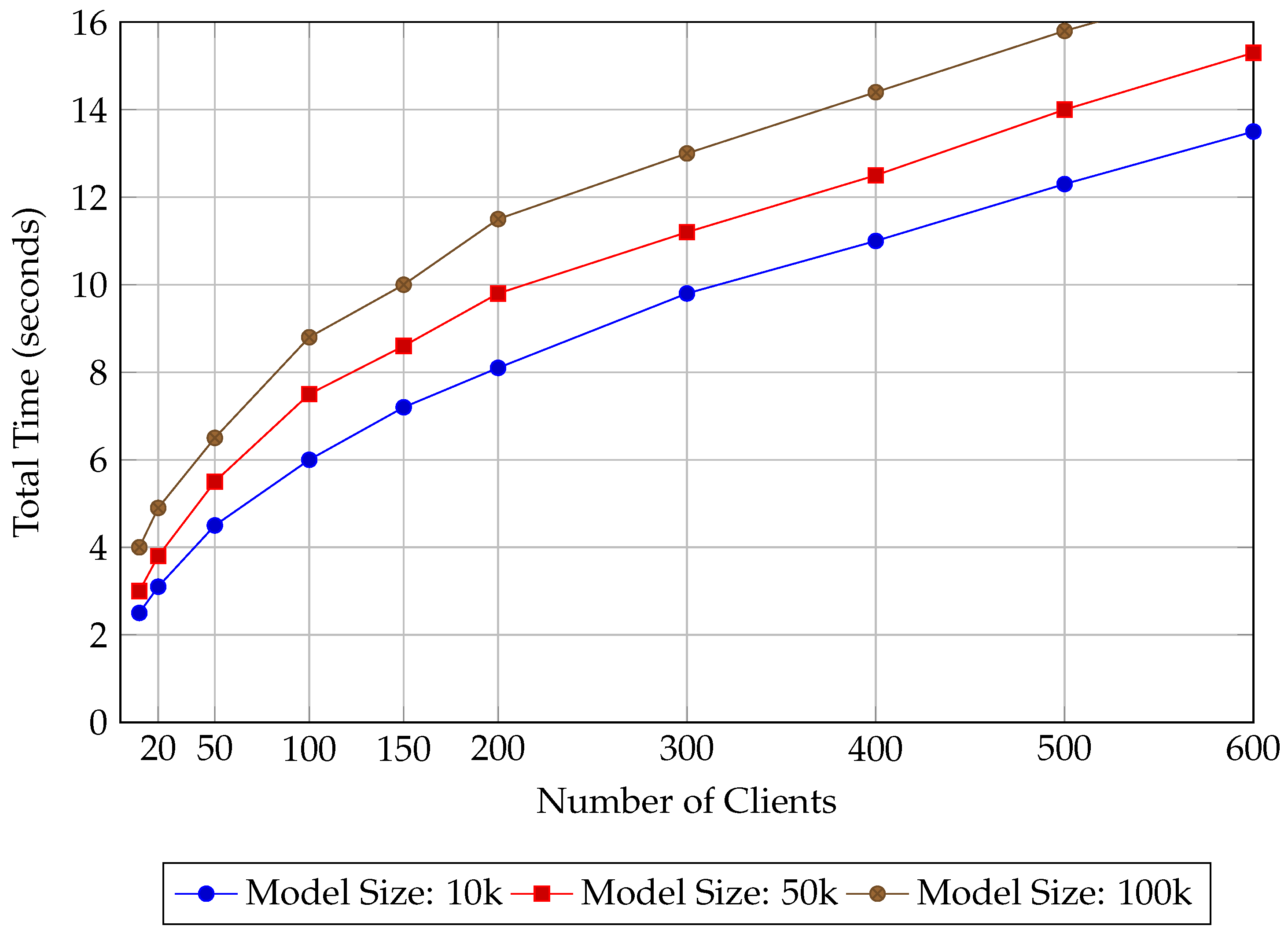
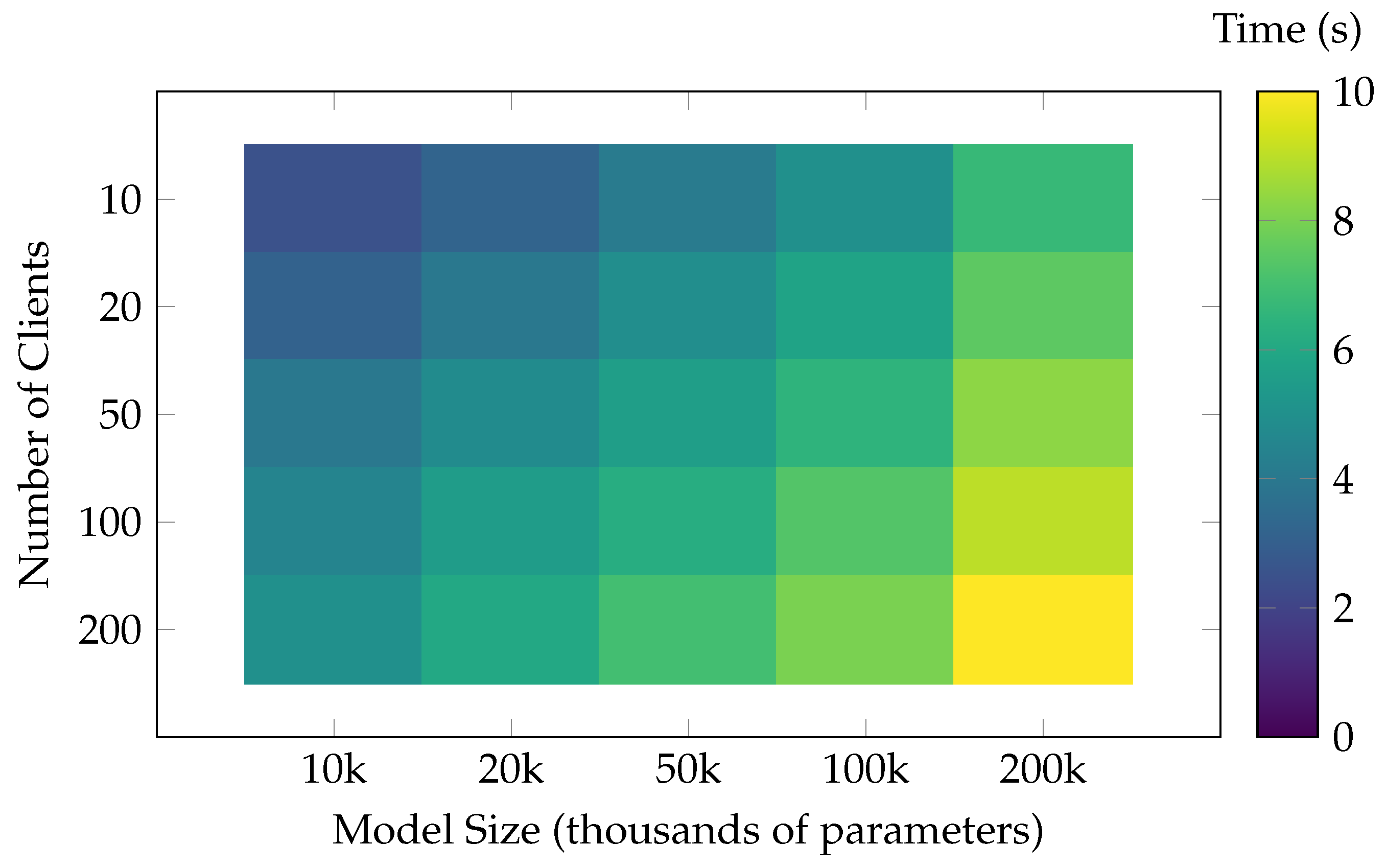
5.2.2. Computational Efficiency and Scalability
5.3. Privacy Protection
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Z.; Wu, Z. Federated Learning-Based Distributed Model Predictive Control of Nonlinear Systems. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; pp. 1256–1262. [Google Scholar]
- Wang, L.; Xu, Y.; Xu, H.; Chen, M.; Huang, L. Accelerating decentralized federated learning in heterogeneous edge computing. IEEE Trans. Mob. Comput. 2022, 22, 5001–5016. [Google Scholar] [CrossRef]
- Qu, L.; Zhou, Y.; Liang, P.P.; Xia, Y.; Wang, F.; Adeli, E.; Fei-Fei, L.; Rubin, D. Rethinking architecture design for tackling data heterogeneity in federated learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10061–10071. [Google Scholar]
- Pei, J.; Liu, W.; Li, J.; Wang, L.; Liu, C. A review of federated learning methods in heterogeneous scenarios. IEEE Trans. Consum. Electron. 2024, 70, 5983–5999. [Google Scholar] [CrossRef]
- Duan, G.R. Robust stabilization of time-varying nonlinear systems with time-varying delays: A fully actuated system approach. IEEE Trans. Cybern. 2022, 53, 7455–7468. [Google Scholar] [CrossRef]
- Hadj Taieb, N. Stability analysis for time-varying nonlinear systems. Int. J. Control 2022, 95, 1497–1506. [Google Scholar] [CrossRef]
- Yin, X.; Zhu, Y.; Hu, J. A comprehensive survey of privacy-preserving federated learning: A taxonomy, review, and future directions. ACM Comput. Surv. (CSUR) 2021, 54, 1–36. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; y Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- Wu, C.; Wu, F.; Lyu, L.; Huang, Y.; Xie, X. Communication-efficient federated learning via knowledge distillation. Nat. Commun. 2022, 13, 2032. [Google Scholar] [CrossRef]
- Chang, Z.L.; Hosseinalipour, S.; Chiang, M.; Brinton, C.G. Asynchronous multi-model dynamic federated learning over wireless networks: Theory, modeling, and optimization. IEEE Trans. Cogn. Commun. Netw. 2024, 10, 1989–2004. [Google Scholar] [CrossRef]
- Chen, L.; Tang, Z.; He, S.; Liu, J. Feasible operation region estimation of virtual power plant considering heterogeneity and uncertainty of distributed energy resources. Appl. Energy 2024, 362, 123000. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, Z.; Li, X.; Cui, Y.; Li, M.; Ban, X. Controlling Partially Observed Industrial System Based on Offline Reinforcement Learning—A Case Study of Paste Thickener. IEEE Trans. Ind. Inform. 2024, 21, 49–59. [Google Scholar] [CrossRef]
- Duchi, J.C.; Jordan, M.I.; Wainwright, M.J. Minimax optimal procedures for locally private estimation. J. Am. Stat. Assoc. 2018, 113, 182–201. [Google Scholar] [CrossRef]
- Zhu, L.; Liu, Z.; Han, S. Deep leakage from gradients. Adv. Neural Inf. Process. Syst. 2019, 32, 14747–14756. [Google Scholar]
- Abadi, M.; Chu, A.; Goodfellow, I.; McMahan, H.B.; Mironov, I.; Talwar, K.; Zhang, L. Deep learning with differential privacy. In Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016; pp. 308–318. [Google Scholar]
- Tang, J.; Korolova, A.; Bai, X.; Wang, X.; Wang, X. Privacy loss in apple’s implementation of differential privacy on macos 10.12. arXiv 2017, arXiv:1709.02753. [Google Scholar]
- Caldas, S.; Konečny, J.; McMahan, H.B.; Talwalkar, A. Expanding the reach of federated learning by reducing client resource requirements. arXiv 2018, arXiv:1812.07210. [Google Scholar]
- Zhao, L.; Hu, S.; Wang, Q.; Jiang, J.; Shen, C.; Luo, X.; Hu, P. Shielding collaborative learning: Mitigating poisoning attacks through client-side detection. IEEE Trans. Dependable Secur. Comput. 2020, 18, 2029–2041. [Google Scholar] [CrossRef]
- Wei, W.; Liu, L.; Wu, Y.; Su, G.; Iyengar, A. Gradient-leakage resilient federated learning. In Proceedings of the 2021 IEEE 41st International Conference on Distributed Computing Systems (ICDCS), Washington, DC, USA, 7–10 July 2021; pp. 797–807. [Google Scholar]
- Xiang, Z.; Li, P.; Chadli, M.; Zou, W. Fuzzy optimal control for a class of discrete-time switched nonlinear systems. IEEE Trans. Fuzzy Syst. 2024, 32, 2297–2306. [Google Scholar] [CrossRef]
- Uçak, K.; Günel, G.Ö. Adaptive stable backstepping controller based on support vector regression for nonlinear systems. Eng. Appl. Artif. Intell. 2024, 129, 107533. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, H.; He, P.; Chen, W.; Liu, X.; Gao, J.; Han, J. On the variance of the adaptive learning rate and beyond. arXiv 2019, arXiv:1908.03265. [Google Scholar]
- Liang, P.P.; Liu, T.; Ziyin, L.; Allen, N.B.; Auerbach, R.P.; Brent, D.; Salakhutdinov, R.; Morency, L.P. Think locally, act globally: Federated learning with local and global representations. arXiv 2020, arXiv:2001.01523. [Google Scholar]
- Smith, V.; Chiang, C.K.; Sanjabi, M.; Talwalkar, A.S. Federated multi-task learning. Adv. Neural Inf. Process. Syst. 2017, 30, 4427–4437. [Google Scholar]
- Yang, Z.; Chen, M.; Wong, K.K.; Poor, H.V.; Cui, S. Federated learning for 6G: Applications, challenges, and opportunities. Engineering 2022, 8, 33–41. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, C.; Lu, J. Parameter self-tuning of SISO compact-form model-free adaptive controller based on long short-term memory neural network. IEEE Access 2020, 8, 151926–151937. [Google Scholar] [CrossRef]
- Lughofer, E.; Sayed-Mouchaweh, M. Adaptive and on-line learning in non-stationary environments. Evol. Syst. 2015, 6, 75–77. [Google Scholar] [CrossRef]
- Hammoud, H.A.A.K.; Prabhu, A.; Lim, S.N.; Torr, P.H.; Bibi, A.; Ghanem, B. Rapid Adaptation in Online Continual Learning: Are We Evaluating It Right? In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 18806–18815. [Google Scholar]
- Hu, W.; Lin, Z.; Liu, B.; Tao, C.; Tao, Z.T.; Zhao, D.; Ma, J.; Yan, R. Overcoming catastrophic forgetting for continual learning via model adaptation. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Shokri, R.; Shmatikov, V. Privacy-preserving deep learning. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 1310–1321. [Google Scholar]
- Gupta, R.; Crane, M.; Gurrin, C. Considerations on privacy in the era of digitally logged lives. Online Inf. Rev. 2021, 45, 278–296. [Google Scholar] [CrossRef]
- Li, J.; Mengu, D.; Luo, Y.; Rivenson, Y.; Ozcan, A. Class-specific differential detection in diffractive optical neural networks improves inference accuracy. Adv. Photonics 2019, 1, 046001. [Google Scholar] [CrossRef]
- Kwon, Y.; Lee, Z. A hybrid decision support system for adaptive trading strategies: Combining a rule-based expert system with a deep reinforcement learning strategy. Decis. Support Syst. 2024, 177, 114100. [Google Scholar] [CrossRef]
- Xiao, Z.; Li, P.; Liu, C.; Gao, H.; Wang, X. MACNS: A generic graph neural network integrated deep reinforcement learning based multi-agent collaborative navigation system for dynamic trajectory planning. Inf. Fusion 2024, 105, 102250. [Google Scholar] [CrossRef]
- Ziller, A.; Usynin, D.; Braren, R.; Makowski, M.; Rueckert, D.; Kaissis, G. Medical imaging deep learning with differential privacy. Sci. Rep. 2021, 11, 13524. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, K.; Chen, X.; Sun, L. Stable Unlearnable Example: Enhancing the Robustness of Unlearnable Examples via Stable Error-Minimizing Noise. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 26–27 February 2024; Volume 38, pp. 3783–3791. [Google Scholar]
- Gong, T.; Kim, Y.; Lee, T.; Chottananurak, S.; Lee, S.J. SoTTA: Robust Test-Time Adaptation on Noisy Data Streams. Adv. Neural Inf. Process. Syst. 2024, 36, 14070–14093. [Google Scholar]
- Zhang, Y.; Zeng, D.; Luo, J.; Fu, X.; Chen, G.; Xu, Z.; King, I. A survey of trustworthy federated learning: Issues, solutions, and challenges. ACM Trans. Intell. Syst. Technol. 2024, 15, 1–47. [Google Scholar] [CrossRef]
| Dataset/Model | Centralized | FL (No DP) | FL (With DP) | Improvement |
|---|---|---|---|---|
| Lorenz (1–1000) | 0.0120 | 0.0147 | 0.0103 | 14.17% |
| Lorenz (1001–2000) | 0.0135 | 0.0160 | 0.0116 | 14.07% |
| Lorenz (2001–3000) | 0.0128 | 0.0155 | 0.0108 | 15.63% |
| Lorenz (3001–4000) | 0.0131 | 0.0163 | 0.0112 | 14.49% |
| Climate (1–5000) | 0.0190 | 0.0210 | 0.0174 | 8.42% |
| Climate (5001–10,000) | 0.0202 | 0.0221 | 0.0181 | 10.40% |
| Overall MSE | 0.0157 | 0.0189 | 0.0143 | 8.91% |
| Dataset/Model | Centralized Model | FL (No DP) | FL (With DP) |
|---|---|---|---|
| Lorenz dataset | 0.0131 | 0.0162 | 0.0115 |
| Climate dataset | 0.0203 | 0.0220 | 0.0188 |
| Accuracy (%) | Loss (%) | Attack Rate (%) | Reduction (%) | Avg. Accuracy (%) | |
|---|---|---|---|---|---|
| No Privacy | 95.8 | 0.0 | 74.5 | 0.0 | 95.5 |
| 5.0 | 95.0 | 0.8 | 45.2 | 39.3 | 94.8 |
| 3.0 | 94.2 | 1.6 | 33.1 | 55.6 | 94.2 |
| 1.0 | 93.6 | 2.2 | 20.6 | 72.3 | 93.4 |
| 0.5 | 92.8 | 3.0 | 14.8 | 80.2 | 92.3 |
| 0.1 | 90.5 | 5.3 | 11.2 | 85.0 | 89.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Yan, X.; Chen, G.; Niu, M.; Tian, X. Towards Federated Robust Approximation of Nonlinear Systems with Differential Privacy Guarantee. Electronics 2025, 14, 937. https://doi.org/10.3390/electronics14050937
Yang Z, Yan X, Chen G, Niu M, Tian X. Towards Federated Robust Approximation of Nonlinear Systems with Differential Privacy Guarantee. Electronics. 2025; 14(5):937. https://doi.org/10.3390/electronics14050937
Chicago/Turabian StyleYang, Zhijie, Xiaolong Yan, Guoguang Chen, Mingli Niu, and Xiaoli Tian. 2025. "Towards Federated Robust Approximation of Nonlinear Systems with Differential Privacy Guarantee" Electronics 14, no. 5: 937. https://doi.org/10.3390/electronics14050937
APA StyleYang, Z., Yan, X., Chen, G., Niu, M., & Tian, X. (2025). Towards Federated Robust Approximation of Nonlinear Systems with Differential Privacy Guarantee. Electronics, 14(5), 937. https://doi.org/10.3390/electronics14050937







