Context Geometry Volume and Warping Refinement for Real-Time Stereo Matching
Abstract
1. Introduction
- We designed a lightweight multi-scale feature extraction structure and a 3D regularization network, transforming traditional 3D convolutions into 3D depthwise separable convolutions with a residual structure. This greatly lowered the model’s computational complexity while boosting its efficiency, leading to notable improvements in both accuracy and speed.
- We introduce contextual geometric attention (CGA), which adaptively fuses contextual information with geometric data to guide the determination of the cost volume in cost aggregation. This effectively improves the model’s accuracy and generalizability.
- We propose a Warped Cost Volume Disparity Refinement (WDR) module, incorporating left–right consistency checking to build the warped cost volume and inputting it, along with reconstruction errors and stereo image feature maps, into a residual network based on dilated convolutions to obtain refined disparity estimates.
2. Related Work
3. Proposed Method
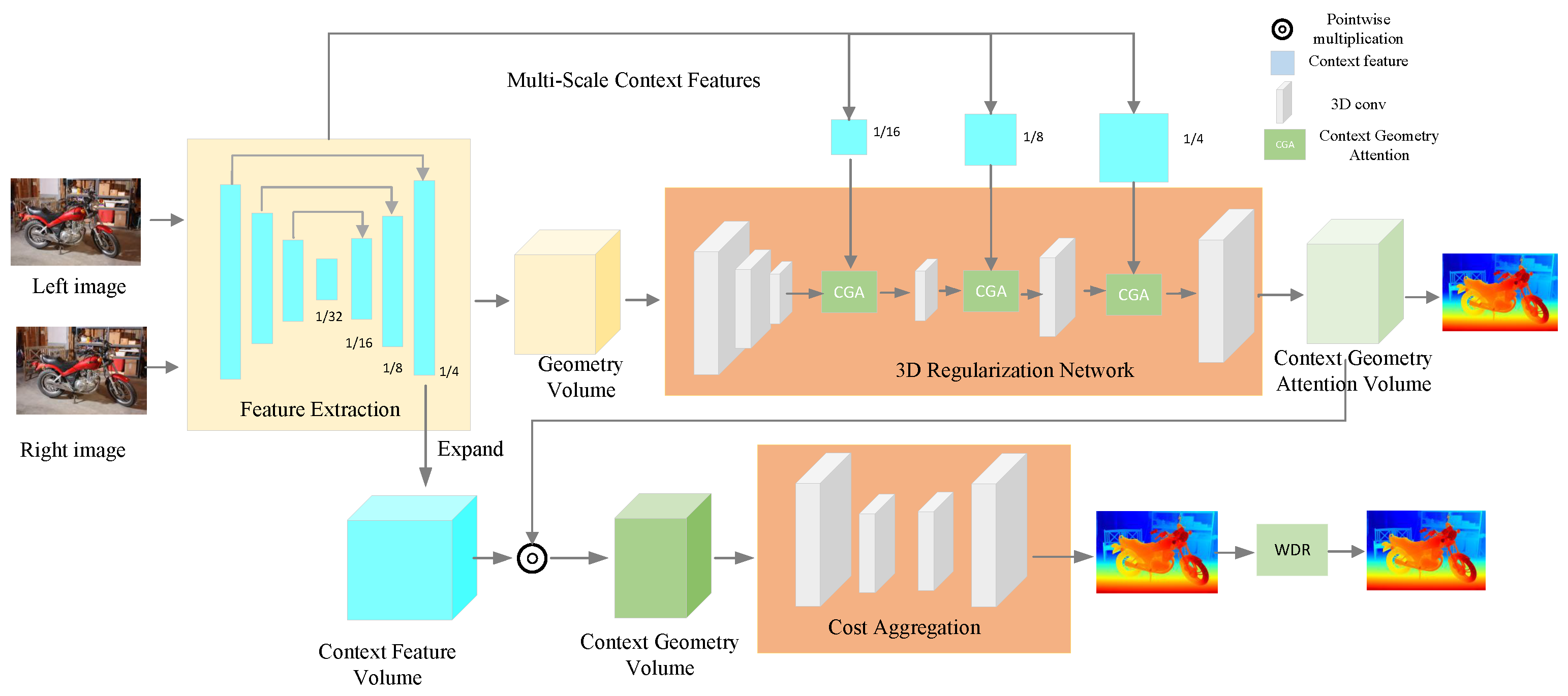
3.1. CGW Architecture
3.2. 3D Depthwise Separable Convolution
3.3. Context Geometry Attention
3.4. Warping Disparity Refinement
3.5. Loss Function
4. Experiment
4.1. Datasets and Evaluation Metrics
4.2. Implementation Details
4.3. Ablation Study
4.3.1. Runtime
4.3.2. Accuracy
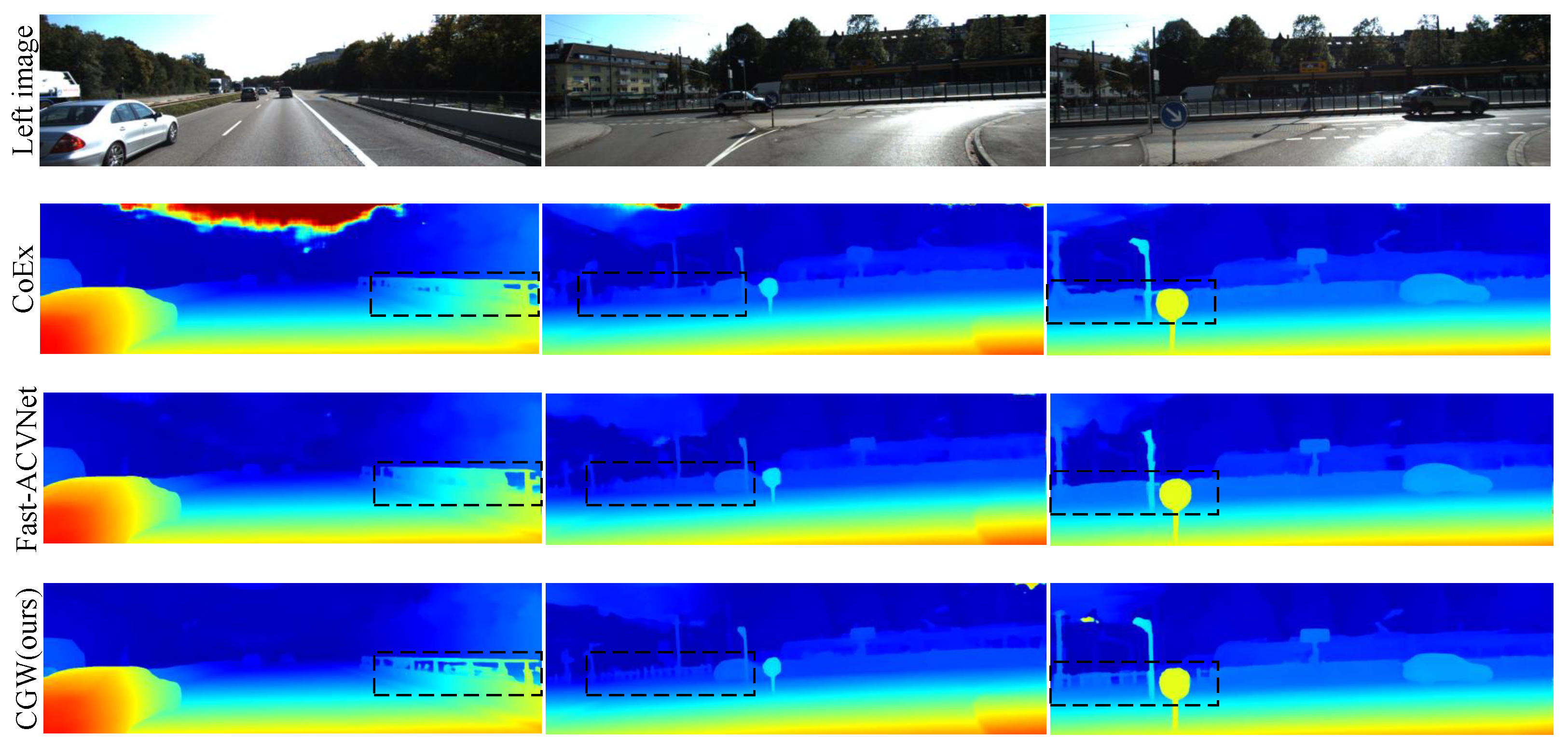
4.4. Comparisons with the State of the Art
4.5. Generalization Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kong, D.; Tao, H. A method for learning matching errors for stereo computation. In Proceedings of the British Machine Vision Conference, Kingston, UK, 7–9 September 2004; Volume 1, p. 2. [Google Scholar]
- Zbontar, J.; LeCun, Y. Stereo matching by training a convolutional neural network to compare image patches. J. Mach. Learn. Res. 2016, 17, 1–32. [Google Scholar]
- Kendall, A.; Martirosyan, H.; Dasgupta, S.; Henry, P.; Kennedy, R.; Bachrach, A.; Bry, A. End-to-end learning of geometry and context for deep stereo regression. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 66–75. [Google Scholar]
- Chang, J.R.; Chen, Y.S. Pyramid stereo matching network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5410–5418. [Google Scholar]
- Guo, X.; Yang, K.; Yang, W.; Wang, X.; Li, H. Group-wise correlation stereo network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3273–3282. [Google Scholar]
- Duggal, S.; Wang, S.; Ma, W.C.; Hu, R.; Urtasun, R. Deeppruner: Learning efficient stereo matching via differentiable patchmatch. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4384–4393. [Google Scholar]
- Zhang, F.; Prisacariu, V.; Yang, R.; Torr, P.H. Ga-net: Guided aggregation net for end-to-end stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 185–194. [Google Scholar]
- Imtiaz, S.M.; Kwon, K.C.; Hossain, M.B.; Alam, M.S.; Jeon, S.H.; Kim, N. Depth estimation for integral imaging microscopy using a 3D–2D CNN with a weighted median filter. Sensors 2022, 22, 5288. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, J. Aanet: Adaptive aggregation network for efficient stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 1959–1968. [Google Scholar]
- Bangunharcana, A.; Cho, J.W.; Lee, S.; Kweon, I.S.; Kim, K.S.; Kim, S. Correlate-and-excite: Real-time stereo matching via guided cost volume excitation. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 3542–3548. [Google Scholar]
- Luo, W.; Lu, Z.; Liao, Q. LNMVSNet: A Low-Noise Multi-View Stereo Depth Inference Method for 3D Reconstruction. Sensors 2024, 24, 2400. [Google Scholar] [CrossRef]
- Xu, G.; Wang, Y.; Cheng, J.; Tang, J.; Yang, X. Accurate and efficient stereo matching via attention concatenation volume. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 46, 2461–2474. [Google Scholar] [CrossRef] [PubMed]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar]
- Li, X.; Zhang, C.; Su, W.; Tao, W. IINet: Implicit Intra-inter Information Fusion for Real-Time Stereo Matching. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024; Volume 38, pp. 3225–3233. [Google Scholar]
- Xu, G.; Cheng, J.; Guo, P.; Yang, X. Attention concatenation volume for accurate and efficient stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 12981–12990. [Google Scholar]
- Smolyanskiy, N.; Kamenev, A.; Birchfield, S. On the importance of stereo for accurate depth estimation: An efficient semi-supervised deep neural network approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1007–1015. [Google Scholar]
- Chang, J.R.; Chang, P.C.; Chen, Y.S. Attention-aware feature aggregation for real-time stereo matching on edge devices. In Proceedings of the Asian Conference on Computer Vision, Kyoto, Japan, 30 November–4 December 2020. [Google Scholar]
- Tankovich, V.; Hane, C.; Zhang, Y.; Kowdle, A.; Fanello, S.; Bouaziz, S. Hitnet: Hierarchical iterative tile refinement network for real-time stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 14362–14372. [Google Scholar]
- Shamsafar, F.; Woerz, S.; Rahim, R.; Zell, A. Mobilestereonet: Towards lightweight deep networks for stereo matching. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2417–2426. [Google Scholar]
- Yee, K.; Chakrabarti, A. Fast deep stereo with 2D convolutional processing of cost signatures. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Snowmass Village, CO, USA, 1–5 March 2020; pp. 183–191. [Google Scholar]
- Khamis, S.; Fanello, S.; Rhemann, C.; Kowdle, A.; Valentin, J.; Izadi, S. Stereonet: Guided hierarchical refinement for real-time edge-aware depth prediction. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 573–590. [Google Scholar]
- Möckl, L.; Roy, A.R.; Petrov, P.N.; Moerner, W. Accurate and rapid background estimation in single-molecule localization microscopy using the deep neural network BGnet. Proc. Natl. Acad. Sci. USA 2020, 117, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Yao, C.; Yu, L.; Wu, Y.; Jia, Y. Parameterized cost volume for stereo matching. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 18347–18357. [Google Scholar]
- Zhong, Y.; Loop, C.; Byeon, W.; Birchfield, S.; Dai, Y.; Zhang, K.; Kamenev, A.; Breuel, T.; Li, H.; Kautz, J. Displacement-invariant cost computation for stereo matching. Int. J. Comput. Vis. 2022, 130, 1196–1209. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Z.; Wang, Q.; Zhang, J.; Wei, G.; Chu, X. Ednet: Efficient disparity estimation with cost volume combination and attention-based spatial residual. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 5433–5442. [Google Scholar]
- Liang, Z.; Guo, Y.; Feng, Y.; Chen, W.; Qiao, L.; Zhou, L.; Zhang, J.; Liu, H. Stereo matching using multi-level cost volume and multi-scale feature constancy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 300–315. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhou, H.; Zhang, Y.; Chen, J.; Yang, Y.; Zhao, Y. High-frequency stereo matching network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 1327–1336. [Google Scholar]
- Shen, Z.; Dai, Y.; Song, X.; Rao, Z.; Zhou, D.; Zhang, L. Pcw-net: Pyramid combination and warping cost volume for stereo matching. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 280–297. [Google Scholar]
- Lipson, L.; Teed, Z.; Deng, J. Raft-stereo: Multilevel recurrent field transforms for stereo matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 218–227. [Google Scholar]
- Xu, G.; Wang, X.; Ding, X.; Yang, X. Iterative geometry encoding volume for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 21919–21928. [Google Scholar]
- Wang, X.; Xu, G.; Jia, H.; Yang, X. Selective-stereo: Adaptive frequency information selection for stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 19701–19710. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Yang, F.; Sun, Q.; Jin, H.; Zhou, Z. Superpixel segmentation with fully convolutional networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 13964–13973. [Google Scholar]
- Shen, Z.; Dai, Y.; Rao, Z. Cfnet: Cascade and fused cost volume for robust stereo matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 13906–13915. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The kitti vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-resolution stereo datasets with subpixel-accurate ground truth. In Proceedings of the Pattern Recognition: 36th German Conference, GCPR 2014, Münster, Germany, 2–5 September 2014; Proceedings 36. Springer: Berlin/Heidelberg, Germany, 2014; pp. 31–42. [Google Scholar]
- Schops, T.; Schonberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A multi-view stereo benchmark with high-resolution images and multi-camera videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 3260–3269. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cheng, X.; Zhong, Y.; Harandi, M.; Dai, Y.; Chang, X.; Li, H.; Drummond, T.; Ge, Z. Hierarchical neural architecture search for deep stereo matching. Adv. Neural Inf. Process. Syst. 2020, 33, 22158–22169. [Google Scholar]
- Zhang, F.; Qi, X.; Yang, R.; Prisacariu, V.; Wah, B.; Torr, P. Domain-invariant stereo matching networks. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part II 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 420–439. [Google Scholar]
- Li, Z.; Liu, X.; Drenkow, N.; Ding, A.; Creighton, F.X.; Taylor, R.H.; Unberath, M. Revisiting stereo depth estimation from a sequence-to-sequence perspective with transformers. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 6197–6206. [Google Scholar]





| Baseline | LW- | 2LW- | EPE | D1 | Params | Runtime |
|---|---|---|---|---|---|---|
| FE | 3DRNER | (PX) | (%) | (M) | (ms) | |
| ✔ | × | × | 0.74 | 2.67 | 3.9 | 61 |
| ✔ | ✔ | × | 0.61 | 2.49 | 2.27 | 50 |
| ✔ | × | ✔ | 0.62 | 2.49 | 2.12 | 45 |
| ✔ | ✔ | ✔ | 0.65 | 2.56 | 1.87 | 29 |
| Model | CGA | WDF | EPE | D1 | >3 px | Runtime |
|---|---|---|---|---|---|---|
| (PX) | (%) | (%) | (ms) | |||
| CGW | × | × | 0.65 | 2.56 | 2.91 | 29 |
| ✔ | × | 0.60 | 2.24 | 2.74 | 31 | |
| × | ✔ | 0.58 | 2.16 | 2.66 | 35 | |
| ✔ | ✔ | 0.54 | 2.06 | 2.56 | 37 |
| Model | EPE (px) | Params (M) | Runtime (ms) |
|---|---|---|---|
| AANet [9] | 0.89 | 3.9 | 62 |
| GwcNet-gc [5] | 0.79 | 6.91 | 320 |
| LEAStereo [43] | 0.78 | 1.81 | 300 |
| BGNet [22] | 1.17 | 2.98 | 25 |
| CoEx [10] | 0.68 | 2.73 | 27 |
| HitNet [18] | 0.55 | - | 55 |
| Fast-ACVNet [12] | 0.64 | 3.9 | 39 |
| CGW (Ours) | 0.54 | 2.75 | 37 |
| Model | KITTI 2012 [38] | KITTI 2015 [39] | Runtime | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 3-noc | 3-all | 4-noc | 4-all | EPE-noc | EPE-all | D1-bg | D1-fg | D1-all | (ms) | |
| PSMNet [4] | 1.49 | 1.89 | 1.12 | 1.42 | 0.5 | 0.6 | 1.86 | 4.62 | 2.32 | 310 |
| GCNet [3] | 1.77 | 2.30 | 1.36 | 1.77 | 0.6 | 0.7 | 2.21 | 6.16 | 2.87 | 900 |
| CFNet [11] | 1.23 | 1.58 | 0.92 | 1.18 | 0.4 | 0.5 | 1.54 | 3.56 | 1.88 | 180 |
| LEAStereo [43] | 1.13 | 1.45 | 0.83 | 1.08 | 0.5 | 0.5 | 1.40 | 2.91 | 1.65 | 300 |
| GWCNet [5] | 1.32 | 1.70 | 0.99 | 1.27 | 0.5 | 0.5 | 1.74 | 3.93 | 2.11 | 200 |
| ACVNet [15] | 1.13 | 1.47 | 0.86 | 1.12 | 0.4 | 0.5 | 1.37 | 3.07 | 1.65 | 280 |
| DispNetC [13] | 4.11 | 4.65 | 2.77 | 3.20 | 0.9 | 1.0 | 4.32 | 4.41 | 4.34 | 60 |
| AANet [9] | 1.93 | 2.41 | 1.46 | 1.87 | 0.5 | 0.6 | 1.99 | 5.39 | 2.55 | 62 |
| BGNet [22] | 1.77 | 2.15 | - | - | 0.6 | 0.6 | 2.07 | 4.74 | 2.51 | 28 |
| CoEx [10] | 1.55 | 1.93 | 1.15 | 1.42 | 0.5 | 0.5 | 1.66 | 3.38 | 1.94 | 33 * |
| HitNet [18] | 1.41 | 1.89 | 1.14 | 1.53 | 0.4 | 0.5 | 1.74 | 3.20 | 1.98 | 55 * |
| Fast-ACVNet [12] | 1.68 | 2.13 | 1.23 | 1.56 | 0.5 | 0.6 | 1.82 | 3.93 | 2.17 | 39 * |
| CGW (ours) | 1.22 | 1.56 | 0.92 | 1.20 | 0.4 | 0.5 | 1.51 | 3.29 | 1.89 | 37 |
| Model | Middlebury | KITTI2012 | KITTI2015 | ETH3D |
|---|---|---|---|---|
| Bad 2.0 | D1-all | D1-all | Bad 1.0 | |
| (%) | (%) | (%) | (%) | |
| GANet [7] | 20.3 | 10.1 | 11.7 | 14.1 |
| CFNet [36] | 15.4 | 5.1 | 6.0 | 5.3 |
| PSMNet [4] | 15.8 | 6.0 | 6.3 | 9.8 |
| DSMNet [44] | 13.8 | 6.2 | 6.5 | 6.2 |
| STTR [45] | 15.5 | 8.7 | 6.7 | 17.2 |
| RAFT-Stereo [29] | 12.6 | - | 5.7 | 3.3 |
| DeepPrunerFast [6] | 38.7 | 16.8 | 15.9 | 36.8 |
| BGNet [22] | 24.7 | 24.8 | 20.1 | 22.6 |
| CoEx [10] | 25.5 | 13.5 | 11.6 | 9.0 |
| CGI-Stereo [11] | 13.5 | 6.0 | 5.8 | 6.3 |
| Fast-ACV [12] | 20.1 | 12.4 | 10.6 | 8.1 |
| CGW (ours) | 11.3 | 5.8 | 5.5 | 5.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, N.; Zhao, N.; Yang, O.; Wu, Q.; Ouyang, X. Context Geometry Volume and Warping Refinement for Real-Time Stereo Matching. Electronics 2025, 14, 892. https://doi.org/10.3390/electronics14050892
Liu N, Zhao N, Yang O, Wu Q, Ouyang X. Context Geometry Volume and Warping Refinement for Real-Time Stereo Matching. Electronics. 2025; 14(5):892. https://doi.org/10.3390/electronics14050892
Chicago/Turabian StyleLiu, Ning, Nannan Zhao, Ou Yang, Qingtian Wu, and Xinyu Ouyang. 2025. "Context Geometry Volume and Warping Refinement for Real-Time Stereo Matching" Electronics 14, no. 5: 892. https://doi.org/10.3390/electronics14050892
APA StyleLiu, N., Zhao, N., Yang, O., Wu, Q., & Ouyang, X. (2025). Context Geometry Volume and Warping Refinement for Real-Time Stereo Matching. Electronics, 14(5), 892. https://doi.org/10.3390/electronics14050892