Building Traceable Redactable Blockchain with Time-Verifiable Chameleon Hash

Abstract

Blockchain is a decentralized digital ledger that records transactions across a distributed network of computers, enabling secure and transparent operations without requiring trust in a central authority. While initially developed for Bitcoin, blockchain technology now underpins many cryptocurrencies and other applications. It serves as an open trust layer without central reliance and is widely used in cryptocurrencies such as Bitcoin and Ethereum. However, this public and permanent open storage has raised concerns about its potential misuse for illegal trades or the distribution of unwanted content. In EuroS&P 2017, Ateniese et al. introduced the concept of the redactable blockchain, which utilizes the trapdoor collision function provided by chameleon hash to rewrite block contents without causing hashing inconsistencies. Recent research has continued to propose solutions for redactable blockchains, leveraging cryptographic algorithms such as chameleon hash and attribute-based encryption (ABE). Current solutions often employ sophisticated cryptographic schemes, such as ABE, but lack sufficient focus on developing secure and scalable solution for practical use. In this work, we propose the time-verifiable policy-based chameleon hash (TPCH) as a candidate solution for practical redaction to rewrite blockchain contents. Our solution for redactable blockchains enables the verification of whether a redaction was executed at a specific time, thereby offering time-based traceability for dominant algorithms in TPCH. Additionally, it restricts misbehavior or abuse of redaction powers by introducing a new trapdoor finding algorithm, Update, in addition to the adapt algorithm Adapt. We formally introduce TPCH with both black-box and white-box constructions. Our experimental and theoretical analysis demonstrates the feasibility and practicality of the proposed solution.

1. Introduction

Blockchain is an open and transparent public ledger commonly used to record the transaction history of cryptocurrencies, such as Bitcoin [1]. One of the defining characteristics of blockchain is its immutability, which is demonstrated by the inability to alter block information once it has undergone consensus authentication. However, with the rapid advancement of blockchain research, the application scenarios for blockchain technology have significantly expanded and diversified [2]. The information recorded in blocks is no longer confined to currency transaction data but has grown substantially in both richness and value. The immutability of blockchains means that once data, such as illegal or abusive content, are added to a blockchain, it cannot be removed or altered. This presents a significant challenge with current blockchain designs. The immutable blockchain can be regarded as a permanent public database, amplifying the negative impact of malicious content. For instance, the malicious uploading of child pornography, copyright-infringing materials, and other inappropriate content to the Bitcoin blockchain can cause permanent harm to victims. Due to the immutability feature, such harmful content cannot be erased from the blockchain.

The immutability of blockchain has recently come under scrutiny due to new erasure requirements imposed by the General Data Protection Regulation’s (GDPR) “right to be forgotten” provision. This regulation grants individuals the right to have their personal information removed from Internet searches and directories under specific circumstances. In EuroS&P 2017, Ateniese et al. [3] introduced the concept of the redactable blockchain (also referred to as mutable blockchain [4]). They replaced the conventional collision-resistant hash function (e.g., SHA-256) in blockchain with a trapdoor one-way hash function, which is known as a chameleon hash (CH).

To rewrite a block indexed as $(m,r)$, where m is the original block content, to $(m^{\prime },·)$ where $m^{\prime }\ne m$ represents the new block content, the modifier must find new chameleon randomness $r^{\prime }$ such that hash consistency is preserved, i.e.,

$$\mathbf{Hash}(m,r)=h=\mathbf{Hash}(m^{\prime },r^{\prime }),$$

where Hash represents the hashing algorithm for CH, and h denotes the chameleon hash value. The CH is associated with a public key $pk$ and offers a trapdoor collision-finding algorithm, Adapt, which allows the private key holder $sk$ (the modifier) to efficiently find hash collisions. This ensures hashing consistency while enabling block modification. This foundational work [3] has motivated further studies on redactable blockchain and garnered significant academic interest in exploring this topic in greater depth [5].

When implementing cryptographic primitives (like CH) for redactable blockchains, addressing security and scalability is crucial for the feasibility of redaction. For security, redaction must be processed securely, addressing issues like key exposure and achieving semantic security (as seen in conventional public-key encryption). Additionally, redaction must be executed efficiently without compromising the system’s throughput. These requirements present challenges in designing a practical CH for redactable blockchain implementation.

In this work, we propose an efficient and secure PCH, which is called time-verifiable policy-based chameleon hash (TPCH). It enables blockchain redaction to be executed in a traceable and efficient manner with necessary security guarantees and access control over redaction privileges. Our work provides a practical solution for rewriting block contents while considering the challenges of security and scalability in one candidate solution for blockchain systems.

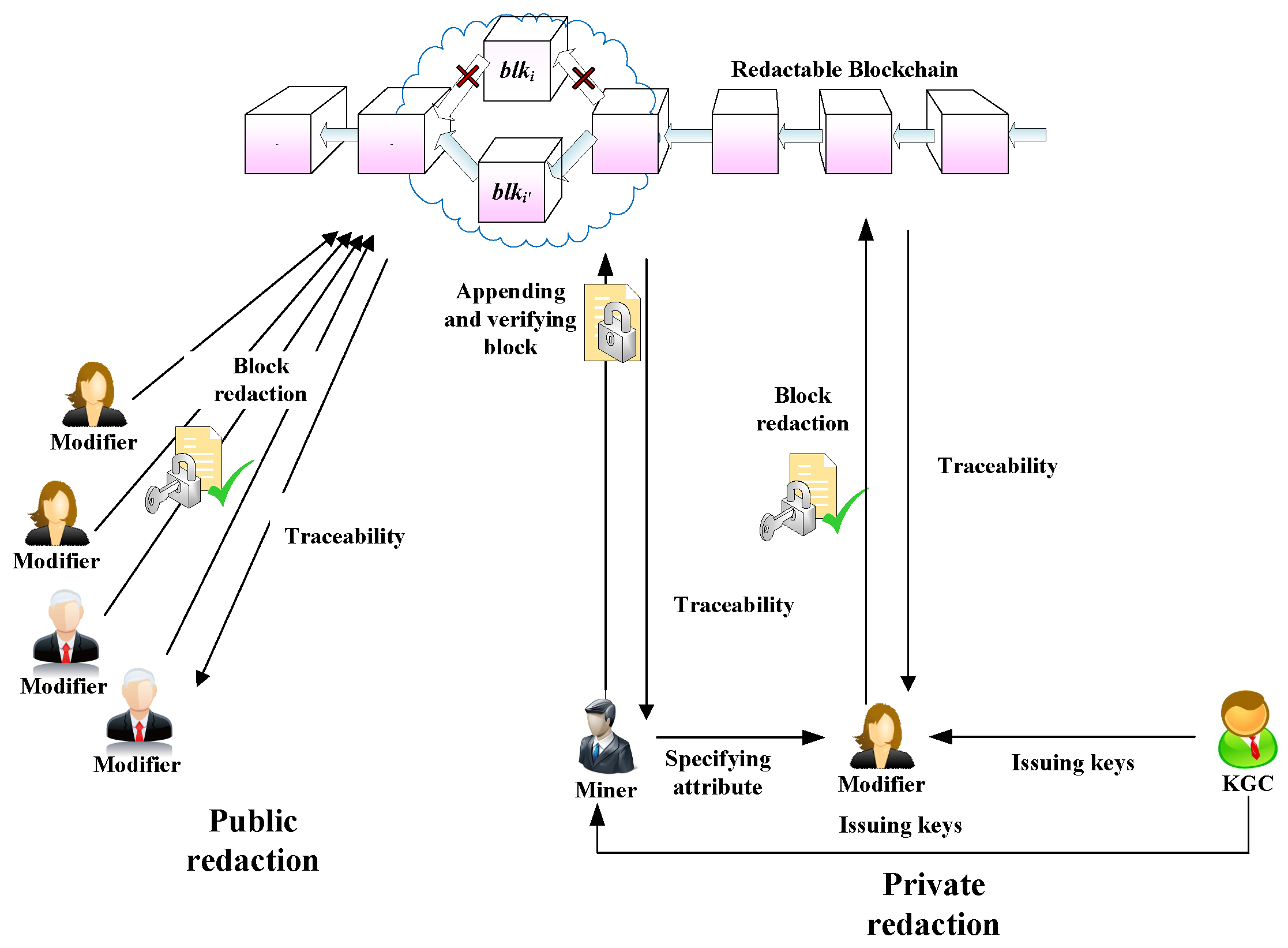
1.1. System Framework

As depicted in Figure 1, our framework supports both private and public redaction for blockchains. Private redaction means only authorized users under an access control policy can conduct redaction. Public redaction means anyone can conduct redaction after a given time period. In Figure 1, a green checkmark indicates permission to perform redaction, while a red checkmark indicates that the original block cannot be accepted after redaction.

In the system, each user utilizes our proposed TPCH for hashing and publishes the transaction. The process begins with each user obtaining a secret and public key pair $(sk,pk)$ from the key generation center (KGC). To append a block, a miner runs the Hash and Ver algorithms to assign a chameleon hash to the block and verify its validity, respectively. The modifier who possesses the desired attributes as specified by the chameleon hash is allowed to run the Adapt and Update algorithms to rewrite the blockchain. Basically, Update is similar to Adapt; however, it provides the ability to find collisions for different times, which is useful for tracing redactions (if we update each time to correspond to the redaction time).

• Key Generation Center (KGC): A trusted entity responsible for assigning a key pair to each user.
• Miner: Trusted entities with privilege to specify an access structure and write a block.
• User: Untrusted entities with read-only access to the blockchain; he cannot modify its contents.
• Modifier: An authorized user who possesses the required attributes according to the access structure, allowing them to rewrite the blockchain.

1.2. Motivations and Challenges

Early solutions for redactable blockchains were too coarse-grained, offering only an all-or-nothing approach to block-level redaction. As suggested by Derler et al. [6], the combination of attribute-based encryption (ABE) and chameleon hash, referred to as policy-based CH (PCH) [6,7], has recently been utilized to achieve fine-grained redaction for blockchain. However, the trivial application of PCH is insufficient to address practical concerns during blockchain redaction. According to Camenisch et al. [8], existing CHs must satisfy indistinguishability (IND) and collision resistance (CR) in order to be securely applied to practical applications. However, traceability is not generally required for CHs to satisfy. Specifically, this security is associated with the notion of “uniqueness”, which was considered a strong security notion by Camenisch et al. (Definition 14 in [8]). Traceability is a necessary requirement for redactable blockchains because it allows for tracing problematic contents (e.g., transactions) or the associated user identity [9] in time-sensitive blockchains. As the identities of users are pseudorandom in blockchain and deanonymization is not our focus, we mainly seek to add time verifiability to chameleon hashes and their applications. Since quick searches on the blockchain based on a given timestamp are allowed, as seen in Bitcoin, traceability is achieved. This also applies to redactable blockchains.

To make each chameleon hash traceable by its generation time, a naive solution is to add a time parameter to each chameleon hash. However, this increases storage complexity and could be maliciously altered by a third party. In fact, each transaction in the blockchain is identified by a unique time parameter. Suppose a timestamp is a 4-byte unsigned integer representing the approximate time when a transaction was generated, and let a block contain 1000 transactions. The size of 1000 timestamps in a block is 4 KB, which will scale linearly as the blockchain grows. Another major problem is that when a block is redacted, we need to maintain hashing consistency and time-based traceability without impairing the basic design or incurring additional storage overhead.

Additionally, there should be countermeasures to prevent the abuse of redaction power. For instance, human error or software bugs may lead to redaction mistakes, such as rewriting a block from m to $m^{″}$ instead of the intended $m^{\prime }$. A naive solution to correct such mistakes would involve initiating another redaction, which is impossible under strict access control policies. To address this, a verification and confirmation step after performing the redaction is needed. Since blockchain systems are time-sensitive, redacted blocks must also remain time-sensitive to satisfy regulatory requirements regarding the timing of redactions. Existing solutions [9] often rely on intensive cryptographic overlays to achieve traceability, which adds complexity. Extending current CHs to naturally support traceability without additional overhead is a significant challenge.

The challenges mentioned above naturally lead to the question: “Can existing CH schemes be designed to support traceability with countermeasures against abuse or misbehavior during redaction?”.

1.3. Contribution

Our contributions are summarized as follows:

• We propose the time-verifiable PCH to achieve practical redaction with traceability and scalable performance. To address the aforementioned issues, we adopt timed-release public key encryption (TPKE) as an alternative solution in our TPCH while also incorporating the ABE-based design. The resulting scheme offers private redaction via ABE for authorized users with the desired attributes and public redaction via TPKE after a given time period for all users (like the way to “mine” a block during the Proof-of-Work consensus [1]). Meanwhile, our underlying CH provides traceability and introduces a new trapdoor collision-finding algorithm, Update, as security enhancements. The former addresses regulation and traceability requirements, while the latter serves as a confirmation mechanism to address misbehaviors in redaction.
• We formally introduce time-verifiable policy-based chameleon hash (TPCH) and utilize the generic transformation proposed by Derler et al. (NDSS 2019) to build a secure time-verifiable policy-based chameleon hash for fine-grained blockchain redaction. We present a formal model, a generic construction, and concrete instantiations of the TPCH scheme. Our experimental and theoretical analyses demonstrate the feasibility of our proposal.
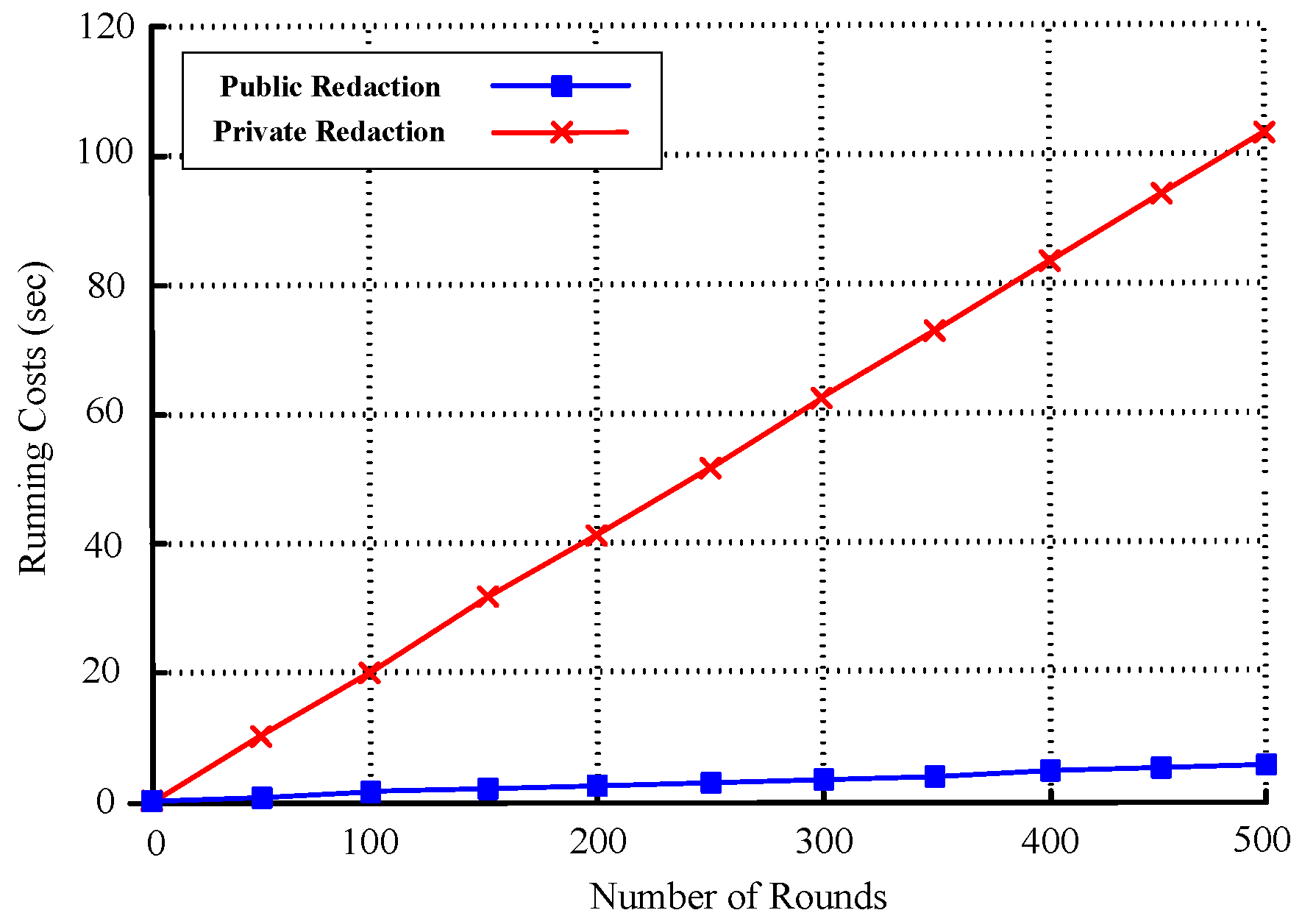
• For the quantitative analysis, the results show that for public redaction, our hashing takes 40 ms for 150 attributes, Adapt takes 290 ms for 100 attributes, and Update takes 295 ms for 50 attributes. For private redaction, our update cost averages 28 ms, and it increases from 0 to 4 s as the number of rounds increases from 0 to 500. These results demonstrate the efficiency of our proposed.

1.4. Related Works

Redactable Blockchain: Politou et al. [4] have conducted comprehensive surveys of redactable blockchains [3], providing detailed overviews of various approaches, including their strengths, limitations, and potential research directions. Current research on redactable blockchains primarily focuses on fine-grained redaction and decentralized redaction [6,10,11,12,13,14]. Implementing redactable blockchains using cryptographic primitives like CP-ABE and CH poses challenges related to practical performance, practical security, and decentralization. Achieving fully decentralized encryption for public redaction is desirable to maintain the decentralized nature of blockchains [3,15], but it presents significant difficulties.

Table 1. Security and functionality comparisons of redactable blockchain.

Scheme	Key Component	Redaction Security						Performance	Practical Functionality
		Hyb	Revo	FR	Trace	Anony	MPC	Efficiency	Fine-Grained	Decentralization	Applying with Coin
AMV+ 17 [3]	CH	✕	✕	✕	✓	✕	✓	Ideal	✕	✓	Bitcoin
TLL+17 [9]	ABE+CH	✕	✕	✕	✓	✕	✕	Acceptable	✕	✕	✕
DMT+19 [16]	Consensus-based voting	✕	✕	✕	✓	✕	✕	Fast	✕	✓	Bitcoin
DSS+19 [6]	ABE and CHET	✕	✕	✕	✓	✕	✕	Not Ideal	✓	✓	✕
XNM+21a [7]	PCH	✕	✓	✕	✕	✓	✕	Ideal	✓	✕	✕
XNM+21b [17]	Time-locked deposit penalty	✕	✕	✕	✕	✕	✕	Efficient	✕	✕	✕
JCH+22 [10]	RSA accumulator	✕	✕	✕	✕	✕	✓	Efficient	✓	✓	✕
MXN+22 [11]	ABE and CHET	✕	✕	✕	✕	✕	✓	Acceptable	✓	✓	✕
XHY+22 [12]	Attribute-based traitor tracing	✕	✕	✕	✓	✕	✕	Efficient	✓	✕	✕
HMR+23 [14]	Trapdoor cryptography	✕	✕	✕	✓	✓	✓	Acceptable	✓	✓	Monero
SCL+23 [18]	Double-trapdoor CH	✕	✕	✕	✕	✕	✕	Acceptable	✕	✕	✓
LMW+23 [19]	Non-interactive threshold CH	✕	✕	✕	✕	✕	✕	Efficient	✕	✓	UTXO
Our TPCH	ABE and TPKE [15]	✓	✓	✓	✓	✕	✕	Efficient (Online)	✓	✓	✕

Denote ✓ as satisfied; ✕ as not satisfied; CH as chameleon hash; PCH as policy-based CH; ABE as attribute-based encryption; UTXO as unspent transaction output model; CHET as chameleon hash with ephemeral trapdoor [8]; TPKE as timed-release public-key encryption [15]; Trace as transaction traceability; Anony as transaction anonymity; Revo as writing privilege revocation; Hyb as hybrid redaction which supports public decryption (e.g., $\mathsf{TPKE}$ [15]) and private decryption (i.e., any decryptions using secrets); FR as forward revocability of CH as mentioned in [7]; MPC as multi-party computation.

shows that most works focus on specific security features like writing privilege revocation, traceability, and anonymity with acceptable experimental performance. Privacy concerns in blockchain redaction have received limited attention [14], and achieving multiple objectives in a single solution remains challenging due to the trilemma of blockchain, i.e., balancing security, privacy, and decentralization. Only a few works successfully encompass more than five of the listed properties in Table 1, such as [14].

Current research on redactable blockchains predominantly focuses on two main areas: fine-grained redaction and decentralized redaction [6,10,11,12,13,14]. The utilization of multi-party computation to achieve decentralized redaction has gained popularity and has been explored in recent works [3,10,11,14]. However, implementing redactable blockchains using CP-ABE, CH, and other cryptographic primitives brings forth several challenges, including practical performance, practical security, and decentralization concerns. Fine-grained redaction, while enabling the precise modification of individual transactions without affecting others, can lead to scalability and performance issues due to the complexity of its designs and access structures. Security considerations arise concerning the revocation of writing privileges, potential malicious disclosures of secret keys [20], etc. Achieving fully decentralized encryption [15] for public redaction, as advocated in the work of Ateniese et al. [3], poses significant challenges but is highly desirable to maintain the decentralized nature of the blockchain framework.

As shown in Table 1, the majority of the listed works have focused on achieving one or two specific security features, such as hybrid redaction, writing privilege revocation, traceability, anonymity, etc. Hybrid redaction refers to the support for both public and private redaction, allowing for decentralization, smart contract alterations, and the maintenance of other public data on the blockchain [21] as well as enabling various decentralized cryptographic services [22]. Notably, the experimental performance of most listed works is deemed acceptable. Approximately half of the works considered fine-grained redaction, schematic decentralization, and the practical implementation of cryptocurrency projects. In summary, researchers have shown increasing interest in addressing security and practical functionality in redactable blockchains. However, an efficient CH scheme with a built-in traceability feature is still missing.

2. Preliminaries and Building Blocks

2.1. Groups and Bilinear Maps

Given two multiplicative groups ${\mathbb{G}}_1$, ${\mathbb{G}}_T$ with the same order p, and let g be the generator of $\mathbb{G}$. A symmetric bilinear pairing is a mapping $\widehat{e}:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$ with the following properties: (1) Bilinearity: $\forall u,v\in {\mathbb{G}}_1$ and $a,b\in {\mathbb{Z}}_p^{*}$, we have $\widehat{e}(u^a,v^b)=\widehat{e}{(u,v)}^{ab}$. (2) Non-degeneracy: $\exists g\in {\mathbb{G}}_1$ such that $\widehat{e}(g,g)\in {\mathbb{G}}_T$ is the generator of ${\mathbb{G}}_T$. (3) Computability: $\forall u,v\in {\mathbb{G}}_1$ to compute $\widehat{e}(u,v)$ is efficient.

2.2. Non-Interactive Zero-Knowledge

Let NIZK = (GenZK, Prove, Verify, SimGen, SimProve) be a simulation-sound non-interactive zero-knowledge (NIZK) proof as

• GenZK$\left(1^{\lambda }\right)\to \mathsf{crs}:$ Input the security parameter $\lambda$; output a common reference string $\mathsf{crs}$.
• Prove $(\mathsf{crs},(x,w\left)\right)\to \pi$: Input $\mathsf{crs}$ and $(x,w)\in R$; output a proof $\pi$.
• Ver $(\mathsf{crs},x,\pi )\to \left(0\mathrm{or}1\right)$: Input $\mathsf{crs}$, x, and $\pi$, and output $\left(0\mathrm{or}1\right)$ indicating acceptance or rejection.
• SimGen $\left(1^{\lambda }\right)\to (\mathsf{crs},td)$: Input the security parameter $1^{\lambda }$ and output a $\mathsf{crs}$ and a trapdoor $td$.
• SimProve $(x,td)\to \left(\pi \right)$: Input x and $td$; output a proof $\pi$.

2.3. Definitions of Timed-Release Public-Key Encryption

Definition 1.

A ($t_e,t_{fd},t_{sd}$) timed-release public-key encryption [15] (TPKE = (KeyGen, Enc, Dec)) is defined as

• KeyGen$\left(1^{\lambda }\right)\to (p{k}_{\mathsf{TPKE}},s{k}_{\mathsf{TPKE}})$: Input the security parameter λ, the KGC runs this algorithm to output a pair of keys $(p{k}_{\mathsf{TPKE}},s{k}_{\mathsf{TPKE}})$. $p{k}_{\mathsf{TPKE}}$ is an implicit input hereafter.
• Enc$\left(m\right)\to \left(c{t}_{\mathsf{TPKE}}\right)$: Input a public key $p{k}_{\mathsf{TPKE}}$ and a message m; the user runs this algorithm to output a ciphertext $c{t}_{\mathsf{TPKE}}$. It runs at most $t_e$ time.
• FDec$(s{k}_{\mathsf{TPKE}},c{t}_{\mathsf{TPKE}})\to m$: The fast decryption algorithm takes as input a secret key $s{k}_{\mathsf{TPKE}}$ and $c{t}_{\mathsf{TPKE}}$ and outputs a message m. It runs in time at most $t_{fd}$.
• SDec$\left(c{t}_{\mathsf{TPKE}}\right)\to m$: The slow decryption algorithm takes as input a public key $pk$ and a $c{t}_{\mathsf{TPKE}}$ and outputs a message m. It runs in time at least $t_{sd}$.

Definition 2.

(IND-CCA in a $(t_p,t_o,ϵ)$-TPKE:) The definition of indistinguishability against a chosen plaintext attack (IND-CCA) for TPKE is formalized through the interaction between the probabilistic polynomial time (PPT) adversary $\mathcal{A}$ and the challenger $\mathcal{C}$, as described in the experiment ${\mathrm{Exp}}_{\mathcal{A},\mathsf{TPKE}}^{\mathsf{IND}-\mathsf{CCA}}$ outlined below. A TPKE must satisfy IND-CCA security in order to be utilized as a secure encryption for our scheme.

• Setup: $\mathcal{C}$ runs $({pk}_{\mathsf{TPKE}}^{*},s{k}_{\mathsf{TPKE}}^{*})\leftarrow$Setup$\left(1^{\lambda }\right)$ and returns $p{k}_{\mathsf{TPKE}}^{*}$ to $\mathcal{A}$.
• Pre-processing Phase: $\mathcal{A}$ launches adaptive queries $c{t}_{\mathsf{TPKE}}$ to oracle ${\mathcal{O}}_{\mathsf{Dec}}$ controlled by $\mathcal{C}$ during pre-processing phase. $\mathcal{C}$ replies with $m_{\mathsf{TPKE}}\leftarrow$FDec$(s{k}_{\mathsf{TPKE}}^{*},c{t}_{\mathsf{TPKE}})$.
• Online Phase: $\mathcal{A}$ submits two equal-length messages $m_0$ and $m_1$ and sends them to $\mathcal{C}$. He flips a random coin $b\in \left\{0,1\right\}$ and returns $c{t}_b^{*}\leftarrow$Enc$(p{k}_{\mathsf{TPKE}}^{*},m_b)$ to $\mathcal{A}$. $\mathcal{A}$ continues to query the oracle in the online phase ${\mathcal{O}}_{\mathsf{Dec}}$ except for the target ciphertext $c{t}_b^{*}$.
• Guess: $\mathcal{A}$ makes a guess $b^{\prime }$ and wins if $b^{\prime }=b$.

A TPKE scheme is said to be IND-CCA and $(t_p,t_o,ϵ)$ secure if for any PPT adversary $\mathcal{A}$ running in time at most $t_p$ in the pre-processing phase and at most $t_o$ in online phase, the following advantage is negligible:

$${\mathsf{Adv}}_{\mathcal{A},\mathsf{TPKE}}^{\mathsf{IND}-\mathsf{CCA}}\left(1^{\lambda }\right)=\left|[\mathsf{Pr}[{\mathbf{Exp}}_{\mathcal{A},\mathsf{TPKE}}^{\mathsf{IND}-\mathsf{CCA}}\left(1^{\lambda }\right)=1]-1/2\right|$$

Remark 1.

Here, we define a stronger security definition than the selective IND-CPA security for ABE, called IND-CCA, in which the adversary is allowed to adaptively query the decryption oracle even after seeing the challenge ciphertext. Therefore, TPKE suffices to level up the security provided by the ABE.

2.4. Definitions of Attribute-Based Encryption

Let ABE = {Setup, KeyGen, Enc, Dec} be the CP-ABE scheme we used in this work.

• Setup$(1^{\lambda },U)\to ({mpk}_{\mathsf{ABE}},ms{k}_{\mathsf{ABE}})$: Given a security parameter $\lambda$ and a universe description U, the KGC runs this algorithm to output the public parameter ${mpk}_{\mathsf{ABE}}$ and the master key $ms{k}_{\mathsf{ABE}}$.
• KeyGen$(ms{k}_{\mathsf{ABE}},S)\to s{k}_S$: Upon input of a master key $ms{k}_{\mathsf{ABE}}$ and an attribute set $S\subseteq U$, the KGC runs this algorithm to output the secret (attribute) key $s{k}_S$.
• Enc$(\mathbb{A},m)\to c{t}_{\mathsf{ABE}}$: Upon input of an access structure $\mathbb{A}$ and a message m, the user runs this algorithm to output a ciphertext $c{t}_{\mathsf{ABE}}$.
• Dec$(s{k}_S,c{t}_{\mathsf{ABE}})\to m$: Upon input of a secret key $s{k}_S$ and a ciphertext $c{t}_{\mathsf{ABE}}$, the user runs this algorithm to output the plaintext m.

Definition 3.

(sIND-CPA in ABE:) The definition of sIND-CPA security for ABE is formalized through the interaction between the PPT adversary $\mathcal{A}$ and the challenger $\mathcal{C}$, as described in the experiment ${\mathrm{Exp}}_{\mathcal{A},\mathsf{ABE}}^{\mathsf{sIND}-\mathsf{CPA}}$ outlined below. An ABE must satisfy sIND-CPA security in order to be utilized as a secure encryption for our scheme.

• Initiation: The adversary declares the challenge access structure ${\mathbb{A}}^{*}$ and sends it to $\mathcal{C}$.
• Setup: $\mathcal{C}$ runs $({mpk}_{\mathsf{ABE}},ms{k}_{\mathsf{ABE}})\leftarrow$Setup$(1^{\lambda },U)$ and returns $mp{k}_{\mathsf{ABE}}$ to $\mathcal{A}$.
• Query Phase: $\mathcal{A}$ launches adaptive queries to oracle ${\mathcal{O}}_{\mathsf{KeyGen}}$ controlled by $\mathcal{C}$ regarding an attribute $S_i$, $\mathcal{C}$ calls $s{k}_i\leftarrow$KeyGen$(ms{k}_{\mathsf{ABE}},S_i)$ and sends $s{k}_i$ to $\mathcal{A}$. The restriction is that each query should not satisfy the challenge access structure, i.e., $S_i\vDash {\mathbb{A}}^{*}$.
• Challenge: $\mathcal{A}$ submits two equal-length messages $m_0$ and $m_1$ and sends them to $\mathcal{C}$. He flips a random coin $b\in \left\{0,1\right\}$ and returns $c{t}_{\mathsf{ABE},b}\leftarrow$Enc$(m_b,{\mathbb{A}}^{*})$ to $\mathcal{A}$.
• Guess: $\mathcal{A}$ makes a guess $b^{\prime }$ and wins if $b^{\prime }=b$.

An ABE scheme is said to be sIND-CPA secure if for any probabilistic polynomial time (PPT) adversary $\mathcal{A}$, the following advantage is negligible:

$${\mathsf{Adv}}_{\mathcal{A},\mathsf{ABE}}^{\mathsf{sIND}-\mathsf{CPA}}(\lambda ,U)=\left|[\mathsf{Pr}[{\mathbf{Exp}}_{\mathcal{A},\mathsf{ABE}}^{\mathsf{sIND}-\mathsf{CPA}}(\lambda ,U)=1]-1/2\right|$$

2.5. Definitions of Time-Verifiable Chameleon Hash

Before presenting the full scheme, we introduce a time-verifiable chameleon hash (TVCH) that satisfies the basic requirements and is secure enough to build the TPCH scheme. However, it is important to note that TVCH alone is insufficient for directly applying to redactable blockchain. We formalize the notion of time-verifiable chameleon hash TVCH = (Setup, KeyGen, Hash, Ver, Adapt, Update), as a variant of chameleon hash with useful properties for achieving redaction. It additionally incorporates a time period t for computing the hash.

• Setup$\left(1^{\lambda }\right)\to {mpk}_{\mathsf{TVCH}}$: Upon input of a security parameter $\lambda$, output the public parameter ${mpk}_{\mathsf{TVCH}}$.
• KeyGen$\left(ms{k}_{\mathsf{TVCH}}\right)\to (p{k}_{\mathsf{TVCH}},s{k}_{\mathsf{TVCH}})$: Upon input of a public parameter $mp{k}_{\mathsf{TVCH}}$, output the public and private keys $p{k}_{\mathsf{TVCH}}$ and $s{k}_{\mathsf{TVCH}}$. For brevity, let $p{k}_{\mathsf{TVCH}}$ be implicit hereafter.
• Hash$(m,t)\to ({\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}})$: Upon input of a message m and a time period t, output a chameleon hash ${\dot{h}}_{\mathsf{TVCH}}$ and a randomness ${\dot{r}}_{\mathsf{TVCH}}$.
• Ver$(({\dot{h}}_{\mathsf{TVCH}},m,{\dot{r}}_{\mathsf{TVCH}}),t)\to b$: Upon input of a triple $(m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}})$, and a time period t, output a decision $b=1$ if $(m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}})$ is valid. Else, output $b=0$.
• Adapt$((m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}}),t,m^{\prime },s{k}_{\mathsf{TVCH}})\to {\dot{r}}_{\mathsf{TVCH}}^{\prime }$: Upon input of a triple $(m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}})$, a time period t, a new message $m^{\prime }$, and a private key $s{k}_{\mathsf{TVCH}}$, output a new randomness ${\dot{r}}^{\prime }$.
• Update$((m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}}),t,t^{″},s{k}_{\mathsf{TVCH}})\to {\dot{r}}_{\mathsf{TVCH}}^{″}$: Upon input of a triple $(m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}})$, two time periods $t\ne t^{″}$, and a private key $s{k}_{\mathsf{TVCH}}$, output a new randomness ${\dot{r}}_{\mathsf{TVCH}}^{″}$.

A TVCH must satisfy the following properties to be considered “secure” enough to be utilized as the basic building block for further design.

• Correctness: All hash and adapt results that are properly conducted should pass verification.
• Indistinguishability: The distribution of randomness ${\dot{r}}^{\prime }$ (from Adapt) is computationally indistinguishable from that of $\dot{r}$ (from Hash).
• Collision resistance (including key exposure freeness): No PPT adversary who has access to the adapt oracle should efficiently find two distinct tuples $((m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}}),t)$ and $((m^{\prime },{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}}^{\prime }),t)$ such that $1=$Ver$((m,{\dot{h}}_{\mathsf{TVCH}},{\dot{r}}_{\mathsf{TVCH}}),t)=$Ver$\left(\right(m^{\prime },{\dot{h}}_{\mathsf{TVCH}},$
  ${\dot{r}}_{\mathsf{TVCH}}^{\prime }),t)$ with non-negligible probability.

3. Security Requirements of Time-Verifiable and Policy-Based Chameleon Hash

Based on the aforementioned TPKE, ABE, and TVCH, we formally model our TPCH in this section. There are several reasons to introduce TPCH instead of directly using TVCH. (1) TVCH is not secure enough for practical applications. According to [6,8], an insecure CH which satisfies the aforementioned security properties (correctness, indistinguishability, and collision resistance) can be transformed into a secure CH with ephemeral trapdoor (CHET) if the underlying CH satisfies the basic requirements as we previously modeled. By extending CHET with ABE, a secure PCH can be constructed for fine-grained redaction. In this work, we follow the above heuristic to construct TPCH by extending TVCH with ABE and TPKE.

3.1. Scheme Overview

Let TPCH = (Setup, KeyGen, Hash, Ver, Adapt, Update) be the time-verifiable policy-based chameleon hash.

• Setup$(1^{\lambda },U)\to (mp{k}_{\mathsf{TPCH}},ms{k}_{\mathsf{TPCH}})$: Input a security parameter $\lambda$ and a universe description U. KGC runs $(mp{k}_{\mathsf{ABE}},ms{k}_{\mathsf{ABE}})\leftarrow$ABE.Setup$(1^{\lambda },U)$, $mp{k}_{\mathsf{TVCH}}\leftarrow$CH.Setup$\left(1^{\lambda }\right)$ and $(p{k}_{\mathsf{TPKE}},s{k}_{\mathsf{TPKE}})\leftarrow$TPKE.Setup$\left(1^{\lambda }\right)$. Let $mp{k}_{\mathsf{TPCH}}\leftarrow (mp{k}_{\mathsf{ABE}},$
  $mp{k}_{\mathsf{TVCH}},p{k}_{\mathsf{TPKE}})$ and $ms{k}_{\mathsf{TPCH}}\leftarrow (ms{k}_{\mathsf{ABE}},s{k}_{\mathsf{TPKE}})$. Output the public parameters $p{k}_{\mathsf{TPCH}}$ and master key $ms{k}_{\mathsf{TPCH}}$.
• KeyGen$(ms{k}_{\mathsf{TPCH}},S)\to (s{k}_{\mathsf{TPCH}},p{k}_{\mathsf{TPCH}})$: Input a master key $ms{k}_{\mathsf{TPCH}}$ and an attribute set S. Parse $ms{k}_{\mathsf{TPCH}}=(ms{k}_{\mathsf{ABE}},s{k}_{\mathsf{TPKE}})$. KGC runs $s{k}_S\leftarrow$ABE.KeyGen$\left(ms{k}_{\mathsf{ABE}}\right)$ and $(s{k}_{\mathsf{TVCH}}^1,p{k}_{\mathsf{TVCH}}^1)\leftarrow$TVCH.KeyGen$\left(mp{k}_{\mathsf{TVCH}}\right)$. Let $s{k}_{\mathsf{TPCH}}\leftarrow (s{k}_S,$
  $s{k}_{\mathsf{TVCH}}^1,s{k}_{\mathsf{TPKE}})$ and $p{k}_{\mathsf{TPCH}}\leftarrow (mp{k}_{\mathsf{ABE}},p{k}_{\mathsf{TVCH}}^1,p{k}_{\mathsf{TPKE}})$. Output secret and public hash key pair $(s{k}_{\mathsf{TPCH}},p{k}_{\mathsf{TPCH}})$. $p{k}_{\mathsf{TPCH}}$ is an implicit input hereafter.
• Hash$({\mathsf{mode}}_{\mathsf{R}},{\mathsf{aux}}_{\mathsf{H}},m)\to (({\dot{h}}_{\mathsf{TPCH}},{\dot{r}}_{\mathsf{TPCH}}),etd)$: Input a redaction request ${\mathsf{mode}}_{\mathsf{R}}$, an auxiliary input ${\mathsf{aux}}_{\mathsf{H}}$, and a message m. The user runs $({\dot{h}}_{\mathsf{TVCH}}^1,{\dot{r}}_{\mathsf{TVCH}}^1)\leftarrow$TVCH. Hash$(p{k}_{\mathsf{TVCH}}^1,$ $m,t)$ and $({\dot{h}}_{\mathsf{TVCH}}^2,{\dot{r}}_{\mathsf{TVCH}}^2)\leftarrow$TVCH.Hash$(p{k}_{\mathsf{TVCH}}^2,m,t)$. Run $c{t}_{\mathsf{TVCH}}^2\leftarrow$ABE.Enc$(\mathbb{A},$${\dot{r}}_{\mathsf{TVCH}}^2)$. Let ${\dot{h}}_{\mathsf{TPCH}}\leftarrow ({\dot{h}}_{\mathsf{TVCH}}^1,{\dot{h}}_{\mathsf{TVCH}}^2,p{k}_{\mathsf{TVCH}}^1)$, ${\dot{r}}_{\mathsf{TPCH}}\leftarrow ({\dot{r}}_{\mathsf{TVCH}}^1,c{t}_{\mathsf{TVCH}}^2)$. Let $etd\leftarrow s{k}_{\mathsf{TVCH}}^2$ be an ephemeral trapdoor. Output a tuple $({\dot{h}}_{\mathsf{TPCH}},{\dot{r}}_{\mathsf{TPCH}},etd)$ including a chameleon hash, a randomness and an encrypted ephemeral trapdoor $c{t}_{etd}$.
• Ver$(p{k}_{\mathsf{TPCH}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t^{\prime })\to \left(0\mathrm{or}1\right)$: Input a public key $p{k}_{\mathsf{TPCH}}$, a chameleon tuple $({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}})$ and a time $t^{\prime }$. User runs $b_1\leftarrow$TVCH.Ver$(p{k}_{\mathsf{TVCH}}^1,$$({\dot{h}}_{\mathsf{TVCH}}^1,m,$${\dot{r}}_{\mathsf{TVCH}}^1),t^{\prime })$ and $b_2\leftarrow$TVCH.Ver$(p{k}_{\mathsf{TVCH}}^2,({\dot{h}}_{\mathsf{TVCH}}^2,m,{\dot{r}}_{\mathsf{TVCH}}^2),t^{\prime })$. If $1=b_1=b_2$, return 1. Otherwise, return $b=0$.
• Adapt$(s{k}_{\mathsf{TPCH}},{\mathsf{mode}}_{\mathsf{R}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t,m^{\prime },etd)\to {\dot{r}}_{\mathsf{TPCH}}^{\prime }$: Input a secret key $s{k}_{\mathsf{TPCH}}$, a redaction request ${\mathsf{mode}}_{\mathsf{R}}$, a tuple $({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}})$, a time t, a new message $m^{\prime }$ and an ephemeral trapdoor $etd$. Run ${\dot{r}}_{\mathsf{TVCH}}^2\leftarrow$ABE.Dec$(\mathbb{A},c{t}_{\mathsf{TVCH}}^2)$. Then, run ${\dot{r}}_{\mathsf{TVCH}}^{\prime 1}\leftarrow$TVCH.Adapt$(({\dot{h}}_{\mathsf{TVCH}}^1,m,{\dot{r}}_{\mathsf{TVCH}}^1),t,m^{\prime },s{k}_{\mathsf{TVCH}})$ and ${\dot{r}}_{\mathsf{TVCH}}^{\prime 2}\leftarrow$TVCH.Adapt
  $(({\dot{h}}_{\mathsf{TVCH}}^2,m^{\prime },{\dot{r}}_{\mathsf{TVCH}}^2),t,m^{\prime },etd)$ where $etd=s{k}_{\mathsf{TVCH}}^2$. Run $c{t}_{\mathsf{TVCH}}^{\prime 2}\leftarrow$ABE.Enc$(\mathbb{A},{\dot{r}}_{\mathsf{TVCH}}^{\prime 2})$. Let ${\dot{r}}_{\mathsf{TPCH}}^{\prime 2}\leftarrow ({\dot{r}}_{\mathsf{TVCH}}^{\prime 1},c{t}_{\mathsf{TVCH}}^{\prime 2})$. Output the new chameleon randomness ${\dot{r}}_{\mathsf{TPCH}}^{\prime 2}$.
• Update$(s{k}_{\mathsf{TPCH}},{\mathsf{mode}}_{\mathsf{R}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t,t^{″},etd)\to {\dot{r}}_{\mathsf{TPCH}}^{″}$: Input a secret key $s{k}_{\mathsf{TPCH}}$, a redaction request ${\mathsf{mode}}_{\mathsf{R}}$, a tuple $({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}})$, two time periods $t,t^{″}$ and an ephemeral trapdoor $etd$. Run ${\dot{r}}_{\mathsf{TVCH}}^2\leftarrow$ABE.Dec$(\mathbb{A},c{t}_{\mathsf{TVCH}}^2)$. Then, run ${\dot{r}}_{\mathsf{TVCH}}^{″1}\leftarrow$TVCH.Update$(s{k}_{\mathsf{TVCH}},({\dot{h}}_{\mathsf{TVCH}}^1,m,{\dot{r}}_{\mathsf{TVCH}}^1),t,t^{″})$ and ${\dot{r}}_{\mathsf{TVCH}}^{″2}\leftarrow$TVCH.Update
  $(etd,({\dot{h}}_{\mathsf{TVCH}}^2,m,{\dot{r}}_{\mathsf{TVCH}}^2),t,t^{″})$ where $etd=s{k}_{\mathsf{TVCH}}^2$. Run $c{t}_{\mathsf{TVCH}}^{″2}\leftarrow$ABE.Enc$(\mathbb{A},c{t}_{\mathsf{TVCH}}^{″2})$. Let ${\dot{r}}_{\mathsf{TPCH}}^{″2}\leftarrow ({\dot{r}}_{\mathsf{TVCH}}^{″1},c{t}_{\mathsf{TVCH}}^{″2})$. Output the new chameleon randomness ${\dot{r}}_{\mathsf{TPCH}}^{″}$.

3.2. Indistinguishability

Definition 4.

Selective Indistinguishability (sIND): Indistinguishability requires that it is computationally difficult to distinguish whether a given randomness corresponds to an output of Hash or Adapt. In comparison with the IND-security in CHET [8], we add an Init phase where the adversary $\mathcal{A}$ declares the target redaction model. We use ${\mathsf{mode}}_{\mathsf{R}}$ to specify the auxiliary hash input ${\mathsf{aux}}_{\mathsf{H}}$. When ${{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{private}”$, TPCH encrypts $etd$ by ABE. When ${{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{public}”$, it uses TPKE instead to encrypt $etd$. The security for sIND between adversary $\mathcal{A}$ and challenger $\mathcal{C}$ is outlined below:

• Init:$\mathcal{A}$ declares the target redaction mode ${{\mathsf{mode}}_{\mathsf{R}}}^{*}$ and attribute set $U^{*}$. We have

  $${\mathsf{aux}}_{\mathsf{H}}^{*}=\left\{\begin{array}{cc}({\mathbb{M}}^{*},{\rho }^{*})\left|\right|t^{*}\hfill & if{{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{private}”\hfill \\ t^{*}\hfill & if{{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{public}”\hfill \end{array}\right.$$
• Setup: $\mathcal{C}$ runsSetup$(1^{\lambda },U^{*})$ and returns $(mp{k}_{\mathsf{TPCH}}^{*},ms{k}_{\mathsf{TPCH}}^{*})$ to $\mathcal{A}$.
  Query Phase: $\mathcal{C}$ picks random $b\in \left\{0,1\right\}$. In addition, $\mathcal{A}$ issues the following queries to $\mathcal{C}$.

  -

  ${\mathcal{O}}_{\mathsf{KeyGen}}\left(S\right)$: ${{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{private}”$, $\mathcal{A}$ can query the decryption key oracle of ABE previously mentioned in ${\mathrm{Exp}}_{\mathcal{A},\mathsf{ABE}}^{\mathsf{sIND}-\mathsf{CPA}}$.

  -

  ${\mathcal{O}}_{{\mathsf{Dec}}_{\mathsf{TPKE}}}\left(c{t}_{\mathsf{TPKE}}\right)$: If ${{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{public}”$, $\mathcal{A}$ can issue a query on the TPKE ciphertext $c{t}_{\mathsf{TPKE}}$ to this oracle during the pre-processing phase. $\mathcal{A}$ is allowed to query in time at most $t_p$ in the pre-processing phase and time at most $t_o$ in the subsequent online phase. To respond, $\mathcal{C}$ runs $M\leftarrow$FDec$(s{k}_{\mathsf{TPKE}},ct)$ and returns M to $\mathcal{A}$. One restriction should apply: the challenged ciphertext should not be queried.

  -

  ${\mathcal{O}}_{\mathsf{HashOrAdapt}}((m,m^{\prime }),{{\mathsf{mode}}_{\mathsf{R}}}^{*},{\mathsf{aux}}_{\mathsf{H}}^{*}):$ $\mathcal{A}$ issues a hash or adapt query on two messages $m,m^{\prime }\in \mathcal{M}$ ($\mathcal{M}$ is the message space), redaction request ${{\mathsf{mode}}_{\mathsf{R}}}^{*}$ and auxiliary hash input ${\mathsf{aux}}_{\mathsf{H}}^{*}$. $\mathcal{C}$ runs $(({\dot{h}}_0,{\dot{r}}_0),{etd}_0)\leftarrow$Hash$(p{k}_{\mathsf{TPCH}}^{*},{{\mathsf{mode}}_{\mathsf{R}}}^{*},{\mathsf{aux}}_{\mathsf{H}}^{*},m^{\prime })$, $(({\dot{h}}_1,{\dot{r}}_1),{etd}_1)\leftarrow$Hash$(p{k}_{\mathsf{TPCH}}^{*},{{\mathsf{mode}}_{\mathsf{R}}}^{*},{\mathsf{aux}}_{\mathsf{H}}^{*},m)$. Further, $\mathcal{C}$ sets ${\dot{r}}_1\leftarrow$Adapt$(s{k}_{\mathsf{TPCH}},{{\mathsf{mode}}_{\mathsf{R}}}^{*},{\mathsf{aux}}_{\mathsf{H}}^{*},({\dot{h}}_1,m,{\dot{r}}_1),m^{\prime },{etd}_1)$. Then, run Ver on $({\dot{h}}_0,m^{\prime },{\dot{r}}_0)$ and $({\dot{h}}_1,m,$${\dot{r}}_1)$ under time period $t^{*}$, respectively; if either of the outputs is 0, return $\mathsf{\perp }$. Otherwise, it flips a coin $b\stackrel{R}{\leftarrow }\left\{0,1\right\}$ and returns the tuple $({\dot{h}}_b,{\dot{r}}_b)$.

• Guess: $\mathcal{A}$ makes a guess $b^{\prime }$ for b.

The advantage of $\mathcal{A}$ in this game is defined as ${\mathsf{Adv}}_{\mathcal{A},\mathsf{TPCH}}^{\mathsf{sIND}}(1^{\lambda },U^{*})=|\mathsf{Pr}[b=b^{\prime }]-{\displaystyle \frac{1}{2}}|$. A TPCH is indistinguishable if any PPT adversary has at most a negligible advantage as above.

3.3. Other Securities

Definition 5.

Insider Collision Resistance (ICR): Insider collision resistance [8] addresses the requirement that even insiders who possess secret keys for certain attributes cannot find collisions for hashes computed with respect to policies that are not satisfied by their keys. The security definition of ICR between an adversary $\mathcal{A}$ and a challenger $\mathcal{C}$ is clear based according to [7]. For space limitations, we omit the details.

Traceability: Our TPCH’s correctness property achieves traceability by extra addition of a time to evaluate the chameleon tuple during collision finding. It allows to test whether a redaction is executed on a specific time, thus offering the redaction a time-based traceability. This traceability is achieved by allowing anyone to verify the validity of the provided hash tuple and time parameter through the Ver.

4. Construction of Time-Verifiable Policy-Based Chameleon Hash

4.1. Design Goals

Our TPCH solution offers time-based traceability for redactions by allowing anyone to input an additional timer period t into the dominant algorithms of TPCH. We also introduce a new collision-finding algorithm, Update, which computes hash collisions for different times t and $t^{″}$. Unlike the traditional collision-finding algorithm Adapt, Update serves as a confirmation step, preventing the modifier from computing arbitrary collisions by restricting redaction to a specific time. Consequently, each chameleon hash becomes traceable, ensuring that redactions are also traceable. Update serves as a confirmation step for Adapt in that it allows to compute arbitrary collisions for time $t^{″}\ne t$ instead of message $m^{\prime }\ne m$. This allows redaction to be reversed or invalidated if enforcing a global time-based policy for the redaction mechanism. For example, asking all redactions to be confirmed immediately after a given time period $t^{″}$, any non-updated chameleon tuple will hence be invalidated and considered outdated. Our TPCH introduces the notion of public and private redaction:

• Public Redaction: Adopts TPKE to encrypt the one-time private key (i.e., ephemeral trapdoor key) for redaction. TPKE offers IND-CCA security for the ciphertext for a given time period. After that, anyone can obtain this ephemeral private key for redaction.
• Private Redaction: Adopts ABE to encrypt the one-time private key for redaction. Only authorized users with designated attributes can obtain the private key to perform redaction.

4.2. Concrete Design

Let the encoding and decoding methods as encode₁ :$\mathbb{G}\to {\mathbb{Z}}_p^{*}$, encode₂: ${\mathbb{Z}}_p^{*}\to {\mathbb{QR}}_N$, ${\mathrm{encode}}_1^{-1}$: ${\mathbb{Z}}_p^{*}\to \mathbb{G}$, and ${\mathrm{encode}}_2^{-1}$: ${\mathbb{QR}}_N\to {\mathbb{Z}}_p^{*}$. Here, ${\mathbb{QR}}_N$ denotes the set of quadratic residues modulo, which is the input and output space of Enc and SDec, respectively, in the employed TPKE [15]. In this paper, the fast decryption algorithm FDec in TPKE was not used.

• Setup$(1^{\lambda },U)\to (mp{k}_{\mathsf{TPCH}},ms{k}_{\mathsf{TPCH}}):$ The KGC runs $(mp{k}_{\mathsf{ABE}},ms{k}_{\mathsf{ABE}})\leftarrow$ABE.Setup$(1^{\lambda },U)$ and $(p{k}_{\mathsf{TPKE}},s{k}_{\mathsf{TPKE}})\leftarrow$TPKE.Setup$\left(1^{\lambda }\right)$ to initiate ABE and TPKE, respectively. Initiate in the following manner: choose two cyclic groups ${\mathbb{G}}_1,{\mathbb{G}}_T$ with order p and generator g. Let $\widehat{e}:{\mathbb{G}}_1\times {\mathbb{G}}_1\to {\mathbb{G}}_T$ be a bilinear map. Let $H_{\tilde{k}}(·)$ be a $\tilde{k}$-keyed collision-resilient hash. Run NIZK.GenZK to derive $\mathsf{crs}$. Let ${mpk}_{\mathsf{TVCH}}\leftarrow ({\mathbb{G}}_1,{\mathbb{G}}_T,g,p,\widehat{e})$. Output the public parameters $p{k}_{\mathsf{TPCH}}$ and master key $ms{k}_{\mathsf{TPCH}}$ as:

  $$\begin{array}{cc}\hfill & mp{k}_{\mathsf{TPCH}}=(mp{k}_{\mathsf{ABE}},mp{k}_{\mathsf{TVCH}}=({\mathbb{G}}_1,{\mathbb{G}}_T,g,p,H_{\tilde{k}},\widehat{e}),\hfill \\ \hfill & \tilde{k},\mathsf{crs},p{k}_{\mathsf{TPKE}}),ms{k}_{\mathsf{TPCH}}=(ms{k}_{\mathsf{ABE}},s{k}_{\mathsf{TPKE}}).\hfill \end{array}$$

  (1)
• KeyGen$(ms{k}_{\mathsf{TPCH}},S)\to (s{k}_{\mathsf{TPCH}},p{k}_{\mathsf{TPCH}})$: Given an attribute set S, the KGC runs $s{k}_S\leftarrow$ABE.KeyGen$(ms{k}_{\mathsf{ABE}},S)$. Then, KGC picks $\tilde{x}\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$; compute $\tilde{h}\leftarrow g^{\tilde{x}}$. Run ${\pi }_{\tilde{h}}\leftarrow$NIZK.Prove$(\mathsf{crs},(\tilde{x},\tilde{h}=g^{\tilde{x}}))$. Output $p{k}_{\mathsf{TPCH}}=(mp{k}_{\mathsf{ABE}},\tilde{h},{\pi }_{\tilde{h}},p{k}_{\mathsf{TPKE}})$ and $s{k}_{\mathsf{TPCH}}=(\tilde{x},s{k}_S)$.
• Hash$({\mathsf{mode}}_{\mathsf{R}},{\mathsf{aux}}_{\mathsf{H}},m)\to (({\dot{h}}_{\mathsf{TPCH}},{\dot{r}}_{\mathsf{TPCH}}),etd)$: Set the auxiliary input ${\mathsf{aux}}_{\mathsf{H}}$ according to redaction request ${\mathsf{mode}}_{\mathsf{R}}$ as

  $${\mathsf{aux}}_{\mathsf{H}}=\left\{\begin{array}{cc}(\mathbb{M},\rho )\left|\right|t,t\in {\mathbb{Z}}_p\hfill & if{\mathsf{mode}}_{\mathsf{R}}=“\mathsf{private}”\hfill \\ t,t\in {\mathbb{Z}}_p\hfill & if{\mathsf{mode}}_{\mathsf{R}}=“\mathsf{public}”\hfill \end{array}\right.$$
  Next, run NIZK.Verify$(\mathsf{crs},\tilde{h},{\pi }_{\tilde{h}})$. If output 0, return $\mathsf{\perp }$. Check if $\tilde{h}\in {\mathbb{G}}^{*}$. If not, return ⊥. Pick $\tilde{r}\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$ and ephemeral trapdoor $etd\stackrel{R}{\leftarrow }{\mathbb{Z}}_p^{*}$. Generate $\mathsf{h}\leftarrow g^{etd}$ and ${\pi }_{\mathsf{h}}\leftarrow$NIZK.Prove$(\mathsf{crs},(etd,\mathsf{h}=g^{etd}))$. Then, compute

  $$\begin{array}{cc}\hfill & \tilde{a}\leftarrow H_{\tilde{k}}\left(m\right|\left|t\right),\tilde{p}\leftarrow {\tilde{h}}^{\tilde{r}},\hfill \end{array}$$

  (2)

  $$\begin{array}{cc}\hfill & {\pi }_{\tilde{p}}\leftarrow \mathbf{NIZK}.\mathbf{Prove}(\mathsf{crs},(\tilde{r},\tilde{p}={\tilde{h}}^{\tilde{r}})).\hfill \end{array}$$

  (3)
  Proceed differently:
  • If ${\mathsf{mode}}_{\mathsf{R}}$= “private”: Set $M\leftarrow {\mathsf{encode}}_{\mathsf{1}}\left(\tilde{r}\right)$. Run $c{t}_{\mathsf{ABE}}\leftarrow$ABE.Enc$\left(\right(\mathbb{M},\rho ),M)$ and let $ct\leftarrow c{t}_{\mathsf{ABE}}$.
  • If ${\mathsf{mode}}_{\mathsf{R}}$ = “public”: Run $\mathbf{M}\leftarrow {\mathsf{encode}}_{\mathsf{2}}\left(\tilde{r}\right)$. Run $c{t}_{\mathsf{TPKE}}\leftarrow$TPKE.Enc$(p{k}_{\mathsf{TPKE}},\mathbf{M})$ and let $ct\leftarrow c{t}_{\mathsf{TPKE}}$.
  Let

  $$\begin{array}{cc}\hfill & b={(\tilde{p}·{\mathsf{h}}^{\tilde{a}})}^t,\dot{h}=(b,\mathsf{h},{\pi }_{\mathsf{h}}),\dot{r}=(\tilde{p},ct,{\pi }_{\tilde{p}}).\hfill \end{array}$$

  (4)
  The hashing algorithm outputs $(({\dot{h}}_{\mathsf{TPCH}},{\dot{r}}_{\mathsf{TPCH}}),etd)$.
• Ver$(p{k}_{\mathsf{TPCH}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t^{\prime })\to \left(0\mathrm{or}1\right)$: The user runs this algorithm for verification:
  • If $\tilde{p}\notin {\mathbb{G}}^{*}$, or $\mathsf{h}\notin {\mathbb{G}}^{*}$, or $\tilde{p}\ne {\tilde{h}}^{\tilde{r}}$, return ⊥.
  • Check if NIZK.Ver$\left({\pi }_{\tilde{p}}\right)=$NIZK.Ver$\left({\pi }_{\mathsf{h}}\right)=$NIZK.Ver$\left({\pi }_{\tilde{h}}\right)=1$ holds. If no, return ⊥.
  • Check if $b={(\tilde{p}·{\mathsf{h}}^{H_{\tilde{k}}\left(m\right|\left|t\right)})}^t$ holds. If yes, output 1. Otherwise, check if $t^{\prime }\ne t$ and $b={(\tilde{p}·{\mathsf{h}}^{H_{\tilde{k}}\left(m\right||t^{\prime })})}^{t^{\prime }}$. If yes, output 0. Otherwise, output ⊥.
• Adapt$(s{k}_{\mathsf{TPCH}},{\mathsf{mode}}_{\mathsf{R}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t,m^{\prime },etd)\to {\dot{r}}_{\mathsf{TPCH}}^{\prime }$: The modifier runs this algorithm. If $m=m^{\prime }$, return ${\dot{r}}_{\mathsf{TPCH}}$. Otherwise, proceed differently according to the redaction request ${\mathsf{mode}}_{\mathsf{R}}$ as

  -

  ${\mathsf{mode}}_{\mathsf{R}}$= “private”:

  • Run TPCH.Ver$(p{k}_{\mathsf{TPCH}},(\dot{h},m,\dot{r}),t)$. If output 0, return ⊥.
  • Compute $\tilde{a}\leftarrow H_{\tilde{k}}\left(m\right|\left|t\right)$ and ${\tilde{a}}^{\prime }\leftarrow H_{\tilde{k}}(m^{\prime }\left|\right|t)$. If $\tilde{a}={\tilde{a}}^{\prime }$, return $\dot{r}$ directly.
  • Run $M\leftarrow$ABE.Dec$(ct,s{k}_S)$ and $\tilde{r}\leftarrow {\mathsf{encode}}_{\mathsf{1}}^{-\mathsf{1}}\left(M\right)$ to recover the encrypted chameleon randomness $\tilde{r}$.
  • Compute

    $${\tilde{r}}^{\prime }\leftarrow {\displaystyle \frac{\tilde{x}\tilde{r}+\tilde{a}·etd-{\tilde{a}}^{\prime }·etd}{\tilde{x}}}$$

    (5)

    and ${\tilde{p}}^{\prime }\leftarrow {\tilde{h}}^{{\tilde{r}}^{\prime }}$. Run $M^{\prime }\leftarrow$encode₁$\left({\tilde{r}}^{\prime }\right)$ and $c{t}^{\prime }\leftarrow$ABE.Enc$(\mathbb{A},M^{\prime })$ to obtain a new ciphertext $c{t}^{\prime }$. Then, run ${\pi }_{{\tilde{p}}^{\prime }}\leftarrow$NIZK.Prove$(\mathsf{crs},({\tilde{r}}^{\prime },{\tilde{p}}^{\prime }={\tilde{h}}^{{\tilde{r}}^{\prime }}))$ to obtain ${\pi }_{{\tilde{p}}^{\prime }}$. Let ${\dot{r}}^{\prime }=({\tilde{p}}^{\prime },c{t}^{\prime },{\pi }_{{\tilde{p}}^{\prime }})$.

  -

  ${\mathsf{mode}}_{\mathsf{R}}$= “public”:

  • Run Ver$(p{k}_{\mathsf{TPCH}},(\dot{h},m,\dot{r}),t)$. Output ⊥ if the output is not 1. Otherwise, compute $\tilde{a}\leftarrow H_{\tilde{k}}\left(m\right|\left|t\right),{\tilde{a}}^{\prime }\leftarrow H_{\tilde{k}}(m^{\prime }\left|\right|t)$. If $\tilde{a}={\tilde{a}}^{\prime }$, return ${\dot{r}}_{\mathsf{TPCH}}$ directly. Otherwise, run $\mathbf{M}\leftarrow \mathbf{TPKE}.\mathbf{SDec}\left(ct\right)$ to obtain $\mathbf{M}$. If $\mathbf{SDec}$ outputs ⊥, return ⊥. Otherwise, run $\tilde{r}\leftarrow$${\mathrm{encode}}_2^{-1}$$\left(\mathbf{M}\right)$ to obtain $\tilde{r}\in {\mathbb{Z}}_p^{*}$.
  • Compute ${\tilde{r}}^{\prime }\leftarrow {\displaystyle \frac{\tilde{x}\tilde{r}+\tilde{a}·etd-{\tilde{a}}^{\prime }·etd}{\tilde{x}}}$ and ${\tilde{p}}^{\prime }\leftarrow {\tilde{h}}^{{\tilde{r}}^{\prime }}$.
  • Run ${\mathbf{M}}^{\prime }\leftarrow$encode₂$\left({\tilde{r}}^{\prime }\right)$ and $c{t}^{\prime }\leftarrow$TPKE.Enc$\left({\mathbf{M}}^{\prime }\right)$ to obtain the new ciphertext $c{t}^{\prime }$. Run ${\pi }_{{\tilde{p}}^{\prime }}\leftarrow$NIZK.Prove$(\mathsf{crs},({\tilde{r}}^{\prime },{\tilde{p}}^{\prime }={\tilde{h}}^{{\tilde{r}}^{\prime }}))$ to obtain ${\pi }_{{\tilde{p}}^{\prime }}$. Let ${\dot{r}}^{\prime }=({\tilde{p}}^{\prime },c{t}^{\prime },{\pi }_{{\tilde{p}}^{\prime }})$.

  The adaption algorithm outputs a new randomness set, ${\dot{r}}^{\prime }=({\tilde{p}}^{\prime },c{t}^{\prime },{\pi }_{{\tilde{p}}^{\prime }})$. Note that we sometimes ignore the subscript in long equations for brevity, i.e., $\dot{r}$ for ${\dot{r}}_{\mathsf{TPCH}}$. It should be clear based on the context.,
• Update$(s{k}_{\mathsf{TPCH}},{\mathsf{mode}}_{\mathsf{R}},({\dot{h}}_{\mathsf{TPCH}},m,{\dot{r}}_{\mathsf{TPCH}}),t,t^{″},etd)\to {\dot{r}}_{\mathsf{TPCH}}^{″}$: The modifier runs this algorithm for update. If $t^{\prime }=t$, return ${\dot{r}}_{\mathsf{TPCH}}$. Else, proceed:

  -

  ${\mathsf{mode}}_{\mathsf{R}}$= “private”:

  • Run TVCH.Ver$((\dot{h},m,\dot{r}),t)$. If output 0 or ⊥, return ⊥. Then, compute $\tilde{a}\leftarrow H_{\tilde{k}}\left(m\right|\left|t\right),{\tilde{a}}^{″}\leftarrow H_{\tilde{k}}\left(m\right||t^{\prime })$. If $\tilde{a}={\tilde{a}}^{″}$, return $\dot{r}$.
  • Run $M\leftarrow$ABE.Dec$(ct,s{k}_S)$ and $\tilde{r}\leftarrow {\mathsf{encode}}_{\mathsf{1}}^{-\mathsf{1}}\left(M\right)$ to recover the encrypted chameleon randomness $\tilde{r}$.
  • Compute

    $${\tilde{r}}^{″}\leftarrow {\displaystyle \frac{t(\tilde{x}\tilde{r}+etd·\tilde{a})-etd·{\tilde{a}}^{″}{t}^{″}}{\tilde{x}{t}^{″}}}$$

    (6)

    and ${\tilde{p}}^{″}\leftarrow {\tilde{h}}^{{\tilde{r}}^{″}}$.
  • Run $M^{″}\leftarrow$encode₁$\left({\tilde{r}}^{″}\right)$ and $c{t}^{″}\leftarrow$ABE.Enc$(\mathbb{A},M^{″})$ to obtain a new ciphertext $c{t}^{″}$. Then, run NIZK.Prove$(\mathsf{crs},{\tilde{r}}^{″},{\tilde{p}}^{″}={\tilde{h}}^{{\tilde{r}}^{″}})$ to obtain ${\pi }_{{\tilde{p}}^{″}}$, respectively. Let ${\dot{r}}^{″}=({\tilde{p}}^{″},c{t}^{″},{\pi }_{{\tilde{p}}^{″}})$.

  -

  ${\mathsf{mode}}_{\mathsf{R}}$= “public”:

  • Run Ver$(p{k}_{\mathsf{TPCH}},(\dot{h},m,\dot{r}),t)$. If output 0 or ⊥, return ⊥. Else, compute $\tilde{a}\leftarrow H_{\tilde{k}}\left(m\right|\left|t\right),{\tilde{a}}^{″}\leftarrow H_{\tilde{k}}(m^{\prime }\left|\right|t)$. If $\tilde{a}={\tilde{a}}^{″}$, return $\dot{r}$.
  • Run TPKE.SDec$(p{k}_{\mathsf{TPKE}},ct)$ to obtain $\mathbf{M}$. If $\mathbf{SDec}$ outputs ⊥, return ⊥. Otherwise, run ${\mathsf{encode}}_{\mathsf{2}}^{-\mathsf{1}}\left(\mathbf{M}\right)$ to obtain $\tilde{r}\in {\mathbb{Z}}_p^{*}$.
  • Compute ${\tilde{r}}^{″}\leftarrow {\displaystyle \frac{t(\tilde{x}\tilde{r}+etd·\tilde{a})-etd·{\tilde{a}}^{″}{t}^{″}}{\tilde{x}{t}^{″}}},{\tilde{p}}^{″}\leftarrow {\tilde{h}}^{{\tilde{r}}^{″}}$.
  • Run ${\mathbf{M}}^{″}\leftarrow$encode₂$\left({\tilde{r}}^{″}\right)$ and $c{t}^{″}\leftarrow$TPKE.Enc$\left({\mathbf{M}}^{″}\right)$ to obtain the new ciphertext $c{t}^{″}$. Run $\mathbf{NIZK}.\mathbf{Prove}(\mathsf{crs},{\tilde{r}}^{″},{\tilde{p}}^{″}={\tilde{h}}^{{\tilde{r}}^{″}})$ to obtain ${\pi }_{{\tilde{p}}^{″}}$. Let ${\dot{r}}^{″}=({\tilde{p}}^{″},c{t}^{″},{\pi }_{{\tilde{p}}^{″}})$.

  This update algorithm outputs ${\dot{r}}^{″}=({\tilde{p}}^{″},c{t}^{″},{\pi }_{{\tilde{p}}^{″}})$.

4.3. Instantiations

For the instantiation of NIZK in both NIZK and TPKE for our TPCH, we refer to [8]. For implementing the concrete TPKE with IND-CCA security, refer to [15]. Specifically, ${\mathbb{QR}}_N$ is the cyclic group of quadratic residues for instantiating TPKE. $\mathbf{M},{\mathbf{M}}^{\prime },{\mathbf{M}}^{″}$ are elements in ${\mathbb{QR}}_N$. Detailed and efficient ABE constructions for our scheme can be found in any ElGamal-type ABE [23].

4.4. Security Analysis of TPCH

Correctness. The correctness of Equations (5) and (6) is shown below:

$$\begin{array}{cccc}\hfill b& ={[{\tilde{p}}^{\prime }·{\mathsf{h}}^{{\tilde{a}}^{\prime }}]}^t\hfill & \hfill & b={[{\tilde{p}}^{″}·{\mathsf{h}}^{{\tilde{a}}^{″}}]}^{t^{″}}\hfill \\ \hfill & ={[{\left(g^{\tilde{x}}\right)}^{{\tilde{r}}^{\prime }}·{\left(g^{etd}\right)}^{{\tilde{a}}^{\prime }}]}^t\hfill & \hfill & ={[{\left(g^{\tilde{x}}\right)}^{{\tilde{r}}^{″}}·{\left(g^{etd}\right)}^{{\tilde{a}}^{″}}]}^{t^{″}}\hfill \\ \hfill & ={[{\left(g^{\tilde{x}}\right)}^{{\displaystyle \frac{\tilde{x}\tilde{r}+etd·\tilde{a}-etd·{\tilde{a}}^{\prime }}{\tilde{x}}}}·{\left(g^{etd}\right)}^{{\tilde{a}}^{\prime }}]}^t\hfill & \hfill & ={[{\left(g^{\tilde{x}}\right)}^{\left({\displaystyle \frac{t(\tilde{x}\tilde{r}+etd·\tilde{a})-etd·{\tilde{a}}^{″}{t}^{″}}{\tilde{x}{t}^{″}}}\right)}·{\left(g^{etd}\right)}^{{\tilde{a}}^{″}}]}^{t^{″}}\hfill \\ \hfill & ={[{\left(g\right)}^{\tilde{x}\tilde{r}+etd·\tilde{a}-etd·{\tilde{a}}^{\prime }}·{\left(g^{etd}\right)}^{{\tilde{a}}^{\prime }}]}^t\hfill & \hfill & ={\left(g\right)}^{\left[t(\tilde{x}\tilde{r}+etd·\tilde{a})-etd·{\tilde{a}}^{″}{t}^{″}\right]}·{\left(g^{etd}\right)}^{{\tilde{a}}^{″}{t}^{″}}\hfill \\ \hfill & ={[{\left(g\right)}^{\tilde{x}\tilde{r}+etd·\tilde{a}}·{\left(g^{etd}\right)}^{({\tilde{a}}^{\prime }-{\tilde{a}}^{\prime })}]}^t\hfill & \hfill & ={\left(g\right)}^{[t(\tilde{x}\tilde{r}+etd·\tilde{a})]}·{\left(g^{etd}\right)}^{{\tilde{a}}^{″}{t}^{″}-{\tilde{a}}^{″}{t}^{″}}\hfill \\ \hfill & ={[{\left(g^{\tilde{x}}\right)}^{\tilde{r}}·{\left(g^{etd}\right)}^{\tilde{a}}]}^t\hfill & \hfill & ={[{\left(g^{\tilde{x}}\right)}^{\tilde{r}}·{\left(g^{etd}\right)}^{\tilde{a}}]}^t\hfill \\ \hfill & ={[\tilde{p}·{\mathsf{h}}^{\tilde{a}}]}^t\hfill & \hfill & ={[\tilde{p}·{\mathsf{h}}^{\tilde{a}}]}^t\hfill \\ \hfill & =b\hfill & \hfill & =b\hfill \end{array}$$

Theorem 1.

Assume the construction 2 of the $\mathsf{CHET}$ system in [8] is strongly indistinguishable; our TPCH scheme is selectively indistinguishable with respect to Definition 4.

Proof. 

Denote Construction 2 of the $\mathsf{CHET}$ system in [8] and our TPCH system as ${\Sigma }_{\mathsf{CHET}}$ and ${\Sigma }_{\mathsf{TPCH}}$, respectively. Suppose there exists a PPT adversary $\mathcal{A}$ that has a non-negligible advantage in selectively breaking ${\Sigma }_{\mathsf{TPCH}}$. We can build a PPT simulator algorithm $\mathcal{B}$ that has a non-negligible advantage in selectively breaking our ${\Sigma }_{\mathsf{CHET}}$. The reduction is clear according to [6]. We only give a part. For simplicity, we set ${{\mathsf{mode}}_{\mathsf{R}}}^{*}=“\mathsf{private}”$. During Init, $\mathcal{B}$ declares and sends $\mathcal{A}$ the challenge hash mode ${\mathsf{mode}}_{\mathsf{H}}^{*}=“\mathsf{private}”$. During Setup, the challenger of ${\Sigma }_{\mathsf{CHET}}$ picks a multiplicative group $\mathbb{G}$ of order p and generator g. Choose $\tilde{k}$ as the the key of hash function $H_{\tilde{k}}(·)$. Run NIZK.Gen$\left(1^{\lambda }\right)$ to derive $\mathsf{crs}$. It returns $mp{k}_{\mathsf{CHET}}=((\mathbb{G},g,p),\tilde{k},\mathsf{crs})$ to $\mathcal{A}$. On receiving $mp{k}_{\mathsf{CHET}}$, $\mathcal{A}$ further completes the TPCH.Setup by running ABE.Setup$\left(1^{\lambda }\right)$ and TPKE.Setup$\left(1^{\lambda }\right)$ to derive $(mp{k}_{\mathsf{ABE}},ms{k}_{\mathsf{ABE}})$ and $(p{k}_{\mathsf{TPKE}},s{k}_{\mathsf{TPKE}})$, respectively. $\mathcal{A}$ sends $mp{k}_{\mathsf{TPCH}}=(mp{k}_{\mathsf{CHET}},mp{k}_{\mathsf{ABE}},p{k}_{\mathsf{TPKE}})$ to $\mathcal{B}$ and keeps $(ms{k}_{\mathsf{ABE}},s{k}_{\mathsf{TPKE}})$ secret. During the Query Phase, for ${\mathcal{O}}_{\mathsf{HashOrAdapt}}$, $\mathcal{A}$ internally uses the HashOrAdapt oracle provided by the challenger of ${\Sigma }_{\mathsf{CHET}}$ to obtain $({\dot{h}}_{\mathsf{CHET}},{\dot{r}}_{\mathsf{CHET}},etd)$. Then, it runs ABE to generate and return $({\dot{h}}_b,{\dot{r}}_b)$. During Guess, $\mathcal{A}$ relays the output of $\mathcal{B}$ as his guess. Now, we observe that all oracles are simulated perfectly, and $\mathcal{A}$ wins with the same probability as $\mathcal{B}$ wins. □

Theorem 2.

Our TPCH is insider collision resistant if the underlying ABE is secure according to Definition 3, and the $(t_e,t_{fd},t_{sd})$-$\mathsf{TPKE}$ [15] is $(t_p,t_o)$-IND-CCA (here, $t_p$ and $t_o$ denote the maximum time allowed for pre-processing and online computing [15]) secure according to Definition 2, and $\mathsf{CHET}$ [8] is private collision-resilient.

Proof. 

Our insider collision resistance of TPCH is based on the insider collision resistance of the underlying $\mathsf{CHET}$ and the security of the underlying $\mathsf{ABE}$ and $\mathsf{TPKE}$. Specifically, we can construct a sequence of games which is straightforward according to the Proof of Theorem 2 in [8]. We omit the details. □

5. Performance Evaluations

Table 2. Complexity comparisons of PCH works.

Reference	Scheme	Properties				Costs (User-Side)
		Revoc	Fine-Grained	On/Off	Delegation	Hash	Adapt
DSS+19 [6]	FAME [24] + RSA-based CH [8]	✕	✓	✕	✕	$\mathcal{O}(\ell ·n)T_e$	$\mathcal{O}(k+n)T_e$
TLL+20 [9]	FAME [24] + DL-based CH [8]	✓	✓	✕	✕	$\mathcal{O}(N+k)T_e$	$\mathcal{O}\left(k\right)T_e$
GWY+21 [26]	AB-KEM [27] (from CP-ABE [25]) + RSA-based CH [8]	✕	✓	✕	✕	$\mathcal{O}\left(1\right)T_e$	$\mathcal{O}\left(1\right)T_e$
XNM+21 [7]	RABE (from FAME [24]) + RSA-based CH [8]	✓	✓	✕	✕	$\mathcal{O}(\ell )T_e$	$\mathcal{O}(\ell )(T_e+T_p)$
XHY+22 [12]	PCH from the Fujisaki–Okamoto transformation	✕	✓	✕	✕	$\mathcal{O}(\ell ·n)T_e$	$\mathcal{O}(k+n)T_e$
Our TPCH	CP-ABE [25] + DL-based CH [8]	✕	✓	✕	✕	$\mathcal{O}(\ell )T_e$	$\mathcal{O}(\ell )(T_e+T_p)$

“Revoc” means the ability to revoke writing privilege or hash. “Fine-grained” means writing privilege, or the target re-written content is split into several parties. “On&off” means supporting pre-computation or outsourced computation. “Delegation” means supporting ciphertext delegation. $T_e$ means exponentiation operation. $T_p$ means pairing operation. Operations like multiplication and inversion are not measured. $\mathbb{M}$ means a matrix with ℓ rows and n columns. k means the size of an attribute set associated with a user. N means the total number of users in the system.

shows a comparison of PCH. The employed ABEs are derived from either FAME [24] or CP-ABE [25], and the employed CHs are all from $\mathsf{CHET}$ [8]. For quantitative evaluations, we implemented our scheme in Java using the JPBC library on a desktop equipped with an i5-11400H CPU running at 2.70 GHz and 16 GB of RAM. For pairings, we used the MNT224 curve, which is the best Type-III curve in PBC for achieving a 96-bit security level. We evaluated our scheme using a policy and attribute set with fixed sizes of 50. We focus on testing the costs of the dominant algorithms, Hash, Adapt, and Update. Since the setup and key generation algorithms, Setup and KeyGen, are one-time costs, we did not evaluate their performance. We apply the CP-ABE from [25] and TPKE from [15] to implement our TPCH. Assume all group operations are performed in a specific group for ease of analysis.

As shown in Figure 2, compared to the base scheme [6], our hashing algorithm Hash is more efficient, scaling more slowly with the number of attributes (ranging from 0 to 250). Specifically, with 150 attributes, our scheme takes 40 ms, while the DSS+19 scheme [6] takes 82 ms for hashing. As shown in Figure 3, our adaptation algorithm Adapt is less efficient than that of [6], scaling faster with the number of attributes (ranging from 0 to 100). Specifically, with 100 attributes, our scheme takes 290 ms, while the DSS+19 scheme [6] takes 142 ms for hashing.

The function and performance of the Update algorithm are similar to those of Adapt. We varied the size of access policies and the number of execution rounds to evaluate its performance in both public and private redaction. As shown in Figure 4, when the size of policies ranges from 1 to 50, our Update algorithm exhibits linear costs relative to the size of policies for private redaction while incurring small costs for public redaction. Specifically, with 50 attributes, it takes 28 ms for public redaction and 295 ms for private redaction. Due to the independence of access policies, our private redaction shows constant costs, which are scalable for extensive implementation. Figure 5 shows that the same trend applies to its performance under an increasing number of execution rounds. Fixing the number of attributes at 20, for 500 execution rounds, it takes 4 s for public redaction and 105 s for private redaction. Due to limited group computations, private redaction is far more efficient and scalable than ABE-based public redaction.

In summary, our TPCH demonstrates efficient performance in public redaction, while its performance in private redaction is heavily influenced by the number of attributes, the size of policies, and the number of execution rounds. This highlights the performance advantages of adopting TPKE for blockchain redaction.

6. Conclusions

To address the accumulation and distribution of unwanted content in blockchains, we follow the idea of redactable blockchains proposed by Ateniese et al. in EuroS&P 2017. In this paper, we propose a time-verifiable, policy-based chameleon hash that allows for the efficient updating of chameleon hashes. Our proposed scheme enables the traceability of redaction time and performs comparably to other schemes. Our experimental and theoretical analyses demonstrate the feasibility of our proposal for practical use. Specifically, our work is scalable and efficient for public redaction, yielding small, sub-linear costs with increasing execution rounds, making it favorable for extensive executions in redactable blockchains. However, our work still has a few inefficiencies in design, such as the performance deficiencies of ABE-based private redaction, which are impacted by various factors and the use of extensive cryptographic primitives. We aim to improve this design in future work by leveraging a lightweight cryptographic framework, such as on/offline ABE, ABE with concise design and constant ciphertexts, and server-aided solutions. These measures will help reduce the heavy loads incurred by existing ABEs.