A Deadlock-Free Deterministic–Adaptive Hybrid Routing Algorithm for Efficient Network-on-Chip Communication
Abstract
1. Introduction
- At the packet injection stage, all deterministic information is calculated, including the positional relationship of the source–destination nodes and hops in both horizontal and vertical directions. The hops and encoded positional relationship (defined as routing direction) are recorded in the head flit of the packet. This step is required only once.
- The output port does not need to be repeatedly calculated during the packet forwarding and the routing calculation unit can be removed. A unique output port can be identified at each hop by decoding the critical information and assessing the free virtual channels (VCs) of alternative directions. The corresponding hops are updated with the packet forwarding. The DAHR algorithm is a combination of deterministic information (directions and hops) and adaptive information (available cache resources). The routing scheme achieves improved average packet latency and saturation throughput without hardware overhead increasing.
2. Related Works
3. Proposed Deterministic–Adaptive Hybrid Routing Algorithm
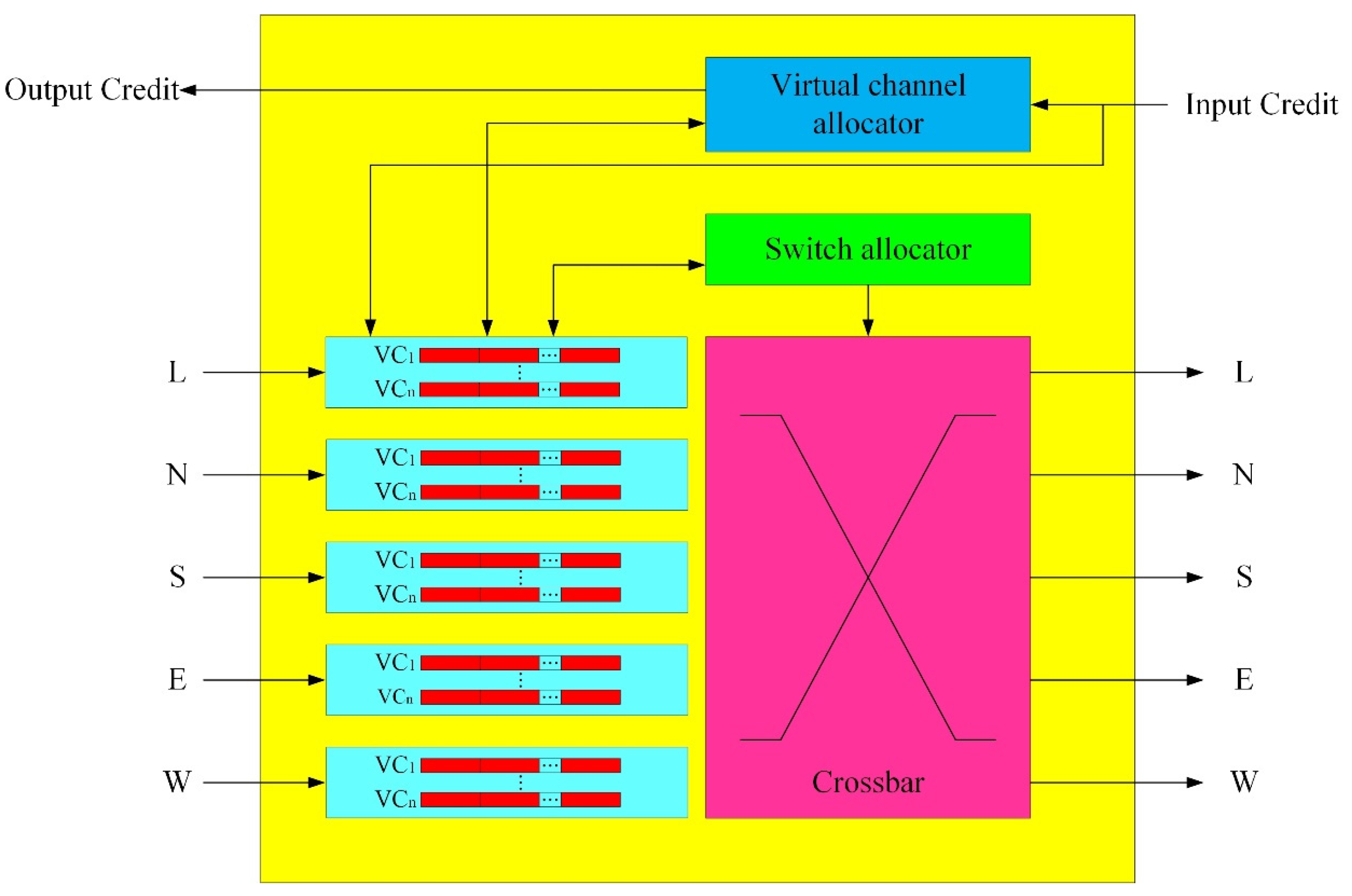
3.1. Working Mechanism of DAHR
3.2. Packet Injection Scheme
3.3. DAHR Algorithm
| Algorithm 1 DAHR Algorithm |
| /* P presents the packet from the upstream router; N, S, W, E and L present the output port; OP presents the output packet */ Input: P carried with RD, X_hop and Y_hop; Output: OP carried with RD and updated X_hop or updated Y_hop; 1: if (X_hop = 0 & Y_hop = 0) //the current node was the destination node 2: L←P; 3: else if (X_hop = 0 &Y_hop ≠ 0) //the current node and the destination node are in the same column 4: { if (RD_Y = 0) 5: N←P; 6: else 7: S←P; } 8: else if (X_hop ≠ 0 &Y_hop = 0) //the current node and the destination node are in the same row 9: { if (RD_X = 0) 10: E←P; 11: else 12: W←P; } 13: else //X_hop ≠ 0 &Y_hop ≠ 0. The current node and destination node are neither in the same row nor the same column 14: { 15: if ({ RD_X, RD_Y} = 00) 16: { 17: if (E_free_VCs > N_free_VCs) 18: E←P; 19: else 20: N←P; 21: } 22: else if ({ RD_X, RD _Y} = 10) 23: { 24: if (N_free_VCs > W_free_VCs) 25: N←P; 26: else 27: W ← P; 28: } 29: else if ({RD _X, RD _Y} = 11) 30: { 31: if (W_free_VCs > S_free_VCs) 32: W←P; 33: else 34: S←P; 35: } 36: else 37: { 38: if (S_free_VCs > E_free_VCs) 39: S←P; 40: else 41: E←P; 42: } 43: update X_hop or Y_hop of P //If the packet is output along X direction, update X_hop in the head flit (X_hop = X_hop-1). If the packet is output along Y direction, update Y_hop in the head flit(Y_hop = Y_hop-1). 44: OP←P |
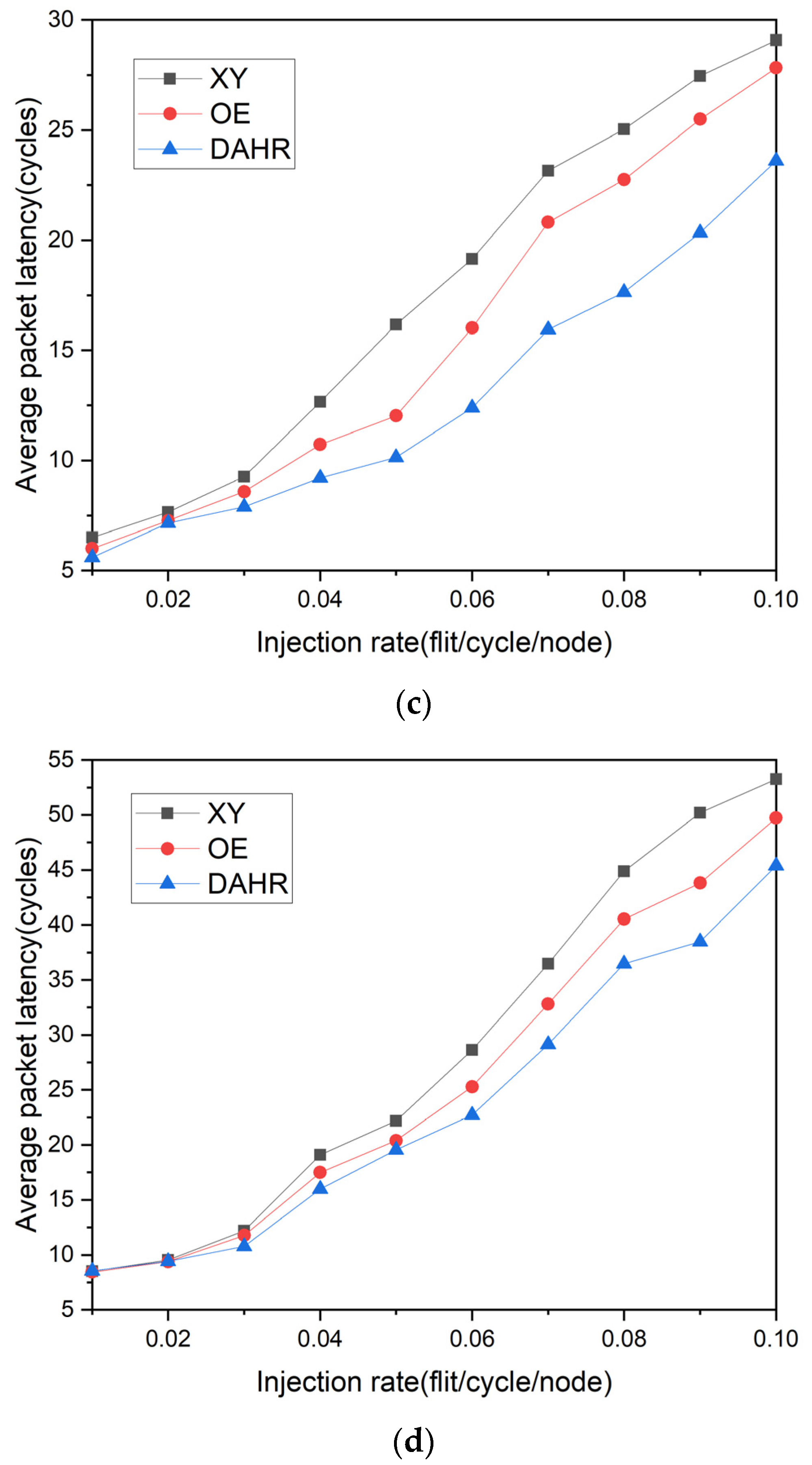
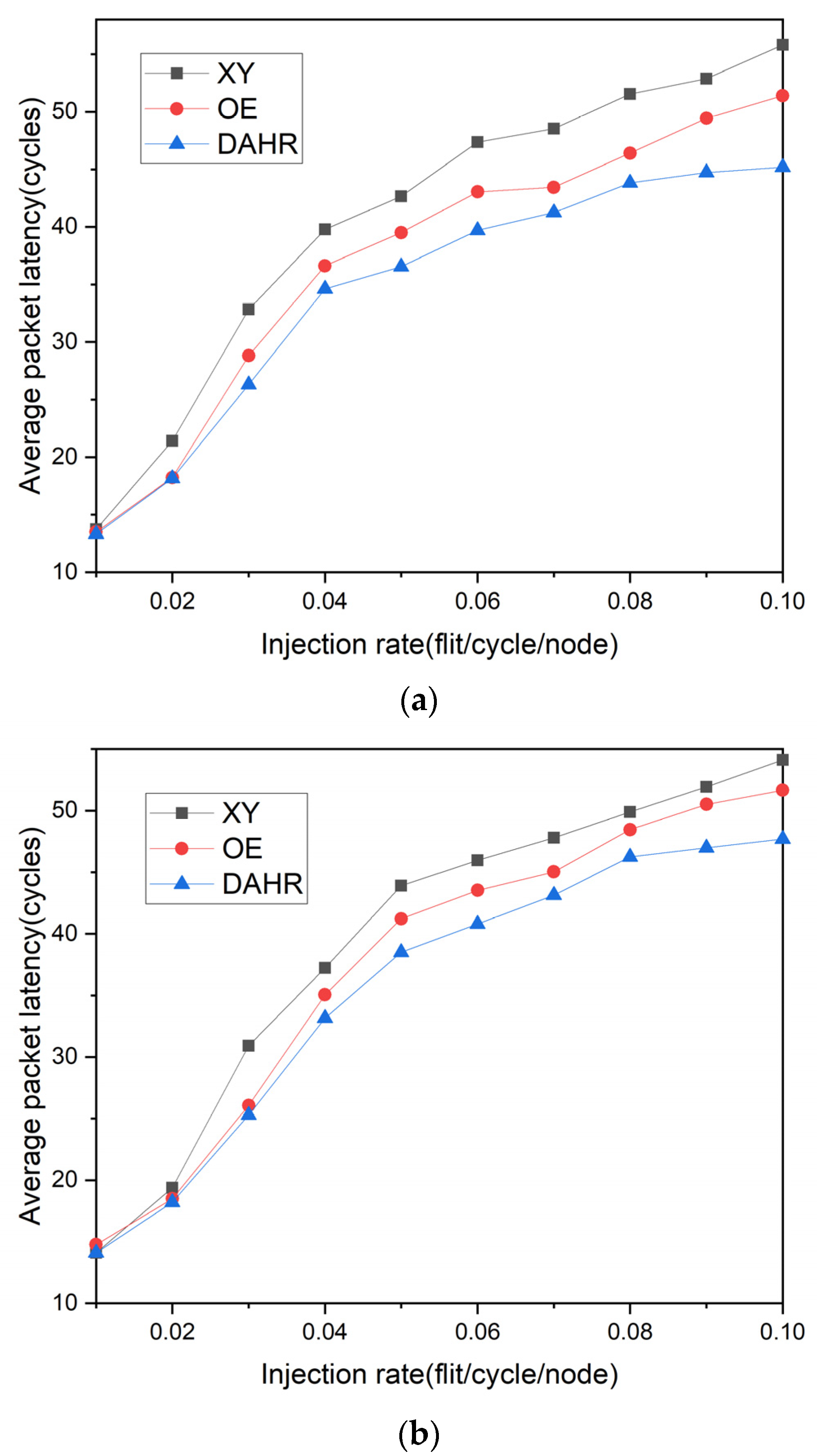
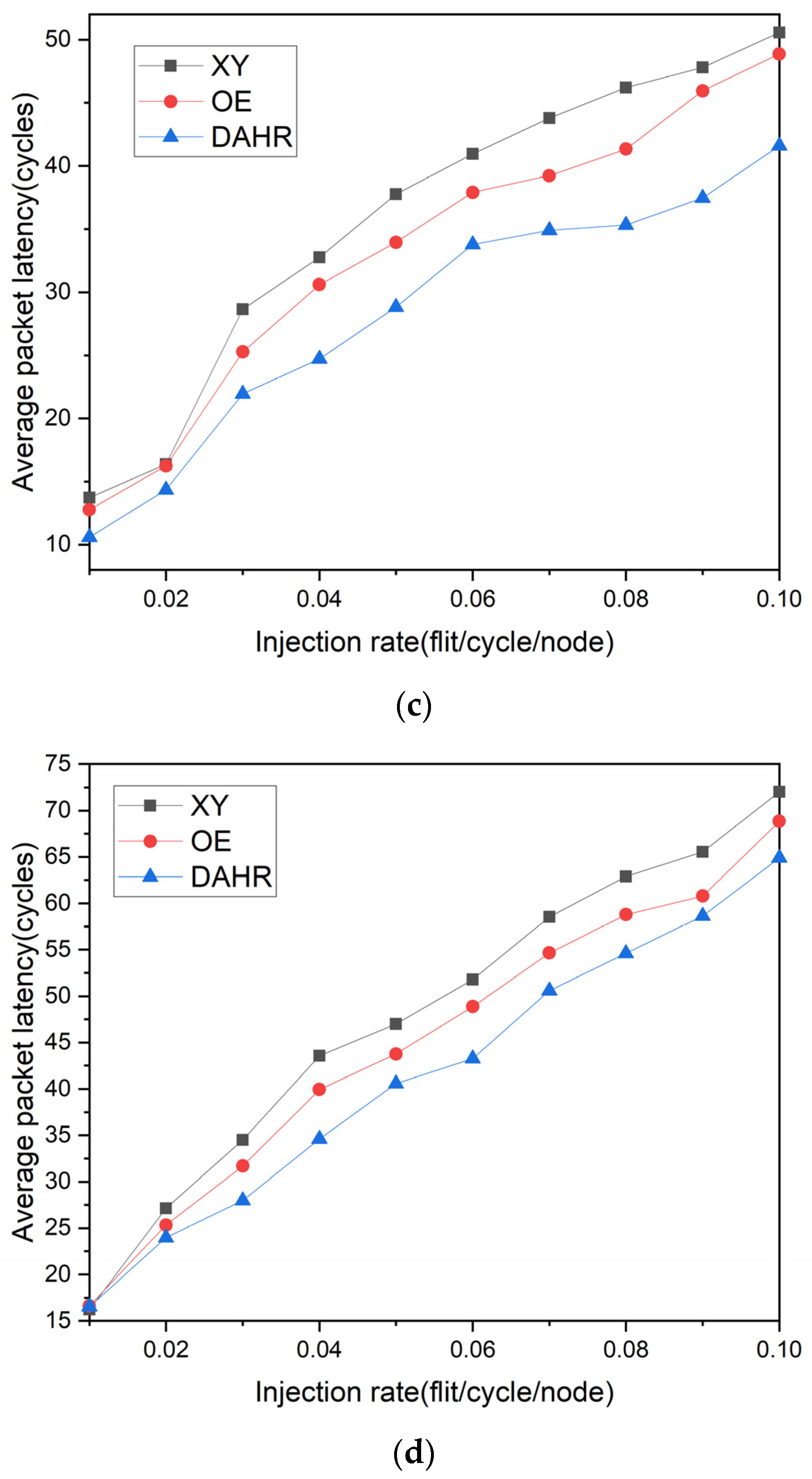
4. Simulation Results and Discussion
4.1. Simulation Settings
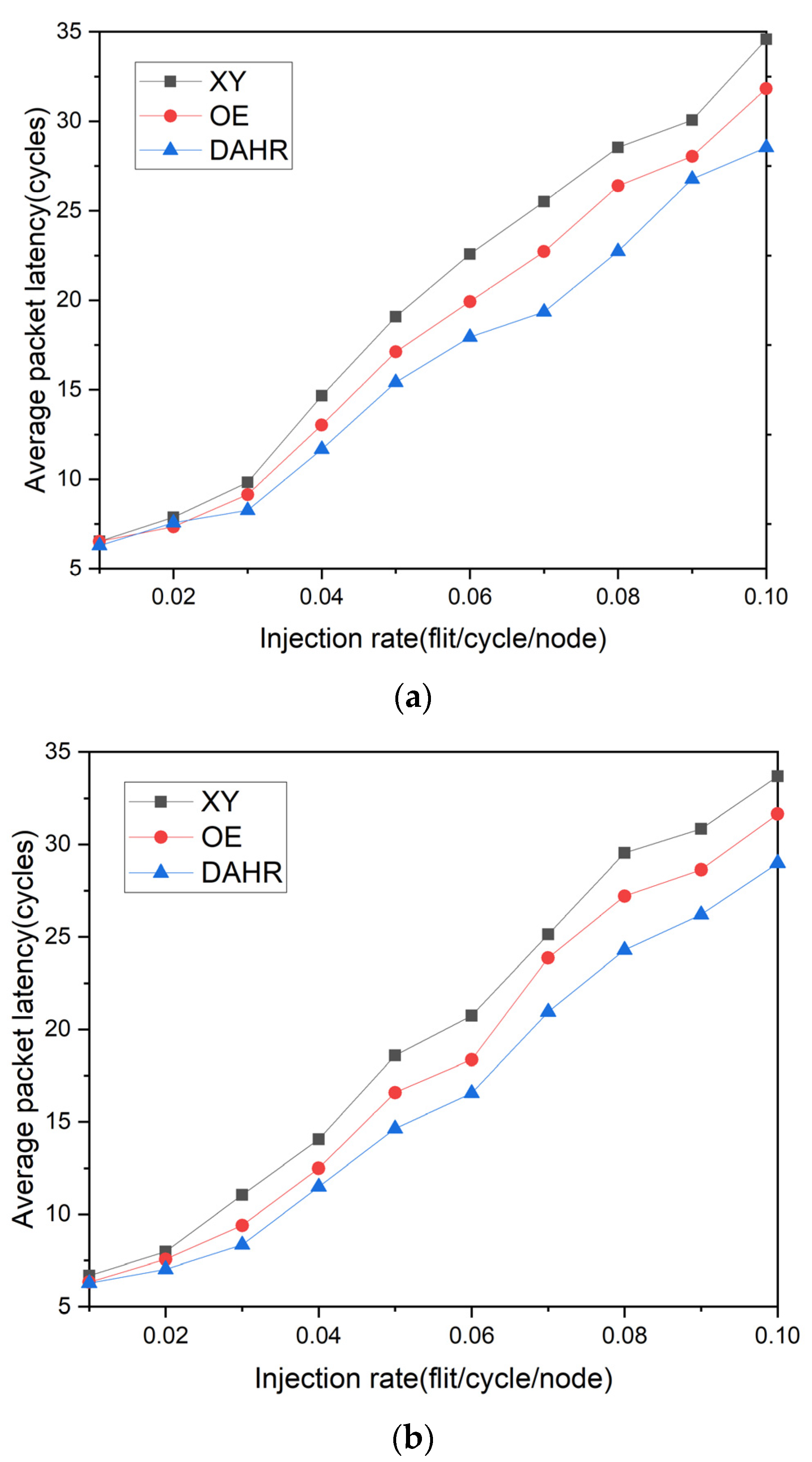
4.2. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ouyang, Y.; Zhang, T.; Li, J.; Liang, H. Fault-tolerant routing for reliable packet transmission in on-chip networks. Microelectron. J. 2024, 153, 106425. [Google Scholar] [CrossRef]
- Xu, C.; Shi, X.; Yang, H.; Wang, Y. 3D network-on-chip data acquisition system mapping based on reinforcement learning and improved attention mechanism. Microelectron. J. 2024, 151, 106323. [Google Scholar] [CrossRef]
- Niu, X.; Li, H.; Liu, F. A Loss-aware Continuous Hopfield Neural Network (CHNN)-based Mapping Algorithm in Optical Network-on-Chip (ONoC). In Proceedings of the 2022 20th International Conference on Optical Communications and Networks (ICOCN), Shenzhen, China, 12–15 August 2022; pp. 1–5. [Google Scholar]
- Balakrishnan, M.T.; Venkatesh, T.G.; Bhaskar, A.V. Design and implementation of congestion aware router for network-on-chip. Integration 2023, 88, 43–57. [Google Scholar] [CrossRef]
- Kaur, S.P.; Ghose, M.; Pathak, A.; Patole, R. A Survey on Mapping and Scheduling Techniques for 3D Network-on-chip. J. Syst. Architect. 2024, 147, 103064. [Google Scholar] [CrossRef]
- Papaphilippou, P.; Chu, T.V. Efficient Deadlock Avoidance for 2-D Mesh NoCs That Use OQ or VOQ Routers. IEEE T. Comput. 2024, 73, 1414–1426. [Google Scholar] [CrossRef]
- Gulzari, U.A.; Salcic, Z.; Farooq, W.; Anjum, S.; Khan, S.; Sajid, M.; Torres, F.S. Comparative analysis of 2D mesh topologies with additional communication links for on-chip networks. Compu. Netw. 2024, 241, 110193. [Google Scholar] [CrossRef]
- Kiasari, A.E.; Jantsch, A.; Lu, Z. A Heuristic Framework for Designing and Exploring Deterministic Routing Algorithm for NoCs. In Routing Algorithms in Networks-on-Chip; Palesi, M., Daneshtalab, M., Eds.; Springer: New York, NY, USA, 2013; pp. 21–39. [Google Scholar]
- Samman, F.A.; Hollstein, T.; Glesner, M. Runtime contention and bandwidth-aware adaptive routing selection strategies for networks-on-chip. IEEE T. Parallel Distrib. 2013, 24, 1411–1421. [Google Scholar] [CrossRef]
- Misbah, M.; Roohie, N.M.; Najeeb-ud-din, H. PAAD (Partially adaptive and deterministic routing): A deadlock free congestion aware hybrid routing for 2D mesh network-on-chips. Microprocess. Microsyst. 2022, 92, 104551. [Google Scholar]
- Zhou, X.; Liu, L.; Zhu, Z.; Zhou, D. A Routing Aggregation for Load Balancing Network-on-Chip. J. Circuit. Syst. Comp. 2015, 24, 1550137. [Google Scholar] [CrossRef]
- Ma, S.; Jerger, N.E.; Wang, Z.; Lai, M.; Huang, L. Holistic Routing Algorithm Design to Support Workload Consolidation in NoCs. IEEE T. Comput. 2014, 63, 529–542. [Google Scholar]
- Dally, W.J.; Seitz, G.L. Deadlock-Free Message Routing in Multiprocessor Interconnection Networks. IEEE Trans. Comput. 1987, 100, 547–553. [Google Scholar] [CrossRef]
- Glass, C.J.; Ni, L.M. The turn model for adaptive routing. J. ACM 1994, 41, 874–902. [Google Scholar] [CrossRef]
- Yu, Z.; Xiang, D.; Wang, X. Balancing Virtual Channel Utilization for Deadlock-Free Routing in Torus Networks. J. Supercomput. 2015, 71, 3094–3115. [Google Scholar] [CrossRef]
- Tsai, W.C.; Lan, Y.C.; Hu, Y.H.; Chen, S.J. Networks on Chips: Structure and Design Methodologies. J. Electr. Comput. Eng. 2012, 2012, 509465. [Google Scholar] [CrossRef]
- Sebastian, J.; Sharma, G. The Pure Zigzag Model for Routing in a NoC. In Proceedings of the 2012 International Conference on Computing, Electronics and Electrical Technologies (ICCEET), Nagercoil, India, 21–22 March 2012; pp. 922–926. [Google Scholar]
- Pedro, V.; Eric, M.; Nan, W. ZigZag: An Efficient Deterministic Network-on-chip Routing Algorithm Design. In Proceedings of the 2017 8th IEEE Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 3–5 October 2017; pp. 1–5. [Google Scholar]
- Abdulelah, G.F.S. A Recursive Deterministic Routing Algorithm for Two Dimensional Mesh Network. Int. J. Comput. Sci. Mob. Comput. 2021, 10, 1–13. [Google Scholar]
- Zhang, B.; Gu, H.; Guo, R. SCRA: A Hybrid Deterministic Routing Algorithm for Aging-Resilient Network-an-Chip. In Proceedings of the Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), Lanzhou, China, 18–21 November 2019; pp. 1455–1458. [Google Scholar]
- Chen, Z.; Zhang, Y.; Peng, Z.; Jiang, J. A Deterministic-Path Routing Algorithm for Tolerating Many Faults on Wafer-Level NoC. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 25–29 March 2019; pp. 1337–1342. [Google Scholar]
- Ebrahimi, M. Fully adaptive routing algorithms and region-based approaches for two-dimensional and three-dimensional networks-on-chip. IET. Comput. Digit. Tec. 2013, 7, 264–273. [Google Scholar] [CrossRef]
- Chiu, G. The Odd-Even Turn Model for Adaptive Routing. IEEE T. Parall. Distr. 2000, 11, 729–738. [Google Scholar] [CrossRef]
- Ascia, G.; Catania, V.; Palesi, M.; Patti, D. Implementation and Analysis of a New Selection Strategy for Adaptive Routing in Networks-on-Chip. IEEE Trans. Comput. 2008, 57, 809–820. [Google Scholar] [CrossRef]
- Syeda, T.A.; Imran, M.M.; Jenia, N.M.; Jenia, A.J.; Chowdhury, Z.I.; Kaiser, M.S. An Adaptive Routing Algorithm for on-chip 2D Mesh Network with an Efficient Buffer Allocation Scheme. In Proceedings of the 2018 International Conference on Computer, Communication, Chemical, Material and Electronic Engineering (IC4ME2), Rajshahi, Bangladesh, 8–9 February 2018; pp. 1–4. [Google Scholar]
- Nosrati, N.; Shahhoseini, H.S. Regional Selection Mechanism for Traffic-balanced Adaptive Routing Algorithms in Mesh-based NoC Architectures. In Proceedings of the 2020 10th International Conference on Computer and Knowledge Engineering (ICCKE), Mashhad, Iran, 29–30 October 2020; pp. 513–518. [Google Scholar]
- Paul, G.; Boris, G.; Stephen, W.K. Regional Congestion Awareness for Load Balance in Networks-on-chip. In Proceedings of the 2008 IEEE 14th International Symposium on High Performance Computer Architecture, Salt Lake City, UT, USA, 16–20 February 2008; pp. 203–214. [Google Scholar]
- Ramanujam, R.S.; Lin, B. Destination-based Adaptive Routing on 2D Mesh Networks. In Proceedings of the 6th ACM/IEEE Symposium on Architectures for Networking and Communications Systems, San Diego, CA, USA, 25–26 October 2010; pp. 1–12. [Google Scholar]
- Ramakrishna, M.; Kodati, V.K.; Gratz, P.V.; Sprintson, A. GCA: Global Congestion Awareness for Load Balance in Networks-on-Chip. IEEE Trans. Parall. Distr. 2016, 27, 2022–2035. [Google Scholar] [CrossRef]
- Seena, V.; Akram, R.; Midia, R. Low-cost Regional-based Congestion-aware Routing Algorithm for 2D Mesh NoC. Int. J. Commun. Syst. 2022, 36, e5360. [Google Scholar]
- Hu, J.; Marculescu, R. DyAD—Smart routing for networks-on-chip. In Proceedings of the DAC04: The 41st Annual Design Automation Conference, San Diego, CA, USA, 7–11 June 2004; pp. 260–263. [Google Scholar]
- Ashok Kumar, S.; Ashima, S. Fuzzy & Neural-based Adaptive & Deterministic Routing Algorithm for Network-on-chip. In Proceedings of the 2018 2nd International Conference on Inventive Systems and Control (ICISC), Coimbatore, India, 19–20 January 2018; pp. 575–579. [Google Scholar]
- Mohammad, T.; Ali, M.N.G.M.; Fatemeh, G.; Pourya, P. A Hybrid Selection Strategy Based on Traffic Analysis for Improving Performance in Networks on Chip. J. Sens. 2022, 2022, 3112170. [Google Scholar]
- Catania, V.; Mineo, A.; Monteleone, S.; Palesi, M.; Patti, D. Noxim: An Open, Extensible and Cycle-Accurate Network on Chip Simulator. In Proceedings of the 2015 IEEE 26th International Conference on Application-specific Systems, Architectures and Processors (ASAP), Toronto, ON, Canada, 27–29 July 2015; pp. 162–163. [Google Scholar]
- Sheibanyrad, A.; Greiner, A.; Miro-Panades, I. Multisynchronous and fully asynchronous NoCs for GALS architectures. IEEE Des. Test. Comput. 2008, 6, 572–580. [Google Scholar] [CrossRef]
- Shang, L.; Peh, L.; Jha, N.K. PowerHerd: A Distributed Scheme for Dynamically Satisfying Peak-Power Constraints in Interconnection Networks. IEEE Trans. Comput.-Aided Design Integr. Circ. Syst. 2006, 25, 92–110. [Google Scholar] [CrossRef]
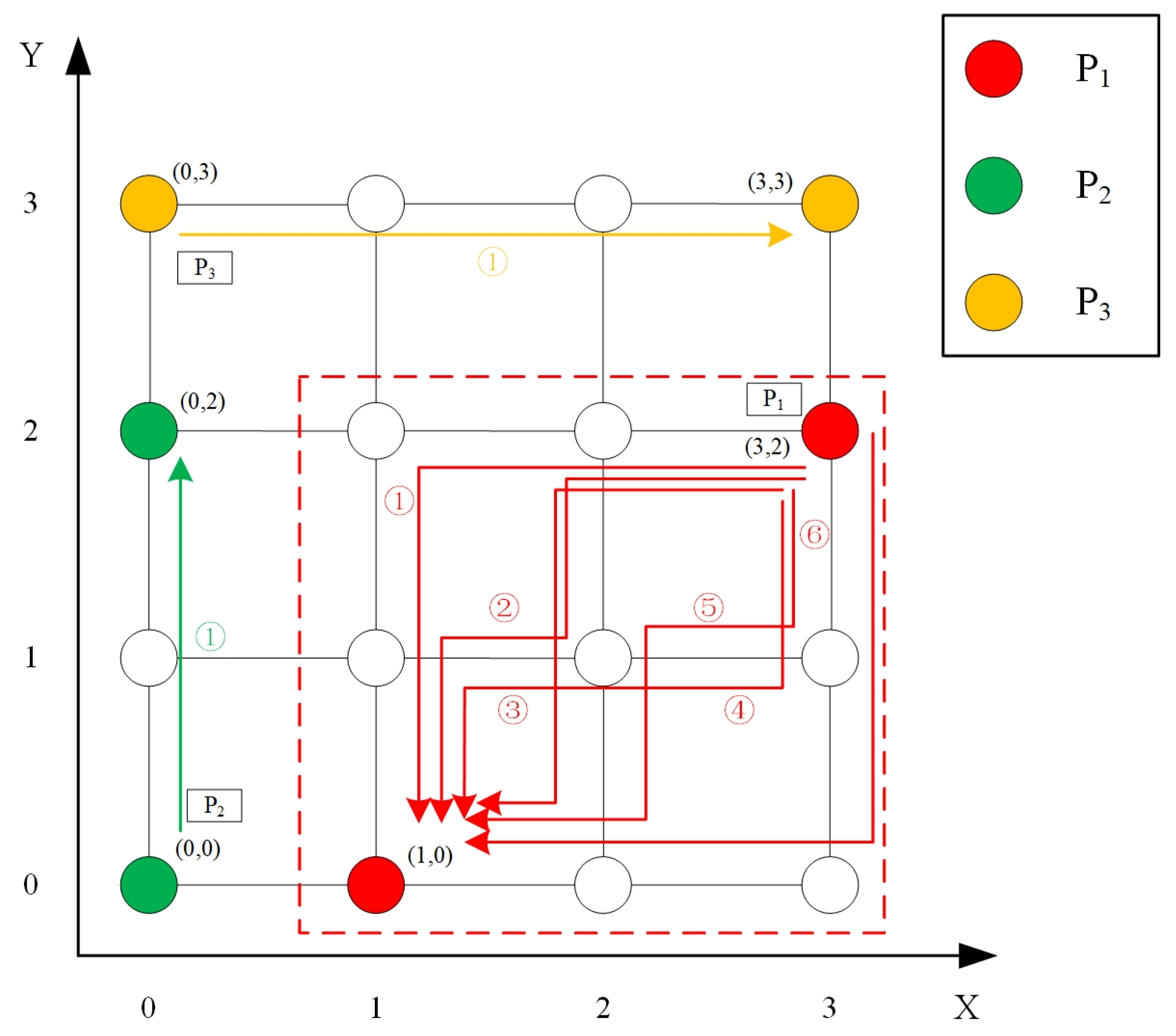

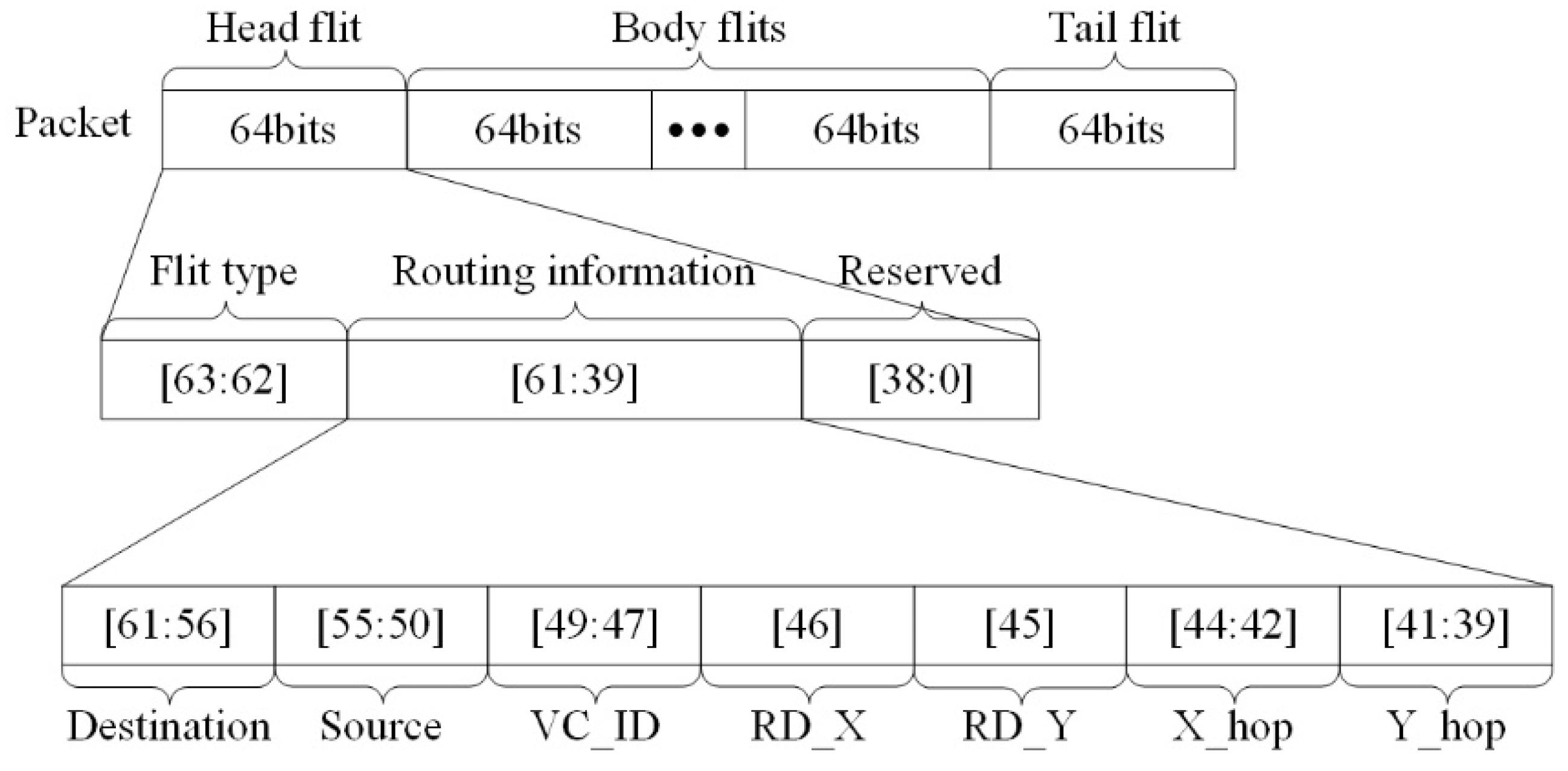




| No. | Coordinate Relationship | X_Hop | Y_Hop | RD_X | RD_Y |
|---|---|---|---|---|---|
| 1 | Xd = Xs, Yd = Ys | 0 | 0 | invalid | invalid |
| 2 | Xd > Xs, Yd > Ys | Xd-Xs | Yd-Ys | 0 | 0 |
| 3 | Xd = Xs, Yd > Ys | 0 | Yd-Ys | invalid | 0 |
| 4 | Xd < Xs, Yd > Ys | Xs-Xd | Yd-Ys | 1 | 0 |
| 5 | Xd < Xs, Yd = Ys | Xs-Xd | 0 | 1 | invalid |
| 6 | Xd < Xs, Yd < Ys | Xs-Xd | Ys-Yd | 1 | 1 |
| 7 | Xd = Xs, Yd < Ys | 0 | Ys-Yd | invalid | 1 |
| 8 | Xd > Xs, Yd < Ys | Xd-Xs | Ys-Yd | 0 | 1 |
| 9 | Xd > Xs, Yd = Ys | Xd-Xs | 0 | 0 | invalid |
| Simulation Settings | Configuration |
|---|---|
| Network scale | 4 × 4 and 8 × 8 (2D mesh) |
| Routing algorithms | XY, OE, DAHR |
| The width of each flit | 64 bits |
| Length of packet | 3~5 flits |
| Buffer size | 5 (flits) × 4 (VCs) |
| Traffic patterns | Bit reversal, Transpose 1, Transpose 2, Hotspot |
| Bit Reversal | Transpose 1 | Transpose 2 | Hotspot | |
|---|---|---|---|---|
| DAHR-XY | 17.5% | 13.9% | 18.8% | 14.8% |
| DAHR-OE | 10.4% | 8.6% | 15.1% | 8.7% |
| Bit Reversal | Transpose 1 | Transpose 2 | Hotspot | |
|---|---|---|---|---|
| DAHR-XY | 19.0% | 11.9% | 17.7% | 9.9% |
| DAHR-OE | 12.0% | 7.6% | 14.8% | 5.8% |
| Bit Reversal | Transpose 1 | Transpose 2 | Hotspot | ||
|---|---|---|---|---|---|
| 4 × 4 mesh | DAHR-XY | 30.6% | 36.3% | 41.5% | 18.0% |
| DAHR-OE | 14.3% | 9.0% | 21.0% | 9.0% | |
| 8 × 8 mesh | DAHR-XY | 39.5% | 35.3% | 33.3% | 19.7% |
| DAHR-OE | 12.5% | 16.9% | 16.7% | 10.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, N.; Yang, Y. A Deadlock-Free Deterministic–Adaptive Hybrid Routing Algorithm for Efficient Network-on-Chip Communication. Electronics 2025, 14, 845. https://doi.org/10.3390/electronics14050845
Ji N, Yang Y. A Deadlock-Free Deterministic–Adaptive Hybrid Routing Algorithm for Efficient Network-on-Chip Communication. Electronics. 2025; 14(5):845. https://doi.org/10.3390/electronics14050845
Chicago/Turabian StyleJi, Ning, and Yintang Yang. 2025. "A Deadlock-Free Deterministic–Adaptive Hybrid Routing Algorithm for Efficient Network-on-Chip Communication" Electronics 14, no. 5: 845. https://doi.org/10.3390/electronics14050845
APA StyleJi, N., & Yang, Y. (2025). A Deadlock-Free Deterministic–Adaptive Hybrid Routing Algorithm for Efficient Network-on-Chip Communication. Electronics, 14(5), 845. https://doi.org/10.3390/electronics14050845







