Edge-of-Chaos Kernel and Dynamic Analysis of a Hopfield Neural Network with a Locally Active Memristor
Abstract
1. Introduction
- (1)
- A third-order circuit of a voltage-controlled memristor with an EOCK is proposed, which can produce a variety of different dynamic phenomena.
- (2)
- The memristor is coupled with an HNN to study the bifurcation behavior at different coupling intensities, and a rare antimonotonicity phenomenon is observed. When one variable in the coupling intensity is changed, bubble bifurcation can be observed. The feasibility is verified with an STM32 hardware board.
2. A Memristor Model and Memristive Circuit
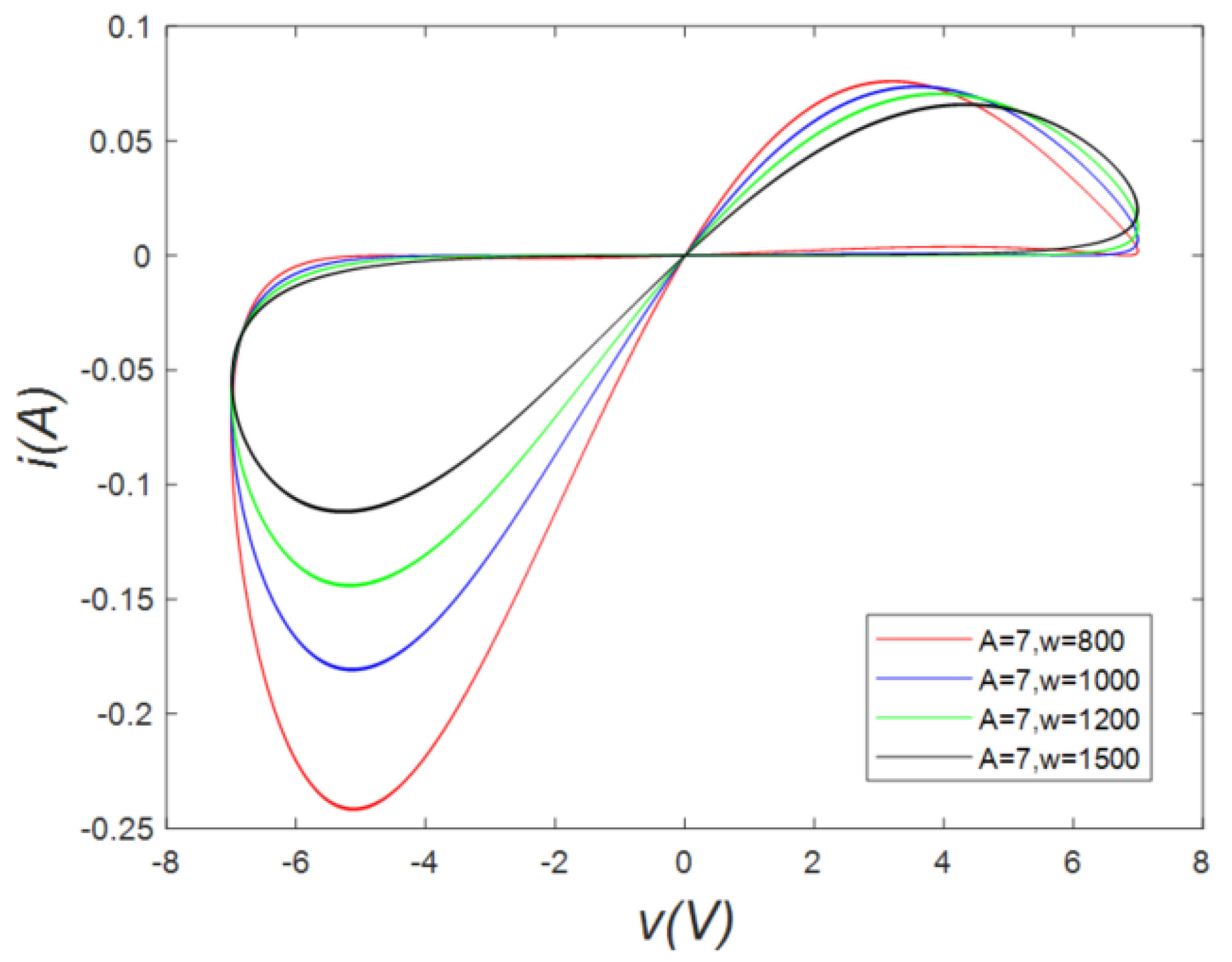
2.1. Hysteresis Loops
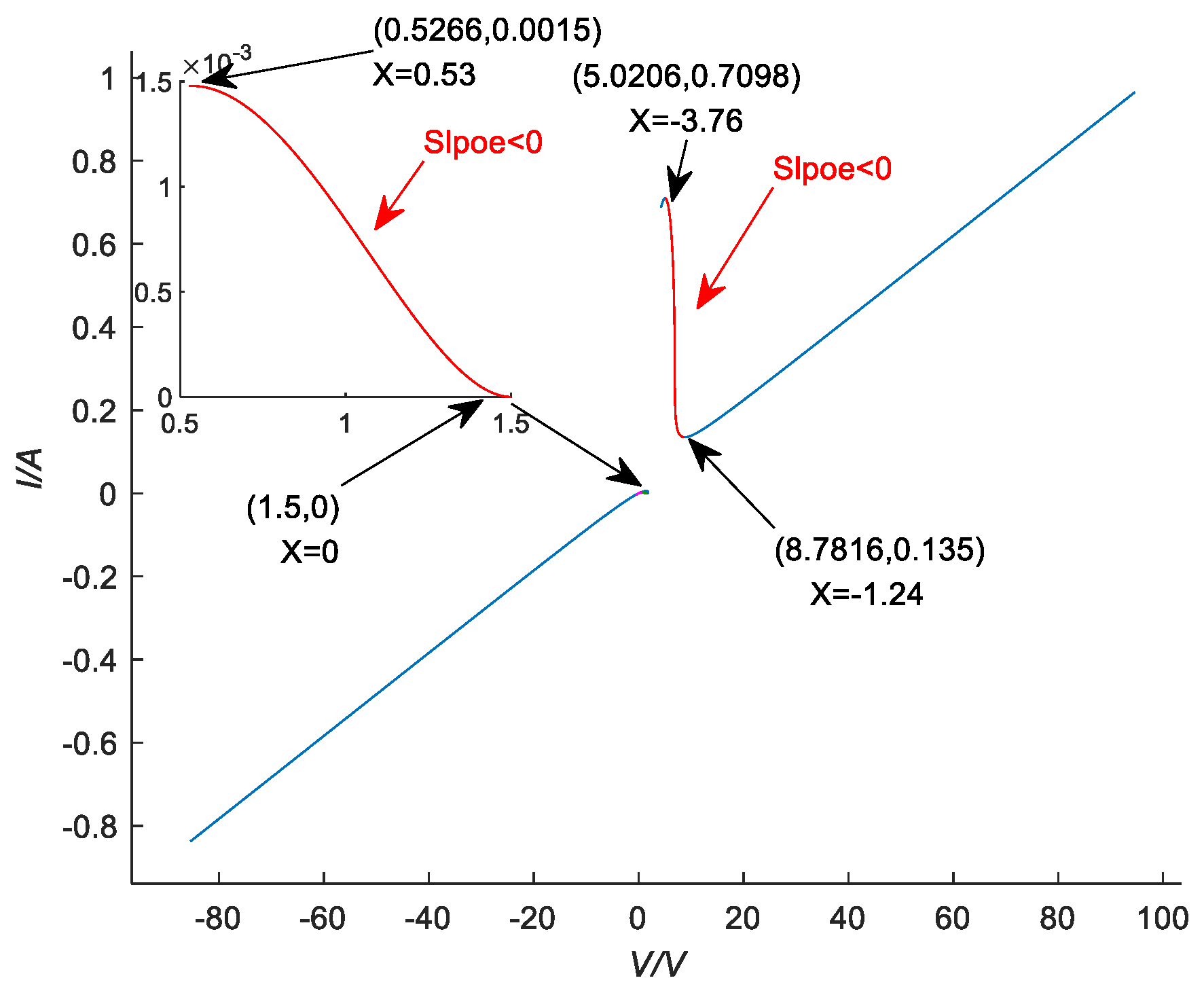
2.2. Locally Active
2.3. Asymptotic Stability
2.4. Edge-of-Chaos Kernel
2.5. A Memristive Circuit with an EOCK
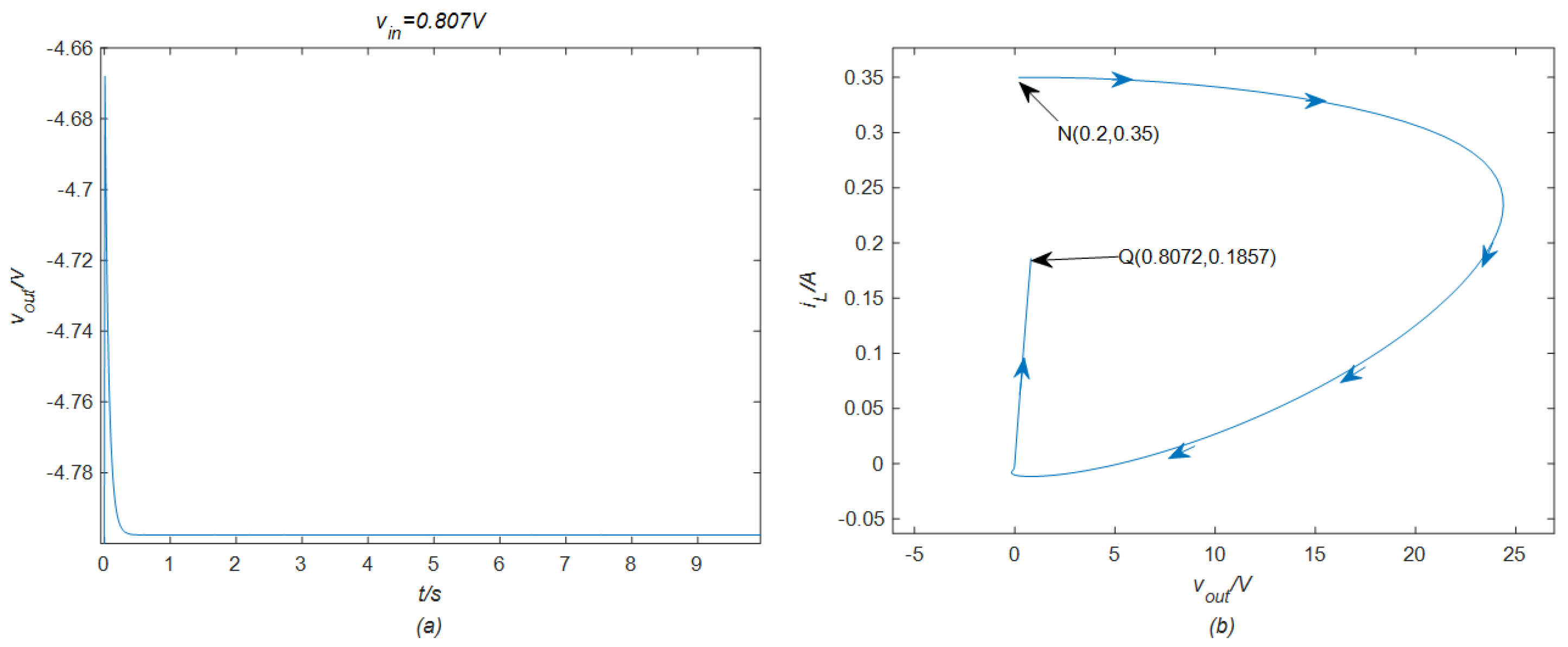
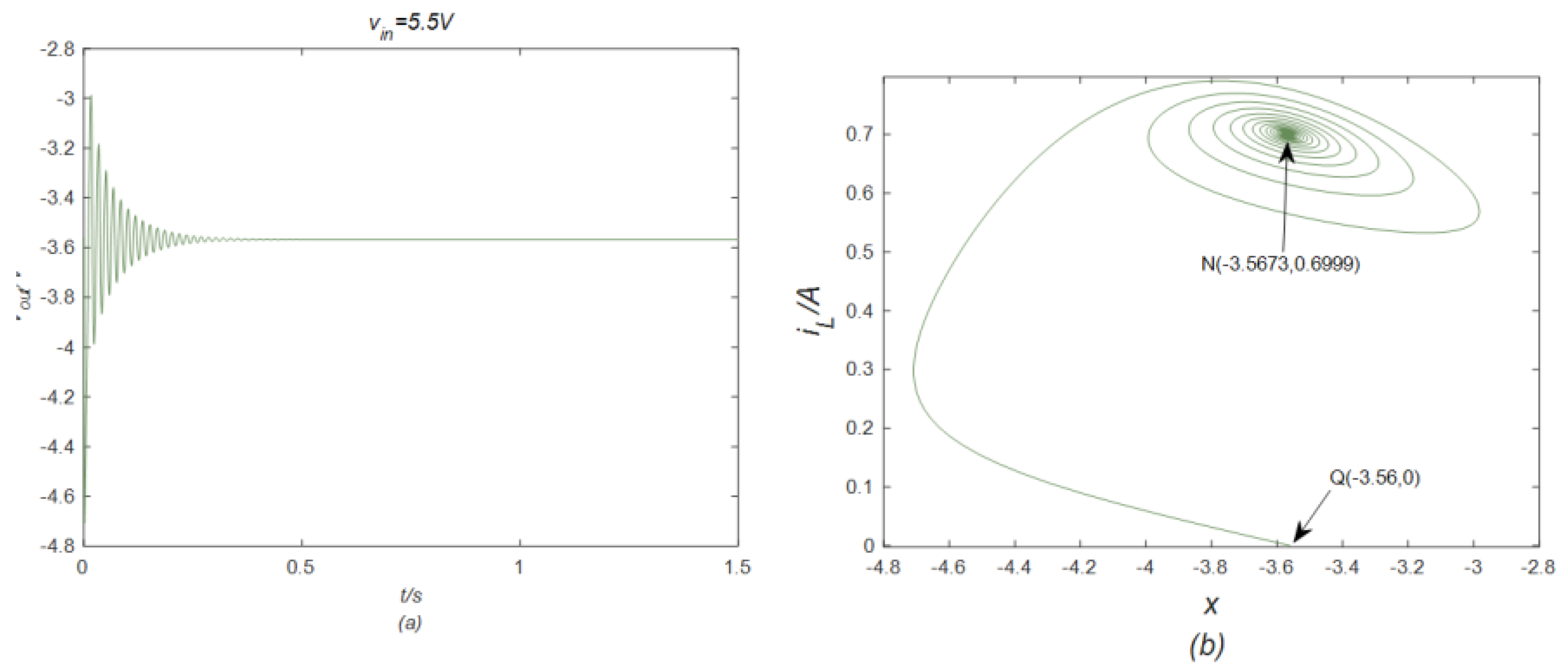
3. EOCK and Neuromorphic Behaviors
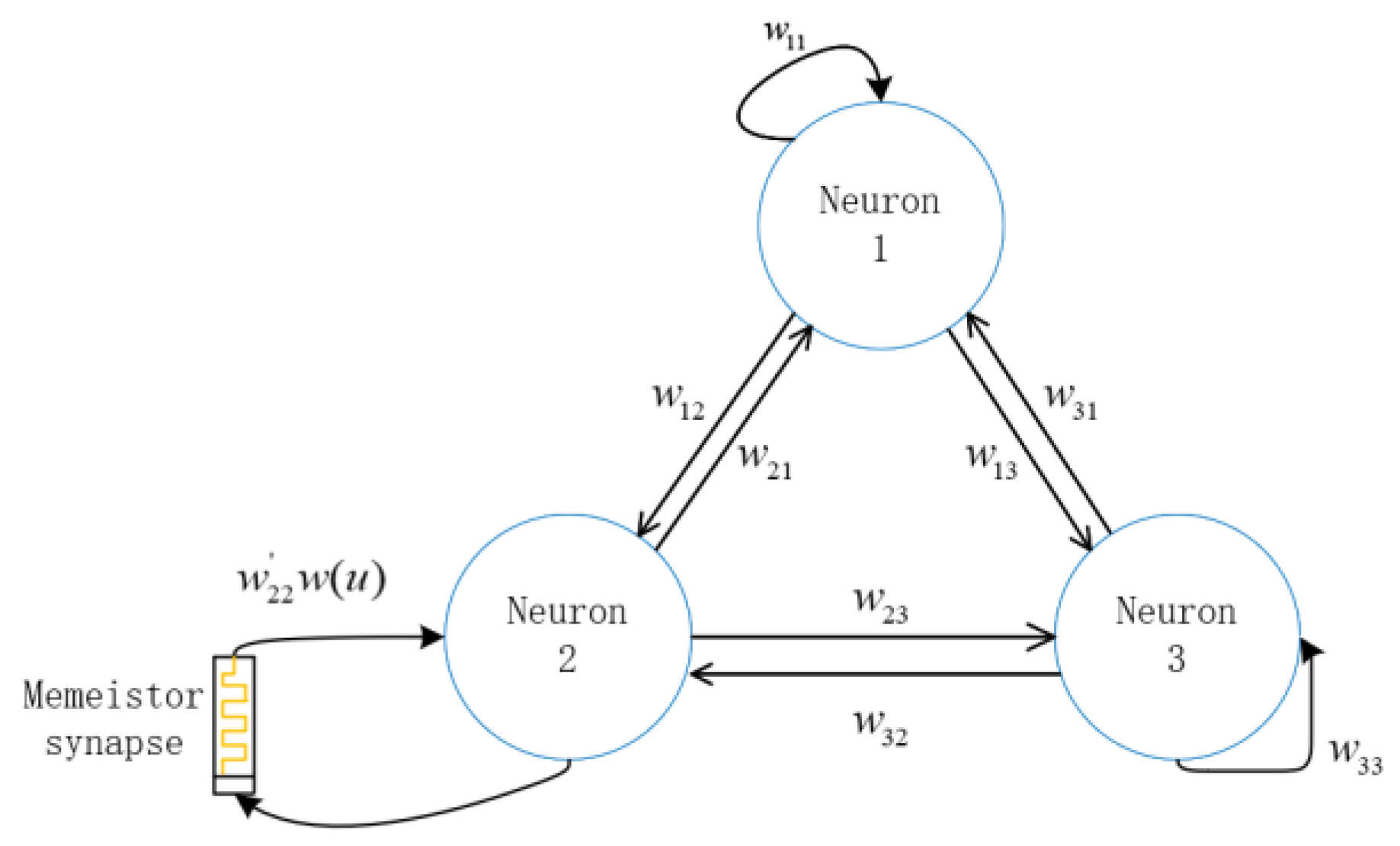
4. Proposed HNN and Its Hardware Implementation
4.1. The Dynamical Behavior of the HNN Model
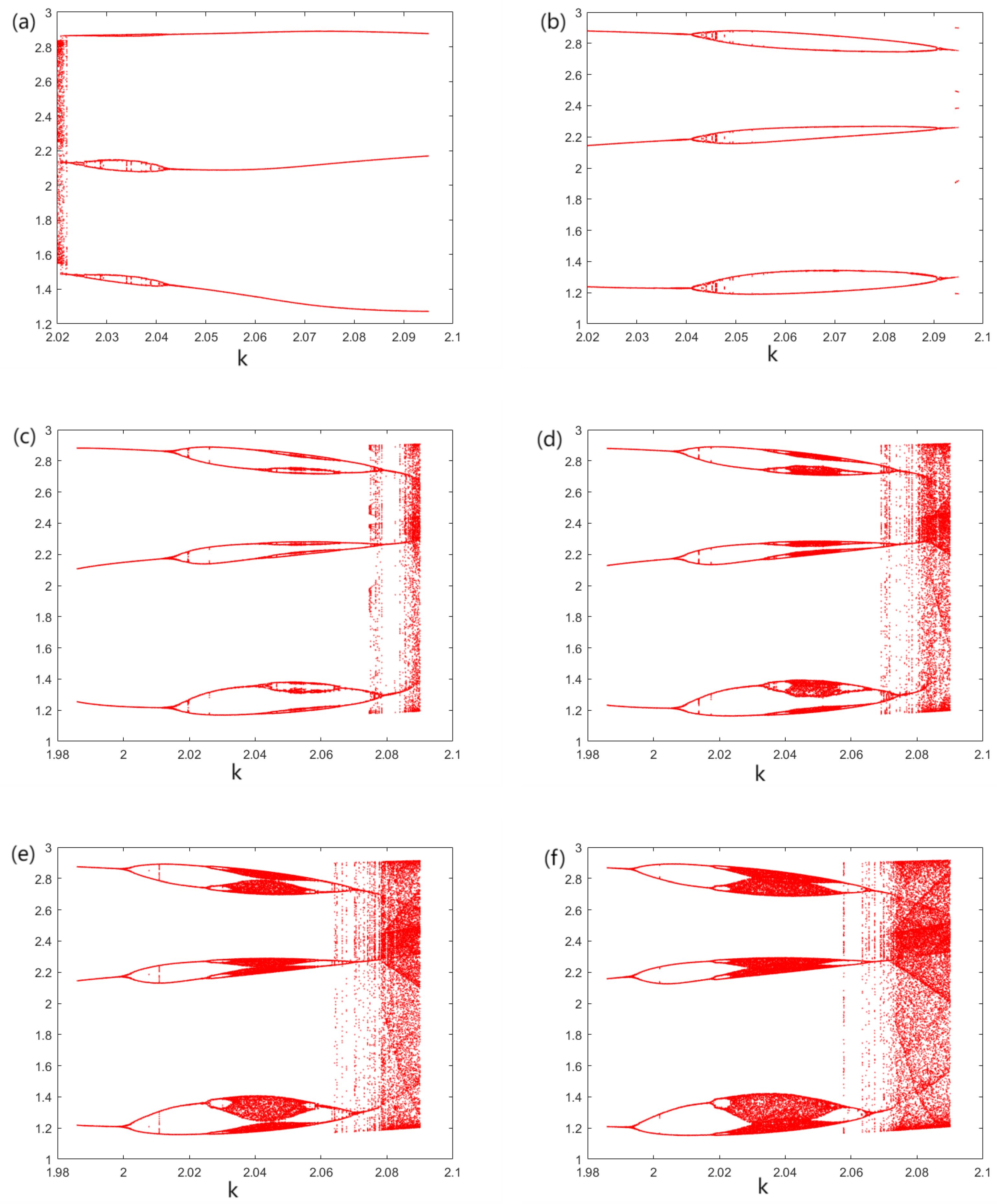
4.2. Dynamical Behavior Analysis
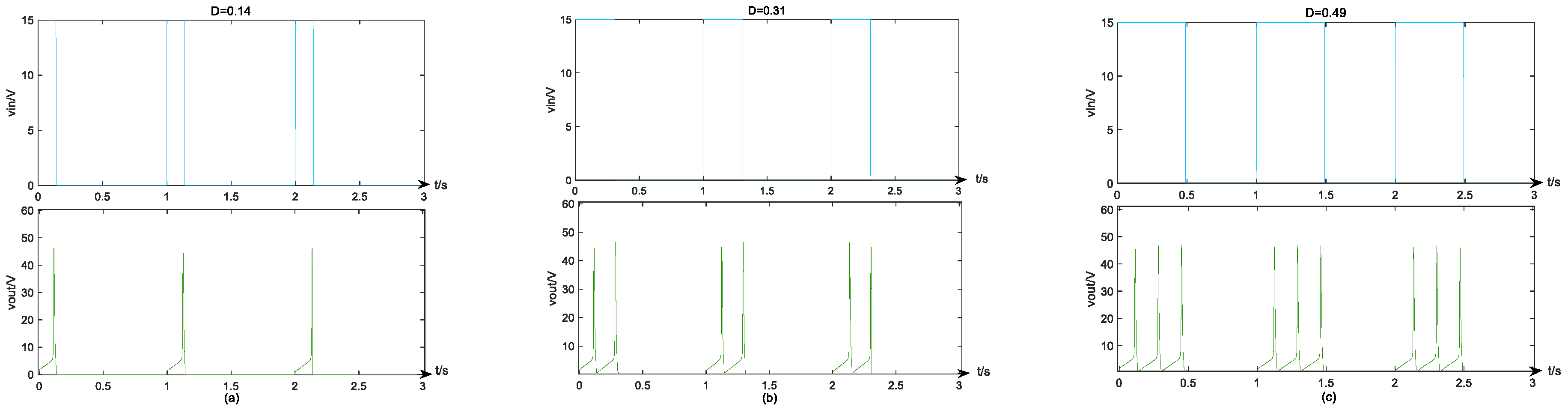
4.3. Validation by STM32 Hardware Board
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nail, B.; Atoussi, M.A.; Saadi, S.; Tibermacine, I.E.; Napoli, C. Real-time synchronisation of multiple fractional-order chaotic systems: An application study in secure communication. Fractal Fract. 2024, 8, 104. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J. Dynamic analysis and circuit design of tunable multi-vortex chaotic systems based on memristors. Nonlinear Dyn. 2024, 112, 14415–14440. [Google Scholar] [CrossRef]
- Zhang, J.; Zuo, J.; Guo, Y.; Hou, J.; Xie, Q. Nonlinear analysis, circuit implementation, and application in image encryption of a four-dimensional multi-scroll hyper-chaotic system. Integration 2024, 95, 102126. [Google Scholar] [CrossRef]
- Zuo, J.; Zhang, J.; Wei, X.; Yang, L.; Cheng, N.; Lv, J. Design and application of multisroll conservative chaotic system with no-equilibrium, dynamics analysis, circuit implementation. Chaos Solitons Fractals 2024, 187, 115331. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, J.; Chen, Y.; Qin, Z.; Zhang, Y.; Ahmad, M.; Woźniak, M. Exploiting robust quadratic polynomial hyperchaotic map and pixel fusion strategy for efficient image encryption. Expert Syst. Appl. 2024, 246, 123190. [Google Scholar] [CrossRef]
- Darani, Y.; Yengejeh, Y.K.; Pakmanesh, H.; Navarro, G. Image encryption algorithm based on a new 3D chaotic system using cellular automata. Chaos Solitons Fractals 2024, 179, 114396. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Q.; Liu, H.; Ren, Y.; Zhang, J.; Zhang, S.; Qian, K.; Wen, H. Exploiting newly designed fractional-order 3D lorenz chaotic system and 2D discrete polynomial hyper-chaotic map for high-performance multi-image encryption. Fractal Fract. 2023, 7, 887. [Google Scholar] [CrossRef]
- Gokyildirim, A.; Akgul, A.; Calgan, H.; Demirtas, M. Parametric fractional-order analysis of Arneodo chaotic system and microcontroller-based secure communication implementation. AEU Int. J. Electron. Commun. 2024, 175, 155080. [Google Scholar] [CrossRef]
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Wang, C.; Luo, D.; Deng, Q.; Yang, G. Dynamics analysis and FPGA implementation of discrete memristive cellular neural network with heterogeneous activation functions. Chaos Solitons Fractals 2024, 187, 115471. [Google Scholar] [CrossRef]
- Li, J.; Wang, C.; Deng, Q. Symmetric multi-double-scroll attractors in Hopfield neural network under pulse controlled memristor. Nonlinear Dyn. 2024, 112, 14463–14477. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Yang, X.; Zi, X.; Xiao, F. A tristable locally active memristor and its application in Hopfield neural network. Nonlinear Dyn. 2022, 108, 1697–1717. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, E.; Guo, Y. A new three-dimensional memristor chaotic circuit design and its application in image encryption. J. Supercomput. 2024, 80, 14694–14724. [Google Scholar] [CrossRef]
- Wang, F.; Wang, F. Design of chaotic circuit based on Knowm memristor. Electron. Lett. 2024, 60, e13294. [Google Scholar] [CrossRef]
- Chen, Y.; Mou, J.; Jahanshahi, H.; Wang, Z.; Cao, Y. A new mix chaotic circuit based on memristor–memcapacitor. Eur. Phys. J. Plus 2023, 138, 78. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, J.; Li, H.; Zuo, J. Nonlinear analysis, circuit design, and chaos optimisation application of multiscroll chaotic attractors based on novel locally active non-polynomial memristor. Nonlinear Dyn. 2024. [Google Scholar] [CrossRef]
- Yao, W.; Liu, J.; Sun, Y.; Zhang, J.; Yu, F.; Cui, L.; Lin, H. Dynamics analysis and image encryption application of Hopfield neural network with a novel multistable and highly tunable memristor. Nonlinear Dyn. 2024, 112, 693–708. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, E. Circuit design and image encryption of CNN chaotic system based on memristor. Eur. Phys. J. B 2024, 97, 100. [Google Scholar] [CrossRef]
- Shi, G.; Wang, C.; Qiao, F.; Lin, R.; Wu, S.; Sun, Y.; Shi, M.; Han, J. A new CMOS-memristor based D-latch with fewer components. Microelectron. J. 2024, 146, 106154. [Google Scholar] [CrossRef]
- Yi, W.; Tsang, K.K.; Lam, S.K.; Bai, X.; Crowell, J.A.; Flores, E.A. Biological plausibility and stochasticity in scalable VO2 active memristor neurons. Nat. Commun. 2018, 9, 4661. [Google Scholar] [CrossRef] [PubMed]
- Slavova, A.; Ignatov, V. Edge of Chaos in Reaction-Diffusion System with Memristor Synapses. In New Trends in the Applications of Differential Equations in Sciences—NTADES 2023; Slavova, A., Ed.; Springer Proceedings in Mathematics & Statistics Volume 449; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Liang, Y.; Guo, H.; Li, Y.; Jin, P.; Wang, G.; Iu, H.H.-C. Theoretical Analysis and Hardware Reproduction of Smale Paradox Based on CCM Neurons and Edge of Chaos. IEEE Trans. Circuits Syst. I Regul. Pap. 2024. early access. [Google Scholar] [CrossRef]
- Chua, L.O. Memristors on ‘edge of chaos’. Nat. Rev. Electr. Eng. 2024, 1, 614–627. [Google Scholar] [CrossRef]
- Chua, L.O. Hodgkin–Huxley equations implies EOCK. Jpn. J. Appl. Phys. 2022, 61, SM0805. [Google Scholar] [CrossRef]
- Zhou, W.; Jin, P.; Dong, Y.; Liang, Y.; Wang, G. Memristor neurons and their coupling networks based on Edge of Chaos Kernel. Chaos Solitons Fractals 2024, 177, 114224. [Google Scholar] [CrossRef]
- Sah, M.; Rajamani, V.; Budhathoki, R.K.; Somasundaram, D.; Chowdhury, S.M. The Simplest Memristor Oscillator is blessed with an Edge of Chaos Kernel. J. Electr. Eng. Technol. 2025, 20, 797–806. [Google Scholar] [CrossRef]
- Panahi, S.; Zainab, A.; Jafari, S.; Ma, J.; Sprott, J.C. Modeling of epilepsy based on chaotic artificial neural network. Chaos Solitons Fractals 2017, 105, 150–156. [Google Scholar] [CrossRef]
- Zhang, J.; Bao, H.; Gu, J.; Chen, M.; Bao, B. Multistability and synchronicity of memristor coupled adaptive synaptic neuronal network. Chaos Solitons Fractals 2024, 185, 115157. [Google Scholar] [CrossRef]
- Xu, W.; Wang, J.; Yan, X. Advances in Memristor-Based Neural Networks. Front. Nanotechnol. 2021, 3, 645995. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, X.J.; Chen, B.; Wu, H.G.; Li, Z.; Bao, H. Dynamical analysis of an improved FitzHugh–Nagumo neuron model with multiplier-free implementation. Nonlinear Dyn. 2023, 111, 8737–8749. [Google Scholar] [CrossRef]
- Bao, H.; Zhu, D.; Liu, W.; Xu, Q.; Bao, B. Memristor synapse-based Morris–Lecar model: Bifurcation analyses and FPGA-based validations for periodic and chaotic bursting/spiking firings. Int. J. Bifurc. Chaos 2020, 30, 2050045. [Google Scholar] [CrossRef]
- Njitacke, Z.T.; Kengne, J. Complex dynamics of a 4D Hopfield neural networks (HNNs) with a nonlinear synaptic weight: Coexistence of multiple attractors and remerging Feigenbaum trees. AEU Int. J. Electron. Commun. 2018, 93, 242–252. [Google Scholar] [CrossRef]
- Shoukui, D.; Ning, W.; Han, B.; Bei, C.; Wu, H.; Quan, X. Memristor synapse-coupled piecewise-linear simplified Hopfield neural network: Dynamics analysis and circuit implementation. Chaos Solitons Fractals 2023, 166, 112899. [Google Scholar]
- Mengjie, H.; Han, B.; Huagan, W.; Quan, X.; Bocheng, B. A single neuron model with memristive synaptic weight. Chin. J. Phys. 2022, 76, 217–227. [Google Scholar]
- Hu, Z.; Wang, C. Hopfield neural network with multi-scroll attractors and application in image encryption. Multimed. Tools Appl. 2024, 83, 97–117. [Google Scholar] [CrossRef]
- Peng, Y.; He, S.; Sun, K. Chaos in the discrete memristor-based system with fractional-order difference. Results Phys. 2021, 24, 104106. [Google Scholar] [CrossRef]
- Qian, K.; Xiao, Y.; Wei, Y.; Liu, D.; Wang, Q.; Feng, W. A Robust Memristor-Enhanced Polynomial Hyper-Chaotic Map and Its Multi-Channel Image Encryption Application. Micromachines 2023, 14, 2090. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Li, B. A uniform chaotic system with extended parameter range for image encryption. Nonlinear Dyn. 2021, 103, 2819–2840. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Yu, F.; Xu, C.; Hong, Q.; Yao, W.; Sun, Y. An Extremely Simple Multiwing Chaotic System: Dynamics Analysis, Encryption Application, and Hardware Implementation. IEEE Trans. Ind. Electron. 2020, 68, 12708–12719. [Google Scholar] [CrossRef]
- Wang, L.; Zou, H. A new emotion model of associative memory neural network based on memristor. Neurcompting 2020, 410, 83–92. [Google Scholar] [CrossRef]
- Yu, F.; Lin, Y.; Yao, W.; Cai, S.; Lin, H.; Li, Y. Multiscroll hopfield neural network with extreme multistability and its application in video encryption for IIoT. Neural Netw. 2025, 182, 106904. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.; Yu, F.; Yao, W.; Cai, S.; Zhang, J.; Lin, H. Memristor-induced hyperchaos, multiscroll and extreme multistability in fractional-order HNN: Image encryption and FPGA implementation. Neural Netw. 2024, 171, 85–103. [Google Scholar] [CrossRef]
- Ding, D.; Chen, S.; Zhang, H.; Yang, Z.; Jin, F.; Liu, X. Firing pattern transition of fractional-order memristor-coupled Hindmarsh–Rose neurons model and its medical image encryption for region of interest. Nonlinear Dyn. 2024, 112, 10529–10554. [Google Scholar] [CrossRef]
- Shooshtari, M.; Través, M.J.; Pahlavan, S.; Serrano-Gotarredona, T.; Linares-Barranco, B. Applying Hodgkin-Huxley Neuron Model for Perovskite Memristor in Circuit Simulation. In Proceedings of the 2024 IEEE International Conference on Metrology for eXtended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), St Albans, UK, 21–23 October 2024; pp. 1077–1082. [Google Scholar]
- Jin, P.; Liang, Y.; Wang, G.; Chen, L.; Iu, H.H.-C.; Chua, L.O. Shortcuts to Edge-of-Chaos Domains of Memristive Circuits and Historic Measurement of Contiguous Triple-Branch V—I Curve of Chua Corsage Memristor. Int. J. Bifurc. Chaos 2022, 32, 2230035. [Google Scholar] [CrossRef]
- Jin, P.; Han, N.; Zhang, X.; Wang, G.; Chen, L. Edge of Chaos Kernel and neuromorphic dynamics of a locally-active memristor. Commun. Nonlinear Sci. Numer. Simul. 2023, 17, 106961. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ma, Y.; Jiang, R.; Yang, Z.; Pu, X.; Li, Z. Edge-of-Chaos Kernel and Dynamic Analysis of a Hopfield Neural Network with a Locally Active Memristor. Electronics 2025, 14, 766. https://doi.org/10.3390/electronics14040766
Zhang L, Ma Y, Jiang R, Yang Z, Pu X, Li Z. Edge-of-Chaos Kernel and Dynamic Analysis of a Hopfield Neural Network with a Locally Active Memristor. Electronics. 2025; 14(4):766. https://doi.org/10.3390/electronics14040766
Chicago/Turabian StyleZhang, Li, Yike Ma, Rongli Jiang, Zongli Yang, Xiangkai Pu, and Zhongyi Li. 2025. "Edge-of-Chaos Kernel and Dynamic Analysis of a Hopfield Neural Network with a Locally Active Memristor" Electronics 14, no. 4: 766. https://doi.org/10.3390/electronics14040766
APA StyleZhang, L., Ma, Y., Jiang, R., Yang, Z., Pu, X., & Li, Z. (2025). Edge-of-Chaos Kernel and Dynamic Analysis of a Hopfield Neural Network with a Locally Active Memristor. Electronics, 14(4), 766. https://doi.org/10.3390/electronics14040766





