Optimization of Cross-Bridge Kelvin Resistor (CBKR) Layout for the Precise Contact Resistance Measurement of TiSi2/n+ Si
Abstract
1. Introduction
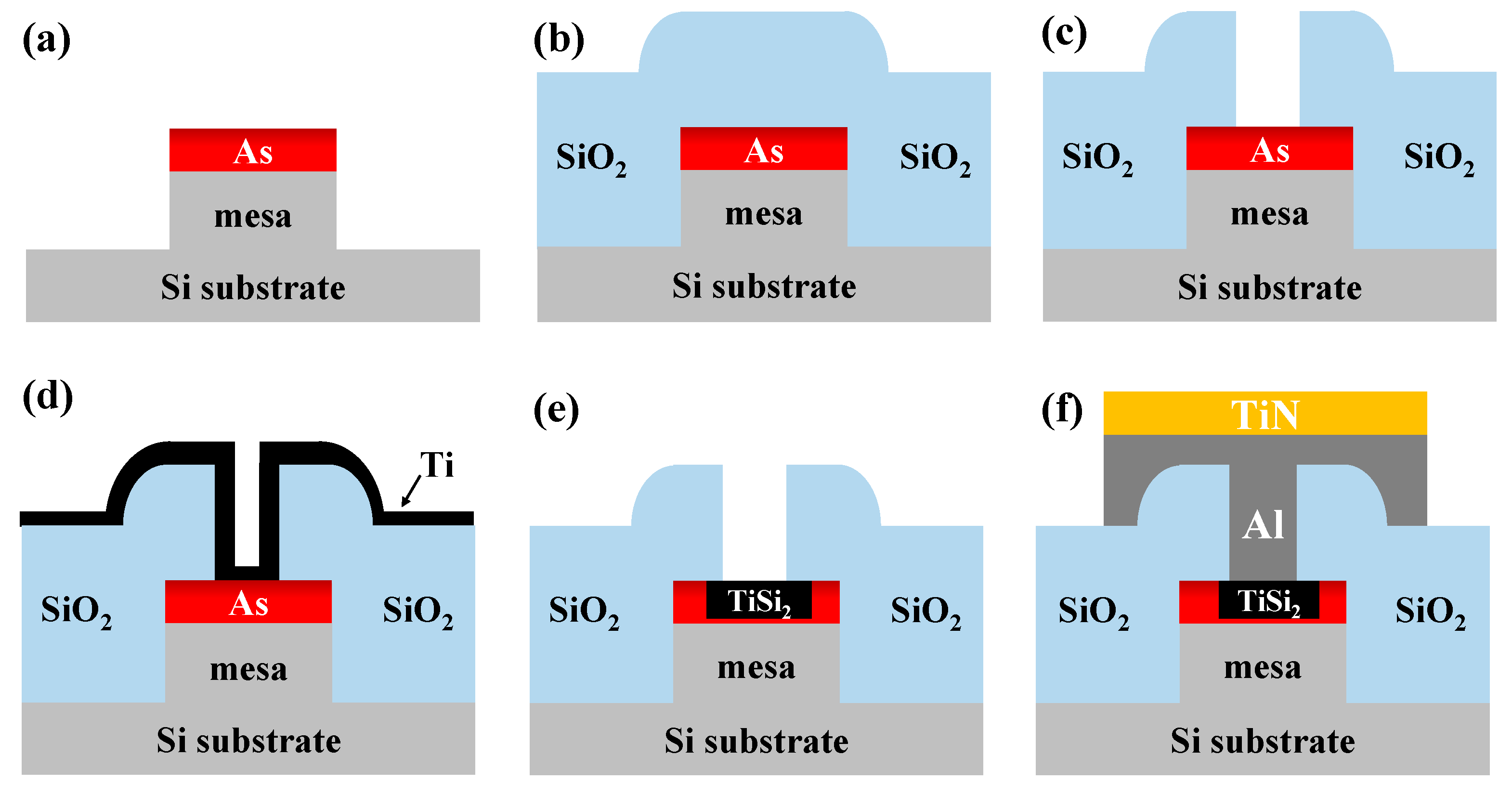
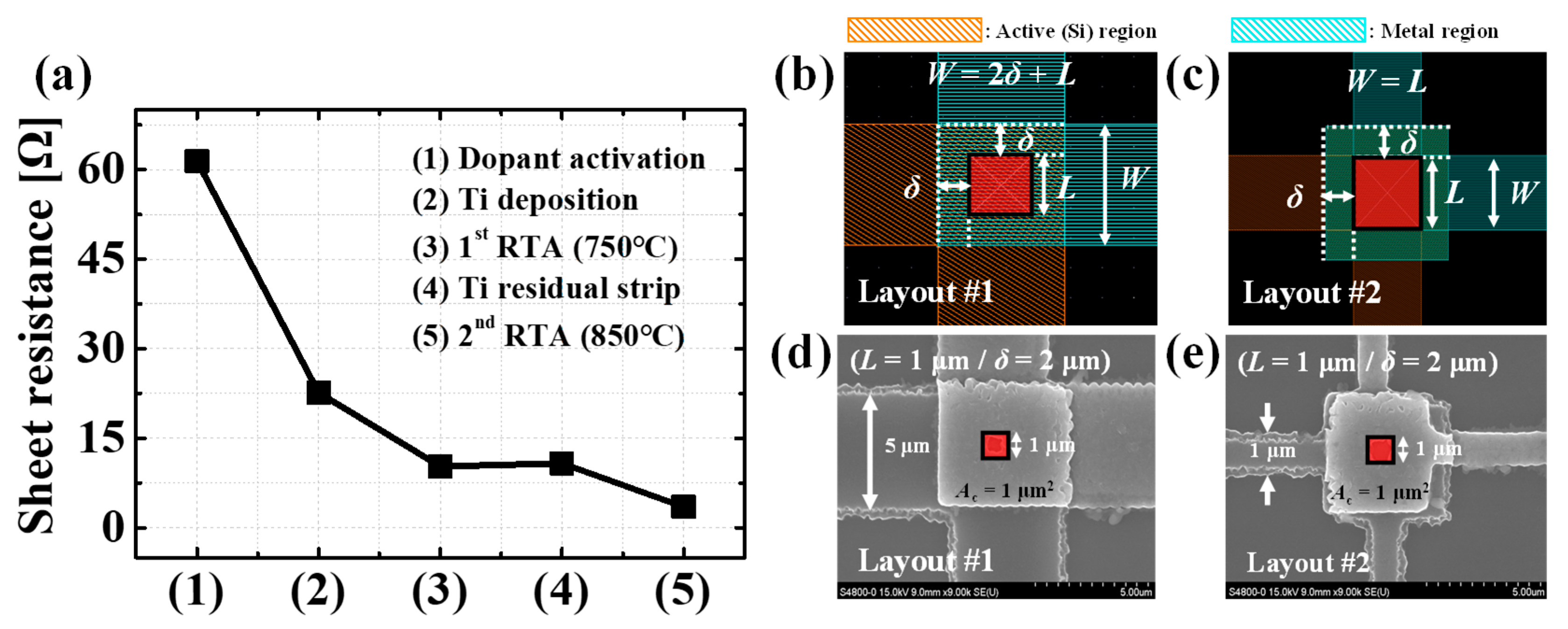
2. Fabrication Process
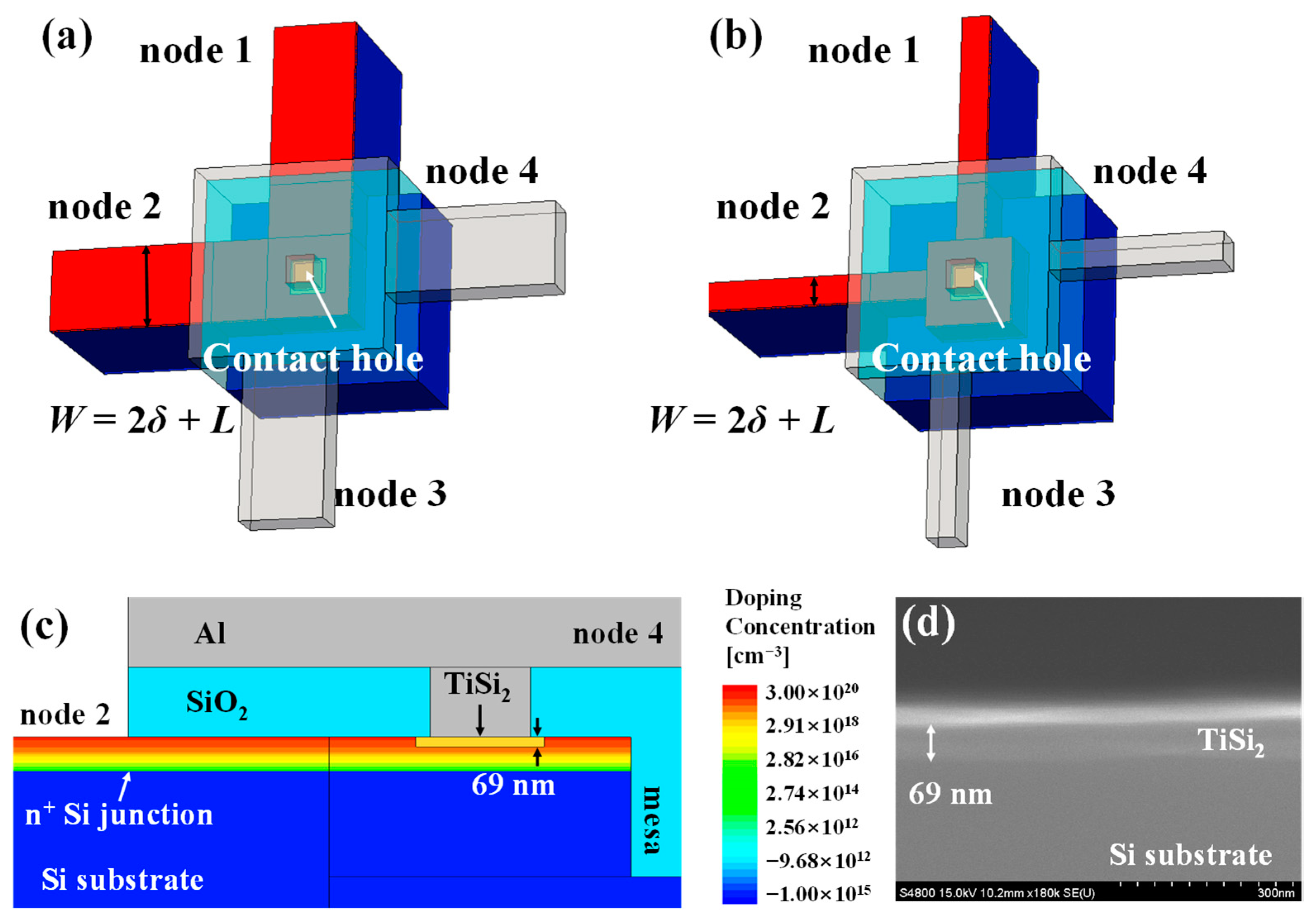
3. Simulation Structures and Extraction Condition
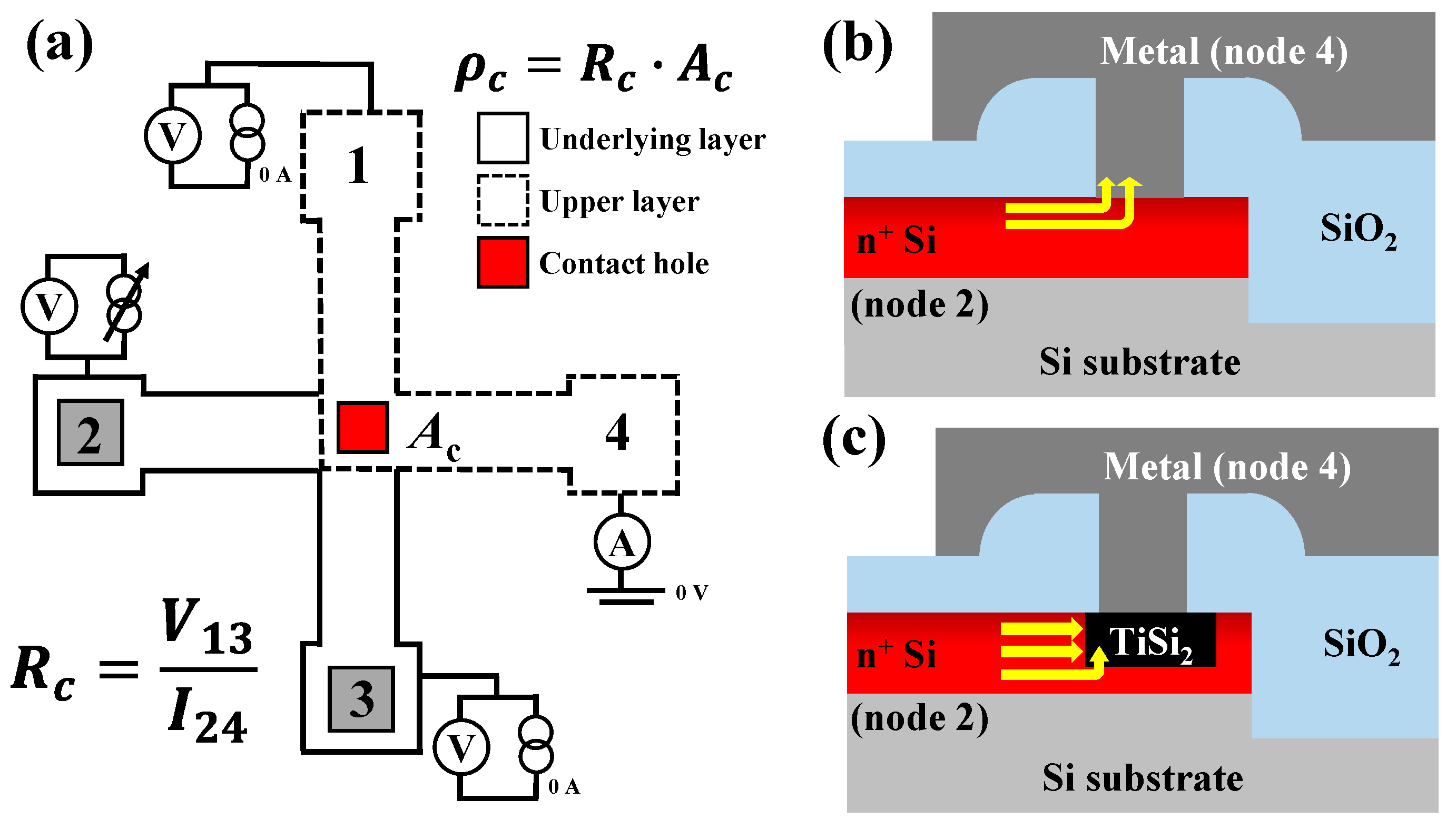
4. Theoretical ρc Calculation
5. Results and Discussion
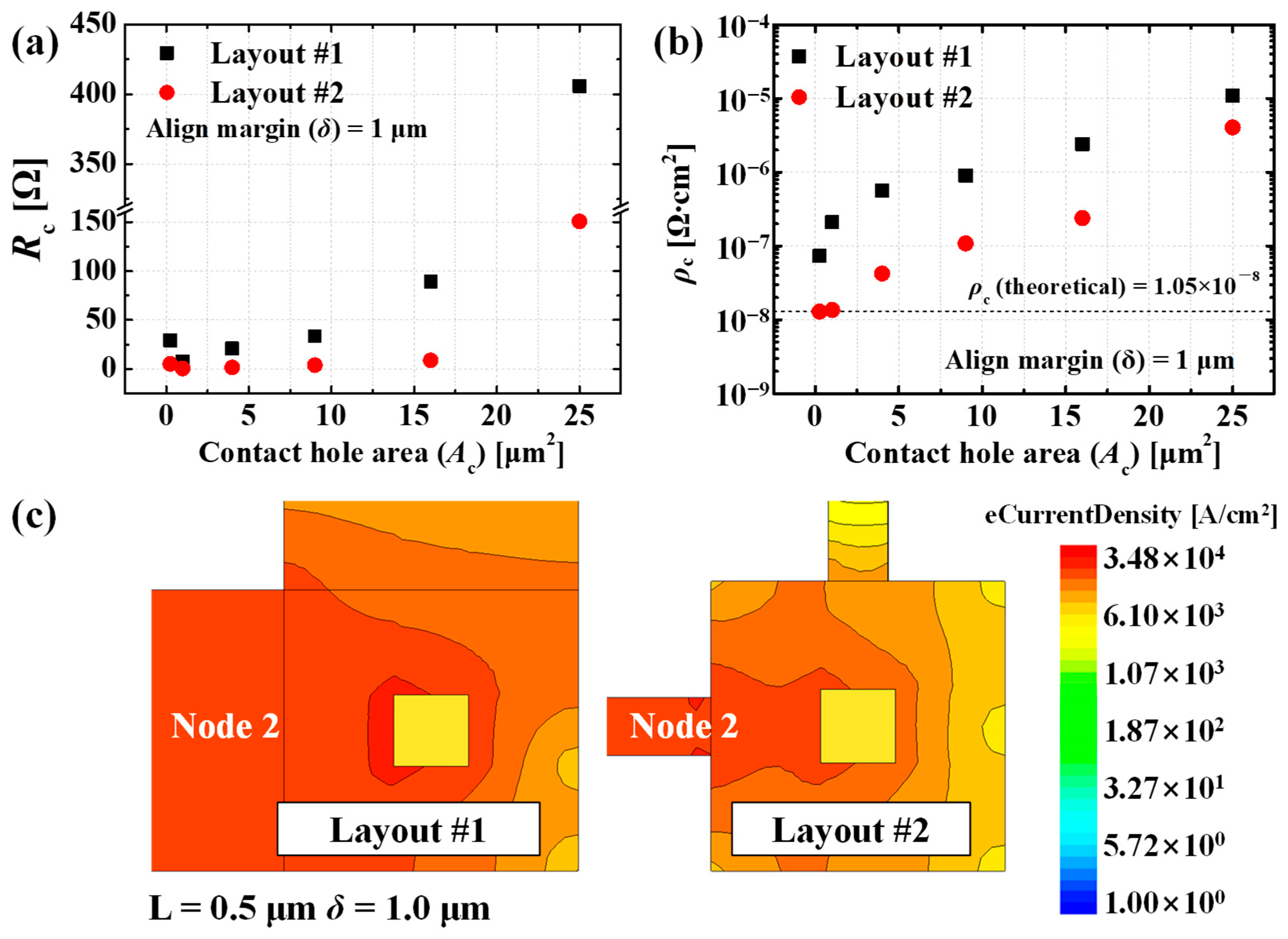
5.1. Layout Comparison
5.2. Contact Hole Area (Ac) Variation
5.3. Align Margin (δ) Variation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Schaller, R.R. Moore’s law: Past, present and future. IEEE Spectr. 1997, 34, 52–59. [Google Scholar] [CrossRef]
- Yu, B.; Chang, L.; Ahmed, S.; Wang, H.; Bell, S.; Yang, C.-Y.; Tabery, C.; Ho, C.; Xiang, Q.; King, T.-J.; et al. FinFET scaling to 10 nm gate length. In Proceedings of the 2002 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 8–11 December 2002; pp. 251–254. [Google Scholar]
- Yoon, J.-S.; Jeong, J.; Lee, S.; Baek, R.-H. Systematic DC/AC performance benchmarking of Sub-7-nm node FinFETs and nanosheet FETs. IEEE J. Electron. Devices Soc. 2018, 6, 942–947. [Google Scholar] [CrossRef]
- Wu, C.C.; Lin, D.W.; Keshavarzi, A.; Huang, C.H.; Chan, C.T.; Tseng, C.H.; Chen, C.L.; Hsieh, C.Y.; Wong, K.Y.; Cheng, M.L.; et al. High performance 22/20nm FinFET CMOS devices with advanced high-K/metal gate scheme. In Proceedings of the 2010 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 6–8 December 2010; pp. 27.1.1–27.1.4. [Google Scholar]
- Bae, G.; Bae, D.I.; Kang, M.; Hwang, S.M.; Kim, S.S.; Seo, B.; Kwon, T.Y.; Lee, T.J.; Moon, C.; Choi, Y.M.; et al. 3 nm GAA Technology featuring Multi-Bridge-Channel FET for Low Power and High Performance Applications. In Proceedings of the 2018 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 1–5 December 2018; pp. 28.7.1–28.7.4. [Google Scholar] [CrossRef]
- Jang, D.; Bury, E.; Ritzenthaler, R.; Bardon, M.G.; Chiarella, T.; Miyaguchi, K.; Raghavan, P.; Mocuta, A.; Groeseneken, G.; Mercha, A.; et al. Self-heating on bulk FinFET from 14nm down to 7nm node. In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 11.6.1–11.6.4. [Google Scholar]
- Mahapatra, S.; Sharma, U. A Review of Hot Carrier Degradation in n-Channel MOSFETs—Part II: Technology Scaling. IEEE Trans. Electron. Devices 2020, 67, 2672–2681. [Google Scholar] [CrossRef]
- AThean, A.V.; Yakimets, D.; Bao, T.H.; Schuddinck, P.; Sakhare, S.; Bardon, M.G.; Sibaja-Hernandez, A.; Ciofi, I.; Eneman, G.; Veloso, A.; et al. Vertical device architecture for 5nm and beyond: Device & circuit implications. In Proceedings of the 2015 Symposium on VLSI Technology (VLSI Technology), Kyoto, Japan, 16–18 June 2015; pp. T26–T27. [Google Scholar]
- Jung, S.-G.; Kim, J.-K.; Yu, H.-Y. Analytical Model of Contact Resistance in Vertically Stacked Nanosheet FETs for Sub-3-nm Technology Node. IEEE Trans. Electron. Devices 2022, 69, 930–935. [Google Scholar] [CrossRef]
- Thompson, S.E.; Parthasarathy, S. Moore’s law: The future of Si microelectronics. Mater. Today 2006, 9, 20–25. [Google Scholar] [CrossRef]
- Yeric, G. Moore’s law at 50: Are we planning for retirement? In Proceedings of the 2015 IEEE International Electron Devices Meeting (IEDM), Washington, DC, USA, 7–9 December 2015; pp. 1.1.1–1.1.8. [Google Scholar]
- Gupta, S.; Manik, P.P.; Mishra, R.K.; Nainani, A.; Abraham, M.C.; Lodha, S. Contact resistivity reduction through interfacial layer doping in metal-interfacial layer-semiconductor contacts. J. Appl. Phys. 2013, 113, 234505. [Google Scholar] [CrossRef]
- Adusumilli, P.; Alptekin, E.; Raymond, M.; Breil, N.; Chafik, F.; Lavoie, C.; Ferrer, D.; Jain, S.; Kamineni, V.; Ozcan, A.; et al. Ti and NiPt/Ti liner silicide contacts for advanced technologies. In Proceedings of the 2016 IEEE Symposium on VLSI Technology, Honolulu, HI, USA, 14–16 June 2016; pp. 1–2. [Google Scholar]
- Qiu, Z.; Zhang, Z.; Ostling, M.; Zhang, S.L. A Comparative Study of Two Different Schemes to Dopant Segregation at NiSi/Si and PtSi/Si Interfaces for Schottky Barrier Height Lowering. IEEE Trans. Electron. Devices 2008, 55, 396–403. [Google Scholar] [CrossRef]
- Yu, H.; Schaekers, M.; Peter, A.; Pourtois, G.; Rosseel, E.; Lee, J.G.; Song, W.-B.; Shin, K.M.; Everaert, J.-L.; Chew, S.A.; et al. Titanium Silicide on Si: P With Precontact Amorphization Implantation Treatment: Contact Resistivity Approaching 1 × 10−9 Ohm-cm2. IEEE Trans. Electron. Devices 2016, 63, 4632–4641. [Google Scholar] [CrossRef]
- Chew, S.A.; Yu, H.; Schaekers, M.; Demuynck, S.; Mannaert, G.; Kunnen, E.; Rosseel, E.; Hikavyy, A.; Dangol, A.; De Meyer, K.; et al. Ultralow resistive wrap-around contact to scaled FinFET devices by using ALD-Ti contact metal. In Proceedings of the 2017 IEEE International Interconnect Technology Conference (IITC), Hsinchu, Taiwan, 16–18 May 2017; pp. 1–3. [Google Scholar]
- Breil, N.; Lavoie, C.; Ozcan, A.; Baumann, F.; Klymko, N.; Nummy, K.; Sun, B.; Jordan-Sweet, J.; Yu, J.; Zhu, F.; et al. Challenges of nickel silicidation in CMOS technologies. Microelectron. Eng. 2015, 137, 79–87. [Google Scholar] [CrossRef]
- Mao, S.; Luo, J. Titanium-based ohmic contacts in advanced CMOS technology. J. Phys. D Appl. Phys. 2019, 52, 503001. [Google Scholar] [CrossRef]
- Stavitski, N.; Klootwijk, J.H.; van Zeijl, H.W.; Kovalgin, A.Y.; Wolters, R.A.M. Cross-Bridge Kelvin Resistor Structures for Reliable Measurement of Low Contact Resistances and Contact Interface Characterization. IEEE Trans. Semicond. Manuf. 2009, 22, 146–152. [Google Scholar] [CrossRef]
- Ono, M.; Nishiyama, A.; Toriumi, A. A simple approach to understanding measurement errors in the cross-bridge Kelvin resistor and a new pattern for measurements of specific contact resistivity. Solid-State Electron. 2002, 46, 1325–1331. [Google Scholar] [CrossRef]
- Kovalgin, A.Y.; Tiggelman, N.; Wolters, R.A.M. An Area-Correction Model for Accurate Extraction of Low Specific Contact Resistance. IEEE Trans. Electron. Devices 2012, 59, 426–432. [Google Scholar] [CrossRef]
- Holland, A.S.; Reeves, G.K.; Leech, P.W. Universal error corrections for finite semiconductor resistivity in cross-Kelvin resistor test structures. IEEE Trans. Electron. Devices 2004, 51, 914–919. [Google Scholar] [CrossRef]
- Loh, W.; Saraswat, K.; Dutton, R. Analysis and scaling of Kelvin resistors for extraction of specific contact resistivity. IEEE Electron. Device Lett. 1985, 6, 105–108. [Google Scholar] [CrossRef]
- Grover, S.; Sahu, S.; Zhang, P.; Davis, K.O.; Kurinec, S.K. Standardization of Specific Contact Resistivity Measurements using Transmission Line Model (TLM). In Proceedings of the IEEE 33rd International Conference on Microelectronic Test Structures (ICMTS), Edinburgh, UK, 4–18 May 2020; pp. 1–6. [Google Scholar]
- Stavitski, N.; Van Dal, M.J.; Lauwers, A.; Vrancken, C.; Kovalgin, A.Y.; Wolters, R.A. Evaluation of Transmission Line Model Structures for Silicide-to-Silicon Specific Contact Resistance Extrac-tion. IEEE Trans. Electron. Devices 2008, 55, 1170–1176. [Google Scholar] [CrossRef]
- Wu, Y.; Xu, H.; Gong, X.; Yeo, Y.C. A Ladder Transmission Line Model for the Extraction of Ultralow Specific Contact Resistivity—Part I: Theoretical Design and Simulation Study. IEEE Trans. Electron. Devices 2020, 67, 2682–2689. [Google Scholar] [CrossRef]
- Aldrich, D.B.; Chen, Y.L.; Sayers, D.E.; Nemanich, R.J.; Ashburn, S.P.; Öztürk, M.C. Stability of C54 titanium germanosilicide on a silicon-germanium alloy substrate. J. Appl. Phys. 1995, 77, 5107–5114. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; pp. 79–124. [Google Scholar] [CrossRef]
- Aboelfotoh, M.O.; Tu, K.N. Schottky-barrier heights of Ti and TiSi2 on n-type and p-type Si(100). Phys. Rev. B. 1986, 34, 2311–2318. [Google Scholar] [CrossRef] [PubMed]
- Schroder, D.K. Semiconductor Material and Device Characterization, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]



| Parameters | Layout #1 | Layout #2 |
|---|---|---|
| Contact hole length (L) | 0.5/1/2/3/4/5 μm | |
| Contact hole area (Ac) | 0.25/1/4/9/16/25 μm2 | |
| Align margin (δ) | 0.2/0.5/1/2/3 μm | |
| Active (W) | 2δ + L | L |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noh, H.; Chae, C.; Jeon, Y.; Oh, D.; Kim, S. Optimization of Cross-Bridge Kelvin Resistor (CBKR) Layout for the Precise Contact Resistance Measurement of TiSi2/n+ Si. Electronics 2025, 14, 762. https://doi.org/10.3390/electronics14040762
Noh H, Chae C, Jeon Y, Oh D, Kim S. Optimization of Cross-Bridge Kelvin Resistor (CBKR) Layout for the Precise Contact Resistance Measurement of TiSi2/n+ Si. Electronics. 2025; 14(4):762. https://doi.org/10.3390/electronics14040762
Chicago/Turabian StyleNoh, Hyungju, Changmin Chae, Yelim Jeon, Dongseok Oh, and Sangwan Kim. 2025. "Optimization of Cross-Bridge Kelvin Resistor (CBKR) Layout for the Precise Contact Resistance Measurement of TiSi2/n+ Si" Electronics 14, no. 4: 762. https://doi.org/10.3390/electronics14040762
APA StyleNoh, H., Chae, C., Jeon, Y., Oh, D., & Kim, S. (2025). Optimization of Cross-Bridge Kelvin Resistor (CBKR) Layout for the Precise Contact Resistance Measurement of TiSi2/n+ Si. Electronics, 14(4), 762. https://doi.org/10.3390/electronics14040762





