Dynamic Multi-Product Integrated Scheduling Algorithm with Urgent Delivery Date
Abstract
1. Introduction
- In the multi-product integrated scheduling, the scheduling advantages of the ‘equipment priority + short time + layer priority’ strategy are integrated, and the initial processing process set of each product is formulated based on the constraint relationship between each process, and the maximum delivery date of each product is determined;
- In multi-product integrated scheduling, the concept of product contribution value is defined to determine the priority processing order of multi-product;
- On the scheduling algorithm, a dynamic adjustment strategy for game processes is proposed. It effectively solves the problem of resource preemption in the process of multi-product processing, dynamically analyzes the relative position relationship between the processes, and realizes the dynamic adjustment of the processing sequence.
2. Problem Description and Analysis
- (1)
- Each process has a unique serial number for identification and corresponds to processing equipment. The processing equipment also has a unique serial number for identification.
- (2)
- The necessary and sufficient condition for each process to start processing is that it has no constraints from previous order constraints.
- (3)
- The start time of each process of each product must be after the start time of its product, and its completion time must be within the delivery date of its product.
- (4)
- The end time of all processes of all products is the total production scheduling time.
3. Algorithm Design and Analysis
3.1. Product Contribution Strategy
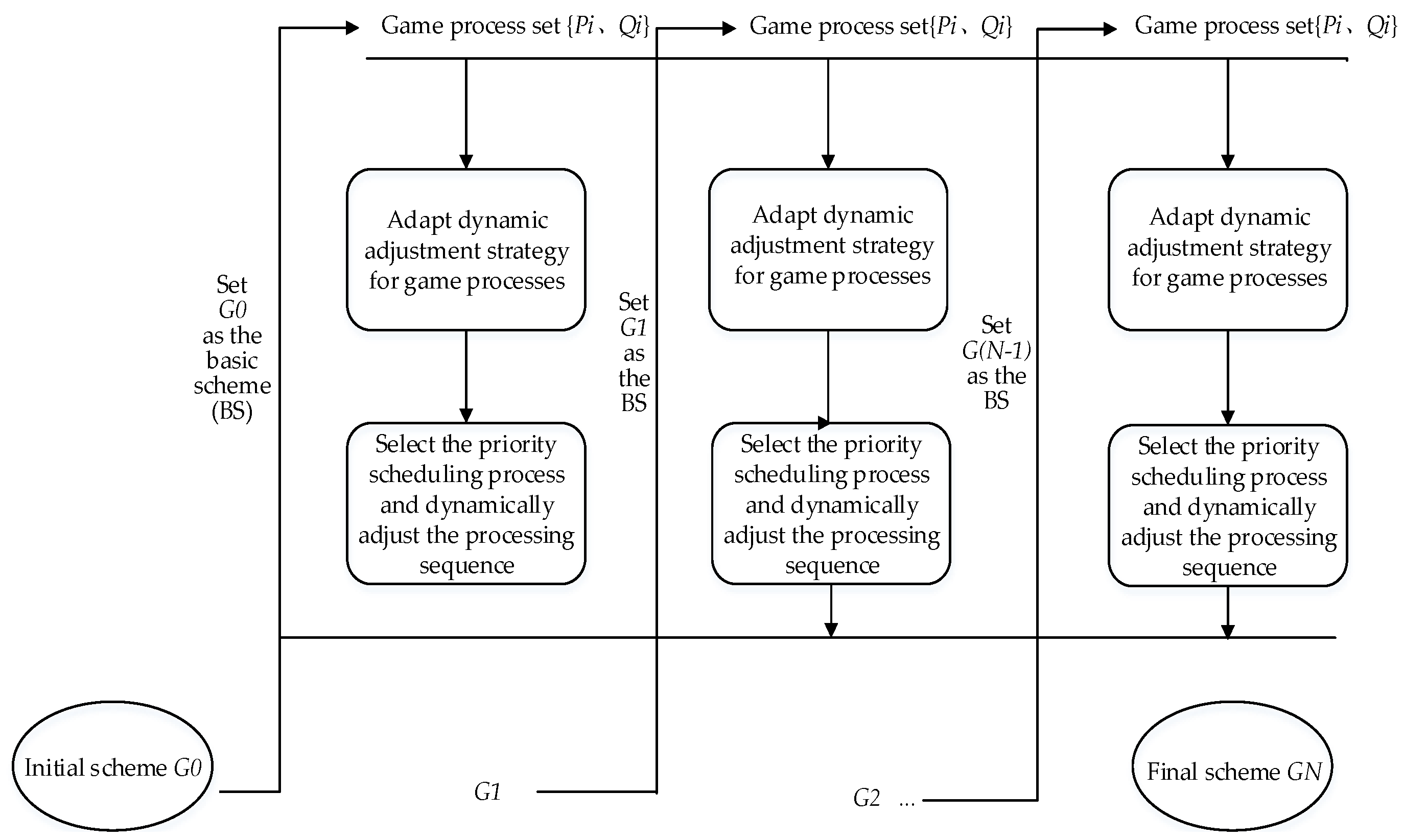
3.2. Dynamic Adjustment Strategy for Game Processes
- (1)
- If the contribution value of product A is greater than that of product B, then schedule the urgent process of A first.
- (2)
- If the contribution value of product A is greater than that of product B, then schedule the process of B first when it is the only urgent process among the game processes.
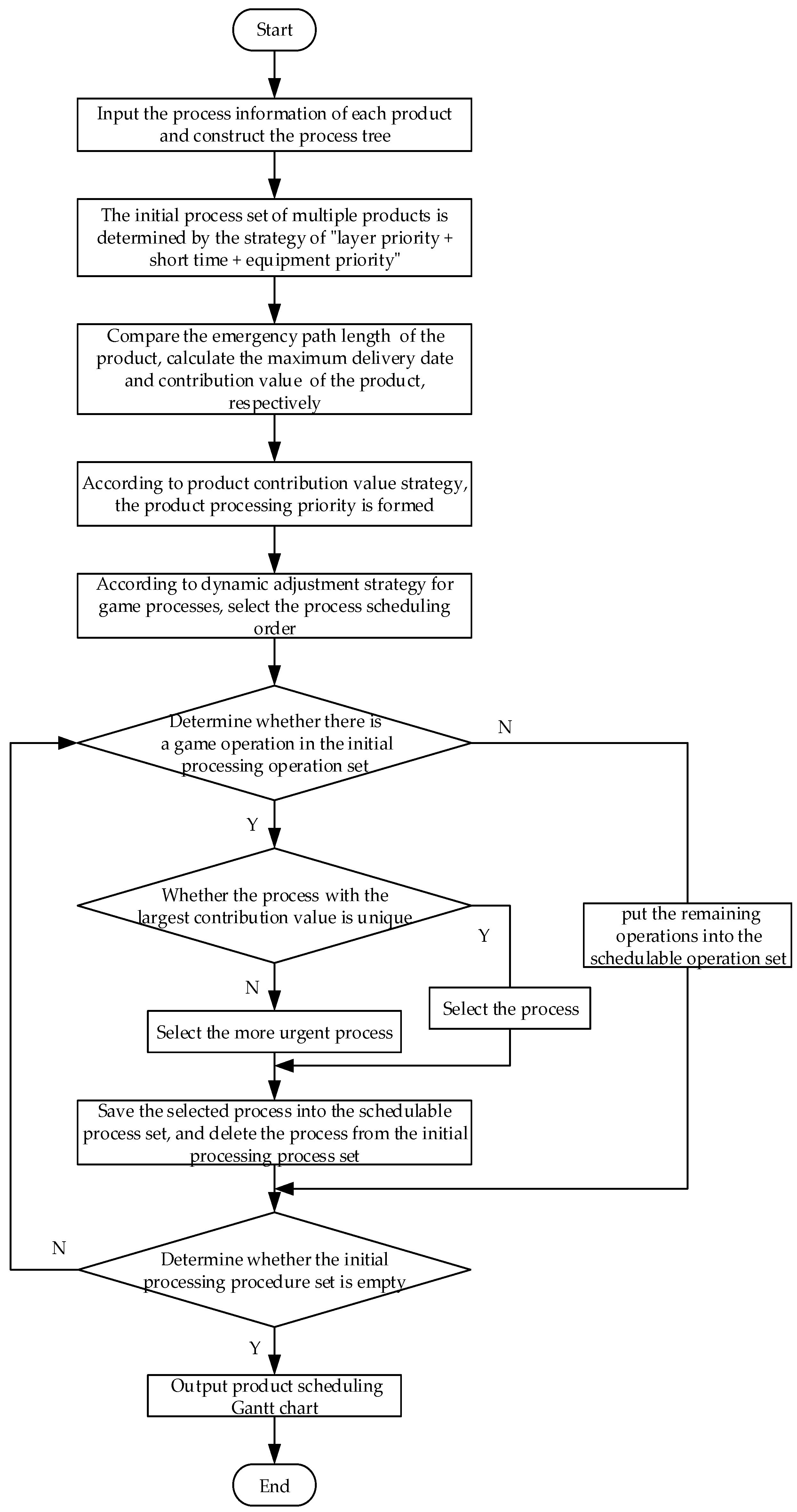
3.3. Algorithm Description
4. Algorithm Time Complexity Analysis
5. Algorithm Example Description
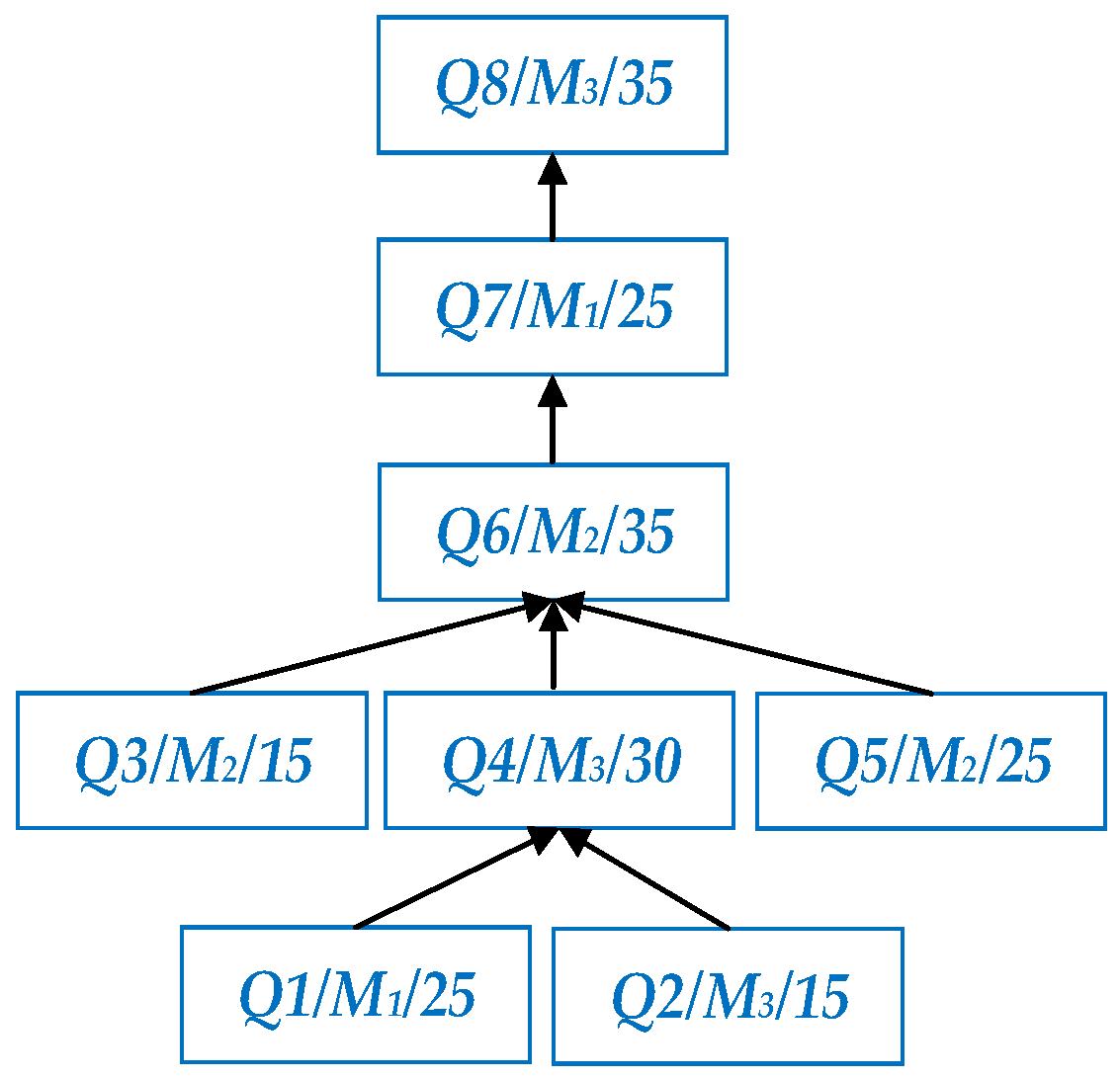
5.1. Initial Process Scheduling Sequence of Multi-Product
5.2. Solve the Maximum Delivery Time
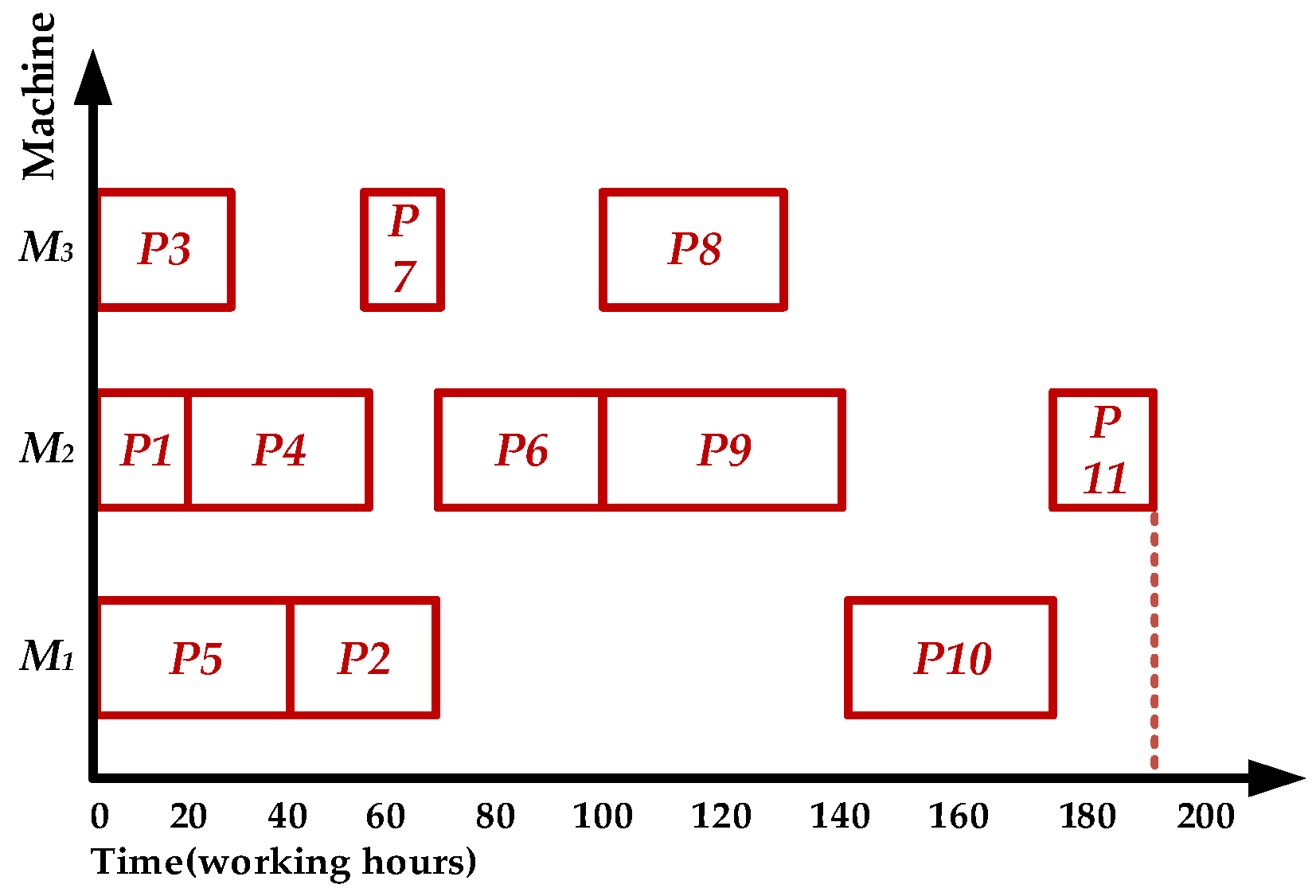
5.3. Game Process Dynamic Adjustment Strategy
6. Experimental Analysis
6.1. Comparison Algorithm
- (1)
- Algorithm based on urgency degree of delivery date (ISA-DDUD). The algorithm adopts priority strategy, long-path strategy, and short-time strategy based on urgency degree to determine the scheduling order of products according to the urgency degree of product priority processing and solve the conflict problem caused by multi-product.
- (2)
- Algorithm considering delivery date constraint (ISA-CDD). The algorithm adopts the strategy of pre-scheduling to solve the required processing time of products, the strategy of product priority with high urgency degree, and the strategy of process insertion during idle period of equipment. It takes the urgency degree as the main basis of product scheduling sequence and uses the idle period of equipment to select the appropriate process for processing.
6.2. Comparative Test Scheduling Results and Evaluation Analysis
- Compared with the ISA-DDUD and the ISA-CDD algorithms, the total processing time of ISA-TDD algorithm reduced by 10 and 30 h, and the reduction rates are 3.8% and 10.5%, respectively.
- The total processing time of the ISA-TDD algorithm is 175 working hours. Compared with the ISA-DDUD and the ISA-CDD algorithms, it reduced by 22.2% and 20.5%, respectively.
- The overall device utilization rate of the ISA-TDD algorithm reached 74.6%. Compared with the ISA-DDUD and the ISA-CDD algorithms, the overall device utilization rate of the ISA-TDD algorithm increased by 4.4% and 4.9%, respectively.
- The delivery time shortening rate of ISA-TDD algorithm is 10%, which is 10% and 3% higher than that of ISA-DDUD and ISA-CDD algorithms, respectively.
6.3. Algorithm Advantage Analysis
- (1)
- The ISA-TDD algorithm adopts the comprehensive strategy of ‘device priority + short time + layer priority,’ relying on the tree structure characteristics of the process, and solves the constraint conflict between the processes through layer-by-layer scheduling.
- (2)
- The ISA-TDD algorithm adopts the product contribution value strategy to determine the product processing order. It fully considered the impact of the urgent path and the number of urgent processes during the scheduling, which effectively reduces the processing time of parallel processes. However, the ISA-DDUD and the ISA-CDD algorithms do not take the impact of these two factors into account, and the equipment has unnecessary idle time during the processing, which extends the processing gap during the scheduling. It leads to a result of delays in the product completion time.
- (3)
- The dynamic adjustment strategy for game processes helps the ISA-TDD algorithm reduce equipment idle time and shorten product processing time. Dynamic adjustment of the processing sequence achieves more efficient resource allocation and quickly realizes the scheduling effect of the process on the equipment. For example, by the ISA-TDD algorithm, the idle time of machine is to and to , which is smaller than that obtained by the ISA-DDUD and the ISA-CDD. For another example, by the ISA-TDD algorithm, the process on the equipment is completed at , which is 20 and 65 hours earlier than that obtained by ISA-DDUD and ISA-CDD, respectively. Meanwhile, the limitation of the ISA-DDUD and the ISA-CDD algorithms is that they do not fully consider the dynamic changes of relative positions between processes, resulting in the overall utilization of the equipment failing to reach the optimal level.
6.4. Analysis of Applicability and Potential Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miao, C.X.; Song, J.X.; Zhang, Y.Z. Single-machine time-dependent scheduling with proportional and delivery times. Asia-Pac. J. Oper. Res. 2023, 40, 2240015. [Google Scholar] [CrossRef]
- Sun, W.J.; Gong, H.; Xu, K.; Shen, A.H. Cooperative games on proportionate flow-shop scheduling problem with due-dates. Control Decis. 2022, 37, 712–720. [Google Scholar]
- Song, C.L. Research on modeling and algorithm of no-wait flow shop scheduling problem with prohibited tardiness. J. Dalian Jiaotong Univ. 2018, 39, 100–105. [Google Scholar]
- Wang, D.Z.; Liu, S.X.; Guo, X.W. A multi-agentevolutionary algorithm for solving total tardiness permutation flow-shop scheduling problem. Acta Autom. Sin. 2014, 40, 548–555. [Google Scholar]
- Rui, Z.; Cheng, W. A double-layered optimization approach for the integrated due date assignment and scheduling problem. Int. J. Prod. Res. 2012, 50, 5–22. [Google Scholar]
- Imanol, E.; Maialen, M.; Roberto, S. Leveraging constraint programming in a deep learning approach for dynamically solving the flexible job-shop scheduling problem. Expert Syst. Appl. 2025, 265, 125895. [Google Scholar]
- Zhu, H.H.; Luo, N.; Li, X.P. A quantum-inspired cuckoo co-evolutionary algorithm for no-wait flow shop scheduling. IET Collab. Intell. Manuf. 2021, 3, 105–118. [Google Scholar] [CrossRef]
- Bilel, M.; Olfa, B.D.; Khaled, G. Solving distributed and flexible job shop scheduling problem using a chemical reaction optimization metaheuristic. Procedia Comput. Sci. 2018, 126, 1424–1433. [Google Scholar]
- Qu, G.Q. Bottleneck focused heuristic algorithm for hybrid flow shop scheduling problem. Inf. Control 2012, 41, 514–521. [Google Scholar]
- Wang, S.Y.; Wang, L.; Xu, Y. An estimation of distribution algorithm for solving hybrid flow-shop scheduling problem. Acta Autom. Sin. 2012, 38, 437–443. [Google Scholar] [CrossRef]
- Xie, Z.Q. Study on operation Scheduling of complex product with constraint among jobs. Ph.D. Thesis, Harbin University of Science and Technology, Harbin, China, 2009. [Google Scholar]
- Liu, X.C.; Zhao, N.; Yang, Z.; Su, Y.H.; Zhou, W. An integrated scheduling algorithm based on dynamically adjusting leaf node processes. Intell. Comput. Appl. 2022, 12, 208–213. [Google Scholar] [CrossRef]
- Berghman, L.; Kergosien, Y.; Billaut, J.C. A review on integrated scheduling and outbound vehicle routing problems. Eur. J. Oper. Res. 2023, 311, 1–23. [Google Scholar] [CrossRef]
- Zeng, L.; Liang, X.B.; Ou, Y.; Ye, L.D. Energy integrated based on multiobjective-constrained optimization evolutionary algorithm. Comput. Integr. Manuf. Syst. 2016, 22, 2668. [Google Scholar]
- Gui, Z.Y.; Yang, J.; Xie, Z.Q. Scheduling algorithm for flexible job shop based on pruning and layering. Control Decis. 2017, 32, 1921–1932. [Google Scholar]
- Xie, Z.Q.; Yang, D.; Ma, M.R.; Yu, X. An improved artificial bee colony algorithm for the flexible integrated scheduling problem using networked devices collaboration. Int. J. Coop. Inf. Syst. 2020, 29, 19. [Google Scholar] [CrossRef]
- Zhou, W.; Ding, X.Y.; Xie, Z.Q. An integrated scheduling algorithm considering the processing capacity of flexible equipment. J. South China Norm. Univ. (Nat. Sci. Ed.) 2024, 56, 110–118. [Google Scholar] [CrossRef]
- Francesco, P.; Luigi, B.; Salvatore, V.; Rocco, A.; Beniamino, D.M. A distributed scheduling framework based on selfish autonomous agents for federated cloud environments. Future Gener. Comput. Syst. 2013, 29, 1461–1472. [Google Scholar]
- Shunsuke, O.; Tomohisa, T.; Jiang, Z.; Yoshio, S. Robust production scheduling using autonomous distributed systems. Key Eng. Mater. 2012, 516, 166–169. [Google Scholar]
- Omid, F.; Mahmoud, H. A collaborative and integrated platform to support distributed manufacturing system using a service-oriented approach based on cloud computing paradigm. Robot. Comput.-Integr. Manuf. 2013, 29, 110–127. [Google Scholar]
- Wu, X.L.; Sun, S.D.; Yu, J.J.; Zhang, H.F. Research on multi-objective flexible job shop scheduling. Comput. Integr. Manuf. Syst. 2006, 5, 731–736. [Google Scholar] [CrossRef]
- Liu, A.J.; Yang, Y.; Xing, Q.S.; Lu, H.; Zhang, Y.D. Dynamic scheduling on multi-objective flexible job shop. Comput. Integr. Manuf. Syst. 2011, 17, 2629–2637. [Google Scholar]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X.S. A discrete firefly algorithm for the multi-objective hybrid flow-shop scheduling problems. IEEE Trans. Evol. Comput. 2013, 18, 301–305. [Google Scholar] [CrossRef]
- Liao, B.F.; Lei, Q.; Wu, W.L.; Song, Y.C.; Guo, W.F. Hybrid teaching-learning-based optimization algorithms for integrated scheduling of multi-workshop collaborations. China Mech. Eng. 2020, 31, 1940. [Google Scholar]
- Xie, Z.Q.; Yu, J.; Chen, D.Y. Integrated scheduling algorithm of two workshops based on the principle of the neighborhood rendering. J. Mech. Eng. 2016, 52, 149–159. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Guo, H.; Su, W.X.; Xin, Y.; Yang, J. Reversal sequence integrated scheduling algorithm of multipe workshop with multi-procedures ended together. J. Jilin Univ. (Eng. Technol. Ed.) 2018, 48, 578–587. [Google Scholar]
- Liu, J.J.; Li, Q.S.; Zeng, C.F.; Chen, Q.X. Flexible assembly flowshop scheduling with batch delivery. Comput. Integr. Manuf. Syst. 2023, 1–25. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Yang, J.; Zhou, Y.; Zhang, D.L.; Tan, G.Y. Dynamic critical paths mult i product manufacturing scheduling algorithm based on operation set. Chin. J. Comput. 2011, 34, 406–412. [Google Scholar] [CrossRef]
- Xie, Z.Q.; Chang, N.N.; Yang, J. Integrated scheduling algorithm based on urgency of delivery date. J. Mech. Eng. 2011, 47, 181–190. [Google Scholar] [CrossRef]
- Li, T.S. Research on Dynamic Multi-Product Integrated Scheduling Algorithm Considering Delivery Date Constraints. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2023. [Google Scholar]



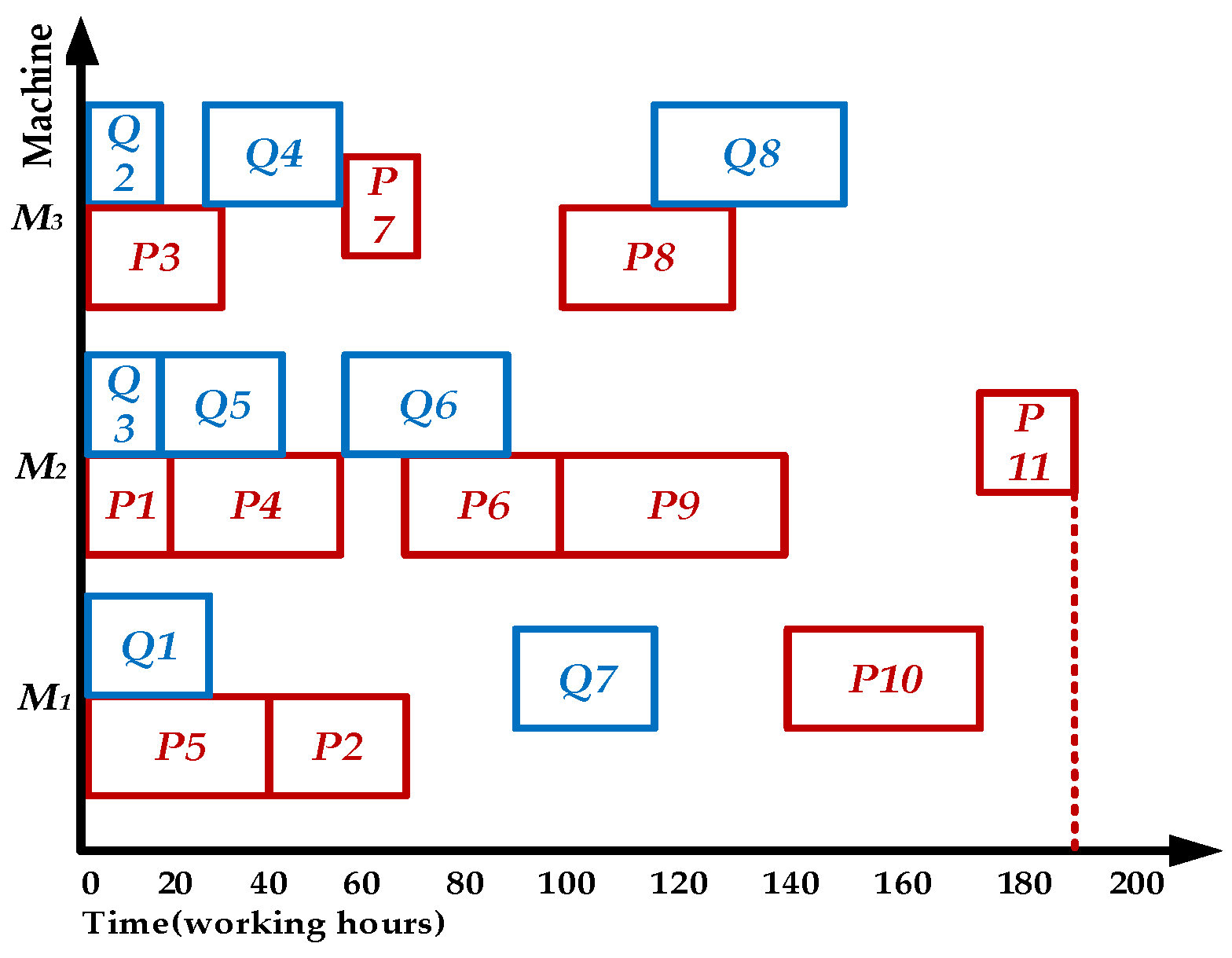
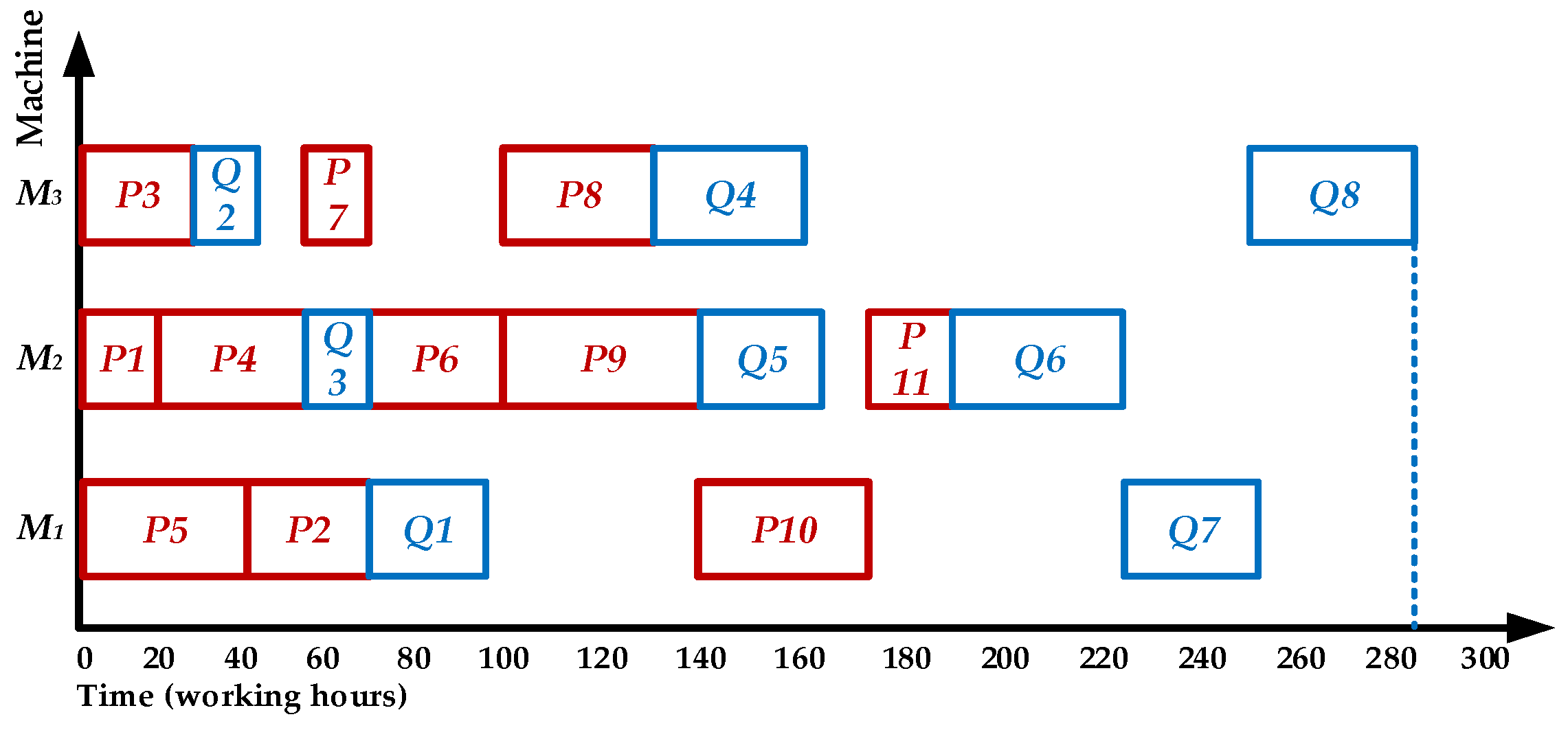

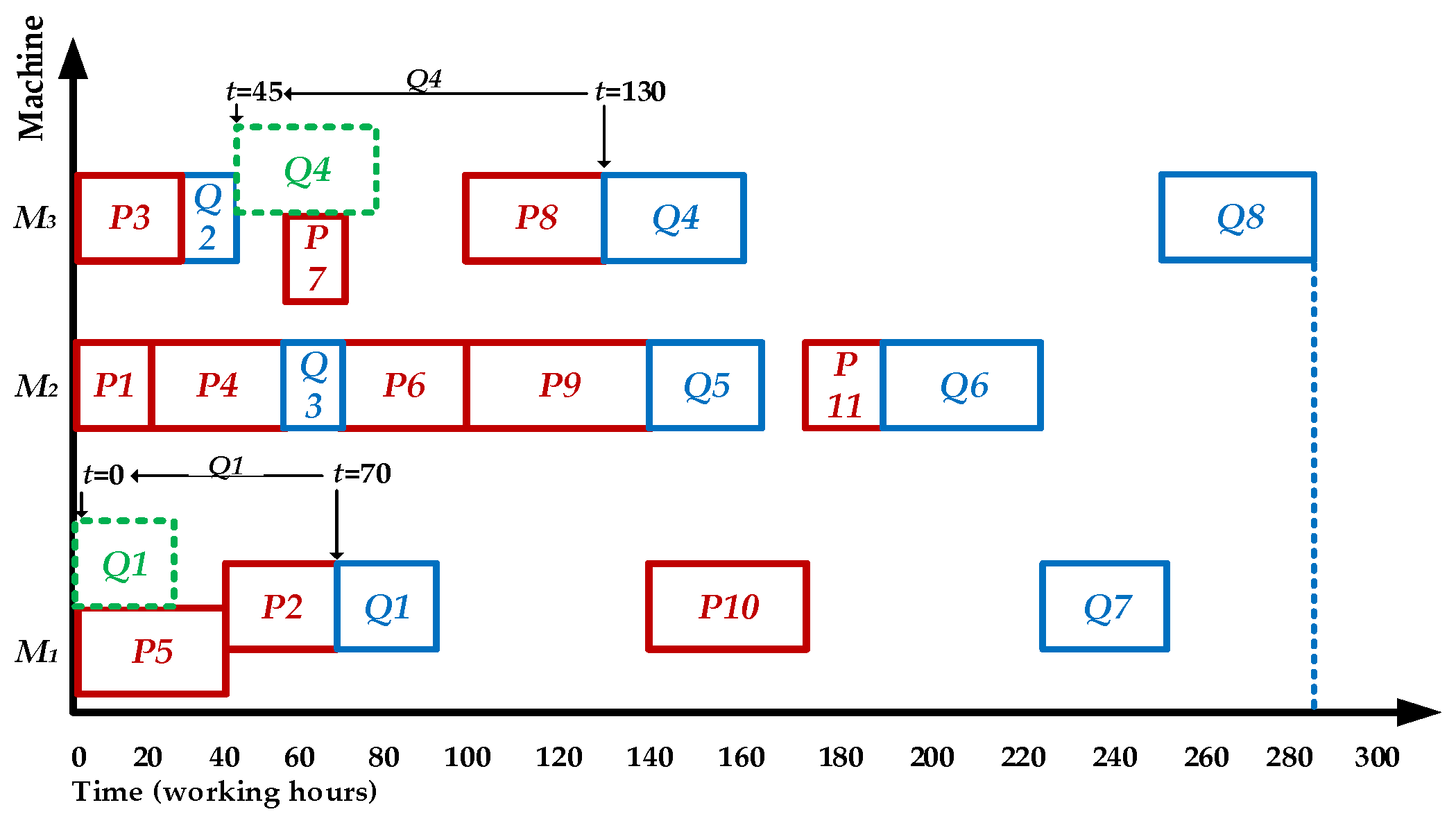
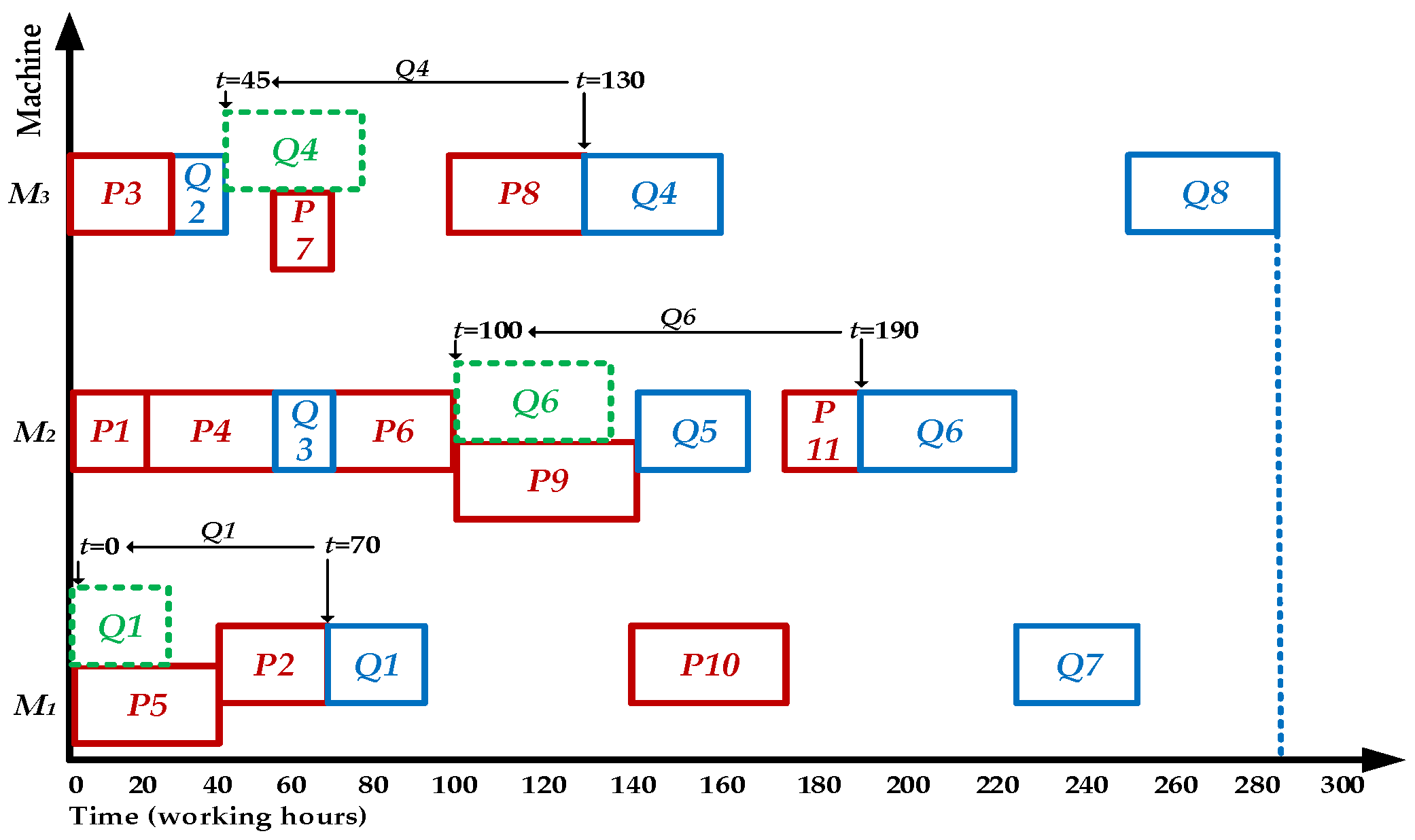
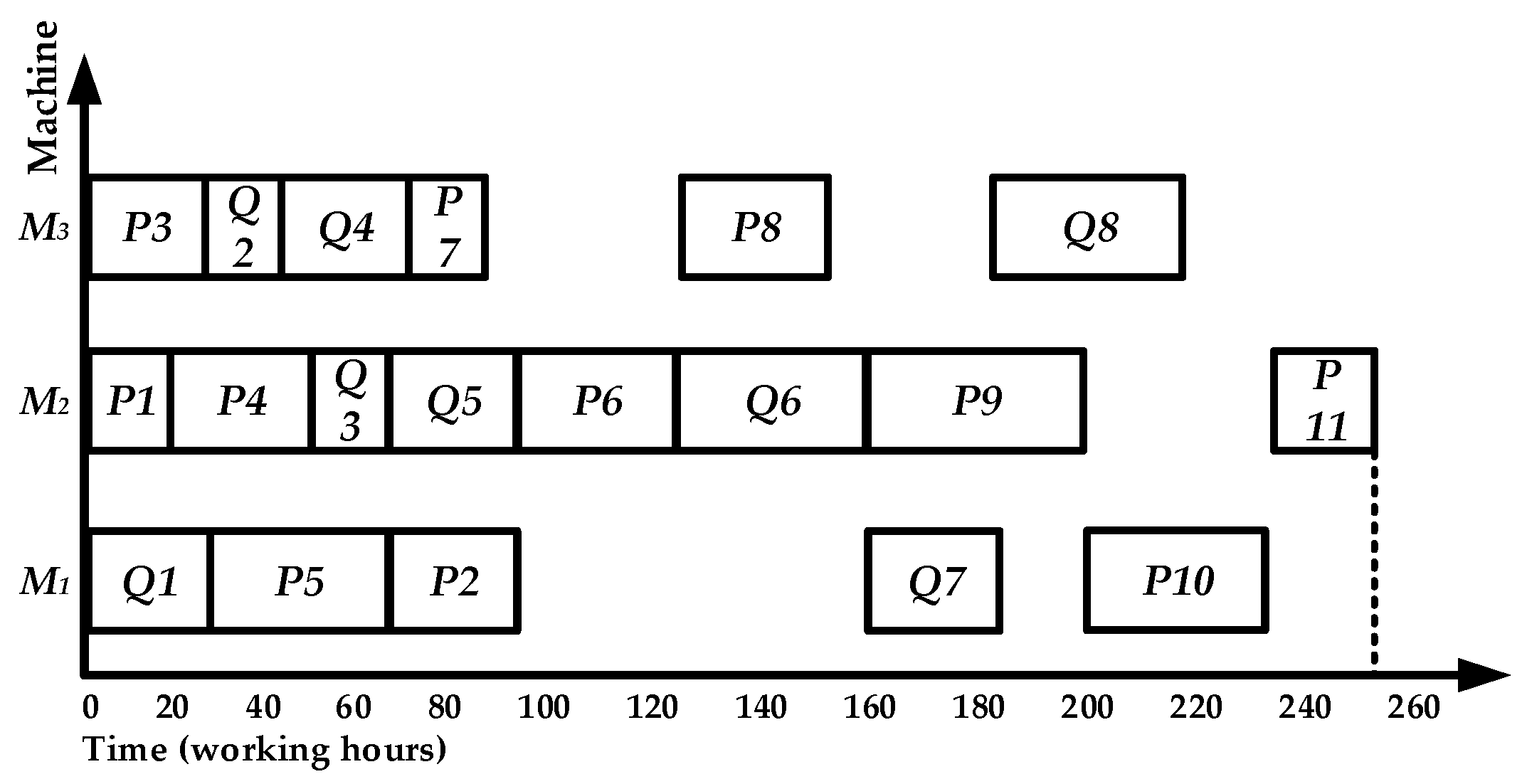
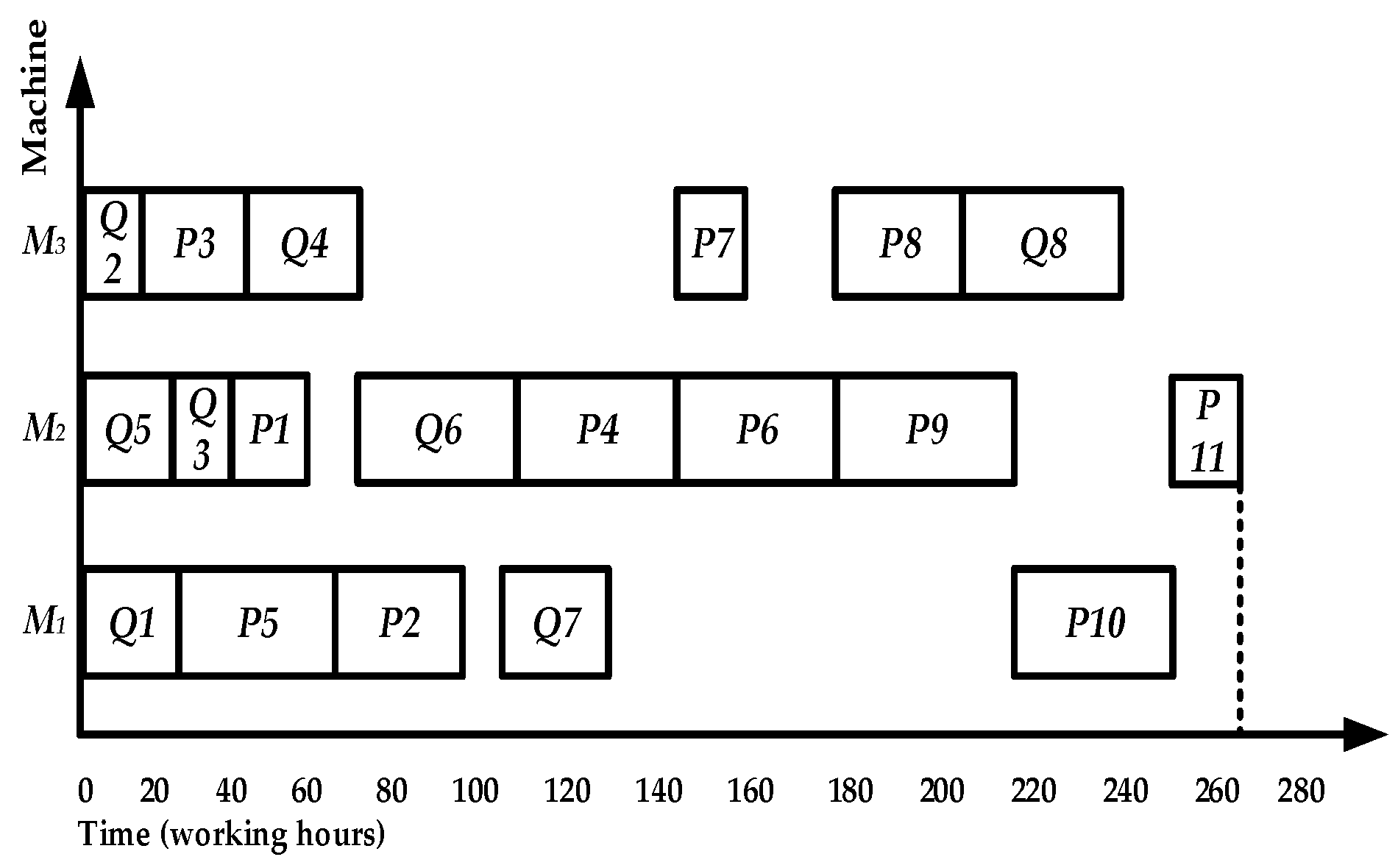
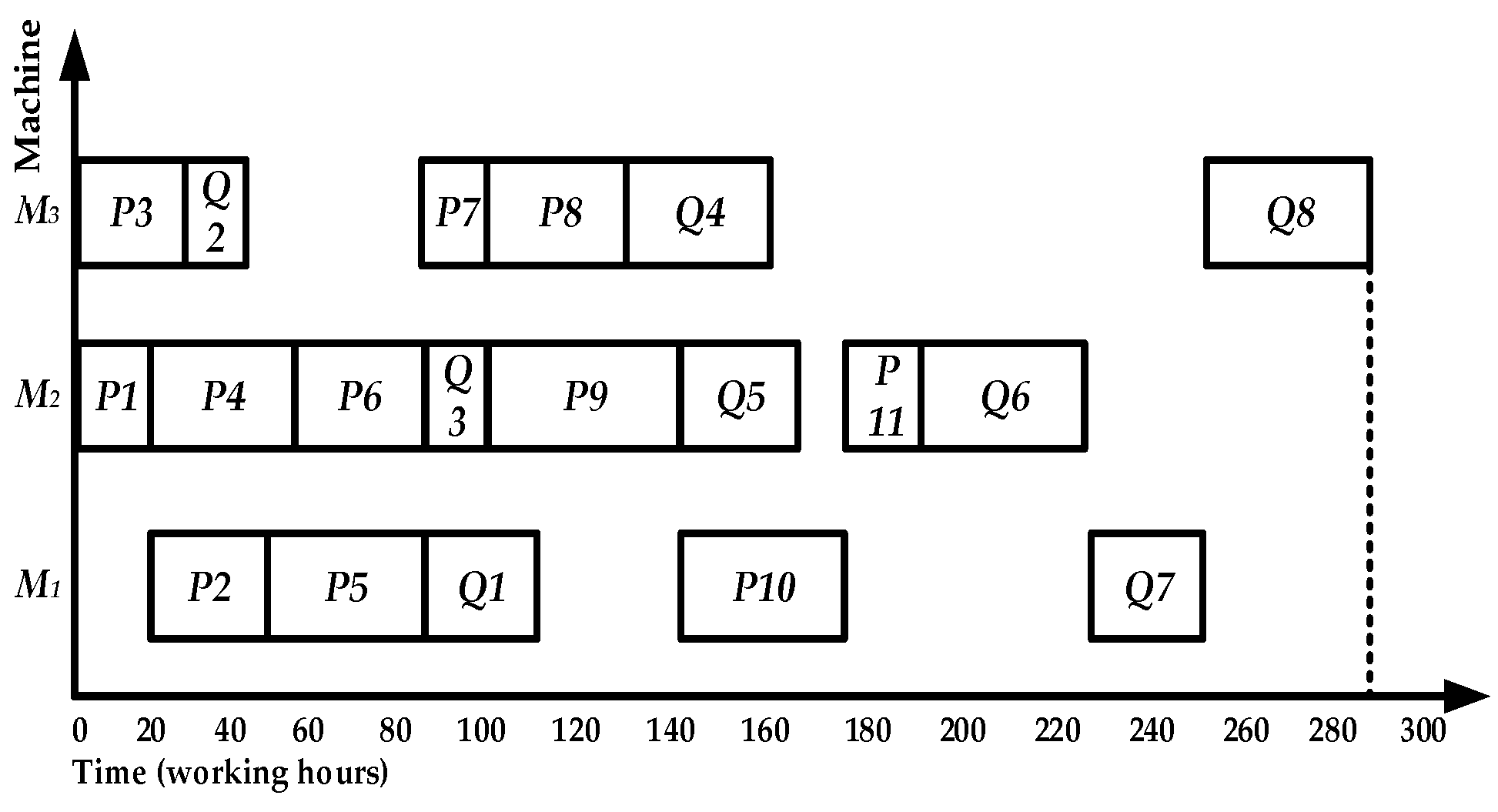
| Product | Original Complete Time | Urgent Path Length | Max Delivery Time | Contribute Value | Schedule Order |
|---|---|---|---|---|---|
| P | 190 | 175 | 285 | 1.84 | 1 |
| Q | 150 | 150 | 285 | 1.11 | 2 |
| Game Process Set | Conflict Machine | Game Result |
|---|---|---|
| {P1, Q3} | M2 | P1 |
| {P4, Q3} | M2 | P4 |
| {P3, Q2} | M3 | P3 |
| {P5, Q1} | M1 | Q1 |
| {P2, Q1} | M1 | Q1 |
| {P6, Q6} | M2 | P6 |
| {P7, Q4} | M3 | Q4 |
| {P9, Q6} | M2 | Q6 |
| Algorithms | Completion Time | Total Idle Time of the Device | Overall Utilization of Equipment | Relative Increase Rate of the Overall Device Utilization | Delivery Shortening Rate |
|---|---|---|---|---|---|
| ISA-DDUD | 265 | 225 | 70.2% | 4.4% | 7% |
| ISA-CDD | 285 | 220 | 69.7% | 4.9% | 0% |
| ISA-TDD | 255 | 175 | 74.6% | ┄┄ | 10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Wang, D.; Zhou, W.; Xie, Z.; Sun, M.; Tan, Z. Dynamic Multi-Product Integrated Scheduling Algorithm with Urgent Delivery Date. Electronics 2025, 14, 693. https://doi.org/10.3390/electronics14040693
Guo J, Wang D, Zhou W, Xie Z, Sun M, Tan Z. Dynamic Multi-Product Integrated Scheduling Algorithm with Urgent Delivery Date. Electronics. 2025; 14(4):693. https://doi.org/10.3390/electronics14040693
Chicago/Turabian StyleGuo, Jianing, Dadong Wang, Wei Zhou, Zhiqiang Xie, Ming Sun, and Zhenjiang Tan. 2025. "Dynamic Multi-Product Integrated Scheduling Algorithm with Urgent Delivery Date" Electronics 14, no. 4: 693. https://doi.org/10.3390/electronics14040693
APA StyleGuo, J., Wang, D., Zhou, W., Xie, Z., Sun, M., & Tan, Z. (2025). Dynamic Multi-Product Integrated Scheduling Algorithm with Urgent Delivery Date. Electronics, 14(4), 693. https://doi.org/10.3390/electronics14040693






