Age-Aware Scheduling for Federated Learning with Caching in Wireless Computing Power Networks
Abstract
1. Introduction
1.1. Related Works
1.2. Contributions and Paper Organization
- To address the trade-off between parameter age and service delays, we propose an FL resource scheduling strategy based on information age perception in WCPNs, which takes advantage of data caching mechanisms. This strategy optimizes the device’s data collection frequency, computation frequency, and spectrum resource allocation to improve global model performance in FL.
- We comprehensively consider the aging of parameters, time-varying channels, random FL request arrivals, and heterogeneous computing capabilities among participating devices. We model the high-dimensional, dynamic, multi-user centralized FL framework system as an MDP and employ the Proximal Policy Optimization (PPO) algorithm to minimize global parameter age, energy consumption, and FL service delays.
- Extensive comparative simulation experiments are conducted to verify the correctness and superiority of our scheme, with an in-depth analysis of the results.
2. Notations
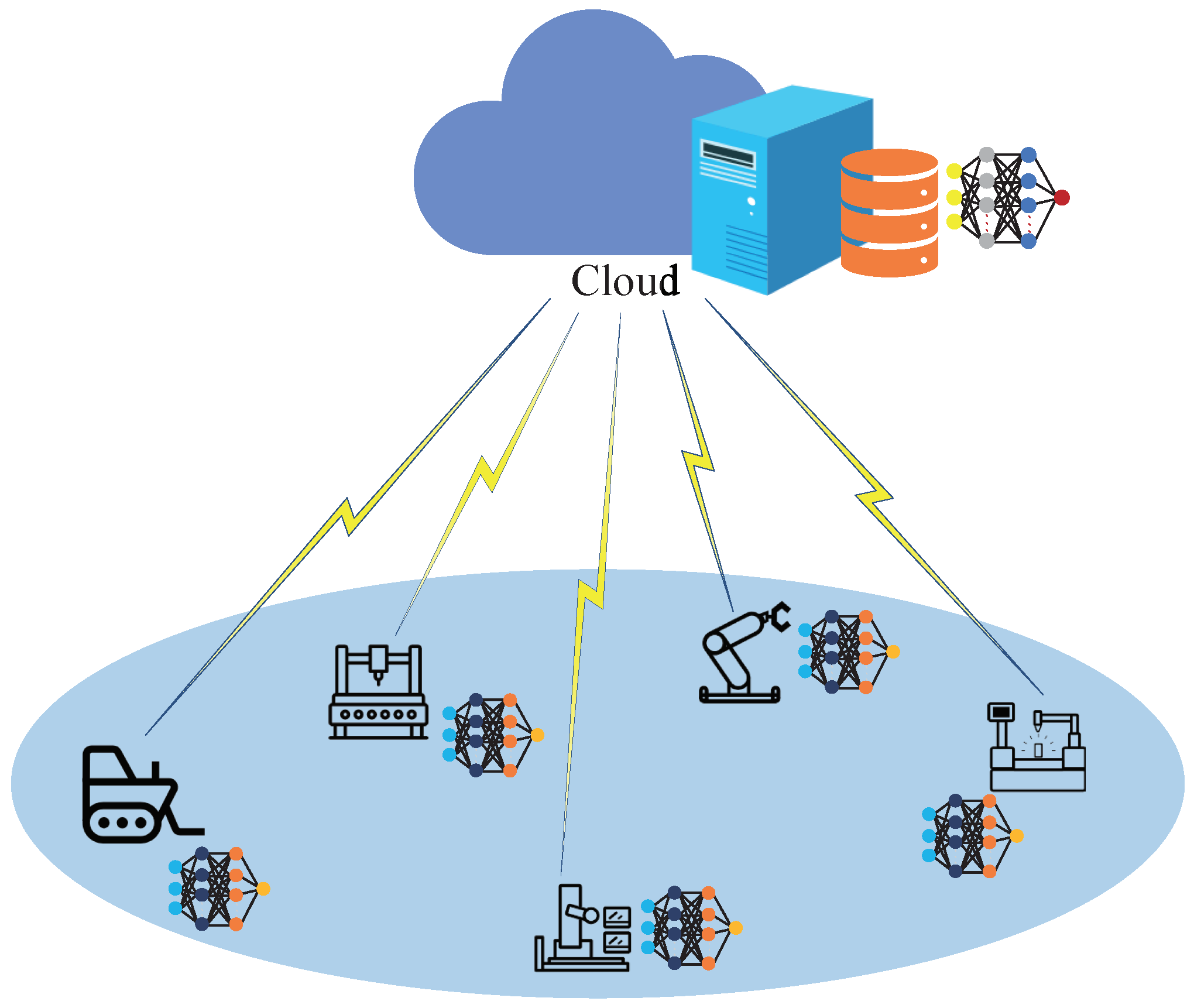
3. System Model and Problem Formulation
3.1. AoI and Service Latency Model
3.1.1. Local Delay and Age of Local Data
3.1.2. Transmission Delay and Age of Model
3.2. Energy Consumption Model
3.2.1. Energy Consumption for Local Training
3.2.2. Energy Consumption for Model Uploads
3.3. Problem Formulation
4. Algorithm
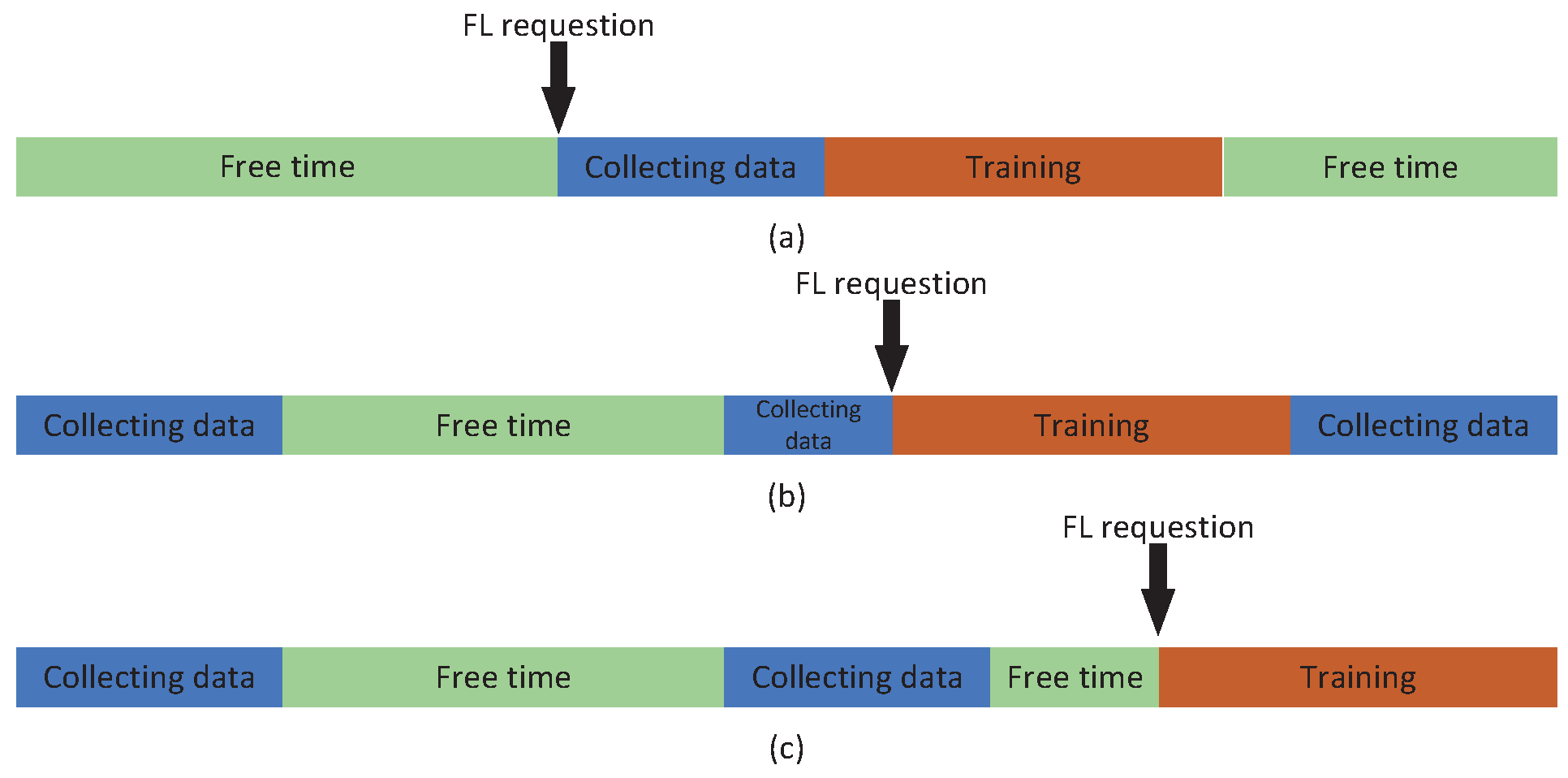
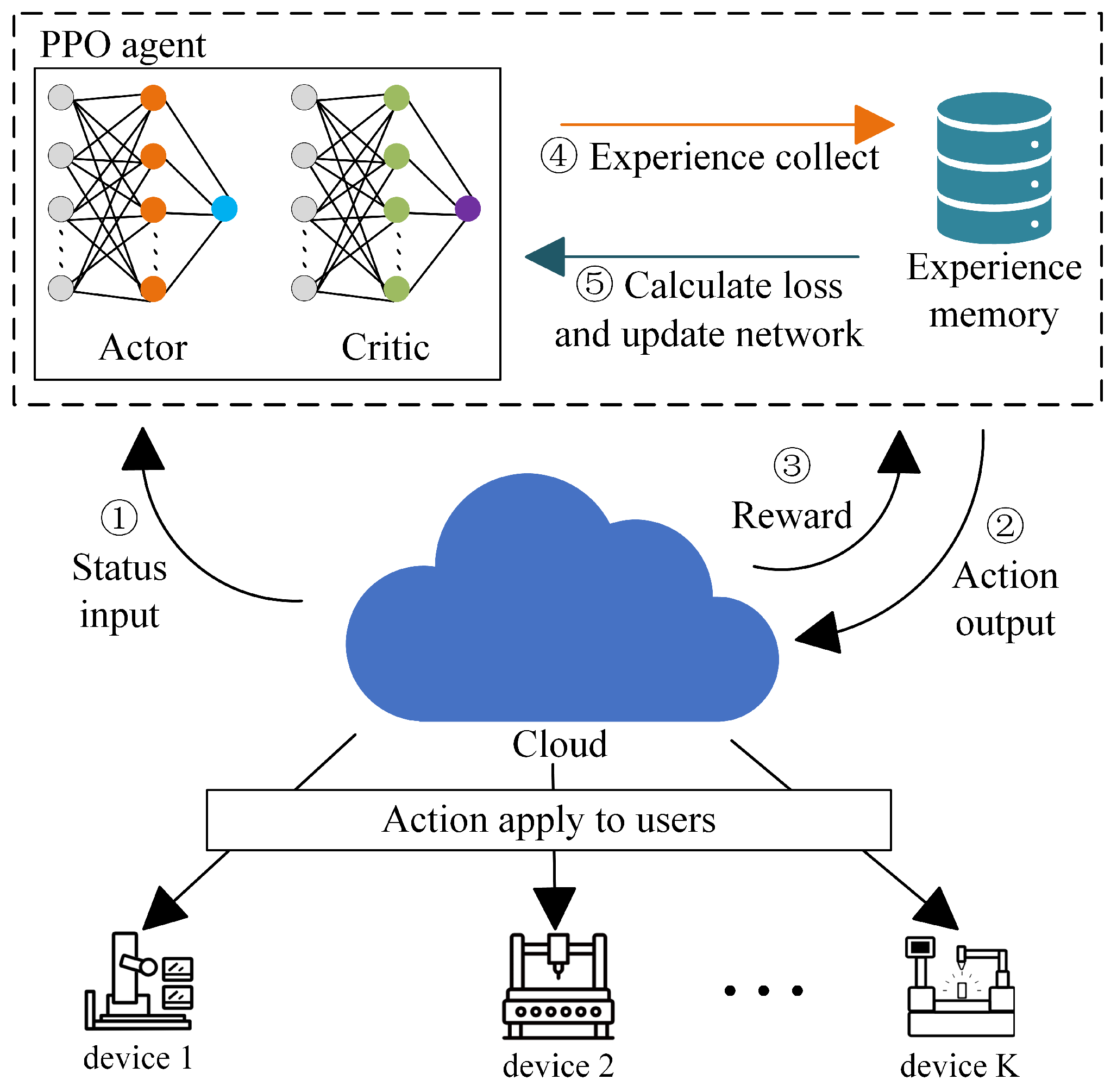
- The WCPN sends the environment state to the PPO agent.
- The PPO agent outputs the optimal decision and evaluation value based on the current state and then returns the decision to the WCPN environment for execution.
- The WCPN environment returns a reward after executing the decision.
- The PPO agent stores relevant data in the experience replay buffer.
- Once the experience replay buffer contains a sufficient amount of data, the parameters of the Actor and Critic networks in the PPO agent are updated.
4.1. MDP Modeling for Optimization Problems
4.1.1. State
4.1.2. Action
4.1.3. Reward
4.2. Double-Cache FL Scheduling Algorithm for Parameter Age Based on PPO
| Algorithm 1: Parameter age-aware PPO double-buffer FL scheduling algorithm |
 |
5. Experiment
5.1. Experimental Settings
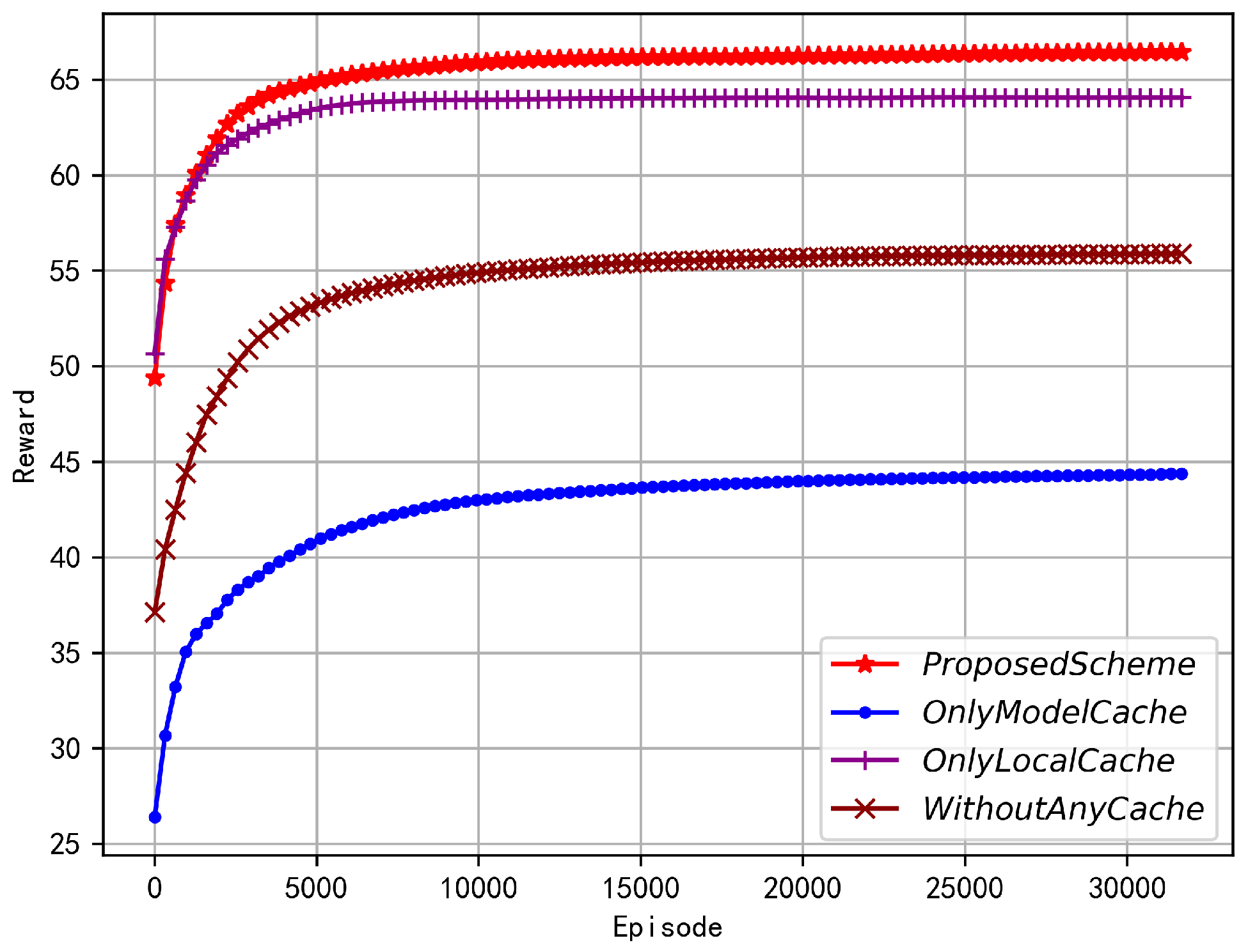
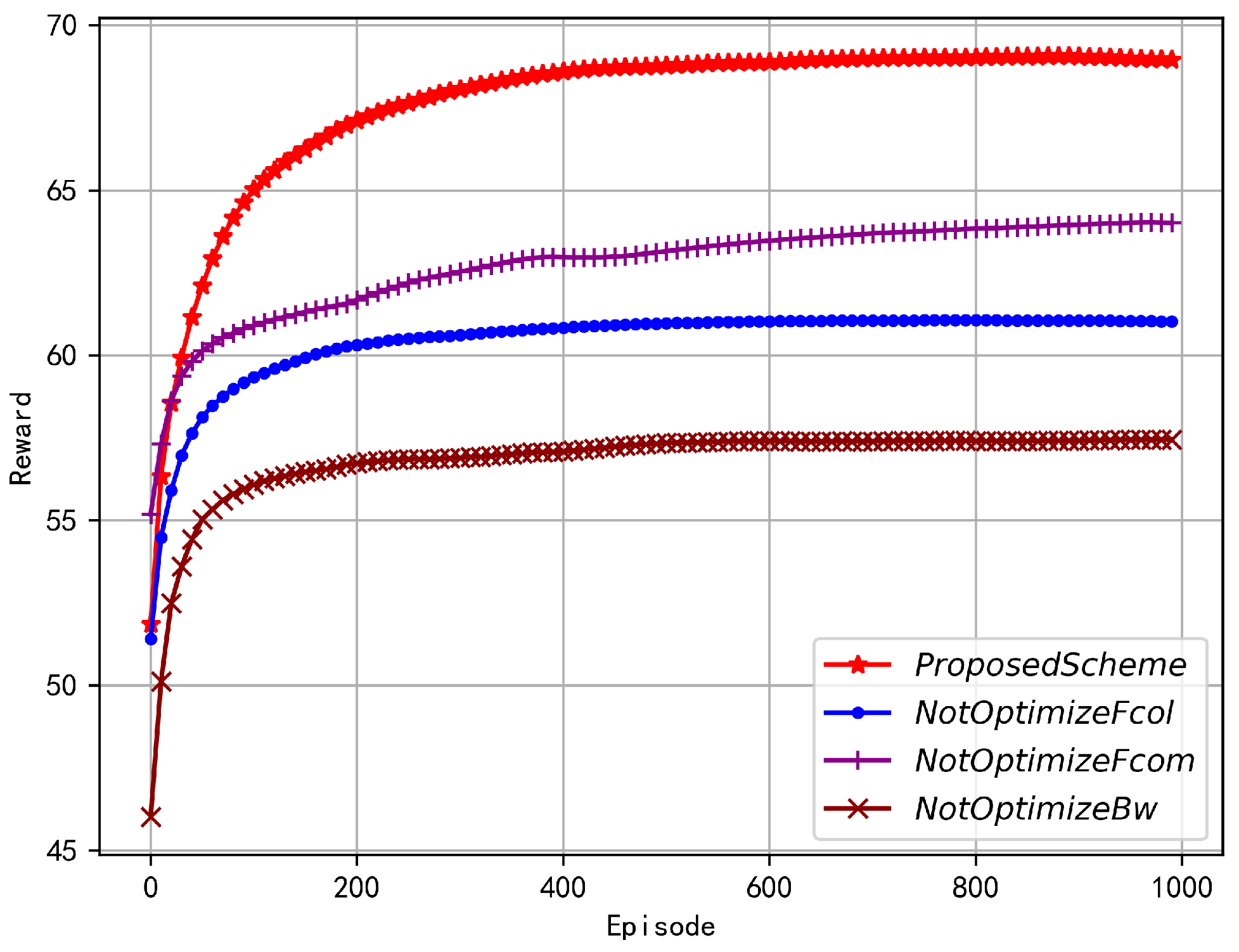
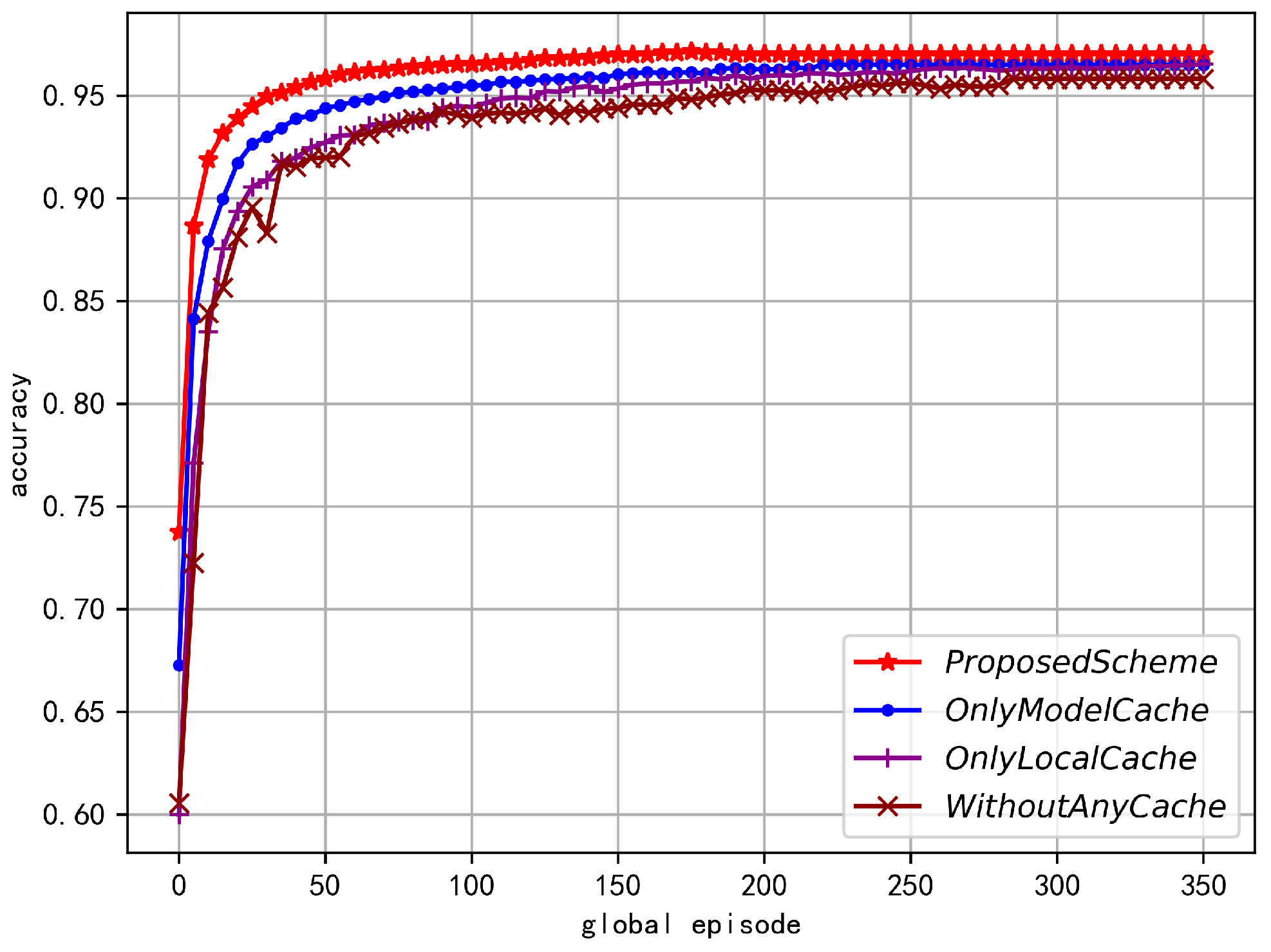
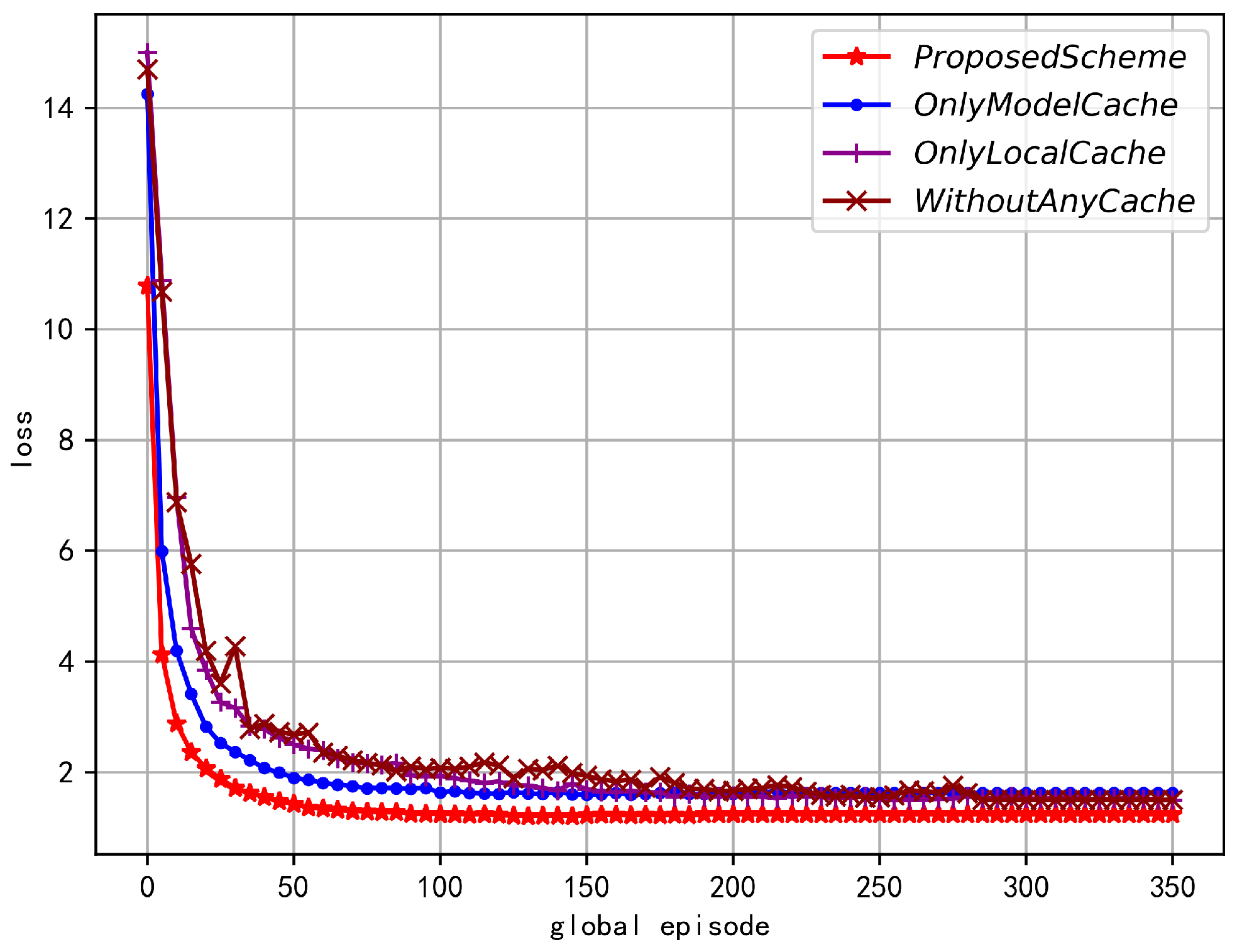
5.2. Numerical Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, Y.; Zheng, X. 6G: A survey on technologies, scenarios, challenges, and the related issues. J. Ind. Inf. Integr. 2020, 19, 100158. [Google Scholar] [CrossRef]
- Sun, W.; Lei, S.; Wang, L.; Liu, Z.; Zhang, Y. Adaptive federated learning and digital twin for industrial internet of things. IEEE Trans. Ind. Inform. 2020, 17, 5605–5614. [Google Scholar] [CrossRef]
- Qu, Y.; Dong, C.; Zheng, J.; Dai, H.; Wu, F.; Guo, S.; Anpalagan, A. Empowering edge intelligence by air-ground integrated federated learning. IEEE Netw. 2021, 35, 34–41. [Google Scholar] [CrossRef]
- McMahan, H.B.; Yu, F.X.; Richtarik, P.; Suresh, A.T.; Bacon, D.; Konečný, J. Federated learning: Strategies for improving communication efficiency. arXiv 2016, arXiv:1610.05492. [Google Scholar]
- McMahan, H.B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B.A. Communication-efficient learning of deep networks from decentralized data. arXiv 2016, arXiv:1602.05629. [Google Scholar]
- Lin, Y.; Han, S.; Mao, H.; Wang, Y.; Dally, W.J. Deep gradient compression: Reducing the communication bandwidth for distributed training. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Letaief, K.B.; Chen, W.; Shi, Y.; Zhang, J.; Zhang, Y.J.A. The roadmap to 6G:CAI empowered wireless networks. IEEE Commun. Mag 2019, 57, 84–90. [Google Scholar] [CrossRef]
- Wang, P.; Sun, W.; Zhang, H.; Ma, W.; Zhang, Y. Distributed and secure federated learning for wireless computing power networks. IEEE Trans. Veh. Technol. 2023, 72, 9381–9393. [Google Scholar] [CrossRef]
- Mao, Y.; You, C.; Zhang, J.; Huang, K.; Letaief, K.B. A survey on mobile edge computing: The communication perspective. IEEE Commun. Surv. Tutor. 2017, 19, 2322–2358. [Google Scholar] [CrossRef]
- Ha, S.; Zhang, J.; Simeone, O.; Kang, J. Coded federated computing in wireless networks with straggling devices and imperfect CSI. arXiv 2019, arXiv:1901.05239. [Google Scholar]
- Reisizadeh, A.; Tziotis, I.; Hassani, H.; Mokhtari, A.; Pedarsani, R. Straggler-resilient federated learning: Leveraging the interplay between statistical accuracy and system heterogeneity. arXiv 2020, arXiv:2012.14453. [Google Scholar] [CrossRef]
- Chen, M.; Poor, H.V.; Saad, W.; Cui, S. Convergence Time Minimization of Federated Learning over Wireless Networks. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Huang, X.; Leng, S.; Maharjan, S.; Zhang, Y. Multi-agent deep reinforcement learning for computation offloading and interference coordination in small cell networks. IEEE Trans. Veh. Technol. 2021, 70, 9282–9293. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Aloqaily, M.; Reisslein, M. FedCo: A federated learning controller for content management in multi-party edge systems. In Proceedings of the 2021 International Conference on Computer Communications and Networks (ICCCN), Athens, Greece, 19–22 July 2021; pp. 1–9. [Google Scholar]
- Sun, W.; Li, Z.; Wang, Q.; Zhang, Y. FedTAR: Task and Resource-Aware Federated Learning for Wireless Computing Power Networks. IEEE Internet Things J. 2023, 10, 4257–4270. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, Z.; Min, G.; Mao, S. Average age of information in wireless powered mobile edge computing system. IEEE Wirel. Commun. Lett. 2022, 11, 1585–1589. [Google Scholar] [CrossRef]
- Zhang, G.; Zheng, Y.; Liu, Y.; Hu, J.; Yang, K. Resource Scheduling for Timely Wireless Powered Crowdsensing with the Aid of Average Age of Information. In Proceedings of the ICC 2024—IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 4161–4166. [Google Scholar] [CrossRef]
- Zhu, J.; Gong, J. Optimizing Peak Age of Information in MEC Systems: Computing Preemption and Non-Preemption. IEEE/ACM Trans. Netw. 2024, 32, 3285–3300. [Google Scholar] [CrossRef]
- Vineeth, B.S.; Thomas, R.C. On the Average Age-of-Information for Hybrid Multiple Access Protocols. IEEE Netw. Lett. 2022, 4, 87–91. [Google Scholar] [CrossRef]
- Moltafet, M.; Leinonen, M.; Codreanu, M. Average Age of Information for a Multi-Source M/M/1 Queueing Model with Packet Management and Self-Preemption in Service. In Proceedings of the 2020 18th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOPT), Volos, Greece, 15–19 June 2020; pp. 1–5. [Google Scholar]
- Zheng, Y.; Hu, J.; Yang, K. Average Age of Information in Wireless Powered Relay Aided Communication Network. IEEE Internet Things J. 2022, 9, 11311–11323. [Google Scholar] [CrossRef]
- Hui, E.T.Z.; Madhukumar, A.S. Mean Peak Age of Information Analysis of Energy-Aware Computation Offloading in IIoT Networks. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, Y.; Zhu, X.; Cao, J.; Sun, S. Optimized Age of Information for Relay Systems with Resource Allocation. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, J.; Gong, J. Optimizing Peak Age of Information in Mobile Edge Computing. In Proceedings of the 2023 35th International Teletraffic Congress (ITC-35), Turin, Italy, 3–5 October 2023; pp. 1–9. [Google Scholar] [CrossRef]
- Wang, X.; Ning, Z.; Guo, S.; Wen, M.; Poor, V. Minimizing the Age of-critical-information: An imitation learning-based scheduling approach under partial observations. IEEE Trans. Mobile Comput. 2021. early access. [Google Scholar] [CrossRef]
- Dai, W.; Zhou, Y.; Dong, N.; Zhang, H.; Xing, E.P. Toward understanding the impact of staleness in distributed machine learning. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019; pp. 1–6. [Google Scholar]
- Buck, D.; Singhal, M. An analytic study of caching in computer systems. J. Parallel Distrib. Comput. 1996, 32, 205–214. [Google Scholar] [CrossRef]
- Fu, F.; Miao, X.; Jiang, J.; Xue, H.; Cui, B. Towards communication-efficient vertical federated learning training via cache-enabled local updates. arXiv 2022, arXiv:2207.14628. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, S.; Wang, Y.; Liu, M.; Xu, K.; Wang, W.; Jiang, X.; Gao, B.; Lu, J. Fedcache: A knowledge cache-driven federated learning architecture for personalized edge intelligence. IEEE Trans. Mob. Comput. 2024, 23, 9368–9382. [Google Scholar] [CrossRef]
- Liu, Y.; Su, L.; Joe-Wong, C.; Ioannidis, S.; Yeh, E.; Siew, M. Cache-Enabled Federated Learning Systems. In Proceedings of the Twenty-Fourth International Symposium on Theory, Algorithmic Foundations, and Protocol Design for Mobile Networks and Mobile Computing, Washington, DC, USA, 23–26 October 2023; pp. 1–11. [Google Scholar]
- Liu, X.; Qin, X.; Chen, H.; Liu, Y.; Liu, B.; Zhang, P. Age-aware Communication Strategy in Federated Learning with Energy Harvesting Devices. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021; pp. 358–363. [Google Scholar] [CrossRef]
- Meng, Q.; Lu, H.; Qin, L. Energy Optimization in Statistical AoI - Aware MEC Systems. IEEE Commun. Lett. 2024, 28, 2263–2267. [Google Scholar] [CrossRef]
- Zhu, Z.; Wan, S.; Fan, P.; Letaief, K.B. Federated Multiagent Actor-Critic Learning for Age Sensitive Mobile-Edge Computing. IEEE Internet Things J. 2022, 9, 1053–1067. [Google Scholar] [CrossRef]
- Xu, J.; Jia, X.; Hao, Z. Research on Information Freshness of UAV-assisted IoT Networks Based on DDQN. In Proceedings of the 2022 IEEE 5th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 16–18 December 2022; pp. 427–433. [Google Scholar] [CrossRef]
- Dong, L.; Zhou, Y.; Liu, L.; Qi, Y.; Zhang, Y. Age of Information Based Client Selection for Wireless Federated Learning With Diversified Learning Capabilities. IEEE Trans. Mob. Comput. 2024, 23, 14934–14945. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, X.; Lin, W. Joint AoI-Aware UAVs Trajectory Planning and Data Collection in UAV-Based IoT Systems: A Deep Reinforcement Learning Approach. IEEE Trans. Consum. Electron. 2024, 70, 6484–6495. [Google Scholar] [CrossRef]
- Hsu, Y.-L.; Liu, C.-F.; Wei, H.-Y.; Bennis, M. Optimized Data Sampling and Energy Consumption in IIoT: A Federated Learning Approach. IEEE Trans. Commun. 2022, 70, 7915–7931. [Google Scholar] [CrossRef]
- Zhang, S.; Li, J.; Luo, H.; Gao, J.; Zhao, L.; Shen, X.S. Towards fresh and low-latency content delivery in vehicular networks: An edge caching aspect. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar]
- Dai, W.; Zhou, Y.; Dong, N.; Zhang, H.; Xing, E.P. Toward Understanding the Impact of Staleness in Distributed Machine Learning. arXiv 2018, arXiv:1810.03264. [Google Scholar]
- Bie, T.; Zhu, X.Q.; Fu, Y.; Li, X.; Ruan, X.; Wang, Q. Safety priority path planning method based on Safe-PPO algorithm. J. Beijing Univ. Aeronaut. Astronaut. 2021, 49, 1–15. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]



| Previous Works | Optimization—Target Focus | Method | Performance in Service Delays | Performance in Parameter Age | Performance in Energy Consumption |
|---|---|---|---|---|---|
| [31] | Mainly on preventing device dropout for parameter-age optimization and less on delays and energy | Energy-harvesting technology | Limited optimization | Good for preventing dropout for age but not comprehensive | Limited consideration |
| [32] | Mainly on AoI tail-distribution analysis and energy minimization and less on FL service delays | Random network calculus (SNC) | Less attention | Focuses on AoI analysis | Focuses on energy minimization |
| [33] | AoI minimization | Hybrid strategy-based multi-modal DRL framework | Does not fully consider FL system dynamics | Focuses on AoI | Does not fully consider energy |
| [37] | AoI-related optimization with DRL | DRL-based approach for AoI | Focuses on AoI, not on FL service delays | Focuses on AoI | Focuses on AoI; not energy-centric |
| Our Work | Multi-objective optimization of global parameter age, energy consumption, and FL service delays | Modeled as MDP and used PPO algorithm and double-cache mechanism | Significant reduction | Lower final global parameter age | Effective energy reduction |
| Symbol | Definition |
|---|---|
| K | Number of smart devices |
| N | Number of iterations for model training or local data buffer length (context-dependent) |
| Threshold age of model | |
| Threshold delay for server to receive model | |
| Coefficient determined by the chip structure of device k | |
| Instantaneous voltage applied to the chip by device k at time t | |
| Voltage threshold to protect the chip | |
| Constant determined by physical factors of the chip | |
| Total floating-point operations (FLOPs) needed to process one data sample for device k | |
| FLOPs of each CPU cycle of device k | |
| Computation frequency of device k at time t | |
| Time for device k to process one data sample, | |
| Data collection frequency of device k | |
| Total number of collected data samples within the time interval between two global iterations for device k | |
| Time delay for device k to collect required data samples at time t | |
| Time delay for user k to perform local model training at time t | |
| , total service time for device k including local training and model upload at time t | |
| Time delay for device k to upload its local model at time t, | |
| Size of the local model of device k at time t | |
| Global maximum available bandwidth | |
| Bandwidth assigned to device k at time t | |
| Data upload rate of device k at time t, | |
| Signal-to-noise ratio from device k to the central server at time t | |
| Power consumed by device k during local training at time t, | |
| Local-phase energy consumption (including data collection and model training processes) of device k at time t | |
| Energy consumption of device k uploading its local model at time t, | |
| Energy consumption generated during the current global iteration | |
| Freshness of device k’s nth group of data at time t | |
| Age of user k’s local model at time t | |
| Latest global model age for global aggregation at time t, | |
| Indicator variable, | |
| Optimization objective function, | |
| State of the environment at decision epoch t, | |
| Action at decision epoch t, | |
| Reward at time t, | |
| Set of parameters for PPO agent’s policy | |
| Actor network parameters in PPO agent | |
| Critic network parameters in PPO agent | |
| Discount factor in PPO algorithm | |
| Advantage function in PPO algorithm | |
| Actor network’s objective function in PPO algorithm | |
| Critic network’s loss function in PPO algorithm | |
| Hyperparameter used to limit the magnitude of policy updates in PPO algorithm |
| Parameter | Description | Value |
|---|---|---|
| K | Number of devices | 6 |
| N | Local data buffer length | 1000 |
| Threshold age of model | 150 | |
| Threshold delay for server receive model | 30 s | |
| Device k’s chip structure coefficient | [0.38988, 0.60998] | |
| Device k’s chip clock frequency | [20, 50] FLOPS | |
| The maximum available computing resources of device k at time t | [2.0, 5.0] GHz | |
| SINR between device k and server at time t | [120, 130] | |
| Global maximum available bandwidth | 100 Mbps |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, X.; Luo, C.; Xie, Z.; Li, Y.; Jiang, L. Age-Aware Scheduling for Federated Learning with Caching in Wireless Computing Power Networks. Electronics 2025, 14, 663. https://doi.org/10.3390/electronics14040663
Zhuang X, Luo C, Xie Z, Li Y, Jiang L. Age-Aware Scheduling for Federated Learning with Caching in Wireless Computing Power Networks. Electronics. 2025; 14(4):663. https://doi.org/10.3390/electronics14040663
Chicago/Turabian StyleZhuang, Xiaochong, Chuanbai Luo, Zhenghao Xie, Yu Li, and Li Jiang. 2025. "Age-Aware Scheduling for Federated Learning with Caching in Wireless Computing Power Networks" Electronics 14, no. 4: 663. https://doi.org/10.3390/electronics14040663
APA StyleZhuang, X., Luo, C., Xie, Z., Li, Y., & Jiang, L. (2025). Age-Aware Scheduling for Federated Learning with Caching in Wireless Computing Power Networks. Electronics, 14(4), 663. https://doi.org/10.3390/electronics14040663







